Improving Vertebral Fracture Detection in C-Spine CT Images Using Bayesian Probability-Based Ensemble Learning
Abstract
1. Introduction
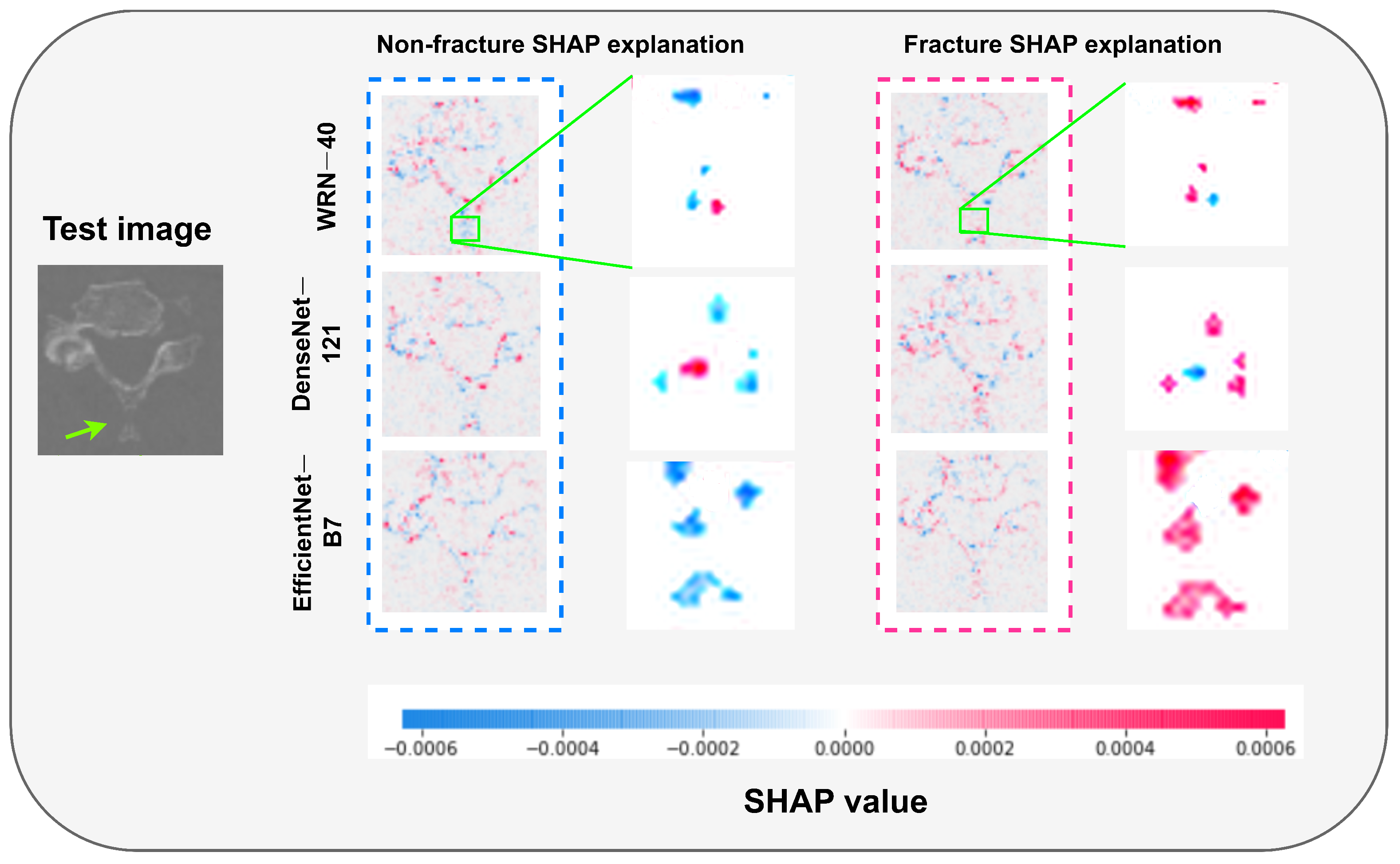
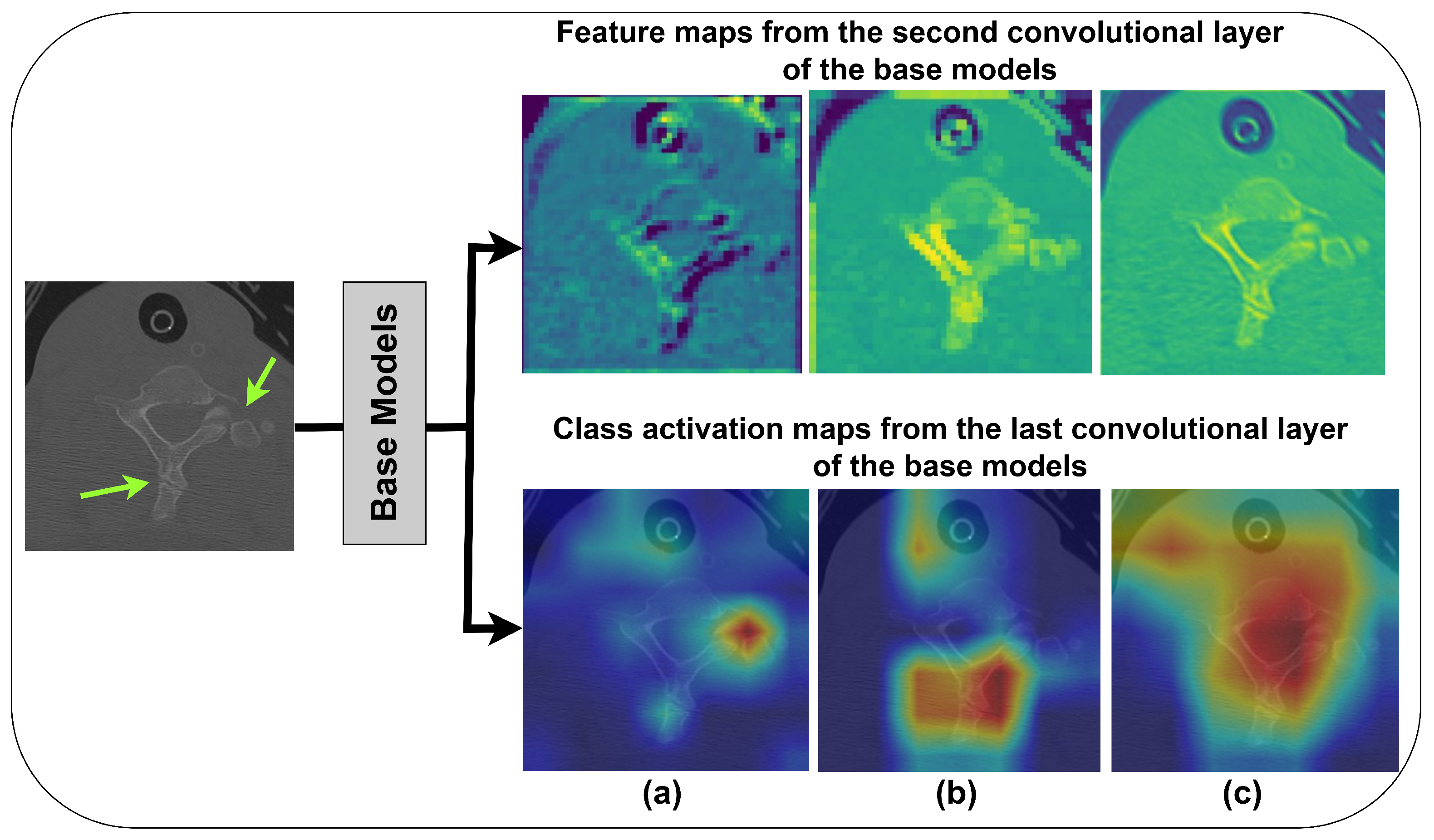
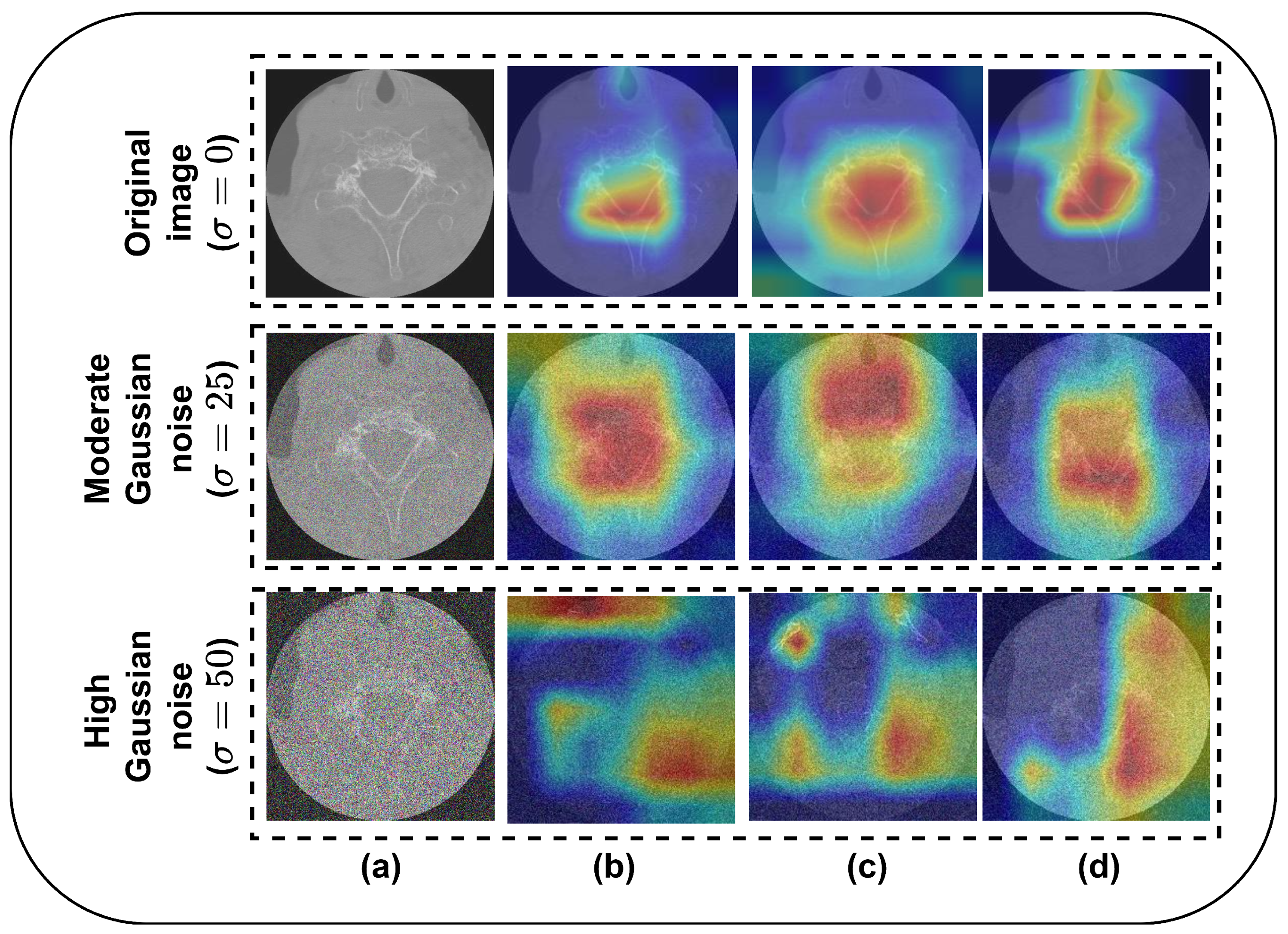
- Training and fine-tuning of three CNNs with 5-fold cross-validation (CV) for VF detection using C-spine CT images and employing them as base learners. Additionally, a base model interpretability analysis is conducted using SHapley Additive exPlanations and the Grad-CAM method.
- To improve the classification performance, a novel ensemble learning approach based on Bayesian probability is proposed.
- To validate the potential of the proposed framework, conventional ensemble learning methods are implemented on our dataset, and then their performance is analyzed and compared with the proposed model in terms of accuracy, specificity, sensitivity, and the F1-score.
2. Materials and Methods
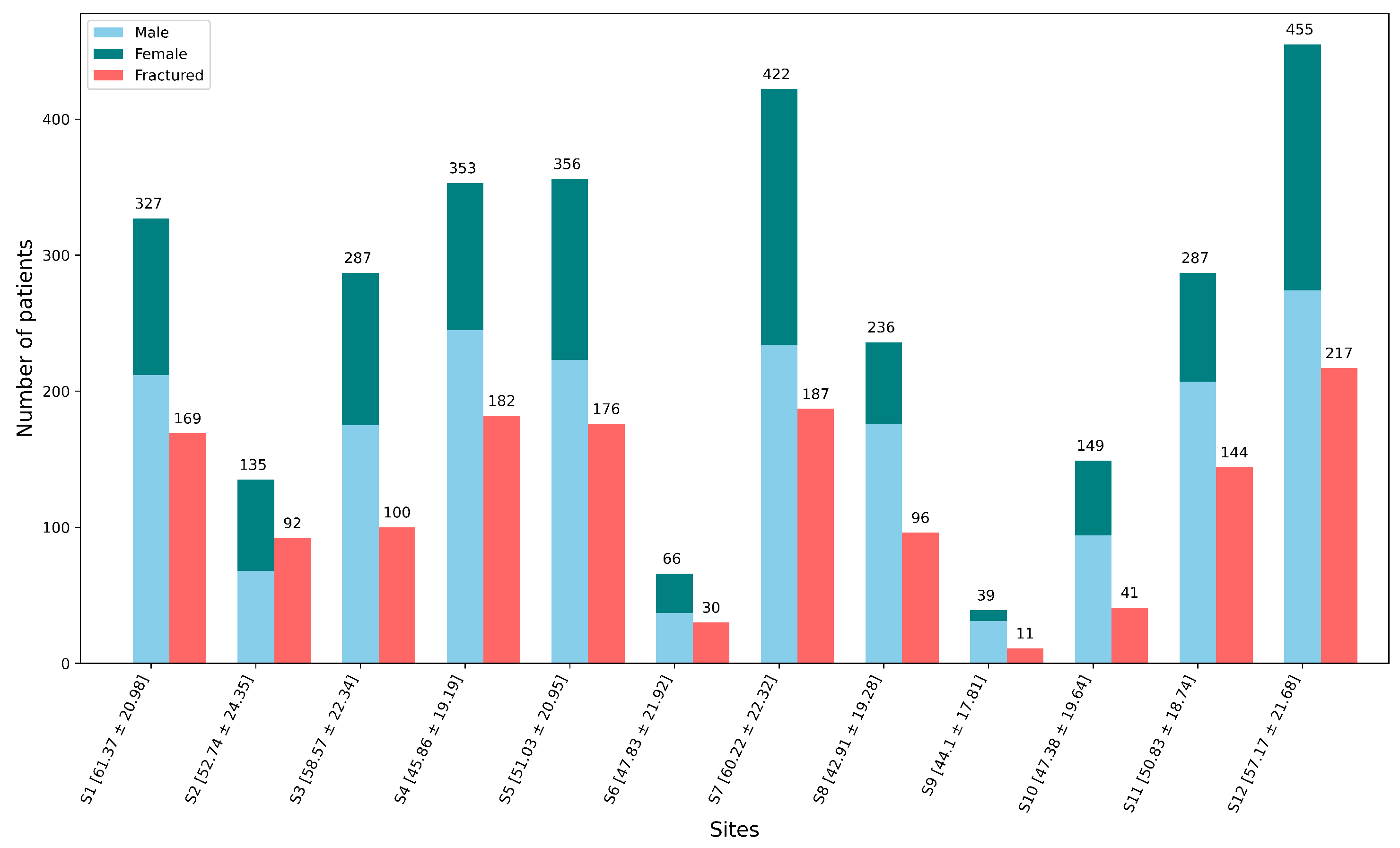
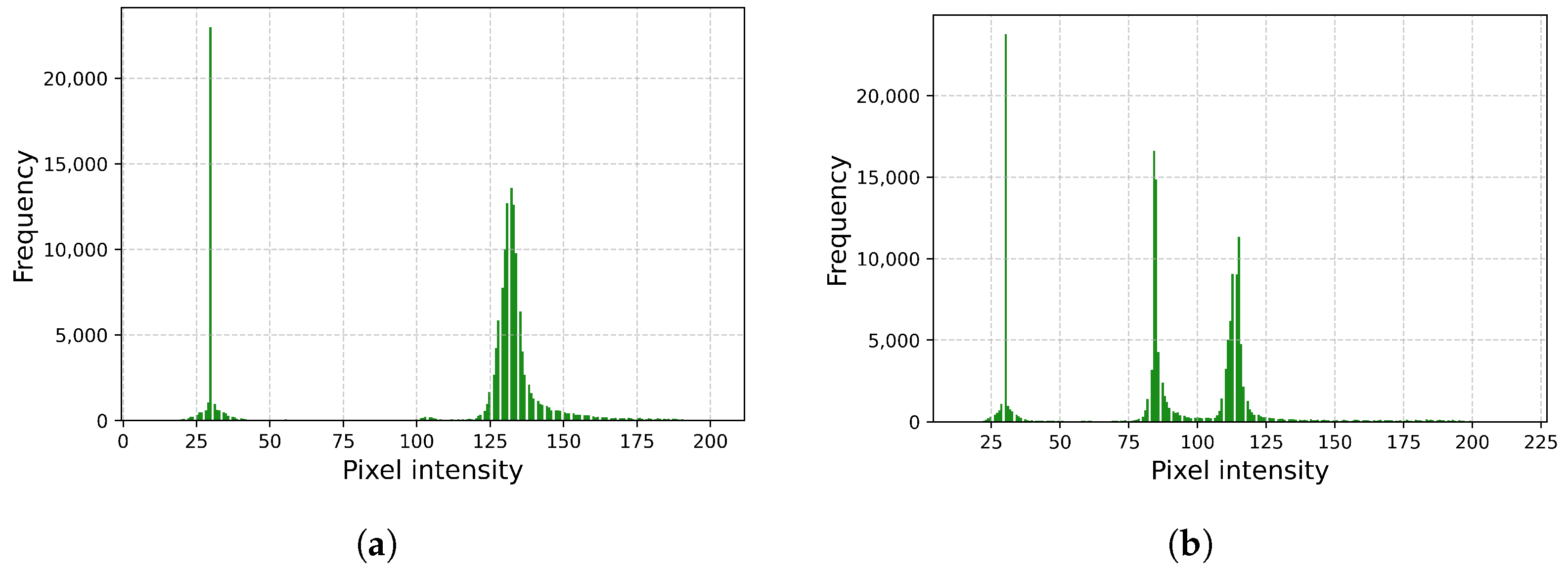
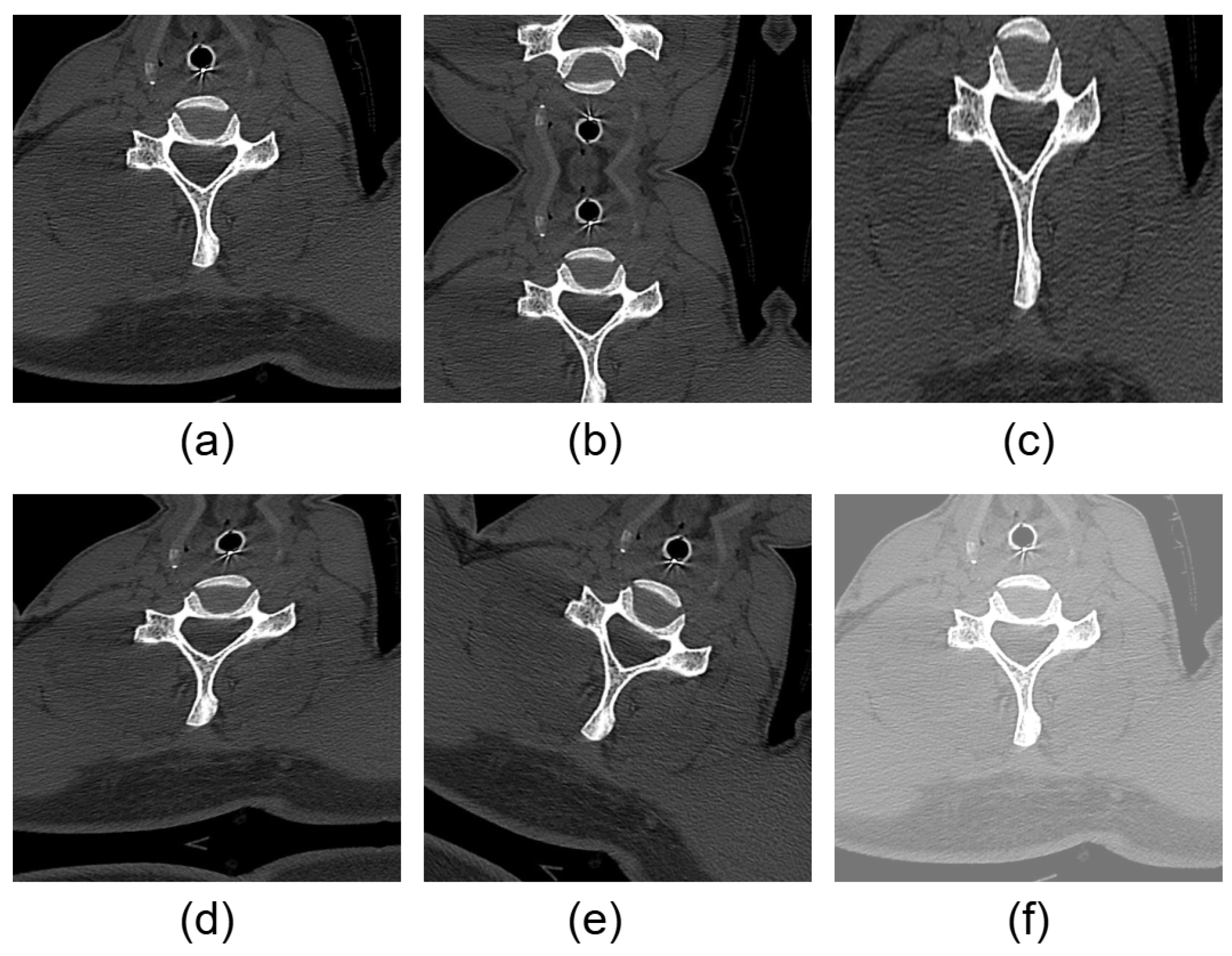
2.1. About Dataset and Its Preprocessing
2.2. Data Augmentation
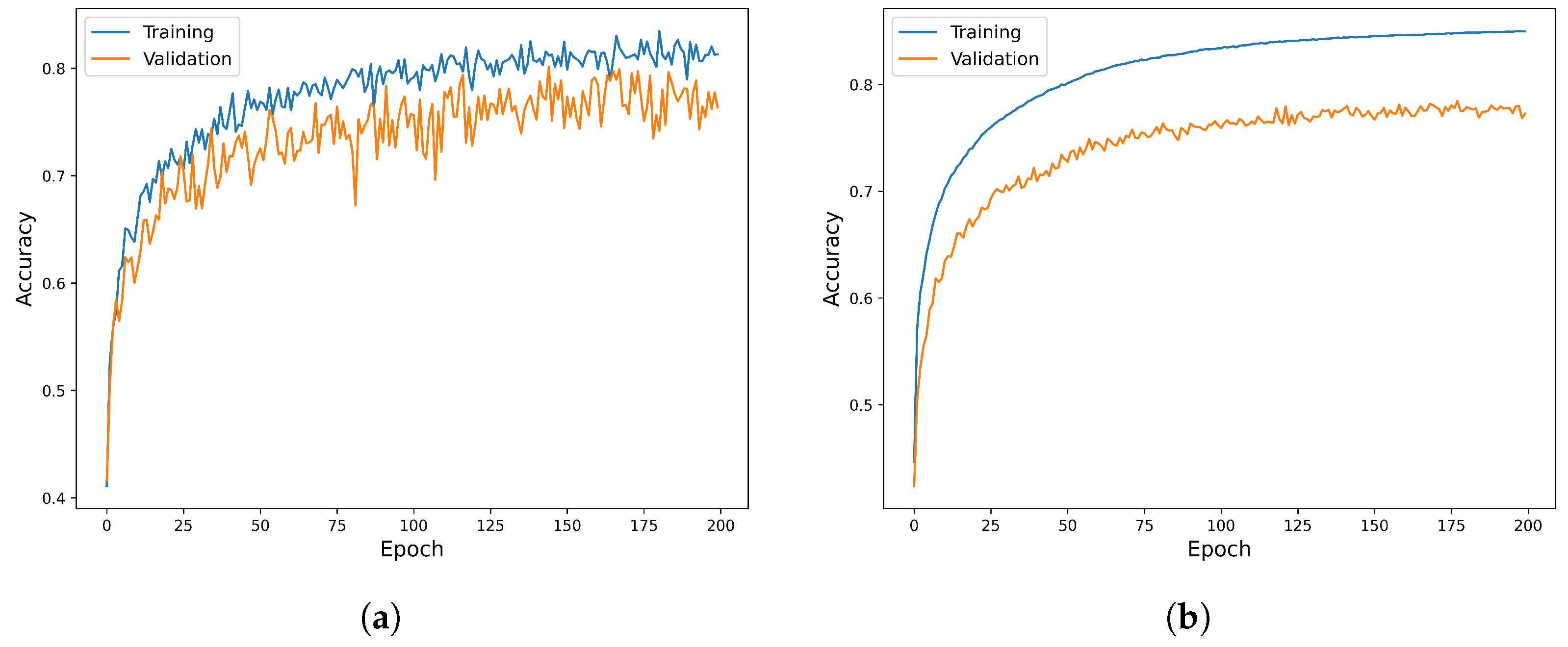
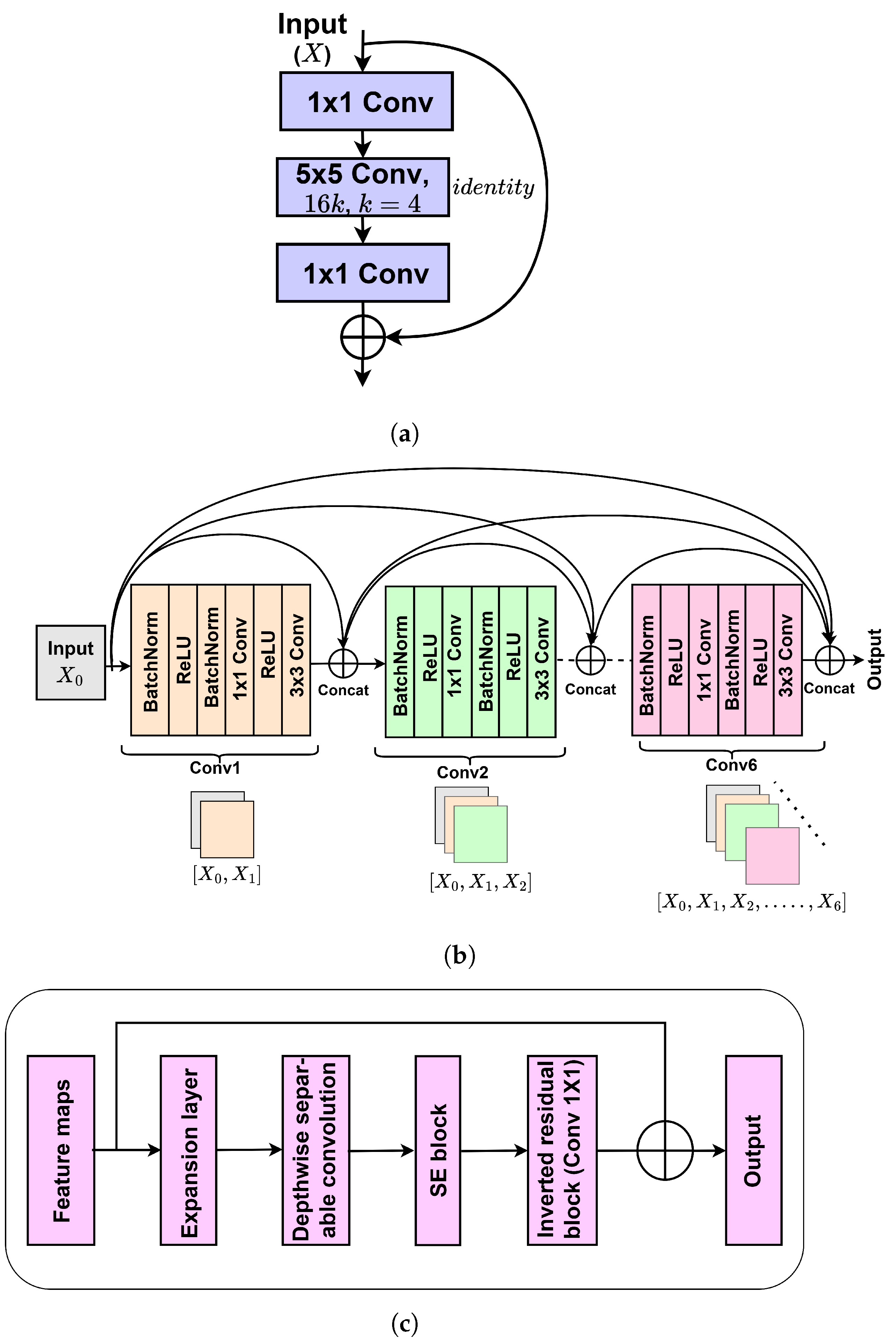
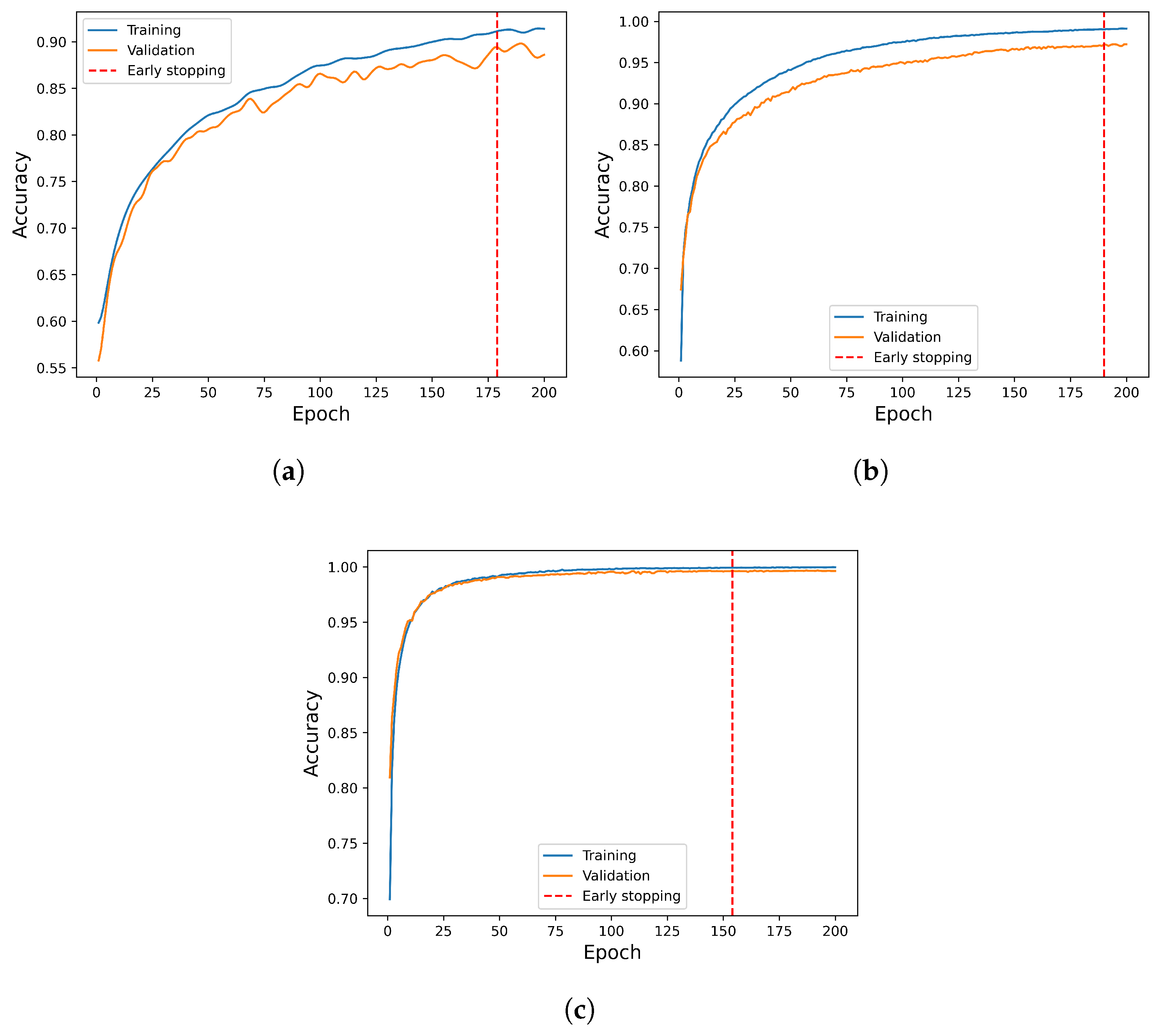
2.3. Base Models’ Training and Their Hyperparameter Optimization
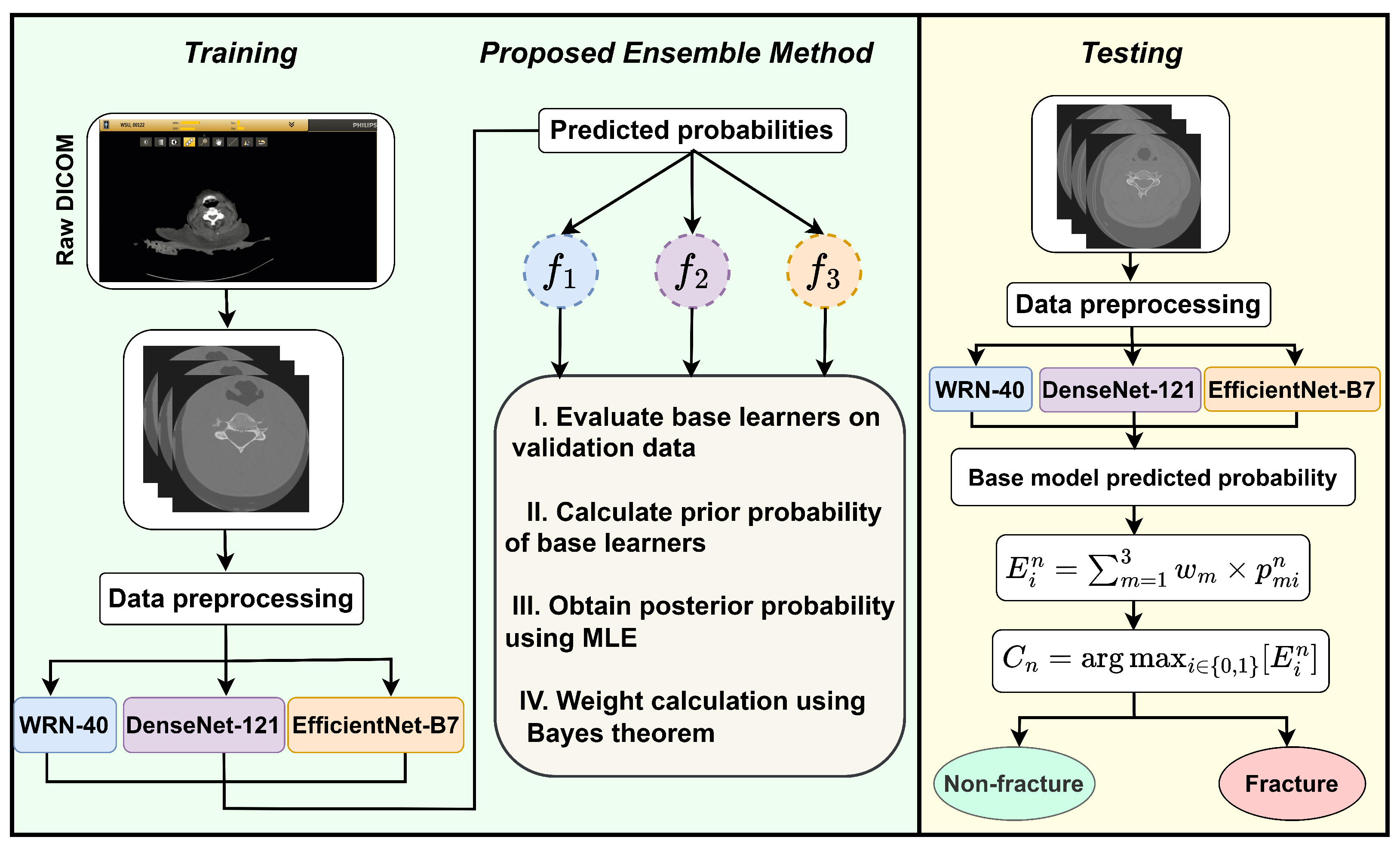
2.4. Proposed Method
| Algorithm 1: Proposed ensemble learning algorithm |
 |
2.5. Experimental Setup
3. Results
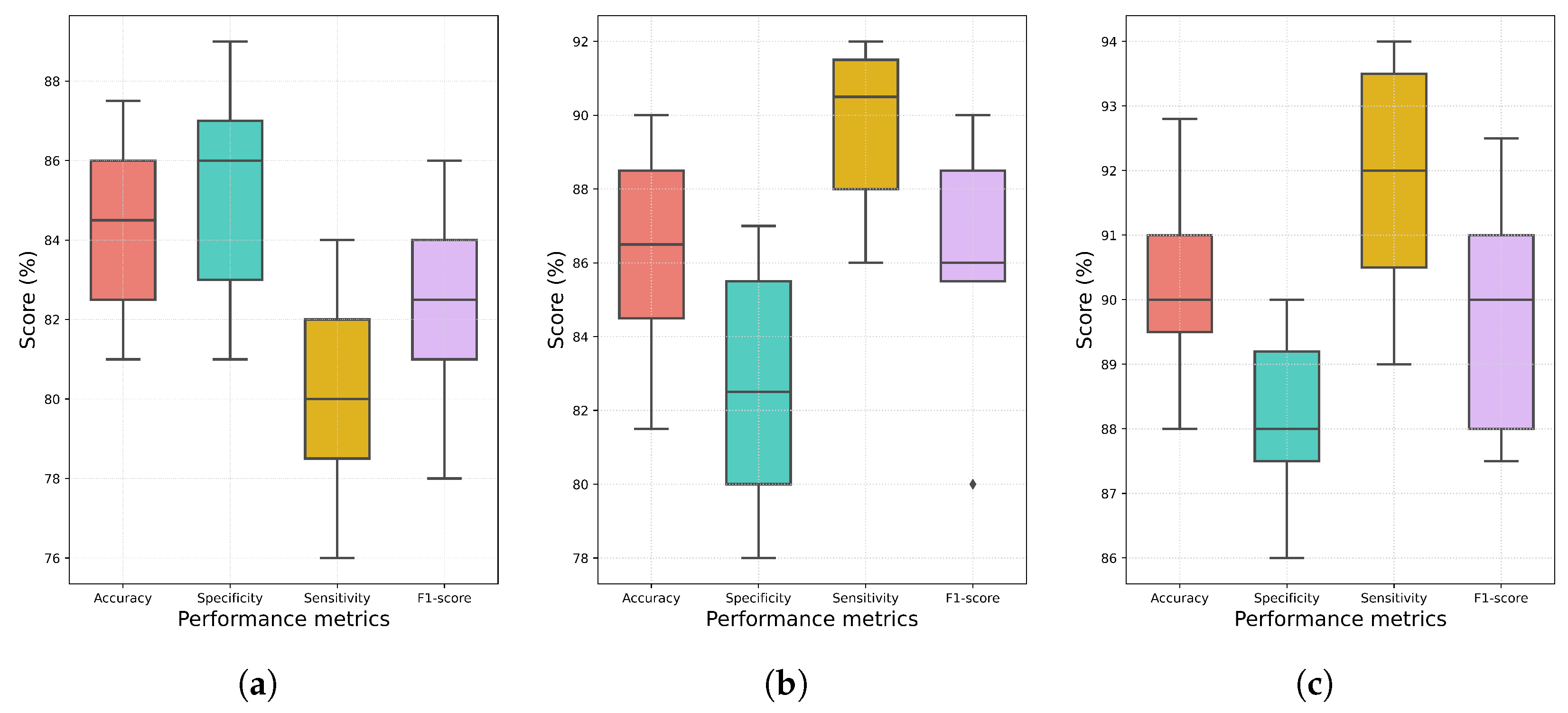
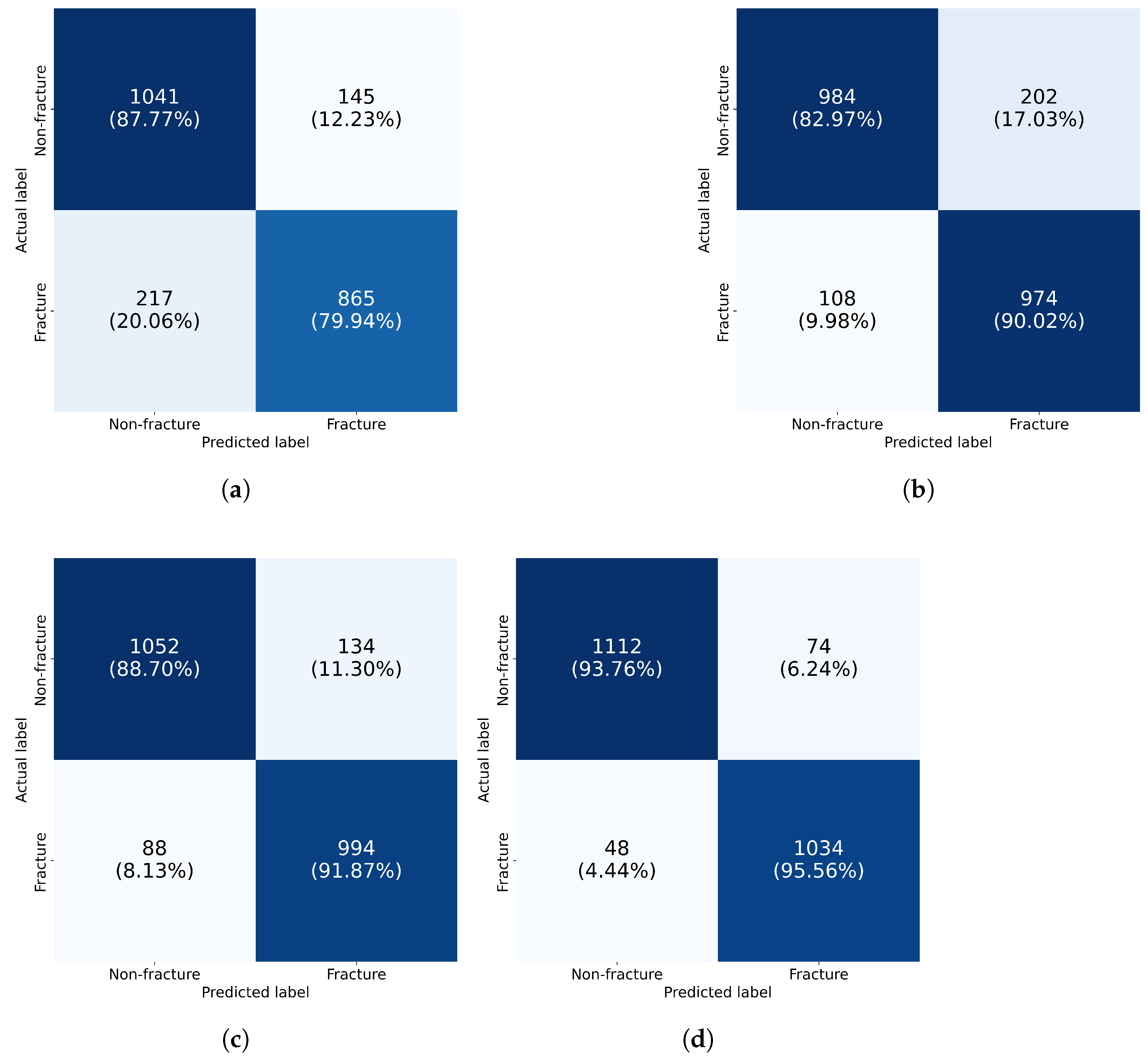
3.1. Evaluation Metrics
3.2. Analysis of Results Obtained from Conventional Ensemble Approaches
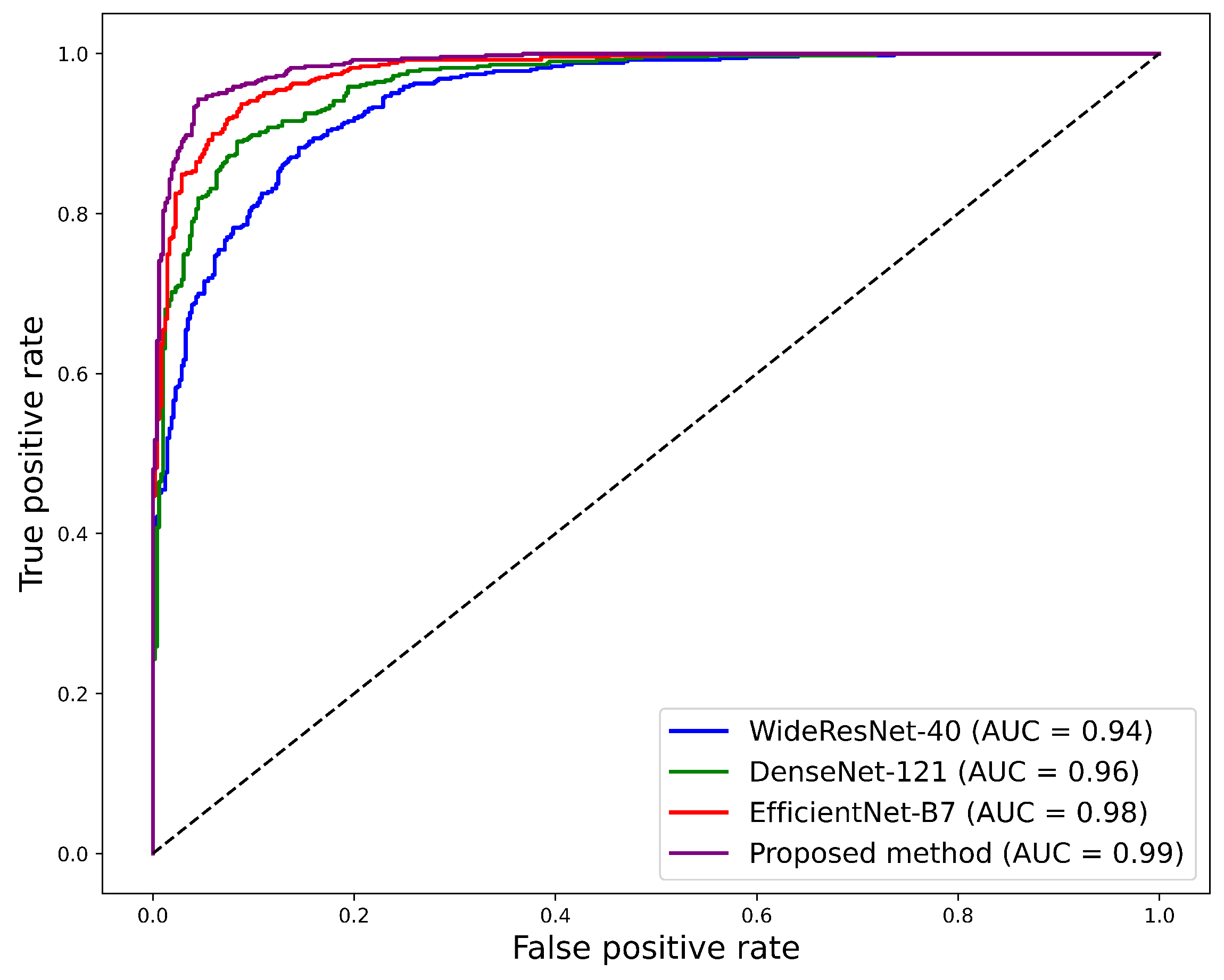
3.3. Performance Analysis of Individual Models and Proposed Ensemble Method
3.4. Comparison with Other Existing Works
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wallace, A.; Hillen, T.; Friedman, M.; Zohny, Z.; Stephens, B.; Greco, S.; Talcott, M.; Jennings, J. Percutaneous spinal ablation in a sheep model: Protective capacity of an intact cortex, correlation of ablation parameters with ablation zone size, and correlation of postablation MRI and pathologic findings. Am. J. Neuroradiol. 2017, 38, 1653–1659. [Google Scholar] [CrossRef] [PubMed]
- Zanza, C.; Tornatore, G.; Naturale, C.; Longhitano, Y.; Saviano, A.; Piccioni, A.; Maiese, A.; Ferrara, M.; Volonnino, G.; Bertozzi, G.; et al. Cervical spine injury: Clinical and medico-legal overview. Radiol. Med. 2023, 128, 103–112. [Google Scholar] [CrossRef] [PubMed]
- Dreizin, D.; Letzing, M.; Sliker, C.W.; Chokshi, F.H.; Bodanapally, U.; Mirvis, S.E.; Quencer, R.M.; Munera, F. Multidetector CT of blunt cervical spine trauma in adults. Radiographics 2014, 34, 1842–1865. [Google Scholar] [CrossRef] [PubMed]
- Karlsson, A.K. Overview: Autonomic dysfunction in spinal cord injury: Clinical presentation of symptoms and signs. Prog. Brain Res. 2006, 152, 1–8. [Google Scholar]
- Hamid, R.; Averbeck, M.A.; Chiang, H.; Garcia, A.; Al Mousa, R.T.; Oh, S.J.; Patel, A.; Plata, M.; Del Popolo, G. Epidemiology and pathophysiology of neurogenic bladder after spinal cord injury. World J. Urol. 2018, 36, 1517–1527. [Google Scholar] [CrossRef]
- Stiller, W. Basics of iterative reconstruction methods in computed tomography: A vendor-independent overview. Eur. J. Radiol. 2018, 109, 147–154. [Google Scholar] [CrossRef]
- Argyros, I.K. The Theory and Applications of Iteration Methods; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Bate, I.; Murugan, M.; George, S.; Senapati, K.; Argyros, I.K.; Regmi, S. On Extending the Applicability of Iterative Methods for Solving Systems of Nonlinear Equations. Axioms 2024, 13, 601. [Google Scholar] [CrossRef]
- Shakhno, S. Gauss–Newton–Kurchatov method for the solution of nonlinear least-squares problems. J. Math. Sci. 2020, 247, 58–72. [Google Scholar]
- Passias, P.G.; Poorman, G.W.; Segreto, F.A.; Jalai, C.M.; Horn, S.R.; Bortz, C.A.; Vasquez-Montes, D.; Diebo, B.G.; Vira, S.; Bono, O.J.; et al. Traumatic fractures of the cervical spine: Analysis of changes in incidence, cause, concurrent injuries, and complications among 488,262 patients from 2005 to 2013. World Neurosurg. 2018, 110, e427–e437. [Google Scholar]
- Bhavya, M.B.S.; Pujitha, M.V.; Supraja, G.L. Cervical Spine Fracture Detection Using Pytorch. In Proceedings of the 2022 IEEE 2nd International Conference on Mobile Networks and Wireless Communications (ICMNWC), Tumkur, Karnataka, 2–3 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–7. [Google Scholar]
- McBee, M.P.; Awan, O.A.; Colucci, A.T.; Ghobadi, C.W.; Kadom, N.; Kansagra, A.P.; Tridandapani, S.; Auffermann, W.F. Deep learning in radiology. Acad. Radiol. 2018, 25, 1472–1480. [Google Scholar] [CrossRef]
- Ma, S.; Huang, Y.; Che, X.; Gu, R. Faster RCNN-based detection of cervical spinal cord injury and disc degeneration. J. Appl. Clin. Med Phys. 2020, 21, 235–243. [Google Scholar] [CrossRef] [PubMed]
- Small, J.; Osler, P.; Paul, A.; Kunst, M. CT cervical spine fracture detection using a convolutional neural network. Am. J. Neuroradiol. 2021, 42, 1341–1347. [Google Scholar] [CrossRef] [PubMed]
- Paik, S.; Park, J.; Hong, J.Y.; Han, S.W. Deep learning application of vertebral compression fracture detection using mask R-CNN. Sci. Rep. 2024, 14, 16308. [Google Scholar] [CrossRef] [PubMed]
- Iyer, S.; Blair, A.; White, C.; Dawes, L.; Moses, D.; Sowmya, A. Vertebral compression fracture detection using imitation learning, patch based convolutional neural networks and majority voting. Informatics Med. Unlocked 2023, 38, 101238. [Google Scholar] [CrossRef]
- Xu, F.; Xiong, Y.; Ye, G.; Liang, Y.; Guo, W.; Deng, Q.; Wu, L.; Jia, W.; Wu, D.; Chen, S.; et al. Deep learning-based artificial intelligence model for classification of vertebral compression fractures: A multicenter diagnostic study. Front. Endocrinol. 2023, 14, 1025749. [Google Scholar] [CrossRef]
- Chen, H.Y.; Hsu, B.W.Y.; Yin, Y.K.; Lin, F.H.; Yang, T.H.; Yang, R.S.; Lee, C.K.; Tseng, V.S. Application of deep learning algorithm to detect and visualize vertebral fractures on plain frontal radiographs. PLoS ONE 2021, 16, e0245992. [Google Scholar] [CrossRef]
- Chen, W.; Liu, X.; Li, K.; Luo, Y.; Bai, S.; Wu, J.; Chen, W.; Dong, M.; Guo, D. A deep-learning model for identifying fresh vertebral compression fractures on digital radiography. Eur. Radiol. 2022, 32, 1496–1505. [Google Scholar] [CrossRef]
- Ono, Y.; Suzuki, N.; Sakano, R.; Kikuchi, Y.; Kimura, T.; Sutherland, K.; Kamishima, T. A deep learning-based model for classifying osteoporotic lumbar vertebral fractures on radiographs: A retrospective model development and validation study. J. Imaging 2023, 9, 187. [Google Scholar] [CrossRef]
- Nicolaes, J.; Liu, Y.; Zhao, Y.; Huang, P.; Wang, L.; Yu, A.; Dunkel, J.; Libanati, C.; Cheng, X. External validation of a convolutional neural network algorithm for opportunistically detecting vertebral fractures in routine CT scans. Osteoporos. Int. 2024, 35, 143–152. [Google Scholar] [CrossRef]
- El Kojok, Z.; Al Khansa, H.; Trad, F.; Chehab, A. Augmenting a spine CT scans dataset using VAEs, GANs, and transfer learning for improved detection of vertebral compression fractures. Comput. Biol. Med. 2025, 184, 109446. [Google Scholar] [CrossRef]
- Guenoun, D.; Quemeneur, M.S.; Ayobi, A.; Castineira, C.; Quenet, S.; Kiewsky, J.; Mahfoud, M.; Avare, C.; Chaibi, Y.; Champsaur, P. Automated vertebral compression fracture detection and quantification on opportunistic CT scans: A performance evaluation. Clin. Radiol. 2025, 83, 106831. [Google Scholar] [PubMed]
- Cheng, L.W.; Chou, H.H.; Cai, Y.X.; Huang, K.Y.; Hsieh, C.C.; Chu, P.L.; Cheng, I.S.; Hsieh, S.Y. Automated detection of vertebral fractures from X-ray images: A novel machine learning model and survey of the field. Neurocomputing 2024, 566, 126946. [Google Scholar] [CrossRef]
- Lin, H.M.; Colak, E.; Richards, T.; Kitamura, F.C.; Prevedello, L.M.; Talbott, J.; Ball, R.L.; Gumeler, E.; Yeom, K.W.; Hamghalam, M.; et al. The RSNA cervical spine fracture CT dataset. Radiol. Artif. Intell. 2023, 5, e230034. [Google Scholar] [PubMed]
- Mandell, J.C.; Khurana, B.; Folio, L.R.; Hyun, H.; Smith, S.E.; Dunne, R.M.; Andriole, K.P. Clinical applications of a CT window blending algorithm: RADIO (relative attenuation-dependent image overlay). J. Digit. Imaging 2017, 30, 358–368. [Google Scholar]
- Sesmero, M.P.; Ledezma, A.I.; Sanchis, A. Generating ensembles of heterogeneous classifiers using stacked generalization. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2015, 5, 21–34. [Google Scholar]
- Zagoruyko, S. Wide residual networks. arXiv 2016, arXiv:1605.07146. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Tan, M.; Le, Q. Efficientnet: Rethinking model scaling for convolutional neural networks. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; PMLR: Cambridge, MA, USA, 2019; pp. 6105–6114. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity mappings in deep residual networks. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part IV 14. Springer: Berlin/Heidelberg, Germany, 2016; pp. 630–645. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 4765–4774. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-cam: Visual explanations from deep networks via gradient-based localization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]
- Ganaie, M.A.; Hu, M.; Malik, A.K.; Tanveer, M.; Suganthan, P.N. Ensemble deep learning: A review. Eng. Appl. Artif. Intell. 2022, 115, 105151. [Google Scholar]
- Zhao, Y.; Gao, J.; Yang, X. A survey of neural network ensembles. In Proceedings of the 2005 International Conference on Neural Networks and Brain, Beijing, China, 13–15 October 2005; IEEE: Piscataway, NJ, USA, 2005; Volume 1, pp. 438–442. [Google Scholar]
- Wolpert, D.H. Stacked generalization. Neural Networks 1992, 5, 241–259. [Google Scholar]
- Pateel, G.; Senapati, K.; Pandey, A.K. A Novel Decision Level Class-Wise Ensemble Method in Deep Learning for Automatic Multi-Class Classification of HER2 Breast Cancer Hematoxylin-Eosin Images. IEEE Access 2024, 12, 46093–46103. [Google Scholar]
- Agapitos, A.; O’Neill, M.; Brabazon, A. Ensemble Bayesian model averaging in genetic programming. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 July 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 2451–2458. [Google Scholar]
- Myung, I.J. Tutorial on maximum likelihood estimation. J. Math. Psychol. 2003, 47, 90–100. [Google Scholar]
- Polikar, R. Ensemble learning. In Ensemble Machine Learning: Methods and Applications; Springer: New York, NY, USA, 2012; pp. 1–34. [Google Scholar]
- Dietterich, T.G. Ensemble methods in machine learning. In Proceedings of the International Workshop on Multiple Classifier Systems, Cagliari, Italy, 21–23 June 2000; Springer: Berlin/Heidelberg, Germany, 2000; pp. 1–15. [Google Scholar]
- Caruana, R.; Niculescu-Mizil, A.; Crew, G.; Ksikes, A. Ensemble selection from libraries of models. In Proceedings of the Twenty-First International Conference on Machine Learning, Banff, AB, Canada, 4–8 July 2004; p. 18. [Google Scholar]
| Hyperparameter | Reference | Chosen Value | ||
|---|---|---|---|---|
| WRN-40 | DenseNet-121 | EfficientNet-B7 | ||
| Learning rate | [0.0001, 0.01] | 0.001 | 0.0001 | 0.0001 |
| Batch size | [16, 128] | 32 | 32 | 32 |
| Optimizer | - | Adam | SGD | Adam |
| Epoch | - | 200 | 200 | 200 |
| Model checkpoint | - | 15 epoch | 15 epoch | 15 epoch |
| Dropout rate | [0, 0.6] | 0.5 | 0.3 | 0.4 |
| Weight decay | ||||
| Data augmentation | - | ✔ | ✔ | ✔ |
| Growth rate | [12, 48] | - | 32 | - |
| Compression factor | [0.1, 1.0] | - | 0.5 | - |
| Width coefficient | [1.0, 2.0] | - | - | 1.5 |
| Depth coefficient | [1.0, 3.0] | - | - | 2.5 |
| Model | Metric | Training | Validation |
|---|---|---|---|
| WRN-40 | Acc | ||
| Spec | |||
| Sens | |||
| F1 | |||
| DenseNet-121 | Acc | ||
| Spec | |||
| Sens | |||
| F1 | |||
| EfficientNet-B7 | Acc | ||
| Spec | |||
| Sens | |||
| F1 |
| Ensemble Method | Acc (%) | Spec (%) | Sens (%) | F1 (%) |
|---|---|---|---|---|
| Majority voting | ||||
| Average probability | ||||
| WAP | ||||
| Proposed |
| Model | Acc (%) | Spec (%) | Sens (%) | F1 (%) | AUC (%) |
|---|---|---|---|---|---|
| WRN-40 | |||||
| DenseNet-121 | |||||
| EfficientNet-B7 | |||||
| ResNet-152 | |||||
| ResNet-200 | |||||
| Proposed |
| Existing Method | Acc (%) | Spec (%) | Sens (%) | F1 (%) | AUC (%) |
|---|---|---|---|---|---|
| Paik et al. [15] | − | ||||
| Xu et al. [17] | |||||
| Iyer et al. [16] | − | ||||
| Small et al. [14] | 92 | 76 | − | − | |
| Chen et al. [18] | − | 72 | |||
| Chen et al. [19] | 74 | 68 | 80 | − | 89 |
| Ono et al. [20] | 89 | 92 | 83 | − | |
| Nicolaes et al. [21] | 93 | 93 | 94 | − | 94 |
| Kojok et al. [22] | 89 | − | − | 90 | − |
| Guenoun et al. [23] | 92 | − | − | ||
| Proposed model | 99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pandey, A.K.; Senapati, K.; Argyros, I.K.; Pateel, G.P. Improving Vertebral Fracture Detection in C-Spine CT Images Using Bayesian Probability-Based Ensemble Learning. Algorithms 2025, 18, 181. https://doi.org/10.3390/a18040181
Pandey AK, Senapati K, Argyros IK, Pateel GP. Improving Vertebral Fracture Detection in C-Spine CT Images Using Bayesian Probability-Based Ensemble Learning. Algorithms. 2025; 18(4):181. https://doi.org/10.3390/a18040181
Chicago/Turabian StylePandey, Abhishek Kumar, Kedarnath Senapati, Ioannis K. Argyros, and G. P. Pateel. 2025. "Improving Vertebral Fracture Detection in C-Spine CT Images Using Bayesian Probability-Based Ensemble Learning" Algorithms 18, no. 4: 181. https://doi.org/10.3390/a18040181
APA StylePandey, A. K., Senapati, K., Argyros, I. K., & Pateel, G. P. (2025). Improving Vertebral Fracture Detection in C-Spine CT Images Using Bayesian Probability-Based Ensemble Learning. Algorithms, 18(4), 181. https://doi.org/10.3390/a18040181









