Elite Multi-Criteria Decision Making—Pareto Front Optimization in Multi-Objective Optimization
Abstract
1. Introduction
2. Literature Review
2.1. Multi-Objective Optimization (MOO)
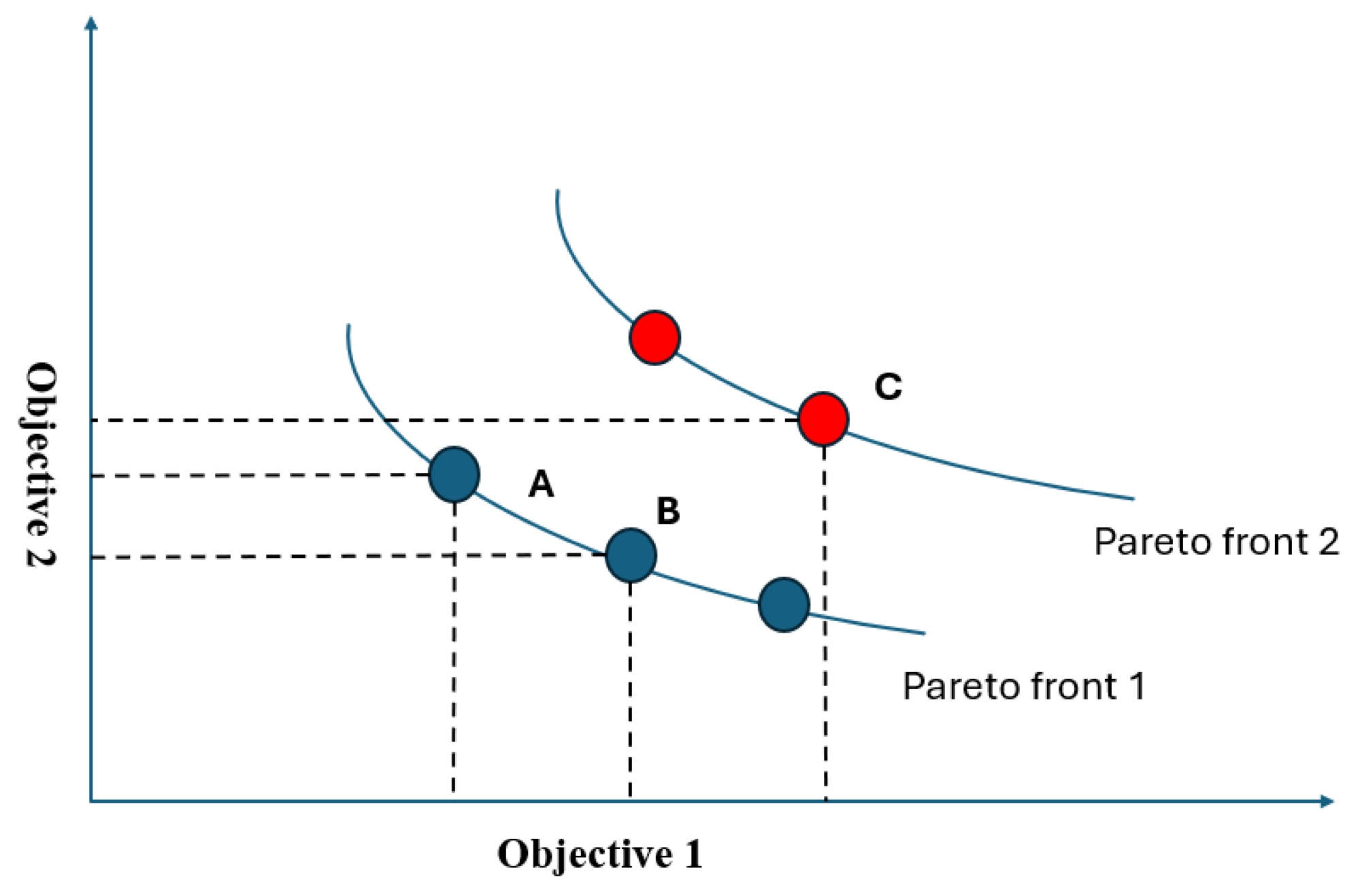
2.2. Pareto Front
- Point A dominates point B in objective 1 and C in both the objectives.
- Point B dominates point A in objective 2 and C in both the objectives.
- Point C is dominated by both A and B points in both the objectives.
2.3. Multi-Criteria Decision Making (MCDM)
2.4. Evolutionary Algorithms (EA)
2.5. Multi-Objective Evolutionary Algorithm (MOEA)
3. Methodology
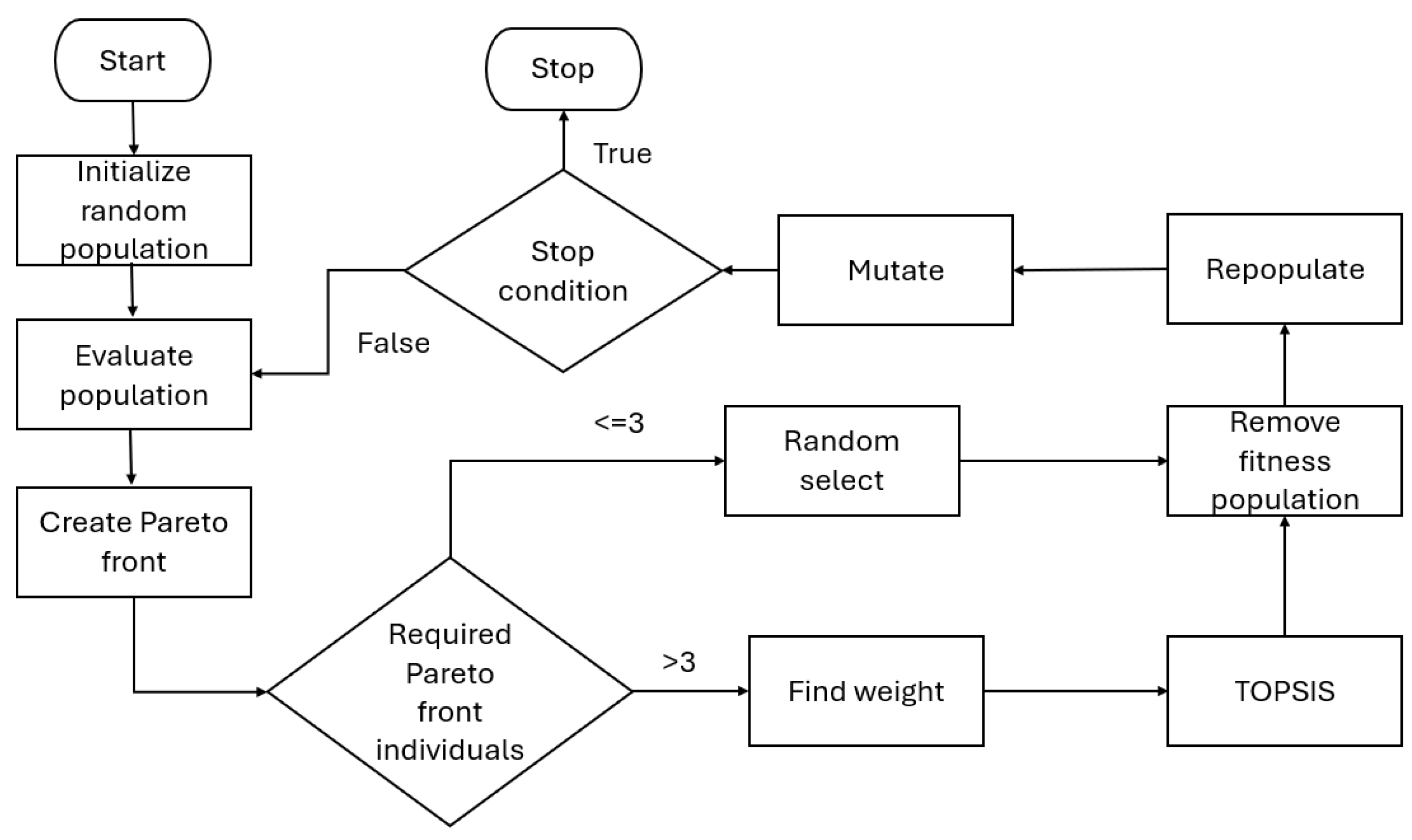
3.1. Algorithm
| Algorithm 1 eMPF selection process |
|
3.1.1. Calculating Weights of Each Objective
- The first step is to normalize the fitness values. The fitness values are normalized using Equation (2),where i is the individual policy, j is the objective number, N is the total number of individual policies, f is the actual fitness value, and F is the normalized fitness value.
- Lastly, the weights () of the objective are calculated using Equation (4),where is the entropy value from the above step, j is the number of objectives, and M is the total number of objectives.
3.1.2. TOPSIS
- Normalize the actual fitness values using Equation (5).where i is the individual policy, j is the objective number, f is the actual fitness value, and F is the normalized fitness value.
- Next, find the fitness weights by taking the product of the weight of each objective with fitness values using the equation as shown below:where is the weight of each objective, and is the normalized fitness value calculated in Equation (5) for the individual policy i and objective j.
- Depending on the value, the best and worst-performing individuals of each objective are selected and flagged as the best or worst individual policy.
- The Euclidean distances between all of the individuals to both the best and worst individuals are calculated and assigned as , where is assigned as the distance to the best individual and is assigned as the distance to the worst individual.
- The last step is to find the degree of approximation using Equation (7),where is assigned to the distance to the best individual, is assigned to the distance to the worst individual from the above calculations, and i is the individual element.
3.2. Performance Evaluation
3.2.1. Pareto Front Spread ()
3.2.2. Generational Distance ()
3.2.3. Pareto Front Spacing ()
3.3. Test Functions
- Binh and Korn Function [33];
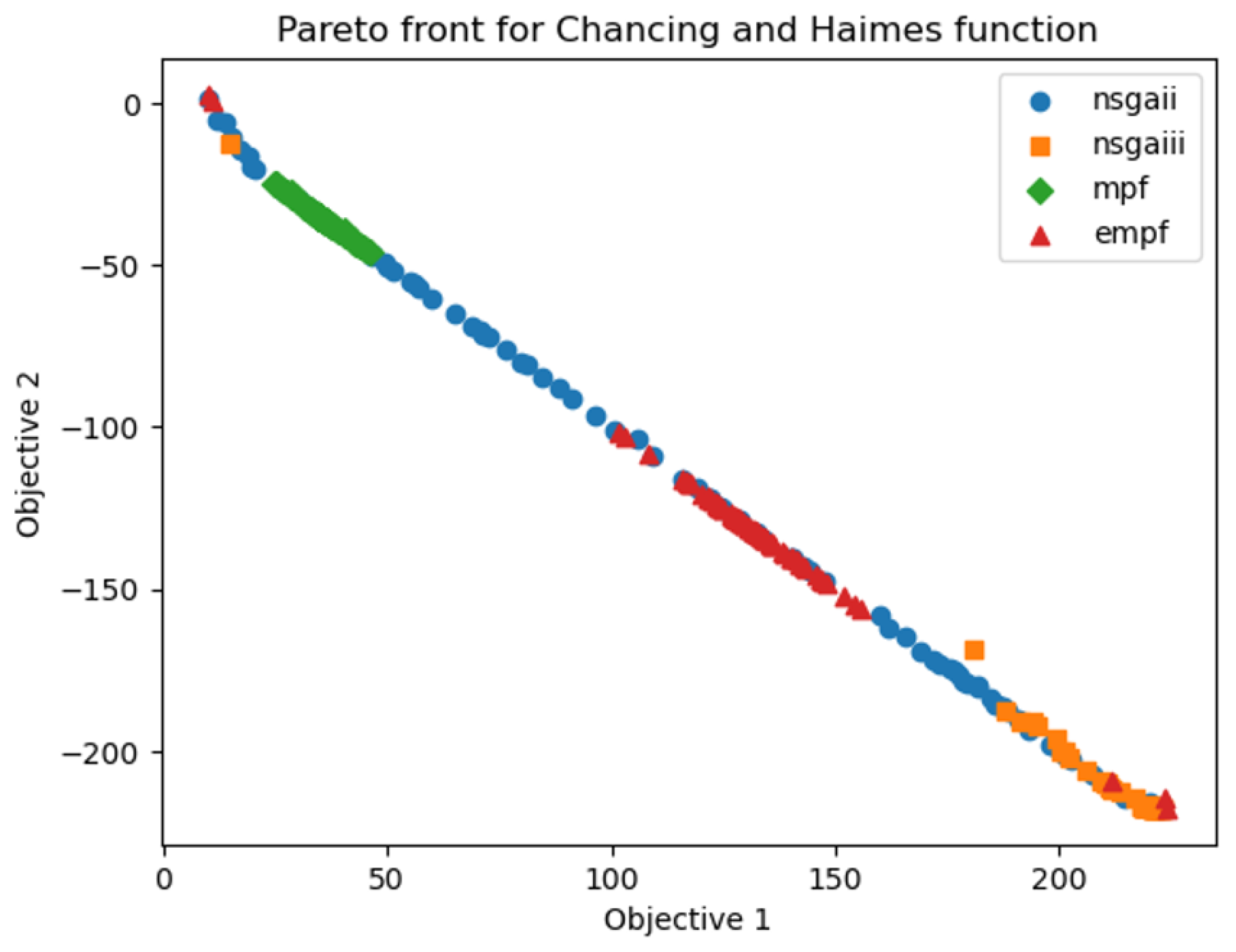
- Chankong and Haimes Function [33];
- Fonseca–Fleming Function [34];
- Test Function 4 [35];
- Kursawe Function [36];
- Schaffer Function N1, and N2 [37];
- Poloni’s Two-Objective Function [38];
- Zitzler–Deb–Thiele’s Function N1, N2, N3, N4, and N6 [39];
- Osyczka and Kundu Function [40];
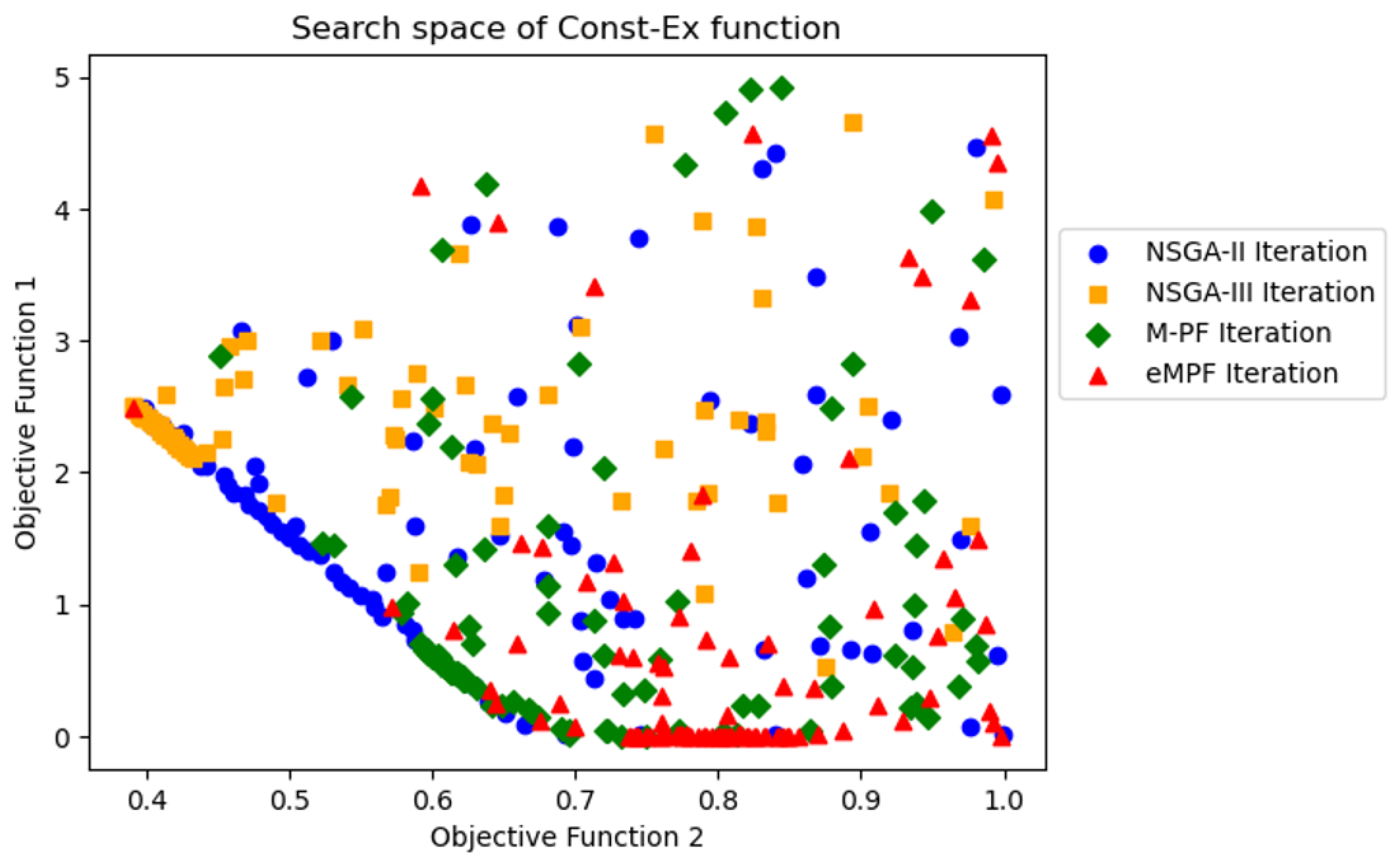
- Constr-Ex Problem;
- VR-UC Test 1, VR-UC Test 2 [41];
- MSGA Test 1 [42];
- Viennet Function [43];
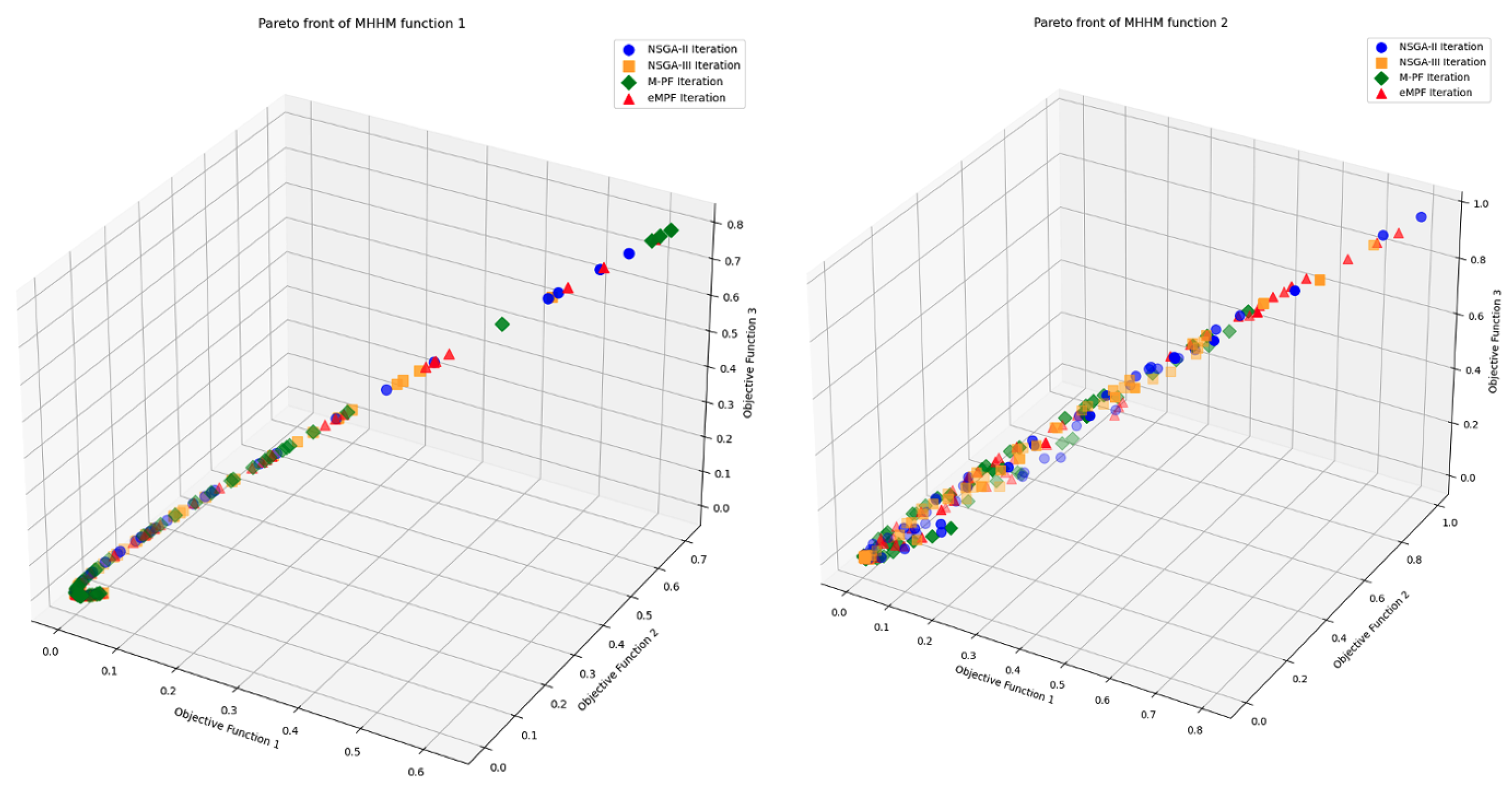
- MHHM1, MHHM2 [44].
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MOO | Multi-Objective Optimization |
| MCDM | Multi-Criteria Decision Making |
| EA | Evolutionary Algorithm |
| TOPSIS | Technique for Order of Preference by Similarity to Ideal Solution |
| NSGA-II | Non-Dominated Sorting Genetic Algorithm-II |
| NSGA-III | Non-Dominated Sorting Genetic Algorithm-III |
| M-PF | Multi-Criteria Decision Making–Pareto Front |
| eMPF | elite Multi-Criteria Decision Making–Pareto Front |
| CCEA | Cooperative Co-evolutionary Algorithms |
Appendix A
| Function | Test Function | Constraints | Search Domain |
|---|---|---|---|
| Binh and Korn Function | |||
| Chankong and Haimes Function | |||
| Fonseca–Fleming Function | |||
| Test Function 4 | 0 | ||
| Kursawe Function | |||
| Schaffer Function N1 | Values of A from 10 to | ||
| Schaffer Function N2 | |||
| Poloni’s Two-Objective Function | where | ; | |
| Zitzler–Deb–Thiele’s Function (ZDT) N1 | |||
| Zitzler–Deb–Thiele’s Function (ZDT) N2 | |||
| Zitzler–Deb–Thiele’s Function (ZDT) N3 | |||
| Zitzler–Deb–Thiele’s Function (ZDT) N4 | |||
| Zitzler–Deb–Thiele’s Function (ZDT) N6 | |||
| Osyczka & Kundu Function | |||
| Constr-Ex Problem | |||
| VR-UC Test 1 | |||
| VR-UC Test 2 | |||
| MSGA Test 1 | |||
| MHHM1 | |||
| MHHM2 | |||
| Viennet Function |
Appendix B
| Test Function | Method | Minimum | Mean | Standard Deviation | |||
|---|---|---|---|---|---|---|---|
| Function 1 | Function 2 | Function 1 | Function 2 | Function 1 | Function 2 | ||
| NSGA-II | 0.000948 | 4.005556 | 52.645992 | 17.283002 | 39.400303 | 12.500695 | |
| Binh and Korn | NSGA-III | 9.332152 | 4.533799 | 100.464088 | 10.277145 | 43.565188 | 13.756248 |
| M-PF | 9.498507 | 10.473067 | 32.993437 | 19.539373 | 18.265393 | 7.521567 | |
| eMPF | 0.002037 | 4.023522 | 14.015699 | 29.174421 | 17.331893 | 5.806211 | |
| NSGA-II | 10.119513 | −217.695484 | 113.45425 | −112.737342 | 62.128512 | 62.677727 | |
| Chankong Haimes | NSGA-III | 96.621684 | −217.730419 | 213.296477 | −210.363403 | 20.65679 | 24.166874 |
| M-PF | 57.01729 | −101.645503 | 80.131923 | −80.211533 | 48.913044 | 48.881173 | |
| eMPF | 10.125042 | −217.686516 | 127.519573 | −127.352052 | 23.87205 | 24.71453 | |
| Fonseca–Fleming | NSGA-II | 0.000034 | 0.000042 | 0.578248 | 0.580166 | 0.296733 | 0.296151 |
| NSGA-III | 0.092419 | 0.032975 | 0.723804 | 0.497992 | 0.153209 | 0.159965 | |
| M-PF | 0.070628 | 0.066346 | 0.609386 | 0.596173 | 0.226319 | 0.233033 | |
| eMPF | 0.000022 | 0.000021 | 0.511756 | 0.499501 | 0.465786 | 0.466366 | |
| NSGA-II | −6.504972 | −8.499939 | −1.534355 | −8.145423 | 3.336720 | 0.277358 | |
| Test Function 4 | NSGA-III | −6.506321 | −8.498921 | −5.331177 | −7.623771 | 3.929542 | 0.229023 |
| M-PF | −6.392928 | −8.316240 | −4.654117 | −7.854135 | 1.901964 | 0.210908 | |
| eMPF | −6.506243 | −8.499792 | −5.808833 | −7.636678 | 2.520614 | 0.161645 | |
| NSGA-II | −19.785629 | −5.138218 | −10.217168 | −2.560673 | 3.696744 | 1.566748 | |
| Kursawe | NSGA-III | −19.800519 | −2.761169 | −12.516551 | −1.290272 | 2.812103 | 0.732146 |
| M-PF | −12.427413 | −3.105100 | −9.705192 | −1.623625 | 0.963143 | 0.812313 | |
| eMPF | −19.823842 | −5.133368 | −12.190258 | −1.771524 | 3.224230 | 1.219680 | |
| NSGA-II | 0.000000 | 0.000000 | 1.309796 | 1.335708 | 1.171495 | 1.178720 | |
| Schaffer function N1 | NSGA-III | 0.458913 | 0.452471 | 2.092166 | 1.548018 | 1.830392 | 1.803354 |
| M-PF | 0.314452 | 0.365226 | 1.484631 | 1.911246 | 1.678226 | 1.713672 | |
| eMPF | 0.000000 | 0.000000 | 1.118533 | 1.121366 | 0.726276 | 0.734062 | |
| NSGA-II | −0.999966 | 0.000000 | 0.519161 | 7.217303 | 1.030891 | 4.693345 | |
| Schaffer function N2 | NSGA-III | −0.824930 | 7.796460 | −0.624833 | 14.028193 | 0.942749 | 4.035698 |
| M-PF | 0.178468 | 3.991629 | 0.742443 | 8.141138 | 1.744642 | 6.828264 | |
| eMPF | −0.999503 | 0.000000 | 2.162599 | 0.964716 | 0.513256 | 1.922794 | |
| NSGA-II | 1.000107 | 0.000011 | 6.867533 | 6.300837 | 5.010289 | 9.464460 | |
| Poloni’s two objectives | NSGA-III | 2.072667 | 8.096344 | 7.516216 | 13.666458 | 7.204542 | 11.749644 |
| M-PF | 2.646164 | 1.748814 | 12.385470 | 3.525388 | 5.237112 | 7.848127 | |
| eMPF | 1.000656 | 0.000035 | 3.790499 | 2.429406 | 2.910871 | 3.427426 | |
| NSGA-II | 0.000016 | 1.830778 | 0.259772 | 3.291023 | 0.295645 | 0.985772 | |
| ZDT’s N1 | NSGA-III | 0.000012 | 1.836794 | 0.294363 | 3.228128 | 0.313797 | 1.012261 |
| M-PF | 0.000016 | 1.852934 | 0.279310 | 3.224510 | 0.302015 | 0.972492 | |
| eMPF | 0.000027 | 1.831970 | 0.284748 | 3.219609 | 0.305802 | 0.967179 | |
| NSGA-II | 0.000020 | 3.360521 | 0.146886 | 4.209470 | 0.265380 | 0.626616 | |
| ZDT’s N2 | NSGA-III | 0.000018 | 3.397406 | 0.150892 | 4.200882 | 0.275458 | 0.627170 |
| M-PF | 0.000015 | 3.389850 | 0.124176 | 4.231827 | 0.244155 | 0.646990 | |
| eMPF | 0.000015 | 3.384750 | 0.154723 | 4.262611 | 0.274839 | 0.691868 | |
| NSGA-II | 0.000015 | 1.197987 | 0.302574 | 3.009383 | 0.295633 | 1.165188 | |
| ZDT’s N3 | NSGA-III | 0.000016 | 1.250750 | 0.288800 | 3.049543 | 0.294440 | 1.148127 |
| M-PF | 0.000015 | 1.230596 | 0.299095 | 3.019458 | 0.296260 | 1.142140 | |
| eMPF | 0.000014 | 1.221293 | 0.306138 | 2.997215 | 0.302244 | 1.155063 | |
| NSGA-II | 0.000014 | 28.918132 | 0.084849 | 64.349782 | 0.174179 | 32.479856 | |
| ZDT’s N4 | NSGA-III | 0.000017 | 30.178694 | 0.077131 | 69.368632 | 0.168524 | 34.873943 |
| M-PF | 0.000011 | 28.018323 | 0.081965 | 65.590350 | 0.166882 | 33.832099 | |
| eMPF | 0.000013 | 27.480261 | 0.105229 | 62.256601 | 0.201626 | 31.532401 | |
| NSGA-II | 0.280775 | 6.356673 | 0.492336 | 7.271715 | 0.278471 | 0.661174 | |
| ZDT’s N6 | NSGA-III | 0.280775 | 6.233513 | 0.499382 | 7.221104 | 0.281440 | 0.653730 |
| M-PF | 0.280775 | 6.276437 | 0.474475 | 7.257931 | 0.269862 | 0.630176 | |
| eMPF | 0.280775 | 6.268319 | 0.491137 | 7.239478 | 0.285670 | 0.677693 | |
| NSGA-II | −258.627419 | 5.194767 | −164.898915 | 28.366042 | 62.986998 | 21.322610 | |
| Osyczka and Kundu | NSGA-III | −258.633516 | 5.433823 | −168.598553 | 29.169913 | 62.053323 | 20.778173 |
| M-PF | −255.080484 | 5.367792 | −162.235317 | 26.606650 | 60.836597 | 18.988171 | |
| eMPF | −257.382419 | 5.312247 | −167.069531 | 28.639926 | 61.643875 | 21.469461 | |
| NSGA-II | 0.390717 | 1.007121 | 0.547760 | 4.747238 | 0.139116 | 2.426397 | |
| Const-Ex | NSGA-III | 0.390230 | 1.515615 | 0.441708 | 7.518592 | 0.093502 | 1.616727 |
| M-PF | 0.445405 | 1.175281 | 0.616617 | 2.902549 | 0.093789 | 1.547132 | |
| eMPF | 0.391615 | 1.004618 | 0.766952 | 1.719732 | 0.099745 | 1.512755 | |
| VR-UC Test 1 | NSGA-II | 0.052761 | 1.000574 | 0.156242 | 17.296326 | 0.193932 | 10.902374 |
| NSGA-III | 0.052718 | 2.866609 | 0.074163 | 31.895484 | 0.086781 | 8.590167 | |
| M-PF | 0.070903 | 2.921766 | 0.144710 | 7.997647 | 0.057197 | 3.582939 | |
| eMPF | 0.053224 | 1.000024 | 0.705932 | 2.339642 | 0.174928 | 5.048489 | |
| VR-UC Test 2 | NSGA-II | −4.995860 | −9.993871 | −4.995082 | −9.992874 | 0.002898 | 0.004093 |
| NSGA-III | −4.995535 | −9.993506 | −4.995059 | −9.992905 | 0.002668 | 0.003992 | |
| M-PF | −4.995112 | −9.993227 | −4.994349 | −9.992267 | 0.003135 | 0.003989 | |
| eMPF | −4.996121 | −9.994576 | −4.995738 | −9.993998 | 0.002667 | 0.003675 | |
| MSGA Test 1 | NSGA-II | 0.234489 | 0.235890 | 0.706906 | 0.709010 | 0.197887 | 0.197780 |
| NSGA-III | 0.549158 | 0.491633 | 0.779350 | 0.734232 | 0.086980 | 0.100268 | |
| M-PF | 0.554772 | 0.531218 | 0.768762 | 0.768141 | 0.051210 | 0.054106 | |
| eMPF | 0.231459 | 0.229316 | 0.661794 | 0.670574 | 0.247905 | 0.247862 | |
| Test Function | Method | Minimum | ||
|---|---|---|---|---|
| Function 1 | Function 2 | Function 3 | ||
| Viennet | NSGA-II | 0.000051 | 15.000000 | −0.099997 |
| NSGA-III | 131,609.806452 | 443,378.967742 | 0.000004 | |
| M-PF | 4292.110524 | 10,870.875716 | −0.002940 | |
| eMPF | 0.000028 | 15.000026 | −0.099998 | |
| MHHM1 | NSGA-II | 9.6666 × | 7.3333 × | 6.33333 × |
| NSGA-III | 6.193743 × | 4.7659963 × | 3.433997 × | |
| M-PF | 2.4781883 × | 7.064937 × | 7.134097 × | |
| eMPF | 1.0666 × | 9.6666 × | 5.3333 × | |
| MHHM2 | NSGA-II | 6.18220 × | 1.7605 × | 2.837620 × |
| NSGA-III | 0.001283 | 0.001229 | 0.00249529 | |
| M-PF | 0.00029338 | 0.0004046536 | 0.0006900754 | |
| eMPF | 6.868939 × | 1.63898 × | 4.5422 × | |
| Test Function | Method | Mean | ||
|---|---|---|---|---|
| Function 1 | Function 2 | Function 3 | ||
| Viennet | NSGA-II | 3.330086 | 15.285244 | 0.053903 |
| NSGA-III | 132,295.691684 | 445,689.241041 | 0.000004 | |
| M-PF | 4607.780516 | 11,696.522534 | 0.001230 | |
| eMPF | 0.572229 | 15.485611 | −0.024929 | |
| MHHM1 | NSGA-II | 0.0034099 | 0.0009104 | 0.00341086 |
| NSGA-III | 0.0013004 | 0.0005224 | 0.00474447 | |
| M-PF | 0.00443803 | 0.002016614 | 0.00459519 | |
| eMPF | 0.0026903 | 0.00020094 | 0.00271158 | |
| MHHM2 | NSGA-II | 0.0054150 | 0.005925 | 0.00555724 |
| NSGA-III | 0.0035569 | 0.003649 | 0.0063590 | |
| M-PF | 0.004642219 | 0.00528738 | 0.005879 | |
| eMPF | 0.0042817 | 0.0046030 | 0.004078 | |
| Test Function | Method | Standard Deviation | ||
|---|---|---|---|---|
| Function 1 | Function 2 | Function 3 | ||
| Viennet | NSGA-II | 2.688537 | 0.511459 | 0.081092 |
| NSGA-III | 6979.937413 | 26,870.603732 | 0.000000 | |
| M-PF | 2278.826105 | 7778.051973 | 0.010432 | |
| eMPF | 0.330933 | 0.328919 | 0.049485 | |
| MHHM1 | NSGA-II | 0.00313115 | 0.00079 | 0.0031071 |
| NSGA-III | 0.0016641 | 0.0004383 | 0.00146057 | |
| M-PF | 0.0045989 | 0.00074356 | 0.004502838 | |
| eMPF | 0.001529 | 0.00059 | 0.0015419 | |
| MHHM1 | NSGA-II | 0.003749 | 0.00417569 | 0.0037675 |
| NSGA-III | 0.001986 | 0.0018050 | 0.0020722 | |
| M-PF | 0.0032253 | 0.0035306 | 0.0034066 | |
| eMPF | 0.0020989 | 0.0021489 | 0.002019 | |
Appendix C
| Test Function | Method | Generational Distance | Spread () | Spacing () |
|---|---|---|---|---|
| Binh and Korn | NSGA-II NSGA-III M-PF eMPF | 0.069016 0.378684 1.333222 0.770759 | 0.938548 1.530796 1.233198 1.584592 | 0.185688 0.554448 1.062628 1.040446 |
| Chankong Haimes | NSGA-II NSGA-III M-PF eMPF | 0.132257 6.711842 1.897858 10.481315 | 0.803492 1.600441 0.99258 1.220204 | 0.216754 3.754718 0.41429 2.947663 |
| Fonseca Fleming | NSGA-II NSGA-III M-PF eMPF | 0.000838 0.002347 0.000664 0.006234 | 0.86052 1.401653 1.134345 1.664327 | 0.001535 0.004618 0.00218 0.006798 |
| Test Function 4 | NSGA-II NSGA-III M-PF eMPF | 0.006338 0.133243 0.020431 0.081445 | 0.938548 1.530796 1.233198 1.584592 | 0.039957 0.287708 0.061413 0.14012 |
| Kursawe | NSGA-II NSGA-III M-PF eMPF | 0.006938 0.70871 0.127039 0.075359 | 0.803527 0.911151 1.19283 0.892111 | 0.336557 0.470105 0.334158 0.45627 |
| Schaffer Function N1 | NSGA-II NSGA-III M-PF eMPF | 0.000985 0.003258 0.003113 0.002111 | 0.772657 1.44585 1.44585 1.274417 | 0.002629 0.007116 0.00495 0.005048 |
| Schaffer Function N2 | NSGA-II NSGA-III M-PF eMPF | 0.001906 0.130632 0.010325 0.096201 | 0.742149 1.514319 1.319566 1.621567 | 0.006122 0.097936 0.023796 0.070892 |
| Poloni’s Two Objectives | NSGA-II NSGA-III M-PF eMPF | 0.0127 0.102661 0.031244 0.186827 | 1.47718 1.789741 1.791253 1.55847 | 0.737613 0.693373 0.664818 0.984685 |
| Zitzler–Deb–Thiele’s N1 | NSGA-II NSGA-III M-PF eMPF | 0.042448 0.052309 0.045381 0.048533 | 0.7066 0.712719 0.721581 0.685075 | 0.074755 0.077806 0.07787 0.147347 |
| Zitzler–Deb–Thiele’s N2 | NSGA-II NSGA-III M-PF eMPF | 0.073596 0.041085 0.068744 0.070442 | 0.697774 0.710485 0.738163 0.712368 | 0.19127 0.113637 0.120021 0.16111 |
| Zitzler–Deb–Thiele’s N3 | NSGA-II NSGA-III M-PF eMPF | 0.032912 0.030987 0.044047 0.040325 | 0.714989 0.660256 0.662726 0.72205 | 0.098628 0.102081 0.111724 0.084448 |
| Zitzler–Deb–Thiele’s N4 | NSGA-II NSGA-III M-PF eMPF | 0.810677 2.272926 2.018945 2.279626 | 0.744636 0.757631 0.786935 0.738201 | 9.043884 7.516822 8.574137 9.78726 |
| Zitzler–Deb–Thiele’s N6 | NSGA-II NSGA-III M-PF eMPF | 0.191495 0.099431 0.065991 0.092465 | 0.685276 0.59864 0.638246 0.69825 | 0.115021 0.140287 0.173285 0.260617 |
| Osycak and Kundu Function | NSGA-II NSGA-III M-PF eMPF | 1.504086 1.294484 1.316762 1.388888 | 1.178373 1.127386 1.132501 1.2232 | 3.283527 2.84922 3.077236 3.686033 |
| Constr-Ex Problem | NSGA-II NSGA-III M-PF eMPF | 0.00495 0.043087 0.02453 0.07408 | 0.714432 1.313374 1.179857 1.683737 | 0.012929 0.067725 0.042256 0.090675 |
| MSGA Test 1 | NSGA-II NSGA-III M-PF eMPF | 0.000538 0.013212 0.012998 0.003187 | 0.972065 1.038185 1.492854 1.242157 | 0.002284 0.015305 0.006631 0.004642 |
| VR-UC Test 1 | NSGA-II NSGA-III M-PF eMPF | 0.01332 0.070166 0.142823 0.38772 | 0.786952 1.427575 1.316431 1.695775 | 0.05018 0.176857 0.190408 0.402943 |
| VR-UC Test 2 | NSGA-II NSGA-III M-PF eMPF | 9.4 × 9.4 × 0.000324 0.000273 | 0.717724 0.636498 0.577738 0.712867 | 0.00000 0.00000 0.00000 0.00000 |
| Vinnet Function | NSGA-II NSGA-III M-PF eMPF | 0.00169 0.627138 1.615187 0.648107 | 0.782624 0.989541 1.21211 1.557092 | 0.015777 0.087255 0.169447 0.095202 |
| MHHM1 | NSGA-II NSGA-III M-PF eMPF | 6 × 2.8 × 1.8 × 2.3 × | 0.772737 1.640253 1.620182 1.688381 | 1.1 × 3.3 × 2.6 × 3.5 × |
| MHHM2 | NSGA-II NSGA-III M-PF eMPF | 0.000401 0.001194 0.000514 0.001207 | 0.651384 0.765195 0.798712 0.702216 | 0.003814 0.001724 0.003292 0.001756 |
References
- Garey, M.R.; Johnson, D.S. Computers and Intractability; Freeman: San Francisco, CA, USA, 1979; Volume 174. [Google Scholar]
- Hooshyar, M.; Huang, Y.M. Meta-heuristic Algorithms in UAV Path Planning Optimization: A Systematic Review (2018–2022). Drones 2023, 7, 687. [Google Scholar] [CrossRef]
- Muñoz, M.A.; Sun, Y.; Kirley, M.; Halgamuge, S.K. Algorithm selection for black-box continuous optimization problems: A survey on methods and challenges. Inf. Sci. 2015, 317, 224–245. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2013, 18, 577–601. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Horn, J.; Nafpliotis, N.; Goldberg, D.E. A niched Pareto genetic algorithm for multiobjective optimization. In Proceedings of the First IEEE Conference on Evolutionary Computation, IEEE World Congress on Computational Intelligence, Orlando, FL, USA, 27–29 June 1994; pp. 82–87. [Google Scholar]
- Gunasekara, R.C.; Mehrotra, K.; Mohan, C.K. Multi-objective optimization to identify key players in social networks. In Proceedings of the 2014 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining (ASONAM 2014), Beijing, China, 17–20 August 2014; pp. 443–450. [Google Scholar]
- Stavroulakis, G.E.; Charalambidi, B.G.; Koutsianitis, P. Review of computational mechanics, optimization, and machine learning tools for digital twins applied to infrastructures. Appl. Sci. 2022, 12, 11997. [Google Scholar] [CrossRef]
- Murray, A.T.; Baik, J. Opensource spatial optimization in GIScience for strategic positioning. Trans. GIS 2023, 27, 646–662. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Goswami, S.S. A comprehensive review of multiple criteria decision-making (MCDM) Methods: Advancements, applications, and future directions. Decis. Mak. Adv. 2023, 1, 25–48. [Google Scholar] [CrossRef]
- Chen, H.; Lu, C.; Feng, L.; Liu, Z.; Sun, Y.; Chen, W. Structural optimization design of BIW using NSGA-III and entropy weighted TOPSIS methods. Adv. Mech. Eng. 2023, 15, 16878132231220351. [Google Scholar] [CrossRef]
- Akbari, M.; Asadi, P.; Rahimi Asiabaraki, H. A Hybrid Method of NSGA-II and TOPSIS to Optimize the Performance of Friction Stir Extrusion. Iran. J. Mater. Form. 2021, 8, 46–62. [Google Scholar]
- Alkayem, N.F.; Cao, M.; Ragulskis, M. Damage diagnosis in 3D structures using a novel hybrid multiobjective optimization and FE model updating framework. Complexity 2018, 2018, 3541676. [Google Scholar] [CrossRef]
- Kesireddy, A.; Carrillo, L.R.G.; Baca, J. Multi-criteria decision making-pareto front optimization strategy for solving multi-objective problems. In Proceedings of the 2020 IEEE 16th International Conference on Control & Automation (ICCA), Singapore, 9–11 October 2020; pp. 53–58. [Google Scholar]
- Méndez, M.; Frutos, M.; Miguel, F.; Aguasca-Colomo, R. Topsis decision on approximate pareto fronts by using evolutionary algorithms: Application to an engineering design problem. Mathematics 2020, 8, 2072. [Google Scholar] [CrossRef]
- Coello Coello, C.A.; González Brambila, S.; Figueroa Gamboa, J.; Castillo Tapia, M.G.; Hernández Gómez, R. Evolutionary multiobjective optimization: Open research areas and some challenges lying ahead. Complex Intell. Syst. 2020, 6, 221–236. [Google Scholar] [CrossRef]
- Roy, B. Problems and methods with multiple objective functions. Math. Program. 1971, 1, 239–266. [Google Scholar] [CrossRef]
- Long, Q.; Wu, X.; Wu, C. Non-dominated sorting methods for multi-objective optimization: Review and numerical comparison. J. Ind. Manag. Optim. 2021, 17. [Google Scholar] [CrossRef]
- Taherdoost, H.; Madanchian, M. Multi-criteria decision making (MCDM) methods and concepts. Encyclopedia 2023, 3, 77–87. [Google Scholar] [CrossRef]
- Stević, Ž.; Durmić, E.; Gajić, M.; Pamučar, D.; Puška, A. A novel multi-criteria decision-making model: Interval rough SAW method for sustainable supplier selection. Information 2019, 10, 292. [Google Scholar] [CrossRef]
- Vaidya, O.S.; Kumar, S. Analytic hierarchy process: An overview of applications. Eur. J. Oper. Res. 2006, 169, 1–29. [Google Scholar] [CrossRef]
- Sarkar, A. A TOPSIS method to evaluate the technologies. Int. J. Qual. Reliab. Manag. 2013, 31, 2–13. [Google Scholar] [CrossRef]
- Borgulya, I. A ranking method for multiple-criteria decision-making. Int. J. Syst. Sci. 1997, 28, 905–912. [Google Scholar] [CrossRef]
- Blickle, T.; Thiele, L. A comparison of selection schemes used in evolutionary algorithms. Evol. Comput. 1996, 4, 361–394. [Google Scholar] [CrossRef]
- Sharma, S.; Kumar, V. A comprehensive review on multi-objective optimization techniques: Past, present and future. Arch. Comput. Methods Eng. 2022, 29, 5605–5633. [Google Scholar] [CrossRef]
- Li, X.; Wang, K.; Liu, L.; Xin, J.; Yang, H.; Gao, C. Application of the entropy weight and TOPSIS method in safety evaluation of coal mines. Procedia Eng. 2011, 26, 2085–2091. [Google Scholar] [CrossRef]
- Trautmann, H.; Rudolph, G.; Dominguez-Medina, C.; Schütze, O. Finding evenly spaced Pareto fronts for three-objective optimization problems. In EVOLVE-A Bridge between Probability, Set Oriented Numerics, and Evolutionary Computation II; Springer: Berlin/Heidelberg, Germany, 2013; pp. 89–105. [Google Scholar]
- Ishibuchi, H.; Masuda, H.; Tanigaki, Y.; Nojima, Y. Modified distance calculation in generational distance and inverted generational distance. In Proceedings of the Evolutionary Multi-Criterion Optimization: 8th International Conference, EMO 2015, Guimarães, Portugal, 29 March–1 April 2015; Part II 8. pp. 110–125. [Google Scholar]
- Riquelme, N.; Von Lücken, C.; Baran, B. Performance metrics in multi-objective optimization. In Proceedings of the 2015 Latin American Computing Conference (CLEI), Arequipa, Peru, 19–23 October 2015; pp. 1–11. [Google Scholar]
- Schott, J.R. Fault Tolerant Design Using Single and Multicriteria Genetic Algorithm Optimization. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1995. [Google Scholar]
- Binh, T.T.; Korn, U. MOBES: A multiobjective evolution strategy for constrained optimization problems. In Proceedings of the Third International Conference on Genetic Algorithms (Mendel 97), Brno, Czech Republic, 25–27 June 1997; Volume 25, p. 27. [Google Scholar]
- Fonseca, C.M.; Fleming, P.J. An overview of evolutionary algorithms in multiobjective optimization. Evol. Comput. 1995, 3, 1–16. [Google Scholar] [CrossRef]
- Kita, H.; Yabumoto, Y.; Mori, N.; Nishikawa, Y. Multi-objective optimization by means of the thermodynamical genetic algorithm. In Parallel Problem Solving from Nature—PPSN IV, Proceedings of the International Conference on Evolutionary Computation—The 4th International Conference on Parallel Problem Solving from Nature, Berlin, Germany, 22–26 September 1996; Proceedings 4; Springer: Berlin/Heidelberg, Germany, 1996; pp. 504–512. [Google Scholar]
- Kursawe, F. A variant of evolution strategies for vector optimization. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Dortmund, Germany, 1–3 October 1990; pp. 193–197. [Google Scholar]
- Schaffer, J.D. Multiple objective optimization with vector evaluated genetic algorithms. In Proceedings of the First International Conference on Genetic Algorithms and Their Applications; Psychology Press: London, UK, 2014; pp. 93–100. [Google Scholar]
- Khatamsaz, D.; Peddareddygari, L.; Friedman, S.; Allaire, D. Bayesian optimization of multiobjective functions using multiple information sources. AIAA J. 2021, 59, 1964–1974. [Google Scholar] [CrossRef]
- Deb, K.; Thiele, L.; Laumanns, M.; Zitzler, E. Scalable multi-objective optimization test problems. In Proceedings of the 2002 Congress on Evolutionary Computation. CEC’02 (Cat. No. 02TH8600), Honolulu, HI, USA, 12–17 May 2002; Volume 1, pp. 825–830. [Google Scholar]
- Osyczka, A.; Kundu, S. A new method to solve generalized multicriteria optimization problems using the simple genetic algorithm. Struct. Optim. 1995, 10, 94–99. [Google Scholar] [CrossRef]
- Rendón, M.V. A non-generational genetic algorithm for multiobjective optimization. In Proceedings of the 7th Interational Conference on Genetic Algorithms, East Lansing, MI, USA, 19–23 July 1997; pp. 658–665. [Google Scholar]
- Lis, J.; Eiben, Á.E. A multi-sexual genetic algorithm for multiobjective optimization. In Proceedings of the 1997 IEEE International Conference on Evolutionary Computation (ICEC’97), Indianapolis, IN, USA, 13–16 April 1997; pp. 59–64. [Google Scholar]
- Vlennet, R.; Fonteix, C.; Marc, I. Multicriteria optimization using a genetic algorithm for determining a Pareto set. Int. J. Syst. Sci. 1996, 27, 255–260. [Google Scholar] [CrossRef]
- Mao, J.; Hirasawa, K.; Hu, J.; Murata, J. Genetic symbiosis algorithm for multiobjective optimization problems. Trans. Soc. Instrum. Control Eng. 2001, 37, 893–901. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kesireddy, A.; Medrano, F.A. Elite Multi-Criteria Decision Making—Pareto Front Optimization in Multi-Objective Optimization. Algorithms 2024, 17, 206. https://doi.org/10.3390/a17050206
Kesireddy A, Medrano FA. Elite Multi-Criteria Decision Making—Pareto Front Optimization in Multi-Objective Optimization. Algorithms. 2024; 17(5):206. https://doi.org/10.3390/a17050206
Chicago/Turabian StyleKesireddy, Adarsh, and F. Antonio Medrano. 2024. "Elite Multi-Criteria Decision Making—Pareto Front Optimization in Multi-Objective Optimization" Algorithms 17, no. 5: 206. https://doi.org/10.3390/a17050206
APA StyleKesireddy, A., & Medrano, F. A. (2024). Elite Multi-Criteria Decision Making—Pareto Front Optimization in Multi-Objective Optimization. Algorithms, 17(5), 206. https://doi.org/10.3390/a17050206






