Abstract
A major area of application of multiobjective path problems and resolution algorithms is telecommunication network routing design, taking into account the extremely rapid technological and service evolutions. The need for explicit consideration of heterogeneous Quality of Service metrics makes it advantageous for the development of routing models where various technical–economic aspects, often conflicting, should be tackled. Our work is focused on multiobjective path problem formulations and resolution methods and their applications to routing methods. We review basic concepts and present main formulations of multiobjective path problems, considering different types of objective functions. We outline the different types of resolution methods for these problems, including a classification and overview of relevant algorithms concerning different types of problems. Afterwards, we outline background concepts on routing models and present an overview of selected papers considered as representative of different types of applications of multiobjective path problem formulations and algorithms. A broad characterization of major types of path problems relevant in this context is shown regarding the overview of contributions in different technological and architectural network environments. Finally, we outline research trends in this area, in relation to recent technological evolutions in communication networks.
1. Introduction
A very important area of the application of shortest path problems in general and multiobjective path problem formulations in particular is telecommunication network design, namely in the context of the development and implementation of advanced routing methods. Routing is a most important network functionality and a key part of network operational design and has strong impacts on network performance both in technical and economic aspects, including the quality of experience of the customers for a given service. Routing methods are essentially focused on the calculation and selection of a loopless path (corresponding to a sequence of network resources or ‘route’) or a set of loopless paths from an originating node to one or multiple terminating node(s)—assuming that the representation of the communication network is a connected network normally composed of arcs of limited transmission capacity—seeking to optimize one or more objective(s) while satisfying certain constraint(s) of a technical/economic nature. Although routing models and methods deal with a number of issues other than path calculation, we can say that at the heart of any routing method, in any communication network application environment, there is the need to calculate one or more paths seeking to satisfy some optimizing criterion/criteria and relevant technical–economic constraints. Telecommunication networks have experienced extremely rapid progress in terms of technologies, architectures and provided services, driven by two major forces: technical innovations and accelerated traffic growth, associated with the demand for more advanced services, such as audio, video services, video conferencing and cloud computing.
These trends and the need for explicit consideration of different Quality of Service (QoS) metrics (usually of heterogeneous nature) in the routing methods make it necessary or advantageous for the development of routing models where various technic–economic aspects, often conflicting, should be tackled. This has fostered, in recent decades, an increasing interest in the development of multiobjective routing models so that QoS constraints and trade-offs between different objectives could be treated in a consistent manner in mathematical terms. It could be noted that, in many situations, taking into account essential characteristics of the network environment, routing models become more effective if different metrics are explicitly applied by considering an adequate set of optimization objectives rather than just aggregating some of them a priori in a single objective function (OF) and transforming the other OFs into constraints as has often been carried out in Operations Research (OR) application models in this area. There are many applications where there is the need for an a priori aggregation of criteria, namely for on-line routing or for off-line automatized dynamic routing with very short route updating times, but even in these cases, there is a potential advantage in addressing explicitly multicriteria modelling since it enables a deeper insight concerning the persecution of several issues regarding the interplay and possible trade-off between some of the criteria.
Thence, it is clear both from an Operations Research and from a network design perspective that it is important to address multiobjective shortest path problems and develop resolution approaches adequate for the envisaged applications in a telecom network routing design which constitutes the major motivation for this work. A state-of-the-art survey on applications of multicriteria decision analysis to telecommunication network design with a section on multicriteria routing methods is in [1], and an overview also with references in this area is included in [2]. A conceptual framework for explicitly multicriteria modelling in QoS-based routing is proposed in [3].
Taking into account the importance of shortest path and -shortest path problems in this context, we pay special attention to these problems after reviewing basic concepts on multiobjective path problems. We present the main formulations of multiobjective path problems also including evidence-relevant theoretical results. Different categories of objective functions will be considered, namely linear and non-linear functions as well as some optimization path problems with an objective function composed of other functions and problems involving uncertainty. We outline the different types of resolution methods for these problems appearing in the scientific literature more relevant to this important application area, not forgetting the approximating approaches. Special emphasis will be given to exact resolution approaches, namely based on the shortest path, -shortest path and dedicated multiobjective shortest path algorithms, having in mind that these algorithms can solve large instances of the problem in execution times compatible with the application context. Also, a classification and overview of relevant algorithms and related contributions concerning different types of problems and of resolution approaches, namely labeling, ranking, recursive and two-phase methods, as well as interactive approaches, will be put forward. Note that focusing this work on exact algorithms is not a severe limitation in many of the path problems because the available resolution approaches enable, in most cases, a fast resolution of large instances of the problems.
It should be emphasized that when multiple and conflicting objectives are explicitly at stake in the path optimization problem, the global optimum does not exist. Thence, the optimal solution is substituted by the concept of an efficient (also known as Pareto optimal) solution set corresponding to a nondominated point set in the objective function space. The designation ‘efficient path’ means a feasible path such that there are no other feasible paths capable of improving the value of one objective function without worsening the value of at least one of the other objective functions. A further distinction has to be made between supported and unsupported nondominated solutions as reviewed in the section on basic concepts.
One of our main purposes in this work, developed in Section 2, is to provide insights into current research trends in the application of Operations Research techniques to solve multiobjective path problems and to outline possible future research directions. In particular, in the first part of this paper, we refer to articles that are focused on path problems and their resolution approaches. We considered works published in scientific journals, conference proceedings, and book chapters. We carried out a search in the following databases: Elsevier, Wiley, Springer, Scopus, IEEExplore, Research Gate, and Google Scholar; we used several keywords such as “multiobjective paths” or “multicriteria paths”. We also present a summary of the main features of the problems in tables, which can help the researchers in comparing the works and exploring new possible configurations.
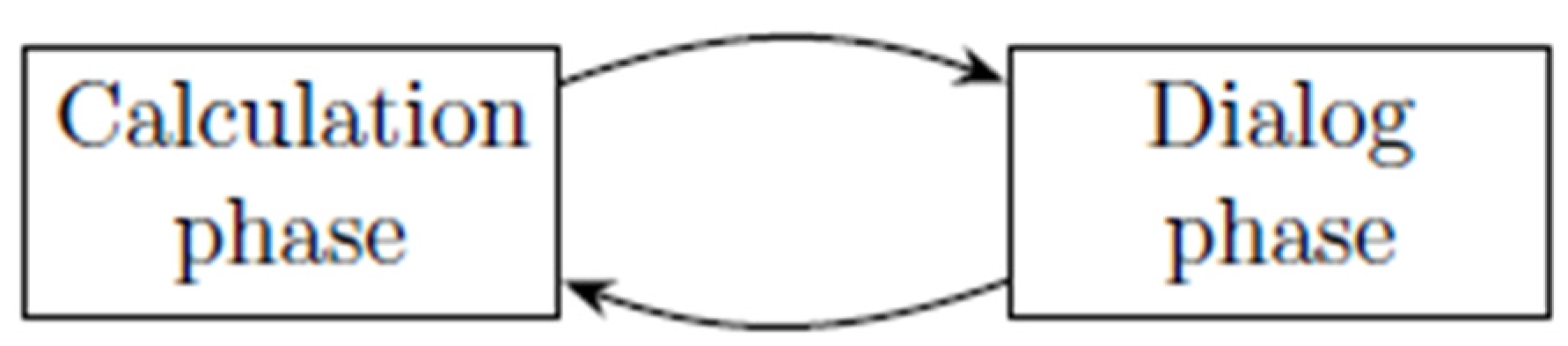
In this paper, we consider three types of algorithms. Firstly, we consider the algorithms for which there is no articulation of preferences of the Decision Maker (DM) (this means that the aggregation of preferences is made a posteriori), so that the algorithms calculate the whole set of efficient solutions. Secondly, we consider those which are characterized by a progressive articulation of preferences of the DM, designated as interactive approaches; Thirdly, we consider those for which there is an a priori articulation of preferences, for instance by building a value/utility function. In the case of interactive approaches (see Figure 1), after each calculation phase leads to one (or several) efficient solution(s), there is a dialogue phase with the DM. This phase is carried out so that a new calculation phase is initiated, and so on. The stopping condition of this procedure depends on the specific characteristics of the interactive procedure.
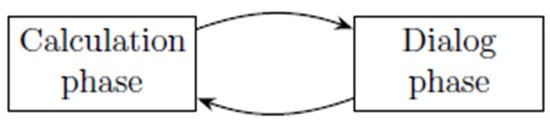
Figure 1.
Interactive process (adapted from [4]).
It should be noted that, concerning interactive procedures, the emphasis on exact algorithms, of course, refers to the calculation phase only, that is, to the phase of calculation of efficient solutions.
A second main purpose of our work is the presentation of an overview of selected papers considered as representative of different types of applications in telecommunication network routing models of multiobjective path problem formulations and of the associated resolution approaches. Note that the extremely rapid evolution of communication technologies, network architectures and provided services had an important impact on various aspects of the developed routing models. In fact, the advantage, in many cases, of explicit consideration of QoS metrics and economic-based metrics either as objectives to be optimized or as constraints has fostered an increasing interest in the development of multicriteria/multiobjective routing models. Note that routing methods deal with a number of issues other than path calculation since the functional technical entities that actually implement the establishment of routes, designated as routing protocols, have to execute several procedures concerning the management of various types of information/data following strict formats, contents and processing rules, dependent on the technical features of the network underlying technology(ies) and architecture.
The possibility of implementing advanced routing methods of multicriteria nature, the advantages of which have been referred to above, is strongly related to the technical capabilities provided by modern network technologies and architectures.
We highlight some technological evolutions in basic communication technologies which had an important impact on routing model developments. Firstly, Multiprotocol Label Switching (MPLS) was developed for packet-switched services (Internet-type services) and enables ‘label-switched paths’ (LSPs) to be established via label-switched routers, so that end-to-end traffic flows can be carried ensuring various QoS requirements. A further extension of MPLS specially developed for optical networks was Generalized MPLS (GMPLS) that provides control functionalities for advanced switching mechanisms, namely wavelength switching, time division multiplexing and fiber (port) switching. In essence, from a logical–functional point of view, this capability is equivalent to circuit-switching or circuit-routing, enabling routing principles perfectly analogous to those of classical multiservice digital telephone networks. Concerning physical transport technologies, Wavelength Division Multiplexing (WDM) and Dense WDM (DWDM) optical technologies enabled the use of tens of wavelengths on each fiber, so that extremely great information rates and enormous traffic carrying capabilities can be implemented associated with flexibility resulting from the possibility of wavelength conversion in the optical switches. Also, the Optical Transport Network (OTN) was designed as the base transport system for the Synchronous Digital Hierarchy (SDH) transmission system and was extended enabling the Internet Protocol (IP) and Ethernet protocols to be supported. It is capable of carrying very large bandwidths and allowing advanced mechanisms in terms of operations, administration, maintenance and provisioning at the level of wavelengths. Note that the interplay between various technologies in distinct functional layers of telecommunication networks enables various network architectures to be used such as IP/MPLS over WDM or IP-over-OTN-over-DWDM that enable the reduction of the needed router capacities and power consumptions and a more efficient utilization of bandwidth. A recent technological paradigm that is having a decisive impact in improving the working and management of current network structures is Software-Defined Networking (SDN). The basic idea behind SDN is the separation between the network control logic and the underlying devices that implement the forwarding of traffic flows, this being achieved by the direct control of specific types of hardware devices by using common management interfaces. This is an important development in a wider trend directed to the ‘softwarization’ of key network functionalities, based on the concept of separation of the functions of the control plane (where the ‘intelligence’ of the routing mechanism is located) from the data/message transport plane. Another area where extremely rapid progresses occurred is mobile networks, driven by the exponential increase in the demand for mobile data and video services, including fast Internet access, associated with the spread of fifth-generation (5G) networks, providing important quantitative and qualitative advancements in terms of bandwidth access (enabling new and better QoS data streaming services) and transmission latency (with more stringent requirements for real-time services). Also, the development of specialized IP-based local wireless networks, namely Wireless Sensor Networks (WSNs) and ad hoc wireless networks (ad hoc WNs), pose specific requirements and limitations to the routing models, resulting from the fully distributed nature of the routing control and the limited capacities of the routers in terms of available network information.
In Section 3 of this paper, we outline background concepts related to telecom network routing models and present an overview of selected papers considered as representative of different types of applications of multiobjective path problem (MOPP) formulations and algorithms. A broad characterization of major types of path problems relevant to telecom routing models, namely single path, path pair and multipath problems (and their main variants) will be mentioned, in the context of the overview of contributions concerning different technological and architectural network environments.
Representative examples of routing models for application in various network environments that involve the formulation of MOPPs will be addressed, focusing on the essential features of the routing model and of the associated MOPP and the resolution approaches that are either exact or approximate. Concerning the types of approaches used for tackling MOPPs in the context of this overview of routing models, we distinguish those that use a primary resolution procedure algorithm(s) specifically dedicated to the calculation of solutions to MOPPs, including heuristics and metaheuristics, from those which use instrumentally, as auxiliary resolution procedures, MOPP-dedicated algorithm(s), including shortest path and -shortest path algorithms. A further distinction will be made by considering a third type of model that involved explicitly, as an objective of the mathematical formulation, the calculation of paths that are solutions to MOPPs by recurring to OR approaches which are not specifically dedicated to path problems, such as network flow, integer linear programming (ILP), mixed integer linear programming (MILP), non-linear programming (NLP) and other more general types of network optimization approaches. The models of the two latter types appear frequently in routing methods where the route/path calculation and selection cannot be mathematically separated from the assignment of node-to-node traffic flows to the selected paths, which happens in all models for which the routing method embodies a teletraffic engineering mechanism. Typical examples are models with traffic splitting, where each node-to-node offered bandwidth can be divided by several paths, models in circuit-switched networks with alternative routing (where a primary route/path and an alternative route are calculated such that the alternative route is used whenever the primary route is blocked) and routing models for GMPLS-based networks using the Resource Reservation Protocol—Traffic Engineering (RSVP-TE) routing protocol. Also, we will refer to a few routing models where multicriteria path problems are formulated through a heuristic multiattribute decision approach using an a priori specification of the system of preferences by using an empirical utility function, common in applications to WSNs and ad hoc WNs, having in mind functional characteristics of these networks.
Finally, in the last section of the paper, we outline general major research trends and challenges in this wide and multifaceted area of application of multiobjective paths problem formulations and algorithms.
2. Overview of Multiobjective Path Problems and Algorithms
2.1. Basic Concepts
Let be a directed graph and be two given nodes in . A path from to in is a sequence , where , , , and . The set of paths from to in , denoted by , can be represented by means of linear constraints, as
where are binary decision variables associated with any arc . Constraints (1) are known as flow balance constraints. Under these conditions, each vector is the indicator vector of a path from to and the arcs with flow form a path from to [5]. We can also write
Let us consider that each arc is associated with cost values, , and that the functions assign a real value to any path in , based on its arc costs, for . The multiobjective path problem can be formulated as an optimization program with linear constraints, considering the previous decision variables for any . The problem can be formulated as
s. t. (1)
The image of the feasible set, , is .
In general, there is no optimal solution to a MOPP since there is not a path in which optimizes all objective functions simultaneously. Thus, in a MOPP, the concept of optimality is replaced by the concept of efficiency (or nondominance). A path is said to be efficient if and only if it does not exist any other path that dominates , that is, such that and . In this case, the image of , , is said to be a nondominated point. Let denote the set of efficient paths in and denote the corresponding set of nondominated points or Pareto front.
We distinguish between supported and unsupported efficient solutions. Supported efficient solutions are efficient solutions for the images which are located on the boundary of the convex hull of the nondominated solution set defined in the objective function space, while the images of unsupported efficient solutions are located in the interior of this hull, in the duality gaps. Details on duality gaps can be seen in [6].
Supported shortest paths can be obtained as optimal solutions of the single-objective weighted shortest path problem (WSPP):
with given weights , for . The set of supported efficient paths will be represented by , and its nondominated image, , denoted by . The remaining efficient solutions in are designated non-supported efficient paths. These cannot be obtained as the solution of a WSPP. The set of non-supported nondominated points, , is represented by .
Two paths are designated as alternative (or equivalent solutions) if . In this paper, the set of all efficient paths is designated as a maximal complete set, and it may contain equivalent solutions. The minimal complete set is a subset of the maximal complete set that contains a single path from any set of equivalent solutions (corresponding to a unique nondominated point).
2.2. Types of Multiobjective Path Problems
We consider three groups of MOPPs. The first group (Section 2.2.1) is the most well known, the multiobjective shortest path problem (MOSPP), where objective functions, to be minimized, are additive (minsum):
Since the MOSPP is the most used path problem in telecommunication network applications, we consider a large number of methods for its resolution and their classification as follows:
- APO—methods using an a posteriori aggregation of preferences, that is, methods that generate the whole set of efficient paths, so that the articulation of preferences is made by the decision maker;
- APR—methods using an a priori aggregation of preferences methods, that is, the problem is a priori transformed into a single objective problem, for instance, by using a utility function. We must refer that, as the different objective functions are modeled prior to the reduction to a single objective problem, the problem remains intrinsically multiobjective. Note that strict-sense lexicographic approaches should be included in this class;
- INT—Interactive methods, that is, methods where the articulation of preferences is progressive, including two successive phases: calculation and dialogue phases. So, a cycle of proposals and reactions continues till a so-called satisfactory compromise is obtained, i.e., some stopping condition is reached.
In the second group (Section 2.2.2), we include, besides minsum functions (for instance, those associated with routing load costs, expressed in terms of the inverse of the available bandwidth in each arc/link of the path), other types of objective functions, for instance, capacity functions such as maxmin or minmax corresponding typically, in routing models, to the optimization of path bottleneck bandwidths.
The third group (Section 2.2.3) refers to specific path combinatorial problems, and we focus on methods dedicated to their resolution based on specific biobjective shortest path techniques.
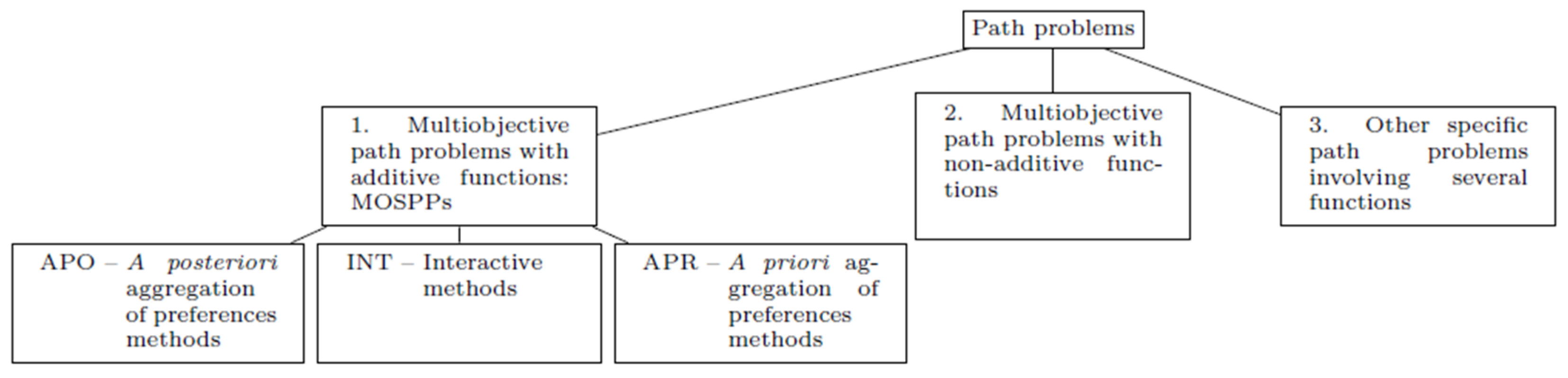
In Figure 2, we summarize the classification of the above referred to problems, considering deterministic formulations only.
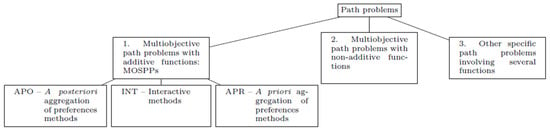
Figure 2.
Classification of multiobjective path problems.
In the next subsections, we will be referring to the main results regarding the considered methods.
In Table 1, Table 2 and Table 3, we summarize some essential features of the mentioned resolution methods as referred to in this paper.
2.2.1. MOPP with Additive Objective Functions
The MOSPP and its more common particular case, the biobjective shortest path problem (BOSPP), have been studied since the early works [7,8]. They proved that, theoretically, the problem is intractable and also that instances of this problem can have an exponential number of Pareto optimal solutions depending on the number of nodes. Despite this characteristic, several exact methods have been proposed for calculating the efficient path solution set. Refs. [9,10] obtained finiteness and boundedness conditions for the MOSPP, assuming that there are no negative cycles for one of the objective functions (cycles for which the value/cost of at least one of the OFs is negative). Furthermore, these studies also proved that, with these assumptions, if the value of any cycle is strictly positive for at least one of the OFs, then every efficient path is an efficient loopless path, and the reverse is also true. In practice, exact algorithms are fast enough to deal with many real applications.
In Table 1, we present a summary of some essential features of exact algorithms for the MOSPPs that are referred to in this subsection by indicating the number of OFs, the essential features of the resolution technique and the class of the resolution method (APO—A posteriori aggregation of preferences; INT—Interactive; or APR—A priori aggregation of preferences) as defined above.
We consider five types of MOSPP algorithms, namely, generalizations of labeling techniques for the single-objective shortest path problem (ls, label setting, and lc, label correcting); parametric methods which compute nondominated supported solutions based on the scalarization of the objective functions depending on a varying parameter (par); ranking methods which list paths in order of cost and eliminate solutions dominated by others (ran); two-phase algorithms which generate the nondominated supported solutions of the problem and afterwards swap duality gap regions to find those that are unsupported nondominated (2p); and recursive algorithms (rec) which extend node labels recursively, therefore following a depth-search policy and generating labels implicitly until a certain point.

Table 1.
Summary of some essential features of exact algorithms for the MOPPs with additive metrics.
Table 1.
Summary of some essential features of exact algorithms for the MOPPs with additive metrics.
| Reference | # Objectives | Technique * | Class |
|---|---|---|---|
| (Hansen 1980) [8] | ls | APO | |
| (Clímaco and Martins 1982) [11] | ran | APO | |
| (Martins 1984) [12] | ls | APO | |
| (Corley and Moon 1985) [13] | lc | APO | |
| (Mote et al., 1991) [14] | 2p | APO | |
| (Stewart and White 1991) [15] | ls | APO | |
| (Tung and Chew, 1992) [16] | ls | APO | |
| (Santos 1999) [9] | ls/lc | APO | |
| (Guerriero and Musmanno 2001) [17] | ls/lc | APO | |
| (Clímaco et al., 2003) [18] | ran | APO | |
| (Mandow and de la Cruz 2010) [19] | lc | APO | |
| (Machuca et al., 2012) [20] | ls | APO | |
| (Xie and Waller 2012) [21] | par | APO | |
| (Demeyer et al., 2013) [22] | ls | APO | |
| (Sanders and Mandow 2013) [23] | ls | APO | |
| (Duque et al., 2015) [24] | rec | APO | |
| (Pulido et al., 2015) [25] | ls | APO | |
| (Machuca and Mandow 2016) [26] | ls | APO | |
| (Giret et al., 2016) [27] | ls | APO | |
| (Sedeño-Noda and Colebrook 2019) [28] | ls | APO | |
| (de las Casas et al., 2021) [29] | ls | APO | |
| (Hu et al., 2021) [30] | ls | APO | |
| (Kergosien et al., 2022) [31] | lc | APO | |
| (de las Casas et al., 2023) [32] | ls | APO | |
| (Hernández et al., 2023) [33] | ls | APO | |
| (Kurbanov et al., 2023) [34] | ls | APO | |
| (Mandow and de la Cruz 2023) [35] | ls | APO | |
| (Current et al., 1990) [36] | 2p | INT | |
| (Murthy and Olson 1994) [37] | 2p | INT | |
| (Henig 1994) [38] | lc | INT | |
| (Coutinho-Rodrigues et al., 1999) [39] | 2p/ran | INT | |
| (Paixão et al., 2003) [40] | lc/ran | APR | |
| (Clímaco et al., 2006) [41] | lc/ran | APR | |
| (Sauvanet and Néron 2010) [42] | lc | APR | |
| (Fouchal et al., 2011) [43] | ls | APR | |
| (Pulido et al., 2014) [44] | ls | APR | |
| (Shirdel and Ramezani-Tarkhorani 2018) [45] | ls | APR | |
| (Pugliese et al., 2020) [46] | 2p/lc | APR |
* ls: label setting; lc: label correcting; par: parametric; ran: ranking; rec: recursive; 2p: two phases.
The works [47,48] present multiobjective combinatorial optimization surveys including sections dedicated to the MOPP; classifications including this type of problem are in [49,50]. Later on, the biobjective shortest path problem (BOSPP) was surveyed in [6,51] and the MOPP in [52]. Computational studies on the multiobjective shortest path problem were presented in [53], considering two OFs, and in [54], the latter including the use of utility functions for defining the next label to be scanned and considering two or more OFs. This study concluded that the features of the network structure have a decisive role in the algorithm performance.
After reviewing the literature concerning the BOSPP, a thorough computational comparison of some of the resolution strategies for this type of problem is presented in [6].
Let us now review the most relevant types of algorithms in each group of methods.
2.2.1.1. APO—A Posteriori Aggregation of Preferences Methods
- (a)
- Maximal Complete Set Computation
Labeling techniques
Labeling algorithms for the MOSPP are generalizations of the single objective labeling methods.
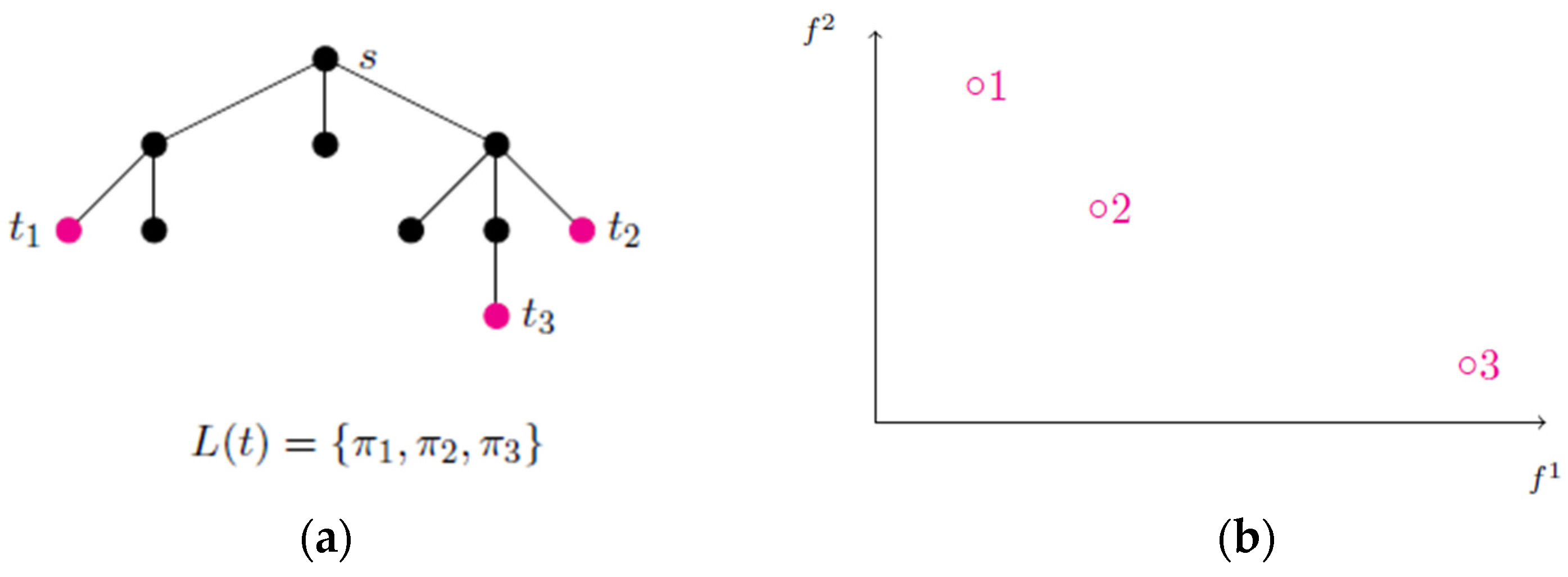
Since we have now more than one objective function the algorithm has to consider more than one path starting in up to each node, implying that more than one label associated with that node is used. Note that the labels associated with one node may dominate one another. This type of algorithm is founded on an adaptation of the Principle of Optimality valid for the shortest path problem that states that every efficient path is formed by efficient subpaths. This can be stated if no cycles with a negative cost exist in the network representation. Like in the single objective problem, these algorithms may be grouped into two types: label setting or label correcting algorithms. The latter type can still be divided into those algorithms that make a label correspond to a path starting in (these are designated as label-selection methods) or those that are characterized by associating a label with each node and representing several paths from to that node so that whenever a label is chosen all the associated paths are expanded by using the network arcs (these are designated as node-selection methods). This technique is outlined in Algorithm 1 and illustrated in Figure 3.
| Algorithm 1: Generic multiobjective labeling method (node selection) | |
| Variables: Let: be the set that stores the nodes which correspond to the labels yet to be examined; the set that stores all the labels which are associated with node ; the objective function vector associated with the path from node to node | |
| Summary: When the algorithm starts, the only label that is considered corresponds to the path . Afterwards, this label is extended using the arcs in . A dominance test is applied to any new label, with an objective function vector , considering the current labels in , ensuring that only nondominated labels are stored. When the algorithm is over, stores the nondominated labels for node , which correspond to the efficient paths from node to node . | |
| 1 | for any node do |
| 2 | |
| 3 | |
| 4 | while set is not empty do |
| 5 | node in |
| 6 | Delete node from set |
| 7 | For any arc do |
| 8 | for any label in set do |
| 9 | If vector is not dominated by any label in set then |
| 10 | Add a new label, corresponding to the vector , to set |
| 11 | Delete any label in set that is dominated by the new label |
| 12 | end if |
| 13 | end for |
| 14 | If set was modified then Insert node in set |
| 15 | end for |
| 16 | end while |
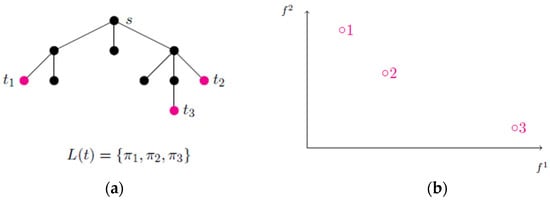
Figure 3.
Labeling techniques: (a) search tree of paths starting at node ; magenta bullets represent the end of efficient paths; (b) nondominated points corresponding to ; magenta circles represent the nondominated points corresponding to efficient paths.
In order to ensure that an efficient path is calculated, the label to be scanned is normally picked in in lexicographic order. The applied dominance test consists of comparing one label cost with the cost of the latest efficient path that was obtained for the biobjective case. In fact, if labels are selected in lexicographic order, then , or and for . The subsequence of a given one formed only by the nondominated labels also satisfies . Let us assume, without loss of generality, that some are not dominated and denote by a label lexicographically greater than . Thence, and implies that and for any associated with the nondominated labels subsequence. Otherwise, if and , then is dominated. Similarly, if then is nondominated, like the former label, but and means that is dominated. Alternatively, for the case where we have more than two OFs, we have to check the cost of all the efficient paths previously obtained. Finally, it should be noted that, similarly to the single objective case, the arc costs should be non-negative so that label setting algorithms may be applied, whereas label correcting methods are valid for finite instances of the MOSPP.
It is important to note that when labels are analyzed in lexicographic order, an efficient path from to is obtained whenever a nondominated label associated with node is selected, meaning that label setting methods calculate these efficient paths along their labeling phase. Otherwise, if label correcting is being used, the efficient paths can only be identified after all the labels are analyzed. The experimental analysis reported in [51,53] indicates that ranking methods for the biobjective shortest path problem (BOSPP) are close to an exhaustive search and consequently less competitive than others. Although there is a dependence on the data structures used in the implementation of the algorithms, it was concluded in [6,17,51] that, in general, label correcting methods are faster than label setting methods, the main reason resulting from the fact that label setting involves the extraction of the label with minimal cost from the set of temporary labels. This task can be completed either by maintaining the set of labels sorted, or by simply selecting the minimal element in the set at every extraction, and both are demanding operations that have to be repeated several times. Furthermore, following [6], node selection can be more advantageous than label selection taking into account that it allows setting several paths terminating at node whenever an arc is being analyzed. Still, the authors in [6] concluded that label-setting and label-correcting methods are the ones with the best performances for most of the instances that these authors evaluated and that the two-phase methods can be competitive with other resolution procedures for the BOSPP. This was concluded after the test of different implementation strategies for each calculation phase, whereas the ranking method using a “near shortest path” procedure (a dynamic programming type procedure) performed poorly. In particular, a ranking approach recurring to a “near shortest path” procedure (alternately identifying nondominated supported solutions and searching within duality gaps) and the two-phase method, investigating different methods for solving the problems arising in phases 1 and 2, were tested. It also investigates the two-phase method considering ranking in phase 2. The addressed near-shortest path method was adapted from the algorithm in [55], enabling the enumeration of all near-shortest loopless paths assuming the network has non-negative arc costs, meaning those with a cost that does not exceed the minimum with a tolerance .
Next, we summarize more recent or particularly relevant references on labeling methods for MOSPPs.
In [8], a generalization of the single objective shortest path algorithm in [56] is presented, considering two objectives. A generalization of Hansen’s algorithm is presented in [12], considering more than two objectives. In the proposed method, the lexicographically lowest label is selected in the set of temporary labels, so that it corresponds to an efficient path. A label correcting algorithm with a form of label generation is described in [13], similarly to the single-objective shortest path problem proposed by [57,58].
The works in [15,19] extend the so-called heuristic search algorithm A* to the multiobjective case: the algorithm Multi-Objective A* (MOA) and the algorithm New Approach to Multi-Objective A* (NAMOA), respectively. The A* algorithm is a path finding method which combines the traditional labeling with a heuristic function that estimates the remaining cost of the path to the terminal node [59]. MOA also uses a labeling method complemented by a node expansion strategy that is guided by a heuristic for the cost of partial paths. NAMOA is based on MOA, but it dynamically uses the cost of the efficient paths found by the algorithm to update the partial solutions that should still be expanded.
Label correcting/setting methods for the MOSPP are investigated in [17]. This work proposes new label-selection and also several node-selection strategies and presents computational experiments. It reports instances of the problem where label selection is the best strategy and others where node selection performs better. Furthermore, it reports that label setting is superior for some instances, whereas label correcting performs better for others. A label-setting algorithm that uses a preference model built a priori for calculating efficiently the exact preferred solutions for the multiobjective shortest path problem is described in [43]. The approach is based on the use of the Choquet integral in the context of a multicriteria decision aid method (see [60]), which can model both relative importance and interactions between criteria. The paper introduces Choquet dominance rules [61] which replace the Pareto dominance, integrated within the algorithm by [12].
In [20], the authors present an analysis and a comparison of the performance of three label-setting algorithms that use heuristic information for improving their efficiency, namely, the procedures MOA and NAMOA referred to above, and the algorithm in [16]. The related paper [26] presents a lower-bound-set calculation procedure for the biobjective shortest path problem to be used for improving the computational efficiency of label-setting algorithms. The method is based on a standard dichotomic search that provides increasingly precise lower-bound sets.
The work in [22] develops two speedup measures for the algorithm presented in [12] using a well-defined stopping condition enabling the search to be terminated as soon as all efficient paths are found and searching the network bidirectionally. That is, dividing the search procedure into a forward search initiated at the origin node and a backward search initiated at the destination node.
Paper [23] develops a parallelized version of a label-setting algorithm for the MOSPP, enabling the calculation of the whole efficient solution set. The procedure is based on the generalization of a priority queue (designated as Pareto queue) for a multiobjective optimization purpose. The authors concluded that the implementation of the developed parallelized algorithm for the biobjective problem yields to an asymptotically lower computational load than the previous sequential type algorithms.
Paper [25] explores the possibility of strengthening the search when the portion of the Pareto front considered to be interesting for further exploration can be initially bounded. A dimensionality reduction technique is applied to label-setting algorithms, which reduces the number of dominance checks. Tests on the application of this technique to problems with three to five objectives are performed; significant reductions in time requirements were obtained. The work [27] addresses the BOSPP and introduces a label-setting algorithm with a dynamic update of the Pareto front. Different exploration strategies are proposed.
Paper [30] extends the ripple-spreading algorithm proposed in [62] for the single-objective shortest path problem of the MOSPP. The ripple-spreading algorithm is an exact method based on labeling, with an approach similar to the pulse algorithm [63] but which defines search areas for each node in order to limit the computation, instead of guiding it recursively. The new algorithm calculates all the efficient paths.
In [29], a label-setting algorithm is introduced for finding a minimal complete set of efficient paths for the MOSPP. The new algorithm is called the Multiobjective Dijkstra Algorithm (MDA). The size of the priority queue used to store the node labels is bounded by the number of nodes in the graph. The new management of the labels allows us to parallelize some of the subroutines. Paper [32] follows up this work, and it equips the MDA with A*-like techniques, with the goal of discarding uninteresting subpaths to be explored at early stages of the algorithm. A key issue is how to store the subpaths. Moreover, the priority queue used in the MDA is combined with a lazy management of paths outside the queue.
An exact algorithm for the MOSPP is developed in [31]. The described algorithm seeks to improve upon a label-correcting algorithm by enabling the removal of unnecessary nodes from the graph and by dynamically updating the bounds for the costs of partial paths.
The work in [34] describes an original algorithmic combination for a one node-to-many nodes MOSPP seeking to achieve a fast solution search. For this purpose, a modification of a multiobjective label-setting algorithm, operating on the cover graph and employing a dimensionality reduction procedure enabling swifter domination checks, is developed. The original procedure preserves the Pareto optimality of the solutions; in addition, it enables the incorporation of existing heuristics for achieving further efficiency improvements.
The authors in [33] introduce efficient, constant-time, dominance tests between labels in labeling algorithms for the BOSPP. The new dominance tests are combined with an algorithm based on the procedure A*.
Also [35] addresses a biobjective shortest path algorithm equipped with efficient pruning checks. In this work, different types of pruning techniques are highlighted, some of them known from the previous literature. The pruning operations are classified depending on the type (op-pruning, cl-pruning, old-filter, new-filter), the moment of their application (eager, early, lazy), and the use of dimensionality reduction. The early pruning technique is introduced, which reduces the computational overhead of lazy op-pruning and filtering.
Parametric techniques
Algorithms of this type compute efficient paths corresponding to supported nondominated solutions based on the scalarization of the objective functions. This scalarization depends on a parameter which varies in order to output the different solutions. It is often used as the first phase of the two-phase method described below.
In [21], a biobjective parametric solution framework is introduced based on an approximate label-setting algorithm for the parameterized and constrained single-objective subproblem. This method finds the supported efficient paths and a large percentage of non-supported efficient paths. In addition, a general projection scheme is proposed to decompose a multiobjective problem into a number of biobjective problems. The introduced parametric algorithm is polynomial in time.
Ranking techniques
Algorithms of this type rank paths in non-decreasing order of one of the objective functions and partition the set of efficient solutions into subsets, , by means of a dominance test, comparing each obtained path with the previous, and selecting the efficient ones. For the biobjective case, the search starts with the lexicographic shortest path with respect to and halts when the minimal value of is achieved.
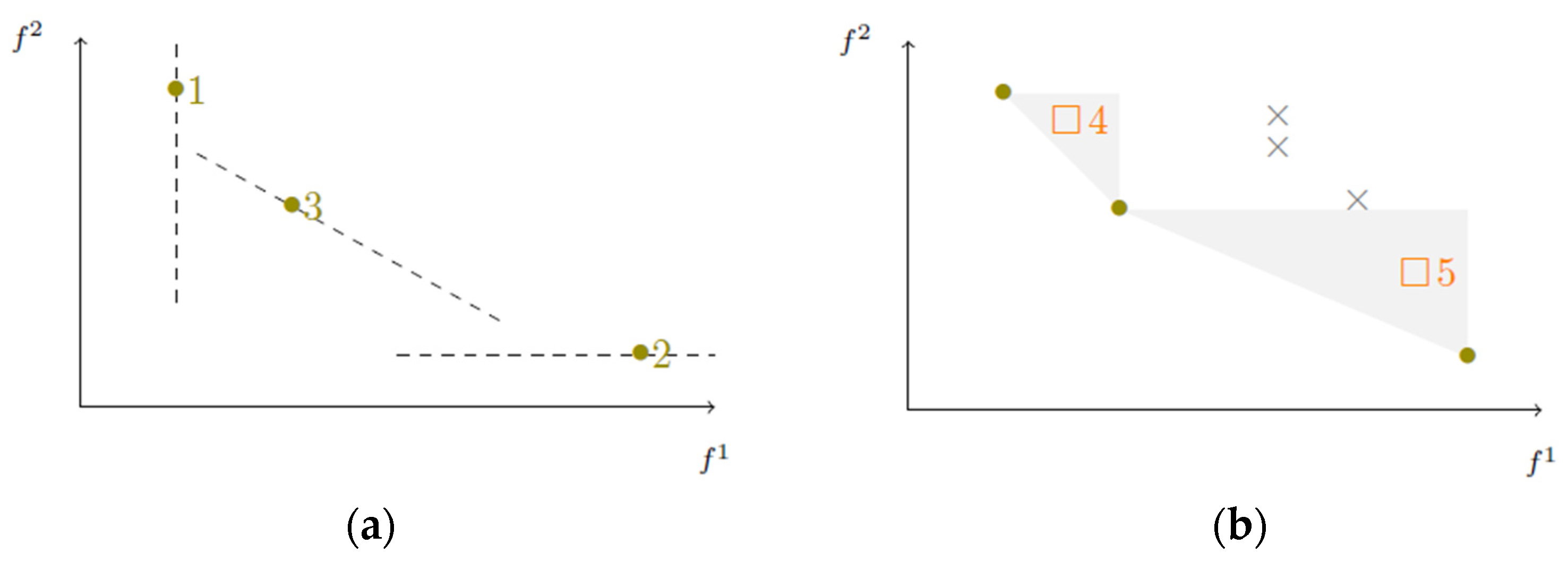
If paths are listed in non-decreasing order of , then the values of efficient paths appear in non-increasing order. The algorithm recurs to a set for storing temporarily any computed path while it is not dominated by any other, and there is no guarantee that it is efficient. Therefore, the algorithm stores in the paths that are candidates to be efficient, and the dominance test for compares with and with , where is the greatest value of for the paths previously determined, whereas is the lowest value of for the same paths. As paths are found in non-decreasing order of , either or . In the first case, is dominated by some other path if ; otherwise, is a candidate to be an efficient path, therefore it is inserted in . In the second case, the paths in are efficient, and is temporarily the only new efficient path candidate in and also the only element calculated so far from the elements in a new set . This technique is summarized in Algorithm 2, and it is illustrated in Figure 4.
| Algorithm 2: Generic biobjective ranking method | |
| Variables: Let be the set that stores potential efficient paths; the set that stores the efficient paths from node to node | |
| Summary: Firstly, the algorithm computes the optimal path with respect to each objective function, also providing , an upper bound on , for any efficient path . Then, the paths from to are listed by nondecreasing order of function and the dominance of each one is checked by comparing its objective function vector with , a pair formed by the worst value of function and the best value of function , respectively, for the paths previously analyzed. A path is included in in case it is not dominated; if it is dominated then it is discarded, and otherwise, it is temporarily stored in . | |
| 1 | for do shortest path with respect to the objective function |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | while do |
| 7 | if then |
| 8 | if then Insert path in set |
| 9 | else |
| 10 | if then |
| 11 | |
| 12 | |
| 13 | end if |
| 14 | end if |
| 15 | else |
| 16 | if then |
| 17 | Insert all the paths in in set |
| 18 | |
| 19 | end if |
| 20 | end if |
| 21 | next shortest path with respect to the objective function |
| 22 | end while |
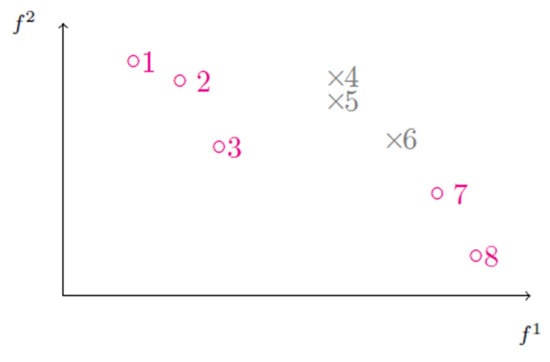
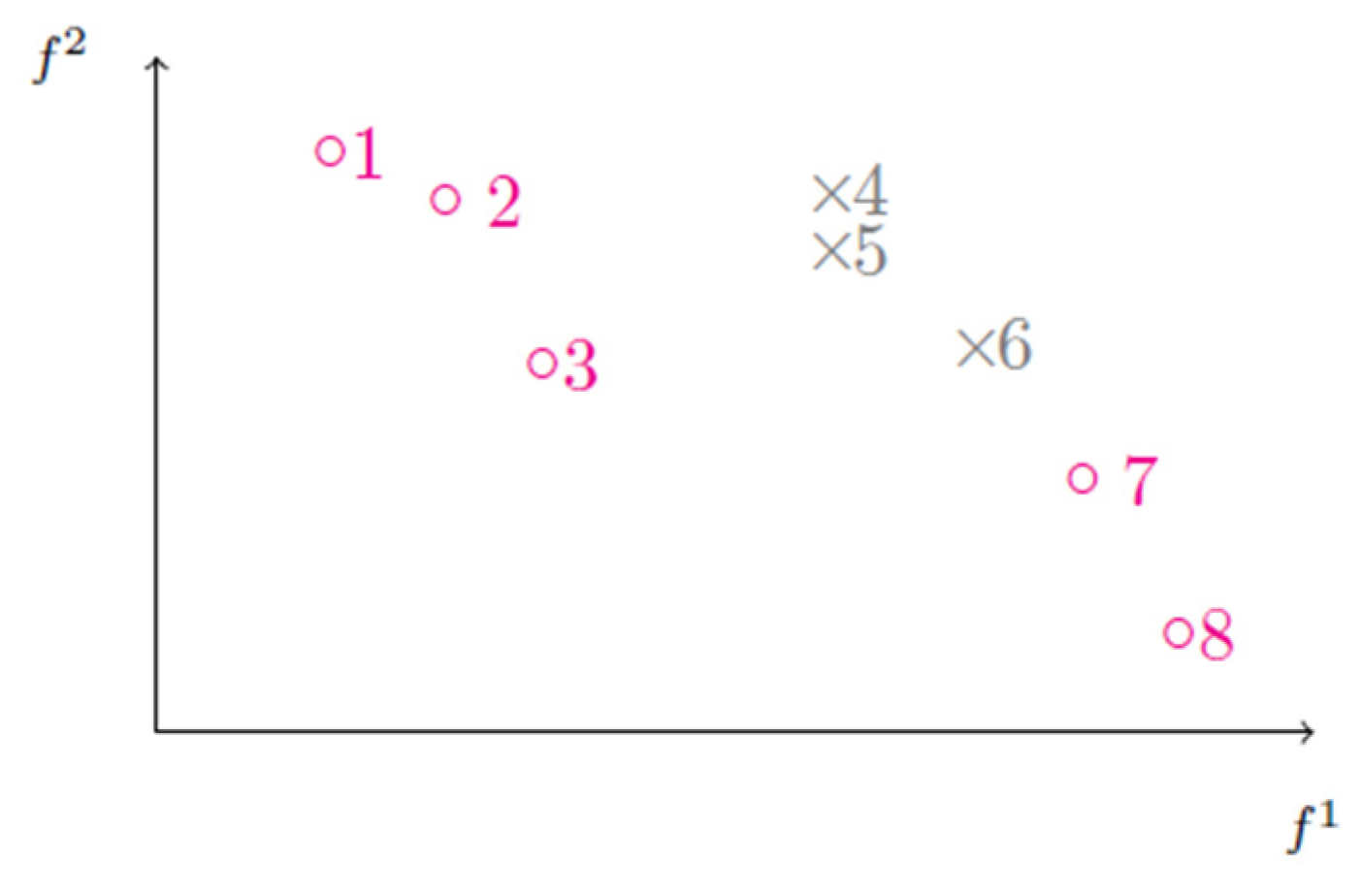
Figure 4.
Ranking technique according to the objective function . Magenta circles represent nondominated points; grey crosses represent dominated points; the numbers indicate the order of calculation of the different points.
Note that when there are more than two OFs, the test of dominance has to take into account all the cost values of the previously determined paths.
The initial proposal of this type of method used the ranking algorithm in [64]. The efficiency of the subroutine used for ranking paths is critical regarding the method’s performance since the dominance test and the stopping condition bound the number of generated solutions. Nevertheless, in the worst cases, the calculation of the complete set can require an exponential number of paths to be listed; although, the results in [65] showed that this limit is never reached for practical problems; the empirical results reported in the studies below also showed reasonable running times.
Path ranking methods can be classified into the following three groups:
- Deletion algorithms: After the shortest path calculation, a new network is constructed with all the original paths except the shortest ones. The repetition of this procedure enables the paths to be listed by order of cost. Various versions of this algorithm were proposed in [64,66,67]. The algorithm in [68] is a recursive method that calculates a new path by obtaining the best alternative to the current path to each node. This can be envisaged as a recursive variant of the method in [67].
- Labeling algorithms: If there are no cycles with negative cost in the network, the -shortest path problem satisfies an extension of the optimality principle, thus paths can be ranked by using labeling methods. To do so, a label is made to represent a path from up to a certain node and at most labels have to be stored for each network node (see [69]).
- Deviation algorithms: In these algorithms any path from to is the deviation from a shorter path, split into an initial subpath common to both paths, a deviation arc and the shortest path from its head up to . Since the shortest path from any node to can be calculated in advance by recurring to a shortest path algorithm, new candidate paths can be generated by selecting the next deviation arc, see [70,71,72].
Among the most efficient algorithms for ranking loopless paths, we cite the deviation algorithms in [71,73,74,75].
Next, we summarize some representative papers using ranking techniques for multiobjective shortest path problems.
The work [9] presents computational experiments for the MOSPP, considering labeling and ranking approaches, in random instances. For two or three objectives, the label-correcting implementation using a first in–first out (FIFO) approach outperformed both label setting and the deletion ranking method in [66]. However, for a small set of tests, a similar implementation using the algorithm in [71] was faster than the remaining ones. Paper [18] deals with a BOSPP with additional constraints, which imposes that paths cannot exceed a maximal bound concerning an additive metric. The work reports experiments where the label setting method is faster than the ranking method using the algorithm in [71]. However, deviation algorithms are very flexible whenever additional constraints are imposed because the non-feasible paths can be discarded at an early phase.
The ranking method in [64] may be used to solve the MOSPP. In [11], it was used for a particular case with two objectives.
Two-phase techniques
These algorithms work in two phases, analogously to what is described in the context of interactive methods for the MOSPP in [36] and in a general biobjective optimization problem context in [76].
In phase 1 of the algorithm, extreme, supported efficient solutions are calculated very often by solving single-objective weighted shortest path problems. In phase 2, the remaining supported and non-supported efficient solutions are calculated by enumeration. Note that, in phase 2, the search space of the solutions is restricted to the duality gaps. Therefore, those problems can be solved faster than by applying pure enumeration to the BOSPP.
The unimodularity property of the constraints is used by [14] in the considered linear programming formulation of the BOSPP. The proposed method solves a parametric shortest path problem for finding the efficient supported solutions. The unsupported solutions are obtained with a label correction method. This approach is illustrated in Figure 5.
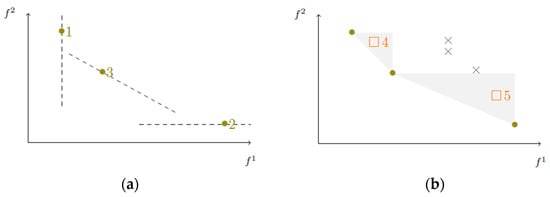
Figure 5.
Two-phase techniques: (a) Phase 1: calculation of supported efficient points; (b) Phase 2: calculation of unsupported efficient points. Green bullets represent supported dominated points. Orange boxes represent unsupported dominated points; grey crosses represent dominated points; the numbers indicate the order of calculation of the different points.
Recursive methods
An exact recursive algorithm (considering non-negative arc costs) is proposed in [24], using implicit enumeration based on the ‘pulse algorithm’ for the constrained shortest path problem given in [63]. Different types of pruning are applied: pruning paths with cycles, pruning based on a dominance test, pruning Nadir points based on upper bounds for each objective function, with both techniques being used in complete and partial paths. These procedures are particularly suited for implicit enumeration. This method is also extended to more than two OFs.
- (b)
- Minimal complete set computation
Labeling techniques
A generalization of Dijkstra’s algorithm to the biobjective shortest path problem is presented in [28], by keeping only one candidate label per node in a priority queue of size . Thence, a novel algorithm for the one node-to-all nodes BOSPP, enabling the determination of all the nondominated points in the objective function space and one efficient path associated with each of these points, is introduced. For the one-to-one BOSPP, the classical bidirectional search scheme is incorporated into the procedure. The proposed procedure also involves pruning strategies so that the computation of unnecessary labels is avoided.
2.2.1.2. INT—Interactive Methods
Paper [36] describes an interactive method for obtaining an approximation to the efficient solution set for the BOPP. The goal of the method is to assist the DM in the selection of the preferred/best trade-off solution within the efficient solution set, working in two phases. The first phase recurs to a Non-Inferior Set Estimation (NISE)-like procedure (enabling a specific order of calculation of supported efficient solutions) [77]; in the second phase of the method, a constrained shortest path problem is solved, enabling a search in specified duality gaps, see [78].
In [37], an interactive method for the BOSPP, which obtains the optimal solutions for a quasi-concave and non-increasing utility function defined by the DM, is proposed. In the first step, the DM evaluates OF values for supported efficient paths. The search region is reduced by carrying out pairwise comparisons until it is defined by two adjacent solutions in terms of costs. Afterwards, a labeling algorithm is applied to the obtainment of the non-supported nondominated points, while the domination cones derived from the pairwise comparisons carried out by the DM cause the search area to shrink.
Paper [38] proposes an interactive method by showing that, given an acyclic network and a preference-order relation, the principle of optimality is valid if and only if the preferences are linear functions with respect to the objectives. It is suggested to use an interactive method for assessment of a value function while using the principle of optimality in the search for an optimal solution. Furthermore, in this process, the DM is asked about the compromises between solutions or to sort paths according to his/her preferences.
The authors in [39] describe an interactive method for finding efficient biobjective shortest paths which is based on the proposal in [36], but now, in phase 2, the ranking of paths is performed, instead of solving constrained shortest path problems.
Paper [42] deals with an application of the MOSPP in the context of cycling routes, and it develops a method focused on finding a well-balanced trade-off path between the objectives. The algorithm follows the Best Compromise A* method, the goal of which is to find a path that minimizes a Chebyshev-weighted norm considering a given reference point. The algorithm follows a labeling approach and includes pruning techniques to enhance its computational performance.
2.2.1.3. APR—A Priori Aggregation of Preferences Methods
Next, we summarize more recent or particularly relevant references on a priori aggregation of preferences methods for MOPPs.
Paper [40] proposes a method that uses different metrics as utility functions based on the norm value associated with each path. Two algorithms for solving the minimum-cost path problem for the proposed metrics are then described.
The authors in [44] introduce an exact label-setting algorithm that obtains the subset of efficient optimal paths which satisfy a set of lexicographic goals, or the subset which minimizes deviation from goals whenever these cannot be fully satisfied. In particular, given an a priori set of goals, the work addresses the problem of finding the subset of Pareto optimal paths which satisfy the goals or, if these cannot be satisfied, finds the subset of Pareto optimal paths which minimize deviation from the goals. This is achieved by means of a multiobjective label-setting algorithm with lower bounds and label expansion that obtains such goal-optimal solutions.
Concerning the works [46,79], the first paper addresses the ‘resource-constrained shortest path problem’, the aim of which is to obtain the shortest path under constraints corresponding to upper bounds on resource consumption along the path. A new resolution method, based on the reference point methodology, is described. Furthermore, the concept of the Chebyshev distance is used for obtaining models and methods enabling upper and lower bounds on the consumption of resources along the paths to be found. The second work addresses the MOSPP and applies a reference point method using a non-additive scalarizing function for finding the ‘best Pareto optimal path’ according to the considered preference-based approach. For this purpose, a reference point-based constrained shortest path problem is formulated. A two-phase method is described for its resolution where, in the first phase, a bound on the optimal solution is computed and used to define the constraints, whereas in the second phase, a labeling algorithm is applied to search for an optimal solution. The proposed method is applied to grid networks.
In [41], a method of analysis of efficient solutions enabling the automated ordering and selection of solutions of a MOPP is proposed and applied to a telecom network routing model based on a BOSPP formulation as it will be referred to in Section 3. The described algorithm is based on a reference point approach such that the paths in a specific priority region in the OF space are ranked by non-decreasing order of a weighted Chebyshev metric. The priority regions are specified from preference thresholds that represent requested and acceptable values previously defined for each OF.
Paper [45] introduces a hybrid method for a MOSPP seeking to generate an efficient path which fulfils the decision maker’s preferences. The method takes advantage of common weights methodology to define the relative importance of some of the objectives, which results in a single-objective shortest path problem.
2.2.2. MOPP with Other Objective Functions
The methods presented here are a posteriori aggregation of preferences methods. Maximal complete set computation and minimal complete set computation approaches are included in the following paragraphs.
In Table 2, we present a summary of some essential features of exact algorithms for the MOPP with non-additive metrics referred to in this subsection by indicating the number of OFs of the addressed problems.

Table 2.
Summary of some essential features of exact algorithms for the MOPP with non-additive metrics.
Table 2.
Summary of some essential features of exact algorithms for the MOPP with non-additive metrics.
| Reference | # Objectives |
|---|---|
| (Martins 1984) [80] | |
| (Current et al., 1985, 1988) [81,82] | |
| (Current et al., 1987) [83] | |
| (Pelegrín and Fernández 1998) [84] | |
| (Gandibleux et al., 2006) [85] | |
| (Pinto et al., 2009, Pinto and Pascoal 2010) [86,87] | |
| (Iori et al., 2010) [88] | |
| (Bornstein et al., 2012) [89] | |
| (Pascoal et al., 2013) [90] | |
| (Torchiani et al., 2017) [91] | |
| (Pascoal 2018) [92] |
- (a)
- Maximal complete set computation
In [80], BOPPs having at least one maxmin objective function are addressed. The other OF can either be of that type or be a minsum or minratio type function. Two algorithms are proposed: the first one enabling the minimal complete set of efficient paths to be found; the second one enabling the maximal complete set to be obtained. Both algorithms can be utilized as long as there is an OF of maxmin type and an algorithm is available for determining the best solution for the other OF. The minimal complete set can be computed in a time of , being the number of maxmin objectives and being the number of operations needed to calculate an optimal path. The papers [81,82] define the maximum covering/shortest path, the minimum covering/shortest path and the maximum population/shortest path problems, the latter being a special case of the former. The problems are formulated as biobjective integer programs. The paper also presents a summary of the results obtained for a sample problem concerning the latter formulation. Also, variants and applications of both problem formulations are shown. Note that these formulations extend the concept of ‘coverage’ used in facility location analysis to network design and routing analysis. The work in [83] puts forward the median shortest path problem (MeSPP), a BOSPP, the objective functions of which are the path length and the travel time required for the demand to reach a node on the path. An algorithm is proposed incorporating a ranking path procedure for identifying efficient solutions. The work in [88] addresses the multi-objective shortest path problem with sum and bottleneck objective functions and introduces a weighted sum aggregate ordering of the labels to be incorporated into label-setting algorithms.
- (b)
- Minimal complete set computation
The authors in [84] address the minsum–maxmin path problem. This work shows that the quickest path problem (QPP) (see Section 2.2.3) is equivalent to a weighted shortest path problem associated with the defined problem. An algorithm enabling the calculation of some specific efficient paths of the minsum–maxmin path problem, based on [93], and a resolution procedure for the QPP (that coincides with the one introduced in [94]) are presented.
In [85], an extension of the label setting algorithm in [12] for the MOPP is presented. This extended version handles one more maxmin OF, , besides the minsum objective functions, , and obtains the efficient paths from to the other nodes. Note that given paths between a given pair of nodes, weakly dominates if , for , and . Thence, the classical version of the optimality principle is not valid in this case because efficient paths may contain weakly efficient subpaths, and consequently, a new dominance test is necessary.
The works [86,87,89] address path problems with two OFs of maxmin type, and a third OF of any kind, assuming that the optimal solution with respect to that function can be found. In the first paper, a polynomial algorithm is presented enabling the generation of the minimal complete set by computing the optimal path in any subgraph where the set of arcs is constrained according to the maxmin values. The second paper seeks to improve the former method by considering the OF values of previous paths to skip some maxmin values, thence reducing the number of subproblems. The same strategy can be applied to other network optimization problems. A labeling procedure for the addressed problem is also developed as a variant of the first procedure which aims at choosing the solutions with the best maxmin value when the cost remains the same. It is shown that the time bound for the first type of algorithms is , being the number of distinct values for each maxmin OF and being the number of operations necessary to obtain the single source–single destination shortest path. As for the labeling procedure, it has time complexity of . Finally, the third work generalizes the algorithm for more than two OFs of maxmin type.
Paper [90] considers a BOPP where two parameters, namely an additive cost value and a label, are assigned to each arc. The first OF of the problem seeks the minimization of the path cost, whereas the aim of the second OF is to obtain the path with a minimal number of different labels. Two algorithms are presented that generate a set of efficient paths. One of the algorithms finds the shortest paths in a sequence of subnetworks of the original one, setting different lower bounds for the number of labels, together with a dominance test for the solutions. The other one uses a breadth-first search (BFS) tree of label combinations together with the calculation of the shortest path associated with each tree node.
The authors in [91] address the shortest path with a shortest detour problem, a problem in which the first OF is the path length (to be minimized), and the second OF (also to be minimized) is the maximal length of a detour path whenever the chosen path is blocked. The relation of this problem to robust optimization is highlighted, and a polynomial time resolution algorithm is proposed, enabling the computation of a minimal complete set of efficient paths. Moreover, it is shown that the number of arcs in the graph is a bound for the number of nondominated points.
In [92], BOPPs are considered, involving the number of hops (or arcs) of a path as one of the OFs and either the path additive cost or the path capacity as the other OF. Labeling algorithms are proposed, which utilize a breadth-first search tree for finding the maximal and the minimal sets of efficient solutions. Dominance rules are derived, and the properties of the used data structure are explored to better suit the number of hops enabling a simplification of the labeling process. For both problems, the minimal complete set can be found in a time of .
2.2.3. Other Specific Path Problems Involving Two Functions
Next, we overview some specific path problems involving two functions. In Table 3, a summary of some essential features of the exact algorithms of the type referred to in this subsection are shown.

Table 3.
Summary of some essential features of exact algorithms for other specific path problems.
Table 3.
Summary of some essential features of exact algorithms for other specific path problems.
| Reference | # Objectives | Problem Type |
|---|---|---|
| (Martins 1984) [95] | minsum/maxmin | |
| (Ahuja 1988) [96] | minsum/max reliability | |
| (Chen and Chin 1990) [97] | quickest | |
| (Rosen et al., 1991) [93] | quickest | |
| (Hansen et al., 1997) [98] | min(max-min) | |
| (Martins and Santos 1997) [94] | quickest | |
| (Boffey et al., 2002) [99] | quickest | |
| (Captivo et al., 2003) [100] | knapsack | |
| (Park et al., 2004) [101] | quickest | |
| (Soroush 2008) [102] | minsum/minsum | |
| (Clímaco and Pascoal 2009) [103] | disjoint path pairs | |
| (Figueira et al., 2010) [104] | knapsack | |
| (Laporte and Pascoal 2011) [105] | minsum with relays | |
| (Calvete et al., 2012) [106] | quickest | |
| (Ruzika and Thiemann 2012) [107] | quickest | |
| (Ghiani and Guerriero 2014) [108] | quickest | |
| (Sedeño-Noda and González-Barrera 2014) [109] | quickest | |
| (Calvete et al., 2017) [110] | quickest | |
| (Pascoal and Clímaco 2020) [111] | shortest disjoint path pairs | |
| (Moghanni et al., 2022) [112] | -shortest dissimilar paths |
- (a)
- Minimal cost–capacity ratio path problem
Paper [95] addresses the minimal cost–capacity ratio path problem by developing a polynomial time algorithm enabling a path from to , which minimizes the cost–capacity ratio to be calculated. The objective function of this problem is as follows:
The proposed algorithm is based on the resolution of the corresponding minsum–maxmin biobjective path problem.
- (b)
- Minimal cost–reliability ratio path problem
Paper [96] addresses the minimum cost–reliability ratio path problem that seeks the determination of a path from to which minimizes the following objective function:
Parametric programming is used (taking into account that the optimal solution to this problem is an efficient path for a biobjective path problem), thence enabling the enumeration of the solutions. A specific sufficiency condition is applied to cut down the enumeration process.
- (c)
- Linear fractional path problem
Paper [102] addresses the linear fractional path problem, the aim of which is the calculation of a simple path between and that minimizes
An exact method for finding an optimal simple path when arc costs associated with the functions in the numerator and denominator are non-negative is proposed. The algorithm uses specific multiobjective optimization related techniques like path preference structures and elimination techniques enabling partial paths that cannot be part of an optimal path to be discarded.
- (d)
- Quickest path problem
The goal of this optimization problem is to find a path that minimizes
for a given .
In a telecommunication network routing context, the function gives the total transmission time of data units between nodes and along path , and and denote the expected delay and the bandwidth (transmission capacity) of arc , respectively. This problem (QPP) was introduced in [113], and a survey on this topic is in [114].
The authors in [97] noted that for constant arc capacities, the QPP is reducible to the shortest path problem. For this purpose, the original network is transformed by creating subnetworks of the original one, with different fixed-capacity lower bounds. The paths in the extended network correspond to the paths from the origin to in with a given capacity; therefore, one of the shortest paths from node to any of the new terminal nodes must be the quickest one. The consideration of different levels for each defined capacity value implicitly solves the problem as a biobjective problem; this is achieved by fixing one of the OF values and obtaining the best path with respect to the other OF. This algorithm runs in a time of and uses memory space of , where denotes the number of values of arc capacities.
In the methods proposed in [93,94], different variants of the resolution strategy are used. In the first paper, the algorithm computes the shortest paths in a sequence of specific subnetworks of the original one, considering fixed lower bounds of the arcs capacity. These subnetworks are obtained by eliminating the arcs with a certain capacity, as new paths are being determined. Like in the previous method, this procedure implicitly solves a biobjective problem. In the second work, the QPP is approached from a biobjective perspective and applies the algorithm for minsum–maxmin problems in [80]. The outcome is very similar to the latter resolution method. These algorithms enable the reduction of the memory space complexity to . In [99], it is noted that the set of arcs of each subnetwork in the sequence used by [93] is always a subset of the previous one, thus a proposal to replace some resolution procedures of the shortest path problem by a simplified version of Dijkstra’s algorithm is put forward. Empirical tests do not demonstrate a significant enhancement in the efficiency of the algorithm.
A label-setting algorithm for obtaining the quickest path is described in [101]. The original network is transformed into another one satisfying an optimality property such that each subpath of a quickest path is also a quickest path. The proposed algorithm avoids enumerating non-efficient paths which have a total transmission time greater than the minimum.
The work in [106] presents algorithms for the quickest path problem and for a related problem seeking the identification of the quickest path, the reliability of which is above a given threshold. The algorithms use an enlarged network like the one proposed in [97] but that considers the number of items to be transmitted. Two approaches are presented for the second problem. The first proposes paths to be ranked in nondecreasing order of transmission time so that the first one which satisfies the reliability constraint is selected. The second approach recurs to an enlarged network and the problem is modified in terms of a constrained shortest path problem.
Minmax versions of robust quickest path problems are proposed and investigated in [107]. The authors propose exact algorithms or fully polynomial-time approximation procedures depending on the complexity of the addressed problems.
In [109], a label-setting algorithm for the quickest path problem is proposed. The algorithm is based on the property that the optimal solution to the problem corresponds to a supported nondominated point in the objective function space of the minsum–maxmin BOPP; note that the procedure does not require enlarging the network representation.
As for [108], it describes a resolution procedure based on obtaining a lower bound of the time-to-target for the QPP, a bound which is embedded into an A* algorithm.
Paper [110] addresses a variant of the quickest path problem in which each arc is associated with the energy consumed during the transmission along the arc, while each node is assigned with a limited power to transmit messages. The aim of the energy-constrained quickest path problem is to obtain the quickest path, the nodes of which can support the transmission of a message of a known size. Algorithms are proposed for this problem as well as to find the complete set of efficient paths for the problem in which the OFs are the transmission time and the total used energy.
- (e)
- Minimum range and ratio path problem
In [98], a study on the following path problems is presented: minrange problem, the aim of which is to find a path with the smallest range of arc lengths, , and the minratio problem, the goal of which is to calculate a path for which the ratio of the largest to the smallest arc length is minimum, that is, with the following objective function:
The optimal solution to these problems is an efficient minsum–maxmin path. The proposed algorithms are based on the enumeration of candidate paths in decreasing order of the objective values, skipping those paths with an OF value greater than or equal to the best known so far. The described algorithms have a time complexity of in directed networks and in undirected networks. The paper also investigates biobjective extensions of these problems.
- (f)
- Knapsack problem
The works [100,104] study the performance of new labeling algorithms devised for finding all of the efficient solutions of the multiobjective integer knapsack problem. The algorithm proposed in the first paper takes advantage of the conversion of the 0–1 knapsack problem into a BOPP over an acyclic network. The second paper describes a generic labeling algorithm for finding all efficient solutions of the multiobjective integer knapsack problem. This algorithm is based on the resolution of the MOPP on an underlying network. Algorithms devised for defining four network modes representing the problem are proposed.
- (g)
- Disjoint path pair problems
Paper [103] proposes an exact method for calculating efficient biobjective shortest pairs of disjoint simple paths. The resolution approach is based on an algorithm for ranking pairs of disjoint simple paths in non-decreasing order of cost [71], which constitutes an adaptation of a path ranking algorithm application to a network obtained from the original one after a specific duplication of the topology. Each path in this transformed network corresponds to a pair of paths in the former one. The obtained listed paths are then put through an effective dominance test. The work in [111] uses an analogous approach for finding pairs of paths that simultaneously minimize the number of arcs that they share and the total cost of the two paths. The performance of the proposed method is assessed also when applied to obtain efficient solutions close to the maximally disjoint path pair (that is, quasi-disjoint pairs, for a given admissible relaxation value).
- (h)
- Shortest path problem with relays
The work in [105] studies the minimum cost path problem with relays (MCPPR). This problem consists of obtaining a shortest path from to , with a resource weight constraint. In order to fulfill this constraint, the path nodes can be utilized as relays, resetting the transported weight to while generating a node-dependent cost. The MCPPR is formulated as a BOPP involving an aggregated function of the path and relay costs and a weight function, dealing with a variant which takes all three functions separately. The paper presents labeling algorithms in which , the bound on the weight of paths, determines the number of node labels. The proposed algorithm for the constrained single objective function version has a time complexity of . Furthermore, the algorithm is extended to consider two additive OFs: the path cost and the relay cost.
- (i)
- Dissimilar paths problem
The problem of finding sets of paths with minimal cost and maximal dissimilarity between them is addressed in [112]. Integer linear formulations for the problem are provided, and an -constrained method to solve them is proposed.
2.3. Approximate Methods
Given their difficulties, NP-hard optimization problems are often approached by approximate methods which work fast while looking for sets of solutions that approximate the efficient ones. Even if shortest path problems can be solved efficiently, when several objectives are considered or the solutions are subject to additional constraints, the instances become harder and, in such cases, exact methods may not be very successful.
An early work concerning an approximate method for solving the MOSPP is [115], where the author proposes a fully polynomial time approximation scheme (FPTAS) to find an approximation to the set of efficient paths. The basic foundation of this algorithm is to use an upper bound on the cost of the paths for every OF, enabling the OF space to be divided into cells such that their size grows exponentially and applying an efficient exact pseudopolynomial algorithm to each cell, namely the algorithm in [12]. The work [116] also introduces a FPTAS for the multiobjective shortest path problem with non-negative and integer arc costs. The algorithm combines a labeling algorithm and a FPTAS proposed in an earlier work by [117]. More recently, [118] proposes an approximation method framework for solving the MOSPP based on three speeding up strategies for labeling algorithms. The authors present a comparison performance study of the proposed approximate methods with other approximate procedures and with exact algorithms, considering random and reference test networks in combinatorial optimization and real-type German power grid networks.
Paper [119] addresses the dynamic MOSPP, which considers arc costs that may vary. It develops an exact algorithm under a FIFO assumption that is used as a starting point for an FPTAS for both the static MOSPP and its dynamic variant.
Several heuristic and metaheuristic approaches have been used to solve some multiobjective problems that are formulated in the context of telecommunication network routing design, as illustrated in more detail in some references in Section 3. Here, we highlight some of these metaheuristics. Two resolution approaches of a multiobjective routing model based on simulated annealing and on tabu search are proposed and tested in [120]. Simulated annealing (SA) has been widely used to solve different optimization problems. It is based on an analogy with the annealing phenomenon in physics, which involves heating and then slowly cooling (in a controlled manner) a material, which will change its physical properties. This technique, in single objective problems, requires a fine tuning of its parameters, so that it may lead to approximate solutions to the optimal solution. Tabu search (TS) is also a widely used metaheuristic procedure in different optimization problems. It is a local neighborhood search technique. In single objective problems, it tries to diversify the areas of the solution space that are explored. This is achieved by an intelligent guidance into those areas by forbidding some moves and allowing the solutions to become worse (i.e., it is possible to escape local optima).
Concerning simulated annealing approaches, next we add two references dedicated to MOPPs [121,122]. These papers investigate an oriented spanning tree (OST)-based simulated annealing for solving the MOSPP as well as the multiobjective constrained shortest path problem, especially for those with non-linear OFs. The test results are compared with those obtained by a recent Evolutionary Algorithm (EA).
Genetic algorithms and EAs are often used to solve multiobjective routing optimization problems. Some examples are in [123,124,125,126]. These algorithms are based on the idea behind the evolution theory by Charles Darwin, such that the resolution procedure mimics the natural selection observed in nature. Different solutions (represented by chromosomes) are found through the application of operations of crossover and recombination, mutation, and selection.
We add some relevant papers on this subject: Non-dominated Sorting Genetic Algorithm II (NSGA-II) [127], Strength Pareto Evolutionary Algorithm 2 (SPEA-2) [128], the Multi-Objective Ant Colony System (MOACS) [129], and Multi-Objective Particle Swarm Optimization (MOPSO) [130]. Furthermore, recent relevant references dedicated to MOPPs are now mentioned.
Papers [131,132] present an evolutionary algorithm for a MOPP in undirected networks. The algorithm differs from the evolutionary algorithms for more general multiobjective optimization problems as it uses an external set to maintain efficient solutions and a different selection strategy.
There is a diversified range of Artificial Intelligence (AI) techniques that may be used for multiobjective optimization problems in this area. An example is in the paper [133], where the authors apply Deep Neural Networks (DNN) and Fuzzy Inference Systems (FIS) to solve a multiobjective Route and Wavelength Assignment (RWA) routing model for Elastic Optical Networks (EONs). In the case of DNNs, they try to mimic the way in which information is processed by the human brain, in order to learn more information and use it to make meaningful decisions. As for FIS, these are systems that use a set of rules (based on fuzzy set theory) to establish relations between features (inputs) and classes (outputs). At the core of this technique lies a reasoning mechanism based on the rules or guidelines, which tries to infer an acceptable output in the context of a problem.
Another example of a metaheuristic applied in this area is the greedy randomized adaptive search procedure (GRASP), used in [134]. This technique starts by (i) generating greedy randomized solutions, i.e., it is based on random solutions, the quality of which is assessed, and the more promising solutions are greedily selected; (ii) afterwards, there is an attempt to improve the considered solutions through a local search procedure.
2.4. Path Problems Dealing with Uncertainty—An Outline
The classical single objective or multiobjective path problems assume that the parameters associated with the arcs are deterministic. However, setting the parameter values is often very difficult, since these values may be subject to several sources of uncertainty and/or imprecision.
Having in mind that path problems dealing with uncertainty/imprecision are not in the core subject of this work, we just briefly refer to shortest path problems involving probabilistic network parameters and to cases where the imprecision of parameters is modelled using fuzzy sets or rough sets.
- (a)
- Stochastic Path Problems
In the work in [135], the authors develop a method for solving a stochastic multiobjective shortest path problem and present an application to a hazardous material transportation case. In [136], a biobjective path problem on a directed multigraph with cycles is studied, where each arc is associated with a survival probability of moving along the arc parameter and the length of the arc. The authors intend to maximize the path survival probability, and to minimize the path length. As it involves the resolution of a NP-complete problem, even in the acyclic case, approximation algorithms are developed. The papers [137,138] deal with an uncertain MOSPP in a ‘weighted connected direct graph’ where two uncertain parameters, cost and time, represented by uncertain variables are associated with the arcs. The authors proposal consists of solving the deterministic transformations of two models. Namely, an expected value model and a chance constrained model of the multiobjective uncertain shortest path problem. Furthermore, the deterministic models resolution uses two multiobjective genetic algorithms, namely nondominated sorting genetic algorithm II (NSGA-II) and multiobjective cross-generational elitist selection, heterogeneous recombination and cataclysmic mutation (MOCHC).
- (b)
- Imprecision in Shortest Path Problems
A shortest path problem on a network in which fuzzy numbers are assigned to the arc lengths is addressed in [139]. An order relation between fuzzy numbers is introduced, allowing us to build an auxiliary problem which enables a resolution for the fuzzy shortest path problem to be derived. The auxiliary problem consists of the calculation of the efficient paths set of a MOSPP, based on the order relation between fuzzy numbers referred to above. Other variants of this problem have been approached in [140,141]. Paper [137] deals with a multiobjective path problem in a directed network, and the associated arc weights are represented as rough variables in order to model the imprecision. The proposed problem resolution involves a modified rough Dijkstra’s labeling algorithm; or, alternatively, a method which considers a rough chance constrained programming technique solved by a Goal Attainment Method and the NSGA-II.
3. Applications to Communication Network Design
3.1. Background Concepts
We should note that the mathematical formulation of a routing model (envisaged as a logical-mathematical system encompassing the assumptions and mathematical entities which enable an unequivocal specification of the route/path calculation and selection problem in a given network environment) typically considers a network representation in terms of a capacitated graph and, in many models, a matrix of node-to-node expected (average) offered demand.
If we wish to have a more complete representation of the factors of the network environment associated with routing methods, then traffic flows (in fact of a stochastic nature), a more general representation, through a ‘teletraffic network’, composed of several mathematical and other logical entities (see e.g., [1,142]), should be used. Furthermore, the nature of real communication networks is very complex, since they are organized, from the point of view of the functional, operational and control/management aspects, in several interrelated layers, which leads to the necessity of considering them as multilayer network structures. An Internet network, for example, in a limited national area, has at least three layers, namely the physical infrastructure (or physical layer, including coaxial cables, optical fiber cables and microwave links), the router topology layer (corresponding to the logical layer) and the third layer (corresponding to the representation of application level and possibly social network flows). This often raises difficult modelling issues in the development of adequate/realistic routing models in a given application context which can have an impact on the mathematical formulation of the path problem(s) defined as a nuclear part of the routing model.
The formulation of the routing models is strongly dependent on various aspects, mainly (i) basic features of the network communication technology (for example, whether it is circuit-switched or equivalent, packet-switched, as in technologies based on IP, or hybrid); (ii) the underlying routing principles (such as static, dynamic, fully distributed, centralized, on-line or off-line routing methods); (iii) the network architecture (for example, IP-over MPLS over WDM); (iv) the QoS features of provided services and service classes, including resilience/protection requirements; (v) the computing capability and network information provided to the route calculation devices (such as switches in circuit-switched networks, routers in IP-based networks or optical-cross connectors in GMPLS optical networks); (vi) the network functional layer where the routing procedure is applied (for example, the logical layer, physical/transport layer or an intermediate layer); and (vii) end-to-end traffic management mechanisms (associated with bandwidth allocation throughout each path for different end-to-end service demands, as in routing methods with explicit bandwidth allocation or traffic splitting).
A general class of routing methods other than the basic class (usually designated as unicast routing where only one node-to-node route/path is calculated for each service demand) is multipath routing that involves the simultaneous calculation of several paths, between two nodes or between two sets of originating and terminating nodes. An important type in this class refers to routing models with explicit reliability requirements/optimization objectives, in which an active/primary path and a backup path/protection path (which will be used for actually carrying the end-to-end communication messages in the event of failure of the active path) have to be computed simultaneously for each pair of origin-destination nodes; this should not be confused with alternative routing (where a secondary path has to be computed and used when the primary or first choice path is blocked due to traffic congestion, typical of circuit-switched networks or of equivalent logical type). The routing methods with built-in reliability requirements are designated in general as resilient routing methods. Another class is designated as multicast routing for which a set of paths has to be calculated from the originating node to a set of destination nodes—point-to-multipoint routing (this is the situation typical of the distributional services supplied by a certain service provider)—or interconnecting two subsets of network nodes—a multipoint-to-multipoint routing model (for example in teleconferencing services in Internet). If all the nodes have to be interconnected, it is designated as broadcast routing and is formulated as a spanning tree problem. If the set of destination nodes is a proper subset of the set of network nodes, the associated multicast routing problem can be formulated as a Steiner tree problem, where the destination nodes and the originating node are the terminal nodes. These types of models using spanning trees or Steiner tree problem formulations are out of the scope of the present work.
Reference books focusing on concepts, techniques, models and algorithms concerning communication network routing methods and protocols for key types of telecommunication network technologies and architectures are [143,144].
3.2. Overview of Selected Papers
Hereafter, we present an overview of selected papers considered as representative of different types of applications in telecom network routing in the scope of this work. As mentioned above, we will distinguish, in each subsection, three types of contributions: those corresponding to routing models that use as primary resolution procedure algorithm(s) specifically dedicated to the calculation of solutions to MOPPs, including heuristics and metaheuristics (these will be referred to in Section 3.2.1); routing models which use instrumentally, as auxiliary resolution procedures, MOPP-dedicated algorithm(s), including shortest path and -shortest path algorithms (these will be referred to in Section 3.2.2); those models that involve explicitly, as the objective (but not necessarily the unique one) of the mathematical formulation, the calculation of paths that are solutions to MOPPs by recurring to Operations Research approaches which are not specifically dedicated to path problems, such as network flow, integer linear programming (ILP), mixed integer linear programming (MILP), non-linear programming (NLP) and other more general types of network optimization approaches that may be designated as ‘network wide routing optimization approaches’, in the sense defined in [145] and, in a multiobjective routing broad context, in [142]. This type of paper will be referred to in Section 3.2.3. Furthermore, throughout this overview we will give examples of contributions concerning different types of path solutions sought by the MOPP formulations referred to in each paper, namely single path node-to-node, path pair node-to-node and multipath node-to-node solutions. Note that each of these types of solutions corresponds to different types of routing models and may have different formulations that have to be contextualized in a particular network environment.
Finally, we refer to a few, specific routing models, where multicriteria path problems are formulated through a multiattribute decision approach using an a priori specification of the system of preferences through an empirical utility function. These approaches were proposed for simplified heuristic multiobjective routing procedures in WSNs and ad-hoc WNs using hop-by-hop routing protocols where the node computation capability is very limited, and the information provided to a node is limited to metrics of the adjacent links (corresponding to arcs of the network graph representation).
We would like to mention that in the late nineteen-nineties/early two-thousands, a new routing paradigm, designated as QoS routing, emerged as a result of the rapid technological evolutions, especially concerning IP-based services. This trend had to do with the need for the development of multiservice networks capable of dealing explicitly with different, heterogeneous QoS metrics. The associated routing models usually included multiple hard constraints or one objective function and several QoS-related constraints. As noted in [1], QoS routing models corresponding to constrained single objective path problem formulations may be considered as ‘first tentative of multicriteria routing modelling’ bearing in mind that a known approach to multicriteria optimization involves the transformation of the OFs into constraints, except one OF, which is to be optimized; in certain conditions, the calculated solution will be Pareto optimal for the associated MOPP which includes some of the former QoS constraint(s) as OFs [146]. This approach to the characterization of models, which should be considered as explicitly multicriteria, was also adopted by the authors in [3]. They propose a conceptual framework concerning the development of explicitly multi-criteria modeling approaches, for multicriteria QoS routing in IP-based networks and put forward a representative example of a routing model using achievement functions defined according to a reference point approach.
The shortest path problems associated with QoS routing models formally are not MOPPs and the number of papers in this area is very large. Nevertheless, we will refer to some relevant works on this type of routing models noting that most exact resolution approaches in this domain were based on shortest path and -shortest path algorithms, and also a number of proposed heuristics/metaheuristics were often based on those types of auxiliary exact algorithms. One of the earliest works in this area is the report [147] which presented an exact algorithm (referred to as constrained Bellman–Ford algorithm) for a constrained shortest path problem in QoS routing design, for calculating minimal cost paths with a delay constraint. It enables the obtainment of successive shortest paths for different values of the right-hand-side constraint on the delay, leading to efficient solutions. Bearing in mind the implicit bicriteria nature of this approach, we could remark that the bicriteria shortest path problem method in [11] could obtain a similar result by using a more efficient procedure.
An early state-of-the-art report on QoS routing up to 1999 is given in [148].
The author of [149] describes a unified treatment of several path calculation problem formulations in QoS routing models (including linear and non-linear objective functions such as in shortest path, widest path, widest-shortest path, most-reliable path and most-reliable shortest path problems) by proposing an ‘algebra of weights’, also enabling us to consider a specific requirement for the implementation of the corresponding hop-by-hop routing procedure on the Internet. For this purpose, it constructs a variant of the Dijkstra algorithm. A review on constrain-based QoS routing models can be seen in [150]. In [151], a formal analysis of complexity issues of the multiconstrained path problem, shows that this problem is NP-complete but not strong NP-complete and also explains reasons why in most practical instances of this problem, in communication network routing, exact resolution methods can be used. A study concerning the comparison of exact algorithms and specific heuristics (-approximation algorithms) for the multiconstrained optimal path problem in QoS routing is shown in [152]. An analysis of the relation between QoS routing problem resolution approaches based on Lagrangean decomposition and the optimization of linear combinations of the OFs (for example, average path delay and path cost) used in multicriteria analysis can be seen in [1] (Section 4.1.2.1).
It is also important to note that, in the context of packet-switched networks and IP-based networks, adequate versions of classical shortest path algorithms have been extensively used as the basis of routing algorithms associated with two classes of routing protocols. These classes are defined in terms of the type of information and information exchange that a node needs (and may need to pass to its neighbors) to compute the shortest paths. The first type comprises link state routing protocols such as Open Shortest Path First (OSPF) and Intermediate System to Intermediate System (IS-IS) which have been commonly used as Internet intra-domain routing protocols and typically use a distributed version of the Dijkstra algorithm. In this case, the current link metric values (arc costs) are to be known by the nodes, and nodes are informed about its changes in a distributed manner (link-state advertisement mechanism). The second type comprises distance-vector routing protocols—where a node needs to know the cost (or ‘distance’) from each of its neighbors to all destination nodes, so that a shortest path may be computed and typically use a distributed version of the Bellman–Ford algorithm. An important example is the Routing Information Protocol (RIP). Extensive analysis of the application of shortest path-based routing algorithms and related protocols can be seen in [143] (Chapter 7) and in [144] (Chapters 2 and 7). Also, an analysis of an NP-hard optimization problem, important in shortest path routing networks, called the ‘weight setting problem’ also designated as ‘shortest path routing allocation problem’, is put forward in these references. In this problem, one seeks the calculation, in a capacitated network, of the costs (or ‘weights’) which should be assigned to the arcs so that the node-to-node traffic demand volumes are carried, assuming that one or various shortest paths are used for any node-to-node connection, aiming at the optimization of a given network objective function, such as minimizing the average delay or the maximal utilized bandwidth in the network. Various basic variants of this problem have been considered in the literature, leading to mixed-integer programming formulations sometimes recurring to duality-based approaches also described in the mentioned references. These types of single-objective formulations and associated resolution methods will not be analyzed in our work. Nevertheless, we will refer to a few representative papers where multiobjective routing models based on shortest path routing methods have been developed.
3.2.1. Models That Use Straightforwardly Algorithm(s) Dedicated to MOPPs
Herein, we refer to representative papers on routing models that use primary resolution method algorithm(s) specifically dedicated to the calculation of solutions to MOPPs, including heuristics and metaheuristics. A summary of some essential features of these models is in Table 4.
In the review on QoS routing models [150], lexicographic formulations of related path problems are addressed, such that there is an a priori articulation of preferences in the path selection (including as optimization objectives bandwidth, delay and number of arcs (or ‘hop count’)) in the context of widest–shortest (where one seeks a path of maximal bottleneck bandwidth (or width) among those of minimal length from source to destination) and shortest–widest path formulations (where the aim is to find a shortest path among those of maximal bottleneck bandwidth (or ‘width’)). This type of lexicographic formulation was also addressed in [149], namely concerning widest–shortest path and most-reliable shortest path problems, by proposing the use of an algebra of weights. Paper [153] addresses techniques based on the derivation of partial order rules for implementation of state-vector routing protocols aimed at seeking lexicographic optimal path solutions in IP-based networks, associated with computation procedures based on shortest path algorithms. These mathematically based procedures are shown to be very useful for efficient heuristic lexicographic routing protocol implementations—designated as ‘dominant paths vectoring protocols’—namely, for widest–shortest path routing.
An example of an efficient combinatorial heuristic resolution for a lexicographic path pair optimization problem with maximal disjointness objectives for application to a resilient routing model in optical GMPLS networks involving the calculation of an active and a protection path (to be used in the event of failure of the active path) can be seen in [154]; the four OFs to be minimized (in this order of priority) are the number of common nodes, the number of common arcs, the number of common failure risks and the total cost of the two paths. The two proposed heuristics are based on extensions of the ‘Trap avoidance’ algorithm [155] and of the ‘weighted Shared Risk Link Group (SRLG) path selection’ algorithm [156]. A closely related lexicographic approach for resilient routing in optical networks is in [157] that addresses a biobjective lexicographic formulation of the protection routing path pair problem which involves the calculation of an active path and a protection path seeking to minimize the number of risks (corresponding to SRLGs) common to the two paths and the two paths cost (in terms of occupied bandwidths). An exact resolution algorithm which combines a path ranking procedure (using the -shortest path algorithm [71]) and a path labeling algorithm is proposed and compared with an ILP formulation in reference test networks.
Paper [158] tackles a problem of multiobjective -disjoint shortest (secure) paths, where the “length” of an edge is associated with information regarding the probability of attacks in a communication network. The multiple “lengths” of each edge are converted into a single “length” given by a weighted sum of “lengths”, where the weight for each criterion depends on the importance assigned to that specific criterion. The weights are defined in very distinct ranges, leading to a lexicographic approach. A generalization of the Dijkstra algorithm is used to devise prioritized multicriteria -shortest (secure) paths. For the specific value of , a prioritized multicriteria -disjoint (node/edge) shortest paths problem is proposed and solved by an approach based on the dynamic programming (DP) approach proposed in [159]. Finally, the problem of finding (if they exist) a set of (edge-)disjoint paths for a source–destination pair, such that each path is the shortest concerning each of the multiple criteria, is tackled and an algorithm is proposed to solve it.
In [160], the description of an application to an Internet stochastic packet routing method of the -quickest path algorithm in [161] is included. The objective function of the corresponding path optimization problem is the expected total transmission time given by the sum of total average delay (an additive metric) and the expected packet transmission time associated with the path bottleneck bandwidth (a non-additive metric) and is solved exactly by that deviation algorithm. The efficiency of the routing method is shown with a stochastic packet traffic simulator using a truncated Pareto distribution.
Note that this type of path ranking calculation method can be very useful in applications to single objective multipath routing and to multicriteria routing models where the path bottleneck bandwidth is a central optimization objective.
Concerning non-lexicographic MOPP formulations, which are the main focus of this work, we will begin by referring to [162]. It is, as far as we know, a first approach to an explicitly multiobjective routing model for telecommunication networks solved with an exact combinatorial algorithm. It presents a biobjective routing model seeking paths with minimal cost and average delay which corresponds to the formulation of a biobjective shortest path problem. This model can be adapted to different additive objective functions associated with different types of end-to-end services in multiservice networks. An exact resolution method was developed which computes efficient paths based on the optimization of weighted sums of the OFs by recurring to the very efficient -shortest path algorithm [71]. Furthermore, QoS requirements are represented in the model through ‘soft constraints’ (which are not directly included in the BOSPP mathematical formulation) concerning ‘acceptable’ and ‘requested’ values for each of those metrics. These values enable the definition of priority regions in the OF space where nondominated solutions can be searched for and can be used in the context of an automatic search procedure of a final routing solution. Paper [18] addresses a multiobjective routing model with two additive objective functions (routing cost in terms of the number of arcs and a ‘load cost’ associated with the available bandwidth in the arcs) and three QoS constraints concerning average delay, delay jitter and bottleneck bandwidth. This corresponds to the formulation of a biobjective constrained shortest path problem previously tackled in a telecom network routing design context by [163] using a rule-based heuristic based on the Dijkstra shortest path algorithm, a heuristic which does not guarantee that the obtained solutions are Pareto optimal. The authors in [18] present an exact resolution approach for calculating the whole set of efficient solutions for this problem by recurring to the biobjective shortest path algorithm in [11] and to the MPS algorithm in [71], for calculating -shortest paths having as objective function the convex combination of the two OFs of the problem. The use of a ranking algorithm in this context was shown to be the more efficient resolution approach (even in networks with up to a few thousand nodes) due to the explicit consideration of the mentioned QoS constraints of the biobjective problem. Note that this type of routing model, although originally formulated for video type traffic in the discontinued Asynchronous Transfer Mode (ATM) based networks, can be applied straightforwardly to current networks with packet-switch-based technologies (such as MPLS–Transport Profile, MPLS-TP) by simple adaptation of the pertinent QoS constraints.
A reference point approach to the important problem of selecting a Pareto optimal solution in the context of a multiobjective shortest path model for a network routing model, considering that the final routing solution has to be defined in an automated manner was presented in [41]. That proposal, in [41], uses an algorithm for minimizing a weighted Chebyshev distance to reference points specified in each priority region; this method is applied to a biobjective video traffic routing problem formulated as a BOPP with various QoS constraints.
A multiobjective routing model for the Internet using a multiobjective path formulation is presented in [164]; the model uses as path metrics number of arcs, total mean delay and residual bandwidth, and it is solved by an exact algorithm that obtains the set of efficient solutions for connections from one node to all the other nodes and a method for selecting a solution that uses a weighted Chebyshev distance to the ideal point. In [125], a multiobjective shortest path problem is also formulated, for application to a QoS routing model, that considers the metrics optimized maximal bandwidth and minimal delay. The MOPP is solved by a genetic algorithm.
The authors in [165] address a new multicriteria approach for routing in IP-based networks using the principle of “routing-as-a-service” such that users/companies may choose from a set of ‘path services’ offered by various network providers competing in an “open marketplace”. This leads to a routing model where paths are calculated and chosen dynamically from a biobjective time-constrained path problem seeking to optimize cost and expected delay under QoS and time-constrained requirements. The resolution method is a dynamic programming procedure that uses Yen’s -shortest path algorithm [73], enabling us to obtain efficient solutions for a given time interval partition, one to be chosen by the customer.
A key path problem in WDM optical network routing is the Route and Wavelength Assignment (RWA) problem which involves, in general, the calculation of lightpaths (topological paths in the optical transport networks) and the assignment of wavelengths to each arc (optical link) along a lightpath (a classic overview in this area is [166]). The work in [167] addresses a formulation of this problem as a multiobjective shortest path problem where the OFs are the number of arcs (optical links), the number of free wavelengths and the path blocking probability. Solutions are obtained with a shortest path algorithm applied to the weighted sum of the objective functions. In [168], there is the development of a biobjective path problem formulation for a RWA problem designated as dynamic lightpath establishment problem with incremental traffic with regards to the topological lightpath calculation subproblem. The first objective function is additive and expressed in the bandwidth usage of the path arcs, and the second is the number of arcs (or ‘hops’), both to be minimized. The exact resolution approach of this key subproblem uses a k-shortest path algorithm and preference thresholds for defining preference regions in the OFs space. The used topological lightpath is selected automatically by using a reference point procedure as in [41]. The choice of wavelengths along the lightpath is performed by a heuristic based on path wavelength bottleneck bandwidth.
The OFs considered in the first level are path costs and the number of arcs of the path, and the second level OFs are bottleneck bandwidth and the expected packet delay on the path. The model is solved exactly by calculating the Pareto optimal solutions of the first-level functions with an exact biobjective shortest path algorithm, which are “filtered” by using bounds defined through the second-level OFs.
Next, we will refer to applications of MOPP algorithms to multipath routing models.
Paper [169] proposes a multiobjective resilient multipath routing model for transport telecom networks, the aim of which is the simultaneous calculation of an active efficient shortest path seeking to minimize ‘load cost’ (an additive bandwidth related metric) and hop count and a maximally disjoint protection path; an exact resolution method is described which is based on a -shortest path algorithm, applied to the convex combination of the two OFs, enabling all supported and unsupported efficient solutions to be obtained. The work [170] presents a biobjective resilient routing model with path protection leading to the formulation of a biobjective maximally SRLG-disjoint/minimal cost path pair problem the aim of which is to minimize the number of risks, corresponding to SRLGs common to both the active and the protection path, and the path pair cost. An exact resolution method enabling the whole set of Pareto optimal solutions to be calculated, based on the algorithm which combines a path ranking method and path labeling in [111], is described and the performance analyzed in reference test networks.
In paper [171], the problem of finding the set of efficient solutions of a MOPP seeking the calculation of paths from one source node to different destination nodes is tackled, for application to cloud computing. The resolution process is based on the extension of a Pareto BFS method proposed in [172], with which it is possible to enumerate all paths from one source node to a destination node and uses a pruning strategy to readily identify the paths which are not efficient.

Table 4.
Summary of some essential features of models that use straightforwardly algorithms dedicated to MOPPs.
Table 4.
Summary of some essential features of models that use straightforwardly algorithms dedicated to MOPPs.
| Reference | # Objectives | Type of Path Problem | Resolution Approach |
|---|---|---|---|
| (Sobrinho 2002) [149] | Multipath; widest–shortest path; most-reliable–shortest path | Lexicographic (a variant of Dijkstra algorithm) | |
| (Sobrinho and Ferreira 2020) [153] | Shortest–widest path; widest–shortest path | Heuristics based on algebraic framework (a lexicographic approach) | |
| (Gomes et al., 2016) [154] | Lexicographic maximally risk–disjoint path pair | Heuristic (based on trap avoidance and weighted sum model) | |
| (Pascoal et al., 2022) [157] | Lexicographic maximally risk–disjoint /minimal cost path pair | Exact a priori lexicographic (path ranking and path labeling) | |
| (Dinitz et al., 2021) [158] | -disjoint shortest (most secure) paths | Lexicographic (based on a weighted sum method) | |
| (Antunes et al., 1999) [162] | Biobjective shortest paths | Exact a priori (based on a weighted sum method) | |
| (Clímaco et al., 2003) [18] | QoS constrained biobjective shortest paths | Exact a priori (based on a weighted sum method) | |
| (Clímaco et al., 2006) [41] | Biobjective path (video traffic) | Exact a priori (based on weighted Chebyshev distance to reference points) | |
| (Beugnies and Gandibleux 2006) [164] | Multiobjective path | Exact (based on a reference point approach using a weighted Chebyshev distance) | |
| (Zheng et al., 2022) [125] | Biobjective path | Metaheuristic (Genetic algorithm) | |
| (Bhat and Rouskas 2016) [165] | -time constrained path problem | Exact a posteriori (uses a dynamic programming procedure) | |
| (Markovic and Acimovic-Raspopovic 2005) [167] | Multiobjective shortest path problem | Exact a priori (uses a weighted sum method) | |
| (Gomes et al., 2009) [168] | Biobjective topological lightpath | Exact a priori (uses a -shortest path method and a reference point approach) | |
| (Clímaco et al., 2007) [160] | Stochastic -quickest path | Uncertainty (solution based on an exact deviation algorithm) | |
| (Gomes et al., 2012) [169] | Biobjective shortest path and maximally disjoint backup path | Exact a posteriori (based on a -shortest path approach regarding a weighted sum OF) | |
| (Craveirinha et al., 2023) [170] | Maximally risk–disjoint/minimal cost path pair | Exact a posteriori (based on a path ranking and path labeling algorithm) | |
| (Xu et al., 2023) [171] | Multicriteria shortest paths (from one source node to multiple destination nodes) | Exact a posteriori (based on a breadth-first search, with pruning to identify paths which are not Pareto optimal) |
3.2.2. Models That Use as Auxiliary Resolution Procedures Shortest Path Dedicated Algorithm(s)
Herein, we refer to representative works describing multicriteria routing models of various types and for different network environments where the resolution approach uses, as auxiliary resolution procedures, algorithms dedicated to single objective or multiobjective path problems. A summary of some essential features of these models is in Table 5.
Paper [173] develops a stochastic multiple-objective dynamic routing model for circuit-switched networks such that the routes for all node-to-node traffic flows may change dynamically. The objective functions of the network-wide optimization model are the mean blocking probability and the maximal node-to-node blocking probability. The resolution method of the model is heuristic, but for calculating candidate paths, blocking probabilities and implied costs [174] are used, leading to a specific auxiliary-constrained biobjective shortest path problem. This is solved exactly with a modified version of the biobjective shortest path algorithmic approach in [41], enabling us to select the paths that are candidates to be efficient. A stochastic hierarchical bilevel multiobjective routing model for MPLS networks with two service classes including fairness objectives is described in [175]. A heuristic resolution method for this complex model is proposed and tested in a reference network which is based on an auxiliary biobjective shortest path sub-model for calculating candidate paths. This sub-model uses ‘marginal implied costs’ (as proposed in [176]) and blocking probabilities and is solved exactly by the method in [41].
The authors in [133] propose a multiobjective RWA routing model for Elastic Optical Networks with spectrum segmentation and shared backup protection (meaning that the bandwidth of a backup path may be shared by several active paths) that seeks to optimize blocking probability and fault restoration ratio. The resolution approach is a metaheuristic, a Deep Neural Network model with a multiobjective Fuzzy Inference System which recurs to Yen´s -shortest path algorithm, and its performance is compared with similar calculation procedures.
The work in [177] proposes a biobjective extension of the shortest path-based routing principle largely used on the Internet and, in general, in shortest path-based routing networks, namely in the context of extensions of the application of link state routing protocols such as OSPF. It considers traffic splitting according to an equal cost multipath (ECMP) split rule and that the paths are calculated with a single objective shortest path algorithm, the weights of which have to be optimized in order to obtain approximate efficient solutions of a biobjective network optimization model. The two OFs of this model are traffic load balancing functions in fully operational and in arc-failure scenarios. This approach leads to a biobjective version of the ‘weight-setting problem’ referred to above. The resolution method is a specialized heuristic that uses a hash function and a diversification technique. Also, a multiobjective formulation of this problem in the context of networks using shortest path routing protocols is proposed in [123]. The authors present an evolutionary metaheuristic for obtaining an approximation to the Pareto front of the associated multiobjective routing model.

Table 5.
Summary of some essential features of routing models that use shortest path dedicated algorithms as auxiliary resolution procedures.
Table 5.
Summary of some essential features of routing models that use shortest path dedicated algorithms as auxiliary resolution procedures.
| Reference | # Objectives * | Type of Model | Approach/Auxiliary Method |
|---|---|---|---|
| (Martins et al., 2005) [173] | Hierarchical stochastic multiobjective | Heuristic/Biobjective stochastic shortest path algorithm | |
| (Girão-Silva et al., 2009) [175] | Hierarchical stochastic multiobjective with two traffic classes | Heuristic/Biobjective stochastic shortest path algorithm | |
| (Lourenço and César 2022) [133] | Stochastic biobjective path pair (resilient routing) | Metaheuristic/-shortest path algorithm | |
| (Yuan 2003) [177] | Shortest path based biobjective routing with traffic splitting | Heuristic (for biobjective weight setting problem)/Shortest path algorithm | |
| (Sousa et al., 2011) [123] | Shortest path based multiobjective routing with traffic splitting | Metaheuristic (for multiobjective weight setting problem)/Shortest path algorithm |
* number of objective functions of the auxiliary resolution procedure.
3.2.3. Models That Include the Resolution of MOPPs by Non-Dedicated Path Approaches
Herein, we overview contributions representative of routing models and path-related models for different types of communication networks such that the mathematical formulation of the model includes multiobjective path problems, solved by approaches not specifically dedicated to MOPPs. A summary of some essential features of these models is in Table 6.
In [178], a very specific problem of route selection for survivable book-ahead guaranteed (BAG) services in MPLS networks is tackled. The authors consider different and potentially conflicting objectives and different survivability requirements for the service requests. The survivable BAG services must be routed without significantly affecting best effort services. To guarantee the survivability, a pair of link-disjoint paths (primary and secondary paths) is calculated by recurring to a MILP formulation, considering four different optimization objectives: residual capacity, routing cost, a penalty cost for non-routed demands and routing revenue. An iterative heuristic is proposed to solve the formulated problem.
A multiobjective routing model for supporting a long-term virtual private network on the Internet is proposed in [134], using an integer multicommodity flow approach with special constraints. This leads to a biobjective path model considering average packet delay and traffic load balancing as OFs. A heuristic of the type Greedy Randomized Adaptive Search procedure is used as the resolution method. A metaheuristic procedure for solving a multiobjective routing problem in MPLS networks is proposed in [124]. In this paper, a variable neighborhood multiobjective genetic algorithm (VN-MGA) is developed, aiming at the minimization of the network cost, the minimization of the number of rejected simultaneous requests and the maximization of arc bandwidth load. Results are compared with those obtained with an ILP solver.
In [179], there is a proposal of a multiobjective routing model for MPLS considering traffic splitting (in terms of bandwidth) leading to a multipath routing problem addressed with a MILP formulation. The OFs are the average packet delay, a traffic load balancing function and the total number of used LSPs (Label-Switched Paths). The resolution method is based on an evolutionary algorithm, and the results are compared with those of an alternative resolution procedure.
Paper [120] presents a metaheuristic resolution approach for the stochastic hierarchical multiobjective routing model for MPLS networks with two service classes including fairness objectives developed in [175]. Two resolution procedures are proposed, the first one a simulated annealing based technique, the second one using a tabu search technique, and both are compared with a specialized heuristic.
The work in [180] describes a multiobjective routing model for MPLS networks, with multiple service types and traffic splitting, considering a network flow approach so that the routing problem is formulated as a multiobjective mixed-integer linear program having as objective functions the routing cost and the load cost in the network links, including a constraint on maximal splitting of each service bandwidth demand. Two exact resolution methods are developed for obtaining the Pareto optimal solutions, the first one based on the classical constraint method in [77] and the second based on the modified constraint method in [181]. This MILP model is extended in [182] to include a path protection resilient routing scheme (without traffic splitting) and solved exactly by the classical constraint method, after enumerating feasible disjoint path pairs for each traffic flow with the aid of an algorithm based on the -shortest path algorithm MPS [71].
A multiobjective routing model for wireless IP-based networks is proposed in [183], seeking to obtain paths which minimize total energy consumption, latency and bit error rate (corresponding to a non-additive metric). The resolution method is based on the optimization of a normalized weighted additive function combining the three OFs, to seek for efficient solutions; a distributed heuristic implementation of the method is described and applied to small test networks.
Paper [184] proposes a biobjective routing model for mobile ad-hoc Wireless Networks that consider minimized energy consumption and link stability as OFs, leading to a dynamic biobjective constrained shortest path formulation. This type of wireless networks is composed of a collection of mobile devices that form a self-organizing temporary network that does not use an underlying telecommunication structure or a centralized control. A heuristic resolution method is used which is based on the optimization of the combination of the two OFs, using an ILP formulation, seeking to account for the dynamic nature of the model and the distributed nature of the routing control. A multiobjective routing model for Wireless Sensor Networks (WSNs) is described in [185]. These networks are composed of sensor nodes installed with the objective of gathering real-time information of specific type(s), in a given area, so that the obtained data are forwarded to an interface node, the sink node. The optimization objectives associated with each node are residual energy, frequency count of packet transmission via a node and number of hops counted from the sink node. The proposed resolution method is a heuristic based on a utility function defined for each node that is the additive aggregation of the OFs, using different weight sets, empirically obtained in terms of the resulting packet loss ratio. Similar types of models and multiattribute resolution approaches are presented in [186] (where the weights are chosen by a ‘weight rating’ method) and [187,188] that use a decision matrix for choosing the next node to be selected in the path.
Note that many multicriteria routing models proposed for WSNs use ‘hop-by-hop’ path calculation heuristics based on a weighted utility function, such that the next node in the path is selected among the adjacent nodes by using a multiattribute model recurring to a performance matrix updated at each step of the procedure. The work in [189] proposes a generic multicriteria routing framework for WSNs regarding the criteria to be addressed and discusses a form of additive aggregation based on technical features of the used routing protocol.
A very particular constrained multipath lexicographic path problem is addressed in [190], aiming at minimizing the number of active paths with the maximal number of arcs in a resilient routing model where active and backup paths (to be used in the event of failure of service path(s)) have to be calculated simultaneously, all with a bounded number of arcs; ILP formulations are used for obtaining exact solutions.
In [191], a specific biobjective path-related problem in packet-switched Software Defined Networks is formulated. The first objective is the minimization of the consumption of the sum of the energy of the switches, the active controllers and the active links. The second objective is the minimization of the sum of all the delays between the active switches and the respective domain controller. An ILP is formulated aiming at the calculation of (i) whether a switch, a controller or a link should be on or off; (ii) whether a path is active; and (iii) which controller should a switch be linked to. A weighted sum method is used for solving the problem and compared with two heuristic procedures.
A ‘critical disruption path problem’ involves the identification of the loopless paths for a source–destination pair, such that their removal will maximize the disruption of the network, in terms of operability. A multiobjective formulation of this problem is proposed in [126]. Considering an induced subgraph obtained when a path is deleted, the tackled problem aims at the minimization of the size of the largest connected component, the maximization of the number of connected components and the minimization of the cost of the disruption path. A MILP formulation is presented, and an evolutionary metaheuristic resolution approach consisting of a hybrid algorithm including modified-NSGA-II and Variable Neighborhood Search (VNS) is used to find an approximation to the Pareto front.

Table 6.
Summary of some essential features of models that include the resolution of MOPPs by non-dedicated path approaches.
Table 6.
Summary of some essential features of models that include the resolution of MOPPs by non-dedicated path approaches.
| Reference | # Objectives | Type of Model | Resolution Approach |
|---|---|---|---|
| (Thirumalasetty and Medhi 2001) [178] | Multiobjective disjoint path pair routing | MILP solved with iterative heuristic | |
| (Resende and Ribeiro 2003) [134] | Biobjective constrained routing | Integer multicommodity flow solved with heuristic (GRASP) | |
| (Onety et al., 2013) [124] | Multiobjective constrained routing | Metaheuristic: genetic algorithm VN-MGA (based on NSGA-II) | |
| (Erbas 2003) [179] | Multiobjective routing with traffic splitting | Metaheuristic: evolutionary algorithm | |
| (Girão-Silva et al., 2009) [120] | Hierarchical stochastic biobjectiverouting with two traffic classes | Metaheuristics: simulated annealing; tabu-search | |
| (Girão-Silva et al., 2015) [180] | Biobjective constrained routing withtwo traffic classes and traffic splitting | MILP solved by exact approach based on a modified constraint method | |
| (Girão-Silva et al., 2017) [182] | Biobjective routing with two trafficclasses and path protection | MILP solved by exact approach based on a modified constraint method and a -shortest path algorithm | |
| (Malakooti and Thomas 2006) [183] | Multiobjective routing | Heuristic using a specific utility function | |
| (Guerriero et al., 2009) [184] | Biobjective constrained dynamic distributed routing | ILP solved by a heuristic | |
| (Bhunia et al., 2014; Das et al., 2015; Suh et al., 2015; Rehena et al., 2017) [185,186,187,188] | Multiobjective constrained dynamic distributed routing | Heuristics using a multiattribute utility function | |
| (Gouveia et al., 2016) [190] | Lexicographic multipath routing with path protection | ILP solved by exact lexicographic approach | |
| (Naseri et al., 2021) [191] | Specific biobjective path related model | ILP solved by a weighted sum method or by heuristics | |
| (Granata and Sgalambro 2023) [126] | Multiobjective critical disruption path model | MILP solved by evolutionary metaheuristic |
4. Conclusions and Trends
Next, after highlighting the essential contents and broad conclusions of this work, we will seek to outline major research trends and challenges in this very wide and multifaceted area of the application of multiobjective path problem formulations and algorithms, in relation to recent technological evolutions in communication networks.
After reviewing basic concepts and presenting main formulations of multiobjective path problems, considering different categories of objective functions, namely linear, non-linear functions and special types of objective functions, we outlined the essential features of different types of resolution methods for these problems appearing in the scientific literature that seemed more relevant to this important application area, not forgetting the approximate approaches. Special emphasis was given to exact resolution approaches. This focus can be justified by the inherent advantage of these methods and by our conclusion that, in many applications, these algorithms can solve large instances of the problems.
Regarding the application of exact algorithms to MOPPs formulated in the context of routing models these should be considered, in many situations, as a possible advantageous first approach, whenever known efficient algorithms are available or can, at least in theory, be developed. This choice should be carefully evaluated, in each particular case.
Despite the relevance of classical NP-completeness analysis in this respect, we note that this is in fact a worst-case analysis. We can say, also from our own research experience, that in many cases, this analysis per se may not be the critical factor in the choice of a resolution method. We concluded that in many applications of multiobjective path problems in this area—as also noted by [151] for QoS routing problems—the predicted worst-case complexity can be much different from execution times in different applications. In many situations, efficient exact algorithms for multiobjective path problems associated with routing models are effective ways of obtaining Pareto optimal solutions in computational times compatible with the application. Multiple examples of the application of exact approaches in this area were referred to in the section above. This does not mean that approximate methods including heuristics and metaheuristics do not play a role of great importance in this very wide area of application of multiobjective path problems. In fact, as noted above, given their inherent resolution difficulties NP-hard optimization problems are often approached by approximate methods which work fast while looking for sets of solutions that approximate the efficient ones. This may be a practical requirement in various applications as it is the case in NP-hard multiobjective problems formulated in the context of routing models in networks of very great dimension and connectivity or involving more complex multilayer network representations and particularly in the case of on-line or dynamic routing models (with very fast updating periods) or in local-area wireless network technologies with switches/routers of limited calculation/information management (for instance, in terms of provided signaling data) capabilities. These specific requirements are naturally related to essential features of the routing protocols associated with a given network technical scenario.
After an outline of background concepts on telecom network routing models, we presented an overview of selected papers considered as representative of different types of applications of multiobjective path problem formulations and algorithms either as direct resolution methods or as auxiliary resolution procedures. Also, an overview of multiobjective routing models formulated in terms of approaches that involve explicitly, as a goal (but usually not the unique one) of the mathematical formulation, the calculation and selection of paths that are solutions to MOPPs by recurring to approaches which are not specifically dedicated to path problems, was presented. This had in mind the fact that these routing models are common in multiple situations. Note that the models of the two latter types appear typically in routing methods where the route/path calculation and selection cannot be mathematically separated from the assignment of node-to-node traffic flows to the selected paths. This happens in routing models for which the routing method embodies a teletraffic engineering mechanism requiring some form of optimization of the bandwidth demand (associated with different end-to-end services) assignment to the arcs of the paths, seeking, on the one hand, the satisfaction of the demand under certain QoS requirements and, on the other hand, the achievement of some form of global network performance optimization, in terms of different network metrics.
Concerning trends and challenges in this research area, as noted above, we begin by noting that the nature of real telecommunication networks is very complex, having in mind that they are organized, in functional, operational and management/control terms, in several interrelated layers, which leads to the necessity of considering them as multilayer networks. This raises difficulties in terms of routing modeling when some inter-layer representation is at stake that also may affect the formulation of the corresponding path problems. An example of the way in which this issue could be tackled, in the context of resilient routing models with path protection, is the concept of Shared Risk Link Group that corresponds to the definition, for each possible failure risk in an element of the physical/transport layer, of the set of arcs in the logical layer which are affected by that risk. The specification of these sets assumes that the mapping of the physical layer onto the logical layer is known, so that this information can be incorporated in the mathematical formulation of the path pair (active path and protection path) problem. This of course has a strong impact in the form of the addressed path problem (either single or multiobjective) and in the corresponding resolution approach (as described in some references referred to in the previous section) since it requires that discrete objective functions specified in terms of operations on finite sets be used. In more complex multilayer modelling situations, a useful mathematical tool may be the definition of ‘multilevel graphs’, as proposed in [192].
In most papers concerning applications of MOPP algorithms to multiobjective telecom network routing models, computational experiments considering different types of network environments are presented. Many of these studies are focused on the performance evaluation of the algorithms in terms of CPU times, usually in reference to topological network structures. In multiple cases, these computational studies also analyze the effects of the application of the proposed routing methods in terms of the resulting network performance measures, using some type of simulation of end-to-end service demands, depending on the network technological and architectural context and on relevant features of the network environment. Specific examples of such computational studies are in references [18,157,170,171]. Also, in a few of the methodological papers in Section 2, real-world applications are presented, see for instance [33,118]. Furthermore, it would be clearly important to evaluate the possible merits and disadvantages of the multiple types of multiobjective routing methods proposed in the literature, in real-world network applications. This would require further empirical studies desirably involving collaborations with network and service operators, on a case by case basis, in the context of future applied research tasks.
Also, the practical implementation requirements and specific limitations (namely related to signaling, information management, control functionalities of routers, switches or optical cross-connectors and other related routing protocol requirements), for the multiple types of multiobjective routing methods proposed in the literature, should be investigated in real-world network application contexts. This would require further empirical R&D studies with real networks involving collaborations with network and service operators and communication software/equipment suppliers, on a case by case basis, and it is a matter that justifies future research.
A problematic area where multiobjective path problem formulations are raising interest is resilient routing involving multiobjective multipath problems. As already noted in [193], the development of multiobjective routing approaches and of resilient routing models, in particular, will enable a mathematically consistent analysis of trade-offs between various route and network performance metrics for different routing methods corresponding to different options in terms of protection or rerouting mechanisms in each layer. This poses a significant challenge since it will require us to address the difficult issue of decomposition of the path optimization model. In routing with path protection, this is associated with the fact that the efficient solutions of the routing/path optimization problem in the physical network level (for instance an OTN optical network structure) are pairs of lightpaths, such that each of these lightpaths may correspond to different feasible paths in the next layer of the network representation (for instance, corresponding to the use of a MPLS-TP protocol technology). Note that in this type of network architecture and modeling approach, the path optimization model would also be multiobjective in this upper layer, thus leading to a complex issue of interrelated problems. Another kind of hierarchical modeling issue, relevant to multilayer networks, involves a hierarchy of the routing/path optimization formulation, which is concerned with the application of well-known optimization methods to multi-level routing, as outlined in [3] in the context of IP-based networks.
These remain challenging methodological questions that deserve future research.
Still in relation to resilient routing, taking into account that many network failures occur as a result of disasters (natural phenomena or as a consequence of human intervention), in such a way that these events have a very strong impact on a certain geographical area (geographically correlated failures, see [194]), there has been an increasing interest in the development of geodiverse routing models. These routing methods have to take into account the geodiversity property of the paths, and this can be modeled in different manners, implying specific types of constraints on the choice of the protection path(s) (a brief review is in [195]). A strategy recurring to -geodiverse shortest paths is described in [196], where a lower bound on the geographic distance between the paths is imposed. Also, resilient routing models with preventive techniques, namely in the case of malicious attacks, have been given attention. A possible strategy is to define specific nodes where the traffic must pass, so that a security inspection is performed to identify possible threats, thence imposing a specific type of topological constraint on the path problems (see examples in [197,198]).
We think that also in the mentioned sub-areas of resilient routing there is room for the investigation of multiobjective routing approaches leading to interesting multiobjective constrained path problems.
Another area where challenging issues concerning the development of multiobjective routing optimization models deserve attention is heterogeneous networks that is networks where an end-to-end connection can (or needs to) use different technological platforms so that a route/path has to traverse several network structures/routing domains, each of them with distinct technical features.
Another issue with impact on multiobjective routing models is the consideration in various network environments of power consumption as a relevant objective function, not only from an economic perspective but foremost, because of the very significant environmental impacts of electrical energy consumption by telecommunication networks and all types of ICT (Information and Communication Technologies) structures in general (for instance, critically relevant vis-à-vis cloud computing). This trend has led to the development of ‘energy-aware routing methods’. An illustrative example is in [199] where a multiobjective routing method, using a heuristic solution for WDM networks, was developed. This study shows that the minimization of power consumption and path blocking probability are conflicting objectives thence fully justifying the consideration of multiobjective routing approaches. This is a research trend where new path problem formulations that incorporate adequate energy consumption objectives/constraints for a given network environment should be developed.
Concerning new modelling aspects related to the new technological platforms, with implications in the form of the formulated MOPPs, this will require, as far as routing models are concerned, the specification of adequate criteria/objectives and constraints, involving technical and often economical aspects, and it is an important preliminary issue. Moreover, adequate resolution methods will have to be selected or developed for new multiobjective problem formulations associated with such models. Examples of new areas of development in this context are multiobjective routing models for anycast flows (traffic patterns of one-to-one of many flows) in cloud computing (see [200]) and certain unicast routing models, such that it is imposed that paths include certain intermediate nodes previously specified. For instance, single objective formulations of this type of problem, in the context of a specific resilient routing method with path protection, were addressed in [197]. These models involve the obtainment of shortest node–disjoint path pairs constrained to visit specific nodes.
Next, we mention some specific modern network technological platforms where it is expected that new routing models possibly involving multiobjective formulations may be developed.
Concerning transport networks, Elastic Optical Networks aim at a more efficient use of the spectrum, by allocating the bandwidth in a flexible way, considering different modulation formats, tailored for each specific application. The problem of routing in EONs is not tackled per se, but rather taking into consideration the allocation of spectrum (Routing and Spectrum Assignment—RSA), sometimes jointly with modulation selection (Routing, Modulation (Level) and Spectrum Assignment—RMSA). There are many approaches for both problems in EONs, with different pros and cons in terms of spectrum fragmentation, modulation formats, quality of transmission, traffic grooming, network survivability, energy efficiency and cost [201]. In [202], a generalization of the Dijkstra algorithm is proposed to tackle the problems of RSA and RMSA where constraints related to the continuity and contiguity of the frequency slot units are taken into account. The problem of RMSA in OTNs is also tackled in [203,204] using different modeling algorithmic approaches.
The sixth generation (6G) of mobile networks also poses new challenges in terms of routing. The need to satisfy the increasingly demanding key performance indicators while optimizing the available network resources is an important aspect to consider. In this context, Software Defined Networking takes a pivotal role in the network management. Furthermore, the use of Artificial Intelligence and Quantum Computing for optimizing routing are foreseen in the near future [205], and there are multiple approaches to deal with routing in these networks. An example using quantum computing is developed in [206] where a single objective and a multiobjective approach of lexicographic type are described, including as optimizing criteria battery consumption and battery cost, respectively.
Finally, another important recent trend with potential impact in this research area is Network virtualization that enables the provision of services by instantiating virtual connections over an existing telecommunication physical infrastructure. Routing in these networks is controlled by the service providers that manage the transport infrastructure. A routing-related problem is the need to guarantee traffic load sharing over multiple paths (thus leading to multipath routing) among different servers (from the perspective of the service provider) or to concentrate the traffic on one particular server (from the perspective of the clients with virtual networks) [207].
Author Contributions
Conceptualization: J.C. (José Craveirinha) and J.C. (João Clímaco); Methodology: J.C. (João Clímaco), J.C. (José Craveirinha), M.P. and R.G.-S.; Formal analysis: J.C. (José Craveirinha), J.C. (João Clímaco), M.P. and R.G.-S.; Investigation: J.C. (José Craveirinha), J.C. (João Clímaco), M.P. and R.G.-S.; Writing—original draft preparation: J.C. (José Craveirinha), J.C. (João Clímaco), M.P. and R.G.-S.; Supervision: J.C. (José Craveirinha) and J.C. (João Clímaco); Writing—review and editing: J.C. (José Craveirinha) and R.G.-S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the Portuguese Foundation for Science and Technology under the project grants UIDB/00308/2020 with the https://doi.org/10.54499/UIDB/00308/2020, and UIDB/00324/2020 with the https://doi.org/10.54499/UIDB/00324/2020.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Clímaco, J.; Craveirinha, J.; Girão-Silva, R. Multicriteria Analysis in Telecommunication Network Planning and Design: A Survey. In Multiple Criteria Decision Analysis—State of the Art Surveys; Greco, S., Ehrgott, M., Figueira, J., Eds.; International Series in Operations Research & Management Science; Springer: New York, NY, USA, 2016; Chapter 26; Volume 233, pp. 1167–1233. [Google Scholar] [CrossRef]
- Clímaco, J.; Craveirinha, J. MCDA/M in Telecommunication Networks—Challenges and Trends. In Advanced Studies in Multi-Criteria Decision Making; Ben Amor, S., Teixeira de Almeida, A., Miranda, J.L., Aktas, E., Eds.; Chapman and Hall/CRC: New York, NY, USA, 2019; Chapter 2. [Google Scholar]
- Wierzbicki, A.P.; Burakowski, W. A conceptual framework for multiple-criteria routing in QoS IP networks. Int. Trans. Oper. Res. 2011, 18, 377–399. [Google Scholar] [CrossRef]
- Clímaco, J.C.; Pascoal, M.M. Multicriteria path and tree problems: Discussion on exact algorithms and applications. Int. Trans. Oper. Res. 2012, 19, 63–98. [Google Scholar] [CrossRef]
- Ahuja, R.K.; Magnanti, T.L.; Orlin, J.B. Network Flows: Theory, Algorithms, and Applications; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- Raith, A.; Ehrgott, M. A comparison of solution strategies for biobjective shortest path problems. Comput. Oper. Res. 2009, 36, 1299–1331. [Google Scholar] [CrossRef]
- Vincke, P. Problèmes multicritères. Cah. Cent. D’études Rech. Opérationelle 1974, 16, 425–439. [Google Scholar]
- Hansen, P. Bicriterion Path Problems. In Multiple Criteria Decision Making Theory and Application, Proceedings of the Third Conference Hagen/Königswinter, West Germany, August 20–24, 1979; Fandel, G., Gal, T., Eds.; Lectures Notes in Economics and Mathematical Systems; Springer: Berlin/Heidelberg, Germany, 1980; Volume 177, pp. 109–127. [Google Scholar] [CrossRef]
- Santos, J.L.E. Uma abordagem ao problema do trajecto óptimo multiobjectivo. Investig. Oper. 1999, 19, 211–226. (In Portuguese) [Google Scholar]
- Martins, E.; Santos, J. The Labeling Algorithm for the Multiobjective Shortest Path Problem; Technical Report 99/005; CISUC, University of Coimbra: Coimbra, Portugal, 1999. [Google Scholar]
- Clímaco, J.C.N.; Martins, E.Q.V. A bicriterion shortest path algorithm. Eur. J. Oper. Res. 1982, 11, 399–404. [Google Scholar] [CrossRef]
- Martins, E.Q.V. On a multicriteria shortest path problem. Eur. J. Oper. Res. 1984, 16, 236–245. [Google Scholar] [CrossRef]
- Corley, H.W.; Moon, I.D. Shortest paths in networks with vector weights. J. Optim. Theory Appl. 1985, 46, 79–86. [Google Scholar] [CrossRef]
- Mote, J.; Murthy, I.; Olson, D.L. A parametric approach to solving bicriterion shortest path problems. Eur. J. Oper. Res. 1991, 53, 81–92. [Google Scholar] [CrossRef]
- Stewart, B.S.; White, C.C., III. Multiobjective A*. J. ACM 1991, 38, 775–814. [Google Scholar] [CrossRef]
- Tung, C.T.; Chew, K.L. A multicriteria Pareto-optimal path algorithm. Eur. J. Oper. Res. 1992, 62, 203–209. [Google Scholar] [CrossRef]
- Guerriero, F.; Musmanno, R. Label Correcting Methods to Solve Multicriteria Shortest Path Problems. J. Optim. Theory Appl. 2001, 111, 589–613. [Google Scholar] [CrossRef]
- Clímaco, J.C.N.; Craveirinha, J.M.F.; Pascoal, M.M.B. A bicriterion approach for routing problems in multimedia networks. Networks 2003, 41, 206–220. [Google Scholar] [CrossRef]
- Mandow, L.; de la Cruz, J.L.P. Path recovery in frontier search for multiobjective shortest path problems. J. Intell. Manuf. 2010, 21, 89–99. [Google Scholar] [CrossRef]
- Machuca, E.; Mandow, L.; de la Cruz, J.L.P.; Ruiz-Sepúlveda, A. A comparison of heuristic best-first algorithms for bicriterion shortest path problems. Eur. J. Oper. Res. 2012, 217, 44–53. [Google Scholar] [CrossRef]
- Xie, C.; Waller, S.T. Parametric search and problem decomposition for approximating Pareto-optimal paths. Transp. Res. B Methodol. 2012, 46, 1043–1067. [Google Scholar] [CrossRef]
- Demeyer, S.; Goedgebeur, J.; Audenaert, P.; Pickavet, M.; Demeester, P. Speeding up Martins’ algorithm for multiple objective shortest path problems. 4OR 2013, 11, 323–348. [Google Scholar] [CrossRef]
- Sanders, P.; Mandow, L. Parallel Label-Setting Multi-objective Shortest Path Search. In Proceedings of the 2013 IEEE 27th International Symposium on Parallel and Distributed Processing, Cambridge, MA, USA, 20–24 May 2013; pp. 215–224. [Google Scholar] [CrossRef]
- Duque, D.; Lozano, L.; Medaglia, A.L. An exact method for the biobjective shortest path problem for large-scale road networks. Eur. J. Oper. Res. 2015, 242, 788–797. [Google Scholar] [CrossRef]
- Pulido, F.J.; Mandow, L.; Pérez-de-la Cruz, J.L. Dimensionality reduction in multiobjective shortest path search. Comput. Oper. Res. 2015, 64, 60–70. [Google Scholar] [CrossRef]
- Machuca, E.; Mandow, L. Lower bound sets for biobjective shortest path problems. J. Glob. Optim. 2016, 64, 63–77. [Google Scholar] [CrossRef]
- Giret, A.; Kergosien, Y.; Sauvanet, G.; Neron, E. An Efficient Label-setting Algorithm for the Bi-objective Shortest Path Problem. In Proceedings of the 5th International Conference on Operations Research and Enterprise Systems (ICORES 2016), Rome, Italy, 23–25 February 2016; pp. 197–203. [Google Scholar] [CrossRef]
- Sedeño-Noda, A.; Colebrook, M. A biobjective Dijkstra algorithm. Eur. J. Oper. Res. 2019, 276, 106–118. [Google Scholar] [CrossRef]
- de las Casas, P.M.; Sedeño-Noda, A.; Borndörfer, R. An Improved Multiobjective Shortest Path Algorithm. Comput. Oper. Res. 2021, 135, 105424:1–105424:14. [Google Scholar] [CrossRef]
- Hu, X.-B.; Gu, S.-H.; Zhang, C.; Zhang, G.-P.; Zhang, M.-K.; Leeson, M.S. Finding all Pareto optimal paths by simulating ripple relay race in multi-objective networks. Swarm Evol. Comput. 2021, 64, 100908:1–100908:18. [Google Scholar] [CrossRef]
- Kergosien, Y.; Giret, A.; Néron, E.; Sauvanet, G. An Efficient Label-Correcting Algorithm for the Multiobjective Shortest Path Problem. INFORMS J. Comput. 2022, 34, 76–92. [Google Scholar] [CrossRef]
- de las Casas, P.M.; Kraus, L.; Sedeño-Noda, A.; Borndörfer, R. Targeted multiobjective Dijkstra algorithm. Networks 2023, 82, 277–298. [Google Scholar] [CrossRef]
- Hernández, C.; Yeoh, W.; Baier, J.A.; Zhang, H.; Suazo, L.; Koenig, S.; Salzman, O. Simple and efficient bi-objective search algorithms via fast dominance checks. Artif. Intell. 2023, 314, 103807:1–103807:20. [Google Scholar] [CrossRef]
- Kurbanov, T.; Cuchý, M.; Vokřínek, J. Fast One-to-Many Multicriteria Shortest Path Search. IEEE Trans. Intell. Transp. Syst. 2023, 24, 10410–10419. [Google Scholar] [CrossRef]
- Mandow, L.; de la Cruz, J.L.P. Improving Bi-Objective Shortest Path Search with Early Pruning. In Proceedings of the 26th European Conference on Artificial Intelligence (ECAI 2023), Kraków, Poland, 30 September–4 October 2023; Gal, K., Nowé, A., Nalepa, G.J., Fairstein, R., Rădulescu, R., Eds.; Frontiers in Artificial Intelligence and Applications. IOS Press: Amsterdam, The Netherlands, 2023; Volume 372, pp. 1680–1687. [Google Scholar] [CrossRef]
- Current, J.R.; Revelle, C.S.; Cohon, J.L. An interactive approach to identify the best compromise solution for two objective shortest path problems. Comput. Oper. Res. 1990, 17, 187–198. [Google Scholar] [CrossRef]
- Murthy, I.; Olson, D.L. An interactive procedure using domination cones for bicriterion shortest path problems. Eur. J. Oper. Res. 1994, 72, 417–431. [Google Scholar] [CrossRef]
- Henig, M.I. Efficient Interactive Methods for a Class of Multiattribute Shortest Path Problems. Manag. Sci. 1994, 40, 891–897. [Google Scholar] [CrossRef]
- Coutinho-Rodrigues, J.M.; Clímaco, J.C.N.; Current, J.R. An interactive bi-objective shortest path approach: Searching for unsupported nondominated solutions. Comput. Oper. Res. 1999, 26, 789–798. [Google Scholar] [CrossRef]
- Paixão, J.M.P.; Martins, E.Q.V.; Rosa, M.S.; Santos, J.L.E. The determination of the path with minimum-cost norm value. Networks 2003, 41, 184–196. [Google Scholar] [CrossRef]
- Clímaco, J.C.N.; Craveirinha, J.M.F.; Pascoal, M.M.B. An automated reference point-like approach for multicriteria shortest path problems. J. Syst. Sci. Syst. Eng. 2006, 15, 314–329. [Google Scholar] [CrossRef]
- Sauvanet, G.; Néron, E. Search for the best compromise solution on Multiobjective shortest path problem. Electron. Notes Discret. Math. 2010, 36, 615–622. [Google Scholar] [CrossRef]
- Fouchal, H.; Gandibleux, X.; Lehuédé, F. Preferred solutions computed with a label setting algorithm based on Choquet integral for multi-objective shortest paths. In Proceedings of the 2011 IEEE Symposium on Computational Intelligence in Multicriteria Decision-Making (MDCM), Paris, France, 11–15 April 2011; pp. 143–150. [Google Scholar] [CrossRef]
- Pulido, F.J.; Mandow, L.; de la Cruz, J.L.P. Multiobjective shortest path problems with lexicographic goal-based preferences. Eur. J. Oper. Res. 2014, 239, 89–101. [Google Scholar] [CrossRef]
- Shirdel, G.H.; Ramezani-Tarkhorani, S. A DEA-based Approach for Finding a Favorable Multi-objective Shortest Path. Croat. Oper. Res. Rev. 2018, 9, 149–164. [Google Scholar] [CrossRef]
- Pugliese, L.D.P.; Granat, J.; Guerriero, F. Two-phase algorithm for solving the preference-based multicriteria optimal path problem with reference points. Comput. Oper. Res. 2020, 121, 104977:1–104977:32. [Google Scholar] [CrossRef]
- Ehrgott, M.; Gandibleux, X. A survey and annotated bibliography of multiobjective combinatorial optimization. OR-Spektrum 2000, 22, 425–460. [Google Scholar] [CrossRef]
- Ehrgott, M.; Gandibleux, X. Multiple Criteria Optimization. State of the Art Annotated Bibliographic Surveys; International Series in Operations Research & Management Science; Springer: New York, NY, USA, 2002; Volume 52. [Google Scholar] [CrossRef]
- Current, J.; Min, H. Multiobjective design of transportation networks: Taxonomy and annotation. Eur. J. Oper. Res. 1986, 26, 187–201. [Google Scholar] [CrossRef]
- Current, J.; Marsh, M. Multiobjective transportation network design and routing problems: Taxonomy and annotation. Eur. J. Oper. Res. 1993, 65, 4–19. [Google Scholar] [CrossRef]
- Skriver, A. A classification of bicriterion shortest path (BSP) algorithms. Asia-Pac. J. Oper. Res. 2000, 17, 192–212. [Google Scholar]
- Tarapata, Z. Selected multicriteria shortest path problems: An analysis of complexity, models and adaptation of standard algorithms. Int. J. Appl. Math. Comp. Sci. 2007, 17, 269–287. [Google Scholar] [CrossRef]
- Huarng, F.; Pulat, S.; Shih, L. A computational comparison of some bicriterion shortest path algorithms. J. Chin. Inst. Ind. Eng. 1996, 13, 121–125. [Google Scholar]
- Paixão, J.M.; Santos, J.L. Labeling Methods for the General Case of the Multi-objective Shortest Path Problem—A Computational Study. In Computational Intelligence and Decision Making: Trends and Applications; Madureira, A., Reis, C., Marques, V., Eds.; Intelligent Systems, Control and Automation: Science and Engineering; Springer: Dordrecht, The Netherlands, 2013; Volume 61, pp. 489–502. [Google Scholar] [CrossRef]
- Carlyle, W.M.; Wood, R.K. Near-shortest and -shortest simple paths. Networks 2005, 46, 98–109. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Ford, L.R. Network Flow Theory; Technical Report P-923; RAND Corporation: Santa Monica, CA, USA, 1956. [Google Scholar]
- Bellman, R. On a routing problem. Q. Appl. Math. 1958, 16, 87–90. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Grabisch, M.; Labreuche, C. A decade of application of the Choquet and Sugeno integrals in multi-criteria decision aid. Ann. Oper. Res. 2010, 175, 247–286. [Google Scholar] [CrossRef]
- Grabisch, M. Fuzzy integral in multicriteria decision making. Fuzzy Sets Syst. 1995, 69, 279–298. [Google Scholar] [CrossRef]
- Hu, X.-B.; Wang, M.; Leeson, M.S.; Di Paolo, E.A.; Liu, H. Deterministic Agent-Based Path Optimization by Mimicking the Spreading of Ripples. Evol. Comput. 2016, 24, 319–346. [Google Scholar] [CrossRef]
- Lozano, L.; Medaglia, A.L. On an exact method for the constrained shortest path problem. Comput. Oper. Res. 2013, 40, 378–384. [Google Scholar] [CrossRef]
- Martins, E.Q.V. An algorithm for ranking paths that may contain cycles. Eur. J. Oper. Res. 1984, 18, 123–130. [Google Scholar] [CrossRef]
- Müller-Hannemann, M.; Weihe, K. Pareto Shortest Paths is Often Feasible in Practice. In Proceedings of the 5th International Workshop on Algorithm Engineering (WAE 2001), Århus, Denmark, 28–31 August 2001; Brodal, G.S., Frigioni, D., Marchetti-Spaccamela, A., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2001; Volume 2141, pp. 185–197. [Google Scholar] [CrossRef]
- Martins, E.; Santos, J. A new shortest paths ranking algorithm. Investig. Oper. 2000, 20, 47–62. [Google Scholar]
- Martins, E.; Pascoal, M.; Santos, J. A new improvement for a shortest paths algorithm. Investig. Oper. 2001, 21, 47–60. [Google Scholar]
- Jiménez, V.M.; Marzal, A. Computing the Shortest Paths: A New Algorithm and an Experimental Comparison. In Proceedings of the 3rd International Workshop on Algorithm Engineering (WAE’99), London, UK, 19–21 July 1999; Vitter, J.S., Zaroliagis, C.D., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 1999; Volume 1668, pp. 15–29. [Google Scholar] [CrossRef]
- Guerriero, F.; Musmanno, R.; Lacagnina, V.; Pecorella, A. A Class of Label-Correcting Methods for the Shortest Paths Problem. Oper. Res. 2001, 49, 423–429. [Google Scholar] [CrossRef]
- Eppstein, D. Finding the k Shortest Paths. SIAM J. Comput. 1998, 28, 652–673. [Google Scholar] [CrossRef]
- Martins, E.Q.V.; Pascoal, M.M.B.; Santos, J.L.E. Deviation algorithms for ranking shortest paths. Int. J. Found. Comput. Sci. 1999, 10, 247–261. [Google Scholar] [CrossRef]
- Jiménez, V.; Marzal, A. A Lazy Version of Eppstein’s K Shortest Paths Algorithm. In Proceedings of the Second International Workshop on Experimental and Efficient Algorithms (WEA 2003), Ascona, Switzerland, 26–28 May 2003; Jansen, K., Margraf, M., Mastrolilli, M., Rolim, J.D.P., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2003; Volume 2647, pp. 179–191. [Google Scholar] [CrossRef]
- Yen, J.Y. Finding the K Shortest Loopless Paths in a Network. Manag. Sci. 1971, 17, 712–716. [Google Scholar] [CrossRef]
- Katoh, N.; Ibaraki, T.; Mine, H. An efficient algorithm for K shortest simple paths. Networks 1982, 12, 411–427. [Google Scholar] [CrossRef]
- Martins, E.Q.V.; Pascoal, M.M.B. A new implementation of Yen’s ranking loopless paths algorithm. 4OR 2003, 1, 121–133. [Google Scholar] [CrossRef]
- Ulungu, E.; Teghem, J. The two-phases method: An efficient procedure to solve biobjective combinatorial optimization problems. Found. Comput. Decis. Sci. 1995, 20, 149–165. [Google Scholar]
- Cohon, J.L. Multiobjective Programming and Planning; Mathematics in Science and Engineering; Academic Press: New York, NY, USA, 1978; Volume 140. [Google Scholar]
- Handler, G.Y.; Zang, I. A dual algorithm for the constrained shortest path problem. Networks 1980, 10, 293–309. [Google Scholar] [CrossRef]
- Pugliese, L.D.P.; Guerriero, F. A Reference Point Approach for the Resource Constrained Shortest Path Problems. Transp. Sci. 2013, 47, 247–265. [Google Scholar] [CrossRef]
- Martins, E.Q.V. On a special class of bicriterion path problems. Eur. J. Oper. Res. 1984, 17, 85–94. [Google Scholar] [CrossRef]
- Current, J.R.; Re Velle, C.S.; Cohon, J.L. The maximum covering/shortest path problem: A multiobjective network design and routing formulation. Eur. J. Oper. Res. 1985, 21, 189–199. [Google Scholar] [CrossRef]
- Current, J.; ReVelle, C.; Cohon, J. The Minimum-Covering/Shortest-Path Problem. Decis. Sci. 1988, 19, 490–503. [Google Scholar] [CrossRef]
- Current, J.R.; Revelle, C.S.; Cohon, J.L. The Median Shortest Path Problem: A Multiobjective Approach to Analyze Cost vs. Accessibility in the Design of Transportation Networks. Transp. Sci. 1987, 21, 188–197. [Google Scholar] [CrossRef]
- Pelegrín, B.; Fernández, P. On the sum-max bicriterion path problem. Comput. Oper. Res. 1998, 25, 1043–1054. [Google Scholar] [CrossRef]
- Gandibleux, X.; Beugnies, F.; Randriamasy, S. Martins’ algorithm revisited for multi-objective shortest path problems with a MaxMin cost function. 4OR 2006, 4, 47–59. [Google Scholar] [CrossRef]
- Pinto, L.L.; Bornstein, C.T.; Maculan, N. The tricriterion shortest path problem with at least two bottleneck objective functions. Eur. J. Oper. Res. 2009, 198, 387–391. [Google Scholar] [CrossRef]
- Pinto, L.L.; Pascoal, M.M.B. On algorithms for the tricriteria shortest path problems with two bottleneck objective functions. Comput. Oper. Res. 2010, 37, 1774–1779. [Google Scholar] [CrossRef]
- Iori, M.; Martello, S.; Pretolani, D. An aggregate label setting policy for the multi-objective shortest path problem. Eur. J. Oper. Res. 2010, 207, 1489–1496. [Google Scholar] [CrossRef]
- Bornstein, C.T.; Maculan, N.; Pascoal, M.; Pinto, L.L. Multiobjective combinatorial optimization problems with a cost and several bottleneck objective functions: An algorithm with reoptimization. Comput. Oper. Res. 2012, 39, 1969–1976. [Google Scholar] [CrossRef]
- Pascoal, M.; Captivo, M.E.; Clímaco, J.; Laranjeira, A. Bicriteria path problem minimizing the cost and minimizing the number of labels. 4OR 2013, 11, 275–294. [Google Scholar] [CrossRef]
- Torchiani, C.; Ohst, J.; Willems, D.; Ruzika, S. Shortest Paths with Shortest Detours: A Biobjective Routing Problem. J. Optim. Theory Appl. 2017, 174, 858–874. [Google Scholar] [CrossRef]
- Pascoal, M. The MinSum-MinHop and the MaxMin-MinHop bicriteria path problems. In Shortest Path Solvers. From Software to Wetware; Adamatzky, A., Ed.; Emergence, Complexity and Computation; Springer: Cham, Switzerland, 2018; Volume 32, pp. 73–98. [Google Scholar] [CrossRef]
- Rosen, J.B.; Sun, S.Z.; Xue, G.L. Algorithms for the quickest path problem and the enumeration of quickest paths. Comput. Oper. Res. 1991, 18, 579–584. [Google Scholar] [CrossRef]
- Martins, E.Q.V.; Santos, J.L.E. An algorithm for the quickest path problem. Oper. Res. Lett. 1997, 20, 195–198. [Google Scholar] [CrossRef]
- Martins, E.Q.V. An algorithm to determine a path with minimal cost/capacity ratio. Discret. Appl. Math. 1984, 8, 189–194. [Google Scholar] [CrossRef]
- Ahuja, R. Minimum cost-reliability ratio path problem. Comput. Oper. Res. 1988, 15, 83–89. [Google Scholar] [CrossRef]
- Chen, Y.L.; Chin, Y.H. The quickest path problem. Comput. Oper. Res. 1990, 17, 153–161. [Google Scholar] [CrossRef]
- Hansen, P.; Storchi, G.; Vovor, T. Paths with minimum range and ratio of arc lengths. Discret. Appl. Math. 1997, 78, 89–102. [Google Scholar] [CrossRef]
- Boffey, T.B.; Williams, R.C.; Pelegrín, B.; Fernandez, P. The Maximum Capacity Shortest Path Problem: Generation of Efficient Solution Sets. RAIRO Oper. Res. 2002, 36, 1–19. [Google Scholar] [CrossRef]
- Captivo, M.E.; Clímaco, J.; Figueira, J.; Martins, E.; Santos, J.L. Solving bicriteria 0-1 knapsack problems using a labeling algorithm. Comput. Oper. Res. 2003, 30, 1865–1886. [Google Scholar] [CrossRef]
- Park, C.K.; Lee, S.; Park, S. A label-setting algorithm for finding a quickest path. Comput. Oper. Res. 2004, 31, 2405–2418. [Google Scholar] [CrossRef]
- Soroush, H.M. Optimal paths in bi-attribute networks with fractional cost functions. Eur. J. Oper. Res. 2008, 190, 633–658. [Google Scholar] [CrossRef]
- Clímaco, J.C.N.; Pascoal, M.M.B. Finding non-dominated bicriteria shortest pairs of disjoint simple paths. Comput. Oper. Res. 2009, 36, 2892–2898. [Google Scholar] [CrossRef]
- Figueira, J.R.; Tavares, G.; Wiecek, M.M. Labeling algorithms for multiple objective integer knapsack problems. Comput. Oper. Res. 2010, 37, 700–711. [Google Scholar] [CrossRef]
- Laporte, G.; Pascoal, M.M.B. Minimum cost path problems with relays. Comput. Oper. Res. 2011, 38, 165–173. [Google Scholar] [CrossRef]
- Calvete, H.I.; del Pozo, L.; Iranzo, J.A. Algorithms for the quickest path problem and the reliable quickest path problem. Comput. Manag. Sci. 2012, 9, 255–272. [Google Scholar] [CrossRef]
- Ruzika, S.; Thiemann, M. Min-Max quickest path problems. Networks 2012, 60, 253–258. [Google Scholar] [CrossRef]
- Ghiani, G.; Guerriero, E. A lower bound for the quickest path problem. Comput. Oper. Res. 2014, 50, 154–160. [Google Scholar] [CrossRef]
- Sedeño-Noda, A.; González-Barrera, J.D. Fast and fine quickest path algorithm. Eur. J. Oper. Res. 2014, 238, 596–606. [Google Scholar] [CrossRef]
- Calvete, H.I.; del-Pozo, L.; Iranzo, J.A. The energy-constrained quickest path problem. Optim. Lett. 2017, 11, 1319–1339. [Google Scholar] [CrossRef]
- Pascoal, M.M.B.; Clímaco, J.C.N. On a relaxed maximally disjoint path pair problem: A bicriteria approach. Int. Trans. Oper. Res. 2020, 27, 2045–2063. [Google Scholar] [CrossRef]
- Moghanni, A.; Pascoal, M.; Godinho, M.T. Finding shortest and dissimilar paths. Int. Trans. Oper. Res. 2022, 29, 1573–1601. [Google Scholar] [CrossRef]
- Moore, M.H. On the Fastest Route for Convoy-Type Traffic in Flowrate-Constrained Networks. Transp. Sci. 1976, 10, 113–124. [Google Scholar] [CrossRef]
- Pascoal, M.M.B.; Captivo, M.E.V.; Clímaco, J.C.N. A comprehensive survey on quickest path problem. Ann. Oper. Res. 2006, 147, 5–21. [Google Scholar] [CrossRef]
- Warburton, A. Approximation of Pareto Optima in Multiple-Objective, Shortest-Path Problems. Oper. Res. 1987, 35, 70–79. [Google Scholar] [CrossRef]
- Breugem, T.; Dollevoet, T.; van den Heuvel, W. Analysis of FPTASes for the multi-objective shortest path problem. Comput. Oper. Res. 2017, 78, 44–58. [Google Scholar] [CrossRef]
- Tsaggouris, G.; Zaroliagis, C. Multiobjective Optimization: Improved FPTAS for Shortest Paths and Non-Linear Objectives with Applications. Theor. Comput. Syst. 2009, 45, 162–186. [Google Scholar] [CrossRef]
- Bökler, F.; Chimani, M. Approximating Multiobjective Shortest Path in Practice. In Proceedings of the Twenty-Second Workshop on Algorithm Engineering and Experiments (ALENEX), Salt Lake City, UT, USA, 5–6 January 2020; pp. 120–133. [Google Scholar] [CrossRef]
- de las Casas, P.M.; Borndörfer, R.; Kraus, L.; Sedeño-Noda, A. An FPTAS for Dynamic Multiobjective Shortest Path Problems. Algorithms 2021, 14, 43. [Google Scholar] [CrossRef]
- Girão-Silva, R.; Craveirinha, J.; Clímaco, J. Hierarchical Multiobjective Routing in MPLS Networks with Two Service Classes—A Meta-Heuristic Solution. J. Telecommun. Inform. Technol. 2009, 3, 20–37. [Google Scholar] [CrossRef]
- Liu, L.; Mu, H.; Luo, H.; Li, X. A simulated annealing for multi-criteria network path problems. Comput. Oper. Res. 2012, 39, 3119–3135. [Google Scholar] [CrossRef]
- Wang, Y.; Li, X.; Ruiz, R. A Fast Algorithm for Finding the Bi-objective Shortest Path in Complicated Networks. In Proceedings of the 2018 IEEE 22nd International Conference on Computer Supported Cooperative Work in Design (CSCWD), Nanjing, China, 9–11 May 2018; pp. 104–109. [Google Scholar] [CrossRef]
- Sousa, P.; Cortez, P.; Rio, M.; Rocha, M. Traffic Engineering Approaches Using Multicriteria Optimization Techniques. In Proceedings of the 9th IFIP TC6 International Conference on Wired/Wireless Internet Communications, WWIC 2011, Vilanova i la Geltrú, Spain, 15–17 June 2011; Masip-Bruin, X., Verchere, D., Tsaoussidis, V., Yannuzzi, M., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2011; Volume 6649, pp. 104–115. [Google Scholar] [CrossRef]
- Onety, R.E.; Tadei, R.; Neto, O.M.; Takahashi, R.H. Multiobjective optimization of MPLS-IP networks with a variable neighborhood genetic algorithm. Appl. Soft Comput. 2013, 13, 4403–4412. [Google Scholar] [CrossRef]
- Zheng, S.; Zheng, C.; Li, W. Research on Multiobjective Shortest Path Based on Genetic Algorithm. In Proceedings of the 2022 2nd International Conference on Computer Science and Blockchain (CCSB), Wuhan, China, 28–30 October 2022; pp. 127–130. [Google Scholar] [CrossRef]
- Granata, D.; Sgalambro, A. A hybrid modified-NSGA-II VNS algorithm for the Multi-Objective Critical Disruption Path Problem. Comput. Oper. Res. 2023, 160, 106363:1–106363:14. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evolut. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm; TIK Report 103; Computer Engineering and Networks Laboratory, ETH Zurich: Zurich, Switzerland, 2001. [Google Scholar] [CrossRef]
- Gao, Y.; Guan, H.; Qi, Z.; Hou, Y.; Liu, L. A multi-objective ant colony system algorithm for virtual machine placement in cloud computing. J. Comput. Syst. Sci. 2013, 79, 1230–1242. [Google Scholar] [CrossRef]
- Coello Coello, C.A.; Lechuga, M.S. MOPSO: A proposal for multiple objective particle swarm optimization. In Proceedings of the 2002 Congress on Evolutionary Computation (CEC’02), Honolulu, HI, USA, 12–17 May 2002; Volume 2, pp. 1051–1056. [Google Scholar] [CrossRef]
- He, F.; Qi, H.; Fan, Q. An Evolutionary Algorithm for the Multi-objective Shortest Path Problem. In Proceedings of the 2007 International Conference on Intelligent Systems and Knowledge Engineering (ISKE 2007), Chengdu, China, 15–16 October 2007; Advances in Intelligent Systems Research. Atlantis Press: Amsterdam, The Netherlands, 2007; pp. 1276–1280. [Google Scholar] [CrossRef]
- Masoumi, Z.; Van Genderen, J.; Sadeghi Niaraki, A. An improved ant colony optimization-based algorithm for user-centric multi-objective path planning for ubiquitous environments. Geocarto Int. 2021, 36, 137–154. [Google Scholar] [CrossRef]
- Lourenço, A.L.F.; César, A.C. A deep neural network with a fuzzy multi-objective optimization model for fault analysis in an elastic optical network. Opt. Switch. Netw. 2022, 43, 100644:1–100644:13. [Google Scholar] [CrossRef]
- Resende, M.G.C.; Ribeiro, C.C. Greedy Randomized Adaptive Search Procedures. In Handbook of Metaheuristics; Glover, F., Kochenberger, G.A., Eds.; International Series in Operations Research & Management Science; Springer: Boston, MA, USA, 2003; Volume 57, pp. 219–249. [Google Scholar] [CrossRef]
- Wijeratne, A.B.; Turnquist, M.A.; Mirchandani, P.B. Multiobjective routing of hazardous materials in stochastic networks. Eur. J. Oper. Res. 1993, 65, 33–43. [Google Scholar] [CrossRef]
- Halman, N.; Kovalyov, M.Y.; Quilliot, A.; Shabtay, D.; Zofi, M. Bi-criteria path problem with minimum length and maximum survival probability. OR Spectr. 2019, 41, 469–489. [Google Scholar] [CrossRef]
- Majumder, S.; Kar, S. Multi-criteria shortest path for rough graph. J. Amb. Intel. Hum. Comput. 2018, 9, 1835–1859. [Google Scholar] [CrossRef]
- Majumder, S.; Kar, M.B.; Kar, S.; Pal, T. Uncertain programming models for multi-objective shortest path problem with uncertain parameters. Soft Comput. 2020, 24, 8975–8996. [Google Scholar] [CrossRef]
- Okada, S.; Soper, T. A shortest path problem on a network with fuzzy arc lengths. Fuzzy Set. Syst. 2000, 109, 129–140. [Google Scholar] [CrossRef]
- Bagheri, M.; Ebrahimnejad, A.; Razavyan, S.; Lotfi, F.H.; Malekmohammadi, N. Solving fuzzy multi-objective shortest path problem based on data envelopment analysis approach. Compl. Intell. Syst. 2021, 7, 725–740. [Google Scholar] [CrossRef]
- Ma, Y.-M.; Hu, X.-B.; Zhou, H. A deterministic and nature-inspired algorithm for the fuzzy multi-objective path optimization problem. Complex Intell. Syst. 2023, 9, 753–765. [Google Scholar] [CrossRef]
- Craveirinha, J.; Girão-Silva, R.; Clímaco, J. A meta-model for multiobjective routing in MPLS networks. Cent. Eur. J. Oper. Res. 2008, 16, 79–105. [Google Scholar] [CrossRef]
- Pióro, M.; Medhi, D. Routing, Flow, and Capacity Design in Communication and Computer Networks; The Morgan Kaufmann Series in Networking; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar] [CrossRef]
- Medhi, D.; Ramasamy, K. Network Routing—Algorithms, Protocols, and Architectures, 2nd ed.; The Morgan Kaufmann Series in Networking; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar] [CrossRef]
- Mitra, D.; Morrison, J.A.; Ramakrishnan, K. Optimization and design of network routing using refined asymptotic approximations. Perform. Eval. 1999, 36–37, 267–288. [Google Scholar] [CrossRef]
- Steuer, R.E. Multiple Criteria Optimization: Theory, Computation, and Application; Probability and Mathematical Statistics; Wiley: Hoboken, NJ, USA, 1986. [Google Scholar]
- Widyono, R. The Design and Evaluation of Routing Algorithms for Real-Time Channels; Technical Report TR-94-024; University of California at Berkeley & International Computer Science Institute: Berkeley, CA, USA, 1994. [Google Scholar]
- van der Zee, M.; Heijenk, G. Quality of Service Routing: State of the Art Report; Report 1/0362-FCP NB 102 88 Uen; Centre for Telematics and Information Technology (CTIT): Enschede, The Netherlands, 1999. [Google Scholar]
- Sobrinho, J. Algebra and algorithms for QoS path computation and hop-by-hop routing in the Internet. IEEE/ACM Trans. Netw. 2002, 10, 541–550. [Google Scholar] [CrossRef]
- Kuipers, F.A.; Korkmaz, T.; Krunz, M.; Van Mieghem, P. A Review of Constraint-Based Routing Algorithms; Technical Report; Delft University of Technology: Delft, The Netherlands, 2002. [Google Scholar]
- Kuipers, F.A.; Van Mieghem, P. Conditions that impact the complexity of QoS routing. IEEE/ACM Trans. Netw. 2005, 13, 717–730. [Google Scholar] [CrossRef]
- Kuipers, F.; Orda, A.; Raz, D.; Van Mieghem, P. A comparison of exact and -approximation algorithms for constrained routing. In Proceedings of the NETWORKING 2006—Networking Technologies, Services, and Protocols; Performance of Computer and Communication Networks; Mobile and Wireless Communications Systems, 5th International IFIP-TC6 Networking Conference, Coimbra, Portugal, 15–19 May 2006; Boavida, F., Plagemann, T., Stiller, B., Westphal, C., Monteiro, E., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2006; Volume 3976, pp. 197–208. [Google Scholar]
- Sobrinho, J.L.; Ferreira, M.A. Routing on Multiple Optimality Criteria. In Proceedings of the SIGCOMM’20: Proceedings of the Annual Conference of the ACM Special Interest Group on Data Communication on the Applications, Technologies, Architectures, and Protocols for Computer Communication, Virtual Event, 10–14 August 2020; pp. 211–225. [Google Scholar] [CrossRef]
- Gomes, T.; Jorge, L.; Melo, P.; Girão-Silva, R. Maximally node and SRLG-disjoint path pair of min-sum cost in GMPLS networks: A lexicographic approach. Photonic Netw. Commun. 2016, 31, 11–22. [Google Scholar] [CrossRef]
- Xu, D.; Xiong, Y.; Qiao, C. Novel algorithms for shared segment protection. IEEE J. Sel. Area Commun. 2003, 21, 1320–1331. [Google Scholar] [CrossRef]
- Oki, E.; Matsuura, N.; Shiomoto, K.; Yamanaka, N. A disjoint path selection scheme with shared risk link groups in GMPLS networks. IEEE Commun. Lett. 2002, 6, 406–408. [Google Scholar] [CrossRef]
- Pascoal, M.; Craveirinha, J.; Clímaco, J. An exact lexicographic approach for the maximally risk-disjoint/minimal cost path pair problem in telecommunication networks. TOP 2022, 30, 405–425. [Google Scholar] [CrossRef]
- Dinitz, Y.; Dolev, S.; Kumar, M. Polynomial Time k-Shortest Multi-criteria Prioritized and All-Criteria-Disjoint Paths. In Proceedings of the Cyber Security Cryptography and Machine Learning. 5th International Symposium, CSCML 2021, Be’er Sheva, Israel, 8–9 July 2021; Dolev, S., Margalit, O., Pinkas, B., Schwarzmann, A., Eds.; Lecture Notes in Computer Science. Springer: Cham, Switzerland, 2021; Volume 12716, pp. 266–274. [Google Scholar] [CrossRef]
- Akhmedov, M. Faster 2-Disjoint-Shortest-Paths Algorithm. In Computer Science—Theory and Applications, Proceedings of the 15th International Computer Science Symposium in Russia (CSR 2020), Yekaterinburg, Russia, 29 June-3 July 2020; Lecture Notes in Computer Science; Fernau, H., Ed.; Springer: Cham, Switzerland, 2020; Volume 12159, pp. 103–116. [Google Scholar] [CrossRef]
- Clímaco, J.C.; Pascoal, M.M.; Craveirinha, J.M.; Captivo, M.E.V. Internet packet routing: Application of a K-quickest path algorithm. Eur. J. Oper. Res. 2007, 181, 1045–1054. [Google Scholar] [CrossRef]
- Pascoal, M.M.; Captivo, M.E.V.; Clímaco, J.C. An algorithm for ranking quickest simple paths. Comput. Oper. Res. 2005, 32, 509–520. [Google Scholar] [CrossRef]
- Antunes, C.H.; Craveirinha, J.; Clímaco, J.; Barrico, C. A multiple objective routing algorithm for integrated communication networks. In Proceedings of the 16th International Teletraffic Congress (ITC16)—Teletraffic Engineering in a Competitive World, Edinburgh, UK, 7–11 August 1999; Key, P., Smith, D., Eds.; Teletraffic Science and Engineering. Elsevier: Amsterdam, The Netherlands; Volume 3b, pp. 1291–1300. [Google Scholar]
- Pornavalai, C.; Chakraborty, G.; Shiratori, N. Routing with multiple QoS requirements for supporting multimedia applications. Telecommun. Syst. 1998, 9, 357–373. [Google Scholar] [CrossRef]
- Beugnies, F.; Gandibleux, X. A multiobjective routing procedure for IP networks. In Proceedings of the 18th International Conference on Multiple Criteria Decision Analysis (MCDM 2006), Chania, Greece, 19–23 June 2006. [Google Scholar]
- Bhat, S.; Rouskas, G.N. On routing algorithms for open marketplaces of path services. In Proceedings of the 2016 IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 22–27 May 2016. [Google Scholar] [CrossRef]
- Assi, C.; Shami, A.; Ali, M.A.; Kurtz, R.; Guo, D. Optical networking and real-time provisioning: An integrated vision for the next-generation Internet. IEEE Netw. 2001, 15, 36–45. [Google Scholar] [CrossRef]
- Markovic, G.; Acimovic-Raspopovic, V. An Adaptive Multi-criteria Routing Algorithm for Wavelength Routed Optical Networks. In Proceedings of the EUROCON 2005—The International Conference on “Computer as a Tool”, Belgrade, Serbia, 21–24 November 2005; pp. 1353–1356. [Google Scholar] [CrossRef]
- Gomes, T.; Craveirinha, J.; Clímaco, J.; Simões, C. A bicriteria routing model for multi-fibre WDM networks. Photonic Netw. Commun. 2009, 18, 287–299. [Google Scholar] [CrossRef]
- Gomes, T.; Martins, L.; Silva, J.; Ferreira, N.G.; Craveirinha, J.; Clímaco, J.; Cadime, R.; Mónica, C. Protected bicriteria paths in transport networks. In Proceedings of the 2012 IV International Congress on Ultra Modern Telecommunications and Control Systems, St. Petersburg, Russia, 3–5 October 2012; pp. 731–737. [Google Scholar] [CrossRef]
- Craveirinha, J.; Pascoal, M.; Clímaco, J. An exact approach for finding bicriteria maximally SRLG-disjoint/shortest path pairs in telecommunication networks. INFOR Inform. Syst. Oper. Res. 2023, 61, 399–418. [Google Scholar] [CrossRef]
- Xu, X.; Liu, X.; Qian, L.; Zhang, N.; Wu, J.; Tang, H. Multi-Criteria Path Finding Using Multi-Queues Based Bidirectional Search for Multiple Target Nodes in Networks. IEEE Access 2023, 11, 101799–101812. [Google Scholar] [CrossRef]
- Chen, X.; Cai, H.; Wolf, T. Multi-criteria Routing in Networks with Path Choices. In Proceedings of the 2015 IEEE 23rd International Conference on Network Protocols (ICNP), San Francisco, CA, USA, 10–13 November 2015; pp. 334–344. [Google Scholar] [CrossRef]
- Martins, L.; Craveirinha, J.; Clímaco, J.N.; Gomes, T. On a bi-dimensional dynamic alternative routing method. Eur. J. Oper. Res. 2005, 166, 828–842. [Google Scholar] [CrossRef]
- Kelly, F. Routing in Circuit-Switched Networks: Optimization, Shadow Prices and Decentralization. Adv. Appl. Probab. 1988, 20, 112–144. [Google Scholar] [CrossRef]
- Girão-Silva, R.; Craveirinha, J.; Clímaco, J. Hierarchical multiobjective routing in Multiprotocol Label Switching networks with two service classes: A heuristic solution. Int. Trans. Oper. Res. 2009, 16, 275–305. [Google Scholar] [CrossRef]
- Craveirinha, J.; Girão-Silva, R.; Clímaco, J.; Martins, L. A Hierarchical Multiobjective Routing Model for MPLS Networks with Two Service Classes. In Proceedings of the 23rd IFIP TC7 Conference on System Modeling and Optimization CSMO 2007, Cracow, Poland, 23–27 July 2007; Korytowski, A., Malanowski, K., Mitkowski, W., Szymkat, M., Eds.; Revised Selected Papers (IFIP Advances in Information and Communication Technology). Springer: Berlin/Heidelberg, Germany, 2009; Volume 312, pp. 196–219. [Google Scholar] [CrossRef]
- Yuan, D. A bicriteria optimization approach for robust OSPF routing. In Proceedings of the 3rd IEEE Workshop on IP Operations & Management (IPOM 2003), Kansas City, MO, USA, 3 October 2003; pp. 91–98. [Google Scholar] [CrossRef]
- Thirumalasetty, S.; Medhi, D. MPLS Traffic Engineering for Survivable Book-Ahead Guaranteed Services; Report; University of Missouri—Kansas City: Kansas City, MO, USA, 2001. [Google Scholar]
- Erbas, S.C. Utilizing evolutionary algorithms for multiobjective problems in traffic engineering. In Proceedings of the INOC 2003: International Network Optimization Conference, Paris, France, 27–29 October 2003; Ben-Ameur, W., Petrowski, A., Eds.; Institut National des Télécommunications: Palaiseau, France, 2003; pp. 207–212. [Google Scholar]
- Girão-Silva, R.; Craveirinha, J.; Clímaco, J.; Captivo, M.E. Multiobjective routing in multiservice MPLS networks with traffic splitting—A network flow approach. J. Syst. Sci. Syst. Eng. 2015, 24, 389–432. [Google Scholar] [CrossRef]
- Messac, A.; Ismail-Yahaya, A.; Mattson, C. The normalized normal constraint method for generating the Pareto frontier. Struct. Multidiscip. Optim. 2003, 25, 86–98. [Google Scholar] [CrossRef]
- Girão-Silva, R.; Craveirinha, J.; Gomes, T.; Martins, L.; Clímaco, J.; Campos, J. A network-wide exact optimization approach for multiobjective routing with path protection in multiservice multiprotocol label switching networks. Eng. Optim. 2017, 49, 1226–1246. [Google Scholar] [CrossRef]
- Malakooti, B.; Thomas, I. A Distributed Composite Multiple Criteria Routing Using Distance Vector. In Proceedings of the 2006 IEEE International Conference on Networking, Sensing and Control, Ft. Lauderdale, FL, USA, 23–25 April 2006; pp. 42–47. [Google Scholar] [CrossRef]
- Guerriero, F.; De Rango, F.; Marano, S.; Bruno, E. A biobjective optimization model for routing in mobile ad hoc networks. Appl. Math. Model. 2009, 33, 1493–1512. [Google Scholar] [CrossRef]
- Bhunia, S.S.; Roy, S.; Mukherjee, N. Adaptive learning assisted routing in Wireless Sensor Network using Multi Criteria Decision model. In Proceedings of the 2014 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Delhi, India, 24–27 September 2014; pp. 2149–2154. [Google Scholar] [CrossRef]
- Das, B.; Bhunia, S.S.; Roy, S.; Mukherjee, N. Multi criteria routing in wireless sensor network using weighted product model and relative rating. In Proceedings of the 2015 Applications and Innovations in Mobile Computing (AIMoC), Kolkata, India, 12–14 February 2015; pp. 132–136. [Google Scholar] [CrossRef]
- Suh, Y.H.; Kim, K.T.; Shin, D.R.; Youn, H.Y. Traffic-Aware Energy Efficient Routing (TEER) Using Multi-Criteria Decision Making for Wireless Sensor Network. In Proceedings of the 2015 5th International Conference on IT Convergence and Security (ICITCS), Kuala Lumpur, Malaysia, 24–27 August 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Rehena, Z.; Roy, S.; Mukherjee, N. Multi-criteria Routing in a Partitioned Wireless Sensor Network. Wirel. Pers. Commun. 2017, 94, 3415–3449. [Google Scholar] [CrossRef]
- Sahli, N.; Jabeur, N.; Khan, I.M.; Badra, M. Towards a Generic Framework for Wireless Sensor Network Multi-Criteria Routing. In Proceedings of the 2012 5th International Conference on New Technologies, Mobility and Security (NTMS), Istanbul, Turkey, 7–10 May 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Gouveia, L.; Patrício, P.; de Sousa, A. Lexicographical minimization of routing hops in hop-constrained node survivable networks. Telecommun. Syst. 2016, 62, 417–434. [Google Scholar] [CrossRef]
- Naseri, A.; Ahmadi, M.; PourKarimi, L. Reduction of energy consumption and delay of control packets in Software-Defined Networking. Sustain. Comput. Infor. Syst. 2021, 31, 100574:1–100574:16. [Google Scholar] [CrossRef]
- Çetinkaya, E.K.; Sterbenz, J.P. A taxonomy of network challenges. In Proceedings of the 2013 9th International Conference on the Design of Reliable Communication Networks (DRCN), Budapest, Hungary, 4–7 March 2013; pp. 322–330. [Google Scholar]
- Rak, J.; Pickavet, M.; Trivedi, K.S.; Lopez, J.A.; Koster, A.M.; Sterbenz, J.P.; Çetinkaya, E.K.; Gomes, T.; Gunkel, M.; Walkowiak, K.; et al. Future research directions in design of reliable communication systems. Telecommun. Syst. 2015, 60, 423–450. [Google Scholar] [CrossRef]
- Long, X.; Tipper, D.; Gomes, T. Measuring the survivability of networks to geographic correlated failures. Opt. Switch. Netw. 2014, 14, 117–133. [Google Scholar] [CrossRef]
- Rak, J.; Girão-Silva, R.; Gomes, T.; Ellinas, G.; Kantarci, B.; Tornatore, M. Disaster resilience of optical networks: State of the art, challenges, and opportunities. Opt. Switch. Netw. 2021, 42, 100619:1–100619:28. [Google Scholar] [CrossRef]
- Godinho, M.T.; Pascoal, M. Implementation of Geographic Diversity in Resilient Telecommunication Networks. In Proceedings of the Operational Research. IO 2022—OR in Turbulent Times: Adaptation and Resilience, Évora, Portugal, 6–8 November 2022; Almeida, J.P., Alvelos, F.P., Cerdeira, J.O., Moniz, S., Requejo, C., Eds.; Springer Proceedings in Mathematics & Statistics. Springer: Cham, Switzerland, 2023; Volume 437, pp. 89–98. [Google Scholar] [CrossRef]
- Martins, L.; Gomes, T.; Tipper, D. Efficient heuristics for determining node-disjoint path pairs visiting specified nodes. Networks 2017, 70, 292–307. [Google Scholar] [CrossRef]
- Ogorodnikov, Y.; Rudakov, R.; Khachai, D.; Khachay, M. A Problem-Specific Branch-and-Bound Algorithm for the Protected Shortest Simple Path Problem with Must-Pass Nodes. IFAC PapersOnLine 2022, 55, 572–577. [Google Scholar] [CrossRef]
- Wiatr, P.; Monti, P.; Wosinska, L. Power savings versus network performance in dynamically provisioned WDM networks. IEEE Commun. Mag. 2012, 50, 48–55. [Google Scholar] [CrossRef]
- Contreras, L.M.; López, V.; de Dios, Ó.G.; Tovar, A.; Muñoz, F.; Azanon, A.; Fernández-Palacios, J.P.; Folgueira, J. Toward cloud-ready transport networks. IEEE Commun. Mag. 2012, 50, 48–55. [Google Scholar] [CrossRef]
- Chatterjee, B.C.; Sarma, N.; Oki, E. Routing and Spectrum Allocation in Elastic Optical Networks: A Tutorial. IEEE Commun. Surv. Tutor. 2015, 17, 1776–1800. [Google Scholar] [CrossRef]
- Szcześniak, I.; Jajszczyk, A.; Woźna-Szcześniak, B. Generic Dijkstra for optical networks. J. Opt. Commun. Netw. 2019, 11, 568–577. [Google Scholar] [CrossRef]
- Olszewski, I. Improved dynamic routing algorithms in elastic optical networks. Photonic Netw. Commun. 2017, 34, 323–333. [Google Scholar] [CrossRef]
- Ruiz, L.; Durán Barroso, R.J.; De Miguel, I.; Merayo, N.; Aguado, J.C.; Abril, E.J. Routing, Modulation and Spectrum Assignment Algorithm Using Multi-Path Routing and Best-Fit. IEEE Access 2021, 9, 111633–111650. [Google Scholar] [CrossRef]
- Bouchmal, O.; Cimoli, B.; Stabile, R.; Olmos, J.J.V.; Monroy, I.T. From classical to quantum machine learning: Survey on routing optimization in 6G software defined networking. Front. Commun. Netw. 2023, 4, 1220227:1–1220227:20. [Google Scholar] [CrossRef]
- Urgelles, H.; Picazo-Martinez, P.; Garcia-Roger, D.; Monserrat, J.F. Multi-Objective Routing Optimization for 6G Communication Networks Using a Quantum Approximate Optimization Algorithm. Sensors 2022, 22, 7570. [Google Scholar] [CrossRef] [PubMed]
- El Amri, A.; Meddeb, A. Optimal traffic routing in the network virtualization context. Int. J. Commun. Syst. 2021, 34, e4846:1–e4846:19. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).