Abstract
Cyclic air braking is a key element for ensuring safe train operation when running on a long and steep downhill railway section. In reality, the cyclic braking performance of a train is affected by its operating environment, speed and air-refilling time. Existing optimization algorithms have the problem of low learning efficiency. To solve this problem, an intelligent control method based on the deep Q-network (DQN) algorithm for heavy-haul trains running on long and steep downhill railway sections is proposed. Firstly, the environment of heavy-haul train operation is designed by considering the line characteristics, speed limits and constraints of the train pipe’s air-refilling time. Secondly, the control process of heavy-haul trains running on long and steep downhill sections is described as the reinforcement learning (RL) of a Markov decision process. By designing the critical elements of RL, a cyclic braking strategy for heavy-haul trains is established based on the reinforcement learning algorithm. Thirdly, the deep neural network and Q-learning are combined to design a neural network for approximating the action value function so that the algorithm can achieve the optimal action value function faster. Finally, simulation experiments are conducted on the actual track data pertaining to the Shuozhou–Huanghua line in China to compare the performance of the Q-learning algorithm against the DQN algorithm. Our findings revealed that the DQN-based intelligent control strategy decreased the air braking distance by 2.1% and enhanced the overall average speed by more than 7%. These experiments unequivocally demonstrate the efficacy and superiority of the DQN-based intelligent control strategy.
1. Introduction
Heavy-haul train transportation has been widely valued around the world due to its advantages such as large capacity, high efficiency and low transportation cost. When heavy-haul trains run on long and steep downhill railway sections, cyclic air braking is needed for controlling the train speed [1]. At present, the utilization of air braking mainly relies on the driving experience of the driver. However, existing braking methods based on drivers’ experience cannot meet the safety and efficiency requirements of heavy-haul train operation [2]. Therefore, it is of great importance to develop an intelligent control strategy for the cyclic braking of heavy-haul trains running on long and steep downhill sections [3].
To date, air braking methods for heavy-haul trains running on long and steep downhill railway sections have been studied in-depth by many researchers. The main solutions can be classified into imitation learning methods based on expert data, numerical solution methods based on an optimal train control models, and reinforcement learning based on a Markov decision process.
In terms of imitation learning based on expert data, it is necessary to provide data on experts’ driving courses during the training stage to simulate an expert’s driving behavior in a supervised manner. For example, Ref. [4] combined expert data with the concept of generative adversarial learning and proposed a representative generative adversarial imitation learning algorithm. Ref. [5] integrated expert data with reinforcement learning to train a new intelligent driving control strategy. The reinforcement learning algorithm supervised by the expert model was able to make the operation more efficient and stable. However, this type of imitation learning method did not directly establish safety assessments and constraints, and the expert data it used failed to fully cover special emergency traffic situations.
In terms of research on numerical solutions based on train optimal control models, Pontryagin’s Maximum Principle (PMP) was employed in ref. [6] to ascertain the most effective driving approach for controlling trains through the use of generalized motion equations. By considering line conditions, such as different slopes and different speed limits, a version of the key equation for train traction energy consumption was proposed, and it was used to calculate the speed of train cyclic braking. Ref. [7] established an optimized model based on a train dynamic model, and integrated the artificial bee colony algorithm to find the appropriate switching points of different states and develop an optimal operation strategy for heavy-haul trains running on long and steep downhill railway sections. Ref. [8] combined an approximate model of data-learning systems with model predictive control to solve planning problems with safety constraints. Ref. [9] considered the energy consumption and comfort of a heavy-haul train when determining the optimal strategy for cyclic braking. Two methods were implemented, including a pseudo-spectral method and a mixed-integer linear programming method, to develop an optimal driving strategy for the train. However, this type of method requires comprehensive data to build the model. Moreover, the accuracy of the model has a strong influence. Therefore, the problem of model bias under complex uncertainty scenarios is prominent.
Reinforcement learning algorithms based on a Markov decision process have been increasingly applied to the intelligent control of trains in recent years. Ref. [10] proposed an optimal model of operation energy consumption leveraging a Q-learning algorithm. Then, a cyclic braking strategy was developed based on the train status value function to solve the problems of train punctuality and energy-saving operation optimization. Ref. [11] designed an intelligent train control method using a reinforcement learning algorithm based on policy gradient. The performance of the agent was continuously optimized to realize the self-learning process of the controller. An improved Q-learning algorithm was proposed in Reference [12]. The target reward for energy consumption and time are updated in different ways. In Reference [13], a Q-SARSA algorithm was proposed by combining Q-learning and the SARSA update rules, which considerably improved the efficiency of subway operations by combining deep fully connected neural networks with it. These methods can achieve cyclic braking, energy savings and emission reduction in a heavy-haul train without the need for a pre-designed reference speed curve. However, the state space in this algorithm is discretized, which results in slow convergence of the optimization algorithm during the learning process and the curse of dimensionality problem. Thereafter, ref. [14] proposed a reinforcement learning algorithm based on two-stage action sampling to solve the combinatorial optimization problem in heavy-haul railway scheduling. This approach not only alleviates the curse of dimensionality but also naturally satisfies the optimization objective and complex constraints. Ref. [15] proposes a reinforcement learning method for multi-objective speed trajectory optimization to simultaneously achieve energy efficiency, punctuality and accurate parking. Ref. [16] employed a double-switch Q-network (DSQ network) architecture to achieve fast approximation of the action value function and enhance the parameter sharing of states and actions. However, the methods used in refs. [14,15,16] still cannot make full use of the large amount of unstructured data generated during train operation, that is, the data utilization rate is reduced. Furthermore, in the design of a train model, the environmental characteristics of heavy-haul trains running on long and steep downhill railway sections are not considered. Therefore, it is difficult to apply such models to the optimal control of heavy-haul trains running on long and steep downhill sections.
Based on the above works, an intelligent algorithm utilizing DQN for the cyclic braking of heavy-haul trains is proposed in this paper to solve the problem of the cyclic air braking of heavy-haul trains traversing lengthy and steep downhill railway sections. The main contributions of this work are as follows:
(1) A model with operation constraints is constructed for heavy-haul trains equipped with a conventional pneumatic braking system and traversing lengthy and steep downhill railway sections. In addition, the performance indexes of a train running on a long and steep downhill section are introduced to evaluate the control performance of the heavy-haul train.
(2) The action value functions are approximated based on a neural network. In accordance with the Q-learning algorithm, the neural network is combined with reinforcement learning to avoid the occurrence of the curse of dimensionality inherent in the Q-learning algorithm. Therefore, this method is suitable for solving the train control problem characterized by continuous state space.
(3) A prioritized experience replay mechanism is proposed. The samples are prioritized and selected according to their importance so that important and high-reward samples are selected and trained more frequently. Therefore, the learning efficiency of the algorithm is improved for important samples, which accelerates the convergence speed of the algorithm. As a result, the performance of the algorithm can be improved.
The rest of this paper is organized as follows: In Section 1, the design of the control model for heavy-haul trains is presented. The constraints of the train operation and the performance indexes of the train control are introduced into the model. The train control problems of a heavy-haul train running on a long and steep downhill section are described in detail. In Section 2, a cyclic air braking method based on the DQN algorithm is established for heavy-haul trains. In Section 3, the validity and robustness of the proposed method are verified via simulation. Finally, the conclusions of this study are summarized in Section 4.
2. Model Construction for Heavy-Haul Trains
2.1. Dynamic Model
During the operation of a heavy-haul train, factors such as track gradient, train composition and on-board mass cause the train to be subjected to diverse forces. In this study, the interaction forces between the cars are not taken into account when calculating the additional resistance. Therefore, the forces imposed on the train during operation mainly include locomotive traction force, braking force (including electric braking and pneumatic braking), basic running resistance and additional resistance. Essentially, a heavy-haul train is a distributed power network system consisting of multiple locomotives and freight cars. According to the Newtonian principle of dynamics, the mathematical expression of each train model can be defined as follows [17]:
Usually, the running resistance encountered by a heavy-haul train during braking on a long and steep downhill section is mainly composed of basic resistance and additional resistance . These resistances depend on the operating speed of the heavy-haul train as well as its physical characteristics [18]. The running resistance is calculated as follows:
According to previous research, the calculation formula of the basic resistance for a heavy-haul train is as follows [19]:
The additional resistance is determined by the section force , the curvature resistance and the tunnel resistance [19], as shown in Equation (4). The specific calculations of these factors [20] are presented in Equation (5):
For heavy-haul trains, the control inputs for the locomotives include the traction force and braking force, whereas the input for freight trains includes only the braking force. There are mainly two types of brake equipment for heavy-haul trains: one is rheostatic brake equipment and the other is pneumatic braking equipment. Rheostatic brake equipment, also known as the regenerative brake, can feed back energy to other locomotives to provide power. A pneumatic braking system achieves braking force by reducing the air pressure in the train’s air braking pipes [21].
The traction force F of a heavy-haul train depends on the relative output ratio of the maximum traction force , while the electric braking force is determined by the maximum electric braking force and its relative output ratio . Therefore, the traction force and electric braking force of a train can be calculated according to Equation (6):
where and are the piecewise functions of the train’s running speed [22]. In addition, it is impossible for each locomotive to output electric braking force and traction force at the same time [23]; thus, the relative output ratio of and is .
The air braking system of a heavy-haul train is its main braking force and the key to ensuring the safety of train operation. Figure 1 is a diagram showing the structural composition of the air braking system of a heavy-haul train [24]. According to Reference [25], in Equation (1) can be calculated based on Equation (7):
where and are intimately associated with the train’s physical characteristics, such as the brake lever and transmission efficiency of locomotives and freight cars, while the service braking coefficient is assigned a value based on the rated pressure p of the air pipes and the corresponding air pressure drop . Therefore, when air braking is applied by heavy-haul trains, the output of the air braking force depends on the air pressure drop [25]. Equation (7) can be rewritten as a function of as follows:
where is a binary variable that determines whether air braking is engaged () or released ().
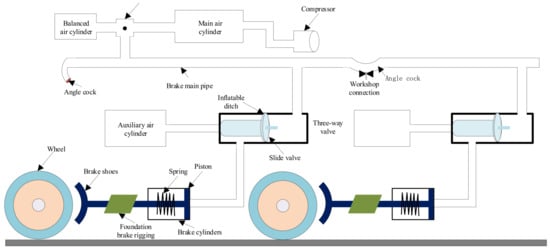
Figure 1.
The compositional structure of the air braking system for heavy-haul trains.
2.2. Running Constraints
The aim of this research on the circulating air braking of a heavy-haul train on a long and steep downhill section is essentially to solve a multi-constraint and multi-objective optimization problem. Considering the actual requirements of train driving control and model design, the running constraints set in this research are as follows:
(1) Air-refill time: When a train operates on a long and steep downhill section, it necessitates the adoption of cyclic braking for speed control. To guarantee sufficient braking force in the next braking cycle, sufficient time should be ensured for refilling the air pipe to its maximum pressure [26]. In other words, the release phase must not be shorter than the minimum air-filling time , as stated in the operating guidelines.
In the above formula, is closely related to the formation of the train and the pressure drop within the train air pipe. For predetermined train parameters, the air-filling time needs to be ascertained.
(2) Speed limit: To ensure safety, the speed of the heavy-haul train cannot exceed the speed limit at any point on the lengthy and steep downhill line stretch. This value often depends on the underlying framework of the railway line or the provisional setup. Additionally, the speed of the train should be greater than the minimum air brake release speed . The specified limit is designated as 40 km/h for a 20,000-ton heavy-haul train formation [19]. Therefore, the speed should meet the following requirement:
(3) Electric braking force: Heavy-haul trains are equipped with both an electric braking system and an air braking system. When the train engages electric braking, the braking current is regulated by adjusting the series excitation resistance of the electric braking system, so as to generate a continuous electric braking force to slow down the running speed of the heavily loaded train. In actual operation, the constraint is the maximum electric braking force [27], so the relative output ratio of the electric braking force should satisfy
2.3. Performance Indicators
This study primarily focuses on the safety and servicing cost of the heavy-haul train operation process. The maintenance cost is expressed by air braking distance. Hence, two indicators are introduced to evaluate the control performance of the heavy-haul train.
(1) Safety: Safety serves as the fundamental prerequisite for train operation. The speed of the heavy-haul train should be kept under the upper limit. Yet, it cannot be lower than . Here, the parameter Y is defined to indicate whether the train speed remains within the speed range.
(2) Air braking distance: As excessive wear will be caused by the friction between wheels and brake shoes when the air brake is engaged for a long distance, a maintenance cost will be generated by the replacement of air brake equipment. By reducing the air brake distance during operation, the maintenance cost can be reduced. Therefore, the air brake distance of a heavy-haul train is defined as Equation (13).
3. DQN Control Algorithm
Reinforcement learning is a machine learning method for goal-oriented tasks. It does not tell the agent how to act, but instead, guides the agent to learn the correct strategy through interaction with the environment. In this section, the train operation process will first be defined as a Markov decision process. Then, a control algorithm based on DQN is proposed to learn the cyclic braking strategy of train operation when running on a long and steep downhill railway section.
3.1. Markov Decision Process
Prior to implementing the DQN algorithm, it is essential to define the control process for train operation when running on a long and steep downhill section as a Markov decision process (MDP), which involves formalizing sequential decision-making. An illustration of the MDP interaction during the operation of heavy-haul trains running on long and steep downhill sections is shown in Figure 2.
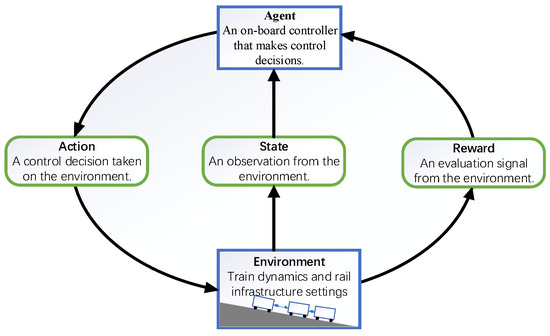
Figure 2.
Illustration of MDP interaction during operation of heavy-haul trains.
The locomotive of a heavy-haul train is described as the agent responsible for making control decisions, while the heavy-haul train’s dynamics and the railway’s underlying structure arrangements are defined as the environment. Assuming that the time interval between two consecutive states is Δt, the control process is evenly divided into N steps with respect to the planned operating time T, and the position, operating speed and operating time of the train are taken as the states of the heavy-haul train.
where is the status of the heavy-haul train at step k, is the position of the train, is the train speed and is the train running time. and represent, respectively, the initial state and final state of the heavy-haul train running on a long and steep downhill section, and their calculation is as follows:
Starting from the initial state of the train, succeeding states in the train control process are determined through actions until the final state is reached. Specifically, at a given train state , the agent chooses the optimal action from all feasible actions. After executing the action , the agent can obtain the next state and receive the corresponding reward . The next state is , which is solely influenced by the current state and action . Its calculation is as follows:
where represents the functional dynamics of the system associated with the heavy-haul train dynamic model, while is denoted as the state–action pair. Notably, the agent lacks prior knowledge of train dynamics. Such knowledge is solely utilized for generating driving experience throughout the interaction and to supply the agent with training data. Herein, the control action refers to the setting of electric braking and the air braking notch.
where is a binary variable, and denotes the relative output ratio of the electric braking force generated by the train locomotive, which is subjected to the constraint condition outlined in Equation (11).
The control output of a heavy-haul train in each cycle is determined solely by the speed and time of the current train. Thus, the control process of a heavy-haul train can be defined by reinforcement learning as a Markov decision process, which is expressed as follows:
3.2. DQN Algorithm Model
In this section, an intelligent control method based on the DQN algorithm is designed for a heavy-haul train running on a long and steep downhill section. The DQN algorithm combines reinforcement learning with deep neural networks to design a neural network that approximates the action value function. By applying the neural network, the curse of dimensionality caused by the discretization of the state space in the Q-learning algorithm is avoided. To solve instability when using a neural network to approximate the action value function, an independent target Q-network updated at regular intervals and a prioritized experience replay mechanism are incorporated into the DQN. Hence, the performance of the DQN algorithm in the cyclic braking control process of the heavy-haul train is further improved. The overall structure of the algorithm is shown in Figure 3.
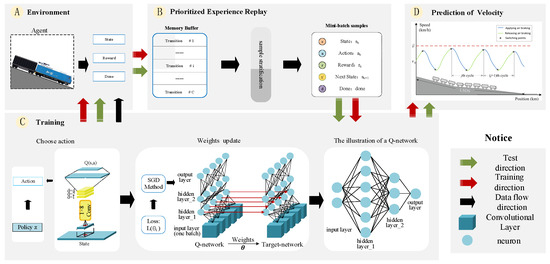
Figure 3.
Overall framework of DQN-based intelligent control algorithm for heavy-haul trains.
The intelligent cyclic air braking system for heavy-haul trains designed in this research consists of a sensing module, a strategy-making module, an action execution module and a reward feedback module. Among them, the sensing module is responsible for collecting the train state information, the strategy-making module devises an optimal braking strategy by using the DQN algorithm, the action execution module converts the strategy into specific braking instructions, and the reward feedback module evaluates the effect of each braking action. The key modules are described in more detail below.
3.2.1. Policy Design
Policy decides how an agent behaves at a specific time step. In this scenario, the train controller is treated as an agent and the state of the heavy-haul train can be described using Equations (14)–(17). Formally, policy is a function that calculates the probability of selecting each potential action relative to the Q function, and its expression is as follows:
where is the mapping policy. The action selection policy consists of two sub-policies, i.e., . Concretely speaking, to assure that the duration of the release air brake release stage satisfies the constraint of minimum air-refilling time in Equation (9), when the air brake release action is selected at the kth step, that is, , then this action ought to be sustained for the subsequent steps, with and . Additionally, the ε-greedy strategy (Equation (21)) is employed to determine the control actions for subsequent stages of the train operation process, wherein an action is chosen randomly with a probability of ε, whereas with the probability of 1 − ε, the action with the largest estimated Q value will be taken.
where is the number of actions in the event of .
3.2.2. Reward Design
The optimization goal of the reinforcement learning problem is reflected by the reward function. For the train control process in question, the operating speed cannot exceed its upper limit to ensure a safe operation. Therefore, the constraint of Equation (10) must be fulfilled. On the condition that the speed exceeds the upper limit or is below the minimum remission speed , a negative reward will be given to the agent. If the heavy-haul train engages in air braking at step k, it will receive a reward of zero. Conversely, if air braking is not engaged, a positive reward will be granted to incentivize the release of air braking. Hence, the specified reward is delineated as listed below:
3.2.3. Prioritized Experience Replay Design
The experience of the heavy-haul train at step k is recorded as a transition , and then, all experiences obtained over many training episodes are stored in the buffer D. The term in an array is a sign signal. If is True, it indicates that the training state is the final state or a negative reward will be imparted. During training, the DQN algorithm updated by means of sampling prioritization is applied to small-batch transitions according to the priority from the memory buffer storing experience. This mechanism enables greater data efficiency, as experiences of higher priority will be more frequently selected for weight updates. Samples are selected probabilistically to ensure that experiences with zero TD error can be sampled. The sampling formula P(i) of the priority experience replay is presented in Equation (23):
where represents the priority of the ith experience sample; α determines the utilization priority; and is defined according to Equation (24),
where is the temporal difference error (TD error), representing the difference between the reward received by the agent after performing an action and the expected reward. is a very small value, taken as 0.001 in this paper. It is used to prevent an experience sample from not being played back into the experience pool after its TD-error value reaches 0.
The smaller the TD error, the smaller the actual difference between the Q value estimated from the sampled data and the target Q value. A small TD error indicates that the agent is able to manage the corresponding situation well and there is no need to sample frequently or to train this experience. When there is significant deviation between the estimated Q value and the target Q value, this indicates that the experience is relative to the strategy currently learned by the agent, that is, the experience value is high, and frequent training should be prioritized to cope with similar changes that could occur. In addition, sampling by priority breaks the strong correlation between successive samples that adversely affects the reinforcement learning algorithm. As a result, it reduces the variance in the learning updates.
3.2.4. Action Value Function Design
Defined as Q(s, a; θ), the action value function demonstrates the quality of the action taken by the agent in a given state. In the form of a formula, the value of an action can be represented as the sum of all rewards that the agent is able to accumulate in subsequent steps, commencing from the current state and action. During the learning process, the agent is coached to choose an action in a manner that optimizes the overall future reward, referred to as the expected return, as shown in the following formula:
The optimal Q function is characterized as the highest cumulative reward attainable by adhering to the policy π upon entering the state s and executing the action a. In the form of Q(s, a), it is a function consisting of two parts: the state value function and the advantage function. The action value function expresses the expected return obtained by executing the action in the specified states, that is, indicating that taking this action is good or bad. The formula for calculating the optimal Q function is presented in Equation (26):
Theoretically, the optimal Q function obeys the Bellman equation, which is shown in Equation (27):
where s′ and a′ denote the state and the potential action at the subsequent time step, respectively.
In the DQN framework, the neural network is employed to approximate the optimal function. The Q function is estimated by the neural network, with the weight parameters denoted as θ (henceforth called the Q-network). Throughout the training process, the Q-network undergoes training through weight adjustments aimed at reducing the mean square error to a minimum, as defined by Equation (27). In this context, the best possible target value, , is approximated with the target value . Thus, the loss function of updating the weight for the network is as follows:
where is the loss of the ith iteration; p is the joint probability distribution of states and actions; θ is the weight parameter of the Q-network in the iteration; and is the weight parameter of the target network. The target network has an identical structure to the Q-network. To revise the Q-network, it is necessary to initially compute the derivative of the loss function concerning θ, and the gradient will be obtained. Then, the stochastic gradient descent (SGD) method is used to update the weight θ as follows:
where λ is the learning rate. The weight of the target network is updated periodically. When the parameters of the Q-network undergo J iterations of updating, a weight will be assigned to the target network to generate a new target network. Then, will be adopted to generate the target value y of the Q-learning to perform subsequent parameter updates J times for the Q-network. Through this approach, the overestimation or training instability caused by the correlation between the Q-network and the target network can be avoided; thus, the algorithm can calculate more accurately and stably, and the convergence speed can be increased.
Algorithm 1 summarizes the control method for heavy-haul trains based on the DQN algorithm.
| Algorithm 1 DQN-Based Intelligent Control Strategy for Circulating Air Brake of the Heavy-Haul Train |
| ///Initialization/// |
| 1: Use weight θ to randomly initialize the Q-network. |
| 2: Use weight = θ to initialize target network . |
|
| ///Process of training/// |
| 4: for episode = 1,…M do |
| 5: initialize the state of train through Equation (13) |
| 6: for k = 0,1,…,N−1 do |
| 7: choose action based on strategy π |
|
|
|
| 11: If done = True, set =; otherwise, |
| 12: calculate the of gradient with respect to weight θ |
| 13: update the weight θ by SGD method |
| 14: update the weight of the target network according to every J perods |
| 15: end for |
| 16: end for |
4. Algorithm Simulation and Analysis
In this study, simulations were carried out with real data obtained for a section of the Shuohuang railway line in China to confirm the efficacy of the proposed algorithm. Firstly, the experimental parameter data setting was introduced. Then, the simulation results were presented and analyzed. The simulations were divided into three parts: the model training process, a practical application performance test, and performance comparison using different algorithms.
4.1. Experimental Parameter Settings
To prove the effectiveness of the intelligent control method, a heavy-haul train weighing 20,000 tons was taken as the object of the simulations. The train formation consisted of 1 HXD1 electric locomotive + 108 freight cars + 1 HXD1 electric locomotive + 108 freight cars. The HXD1 electric locomotive had the abilities of traction and regenerative braking. The whole train was equipped with air braking. For specific train parameters, see Table 1.

Table 1.
Train parameters.
Based on the data for the section spanning from Longgong Station to Beidaniu Station of the Shuozhou–Huanghua Line, simulations were carried out to obtain a speed curve of the heavy-haul train running on a long and steep downhill section. The operation section had a total length S = 23,800 m, with a gradient of 10–12‰ for the extended and precipitous downhill stretch. The speed limit on this line was 80 km/h. The specific data are presented in Table 2.

Table 2.
Route information.
The parameter settings of Algorithm 1 used in this paper are listed in Table 3:

Table 3.
Algorithm hyperparameters.
4.2. Simulation Experiment Verification
4.2.1. Model Training Process
In this study, simulations were carried out under different parameters and training cycles with the proposed DQN algorithm for verification purposes. Under the specified circumstances, the time interval Δt was 100 s. In addition, the initial speed of the heavy-haul train running on a long and steep downhill section was 65 km/h. The change curve of the cumulative reward obtained using the proposed algorithm is shown in Figure 4. As shown in Figure 4a–c, the learning rates were determined to be 0.03, 0.003 and 0.0003, respectively, for the cumulative reward curve that changes depending on the number of episodes in different experiments. It is evident that during the short-term training period, the total cumulative reward gradually increases and converges in a good direction after training, as shown in Figure 4a–c. It should be noted that the best training performance is in Figure 4b, where the learning rate was determined to be 0.003. The average total reward’s evolution curve exhibits a swifter and more consistent convergence rate, along with a higher convergence value. Consequently, a learning rate of 0.003 was selected for the other experiments.
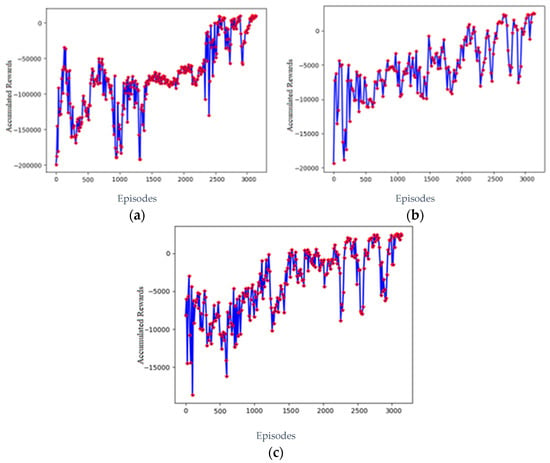
Figure 4.
Change curves of cumulative reward at different learning rates: (a) the learning rate λ of DQN algorithm is 0.03; (b) the learning rate λ of DQN algorithm is 0.003; (c) the learning rate λ of DQN algorithm is 0.0003.
Figure 5 shows the change curve of the total cumulative reward with the number of training episodes at a learning rate of 0.003 and a training period of 10,000 episodes. It also illustrates the change curve of the cumulative reward after the algorithm has converged. The other parameters of the DQN algorithm are the same as those shown in Table 3.
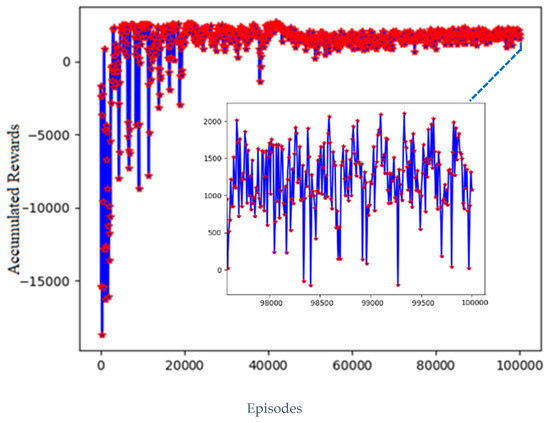
Figure 5.
Change curve of total cumulative reward of the DQN algorithm with λ = 0.003.
It can be seen from Figure 5 that in the 10,000-episode training experiment, the fluctuation range of the cumulative reward gradually decreases as the number of training episodes increases. From the change curve of the cumulative reward, it seems that the cumulative reward was maintained at a significant level within a designated range upon practice when executed about 5000 times, and the average cumulative reward converged to about 1400. After training was executed 10,000 times, the average cumulative reward remained at 1450, indicating that the proposed algorithm is convergent.
4.2.2. Practical Application Performance Test
Figure 6a,b exhibit the outputs of the air braking force and electric braking force during the control process of the DQN algorithm, respectively. The curve in Figure 7 shows the train speed controlled by the DQN algorithm. With the above parameter, i.e., the index Done was 1 with a learning rate of 0.003, the speed of the train was kept within the limitation range during the operation. This means that the agent had learned a safe and feasible control strategy during the test simulations to ensure the safe operation of the heavy-haul train. Moreover, it is evident from Figure 6 and Figure 7 that during the process of train control, cyclic air braking was engaged when the train was running on the long and steep downhill section. Specifically, air braking was not applied during the initial 80 s. Since the overall braking force was not sufficient to decelerate the heavy-haul train, the train speed increased during this period. In the following 100 s, air braking and electric braking were utilized concurrently ( and = 0.8), resulting in the train’s velocity dropping from 76 km/h to 52 km/h. Subsequently, air braking was discontinued, while electric braking was maintained constantly for the next 100 s ( and = 0.8). At 210 s, the train speed reached 78 km/h. At this moment, air braking was reactivated to reduce the train’s velocity ( and = 0.8).
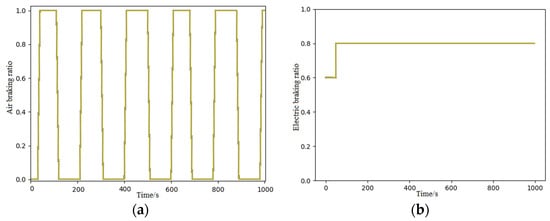
Figure 6.
Output of brake command during braking: (a) output of air braking; (b) output of electric braking.
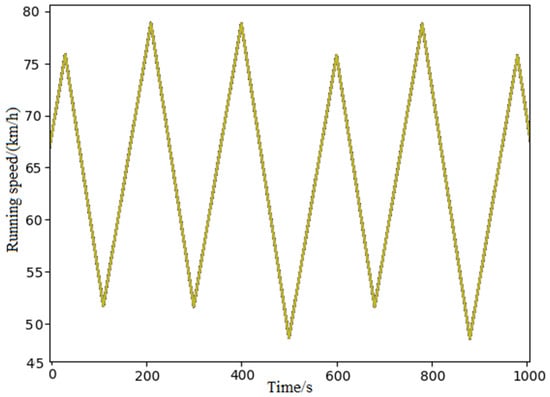
Figure 7.
Control Strategy for Running Speed of The Heavy-Haul Train.
Herein, an intelligent air braking strategy employing the DQN algorithm was used to implement five braking cycles for a heavy-haul train running on a long and steep downhill railway section. This approach ensured the safety of train operation. Furthermore, Figure 7 unequivocally illustrates that the train’s safe operation indicator Y maintains a value of 1, which signifies that the train velocity consistently remains within the predefined safety limits during its entire operation. Figure 7 shows that the DQN agent in the experiment learned a safe and feasible control strategy to ensure the safe operation of heavy-haul trains. It can be seen that after training, the algorithm is able to control the train speed by applying the air brakes before the train reaches the maximum speed of 80 km/h under the premise of a slope speed of 68 km/h, and by releasing the air brakes before the speed drops below the minimum release speed of 40 km/h after braking. This is done to ensure the train can maintain safe operation until it exits the long downhill section.
4.2.3. Comparison of Algorithm Performance
To prove the superiority of the DQN algorithm in dealing with the cyclic braking of a heavy-haul train running on a long and steep downhill section, the optimization results with the above settings were compared with those of the Q-learning algorithm [10]. The key parameters of the Q-learning algorithm were as follows: the learning rate λ was 0.05, the maximum number of iterations M was 100,000, the discount rate γ was 0.95, the acquisition probability ε was 0.1, and the state transition interval Δt was 10.
It can be seen from Table 4 that compared with the results of the Q-learning algorithm from [10], the proposed algorithm based on DQN is superior in terms of braking distance, braking efficiency and operation efficiency during the cyclic braking of a heavy-haul train running on a long and steep downhill section. The safe operation of the train is, thus, effectively ensured.

Table 4.
Comparison of simulation results.
From Table 4, it can be observed that under the same conditions and with the same hyperparameter settings, the DQN algorithm, which is focused on air braking distance, actual running time and the train’s average speed, shows superiority in braking distance and running efficiency when heavy-haul trains perform cyclic air braking on long downhill sections. Our findings reveal that the DQN-based intelligent control strategy decreased the air braking distance by 2.1% and enhanced the overall average speed by over 7%. These results unequivocally demonstrate the efficacy and superiority of the DQN-based intelligent control strategy. Our experimental results indicate that the DQN algorithm proposed in this paper effectively ensures the safety of train operation.
5. Conclusions
In this article, we explore the optimal working condition (braking and braking release) transition during cyclic braking when a heavy-haul train is running on a long and steep downhill section. Aiming at obtaining the shortest air brake distance and the highest operating efficiency, various constraints of the actual operation are considered at the same time, including factors such as the air-refilling time of the auxiliary reservoir, operating speed and operation action switch. The main conclusions are as follows:
(1) To achieve the optimization of multiple objects, a mathematical model is established for a heavy-haul train running on a long and steep downhill section. An intelligent cyclic braking system design based on the DQN algorithm is introduced for the train to adapt to a variety of complex operation environments and line conditions. To improve the convergence speed of the algorithm, the priority experience replay mechanism is used instead of ordinary experience replay. By prioritizing experiences, the agent can choose experiences with a higher priority for learning. In this way, the agent can more quickly learn important experiences that are more conducive to the rapid convergence of the algorithm. As a result, it improves the performance of the control algorithm.
(2) To verify the performance of the proposed DQN algorithm, comparative simulations were carried out and tested with different parameters. The simulation results show that the DQN algorithm proposed in this article exhibits better optimization performance and can effectively generate train driving speed curves that fulfill the specified constraints. This provides a valuable reference for the application of cyclic braking in heavy-haul trains running on long and steep downhill sections.
This study primarily focuses on the intelligent control of a cyclic air braking strategy for heavy-haul trains. However, during the research phase, we failed to comprehensively consider all environmental factors that could affect braking effectiveness. In particular, weather conditions (such as temperature, humidity and wind speed), track conditions (such as track flatness and friction coefficient) and variations in train load were not within the scope of our research. In future, we plan to conduct in-depth research on these environmental factors to evaluate the braking performance of heavy-haul trains more comprehensively under different conditions. In addition, the proposed DQN algorithm could be further improved and a more efficient network structure could be developed. This, in turn, could improve the performance of cyclic air braking with respect to heavy-haul trains.
Author Contributions
Conceptualization, C.Z.; Formal Analysis, J.H.; Funding Acquisition, C.Z.; Investigation, L.J.; Methodology, S.Z.; Resources, L.J.; Software, S.Z.; Validation, J.H.; Writing—Original Draft, S.Z.; Writing—Review and Editing, L.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Nos. 62173137, 52172403, 62303178) and the Project of the Hunan Provincial Department of Education, China (Nos. 23A0426, 22B0577).
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| M | Sum of the masses of all carriages | Acceleration of heavy-haul train | |
| F | Locomotive traction force | Running speed of train | |
| Output electric braking force | Output air brake force | ||
| Maximum electric brake force | Maximum traction force | ||
| Resistance of train | g | Gravity acceleration | |
| Upper limit of train running speed | Minimum release speed of air braking | ||
| Relative output ratio of traction force | Relative output ratio of the electric braking force | ||
| Equivalent emergency brake ratio of air braking | Equivalent friction coefficient of air braking | ||
| R | Curve radius | Tunnel length | |
| Service brake coefficient of air braking | i | Gradient of the line section | |
| Running resistance constant | Air brake distance | ||
| Time point of engaging air brake in the (j + 1)th cycle | Time point of releasing air brake in the jth cycle |
References
- Zhang, Z. Optimization Analysis of Smooth Operation for Ten-Thousand Ton Trains of Shuohuang Railway; Southwest Publishing House: Chengdu, China, 2017. [Google Scholar]
- Lu, Q.; He, B.; Wu, M.; Zhang, Z.; Luo, J.; Zhang, Y.; He, R.; Wang, K. Establishment and analysis of energy consumption model of heavy-haul train on large long slope. Energies 2018, 11, 965. [Google Scholar] [CrossRef]
- Dong, S.; Yang, S.; Yang, C.; Ni, W. Analysis of Braking Methods for Express Freight Train on Long Ramp. Mod. Mach. 2022, 2, 28–34. [Google Scholar]
- Kuefler, A.; Morton, J.; Wheeler, T.; Kochenderfer, M. Imitating Driver Behavior with Generative Adversarial Networks. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; IEEE: New York, NY, USA, 2017. [Google Scholar]
- Yang, H.; Wang, Y.; Li, Z.; Fu, Y.; Tan, C. Expert supervised SAC reinforcement learning for optimizing the operation of heavy-duty trains. Control Theory Appl. 2022, 39, 799–808. [Google Scholar]
- Howlett, P. An optimal strategy for the control of a train. Anziam J. 1990, 31, 454–471. [Google Scholar] [CrossRef]
- Huang, Y.; Su, S.; Liu, W. optimization on the Driving Curve of Heavy Haul Trains Based on Artificial Bee Colony Algorithm. In Proceedings of the 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), Rhodes, Greece, 20–23 September 2020; IEEE: New York, NY, USA, 2020. [Google Scholar]
- Du, L. Model Based Security Reinforcement Learning. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2021. [Google Scholar]
- Wang, Y.; De Schutter, B.; van den Boom, T.J.; Ning, B. Optimal trajectory planning for trains—A pseudo spectral method and a mixed integer linear programming approach. Transp. Res. Part C Emerg. Technol. 2013, 29, 97–114. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, Q.; Zhang, Z. A Study on Energy-Saving Optimization for High Speed Railways Based on Q-learning Algorithm. Railw. Transp. Econ. 2019, 41, 111–117. [Google Scholar]
- Zhang, M.; Zhang, Q.; Liu, W.; Zhou, B. A Policy-Based Reinforcement Learning Algorithm for Intelligent Train Control. J. China Railw. Soc. 2020, 42, 69–75. [Google Scholar]
- Zhang, W.; Sun, X.; Liu, Z.; Yang, L. Research on Energy-Saving Speed Curve of Heavy Haul Train Based on Reinforcement Learning. In Proceedings of the 2023 IEEE 26th International Conference on Intelligent Transportation Systems (ITSC), Bilbao, Bizkaia, 24–28 September 2023; IEEE: New York, NY, USA, 2023; pp. 2523–2528. [Google Scholar]
- Sandidzadeh, M.A.; Havaei, P. A comprehensive study on reinforcement learning application for train speed profile optimization. Multimed. Tools Appl. 2023, 82, 37351–37386. [Google Scholar] [CrossRef]
- Wu, T.; Dong, W.; Ye, H.; Sun, X.; Ji, Y. A Deep Reinforcement Learning Approach for Optimal Scheduling of Heavy-haul Railway. IFAC-PapersOnLine 2023, 56, 3491–3497. [Google Scholar] [CrossRef]
- Lin, X.; Liang, Z.; Shen, L.; Zhao, F.; Liu, X.; Sun, P.; Cao, T. Reinforcement learning method for the multi-objective speed trajectory optimization of a freight train. Control Eng. Pract. 2023, 138, 105605. [Google Scholar] [CrossRef]
- Tang, H.; Wang, Y.; Liu, X.; Feng, X. Reinforcement learning approach for optimal control of multiple electric locomotives in a heavy-haul freight train: A Double-Switch-Q-network architecture. Knowl.-Based Syst. 2020, 190, 105173. [Google Scholar]
- Wang, M.Y.; Kou, B.Q.; Zhao, X.K. Analysis of Energy Consumption Characteristics Based on Simulation and Traction Calculation Model for the CRH Electric Motor Train Units. In Proceedings of the 2018 21st International Conference on Electrical Machines and Systems (ICEMS), Jeju, Republic of Korea, 7–10 October 2018; IEEE: New York, NY, USA, 2018; pp. 2738–2743. [Google Scholar]
- Yu, H.; Huang, Y.; Wang, M. Research on operating strategy based on particle swarm optimization for heavy haul train on long down-slope. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; IEEE: New York, NY, USA, 2018; pp. 2735–2740. [Google Scholar]
- Huang, Y.; Bai, S.; Meng, X.; Yu, H.; Wang, M. Research on the driving strategy of heavy-haul train based on improved genetic algorithm. Adv. Mech. Eng. 2018, 10, 1687814018791016. [Google Scholar] [CrossRef]
- Su, S.; Tang, T.; Li, X. Driving strategy optimization for trains in subway systems. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2018, 232, 369–383. [Google Scholar] [CrossRef]
- Niu, H.; Hou, T.; Chen, Y. Research on Energy-saving Operation of High-speed Trains Based on Improved Genetic Algorithm. J. Appl. Sci. Eng. 2022, 26, 663–673. [Google Scholar]
- Zhang, Z. Train Traction Calculation; China Railway Press: Beijing, China, 2013. [Google Scholar]
- Su, S.; Wang, X.; Cao, Y.; Yin, J. An energy-efficient train operation approach by integrating the metro timetabling and eco-driving. IEEE Trans. Intell. Transp. Syst. 2019, 21, 4252–4268. [Google Scholar] [CrossRef]
- Ma, H. Research on Optimization Control of Long Downhill Braking Process for Heavy Haul Trains. Master’s Thesis, East China Jiaotong University, Nanchang, China, 2019. [Google Scholar]
- Wu, J. Train Traction Calculation; Southwest Jiaotong University Press: Chengdu, China, 2013; pp. 50–141. [Google Scholar]
- Wei, W.; Jiang, Y.; Zhang, Y.; Zhao, X.; Zhang, J. Study on a Segmented Electro-Pneumatic Braking System for Heavy-Haul Trains. Transp. Saf. Environ. 2020, 2, 216–225. [Google Scholar] [CrossRef]
- Su, S.; Tang, T.; Xun, J.; Cao, F.; Wang, Y. Design of Running Grades for Energy-Efficient Train Regulation: A Case Study for Beijing Yizhuang Line. IEEE Intell. Transp. Syst. Mag. 2019, 13, 189–200. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).