Abstract
Phasor measurement units (PMUs) are deployed at power grid nodes around the transmission grid, determining precise power system monitoring conditions. In real life, it is not realistic to place a PMU at every power grid node; thus, the lowest PMU number is optimally selected for the full observation of the entire network. In this study, the PMU placement model is reconsidered, taking into account single- and multi-capacity placement models rather than the well-studied PMU placement model with an unrestricted number of channels. A restricted number of channels per monitoring device is used, instead of supposing that a PMU is able to observe all incident buses through the transmission connectivity lines. The optimization models are declared closely to the power dominating set and minimum edge cover problem in graph theory. These discrete optimization problems are directly related with the minimum set covering problem. Initially, the allocation model is declared as a constrained mixed-integer linear program implemented by mathematical and stochastic algorithms. Then, the integer linear problem is reformulated into a non-convex constraint program to find optimality. The mathematical models are solved either in binary form or in the continuous domain using specialized optimization libraries, and are all implemented in YALMIP software in conjunction with MATLAB. Mixed-integer linear solvers, nonlinear programming solvers, and heuristic algorithms are utilized in the aforementioned software packages to locate the global solution for each instance solved in this application, which considers the transformation of the existing power grids to smart grids.
1. Introduction
Energy management systems (EMSs) play a vital function, serving as the backbone of smart power grids for monitoring, control, and state estimation [1,2,3,4], while Supervisory Control and Data Acquisition (SCADA) systems are crucial for their implementation of monitoring and control [1,2,3,4,5].
The state of the power system is determined to be the assignment of the phasor voltage quantities, electrical current quantities to branches, and power values to generators and loads. One way to transform the existing power system to a “modern” grid is to measure its state in actual time, which requires continuous monitoring [1,2,3,4,5]. The state of a power network is said to be observed in the case of measuring the state variables, such as the phasors voltage at nodes and phasor currents running in the lines.
Sensors are installed at appropriate nodes in the power network to measure the state variables’ quantity, which is telemetered to the central control. The electricity companies are required to continually observe the state variables [1,2,3,4,5,6].
In order to observe the power network state, phasor measurement units (PMUs) are utilized for gathering data and sending them to the system operator [1,2,3,4].
The power system can be made fully observable by utilizing solely PMUs. In this case, the state estimation formulation is linear and solved without the needed iterative schemes [2,4,6]. PMUs are installed at substations and are crucial devices for system operation and control due to the measuring of the phasor voltages and phasor currents running the transmission lines. Global time reference can accurately measure these types of phasors, even from remote physical locations within a designated power system [1,2,3,4,5,6,7].
Traditionally, state estimation (SE) is implemented using the SCADA system, whereas with the utilization of PMUs, hybrid state estimators based on SCADA-PMU and linear state estimators based on PMUs have emerged [2,3,4,6].
SE is the most significant tool of the EMS, giving the transmission system operator an actual-time understanding of the current operation [2,3,4,6].
In these circumstances, SE helps the system operator maintain the power grid to be reliable, secure, and economical in its service [1,2,3,4,5,6]. Furthermore, SE supports the monitoring and control application in the EMS [1,2,3,4,5,6]. SE procedures have undergone a great improvement since the introduction of the PMU [1,2,3,4,5,6]. The literature illustrates different methods to implement and solve the state estimation application [2,3,4,6].
The SE model is classified as static or dynamic [1,2,3,4,5,6]. State estimation models based on a limited PMU number were recently presented in [2,3,4,5,6]. The static algorithm principally relies on a WLS algorithm, utilizing data calculated at a given time [2,3,4,6]. By comparison, a SE model based on a dynamic response and Kalman filter is presented in [6]. Both SE models are based on a mixed set including conventional measurements as well as a limited PMU number [1,2,3,4,5,6].
In a modern transmission system, telemetry relies on the SCADA and the wide-area monitoring system (WAMS) [1,2,3,4,5]. The WAMS is made of PMUs and phasor data concentrators (PDCs) and their communication networks [1,2,3,4,5,6]. PMUs play an essential part in the observation of the power transmission network [1,2,3,4,5,6].
This fact has caused a paradigm shift in the architecture of power grids, increasing the utilization of PMUs with their installation at selected power grid nodes [1,2,3,4,5,6]. PMUs have led to reconsideration of the way the state estimation is executed for reliable monitoring of the power grid state [1,2,3,4,5,6].
PMUs comprise the most commonly obtainable vital measurement infrastructures that consider synchro phasor technology [1,2,3,4,5,6]. A PMU enables real-time measuring data, which are the phasor voltage of the placing node and the phasor currents running in the branches running from that network bus [1,2,3,4,5,6].
The real-time data are collected and sent to the phasor data concentrator (PDC), enabling it able to undertake applications such as monitoring, control, and network stability [1].
This measuring fact allows real-time monitoring, which is important for energy management system applications [1,2,3,4,5,6].
With the utilization of PMUs, the SE procedure is now able to work more accurately in large power networks, as it incorporates phasor voltage measurements at network buses and current measurements through connection lines [1,2,3,4,5,6,7,8,9,10,11,12].
In the last decade, utilities have made significant investments in enhancing the actual-time monitoring and power transmission grid control applications [1,2,3,4,5,6,7,8,9,10,11,12]. All over the world, many utility industries have installed large numbers of PMUs to render their optimal deployment at substations [7,8,9,10,11].
The deployment of synchronized sensors is still continuing and somehow is in slow progress, mainly due to economic and technical restrictions [5].
Due to the high cost of installing a PMU at every power grid node in the WAMS implementation to attain full observability, it is significant to take into account the best PMU position sites through a solvable OPP problem [7,8,9,10,11].
Hence, the OPP problem still stands, giving a full network observation of the power grid state while the entire cost investment is minimized [7,8,9,10,11]. A PMU is placed at the installation bus and computes the phasor voltage at that bus and all the phasor current lines running from that bus with the assumption that the monitoring device has an unlimited number of channels [4,6,7,8,9,10,11].
Over two decades of research, a plethora of significant papers has emerged to tackle the OPP problem. They aim to ascertain the optimal PMU number needed and strategically position them to ensure the power grid achieves full observability [4,8,9,10,11,12,13,14].
Many of these papers delve into various strategies for solving the OPP problem, with a primary focus on achieving full observability while satisfying zero–one constraints on a minimum objective function bound [4,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]. Some interesting research studies have been published recently in the OPP domain [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67].
The pioneering work is to address the OPP-based model on optimization [28,29,30,31,32] using a zero–one integer linear programming (ILP) model, and some interesting research works have been published in the OPP domain in the recent past [33,34,35,36].
Mathematical algorithms are utilized in the OPP problem solving [31,32,33,34,35,36,37,38,39,40,41,42], whereas heuristic algorithms are also implemented to handle the integer program’s inequality to examine the solution, thereby yielding heuristically sound knowledge [39,43,44,45,46,47,48,49,50,51,52,53,54,55].
In the past years, the initial OPP formulation has become more and more attractive in the incorporation of intellectually demanding tasks under operating conditions [7,8,9,10,11].
These OPP models consider relative constraints to satisfy these issues without sacrificing the entire observability [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55].
Many research works on OPP rely on a cumulative single objective function that is minimized subject to a constraint function defined on specific decision bounds [32,33,34,35,36,37,38,39,40,41]. On the contrary, a two-product objective minimization model is proposed in [42,47,49,51] to find those optima points with a maximum system observability index declared in [33,37,38,41,42,51].
The optimization problem in [37,38,42,43,44,45,47,49,51] considers obtaining more than one objective product. This multi-objective function consists of two conflicting products for the consideration of those solutions satisfying complete and maximum observability at the same time.
The impact of ZI buses is considered for further minimization of PMU cost installation at substations [35,40,46,47,48]. Despite this, with unknown tap ratios, uniform behavior among all ZI buses may lead to situations where a topological observability analysis does not ensure a numerical observability [34,35].
Likewise, it may be the case that the consideration of ZI buses does not necessarily further minimize the PMU cost allocation at power grid buses [54].
In real-life, each PMU device has a restricted number of channels and thus a more realistic configuration of the PMUs is taken into consideration with a varying channel capacity [47,52,56,57,58,59,60,61,63,64,65,66,67].
Therefore, the restriction in the channel limit capacities is taken into consideration to implement a more reasonable configuration of PMUs in grids [56,57,58,59,60,61,62,63,64,65,66,67].
In this study, we consider the extra limitation regarding the channel capacity, and propose mathematical and heuristic algorithmic schemes to solve the OPP focused on finding the true solutions including the PMU locations and the branches being observed.
Mathematics, heuristic algorithms, and derivative-free optimizers (DFO) are adopted to solve the OPP problem for the implementation of the installation of PMUs with a limited channel capacity per a PMU optimally installed at selected power grid nodes.
As a result, we present the mathematical formulations, the solution algorithms, the PMU locations, and the branch assignments related to the best PMU sites. All findings are displayed in tables and plot diagrams to validate our algorithmic approach.
2. Consideration of This Study
The OPP problem delivers an adequate number of PMUs for observing a power grid and defines the health of a power grid [1,2,3,4,5,6,7,8,9,10,11,12]. PMUs are placed at power network nodes, i.e., substations to which transmission lines, generators, and loads are joined [34,35].
Due to lack of a communication facility at some substations [36,39,65], the PMU’s cost placement is further increased and it is forbidden to be placed at substations with a lack of communication facilities [1,34,35,36].
Hence, it is still significant to optimize/minimize the number of PMUs placed within the power grid transmission system [36,37,38,41,42,51]. The optimization output gives an appropriate number of PMUs that is sufficient to monitor the power system [37,38,41,51]. In practice, PMU manufacturers yield a few types of PMU, with distinct functions and varying channel capacities [56,59,60,61,63,64,65,66,67].
As a consequence, specific algorithms are studied for optimally placing PMUs with a restricted number of channels at power nodes [60]. We consider an extra constraint function to the allocation problem related to the number of channels to keep complete network observability [56,59,60,61,63,64,65,66,67].
We develop PMU placement models with multiple channels as well as a single-line placement model to detect PMU sites related to branch assignments. The optimization model is also interpreted as a minimum edge cover, otherwise known as a node set covering problem [15]. Single-line PMUs are also known as a unit channel capacity [61].
A single-line PMU is able to measure the voltage phasor of the related bus, and the phasor current of only one of the branch incidents to the bus where the PMU is placed [60,61]. So, in the monitoring of the phasor’s voltages of grid nodes, PMU measurements are significant in observing the transmission grid lines [61].
Thus, each PMU enables it to make better line capability observation with PMU measurements [56,58,60,61,64]. As a result, the installation of single-line PMUs could be a standard practice interpreted as a minimum edge covering problem [28,29,30,31,61].
So, the node set covering problem interprets the above strategy in graph theory [28,29,30,31]. In practice, it can be used primarily in industries such as utility companies to construct a modern grid with the capability of optimal “branch” placement of PMUs [61].
Furthermore, the manufacturers supply PMUs with a varying number of channels and PMU cost ranges analogous to channel restriction. Some works study this combinatorial problem considering a restricted number of channels, which is a more realistic OPP scenario [56,57,58,59,60,61,62,63,64,65,66,67,68,69]. The principal constitution of this study is threefold:
- (1)
- To achieve the proper PMU number by optimizing a linear or a quadratic cost function under a topological constraint function considering the limitation of the PMU channel limit capacity.
- (2)
- To accomplish this task, branch-and-bound algorithms [37], sequential quadratic programming [42], interior-point methods [42], generalized pattern search algorithms [41,70,71], genetic algorithms [51], and binary swarm optimization [51] are utilized to achieve optimality.
- (3)
- We focus on finding the proper PMU number with a branch assignment set solution with a fixed number of channels.
Our aim is to reconsider the ILP-based model under a limited PMU number [56,57,58] in the YALMIP environment [37,38]. GA and BSPO are able to handle the ILP model’s constraints, and finally an equivalent nonlinear model is given to find optimality.
We tested the algorithmic models on the classical IEEE power systems. BBA gives the solution under a strict optimality warranty followed by evolutionary algorithms’ solutions with the same quality and quantity [37,38,41,42,51]. ZI buses are the buses without generation or load consumption [32,33,34,35,39,40].
In actual conditions, buses are mainly substations, as noted in [34,35,54], and the substation’s internal consumption is something that cannot be ignored [34,35,39]. Specifically, the substation itself needs energy to operate [34]. For example, energy is required for the substation control and protection system [68,69]. Substations also need energy for the cooling fans (ONAN/ONAF) and the on-load tap changer of transformers, uninterruptible power supplies (UPSs), fire extinguishing systems, lighting fixtures, floodlights, and battery chargers [68,69]. Moreover, the observability scenario based on a topological approach, which does not always ensure numerical observability, is also avoided by treating ZI buses as normal buses [34,35,39,46].
Thus, simulation results are produced by mathematical and heuristic algorithms when ZI buses are not taken into account for the practical power systems, following recently published papers in the relative research domain [34,37,41,42,51].
Since the ZI’s effect will not be included in the PMU arrangement procedure [34,37,41,51], each power network bus is fully observed, either by a PMU placed at that node or by other PMUs placed at the incident network nodes [34,37,41,42,51].
To present an OPP model based on a restricted number of channels, ILP [37,38], DFO solvers [41,51], NLP [41], and a BPSO [51] are utilized to find the exact solution avoiding near-to-optimal solutions. The solvers produce the PMU number and the branch assignments for a varying number of measurement channels.
The placement problem is optimized in three stages. Integer linear, heuristic, and nonlinear models are simulated using specialized optimization libraries [72,73,74,75,76]. As a guide in minimizing these placement problems, optimization tactics can be followed by the reader in previous authors’ cited works [37,38,41,42,51].
The proposed models are well optimized by BBA, SQP, IPMs, GPSA, Gas, and BPSO towards an optimum point. We derive not only the PMU number but also the branch assignments for ranging channel capacity. The BBA solutions are given within an absolute zero gap, which means no better solution can be found [37,38,41,42,51].
3. Contribution of This Study
PMU brings a revolution to the manner in which power networks are observed and operated. Most of the works assume that these monitoring devices have an unrestricted amount of channel capacity to measure as many phasors’ voltage and currents running the lines as are required. In real conditions, manufacturers produce PMUs with different characteristics.
One characteristic is the channel limit capacity, which allows the PMU’s availability onto the market with a varying cost [52]. Therefore, an optimal investment can be made based on the selection of appropriate PMU types utilizing efficient algorithms.
This decision leads to a decrease in the cost of hardware needed for the development of the WAMS system based on synchronized measurements [52].
In this study, we consider that optimal PMU numbers are installed around the power grid having a restricted number of measurement channels. Although there exist some works in this domain [56,57,58,59,60,61,62,63,64,65,66,67], we present a revised optimization model and a number of algorithms related to its solution. The solution of this model will keep the network completely observable relying only on synchronized measurements [37].
This study takes into account the realistic scenario where the channel capacity is varied to measure phasors’ voltage and current running in the connectivity lines and produces global solutions with strict optimality conditions [13,14,15,16,17,18,19,20,21].
The optimization study does not consider the existence of ZI buses at this time. This approach does not take away any truth of models presented in [40,56,57,58,59,60,61,62,63,64,65,66,67] when ZI, active injections, and flow measurements are taken into account for further consideration.
Our aim is to give a comprehensive output of our algorithmic approach to the PMU allocation problem solving based on BBA considering a restricted number of channel capacities. Furthermore, we examine how the entire observability is preserved with less measurement redundancy in the state estimation [1,2,3,4,6].
To extend the mentioned target, we illustrate a number of algorithmic models to enhance our approach. In this direction, we adopt nonlinear, derivative-free, and heuristic algorithms to find alternative PMU set solutions with the branch assignments covered to keep the system functional and observable. Our primary outputs are:
- We create an algorithmic connection between the OPP based-model with a restricted channel capacity and the optimal solutions produced by the suggested mathematical and heuristic algorithms.
- The branch-and-bound algorithm is used in a comparison study with nonlinear and heuristic algorithms.
- We present a state-of-the-art solution produced by the integer program solving with a zero absolute gap calculated with zero percentage gap tolerances; this means that this solution is a global one returned by the solver.
- We extend the ILP model into a heuristic search of the feasible set to show that evolutionary algorithms can efficiently perform the optimization following the BBA’s solution.
- Finally, a novel nonlinear program is created and solved by either continuous algorithms or a BBA embedded in the SCIP optimizer performed in MATLAB.
4. Materials and Methods
Despite the fact the PMU’s cost was recently reduced, it cannot be workable to place a PMU at every power grid node in a large-size transmission grid [7,8,9,10,11].
Hence, it has an important value to attain complete observability and maximum redundancy with an optimal number of PMUs placed at buses within the power grid [33,37,41,43,44,45,47,49,51].
Many research works have considered the ZI’s bus presence to further reduce the entire PMU number needed to attain power grid observability [32,33,35,36,39,40,43,44,45,46,47,48,49,50,52,53,54]. A PMU-PDC monitoring system is designed in [55].
Considering the unknown tap ratios [68,69], having all ZI nodes behave in a similar manner can provide guidance for schemes where the topological observability may not secure numerical observability being fulfilled [35,40,46].
Our aim is observability analysis based on a restricted number of channels per PMU device. Hence, a minimum number of such devices are optimally placed around the power transmission grid. The whole power network must be fully monitored using an optimal PMU number [37,38,41,51,56,57,58].
A PMU device placed at a network bus supplies the system operator with direct measurements, whereby Kirchhoff’s voltage law and Ohm’s law are utilized to compute the pseudo measurements that are essential to maintain the system observability [31].
Optimal PMU placement models are suggested where the PMU number is found when a linear or quadratic cost function is optimized subject to several topological or numerical observability constraints in [37,38,41,42,51]. The decision vector ranges in either a binary or a continuous domain [37,38,41,51].
At first, the OPP formulation was suggested in an integer linear program [31,32,33] and a powerful ILP solver was used to obtain an optimal solution [35,36,37,38,41,51]. Then, 0/1 semi-definite and nonlinear programs have been proposed to find an optimal solution from an alternative optimization point of view [37,40].
All optimization models are robust in the implementation, with excellent outcomes ensuring the topological or the numerical approach in the state estimation tool [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67].
The high cost of PMUs related to installation limitations and commissioning procurement in substations is still a practical restriction over the wide-area power grid [36,37,38,41,51]. The PMU cost is further increased by keeping the same ratio with the number of channels [36,56,58,59,60,61,63,64,65,66,67].
In the bibliography, most articles have supposed an unlimited number of measurement channels for the PMU allocation problem solving [4,7,8,9,10,11].
The restricted number of channels within a PMU monitoring device is an extra constraint involved in the optimization model related to finding the best PMUs to ensure the complete observability scenario [36,56,58].
This realistic assumption about PMU limit capacity can have an effect on the PMU arrangement in the power grid with or without contingency scenarios [56,58]. Certainly, if the amount of PMU channel capacity is less than the number of connectivity lines to a power grid node, a combinatorial number of possible branch phasor current measurements can be found in this realistic scenario [56,57,58].
In such a realistic scenario, PMU monitoring devices are constructed with a restricted number of channels. A single PMU can be lost depending on the amount of current channel capacity embedded in a PMU device [53,54]. Hence, the measurement redundancy task is very significant for the effective utilization of SE [2,3,4,6].
We consider mathematical and heuristic models, with the problem solving being presented using BBA, nonlinear algorithms, derivative-free optimizers, and a BPSO.
This paper completes previous authors’ papers [37,38,41,42,51], filling the gap relating to the certainty of reaching a global solution or a near-to-optimum point considering a restricted number of measurement channels [56,57,58,59,60,61].
5. Optimization Models Studied for the OPP Model
PMUs are placed at substations in which transmission lines, generators, and loads are adjoined [29,31,60]. Specific reasons, such as the PMU’s high cost and communication facilities not existing in some substations, increase the entire cost of installation [7,37,38,41,51,55,60].
Thereby, the power utility industries desire a reasonable number of channels per a PMU device to determine the entire cost of the investment. In addition to that consideration, an optimal PMU placement is essential in the research domain [37,38,41,42,51].
The initial step is to identify if the solution achieved by the optimization algorithm is feasible or not. In the case of producing the sequence of points, we first derive a feasible estimate point in which the objective value is less than the older one on the previous trial point [13,14,15,16,17,18,19,20,21].
Such a task between a feasible and an infeasible point is crucial to achieve optimality. What we desire is to deliver the optimum point over the feasible region constituted by the objective, the constraint function, and the decision bounds [21,22,23,24,25]. Therefore, the aim is to identify the feasibility and optimality of the response space solutions. Although there exist a few works in this domain [56,57,58,59,60,61,62,63,64,65,66,67], there is no possible combination of the PMU number and the appropriate locations.
This work proposes an OPP-based model considering the limited number of channels per PMU device using extended ILP models initially presented in [56,57,58] and [60] where a set cover problem is introduced [28,29,30,31]. The suggested optimization models have been solved by BBA, heuristic algorithms, and nonlinear algorithms.
Heuristic algorithms work together with BBA to find a solution of the same quantity and quality in a minimal running time [25,26]. Furthermore, transforming the binary-integer programming into a nonlinear polynomial model shows the robustness required to find a proper number of PMUs and their placement sites for a fixed number of channels [13,14,15,16,17,18,19,20,21,22,23,24]. The numerical optimization challenge is to run mathematical as well as heuristic algorithms, including BBA, SQP, IPMs, GPSA, GA, and BPSO, to discover the best combination between the proper PMU number and the upper bound of channel capacity without increasing the cost of installation [56,57,58,59,60].
- ✓
- Observability of the graph
Graphs are useful models for many problems considered in combinatorial optimization [28,29,30,31]. Let be a graph depicting a power transmission system, where a vertex depicts a power network node and an edge is a connectivity line by which two graph vertices are joined [28,29,30,31].
Each power network node represents a substation where generators, loads, and transmission lines are joined. Let be a defined PMU set solution on a graph and the set of monitored vertices [28,29,30,31]. The observability of is determined by the two rules relying on electrical laws below [28,29,30,31].
Rule 1: If a PMU is installed on an edge, then vertices and are monitored.
Rule 2: If a monitored vertex has all its neighbours monitored, save one, then this vertex is monitored.
By rule R1, the PMU installed at calculates the voltage at and the current on . Using Ohm’s law, we can work out the voltage at the vertex . Then vertices are observed [28,29,30,31].
By rule R2, if a vertex and all its neighbors are monitored, except a single vertex , then utilizing Ohm’s law we define the current on for knowing the currents on all (), we can work out the current on utilizing Kirchhoff’s law [28,29,31]. Then, the voltage at and the current on are measured, and we define the voltage on using Ohm’s law. Hence, is observed [28,29,30,31].
Definition 1.
Statement of the Power Dominating Set Problem:
The power dominating set is the OPP problem which determines an optimal PMU number with a varying number of channel capacities.
Definition 2.
Statement of the Power Edge Set Problem:
The power edge set is the OPP problem which utilizes a single-line PMU and determines a proper number of them for installation.
5.1. Binary-Integer Programming Model Considering an Unlimited Number of Channel Capacities
The integer programming models declare the integer variables representing “yes” or “no” decisions, meaning that they are taking two values, i.e., zero or one [13,14,15,16]. Such integer problems are declared as follows [13,14,15,16,17,18]:
where is defined as a Boolean constraint, and the number of the decision variables. The problem’s solution is the set of assignment values that produces the best objective value while the logical constraints are satisfied [13,14,15,16].
Consider an event that may or may not happen, and assume that we choose between these two options. To make such a decision, a binary variable is as follows [13,14,15,16]:
Therefore, a decision is required to solve the optimization problems. In such kinds of problems, the possible answers are “yes” or “no” [13,14,15,16], which are interpreted as zero or one [16]. This kind of problem is a zero–one linear program in which the variables range in the decision domain [13,14,15,16,17,18].
Therefore, a BBA is needed that enforces the assignment decision model to result in a “yes” or “no” output [37,38,41,51]. The power grid is completely monitored if the phasor voltage is calculated for each network node either in a direct or indirect way [29].
We adopt a logical relationship for declaring those decisions followed by a linear constraint function [13,14,15,16,37,38,41,42,43,44,51].
With an unrestricted channel capacity, a PMU is placed at a node that can monitor all the buses through the connectivity lines between that bus and its neighboring buses [32]. The OPP model needs a decision value equal to zero or one [16].
Thereby, the OPP problem is originally declared in a integer program [13,14,15,16,17,18]. Let us define the programming model related to the power grid with n nodes [31,32,33,34,35,36,37,38,41,51].
Given an n—bus power network and considering that the PMU channel availability permits us to calculate the phasor voltage at the installation node and the line phasor currents emanating from that node [37,38,41,51]. the minimization model is structured considering an unlimited number of channel capacities [37,38,41,51].
Definition 3.
Statement of the decision variables’ nature in the decision-making problem:
The decision variables are stated to be as follows [37,38,41,51]:
The binary-integer model is declared as [32,33,37,38,41,51]:
Let us determine the power grid connectivity matrix as [32,33,37,38,41,42,51]:
The inequality constraint function is based on a multiple-choice decision and logical constraints [13,14,15,16,37,38,41,51]. The investment must be at least one of the obtainable options that satisfy the Boolean logic constraint function [37,38,41,51], where is a binary decision variable placement vector whose elements are stated if the sensor device is placed at a node or not [37,38,41,51].
The objective function (3) represents the entire cost investment. The constraints are declared in force for each decision variable, and the objective function is minimized subject to a set of inequality constraints defined on a binary domain [37,38,41,51].
The binary-integer model is solved by a BBA. The focus is to adopt the BBA, which is utilized to solve relaxed programming problems to achieve bounds on the objective function value of the original MILP model within a binary domain [13,14,15,16,17,18].
The BBA solves LP-relaxed problems where the binary restriction on the decision variables is substituted by the relaxed restriction [13,14,15,16,17,18].
The next steps of the algorithms are to implement and solve the linear relaxed problems [37,38,41,51]. If the algorithm’s output is integer, then the solution is achieved [13,14,15,16,17,18]. In a different outcome, two sub-problems are constructed by utilizing a branch methodology on a fractional variable [37,38,41,51]. The gap between the upper and lower bounds is inside a pre-given tolerance [13,14,15,16,37,38,41,51].
The upper bound is the incumbent cost value, and the current lower bound is the minimum quantity of the lower bounds produced by finding a solution to the candidate sub-problems [13,14,15,16,37,38,41,51]. To run this optimization process, MILP solvers can be called to achieve an accurate solution point within a range given by the users.
Definition 4.
The optimality gap is stated as follows:
Definition 5.
Definition of the percentage relative gap:
The termination criterion equal to the optimality gap means that a global solution has been reached [13,14,15,16,37,38,41,51]. The incumbent solution is the best solution delivered by the repetitive strategy in the BBA search tree [13,14,15,16].
The tolerance gap is a need for a successful termination of the BBA [13,14,15,16,37,38,41,51]. The optimization procedure leads to a ϵ-optimality criterion [13,14,15,16].
The relative absolute gap is a criterion to measure how close the solution is to being global [13,14,15,16]. The steps of the BBA implementation are outlined in Algorithm 1.
| Algorithm 1: Steps of BBA methodology |
| 1. Calculate the lower bound: A procedure is used to achieve the lower bound on the objective function to solve the given sub-problem and deliver an estimated point. |
| 2. Calculate the upper Bound: An upper bound is evaluated to give the solution. |
| 3. Branching method: The sub-problem is portioned to deliver more than two children by a procedure strategy |
| 4. Methodology search: A search order is programmed to construct the binary tree. |
| 5. If the stopping criterion is satisfied, then end up the iterative scheme. |
| 6. The BBA ends delivering a solution as an output. |
Τhe integer program can be solved utilizing genetic algorithms and binary particle swarm optimization [18,51]. They follow a probabilistic search of the feasible region due to a random selection of the initial population, searching and finding an optimum solution [25,26,51]. Strategies such as special creation, crossover, and mutation functions are utilized to enforce the variables to be declared in the integer problem solving [72]. GA tries to minimize a penalty function, not necessarily the fitness one, and a penalty term is added to consider any infeasibility while the feasible region is explored [25,26,27,50,51]. The penalty function is performed with a binary tournament choice to find individuals for subsequent generations [25,26,50,51].
If the member is feasible, the penalty function value of a member included in the population is the fitness function [51]. Otherwise, the objective function counts the maximum fitness function among feasible members of the population, plus a sum of the constraint violations in case of an infeasible point if the member is found to be infeasible [72]. The steps of the GA code are outlined in Algorithm 2. The flowchart is given in Figure 1.
| Algorithm 2: Steps of GA implementation |
| 1 Set ; starting from the population ; |
| 2 Estimate ; |
| 3 If the stopping criterion is completed, then end up the iterations; |
| 4 Choose from ; |
| 5 Evolve to create ; |
| 6 Set , go to step 2. |
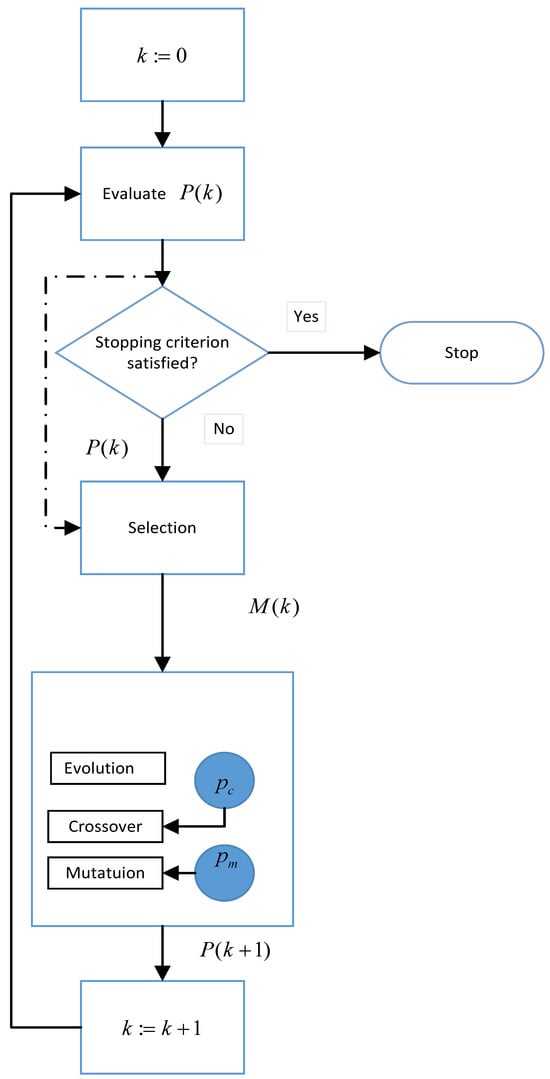
Figure 1.
Flowchart of genetic algorithm.
Particle swarm optimization (PSO) does not utilize mutation and crossover parameters [25,26,39,48,51]. PSO is easily implemented without using encoding or decoding of the parameters into binary strings, such as those in genetic algorithms which can also utilize real-number strings [25,26,39,48,51].
PSO searches the feasible regions by utilizing trajectories of particles in a quasi-stochastic manner. A deterministic strategy and a heuristic strategy are implemented for the PSO [25,26,39,48,51].
Each particle is attracted toward the position of the current global best and its own best location in history, while it has a tendency to move accidentally at the same time.
When a particle detects a location that is better than any previously found locations, then it updates it as the new current best for the particle [25,26,39,48,51].
There is a current best for all particles at any time during the iterative scheme. The target is to detect the global best among all the current best solutions so that the objective will no longer improve after a number of iterations [25,26,39,48,51].
An inertial weight parameter is used to properly tune the optimization mechanism between the local and global best of the particles at each trial estimated point. This optimization factor is used to give an accurate solution within specific tolerances criteria.
The inertia weight is utilized to balance the global exploration and local exploitation [51]. We use the linear decreasing inertia weight in Equation (12) [25,26,27,51].
Although PSO was proposed to optimize unconstrained optimization problems, it can also solve constraint optimization problems. The PSO is proposed to locate the optimality handling the constraint function in an appropriate way. A mechanism is utilized when the particle’s best position and the swarm global optimal position are updated [21]. To explore the feasible region, a feasibility restriction is utilized to evaluate the constraint violation and deliver a feasible and optimal solution [25,27,39,47,48,51].
The PSO code is depicted in Algorithm 3 and the flowchart is given in Figure 2 [25,26].
| Algorithm 3: Steps of PSO implementation |
| Objective function . |
| Initialize locations and velocity of particles. |
| Determine from at (). |
| while (criterion) |
| (Iteration counter) |
| For loop over all particles and all dimensions |
| Produce new velocity |
| Compare new locations |
| Assess objective functions at new locations |
| Deliver the current best for each particle |
| end ε |
| Deliver the current global best |
| end while |
| output the final results and |
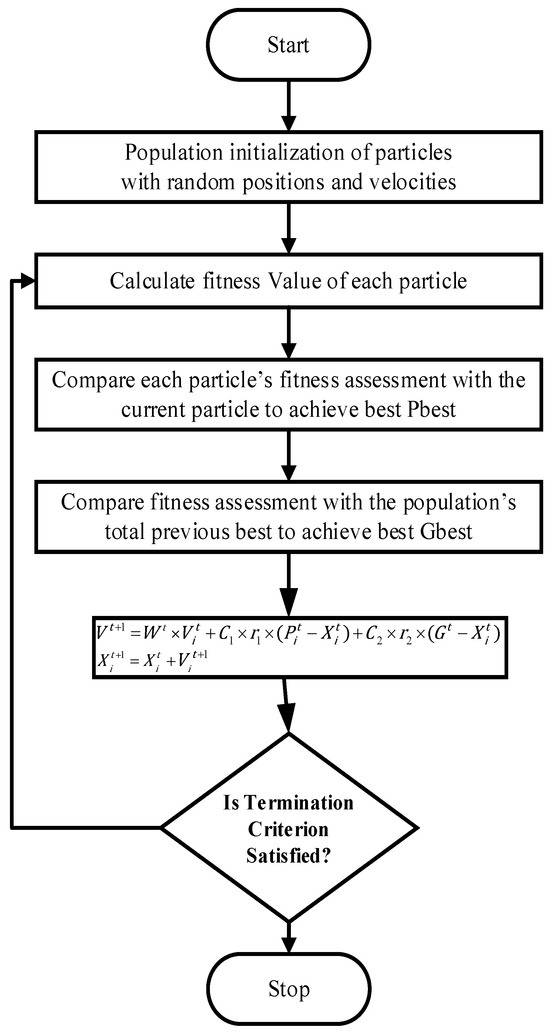
Figure 2.
The flow chart of particle swarm optimization.
5.2. Constrained Binary-Integer Programming Model with a Fixed Number of Channels
The widespread adoption of PMUs is gradually advancing but faces impediments from technical limitations and economic factors, thus hindering its pace [56,57,58].
In actual conditions, every PMU has a limited number of channels, and therefore we need a more realistic installation of PMUs in a way to further decrease the cost of the investment [47,56,57,59,60,61,62,63,64,65,66,67].
Every PMU produced by the industry has a restricted number of channels for installation at a substation [52,56,57,58,59,60]. The number of branches adjacent to a power grid node in which a PMU is placed is known as channel capacity [60].
Considering the channel limitation capacities there is a reasonable query: which is the appropriate set of topological constraints to lead to a least PMU number with an adequate number of observed branches without sacrificing the entire observability at all [52,56,57,58,60].
Here we implement the OPP-based model when the number of measurement channels is restricted and the zero-injection buses are not assumed in the formulation.
We have taken into account a PMU which has an number of channels and is placed at a bus within the power grid [47,56,57,58,59,60,61,62,63,64,65,66,67].
We also consider that the bus is adjacent to number of buses [56,57,58]. If the number of channels is greater than the number of neighbors , then a single PMU installed at the bus will give the phasor voltages at all its neighbor buses [56,57,58].
Differently, there will be combinations of possible channel assignments to branches adjacent to bus [56,57,58,59,60,61,62,63,64,65,66,67]:
where is the number of lines joined to bus k, and is the pre-given channel limit for the PMUs [56,57,58,59,60,61,62,63,64,65,66,67]. The number of these combinations is defined by [56,57,58,59,60,61,62,63,64,65,66,67]:
where:
is the number of branches, is the number of available channels, and is the number of combinations of possible channel arrangements to lines adjacent to the related bus [56,57,58,59,60,61,62,63,64,65,66,67].
The channel limit constraint function can be adopted so that a PMU posed at a node will monitor its adjacent nodes by choosing a suitable combination of L [56,57,58].
The OPP is declared using the integer linear programming model based on a restricted number of channels, and can be declared as follows [56,57,58]:
where and the matrix consists of rows representing the possible combinations [56,57,58,59,60,61,62,63,64,65,66,67].
represents a PMU placement design that gives a combination where one bus is dominant and observes the neighboring buses [56,57,58].
This optimization problem is equivalent to the set covering problem [28,29,31], that is, the problem of seeking out the smallest number of subsets in the family of sets that constitutes the rows of the matrix [56,57,58,59,60,61,62,63,64,65,66,67].
Hence, a PMU placement is derived in which each element observes a subset of buses [60]. Y is a placement vector and is formulated by , where m is the number of subsets [56,57,58]. Each subset is constituted by a set of buses where the center bus observes some of the neighboring buses. The center bus is the dominant bus and is the first entry in the subset, as noted in [60].
The Y placement vector’s nonzero entries will indicate the rows of related grid nodes, voltage angles of which can be monitored by these synchronized measurements [56,57,58]. PMU locations are derived and its bus observes a subset of its neighboring buses with the branch assignments [60,61,62,63,64,65,66,67].
Thereby, we can derive the PMU locations and the branch assignments, which mean the lines directly observed by the dominant bus or center bus.
Algorithm 4 presents the MILP solver implementation considering a multi-channel capacity. We define the objective function, the binary connective matrix, the unity vector and the lower and upper bound of the decision variables. The MILP routine is invoked to deliver the upper bound for the minimization problem [13,14,15,16,72,73,74,75,76,77,78,79,80,81].
| Algorithm 4: Steps of MILP Solver implementation |
| MILP Algorithm: Optimal Placement of PMU with multi-channel capacity |
| 1. The set of implementation costs, ; |
| 2. Set of possible combinations including a number of nodes; |
| 3. Define a set of variables Y ; |
| 4. Define binary connectivity matrix; |
| 5. ; objective function considering costs; |
| 6. /* solving the problem of mixed integers; |
| 7. programming*/ |
| 8. Invoke MILP solver in MATLAB environment; |
| 9. solve placement minimizing using mip; |
| 10. |
| 11. Solution (display combinations by which a PMU location is the Center and the other locations representing the PMUs directly observed); |
| 12. Solve linear relaxation problems of the initial MILP model |
| 13. Tighten LP via cutting planes and domain propagation |
| 14. Search for feasible solutions via primal heuristics for the MILP model |
| 15. Branch on variables |
| 16. Output: a binary-feasible solution to the MILP model |
| ✓ Exit: MILP status (optimal or infeasible) and solution |
| ✓ Absolute gap: |
| ✓ Relative gap: 100 (U − L)/(abs(U) + 1) |
The MILP solver solves the linear programming relaxations and allows temporarily the integer decision variables to be continuous [13,14,15,16,17,18,37,38,41,51,72,73,74,75,76,77,78,79,80,81].
Dual-simplex or primal-simplex algorithms finally solve the relaxed problems in the relaxed decision variable range [13,14,15,16,17]. The iterative process is completed within specific criterions to achieve an accurate solution [19,20,21]. To conclude, four tasks require attention when the integer problem is solved by a BBA scheme [14]:
- Formulation so that the absolute gap is small;
- Heuristic computations are needed to find a good lower bound;
- Branching;
- Node selection.
The MILP solver ends up as the process with an optimality gap, which is given counting the upper bound and the lower bound estimated points [13,14,15,16,17,18,37,38,41,51,72,73,74,75,76,77,78,79,80,81].
This gap is determined as the optimal value where is the best integer solution and is the lower bound. If the absolute gap is found equal to zero, the solver returns a solution at the globally optimum point [37,38,41,51,72,73,74,75,76,77,78,79,80,81].
5.3. Constrained Binary-Integer Programming Model with a Single-Line PMU
Instead of using multi-channel PMUs, single-line PMUs observe a single line by calculating the running current in the line and the phasors’ voltage at the end point of that line [61]. The problem is referred to as the minimum edge cover problem in graph theory and it is directly related to the minimum set covering problem, which is a combinatorial optimization problem [28,29,30,31].
An edge cover of a graph is a subset of edges such that for any , there exists such that is an endpoint of . As given in the definition, the power edge set (PES) problem is as follows [28,29,30,31,37,38,41,51]:
Definition 6.
Declaration of the edge cover problem:
Given a , find an edge subset of minimum cardinality such that a placement of PMUs on edges over yields the full observability of the graph [28,29,31]. It is noticed that the OPP finds a subset of nodes such that the whole graph is topologically observable similar to the “set covering problem” [28,29,30,31].
The problem solving goal is to monitor a single branch, namely the sending end node voltage and the sending end current flow towards the receiving end bus [61]. We note that single-line PMUs are placed at either end of the line since, in either case, both end bus voltages will be calculated due to the availability of the line current [61].
Thus, the problem is declared in installing PMUs to lines and not to nodes. If a PMU is considered to be a line, it can be installed arbitrarily at either end of that line without changing the output of the observability-based model [61,64].
Thereby, the optimal branch phasor current measurement problem is to discover the minimum set of line phasor currents such that a power node is monitored by, at least and at most, one line phasor current [28,29,30,31,61].
The problem is declared as a binary-integer program, that is, a set covering problem, or otherwise a minimum edge set problem [28,29,30,31,61]. An edge cover is a subset of edges determined similarly to the vertex cover, that is, a collection of graph edges so as a union of edge endpoints relating to the vertex set of the graph [28,29,30,31,61].
The solution of the edge cover problem gives the smallest possible number of edges for a specific graph [28,29,31,61]. In this paragraph, we study the OPP model with one channel, such that to guarantee a complete observability of the whole graph [28,29,30,31,32].
If a PMU is selected for a branch, it can be installed arbitrarily at either end of that branch without changing the outcome of network observability analysis [31,60,61].
Thus, it confirms the observation that the matching is perfect [28,29]. This is true if it covers every vertex of the graph, that is, every vertex is within exactly one edge of the matching where an edge is shown as a set of two different vertices [31,60,61].
This case considers the PMU where the PMU installed at a bus monitors a single line by computing the voltage phasor and the phasor current running this line [60,61].
A PMU number is computed to maintain the whole observability [60,61]. Let us assume a system consists of buses and branches [78]. The OPP problem is declared in a binary-integer programming format [61]:
where [31,60,61]:
5.4. Constrained Mixed-Integer Nonlinear Programming Formulation
The minimization problem is stated as a nonlinear model following the binary-integer programming. A linear cost function is minimized subject to a set of polynomial constraints within a binary decision bound. Assume that the optimization problem is declared as follows [19,20,21,22,23,24,25,26]:
where:
A combination of buses can be derived by declaring a constraint function as [20]:
where are unknown optimization variables and each variable is a possible subset of buses where a center bus exists monitoring a set of its neighboring buses in the power transmission grid [60].
The mathematical model is solved by the SCIP solver utilizing LP solvers named SoPlex and IPOPT for solving the nonlinearities [73,74]. Finally, a BBA tree is constructed through linearized strategies towards optimality [37,38,41,51,72,73,74,75,76,79,81].
To estimate the quality of the solution, the user examines the optimality gap [81]. The optimal solution is obtained inside an 0.00% tolerance criterion, which is accurately calculated during the repetitive BBA algorithmic scheme [37,38,42,51]. This tolerance criterion is required to end the termination with a successful output [37,38,42,51].
5.5. Constrained Nonlinear Programming Model
Suppose (P) is the optimization problem [19,20,21]:
For some is generally defined on [19,20,21,82]. In mathematical algorithms, optimization is executed relying on gradient-based algorithms for minimizing or maximizing the objective function in the problem [19,21,41] or building a binary tree by utilizing BBA as shown in [13,14,15,37,38,41,42,51].
Definition 7.
Statement of the local minimizer of the (P) problem.
We declare that is a local minimum of the minimization problem if ≤ , where N is a neighborhood of the local minimizer, if there exists such that whenever satisfying .
The objective value is a local minimum of the optimization problem where is the feasible region of the optimization problem [19,20,21].
Definition 8.
Statement of the global minimizer of the (P) problem.
We declare that is a strict global minimizer of the minimization problem if [19,20,21].
The objective value is a strict global minimum of the optimization problem, where is the feasible region of the optimization problem [19,20,21].
The objective function can have a strict global minimizer at only one solution point. It is possible to have non-strict global solution at several points [19,20,21].
Even though the minimum could be global, there can be more than one minimizer at the least objective value [19,20,21].
Definition 9.
Statement of the (P) problem.
Problem (P) is declared in general as NP-complete [19,20,21] and one is in many cases satisfied with the determination of a local minimum point, which can be reached by calling some nonlinear algorithms [13,14,15,19,20,21,22,23,24].
Such kinds of nonlinear algorithms are based on local search of a neighborhood in the feasible set constituted by the objective function, the constrained function, and bounds to hopefully finding a good local minimum point [19,21,22,23,24].
Such algorithms estimate a trial point at the current iteration, which is some feasible point solution belonging to the feasible region [19,20,21,22,23,24].
Starting from a first estimated solution, a sequence of trial points is generated, , which is hoped to converge to an optimum point [19,20,21,22,23,24].
That point must satisfy the Karush–Kuhn–Tucker (KKT) optimality conditions within a given ϵ-tolerance [19,20,21,22,23,24,41,73,82].
Then, KKT is necessary for determining a local minimum of (P). These optimality conditions are required for a trial point to be characterized as a local minimum point, and actually, yet for a stationary point of the Lagrangian function. Hence, any stationary point must satisfy these sufficient and required conditions for locality [19,20,21,22,23,24].
In such optimality conditions, the real question if the local minimizer of the cost function is global at the same time becomes a reasonable query [37,41,42,51].
As the reader may understand, in such NP-complete problems, the difficulty lies in finding a good approximation of the true optimal solution point [17,18,19,37,38,41,51]. For that needed purpose, some sufficient conditions are required to characterize if a solution point is a global one or not [19,20,21,22,23,24,25,26].
First-order and second-order conditions are able to work together for non-convex optimization problems by determining local minimum points strongly relying on the selection of the initial point [19,20,21,22,23,24,25].
We can use local algorithms such as interior-point methods (IPMs) and sequential quadratic programming (SQP) methods to find locality, and if we adopt multi-start initialization techniques [41], a global solution can be reached with high probability [19,20,21,22,23,24,25].
SQP algorithms solve a sequence of optimization sub-problems, each of which optimizes a quadratic model of the objective under a linearization of the constraint function.
The nonlinear algorithms can reach a local solution in a reasonable running time [19,20,21]. The other option is to adopt a global optimizer routine to determine a global minimum point but at a slower time [19,20,21,22,23,24,25,37,38].
Furthermore, derivative-free optimizers (DFOs) are adopted to handle such a kind of nonlinear programming model [22,41,70,71].
DFO is a totally free direct-search algorithm that calculates the gradient of the objective and constraint functions per iteration [22,41,70,71].
Direct-search algorithms guarantee global convergence to a local solution with optimality conditions fully satisfied [22,41,70,71]. For that convergence, the Clarke calculus is adopted for handling non-smooth functions [22,41,70,71].
The generalized pattern search algorithm (GPSA) is a direct-search algorithm perfectly suited to PMU allocation problem solving [22,41,70,71]. The search methodology is implemented to estimate a limited number of trial points [22,41,70,71].
GPSA executes a global exploration of the feasible set and permits us to optimize the programming model [22,41,70,71]. Τhe aim is to find a local solution point [22].
In the case of failing to find any improvement, the poll suggests trial points in the neighborhood of the incumbent solution relying on suitable optimality conditions [22,41].
The poll methodology guarantees that the algorithm has a global convergence property and that a local minimum can be reached [22,41,70,71].
This optimization problem is smooth but many local minimum points can be found by gradient-based algorithms or derivative-free optimizers [20,41,70,71]. The nonlinear optimization algorithms usually present the general iterative scheme for the optimization problem of the form in Algorithm 5 [19,20,21,22,23,82]:
| Algorithm 5: Steps of nonlinear algorithms |
| Step 0: initial estimate , we set the iterative number equal to zero, |
| Step 1: Computation of the search direction |
| Step 2: Computation of step-length such as: |
| , |
| Step 3: |
| Step 4: if , then stop. Otherwise, set and go to step 1. |
is solved either with SQP or IPMs [19,20,21]. The objective function is declared in a quadratic form and the minimization problem is formulated as follows [19,20,21,22,23,24,25,41]:
where are differentiable functions. Furthermore, nonlinear inequality constraints can be formed in this formulation by utilizing slack variables [19,20,21].
The IPM strategy achieves a solution by approximately solving a sequence of barrier problems of the following format [19,20,21,24,25,41,72,73]:
where μ is a barrier parameter that is reducing and converges to zero [19,20,21]. For this solution, Newton (or quasi-Newton) methods are utilized for convergence [19,20,21] whereas some algorithms utilize SQP (or trust-region) methods [19,20,21].
The Newton methods utilize a search direction strategy from solving a Newton equation of the perturbed optimality system [19,20,21]. To obtain a local convergence algorithm in a fast manner, the barrier parameter needs to be updated carefully [19].
The SQP and IPMs are performed through the Fmincon optimizer function included in the MATLAB optimization toolbox [41]. The optimizer solver is able to initialize the iterative process using a multi-start search procedure in order to terminate to a local solution point, which is approximately the global one with high accuracy [72].
Furthermore, IPMs can be performed by calling the IPOPT solver and reaching a local point [73]. Both algorithms end the iterative process with specific tolerances [19,20,21]. The criteria tolerances are adequate to guarantee convergence to a local point [21].
The objective function is estimated at each iteration taking into account specific tolerances such as the and the function tolerance [19,20,21,41,72,73].
Furthermore, the constraint tolerance is considered an upper limit for any constraint violation at each iteration [21]. The constraint function magnitude must not exceed the constraint tolerance to avoid the violation of the feasibility [19,20,21,41,72,73,79].
Considering the importance of the selection option in handling the constraint function, a variety of mathematical and heuristic algorithms are adopted for solving the OPP-based model with a limited amount of channel capacity. Our aim is the following:
- Instead of searching local solution points for the optimization models, we examine all the sufficient and guaranteed optimality conditions for finding global solutions.
- Hence the testing of optimality yields the exact solutions by utilizing the BBA, SQP, IPMs, GPSA, and BPSO for simulation purposes.
All mathematical algorithms evaluate a linear objective of a quadratic function through the iterations required to first ensure a feasible trial point, and then optimality, etc. [13,14,15,16,19,20,21,37,38,41,42,51,82].
The other concern is how to improve the performance of convergence towards an optimal solution using BBA, nonlinear, and heuristic algorithms [37,38,41,42,51].
Finally, the simulation running of the algorithms reveals the possible combinations of PMUs, the PMU locations, and the branch assignments [56,57,58,59,60,61].
6. The IEEE-14-Bus System for Illustrating the Mathematical Models and Numerical Results Obtained by the Optimization Procedure
In line with the power grid utility industry’s concern, the number of constraints is increasing and it is strongly dependent on the quantity of channel capacity [56,57,58,60,61]. We first declare the integer program and the mixed-integer nonlinear program, and finally obtain the pure nonlinear mathematical models [13,14,15,23].
The integer program is declared with a linear objective function to be minimized under specific inequality constraints under a topological analysis.
We consider that the power grid is fully observable with an appropriate PMU number under the channel restriction capacity. The solution is given by BBA, Gas, and BPSO. Then, we transform it into a nonlinear model solved by BBA. Finally, we examine the conditions under which the pure nonlinear problem is solved using SQP, IPMs, and GPSA. As a benchmark case study, we use the IEEE-14-bus system and a binary-integer linear program is firstly studied following the works of Korkali et al. [56,57,58].
The matrix B, which consists of rows representing the possible combinations, is depicted in Equation (32) for the IEEE-14-bus system (Figure 3) [52,56,57,58,59,60,62,63,64].
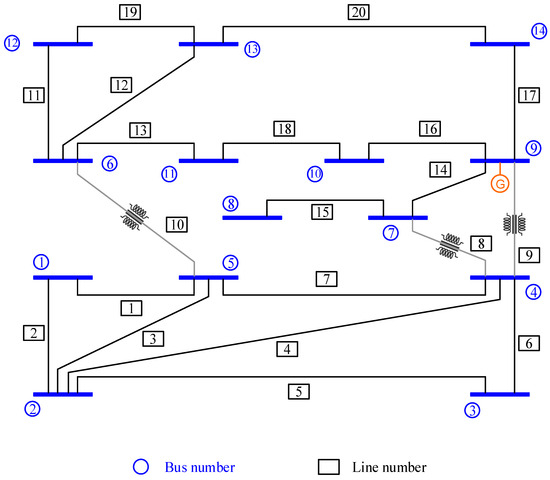
Figure 3.
IEEE-14-bus system.
Suppose that the channel limit is equal to four, that is , and the possible number combinations are equal to 18, [56,57,58,60]. The set of all subsets in the case of considering four channels is the following [60]:
Each first entry of the subset is the center bus used to monitor the adjacent buses. For example, 2 is the center in the second subset, 8 is the center in the 12th subset, 10 is the center in the 14th subset, and 13 is the center in the 17th set [60].
When , and solving the ILP model for the IEEE-14-bus network in Figure 3, four combinations are derived, that is, {2, 12, 14, 17}. Assume that ; declare a binary decision variable such that if a PMU is placed at the center of the subset of the family S, and otherwise, where s is an index within the family of the subsets [60].
The algorithm has chosen as a solution the set {2, 12, 14, 17}. From that subset, and considering the yes or no decision [15], a PMU placement is obtained in which the center is declared as 1 in the placement vector and monitors all buses inside that subset [60].
The algorithmic scheme delivers PMUs installed at buses , which are centers of the subsets, respectively [60]. Thus, the placement result is a binary vector with “yes” or “no” decisions [13,14,15,16,17,18].
Furthermore, the algorithms identify not only the PMU location, but also the branch assignments considering the extra restriction, which is a fixed amount of capacity. The solution is adequate to decrease the entire cost without sacrificing observability. For example, the PMU at bus 2 monitors buses 2, 1, 3, 4, and 5. The PMU locations are {2, 8, 10, 13}, where the branch assignments are the PMU channels presented in Table 1.

Table 1.
Channel capacity, PMU number, PMU locations, and PMU channels.
The above results are produced by executing YALMIP’s BBA and the log file is presented in Algorithm 6 [75,77]. YALMIP’s BBA optimizes the integer model declared in Equations (33)–(35). The log file is presented in Algorithms 6 and 7 [37,38,72,74,75,76,77,79,80].
The binary decision variable is displayed in Table 1 and it is a placement in which each element is the combination related to the center bus [56,57,58,59,60,61].
The outcome presents a PMU set solution with all network buses observed. One bus serves as the center interconnected with neighboring buses through branches, such that all buses are reachable by synchronized measurements and make the power grid fully observable [56,57,58,59,60,61,62,63,64,65,66,67].
The set {2, 12, 14, 17} corresponds to PMU locations, namely {2, 8, 10, 13} illustrated in Figure 3. A PMU placed at bus 2 will monitor buses 1, 2, 3, 4 and 5; the one at bus 8 will monitor buses 7 and 8; the one at bus 10 will monitor buses 9, 10, and 11; and the one at bus 13 will monitor buses 6, 12, 13, and 14. Then, the observability is preserved.
Thus, the system observability is preserved with the best trade-off relationship between the channel restriction capacity and the best PMU locations. Hence, we succeed in finding PMU set solutions which observe branches with an increased redundancy.
Algorithms 6 and 7 present the output logs produced by BBA optimizing the integer programs [14,15,16]. The solution is achieved within a 0.00% optimality criterion [15].
| Algorithm 6: Steps of optimizing YALMIP’s BBA |
| + Solver chosen : BMIBNB |
| + Processing objective function |
| + Processing constraints |
| + Branch and bound started |
| * Starting YALMIP global branch & bound. |
| * Upper solver : INTLINPROG |
| * Lower solver : INTLINPROG |
| * LP solver : INTLINPROG |
| * -Extracting bounds from model |
| * -Performing root-node bound propagation |
| * -Calling upper solver + Calling INTLINPROG |
| (Found a solution!) |
| * -Branch-variables : 0 |
| * -More root-node bound-propagation |
| * -Performing LP-based bound-propagation |
| * -And some more root-node bound-propagation |
| * Starting the b&b process |
| Node Upper Gap (%) Lower Open Time |
| + Calling INTLINPROG |
| 1 : 4.00000E+00 0.00 4.00000E+00 0 0s Poor lower bound |
| * Finished. Cost: 4 (lower bound: 4, relative gap 0%) |
| * Termination with all nodes pruned |
| * Timing: 38% spent in upper solver (1 problems solved) |
| * 19% spent in lower solver (1 problems solved) |
| * 1% spent in LP-based domain reduction (0 problems solved) |
| * 1% spent in upper heuristics (0 candidates tried) |
| ans = |
| Columns 1 through 15 |
| 0 1 0 0 0 0 0 0 0 0 0 1 0 1 0 |
| Columns 16 through 18 |
| 0 1 0 |
| ans = |
| 2 12 14 17 |
| Algorithm 7: Steps of optimizing YALMIP’s BBA |
| + Solver chosen : BMIBNB |
| + Processing objective function |
| + Processing constraints |
| + Branch and bound started |
| * Starting YALMIP global branch & bound. |
| * Upper solver : INTLINPROG |
| * Lower solver : INTLINPROG |
| * LP solver : INTLINPROG |
| * -Extracting bounds from model |
| * -Performing root-node bound propagation |
| * -Calling upper solver + Calling INTLINPROG |
| (Found a solution!) |
| * -Branch-variables : 0 |
| * -More root-node bound-propagation |
| * -Performing LP-based bound-propagation |
| * -And some more root-node bound-propagation |
| * Starting the b&b process |
| Node Upper Gap (%) Lower Open Time |
| + Calling INTLINPROG |
| 1 : 2.64286E+00 0.00 2.64286E+00 0 0s Poor lower bound |
| * Finished. Cost: 2.6429 (lower bound: 2.6429, relative gap 0%) |
| * Termination with all nodes pruned |
| * Timing: 27% spent in upper solver (1 problems solved) |
| * 12% spent in lower solver (1 problems solved) |
| * 1% spent in LP-based domain reduction (0 problems solved) |
| * 1% spent in upper heuristics (0 candidates tried) |
| Columns 1 through 15 |
| 0 1 0 0 0 0 0 0 0 1 1 0 1 0 0 |
| Columns 16 through 18 |
| 0 0 0 |
| 2 10 11 13 |
An optimal solution was achieved with an absolute gap equal to zero, which means a better solution cannot be delivered by the iterative process [13,37,38,41,51].
Considering the case of the unlimited PMU channel capacity [31,32,33,40,46], the best system observability index was found in [33,37,38,41,42,43,44,45,47,51].
We declare a b-objective optimization model to find solutions with a higher observability index. The mathematical programming model is stated in a ILP domain [14]:
where , , [56,57,58], and is the number of power grid nodes. Table 1 presents the log file produced by BBA [37,38,41,51,75,77].
For the minimization problem, the BBA builds a sequence of sub-problems to try to find an optimum point solution [72,79,80]. The solution of the relaxed problems gives the upper and lower bounds on the objective function solution [72,74,75,76,79,80,81].
The first upper bound is any feasible point whereas the first lower bound is the solution to the relaxation problem. The upper bound is the objective’s function bound.
Τhe algorithm constantly estimates the upper bound and lower bound to reach optimality for the minimization problem [17,72,74,75,76,79,80,81].
For the minimization problem studied in this paper, the upper bound is assumed to be the solution to the problem solving. The lower bound is the reason for closing the absolute tolerance gap delivering a global solution point [74,75,79,80].
The solver returns a solution within an 0.00% optimality criterion, proving that no better optimum can be achieved. Thereby, the solution is a global optimum point.
The optimal result is interpreted as follows: From Equation (33), we found the bus combination set solutions: . Each first entry in each subset is the center bus, which is the dominant bus, and that bus is installed as a PMU [60], i.e., the PMU set solution [60]. We definitely achieved a set solution with the maximum observability index for a fixed channel capacity . The branch assignments are observed by optimal placement of PMUs at power nodes and are as follows:
When , solving the ILP model for the IEEE-14-bus network in Figure 3, four combinations are derived, that is, {2, 10, 11, 13}. The algorithmic scheme delivers PMUs installed at buses of subsets .
The PMU locations are {2, 6, 7, 9}, where the branch assignments are displayed in Table 2 [64]. The ILP model with a single line is optimized with the intlinprog optimizer function [37,38,41,51]. Optimal set solutions are derived and presented in Table 3 for the IEEE-14-bus, 30-bus, 57-bus, and 118-bus systems. Each number reflects a line where a single-line PMU is assigned across the two-points of the line [61].

Table 2.
Channel capacity, PMU number, PMU locations, and PMU channels.

Table 3.
Algorithm BBA: Optimizing the ILP model with a single line.
Two set configurations are derived based on the strategy by which the linear programming relaxations are solved. We utilize the primal-simplex algorithm and the dual-simplex algorithm to deliver a binary feasible solution for the initial model.
We present the PMU numbers, PMU locations, and the related PMU channels for the IEEE-14-bus system in Table 4 and Table 5 [78]. Two instances are studied. The first gives results produced by minimizing a one-product objective function [56,57,58].

Table 4.
Optimizing the ILP with multiple lines for IEEE-14 bus.

Table 5.
Algorithm BBA: Optimizing the b-objective ILP with multiple lines for IEEE-14 bus.
The second produces results by optimizing a b-objective function under a set of inequality constraints [41,51]. The b-objective is minimized under a certain number of constraints so that an optimal point can be determined [38,41,51]. Intlinprog removes the decision bound integrality and permits all variables to be temporarily real [17,18].
The solution was found by solving the relaxed problems in the BBA construction tree and this solution is feasible and optimal for the initial MILP [13,14,15,21]. Each instance was derived within the pre-specified stopping and tolerance criterion [13,14,15,16,19,21]. BBA utilizes the optimality gap as a stopping criterion to end the iterative scheme [13,14,15,16]. It is calculated for all instances returning a zero value.
We observe that the placement set gives an optimum point where each center observes the maximum number of power nodes [78]. Each subset is a connected dominating set with the characteristic that each center is a vertex reaching any other vertex inside that subset by a connectivity line [30,60]. Therefore, the observability is attained even in a restricted channel capacity scenario, as noted in [56,57,58,59,60,61,62].
In the meantime, we suggest a mixed-integer nonlinear program that leads to optimality and works together with a similar formulation in the continuous domain. We perform the integer nonlinear programming using a global BBA embedded in the YALMIP toolbox and the log files produce the desired output [37,38,75,77].
The nonlinear integer programming model is declared using the IEEE-14-bus system. The polynomial constraint function is written. The objective function is minimized subject to a set of equality constraints within binary decision variables [19,20,21,37,38]. The instance is solved as an empty entry, when the coincides with the best value whereas the closes the optimality gap [37,38,41,51,72,74,75,76,79,80]. Therefore, the nonlinear integer programming model is exactly solved by calling the BBA embedded in the SCIP optimizer function [74].
is an integer decision variable that takes two values, i.e., 0 or 1 [16]. The value 1 means the PMU combination is installed at the center bus [60]. The nonlinear programming is well posed given that the number of equality constraints is fewer than the number of the decision variables [19,20,21,22,23,24,70,82]. Using the IEEE-14 bus and the two instances, two optimal results are derived for a fixed-channel equal to four [64]. The first model optimizes an objective function with one product and the second a b-objective (Equation (35)) to find a better redundancy, as declared in [41,51].
Optimizing the augmented objective function, we increase the measurement redundancy and find a better optimal solution. The problem can be written in a compact form. We combine discrete decision variables, a linear objective function, and non-convexities in the constraint function and a global optimization execution.
We solve two instances, namely with one objective and a two-product function optimization model. The mathematical model is generally stated as follows [23,24]:
where y is the objective function and w is a unity vector [56,57,58].
The nonlinear program is solved by BBA [37,38,74,75,76,81]. YALMIP’s BBA and SCIP (Solve Constraint Integer Programming) optimizer tools can solve the nonlinear program. A solution is found within an optimality gap given by [72,74,75,76,80,81]:
The MILP optimizer routine ends the iterative process with an optimal solution when the absolute gap between the upper and lower bounds is less by the default value. The default value can be either 1 × 10−6 or 1 × 10−10. The optimal solution was found within a minimum value [72,74,75,76,79,80,81]. The upper and the lower bounds are computed in this instance. YALMIP’s BBA invokes local and MILP optimizer routines to build the BBA tree [37,38,74,75,76,79]. Fmincon delivers the upper bound whereas the lower bound is solved by the SCIP optimizer through linear programming relaxations [37,38,75]. Furthermore, the lower bound can be calculated using intlinprog, MOSEK, and Gurobi [72,74,75,76,79,80,81].
YALMIP’s BBA initially tries to discover the best feasible solution; then, calculations are implemented by the local [73] and lower solvers [80]. An LP-based domain reduction computation as well as some needed heuristic computations are performed to obtain the solution inside the -optimality criterion [13,14,15,16,79].
The optimization terminates when the difference between those bounds computed by YALMIP’s BBA routine is within the default value of the absolute gap [37,38,75].
As we observed, the upper bound is the best solution for the minimization process, whereas the lower bound minimizes the gap (lower bound: 4, relative gap 0%), as displayed in the output log in Table 6 [75]. Finally, the termination ends with all nodes pruned, as displayed in the output log of YALMIP’s BBA [37,38,74,75,76,77,79].

Table 6.
Algorithm BBA: Steps of optimizing YALMIP’s BBA.
Table 6, Table 7, Table 8, Table 9, Table 10, Table 11, Table 12, Table 13 and Table 14 illustrate results towards optimality [37,38]. The number of branch variables is equal to the number of possible combinations [60].

Table 7.
Channel capacity, PMU number, PMU locations, and PMU channels.

Table 8.
Algorithm BBA: Steps of optimizing YALMIP’s BBA.

Table 9.
Channel capacity, PMU number, PMU locations, and PMU channels.

Table 10.
Optimizing mixed-integer nonlinear program with multiple lines for IEEE-14 bus.

Table 11.
Algorithm GPSA: Steps of optimizing the GPSA.

Table 12.
Algorithm SQP: Steps of optimizing the SQP methods.

Table 13.
Algorithm IPOPT: Steps of optimizing the interior-point methods.

Table 14.
Channel capacity, PMU number, PMU locations, and PMU channels.
Further, we can select an upper bound of channel capacity to reduce the cost of installation (Table 4 and Table 5). Recent research reveals that the upper bound of capacity is four without sacrificing the essential task of observability [56,57,58,59,60,61,62,63,64,65,66,67].
The ILP solver gives a precise solution inside a 0.00% criterion, meaning that this solution is the optimal and no better solution exists [13,14,15,16]. With this computational method, YALMIP’s BBA identifies two root-nodes delivering a globally solution [37,38,41,51,74,75,76,79,80]. We also solve the mixed-integer non-convex nonlinear program to with a spatial branch-and-bound algorithm (s-BBA) [37,38,74].
An s-BBA is performed using an LP solver named SoPlex with the IPOPT optimizer function to find global optimality within 0.00% [74,75,76,79,80,81].
SCIP utilizes SoPlex for solving the linear relaxation sub-problem and IPOPT to solve the nonlinear problems to determine the optimality [41,73,74]. For the particular instances, the optimizer function detects a globally optimal solution [37,38,41,51,73,74,75,76]. Both instances were solved and the optimal results are presented in Table 10.
As we noticed, the upper bound takes the lead on finding the objective bound, with an equal lower bound calculated to return an optimal solution within a 0.00% criterion [75].
The lower bound is found to be equal to four with a 0.00% relative gap, as displayed in the log output. At the final root-node, the two bounds are found to be equal. Therefore, the BBA finishes the iterative process with a global solution point [14,37,38,42,51].
The YALMIP global branch and bound detects an upper bound with the help of the local optimizer function, while the lower bound is calculated by solving linear programming relaxations and appropriate branch strategies utilizing an LP solver [13,14,37,38,75,77].
YALMIP’s BBA ends the iterative process when the absolute gap is less than the default value. As observed, the solution is the upper bound while the lower bound closes the gap (lower bound: 2.6429, relative gap 0%) [13,14,37,38,75,77]. We have noticed that the BBA tree ends with two root-nodes; therefore, the solution process is fast. The computations were performed without computational complexity, as the log files show [17].
Then, we optimize the nonlinear integer programming in a continuous domain where a quadratic objective function is minimized under a set of polynomial constraints and a decision variable bound [19,20,21,22,23,24,41]. The nonlinear programming is declared in the feasible region Ω as follows [19,20,21,41,72,73]:
where [19,20,21].
The optimization problem is non-convex, for which GPSA, SQP, and IPMs exist for its solution [19,20,21,22,23,24,41,70,71,72]. The GPSA optimizes the nonlinear programming model considering channel capacity equal to 4, [64]. GPSA is performed through patternsearch included in the global optimization library of MATLAB [22,41,70,71,72].
Patternsearch uses, as a poll method, the gpspositivebasisnp1 strategy, and as the search method, the GPSPositiveBasis2N methodology [22,41,70,71,72]. The iterative scheme ends based on the calculation of the mesh size [22,41,70,71,79].
The optimization ends due to the fact that the mesh size is less than the pre-given mesh size tolerance [21,22,41,70,71,72]. Therefore, the local solution satisfies the pre-given tolerance criteria in order to avoid any constraint violation [41,70,71,72]. Thus, a feasibility and local optimality is derived [21]. The log files produced by patternsearch are shown in Table 11 [22,41,70,71,72].
The optimal result is . Each combination is related to the power grid node. From Equation (33), we derive the subset combinations . For a specific number of channel capacity, we derive a set solution including four PMUs optimally placed around the grid [56].
We present a set solution with the branch assignments of the incident lines to each PMU installed at the related bus.
The SQP optimizes the nonlinear programming model considering channel capacity equal to 4, [64]. The log files produced by fmincon included in the Optimization Library of MATLAB are shown in Table 12 [41,72]. SQP runs the nonlinear programming model, spending reasonable function evaluations per iterations [19,20,21].
The SQP method is invoked through the Fmincon optimizer function to the nonlinear problem solving [19,20,21]. A feasible and a local solution are achieved at the final iteration without any constraint violation (feasibility = 0.000e+00 (Table 12)). The local minimizer satisfies the constraint function, as shown in the log file produced [20,21].
A possible infeasibility of the unity step-length may be presented close to a local solution point, destroying the super-linear convergence speed [82]. This phenomenon is called the Maratos effect [82]. As we observed, the step-length is acceptable for the line search conditions. Through the simulation results, we prove that holds eventually. is the solution of the quadratic programming problem, whereas the SQP estimates the solution from one trial point to the other [19,20,82]. Despite the fact that the merit function is a non-smooth function, the step-length is unity and the Maratos effect is avoided, thus preserving the super-linear convergence towards optimality [82].
The objective function was found to be non-decreasing in any feasible direction based on the tuning parameters declared by the user’s program. The relative first-order optimality quantity is less than the default value, the maximum constraint violation is zero, and the local minimum is inside the optimality tolerance [19,20,21,42].
The optimization finishes the iterations due to the fact that the objective function was found to be non-reducing in any feasible direction [72]. The optimality tolerance and the constraint violations are found within the pre-given tolerances, showing that optimality is achieved [72]. Therefore, the solution is feasible and a local minimum at the same time [21].
The optimal result is . Each combination is related to the power node. From Equation (33), the subset combinations are derived as follows: . This combination of subsets gives the set solution with the following branch assignments:
IPOPT is a primal-dual interior-point method based on a line search filter strategy to discover a local solution of the nonlinear program without considering the decision bound [20,73]. The interior-point methods optimize the nonlinear programming model considering channel capacity equal to 4, . The log file is displayed in Table 13 [19,20,21,73]. The IPOPT: Interior Point NL Solver ends the iterations after spending 21 iterations in a robust MATLAB code [73]. A restoration phase of the filter process is implemented followed by some heuristic computations to enhance the entire optimization [20].
The IPOPT optimizer utilizes a feasibility restoration phase in calculating the optimality. The target is to compute a new iteration while the infeasibility is decreased at every computation step [42,73]. Therefore, a local solution is reached with the calculation of the infeasibility during the iterative process, with the aim to decrease it. The solution is returned by the IPOPT solver with a dual infeasibility quantity without giving any constraint violation [42,73]. Therefore, a feasible and local solution is delivered [19,20].
The optimal result is . From Equation (33), we derive the following subset combinations: . This combination gives the following set solution: . The branch assignments are as follows:
GPSA, SQP, and IPMs end the iterations without calculating infeasibility at the final iteration [42]. The local solution is located and the placement vector is the proper output of the minimization of the objective function under the related constraints [21].
Heuristic algorithms are also utilized to handle and solve the binary-integer program [18,25,26,39,44,45,46,47,48,49,50,51]. It is valuable to mention that GAs and BPSO are utilized for PMU allocation problem solving since these algorithms can produce accurate solutions within a reasonable time frame [5]. BPSO and GAs optimize the BILP model giving the best PMU number with appropriate branch assignments to keep the entire system observability [25,26]. Considering channel capacity , the following results are produced. BPSO derives the combination [78,83]. From Equation (33), we derive the subset combinations . This combination gives the following set solution: . The branch assignments are:
GA derives the combination: . From Equation (33), we derive the subset combinations [60] . This combination gives the following set solution: . The branch assignments are:
The major concern of this research study is to examine the channel capacity’s effect on finding a set of PMUs with the selected number of channels [56,57,58]. As a result, our aim is to identify the algorithmic scheme for designing wide-area observability and to determine the PMU placement set for WAMS application in real time [1,2,3,4,5,6,7,8].
Considering a pre-given number of available channels, we derive not only the PMU locations but also the branches being measured (Table 4, Table 5, Table 10 and Table 14). Thereby, a number of measurements are obtained based on PMUs placed at buses with the adjacent current available but strongly depending on the channel limit [56,57,58,60,62,63,64].
Intlinprog optimizes the integer programming model in two stages [72,79,80]. Initially, we optimize the model (Equations (16)–(18)) and, then, we produce results by optimizing the mathematical model (Equations (35)–(37)) [37,38,41,51,72,74,75,76,79,80].
The optimal results are attained inside an absolute as well as relative gap equal to zero. The solutions are globally found for the IEEE-14-bus system [78,83,84,85].
Some plots are derived illustrating the best objective function value, the PMU subsets that are interpreted by the PMU locations, and the covered branches incident to each PMU placement entry. We show that a solution with the best redundancy is achieved for a fixed channel capacity superior to those solutions derived in [64,65,66,67].
The plot diagrams displayed in Figure 4 and Figure 5 show the results produced by optimizing the mathematical model (Equations (16)–(18)). The subsets are {2, 12, 14, and 17} and the PMU placement is {2, 8, 10, and 13}. The branch assignments are {2-1, 2-3, 2-4, and 2-5, 8-7, 10-9, 10-11, 13-6, 13-12, 13-14}. Furthermore, a plot diagram shows the results produced by optimizing the mathematical model (Equations (35)–(37)) [74,75,76,79,80,81,85]. The subsets are {2, 10, 11, and 13} and the PMU placement is {2, 6, 7, and 9} with best redundancy.
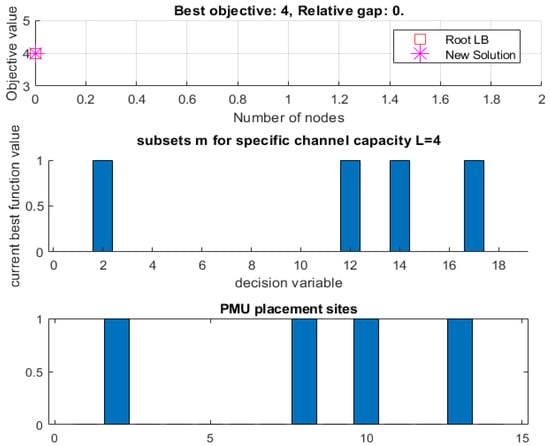
Figure 4.
Plots derived by the intlinprog optimizer in the MATLAB optimization library.
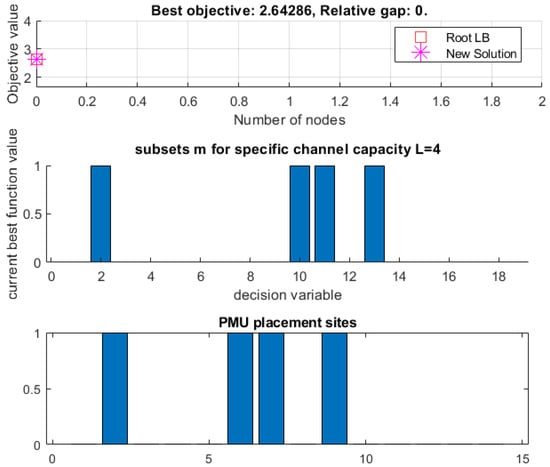
Figure 5.
Plots derived by the intlinprog optimizer in the MATLAB optimization library.
The branch assignments are the following: {2-1, 2-3, 2-4, 2-5, 6-5, 6-11, 6-12, 6-13, 7-4, 7-8, 7-9, 9-4, 9-7, 9-10, 9-14} [60]. That optimal result has the best system redundancy index, as declared in [33,37,38,41,42,43,44,45]. We succeed in finding the best trade-off relationship between PMU locations and observed channels for a fixed channel restriction.
7. Results
Many research articles assume that each PMU device is supplied with unrestricted channel measurements to observe the phasor currents running all incident connectivity lines to the bus equipped with a synchronized monitoring device [37,38,41,51].
In the majority of real PMU problem applications, due to economic restrictions, PMUs are selected with a restricted channel capacity to be placed at substations within the power grid [56,57,58,59,60,61,62,63,64,65,66,67]. As shown in the literature, if one supplementary channel is joined to the commercial PMU, the cost increases by approximately 6.5–20% [7,8,9,10,11].
Our implementation takes into account the bounds on the PMU number channel capacity [56,57,58,59,60,61,62,63,64,65,66,67], but these attempts have shown PMU locations without branch assignments and no optimality was taken into account for achieving a global solution [13,14,16,17,18,19,20,21,24].
Therefore, a channel limit capacity is taken into account for further consideration and filling the gap about the uncertainties if the solution is a local or global solution.
We utilize mathematical and heuristic algorithms to determine all the possible combinations of buses and how the best number of PMUs and their locations are produced [37,38,41,51]. The entire observability is ensured by utilizing PMUs with a minimum measurement channel, which numbers four [56,57,58,59,60,64,65,66,67].
In order to be realistic with observability analysis, the OPP problem is revisited taking a restricted number of channels and solving it from the optimization point of view. It is noticed that BBA, SQP, IPM, GPSA, GA, and BPSO are able to find the proper number of PMUs and their related placement sites to monitor the power grid under complete and maximum observability scenarios [37,41,51].
We utilize the BBA [37], GPSA [41], SQP [41], IPMs [41], GA [51], and BPSO [51] to determine the proper PMU number and the related branch assignments in case of limited channel capacity [64]. Simulation results are presented to the optimal PMU placement implementation, either with one-channel or multi-channel capacity [56,61].
To illustrate results in this section, the relative PMU number and associated PMU placement locations with branch assignments are presented. The results considering the existence of ZIBs will not be included in this study as presented in [56,57,58,60,64,65,66,67]. However, this does not take away from the truth of the proposed algorithmic scheme, and the outputs are the optimum points when ZIBs are not considered [34,37].
Aimed at the minimization problem solving considering a restricted number of measurement channels, minimization modeling is utilized to produce optimal solutions in minimal running time.
More exactly, a binary constraint integer program and a nonlinear constraint program are solved together towards optimality [42]. They produce suitable cost-efficient solutions based on an appropriate amount of channel capacity per PMU device placed at a node within the power grid [56,57,58,59,60,61,62,63,64,65,66,67].
The MILP solver is invoked to deliver the best upper bound to the minimization problem solving [75,79]. The MILP solver solves the LP-relaxation problems with all integer variables to be temporarily continuous [13,14,15,37,38,41,51,72,74,79,80].
If the solution to the relaxed problems entails integers, the solution is the optimum. Otherwise, the iterative scheme continues until the non-integer variables are eliminated [13,14,15,72,74,79,80]. For that, a branching process is followed [79].
Once the process ends for all the decision variables, all the integer solutions are compared. These solutions are achieved by different PMU channels. These solutions are considered to be the optimal point solutions.
As a result, we present the best PMU number as well as the branch assignments considering a restricted number of channels. Those solutions are achieved within zero absolute and relative gaps, showing that optimality is reached [37,38,41,51].
Table 15 illustrates the best objective function value for benchmark power networks considering a varying number of channels [56]. As we observed, the measurement redundancy is maximized for a fixed channel capacity. Mathematical and heuristic algorithms produce the number and locations of PMUs for a restricted number of channels.

Table 15.
Optimal PMU number with a restricted channel capacity for IEEE system.
This scenario is more closely linked to the utility industry’s attention for installation at buses/substations within the power grid [56,57,58,59,60,61]. We use mathematical and heuristic algorithms as an optimization guide to our previous efforts [37,38,41,51].
The branch-and-bound algorithm [37], nonlinear algorithms [41], derivative-free optimizer [41,51], and heuristic algorithm [41] find the optimal solution. PMUs are optimally selected with fewer channels, which is more economical than utilizing PMUs with variant channels. As a result, investment can be saved without giving up the power network observability [35,37,38,41,42,51].
Later, we transform the binary-integer program [56,57,58] into an equivalent nonlinear program solved by SQP [41], IPMs [41], and a GPSA [41] to show convergence to desired local solution points, which are characterized as global solutions.
We utilize a GA [51] and BPSO [51] to handle the ILP’s constraints to show convergence to an optimal solution without violation of the constraint function [21]. GAs and GPSA are considered derivative-free optimizers [22,41,70] and proper optimizer tools for optimizing the OPP problem [41,51,72,73,74,75,76,79,80].
The GPSA is a direct-search algorithm for nonlinear problem-solving. The nonlinear iterative algorithms may be trapped in a local optimum point. The GPSA has the ability to deliver a global solution with increased accuracy [22,41,70,71].
The solution algorithm is a derivative-free optimizer, and more function estimations are needed during the iterative scheme towards optimality [22,25,26,41,70,71].
Two steps are needed to start the iterative scheme and achieve some solution. The poll step is a local descent strategy to compute suitable steps to give a solution that is relatively close to the locality [19,20,21,22,41,70,71,75].
After that, a search step is utilized to search the feasible region in a global way and thus to avoid being trapped in a local optimum [19,20,21,22,41,70,71].
This algorithm can find a global solution with a higher potential action. For that achievement, the search step is an essential algorithmic application to terminate the iterative with success [19,20,21,22,41,70], and redundancy is increased considering multi-channel PMU capacities [56,57,58,59,60,61]. We can increase the redundancy of measurements by minimizing the objective function under the inequality constraints while the decision variables are binary [13,14,15,16,17,18]. The maximum measurement values are 19, 52, 72, and 164 for the 14-, 30-, 57-, and 118-bus networks, respectively [33,37,38,41,42,43,44,45,47,51].
The maximum observability is achieved for for the 14-, 30-, 57-, and 118-bus networks [83]. Table 15 illustrates the channel limit capacity, the PMU number, and the related measurement redundancy for both mathematical models being optimized in this study. The PMUs with more than four channels increase the cost installation at selected nodes in the power transmission grid [56,57,58,60,64,65,66,67].
As shown, we found the specific channels by which the redundancy is maximized. We use the IEEE-57 bus system to produce some optimal results with channel restriction capacity for a comparative study with those shown in [65,66].
Firstly, we optimize the one-product objective function in binary-integer programming format, and then, the b-objective mathematical model is optimized in a computational way similar to that presented in [37,38,41,51]. In the second instance, we succeed in finding an optimal result. The optimal result is superior to those presented in [65,66].
This optimal result is with the maximum observed branches incident to each PMU optimally selected and well posed at strategically power transmission grid nodes to keep the entire system observable. The solution is the best found under this contingency.
This solution is achieved when the gaps between the upper and lower bounds on the objective function are equal so that their difference is zero. The absolute MIP optimality gap is calculated inside a default value (1 × 10−6) declared in [72,76,79,80].
is found with a zero value in conjunction with a relative gap calculated inside a default value (1 × 10−4) declared in [72,76,79,80,81,84,85,86,87,88].
Intlinprog optimizer functions solved the integer program [80]. We detect the upper bound, which is the incumbent objective value for the minimization problem, whereas the lower bound closes the gap to find the globally optimal solution [41,74]. In this case, an optimality certificate is produced by the integer program solver [14].
Furthermore, and are both found to be equal to 0 [76,80]. The plots present the best objective value within a zero-valued relative gap as well as the possible combinations connected with the center buses, which are the main entries in the PMU placement set. Finally, the PMU placement sites are presented in the plots [60].
Figure 6 and Figure 7 illustrate the plot diagrams derived by the entire BBA optimization executed by intlinprog included in the MATLAB optimization library with relative gap equal to zero [72,79,80]. Table 16 and Table 17 depict the PMU locations and the branch assignments for the IEEE-57 system [83] and channel capacity [56,57,60,65,66].
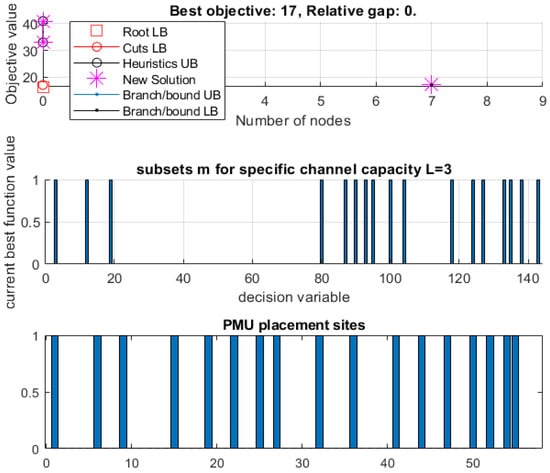
Figure 6.
Plots derived by the intlinprog optimizer in the MATLAB optimization library. Subsets: {3, 12, 19, 80, 87, 90, 93, 95, 100, 104, 118, 124, 127, 133, 135, 138 143} [60].
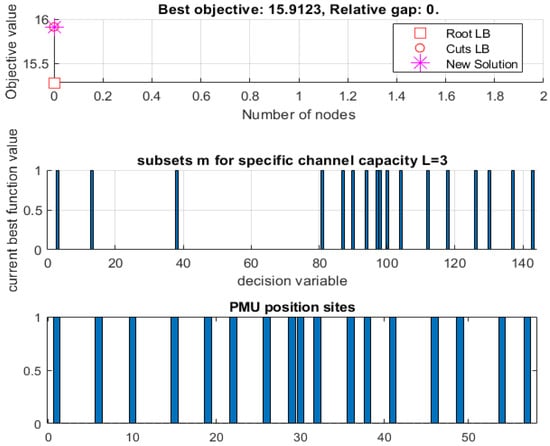
Figure 7.
Plots derived by the intlinprog optimizer in the MATLAB optimization library. Subsets: {3, 13, 38, 81, 87, 90, 94, 97, 98, 100, 104, 112, 118, 126, 130, 137, 143} [60].

Table 16.
Optimal PMU number with channel capacity with redundancy term equal to 59.

Table 17.
Optimal PMU number with channel capacity with redundancy term equal to 62.
The number of the subsets for the IEEE-57 bus is equal to 143 [60]. As we observed, intlinprog optimizes the b-objective optimization model. Optimal results are derived where maximum branches are covered and they are adjacent to the center buses [61].
Thereby, we achieved a PMU optimal set solution with an increased measurement redundancy, which is superior to those found in [65,66], and optimized by a single function considering all the decision variable weights to be unity [56,57,58,59,60,61,62,63,64,65,66,67].
With the presentation of the results, it has been shown that the dual bound is assumed to be the optimal objective function bound, whereas the primal bound minimizes the optimality gap giving a solution within the 0.00% optimality criterion [80].
We also use IPOPT, the interior-point optimizer function, which is written in C++ and released as open-source code under the Eclipse Public License (EPL) [20,42,73].
IPOPT converges rapidly with a super-linear speed. Barrier methods are utilized with exact Hessian and sparse Newton methodologies that are significantly in problem-solving [19,20,21]. Therefore, the second-order optimality conditions are satisfied [19,20,21,22,23,24,25].
We test IPOPT on the IEEE-57 bus system with channel capacity equal to four. The number of subsets for the IEEE-57 bus is equal to 97 [60,65].
We achieve a PMU set solution with the maximum observed branches at once (Figure 8). We present the plot diagram as well as the tabulated optimal results, as follows [73] (Table 18).
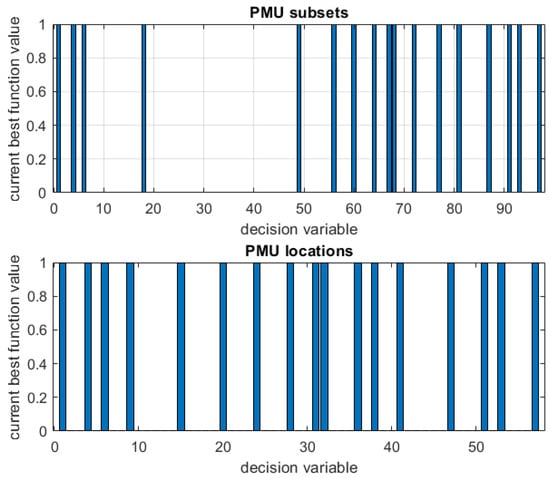
Figure 8.
Plots derived by the IPOPT optimizer in the MATLAB optimization library. PMU subsets: {1, 4, 6, 18, 49, 56, 60, 64, 67, 68, 72, 77, 81, 87, 91, 93, 97}.

Table 18.
Optimal PMU number with channel capacity with redundancy term equal to 68.
We also give the PMU combinations, PMU set solutions, and branch assignments produced by calling the GA solver included in the global optimization library [72]. We run the binary-integer program on the IEEE-57 bus system in order to give a derivative-free approach in optimizing the OPP model based on channel capacity restriction [22] (Figure 9).
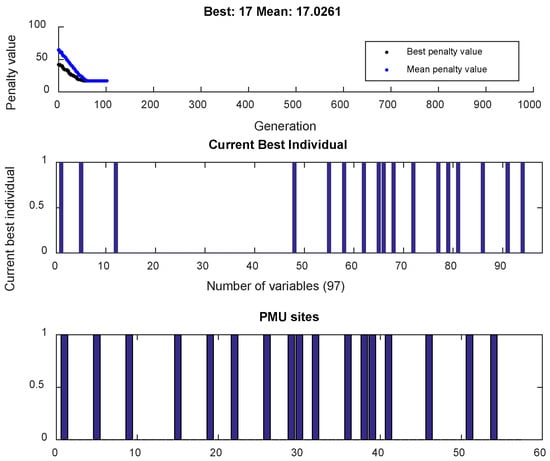
Figure 9.
Plots derived by the GA optimizer in the MATLAB optimization library. Subsets: {1, 5, 12, 48, 55, 58, 62, 65, 66, 68, 72, 77, 79, 81, 86, 91, 94}.
Considering the power network size, we select the population initialized as bit strings in a double vector matrix. Thus, we avoid premature convergence to a local solution point and a global one is reached within specific tolerance criteria [51,72] (Table 19).

Table 19.
Optimal PMU number with channel capacity with redundancy term equal to 65.
We also give the PMU combinations, PMU set solutions, and branch assignments produced by calling BPSO [51]. We run the binary-integer program on the IEEE-57 bus system in order to give an optimal solution with a best redundancy index equal to 68 considering the channel restriction [22]. The optimal result is superior to those produced by SDP in [64,65]. The plot diagram is depicted in Figure 10.
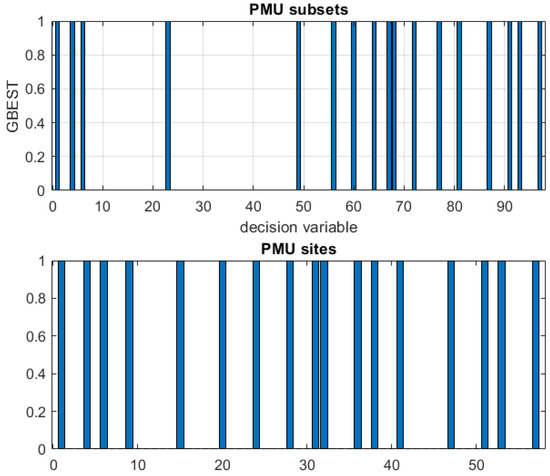
Figure 10.
Plots derived by BPSO. PMU subsets: {1, 4, 6, 23, 49, 56, 60, 64, 67, 68, 72, 77, 81, 87, 91, 93, 97}.
The utilization of BPSO results in PMU locations and branch assignments is superior to those presented in [47]. The PMU locations and the related branch assignments are displayed in Table 20. We achieve a set solution with the best redundancy. For , we increased the number of branches observed by the PMU numbers.

Table 20.
Optimal PMU number with channel capacity with redundancy term equal to 68.
8. Discussion
Keeping in mind the latest advancements in mixed-integer programming, mixed-integer nonlinear programming, and nonlinear programming [13,14,15,16,72,73,74,75,76,79,80,84,85], the targets of this study are (I) to declare the OPP problem model under the consideration of channel capacity, and (II) to compare the computational and simulation results derived by different solutions in order to reach a global solution [19,20,21,22,23,26,72,73,74,75,76,79,80,84,85].
The key factor of this study is to identify the channel capacity’s effect of a specified PMU type on the OPP based-model solution for wide-area system observability.
Our goal is to achieve global solutions using BBA, SQP, IPMs, GAs, BPSO, and GPSA. Initially, a feasible and optimal solution is derived by utilizing the BBA [74,75,76,79,80]. Then, the binary-integer program is transformed into a heuristically solution through the utilization of GAs and BPSO [25,26,39,47,48,50,51].
GA utilizes a parameter penalty for approaching and handling the integer program’s constraints [25,26,50,51,72]. Fewer restrictions are needed in the implementation of the BPSO to find optimality [39,47,48,50,51].
The binary-integer program is transformed into a mixed-integer nonlinear program towards optimality [51]. Thereby, optimum points are derived with sufficient accuracy; they are characterized as global points [16,37,38,41,51,72,74,75,76,79,80].
Finally, some nonlinear algorithms are used to minimize the pure nonlinear programming model. The principal core of the proposed modeling formulation is the way it is defined for the obtainable PMU number channel capacities [56,57,58,59,60,61,62,63,64,65,66,67].
This implementation does not consider the impact of ZI buses to further decrease the PMU number, following [39,56,57,58]. The topological analysis does not always ensure numerical observability taking into account the existence of ZI buses [39,40,46].
The numerical outcome illustrates that the suggested binary-integer model, as well as polynomial formulations, can be implemented and solve the OPP problem with accuracy. The optimization confirms that the OPP-based model on a restricted number of channels is minimized to render the power system completely observable.
An extensive algorithmic approach was studied and binary-integer programming in heuristically and nonlinear programming models is presented. Thus, the mathematical or heuristic models deliver not only the PMU locations but also the branch assignments. We simulate those programming models with a branch-and-bound algorithm, nonlinear algorithms, derivative-free optimizer, and evolutionary algorithm to find alternative PMU set solutions with branch assignments [13,14,15,16,17,19,20,21,23,70,71].
All algorithms are convergent to a desired outcome with a varying number of channels, including PMU locations as well as current line assignments [57,58,60,64].
The accessibility of the monitoring channels is taken into consideration in the mathematical and the heuristic models in this study. Hence, the target is to produce optimal results that are as realistic as possible by the proposed algorithmic models.
The simulation illustrates that the network observability is achieved with accurate reliability. Since the evolutionary algorithms do not supply a sufficient optimality gap between their estimated solution and the true optimum point, the results produced by GA and BPSO are compared to those found by the ILP model [34,47,51]. As the simulation results show, heuristic algorithms guarantee global optimality [25,26,51].
The PMU model based on a restricted number of channels presented in this paper is a complete programming package; it can produce ILP solutions for the classical IEEE power systems within a zero optimality gap [13,14,15,16,17].
Based on this feedback, we simulate the robustness of the evolutionary algorithms to handle the ILP constraints, and thereby produce solutions that are as equally important and have the same quality as those derived by the ILP modeling approach [25,26,37,38,41,44,45,46,47,51].
SQP and IPMs perform the optimization, delivering a local solution point instead of reaching a global one [19,20,21,42]. Generalized pattern search and genetic algorithms work together to deliver optimal solutions for the OPP instances [41,70,71,75].
We extend this BILP model, giving not only the PMU possible combinations but also the number of PMUs and their locations for a fixed number of channels [64]. Our realistic algorithmic approach outperforms the SDP approach in producing more than one solution for a varying number of measurement channels [64,65,66,67].
Finally, the proposed nonlinear programming (NLP) model is optimized under a linear or quadratic objective function subject to a polynomial constraint to find appropriate local solution points. The execution of the MATLAB programming code is illustrated with a detailed optimization study based on the specific instances.
An evaluation of the achieved simulation results is presented in the appendices (Appendix A and Appendix B). Finally, all the algorithms result in a global solution in a minimal time.
The objective function is no longer improved for limit channels bigger than four channels per PMU device [47,56,60,64]. Hence, we reduce the cost installation.
Thereby, we succeed in determining the optimal number of PMUs with the appropriate number of channels without sacrificing the system observability.
9. Final Remarks and Future Study
In this study, the OPP problem is reconsidered with the target of considering that the node voltage phasor and all current phasors running the connectivity lines incident to that node can be obtainable.
To be accurate in the declaration of this study, the minimization model is rewritten where a channel limit capacity is considered. Each PMU may vary in terms of the number of channels to observe the voltage phasor at the node in which it is installed, as well as a number of branches observed through the channel capacity restriction.
The innovation of this paper lies in using mathematical and heuristic algorithms that optimize the OPP-based model on a restricted number of channels. Utilizing these algorithms, a global solution is reached by mathematical and heuristic algorithms.
An algorithmic scheme is adopted utilizing the ideas of the mathematical and heuristic algorithms, building up a procedure and a global problem solving. The new algorithmic placement model results in theoretical and calculation improvements in developing the OPP placement based on a restricted number of channels.
Optimum points are derived, minimizing further the entire cost installation. As we prove, the optimal number of channels, to achieve complete observability with a reduced cost, is four. Furthermore, we present solutions with higher or highest observability, but the quantities highly depend on the number of channels [56,57,58,59,60,61,62,63,64,65,66,67]. This study presents an unambiguous combinatorial methodology, splitting into integer linear and nonlinear domains to solve the PMU allocation model, considering the effect of the restricted channel capacity per monitoring device. We study mathematical models for the varying-channel OPP based-formulation to derive appropriate and accurate solutions.
We focus on a binary-integer model and an equivalent nonlinear programming model that produces globally optimal solutions. We illustrate that these optimization models are easy to implement and solvable by commercial or open-course solvers [72,73,74,75,76,79,80,81,82,83,84,85].
BBA runs the binary-integer program, whereas SQP, IPMs, and GPSA optimize the mathematical programming models to find the desired outcome in minimal runtime.
Additionally, our numerical results call into question the utilization of the heuristic algorithms’ solution for the problem solving for the OPP model based on a restricted number of channels. BPSO and GA were suggested for the classical OPP problem, with an unlimited number of channels being solved in [25,26,39,47,48,50,51,72].
GA is known to execute the BIP and generate a global solution within a reasonable runtime [25,26,51]. Comparatively, BPSO offers simpler implementation than GA and demonstrates comparable results in terms of both quality and quantity, as evidenced in [51].
Following the simulation run, PMU site positions were determined along with corresponding branch assignments, allowing for the derivation of the number of channels, PMU assignments, and monitored channels within a fixed channel capacity.
This assessment incorporates considerations such as restricted PMU channel capacity, voltage measurements, power flows across connectivity lines, injections at power grid nodes, and higher voltage nodes [5]. The forthcoming PMU placement is anticipated to furnish all requisite information for the state estimation model, ensuring reliable monitoring. In such contexts, leveraging graphics processing units (GPUs) and deep neural networks in state estimation applications will prove indispensable, indicative of the growing adoption of GPU architecture in smart grid applications [3,5].
Author Contributions
N.P.T., Forming of the algorithmic idea, N.P.T., Consideration of the Study, N.P.T., Mathematical Analysis, N.P.T., Problem-Solving, N.P.T., Organization and Integration of the main body of the research, N.P.T., MATLAB Implementation, N.P.T., MATLAB Results Validation, N.P.T., Writing—Original Manuscript, R.B., Software, R.B., Interpretation of Results, R.B., Review, Editing and writing, C.A.T., Investigation, C.A.T., Data Analysis, C.A.T., Engineering Analysis, A.P.M., Forming Analysis, A.P.M., Software, A.P.M., Engineering Analysis. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The authors confirm that the data supporting the findings of this study are cited within the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
To illustrate the results, possible combinations, PMU locations, and branch assignments are derived by mathematical and heuristic algorithms. The optimization results from the existence of ZIBs will not be accounted for at this time [34,37,38,41,51].
However, this does not take away from the truth of the approach presented in [56,57,58,59,60,61,62,63,64,65,66,67] when ZIBs and conventional measurements are taken into consideration to further reduce the PMU in numbers [40].
Although the formulations in the literature take into consideration zero injection existing in the power grid, active injections, and flow measurements [64,65,66,67], the impacts of such measurements are not illustrated in this study. However, this does not take away from the truth of the presented results, and results are feasible and optimal without the consideration of the above-mentioned measurements. We adopt combinatorial optimization as well as continuous optimization. BBA, Gas, and BPSO handle decision variables to take binary values to optimize the mathematical models.
Alternatively, SQP, IPMs, and GPSA handle decision variables to take real values, rather than discrete variables such as binary. The algorithm, in either the binary or continuous domain, produces solutions within tolerances and feasibility criteria [13,14,15,16,17,18,19,20,21,22,23,24,25].
Appendix B
In this study, we outlined the mathematical and heuristic algorithms used, providing the exact solutions together with log files [72,73,74,75,76,79,80,83,84]. BBA is the suitable algorithm for minimizing the integer program [13,14,15,16,17,37,38,42,51].
Table A1, Table A2, Table A3, Table A4, Table A5, Table A6, Table A7, Table A8, Table A9 and Table A10 illustrate the optimization performed by mathematical and heuristic algorithms [19,20,21,22,23,24,25,26]. Table 20, Table A2, Table A4, Table A6, Table A7 and Table A8 illustrate the PMU locations with the related branch assignments for channel capacity . We optimize the one-product objective function as well as the b-objective under a set of constraints.
We perform the integer program using the MOSEK optimizer engine (Table A1 and Table A3) [76,81]. The ILP solver optimizes the mathematical model utilizing the 30-bus system as a benchmark system [83]. We consider as a restriction [56,57,58,59,60,61,62,63,64,65,66,67].
Optimizing the objective function with one product, we found that the optimal PMU number is 10 together with the branch assignments. Then, we optimize the b-objective function to find a solution with higher measurement redundancy [37,38].
The integer linear problem is divided into two sub-problems, whereas the binary restriction is relaxed [74,75,76,79,80]. The sub-problems are repeatedly solved utilizing the primal-simplex or dual-simplex [15,16,17,18,36,37,75,76,84,85].
Non-integer solutions are found by the linear programming relaxations that work for upper bounds and integer solutions work for lower bound [36,37,41,51].
The optimizer function utilizes a BBA adopting a heuristic approach to determine feasible solutions and, also, a cut generation is adopted [72]. Additionally, cut linear inequality constraints are adopted so that the function adds to the model solving [79,80].
The inequality constraints restrict the feasible set of the linear programming relaxations so that their solutions are calculated as integer-valued entries [13,14,15,16,17,18].
In order to evaluate the quality of any incumbent solution related to its objective value, one may examine the optimality gap. This optimality criterion calculates how much the incumbent and the optimum point can deviate in the worst-case scenario [88].
Absolute and relative optimality gaps give valuable feedback to determine termination criteria for the mixed-integer optimizer functions [81]. The aim is to end the optimization procedure the moment that the quality of the incumbent solution, calculated in terms of the absolute or relative gap, is good enough [72,74,75,76,79,80,84,85].
As observed, YALMIP’s BBA solves the integer program with the help of the MOSEK solver and finds a solution at one root-node for the two case studies [75,76].
The SCIP optimizer function optimizes the nonlinear program while the optimal solution is attained inside an optimality gap [13,14,15,16,72,74,75,76,79,80,81].
The optimality gap is calculated by [74]. We calculate the primal and dual bounds, and their difference leads to a zero optimality gap [15,36,37]. Hence, the ILP solver converges to an optimum point with a zero absolute gap [80]. Table A1, Table A3, Table A5 and Table A7 illustrate the performance of BBA in optimizing the mathematical models to locate a global solution [37,38,41,51].
As we noticed, the primal bound takes the lead in the minimization process, with an equal upper bound evaluated to attain zero-gap tolerance [75,79]. The dual bound minimizes the gap so the solution is attained within the 0.00% criterion [37,38,75,79,81].
Thereby, no better solution can be further derived by the optimization process. This solution is a global one, as the SCIP solution status declares. The relative output logs are displayed in Table A5 and Table A7, confirming that an accurate solution is achieved [74,75,81].

Table A1.
Algorithm BBA: Steps of optimizing YALMIP’s BBA.
Table A1.
Algorithm BBA: Steps of optimizing YALMIP’s BBA.
| + Processing objective function |
| + Processing constraints |
| + Branch and bound started |
| * Starting YALMIP global branch & bound. |
| * Upper solver : MOSEK |
| * Lower solver : MOSEK |
| * LP solver : MOSEK |
| * -Extracting bounds from model |
| * -Performing root-node bound propagation |
| * -Calling upper solver + Calling Mosek |
| (no solution found) |
| * -Branch-variables : 0 |
| * -More root-node bound-propagation |
| * -Performing LP-based bound-propagation |
| * -And some more root-node bound-propagation |
| * Starting the b&b process |
| Node Upper Gap (%) Lower Open Time |
| + Calling MOSEK |
| 1 : 1.00000E+01 0.00 1.00000E+01 0 0s Solution found by heuristics |
| * Finished. Cost: 10 (lower bound: 10, relative gap 0%) |
| * Termination with all nodes pruned |
| * Timing: 33% spent in upper solver (2 problems solved) |
| * 16% spent in lower solver (1 problems solved) |
| * 1% spent in LP-based domain reduction (0 problems solved) |
| * 3% spent in upper heuristics (1 candidates tried) |
| ans = |
| 1 5 42 43 58 61 70 75 77 79 |
| Optimal PMU numbers: 10 |
| best function value: 10 |
The iteration scheme ends at the root-node because the objective value is inside an absolute gap tolerance of the optimal value; (the default value by the MIP intlinprog solver of MATLAB) [37,38,41,51,72,74,75,76,79,80,84,85].
BBA delivers a global solution avoiding being trapped in a sub-optimum point.

Table A2.
Channel capacity, PMU number, PMU locations, and PMU channel.
Table A2.
Channel capacity, PMU number, PMU locations, and PMU channel.
| L | nPMU | PMU Locations | PMU Channels |
|---|---|---|---|
| 4 | 10 | 1, 2, 6, 9, 10, 12, 18, 23, 25, 27 | {1-2, 1-3} {2-5, 2-7} {6-8, 6-28} {9-6, 9-10, 9-11} {10-17, 10-20, 10-21, 10-22} {12-4, 12-13, 12-14, 12-16} {18-15, 18-19} {23-25, 23-24} {25-24, 25-26, 25-27} {27-25, 27-28, 27-29, 27-30} |

Table A3.
Algorithm BBA: Steps of optimizing YALMIP’s BBA.
Table A3.
Algorithm BBA: Steps of optimizing YALMIP’s BBA.
| + Solver chosen : BMIBNB |
| + Processing objective function |
| + Processing constraints |
| + Branch and bound started |
| * Starting YALMIP global branch & bound. |
| * Upper solver : MOSEK |
| * Lower solver : MOSEK |
| * LP solver : MOSEK |
| * -Extracting bounds from model |
| * -Performing root-node bound propagation |
| * -Calling upper solver + Calling Mosek |
| (no solution found) |
| * -Branch-variables : 0 |
| * -More root-node bound-propagation |
| * -Performing LP-based bound-propagation |
| * -And some more root-node bound-propagation |
| * Starting the b&b process |
| Node Upper Gap (%) Lower Open Time |
| + Calling MOSEK |
| 1 : 8.46667E+00 0.00 8.46667E+00 0 0s Solution found by heuristics |
| * Finished. Cost: 8.4667 (lower bound: 8.4667, relative gap 0%) |
| * Termination with all nodes pruned |
| * Timing: 45% spent in upper solver (2 problems solved) |
| * 21% spent in lower solver (1 problems solved) |
| * 1% spent in LP-based domain reduction (0 problems solved) |
| * 2% spent in upper heuristics (1 candidates tried) |
| ans = |
| 2 4 6 43 58 61 67 70 77 79 |
| Optimal PMU numbers: 10 |
| best function value: 8.466667e+00 |
YALMIP’s BBA ends when the absolute gap is less than a pre-given tolerance [75,77]. Furthermore, the relative gap is given as a certificate of meeting a ε-sub optimality criterion [15]. The optimization ends by giving a global solution within 0.00% optimality [13,14,15,37,38,41,51]. Thus, a global solution is achieved [37,38,80].

Table A4.
Channel capacity, PMU number, PMU locations, and PMU channels.
Table A4.
Channel capacity, PMU number, PMU locations, and PMU channels.
| L | nPMU | PMU Locations | PMU Channels |
|---|---|---|---|
| 4 | 10 | 2, 4, 6, 9, 10, 12, 15, 18, 25, 27 | {2-1, 2-4, 2-5, 2-6} {4-2, 4-3, 4-6, 4-12} {6-2, 6-4, 6-7, 6-8} {9-6, 9-10, 9-11} {10-17, 10-20, 10-21, 10-22} {12-4, 12-13, 12-14, 12-16} {15-12, 15-14, 15-18, 15-23} {18-15, 18-19} {25-24, 25-26, 25-27} {27-25, 27-28, 27-29, 27-30} |

Table A5.
Solving the mixed-integer-nonlinear program using the SCIP function.
Table A5.
Solving the mixed-integer-nonlinear program using the SCIP function.
| Mixed-Integer Nonlinear Program (MINLP) Optimization |
| min f(x) |
| s.t. lb <= x <= ub |
| cl <= c(x) <= cu |
| xi = Integer/Binary |
| Problem Properties: |
| # Decision Variables: 82 |
| # Constraints: 276 |
| # Bounds: 164 |
| # Binary Variables: 82 |
| # Nonlinear Equality: 30 |
| Solver Parameters: |
| Solver: SCIP |
| Objective Gradient: @(x)mklJac(fun,x) |
| Constraint Jacobian: @(x)mklJac(nlcon,x) |
| Jacobian Structure: Supplied |
| time | node | left |LP iter|LP it/n| mem |mdpt |frac |vars |cons |cols |rows |cuts |confs|strbr| dual bound | primal bound | gap |
| T 0.1s| 1 | 0 | 0 | - |2520k| 0 | - | 690 | 942 | 690 | 637 | 0 | 0 | 0 | -- |6.500000e+001 | Inf |
| b 0.1s| 1 | 0 | 0 | - |2457k| 0 | - | 690 | 942 | 690 | 637 | 0 | 0 | 0 | -- |1.800000e+001 | Inf |
| 0.1s| 1 | 0 | 307 | - |2453k| 0 | 7 | 690 | 942 | 690 | 637 | 0 | 0 | 0 |1.000000e+001 |1.800000e+001 | 80.00 |
| 0.1s| 1 | 0 | 324 | - |2542k| 0 | 13 | 690 | 942 | 690 | 641 | 4 | 0 | 0 |1.000000e+001 |1.800000e+001 | 80.00 |
| 0.1s| 1 | 0 | 327 | - |2612k| 0 | 0 | 690 | 942 | 690 | 643 | 6 | 0 | 0 |1.000000e+001 |1.800000e+001 | 80.00 |
| * 0.1s| 1 | 0 | 327 | - |2620k| 0 | - | 690 | 942 | 690 | 643 | 6 | 0 | 0 |1.000000e+001 |1.000000e+001 | 0.00 |
| SCIP Status : problem is solved [optimal solution found] |
| Solving Time (sec) : 0.12 |
| Solving Nodes : 1 |
| Primal Bound : +1.00000000000000e+001 (3 solutions) |
| Dual Bound : +1.00000000000000e+001 |
| Gap : 0.00 |
| 1 2 18 43 58 64 67 71 77 82 |
| Optimal PMU numbers: 10 |
| best function value: 10 |
| BBNodes: 1 |
| BBGap: 0 |
| Time: 0.5361 |
| Algorithm: ‘SCIP: Spatial Branch and Bound using IPOPT and SoPlex’ |
| Status: ‘Globally Integer Optimal’ |

Table A6.
Channel capacity, PMU number, PMU locations, and PMU channels.
Table A6.
Channel capacity, PMU number, PMU locations, and PMU channels.
| L | nPMU | PMU Locations | PMU Channels |
|---|---|---|---|
| 4 | 10 | 1, 2, 6, 9, 10, 12, 15, 19, 25, 27 | {1-2, 1-3} {2-1, 2-4, 2-5, 2-6} {6-2, 6-7, 6-8, 6-28} {9-6, 9-10, 9-11} {10-17, 10-20, 10-21, 10-22} {12-13, 12-14, 12-15, 12-16} {15-12, 15-14, 15-18, 15-23} {19-18, 19-20} {25-24, 25-26, 25-27} {27-29, 27-30} |

Table A7.
Solving the mixed-integer nonlinear program using the SCIP optimizer.
Table A7.
Solving the mixed-integer nonlinear program using the SCIP optimizer.
| Mixed-Integer Nonlinear Program (MINLP) Optimization |
| min f(x) |
| s.t. lb <= x <= ub |
| cl <= c(x) <= cu |
| xi = Integer/Binary |
| Problem Properties: |
| # Decision Variables: 82 |
| # Constraints: 276 |
| # Bounds: 164 |
| # Binary Variables: 82 |
| # Nonlinear Equality: 30 |
| Solver Parameters: |
| Solver: SCIP |
| Objective Gradient: @(x)mklJac(fun,x) |
| Constraint Jacobian: @(x)mklJac(nlcon,x) |
| Jacobian Structure: Supplied |
| time | node | left |LP iter|LP it/n| mem |mdpt |frac |vars |cons |cols |rows |cuts |confs|strbr| dual bound | primal bound | gap |
| T 0.1s| 1 | 0 | 0 | - |2550k| 0 | - | 690 | 942 | 690 | 637 | 0 | 0 | 0 | -- |5.540000e+001 | Inf |
| b 0.2s| 1 | 0 | 0 | - |2487k| 0 | - | 690 | 942 | 690 | 637 | 0 | 0 | 0 | -- |1.560000e+001 | Inf |
| * 0.2s| 1 | 0 | 319 | - |2492k| 0 | - | 690 | 942 | 690 | 637 | 0 | 0 | 0 |8.466667e+000 |8.466667e+000 | 0.00 |
| 0.2s| 1 | 0 | 319 | - |2492k| 0 | - | 690 | 942 | 690 | 637 | 0 | 0 | 0 |8.466667e+000 |8.466667e+000 | 0.00 |
| SCIP Status : problem is solved [optimal solution found] |
| Solving Time (sec) : 0.17 |
| Solving Nodes : 1 |
| Primal Bound : +8.46666666666667e+000 (3 solutions) |
| Dual Bound : +8.46666666666667e+000 |
| Gap : 0.00 |
| 2 4 18 43 56 64 67 72 77 79 |
| Optimal PMU numbers: 10 |
| BBNodes: 1 |
| BBGap: 0 |
| Time: 0.3718 |
| Algorithm: ‘SCIP: Spatial Branch and Bound using IPOPT and SoPlex’ |
| Status: ‘Globally Integer Optimal’ |

Table A8.
Channel capacity, PMU number, PMU locations, and PMU channels.
Table A8.
Channel capacity, PMU number, PMU locations, and PMU channels.
| L | nPMU | PMU Locations | PMU Channels |
|---|---|---|---|
| 4 | 10 | 2, 4, 6, 9, 10, 12, 15, 20, 25, 27 | {2-1, 2-4, 2-5, 2-6} {4-2, 4-3, 4-6, 4-12} {6-2, 6-7, 6-8, 6-28} {9-6, 9-10, 9-11} {10-9, 10-17, 10-21, 10-22} {12-13, 12-14, 12-15, 12-16} {15-12, 15-14, 15-18, 15-23} {20-10, 20-19} {25-24, 25-26, 25-27} {27-25, 27-28, 27-29, 27-30} |
For the 30-bus system, we found the set solutions for a fixed channel capacity [65]. Table A6 and Table A8 illustrate the best PMU number and the branch assignments related to each entry included in the PMU placement vector. Considering this, we optimize the two mathematical models to achieve PMU locations and related branch assignments.
The first optimizes a one product objective, whereas the second optimizes the b-objective function. We succeed in finding PMU solutions covering branches with higher redundancy related to previous results presented in [64,65,66,67]. Thus, we achieve better results to those found in [57,58,59,60,61,62,63,64,65,66,67] for a fixed amount of channel capacity [65].

Table A9.
Channel capacity, PMU number, PMU locations, and PMU channels.
Table A9.
Channel capacity, PMU number, PMU locations, and PMU channels.
| Binary Swarm Optimization | |||
|---|---|---|---|
| L | nPMU | PMU Locations | PMU Channels |
| 4 | 10 | 1, 2, 6, 10, 11, 12, 19, 24, 26, 29 | {1-2, 1-3 {2-1, 2-4, 2-5, 2-6 {6-7, 6-8, 6-9, 6-28 {10-6, 10-17, 10-21, 10-22 {11-9 {12-13, 12-14, 12-15, 12-16 {19-18, 19-20 {24-22, 24-23, 24-25 {26-25 {29-27, 29-30} |
| 4 | 10 | 2, 4, 6, 9, 10, 12, 15, 18, 25, 27 | {2-1, 2-4, 2-5, 2-6 {4-2, 4-3, 4-6, 4-12 {6-2, 6-7, 6-8, 6-28 {9-6, 9-10, 9-11 {10-17, 10-20, 10-21, 10-22 {12-4, 12-13, 12-15, 12-16 {15-12, 15-14, 15-18, 15-23 {18-15, 18-19 {25-24, 25-26, 25-27 {27-29, 27-30} |
| Genetic Algorithms | |||
| 4 | 10 | 3, 6, 7, 10, 11, 12, 15, 19, 25, 29 | {3-1, 3-4 {6-2, 6-8, 6-9, 6-28 {7-5, 7-6 {10-17, 10-20, 10-21, 10-22 {11-9 {12-4, 12-13, 12-15, 12-16 {15-12, 15-14, 15-18, 15-23 {19-20, 19-18 {25-24, 25-26, 25-27 {29-27, 29-30} |
| 4 | 10 | 2, 4, 6, 9, 10, 12, 15, 19, 25, 27 | {2-1, 2-4, 2-5, 2-6 {4-2, 4-3, 4-6, 4-12 {6-4, 6-7, 6-8, 6-28 {9-6, 9-10, 9-11 {10-17, 10-20, 10-21, 10-22 {12-13, 12-14, 12-15, 12-16 {15-12, 15-14, 15-18, 15-23 {19-18, 19-20 {25-24, 25-26, 25-27 {27-25, 27-28, 27-29, 27-30} |
As observed in Table A5 and Table A7, the primal bound on the objective function value is calculated for the minimization problem. SCIP computes the difference between the primal and dual bounds on the objective function in the BBA tree implementation [74].
is found to be equal to zero [79,80]. The solution status illustrates that “Globally Integer Optimal” has been detected [74,79].
Table A9 and Table A10 presents the optima points derived by mathematical and heuristic algorithms considering a fixed channel capacity . Table A7 and Table A8 present the PMU numbers, the PMU locations, and the observed branches obtained by SQP, IPMs, GPSA, GAs, BPSO, and BBA [41,51,72,73,74,75,76,79,80,84,85,86,87,88].
We derive not only the PMU locations, but also the channels being observed that lead to the measurement of the redundancy, as illustrated in Table 15. BBA, GA, and BSO optimize the integer program, while SQP, IPMs, and GPSA optimize the nonlinear program to find the best solutions under this contingency [41,51]. SQP and IPMs are local search algorithms detecting local minimizers at the desired objective function value for the specific minimization problem [19,20,21,25,41].
SQP and IPMs are theoretically efficient algorithms, and they are also computational methods that are not wasteful [19,20,41]. SQP, IPMs, and GPSA emphasize the search of a neighborhood of a local point, and the solution is not the global optimum in case of minimizing non-convex nonlinear problems [19,20,22,25,41,70,71].
All algorithms deliver solutions as the iterations go to the final stage, where the tolerance and feasible criteria are fulfilled so as an optimal result is reached [21].
Furthermore, we derive solutions for channel capacity utilizing the COIN-OR Branch and Cut solver (CBC) optimizer routine written in C++ [84].
CBC utilizes a Branch and Cut using CLP with a solution status declared “Integer Optimal” [84]. Furthermore, the GLPK Simplex Optimizer utilizes a revised simplex algorithm to find an INTEGER OPTIMAL SOLUTION within a 0.0% criterion [26,85]. Finally, some MILP results are provided by using Gurobi to find global solutions [86,87,88].
This computational approach permits us to avoid local or sub-optimum points, and globally optimal solutions can be identified with accuracy under specific tolerances [21].
Mathematical and heuristic algorithms return optimal solutions with the best trade-off relationship between the optimal PMU locations and the branch assignments.

Table A10.
Channel capacity, PMU number, PMU locations, and PMU channels.
Table A10.
Channel capacity, PMU number, PMU locations, and PMU channels.
| Sequential Quadratic Programming | |||
| L | nPMU | PMU locations | PMU channels |
| 3 | 10 | 1, 7, 8, 10, 11, 12, 15, 20, 25, 29 | {1-2, 1-3 {7-5, 7-6 {8-6, 8-28 {10-17, 10-21, 10-22 {11-9 {12-4, 12-13, 12-16 {15-14, 15-18, 15-23 {20-10, 20-19 {25-24, 25-26, 25-27 {29-27, 29-30} |
| 4 | 10 | 3, 5, 10, 11, 12, 19, 23, 26, 27, 28 | {3-1, 3-4 {5-2, 5-7 {10-17, 10-20, 10-21, 10-22 {11-9 {12-13, 12-14, 12-15, 12-16 {19-18, 19-20 {23-15, 23-24 {26-25 {27-25, 27-28, 27-29, 27-30 {28-6, 28-8, 28-27} |
| Interior-Point Methods | |||
| 3 | 10 | 1, 5, 8, 10, 11, 12, 19, 23, 26, 29 | {1-3, 1-4 {5-2, 5-7 {8-6, 8-28 {10-17, 10-21, 10-22 {11-9 {12-13, 12-14, 12-16 {19-18, 19-20 {23-15, 23-24 {26-25 {29-27, 29-30} |
| 4 | 10 | 2, 4, 6, 10, 11, 12, 19, 23, 25, 27 | {2-1, 2-4, 2-5, 2-6 {4-2, 4-3, 4-6, 4-12 {6-2, 6-7, 6-8, 6-28 {10-6, 10-17, 10-21, 10-22 {11-9 {12-13, 12-14, 12-15, 12-16 {19-18, 19-20 {23-15, 23-24 {25-24, 25-26, 25-27 {27-25, 27-28, 27-29, 27-30} |
| Generalized Pattern Search Algorithm | |||
| 3 | 10 | 2, 4, 6, 10, 11, 12, 19, 23, 25, 27 | {2-1, 2-4, 2-5 {4-2, 4-3, 4-6 {6-7, 6-8, 6-28 {10-17, 10-21, 10-22 {11-9 {12-13, 12-14, 12-16 {19-18, 19-20 {23-15, 23-24 {25-24, 25-26, 25-27 {27-25, 27-29, 27-30} |
| 4 | 10 | 1, 2, 6, 10, 11, 12, 18, 24, 25, 29 | {1-2, 1-3 {2-1, 2-4, 2-5, 2-6 {6-7, 6-8, 6-10, 6-28 {10-17, 10-20, 10-21, 10-22 {11-9 {12-13, 12-14, 12-15, 12-16 {18-15, 18-19 {24-22, 24-23, 24-25 {25-24, 25-26, 25-27 {29-27, 29-30} |
| Genetic Algorithms | |||
| 3 | 10 | 3, 5, 8, 10, 11, 12, 18, 24, 26, 27 | {3-1, 3-4 {5-2, 5-7 {8-6, 8-28 {10-17, 10-20, 10-21 {11-9 {12-13, 12-14, 12-16 {18-15, 18-19 {24-22, 24-23, 24-25 {26-25 {27-25, 27-29, 27-30} |
| Genetic Algorithms | |||
| 4 | 10 | 2, 3, 6, 9, 10, 12, 15, 19, 25, 27 | {2-1, 2-4, 2-5, 2-6 {3-1, 3-4 {6-4, 6-7, 6-8, 6-9 {9-6, 9-10, 9-11 {10-9, 10-17, 10-21, 10-22 {12-4, 12-13, 12-15, 12-16 {15-12, 15-14, 15-18, 15-23 {19-18, 19-20 {25-24, 25-26, 25-27 {27-25, 27-28, 27-29, 27-30} |
| Binary Particle Swarm Optimization | |||
| 3 | 10 | 2, 4, 6, 9, 10, 12, 18, 24, 26, 29 | {2-1, 2-4, 2-5 {4-2, 4-3, 4-12 {6-7, 6-8, 6-28 {9-6, 9-10, 9-11 {10-17, 10-20, 10-21 {12-13, 12-14, 12-16 {18-15, 18-19 {24-22, 24-23, 24-25 {26-25 {29-27, 29-30} |
| 4 | 10 | 3, 6, 7, 9, 10, 12, 18, 24, 26, 29 | {3-1, 3-4 {6-2, 6-8, 6-9, 6-28 {7-5, 7-6 {9-6, 9-10, 9-11 {10-6, 10-17, 10-20, 10-21 {12-13, 12-14, 12-15, 12-16 {18-15, 18-19 {24-22, 24-23, 24-25 {26-25 {29-27, 29-30} |
| CBC Branch and Cut Algorithm | |||
| 3 | 10 | 2, 4, 6, 9, 10, 12, 18, 24, 25, 27 | {2-1, 2-4, 2-5 {4-2, 4-3, 4-6 {6-2, 6-7, 6-8 {9-6, 9-10, 9-11 {10-17, 10-20, 10-21 {12-13, 12-14, 12-16 {18-15, 18-19 {24-22, 24-23, 24-25 {25-24, 25-26, 25-27 {27-28, 27-29, 27-30} |
| 4 | 10 | 2, 4, 6, 9, 10, 12, 15, 19, 25, 27 | {2-1, 2-4, 2-5, 2-6 {4-2, 4-3, 4-6, 4-12 {6-2, 6-7, 6-8, 6-10 {9-6, 9-10, 9-11 {10-6, 10-17, 10-21, 10-22 {12-13, 12-14, 12-15, 12-16 {15-12, 15-14, 15-18, 15-23 {19-18, 19-20 {25-24, 25-26, 25-27 {27-25, 27-28, 27-29, 27-30} |
| SCIP Spatial Branch-and-Bound Algorithm | |||
| 3 | 10 | 3, 5, 6, 9, 10, 12, 15, 19, 25, 27 | {3-1, 3-4 5-2, 5-7 6-4, 6-7, 6-8 9-6, 9-10, 9-11 10-17, 10-21, 10-22 12-13, 12-15, 12-16 15-12, 15-14, 15-23 19-18, 19-20 25-24, 25-26, 25-57 27-28, 27-29, 27-30} |
| 4 | 10 | 3, 5, 6, 9, 10, 12, 15, 18, 25, 27 | {3-1, 3-4 5-2, 5-7 6-2, 6-4, 6-7, 6-8 9-6, 9-10, 9-11 10-17, 10-20, 10-21, 10-22 12-13, 12-14, 12-15, 12-16 15-12, 15-14, 15-18, 15-23 18-15, 18-19 25-24, 25-26, 25-27 27-25, 27-28, 27-29, 27-30} |
| Gurobi: Branch-and-Bound Algorithm | |||
| 3 | 10 | 2, 3, 6, 9, 10, 12, 18, 24, 26, 27 | {2-1, 2-5, 2-6 3-1, 3-4 6-7, 6-8, 6-28 9-6, 9-10, 9-11 10-17, 10-20, 10-21 12-13, 12-14, 12-16 18-15, 18-19 24-22, 24-23, 24-25 26-25 27-25, 27-29, 27-30} |
| 4 | 10 | 1, 2, 6, 9, 10, 12, 18, 24, 25, 27 | {1-2, 1-3 2-1, 2-4, 2-5, 2-6 6-7, 6-8, 6-9, 6-10 9-6, 9-10, 9-11 10-17, 10-20, 10-21, 10-22 12-4, 12-13, 12-14, 12-16 18-15, 18-19 24-22, 24-23, 24-25 25-24, 25-26, 25-27 27-25, 27-28, 27-29, 27-30} |
| MOSEK: Branch-and-Bound Algorithm | |||
| 3 | 10 | 1, 2, 6, 9, 10, 12, 15, 20, 25, 27 | {1-2, 1-3 2-1, 2-5, 2-6 6-4, 6-7, 6-8 9-6, 9-10, 9-11 10-17, 10-21, 10-22 12-13, 12-14, 12-16 15-12, 15-18, 15-23 20-10, 20-19 25-24, 25-26, 25-27 27-28, 27-29, 27-30} |
| 4 | 10 | 1, 5, 6, 9, 10, 12, 18, 23, 25, 27 | {1-2, 1-3 5-2, 5-7 6-8, 6-28 9-6, 9-10, 9-11 10-17, 10-20, 10-21, 10-22 12-4, 12-13, 12-14, 12-16 18-15, 18-19 23-15, 23-24 25-24, 25-26, 25-27 27-25, 27-28, 27-29, 27-30} |
| GLPK: Revised Simplex to Build the BBA Tree | |||
| 3 | 10 | 2, 4, 6, 10, 11, 12, 19, 23, 25, 27 | {2-1, 2-4, 2-5 4-2, 4-3, 4-6 6-7, 6-8, 6-28 10-17, 10-21, 10-22 11-9 12-13, 12-14, 12-16 19-18, 19-20 23-15, 23-24 25-24, 25-26, 25-27 27-25, 27-29, 27-30} |
| 4 | 10 | 3, 5, 6, 9, 10, 12, 18, 24, 26, 29 | {3-1, 3-4 5-2, 5-7 6-2, 6-7, 6-8, 6-28 9-6, 9-10, 9-11 10-9, 10-17, 10-20, 10-21 12-4, 12-13, 12-14, 12-16 18-15, 18-19 24-22, 24-23, 24-25 26-25 29-27, 29-30} |
| GLPK: Revised Simplex to Build the BBA Tree | |||
| Optimizing the b-objective function leading to a set with increased redundancy | |||
| 3 | 10 | 2, 4, 6, 9, 10, 12, 15, 20, 25, 27 | {2-1, 2-4, 2-5 4-2, 4-3, 4-6 6-7, 6-8, 6-28 9-6, 9-10, 9-11 10-17, 10-21, 10-22 12-4, 12-13, 12-16 15-14, 15-18, 15-23 20-10, 20-19 25-24, 25-26, 25-27 27-25, 27-29, 27-30 |
| 4 | 10 | 2, 4, 6, 9, 10, 12, 15, 18, 25, 27 | {2-1, 2-4, 2-5, 2-6 4-2, 4-3, 4-6, 4-12 6-2, 6-7, 6-8, 6-28 9-6, 9-10, 9-11 10-17, 10-20, 10-21, 10-22 12-4, 12-13, 12-14, 12-16 15-12, 15-14, 15-18, 15-23 18-15, 18-19 25-24, 25-26, 25-27 27-25, 27-28, 27-29, 27-30} |
| GLPK: Revised Simplex to Build the BBA Tree | |||
| Optimizing the b-objective function leading to a set with increased redundancy | |||
| 3 | 10 | 2, 4, 6, 9, 10, 12, 15, 20, 25, 27 | {2-1, 2-4, 2-5 4-2, 4-3, 4-6 6-7, 6-8, 6-28 9-6, 9-10, 9-11 10-17, 10-21, 10-22 12-4, 12-13, 12-16 15-14, 15-18, 15-23 20-10, 20-19 25-24, 25-26, 25-27 27-25, 27-29, 27-30 |
| 4 | 10 | 2, 4, 6, 9, 10, 12, 15, 18, 25, 27 | {2-1, 2-4, 2-5, 2-6 4-2, 4-3, 4-6, 4-12 6-2, 6-7, 6-8, 6-28 9-6, 9-10, 9-11 10-17, 10-20, 10-21, 10-22 12-4, 12-13, 12-14, 12-16 15-12, 15-14, 15-18, 15-23 18-15, 18-19 25-24, 25-26, 25-27 27-25, 27-28, 27-29, 27-30} |
References
- Phadke, A.G.; Thorp, J.S. Synchronized Phasor Measurements and Their Applications, 2nd ed.; Springer: New York, NY, USA, 2017. [Google Scholar]
- Darmis, O.; Korres, G. A Survey on Hybrid SCADA/WAMS State Estimation Methodologies in Electric Power Transmission Systems. Energies 2023, 16, 618. [Google Scholar] [CrossRef]
- Monti, A.; Sadu, A.; Tang, J. Chapter 8—Wide Area Measurement Systems: Applications. In Phasor Measurement Units and Wide Area Monitoring Systems; Academic Press: Cambridge, MA, USA, 2016; pp. 177–234. [Google Scholar]
- Cheng, G.; Lin, Y.; Abur, A.; Gómez-Expósito, A.; Wu, W. A Survey of Power System State Estimation Using Multiple Data Sources: PMUs, SCADA, AMI, and Beyond. IEEE Trans. Smart Grid 2024, 15, 1129–1151. [Google Scholar] [CrossRef]
- Varghese, C.H.; Shah, B.; Azimian, B.; Pal, A.; Farantatos, E. Deep Neural Network-Based State Estimator for Transmission System Considering Practical Implementation Challenges. J. Mod. Power Syst. Clean Energy 2024. early access. [Google Scholar]
- Todescato, M.; Carli, R.; Schenato, L.; Barchi, G. Smart Grid State Estimation with PMUs Time Synchronization Errors. Energies 2020, 13, 5148. [Google Scholar] [CrossRef]
- Johnson, T.; Moger, T. A critical review of methods for optimal placement of phasor measurement units. Int. Trans. Electr. Energy Syst. 2020, 31, e12698. [Google Scholar] [CrossRef]
- Ahmed, M.M.; Amjad, M.; Qureshi, M.A.; Imran, K.; Haider, Z.M.; Khan, M.O. A Critical Review of State-of-the-Art Optimal PMU Placement Techniques. Energies 2022, 15, 2125. [Google Scholar] [CrossRef]
- Biswal, C.; Sahu, B.K.; Mishra, M.; Rout, P.K. Real-Time Grid Monitoring and Protection: A Comprehensive Survey on the Advantages of Phasor Measurement Units. Energies 2023, 16, 4054. [Google Scholar] [CrossRef]
- Paramo, G.; Bretas, A.; Meyn, S. Research Trends and Applications of PMUs. Energies 2022, 15, 5329. [Google Scholar] [CrossRef]
- Menezes, T.S.; Barra, P.H.A.; Dizioli, F.A.S.; Lacerda, V.A.; Fernandes, R.A.S.; Coury, D.V. A Survey on the Application of Phasor Measurement Units to the Protection of Transmission and Smart Distribution Systems. Electr. Power Compon. Syst. 2023, 1, 1–18. [Google Scholar] [CrossRef]
- Fotopoulou, M.; Petridis, S.; Karachalios, I.; Rakopoulos, D. A Review on Distribution System State Estimation Algorithms. Appl. Sci. 2022, 12, 11073. [Google Scholar] [CrossRef]
- Wolsey, L.A. Integer Programming; John Willey and Sons: Hoboken, NJ, USA, 2020. [Google Scholar] [CrossRef]
- Conforti, M.; Cornuéjols, G.; Zambelli, G. Integer Programming, Graduate Texts in Mathematics; Springer: Berlin/Heidelberg, Germany, 2014; Volume 271. [Google Scholar]
- Chen, D.S.; Batson, R.G.; Dang, Y. Applied Integer Programming: Modelling and Solution; John Wiley and Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Sarma, E.; Xedoses, P.; Doksa, H. Springer optimization and its applications (Springer) Literature review. In Multicriteria Portfolio Construction with Python; Springer: Berlin/Heidelberg, Germany, 2020; Volume 163. [Google Scholar]
- Ganian, R.; Ordyniak, S. Solving Integer Linear Programs by Exploiting Variable-Constraint Interactions: A Survey. Algorithms 2019, 12, 248. [Google Scholar] [CrossRef]
- Brajević, I. A Shuffle-Based Artificial Bee Colony Algorithm for Solving Integer Programming and Minimax Problems. Mathematics 2021, 9, 1211. [Google Scholar] [CrossRef]
- Durenberger, D.G.; Yonge, Y. Linear and Nonlinear Programming, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Necedah, J.; Wright, S. Numerical Optimization; Springer Series in Operations Research and Financial Engineering; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Chinneck, J.W. Feasibility and Infeasibility in Optimization: Algorithms and Computational Methods; International Series in Operations Research & Management Science; Springer: Cham, Switzerland, 2008. [Google Scholar]
- Rios, L.M.; Sahinidis, N.V. Derivative-Free Optimization: A Review of Algorithms and Comparison of Software Implementations. J. Glob. Optim. 2013, 56, 1247–1293. [Google Scholar] [CrossRef]
- Sahinidis, N.V. Mixed-Integer Nonlinear Programming 2018; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Liberti, L.; Maculan, N. Global Optimization: From Theory to Implementation, Nonconvex Optimization and Its Applications; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Yang, X.S. Engineering Optimization: An Introduction with Metaheuristic Applications; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Özlü, İ.A.; Baimakhanov, O.; Saukhimov, A.; Ceylan, O. A Heuristic Methods-Based Power Distribution System Optimization Toolbox. Algorithms 2022, 15, 14. [Google Scholar] [CrossRef]
- Nardin, A.; D’Andreagiovanni, F. A Quantum-Inspired Ant Colony Optimization Algorithm for Parking Lot Rental to Shared E-Scooter Services. Algorithms 2024, 17, 80. [Google Scholar] [CrossRef]
- Diestel, R. Graph Theory; Springer: Berlin/Heidelberg, Germany, 2017; Volume 173, pp. 59–172. [Google Scholar]
- Haynes, T.W.; Hedetniemi, S.M.; Hedetniemi, S.T.; Henning, M.A. Domination in Graphs Applied to Electric Power Networks. SIAM J. Discret. Math. 2002, 15, 519–529. [Google Scholar] [CrossRef]
- Sun, O.; Fan, N. The probabilistic and reliable connected power dominating set problems. Optim. Lett. 2019, 13, 1189–1206. [Google Scholar] [CrossRef]
- Poirion, P.L.; Toubaline, S.; D’Ambrosio, C.; Liberti, L. The power edge set problem. Networks 2016, 68, 104–120. [Google Scholar] [CrossRef]
- Xu, B.; Abur, A. Observability Analysis and Measurement Placement for Systems with PMUs. In Proceedings of the IEEE PES Power Systems Conference and Exposition, New York, NY, USA, 10–13 October 2004; pp. 2–5. [Google Scholar]
- Dua, D.; Dambhare, S.; Gajbhiye, R.K.; Soman, S.A. Optimal Multistage Scheduling of PMU Placement: An ILP Approach. IEEE Trans. Power Deliv. 2008, 23, 1812–1820. [Google Scholar] [CrossRef]
- Pal, A.; Sánchez, A.G.A.; Thorp, J.S.; Centeno, V.A. A Community-based Partitioning Approach for phasor Measurement Unit Placement in Large systems. Electr. Power Compon. Syst. 2016, 44, 1317–1329. [Google Scholar] [CrossRef]
- Pal, A.; Vullikanti, A.K.S.; Ravi, S.S. A PMU Placement Scheme Considering Realistic Costs and Modern Trends in Relaying. IEEE Trans. Power Syst. 2017, 32, 552–561. [Google Scholar] [CrossRef]
- Ghamsari-Yazdel, M.; Esmaili, M.; Amjady, N. Optimal substation-based joint allocation of PMUs and measuring channels considering network expansion planning. Int. J. Electr. Power Energy Syst. 2019, 106, 274–287. [Google Scholar] [CrossRef]
- Theodorakatos, N.P.; Babu, R.; Moschoudis, A.P. The branch-and-bound algorithm in optimizing mathematical programming models to achieve power grid observability. Axioms 2023, 12, 1040. [Google Scholar] [CrossRef]
- Theodorakatos, N.P.; Moschoudis, A.P.; Babu, R. Calculating Global Minimum Points to Binary Polynomial Optimization Problem: Optimizing the Optimal PMU Localization Problem as a Case-Study. J. Phys. Conf. Ser. 2024, 2701, 012001. [Google Scholar] [CrossRef]
- Pal, A.; Jones, K.D.; Mishra, C.; Centeno, V.A. Binary particle swarm optimisation-based optimal substation coverage algorithm for phasor measurement unit installations in practical systems. IET Gener. Transm. Distrib. 2016, 10, 555–562. [Google Scholar]
- Korres, G.N.; Manousakis, N.M.; Xygkis, T.C.; Lofberg, J. Optimal phasor measurement unit placement for numerical observability in the presence of conventional measurement using semi-definite programming. IET Gener. Transm. Distrib. 2015, 9, 2427–2436. [Google Scholar] [CrossRef]
- Theodorakatos, N.P.; Lytras, M.; Babu, R. A Generalized Pattern Search Algorithm Methodology for solving an Under-Determined System of Equality Constraints to achieve Power System Observability using Synchrophasors. J. Phys. Conf. Ser. 2021, 2090, 012125. [Google Scholar] [CrossRef]
- Theodorakatos, N.P.; Lytras, M.D.; Moschoudis, A.P.; Kantoutsis, K.T. Implementation of optimization-based algorithms for maximum power system observability using synchronized measurements. AIP Conf. Proc. 2023, 2872, 120006. [Google Scholar]
- Xia, N.; Gooi, H.B.; Chen, S.X.; Wang, M.Q. Redundancy based PMU placement in state estimation. Sustain. Energy Grids Netw. 2015, 2, 23–31. [Google Scholar] [CrossRef]
- Ramasamy, S.; Koodalsamy, B.; Koodalsamy, C.; Veerayan, M.B. Realistic method for placement of phasor measurement units through optimization problem formulation with conflicting objectives. Electr. Power Compon. Syst. 2021, 49, 474–487. [Google Scholar] [CrossRef]
- Singh, S.P.; Singh, S.P. A Multi-objective PMU Placement Method in Power System via Binary Gravitational Search Algorithm. Electr. Power Compon. Syst. 2017, 45, 1832–1845. [Google Scholar] [CrossRef]
- Koutsoukis, N.C.; Manousakis, N.M.; Georgilakis, P.S.; Korres, G.N. Numerical observability method for optimal phasor measurement units placement using recursive Tabu search method. IET Gener. Transm. Distrib. 2013, 7, 347–356. [Google Scholar] [CrossRef]
- Hanis, N.; Rahman, A.; Zobaa, A.F. Binary PSO Algorithm for Optimal PMUs Placement. IEEE Trans. Ind. Inform. 2017, 13, 3124–3133. [Google Scholar]
- Maji, T.K.; Acharjee, P. Multiple Solutions of Optimal PMU Placement Using Exponential Binary PSO Algorithm for Smart Grid Applications. IEEE Trans. Ind. Appl. 2017, 53, 2550–2559. [Google Scholar] [CrossRef]
- Dalali, M.; Karegar, H.K. Optimal PMU placement for full observability of the power network with maximum redundancy using modified binary cuckoo optimization algorithm. IET Gener. Transm. Distrib. 2016, 10, 2817–2824. [Google Scholar] [CrossRef]
- Müller, H.H.; Castro, C.A. Genetic algorithm-based phasor measurement unit placement method considering observability and security criteria. IET Gener. Transm. Distrib. 2016, 10, 270–280. [Google Scholar] [CrossRef]
- Theodorakatos, N.P.; Moschoudis, A.P.; Lytras, M.D.; Kantoutsis, K.T. Research on optimization procedure of PMU positioning problem achieving maximum observability based on heuristic algorithms. AIP Conf. Proc. 2023, 2872, 120032. [Google Scholar]
- Rezaeian Koochi, M.H.; Dehghanian, P.; Esmaeili, S. PMU Placement with Channel Limitation for Faulty Line Detection in Transmission Systems. IEEE Trans. Power Deliv. 2020, 35, 819–827. [Google Scholar] [CrossRef]
- Tshenyego, O.; Samikannu, R.; Mtengi, B.; Mosalaosi, M.; Sigwele, T. A Graph-Theoretic Approach for Optimal Phasor Measurement Units Placement Using Binary Firefly Algorithm. Energies 2023, 16, 6550. [Google Scholar] [CrossRef]
- Rather, Z.H.; Chen, Z.; Thøgersen, P.; Lund, P.; Kirby, B. Realistic Approach for Phasor Measurement Unit Placement: Consideration of Practical Hidden Costs. IEEE Trans. Power Deliv. 2015, 30, 3–15. [Google Scholar] [CrossRef]
- Singh, S.P.; Singh, S.P. Optimal cost wide area measurement system incorporating communication infrastructure. IET Gener. Transm. Distrib. 2017, 11, 2814–2821. [Google Scholar] [CrossRef]
- Korkali, M.; Abur, A. Placement of PMUs with Channel Limits. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009. [Google Scholar]
- Korkali, M. Robust wide-area fault visibility and structural observability in power systems with synchronized measurement units. In Advances in Electric Power and Energy: Static State Estimation; IEEE: New York, NY, USA, 2020; pp. 209–230. [Google Scholar]
- Korkali, M.; Abur, A. Impact of network sparsity on strategic placement of phasor measurement units with fixed channel capacity. In Proceedings of the 2010 IEEE International Symposium on Circuits and Systems, Paris, France, 30 May–2 June 2010; pp. 3445–3448. [Google Scholar]
- Baba, M.; Nor, N.B.M.; Aman Sheikh, M.; Irfan, M.; Tahir, M. A Strategic and Significant Method for the Optimal Placement of Phasor Measurement Unit for Power System Network. Symmetry 2020, 12, 1174. [Google Scholar] [CrossRef]
- Fan, N.; Watson, J.P. On integer programming models for the multi-channel PMU placement problem and their solution. Energy Syst. 2014, 6, 1–19. [Google Scholar] [CrossRef]
- Emami, R.; Abur, A. Robust measurement design by placing synchronized phasor measurements on network branches. IEEE Trans. Power Syst. 2010, 25, 38–43. [Google Scholar] [CrossRef]
- Andic, C.; Ozturk, A.; Turkay, B. Power system state estimation using a robust crow search algorithm based on PMUs with limited number of channels. Electr. Power Syst. Res. 2023, 217, 109126. [Google Scholar] [CrossRef]
- Shafiullah, M.; Hossain, M.I.; Abido, M.A.; Abdel-Fattah, T.; Mantawy, A.H. A Modified Optimal PMU Placement Problem Formulation Considering Channel Limits under Various Contingencies. Measurement 2019, 135, 875–885. [Google Scholar] [CrossRef]
- Manousakis, N.M.; Korres, G.N. Optimal placement of PMUS considering scada measurements and fixed channel capacity by semidefinite programming. In Proceedings of the MedPower 2014, Athens, Greece, 2–5 November 2014; pp. 1–6. [Google Scholar]
- Manousakis, N.M.; Korres, G.N. Optimal PMU placement for numerical observability considering fixed channel capacity—A semidefinite programming approach. IEEE Trans. Power Syst. 2016, 31, 3328–3329. [Google Scholar] [CrossRef]
- Manousakis, N.M.; Korres, G.N. Semidefinite programming for optimal placement of PMUs with channel limits considering pre-existing SCADA and PMU measurements. In Proceedings of the 2016 Power Systems Computation Conference (PSCC), Genoa, Italy, 20–24 June 2016. [Google Scholar]
- Manousakis, N.M.; Korres, G.N. Optimal PMU arrangement considering limited channel capacity and transformer tap settings. IET Gener. Transm. Distrib. 2020, 14, 5984–5991. [Google Scholar] [CrossRef]
- Qi, B.; Yuan, Y.; Yang, Y.; Bu, Q.; Chen, J. Chapter 1—Overview of Smart Substations; Yuan, Y., Yang, Y., Eds.; IEC 61850-Based Smart Substations; Academic Press: Cambridge, MA, USA, 2019; pp. 1–24. [Google Scholar]
- Li, J.; Huang, Q.; Li, P.; Huang, H.; Zhang, L. Chapter 8—Intelligent Status Monitoring System for Smart Substations; Yuan, Y., Yang, Y., Eds.; IEC 61850-Based Smart Substations; Academic Press: Cambridge, MA, USA, 2019; pp. 255–305. [Google Scholar]
- Bogani, C.; Gasparo, M.; Papini, A. Generalized pattern search methods for a class of nonsmooth optimization problems with structure. J. Comput. Appl. Math. 2009, 229, 283–293. [Google Scholar] [CrossRef]
- Hosseini, S.S.S.; Gandomi, A.H.; Nemati, A.; Hosseini, S.H.S. Reactive Power and Voltage Control Based on Mesh Adaptive Direct Search Algorithm. In Engineering and Applied Sciences Optimization; Springer: Berlin/Heidelberg, Germany, 2015; pp. 217–231. [Google Scholar]
- The MathWorks Inc. Optimization Toolbox for Use with MATLAB R®. User’s Guide for Mathwork. 2016. Available online: www.mathworks.com (accessed on 15 February 2024).
- Available online: https://coin-or.github.io/Ipopt/ (accessed on 15 February 2024).
- Bestuzheva, K.; Besançon, M.; Chen, W.K.; Chmiela, A.; Donkiewicz, T.; van Doornmalen, J.; Eifler, L.; Gaul, O.; Gamrath, G.; Gleixner, A.; et al. Enabling research through the SCIP optimization suite 8. 0. ACM Trans. Math. Softw. 2023, 49, 1–21. [Google Scholar] [CrossRef]
- Available online: https://yalmip.github.io/_posts/tutorials/2016-09-17-globaloptimization/ (accessed on 15 February 2024).
- Parametric Fusion (MOSEK 10.1). Available online: https://www.mosek.com (accessed on 15 February 2024).
- Löfberg, J. YALMIP: A toolbox for modeling optimization in MATLAB. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 2–4 September 2004; pp. 284–289. [Google Scholar]
- Zimmerman, R.D.; Murillo-Sánchez, C.E.; Thomas, R.J. MATPOWER: Steady-state operations, planning, and analysis tools for power systems research and education. IEEE Trans. Power Syst. 2010, 26, 12–19. [Google Scholar] [CrossRef]
- Available online: https://www.mathworks.com/help/optim/ug/mixed-integer-linear-programming-algorithms.html (accessed on 15 April 2024).
- Available online: https://www.mathworks.com/help/optim/ug/intlinprog.html (accessed on 15 April 2024).
- Available online: https://docs.mosek.com/latest/cxxfusion/mip-optimizer.html (accessed on 15 April 2024).
- Maratos, N.G. Exact Penalty Function Algorithms for Finite Dimensional and Optimization Problems. Ph.D. Thesis, Imperial College of Science and Technology, University of London, London, UK, 1978. [Google Scholar]
- Available online: https://icseg.iti.illinois.edu/power-cases/ (accessed on 15 February 2024).
- Available online: https://coin-or.github.io/Cbc/intro.html (accessed on 15 February 2024).
- Available online: https://www.gnu.org/software/glpk/ (accessed on 15 February 2024).
- Available online: https://www.gurobi.com/ (accessed on 15 April 2024).
- Available online: https://www.gurobi.com/documentation/current/refman/mipgapabs.html (accessed on 15 April 2024).
- Available online: https://www.gurobi.com/documentation/current/refman/mipgap2.html (accessed on 15 April 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).