Multi-Augmentation-Based Contrastive Learning for Semi-Supervised Learning

Abstract

Semi-supervised learning has been proven to be effective in utilizing unlabeled samples to mitigate the problem of limited labeled data. Traditional semi-supervised learning methods generate pseudo-labels for unlabeled samples and train the classifier using both labeled and pseudo-labeled samples. However, in data-scarce scenarios, reliance on labeled samples for initial classifier generation can degrade performance. Methods based on consistency regularization have shown promising results by encouraging consistent outputs for different semantic variations of the same sample obtained through diverse augmentation techniques. However, existing methods typically utilize only weak and strong augmentation variants, limiting information extraction. Therefore, a multi-augmentation contrastive semi-supervised learning method (MAC-SSL) is proposed. MAC-SSL introduces moderate augmentation, combining outputs from moderately and weakly augmented unlabeled images to generate pseudo-labels. Cross-entropy loss ensures consistency between strongly augmented image outputs and pseudo-labels. Furthermore, the MixUP is adopted to blend outputs from labeled and unlabeled images, enhancing consistency between re-augmented outputs and new pseudo-labels. The proposed method achieves a state-of-the-art performance (accuracy) through extensive experiments conducted on multiple datasets with varying numbers of labeled samples. Ablation studies further investigate each component’s significance.

1. Introduction

In recent years, deep learning has rapidly advanced and achieved remarkable results in various fields, such as image classification [1,2], object detection [3,4], clustering [5,6], semantic segmentation [7,8], and more. However, the success of deep learning is heavily reliant on large-scale, high-quality labeled datasets [9].

However, collecting labeled data can be expensive and time-consuming, especially when expert annotation is required, which is unaffordable for the countless everyday learning demands in modern society. Semi-supervised learning [10,11] addresses the scarcity of labeled samples by leveraging a combination of a small labeled dataset and a substantial amount of unlabeled data for model training, thus alleviating the dependency on extensive labeled datasets. This has led to a plethora of SSL methods designed for various fields [12,13,14,15,16,17,18,19]. Traditional semi-supervised learning methods involve training models to predict artificial labels for unlabeled images, which are then incorporated as supplementary inputs during training. However, these approaches, such as the pseudo-labeling method [20,21] (also known as self-training [22,23,24,25,26]), face limitations due to their reliance on initial training with labeled samples prior to generating pseudo-labels for unlabeled samples, resulting in reduced effectiveness when labeled data are scarce.

Consistency regularization [27,28,29,30] -based semi-supervised learning methods (also commonly referred to as contrastive learning [31,32,33,34]) tackle this challenge by treating both labeled and unlabeled input images, along with their augmented versions, as positive pairs. These consistency regularization-based methods in deep learning operate under the assumption that, even after applying data augmentation [35,36,37], the classifier should maintain consistent class probabilities for unlabeled samples, implying that the semantic content remains unchanged. The augmented versions of an input image should exhibit greater similarity to the original image compared to other unrelated images. To adhere to this assumption, researchers introduce perturbations to the input samples through data augmentation, thereby generating augmented samples that are similar to the original data.

While the aforementioned algorithms have significantly contributed to improving learning accuracy in situations where labeled data are limited, they exhibit a notable decline in performance when confronted with a scarcity of labeled samples. This decline can be primarily attributed to the inability to fully leverage the informative content present in the unlabeled data, leading to an overreliance on the limited labeled samples.

Different from approaches that typically enforce consistency between the model outputs of strongly augmented unlabeled images and weakly augmented unlabeled images (using pseudo-labels or soft labels), MAC-SSL introduces a moderate augmentation step, where the model outputs of moderately augmented unlabeled images collaborate with the model outputs of weakly augmented images to derive pseudo-labels for the unlabeled images. Subsequently, the consistency (contrastive loss) between the model outputs of strongly augmented images and the pseudo-labels is enforced. Furthermore, inspired by MixMatch [33], the MixUP [38] is adopted to combine the three different outputs of unlabeled images and the outputs of labeled images to obtain further augmentation, which ensures consistency (unsupervised loss) between the model outputs of the re-augmented images and the newly generated pseudo-labels derived from the mixed labels or pseudo-labels.

The main contributions of this article are summarized as follows:

(1)

A novel moderate augmentation technique is introduced, which is incorporated into two distinctive losses.

(2)

Numerous experiments demonstrate that MAC-SSL achieves state-of-the-art (SOTA) results across all standard benchmark datasets (Section 3.3).

(3)

The conducted ablation experiments illustrate the excellent performance of MAC-SSL (Section 3.4).

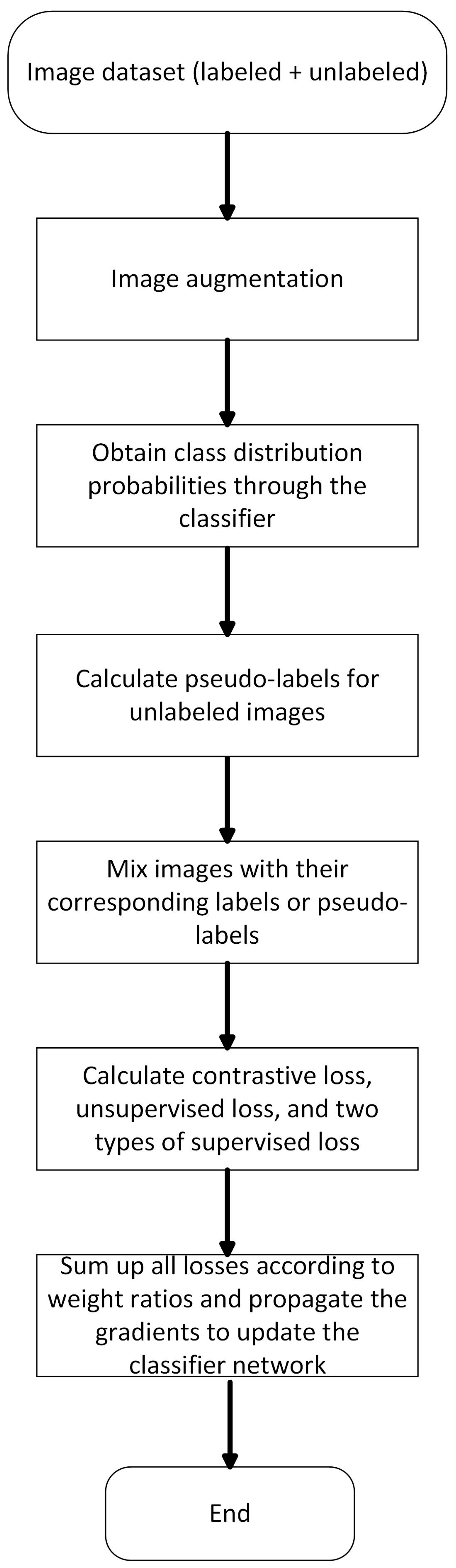
2. Method

This section provides a detailed introduction to the proposed MAC-SSL algorithm. For an $L$-class classification problem, we let $\mathcal{X}=((x_b,q_b);b\in (1,\dots ,B))$ represent a batch of $B$ labeled examples with $L$ classes where $x_b$ is the training sample and $q_b$ is the corresponding one-hot encoded label, and we let $\mathcal{U}=(u_b;b\in (1,\dots ,\mu B))$ represent a batch of $\mu B$ unlabeled examples, where $\mu$ is a hyperparameter that determines the relative sizes of $\mathcal{X}$ and $\mathcal{U}$.

2.1. Data Augmentation

Data augmentation is performed on both labeled and unlabeled data. There are three different levels of augmentation strategies used, and in increasing order of intensity, they are weak augmentation, moderate augmentation, and strong augmentation. Weak augmentation refers to a standard flip-and-shift augmentation strategy. Specifically, it randomly flips an image horizontally with a 50% probability and randomly translates the image by 12.5% in the horizontal or vertical direction. Moderate augmentation involves applying Augmix [39] to weakly augmented samples, following the configuration specified in Augmix [39] and Augmix’s pseudocode visible Algorithm 1. Strong augmentation applies RandAugment [40] to weakly augmented samples, following the configuration specified in RandAugment [40].

For the labeled data batch $\mathcal{X}$, a “weak” augmentation strategy is employed. For the unlabeled data batch $\mathcal{U}$, a combination of “weak”, “moderate”, and “strong” augmentation techniques is employed. The weak augmentation strategy is identical to that employed for $\mathcal{X}$.

By employing the weak, moderate, and strong augmentation strategies, the following augmented data batches are generated: the weakly augmented labeled data batch ${\mathcal{X}}^{\prime }$, the weakly augmented unlabeled data batch ${\mathcal{U}}_w^{\prime }$, the moderately augmented unlabeled data batch ${\mathcal{U}}_m^{\prime }$, and the strongly augmented unlabeled data batch ${\mathcal{U}}_s^{\prime }$.

The data augmentation process described above is illustrated in Figure 1.

Algorithm 1 AugMix

1: Input: Original image $x_{orig}$, Operations $\mathcal{O}=rotate,\dots ,posterize$.

2: function AugmentAndMix $(x_{orig},k=3,\alpha =1)$

3:    Fill $x_{aug}$ with zeros of same shape as $x_{orig}$

4:    Sample mixing weights $(w_1,w_2,\dots ,w_k)~$Dirichlet $(\alpha ,\dots ,\alpha )$    ▷ Dirichlet denotes Dirichlet distribution

5:    for $i=1$ to $k$ do

6:       $o{p}_1,o{p}_2,o{p}_3~\mathcal{O}$                   ▷ Sample augmentation operation

7:       Compose operations with varying depth $o{p}_{12}=o{p}_2\circ o{p}_1,o{p}_{123}=o{p}_3\circ o{p}_{12}$ ▷ $\circ$ denotes composition of operations

8:       Sample uniformly from one of these operations $chain~\{o{p}_1,o{p}_{12},o{p}_{123}\}$

9:       $x_{aug}+=w_i\cdot chain(x_{orig})$   ▷ Addition is elementwise, $\cdot$ denotes that attach weights to each augmentation operation.

10:    end for                   ▷ Completion of the augmetation process

11:    Sample weight $m~\mathrm{Beta}(\alpha ,\alpha )$

12:    Interpolation with rule $x_{augmix}=m{x}_{orig}+(1-m)x_{aug}$    ▷ Completion of the mix process

13:    return $x_{augmix}$

14: end function

15: $x_{am}=$ AugmentAndMix $(x_{orig},3,1)$        ▷ $x_{am}$ is stochastically generated by the function AugmentAndMix $(x_{orig},k=3,\alpha =1)$.

16: return $x_{am}$.

2.2. Pseudo-Labels Generating

The process of generating pseudo-labels is depicted in Figure 2. MAC-SSL leverages the model outputs $p_{wb}^{u\prime }=p(q|u_{wb}^{\prime })$ and $p_{mb}^{u\prime }=p(q|u_{mb}^{\prime })$ obtained from its weakly augmented and moderately augmented versions $u_{wb}^{\prime }$ and $u_{mb}^{\prime }$, respectively, to compute an average prediction $p_b^u$ for each unlabeled sample $u_b$ in $\mathcal{U}$. It is worth noting that $p(q|u)$ represents the model’s output for $u$. Subsequently, a “Sharpening” [33] operation is applied to $p_b^u$ to generate the pseudo-label $q_b^u$ for $u_b$. The corresponding computational steps are described as follows:

$$p_b^u=\frac{1}{2}\left(p_{wb}^{u\prime }+p_{mb}^{u\prime }\right) \mathrm{and}$$

(1)

$$q_b^u=\mathrm{Sharpen}\left(p_b^u,T\right),$$

(2)

where the Sharpening operation is defined as follows:

$$\mathrm{Sharpen}{\left(p,T\right)}_i:=\frac{p_i^{\frac{1}{T}}}{{\displaystyle \sum _{j=1}^L{p}_j^{\frac{1}{T}}}},$$

(3)

where $p$ represents an input categorical distribution (specifically in MAC-SSL, $p$ is the average class prediction generated from the model outputs $p_{wb}^{u\prime }$ and $p_{mb}^{u\prime }$, denoted as $p_b^u$) and $T$ is a hyperparameter that signifies the “temperature [41]” of the class distribution. As $T\to 0$, the output of $\mathrm{Sharpen}(p,T)$ will approach a “one-hot” distribution. Since $q_b^u=\mathrm{Sharpen}(p_b^u,T)$ will be used as a target for the model’s prediction for augmentations of $u_b$, lowering the temperature encourages the model to produce lower-entropy predictions. $T$ is set to a small value in this paper.

Figure 2. Process of pseudo-label generating.

Figure 2. Process of pseudo-label generating.

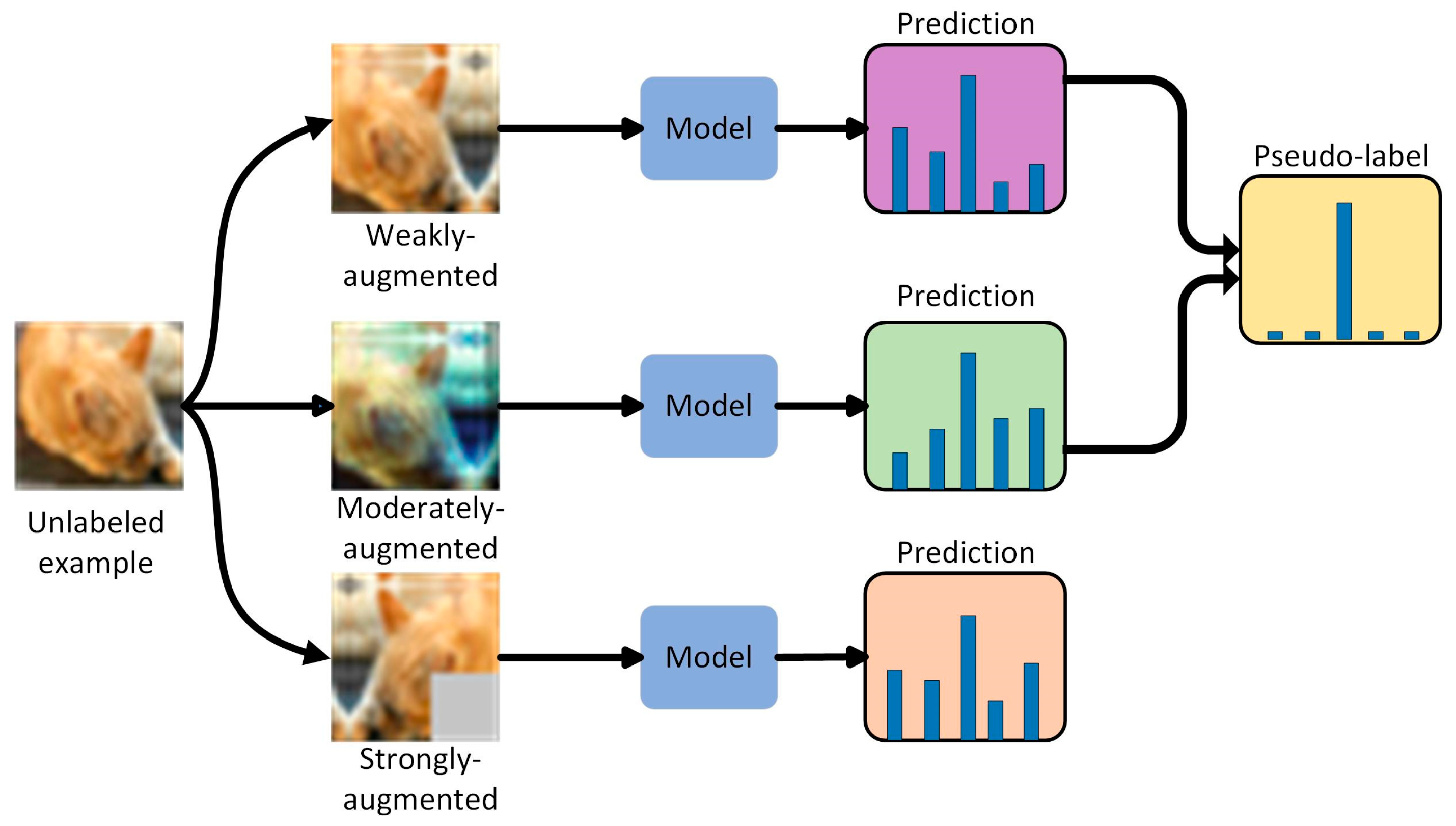
2.3. MixUP

MixUP is employed for semi-supervised learning, distinguishing itself from prior approaches that solely mix images. MAC-SSL involves mixing both labeled samples with ground-true labels and unlabeled samples with pseudo-labels (generated as described in Section 2.2). For a pair of samples with their respective label predictions $(x_1,q_1)$ and $(x_2,q_2)$, when $x_1$ is a labeled sample, $q_1$ represents the true label. When $x_1$ is an unlabeled sample, $q_1$ represents the generated pseudo-label. The same applies to $x_2$ and $q_2$. The MixUP technique employed can be described as follows:

$$\lambda ~\mathrm{Beta}(\alpha ,\alpha ),$$

(4)

$${\lambda }^{\prime }=\max (\lambda ,1-\lambda ),$$

(5)

$$(x_1^{\prime },q_1^{\prime })={\lambda }^{\prime }(x_1,q_1)+(1-{\lambda }^{\prime })(x_2,q_2), \mathrm{and}$$

(6)

$$(x_2^{\prime },q_2^{\prime })={\lambda }^{\prime }(x_2,q_2)+(1-{\lambda }^{\prime })(x_1,q_1),$$

(7)

where $(x_1^{\prime },q_1^{\prime })$ represents the new sample generated by mixing with $x_1$ as the base (${\lambda }^{\prime }$ is a value close to 1), $(x_2^{\prime },q_2^{\prime })$ represents the new sample generated by mixing with $x_2$ as the base, and $\alpha$ is a hyperparameter. The specific calculation steps for Equation (6) are as follows:

$$x_1^{\prime }={\lambda }^{\prime }{x}_1+(1-{\lambda }^{\prime })x_2 \mathrm{and}$$

(8)

$$q_1^{\prime }={\lambda }^{\prime }{q}_1+(1-{\lambda }^{\prime })q_2,$$

(9)

and the specific calculation steps for Equation (7) are as follows:

$$x_2^{\prime }={\lambda }^{\prime }{x}_2+(1-{\lambda }^{\prime })x_1 \mathrm{and}$$

(10)

$$q_2^{\prime }={\lambda }^{\prime }{q}_2+(1-{\lambda }^{\prime })q_1.$$

(11)

The mixing process in the algorithm is presented in line 15 of Algorithm 2.

Algorithm 2 MAC-SSL

1: Input: Batch of labeled examples $\mathcal{X}=((x_b,q_b);b\in (1,\dots ,B))$, batch of unlabeled examples $\mathcal{U}=(u_b;b\in (1,\dots ,\mu B))$, ratio of sample size $\mu$, sharpening temperature $T$, Beta distribution parameter $\alpha$ for MixUp, unlabeled loss weight ${\lambda }_u$, contrastive loss weight ${\lambda }_c$.

2: for $b=1$ to $B$

3:    $x_b^{\prime }=$ Weak-Augment $(x_b)$

4: end for

5: for $b=1$ to $\mu B$

6:    $u_{wb}^{\prime }=$ Weak-Augment $(u_b)$, $u_{mb}^{\prime }=$ Moderate-Augment $(u_b)$, $u_{sb}^{\prime }=$ Strong-Augment $(u_b)$

7:    $p_{wb}^{u\prime },p_{mb}^{u\prime },p_{sb}^{u\prime }=p(q|u_{wb}^{\prime }),p(q|u_{mb}^{\prime }),p(q|u_{sb}^{\prime })$

8:   $p_b^u=\frac{1}{2}(p_{wb}^{u\prime }+p_{mb}^{u\prime })$              ▷ Compute average predictions of $u_{wb}^{\prime }$ and $u_{mb}^{\prime }$

9:   $q_b^u=Sharpen(p_b^u,T)$   ▷ Apply temperature sharpening to the average prediction (see Equation (3))

10: end for

11: ${\mathcal{X}}^{\prime }=((x_b^{\prime },q_b);b\in (1,\dots ,B))$,

12: ${\mathcal{U}}_w^{\prime }=(u_{wb}^{\prime };b\in (1,\dots ,\mu B))$, ${\mathcal{U}}_m^{\prime }=(u_{mb}^{\prime };b\in (1,\dots ,\mu B))$, ${\mathcal{U}}_s^{\prime }=(u_{sb}^{\prime };b\in (1,\dots ,\mu B))$

13: $\mathcal{W}=\mathrm{Shuffle}(Concat({\mathcal{X}}^{\prime },{\mathcal{U}}_w^{\prime },{\mathcal{U}}_m^{\prime },{\mathcal{U}}_s^{\prime }))$      ▷ Combine and shuffle labeled and unlabeled data

14: ${\mathcal{X}}^{″}=(\mathrm{MixUp}({\mathcal{X}}^{\prime },{\mathcal{W}}_i);i\in (1,\dots ,B))$                                                  ▷ see Section 2.3

15: ${\mathcal{U}}_w^{″}=(\mathrm{MixUp}({\mathcal{U}}_w^{\prime },{\mathcal{W}}_{i+B});i\in (1,\dots ,\mu B))$, ${\mathcal{U}}_m^{″}=(\mathrm{MixUp}({\mathcal{U}}_m^{\prime },{\mathcal{W}}_{i+B+\mu B});i\in (1,\dots ,\mu B))$,

${\mathcal{U}}_s^{″}=(\mathrm{MixUp}({\mathcal{U}}_s^{\prime },{\mathcal{W}}_{i+B+2\mu B});i\in (1,\dots ,\mu B))$

16: ${\mathcal{L}}_x$$=\frac{1}{B}{\displaystyle \sum _{b=1}^{B}H}(q_b,p(q|x_b))$                                                        ▷ Equation (12)

17: ${\mathcal{L}}_{xm}$$=\frac{1}{B}{\displaystyle \sum _{b=1}^{B}H}(q_b^{\prime },p(q|x_b^{″}))$                                                        ▷ Equation (13)

18: ${\mathcal{L}}_u=\frac{1}{\mu B}{\displaystyle \sum _{b=1}^{\mu B}(\Vert }{q}_b^{u\prime }-p(q\mid u_{wb}^{″}){\Vert }_2^2+\Vert q_b^{u\prime }-p(q\mid u_{mb}^{″}){\Vert }_2^2+\Vert q_b^{u\prime }-p(q\mid u_{sb}^{″}){\Vert }_2^2)$                                   ▷ Equation (14)

19: ${\mathcal{L}}_c=\frac{1}{\mu B}{\displaystyle \sum _{b=1}^{\mu B}f}(\max (p_b^u)\ge \tau )H\left(p_b^u,p(q\mid u_{sb}^{\prime })\right)$                                                ▷ Equation (15)

20: $\mathcal{L}={\mathcal{L}}_x+{\mathcal{L}}_{xm}+{\lambda }_u{\mathcal{L}}_u+{\lambda }_c{\mathcal{L}}_c$                                                     ▷ Equation (16)

21: return $\mathcal{L}$

2.4. The Proposed MAC-SSL

MAC-SSL generates one batch of augmented labeled data, denoted as ${\mathcal{X}}^{\prime }$, and three batches of augmented unlabeled data, where ${\mathcal{U}}_w^{\prime }$, ${\mathcal{U}}_m^{\prime }$, and ${\mathcal{U}}_s^{\prime }$. ${\mathcal{X}}^{\prime }$ represent the labeled data batch after weak augmentation and ${\mathcal{U}}_w^{\prime }$, ${\mathcal{U}}_m^{\prime }$, and ${\mathcal{U}}_s^{\prime }$ represent the unlabeled data batches after weak, moderate, and strong augmentations, respectively. The average prediction distribution $p_b^u$ is computed using the model outputs $p_{wb}^{u\prime }$ and $p_{mb}^{u\prime }$ from ${\mathcal{U}}_w^{\prime }$ and ${\mathcal{U}}_m^{\prime }$, respectively (see Equation (1)), which are then used to generate the pseudo-labels $q_b^{u\prime }$ for the unlabeled data batch (see Equation (2)). Subsequently, ${\mathcal{X}}^{\prime }$ and ${\mathcal{U}}_w^{\prime }$, ${\mathcal{U}}_m^{\prime }$, and ${\mathcal{U}}_s^{\prime }$ are mixed to generate the mixed weakly augmented labeled data batch ${\mathcal{X}}^{″}$ and the mixed weakly augmented unlabeled data batches ${\mathcal{U}}_w^{″}$, the mixed moderately augmented unlabeled data batch ${\mathcal{U}}_m^{″}$, and the mixed strongly augmented unlabeled data batch ${\mathcal{U}}_s^{″}$, respectively. Likewise, the ground-true label $q_b$ and pseudo-label $q_b^u$ are also mixed to obtain the corresponding pseudo-labels $q_b^{\prime }$ and $q_b^{u\prime }$ for ${\mathcal{X}}^{″}$ and ${\mathcal{U}}_w^{″}$, ${\mathcal{U}}_m^{″}$, and ${\mathcal{U}}_s^{″}$, respectively (see Section 2.3). The complete MAC-SSL framework is illustrated in Figure 3, and a flowchart of the MAC-SSL process is presented in Figure 4.

The loss function of MAC-SSL consists of the following four components: supervised classification loss ${\mathcal{L}}_x$, mixed supervised classification loss ${\mathcal{L}}_{xm}$, unsupervised classification loss ${\mathcal{L}}_u$, and contrastive loss ${\mathcal{L}}_c$.

${\mathcal{L}}_x$ is the supervised classification loss on $\mathcal{X}$, which is defined as the cross-entropy between the ground-true label and the model prediction, as follows:

$${\mathcal{L}}_x=\frac{1}{B}{\displaystyle \sum _{b=1}^{B}H}(q_b,p(q|x_b)),$$

(12)

where $p(q|x_b)$ is the model’s prediction for $x_b\in \mathcal{X}$ and $H$ denotes the cross-entropy between $q_b$ and $p(q|x_b)$.

Regarding ${\mathcal{L}}_{xm}$, it is the supervised classification loss on ${\mathcal{X}}^{″}$. It is defined as the cross-entropy between the pseudo-label and the model prediction, as follows:

$${\mathcal{L}}_{xm}=\frac{1}{B}{\displaystyle \sum _{b=1}^{B}H}(q_b^{\prime },p(q|x_b^{″})),$$

(13)

where $q_b^{\prime }$ is the pseudo-label, $p(q|x_b^{″})$ is the model’s prediction for $x_b^{″}\in {\mathcal{X}}^{″}$, and $H$ denotes the cross-entropy between $q_b^{\prime }$ and $p(q|x_b^{″})$.

The unsupervised classification loss, ${\mathcal{L}}_u$, is defined on ${\mathcal{U}}_w^{″}$, ${\mathcal{U}}_m^{″}$, and ${\mathcal{U}}_s^{″}$. It is computed as the mean squared error between the pseudo-label $q_b^{u\prime }$ and the three model predictions $p(q|u_{wb}^{″})$, $p(q|u_{mb}^{″})$, and $p(q|u_{sb}^{″})$ as follows:

$${\mathcal{L}}_u=\frac{1}{\mu B}{\displaystyle \sum _{b=1}^{\mu B}(\Vert }{q}_b^{u\prime }-p(q\mid u_{wb}^{″}){\Vert }_2^2+\Vert q_b^{u\prime }-p(q\mid u_{mb}^{″}){\Vert }_2^2+\Vert q_b^{u\prime }-p(q\mid u_{sb}^{″}){\Vert }_2^2),$$

(14)

where $u_{wb}^{″}$, $u_{mb}^{″}$, $u_{sb}^{″}\in {\mathcal{U}}_w^{″}$, ${\mathcal{U}}_m^{″}$, and ${\mathcal{U}}_s^{″}$ and $p(q|u_{wb}^{″})$, $p(q|u_{mb}^{″})$, and $p(q|u_{sb}^{″})$ are the model’s predictions for $u_{wb}^{″}$, $u_{mb}^{″}$, and $u_{sb}^{\prime \prime }$, respectively.

The contrastive loss, ${\mathcal{L}}_c$, is established between ${\mathcal{U}}_w^{\prime }$, ${\mathcal{U}}_m^{\prime }$, and ${\mathcal{U}}_s^{\prime }$. The object in this case is to maintain a certain level of strength in the optimization of the model on ${\mathcal{U}}_s^{\prime }$. Therefore, a threshold, $\tau$, is employed to $p_b^u$, and instead of converting $p_b^u$ into pseudo-labels, the predicted distribution’s state is directly utilized to constrain the model’s output, $p(q|u_{sb}^{\prime })$, which is also a predicted distribution, on ${\mathcal{U}}_s^{\prime }$ using cross-entropy. ${\mathcal{L}}_c$ can be calculated as follows:

$${\mathcal{L}}_c=\frac{1}{\mu B}{\displaystyle \sum _{b=1}^{\mu B}f}(\max (p_b^u)\ge \tau )H\left(p_b^u,p(q|u_{s{b}^{\prime }})\right),$$

(15)

where $u_{sb}^{\prime }\in {\mathcal{U}}_s^{\prime }$ and $p(q|u_{sb}^{\prime })$ are the model’s predictions for $u_{sb}^{\prime }$, $H$ denotes the cross-entropy between the distribution $p_b^u$ and $p(q|u_{sb}^{\prime })$, and $f(•)$ represents 1 if the inequality in the parentheses holds (and it is otherwise 0).

By combining the aforementioned loss functions, the loss function of MAC-SSL is defined as follows:

$$\mathcal{L}={\mathcal{L}}_x+{\mathcal{L}}_{xm}+{\lambda }_u{\mathcal{L}}_u+{\lambda }_c{\mathcal{L}}_c,$$

(16)

where ${\lambda }_u$ and ${\lambda }_c$ are trade-off hyper-parameters that control the weights of the unsupervised loss ${\mathcal{L}}_u$ and the contrastive loss ${\mathcal{L}}_c$, respectively.

This design takes into account the different characteristics of the data by comprehensively utilizing different types of data and loss functions, enabling the model to learn the features of the data more comprehensively and, thus, improve its performance. Specifically, the benefits of such comprehensive utilization are reflected in the following aspects:

(1)

Integration of information from different types of data: This model combines labeled and unlabeled data, applying different types of loss functions to both. ${\mathcal{L}}_x$ and ${\mathcal{L}}_{xm}$ utilize the true labels of labeled data, ${\mathcal{L}}_u$ utilizes pseudo-labels of unlabeled data, and ${\mathcal{L}}_c$ performs contrastive learning on unlabeled data. By comprehensively utilizing these different types of data and loss functions, the model can learn the features of the data more comprehensively, thereby improving its performance.

(2)

Enhancing the model’s generalization ability: Integrating different types of loss functions can improve the model’s generalization ability. ${\mathcal{L}}_x$ and ${\mathcal{L}}_{xm}$ help the model learn accurate classification decisions on labeled data, while ${\mathcal{L}}_u$ and ${\mathcal{L}}_c$ can help the model utilize information from unlabeled data to enhance its generalization ability.

(3)

Strengthening the model’s understanding of the data: Different types of loss functions allow the model to understand the data from different perspectives. ${\mathcal{L}}_x$ and ${\mathcal{L}}_{xm}$ help the model understand the true labels of the data, while ${\mathcal{L}}_u$ and ${\mathcal{L}}_c$ enable the model to learn the distribution and features of the data from unlabeled data, thereby improving the model’s robustness.

The full MAC-SSL algorithm is presented in Algorithm 2.

3. Results

MAC-SSL was evaluated on several benchmarks for SSL image classification (see Section 3.2). Furthermore, ablation experiments were conducted on each of MAC-SSL’s components to analyze their individual contributions (see Section 3.3).

3.1. Implementation Details

• Datasets and metrics: MAC-SSL was experimentally validated on the CIFAR-10 [42], CIFAR-100 [42], and SVHN [43] datasets, as shown in Figure 5.
  • CIFAR-10: The CIFAR-10 dataset is a widely used benchmark in the field of computer vision. It consists of 60,000 color images, each sized at 32 × 32 pixels, belonging to 10 different classes. These classes include common objects such as airplanes, automobiles, cats, birds, dogs, and more. The dataset is divided into 50,000 training images and 10,000 test images, with an equal distribution of images across the classes.
  • CIFAR-100: Similar to CIFAR-10, CIFAR-100 is another dataset used for image classification tasks. It contains 60,000 images, each also sized at 32 × 32 pixels, but it is divided into 100 fine-grained classes. Each class represents a specific object or concept, such as insects, food containers, trees, fish, and so on. The dataset is split into 50,000 training images and 10,000 test images, with a balanced distribution of images across the classes. Classifying CIFAR-100 is more difficult than CIFAR-10 due to its larger number of categories.
  • SVHN (Street View House Numbers): The SVHN dataset is focused on digit recognition tasks. It consists of real-world images taken from Google Street View that contain house numbers. Each image in SVHN contains multiple digits (from zero to nine). The images are of varying sizes but are predominantly sized at 32 × 32 pixels. SVHN is divided into a training set with 73,257 images and a test set with 26,032 images.
• Experiment setting: All experiments were implemented using PyTorch and conducted on an Ubuntu system server with four NVIDIA 3090 GPUs and 128 GB of memory, and they followed SSL evaluation methods. The experiments were conducted using the “Wide ResNet-28” model from [44]. Training for the CIFAR-10 [42] and SVHN [43] datasets continued for 300 epochs until convergence. A batch size of 64 was used with the Wide ResNet-28-2 model, which has 1.47 M parameters. Due to computational limitations, a batch size of up to 32 was used for the CIFAR-100 [42] dataset in MAC-SSL, while for the other methods, the batch size remained at 64. The Wide ResNet-28-8 model with 23.46 M parameters was utilized for the CIFAR-100 training. For the selection of hyperparameters, we employed a random search. The hyperparameter $\mu$, controlling the sample ratio, was set to 5. The weight hyperparameter ${\lambda }_u$ was set as $\frac{currentepoch}{totalepoch}\times 75$, and ${\lambda }_c$ was set to 1. The learning rate was set to 0.01 for CIFAR-10, CIFAR-100, and SVHN. The threshold $\tau$ was set to 0.95. The training employed the SGD optimizer with cosine weight decay. Exponential moving average (EMA) with a decay rate of 0.999 was utilized for evaluating the models. Of note, for SVHN, we applied strong augmentation using RandAugment [40] on top of moderate augmentation, referred to as MAC-SSL-II. This differed from CIFAR-10/100. Each epoch involved 1024 steps of training, and checkpoints were saved at each epoch. The average accuracy of the last 20 checkpoints was recorded. This approach simplified the analysis process.

For the SOTA algorithms used in the comparative experiments, we reproduced results by obtaining their source code and maintaining the original settings mentioned in the code. For some datasets that were not included in their original code, we added them ourselves and used the hyperparameters specified in the respective papers. The source code for the comparative algorithms can be downloaded from the authors’ or reproducers’ homepages, except for Mean-Teacher [32] (reproduced by ourselves). The codes for CoMatch¹ [34], MixMatch² [33], ICT³ [45], VAT³ [46], Temporal-ensembling³ [30], and Pimodel³ [30] are available on their respective authors’ or reproducers’ homepages.

3.2. Comparison Algorithms

(1)

To demonstrate the superiority of MAC-SSL, performance comparison experiments were conducted with the following seven state-of-the-art semi-supervised algorithms:

(2)

CoMatch [34] combines pseudo-based, contrast-loss-based, and graph-based models to improve model performance with limited labeled data. It jointly learns class probabilities and low-dimensional embeddings, enhancing the quality of pseudo-labels by imposing a smoothness constraint on the class probabilities.

(3)

MixMatch [33] optimizes both supervised and unsupervised losses. It utilizes cross-entropy for supervised losses and mean square errors (MSEs) between predictions and generated pseudo-labels for unsupervised losses. MixMatch constructs pseudo-labels through data augmentation and improves their quality using the Sharpen function. MixUP [38] interpolation is also employed to create virtual samples.

(4)

Mean-Teacher [32] employs a student–teacher approach for SSL. The teacher model is based on the average weights of a student model in each update step. Mean-Teacher utilizes MSE loss as the consistency loss between two predictions and updates the model using exponential moving average (EMA) to control the update speed.

(5)

ICT [45] extends MixUP by interpolating unlabeled data, generating diverse mixed samples. It enforces consistency across different interpolation ratios using regularization. ICT trains a model by constraining predictions of mixed data to align with mixed predictions of original data. It effectively utilizes unlabeled data, particularly in scenarios with limited labeled data, resulting in improved generalization capabilities.

(6)

VAT [46] replaces data augmentation with adversarial transformations. It perturbs input data through adversarial transformations, leading to lower classification errors.

(7)

Temporal-ensembling [30] is a method based on temporal ensembling that improves model consistency and robustness by using an exponential moving average of historical prediction results during training. It trains the model by minimizing the consistency loss between the predictions of unlabeled data and the true labels of labeled data.

(8)

Pimodel [30] is a method based on data augmentation and consistency regularization. It generates virtual samples using data augmentation and trains the model by applying consistency constraints between labeled and unlabeled data.

3.3. Performance Comparison

• CIFAR-10: For CIFAR-10, performance comparison experiments were conducted with six baselines, including MixMatch [33], Mean-Teacher [32], ICT [45], VAT [46], Temporal-ensembling [30], and Pimodel [30]. The accuracy of these methods was evaluated with a varying number of labeled samples from 250 to 4000 (as is standard practice). The result can be seen in Figure 6. It can be observed that MAC-SSL was significantly superior to all other methods, especially when labeled samples were scarce, such as with 250 labels and 500 labels. MAC-SSL outperformed the second-best method, MixMatch, by 6.82% and 7.02%, respectively. These results highlight MAC-SSL’s ability to effectively utilize information from unlabeled data, thereby delivering a strong performance even in a scenario with limited labeled samples.
• CIFAR-100: To further demonstrate the effectiveness of MAC-SSL, we conducted comparative experiments on CIFAR-100. The baselines for comparison were the same as those used for CIFAR-10. The CIFAR-100 evaluation involved a varying number of labeled samples ranging from 400 to 2500. The results are presented in Figure 7. Upon observation, it can be seen that MAC-SSL achieved the best performance. When the number of labeled samples was 400, which means only 4 labeled samples per class, MAC-SSL outperformed the second-best method, MixMatch, by 16.58%. It is also noteworthy that as the number of labeled samples decreased, MAC-SSL brought even greater improvements, further validating the ability of the proposed method to effectively utilize information from unlabeled samples.
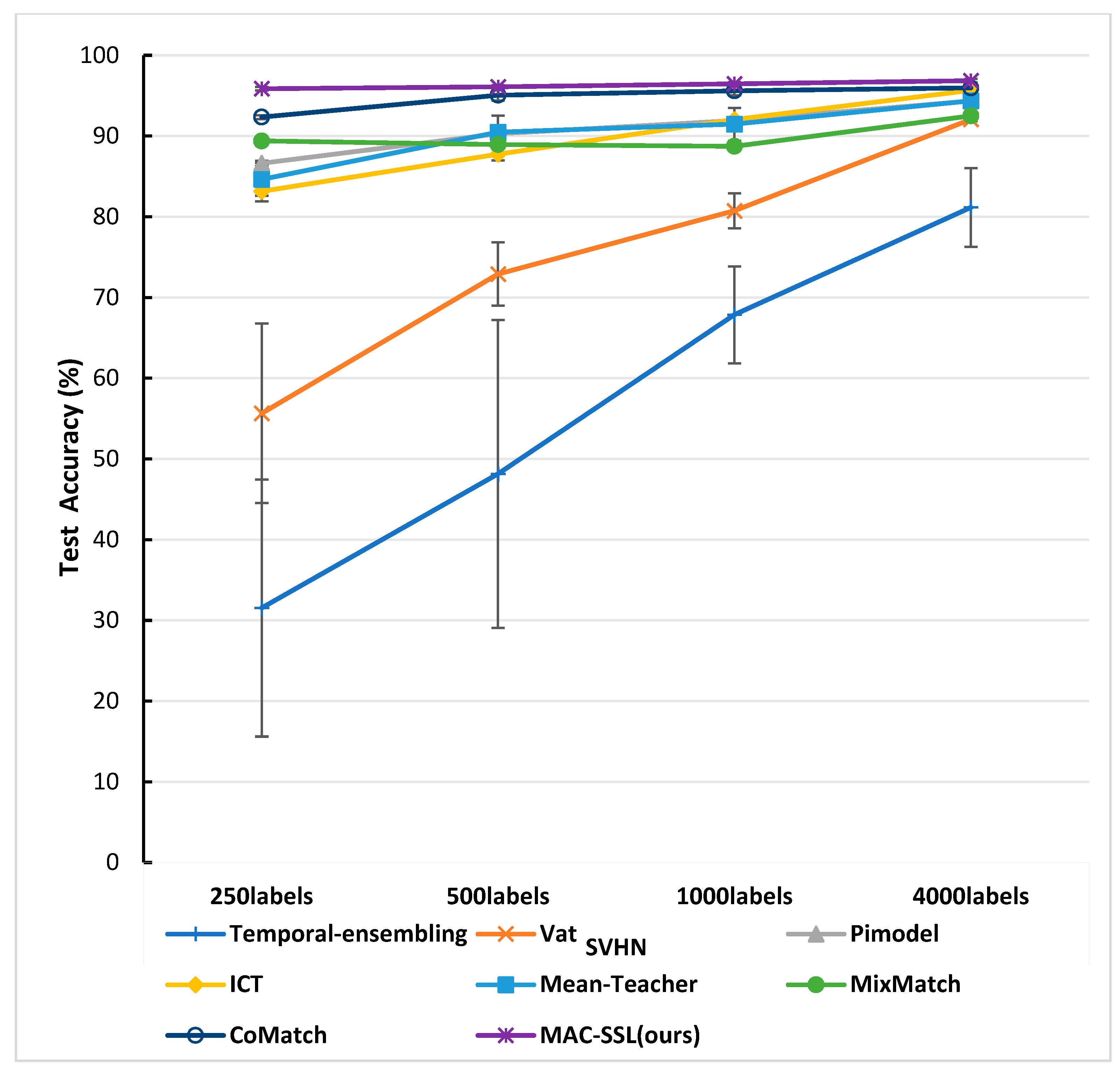
• SVHN: We conducted comparative experiments on the SVHN dataset and, in addition to CIFAR-10 and CIFAR-100, included CoMatch as one of the baselines. The accuracy of these methods was evaluated with varying numbers of labeled samples ranging from 250 to 4000. The experimental results are presented in Figure 8. As observed earlier, MAC-SSL achieved the best results and demonstrated greater improvements when the number of labeled samples was reduced. This once again confirmed the effectiveness of MAC-SSL and its ability to fully utilize unlabeled samples.

Through the conducted experiments, the proposed method demonstrated superior performance compared to all other existing methods, particularly in scenarios with limited availability of labeled samples. The key advantage of our approach was its ability to effectively leverage the valuable information contained within unlabeled samples, which is often overlooked by other methods’ data augmentation techniques. MAC-SSL stood out by generating reliable positive sample pairs through three distinct augmentation techniques, thereby enhancing the regularization benefits. Furthermore, by incorporating MixUP with augmented images and their corresponding labels or pseudo-labels, our model exhibited enhanced generalization capabilities and achieved efficient convergence.

Notably, MAC-SSL exhibited exceptional classification performances across multiple benchmark datasets, including CIFAR-10, CIFAR-100, and SVHN. These results highlight the versatility and robustness of our approach, especially in scenarios where labeled samples are scarce. The promising outcomes achieved by MAC-SSL validate its potential as a valuable contribution to the field, addressing the challenges associated with limited labeled data and demonstrating its efficacy in improving classification performance.

We also present in Figure 9 the test accuracy and test loss during the training process on the CIFAR-10 dataset with 1000 labeled samples using the different methods. It can be observed that MAC-SSL achieved rapid convergence, attaining the highest accuracy and nearly the lowest loss (with only a slight increase in loss towards the end). This further demonstrated the effectiveness and stability of MAC-SSL.

3.4. Ablation Experiment

Additional ablation experiments were conducted to examine the roles of the different components in MAC-SSL and evaluate the impacts of certain parameters. Specifically, we measured the effects of the following:

(1)

Investigating the effects of different strong augmentation strategies: directly using RandAugment (MAC-SSL) and using RandAugment after applying moderate augmentation (MAC-SSL-II)

(2)

Using different sample ratio hyperparameter $\mu$ values ranging from 1 to 9

(3)

Removing temperature sharpening (i.e., setting $T=1$)

(4)

Performing MixUP between labeled examples only, unlabeled examples only, and without mixing across labeled and unlabeled examples

(5)

Using the mean class distribution over two augmentations (i.e., weak and moderate augmentations) or using the class distribution for a single augmentation (i.e., only weak augmentation)

(6)

Employing weak augmentation, moderate augmentation, and strong augmentation, as well as the scenario where only weak augmentation and strong augmentation were utilized (with the class distribution being used only for weak augmentation)

The ablation experiments were conducted on the CIFAR-10 and SVHN datasets, and the results are shown in

Table 1. Ablation study results (a). All values indicate accuracy (%).

Method	CIFAR-10 (µ = 5)
	40 Labels	500 Labels	1000 Labels	4000 Labels
MAC-SSL (base for CIFAR10)	87.36 ± 0.09	93.93 ± 0.1	94.32 ± 0.18	94.96 ± 0.09
MAC-SSL-II (base for SVHN)	90.22 ± 0.14	93.29 ± 0.07	93.97 ± 0.08	94.91 ± 0.07
MAC-SSL/MAC-SSL-II without temperature sharpening (T = 1)	–	–	93.31 ± 0.08	–
MAC-SSL/MAC-SSL-II without MixUP	–	–	91.88 ± 0.11	–
MAC-SSL/MAC-SSL-II with MixUP on labeled only	–	–	90.07 ± 0.14	–
MAC-SSL/MAC-SSL-II with MixUP on unlabeled only	–	–	93.97 ± 0.35	–
MAC-SSL/MAC-SSL-II with MixUP on separate labeled and unlabeled	–	–	92.36 ± 0.42	–
MAC-SSL/MAC-SSL-II without distribution averaging	–	–	91.6 ± 0.18	–
MAC-SSL/MAC-SSL-II without moderate augmentation	–	–	94.18 ± 0.24	–

,

Table 2. Ablation study results (b). All values indicate accuracy (%). For SVHN, MAC-SSL-II was the base.

Method	SVHN (µ = 5)
	250 Labels	1000 Labels
MAC-SSL (base for CIFAR10)	95.35 ± 0.1	95.65 ± 0.08
MAC-SSL-II (base for SVHN)	95.87 ± 0.06	96.46 ± 0.04
MAC-SSL/MAC-SSL-II without temperature sharpening (T = 1)	–	95.95 ± 0.05
MAC-SSL/MAC-SSL-II without MixUP	–	94.83 ± 0.12
MAC-SSL/MAC-SSL-II with MixUP on labeled only	–	94.02 ± 0.13
MAC-SSL/MAC-SSL-II with MixUP on unlabeled only	–	96.17 ± 0.06
MAC-SSL/MAC-SSL-II with MixUP on separate labeled and unlabeled	–	96.06 ± 0.04
MAC-SSL/MAC-SSL-II without distribution averaging	–	96.44 ± 0.04
MAC-SSL/MAC-SSL-II without moderate augmentation	–	95.50 ± 0.06

and

Table 3. Ablation study results (c). All values indicate accuracy (%).

Method	CIFAR-10 (1000 Labels)
	µ = 1	µ = 3	µ = 5	µ = 7	µ = 9
MAC-SSL	89.47 ± 0.14	93.18 ± 0.08	94.32 ± 0.18	94.55 ± 0.08	96.46 ± 0.04
MAC-SSL-II	88.49 ± 0.18	92.96 ± 0.17	93.96 ± 0.08	94.5 ± 0.09	94.85 ± 0.11

. It was observed that each component contributed to the performance of MAC-SSL, and incorporating MixUP solely on labeled samples resulted in the largest performance loss, even surpassing the impact caused by not using MixUP at all. This indicated that unlabeled samples contributed significantly to the training process, as the information contained within a large volume of unlabeled samples exceeded that of a small number of labeled samples. MAC-SSL was able to fully utilize the information embedded within the unlabeled samples, resulting in remarkable performance.

Applying RandAugment in addition to moderate augmentation as the strong augmentation strategy proved to be more effective on the SVHN dataset. MAC-SSL also yielded superior results with a small number of labeled samples and an increased number of unlabeled samples (an increased $\mu$). Notably, it outperformed the conventional strong augmentation strategy on the CIFAR-10 dataset with 40 labeled samples, as well as on the CIFAR-10 dataset with 1000 labeled samples when $\mu =9$.

4. Discussion

The paper introduces MAC-SSL, which proposes a novel approach to leverage the valuable information within unlabeled samples in semi-supervised learning tasks. Unlike traditional methods that rely on pseudo-labels or soft labels to enforce consistency between strongly and weakly augmented unlabeled images, MAC-SSL incorporates a moderate augmentation step. This step combines the model outputs of moderately augmented unlabeled images with those of weakly augmented unlabeled images to generate pseudo-labels. Subsequently, the model outputs of strongly augmented images are enforced to be consistent with the pseudo-labels. Additionally, inspired by MixMatch, MixUP is adopted to combine the outputs of unlabeled images with those of labeled images, augmenting the data and ensuring consistency between the model outputs of the re-augmented images and the newly generated pseudo-labels derived from mixed labels or pseudo-labels.

The experimental results demonstrate the superior performance of MAC-SSL compared to existing methods, particularly in scenarios with limited labeled samples. MAC-SSL effectively leverages the valuable information within unlabeled samples, which other methods often overlook in their data augmentation techniques. MAC-SSL generates reliable positive sample pairs through three distinct augmentation techniques, enhancing the regularization benefits. Moreover, the integration of MixUP with augmented images and their corresponding labels or pseudo-labels improves the generalization capabilities of the model and facilitates efficient convergence.

Evaluation on the CIFAR-10, CIFAR-100, and SVHN benchmark datasets consistently showed that MAC-SSL outperformed the other methods, especially with limited labeled samples. For CIFAR-10, MAC-SSL achieved significant accuracy improvements over the second-best method, MixMatch, with increases of 6.82% and 7.02% when only 250 and 500 labeled samples were available, respectively. Similarly, MAC-SSL surpassed MixMatch by 16.58% on CIFAR-100 even with as few as 400 labeled samples. The experiments on the SVHN dataset further validated the effectiveness of MAC-SSL in fully leveraging unlabeled samples for a superior performance.

The ablation studies provided insights into the roles of different components in MAC-SSL and the impacts of various parameters. Utilizing unlabeled samples through MixUP was found to be crucial, as removing MixUP solely on unlabeled samples resulted in an even greater performance loss compared to not using MixUP. Furthermore, MAC-SSL demonstrated superior results with a small number of labeled samples and an increased number of unlabeled samples, highlighting the importance of leveraging a large volume of unlabeled samples. The choice of a strong augmentation strategy, the sample ratio hyperparameter, the temperature sharpening, and the combination of weak, moderate, and strong augmentations also impacted the performance of MAC-SSL, showcasing the effectiveness of these design choices.

While the increased augmentation consumes more computational resources, the performance improvements achieved by MAC-SSL justify the additional cost. Future research can explore strategies to optimize the computational efficiency of MAC-SSL without compromising its effectiveness, such as excluding backpropagation on weakly augmented unlabeled samples. Additionally, the current trend of using large-scale models suggests that employing pre-trained models will lead to further breakthroughs in the future. Finally, larger and more complex datasets such as ImageNet [47], as well as specialized and widely used datasets for semi-supervised learning such as medical image datasets, are also within our scope of consideration. In the future, we plan to conduct more extensive experiments on these datasets.

In conclusion, the experiments and ablation studies demonstrated the superiority of MAC-SSL in semi-supervised learning scenarios, particularly with limited labeled samples. MAC-SSL effectively leverages the valuable information within unlabeled samples, resulting in improved classification performances across multiple benchmark datasets. The integration of moderate augmentation, collaboration between weak and moderate augmented unlabeled samples, and the use of MixUP enhance the regularization benefits and generalization capabilities of MAC-SSL. MAC-SSL makes a valuable contribution to the field by addressing the challenges associated with limited labeled data, demonstrating its efficacy in improving classification performance. Future research can explore extensions and modifications to further enhance MAC-SSL’s performance or investigate its applicability in other domains and datasets.

5. Conclusions

Herein, we proposed MAC-SSL, a semi-supervised learning method that leverages contrastive learning with multiple augmentation strategies. Through extensive comparative experiments in the field of semi-supervised learning, MAC-SSL demonstrated remarkable performance improvements compared to other methods, showcasing its effectiveness and generality. Ablation experiments further emphasized the significance of each component in MAC-SSL and uncovered its potential for further enhancements, such as achieving a better performance with a larger $\mu$. Moving forward, we are interested in exploring the effectiveness of MAC-SSL in different domains. Additionally, we aim to streamline the algorithm while maintaining its performance and investigate methods to ensure its effectiveness in scenarios with fewer labeled samples.

In future work, the application of MAC-SSL to different domains and its effectiveness in those domains will be explored. Additionally, efforts will be made to simplify the algorithm while maintaining its performance to improve usability. Furthermore, research will be conducted to ensure the effectiveness of the method in scenarios with even fewer labeled samples. Lastly, in an era of large models, the utilization of pre-training models will also be further explored.