1. Overview
Combinatorial issues that deal with network optimization problems have motivated several branches of computational science, also thanks to the huge real-world contexts in which they find application (e.g., bioinformatics [
1], sensor networks [
2], biology [
3], information retrieval [
4] and, more recently, natural language processing [
5]). Most of these problems are intractable (NP-hard). Minimum Vertex Cover (MVC) or its weighted version (MWVC) [
6,
7,
8], Maximum Clique (MC) [
9,
10] or Traveling Salesman (TS) [
11,
12] are notable examples of NP-hard problems [
13] over graphs for which various approximation algorithms or heuristics solvers have been proposed as effective alternatives to exact exponential methods [
14,
15].
In recent years, the use of Deep-Learning (DL) approaches has been proposed for solving NP-hard problems over graphs in a purely data-driven fashion. Among these, the most notable are Pointer Networks [
16] and Neural Networks with Dynamic External Memory [
17].These approaches are classical end-to-end learning frameworks based on the usage of neural networks extended with recent DL mechanisms such as neural attention or external memory. Nevertheless, the general DL architectures and the strictly data-driven learning approaches proposed in these pioneering works have been criticized for being too generic and for not considering the peculiarity of different graph problems [
18], thus not providing theoretical guarantees. More effective research investigation directions are based on using Reinforcement Learning (RL) [
18,
19,
20,
21,
22] or Graph Neural Networks (GNNs) [
23,
24] not in an end-to-end fashion, but with a two-stage approach: a first stage in which they learn a representation of the graph (with DL techniques like GNNs, in a representation learning fashion), and a second stage in which this representation is used to build the solution to the combinatorial optimization problem using an autoregressive machine-learning-based procedure (e.g., with RL), or using greedy algorithms or local search. It has been shown that representation learning-based approaches are better in building solutions to combinatorial optimization over graphs with respect to end-to-end approaches, but the majority of the proposed research shares some drawbacks [
25,
26]:
In many graph-based combinatorial optimization problems, the global information of the graph is needed for solving the problem; however, existing graph learning models, especially GNN, only aggregate local information from neighbors. Roughly speaking, this is because GNNs are based on the neural message-passing framework, i.e., to build node representations, they follow an iterative schema of updating node representations based on the aggregation from nearby nodes. The role of the aggregation function is to aggregate information from its neighborhood and pass on the information to the next layer. More global information can be obtained by adding more message-passing layers; however, this can cause over-smoothing, a non-trivial phenomenon according to which, after several iterations of GNN message passing, the representations for all the nodes in the graph can become very similar to one another. Therefore, neural message-passing iterations are generally kept low, thus not effectively encoding global information of graphs.
General DL architectures are used to solve different types of combinatorial optimization problems (MVC, TS, MC); however, each problem has its own characteristics and constraints. Encoding inductive bias into DL architectures to better capture the characteristics of the combinatorial optimization problem is often missing.
Many approaches do not integrate or take into account traditional heuristics even though identifying the operations of traditional heuristics of a combinatorial optimization problem and integrating such operations appropriately into the learning procedure or in the methodology can benefit the learning-based methods.
In this paper, we focus on the MVC problem, a traditional NP-hard optimization problem of finding the minimum sized subset
of nodes of an undirected graph
such that every edge in
G has at least one endpoint in
. The interest in the MVC problem is motivated by its many real-world applications and by its recent extension to the less explored context of temporal networks [
27]. Theoretical analyses indicate that the MVC problem is NP-hard and the associated decision problem is NP-complete [
13]. Moreover, it is NP-hard to approximate MVC within any factor smaller than
for any
assuming
[
28] and within constant factor smaller than two assuming the Unique Game Conjecture [
29], although an approximation ratio of
has been proposed [
30]. Despite this, MVC has several simple 2-factor approximations: e.g., in [
31], where the authors propose a local-ratio algorithm for computing an approximate vertex cover; the algorithm greedily reduces the costs over edges, iteratively building a cover. The worst-case runtime of this implementation is
, where
n is the number of nodes and
m the number of edges in the graph. An implementation of such an algorithm is available in [
32]. If, on the one hand, 2-factor approximations are very useful for their low complexity, on the other hand, they produce results that are quite far from the optimum. Various exact algorithms or heuristic algorithms have been proposed to overcome this problem. Exact methods, which mainly include Integer Linear Programming (ILP) [
33], branch-and-bound algorithms [
34,
35,
36,
37], and fixed-parameter tractable algorithms [
38] guarantee the optimality of their solutions, but may fail to give a solution within reasonable time for large or medium-size instances. Heuristic algorithms, like NuMVC [
39] and FastVC [
40], which are mainly based on local search, cannot guarantee the optimality of their solutions, but they can find satisfactory near-optimal solutions for large and hard instances within reasonable time. These heuristic-based approaches have become state-of-the-art for many real-world use cases, and they have also inspired heuristic-based algorithms for the weighted version of the problem [
41,
42]. More recently, as for other combinatorial optimization problems over graphs, the research trend for MVC has moved towards the adoption of DL techniques with RL as in [
21] or GNN as in [
23]. However, these solutions suffer from the main drawbacks of other DL-based approaches for combinatorial optimization over graphs, i.e., they build graph representations considering only local information, they adopt general DL techniques without customizing them according to the nature of the specific combinatorial problem, and they do not take advantage of the state-of-the-art heuristics for such problem by integrating them into the learning methodology.
In this research, we propose a custom DL-based approach to solve the MVC problem by addressing these three main challenges: (1) build a suitable graph representation at the node level using both global and local information; (2) customize a common DL approach based on attention to reflect the combinatorial structure of MVC problems; (3) integrate the DL methodology with state-of-the-art heuristics to take advantage of them. The proposed approach, which we named Attention with Complement Information (ACI), is based on an encoder–decoder architecture that adopts the attention mechanism and a memory network to build node representation exploiting both the adjacency matrix and its complement. In this way, (1) an MVC-biased representation of the graph is built considering both local and global information, and (2) we adapt a common DL approach to the MVC problem. We also propose to use the representation obtained within a state-of-the-art heuristic to produce a final covering set, thus (3) taking advantage of it, also from a theoretical perspective.
Our experimental results suggest that the proposed methodology can learn suitable node representation for combinatorial problems. Indeed, on the one hand, we tested our models against a fast 2-factor approximation algorithm and a widely adopted state-of-the-art heuristic, showing that, on average, the methodology is able to outperform both the 2-factor approximation algorithm and the heuristic in finding a vertex cover of the smallest possible size, scaling well also with larger instances, from the other, we explore the representation capabilities of our approach with visual artifacts, providing evidence of the fact that the methodology is able to represent nodes reflecting the combinatorial structure of the problem.
The remainder of the paper is organized as follows: in
Section 2, we provide the basic concepts from graph theory to understand the MVC problem, with a focus also on the attention mechanism and memory networks that have been adopted in the proposed solution. In
Section 3, we provide the details of our methodology, and in
Section 4, our experimental results are discussed together with training and test datasets, selected network hyperparameters, and evaluation metrics. Moreover, a discussion on the expressive power of the proposed methodology with respect to representation learning is reported; finally,
Section 5 suggests some hints on future research directions.
2. Basic Concepts and Problem Definition
In this section, we first introduce basic concepts about graphs and the MVC problem; then, we introduce the basics of the DL techniques adopted in this research.
Definition 1 (Graph)
. A Graph is a pair , where N is the set of nodes and E is the set of edges, such that each element of E is a pair of element of N.
An edge that links two nodes and can be denoted as . Moreover, if E is not a symmetric relation, the graph is said to be undirected, and if edges are not weighted, the graph is said to be unweighted. Since we focus on these kinds of graphs, in the following, we will generally refer to graphs as unweighted, undirected graphs.
At the node level, graphs can be represented by features that describe structural graph information. Node degree, i.e., the quantity of direct neighbors of a node (or the number of incident edges), is one of the most commonly used since it can naturally indicate the importance of a node within the graph. As for node-level description, graph-level features can be used. Among the most commonly used, density conceptually provides an idea of how much connected a graph is and is measured by the ratio between edges and nodes within a graph, . Another relevant concept is clique, i.e., a set of vertices, all pairs of which are adjacent.
Definition 2 (Minimum Vertex Cover)
. Given an unweighted undirected graph , a vertex cover is a subset of . A minimum vertex cover is a vertex cover of the smallest possible size.
This problem can be formulated as the following integer linear program:
where the objective function consists of minimizing the number of nodes belonging to the covering set, such that every edge of the graph is covered (
) and every vertex is either in the vertex cover or not (
).
With the above definitions we can state our objective as follows: Given an unweighted undirected graph , with N nodes and E edges and a minimum vertex cover of G, we want to find a parametric function which is able to map the input graph G to the set of covering nodes , .
The MVC problem does not have a unique optimal solution. The solution, i.e., the minimum covering set, mainly depends on the order according to which edges or nodes are scanned to determine whether they should be part of it.
As an example, a very simple approximated approach to solving the problem consists of starting from the set
E of all edges, where edges are arbitrarily ordered (suppose, without loss of generality, that they are named with capital letters, and they are ordered lexicographically). The approach consists of iteratively scanning this set so that at each iteration, edge
is picked, and nodes
u and
v are added to the final covering set
. Then, all the other edges in
E, which are either incident to
u or
v are removed. This is carried out until
E is empty.
represents the final solution.
Figure 1 shows an example of this. By applying the described approach to the left-side graph, assuming that edges are ordered lexicographically since edge
is the first scanned, the results would be
. By changing the name of the edges (right-side graph) and applying the same procedure using the lexicographical order, the first scanned edge would be
. Thus, the final result would be
.
In general, iterative algorithms (either approximated or exact) do not pick edges or nodes completely at random, but they order them according to some heuristic or criterion as in [
37,
39,
40]. However, it is clear that, according to these approaches, the order according to which edges are picked from the initial set highly influences the final result since the fact that a node is already part of the final solution has an impact on the fact that another node should be part of it. In our example in
Figure 1, the fact that node 3 is already part of the solution implies that node 4 should not be part of it and vice versa. Informally, this means that, given an ordered sequence of nodes, the probability that a node is part of the final solution depends on the probability that the previous nodes in the sequence are already part of the solution.
Thus, given a sequence of nodes, , we want to model the probability of the event “ is part of the covering set” for each , assuming that this event is conditioned to each event “ is part of the covering set” for each . Supposing that each event can be described as a random variable , what we want to model, according to probability theory, is the joint probability distribution of all the random variables , which according to the chain rule, can be modeled as . Moreover, we can consider that the probability distribution of the covering nodes can be represented as a sequence of nodes ordered according to their probability of belonging to the covering set. Let us call this sequence . The probability of belonging to the covering set is, of course, determined by the representation of nodes itself. Let us call it . Indeed, we assume that each node , with index i, can be represented as a vector according to a parametric function that maps each input node to a latent representation . According to this, the previous conditioned probability distribution is evaluated on a sequence of nodes conditioned by their representation .
We can now formally define the problem that we want to solve.
Problem 1 (Minimum Vertex Cover Biased Nodes Embedding)
. Given a graph , with and a training pair , where is a sequence of node embeddings, representing the latent representation of nodes, and is a sequence of nodes, we want to model the conditional probability using a parametric model to estimate the terms of the probability chain rulelearning the parameter of the model by maximizing the conditional probabilities for the training set In this way, we reduce the MVC problem to a binary classification problem, i.e., given a graph as input, we want to assign to each node of the graph a probability term such that the node is assigned to the covering set if and only if the value of the probability term is higher than a given threshold value (e.g., 0.5).
2.1. Attention
The attention mechanism was introduced by Bahadanau et al. [
43] to improve the performance of encoder–decoder models for machine translation. Encoder–decoder models work on an input sequence by first building a compact and meaningful representation in a latent space and then using that representation to construct the target output sequence. Before the introduction of attention, such models worked focusing on the entire input sequence, giving equal importance to all its parts. In general, given an input sequence
, the role of the encoder is to generate an embedded representation
for each
of the sequence. Given this representation, the role of the decoder is to produce the target output
by focusing on
and on the previous output
of the decoder by applying a function
like a feed-forward neural network,
.
In general, we can think of feed-forward neural networks as stacked parameterized linear models to which a non-linear activation function is applied. Thus, given an input
and a single parameterized linear model
, also known as hidden layer, the output
of a feed-forward neural network is:
where
and
are learnable weight matrices for input-to-hidden and hidden-to-output connections, respectively,
and
are learnable bias parameters,
g is a non-linear activation function, like tangent-hyperbolic function used to add non-linearity, and
f is a function, like a SoftMax function for classification problem, used to convert the output of the feed-forward neural network to a conditional probability distribution over the input. In the following, we will refer to the hidden-layer transformation
also as
dense layer, and we will mainly use as activation function the ReLU activation function [
44].
In the case of the original encoder–decoder model, this function directly uses
as it comes out from the encoder without weighing it with respect to a score value that represents the relevance of that part of the input within the sequence. To assign weights to take care of differences within the input sequence, Bahadanau suggests computing a
context vector to be fed to the decoder at each timestamp. Equation (
5) shows the procedure to compute this context vector
.
First, it is necessary to calculate an alignment scores , computed applying a function , like a feed-forward neural network, to each encoded hidden state and to the previous decoder output , so that the more relevant input of the sequence is in producing the current output (i.e., the more an input is aligned to an output), the higher its value is. The context vector is then computed by a weighted sum of all T encoder hidden states, where the weights are obtained by applying a SoftMax normalization to the alignment score. In this way, instead of passing directly the hidden state together with the previous decoder output state to the decoder to compute the output, the decoder is fed with a vector that represents the input but which is scaled according to its importance (expressed by ) in the input sequence to determine the output.
This mechanism has been reformulated into a general form that applies to any sequence-to-sequence task [
45], making use of three main components, namely
queries,
keys and
values, such that query corresponds to the previous decoder output
, while values and keys to the encoded inputs
. The idea is that of trying to identify, given the previous output state
(the query), which encoded inputs
(the keys) are the best to produce the new output state and, once identified, to compute the relative weights (alignment scores) using the previous output state
(the query) and the encoded inputs
(the values, corresponding to the identified key). According to this framework, the attention function can be described as mapping a query and a set of key-value pairs to an output. The output (the context vector),
, is computed as a weighted sum of the values
, where the weights,
, assigned to each value is computed by the alignment score of the query with the corresponding key,
. The attention function can, thus, be computed on a set of queries, keys, and values simultaneously, packed together into matrices
Q,
K and
V. The matrix of outputs is computed as
where
is the dimension of queries and keys. This model can also be enhanced with
positional encoding, i.e., information about the relative or absolute position of the tokens in the sequence, to let the attention scores also focus on the order of the elements in the sequence.
2.2. Memory Networks
Despite feed-forward neural networks, recurrent neural networks (RNNs) [
46] are used to model sequential data and to tackle time dimension. RNNs process one element of the input sequence at a time, and they model short-term dependencies by building their output, taking into account both the input at a given timestamp and the network output at the previous timestamp. Thus, RNNs model short-term dependencies using backward connections from a hidden layer of the network to the previous one, i.e., the state of a hidden layer
(with
) depends both on the input
(with
) at a given timestamp
t and on the previous hidden state of the network
. A non-linear transformation of this contributes to defining the final output of an RNN as described in Equation (
4):
where
,
and
are learnable weight matrices for hidden-to-hidden, input-to-hidden and hidden-to-output connections, respectively,
and
are learnable bias parameters,
g and
f functions as in the feed-forward neural network.
Long short-term memory (LSTM [
47]) networks have been proposed to extend to longer time periods, the possibility to take into account time dependencies. In a current LSTM, “past relevant inputs” are stored in a cell memory vector, which is determined by
where
input gate ,
forget gate and
output gate are functions with values in range
, that, respectively, determine the quantity of input, past information and current hidden state to be stored into the cell memory, and thus to be used to produce the output.
∗ denotes element-wise multiplication, is the previous cell value, while is the candidate value for current cell memory, and is the final hidden state.
In LSTM, the forget gate plays a crucial role in enabling the network to capture long-term dependencies. If , previous memory values will be preserved; thus, even distant inputs can take part in output computation. On the other hand, if , the connection with previous cell values is lost. Thus, the model tends to forget long-term events and to remember only short-term ones.
Given an input sequence
, it has been shown [
48] that LSTM can be used to model the conditional probability
as a function of the network output
as:
4. Experimental Evaluation
To train the neural model proposed, we create a synthetic dataset composed of randomly generated graphs. The final training dataset is composed of 3000 graphs for training and 600 graphs for validation with a random number of nodes between 5 and 2000. Half of the instances are relatively simple, with a random number of edges between the number of nodes itself and 1.5 times the number of nodes, i.e., low-density instances, and half more complex, with a random number of edges between 5 and 500 times the number of nodes, i.e., high-density instances. Given the number of nodes and the number of edges (iteratively extracted from a uniform distribution as described above), instances are built by choosing a graph uniformly at random from the set of all graphs with the given number of nodes and the given number of edges according to the method described in [
50]. For each graph from the simple instances, we compute the cover using a branch-and-bound algorithm [
51] to solve exactly the integer linear program formulated in Equation (
1), setting as upper bound the initial number of nodes (updated each time to the size of the best solution found), as lower bound the dimension of the current vertex cover plus the dimension of the best vertex cover found for the subproblem considered and starting search from the node with highest degree in the subproblem considered. For each graph from the hard instances, instead, we compute the cover using the FastVC algorithm [
40] by setting a cutoff time of 10 s, a maximum number of iterations of 30, and, since FastVC is non-deterministic, for each graph we run the algorithm 5 times and use as ground truth the best solution found. We decided to choose two distinct approaches to build the ground truth first because there is not a publicly available dataset with exact solutions that could fit our case and then because the ILP exact solver can only produce results for very low-density simple instances since the computation time for hard instances is too high for development. Thus, we decided to use simple cases with exact solutions and hard cases with approximate solutions, supposing that if the model can generalize well, simple instances with exact solutions may also let the model learn to produce better solutions for hard cases. We decided to use FastVC since it has been proven in [
40] that this is the best-performing heuristic with respect to the other heuristics proposed, like NuMVC [
39].
For the same reason, to test the methodology, we build 3 distinct datasets:
4.1. Hyperparameters and Training Results
As far as the common neural network’s hyperparameters are concerned, the network has been trained for 100 epochs, with a batch size
and Adam [
53] with initial learning rate
as optimizer. Both the
Input Embedding and the
Positional Embedding produce a node representation with an embedding dimension
. In the encoder, after the ACI layer, we stacked three dense layers that convert the dimension of the context vector first to
(with
N maximum number of nodes in the graphs, i.e., 2000), then to
and finally produce and embedded vector of size
. In the decoder, we used only one LSTM layer that converts the dimension of the embedded vector from
to
.
We trained the network on a MacBook Pro (2017) with 16 GB of RAM and a 3.1 GHz Intel Core i7 quad-core CPU, and it takes 7 h and 32 m to complete the training.
To ensure that the neural model actually learns how to assign good probability estimates, we measure the network with respect to the classification task for which it is trained. As described in
Section 3.3, we train the network minimizing the negative log-likelihood loss function over the log-SoftMax activation function, measuring the performance comparing, for each node of the input graph, the predicted class probability (1, if the corresponding node is a covering node, 0 otherwise) with the desired output. Thus, to be sure that the model properly learns how to assign such estimates, we measure the model using the common metrics for binary classification problems:
Accuracy,
Precision and
Recall, by considering a threshold value for the probability estimates of 0.5 (i.e., if the probability estimate is higher than 0.5, the outcome of the model is 1. Otherwise it is 0). Accuracy measures how often the model correctly predicts the outcome and is measured as the ratio between the number of correct predictions (the sum of true positives and true negatives) and the total number of predictions. Precision measures how often the model correctly predicts the positive class and can be computed as the ratio between the number of correct positive predictions (true positives) and the total number of instances the model predicted as positive (the sum of true and false positives). Recall measures how often the model correctly identifies positive instances from all the actual positive samples in the dataset and can be computed as the ratio between the number of true positives and the number of positive instances (the sum of true positives and false negatives). We measured these three metrics over the two synthetically generated datasets, which, considered together, are composed of a total of 92 graphs with 92,650 nodes. Therefore, these metrics are calculated considering a support of 92,650 samples. Results are shown in
Table 1. As we can see, the results show a good percentage for all the metrics (always higher than 82%). This confirms the fact that the probability estimates produced by the neural model actually reflect the real ones. It is important to note, however, that such metrics are not suitable to evaluate the entire methodology with respect to the MVC task for two main reasons: (1) the model is trained to produce probability estimates in a data-driven fashion, thus without constraints that force the final classification to be a minimal cover (this is achieved by the iterative algorithm proposed described in the following); (2) the MVC problem does not have a unique solution, thus even if the model were able to produce probability estimates that result in a minimal cover, if the minimal cover estimated is not exactly the same as the one given as ground truth to be compared against, it would result in poor performance metrics. Therefore, to measure the entire methodology, we rely on a different metric (described in the next paragraph) that takes these aspects into account.
4.2. Percentage Improvement
To measure the performance of our model for each of the three datasets, since MVC sets may not be unique, we compare the length of the covering sets produced by our ACI-based methodology and by the FastVC heuristic with the length of the covering sets produced by the baseline algorithm used to build the ground truth (ILP solver for the first test set or the 2-factor approximation for the second and third test set), normalizing the distance with respect to the biggest cover obtained by the baseline and the compared method as in the following equation,
where
I is the percentage improvement,
is the size of the cover produced by the corresponding baseline algorithm, and
is the size of the cover produced by the compared methodology.
To compare the results of our methodology with the state-of-the-art solutions FastVC heuristic, we set a cutoff time of 10 s, and a maximum number of iterations of 30, and we ran the algorithm 5 times and used the best solution found.
Table 2 reports the comparison between the results of our methodology and the FastVC heuristic for Dataset 1 and Dataset 2. In the first case, the average improvement represents the average distance of the computed solution from the exact solution. In this case, our methodology can outperform FastVC in better approximating the solution. Indeed, the ACI-based method allows the obtaining of an average distance of −7.21% against the larger distance of −10.61% of FastVC. In the second case, instead, both our methodology and the FastVC heuristic can outperform the 2-factor approximation algorithm, our solution by a percentage of 3.26% and the FastVC heuristic by a percentage of 2.70%. Thus, the proposed methodology can also outperform the FastVC heuristic in this case. These results confirm the fact that the neural model achieves the task of producing probability estimates that actually reflect the combinatorial structure of the problem since, if used together with the iterative algorithm as heuristic to compute a minimal vertex cover, on average, they produce a better approximation than the 2-factor approximation algorithm and than the FastVC heuristic. Another interesting consideration concerns computation time. Clearly, the exact ILP solver is the slowest algorithm, even though instances are relatively small, while the 2-factor approximation is by far the fastest. When it comes to our proposed solution, by analyzing the results, we can see that the computation time is very similar both with low-density instances and with high-density instances. It is important to consider that, on average, 0.19 s are required by the neural model at inference time to produce the node score probability. The rest is used to compute the covering set. The fact that the average time does not increase too much from Dataset 1 with simpler instances to Dataset 2 with harder instances means that our methodology, in general, scales well. As far as FastVC is concerned, the average time considered is the required time to compute the cover, thus the sum of the required times for each run of the algorithm (5 in total for each instance). We can see that, in this case, with low-density instances, the algorithm is very fast. With high-density instances, the required time is almost quadrupled. Of course, the average time is still relatively small; however, this highlights the limits in the scalability of such an algorithm.
The same considerations can be done by analyzing the results over Dataset 3, composed of the publicly available DIMACS benchmark graphs [
52]. The results are shown in
Table 3. On average (average results are highlighted in the last line), the ACI-based approach produces a percentage improvement of 2.91% with respect to the 2-factor approximation algorithm, while the FastVC heuristic (with the same configuration and number of runs) obtains a percentage improvement of 1.43%. Thus, in this case, even though both algorithms produce a better covering set with respect to the 2-factor approximation algorithm, our proposed solution can also outperform the FastVC heuristic. Even considering execution time, results over Dataset 3 are in line with results over Dataset 1 and 2. Indeed, on average, the ACI-based method requires 0.25 s, while FastVC requires 0.33 s (against the 0.02 s of the 2-factor approximation). It is important to notice that actually, on small instances (e.g., johnson8-2-4), the time required by FastVC is very small compared with the ACI-based method; however, it increases a lot when considering harder instances (e.g., C2000-5, hamming10-2) differently from the ACI-based method where the increase in the computation time is limited. This further confirms the fact that our approach scales better than FastVC with harder instances.
It is important to note that our methodology only fits for graphs with no more than 2000 nodes. This is not a strong limit for many real-world applications like network design, sensor network, resource allocation, or text tasks [
2,
4,
5]. To test the methodology with larger graphs, it would be necessary to retrain the neural model by modifying the maximum size of the graph to be expected as input. However, we did not explore this aspect of the research further.
4.3. Nodes Representation
Another important aspect of our approach concerns the capability of the network, particularly of the ACI-based method, to produce a good representation of the nodes with respect to the optimization target defined by the MVC problem. To understand whether the network can perform a proper mapping of the embedded input nodes into a d-dimensional space, we plot some points considering the representation of the nodes as obtained from the output of the ACI layer of the network, namely the context vector
U. Since the network has been trained to produce an encoding embedding in a 32-dimensional space, we only visualize a scatterplot of the nodes by taking two of the 32 components at a time. We only visualize the results with respect to the first four components since the behavior is similar for the others as well. In
Figure 4, we can see the representation of the nodes of a graph with 25 nodes and 50 edges. The orange points are the points associated with covering nodes according to the exact solution, while the blue ones are those that do not correspond to covering nodes. In general, we can see that the network is able to map the points in a space where covering nodes and non-covering nodes belong to different regions (almost linearly separable) and with a clear ordering.
This representation is built considering node features so that similar nodes are closer in this representation space.
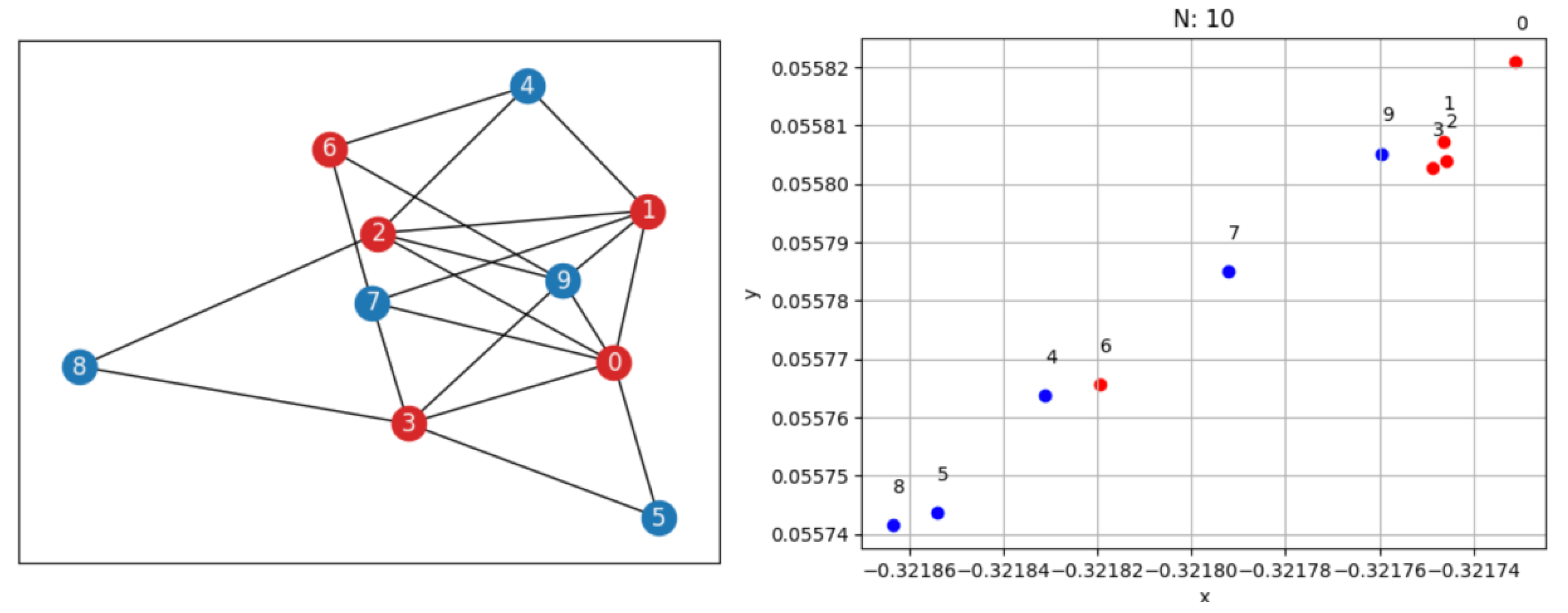
Figure 5 shows an example of this. In the picture, we can see the input graph (with 10 nodes and 15 edges), with covering nodes represented in red and non-covering nodes represented in blue. Together with the graph, the representation of the nodes (with respect to 2 random dimensions of the context vector) is visualized by tagging each point with the corresponding index of the node and color. From the picture, we can see that, as an example, nodes 1 and 2 are close to each other. Indeed, they both have a degree equal to 5, and they are both connected to nodes 4, 9, and 0. Therefore, they are very similar. Analogous reasoning can be done for node 3, which is very similar to 2 and 1, and for nodes 8 and 5, which are very similar to each other. Moreover, if, on the one hand, this representation is interesting and reasonable, the final probability estimates which are built considering this representation, do not perfectly reflect this representation since, as an example, considering the graph in
Figure 5, nodes 9 and 8 have a higher probability score with respect to node 0 (the final order with respect to the probability score is: 1, 3, 2, 9, 8, 0, 6, 4, 5, 7). This means that the decoder component of the network also plays a very important role in producing the final result. Moreover, the order produced is quite far from the order that we would obtain, considering only the degree. Thus, it is not surprising that the result obtained using these probability estimates in the ConstructVC algorithm is different from the result obtained using the degree (as for FastVC).
The fact that our methodology outperforms the FastVC heuristic, instead, makes clear that the implemented approach manages to reflect the combinatorial structure of MVC problems and that the probability estimates produced by our neural model are a better driver for building the MVC with respect to node degree. This is due to the fact that, on the one hand, we build node representations considering both local and global information by applying the attention mechanism directly to the adjacency matrix, and on the other hand, it is due to the fact that the customization proposed, which reflects common heuristics procedures to build the MVC, actually induces a good bias to represents nodes with respect to the specific problem considered. Specifically, these results show that the proposed customization of the attention mechanism manages the task of assigning a higher score to nodes that should be part of the MVC set, making the iterative algorithm proposed a good approach to build the final covering set.
5. Conclusions and Future Works
In this paper, we have presented an approach to solving MVC problems over graphs, mainly using attention. In designing the approach, we tried to tackle three main issues related to the DL-based approach for combinatorial optimization over graphs: (1) build a suitable graph representation at node level using both global and local information; (2) customize a common DL approach to reflect the combinatorial structure of the MVC problem; (3) integrate the DL methodology with state-of-the-art heuristics to take advantage of them.
To cope with issues 1 and 2, we proposed a methodology that makes use of what we called Attention with Complement Information, i.e., a mechanism of attention which first of all is applied over graphs adjacency matrix to use both local and global information, and then that takes as input not only the matrix itself but also the complement of the matrix, following the intuition, commonly implied also by many state-of-the-art heuristics, that in order to identify candidate nodes to a covering set, it could be useful to know their interaction with other nodes and that the complement of such interaction may provide a better scoring when two nodes have similar interactions. We then use the output of such attention mechanism, properly transformed, as input to an LSTM-based decoder network followed by a SoftMax activation layer to produce the final probability distribution.
We showed that our methodology can outperform not only a common 2-factor approximation algorithm for MVC but also a widely used state-of-the-art heuristic known as FastVC both on low-density graphs and on higher-density graphs. Moreover, if our approach is relatively slower with low-density graphs with respect to both the 2-factor approximation algorithm and the FastVC heuristic, it scales much better than FastVC on higher-density graphs. This represents a great advantage, also meaning that for MVC tasks on graphs of comparable size to the ones used to train our neural model, our methodology should be preferred to other state-of-the-art approaches.
Finally, we also proved that our attention mechanism with complement information manages to draw a proper representation of the nodes according to the combinatorial nature of the MVC problem. This is extremely important since it demonstrates that our work manages to address the three main issues of the DL-based approach for combinatorial optimization over graphs. As far as we know, this makes our proposal one of the firsts to address these main challenges successfully. Nonetheless, another advantage of our methodology is that we provide a new validated method to build node embeddings in a meaningful way. The embeddings produced, indeed, could be used and tested also for different task-related MVC problems. In this research, we have explained that there is a strong similarity between the iterative algorithm proposed to build the final solution of our method and the iterative algorithm used by FastVC to initialize its solution. However, in FastVC, after initializing the solution, the authors propose to refine the solution by changing the nodes in the covering set according to a cost-effective heuristic called Best from Multiple Selections (BMS). Thus, a possible future direction of this work could be that of understanding how, by applying the BMS heuristic, we could improve the results and in which time.
We consider this work as a step towards a new family of solvers for NP-hard problems that leverages and customize DL properly, and, in particular, we will try to extend the results of such work also on the less explored context of temporal networks, where many combinatorial NP-hard problems, like the minimum timeline cover [
27,
54], do not have an approximate solution.