Abstract
The exploration of the energy landscape of a chemical system is essential for understanding and predicting its observable properties. In most cases, this is a challenging task due to the high complexity of such landscapes, which often consist of multiple, possibly hierarchical basins that are difficult to locate and thoroughly explore. In this study, we introduce a novel method, called IGLOO (Iterative Global Exploration and Local Optimization), which aims to achieve a more efficient global exploration of the conformational space compared to existing techniques. The method utilizes a tree-based exploration inspired by the Rapidly exploring Random Tree (RRT) algorithm originating from robotics. IGLOO dynamically adjusts its exploration strategy to both homogeneously scan the landscape and focus on promising regions, avoiding redundant exploration. We evaluated IGLOO using models of two polypeptides and compared its performance to the traditional basin-hopping method and a hybrid method that also incorporates the RRT algorithm. We find that IGLOO outperforms both alternative methods in terms of efficiently and comprehensively exploring the molecular conformational space. This approach can be easily generalized to other chemical systems such as molecules on surfaces or crystalline systems.
1. Introduction
Cost functions appear in many fields of science, economics, and engineering, wherever issues concerning the optimization, typically the minimization or maximization, of some (scalar) quantity—the so-called cost—are raised [1]. Classical examples are the cost of a business strategy, the fitness of biological species or individuals, the objective function value of a trajectory in an optimal control problem, or the potential energy of an arrangement of atoms in space. Given a state space of the system of interest, the cost function assigns a real number to each state of the system; such a state is often called a microstate, configuration, or conformation (in the case of chemical systems), or a legitimate solution to a combinatorial optimization problem. Here, the state space can be a discrete set of states, like the nodes of a graph (often called a metagraph in the context of cost function analysis [2]), or exhibit a continuous structure, like a subspace of . Together with the neighborhood structure of the state space—in the case of a discrete state space, the connectivity of the metagraph—, the cost function can be represented by a so-called cost function landscape, which usually contains a multitude of local minima that are separated by a complex barrier structure. In this context, one should note that the choice of connectivity or neighborhood is essentially left to the researcher him/herself; since the choice of the neighborhood implicitly defines the dynamics of the system in most cases, one often speaks of the neighborhood in terms of the moveclass of the system—a terminology derived from the description of the exploration algorithms that are designed to study the landscape. Often, the number of local minima grows exponentially or even factorially with some parameter that represents the size of a system, such as the number of cities in a travelling salesman problem [3,4], the number of spins in a magnetic material, or the number of atoms in a cluster or molecule [5]. For more general aspects of cost function, fitness, or energy landscapes, we refer to the literature [1].
In the case of a chemical or physical system, one frequently encounters the (potential) energy of the system as the quantity to be studied or minimized, and thus one speaks of the energy landscape of, e.g., the molecule of interest. Furthermore, in the case of such systems, the landscape is of much greater importance than just as a tool to find the lowest energy, since the laws of physics that describe the evolution of the system are embedded in the local shape of the potential energy surface (PES): the gradient of the potential energy yields the forces acting on the atoms, and thus prescribes the subsequent trajectory of, e.g., the atoms belonging to a molecule, such as the vibrations or translational motion of the molecule.
Thus, the study of the energy landscape of physical and chemical systems usually goes far beyond the obvious task of identifying the global minimum; for example, all low-energy local minima surrounded by high enough barriers on the landscape correspond to (meta)stable configurations of, e.g., the molecule, which can be observed or synthesized, in principle, or transformed into each other. Therefore, determining all low-energy minima of a chemical system ranks as a goal of similar importance as finding the global minimum [1].
Furthermore, after the initial step of finding not only the global minimum but also as many side-minima as possible, one would study the energy barriers and entropy barriers of the system separating these minima. This requires the design and implementation of new classes of algorithms that, e.g., identify saddle points between local minima [6,7], or measure the entropic barriers between basins for portions of the landscape restricted to lie below energy lids, such as the threshold algorithm [8].
However, in a large number of instances, just identifying the global minimum without any prior information about the cost function landscape is already a highly nontrivial task that typically requires an enormous computational effort. This is due to the large size of the state space—prohibiting an exhaustive search via testing every microstate—and due to the complexity of the barrier structure, which makes straightforward steepest descent gradient-based minimizations (for continuous landscapes) or random downhill walks ineffective. Although some improvement is achieved by combining such greedy downhill algorithms with a systematic (nearly exhaustive) grid-like selection of starting points for the local minimization [9], this combination is still not very efficient in identifying the global minimum of the system, due to the enormous size of the state space and the large number of local minima present. Moreover, many of these minima would be rediscovered many times, thus resulting in a massive oversampling of the landscape’s minima.
As a consequence, researchers in many fields have developed a plethora of global optimization algorithms, many of which are variations of some “classical” ones, such as genetic algorithms (GA) [10], simulated annealing (SA) [11], or branch-and-bound algorithms (BB) [12]. Among these are the bounce algorithm [13], the great-deluge algorithm [14], threshold accepting [15], particle swarm optimization [16], the tabu algorithm [17], thermal cycling [18], and evolutionary algorithms [19,20,21], just to name a few—for an overview, we refer to the literature [1,22,23,24]. Many of these methods are inspired by physical processes, e.g., molecular dynamics simulations [25,26] or thermal cycling [18], and by biology, e.g., the evolutionary [19] or genetic algorithms [10,27], while others are based on general energy landscape considerations as, e.g., the great-deluge [14] or the tabu [17] algorithms.
These basic—in principle generally applicable—algorithms are often specially adapted to certain classes of systems and energy landscapes, e.g., for the prediction of the conformers of molecules, such as the rotamers of chain-like molecules such as proteins or polysaccharides. Since one usually restricts the structure generation to molecules with a given bond network, only limited changes in the bond lengths are allowed, and the main degrees of freedom that are varied during the search are the bond angles and dihedral (torsion) angles. Ideally, one would compute the energy on the ab initio level. However, because of the high computational expense of quantum mechanical calculations, one commonly employs empirical molecular modeling potentials instead, possibly adding penalty terms that restrict the bond lengths and angles to certain “allowed” ranges which are physically and chemically sensible—according to experimental data and/or results from ab initio calculations. Such limits can be either implemented as parts of the energy function or via the moveclass, i.e., no new test configuration is allowed that violates these constraints. Moveclasses with such constraints on the allowed configurations are sometimes called “rule-based conformation generators” [24]; they are employed in the context of molecular structure prediction by, e.g., the OMEGA [28] method; for a review of these and other approaches, we refer to the literature [24].
Trying to find the optimal combination of computational speed, quality of the candidates—both regarding their energy and the accuracy of the parameters of the physical structure obtained—, and diversity of the solutions in the set of generated candidates, is a great challenge for systems that exhibit complex multi-minima landscapes. In particular, the goal to explore a wide range of the state space without losing much computational time by having to laboriously cross many energetic barriers as in, e.g., MD simulations, has led to the introduction of algorithms that attempt to perform large moves on the landscape without wasting too much time in exploring uninteresting high-energy regions of the landscape. Such so-called jumpmoves are common features of many modern algorithms, and an optimal choice of the moveclass is crucial for the success of a global optimization procedure [8]; for example, one class of searches which combines every jumpmove automatically with a local deterministic (gradient-based) or stochastic (downhill random walk) minimization, and therefore moves from local minimum to local minimum, has been called the basin-hopping algorithm (BH) [29,30]. Similarly, the genetic algorithms, which belong to the class of multi-walker algorithms that generate new states from two (or more) old states by combining their parameter values, are nowadays often combined with a local minimization of the newly generated state [31]. Nevertheless, oversampling is still a major problem. Even though the multiple discovery of the same minima is often interpreted as the heuristic criterion of the success (sometimes called “convergence”) of the global optimization, thus turning oversampling from a bug into a feature, performing orders of magnitude more local optimizations than necessary greatly reduces the efficiency of the search algorithm.
Due to the wide variety of fields where global optimizations of cost functions take place, many of these algorithms have been re-invented, or have been transferred from one area of applications to another, where one often has to adapt the original algorithm to the specific aspects of the new class of systems under consideration. An example of such a transfer with adaptation is the application of the RRT (Rapidly exploring Random Tree) algorithm [32], which was developed in the field of robotics to solve the so-called motion planning problem [33], to the field of chemistry. Indeed, solving the robot motion planning problem requires algorithms to explore the state space of the robot system aiming to find feasible trajectories between an initial and a final state. The same type of algorithms, with some adaptations, can be applied to explore the energy landscape of atomic or molecular systems [34].
Of particularly great potential to yield a qualitative and not only quantitative improvement in the development of global optimization algorithms are those methods which combine tools and (sub)-algorithms from different fields into a new type of algorithm. In this study, we present the IGLOO (Iterative Global Exploration and Local Optimization) algorithm, which combines concepts from the RRT algorithm and the threshold algorithm to efficiently explore the low-energy regions of the landscape. In the past, an earlier version of this algorithm has been successfully applied to the study of disaccharide molecules on metal surfaces, predicting the shape of the molecules on the surface and thus allowing an interpretation of the STM (Scanning Tunneling Microscopy) images obtained in the experiment [35].
In the present investigation, we analyze the performance of this algorithm in detail, using two chain-type molecules as examples. The outcomes of these global optimizations are compared to the performance of two similar types of algorithms, a classical basin-hopping algorithm [36] and a hybrid BH-RRT algorithm [37].
2. Materials and Methods
This section is structured in a top-down manner. First, the main principles of the global optimization algorithms considered in this comparative study are described. They are presented from the simplest to the most complex one: basin-hopping (BH), hybrid BH-RRT (HYBRID), and IGLOO. In our implementation, and for the sake of a fair comparison, these algorithms apply the same techniques to perform sampling and local optimization. These techniques as well as other implementation details are presented in the second subsection. The last subsection describes the molecular model and potential energy function considered for this investigation.
2.1. Global Optimization Algorithms
2.1.1. Basin-Hopping (BH)
Basin-hopping is the popular name [30] given to a “Monte Carlo-minimization” method initially proposed ten years earlier [29]. The basic version of this algorithm, usually called monotonic basin-hopping [36] is presented in Algorithm 1. Starting from a given initial configuration q, this algorithm iterates the following steps until one of the conditions in the function StoppingCriteria is satisfied (see Section 2.2): (line 3) a relatively large-amplitude perturbation is applied to the current conformation q, aiming to escape from local basins; (line 4) a new conformation is generated by local energy minimization from the perturbed conformation ; (line 5) the transition to the new local minimum is accepted or rejected based on the usual MetropolisTest [38]. Following this stochastic acceptance test, the new conformation is accepted if its energy is lower than or equal to the one of the previous conformation q. Otherwise, it is accepted with a probability that decreases exponentially with the positive energy difference between the two configurations. The implementation of BH used for the comparative analysis in this work follows a multistart procedure, as presented in Algorithm 2. Aiming to cover the space more globally, it performs several rounds of the monotonic-BH algorithm, starting from randomly sampled conformations generated by the function SampleRoot. Note that we successfully applied this implementation of BH in previous work [39].
| Algorithm 1: Monotonic-Basin-Hopping |
 |
| Algorithm 2: Multistart-Basin-Hopping |
 |
2.1.2. Hybrid-BH-RRT (HYBRID)
The HYBRID algorithm [37] combines the underlying principles of two methods: BH and RRT [32]. RRT is a popular algorithm in the robotics community, originally developed to plan the motions of robotic systems, and subsequently extended and applied to explore the conformational space of molecules [34,39]. RRT performs an iterative stochastic process that, starting from a given state, incrementally builds a tree that tends to cover the reachable regions of the search space. The tree’s growth is guided by an intrinsic “Voronoi bias”, enabling it to expand rapidly into unexplored regions. The idea of the HYBRID algorithm is to interleave exploration stages following the BH heuristic (i.e., digging into low-energy basins) and stages applying the RRT approach (i.e., biasing the search towards unexplored regions).
The pseudo-code in Algorithm 3 presents the main steps of HYBRID. The implementation applied in this work involves a mechanism similar to the multistart-BH, in which the exploration starts from different initial configurations sampled by the function SampleRoot. The number of initial configurations is defined in the parameters P and tested inside the function MaxNumberRoots. Then, the algorithm follows the main steps of RRT: (line 6) a conformation is randomly sampled in the whole conformational space; (line 7) the nearest conformation to among the already explored minima contained in is selected; (line 8) the basic tree expansion step in the original RRT algorithm is replaced by an execution of the monotonic-BH algorithm starting from the selected . Since the probability of a conformation to be selected for expansion is proportional to the volume of its associated Voronoi cell (i.e., the subset of points in the conformational space closer to than to any other conformation contained in the tree), the tree tends to grow towards the least explored regions of the space. Note that the parameters used for the monotonic-BH within the HYBRID algorithm should ensure that the number of iterations of perturbation and local minimization stages is relatively small compared to the number of iterations within the multistart-BH, so that the efficiency of the exploration via the coupling of the BH with the RRT algorithm will be enhanced.
2.1.3. Iterative Global Exploration and Local Optimization (IGLOO)
Similar to the HYBRID algorithm, IGLOO relies on the exploration strategy of the robotics-inspired RRT algorithm. However, the exploration and local minimization steps are nested in a different way. The pseudo-code of IGLOO is presented in Algorithm 4. The first part of the algorithm (lines 2–5) samples n conformations that will be used as the initial roots of the exploration trees. These trees are constructed by the function TRRT-Exploration (line 7), which implements a multi-tree variant of the RRT algorithm that considers an energy threshold as a constraint for the exploration. This algorithm will be described in Section 2.2. Then, local energy minimization is performed from each of the conformations corresponding to the nodes of these trees (lines 8–10). The resulting set of local minima is filtered to eliminate conformations that are too similar, and to reduce the number of local minima taken into account for the following steps (line 11). Note that although the TRRT-Exploration generates conformations with a good dispersion in , the subsequent local minimization usually produces clusters of conformations. The UpdateParameters function (line 12) adapts the energy threshold, the exploration step size, and the maximum number of roots for the next iteration of the algorithm. The three main steps of IGLOO—global exploration, local minimization, and filtering—are iterated until one of the conditions in the function StoppingCriteria is satisfied. To illustrate the behavior of IGLOO, Figure A1 provided in the appendix section presents results obtained along several iterations of the algorithm to find low-energy conformations of a simple system that has frequently been used in theoretical works: the alanine dipeptide.
| Algorithm 3: Hybrid-BH-RRT |
 |
| Algorithm 4: IGLOO |
 |
2.2. Implementation Details
This section provides more detailed explanations of the main functions implemented in the algorithms described above:
SampleRoot: This function randomly samples a conformation q from the domain defined for the conformational space variables . This conformation is locally minimized using the LocalMinimization function described below. If the set already contains other local minima, the distance between the new sample and the previous ones is computed, and the new sample is rejected if the minimum value of these distances is below a given threshold defined in the set of parameters P. In that case, the process is repeated until the new sample is sufficiently far from all the others. This strategy is inspired from the Poisson disk sampling process [40], and aims to guarantee a good dispersion of the points used to initialize the exploration.
LargeAmplitudePerturbation: As is generally done in Monte Carlo-type methods, this “random move” is not applied to all the variables simultaneously, but to a subset of them at each iteration. In the implementation used in this work, the LargeAmplitude- Perturbation is applied to a single variable at a time (we tested random moves applied to several variables simultaneously but the results did not improve for the test systems presented below). More precisely, these large-amplitude moves are applied only to a subset of the conformational space variables considered to be the most important ones, whereas the LocalMinimization function, explained below, operates on all the variables. Section 2.3 will explain the main and secondary variables for the type of molecules considered in this work. The bounds for the amplitude of the perturbation (i.e., the minimum and maximum step size) are defined in the set of parameters P. A random value between these bounds is sampled at each iteration.
LocalMinimization: The local minimization is based on a simple Monte Carlo method at very low temperature. Although this type of stochastic algorithm is in general less computationally efficient than deterministic gradient-based approaches, it is also less sensitive to local traps. Moreover, it does not require the computation of the derivatives of the objective function, which can be difficult and expensive in some cases. The algorithm iteratively applies small random perturbations to the current conformation, which are accepted or rejected based on the Metropolis test (as for the BH algorithm). As the temperature parameter used in this test is very low, the probability of accepting a locally perturbed conformation that increases energy is also very low, but not zero, allowing minimization to escape from small energy basins.
Our implementation considers two types of variables, main and secondary, as defined in Section 2.3. At each iteration, one of the two groups is alternatively selected. Then, a number of variables inside the group is randomly selected. The probability to perturb one or several variables is adapted with the number of iterations. During the first iterations, the probability of selecting one or several variables is of 50% in each case. Once a threshold percentage of rejected Metropolis tests is reached within a given number of consecutive iterations, only one variable is selected. The amplitude of the random perturbation applied to the selected variable(s) is adjusted between a maximum and a minimum value defined in the set of parameters P. Using a similar buffer strategy, this amplitude decreases each time that 50% of the Metropolis tests is rejected. To prevent the amplitude from decreasing too quickly, the buffer is reset after each amplitude reduction. The algorithm iterates until a stopping condition is satisfied. Similarly to the StoppingCriteria function explained below, the considered criteria are a maximum number of iterations, a limited computing time, or estimated convergence, based on a maximum number of consecutive rejections of Metropolis test.
TRRT-Exploration: The exploration algorithm implemented in this work combines ideas of the Transition-based RRT (TRRT) [34] and the threshold algorithm [8]. The pseudo-code is presented in Algorithm 5. The algorithm constructs several exploration trees starting from the given set of roots, aiming to cover the reachable regions of the conformational space. These trees are constructed by iterating the following steps:
- (line 3) One of the trees is randomly selected.
- (line 4) A conformation is randomly sampled in a domain containing the selected tree. In practice, a convex polytope in is computed for each tree, and updated when the tree grows. This polytope is enlarged in proportion to the size of the exploration step, and a conformation is randomly sampled within it.
- (line 5) The nearest conformation to , , stored in the nodes of the selected tree is chosen for extension.
- (line 6) A new conformation is created by extending in the direction of . This extension is implemented by moving along the interpolated path between and of a given step size, provided in the set of parameters P.
- (lines 7–8) A new node containing will be added to the corresponding tree if it satisfies a set of constraints. More precisely, the function ValidConformation tests the absence of clashes between non-bonded atoms and that the potential energy of the conformation is below a given threshold (defined in the set of parameters P). The function AddNode creates a new node and performs the merging of two trees when can be connected to a neighboring node in another tree.
The algorithm stops when StoppingCriteria based on a maximum number of iterations or on a limited computing time are satisfied.
| Algorithm 5: TRRT-Exploration |
 |
FilterConformations: The aim of this function is to reduce the number of local minima from which the next iteration of the IGLOO algorithm is initialized.
Similarity between conformations is based on two criteria: (i) the angular root-mean-square deviation (RMSD) between the values of the main variables; (ii) the difference between each main dihedral value. Two conformations are considered to be too similar if these two values are below given thresholds. In that case, the conformation with higher energy is removed.
StoppingCriteria: Several types of conditions can be considered to determine the end of the iterative process performed by the algorithms. They are based on: (i) a maximum number of iterations; (ii) a limited computing time; (iii) estimated convergence, based on the evolution of the lowest energy value (i.e., the global optimum). All these conditions are evaluated, and the first one to be satisfied stops the algorithm.
2.3. Molecular Model and Energy Function
For the comparative analyses of the algorithms presented in Section 3, we chose models of two polypeptides. We considered all-atom models, but assuming constant values for bond lengths and bond angles (i.e., the so-called rigid geometry assumption). Therefore, the conformational space variables we considered, , consisted of all the bond torsions. As mentioned above, these variables are divided into two groups: the main variables involve all the backbone dihedral angles except the first one and the last one, and the secondary variables involve these two terminal backbone angles and the dihedral angles of the side-chains. The angular step size for the global exploration was empirically determined for each method/molecule pair. For the evaluation of the potential energy, we employed the AMBER parm96 force-field with an implicit representation of the solvent using the Generalized Born Approximation [41].
2.4. Software Availability
The algorithms presented in this section have been implemented in the Molecular Motion Algorithms (MoMA) software suite: https://moma.laas.fr/. This software is a prototype used for research purposes. The version used corresponds to the June 2023 release. Binaries can be provided upon request to the authors.
3. Results and Discussion
To analyse the performance of the algorithms, two molecules with different size and conformational behavior were chosen, as they allow different properties to be evaluated. The first molecule, Met-enkephalin, is an endogenous opioid pentapeptide (Tyr-Gly-Gly-Phe-Met) exhibiting a stable conformational state and various metastable ones [42]. The second molecule, referred to as df-c-Myb in the following, is an heptapeptide (Ace-Lys-Gln-Cys-Arg-Glu-Arg-Ala-NMe) derived from the recognition helix of the c-Myb DNA-binding protein [43]. It presents a more complex PES containing regions of the conformational space characterised by different structural motifs [44]. A good characterization of the PES of these two molecules therefore requires an algorithm able to accurately locate the global minimum while exhaustively exploring the diversity of local minima, both with a high convergence rate. In the following, the performance of the three algorithms presented in Section 2.1 will be compared on the basis of (i) their convergence towards the global energy minimum, () the associated atomic structures and computing costs, and () their ability to explore different regions of the conformational space of the df-c-Myb PES corresponding to three different structural motifs: an -helix (HLX) and two -hairpins (HPN1 and HPN2). Note that we have used parallelized versions of the three algorithms. Therefore, the computing times mentioned below correspond to the sum of the CPU time for each thread. Given that we used 45 threads and that the speedup of the parallel version is almost linear with the number of threads, the wall-clock time is approximately the total CPU time divided by 45.
Figure 1 shows the evolution of the observed minimum energy as a function of the CPU time for the molecules used in our analyses. Here we depict, as a function of time, the value of the minimum energy averaged over 10 runs, together with a quartile-based estimate of the spread of the minimum energies observed. In the plot at the top, corresponding to Met-enkephalin, the IGLOO curve remains below the BH and HYBRID ones throughout the exploration. The IGLOO lowest energy decreases very rapidly until around s, after which the slope decreases markedly and the average energy improves very little beyond s. The overall behaviour of the HYBRID algorithm is similar to that of IGLOO but with a smaller initial slope and a stagnation of the observed minimum energy after s. The BH curve looks very different, with a much shallower slope and large plateaus. After s of exploration, the IGLOO energy (−224.43 kcal/mol) is much lower than the energies of the other two algorithms (−221.63 kcal/mol for HYBRID and −221.77 kcal/mol for BH, respectively). The curves representing the evolution of the lowest energy of df-c-Myb (Figure 1, bottom panel) show a better performance of IGLOO in terms of convergence towards the minimum energy (−628.75 kcal/mol after s) compared to BH (−626.04 kcal/mol) and HYBRID (−622.86 kcal/mol). The IGLOO curve has an almost constant slope up to s, exploration time at which the average minimum energy reaches a plateau. Although its approach to low minimum energies is slower at the beginning, IGLOO surpasses the two other algorithms beyond s.
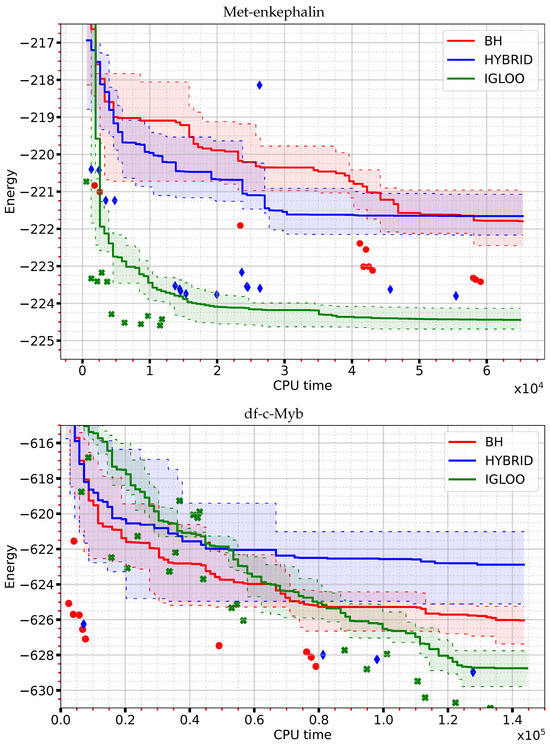
Figure 1.
Evolution of the Met-enkephalin (top) and df-c-Myb (bottom) lowest energy (in kcal/mol) for BH (red), HYBRID (blue) and IGLOO (green) algorithms as a function of CPU time (in s). The solid lines represent the average value over ten runs of each algorithm. The variability of their performance is illustrated by the colored area between the first and third quartile (dashed lines). Outliers are represented by red circles (BH), blue diamonds (HYBRID), and green crosses (IGLOO).
The variability of the performance of the algorithms is illustrated by their first and third quartiles shown as dotted lines in Figure 1. These quartiles were computed from 10 independent runs of the algorithms, using time frames of 650 s for Met-enkephaline and 1450 s for df-c-Myb. For the Met-enkephalin and df-c-Myb, IGLOO exhibits an interquartile mean value of and , respectively, vs. and , respectively, for HYBRID, and and , respectively, for BH. This reflects a lower variability of the results obtained from different executions of IGLOO compared to the two other methods. Due to the stochastic nature of the three algorithms, some runs deviate from their average behavior, as illustrated by the outliers shown in Figure 1. This confirms the need for a sufficient number of runs to obtain sufficient statistics for a meaningful comparative analysis of these methods. In summary, at short exploration times, the IGLOO algorithm locates structures of lower energy than the BH and HYBRID algorithms and with lower variability, demonstrating its ability to rapidly explore the PES with the objective of finding the global minimum.
The lowest-energy structures identified by each global optimization method during long runs are depicted in Figure 2 for Met-enkephalin, and in Figure 3 for df-c-Myb, together with their energy and the execution time at which they were found. Regarding Met-enkephalin, the structures found by the three algorithms are similar and have very similar energies. The structure obtained by IGLOO was the one with the lowest-energy, followed by BH (+0.41 kcal/mol) and HYBRID (+0.80 kcal/mol). These energy differences come from the side-chain of residue 5 which breaks the stabilizing stacking interaction between the phenol group of residue 1 and the phenyl group of residue 4. The time needed for IGLOO to discover the lowest-energy structure of Met-enkephalin is around 2 and 20 times shorter than the one needed for the HYBRID and BH algorithms, respectively, to locate their optimal structures (which are still slightly less energetically favorable than the one found by IGLOO). This confirms the better performance of IGLOO in terms of convergence to the global minimum.
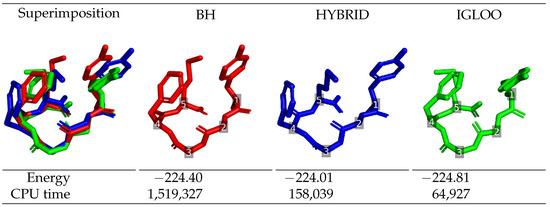
Figure 2.
Met-enkephalin lowest-energy structure found by BH (red), HYBRID (blue) and IGLOO (green) and associated energy (in kcal/mol) and CPU time (in s). Residue numbers are depicted in white.
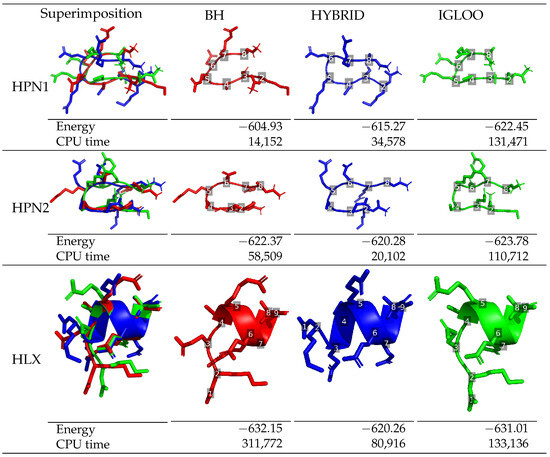
Figure 3.
df-c-Myb HPN1, HPN2 and HLX lowest-energy structures found by BH (red), HYBRID (blue) and IGLOO (green) and associated energy (in kcal/mol) and CPU time (in s). Residue numbers are depicted in white.
The lowest-energy structures of df-c-Myb corresponding to each of the structural motifs (HPN1, HPN2 and HLX) are presented in Figure 3 for each of the three algorithms, including the time step when the structures were observed. A secondary structure was classified as a hairpin when it contains a -turn H-bond (NH-O for HPN1 and NH-O for HPN2) associated to at least one inter-strand H-bond. The possible inter-strand H-bonds are NH-O, NH-O, NH-O and NH-O for HPN1 and NH-O, NH-O, NH-O and NH-O for HPN2. A secondary structure was classified as a helix when it contains at least two hydrogen bonds among NH-O, NH-O, NH-O, NH-O and NH-O. A H-bond was considered to be present when the distance between a donor and an acceptor atom was shorter than a threshold value set to 3.3 Å. The three global optimization methods all succeed in visiting the three structural motif regions: HPN1, HPN2, and HLX. However, the methods differ in their ability to locate the lowest-energy structure for each motif. In the case of hairpins, IGLOO found a more favorable minimum than the ones obtained by BH (+17.52 kcal/mol for HPN1 and +1.41 kcal/mol for HPN2) and the HYBRID algorithm (+7.18 kcal/mol for HPN1 and +3.5 kcal/mol for HPN2). The performance with respect to the low-energy minima exhibiting helices diverges from that of the hairpins, with the BH method finding the best minimum; the best structures found by IGLOO and the HYBRID algorithm having energies 1.14 kcal/mol and 11.89 kcal/mol higher than the best one of the BH structure, respectively. We note that while the BH method finds low-energy helices, it encounters difficulties in the case of hairpins. The HYBRID algorithm explores the different regions of the PES but seems to perform poorly when it comes to refining the explorations locally. Finally, IGLOO manages to quickly identify diverse regions and perform refined local exploration of these regions, where the best minima in each region were found at similar CPU times during the simultaneous multi-basin exploration of the IGLOO runs.
The two-dimensional projection of the minimized conformations issued from df-c-Myb PES explorations is depicted in Figure 4 for three evenly distributed CPU times (, and s). The two dimensions of the projection, the CC and CC interatomic distances, were chosen because they allow a clear spatial separation of the structural motifs of interest. Regions corresponding to HPN1, HPN2 and HLX structures can thus be approximately delineated on the 2D projection (ovals). The dark dots present on the and s snapshots correspond to minima already located at the CPU time of the previous snapshot, i.e., and s respectively.
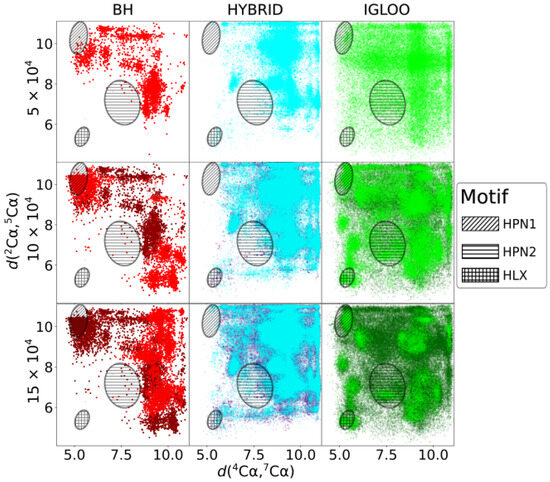
Figure 4.
Distribution of minimized conformations of df-c-Myb on a two-dimensional projection at three different CPU times (in s) for BH (red), HYBRID (blue), and IGLOO (green). The two dimensions are defined by the CC and CC interatomic distances (in Å). HPN1, HPN2 and HLX regions are depicted by oblique hatches, horizontal hatches and grids, respectively. On each thumbnail, the dark dots correspond to the minima already located during the CPU time corresponding to the previous thumbnail.
The BH method struggles to explore the PES of df-c-Myb correctly, with some areas visited very infrequently (HPN2) or not at all (HLX) after s of exploration, while the others are heavily oversampled. Indeed, very long times are needed to explore the conformational space corresponding to the helices, as shown by the ∼ s needed to locate a low-energy helix (Figure 3). The BH local exploration also sometimes appears to be of poor quality, as evidenced by the high energy of the most stable HPN1 hairpin found by this algorithm, even though the algorithm has sampled a large part of the corresponding PES region.
The initial space visited by the HYBRID algorithm is more extended than the one visited by the BH method. After s of exploration, minima are found in the three zones corresponding to the structural motifs. However, during the subsequent exploration, the algorithm concentrates on areas that have already been explored or those that are close to them, and struggles to extend the exploration to previously unvisited regions. Some areas therefore remain unexplored after s while others appear to be oversampled. A major weakness of the HYBRID algorithm lies in its inability to properly explore locally: although the zones corresponding to the HPN1, HPN2, and HLX motifs are visited, the energies of the corresponding low-energy isomers found by the algorithm remain relatively high (Figure 3).
Finally, the IGLOO algorithm extends its initial exploration to the whole space and then concentrates on certain zones, including those corresponding to hairpins and helices. Its local refinement is also highly efficient, with the energy of the most stable isomer found by this method being the lowest one in the case of HPN1 and HPN2 and competitive for HLX (Figure 3). In summary, the BH method and the HYBRID algorithm struggle to cover the space to be explored, oversample certain areas, and show poor performance relative to local refinement. In contrast, the IGLOO algorithm explores the PES in a comprehensive fashion, focusing iteratively on the relevant basins. Furthermore, we note that IGLOO already reaches these relevant basins quite early during the search and thus allows to identify promising low-energy conformations with a rather small computational effort.
4. Conclusions and Outlook
In this study, we have presented a new global optimization algorithm, IGLOO, which combines the basic features of the RRT algorithm from the field of robotics, of the threshold algorithm that has in the past been used to study energy landscapes of various chemical and physical systems, and of repeated local stochastic quenches. Both the RRT and the threshold algorithm explore the landscape in many ways “orthogonal” to the standard global optimization and exploration procedures such as GA, SA, or BH. However, when combined with a moderately greedy local optimization algorithm, we find that IGLOO demonstrates a faster convergence to low-energy minima at a lower computational cost than the other two algorithms we have tested as a comparison (BH and HYBRID), even though they share tools such as frequent minimizations (BH and HYBRID) and the exploration capabilities of the RRT algorithm (HYBRID). In particular, IGLOO achieves a much smoother coverage of all important low-energy regions of the landscape and exhibits a high efficiency in exploring these zones on the landscape. Considering the tools common with the other algorithms, it appears that the threshold criterion likely makes a difference as it tends to focus the search on the low-energy regions of the landscape, without overly constraining the subsequent search inside these regions. In particular, by reducing the importance of lower-level energy barriers but still allowing the RRT-part of the search algorithm to stay in large regions that lie below a (possibly characteristic) threshold energy of the system, the combination of RRT, threshold, and local minimization results in a relatively fast yet efficient and homogeneous coverage of the various low-energy regions of the landscape.
In this “proof-of-principle” study, we have illustrated the ability of IGLOO to identify a representative set of low-energy conformations of flexible peptides. Nevertheless, we can envisage many other applications. A particularly interesting application would be the search for conformers of (small) organic molecules in the context of virtual screening for drug discovery, where IGLOO could be competitive with respect to other algorithms [24] thanks to its ability to rapidly find diverse low-energy conformations. IGLOO could also be applied to the generation of accessible conformations from a given one with minor modifications of the algorithm, incorporating additional features of the threshold algorithm. Indeed, the main aspect to be changed is the initial iteration of the algorithm, which should start from a given conformation instead of a set of randomly sampled states, and the energy threshold(s) controlling the accessibility should be initialized at the desired value(s). Going further, IGLOO could find applications in many other fields beyond molecular modeling, wherever global optimization methods are useful, including hyperparameter optimization in machine learning [45]. Note, however, that due to the RRT-based exploration, IGLOO requires the definition of a suitable distance metric in the search space, which is not straightforward for all types of problems.
Concerning potential future applications of IGLOO to various types of chemical systems consisting of one or more molecules, either isolated or on a surface or within a medium, two issues are expected to arise: (i) the quality of the energy function, and (ii) the dimensionality and topology of the configuration space that needs to be explored. Regarding the energy function, full quantum mechanical evaluations of the energy are computationally very expensive and thus always a stretch for global landscape exploration. Nevertheless, energy functions with a good balance between accuracy and computational efficiency, e.g., based on density functional-based tight-binding (DFTB) [46], are available and have been successfully employed to globally explore energy landscapes of chemical systems [47].
The issue of the configuration space that needs to be smoothly but efficiently explored is a much more subtle one. We note that it will also appear in any application of IGLOO as a general global optimization algorithm for cost function landscapes drawn not only from robotics and chemistry but also from physics, biology, or economics. The concern here is the question whether the (T)RRT exploration methodology can be employed beyond compact state spaces such as the n-dimensional torus for a chain molecule or a multi-link robot arm where n angular variables characterize the microstates of the system. One class of systems for which (T)RRT appears to be very suitable are the landscapes of periodic approximants to crystalline solids, where the atom coordinates also exhibit a torus-like topology. While the threshold control and the stochastic quenches have proven their worth in many global landscapes studies, testing the (T)RRT feature of IGLOO for other classes of energy landscapes will be an important direction of future research.
The extension of IGLOO to a large variety of cost function problems will, of course, be accompanied by the fine-tuning of the current version of IGLOO, optimizing the parameters of the algorithm and possibly developing adaptive mechanisms for selection and modifying the IGLOO’s control parameters based on information gathered about the landscape. Finally, the graph generation and exploration feature of the (T)RRT part of IGLOO should be a valuable tool for an efficient search for transition path candidates on the energy landscape. Combining this with the measurement of probability flows provided by the threshold algorithm could result in a promising approach for efficiently gaining deeper insights into the barrier structure of an energy landscape, which controls the stability of the minima configurations of a chemical system and governs the transformations among these structures and phases.
Another interesting direction for future work would be the extension of IGLOO to address general problems with high-dimensional state spaces. Up to now, we have successfully tested IGLOO on problems involving several dozen variables, but we can imagine difficulties in tackling problems involving hundreds or thousands of variables, which represent a huge challenge for global exploration. This extension may require a sophisticated parallel implementation of the algorithm. For the investigation presented in this work, we employed a basic multi-threading strategy exploiting the shared-memory architecture of current multi-core CPUs. The execution on larger computer clusters would need a more in-depth strategy, avoiding unnecessary communication between processes. Our previous work on the parallelization of RRT-like algorithms based on an automatic subdivision of space [48] could be a good starting point. In addition to the “high-level” parallelization of the algorithm for efficient execution on multiple CPUs, one can also envisage GPU-accelerated calculation of certain “low-level” functions inside the algorithm, such as energy or distance calculations. Thus, we expect IGLOO to prove to be a highly versatile tool for global optimization tasks and for the global exploration of complex energy landscapes in the future.
Author Contributions
Conceptualization, J.C.S. and J.C.; Funding acquisition, C.M.-R., N.T. and J.C.; Investigation, W.M.; Methodology, W.M., A.C. and J.C.; Resources, N.T. and J.C.; Software, W.M., A.C. and J.C.; Supervision C.M.-R., N.T. and J.C.; Visualization: W.M., C.M.-R., N.T. and J.C.; Writing—original draft: W.M., J.C.S., N.T. and J.C.; Writing—review & editing: W.M., C.M.-R., J.C.S., N.T. and J.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the “Institut National des Sciences Appliquées de Toulouse” through the DEFIANT project.
Data Availability Statement
The data generated in the course of this work has been deposited in Zenodo: https://doi.org/10.5281/zenodo.8428004.
Acknowledgments
This work was granted access to the HPC resources of CALMIP supercomputing center under the allocation p19055.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Illustrative Example of IGLOO’s Performance on the Alanine Dipeptide
To illustrate the behavior of IGLOO, Figure A1 presents results obtained along several iterations of the algorithm to find low-energy conformations of the alanine dipeptide. This molecule corresponds to an alanine residue acetylated in its N-terminus and methylamidated in its C-terminus. Due to its relatively complex energy landscape, despite its small size, alanine dipeptide has been frequently used as test-system in theoretical work (e.g., [49,50,51,52]). It is well known that the two backbone dihedral angles of the alanine residue, and , are good descriptors of the conformational space of this molecule. The background images in Figure A1 represent projections of the energy landscape on these two variables for four different values of an energy threshold: (a) 0 kcal/mol, (b) −20 kcal/mol, (c) −35 kcal/mol, (b) −40 kcal/mol. These landscapes were obtained by systematic grid sampling of the and angles with constant step-size followed by local minimization of the other variables. Note that these two-dimensional (2D) landscapes were computed for illustrative purposes, but they were not used for the exploration performed by IGLOO, which operates in the full-dimensional space. In this particular case, IGLOO explores a seven-dimensional space, corresponding to all the variable dihedral angles of the alanine dipeptide.
The four images in Figure A1a–d represent the result of the exploration of IGLOO at the end of four iterations. They show its ability to explore globally but roughly during the first iterations (Figure A1a,b), before being focused on the lowest-energy basins (Figure A1c,d), with the aim to accurately identify a representative set of distinct low-energy conformations.
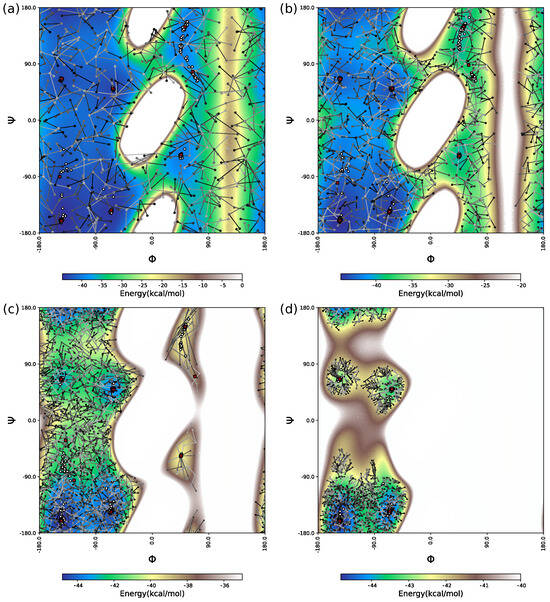
Figure A1.
Two-dimensional projections, using the and dihedral angles, of explored conformations of the alanine dipeptide after four iterations (a–d) of the IGLOO algorithm. Each sampled conformations is depicted with a point, and it is connected to its parent node in the tree by an edge. Each point and edge is colored on a gradient from gray to black, providing information on the order in which the conformations were sampled. The first conformations sampled are in light gray, the last in black. Once locally minimized, conformations are represented by white circles. Nodes selected as roots for the next iteration, which correspond to representative conformations in the different basins, are depicted by red crosses. (a) Extensive exploration of the potential energy surface with an energy threshold allowing the global exploration and the crossing of high-energy barriers. (b) Reduction of the exploration step, inducing closer proximity of the nodes, and of the energy threshold, revealing lower barriers. (c) Further reduction of the exploration step and energy threshold allows the achievement of a resolution enabling basin separation. (d) The threshold value reached limits the exploration to low-energy basins.
References
- Schön, J.C. Energy landscapes in inorganic chemistry. In Comprehensive Inorganic Chemistry III; Reedijk, J., Poeppelmeier, K., Eds.; Elsevier: Amsterdam, The Netherlands, 2023; pp. 262–392. [Google Scholar]
- Mosegaard, K. Resolution analysis of general inverse problems through inverse Monte Carlo sampling. Inverse Probl. 1998, 14, 405. [Google Scholar] [CrossRef]
- Flood, M.M. The Travelling-Salesman Problem. Oper. Res. 1956, 4, 1–137. [Google Scholar] [CrossRef]
- Sibani, P.; Schön, J.C.; Salamon, P.; Andersson, J.O. Emergent hierarchies in complex systems. Europhys. Lett. 1993, 22, 479–485. [Google Scholar] [CrossRef]
- Berry, R.S. Potential Surfaces and Dynamics: What Clusters Tell Us. Chem. Rev. 1993, 93, 2379–2394. [Google Scholar] [CrossRef]
- Banerjee, A.; Adams, N.; Simmons, J.; Shepard, R. Search for stationary points on surfaces. J. Phys. Chem. 1985, 89, 52–57. [Google Scholar] [CrossRef]
- Baker, J.; Hehre, W.J. Geometry Optimization in Cartesian Coordinates—The End of the Z-Matrix. J. Comput. Chem. 1991, 12, 606–610. [Google Scholar] [CrossRef]
- Neelamraju, S.; Oligschleger, C.; Schön, J.C. The threshold algorithm: Description of the methodology and new developments. J. Chem. Phys. 2017, 147, 152713. [Google Scholar] [CrossRef]
- van Eijck, B.P.; Mooij, W.T.M.; Kroon, J. Attempted Prediction of the Crystal Structures of Six Monosaccharides. Acta Cryst. B 1995, 51, 99–103. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; The MIT Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Little, J.D.C.; Murty, K.G.; Sweeney, D.W.; Karel, C. An algorithm for the traveling salesman problem. Oper. Res. 1963, 11, 972–989. [Google Scholar] [CrossRef]
- Müller-Krumbhaar, H. Fuzzy Logic, m-Spin Glasses and 3SAT. Europhys. Lett. 1988, 7, 479–484. [Google Scholar] [CrossRef]
- Dueck, G. New Optimization Heuristics. The Great-Deluge Algorithm and the Record-to-Record Travel. J. Comp. Phys. 1993, 104, 86–92. [Google Scholar] [CrossRef]
- Dueck, G.; Scheuer, T. Threshold Accepting: A general purpose optimization algorithm appearing superior to simulated annealing. J. Comp. Phys. 1990, 90, 161–175. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Glover, F. Tabu search—A tutorial. Interfaces 1990, 20, 74–94. [Google Scholar] [CrossRef]
- Möbius, A.; Neklioudov, A.; Diaz-Sanchez, A.; Hoffmann, K.H.; Fachat, A.; Schreiber, M. Optimization by Thermal Cycling. Phys. Rev. Lett. 1997, 79, 4297–4301. [Google Scholar] [CrossRef]
- Spendley, W.; Hext, G.R.; Hindsworth, F.R. Sequential Application of Simplex Designs in Optimization and Evolutionary Operation. Technometrics 1962, 4, 441–461. [Google Scholar] [CrossRef]
- Bush, T.S.; Catlow, C.R.A.; Battle, P.D. Evolutionary programming technique for predicting inorganic crystal structures. J. Mater. Chem. 1995, 5, 1269. [Google Scholar] [CrossRef]
- Woodley, S.M. Prediction of Crystal Structures Using Evolutionary Algorithms and Related Techniques. Struct. Bond. 2004, 110, 95. [Google Scholar]
- Schön, J.C.; Jansen, M. Determination, Prediction, and Understanding of Structures Using the Energy Landscape Approach—Part I+II. Z. Kristallogr.-Cryst. Mater. 2001, 216, 361–383. [Google Scholar] [CrossRef]
- Oganov, A.R. (Ed.) Modern Methods of Crystal Structure Prediction; John Wiley & Sons: Weinheim, Germany, 2011. [Google Scholar]
- Hawkins, P.C.D. Conformation Generation: The State of the Art. J. Chem. Inf. Model. 2017, 57, 1747–1756. [Google Scholar] [CrossRef]
- Alder, B.J.; Wainwright, T.E. Phase Transitions for a Hard Sphere System. J. Chem. Phys. 1957, 27, 1208–1209. [Google Scholar] [CrossRef]
- Huber, T.; van Gunsteren, W.F. SWARM-MD: Searching Conformational Space by Cooperative Molecular Dynamics. J. Phys. Chem. 1998, 102, 5937–5943. [Google Scholar] [CrossRef]
- Holland, J.H. Outline for a logical theory of adaptive systems. J. Assoc. Comp. Machin. 1962, 3, 297–314. [Google Scholar] [CrossRef]
- Hawkins, P.C.D.; Skillman, A.G.; Warren, G.L.; Ellingson, B.A.; Stahl, M.T. Conformer Generation With OMEGA: Algorithm and Validation Using High Quality Structures from the Protein Data Bank and Cambridge Structure Database. J. Chem. Inf. Model. 2010, 50, 572–584. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Scheraga, H.A. Monte Carlo-minimization approach to the multiple-minima problem in protein folding. Proc. Natl. Acad. Sci. USA 1987, 84, 6611–6615. [Google Scholar] [CrossRef]
- Wales, D.J.; Doye, J.P. Global optimization by basin-hopping and the lowest energy structures of Lennard-Jones clusters containing up to 110 atoms. J. Phys. Chem. A 1997, 101, 5111–5116. [Google Scholar] [CrossRef]
- Deaven, D.M.; Ho, K.M. Molecular geometry optimization with a genetic algorithm. Phys. Rev. Lett. 1995, 75, 288–291. [Google Scholar] [CrossRef]
- LaValle, S.M.; Kuffner, J.J. Randomized Kinodynamic Planning. Int. J. Robot. Res. 2001, 20, 378–400. [Google Scholar] [CrossRef]
- LaValle, S.M. Planning Algorithms; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Jaillet, L.; Corcho, F.J.; Pérez, J.J.; Cortés, J. Randomized tree construction algorithm to explore energy landscapes. J. Comput. Chem. 2011, 32, 3464–3474. [Google Scholar] [CrossRef]
- Abb, S.; Tarrat, N.; Cortés, J.; Andriyevsky, B.; Harnau, L.; Schön, J.C.; Rauschenbach, S.; Kern, K. Carbohydrate Self-Assembly at Surfaces: STM Imaging of Sucrose Conformation and Ordering on Cu(100). Angew. Chem. Int. Ed. 2019, 58, 8336–8340. [Google Scholar] [CrossRef]
- Locatelli, M.; Schoen, F. Global optimization based on local searches. Ann. Oper. Res. 2016, 240, 251–270. [Google Scholar] [CrossRef]
- Roth, C.A.; Dreyfus, T.; Robert, C.H.; Cazals, F. Hybridizing rapidly exploring random trees and basin hopping yields an improved exploration of energy landscapes. J. Comput. Chem. 2016, 37, 739–752. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Devaurs, D.; Molloy, K.; Vaisset, M.; Shehu, A.; Siméon, T.; Cortés, J. Characterizing energy landscapes of peptides using a combination of stochastic algorithms. IEEE Trans. Nanobiosci. 2015, 14, 545–552. [Google Scholar] [CrossRef] [PubMed]
- Gamito, M.N.; Maddock, S.C. Accurate Multidimensional Poisson-Disk Sampling. ACM Trans. Graph. 2009, 29, 1–19. [Google Scholar] [CrossRef]
- Ponder, J.W.; Case, D.A. Force fields for protein simulations. Adv. Protein Chem. 2003, 66, 27–85. [Google Scholar]
- Ando, H.; Ukena, K.; Nagata, S. (Eds.) Front Matter for Volume 1. In Handbook of Hormones, 2nd ed.; Academic Press: San Diego, CA, USA, 2021; pp. i–ii. [Google Scholar]
- Ogata, K.; Morikawa, S.; Nakamura, H.; Hojo, H.; Yoshimura, S.; Zhang, R.; Aimoto, S.; Ametani, Y.; Hirata, Z.; Sarai, A.; et al. Comparison of the free and DNA-complexed forms of the DMA-binding domain from c-Myb. Nat. Struct. Biol. 1995, 2, 309–320. [Google Scholar] [CrossRef]
- Higo, J.; Ito, N.; Kuroda, M.; Ono, S.; Nakajima, N.; Nakamura, H. Energy landscape of a peptide consisting of α-helix, 310-helix, β-turn, β-hairpin, and other disordered conformations. Protein Sci. 2001, 10, 1160–1171. [Google Scholar] [CrossRef]
- Feurer, M.; Hutter, F. Hyperparameter Optimization. In Automated Machine Learning: Methods, Systems, Challenges; Hutter, F., Kotthoff, L., Vanschoren, J., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 3–33. [Google Scholar]
- Rapacioli, M.; Heine, T.; Dontot, L.; Buey, M.Y.; Tarrat, N.; Spiegelman, F.; Louisnard, F.; Cuny, J.; Morinière, M.; Dubosq, C.; et al. deMonNano Experiment. 2023. Available online: http://demon-nano.ups-tlse.fr/ (accessed on 1 July 2023).
- Salomon, G.; Tarrat, N.; Schön, J.C.; Rapacioli, M. Low-Energy Transformation Pathways between Naphtalene Isomers. Molecules 2023, 28, 5778. [Google Scholar] [CrossRef]
- Estaña, A.; Molloy, K.; Vaisset, M.; Sibille, N.; Siméon, T.; Bernadó, P.; Cortés, J. Hybrid parallelization of a multi-tree path search algorithm: Application to highly-flexible biomolecules. Parallel Comput. 2018, 77, 84–100. [Google Scholar] [CrossRef]
- Brooks, C.; Case, D.A. Simulations of peptide conformational dynamics and thermodynamics. Chem. Rev. 1993, 93, 2487–2502. [Google Scholar] [CrossRef]
- Bolhuis, P.G.; Dellago, C.; Chandler, D. Reaction coordinates of biomolecular isomerization. Proc. Natl. Acad. Sci. USA 2000, 97, 5877–5882. [Google Scholar] [CrossRef] [PubMed]
- Chodera, J.D.; Swope, W.C.; Pitera, J.W.; Dill, K.A. Long-Time Protein Folding Dynamics from Short-Time Molecular Dynamics Simulations. Multiscale Model. Simul. 2006, 5, 1214–1226. [Google Scholar] [CrossRef]
- Okumura, H.; Okamoto, Y. Temperature and Pressure Dependence of Alanine Dipeptide Studied by Multibaric–Multithermal Molecular Dynamics Simulations. J. Phys. Chem. B 2008, 112, 12038–12049. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).