A Greedy Pursuit Hierarchical Iteration Algorithm for Multi-Input Systems with Colored Noise and Unknown Time-Delays
Abstract
1. Introduction
- The multi-variable systems model is recast based on the framework of CS by using the hierarchical identification principle.
- The unknown true internal noise items of the recast sparse model in the presented algorithm are replaced by their estimation values according to the hierarchical principle.
- The presented algorithm constructs a kernel matrix to find the locations of key parameters and reduce the estimated dimension and computational cost by using greedy pursuit search, in which only limited sampled data are used.
- The parameters and time delays are estimated simultaneously by using the presented algorithm.
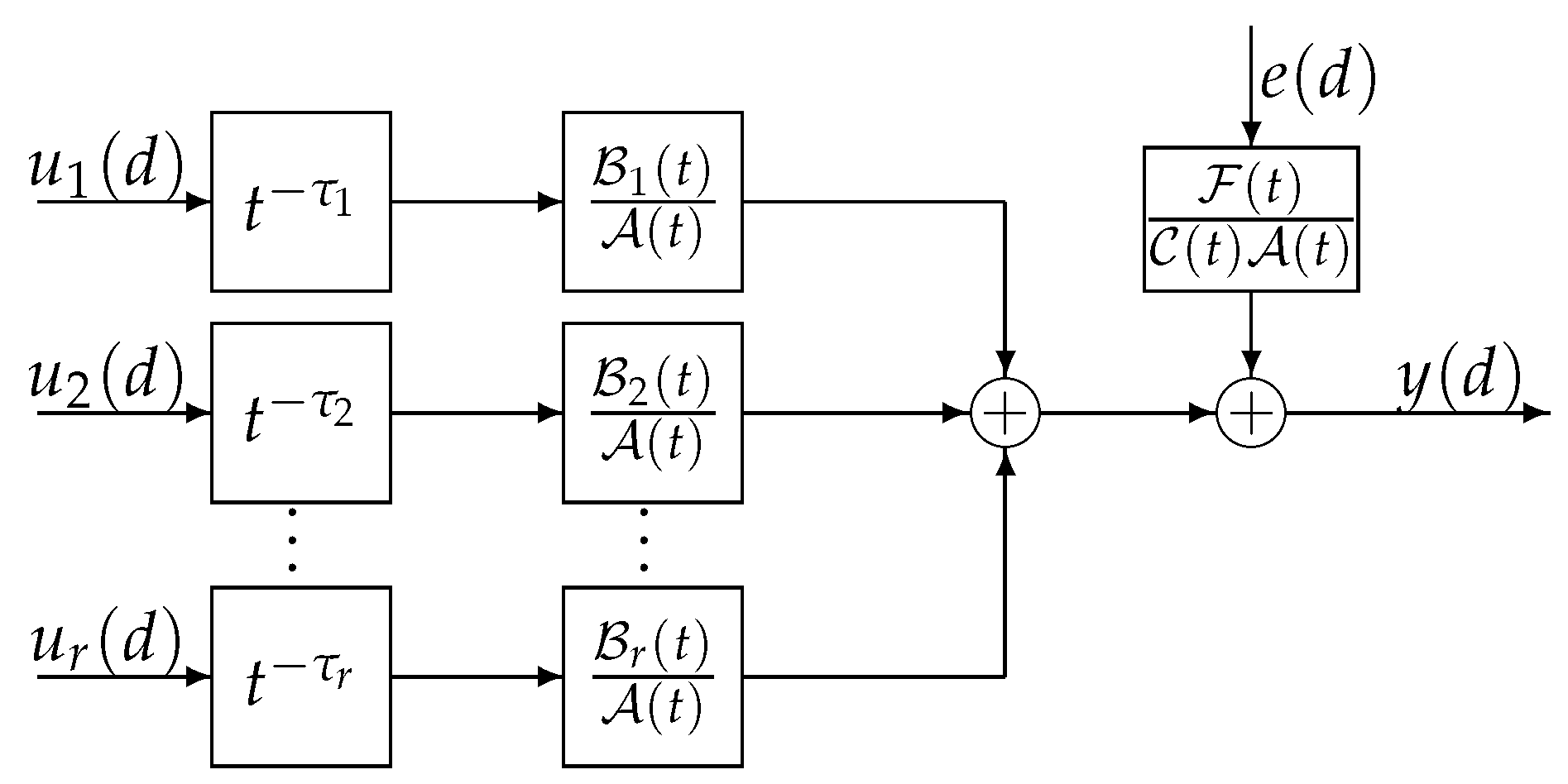
2. Systems Model
3. Greedy Pursuit Hierarchical Iterative Parameter Estimation Algorithm
- Define l and collect sampled data : to form Y.
- To initialize external iteration: let , , , be a random number, and give allowable error and .
- Form by Equation (20), and by
- Begin the internal iteration. Let , , and , .
- If , complete the iteration stage and receive the final estimate ; otherwise, let and turn to step 4.
4. Simulation Experiments
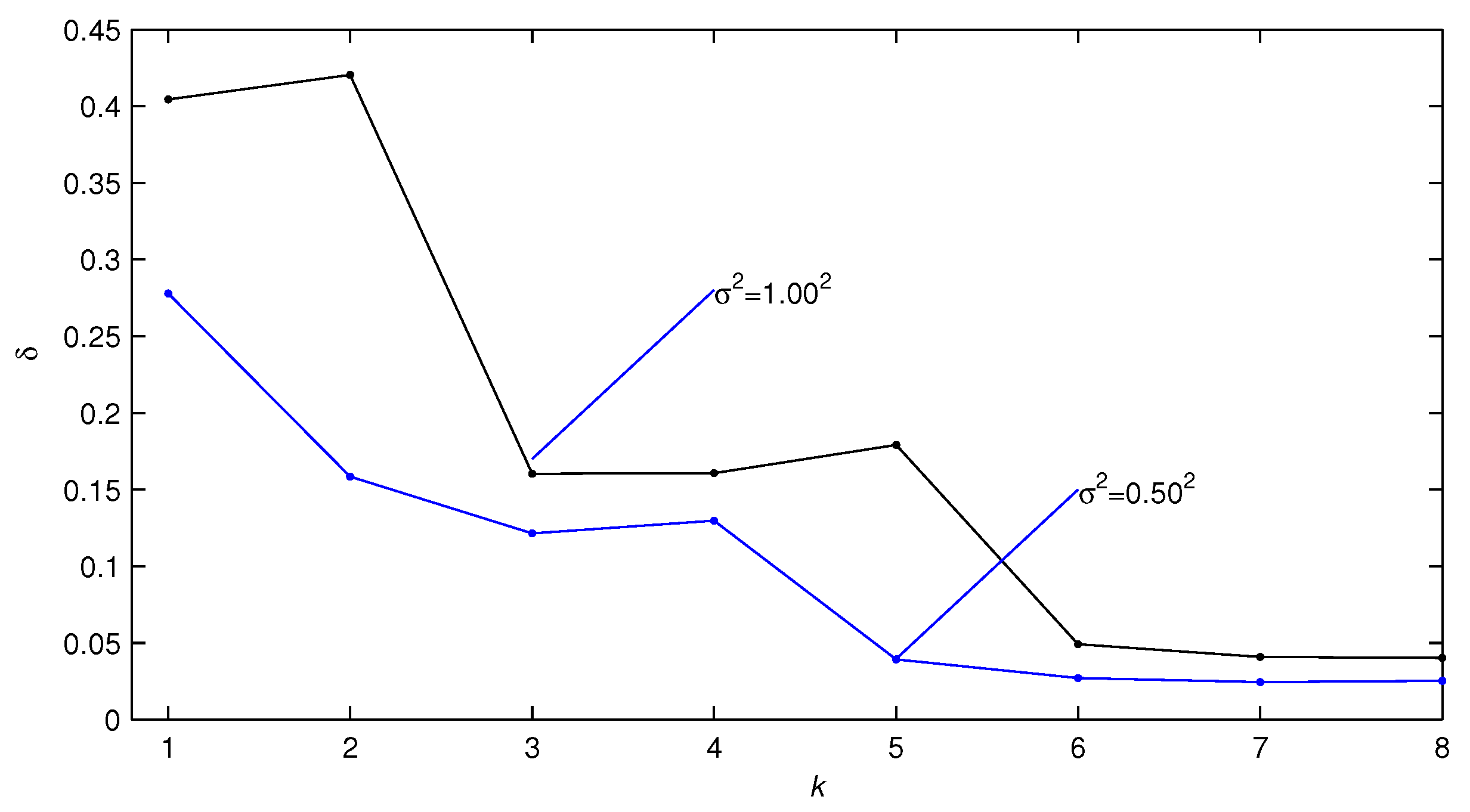
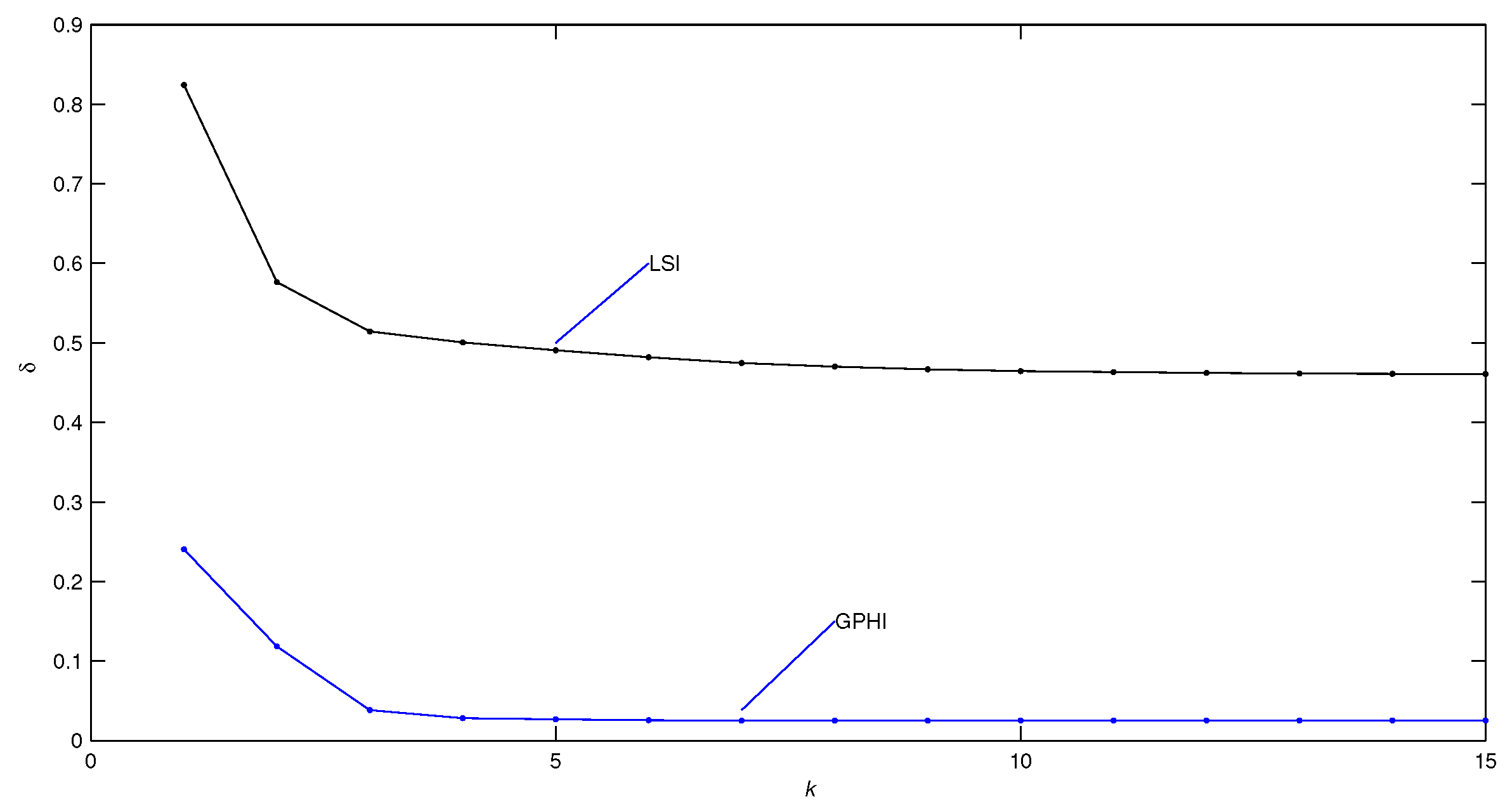
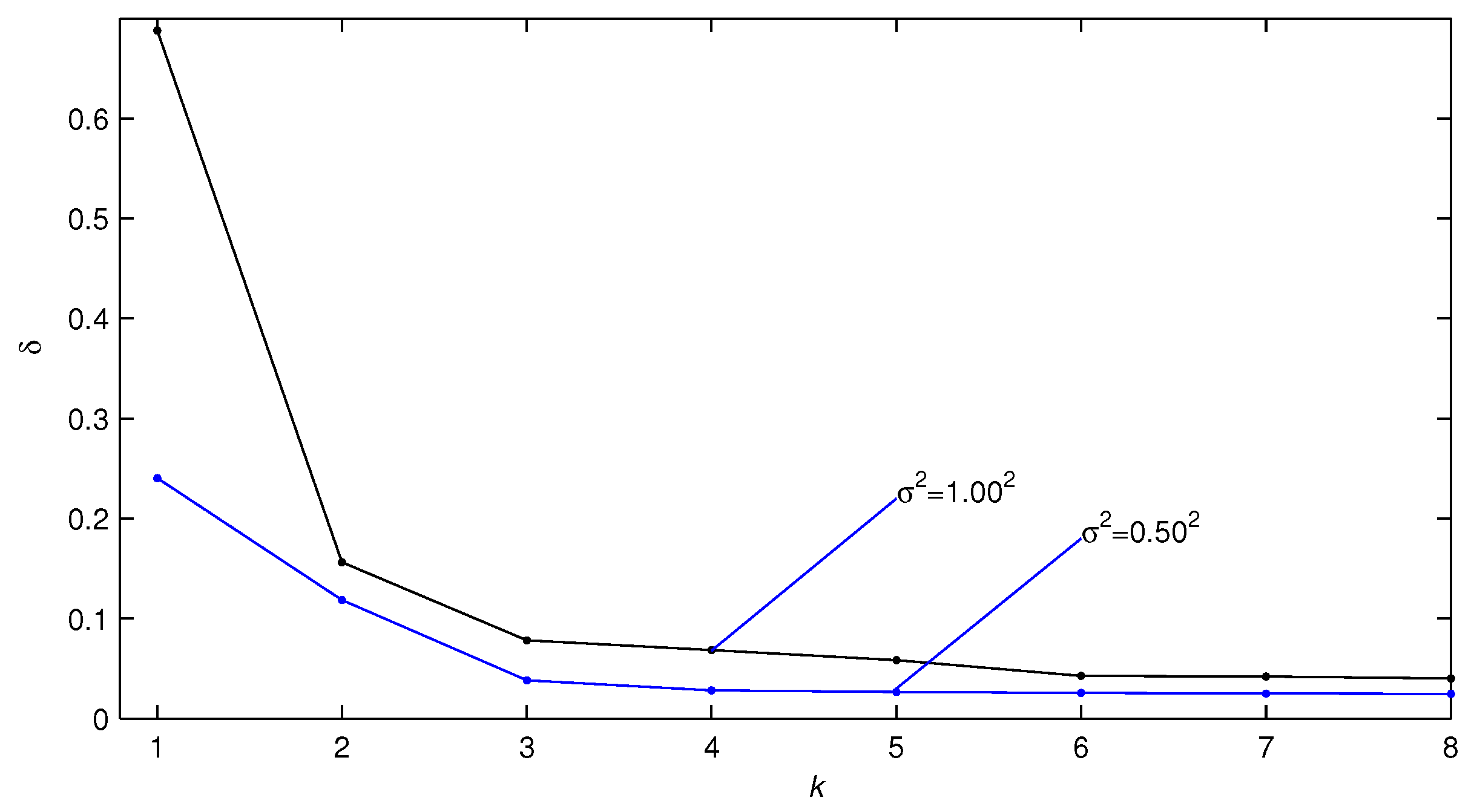
- Compared with the traditional LSI algorithm, the GPHI algorithm can use the limited sampled data to achieve higher parameter estimation accuracy—see Figure 9.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ljung, L. System Identification: Theory for The User, Information and System Science Series; Tsinghua University Press: Beijing, China, 2002. [Google Scholar]
- Ding, F. System Identification—New Theory and Methods; Science Press: Beijing, China, 2013. [Google Scholar]
- Ding, F. System Identification—Performance Analysis for Identification Methods; Science Press: Beijing, China, 2014. [Google Scholar]
- Ding, F. System Identification—Multi-innovation Identification Theory and Methods; Science Press: Beijing, China, 2016. [Google Scholar]
- Xu, J.; Tao, Q.; Li, Z.; Xi, X.; Suykens, J.A.; Wang, S. Efficient hinging hyperplanes neural network and its application in nonlinear system identification. Automatica 2020, 116, 108906. [Google Scholar] [CrossRef]
- Zhang, C.M.; Lu, Y. Study on artificial intelligence: The state of the art and future prospects. J. Ind. Inf. Integr. 2021, 23, 00224. [Google Scholar] [CrossRef]
- Chen, J.; Huang, B.; Gan, M.; Chen, P. A novel reduced-order algorithm for rational model based on Arnoldi process and Krylov subspace. Automatica 2021, 129, 109663. [Google Scholar] [CrossRef]
- Li, Y.; Yu, K. Adaptive fuzzy decentralized sampled-data control for large-scale nonlinear systems. IEEE Trans. Fuzzy Syst. 2022, 30, 1809–1822. [Google Scholar] [CrossRef]
- Skarding, J.; Gabrys, B.; Musial, K. Foundations and modeling of dynamic networks using dynamic graph neural networks: A survey. IEEE Access 2021, 9, 79143–79168. [Google Scholar] [CrossRef]
- Liu, Y.A.; Tang, G.S.D.; Liu, Y.F.; Kong, Q.K.; Wang, J. Extended dissipative sliding mode control for nonlinear networked control systems via event-triggered mechanism with random uncertain measurement. Appl. Math. Comput. 2021, 396, 125901. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Q.Y.; Ding, F.; Alsaedi, A.; Hayat, T. Recursive identification of bilinear time-delay systems through the redundant rule. J. Frankl. Inst. 2020, 357, 726–747. [Google Scholar] [CrossRef]
- Gu, Y.; Liu, J.; Li, X.; Chou, Y.; Ji, Y. State space model identification of multirate processes with time-delay using the expectation maximization. J. Frankl. Inst. 2019, 356, 1623–1639. [Google Scholar] [CrossRef]
- Fei, Q.L.; Ma, J.X.; Xiong, W.L.; Guo, F. Variational Bayesian identification for bilinear state space models with Markov-switching time delays. Int. J. Robust Nonlinear Control 2020, 30, 7478–7495. [Google Scholar] [CrossRef]
- Ding, F.; Wang, X.H.; Mao, L.; Xu, L. Joint state and multi-innovation parameter estimation for time-delay linear systems and its convergence based on the Kalman filtering. Digit. Signal Process. 2017, 62, 211–223. [Google Scholar] [CrossRef]
- Ding, F.; Ma, H.; Pan, J.; Yang, E.F. Hierarchical gradient and least squares-based iterative algorithms for input nonlinear output-error systems using the key term separation. J. Frankl. Inst. 2021, 358, 5113–5135. [Google Scholar] [CrossRef]
- Ding, F.; Liu, X.M.; Hayat, T. Hierarchical least squares identification for feedback nonlinear equation-error systems. J. Frankl. Inst. 2020, 357, 2958–2977. [Google Scholar] [CrossRef]
- Ding, F.; Wang, X.H.; Chen, Q.J.; Xiao, Y.S. Recursive least squares parameter estimation for a class of output nonlinear systems based on the model decomposition. Circ. Syst. Signal Process. 2016, 35, 3323–3338. [Google Scholar] [CrossRef]
- Chen, T.; Ohlsson, H.; Ljung, L. On the estimation of transfer functions, regularizations and Gaussian processes—Revisited. Automatica 2012, 48, 1525–1535. [Google Scholar]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar]
- Candès, E.J.; Wakin, M.B. An introduction to compressive sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Tropp, J.A. Greed is good: Algorithmic results for sparse approximation. IEEE Trans. Inf. Theory 2004, 50, 2231–2242. [Google Scholar] [CrossRef]
- Liu, Y.J.; You, J.Y.; Ding, F. Iterative identification for multiple-input systems based on auxiliary model-orthogonal matching pursuit. Control Decis. 2019, 34, 787–792. [Google Scholar]
- You, J.Y.; Liu, Y.J.; Chen, J.; Ding, F. Iterative identification for multiple-input systems with time-delays based on greedy pursuit and auxiliary model. J. Frankl. Inst. 2019, 356, 5819–5833. [Google Scholar]
- You, J.Y.; Liu, Y.J. Iterative identification for multivariable systems with time-delays based on basis pursuit de-noising and auxiliary model. Algorithms 2018, 11, 180. [Google Scholar] [CrossRef]
- Tao, T.Y.; Wang, B.; Wang, X.H. Parameter and time delay estimation algorithm based on gradient pursuit for multi-input C-ARMA systems. Control Decis. 2022, 37, 2085–2090. [Google Scholar]
- Wang, D.Q.; Li, L.W.; Ji, Y.; Yan, Y. Model recovery for Hammerstein systems using the auxiliary model based orthogonal matching pursuit method. Appl. Math. Model. 2017, 54, 537–550. [Google Scholar] [CrossRef]
- Mao, Y.W.; Ding, F.; Liu, Y.J. Parameter estimation algorithms for Hammerstein time-delay systems based on the orthogonal matching pursuit scheme. IET Signal Process. 2017, 11, 265–274. [Google Scholar] [CrossRef]
- Troop, J.A. Just relax: Convex programming methods for identifying sparse signals in noise. IEEE Trans. Inf. Theory 2006, 52, 1030–1051. [Google Scholar] [CrossRef]
- Ding, F. System Identification—Iterative Search Principle and Identification Methods; Science Press: Beijing, China, 2018. [Google Scholar]
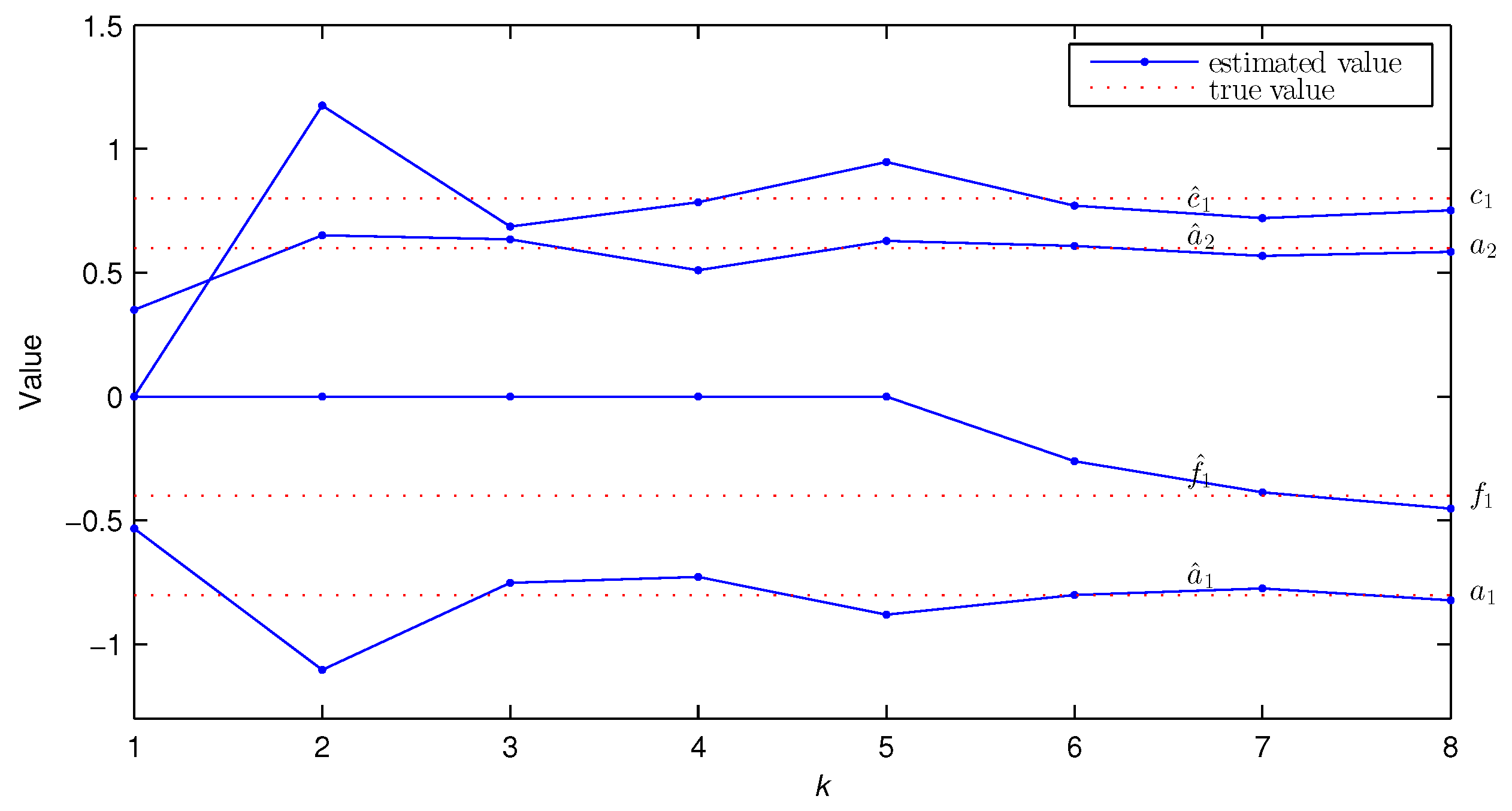
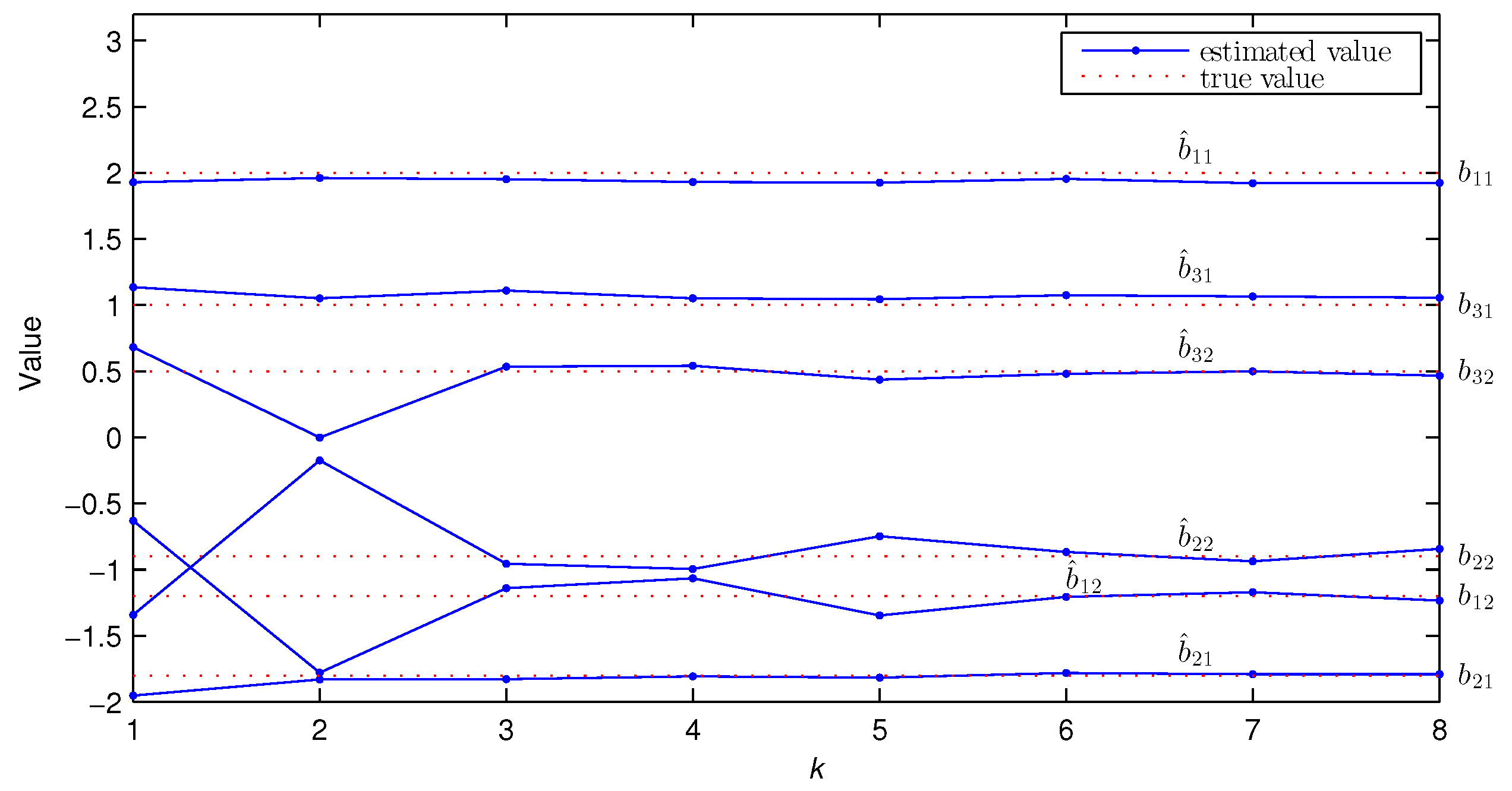
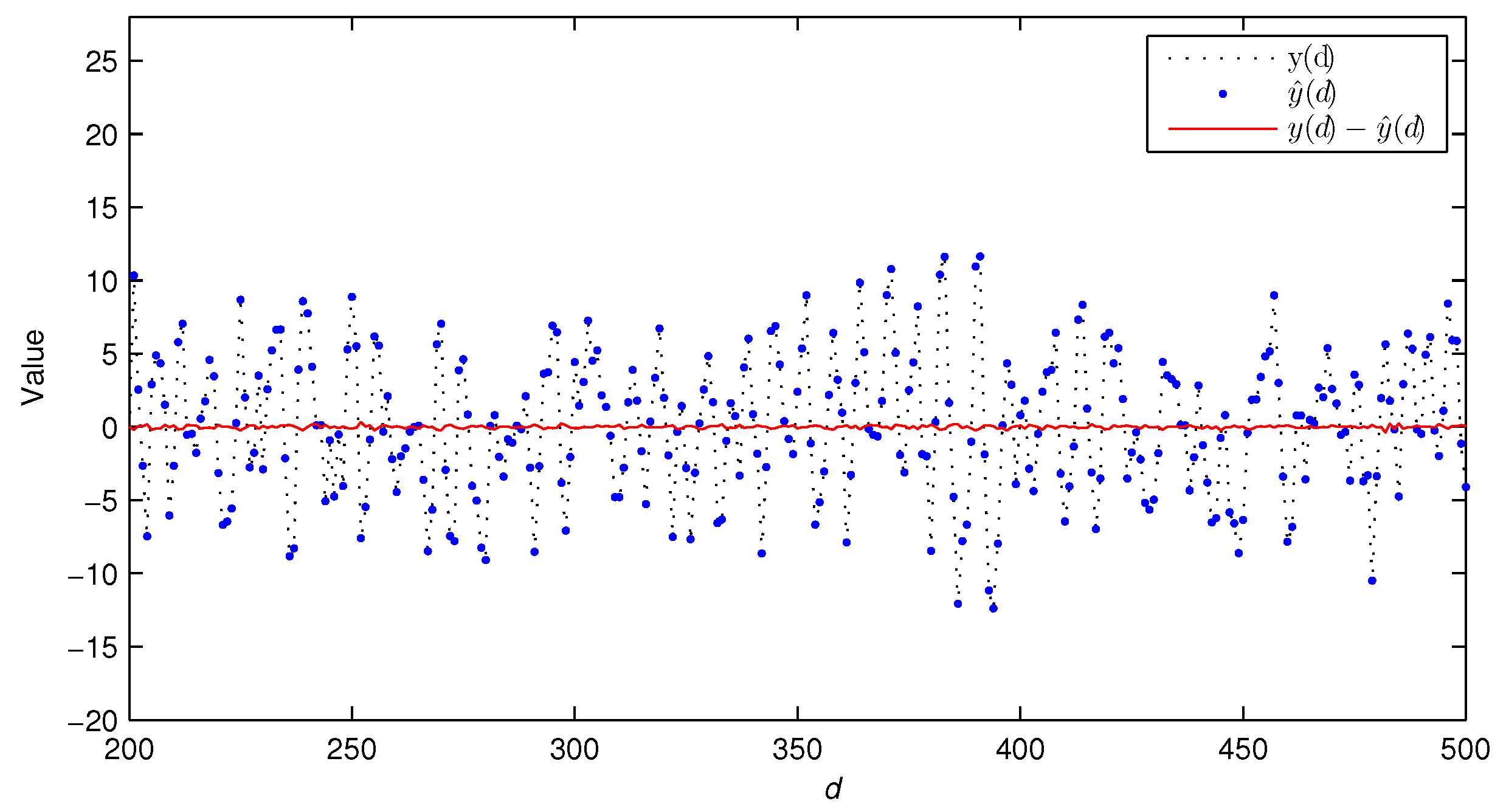
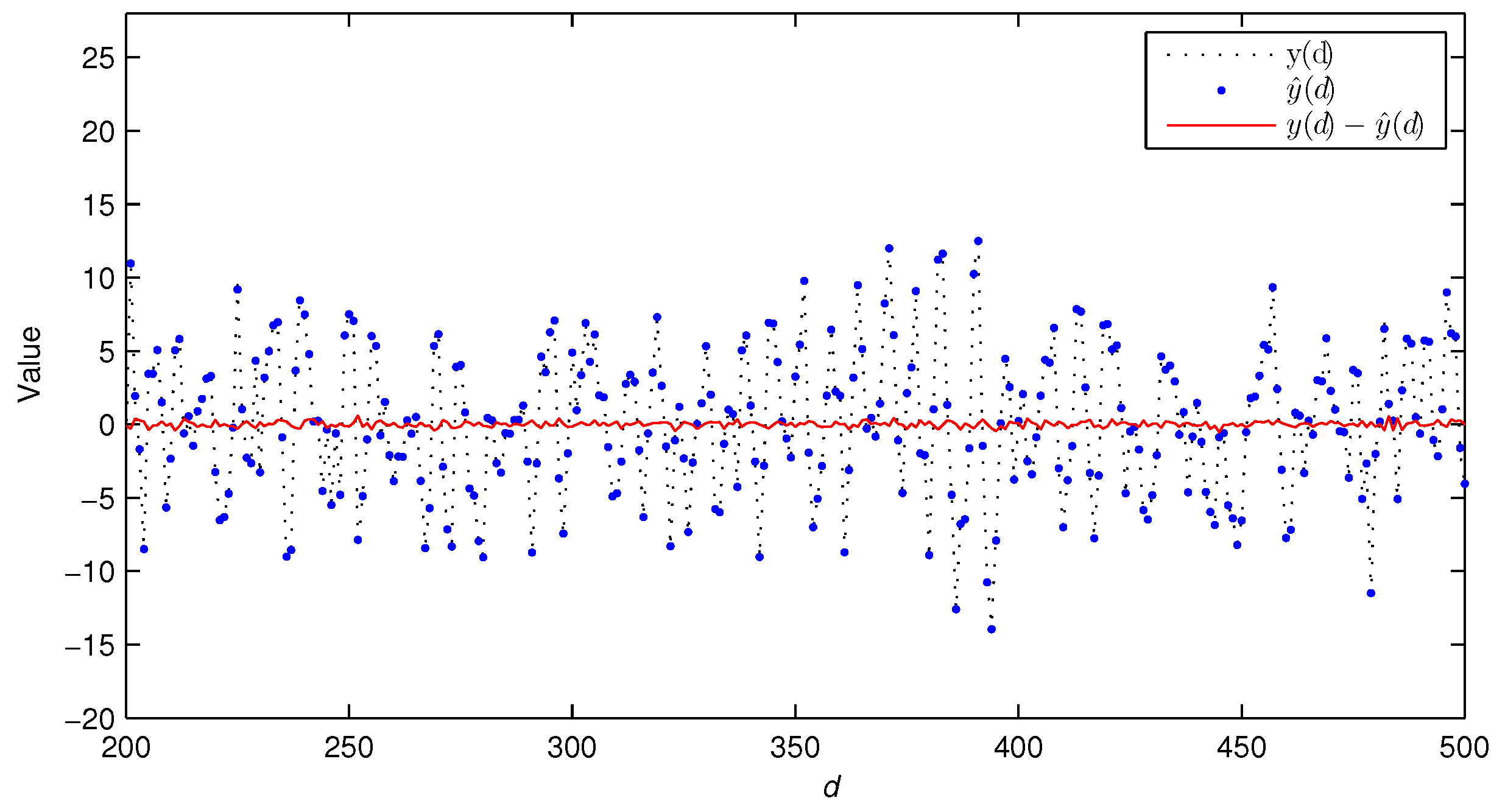
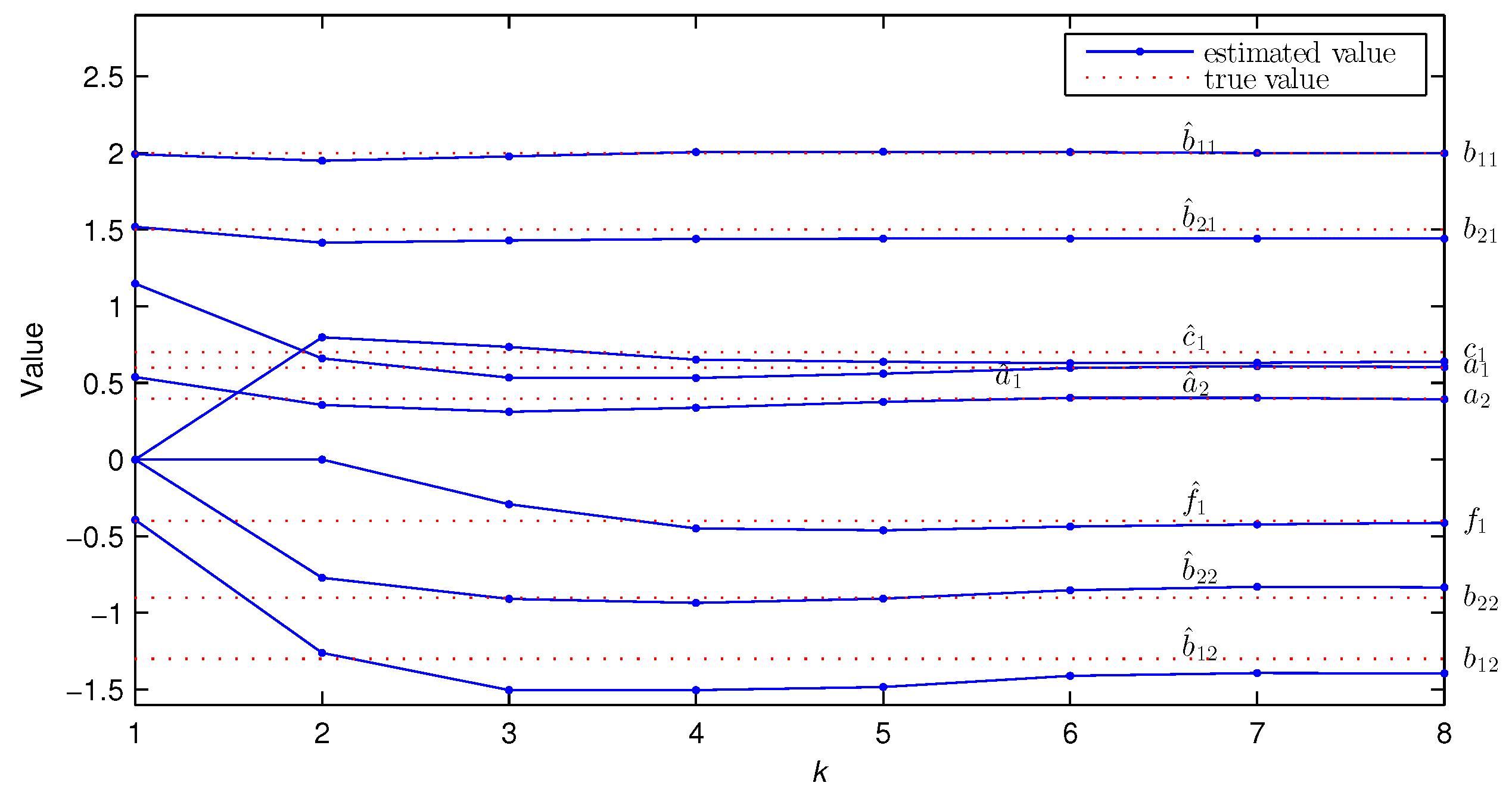
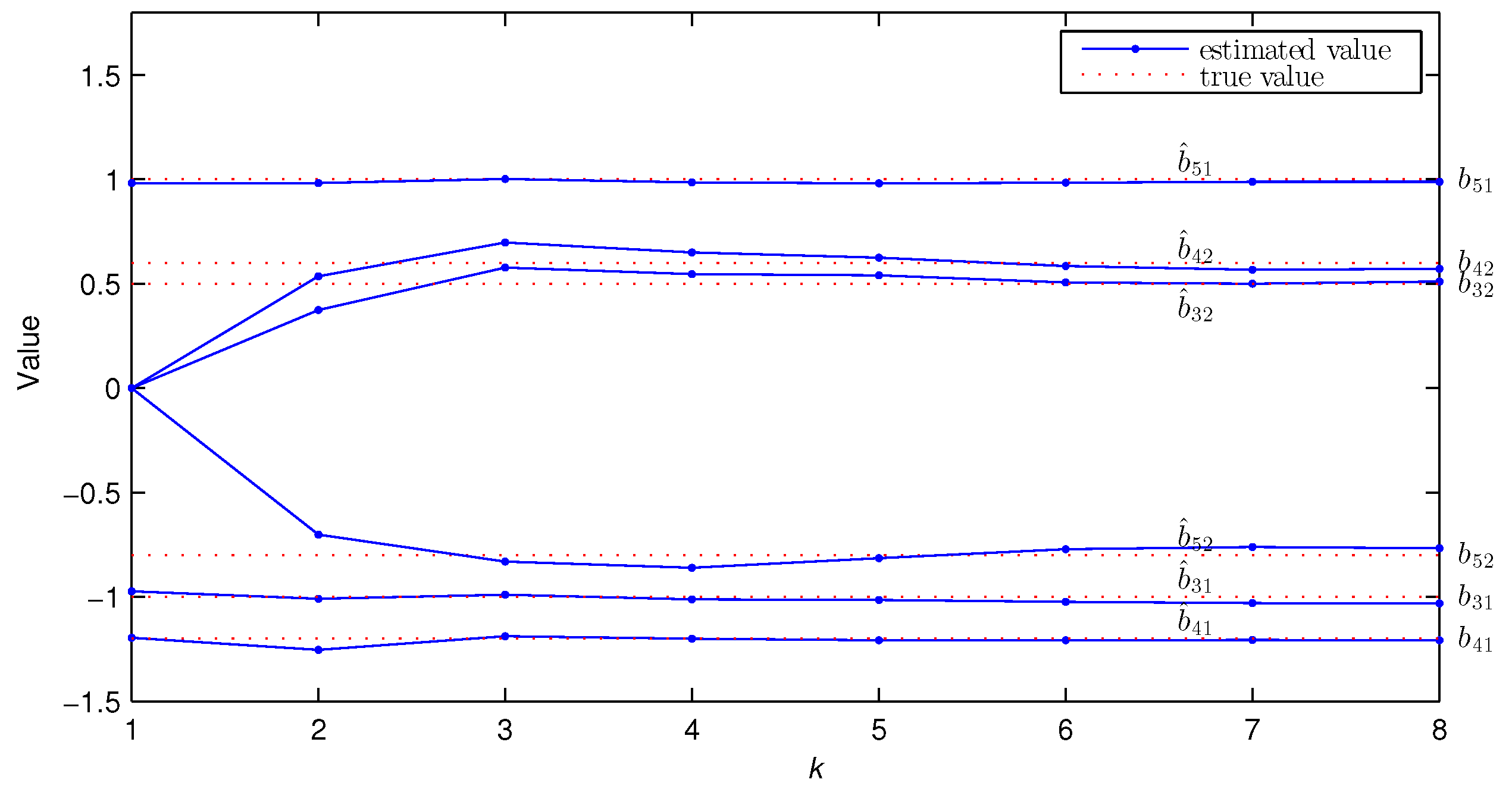
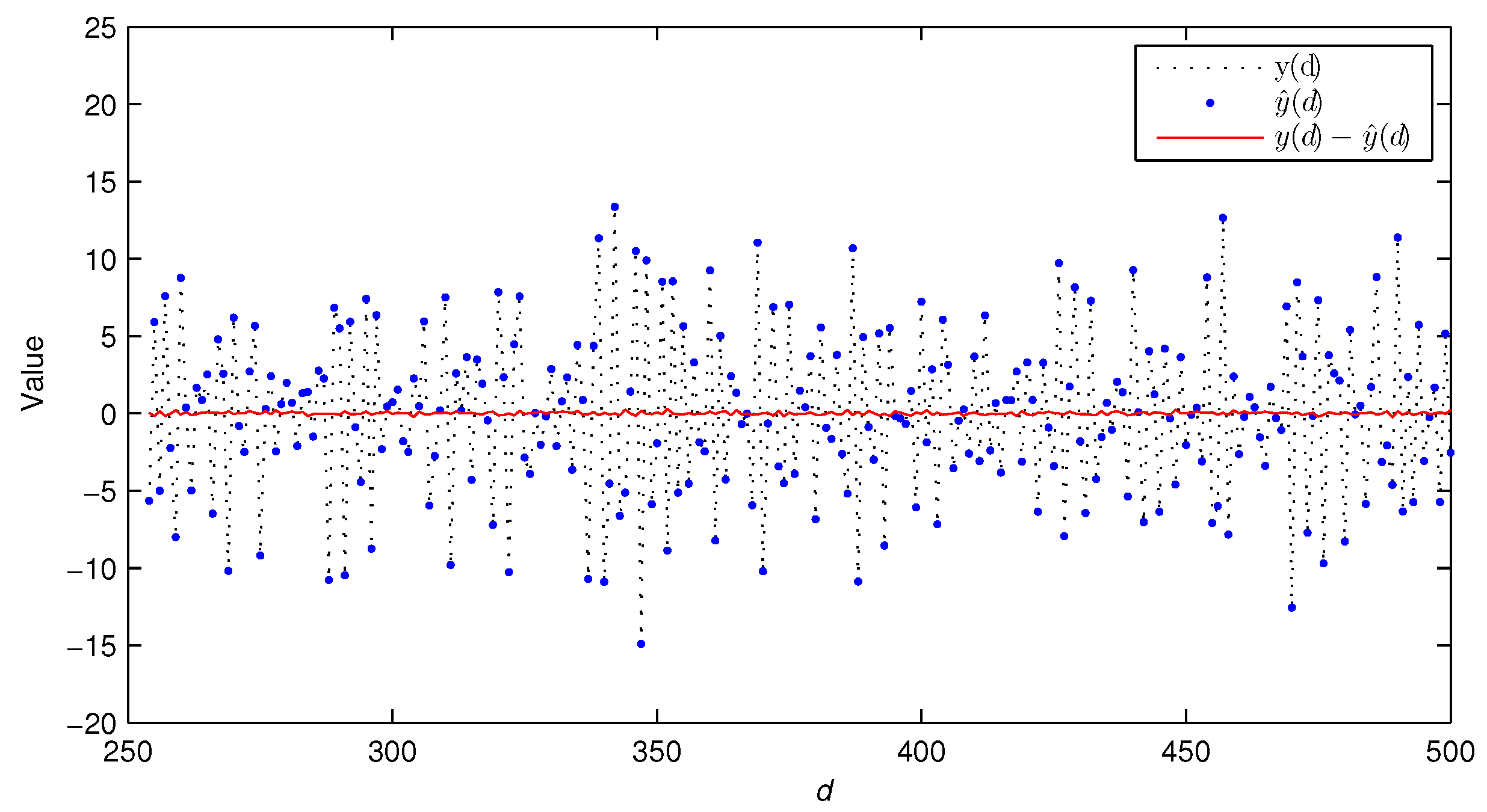
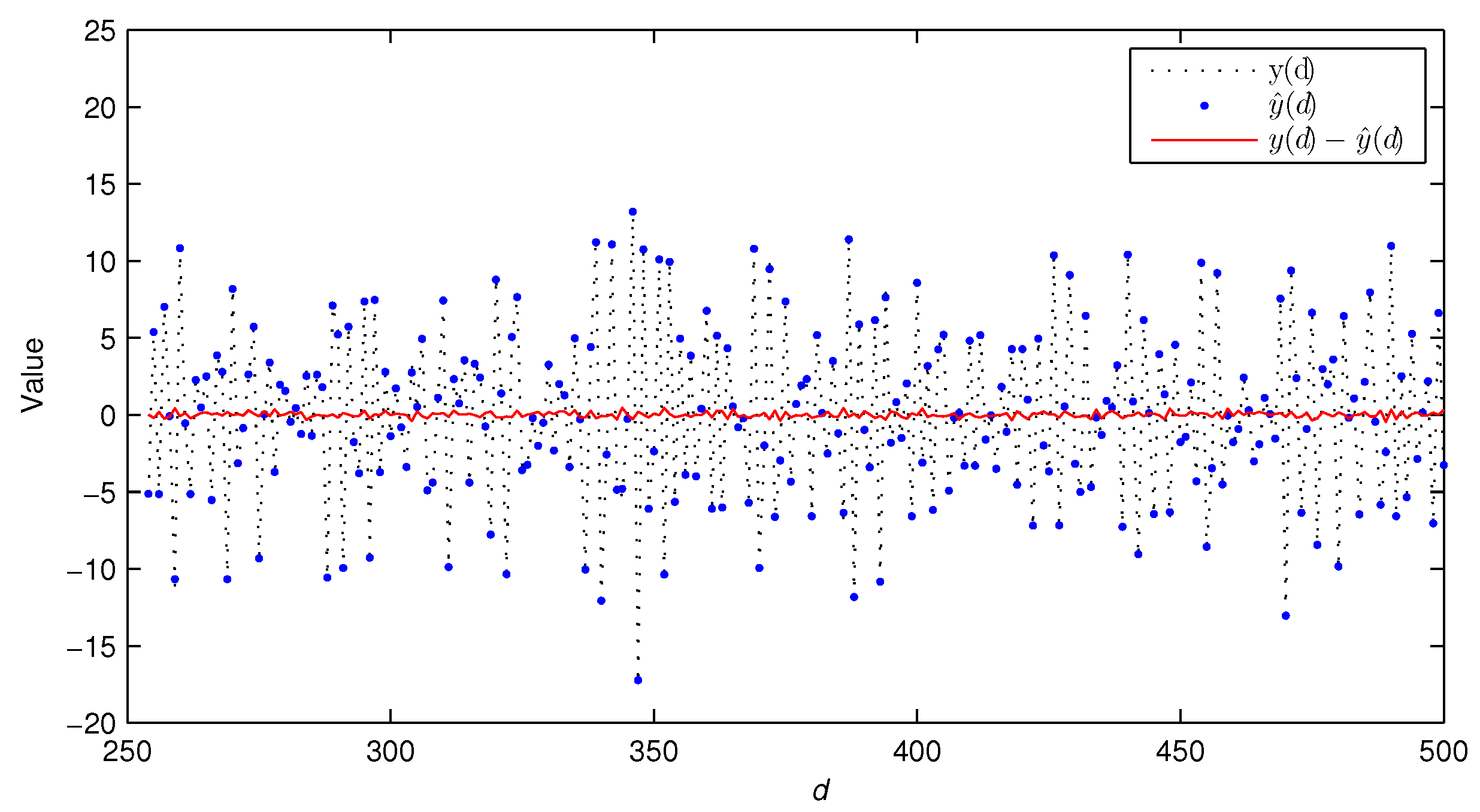
| k | % | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
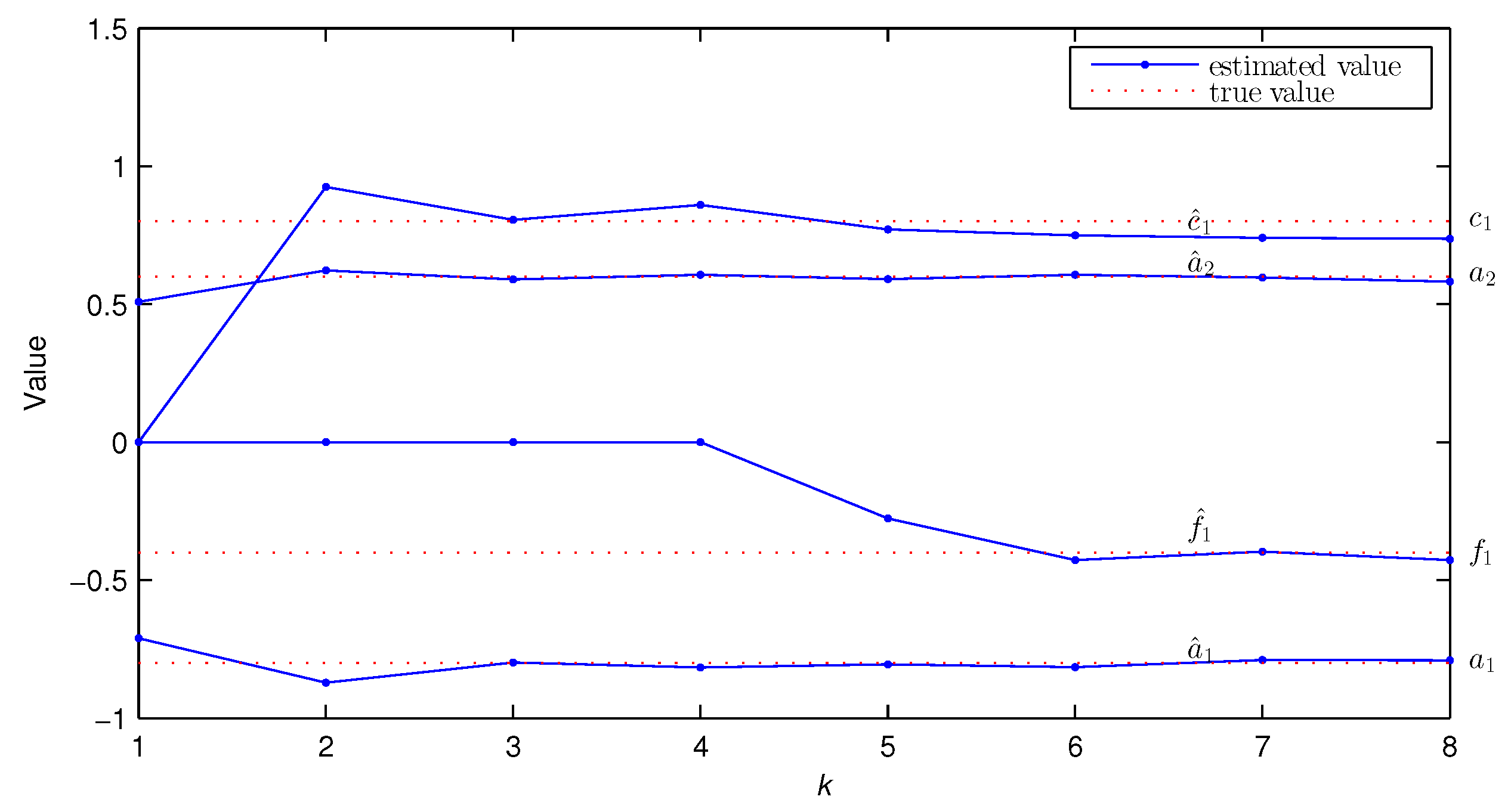
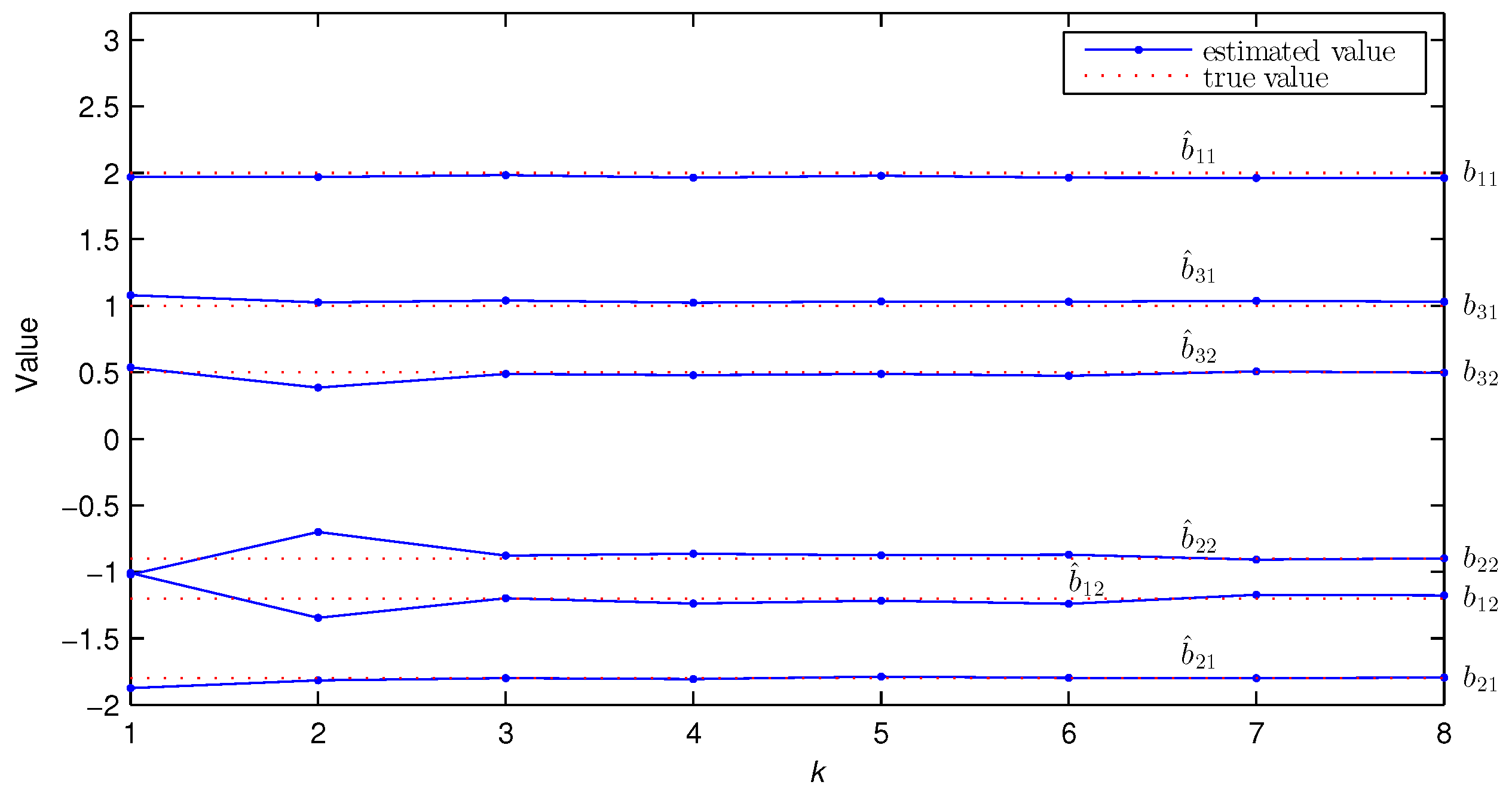
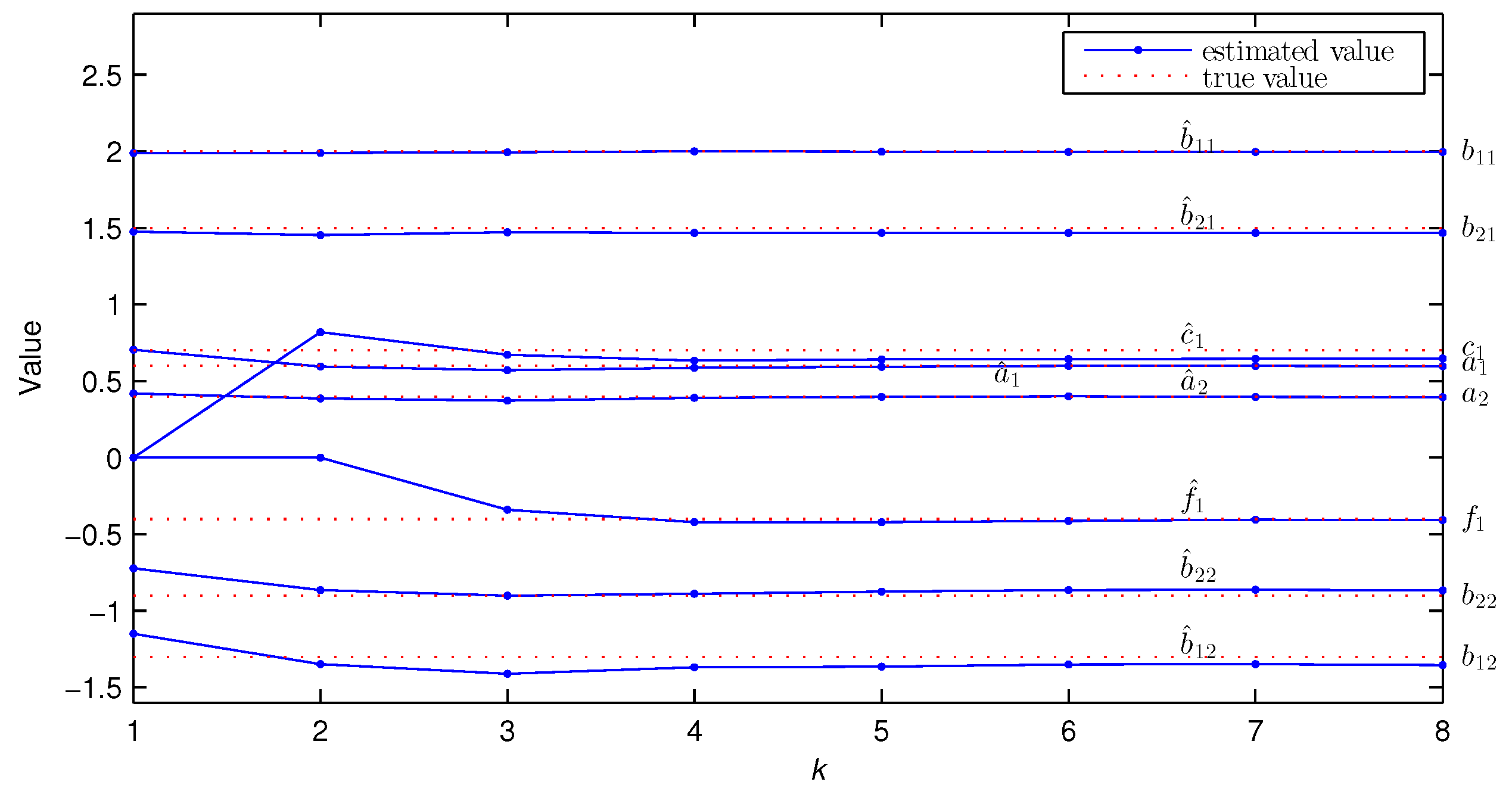
| 1 | −0.7107 | 0.5090 | 1.9694 | −1.0090 | −1.8753 | −1.0219 | 1.0790 | 0.5366 | 0.0000 | 0.0000 | 27.7831 | |
| 2 | −0.8717 | 0.6218 | 1.9681 | −1.3473 | −1.8160 | −0.7010 | 1.0268 | 0.3843 | 0.9248 | 0.0000 | 15.8395 | |
| 3 | −0.7982 | 0.5895 | 1.9816 | −1.1991 | −1.7996 | −0.8780 | 1.0396 | 0.4889 | 0.8053 | 0.0000 | 12.1355 | |
| 5 | −0.8052 | 0.5905 | 1.9772 | −1.2174 | −1.7890 | −0.8756 | 1.0339 | 0.4876 | 0.7704 | −0.2763 | 3.9074 | |
| 8 | −0.7905 | 0.5818 | 1.9615 | −1.1770 | −1.7950 | −0.9001 | 1.0299 | 0.4972 | 0.7374 | −0.4265 | 2.5213 | |
| 1 | −0.5319 | 0.3512 | 1.9279 | −0.6311 | −1.9520 | −1.3414 | 1.1347 | 0.6812 | 0.0000 | 0.0000 | 40.4417 | |
| 2 | −1.1028 | 0.6513 | 1.9611 | −1.7779 | −1.8306 | −0.1742 | 1.0516 | 0.0000 | 1.1758 | 0.0000 | 42.0247 | |
| 3 | −0.7517 | 0.6354 | 1.9523 | −1.1405 | −1.8269 | −0.9556 | 1.1100 | 0.5334 | 0.6873 | 0.0000 | 16.0285 | |
| 5 | −0.8796 | 0.6296 | 1.9260 | −1.3454 | −1.8156 | −0.7463 | 1.0452 | 0.4368 | 0.9477 | 0.0000 | 17.9049 | |
| 8 | −0.8218 | 0.5847 | 1.9238 | −1.2333 | −1.7917 | −0.8439 | 1.0565 | 0.4663 | 0.7521 | −0.4519 | 4.0108 | |
| True values | −0.8000 | 0.6000 | 2.0000 | −1.2000 | −1.8000 | −0.9000 | 1.0000 | 0.5000 | 0.8000 | −0.4000 | ||
| Sampled Data Length L | 400 | 500 | 600 | 700 | 800 | 1000 |
|---|---|---|---|---|---|---|
| Estimation error | 2.3931 | 2.591 | 2.0535 | 1.6165 | 1.9868 | 2.2789 |
| Estimation error | 6.1781 | 5.9393 | 4.1059 | 4.3916 | 3.6913 | 4.5132 |
| Parameter | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Location | 1 | 2 | 9 | 10 | 48 | 49 | 83 | 84 | 93 | 94 |
| k | % | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
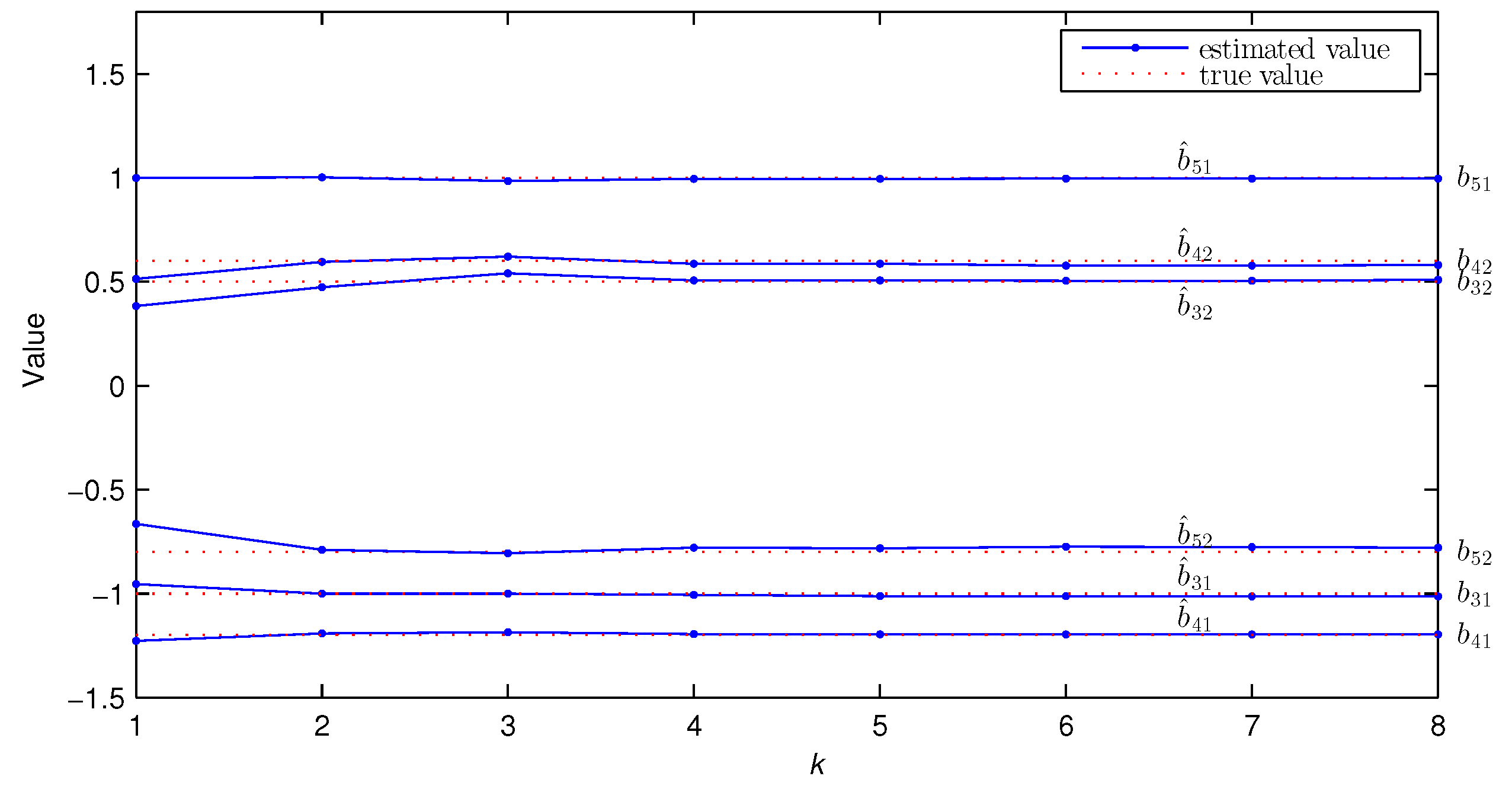
| 1 | 0.7043 | 0.4193 | 1.9900 | −1.1505 | 1.4756 | −0.7222 | −0.9542 | 0.3833 | −1.2275 | 0.5137 | 0.9985 | −0.6643 | 0.0000 | 0.0000 | 24.0379 | |
| 2 | 0.5958 | 0.3868 | 1.9909 | −1.3471 | 1.4534 | −0.8632 | −0.9999 | 0.4732 | −1.1926 | 0.5949 | 1.0018 | −0.7892 | 0.8209 | 0.0000 | 11.8417 | |
| 3 | 0.5702 | 0.3731 | 1.9940 | −1.4102 | 1.4709 | −0.9009 | −1.0007 | 0.5398 | −1.1864 | 0.6208 | 0.9846 | −0.8065 | 0.6720 | −0.3408 | 3.8284 | |
| 5 | 0.5937 | 0.3974 | 1.9985 | −1.3644 | 1.4680 | −0.8740 | −1.0119 | 0.5066 | −1.1964 | 0.5860 | 0.9948 | −0.7824 | 0.6427 | −0.4213 | 2.6627 | |
| 8 | 0.5971 | 0.3944 | 1.9958 | −1.3538 | 1.4675 | −0.8662 | −1.0131 | 0.5092 | −1.1959 | 0.5802 | 0.9964 | −0.7793 | 0.6478 | −0.4059 | 2.4836 | |
| 1 | 1.1487 | 0.5378 | 1.9923 | −0.3923 | 1.5176 | 0.0000 | −0.9743 | 0.0000 | −1.1962 | 0.0000 | 0.9823 | 0.0000 | 0.0000 | 0.0000 | 68.7931 | |
| 2 | 0.6610 | 0.3569 | 1.9489 | −1.2599 | 1.4150 | −0.7717 | −1.0095 | 0.3747 | −1.2543 | 0.5356 | 0.9832 | −0.7020 | 0.7977 | 0.0000 | 15.6424 | |
| 3 | 0.5342 | 0.3111 | 1.9775 | −1.5040 | 1.4303 | −0.9078 | −0.9906 | 0.5777 | −1.1896 | 0.6985 | 1.0027 | −0.8310 | 0.7349 | −0.2909 | 7.8178 | |
| 5 | 0.5616 | 0.3767 | 2.0078 | −1.4832 | 1.4422 | −0.9073 | −1.0159 | 0.5403 | −1.2081 | 0.6244 | 0.9810 | −0.8144 | 0.6377 | −0.4610 | 5.8361 | |
| 8 | 0.6041 | 0.3931 | 1.9989 | −1.3938 | 1.4410 | −0.8344 | −1.0317 | 0.5114 | −1.2076 | 0.5711 | 0.9894 | −0.7675 | 0.6391 | −0.4123 | 4.0277 | |
| True values | 0.6000 | 0.4000 | 2.0000 | −1.3000 | 1.5000 | −0.9000 | −1.0000 | 0.5000 | −1.2000 | 0.6000 | 1.0000 | −0.8000 | 0.7000 | −0.4000 | ||
| Sampled Data Length L | 300 | 400 | 500 | 600 | 700 | 800 | 1000 |
|---|---|---|---|---|---|---|---|
| Estimation error | 2.3844 | 1.7831 | 1.9832 | 2.5122 | 2.4627 | 2.388 | 1.8807 |
| Estimation error | 3.641 | 3.2164 | 4.055 | 4.7375 | 4.5741 | 4.1934 | 3.2887 |
| Parameter | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Location | 1 | 2 | 12 | 13 | 76 | 77 | 118 | 119 | 183 | 184 | 220 | 221 | 253 | 254 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, R.; Tao, T. A Greedy Pursuit Hierarchical Iteration Algorithm for Multi-Input Systems with Colored Noise and Unknown Time-Delays. Algorithms 2023, 16, 374. https://doi.org/10.3390/a16080374
Du R, Tao T. A Greedy Pursuit Hierarchical Iteration Algorithm for Multi-Input Systems with Colored Noise and Unknown Time-Delays. Algorithms. 2023; 16(8):374. https://doi.org/10.3390/a16080374
Chicago/Turabian StyleDu, Ruijuan, and Taiyang Tao. 2023. "A Greedy Pursuit Hierarchical Iteration Algorithm for Multi-Input Systems with Colored Noise and Unknown Time-Delays" Algorithms 16, no. 8: 374. https://doi.org/10.3390/a16080374
APA StyleDu, R., & Tao, T. (2023). A Greedy Pursuit Hierarchical Iteration Algorithm for Multi-Input Systems with Colored Noise and Unknown Time-Delays. Algorithms, 16(8), 374. https://doi.org/10.3390/a16080374




