Abstract
An algorithm is presented for the construction of an asymptotic approximation of a stable stationary solution to a diffusion equation system in a two-dimensional domain with a smooth boundary and a source function that is discontinuous along some smooth curve lying entirely inside the domain. Each of the equations contains a small parameter as a factor in front of the Laplace operator, and as a result, the system is singularly perturbed. In the vicinity of the curve, the solution of the system has a large gradient. Such a problem statement is used in the model of urban development in metropolitan areas. The discontinuity curves in this model are the boundaries of urban biocenoses or large water pools, which prevent the spread of urban development. The small parameter is the ratio of the city’s outskirts linear size to the whole metropolis linear size. The algorithm includes the construction of an asymptotic approximation to a solution with a large gradient at the media interface as well as the steps for obtaining the existence conditions. To prove the existence and stability theorems, we use the upper and lower solutions, which are constructed as modifications of the asymptotic approximation to the solution. The latter is constructed using the Vasil’yeva algorithm as an expansion of a small parameter exponent.
1. Introduction
Boundary value problems for partial differential equations provide models of physical processes in media with discontinuous characteristics [1,2,3]. In connection with this, questions arise about the existence and smoothness classes of solutions to these problems, as well as the suitable difference methods for their numerical solution. In the literature, one can find a variety of publications concerning the existence of non-classical solutions for equations with discontinuous coefficients. In [4], extensive material on the properties of generalized solutions to elliptic and parabolic equations with inhomogeneities can be found, and theorems on the comparison principle are formulated and proven. In [5], the existence theorems for strong solutions to boundary value problems for elliptic equations with inhomogeneities of the Caratheriodori type are proven. The definition of the upper and lower solutions is formulated, and the comparison principle is proven. The same procedure was carried out for parabolic equations in these works [6,7]. There are few works on systems of equations with discontinuous terms [8,9,10].
Here, we present an algorithm for the construction of an asymptotic approximation of a stable stationary solution to a system of diffusion equations with discontinuous sources by using the example of one model problem.
The statement of the problem considered in this paper arose in the course of developing a model for megacities’ growth [11,12]. According to this model, the expansion of urban development is described using a system of autowave diffusion equations. Large megacities are characterized by a mosaic structure when densely built-up areas alternate with urban biocenoses, such as parks or large reservoirs. The boundaries of biocenoses can be interpreted mathematically as media interfaces. At the interface, a sharp transition layer is formed from dense urban development to an almost natural landscape. The model also takes into account the influence of inhibitors, which are factors that prevent development. In [11], such a factor was the area of destroyed green spaces, which was limited by regulations, and in [12], it was the cost per square meter of built-up area. We call the area in which the activator and inhibitor change sharply from their values in the urban environment to the values within biocenoses the internal transition layer. The linear size of the transition layer is small compared with the linear size of the metropolis, and thus the mathematical formulation of the model contains a small parameter. Based on the physical meaning, the width of the transition layer of the activator is an order of magnitude smaller than that of the inhibitor; that is, the transition layer has two scales. This is taken into account in the model due to the different powers of the small parameter as a factor in front of the Laplace operator in the diffusion equations. Note that such an occurrence of a small parameter makes the problem singularly perturbed.
The functions on the right side of the system of equations contain information about the interaction between the activator and the inhibitor. In its meaning, the activator enhances the action of the inhibitor, and the inhibitor slows down the action of the activator. Mathematically, this can be specified using the so-called quasi-monotonicity conditions, which are conditions on the sign of the derivative of the source function in any equation with respect to the argument corresponding to that solution component that is a parameter in this equation.
A system of equations similar to the present work in the case of smooth right-hand sides was considered in [13]. However, in this work, a system was considered with quasi-monotonicity conditions with the same negative signs of the mentioned derivatives. In this paper, we consider all four different versions of the quasi-monotonicity conditions, for which the upper and lower solution method is presented in [14].
The novelty of this work should be noted:
- A technique is developed for studying problems with internal transition layers for systems of parabolic and elliptic equations with discontinuous functions on the right-hand side in two-dimensional domains. Earlier in [15], for simplicity, we studied a similar problem on a segment. In this paper, we show how the algorithm for the construction of an asymptotic approximation to the solution can be developed for the case of a problem in two-dimensional domains. Furthermore, in Section 3.4, we demonstrate the application of this algorithm using the example of a system of equations that was used in the megacity development model [11,12].
- The substantiation of the existence of smooth solutions to elliptic and parabolic problems with functions on the right-hand side that have jumps along a smooth curve in a two-dimensional domain is carried out.
The main contributions of this work are the following:
- The present work is the final study of one aspect of the mathematical validation of the megacity development model. The proof of the existence of a stable stationary solution with a large gradient in the vicinity of the media discontinuity line makes the numerical solution of this problem justified, regardless of the applied solution schemes.
- The developed algorithm can also be applied to other biophysical problems, such as the appearance of spots on animal skins [16].
2. Materials and Methods
We consider the following problem:
where is a connected domain in the coordinate space with a closed smooth boundary ; is a small parameter; is the derivative with respect to the internal normal to the curve ; and the functions , are smooth in and satisfy the matching conditions
It is assumed that the functions and have jumps on some surface , where is a simple, smooth closed curve lying entirely in the domain D:
where and . For definiteness, we assume that is the domain enclosed between the internal curve and the boundary . In turn, is the domain bounded by . The construction of an asymptotic approximation to the solution is a generating part of the algorithm. A requirement for the functions and to be sufficient to construct the nth-order asymptotic is that these functions are of a class , where and are some permissible intervals for changing variables u and v, respectively. In order to appreciate the behavior of the solution, it is enough to construct its asymptotic approximation of the zero or first order. When proving the existence and stability theorems, we use the possibility of constructing an asymptotic approximation of the order .
We define the solution to Problem (1) as follows:
Definition 1.
Obviously, the stationary solution to Problem (1) is the solution to the following elliptic problem:
We will assume that the solution to this problem is in the sense of the following definition:
Definition 2.
We are interested in a stationary solution with a large gradient at the media interface. The algorithm that we present allows us to construct an asymptotic approximation of such a solution and obtain the conditions for its existence. It consists of the following steps:
- Construction of an asymptotic approximation to the solution using the Vasil’eva algorithm [17];
- Construction of the upper and lower solutions, using the asymptotic method of differential inequalities as modifications of the asymptotic approximation [18];
- Proof of the existence of a solution through the method of monotone iterations [14];
- Proof of the stability of the solution through the barrier method [18].
3. Results
In the course of applying the algorithm, we obtained propositions under which Problems (1) and (3) have a solution with a large gradient in the vicinity of the curve .
Proposition 1.
There is an isolated solution to each of the equations
on , and the inequalities hold:
Furthermore, we denote .
Proposition 2.
There is an isolated solution to each of the equations on the set , and the inequalities hold:
In this paper, we study a stationary solution to Problem (3) that is close to the functions in the domain and to the functions in which changes sharply from the values of up to in a small vicinity of the curve . In what follows, we will refer to this vicinity as the internal transition layer.
The next proposition is called the “quasi-monotonicity conditions”.
Proposition 3.
Let one of four pairs of inequalities hold
for all with .
When constructing asymptotic approximations for solutions to boundary value problems with internal transitional and boundary layers, an important stage is the study of the so-called adjoint equations [17]. In this paper, the properties of the adjoint problems determine the existence of functions that describe the internal transition layer. To construct these functions, it is expedient to use local coordinates in a small vicinity of the curve in the same way as in [19].
We denote with the normal to the curve directed inside the domain . We introduce local coordinates in as follows:
The r coordinate is considered positive if and negative if .
As noted in the introduction, the transition layer has two spatial scales. Therefore, to describe the behavior of the solution in the transition layer, it is necessary to introduce two different stretched variables:
The existence and properties of the transition layer functions are related to the existence and properties of the solutions and to the following (adjoint) problems:
It is known [20,21] that under Propositions 1 and 2, there are nonempty sets such that the solution to each of the problems (Equations (6) and (7)) exists if and .
We denote
With admissible values and for any , there exists a phase trajectory entering the point on the phase plane when and a phase trajectory entering the point when . These phase trajectories can be written explicitly as
With admissible values and for any , there exist phase trajectories entering the respective points on the phase plane :
To construct an asymptotic approximation of the solution with an internal transition layer to Problem (3), it is necessary to require that nonempty intersections of the sets of admissible values and exist. In this case, we can introduce the functions
We have one more proposition:
Proposition 4.
Let be the unique solution to the equation and the function be the unique solution to the equation .
Let some vicinity of the function belongs entirely to the set , and let some vicinity of the function entirely belongs to the set . Then, the inequalities hold:
Remark 1.
Remark 2.
The inequalities from Proposition 4 are equivalent to
Furthermore, we introduce the functions
on the sets for functions with the superscript “” and for functions with the superscript “”, and introduce the notation
Proposition 5.
Let in the domains , and for the relations hold:
3.1. Algorithm for the Construction of an Asymptotic Approximation of the Solution to the Stationary Problem
The nth-order asymptotic representation of the solution that has an internal transition layer in the vicinity of for Problem (3) is built separately in each of the domains :
The asymptotic representations and consist of the regular part functions depending on , which we will mark with an overline, and functions of the transition layer of two scales: Q-functions and M-functions, depending on the stretched variables and , respectively, which are defined by the equalities in Equation (5). The asymptotic representations and , in addition to the regular part and the transition layer functions, also include boundary functions of two scales that describe the solution in the vicinity of the boundary . To determine them, local coordinates like those in Equation (4) and stretched variables and are introduced in the vicinity of the boundary.
In turn, each component of the asymptotic representation is a sum over small parameter exponents:
The functions and , as well as and , are matched continuously on the curve in such a way that the equalities are fulfilled:
where and are the functions mentioned in Proposition 4. The functions and , at each step k are determined from the equalities of the derivatives of the functions , :
Furthermore, in the text, we will use the notations
The same notations will be used for the derivatives of the functions f and g.
3.1.1. The Regular Part of the Asymptotic Representation
The functions of the regular part, and , , are defined in such a way that the following equalities are satisfied:
In order to obtain the equations from which the regular part functions are determined, it is necessary to expand the functions on the left side of these equalities according to the Taylor formula and equate the coefficients at the same powers of epsilon.
In particular, in the zeroth order, Propositions 1 and 2 imply
The kth-order functions and , , are the solutions to systems of equations
where the notation in Equation (17) is used and , are the known functions, particularly
The systems in Equation (19) are solvable due to Propositions 1–3.
3.1.2. The Transition Layer Functions
The transition layer functions describe a sharp change in the solution in the vicinity of the curve . To determine them, we introduce the local coordinates determined by Equation (4) and the stretched variables and defined by the equalities in Equations (5). In this case, the operator is transformed as follows [19]:
where , , are known differential operators of the first or second order [19] and denotes the curvature. We assume that the curvature has a positive sign at the point if the center of the circle of curvature at this point is in the region .
The systems of equations for the transition layer functions are obtained in the standard way [17] by equating the coefficients at the same powers of in the Taylor expansion of the equalities
Here, we denote
and we define the functions in the same way;
The functions are defined by analogy with .
Proceeding in this way, we will obtain differential equations for the functions , and finite equations for the functions , . We set the supplementary condition of decreasing to zero at infinity for the differential equations and also the conditions at and for the functions , in such a way that the equalities in Equation (15) are satisfied in the ith order.
The functions and turn out to be trivial.
Furthermore, we denote
From the equalities in Equation (20) in the zeroth order, we obtain the expressions for the functions :
Next, we aggregate the zero-order terms in the Taylor expansions of the equalities in Equation (21) and substitute the expressions for into the resulting equalities. The equations we obtain this way coincide with Equation (6). We solve these equations on half-lines and with additional conditions at infinity and the condition for , which is obtained from the equality in the second line of Equation (15):
As noted at the beginning of Section 3, the functions exist if is small enough that the values of the function satisfy Proposition 4, and the following estimates are valid [20,21]:
where C and are positive constants.
We denote
For the functions , from the equalities in Equation (22), we obtain equations that coincide with the adjoint equation (Equation (7)). We set for them the conditions from the first equality in Equation (15) and conditions at infinity:
The functions exist if is sufficiently small and they have exponential estimates [20,21]:
where C and are positive constants.
We obtain the higher terms of the asymptotic representation (of the order ) in successive steps:
- We determine the functions from the equations obtained from Taylor expansion in the small parameter of the equalities in Equation (23) with supplementary conditions at infinity:where are known exponentially decreasing functions (see [17]).
- From the equalities in Equation (20), algebraic equations are obtained, from which we define the functions :where are known functions decreasing exponentially to zero as ; in the first order they are as follows:Here, we have taken the identities into account and the first part of Equation (19) for .
- From the equalities in Equation (21) with known expressions for , we obtain equations for the functions . We solve them on the half-lines and respectively, with the supplementary conditions at infinity and at :The functions are known at each step; in the first order they are expressed asHere, the identities and the second part of Equation (19) for are taken into account. The functions , decrease exponentially to zero as .
- We determine the functions. The equations for them are obtained from the equalities in Equation (22). These functions are defined as the solutions to the problemswhere are known exponentially decreasing functions as . In particular, we have
The transition layer functions have estimates [17]:
where C and are positive constants.
3.1.3. Matching of the Asymptotic Approximation Derivatives
Taking into account the expansions in Equations (13) and (14), we can represent the conditions for matching derivatives (Equation (16)) as
where the functions , are defined by the expressions in Equation (10):
and similarly for , , .
The conditions for matching of the derivatives in Equation (16) in the zeroth order are satisfied due to Proposition 4. The coefficients and of the expansions in Equation (15) are determined from the equations obtained from the equalities in Equation (25):
These equations are solvable due to Proposition 4. Here, , are known functions; in the first order these functions are as follows:
3.1.4. Boundary Functions
The boundary functions for this problem were obtained in earlier works [22,23].
3.2. Algorithm for the Construction of the Upper and Lower Solutions Using the Asymptotic Method of Differential Inequalities
We denote
Here, as above, is the normal to the curve at the point directed inside the domain .
We use the definition of the upper and lower solutions of Problem (3) according to what is given in [14] (see also [15]):
Definition 3.
Pairs of functions and of the class are called the upper and lower solutions to Problem (3), respectively, if the following inequalities hold:
- (A1).
- ,,;
- (A2).
- ;
- (A3).
- , , ;
- (A4).
- .
Following [14], we then replace Condition (A2) for each particular type of quasi-monotonicity with the corresponding more stringent condition
3.2.1. Construction of the Upper and Lower Solutions
The asymptotic method of differential inequalities is essentially an algorithm that allows one to construct the upper and lower solutions based on an asymptotic expansion in powers of a small parameter [13,18]. We will apply this method using the nth-order asymptotic representation, by which we mean the functions in Equations (12)–(14) with the parameters and (see Equation (15)) replaced by , .
The upper and lower solutions to Problem (3), as well as the asymptotic approximation in Equation (12), will be constructed separately in the domains and :
where
The terms and were added to ensure the fulfillment of the inequalities in Condition (A3). For this, we choose the constants and to be sufficiently large positives (see [23]), and are included to achieve continuity of the functions on . They eliminate small residuals in the condition of continuous matching introduced by the boundary layer functions. The terms and eliminate jumps of order no lower than for the functions on the curve .
We include the functions and in the upper and lower solutions to fulfill Condition (A2) far from the internal transition layer. For these functions, we have the systems of equations
where A and B are positive constants. Notations like those in Equation (17) are used here. These systems are uniquely solvable given Propositions 1–3 and 5 (the latter for quasi-monotonicities of the NP and PN types), and their solutions are strictly positive (see [23]).
The functions , are defined for , and , for , in such a way as to remove residuals in the inequalities in Condition (A2) (the second line) that the functions and introduce near the transition layer. To satisfy the inequalities in Equation (26), we define these functions as the solutions to
Here, we have
and , and are some positive constants that can be chosen in a way to provide positive values of the functions , .
By expressing , we come to the problems for the functions . Note that the equations for these functions are specific to various types of quasi-monotonicities:
Here, are the functions defined by the expressions in Equation (11) and
We choose the constant so that for all , the inequalities hold; the value in the expression in Equation (35) is chosen large enough, and is chosen small enough to provide the negativeness of the functions in the corresponding domains and . This guaranties that the solutions to Problems (33) are strictly positive, and we can obtain these functions explicitly:
where are defined in Equation (8).
In order for the solutions to Problems (34) in the case of the NP and PN types of quasi-monotonicities to be strictly positive, Proposition 5 is required. In this case, the functions are written as
where are the solutions to
These functions are strictly positive and decrease exponentially to zero as (see [14,15] (T. 9.3 p. 354)), and for all , the inequalities hold [15]:
The functions , expressed with the equalities in the first line of Equation (32), also turn out to be positive since Proposition 1 is satisfied. They have estimates like that in Equation (24) as well as the functions .
The functions remove residuals in the inequalities in Condition (A2) (the first line), introduced by the functions , , in the transition layer. We set them as the solutions to
where is a positive value and has the sense of the notation from Equation (18):
The solutions to Problems (37) can be explicitly expressed:
The constant is chosen so that the first terms in the expressions for are positive, (this is possible due to the positiveness of the functions ; see Equation (9).) and is chosen to be large enough and the positive constant small enough so that the functions are strictly negative. Then, the values of are strictly positive for and . Like all transition layer functions, have estimates like those in Equation (24).
We define the functions as the solutions to
where are known functions with estimates like those in Equation (24).
3.2.2. Proof of the Inequalities in Conditions (A1–A4)
In the previous section, we built the functions , . Now, we have to prove that these functions satisfy Conditions (A1–A4) for sufficiently small values and thus are indeed the upper and lower solutions of Problem (3). We will carry this out using the example of the upper solution.
The functions , , , and are defined so that they take strictly positive values in their domains. This ensures that Condition (A1) is satisfied.
We have built the asymptotic approximation in such a way that for any type of quasi-monotonicity, these inequalities are true (see the equalities in Equations (20)–(23)), as well as Equations (31), (32), (37) and (39):
This provides fulfillment of the inequalities in Equation (26) for sufficiently small values and positive constants A, B, and .
Condition (A3) is proven in the same way as in [23].
The differences in the derivatives of the U and V components of the upper solution in Condition (A4) can be expressed as follows:
Using the explicit form (Equation (38)) of the functions , we can obtain the expression for the jump of the derivatives of the upper solution’s U component on the curve that is valid for each type of quasi-monotonicity:
where the function is bounded and independent on . Here, we use the expression in Equation (10) (the second line). Due to Proposition 4, it is sufficient to choose the value to be sufficiently large so that the expression on the right-hand side is positive, and thus Condition (A4) for the upper solution’s U component is satisfied.
For the jump of the derivative of the V component of the upper solution in the case of NN and PP types of quasi-monotonicities, we have
where we use the expression in Equation (10) (the first line).
In the case of NP and PN types of quasi-monotonicities, the jump of the derivatives is
In each case, the function is bounded and independent on Taking into account Proposition 4 for a quasi-monotonicity of the NN or PP type, or taking into account the inequalities in Equation (36) for the NP or PN type, one ensures that the expression on the right side for the difference of the derivatives of the V component is positive by choosing the value of to be large enough. Thus, Condition (A4) will be satisfied for the V component.
3.3. Existence and Stability Results
Theorem 1.
Assuming Propositions 1–4 and 5 (the latter for quasi-monotonicities of the NP and PN types), for sufficiently small values, there exists a solution to Problem (3) in the sense of Definition 2, for which the pair of functions is an asymptotic approximation uniform in with an accuracy of ; in other words, we have
where C is a positive constant independent on ε.
Proof of Theorem 1.
The proof of this theorem is based on the following statement:
Lemma 1.
Let there be the pairs of functions and , which are the upper and lower solutions in the sense of Definition 3, respectively. Then, there exists at least one solution to Problem (3) in the sense of Definition 2 for which the following inequalities hold:
The proof of Lemma 1 can be carried out using the method of monotone iterations [14]. However, in [14] elliptic systems with continuous right-hand sides are dealt with. In the case of the system in Equation (3) with the right-hand sides of Equation (2), the proof given in [15] for the one-dimensional case is applicable, with reference to [5] regarding the smoothness of the solutions to linear problems for the terms of iterative sequences as well as reference to properties of the volume potential (see [24]) regarding the smoothness of the solution to Problem (3).
From Lemma 1, given the upper and lower solutions defined by the Equations (27)–(30), it follows that Problem (3) has a solution for which the inequalities in Equation (41) are valid. From here, we have
The differences on the left and right sides of each double inequality have the order (see Equations (27)–(30)), and the same order is for the differences To obtain the estimate (Equation (40)) from these inequalities, we just have to replace the index n with . □
Theorem 2.
Assuming Propositions 1–4 and 5 (the latter for quasi-monotonicities of the NP and PN types), for sufficiently small values, the stationary solution to Problem (1) is locally unique as a solution to Problem (3) and asymptotically stable in the sense of Lyapunov, with a domain of attraction no less than .
The proof of the theorem can be carried out similarly to one from [15] by rewriting it for the two-dimensional case and using the properties of the volume potential [25].
3.4. Example
As an example, let us consider the problem in the unit disk D such that , bounded by the circle :
In the case of positive and , this problem belongs to the “PN” type of quasi-monotonicity.
Let be an ellipse . Hence, and :
In the domain , we have . Assuming , the equation has a unique root , and therefore
In the domain , we have . The equation has three roots:
Only the function satisfies Proposition 1, and therefore
The functions exist for each , and the functions exist for . The equation has the unique solution , and the equation has the unique solution . Aside from that, for the expressions mentioned in Remark 2, we have
Thus, Propositions 1–5 are valid for Problem (42).
The corresponding stationary problem therefore has the following zeroth-order asymptotic approximation to its solution:
Here, we have and the function is the solution to the problem
Also in (45), The functions are the solutions to the problems
where the functions are given in Equations (43) and (44). The solutions to Problems (46) and (47) can be obtained numerically.
Figure 1a,b shows the zeroth-order asymptotic approximation in the case .
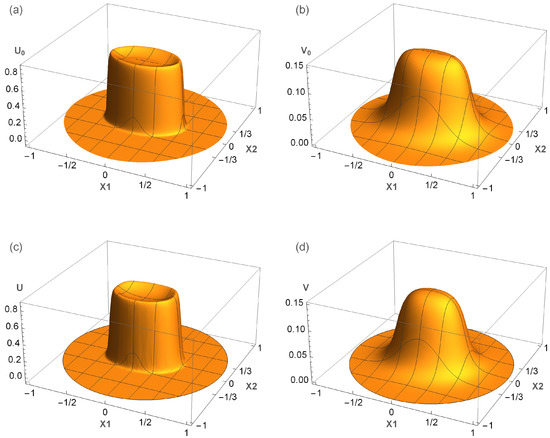
Figure 1.
The zeroth-order asymptotic approximation to the stationary solution to Problem (42): (a) U component and (b) V component. For the stabilized numerical solution: (c) U component and (d) V component. In each case .
Furthermore, we can solve Problem (42) numerically by setting the initial conditions as , . Note that these initial functions satisfy the propositions of Theorem 2. Over a rather long period of time, the numerical solution stabilizes to the stationary solution to Problem (42).
Figure 2 shows the graphs of the functions , depending on the argument and the sum on the same argument. The influence of the “slow” transition layer function can be seen quite clearly on the graphs in domain .
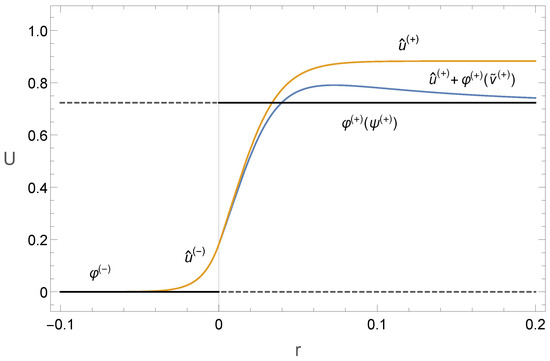
Figure 2.
The graphs of the functions , depending on the argument (yellow line) and the sum (blue line) on the same argument.
The numerical results were obtained using Wolfram Mathematica 12.1 with the native finite element method (FEM) extension. The calculations were performed by the standard NDSolve function with the custom parameters Method -> {“FiniteElement”, “MeshOptions” -> {MaxCellMeasure -> 0.00025}}, where MaxCellMeasure -> 0.00025 provided an extremely fine mesh over the unit disk with the center at (0,0). It is worth noting that WM 12.1 automatically took into account the discontinuities in and during mesh creation (by putting vertices onto the elliptic discontinuity curve) and during computations.
4. Discussion
The algorithm that we have presented here can be used to study singularly perturbed boundary value problems with internal transition and boundary layers. It is based on the asymptotic method of differential inequalities, which contains a technique for constructing upper and lower solutions as modifications of the asymptotic approximation to the solution. In turn, the presence of upper and lower solutions guarantees the existence of a solution that is uniformly approximated by the constructed asymptotics. In addition, the constructed upper and lower solutions can be further used in the barrier method to prove the asymptotic stability of the solution [26].
Since the application of the proposed algorithm leads to a proof of the existence and stability of the solution, it can be used to justify various models based on the diffusion equation.
The results of this study can be used to develop efficient numerical methods for solving stiff problems, particularly to create suitable grids [27,28].
For practical purposes, it is sometimes convenient to solve the problem numerically in a rectangular region. In this case, the algorithm for constructing the corner boundary functions should be added to the proposed algorithm [17,29,30].
5. Conclusions
It is no secret that the formulation of model problems often goes beyond the known theoretical studies on the existence of solutions. Predictions according to such models are often made only on the basis of numerical calculations. Despite the fact that numerical methods for solving parabolic equations are being actively developed [31,32], calculations cannot always be carried out with sufficient accuracy. Therefore, justification of the existence of solutions with certain properties is an actual area of mathematical research. The algorithm presented in our work allows us to partially solve the question of the applicability of the model for the development of megacities based on the FitzHugh–Nagumo system, namely the existence and stability of a solution that has a large gradient at the boundary of the environmental characteristics’ discontinuity.
Author Contributions
Conceptualization, N.N. and N.L.; methodology, B.T. and N.L.; software, B.T.; validation, B.T.; formal analysis, B.T.; writing—original draft preparation, N.L.; writing—review and editing, B.T.; supervision, N.N.; project administration, N.N.; funding acquisition, N.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Russian Science Foundation grant number 23-11-00069.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pavlenko, V.N.; Potapov, D.K. Elenbaas Problem of Electric Arc Discharge. Math. Notes 2018, 103, 89–95. [Google Scholar] [CrossRef]
- Bögelein, V.; Duzaar, F.; Gianazza, U. Sharp boundedness and continuity results for the singular porous medium equation. Isr. J. Math. 2016, 214, 259–314. [Google Scholar] [CrossRef]
- Bögelein, V.; Duzaar, F.; Marcellini, P.; Scheven, C. Doubly Nonlinear Equations of Porous Medium Type. Arch. Ration. Mech. Anal. 2018, 229, 503–545. [Google Scholar] [CrossRef]
- Carl, S.; Le, V.K.; Motreanu, D. Nonsmooth Variational Problems and Their Inequalities Comparison Principles and Applications; Springer Science+Business Media, LLC: New York, NY, USA, 2007; pp. 10–210. [Google Scholar]
- Pavlenko, V.N.; Ul’yanova, O.V. The method of upper and lower solutions for elliptic-type equations with discontinuous nonlinearities. Russ. Math. (Iz. VUZ) 1998, 42, 65–72. [Google Scholar]
- Pavlenko, V.N.; Ul’yanova, O.V. Method of Upper and Lower Solutions for Parabolic-Type Equations with Discontinuous Nonlinearities. Differ. Equ. 2002, 38, 520–527. [Google Scholar] [CrossRef]
- De Coster, C.; Obersnel, F.; Omari, P.A. A qualitative analysis via lower and upper solutions of first order periodic evolutionary equations with lack of uniqueness. In Handbook of Differential Equations: Ordinary Differential Equations; Cañada, A., Drábek, R., Fonda, A., Eds.; Elsevier B.V.: Amsterdam, The Netherlands, 2006; Volume 3, pp. 203–339. [Google Scholar]
- Pavlenko, V.N.; Potapov, D.K. Existence of Semiregular Solutions of Elliptic Systems with Discontinuous Nonlinearities. Math. Notes 2021, 110, 226–241. [Google Scholar] [CrossRef]
- Pavlenko, V.N.; Potapov, D.K. Variational method for elliptic systems with discontinuous nonlinearities. Sb. Math. 2021, 212, 726–744. [Google Scholar] [CrossRef]
- Carl, S.; Motreanu, D. Extremal solutions for nonvariational quasilinear elliptic systems via expanding trapping regions. Monatshefte Math. 2017, 182, 801–821. [Google Scholar] [CrossRef]
- Sidorova, A.E.; Levashova, N.T.; Semina, A.E.; Mel’nikova, A.A. The Application of a Distributed Model of Active Media for the Analysis of Urban Ecosystems Development. Math. Biol. Bioinform. 2018, 13, 454–465. [Google Scholar] [CrossRef]
- Levashova, N.T.; Sidorova, A.E.; Semina, A.E.; Ni, M. A spatio-temporal autowave model of shanghai territory development. Sustainability 2019, 11, 3658. [Google Scholar] [CrossRef]
- Butuzov, V.F.; Levashova, N.T.; Mel’nikova, A.A. A steplike contrast structure in a singularly perturbed system of elliptic equations. Comput. Math. Math. Phys. 2013, 53, 1239–1259. [Google Scholar] [CrossRef]
- Pao, C.V. Nonlinear Parabolic and Elliptic Equations; Plenum Press: New York, NY, USA, 1992; pp. 381–408. [Google Scholar]
- Levashova, N.T.; Tishchenko, B.V. Existence and stability of the solution to a system of two nonlinear diffusion equations in a medium with discontinuous characteristics. Comput. Math. Math. Phys. 2021, 61, 1811–1833. [Google Scholar] [CrossRef]
- Murray, J.D. Mathematical Biology. II: Spatial Models and Biomedical Applications, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 141–252. [Google Scholar]
- Vasil’eva, A.B.; Butuzov, V.F.; Kalachev, L.V. The Boundary Function Method for Singular Perturbation Problems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1995; pp. 83–88. [Google Scholar]
- Nefedov, N.N. Development of methods of asymptotic analysis of transition layers in reaction–diffusion–advection equations: Theory and applications. Comput. Math. Math. Phys. 2021, 61, 2068–2087. [Google Scholar] [CrossRef]
- Nefedov, N.N.; Sakamoto, K. Multi-dimensional stationary internal layers for spatially inhomogeneous reaction-diffusion equations with balanced nonlinearity. Hiroshima Math. J. 2003, 33, 391–432. [Google Scholar] [CrossRef]
- Fife, P.C.; McLeod, J.B. The approach of solutions of nonlinear diffusion equations to travelling front solutions. Arch. Ration. Mech. Anal. 1977, 65, 335–361. [Google Scholar] [CrossRef]
- Volpert, A.I.; Volpert, V.A.; Volpert, V.A. Traveling Wave Solutions of Parabolic Systems; American Mathematical Society: Providence, RI, USA, 1994; pp. 39–45. [Google Scholar]
- Butuzov, V.F.; Nedelko, I.V. Asymptotic stability of solutions of singularly perturbed boundary value problems with boundary and internal layers. Differ. Equ. 2000, 36, 224–235. [Google Scholar] [CrossRef]
- Tishchenko, B.V. Existence, local uniqueness and asymptotic stability of the boundary layer type solution of the Neumann problem for the two equation nonlinear system with different powers of a small parameter. Mosc. Univ. Phys. Bull. 2021, 76, 296–304. [Google Scholar] [CrossRef]
- Gilbarg, D.; Trudinger, N.S. Elliptic Partial Differential Equa-tions of Second Order; Springer: Berlin, Germany, 1977; pp. 51–72. [Google Scholar]
- Friedman, A. Partial Differential Equations of Parabolic Type; Roert E. Krieger Publishing Company: Malabar, FL, USA, 1983; pp. 7–14, 144–148. [Google Scholar]
- Melnikova, A.A. Existence and stability of a front-type periodic solution of a two-component system of parabolic equations. Comput. Math. Math. Phys. 2019, 59, 1131–1147. [Google Scholar] [CrossRef]
- O’Riordan, E.; Quinn, J. Parameter-uniform numerical method for some linear and nonlinear singularly perturbed convection–diffusion boundary turning point problems. BIT Numer. Math. 2011, 51, 317–337. [Google Scholar] [CrossRef]
- Lukyanenko, D.V.; Borzunov, A.A.; Shishlenin, M.A. Solving coefficient inverse problems for nonlinear singularly perturbed equations of the reaction-diffusion-advection type with data on the position of a reaction front. Commun. Nonlinear Sci. Numer. Simul. 2021, 99, 105824. [Google Scholar] [CrossRef]
- Andreev, V.B.; Kopteva, N. Pointwise approximation of corner singularities for a singularly perturbed reaction-diffusion equation in an L-shaped domain. Math. Comp. 2008, 77, 2125–2139. [Google Scholar] [CrossRef]
- Kellogg, R.B.; Kopteva, N. A singularly perturbed semilinear reactiondiffusion problem in a polygonal domain. J. Differ. Equ. 2010, 248, 184–208. [Google Scholar] [CrossRef]
- Wang, F.; Fan, C.M.; Zhang, C.; Lin, J. A Localized Space-Time Method of Fundamental Solutions for Diffusion and Convection-Diffusion Problems. Adv. Appl. Math. Mech. 2020, 12, 940–958. [Google Scholar] [CrossRef]
- Wang, F.; Wang, C.; Chen, Z. Local knot method for 2D and 3D convection–diffusion–reaction equations in arbitrary domains. Appl. Math. Lett. 2020, 105, 106308. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).