Abstract
We consider the estimation of the marginal likelihood in Bayesian statistics, with primary emphasis on Gaussian graphical models, where the intractability of the marginal likelihood in high dimensions is a frequently researched problem. We propose a general algorithm that can be widely applied to a variety of problem settings and excels particularly when dealing with near log-concave posteriors. Our method builds upon a previously posited algorithm that uses MCMC samples to partition the parameter space and forms piecewise constant approximations over these partition sets as a means of estimating the normalizing constant. In this paper, we refine the aforementioned local approximations by taking advantage of the shape of the target distribution and leveraging an expectation propagation algorithm to approximate Gaussian integrals over rectangular polytopes. Our numerical experiments show the versatility and accuracy of the proposed estimator, even as the parameter space increases in dimension and becomes more complicated.
1. Introduction
In Bayesian inference, many tasks, such as model selection, averaging, and comparison, rely on being able to compute the marginal likelihood (or model evidence) in order to form the Bayes factor. The marginal likelihood is the normalizing constant of a posterior distribution, which plays a particularly important role in probabilistic graphical models. Suppose is a general Gibbs distribution defined on , , with
In a Bayesian setup, is the negative log posterior. Since is typically complicated, and the space over which we are integrating tends to be high-dimensional, the resulting integral is usually intractable. This calculation is exacerbated further for Gaussian graphical models (GGM) [1,2] because the integral is taken over a specialized subset of positive definite matrices.
Generic algorithms for approximating the marginal likelihood include Laplace’s method [3], the harmonic mean estimator [4,5], the corrected arithmetic mean estimator [6], annealed importance sampling [7], Chib’s method [8], (warp) bridge sampling [9,10], and nested sampling [11]. More recent developments include the integrated nested Laplace approximation [12] and the expectation propagation–approximate Bayesian computation algorithm [13]. While these methods can be applied to many marginal likelihood estimation problems, they do not provide a straightforward way to deal with the specificity of GGMs and the positive definite restriction on the precision matrices. Additionally, many of these aforementioned methods tend to rely on high-quality MCMC samples and have numerous problem-specific model settings that limit the overall practicality.
While there have been developments that specifically target the marginal likelihood of GGMs [14], the stringent prior restrictions (inverse-Wishart and hyper-inverse Wishart) prevent many of these approaches from being used in broader contexts. Furthermore, there exists substantial literature on inference for both decomposable [15] and non-decomposable [16,17,18] graphs; however, the need for more general and scalable algorithms is ever present. This has consequently led to dedicated methods for sampling from the G-Wishart distribution and conducting model comparison [19,20,21]. Also relevant is the availability of the G-Wishart normalizing constant in closed form [22], but the viability of these results is limited when considering most high-dimensional graphs of practical interest. Bhadra et al. [23] propose an application of Chib’s method and a telescoping decomposition of the precision matrix that simplifies the ensuing marginal likelihood calculations, but the main advantages of this approach are seen with element-wise priors, and in most cases, the time complexity is on par with other GGM-specific methods.
A recent approach that combines some of the probabilistic ideas from MCMC-based methods while drawing inspiration from quadrature is the hybrid estimator [24]. This method moves away from an over-reliance on MCMC samples, as these can be time-consuming to obtain if the likelihood is expensive to evaluate. Rather, the MCMC samples are utilized during a preliminary step to learn a partition of the parameter space in order to identify regions of posterior concentration. By making local approximations to the negative log posterior over these partition sets, the the hybrid algorithm simplifies the integral and forms a piecewise estimate of the marginal likelihood. The high-probability partition of the parameter space yields multiple benefits. First, the areas of the parameter space that admit finer partitions encourage precise approximations to the log posterior. More importantly, this partitioning routine redirects attention away from regions that have little to no contribution to the posterior distribution, saving both time and computation.
The hybrid estimator establishes the foundation for a promising way to estimate the marginal likelihood, and the experimental results demonstrate its competitiveness with other well-known estimators in various problem settings [24]. Moreover, the methodology’s generality makes it convenient to refine the algorithm so that it can be applied to more specific problem setups. With the ultimate goal of accurately computing the marginal likelihood for GGMs, we introduce an alternative parametrization of precision matrices and restrict our scope to target the normalizing constants of a specific class of densities—unimodal densities that are approximately log-concave around the mode. In this paper, we leverage core ideas of the hybrid estimator in conjunction with higher order approximations to the negative log posterior for accuracy, as well as expectation propagation techniques for scalability. This results in a novel estimator that is suitably equipped for high-dimensional problems. We call the estimator that arises from these modifications the EP-guided second-order modified hybrid estimator (EPSOM-Hyb).
After verifying the accuracy of EPSOM-Hyb in initial experiments for decomposable graphs, we further extend the methodology to better handle non-decomposable GGMs. By incorporating junction tree (JT) representations of connected graphs, we enhance the computational efficiency of the marginal likelihood calculation. This leads to a GGM-specific estimator, denoted EPSOM-HybJT. Our contribution is multifaceted; despite the introduction of higher-order terms that inherently bring additional computational challenges to the hybrid estimator framework, we maintain practical utility in the EPSOM-Hyb methodology. This approach leads to an estimator that not only excels in highly specific problem settings, but also outperforms well-established estimators. Our experiments indicate that EPSOM-HybJT is more accurate and more than 100 times faster in higher dimensions than other viable estimators.
The outline of the paper is as follows. In Section 2, we provide the background for the hybrid estimator so that the modifications that we propose in Section 3 to formulate the EPSOM-Hyb estimator have relevant context. In Section 4, we investigate the performance of the EPSOM-Hyb estimator for GGMs, and we also develop the EPSOM-HybJT estimator. In Section 5, we conclude and briefly discuss future work.
2. The Hybrid Estimator
We first review the salient details of the hybrid estimator as a means of providing background on the existing work and establishing context for our development of the EPSOM-Hyb estimator. As an initial step, the hybrid algorithm learns a dyadic partition of the parameter space that helps identify high-probability regions of the target distribution. In order to accomplish this, we form covariate–response pairs, , using MCMC samples from the target distribution and evaluating them with . Clearly, we make the assumption of being able to sample from and evaluate , but both of these are basic requirements in many MCMC-based algorithms. We can then use a regression tree algorithm to obtain optimal splits of the parameter space, where each of the partition sets is the hyper-rectangle that defines the corresponding leaf node in the fitted tree. The hybrid estimator uses the classification and regression tree (CART) algorithm [25], which returns a partition of the parameter space that can be further restricted to the compactification A of by setting A to be bounding box defined by the range of the posterior samples: , where is the l-th coordinate of the j-th sample. Thus, the resulting partition is a dyadic partition of the compact set A. We work with a compactification of the parameter space as a means of eliminating low-probability regions of the domain whose contributions to the integral in Equation (1) are negligible. This is particularly useful in Bayesian contexts where the posterior concentrates with increasing sample size [26,27].
Next, we formulate the piecewise estimator to defined over the compact set ,
where , , and for all . We set , a representative point in that is constant in u. Since each is a hyper-rectangle, the hybrid estimator reduces to
Here, denotes the d-dimensional volume of a set B.
3. The Epsom-Hyb Estimator
In the discourse that follows, we propose some key modifications to the hybrid algorithm to develop a novel estimator better suited for tackling higher-dimensional problems. For the initial development, we do not restrict our analysis to posterior distributions and illustrate the modified algorithm in the general case of log-concave target densities. Our additional assumption about the shape of is employed only to ensure that the Hessian is positive definite everywhere and can, in fact, be relaxed to unimodal densities that are approximately log-concave in a suitable neighborhood around the mode. This assumption is widely satisfied by Bayesian posteriors in regular parametric models, and due to the Bernstein–von Mises phenomenon, most regular posterior distributions are approximately log-concave with sufficiently large sample size [28].
As before, we work with a compactification of the parameter space, for which we have a dyadic partition obtained through the same tree-fitting procedure as before. However, instead of the constant approximation to within each partition set in , we first retain the general estimator given in Equation (2),
Below, we highlight three fundamental features of the EPSOM-Hyb algorithm that distinguish it from the hybrid algorithm, followed by detailed discussions of each step. See Algorithm 1 for a formal statement of the EPSOM-Hyb estimation procedure.
- In Equation (2), we take to be a local approximation to constructed using a second-order Taylor expansion of around a representative point .
- The second-order Taylor approximation complicates the calculation of the integrals in Equation (4). We address the intractability of the resulting integral using an expectation propagation (EP) algorithm that targets high-dimensional Gaussian integrals.
- We exploit the unimodality of to identify suitable points within each partition set around which we perform the Taylor expansion required for .
| Algorithm 1: EPSOM-Hyb |
 |
3.1. Local Approximation Using a Taylor Expansion
We revisit Equation (2) and consider the following piecewise quadratic approximation to ,
where is a representative point of . This improves upon the initial idea of the piecewise constant approximation in the hybrid methodology by introducing a second-order Taylor approximation. By introducing higher-order terms, we trade the convenient simplification of the integral in Equation (3) for increased local accuracy of the approximation. Upon exponentiating the approximation in Equation (5), we observe that the second exponential in the summation below is proportional to a Gaussian density,
where and represent the gradient vector and the Hessian matrix of evaluated at , respectively. Since is log-concave, the Hessian matrix is positive definite, and hence invertible. Integrating the exponential above, we arrive at the following approximation to :
Here, , , and . Before can serve as a viable estimator for , we must address the remaining questions of how to determine the value of each and how to compute the intractable Gaussian integrals in Equation (6). In the next two sections, we provide scalable methods to accomplish these tasks. It is worth noting that the original hybrid estimator does not face the same intractability issue due to the simplistic nature of the constant approximation used in Equation (3). Our incorporation of higher-order terms complicates the subsequent calculation, which necessitates a scalable algorithm like EP to compute the truncated Gaussian integrals.
3.2. Estimating Truncated Gaussian Probabilities
Despite the prevalence of Gaussian densities in statistical modeling, multivariate Gaussian probabilities remain difficult to compute, as they typically require high-dimensional integration. Numerical integration [29] is a common solution, but it is prohibitively expensive in the number of points required, thus preventing it from being a scalable solution in the high-dimensional space in which we wish to operate. A more recent alternative that specifically targets truncated normal distributions is the minimax tilting method [30], and while we used this method in the initial development of our algorithm, it failed to produce accurate results beyond trivial settings. This ultimately led us to consider more computationally efficient integration techniques, such as expectation propagation [31], which is widely used to compute approximate integrals. To better understand how the expectation propagation (EP) algorithm can be applied to the intractable Gaussian integral in the previous section, we lay out some preliminary groundwork for the EP algorithm. Starting with the Gaussian distribution , we define the un-normalized truncated distribution . The Gaussian probability of interest can be written as:
Cunningham et al. [32] propose a framework for approximating that consists of two main approximations. The first approximation is a tractable distribution q that minimizes the Kullback–Leibler (KL) divergence between p and q, denoted . However, the intractability of p complicates the minimization and subsequently requires another approximation, for which we instead work with a simplified representation of p. Namely, we replace with the product of a prior distribution and factors , such that
In order to facilitate tractability, we assume , where is the i-th coordinate of x, and are simply the lower and upper bounds of integration, respectively. Then, the target integral in Equation (7) can be written as
We proceed to approximate each of the intractable factors with a tractable, un-normalized Gaussian , which produces the final approximation q of p. More specifically, we take q to mirror the product form of p,
where the parameters of these unnormalized Gaussian distributions, , admit closed form updates that are the result of an iterative moment matching scheme. From this, we observe that by estimating the normalizing constant of q, we also obtain an approximation for the normalizing constant of the target distribution p. See Equations (21)–(23) from Cunningham et al. [32] for the closed-form updates for each of these parameters and more details regarding the relevant notation. Essentially, the EP algorithm iteratively constructs the approximating distribution to minimize , which in turn approximately minimizes . Here, is defined as the cavity distribution. By running the EP algorithm to convergence, we can calculate the following mean and covariance parameters of the normal distribution q,
where is the i-th standard basis vector. With this, we also obtain a closed-form expression for the normalizing constant of q,
which approximates the Gaussian probability in Equation (7). It is worth noting that the algorithm is still valid for arbitrary factors , albeit with different parameter updates. Our simplistic choice of to be the indicator function defined over the constant lower and upper limits of integration reflects the rectangular nature of the partition sets used in the Hybrid-EP estimator.
With this, recall the Gaussian integral in Equation (6),
Taking , we observe that the above integral is exactly the one given in Equation (7). Thus, we can directly use the algorithm to obtain an estimate for the Gaussian probability in Equation (8). Another benefit of using the EPMGP algorithm is its exceptional accuracy when the constraint set is rectangular, which coincides with our setup, where is a d-dimensional hyper-rectangle.
3.3. Selecting the Candidate Point in Each Partition Set
The final piece of EPSOM-Hyb is the point used in the piecewise Taylor approximation in Equation (5). In our unimodal setup, a natural choice for each partition set’s representative point is one that is closest to the global mode of . More specifically, if is the global mode, then . Conveniently, we can obtain the global mode of using Newton’s method with little additional effort because we already have expressions for the gradient and Hessian of as part of the approximation in Equation (6). With this, all components of EPSOM-Hyb are accounted for and can be summarized in Algorithm 1.
4. Application to Gaussian Graphical Models
Next, we investigate the performance of EPSOM-Hyb on marginal likelihood estimation for GGMs. Let be an undirected graph with vertex set and edge set E. Define as the set of symmetric matrices and as the cone of positive definite matrices in . Let , , where . Then, the likelihood can be written as follows,
Further, X satisfies the GGM with graph G, where G dictates the conditional dependence structure and restricts the sparse concentration matrix so that if and only if , and and are conditionally independent if and only if . Hence, an undirected graphical model corresponding to G restricts the inverse covariance matrix to a linear subspace of the cone of positive definite matrices.
We first consider decomposable GGMs where the tractability of the marginal likelihood makes it easy to evaluate estimates. In Section 4.2, we broaden our focus to general, non-decomposable graphs. To address the additional computational challenges that accompany non-decomposable graphs and high-dimensional parameter spaces, we propose an extension to EPSOM-Hyb that facilitates dimension reduction and drastically reduces the time complexity of the normalizing constant calculation. In the following GGM experiments, we refer to the estimator from Atay-Kayis and Massam [17] as GNORM, which is well-established for general graphs and can be computed easily using BDgraph [33].
4.1. Hyper Inverse-Wishart Induced Cholesky Factor Density
We first consider the case where G is decomposable. The hyper-inverse Wishart (HIW) distribution [34] for and the corresponding induced class of distributions [14] for are attractive choices for priors. Given G, we place a hyper-inverse Wishart prior on , where is the degrees of freedom and is fixed. The HIW distribution is defined over the cone of positive definite matrices, with the corresponding density:
Despite being able to sample from the posterior distribution, , we cannot directly carry out the EPSOM-Hyb algorithm. Since samples are drawn from a sub-manifold of , proceeding to obtain a partition over does not guarantee that a given point in the partition can be reconstructed to form a valid covariance matrix. As such, we circumvent this issue by working with an alternative representation of given by the Cholesky decomposition . Provided that the vertices of G are enumerated according to a perfect vertex elimination scheme, the upper triangular matrix observes the same sparsity as . Consequently, we need only compute the induced prior on the nonzero elements of , which, together with the likelihood in Equation (9), gives us an explicit expression for the negative log posterior . The determinant of the Jacobian matrix J of the transformation is given by , where the i-th row of has exactly nonzero elements [14]. Further, the distribution of has the strong hyper-Markov property [35], so we can ascertain mutual independence of the rows of . Then, we can specify the joint density of the free elements of as follows,
Recall that we also require expressions for the gradient and Hessian of , both of which are provided in Appendix D. Putting these ideas together, we can employ the EPSOM-Hyb estimation framework by drawing samples from the posterior distribution, taking the Cholesky factor of each sample, and computing using the likelihood in Equation (9) and the prior in Equation (11). While this procedure appears to be quite simple, the implications are significant; if we have a different prior on for which we can do the posterior computation, all other aspects of the algorithm would remain the same. All that is required is a way to sample from the posterior of and an expression for the Jacobian of the corresponding transformation.
In our simulations, we emulate a high-dimensional setting by stacking the adjacency matrix of the decomposable graph in Figure 1 multiple times along a block diagonal to construct larger graphs, e.g., , where is the adjacency matrix of and r is the number of times we stack the graph. For , we form the graphs , which have free elements, respectively. Drawing data that satisfy their corresponding GGMs and taking , and , we can sample from the posterior distribution and compute the marginal likelihood estimates. Among the generic methods mentioned in Section 1, only the bridge sampling estimator (BSE) and the warp bridge sampling estimator (WBSE) are viable and accurate methods for computing the marginal likelihood. As seen in Table 1, both BSE and WBSE are competitive with EPSOM-Hyb when , but the quality of the former two estimators deteriorates when . The relatively small error of EPSOM-Hyb in this high-dimensional graphical models setting is particularly encouraging. Interestingly, GNORM fails to produce sensible estimates for these high-dimensional graphs.
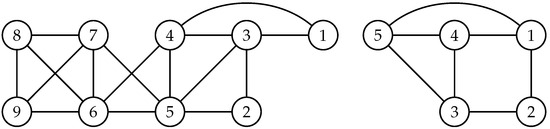
Figure 1.
(left), an undirected, decomposable graph, and (right), an undirected, non-decomposable graph.

Table 1.
Mean, average error (AE), and root mean squared error (RMSE) for the approximations to the log normalizing constant of the distribution. has 72 vertices with 200 parameters and has 90 vertices and 250 parameters. Estimates are reported over 100 replications, each using 1000 samples from the true posterior.
4.2. G-Wishart Prior for General Graphs
In contrast with the previous section, we now broaden the scope of examples and consider general, non-decomposable graphs. For the conditional general graph G, a popular choice for the prior is the G-Wishart prior on , , which has the following density,
Here, are positive definite matrices, and . While the density expression is similar to that of the HIW density, the tractability of the normalizing constant is no longer assumed. The normalizing constant that we wish to compute is of the form
where . Here, .
G-Wishart-Induced Cholesky Factor Density
We first establish some of the notations relevant to the GW density. For , define and Then, let , and , where if or if , and otherwise. Set to be the number of 1’s in the i-th column of A. Proceeding in a similar fashion as in the HIW example, we take the Cholesky decomposition of and , where . We make an additional change of variable . The Jacobian of the first transformation is identical to the one given in Section 4.1, and the determinant of the Jacobian of the second transformation is given by . Putting this all together, we can rewrite the normalizing constant as an integral over the free variables of ,
where , , and . Taking the logarithm of the integrand above, we can write the following expression for ,
where . Another key difference between the GW and HIW setups is how the non-free elements interact with the objective function . In the case of decomposable G, the Cholesky factor observes the same sparsity pattern as the adjacency matrix of G. This simplifies the evaluation of , as can then be evaluated over the nonzero elements of . However, in the case of non-decomposable G, the sparsity in G is not necessarily reflected in the Cholesky factors. Therefore, has nonzero contribution from the non-free elements, denoted as . Using Lemma 2 [17], we can express the non-free elements, for and , recursively in terms of the free elements,
Subsequent expressions for the gradient and Hessian of can be found in Appendix E.
4.3. Junction Tree Representation
In order to combat the computational overhead associated with larger graphs, we modify EPSOM-Hyb to first break down the graph into subgraphs according to its topology using a junction tree representation, which exists for all connected graphs. By leveraging the attractive properties of junction tree representations, we not only achieve significant computational speedup in the marginal likelihood calculation, but we can also more adequately handle general graphs. We briefly discuss the properties of decomposable versus non-decomposable graphs and how their respective junction tree representations can simplify the normalizing constant calculation. A junction tree representation of a graph decomposes the graph into a sequence of interconnecting subgraphs separated by complete subgraphs [36], which has the following form:
In , each prime component is a proper subgraph of G, each separator is a complete subgraph of G, and each is the intersection of with all the previous components . If any of the prime components found by this decomposition procedure is not complete and cannot be further decomposed, then G is non-decomposable [37]. With these concepts in place, we recall the original goal of marginal likelihood estimation but look to include the intermediate step of obtaining the junction tree representation of the graph. By working with the smaller prime components, we can overcome the complexity associated with the original high-dimensional graph. Moreover, we can take advantage of the distributional properties of the complete prime components.
Concretely, suppose we have data satisfying the GGM with a graph G and corresponding junction tree , as given in Equation (17). Let and represent the prime component and separator sequences, respectively. If all of the prime components are complete (cliques), we denote the clique sequence as . Regardless of the decomposability of G, we can use to express the joint density of X given ,
where and represent the submatrices corresponding to the subgraphs P and S, respectively. We first consider the case where G is decomposable, with . Then, the prior density factorizes over the cliques and separators,
The completeness of the prime components admits distributional properties that make the normalizing constants tractable. In particular, the prior density on is the inverse-Wishart (IW). Putting this together with the likelihood given in Equation (18), we deduce that the marginal likelihood also factorizes over the cliques and separators as follows,
Here, . For a decomposable graph, the factorization of the likelihood and IW prior over the cliques and separators yields a product of tractable normalizing constants. Exact formulae for , and can be found in Equations (A4) and (A5).
We can easily generalize the calculations above to accommodate non-decomposable graphs with GW priors. Since the GW density in Equation (12) has a similar form to the HIW density, the marginal likelihood calculation also factorizes over prime components and separators. The difference from the previous calculation is that for decomposable G, the product in Equation (21) is taken over the cliques , whereas in the GW case, the product is taken over prime components , which may or may not be complete. Since normalizing constants for the non-complete prime components are generally intractable, they typically require MCMC estimation.
Essentially, the factorized representation of the marginal likelihood induced by the junction tree representation of G splits the original calculation involving the entire graph G into sub-problems involving the prime components and separators. When is complete, we can rely on the closed form IW normalizing constant. For non-complete , we take the corresponding parameters, , and write the normalizing constant for the non-complete prime component as
Although this quantity remains intractable, it poses a lower dimensional problem for which we can use the procedure outlined in Section 4.2 along with the EPSOM-Hyb algorithm. The posterior normalizing constant can be similarly computed. After computing the normalizing constants for each of the prime components and separators, the individual approximations are summed together to form the log normalizing constant approximation corresponding to the original graph G. These steps make up the EPSOM-HybJT algorithm, which is outlined in Algorithm 2.
4.3.1. Experiment 1: Block Diagonal Graph Structure
Consider a graph formed by stacking the adjacency matrix of (given in Figure 1) r times along a block diagonal. Using the notation in Section 4.1, , for . Similarly, for a randomly generated scale matrix , the corresponding scale matrix for is , where denotes the dimension of the vertex set of . For specific graphs, the corresponding GW normalizing constants can be computed analytically. In particular, for , we can use the formula in Equation (4.1) from Uhler et al. [22] to compute , which can then be plugged into Equation (13) to obtain the normalizing constant of . Since explicitly uses to create its dependence structure, we can then easily calculate the normalizing constant of .
The results in Table 2 indicate that both GNORM and EPSOM-HybJT produce accurate estimates, with EPSOM-HybJT having a slightly lower relative error. However, the time savings that accompany EPSOM-HybJT are substantial. In the case of , GNORM is notably faster, but for high-dimensional graphs, there is a dramatic slowdown. Indeed, for , GNORM is more than 100 times slower than EPSOM-HybJT.
| Algorithm 2: EPSOM-HybJT |
 |

Table 2.
Mean estimate, mean relative error (MRE), and relative runtime of EPSOM-HybJT and GNORM approximations to the log normalizing constant of the density. has vertices and free elements. Here, and . Estimates are reported over 20 replications, each using 1000 samples from the target distribution. The runtime of the GNORM algorithm is calculated relative to the runtime of the EPSOM-HybJT algorithm.
4.3.2. Experiment 2: Normalizing Constants of General Graphs
Next, we investigate the performance of the two estimators for more general graphs. The results of the previous experiment showed that both GNORM and EPSOM-HybJT are very close to the true normalizing constants. For general graphs that do not satisfy the conditions that previously allowed us to calculate the exact GW normalizing constant, we compare the values of the GNORM and EPSOM-HybJT estimates against each other and keep track of the runtime relative to that of the EPSOM-HybJT algorithm when . In Table 3, for , very little separates the log normalizing constant estimates, and GNORM even demonstrates its strength in low dimensions with a runtime that is about 50 times faster than EPSOM-HybJT for . However, EPSOM-HybJT flips the script in all subsequent experiments and scales better as p grows. For , the GNORM estimator fails to give a finite estimate for the log normalizing constant.

Table 3.
Mean estimate, standard deviation, and relative runtime of EPSOM-HybJT and GNORM approximations to the log normalizing constant of the . Here, is not block-diagonal. Estimates are reported over 20 replications, each using 1000 samples from the corresponding G-Wishart distribution. The runtime of the GNORM algorithm is calculated relative to the runtime of the EPSOM-HybJT algorithm.
In these experiments, each graph is generated using Bernoulli draws to determine the existence of its edges and checked to ensure that the graph is non-decomposable; otherwise, this would simply reduce the problem to a summation of tractable IW constants and would be unable to fairly assess the approximating ability of EPSOM-HybJT. Contrast these results with the examples from the previous section where the scale matrix was assumed to be block-diagonal and the dependence structure was relatively simple. In those simpler settings, GNORM retains its accuracy even for high-dimensional graphs, albeit with a much slower runtime. Evidently, the added complexity induced by a nontrivial dependence structure contributes to the computational burden that cannot be easily overcome using standard methods.
4.4. Software Contribution
With the architecture in place for both the EPSOM-Hyb algorithm and its junction tree extension, we are equipped with the necessary tools for computing normalizing constants for general cases, as well as GGM-specific examples. For ease of use, EPSOM-Hyb is implemented in the hybrid package. Note that the hyperparameter initialization in line 26 of Figure A1 refers to problem-specific hyperparameters, rather than algorithm-specific hyperparameters or settings. We emphasize that other than supplying a sampler for the target distribution and functions to evaluate and its gradient and Hessian, the EPSOM-Hyb methodology does not require hyperparameter tuning or convergence monitoring, beyond Newton’s method for finding the global mode of the unimodal target distribution, as described in Section 3.3. Recognizing the intricacy of the EPSOM-HybJT algorithm and the difficulty of having to manually combine the EPSOM-Hyb and the junction tree methodologies, we have developed an additional package dedicated specifically to estimating the normalizing constant of G-Wishart densities. The R package graphml serves as a black box method that seamlessly integrates the junction tree algorithm into the existing EPSOM-Hyb methodology without any user input other than the adjacency matrix representation of the graph and the G-Wishart density parameters. See Appendix A and Appendix B for more details regarding the installation and use of these packages. Additionally, in the package repositories, we provide the R programs that replicate the experimental results reported in this paper.
5. Discussion
Our methodological contributions are twofold: firstly, we developed EPSOM-Hyb as a general algorithm for computing the normalizing constant of log-concave densities, and secondly, we extended this methodology to specifically target the marginal likelihood of non-decomposable GGMs. While the GNORM estimator from Atay-Kayis and Massam [17] is a valuable tool that performs well for simpler and lower-dimensional graph structures, it is evident that more scalable and robust solutions are needed in the nontrivial problem settings presented in this paper. By taking advantage of junction tree representations of connected graphs and pairing them with the EPSOM-Hyb methodology, we significantly simplify the normalizing constant calculation for GGMs. The resulting EPSOM-HybJT algorithm is not only able to compete with other widely accepted estimators, but it also presents itself as a scalable solution for high-dimensional scenarios where other methods either fail to produce sensible results or succumb to time complexity constraints.
We recognize that the junction tree representation of a connected graph can be integrated into the GNORM methodology to create a more robust algorithm, leading to substantial time savings in subsequent normalizing constant calculations. However, such an implementation is presently unavailable. In the meantime, our contributions represent a universal method for marginal likelihood estimation that can be easily adapted to be as accurate and significantly faster than specialized methods for graphical models. Finally, while our methodologies empirically demonstrate their competitiveness across a variety of examples, many popular and long-established marginal likelihood estimation methods are accompanied by strong theoretical guarantees. As such, this remains an area of future work and development.
Author Contributions
Conceptualization, A.B. and D.P.; methodology, E.C. and Y.N.; software, E.C.; validation, Y.N.; formal analysis, E.C.; investigation, E.C.; resources, A.B. and D.P.; data curation, E.C. and Y.N.; writing—original draft preparation, E.C.; writing—review and editing, Y.N., A.B. and D.P.; visualization, E.C.; supervision, A.B. and D.P.; project administration, A.B.; funding acquisition, A.B. and D.P. All authors have read and agreed to the published version of the manuscript.
Funding
Pati and Bhattacharya acknowledge support from NSF DMS (2210689).
Informed Consent Statement
Not applicable.
Data Availability Statement
No datasets were used in this article. Simulations and examples can be replicated using the scripts made available in the following repositories: https://github.com/echuu/hybrid (accessed on 12 May 2024) and https://github.com/echuu/graphml (accessed on 12 May 2024).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| GGM | Gaussian Graphical Model |
| JT | Junction Tree |
| KL | Kullback–Leibler |
| IW | Inverse Wishart |
| HIW | Hyper-Inverse Wishart |
| GW | G-Wishart |
| MCMC | Markov Chain Monte Carlo |
| EP | Expectation Propagation |
| CART | Classification and Regression Tree |
| EPSOM-Hyb | EP-guided Second-Order Modified Hybrid |
| EPSOM-HybJT | EP-guided Second-Order Modified Hybrid Junction Tree |
| BSE | Bridge Sampling Estimator |
| WBSE | Warp Bridge Sampling Estimator |
| AE | Average Error |
| MRE | Mean Relative Error |
Appendix A. General Use of the hybrid Package
We developed hybrid [38], an R package that allows practitioners to easily compute estimates of the log-marginal likelihood. In Figure A1, we provide a snippet of code to demonstrate how both the hybrid approximation and the EPSOM-Hyb approximation can be used in practice. For the hybrid method, users only need to provide a way to evaluate the negative log posterior and a sampler for the target distribution . After drawing the samples using a user-defined sample_post() function and evaluating them using the hybrid::preprocess() function, we can calculate the log-marginal likelihood estimate with the hybrid::hybml_const() function.
For EPSOM-Hyb, users will need to supplement the input of the hybrid method with function definitions for the gradient vector and Hessian matrix of . These function definitions, along with the posterior samples, are then passed into the hybrid::hybml() function. Optionally, a representative point (typically the global mode) can be supplied to the function call to play the role of as defined in Section 3.3, but in the case where no point is given, the implementation will take to be the point with the highest posterior mass. We emphasize that beyond specifying the model and supplying a sampler, which is typically required in all other competing methods, there are no hyperparameters to tune and no problem-specific settings that require modification or attention. This makes our solution one of the few black box marginal likelihood estimation methods that has been empirically shown to scale well with dimension and accommodate complex parameter spaces. The repository that contains the source code for these algorithm implementations can be found at https://github.com/echuu/hybrid, accessed on 12 May 2024. The repository also contains installation instructions and a working example.

Figure A1.
Demonstration of how to use hybrid package in R. This package contains the implementation for both the Hybrid and EPSOM-Hyb algorithms for estimating the log normalizing constant of a target distribution.
Appendix B. General Use of the Graphml Package
While the graphical modeling examples can be adapted to be used with the hybrid package, we have also developed a package specific to graphical models that further simplifies the process of weaving together the EPSOM-Hyb methodology with the junction tree representation of general graphs—as discussed in Section 4.3 and presented in Algorithm 2—because of the importance of the normalizing constant calculation in graphical modeling literature. With the graphml [39] package, we can easily use the EPSOM-HybJT methodology to compute the normalizing constant of the G-Wishart density given the adjacency matrix for a general graph, the scale matrix, the degrees of freedom, and the number of MCMC samples to be drawn from the corresponding G-Wishart density.

Figure A2.
Demonstration of how to use graphml package in R. This package contains the implementation of the EPSOM-HybJT algorithm for estimating the log normalizing constant of G-Wishart densities. Atay’s estimator can similarly be computed using the gnorm function from the BDgraph package.
We juxtapose the code necessary for computing the GNORM estimate via the BDgraph package to demonstrate the comparable ease of use of the graphml package. We use the C++ implementation of junction tree representation [40], which can be found at https://www2.stat.duke.edu/~mw/mwsoftware/GGM/index.html (accessed on 10 April 2024). We adapt their implementation into the graphml package since the original C++ implementation is not directly importable in . Recall that for the general hybrid package, we require user-defined functions for the objective function, gradient, and Hessian, whereas, in this package, all of these functions are already optimally implemented. In the case of the G-Wishart density, these functions are quite cumbersome to write because of the recursive structure, so removing this from the list of user responsibilities is especially convenient. The Github repository that contains the source code for this package can be found at https://github.com/echuu/graphml (accessed on 12 May 2024).
Appendix C. Hyper-Inverse Wishart Density
We introduce some notation to help us obtain a closed form for the marginal likelihood in the case of a decomposable graph G. For an matrix X, is defined as the sub-matrix of X consisting of columns with indices in the clique C. Let , where is the ith column of . If , where , then . For any square matrix , define where , is the cardinality of the clique C, and the order of entries carries into the new sub-matrix . Therefore, .
Decomposable graphs correspond to a special kind of sparsity pattern in , henceforth denoted . Suppose we have a distribution on the cone of positive definite matrices with degrees of freedom and a fixed positive definite matrix D such that the joint density factorizes on the junction tree of the given decomposable graph G as
where for each , has the density
where . Here, denotes the inverse-Wishart distribution with degrees of freedom b and a fixed positive definite matrix D with normalizing constant
Note that we can establish equivalence to the parametrization used in Section 4.1 by taking . Since the joint density in Equation (9) factorizes over cliques and separators in the same way as in Equations (A1) and (A2),
Using the above equations, we can obtain the marginal likelihood,
where
Appendix D. Hyper-Inverse Wishart Objective Function
Recall that we take the Cholesky decomposition of , where is upper triangular. Using Equations (9) and (11), we define . Even though is expressed as a function of the upper Cholesky factor , it is inherently a function of only the free elements of . As a result, the gradient of is defined element-wise,
Similarly, the Hessian can be computed element-wise,
where , , and .
Appendix E. G-Wishart Objective Function
Next, we provide the calculation details for the derivation of the gradient and Hessian of , as defined in Equation (15). First, we can compute the terms of the gradient element-wise by taking the derivative of with respect to the free elements of ,
Note that because the non-free elements are functions of the free elements, each gradient term involves additional recursive derivative calculations. As given in Equation (16), for and ,
Finally, using the expression for the gradient in Equation (A6), we can perform a similar calculation for the Hessian. The elements on and above the diagonal are defined as follows,
Below, we provide the derivation for the partial derivative terms of the non-free elements taken with respect to the free elements by again starting with the recursive definition of in Equation (16). In the following calculations, we define , where where . We consider two cases.
- Case 1: for , , , and coming after , we have
- Case 2: for , and , we obtain the derivative:
- In case 1, each term in the outer summation in Equation (A9) can be computed as:These scalar, element-wise quantities can be substituted back into the piecewise definitions of the gradient and Hessian matrices, as given in Equations (A6) and (A8), respectively.
References
- Lauritzen, S.L. Graphical Models; Clarendon Press: Oxford, UK, 1996; Volume 17. [Google Scholar]
- Maathuis, M.; Drton, M.; Lauritzen, S.; Wainwright, M. Handbook of Graphical Models, 1st ed.; CRC Press, Inc.: Boca Raton, FL, USA, 2018. [Google Scholar]
- Tierney, L.; Kadane, J.B. Accurate Approximations for Posterior Moments and Marginal Densities. J. Am. Stat. Assoc. 1986, 81, 82–86. [Google Scholar] [CrossRef]
- Newton, M.A.; Raftery, A.E. Approximate Bayesian Inference with the Weighted Likelihood Bootstrap. J. R. Stat. Soc. Ser. B 1994, 56, 3–26. [Google Scholar] [CrossRef]
- Lenk, P. Simulation Pseudo-Bias Correction to the Harmonic Mean Estimator of Integrated Likelihoods. J. Comput. Graph. Stat. 2009, 18, 941–960. [Google Scholar] [CrossRef]
- Pajor, A. Estimating the Marginal Likelihood Using the Arithmetic Mean Identity. Bayesian Anal. 2017, 12, 261–287. [Google Scholar] [CrossRef]
- Neal, R.M. Annealed importance sampling. Stat. Comput. 2001, 11, 125–139. [Google Scholar] [CrossRef]
- Chib, S. Marginal Likelihood from the Gibbs Output. J. Am. Stat. Assoc. 1995, 90, 1313–1321. [Google Scholar] [CrossRef]
- Meng, X.L.; Wong, W.H. Simulating ratios of normalizing constants via a simple identity: A theoretical exploration. Stat. Sin. 1996, 6, 831–860. [Google Scholar]
- Meng, X.L.; Schilling, S. Warp Bridge Sampling. J. Comput. Graph. Stat. 2002, 11, 552–586. [Google Scholar] [CrossRef]
- Skilling, J. Nested sampling for general Bayesian computation. Bayesian Anal. 2006, 1, 833–859. [Google Scholar] [CrossRef]
- Hubin, A.; Storvik, G. Estimating the marginal likelihood with Integrated nested Laplace approximation (INLA). arXiv 2016, arXiv:1611.01450. [Google Scholar] [CrossRef]
- Barthelmé, S.; Chopin, N. Expectation-Propagation for Likelihood-Free Inference. arXiv 2011, arXiv:1107.5959. [Google Scholar] [CrossRef]
- Roverato, A. Cholesky decomposition of a hyper inverse Wishart matrix. Biometrika 2000, 87, 99–112. [Google Scholar] [CrossRef]
- Giudici, P.; Green, P. Decomposable graphical Gaussian model determination. Biometrika 1999, 86, 785–801. [Google Scholar] [CrossRef]
- Dellaportas, P.; Giudici, P.; Roberts, G. Bayesian inference for nondecomposable graphical Gaussian models. Sankhyā Indian J. Stat. 2003, 65, 43–55. [Google Scholar]
- Atay-Kayis, A.; Massam, H. A Monte Carlo method for computing the marginal likelihood in nondecomposable Gaussian graphical models. Biometrika 2005, 92, 317–335. [Google Scholar] [CrossRef]
- Khare, K.; Rajaratnam, B.; Saha, A. Bayesian inference for Gaussian graphical models beyond decomposable graphs. arXiv 2015, arXiv:1505.00703. [Google Scholar] [CrossRef]
- Piccioni, M. Independence Structure of Natural Conjugate Densities to Exponential Families and the Gibbs’ Sampler. Scand. J. Stat. 2000, 27, 111–127. [Google Scholar] [CrossRef]
- Rajaratnam, B.; Massam, H.; Carvalho, C.M. Flexible covariance estimation in graphical Gaussian models. Ann. Stat. 2008, 36, 2818–2849. [Google Scholar] [CrossRef]
- Lenkoski, A. A Direct Sampler for G-Wishart Variates. Stat 2013, 2, 119–128. [Google Scholar] [CrossRef]
- Uhler, C.; Lenkoski, A.; Richards, D. Exact Formulas for the Normalizing Constants of Wishart Distributions for Graphical Models. Ann. Stat. 2018, 46, 90–118. [Google Scholar] [CrossRef]
- Bhadra, A.; Sagar, K.; Banerjee, S.; Datta, J. Graphical Evidence. arXiv 2022, arXiv:2205.01016. [Google Scholar] [CrossRef]
- Chuu, E.; Pati, D.; Bhattacharya, A. A Hybrid Approximation to the Marginal Likelihood. In Proceedings of the AISTATS, San Diego, CA, USA, 13–15 April 2021. [Google Scholar]
- Breiman, L. Classification and Regression Trees; Wadsworth International Group: Franklin, TN, USA, 1984. [Google Scholar]
- Kleijn, B.J.K.; van der Vaart, A.W. Misspecification in infinite-dimensional Bayesian statistics. Ann. Statist. 2006, 34, 837–877. [Google Scholar] [CrossRef]
- Ghosal, S.; Van Der Vaart, A. Convergence rates of posterior distributions for noniid observations. Ann. Stat. 2007, 35, 192–223. [Google Scholar] [CrossRef]
- Vaart, A.W.v.d. Asymptotic Statistics; Cambridge Series in Statistical and Probabilistic Mathematics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar] [CrossRef]
- Genz, A. Numerical Computation of Multivariate Normal Probabilities. J. Comput. Graph. Stat. 1992, 1, 141. [Google Scholar] [CrossRef]
- Botev, Z.I. The normal law under linear restrictions: Simulation and estimation via minimax tilting. J. R. Stat. Soc. Ser. B 2016, 79, 125–148. [Google Scholar] [CrossRef]
- Minka, T.P. Expectation Propagation for approximate Bayesian inference. arXiv 2013, arXiv:1301.2294. [Google Scholar] [CrossRef]
- Cunningham, J.P.; Hennig, P.; Lacoste-Julien, S. Gaussian probabilities and expectation propagation. arXiv 2011, arXiv:1111.6832. [Google Scholar]
- Mohammadi, R.; Wit, E.C. BDgraph: An R Package for Bayesian Structure Learning in Graphical Models. J. Stat. Softw. 2019, 89, 1–30. [Google Scholar] [CrossRef]
- Diaconis, P.; Ylvisaker, D. Conjugate priors for exponential families. Ann. Stat. 1979, 7, 269–281. [Google Scholar] [CrossRef]
- Dawid, A.P.; Lauritzen, S.L. Hyper Markov laws in the statistical analysis of decomposable graphical models. Ann. Statist. 1993, 21, 1272–1317. [Google Scholar] [CrossRef]
- Robertson, N.; Seymour, P. Graph minors. II. Algorithmic aspects of tree-width. J. Algorithms 1986, 7, 309–322. [Google Scholar] [CrossRef]
- Fitch, A.M.; Jones, M.B.; Massam, H. The Performance of Covariance Selection Methods That Consider Decomposable Models Only. Bayesian Anal. 2014, 9, 659–684. [Google Scholar] [CrossRef]
- Chuu, E. hybrid: Hybrid Approximation to the Marginal Likelihood, R package version 1.0.; 2022. Available online: https://proceedings.mlr.press/v130/chuu21a.html (accessed on 10 May 2024).
- Chuu, E. graphml: Hybrid Approximation for Computing Normalizing Constants of G-Wishart Densities. R package, version 1.0. 2022. [Google Scholar]
- Jones, B.; Carvalho, C.; Dobra, A.; Hans, C.; Carter, C.; West, M. Experiments in Stochastic Computation for High-Dimensional Graphical Models. Stat. Sci. 2005, 20, 388–400. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).