A State of the Art Review of Systems of Linear Inequalities and Related Observability Problems
Abstract
1. Introduction and Motivation
2. Systems of Linear Equations
2.1. Homogeneous Systems of Linear Equations
2.2. Complete Systems of Linear Equations
The Plate Scanning Example
2.3. Compatibility of Systems of Linear Equations
A Symbolic Compatibility Example
2.4. Some Software Available
3. Systems of Linear Inequalities
3.1. Homogeneous Systems of Linear Inequalities
Example of a Homogeneous System of Linear Inequalities
3.2. Complete Systems of Linear Inequalities
Example of a Complete System of Linear Inequalities
3.3. Compatibility of a Complete System of Linear Inequalities
- Replace each inequality “greater than or equal” with an “equality” by simply subtracting a new non-negative variable, one per each inequality.
- Replace each inequality “less than or equal” with an “equality”, a new non-negative variable, one per inequality.
- Replace all non-positive unknowns with others equal to themselves but with the sign changed.
- Replace all unknowns not restricted in sign with a new , where is a common non-negative unknown and .
3.3.1. Example of Compatibility of the Particular Case of Complete System of Linear Inequalities
3.3.2. Example of Compatibility of the General Case of Complete System of Linear Inequalities
- The inequalities “greater than or equal” and “less than or equal” are replaced by equalities:
- We replace the unrestricted unknowns and by and , respectively:
3.4. Working with Compatible Systems of Inequalities
3.5. Another Approach to Compatible Systems of Inequalities
3.6. Some Software Available
4. Observability
4.1. Complete and No Observability at All
4.2. Partial Observability
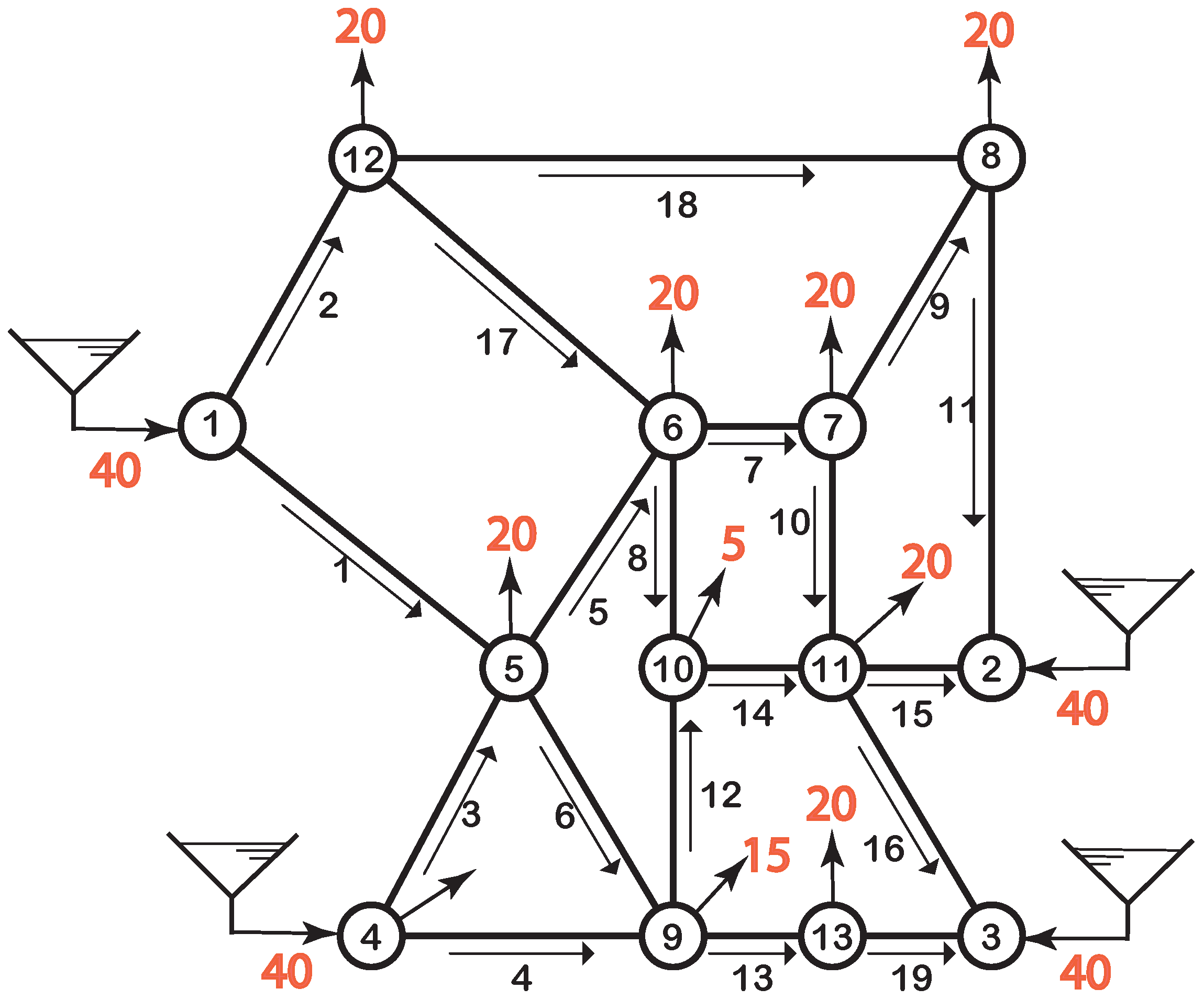
Example of the Water Supply Problem
5. Linear Programming
5.1. Discussion of the Boundedness or Unboundedness and Uniqueness or Multiplicity of Solutions
- If is non-null, the problem is unbounded. It is sufficient to choose a non-null component of this vector and associate with the corresponding coefficient a very large (positive) or very small (negative) value, depending on its sign, positive or negative, respectively, to obtain a value as small as desired.
- If is null and is non-null and has a negative component, the problem is unbounded. By choosing a negative component of that vector and associating with the corresponding coefficient a very large value (positive), we obtain a negative value as small as desired.
- If is null and is non-negative, the problem is bounded. The term is non-negative, that is, bounded from below.
- If the vectors and are null, the problem is bounded. The term is bounded from below.
5.2. Illustrative Examples

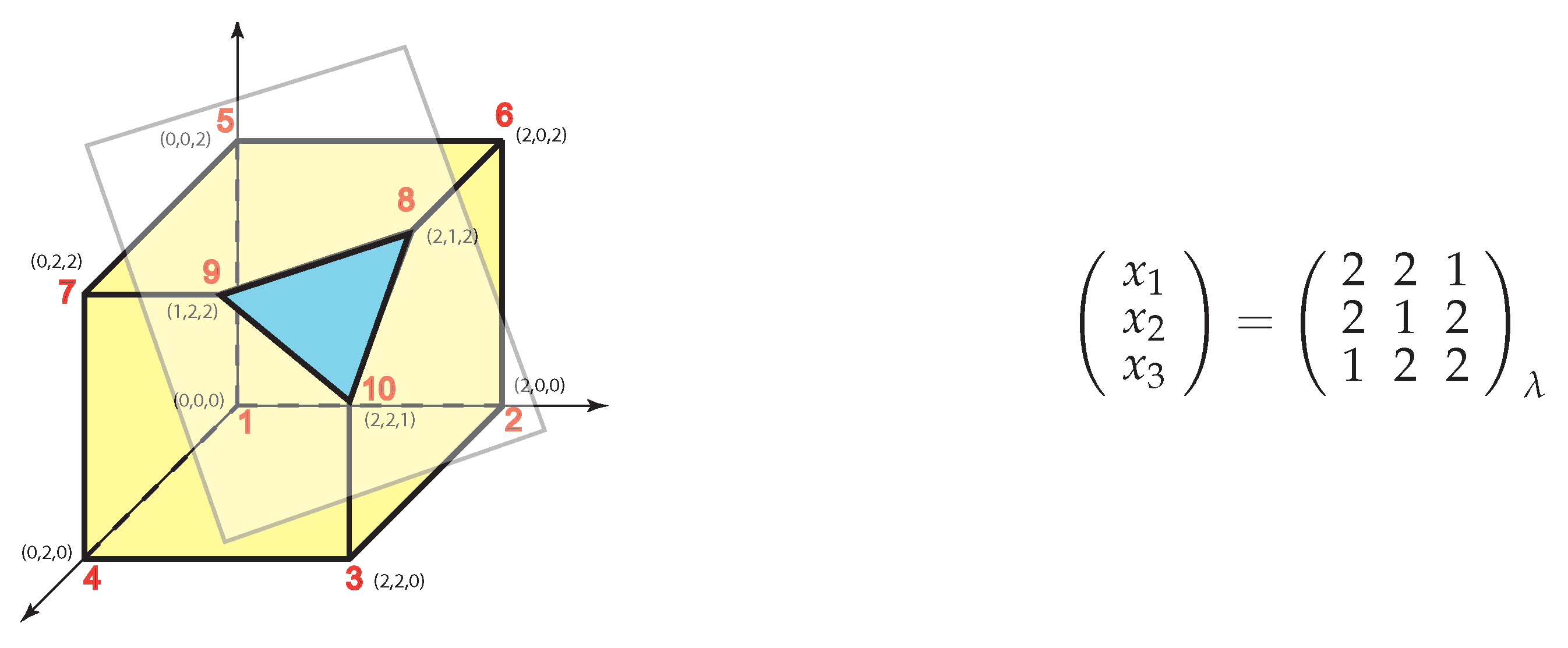 Note that all solutions have been obtained.
Note that all solutions have been obtained.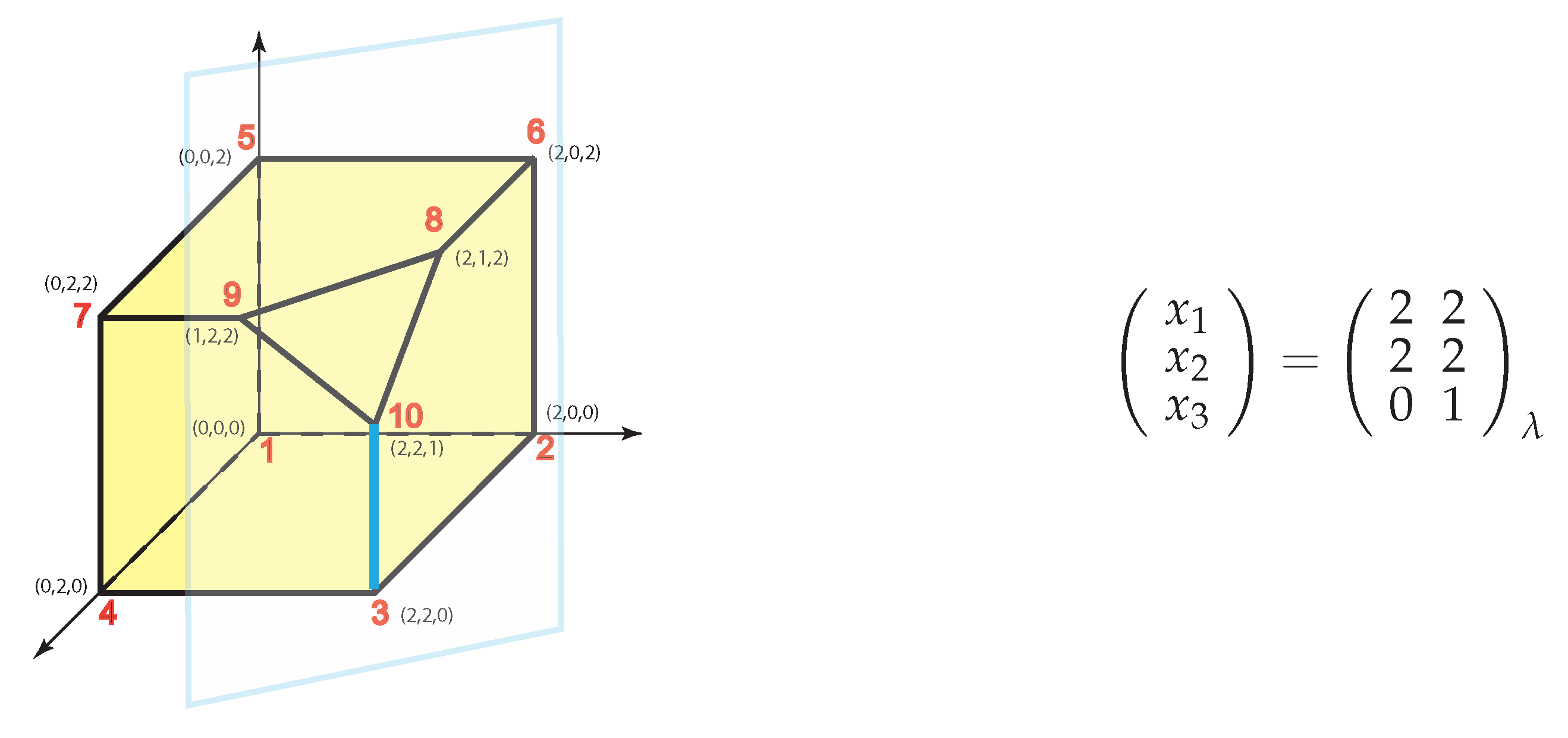 Note that all solutions have been obtained.
Note that all solutions have been obtained.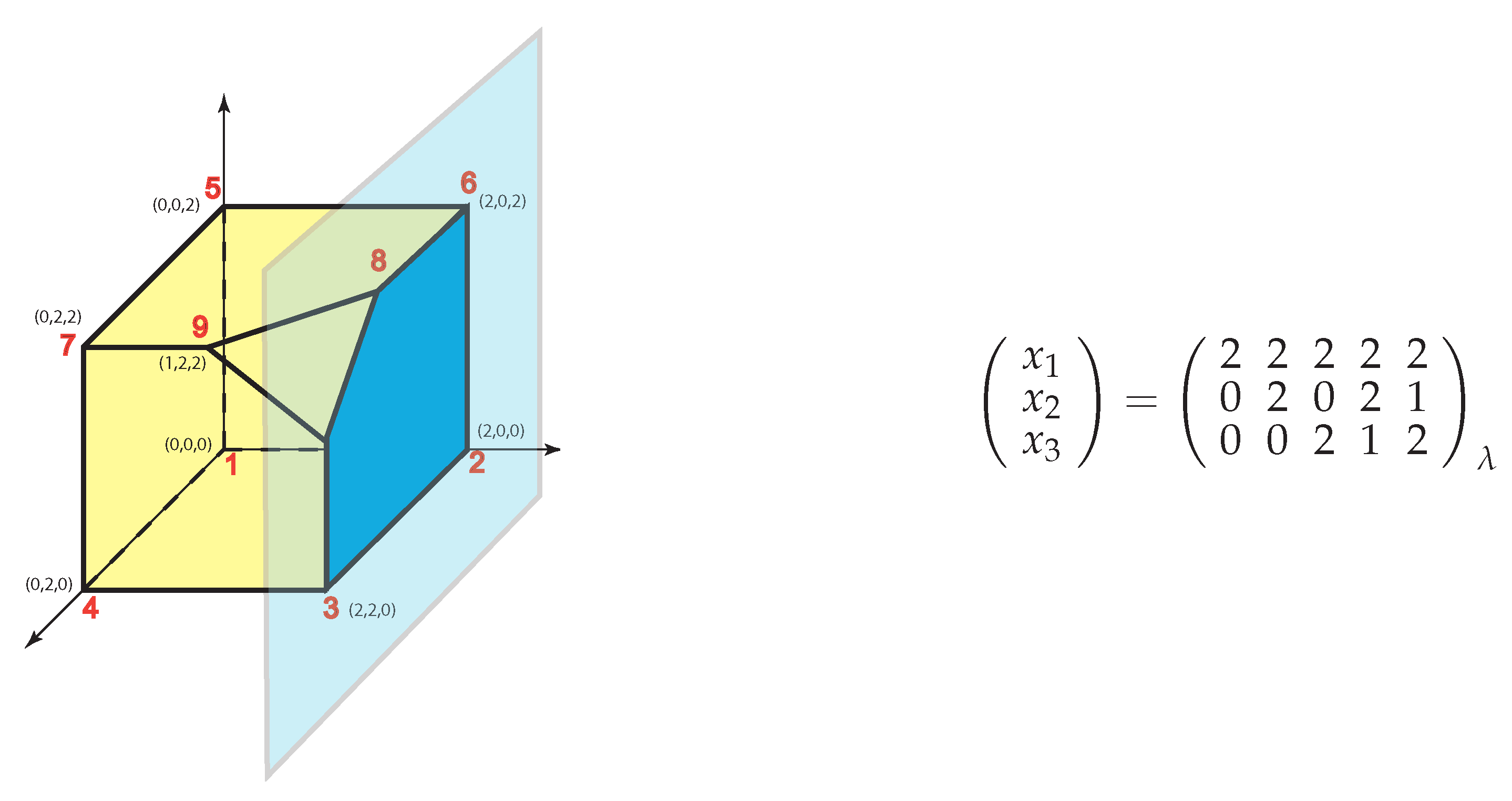 Again, note that all solutions have been obtained.
Again, note that all solutions have been obtained.5.3. Some Software Available
6. Examples of Applications
6.1. Application to Artificial Intelligence Problems
6.2. Application to Traffic Problems
- The problem of optimizing the use of scanning resources for the estimation of route flows in traffic networks is dealt with in [40], where the authors analyze three problems: (a) how to minimize the number of cameras required for estimating a given subset of route flows, (b) finding the links to be scanned when n cameras are available, and (c) solving the same problems when errors are present. Finally, the Nguyen Dupuis, a small-sized and well-known network example, and the case of the city of Ciudad Real in Spain, are used to illustrate the methodology.
- The problem of observability of subsets of flows in terms of another subset , when simultaneously different types of flows, links, nodes, routes, origin–destination (OD), plate scanned, etc., are considered, is discussed in [7]. There are two problems considered: (a) which flows in can be calculated in terms of the observed flows , and (b) find the subset of flows that needs to be observed to obtain the flows in . In addition, important theorems providing necessary and sufficient conditions for solving these two problems are given and they are illustrated by its application to three simple examples.
- The observability problem in traffic networks and the optimal location of scanning and counting devices, the treatment of plate scanning information, and the associated flow amount of information measured is dealt with. In addition, the problem of the optimal location of counters and plate scanning cameras is analyzed and illustrated with some illustrative and real examples.
6.3. Applications to Algebra Problems
- A pivoting transformation or algorithm, to obtain the orthogonal linear subspace to a given linear subspace is presented in [6], by explaining the meaning of the tables resulting after introducing each generator of the initial linear subspace. In addition, this algorithm allows us to solve many problems of linear algebra avoiding some painful classical methods, such as calculating the rank of a matrix, its inverse and determinant, updating inverses and determinants of a matrix after changing rows or columns, identifying linearly dependent vectors, etc.
- The algorithm, to obtain the dual cone of a given cone, is presented in some detail in [17]. This algorithm obtains, at the i-th step, the dual cone of the cone generated by the first generators of the initial cone. This algorithm is useful to solve a wide collection of algebra problems that can be solved if one uses the point of view of polarity, such as checking if a vector belongs to a cone, obtaining minimal representations of cones as the sum of a linear subspace and an acute cone, obtaining the cone intersection of two given cones, etc.Finally, the proposed methods and applications are illustrated with some examples.
- An interesting method that implies systems of linear equations subject to data with rounding errors is presented in [41], where, due to the errors, the linear system becomes incompatible. Thus, instead of solving the system, a least squares problem is solved, leading to another linear system. The methods mentioned in the present paper suggest alternative solutions to the problem.
- The problem of systems of linear equations when the less than or equal to, equal to or greater than, or equal to relations can be selected is solved in [20]. The proposed algorithm provides the necessary information to solve this problem, where the operators in each linear relation are chosen as wished. In addition, the algorithm permits obtaining the dual cone of the cone defined by any subset of constraints. Some examples illustrate the methodology.
7. Conclusions
- There exist a wide collection of methods and algorithms to deal with the problem of solving systems of linear inequalities and related problems, but they appear in some areas of mathematical specialities which are far from other applied areas in which these systems appear in a natural way.
- This causes a general state of ignorance about the possibilities of using these methods and algorithms to solve real and important problems in which they play an important role.
- People in general have a great degree of ignorance about the algebraic structures of polyhedra as the sum of a linear subspace plus an acute cone plus a polytope. In particular they ignore that for bounded problems this solution degenerates to a polytope, which is, with difference, the most frequent in real applications.
- The existing software able to solve systems of linear inequalities is not easily available, so that in practice this software is not commonly used in spite of its close relation with the problems mentioned. In addition, the software should be free to use.
- There is a need for publications describing the multiple applications of systems of linear inequalities. The actual lack of available examples and their poor diffusion is the cause of the slow rate of important advances in science and engineering.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Swart, G. Finding the convex hull facet by facet. J. Algorithms 1985, 6, 17–48. [Google Scholar] [CrossRef]
- Avis, D.; Fukuda, K. A pivoting algorithm for convex hulls and vertex enumeration of arrangements and polyhedra. Discret. Comput. Geom. 1992, 8, 295–313. [Google Scholar] [CrossRef]
- Ziegler, G.M. Lectures on Polytopes; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 152. [Google Scholar]
- Dyer, M.E. The Complexity of Vertex Enumeration Methods. Math. Oper. Res. 1983, 8, 381–402. [Google Scholar] [CrossRef]
- Pang, L.P.; Spedicato, E.; Xia, Z.Q.; Wang, W. A method for solving the system of linear equations and linear inequalities. Math. Comput. Model. 2007, 46, 823–836. [Google Scholar] [CrossRef]
- Castillo, E.; Cobo, A.; Jubete, F.; Pruneda, R.E.; Castillo, C. An Orthogonally Based Pivoting Transformation of Matrices and Some Applications. SIAM J. Matrix Anal. Appl. 2001, 22, 666–681. [Google Scholar] [CrossRef]
- Castillo, E.; Gallego, I.; Sánchez-Cambronero, S.; Rivas, A. Matrix Tools for General Observability Analysis in Traffic Networks. IEEE Trans. Intell. Transp. Syst. 2010, 11, 799–813. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Book Review: Numerical recipes: The art of scientific computing. by W. H. Press, B. P. Flannery, S. A. Teukolsky and W. T. Vetterling, Cambridge University Press, 1986, pp. xx + 818, price £25.00. J. Mol. Struct. 1987, 161, 349. [Google Scholar] [CrossRef]
- Spedicato, E.; Bodon, E.; Del Popolo, A.; Xia, Z. ABS Algorithms for Linear Systems and Optimization. arXiv 2001, arXiv:math/0105056. [Google Scholar]
- Abaffy, J.; Broyden, C.; Spedicato, E. A class of direct methods for linear systems. Numer. Math. 1984, 45, 361–376. [Google Scholar] [CrossRef]
- Abaffy, J.; Spedicato, E. ABS Projection Algorithms: Mathematical Techniques for Linear and Nonlinear Equations; Prentice-Hall, Inc.: Hoboken, NJ, USA, 1989. [Google Scholar]
- Nicolai, S.; Spedicato, E. A bibliography of the ABS methods. Optim. Methods Softw. 1997, 8, 171–183. [Google Scholar] [CrossRef]
- Spedicato, E.; Bodon, E.; del Popolo, A.; Xia, Z. ABS algorithms for linear systems and optimization: A review and a bibliography. Cent. Eur. J. Oper. Res. 1999. [Google Scholar]
- Spedicato, E.; Bodon, E.; Xia, Z.; Mahdavi-Amiri, N. ABS methods for continuous and integer linear equations and optimization. Cent. Eur. J. Oper. Res. 2010, 18, 73–95. [Google Scholar]
- Demmel, J.W. Applied Numerical Linear Algebra; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1997. [Google Scholar] [CrossRef]
- Higham, N.J. Accuracy and Stability of Numerical Algorithms, 2nd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2002. [Google Scholar] [CrossRef]
- Castillo, E.; Jubete, F. The Γ-algorithm and some applications. Int. J. Math. Educ. Sci. Technol. 2004, 35, 369–389. [Google Scholar] [CrossRef]
- Castillo, E.; Cobo, A.; Jubete, F.; Pruneda, R.E. Orthogonal Sets and Polar Methods in Linear Algebra: Applications to Matrix Calculations, Systems of Equations, Inequalities, and Linear Programming; Wiley Interscience. John Wiley and Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Pillers Dobler, C. A Matrix Approach to Finding a Set of Generators and Finding the Polar (Dual) of a Class of Polyhedral Cones. SIAM J. Matrix Analuysis Appl. 1994, 15, 796–803. [Google Scholar] [CrossRef]
- Castillo, E.; Jubete, F.; Pruneda, R.; Solares, C. Obtaining simultaneous solutions of linear subsystems of inequalities and duals. Linear Algebra Its Appl. 2002, 346, 131–154. [Google Scholar] [CrossRef]
- Contesse, L. A general algorithm for determining all essential solutions and inequalities for any convex polyhedron. Ann. Oper. Res. 1994, 50, 187–218. [Google Scholar] [CrossRef]
- McMullen, P.G.M. Ziegler Lectures on polytopes (Graduate Texts in Mathematics, Vol. 152, Springer-Verlag, Berlin-Heidelberg-New York-London-Paris-Tokyo-Hong Kong 1995), ix 370 pp., softcover: 3 540 94365 X, £21, hardcover: 3 540 94329 3, £47. Proc. Edinb. Math. Soc. 1996, 39, 189–190. [Google Scholar] [CrossRef][Green Version]
- Matheiss, T.H.; Rubin, D.S. A Survey and Comparison of Methods for Finding All Vertices of Convex Polyhedral Sets. Math. Oper. Res. 1980, 5, 167–185. [Google Scholar] [CrossRef]
- Dyer, M.; Proll, L. An improved vertex enumeration algorithm. Eur. J. Oper. Res. 1982, 9, 359–368. [Google Scholar] [CrossRef]
- Motzkin, T.S.; Raiffa, H.; Thompson, G.L.; Thrall, R.M. The double description method. Contrib. Theory Games 1953, 2, 51–73. [Google Scholar]
- Fukuda, K.; Prodon, A. Double description method revisited. In Franco-Japanese and Franco-Chinese Conference on Combinatorics and Computer Science; Deza, M., Euler, R., Manoussakis, I., Eds.; Springer: Berlin/Heidelberg, Germany, 1996; pp. 91–111. [Google Scholar]
- Esmaeili, H.; Mahdavi-Amiri, N. Solving some linear inequality systems and LP problems in real and integer spaces via the ABS algorithm. QDMSIA13 2000. [Google Scholar]
- Zhao, J. A class of direct methods for solving linear inequalities. J. Numer. Math. Chin. Univ. 1989, 3, 231–238. [Google Scholar]
- Shi, G. An ABS algorithm for generating nonnegative solutions of linear systems. In Proceedings of the First International Conference on ABS Algorithms, Luoyang, China, 2–6 September 1991; pp. 54–57. [Google Scholar]
- Gill, P.E.; Golub, G.H.; Murray, W.; Saunders, M.A. Methods for modifying matrix factorizations. Math. Comp. 1974, 28, 505–535. [Google Scholar] [CrossRef]
- Zhang, L. A method for finding a feasible point of inequalities. In Proceedings of the First International Conference on ABS Algorithms, Luoyang, China, 2–6 September 1991; pp. 131–137. [Google Scholar]
- Zhang, L. An algorithm for the least Euclidean norm solution of a linear system of inequalities via the Huang ABS algorithm and the Goldfarb–Idnani strategy. Rep. DMSIA 1995, 95. [Google Scholar]
- Xia, Y.; Wang, J.; Hung, D.L. Recurrent neural networks for solving linear inequalities and equations. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1999, 46, 452–462. [Google Scholar]
- Xu, F.; Li, Z.; Nie, Z.; Shao, H.; Guo, D. Zeroing Neural Network for Solving Time-Varying Linear Equation and Inequality Systems. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 2346–2357. [Google Scholar] [CrossRef] [PubMed]
- Chvatal, V. Linear Programming; Macmillan: New York, NY, USA, 1983. [Google Scholar]
- Padberg, M. Linear Programming and Extensions; Springer: Berlin, Germany, 1995. [Google Scholar]
- Scrucca, L. Entropy-Based Anomaly Detection for Gaussian Mixture Modeling. Algorithms 2023, 16, 195. [Google Scholar] [CrossRef]
- La Grassa, R.; Gallo, I.; Vetro, C.; Landro, N. Learning to Navigate in the Gaussian Mixture Surface. In International Conference on Computer Analysis of Images and Patterns; Tsapatsoulis, N., Panayides, A., Theocharides, T., Lanitis, A., Pattichis, C., Vento, M., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 414–423. [Google Scholar]
- Karras, C.; Karras, A.; Giotopoulos, K.C.; Avlonitis, M.; Sioutas, S. Consensus Big Data Clustering for Bayesian Mixture Models. Algorithms 2023, 16, 245. [Google Scholar] [CrossRef]
- Castillo, E.; Gallego, I.; Menéndez, J.M.; Rivas, A. Optimal Use of Plate-Scanning Resources for Route Flow Estimation in Traffic Networks. IEEE Trans. Intell. Transp. Syst. 2010, 11, 380–391. [Google Scholar] [CrossRef]
- Lukyanenko, D. Parallel Algorithm for Solving Overdetermined Systems of Linear Equations, Taking into Account Round-Off Errors. Algorithms 2023, 16, 242. [Google Scholar] [CrossRef]

| Three ways of checking if a vector belongs to a linear subspace |
| Three ways of obtaining the intersection of two subspaces |
| OD | Route Number (r) | Links | w | ||||
|---|---|---|---|---|---|---|---|
| 1-3 | 1 | 1 | 2 | {1} | |||
| 1-6 | 2 | 1 | 5 | 6 | {1,5,6} | ||
| 2-3 | 3 | 2 | - | - | |||
| 2-3 | 3 | 5 | 8 | {5,8} | |||
| 2-5 | 4 | 5 | {5} | ||||
| 2-6 | 5 | 5 | 6 | {5,6} | |||
| 3-1 | 6 | 9 | {9} | ||||
| 3-2 | 7 | 9 | 1 | {1,9} | |||
| 4-5 | 8 | 4 | 1 | 5 | {1,4,5} | ||
| 5-1 | 9 | 8 | 9 | {8,9} | |||
| 5-1 | 9 | 6 | 7 | 3 | 4 | {4,6} | |
| 5-1 | 9 | 6 | 7 | 9 | {6,9} | ||
| Three ways of checking if a vector belongs to a cone |
| Three ways of obtaining the intersection of two subspaces |
| 0 | 0 | −1 | 1 | 0 | 0 | 1 | |
| −1 | 0 | 0 | 0 | 0 | 1 | 1 | |
| 0 | −1 | 0 | 0 | 1 | 0 | 1 | |
| 0 | 0 | 0 | −2 | −2 | −2 | −5 | |
| 1 | 1 | 1 | 2 | 5 | 3 | 8 | |
| 2 | 2 | 4 | 3 | 6 | 4 | 9 | |
| 5 | 3 | 5 | 6 | 7 | 7 | 10 | |
| 10 | 9 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castillo, E. A State of the Art Review of Systems of Linear Inequalities and Related Observability Problems. Algorithms 2023, 16, 356. https://doi.org/10.3390/a16080356
Castillo E. A State of the Art Review of Systems of Linear Inequalities and Related Observability Problems. Algorithms. 2023; 16(8):356. https://doi.org/10.3390/a16080356
Chicago/Turabian StyleCastillo, Enrique. 2023. "A State of the Art Review of Systems of Linear Inequalities and Related Observability Problems" Algorithms 16, no. 8: 356. https://doi.org/10.3390/a16080356
APA StyleCastillo, E. (2023). A State of the Art Review of Systems of Linear Inequalities and Related Observability Problems. Algorithms, 16(8), 356. https://doi.org/10.3390/a16080356






