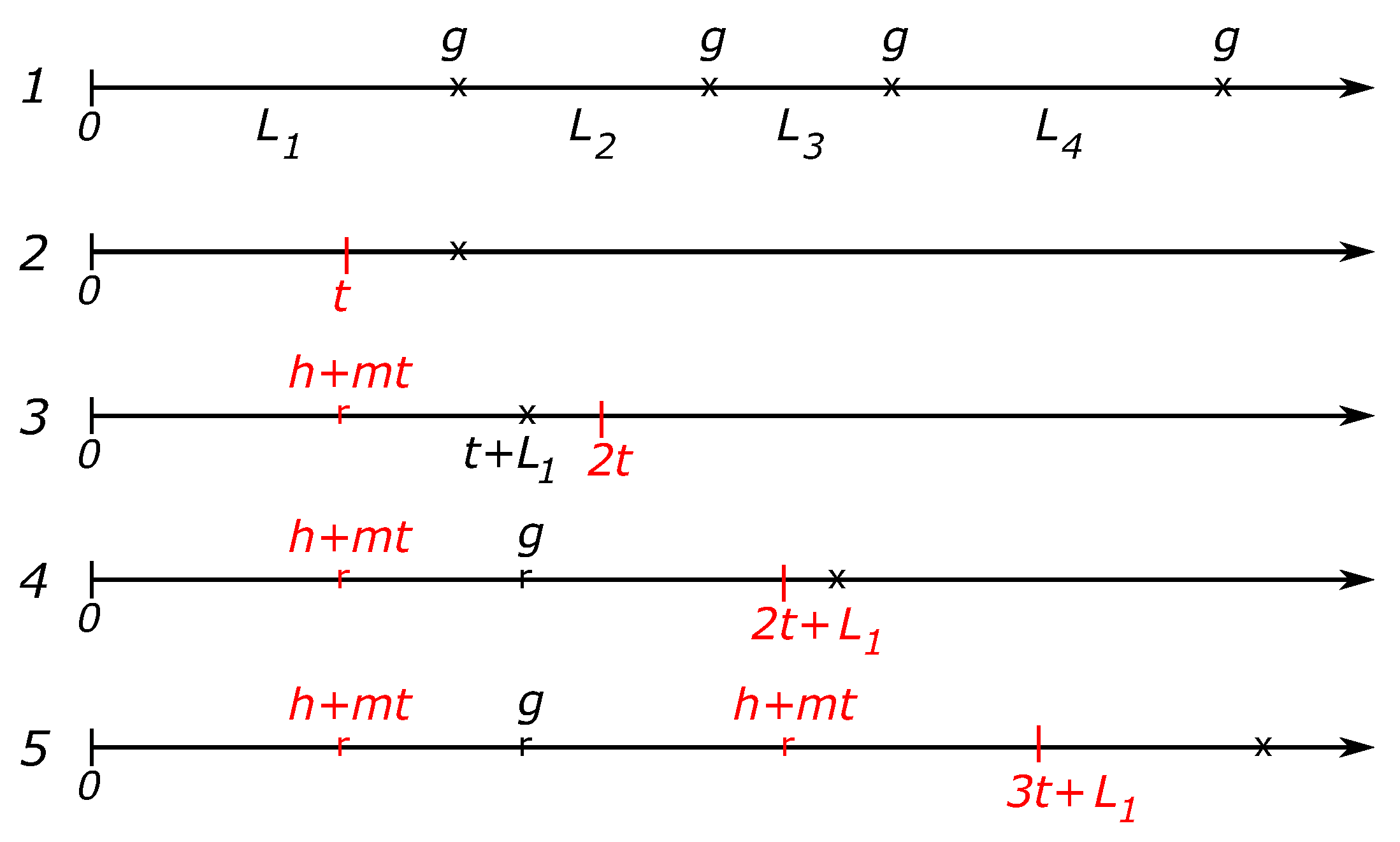Optimal Maintenance Schedule for a Wind Power Turbine with Aging Components

Abstract

Wind power is one of the most important sources of renewable energy available today. A large part of the cost of wind energy is due to the cost of maintaining wind power equipment. When a wind turbine component fails to function, it might need to be replaced under circumstances that are less than ideal. This is known as corrective maintenance. To minimize unnecessary costs, a more active maintenance policy based on the life expectancy of the key components is preferred. Optimal scheduling of preventive maintenance activities requires advanced mathematical modeling. In this paper, an optimal preventive maintenance algorithm is designed using the renewal-reward theorem. In the multi-component setting, our approach involves a new idea of virtual maintenance that allows us to treat each replacement event as a renewal event even if some components are not replaced by new ones. The proposed optimization algorithm is applied to a four-component model of a wind turbine, and the optimal maintenance plans are computed for various initial conditions. The modeling results clearly show the benefit of PM planning compared to a pure CM strategy (about 30% lower maintenance cost).

1. Introduction

Wind power technology is one of the most efficient sources of renewable energy available today [1]. A large part of the wind energy cost is due to the cost of maintaining wind power equipment (e.g., 25–30% of the total lifecycle costs for offshore wind farms) [2]. The corrective maintenance (CM) of a turbine component, performed after it breaks down, is usually more expensive than a preventive maintenance (PM) event, as some of the equipment is replaced in a planned manner. However, if PM activities are scheduled too frequently, the maintenance costs become unreasonably high, which entails the necessity of a maintenance schedule minimizing the expected replacement, logistic, and downtime costs.

There is a broad body of literature devoted to various optimization models of maintenance scheduling. Here, we name just a few of the relevant papers that influenced our own approach. In the article by Lee and Cha [3], some general PM optimization models are presented. The effect of a PM action has been classified into three categories: failure rate reduction, the decrease in the deterioration speed, and age reduction. The paper concludes that it can be profitable to perform PM. Compared to our setting, this paper considers a one-component system and relies on a different survival function.

The article [4] looks at opportunistic maintenance, which is a special kind of preventive maintenance. When one component breaks down, the maintenance personnel attending to the broken component might as well maintain other aged components to save some logistics costs. This is extremely beneficial for offshore wind farms due to the large set-up costs.

In [5], optimization algorithms are developed to determine optimal PM schedules in repairable and maintainable systems. It was demonstrated that higher set-up costs make simultaneous PM activities advantageous. However, the suggested models are nonlinear, which means they are computationally hard to solve.

Our paper suggests a new optimization algorithm aiming at a PM plan $({\mathit{x}}_s,{\mathit{y}}_s)$—see Section 6—which proposes the next time for the replacement of one or several components at a minimal maintenance cost $f_{(s,\mathit{a})}\left({\mathit{y}}_s\right)$ estimated for the whole planning time period $[s,T]$, subject to certain linear constraints on $({\mathit{x}}_s,{\mathit{y}}_s)$. Here, T is the life length of the wind turbine, $s\in [0,T)$ is the starting time of the planning period, and $\mathit{a}=(a^1,\dots ,a^n)$ is the vector of component ages at time s.

The age dynamics of our algorithm are based on the discrete Weibull distribution; see [6]. To account for the component deterioration due to aging, we assume that the PM cost increases as a linear function of the component’s age at the moment of replacement. Previously, the PM replacement cost was usually treated as an age-independent constant; see for example [7,8]. Our approach, focusing on age dependence, should be compared to that of [9], where the maintenance cost is assumed to depend on the total damage. Another relevant paper [10] quantifies the maintenance cost of a component using the reliability distribution.

Our definition of the objective function requires an application of the classical renewal-reward theorem; see for example [11]. This approach is quite straightforward in the one-component case, as explained in Section 2. In the multiple-component case, however, when the true renewal events (when all components are replaced simultaneously) are rarely encountered, our approach requires some kind of pseudo-renewal events. To this end, in Section 5, we introduce the key idea of the virtual maintenance replacement cost $b_{(t,a)}$ for a generic component with age a at time t.

Section 7 presents two sensitivity analyses and two case studies treating a four-component model of the wind power turbine. In particular, it was demonstrated that under the additional assumptions of [7], the new model produces similar results to those obtained in [7] but at a higher computational speed. Some technical proofs of our claims are postponed until the end of the paper.

2. A Single-Component Model

We start our exposition of the model by turning to the one-component case. Without planned PM activities, the maintenance cost flow is described by line 1 of Figure 1.

Here, the consecutive failure times (depicted by crosses) form a renewal process with independent inter-arrival times $L_1,L_2,\dots$ each having the same Weibull distribution W$(\theta ,\beta )$. After each failure, the broken component is replaced by a new one, and the incurred replacement cost is g. According to the classical renewal-reward theorem, the long-term time-average reward (the maintenance cost in the current setting) is $c=\frac{g}{\mathrm{E}\left(L\right)}$, where $E\left(L\right)$ is the expected value of the random variable L.

Lines 2–5 in Figure 1 introduce the renewal-reward model used to compute the time-average maintenance cost $q_t$ based on the PM planning strategy: plan the next PM replacement at time t after each replacement. Line 2 describes a scenario where the first failure occurs after the planned PM time and the first replacement is performed at time t, so the failure is avoided. The corresponding PM replacement cost is assumed to be a linear function $h+tm$ of the component’s age at the time of a PM replacement.

According to line 3, after the PM replacement was performed at the cost $h+tm$, the next failure occurred before the next PM planned time $2t$. As a consequence, the second replacement was performed in a CM regime incurring the cost g; see line 4. Line 4 says that following the second replacement, the next PM is planned at time $2t+L_1$, that is, at time t after the failure time $t+L_1$. According to the placement of a cross on line 4, we see on line 5 that the third replacement is performed in the PM regime and the next PM time is scheduled at time $3t+L_1$.

Recall that a random variable L has a Weibull distribution W$(\theta ,\beta )$ if

$$\mathrm{P}(L>t)=e^{-\theta t^{\beta }},t\ge 0,$$

where $\theta >0$ is a scale parameter and $\beta >1$ is a shape parameter of W$(\theta ,\beta )$. The mean value of L

$$\mu ={\theta }^{-1/\beta }\mathrm{\Gamma }(1+\frac{1}{\beta })$$

is computed using the gamma function. The age dependence in the continuous time setting is best viewed in terms of the hazard function $\theta \beta t^{\beta -1}$, telling how fast the failure rate increases with the component’s age t. In this paper, we use the discrete-time version of the Weibull distribution

$$\mathrm{P}(L>t)=e^{-\theta t^{\beta }},t=0,1,2,\dots ,$$

so that

$$\mathrm{P}(L=t)=e^{-\theta {(t-1)}^{\beta }}-e^{-\theta t^{\beta }},t=1,2,\dots$$

Using these expressions and the renewal-reward theorem, we arrive at the following explicit formula involving the key parameters of the one-component model $(\theta ,\beta ,g,h,m)$. The proof of this result (as well as the forthcoming Proposition 2) is given at the end of the paper.

Proposition 1.

Think of an infinite planning horizon and a recurrent strategy of planning the next PM at time t after each replacement event. Then, the time-average maintenance cost is the following function

$$q_t=\frac{(1-e^{-\theta t^{\beta }})g+e^{-\theta t^{\beta }}(h+mt)}{{\sum }_{k=1}^t(e^{-\theta {(k-1)}^{\beta }}-e^{-\theta k^{\beta }})k+e^{-\theta t^{\beta }}t}$$

of the planning time t.

As a check, one can send t to infinity and observe that this results in $q_t\to \frac{g}{\mathrm{E}\left(L\right)}$, the average maintenance cost in the absence of PM activities.

Minimizing the function $q_t$ over the possible planning times t produces a constant

$$c=\underset{t\ge 1}{min}\frac{(1-e^{-\theta t^{\beta }})g+e^{-\theta t^{\beta }}(h+mt)}{{\sum }_{k=1}^t(e^{-\theta {(k-1)}^{\beta }}-e^{-\theta k^{\beta }})k+e^{-\theta t^{\beta }}t},$$

(1)

which we will treat as the long-term maintenance cost per unit of time for the component in question. Notice that according to this formula, c is independent of the planning period $[s,T]$.

3. Optimal Maintenance Algorithm in the One-Component Case

In this section, we propose an optimization algorithm for PM scheduling during a discrete-time interval

$$[s,s+1,\dots ,T-1,T]$$

assuming that at time s the component in use is of age a. If $a=0$, we say that at the beginning of the planning period, the component was as good as new. This will allow us to find an optimal time $t_{(s,a)}$ for the next PM by minimizing the total maintenance cost during the whole planning period.

Definition 1.

For the one-component model with a planning period $[s,T]$, we call a PM plan any vector

$${\mathit{x}}_s=(x_{s+1},\dots ,x_{T+1})$$

with binary components satisfying a linear constraint

$$\begin{array}{c}\hfill \sum _{t=s+1}^{T+1}{x}_t=1,x_{s+1}\in \{0,1\},\dots ,x_{T+1}\in \{0,1\}.\end{array}$$

(2)

For the given planning period $[s,T]$, we define the total maintenance cost $Q_{(s,a)}(t,u)$ as a function of the planning time t for the next PM and the failure time u of the component in use. For $t\in [s+1,T]$, we put

$$\begin{array}{c}\hfill Q_{(s,a)}(t,u)=\left\{\begin{array}{cc}g+(T-u)c,\hfill & \mathrm{if}u\le t\hfill \\ h+(t-s+a)m+(T-t)c,\hfill & \mathrm{if}u>t\hfill \end{array}\right.\end{array}$$

(3)

or using indicator functions,

$$Q_{(s,a)}(t,u)=[g+(T-u)c]1_{\{u\le t\}}+[h+(t-s+a)m+(T-t)c]1_{\{u>t\}}.$$

We also put

$$Q_{(s,a)}(T+1,u)=[g+(T-u)c]1_{\{u\le T\}}.$$

This formula recognizes two possible outcomes:

• If $\{u\le t\}$, then the breakdown happens before the planned PM time, and the expected total maintenance cost is estimated to be $g+(T-u)c$, with c given by (1),
• If $\{u\ge t+1\}$, so that there is no breakdown before the planned PM time, then the expected total maintenance cost is estimated to be

  $$h+(t-s+a)m+(T-t)c.$$

If at the starting time s of the planning period, the component in use has age $a\ge 1$, and we will use a special notation $s+L_a$ for the first failure time, where

$$L_a\stackrel{d}{=}\{L-a|L>a\},$$

is defined in terms of the full life length L of a genetic component. If L has a discrete W$(\theta ,\beta )$ distribution, then

$$\mathrm{P}(L_a>t)=exp\left\{\theta \left(a^{\beta }-{(a+t)}^{\beta }\right)\right\},t\ge 0.$$

Putting $u=s+L_a$ into the formula for $Q_{(s,a)}(t,u)$, we arrive at a random variable

$$\begin{array}{c}\hfill F_{(s,a)}\left({\mathit{x}}_s\right)=\sum _{t=s+1}^{T+1}{Q}_{(s,a)}(t,s+L_a)x_t\end{array}$$

that gives us the total maintenance cost of the PM plan ${\mathit{x}}_s$. Averaging over $L_a$, we obtain the objective function

$$f_{(s,a)}\left({\mathit{x}}_s\right)=\mathrm{E}\left(F_{(s,a)}\left({\mathit{x}}_s\right)\right)$$

as the expected maintenance cost of the PM plans ${\mathit{x}}_s$. Now we are ready to define the optimal maintenance plan as the solution to the following optimization problem:

$$\begin{array}{cc}\hfill \mathrm{minimize}& f_{(s,a)}\left({\mathit{x}}_s\right)\hfill \\ \hfill \mathrm{subject}\mathrm{to}& \mathrm{linear}\mathrm{constraints}\left(2\right).\hfill \end{array}$$

Let $t_{(s,a)}$ be the PM time proposed by the solution of the minimization problem above, and notice that

$$t_{(0,0)}=\mathrm{argmin}\left(q_t\right).$$

The following proposition states a consistency property for the set of optimal times $t_{(s,a)}$, providing intuitive support for the suggested approach.

Proposition 2.

Suppose for some positive δ,

$$t_{(s,a)}>s+\delta .$$

If $t_{(s,a)}\le T$, then

$$t_{(s+\delta ,a+\delta )}=t_{(s,a)}.$$

4. Multiple-Component Model

In this section, we expand our one-component model to the cases with $n\ge 2$ components. We now think of a wind turbine consisting of n components with the j-th component having a life length $L^j$ distributed according to a Weibull distribution W$({\theta }^j,{\beta }^j)$, where parameters $({\theta }^j,{\beta }^j)$ may differ for different $j=1,\dots ,n$. We will assume that components may require different replacement costs:

• $g_0=$ the shared logistic and downtime costs associated with a CM activity,
• $g^j=$ the component-specific CM cost,
• $h_0=$ the fixed logistic cost plus the downtime cost during a PM activity,
• $h^j+t{m}^j=$ the component-specific PM replacement cost for j-th component at age t.

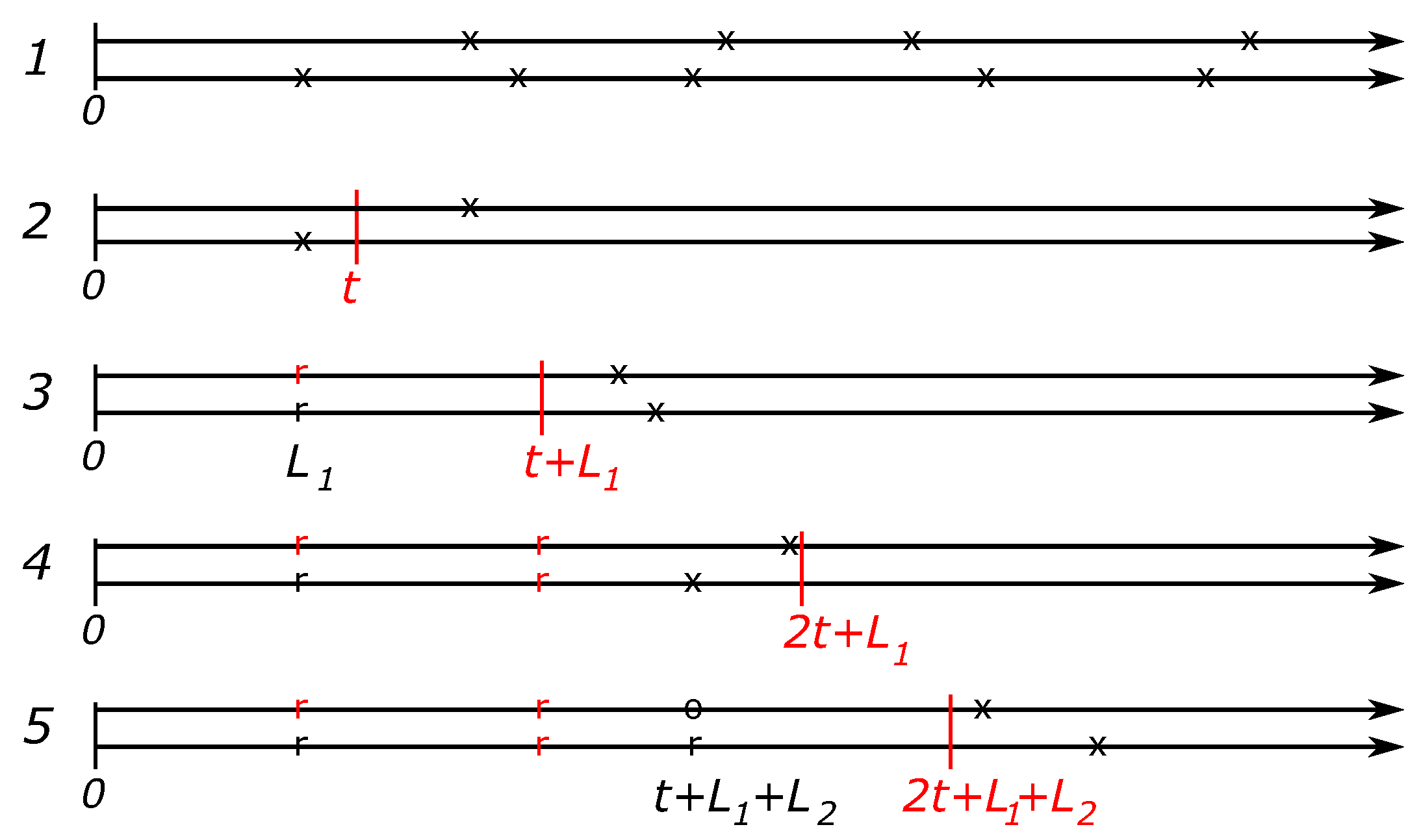
To be able to update the Formula (1) of the minimal time-average maintenance cost, we would need to determine the times of total renewal of the system that are not readily available in the multiple component setting. For an illustration, turn to Figure 2 dealing with the case of $n=2$ components.

Even in the absence of PM activities—see line 1—it is clear that the classical renewal-reward theorem is not directly applicable. Our solution to this problem is to treat each replacement event as total renewal events, sometimes by performing opportunistic maintenance and, in some cases, by increasing the cost function to reflect the future additional age-related replacement costs. This idea is illustrated by lines 2–5 in Figure 2.

Consider a strategy in which the next PM activity is planned at time t after each replacement. Line 2 depicts a case in which the second component is broken first and before the time t of the next PM. As shown by line 3, both components are replaced at the failure time $L_1$, and the next PM is planned at time $L_1+t$. In this way, the time $L_1$ can be viewed as the total renewal time of the two-component system. The incurred replacement cost is

$$g_0+g^2+h^1+L_1{m}^1.$$

Since, according to the line 3, both components break down after the planned time $t+L_1$ for the next PM, both components are replaced in the PM regime so that the incurred replacement cost is

$$h_0+h^1+t{m}^1+h^2+t{m}^2.$$

Continuing in this way by replacing both components at each maintenance event, we arrive at a renewal-reward process described in the general setting as follows.

Assume that we start at time 0 with n new components and denote by

$$L=min(L^1,\dots ,L^n)$$

the time of the first failure. With independence, we have

$$\mathrm{P}(L>t)=\mathrm{P}(L^1>t)\cdots \mathrm{P}(L^n>t)=exp\{-{\theta }^1{t}^{{\beta }^1}-\dots -{\theta }^n{t}^{{\beta }^n}\}.$$

Thus, if we plan our next PM at time t after each maintenance replacement, the first renewal time is $X=X\left(t\right)$ with

$$X=L\wedge t=L·1_{\{L\le t\}}+t·1_{\{L>t\}}$$

(4)

and the corresponding reward value $\tilde{R}=\tilde{R}\left(t\right)$ is computed as

$$\tilde{R}=\left(\sum _{j\in \gamma }{g}^j+\sum _{j\notin \gamma }(h^j+L{m}^j)+g_0\right)1_{\{L\le t\}}+\left(\sum _{j=1}^n(h^j+t{m}^j)+h_0\right)1_{\{L>t\}},$$

where

$$\gamma =\{j:L^j=L\}$$

is the subset of components that would be replaced at the first failure. The renewal-reward theorem allows us to express the time-average maintenance cost $\frac{\mathrm{E}\left(\tilde{R}\right)}{\mathrm{E}\left(X\right)}$ as an explicit function of the planning time t.

However, replacing all of the components at each maintenance event irrespective of the ages of the components in use is definitely a suboptimal strategy. If, at a maintenance event, some component j is in working condition and its current age a is rather small, then it might be more beneficial to let it continue working. To still be able to use the renewal argument in such a case, we introduce the idea of a virtual replacement. We replace the previous naive formula for reward $\tilde{R}$ with a more sophisticated one

$$R=\left(\sum _{j\in \gamma }{g}^j+\sum _{j\notin \gamma }{B}_L^j+g_0\right)1_{\{L\le t\}}+\left(\sum _{j=1}^n{B}_t^j+h_0\right)1_{\{L>t\}},$$

where

$$B_a^j=(h^j+a{m}^j)\wedge b_a^j$$

chooses the minimum between two age-specific costs: the preventive replacement cost and the virtual replacement cost; see Section 5. The renewal-reward theorem implies that the time-average maintenance cost $\frac{\mathrm{E}\left(R\right)}{\mathrm{E}\left(X\right)}$ is computed as the following function of the planning time t,

$$q_t=\frac{{\mathrm{E}}_t({\sum }_{j\in \gamma }{g}^j+{\sum }_{j\notin \gamma }{B}_L^j+g_0)+({\sum }_{j=1}^n{B}_t^j+h_0)\mathrm{P}(L>t)}{{\mathrm{E}}_t\left(L\right)+t\mathrm{P}(L>t)},$$

where ${\mathrm{E}}_t\left(Z\right)$ stands for $\mathrm{E}(Z·1_{\{L\le t\}})$. Now, after minimizing $q_t$ over t, we define the desired constant as

$$c=\underset{t\ge 1}{min}\frac{{\mathrm{E}}_t({\sum }_{j\in \gamma }{g}^j+{\sum }_{j\notin \gamma }{B}_L^j+g_0)+({\sum }_{j=1}^n{B}_t^j+h_0)\mathrm{P}(L>t)}{{\mathrm{E}}_t\left(L\right)+t\mathrm{P}(L>t)}.$$

(5)

5. Virtual Replacement Cost

Returning to the one-component model and focusing on an arbitrary component j, observe that in this one-component case, the model parameters are $g=g_0+g^j$, $h=h_0+h^j$, $\theta ={\theta }^j$, $\beta ={\beta }^j$, and $m=m^j$. Using this set of parameters, we introduce the virtual replacement cost function $b_{(t,a)}^j=b_{(t,a)}$ as a function of the current time t and the current age a of the component in question.

Since $f_{(s,a)}^{*}$ is the total cost of the optimal PM-plan in the one-component set, in terms of this cost function, the virtual replacement cost is defined by the difference

$$b_{(t,a)}=f_{(t,a)}^{*}-f_{(t,0)}^{*}.$$

(6)

This difference evaluates the extra maintenance cost over the time period $[t,T]$ due to the component’s age a at the starting time t of the observation period. The larger a is, the higher the expected maintenance cost. The function

$$b_a=b_{(0,a)}$$

will be treated as the long-term virtual replacement cost of the component of age a.

Proposition 3.

If $t_{(0,0)}+s\le T$, then $b_{(s,a)}=b_a$ and

$$t_{(s,a)}=t_{(0,0)}+s-a.$$

(7)

In the manner described above, we can define $b_{(t,a)}^j=b_{(t,a)}$ and $b_a^j=b_a$ for all $j=1,\dots ,n$.

6. Optimal Maintenance Algorithm for Multiple Components

For the planning period $[s,T]$, we call a PM plan in the multi-component setting any array $({\mathit{x}}_s,{\mathit{y}}_s,z)$, where

$$({\mathit{x}}_s,{\mathit{y}}_s)=\{x_t^j,y_t:1\le j\le n,s+1\le t\le T\}$$

and all components are binary $x_t^j,y_t,z\in \{0,1\}$ subject to the following linear constraints

$$\begin{array}{cc}\hfill & y_t\ge x_t^j,t=s+1,\dots T,j=1,\dots ,n,\hfill \end{array}$$

(8a)

$$\begin{array}{cc}\hfill & \sum _{t=s+1}^T{y}_t=1-z,\hfill \end{array}$$

(8b)

$$\begin{array}{cc}\hfill & \sum _{i=1}^n{x}_t^j\ge y_t,t=s+1,\dots T.\hfill \end{array}$$

(8c)

The equality $x_t^j=1$ means that the plan $({\mathit{x}}_s,{\mathit{y}}_s,z)$ suggests a PM replacement of the j-th component at time t. On the other hand, the equality $y_t=1$ means that according to the plan, $({\mathit{x}}_s,{\mathit{y}}_s,z)$ at least one of the components should be replaced at time t; this is guaranteed by constraint (8c) (constraint (8a) allows for several components to be replaced at such a time t). The equality $z=1$ means that no PM is planned during the whole time period $[s+1,T]$. This is guaranteed by constraint (8b).

Given the current ages of n components

$$\mathit{a}=(a^1,\dots ,a^n),$$

the first failure time is $s+L_{\mathit{a}}$, where

$$L_{\mathit{a}}=min(L_{a^1}^1,\dots ,L_{a^n}^n).$$

Putting

$$\gamma =\{j:L_{a^j}^j=L_{\mathit{a}}\}$$

we first mention a naive formula for the cost ${\tilde{F}}_{(s,\mathit{a})}$ assigned to a PM plan $({\mathit{x}}_s,{\mathit{y}}_s,z)$ assuming that, at each maintenance event, all n components are replaced by the new ones. With

$$\begin{array}{cc}\hfill {\tilde{C}}_{\mathit{a}}& =g_0+(T-s-L_{\mathit{a}})c+\sum _{j\in \gamma }{g}^j+\sum _{j\notin \gamma }(h^j+(L_{\mathit{a}}+a^j)m^j),\hfill \\ \hfill {\tilde{P}}_{\mathit{a}}& =h_0+(T-t)c+\sum _{j=1}^n(h^j+(t-s+a^j)m^j),\hfill \end{array}$$

where c is given by (5), put

$$\begin{array}{cc}\hfill {\tilde{F}}_{(s,\mathit{a})}({\mathit{y}}_s,z)=\sum _{t=s+1}^T& ({\tilde{C}}_{\mathit{a}}{1}_{\{s+L_{\mathit{a}}\le t\}}+{\tilde{P}}_{\mathit{a}}{1}_{\{s+L_{\mathit{a}}>t\}})y_t+{\tilde{C}}_{\mathit{a}}{1}_{\{s+L_{\mathit{a}}\le T\}}z.\hfill \end{array}$$

Here, the last term describes the option of planning no PM activity. This formula should be modified to incorporate the virtual replacement costs:

$$\begin{array}{c}\hfill F_{(s,\mathit{a})}({\mathit{y}}_s,z)=\sum _{t=s+1}^T\left(C_{\mathit{a}}{1}_{\{s+L_{\mathit{a}}\le t\}}+P_{\mathit{a}}{1}_{\{s+L_{\mathit{a}}>t\}}\right)y_t+{\tilde{C}}_{\mathit{a}}{1}_{\{s+L_{\mathit{a}}\le T\}}z,\end{array}$$

where

$$\begin{array}{cc}\hfill C_{\mathit{a}}& =g_0+(T-s-L_{\mathit{a}})c+\sum _{j\in \gamma }{g}^j+\sum _{j\notin \gamma }(h^j+(L_{\mathit{a}}+a^j)m^j)\wedge b_{(s+L_{\mathit{a}},a^j+L_{\mathit{a}})}^j,\hfill \\ \hfill P_{\mathit{a}}& =h_0+(T-t)c+\sum _{j=1}^n(h^j+(t-s+a^j)m^j)\wedge b_{(s+L_{\mathit{a}},a^j+L_{\mathit{a}})}^j.\hfill \end{array}$$

Notice that the total cost function $F_{(s,\mathit{a})}({\mathit{y}}_s,z)$ does not explicitly depend on ${\mathit{x}}_s$. The role of ${\mathit{x}}_s$ becomes explicit through the following additional constraint

$$\begin{array}{c}\hfill (h^j+(a^j+t-s)m^j)x_t^j+b_{(t,a^j+t-s)}^j(y_t-x_t^j)=B_{(t,a^j+t-s)}^j{y}_t,\\ \hfill t=s+1,\dots T,j=1,\dots ,n.\end{array}$$

(9)

This says that if $y_t=1$, that is, if a PM for at least one component is scheduled at time t, then for each component j, there is a choice between two actions at time t: either perform a PM, so that $x_t^j=1$ and $y_t-x_t^j=0$, or do not perform a PM and compensate for the current age of the component by increasing the cost function using the virtual replacement cost value (which corresponds to $x_t^j=0$ and $y_t-x_t^j=1$).

The optimal maintenance plan is the solution to the linear optimization problem:

$$\begin{array}{cc}\hfill \mathrm{minimize}& f_{(s,\mathit{a})}({\mathit{y}}_s,z)=\mathrm{E}\left(F_{(s,\mathit{a})}({\mathit{y}}_s,z)\right)\hfill \\ \hfill \mathrm{subject}\mathrm{to}& \mathrm{linear}\mathrm{constraints}\left(8\mathrm{a}\right),\left(8\mathrm{b}\right)\left(8\mathrm{c}\right)\mathrm{and}\left(9\right),\hfill \\ \hfill & x_t^j\in \{0,1\},t=s+1,\dots T,j=1,\dots ,n,\hfill \\ \hfill & y_t\in \{0,1\},t=s+1,\dots T,\hfill \\ \hfill & z\in \{0,1\}.\hfill \end{array}$$

This optimization problem is solved using the standard approach for the case when all variables are binary, and the objective function is a linear function of the variables $(y_{s+1},\dots ,y_T)$ and z. According to constraint (8b), only one of the variables $(y_{s+1},\dots ,y_T,z)$ can be equal to 1, so by selecting the variable with the smallest coefficient, we can determine which one is equal to 1. As a result, we can determine the optimal values of the target variables ${\mathit{x}}_s$ subject to the remaining constraints.

7. Case Studies

This section contains five computational studies with our algorithm applied to a four-component model of a wind power turbine described below.

Table 1. Base values for the model with $n=4$ components.

Component (j)	${\mathit{g}}^{\mathit{j}}$, CM Replacement Cost (USD 1000)	${\mathit{m}}^{\mathit{j}}$, Value Loss per Month (USD 1000)	Weibull Shape ${\mathit{\beta }}^{\mathit{j}}$	Weibull Scale ${\mathit{\theta }}^{\mathit{j}}$
Rotor $(j=1)$	162	0.5	3	1 × ${10}^{-6}$
Main Bearing $(j=2)$	110	0.25	2	6.4 × ${10}^{-5}$
Gearbox $(j=3)$	202	1	3	1.95 × ${10}^{-6}$
Generator $(j=4)$	150	0.45	2	8.26 × ${10}^{-5}$

lists the four components in question and summarizes the basic values of the model parameters, where the suggested values of $(g^j,{\beta }^j,{\theta }^j)$ are taken from the paper [12].

The cost unit is USD 1000, and the time unit is one month. In accordance with paper [13], the lifetime of the wind turbine is assumed to be 20 years, so $T=240$. Other basic values of the model are

$$g_0=100,h_0=10,h^1=65,h^2=40,h^3=80,h^4=60.$$

7.1. Sensitivity Analysis 1

In this section, we focus on the generator component of the four-component model and have a closer look at the cost function of age a

$$B_a^4=(h^4+a{m}^4)\wedge b_a^4$$

for different values of the parameters, where $(g,h_0,h^4,m^4)$ keep the values for the other parameters of the model unchanged.

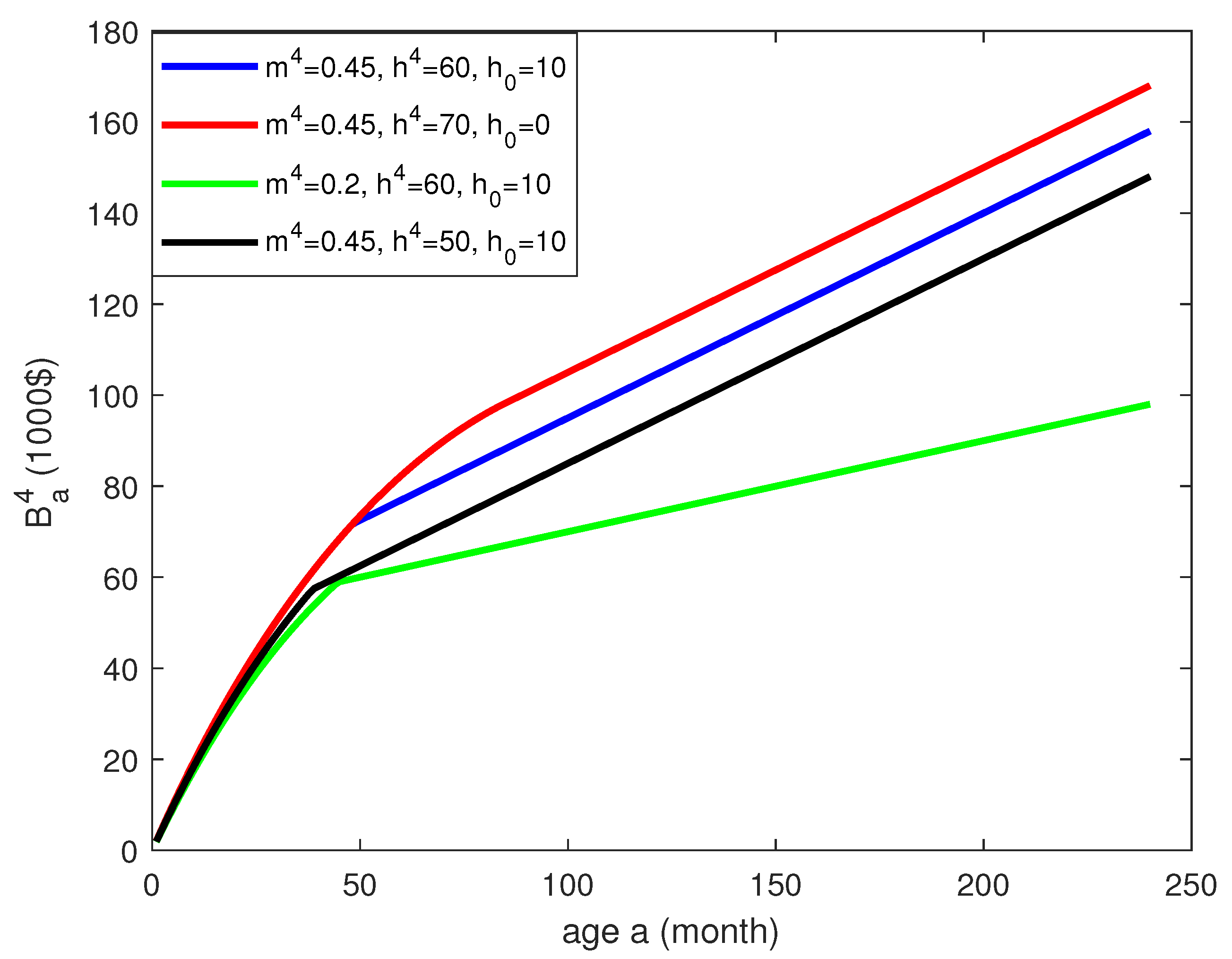
Figure 3 summarizes the results of this sensitivity analysis. The blue line in Figure 3 describes the function $B_a^4$ of age for the baseline set of parameter values. For small values of the age variable a, the cost function $B_a^4=b_a^4$ grows in a concave manner and beyond some critical age takes the linear form $B_a^4=h^4+a{m}^4$.

The red line shows what happens if we reduce $h_0$ but keep the sum $h^4+h_0$ unchanged. We see that the initial concave part of the curve is the same but the critical age becomes larger.

The green line indicates a drop in the cost function $B_a^4$ in response to the lowering of the monthly value loss parameter $m^4$. Finally, the black line shows the cost reduction caused by a smaller value of $h^4$. The black, blue, and red straight lines have the same slope because of the shared parameter value $m^4=0.45$.

7.2. Sensitivity Analysis 2

One of the most crucial parameters of our model is m, the monthly value depreciation of a genetic component. In this section, we consider the one-component model taking the rotor component as an example. We study how the optimal time to perform the next PM increases as $m=m^1$ becomes larger. All other parameters are fixed at their primary values.

Recall the formula for the time-average maintenance cost in the one-component setting:

$$q_t=\frac{(1-e^{-\theta t^{\beta }})g+e^{-\theta t^{\beta }}(h+mt)}{{\sum }_{k=1}^t(e^{-\theta {(k-1)}^{\beta }}-e^{-\theta k^{\beta }})k+e^{-\theta t^{\beta }}t},$$

where t is the planning time for the next PM. Considered as a function of m, the average cost $q_t$ is a linear function as depicted on the right panel of Figure 4 for different values of the planning time t.

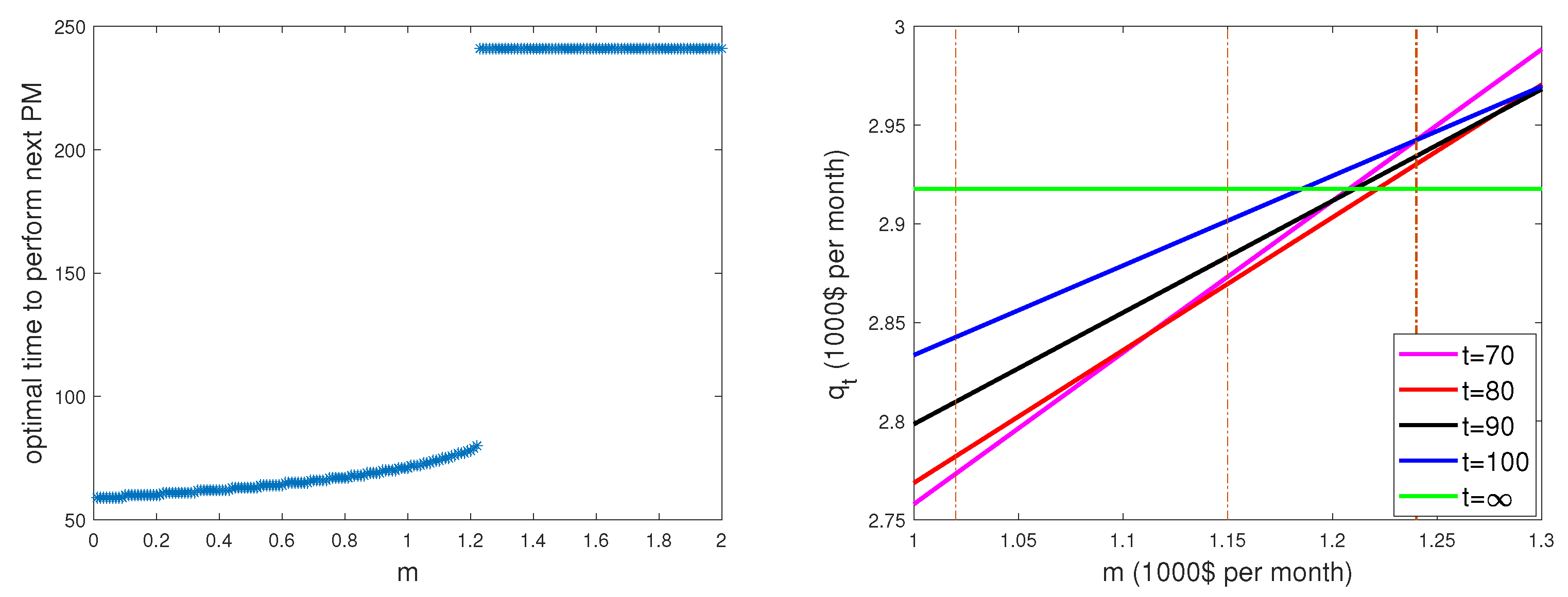
The left panel of Figure 4 reveals an interesting phenomenon: there exists a critical value $m_0$ of the parameter m, beyond which the optimal PM plan is to never perform a PM activity. Indeed, at the value $m_0=1.22$, we observe a jump from optimal planning time $t=80$ up to $t=T$, which is equivalent to $t=\infty$ for no planned PM.

The sudden jump on the left panel graph is explained on the right panel by comparing $q_t$ for different values of t. The five straight lines compare $q_{70},q_{80},q_{90},q_{100},q_{\infty }$ with respect to different values of the parameter m. For $m=1.02$, the minimal cost among the five options is given by $q_{70}$. For $m=1.15$, the minimal cost is given by $q_{80}$. For $m=1.25$, the minimal cost is given by $q_{\infty }$. It is also clear that starting the horizontal line for all $m>1.22$, corresponding to $t=\infty$, always gives the minimum cost.

7.3. Sensitivity Analysis 3

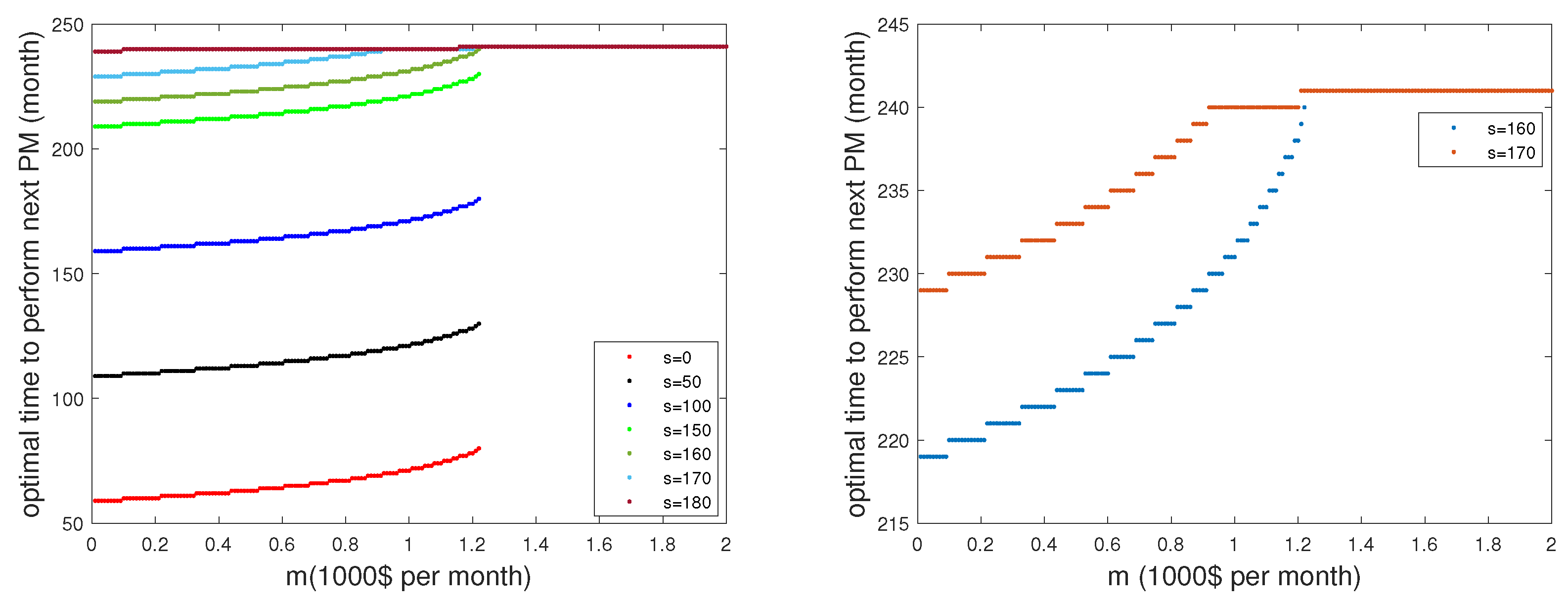
In this section, we illustrate the relation (7) for the one component (rotor). Figure 5 compares the optimal times $t_{(s,0)}$ for different starting times s of the planning period.

The curves confirm the stated relation $t_{(s,0)}=t_{(0,0)}+s$. They also emphasize that for s closer to T, the approximation $(T-s)c$ of the maintenance costs in (3) becomes rather hoarse for our model to give a reasonable answer. A recent paper [14] proposes an optimization model with special attention to the planning period near the end time T.

However, relation (7) allows an effective time-effective implementation of our algorithm as a key ingredient of an app (for s not too close to T) by pre-calculating the constants $t_{(0,0)}^j$.

7.4. Case Study 1

This section deals with the full model of four components. The results for different initial ages of four components are shown in

Table 2. The next PM plan for 4 components with different initial ages.

Initial Ages	$\mathit{j}=1$	$\mathit{j}=2$	$\mathit{j}=3$	$\mathit{j}=4$	PM	CM
$(0,0,0,0)$	62	x	62	x	9.937	13.756
$(30,30,30,30)$	32	x	32	x	10.815	15.064
$(30,30,0,30)$	46	x	46	46	10.469	14.868
$(20,60,0,30)$	47	47	47	47	10.458	14.668
$(0,0,40,0)$	x	x	12	x	10.364	14.229

.

Comparing the first two cases, we find that $62=30+32$, in accordance with Proposition 2. The two rightmost columns compare monthly maintenance costs for PM planning and the pure CM strategy (no PM planning). Note that the maintenance cost becomes larger if the components are older at the start. On the other hand, according to Table 2, the PM planning may save around USD 4000 per month, which is around $30\%$, compared to the pure CM strategy. In all five scenarios presented in Table 2, the optimal maintenance plan includes a PM activity for the gearbox. In four of the cases, a PM for the rotor is suggested. This is due to the higher replacement costs and failure frequency of the gearbox and the rotor. Notably, in one of the scenarios, the optimal maintenance plan suggests performing PM on all four components simultaneously. (The pure CM monthly costs are obtained by choosing a parameter m value so high that it is never beneficial to plan a PM activity.)

7.5. Case Study 2

Here, the optimization model developed in this paper is compared with the NextPM model from the paper [7]. To adapt to the assumption of age-independent PM costs of the paper [7], we set $m^j=0$ for all j. We put $h^1=36.75$, $h^2=23.75$, $h^3=46.75$, $h^4=33.75$, and $g_0=h_0=d$ for the values $d=1,5,10$ considered in the paper [7].

The following

Table 3. A comparison of the earlier NextPM algorithm and the algorithm of this paper.

$\mathit{d}=1$	1	2	3	4	Monthly Maintenance Cost	CPU Time
NextPM	x	x	43	x	4.731	49 s
New algorithm	x	x	43	x	4.703	2 s
$\mathit{d}=\mathbf{5}$	1	2	3	4	Monthly Maintenance Cost	CPU Time
NextPM	50	50	50	50	4.964	54 s
New algorithm	51	51	51	51	4.881	2 s
$\mathit{d}=\mathbf{10}$	1	2	3	4	Monthly Maintenance Cost	CPU Time
NextPM	52	52	52	52	5.061	55 s
New algorithm	52	52	52	52	5.040	2 s

juxtaposes the results produced by the two methods. It turns out that the optimal maintenance plans obtained by these two algorithms are almost identical across different scenarios, demonstrating the accuracy of the new algorithm. Importantly, the new algorithm runs 25 times faster than the NextPM algorithm.

8. Conclusions and Future Work

This paper introduces a new optimization algorithm relying on the renewal-reward theorem. In the multi-component setting, a new concept called the virtual replacement is introduced, allowing us to treat each replacement event as a renewal event, even when some components are not actually replaced with new ones. The new algorithm is illustrated by careful simulation studies in the framework of a four-component system of a wind turbine, searching for optimal maintenance plans under various initial conditions.

In sensitivity analysis 1, we conducted a detailed study on the replacement cost of a single component based on its age a at a potential replacement moment t. Our findings indicate that the replacement cost of the component increases as the parameter a increases. For the component with a below a certain critical value, the component is deemed to be in a sufficiently good condition to not require a replacement. However, when the age a exceeds the critical value, the optimal solution is to plan for a PM activity at the time t.

Sensitivity analysis 2 examines the influence of the crucial parameter m representing the monthly value depreciation of a generic wind turbine component. Our results show that as m increases, the optimal PM time for the component also increases. When m is large enough, the optimal solution is to never perform the PM activity.

Sensitivity analysis 3 deals with the effect of the starting time s of the scheduling period $[s,T]$. For a single-component system, we have observed that as long as s is not too close to T, the optimal solution is to perform a PM when the component in question reaches a certain critical age.

Case study 1 estimates that compared to the pure CM strategy, our optimization algorithm on average saves around $30\%$ of the maintenance costs. In case study 2, we compared our new algorithm with an earlier algorithm NextPM from [7]. The study demonstrates that the new algorithm yields precise outcomes while significantly reducing CPU processing time. Compared to the NextPM algorithm, our new algorithm has the advantage of being able to handle age-dependent PM costs.

The algorithm of this paper can handle only replacement maintenance activities. In the future, it would be worthwhile to study how other maintenance activities, such as inspection and minor or major repair, affect the optimal PM scheduling plan. Another interesting development would be to consider the case in which the PM replacement cost is a non-linear function of the component’s age. Finding the optimal PM scheduling plan in this case is an interesting and challenging problem.

9. Proofs of Propositions

Proof of Proposition 1.

We will need the following result from the renewal theory; see for example [11]. Let

$$(X_i,R_i),i=1,2,\dots$$

be independent and identically distributed pairs of possibly dependent random variables: $X_i$ values are positive inter-arrival times and $R_i$ values are associated rewards. The cumulative reward process is defined as

$$W\left(u\right)=R_1+\dots +R_{N\left(u\right)},$$

where $N\left(u\right)$ is the number of renewal events up to time u, that is, $N\left(u\right)=k$ if

$$X_1+\dots +X_k\le u<X_1+\dots +X_{k+1}.$$

According to the renewal-reward theorem, the per unit of time reward

$$\frac{W\left(u\right)}{u}\to \frac{\mathrm{E}\left(R\right)}{\mathrm{E}\left(X\right)},u\to \infty$$

almost surely converges.

Recall that the full maintenance cost of the gearbox due to a CM is g, and a similar cost for a PM is $(ma+h)$, where a is the gearbox age at the replacement. Thus, if we plan our next PM for a new gearbox at time t after each renewal event, then the corresponding renewal-reward process has inter-arrival time $X=X\left(t\right)$ with

$$X\left(t\right)=L\wedge t=L·1_{\{L\le t\}}+t·1_{\{L\ge t+1\}}$$

(10)

and the reward $R=R\left(t\right)$ with

$$R\left(t\right)=g{1}_{\{L\le t\}}+(tm+h)1_{\{L\ge t+1\}}.$$

(11)

Since

$$\begin{array}{cc}\hfill \mathrm{E}\left(X\right)& =\mathrm{E}(L·1_{\{L\le t\}})+t\mathrm{P}(L\ge t+1)=\sum _{k=1}^t(e^{-\theta {(k-1)}^{\beta }}-e^{-\theta k^{\beta }})k+e^{-\theta t^{\beta }}t,\hfill \\ \hfill \mathrm{E}\left(R\right)& =g\mathrm{P}(L\le t)+(tm+h)\mathrm{P}(L\ge t+1)=(1-e^{-\theta t^{\beta }})g+e^{-\theta t^{\beta }}(tm+h),\hfill \end{array}$$

the renewal-reward theorem implies that the time-average maintenance cost is computed as the following function of the planning time t

$$q_t=\frac{\mathrm{E}\left(R\right)}{\mathrm{E}\left(X\right)}=\frac{(1-e^{-\theta t^{\beta }})g+e^{-\theta t^{\beta }}(tm+h)}{{\sum }_{k=1}^t(e^{-\theta {(k-1)}^{\beta }}-e^{-\theta k^{\beta }})k+e^{-\theta t^{\beta }}t}.$$

□

Proof of Proposition 2.

By the definition of $t_{(s,a)}$ we have

$$\mathrm{E}\left(Q_{(s,a)}(t_{(s,a)},s+L_a)\right)\le \mathrm{E}\left(Q_{(s,a)}(t,s+L_a)\right),t=s+1,\dots ,T+1.$$

To prove the assertion, it is sufficient to verify that

$$\begin{array}{cc}\hfill \mathrm{E}\left(Q_{(s+\delta ,a+\delta )}(t_{(s,a)},s+\delta +L_{(a+\delta )})\right)& \le \mathrm{E}\left(Q_{(s+\delta ,a+\delta )}(t,s+\delta +L_{(a+\delta )})\right),\hfill \end{array}$$

(12)

for $t=s+\delta +1,\dots ,T+1$.

To derive (12), we will introduce a special notation

$$\begin{array}{cc}\hfill B\left(t\right)& =g+(T-t)c,\hfill \\ \hfill \widehat{B}(t,u)& =tm+h+(T-u)c,\hfill \end{array}$$

and notice that for $t\le T$

$$\begin{array}{cc}\hfill \mathrm{E}\left(Q_{(s,a)}(t,s+L_a)\right)& =\sum _{u=1}^{t-s}B(s+u)\mathrm{P}(L-a=u|L>a)\hfill \\ \hfill & +\widehat{B}(t-s+a,t)\mathrm{P}(L-a>t-s|L>a)\hfill \end{array}$$

or in other words,

$$\begin{array}{cc}\hfill \mathrm{P}(L>a)\mathrm{E}\left(Q_{(s,a)}(t,s+L_a)\right)& =\sum _{u=1}^{t-s}B(s+u)\mathrm{P}(L=a+u)\hfill \\ \hfill & +\widehat{B}(t-s+a,t)\mathrm{P}(L>a+t-s).\hfill \end{array}$$

On the other hand, we have, similarly,

$$\begin{array}{c}\mathrm{P}(L>a+\delta )\mathrm{E}\left(Q_{(s+\delta ,a+\delta )}(t,s+\delta +L_{(a+\delta )})\right)\hfill \\ =\sum _{u=1}^{t-s-\delta }B(s+\delta +u)\mathrm{P}(L=a+\delta +u)+\widehat{B}(t-s+a,t)\mathrm{P}(L>a+t-s).\hfill \end{array}$$

The key observation leading to (12) is that the difference

$$\begin{array}{cc}\hfill \mathrm{P}(L>a)\mathrm{E}\left(Q_{(s,a)}(t,s+L_a)\right)& -\mathrm{P}(L>a+\delta )\mathrm{E}\left(Q_{(s+\delta ,a+\delta )}(t,s+\delta +L_{(a+\delta )})\right)\hfill \\ \hfill & =\sum _{u=1}^{\delta }B(s+u)\mathrm{P}(L=a+u)\hfill \end{array}$$

is independent of t. In view of this fact, it is clear that the earlier observed inequality

$$\mathrm{P}(L>a)\mathrm{E}\left(Q_{(s,a)}(t_{(s,a)},s+L_a)\right)\le \mathrm{P}(L>a)\mathrm{E}\left(Q_{(s,a)}(t,s+L_a)\right)$$

entails

$$\begin{array}{cc}\hfill \mathrm{P}(L>a+\delta )\mathrm{E}& (Q_{(s+\delta ,a+\delta )}(t_{(s,a)},s+\delta +L_{(a+\delta )}))\hfill \\ \hfill & \le \mathrm{P}(L>a+\delta )\mathrm{E}\left(Q_{(s+\delta ,a+\delta )}(t,s+\delta +L_{(a+\delta )})\right),\hfill \end{array}$$

which immediately implies (12). □

Proof of Proposition 3.

If $t\le T$, then, according to (3)

$$Q_{(s,0)}(t,L)=[g+(T-s-L)c]·1_{\{s+L\le t\}}+[h+(t-s)m+(T-t)c]·1_{\{s+L>t\}},$$

and

$$\begin{array}{cc}\hfill \mathrm{E}\left(Q_{(s,0)}(t,L)\right)-(T-s)c=& g\mathrm{P}(L\le t-s)+(h+(t-s\left)m\right)\mathrm{P}(L>t-s)\hfill \\ & -c(\mathrm{E}\left(L{1}_{\{L\le t-s\}}\right)+(t-s)\mathrm{P}(L>t-s))\hfill \\ & =\mathrm{E}\left(R(t-s)\right)-c\mathrm{E}\left(X(t-s)\right)=(q_{t-s}-c)\mathrm{E}\left(X(t-s)\right),\hfill \end{array}$$

where in the last line we use notation (10) and (11). Since by definition, $c\le q_{t-s}$, the obtained equality

$$\mathrm{E}\left(Q_{(s,0)}(t,L)\right)=(T-s)c+(q_{t-s}-c)\mathrm{E}\left(X(t-s)\right)$$

implies that, provided $t_{(0,0)}+s\le T,$

$$f_{(s,0)}^{*}=\underset{t}{min}\mathrm{E}\left(Q_{(s,0)}(t,L)\right)=(T-s)c,$$

and we conclude

$$f_{(s_1,0)}^{*}-f_{(s_2,0)}^{*}=(s_2-s_1)c.$$

(13)

Furthermore, we see that

$$t_{(s,0)}=t_{(0,0)}+s,$$

which, together with Proposition 2, yields (7).

It remains to prove that $b_{(s,a)}=b_a$, or equivalently,

$$f_{(s,a)}^{*}=f_{(0,a)}^{*}-sc.$$

Since

$$\begin{array}{cc}\hfill f_{(s,a)}^{*}& =\mathrm{E}\left(Q_{(s,a)}(t_{(s,a)},s+L_a)\right)=\mathrm{E}\left(Q_{(s,a)}(t_{(0,a)}+s,s+L_a)\right)\hfill \\ \hfill & =\mathrm{E}((g+(T-s-L_a)c)1_{\{L_a\le t_{(0,a)}\}}\hfill \\ \hfill & +(h+m(t_{(0,a)}+a)+(T-t_{(0,a)}-s)c)1_{\{L_a>t_{(0,a)}\}})\hfill \\ \hfill & =\mathrm{E}\left(Q_{(0,a)}(t_{(0,a)},L_a)\right)-sc=f_{(0,a)}^{*}-sc.\hfill \end{array}$$

This finishes the proof of Proposition 3. □