Abstract
For multimodal multi-objective optimization problems (MMOPs), there are multiple equivalent Pareto optimal solutions in the decision space that are corresponding to the same objective value. Therefore, the main tasks of multimodal multi-objective optimization (MMO) are to find a high-quality PF approximation in the objective space and maintain the population diversity in the decision space. To achieve the above objectives, this article proposes a zoning search-based multimodal multi-objective brain storm optimization algorithm (ZS-MMBSO). At first, the search space segmentation method is employed to divide the search space into some sub-regions. Moreover, a novel individual generation strategy is incorporated into the multimodal multi-objective brain storm optimization algorithm, which can improve the search performance of the search engineering. The proposed algorithm is compared with five famous multimodal multi-objective evolutionary algorithms (MMOEAs) on IEEE CEC2019 MMOPs benchmark test suite. Experimental results indicate that the overall performance of the ZS-MMBSO is the best among all competitors.
1. Introduction
Multimodal multi-objective optimization problems (MMOPs) have become a research hot spot in recent years. As we know, there are at least two conflicting objectives in multi-objective optimization problems (MOPs) [1,2,3]. However, for actual problems, some of them have multiple equivalent Pareto optimal solutions in the decision space that are corresponding to the same objective value. These special MOPs are termed as MMOPs [4]. Clearly, how to maintain the population diversity in the decision space and find the high-quality Pareto front (PF) approximation in the objective space are two challenging tasks.
In order to effectively solve MMOPs, the niching methods [5,6,7,8], the diversity maintenance technique [9], and multiple population strategies [10,11] have been incorporated into multi-objective evolutionary algorithms (MOEAs), such as the decision space-based niching NSGAII (DN-NSGAII) [4] and the multi-objective particle swarm optimization (PSO) based on the self-organizing mechanism (SMPSO-MM) [12]. Besides the above “soft isolation” methods, the “hard isolation” methods (i.e., Zoning search (ZS)) [13] is employed to reduce the solution complexity of MMOPs. Subsequently, the ZS with an adaptive resource-allocating method is proposed by Fan et al. [14], which can further improve the solution efficiency of the ZS. From the above studies, it is clear that the previous studies focused on how to preserve the equivalent Pareto optimal solutions. Additionally, search engineering is also important for solving MMOPs as it can greatly affect the population diversity throughout the evolution. Like other meta-heuristics algorithms, brain storm optimization (BSO) [15,16] has good global exploration ability and is suitable for solving different types of MOPs. Moreover, existing studies [17,18,19,20,21] show that the BSO is a competitive method to solve multimodal optimization problems. Therefore, the BSO may be an effective method to solve MMOPs.
In the present study, a zoning search-based multimodal multi-objective brain storm optimization (ZS-MMBSO) is proposed. In the ZS-MMBSO, the ZS [13] is used to divide the decision space, which can reduce the search complexity and improve the population diversity. In addition, a novel individual generation strategy is proposed which can enhance the exploration capability in the early stage and the exploitation ability in the later stage. Note that a “soft isolation” method (i.e., K-means) is used in the BSO. Therefore, the proposed algorithm uses both “soft isolation” and “hard isolation” to locate and preserve the equivalent solutions. In this paper, five famous multimodal multi-objective evolutionary algorithms (MMOEAs) are chosen to compare with the ZS-MMBSO on 22 MMOPs introduced in IEEE CEC2019 [22]. The experimental results indicate that compared with other well-known MMOEAs, the ZS-MMBSO is competitive in solving MMOPs.
The remaining parts of this article are as follows: The basic concepts of the MOPs, the performance metric, and the BSO are introduced in Section 2. In Section 3, the relevant work in the field of MMO is reviewed. Section 4 shows the details of the ZS-MMBSO. And in Section 5, the experimental results and analyses are reported. Section 6 summarizes the conclusions.
2. Preliminaries
2.1. Multi-objective Optimization Problems
The definition of the MOPs is as follows [1,2,3]:
where x is an n-dimensional decision vector in the decision space Ω; F (x) = [f1(x), f2(x), …, fm(x)] T is an objective vector containing m objectives in the objective space. and are the boundaries of the i-th decision vector, respectively.
The following are the basic concepts of MOPs:
Definition 1.
(Pareto Dominance): For the vector u= [u1, u2, …, um]T and v = [v1,v2,…, vm]T, if , uj ≤ vj, and , us < vs, then the vector u dominates another vector v, expressed as .
Definition 2.
(Pareto Optimal Set): For a solution x* ∈ Ω, if there is no other solution x ∈ Ω which satisfied , x* is called the Pareto optimal solution. All Pareto optimal solutions constitute PS, denoted by X*.
Definition 3.
(Pareto Front): All objective vectors corresponding to PS form Pareto front (PF), denoted as
2.2. Performance Metric
To demonstrate the effectiveness of MMOEAs, various performance metrics have been proposed, such as the Pareto set proximity (PSP) [23] and the hypervolume (HV) [24].
- (1)
- The PSP is calculated as follows:
- (2)
- The calculation method for HV is as follows:
2.3. Brain Storm Optimization
Shi [25] proposed the brain storm optimization (BSO) in 2011. In the BSO, the population is composed by N individuals, and each individual simulated the idea generated in the brainstorming process. Then the population is updated through the convergence and divergence operators. As a convergence operation, the clustering method is employed to divide the population. Then, the BSO can effectively improve the population diversity by selecting different individuals from a single cluster or multiple clusters for mutation.
The specific steps are as described below:
Step 1: Randomly generate N initial individuals and evaluate them.
Step 2: The initial population is clustered into multiple groups by the K-means method. Moreover, for each cluster, individuals are sorted and the best one is recorded as the cluster center.
Step 3: Randomly select a cluster center and generate a new individual to replace it.
Step 4: The new individual is produced as follows [25]:
If rand < p1 then
Else
End
where u is generated from 1 to N, is the u-th selected individual in the t-th iteration; xc1 and xc2 are random cluster centers; xr1 and xr2 are random individuals from two stomatic clusters. p1 is the probability to choose the individual from one cluster [25]. p2, p3, and c are random number between 0 and 1. When rand < p1, Equation (4) is used to select the individual, otherwise, Equation (5) is employed. And then, for the selected individuals, the Gaussian mutation is employed to generate new individuals.
where is the u-th new individual in the t + 1-th generation; N(μ, σ) is the Gaussian distribution function with mean μ and standard deviation σ. T represents the maximum number of iterations; rand is a random value between 0 and 1; z is a slope.
Step 5: Evaluate new individuals and select the population for next generation.
Step 6: If the maximum number of iterations is reached, output the final solution, otherwise go to step 2.
3. Related Work
Finding the high-quality PF and preserving all equivalent Pareto solutions are two main tasks in the MMO. A large number of MMOEAs have been proposed to achieve the above objectives. For example, the Omni-optimizer proposed by Deb and Tiwari [26] introduced the crowding distance into the decision space. The results indicate that Pareto solutions with the same objective value can be effectively retained. Then, Liang et al. [4] designed a decision space-based niching NSGAII (DN-NSGAII). Experiments show that the proposed algorithm preserves almost all the PSs. In Ref. [23], a multi-objective PSO using ring topology and special crowding distance (SCD) (MO_Ring_PSO_SCD) has been proposed. The ring topology is introduced to form stable neighborhoods. The SCD is a measurement method that comprehensively considers the density of the population. Their results exhibit that the proposed algorithm is effective in solving the MMOPs. In Ref. [12], a multi-objective PSO with a self-organizing map network (SMPSO-MM) is proposed. The self-organizing map network is utilized to establish multiple neighborhoods. The results expound that the proposed algorithm is superior to the compared algorithms. In Ref. [27], Zhang et al. proposed a two-stage search framework. The global search is applied in the first stage to identify as many optimal solutions as possible. Then, the DBSCN clustering with adaptive neighborhood radius is employed to enhance the local search ability. Their results demonstrate that the two-stage search framework is effective. In Ref. [28], the reference point strategy is used to construct the neighborhood and the dominant radius of each Pareto front is utilized to distinguish whether the individual is a local optimal solution. From the results, the proposed algorithm can effectively locate the local solutions. At the same time, the evolutionary algorithm using the hierarchy sorting [29] is proposed to locate the global and local PSs. In order to ensure population diversity, an evaluation method for the local convergence of the population is introduced in the hierarchy sorting. The simulation results demonstrate that the proposed algorithm can maintain both the global and local PSs. To improve the distribution of Pareto optimal solutions, a niche backtracking search algorithm is proposed by Hu et al. [30]. In the proposed algorithm, a novel mutation strategy, which is based on affinity propagation clustering and an adaptive local search, is employed. The achieved results show that the solutions obtained by the proposed algorithm are uniformly distributed in the decision space. Hu et al. [31] adopted two parallel offspring generation mechanisms to improve the population diversity, while the reverse vector mutation strategy and niching local search scheme were used to balance convergence and diversity. From the experimental results, it can be found that the proposed method outperforms its competitors in most functions. In Ref. [32], a decomposition-based algorithm is proposed to address MMOPs, and a density-based estimation strategy is designed to estimate the number of PSs. And the mean-shift algorithm is used to partition the population. Their results expound that the proposed algorithm can find and maintain multiple PSs. To solve the problem of excessive convergence, Ref. [33] introduced the adaptive parameter control method to promote the convergence of population. The adaptive sub-population size is used to balance the convergence of the population in each region. The results exhibit that the proposed algorithm is effective in solving the MMOPs with multiple solution sets. Ming et al. [34] proposed a co-evolutionary algorithm, in which the convergence-relaxed population is used to assist the convergence-first population in locating more PSs, and the objective relaxation method is employed to complement previously undetected areas. The results validate the performance of the proposed algorithm is better than that of six advanced MMOEAs.
Most of the above-mentioned studies adopted the niching approaches to solve the MMOPs. Besides the “soft isolation” methods, “hard isolation” methods have been also proposed. In Ref. [13], Fan and Yan proposed the ZS strategy to maintain the population diversity in the decision space. The effectiveness of the ZS is systematically evaluated on 11 test functions. In Ref. [35], in order to distinguish the potentials of each subspace, the reinforcement learning method is used to dynamically allocate computing resources to each subspace. From the results, it is an effective strategy to assist the ZS in solving the MMOPs. Ji et al. [36] proposed a ZS and transfer learning-based MMEAs, in which transfer learning is employed to realize the information sharing between similar subspaces. The simulation results indicate that the proposed strategy is competitive.
4. Proposed Algorithm
How to locate and preserve the equivalent PSs in the decision space is important for the MMO. And reducing the complexity of MMOPs and improving the global search capability may be effective. To achieve the above objectives, the ZS-MMBSO is proposed. In the ZS-MMBSO, the ZS strategy [13] is employed to reduce the size of the search space, the improved BSO is utilized to improve the global search ability.
4.1. Search Space Segmentation
To reduce the complexity of MMOPs, the ZS is utilized to divide the decision space into some sub-regions. As in the previous study [13], randomly selecting h(1 ≤ h ≤ n) decision variables, and then each of them is divided into e equal parts. Therefore, the number of subspaces is set to w = eh.
4.2. Novel Individual Generation Strategy
Although the BSO has good performance in multimodal optimization, a fixed search pattern may be difficult to adapt to different evolutionary stages. Therefore, a novel individual generation strategy is proposed.
In the novel individual generation strategy, the Gaussian mutation has a higher probability to be selected in the early stage, and the DE/current-to-best/1 is employed in the latter stage. The main reason is that the Gaussian mutation can effectively explore the entire decision space and quickly find the area where the optimal solution may exist, while the DE/current-to-best/1 has good exploitation ability and can promote population convergence.
The steps of the novel individual generation strategy are as follows:
If rand < p1 then
Else
End if
If rand < t/T then
Else
End
where is the u-th selected individual in the t-th iteration; xr1 and xr2 are random individuals from two different stomatic clusters; xc1 is a random cluster center; xnd is a non-dominated solution from the k-th cluster; Random individuals from the k-th cluster are denoted as xn1 and xn2. p1 is a pre-set probability parameter that determines the individuals for mutation is from the single cluster or multiple clusters. p2, p3, and c are random number between 0 and 1. The remaining parameters remain consistent with the original reference [25]. F is the scale factor.
4.3. Main Framework of the Proposed Algorithm
The main framework of the proposed ZS-MMBSO is shown in Algorithm 1. Line 1 is the search space segmentation strategy which is used to divide the decision space. For each subspace, a population POP is randomly initialized (line 3). Line 5 is the judgment of the algorithm termination criterion. In Line 6, the K-means clustering is performed on the population POP. For each cluster, the non-dominated_scd_sort method [23] is employed in lines 7 to 9. The non-dominated individuals in k-th cluster Ck are stored in NDk, and the optimal individual is stored in the cluster center archive CA. In lines 10 to 12, it is a certain probability that a cluster center will be replaced by a new individual. The probability parameter is the same as the original BSO [25]. In lines 13 to 17, offspring individuals are generated by the novel individual generation strategy in Section 4.2. The individuals in the offspring population and the population POP are sorted by the non-dominated_scd_sort method (line 18). The top N individuals are selected for the next iteration. If the stopping criterion is not met, the procedures in Lines 5–19 will be run iteratively. Otherwise, the non-dominated individuals in each subspace Sd are recorded as PSd and PFd in line 20. At last, the final PS and PF are selected.
| Algorithm 1. Framework of ZS-MMBSO |
| Input: the number of subspaces: w; maximum number of iterations: T; the number of the cluster: K; cluster center archive: CA; the archive of the individuals in the k-th cluster: Ck; the archive of the non-dominated individuals in the k-th cluster: NDk; the number of the individuals in Ck: |Ck| 1: Search space segmentation via Section 4.1. 2: for each subspace Sd in S1, S2, ..., Sw do 3: Initialize the population POP. 4: t = 1 5: if t < T then 6: Use the K-means method to divide POP into K subpopulations. 7: for k = 1 → K do 8: The non-dominated_scd_sort method is used to sort individuals in the k-th cluster Ck. The non-dominated individuals of Ck are stored in NDk and the optimal individual in the Ck is stored in CA. 9: end for 10: if rand < 0.2 then 11: Randomly select an individual from the CA, and it is replaced by the new individual, which is randomly generated within the search space. 12: end if 13: for k = 1 → K do 14: for l = 1 → |Ck| do 15: Generate offspring individuals via a novel individual genera-tion strategy in Section 4.2. 16: end for 17: end for 18: Perform the non-dominated_scd_sort method to choose the population for next iteration. 19: end if 20: Record the non-dominated individuals in Sd as PSd and PFd. 21: end for 22: PS = Selection (PS1∪PS2∪…∪PSw) and PF = Selection (PF1∪PF2∪…∪PFw). Output: PS and PF |
5. Experimental Results and Analyses
To evaluate the performance of the ZS-MMBSO, it is compared with five famous MMOEAs, which are the SMPSO_MM [12], the MMGPE [37], the MMODE_CSCD [6], the MMODE_ICD [38], and the ZS-MO_Ring_PSO_SCD [13]. The IEEE CEC2019 [22] MMOPs benchmark suite is employed to assess the performance of these comparison algorithms. Additionally, the experimental results are analyzed by Wilcoxon’s rank sum test [39] and Friedman’s test [40], and the significance level is set to be 0.05. “+”, “-” and “=” indicate that the ZS-MMBSO is better, worse, or similar to the comparison algorithm.
5.1. Experimental Settings
The parameter settings of the selected MMOEAs are recommended by their original references [6,12,13,37,38]. For all compared algorithms, the maximum number of function evaluations and the population size are set to 80,000 and 800, respectively. All algorithms are implemented by using MATLAB (R2021a) and run independently for 20 times on each test problem. Additionally, some parameter settings of the ZS-MMBSO are as follows: F is set to 0.5 to scale the difference vectors; the pre-set probability parameter p1 is equal to 0.8; the number of clusters in K-means clustering is set to 20.
5.2. Comparison with Other Algorithms
Table 1 and Table 2 record the mean values and standard deviations of PSP and HV, respectively. The best results are highlighted in bold, and the results are statistically analyzed by Wilcoxon’s rank sum test.

Table 1.
Mean and standard deviation values of PSP obtained by different algorithms.

Table 2.
Mean and standard deviation values of HV obtained by different algorithms.
From Table 1, it is observed that the ZS-MMBSO significantly outperforms the SMPSO_MM, the MMGPE, the MMODE_CSCD, and the ZS-MO_Ring_PSO_SCD in terms of PSP on all MMOPs. The main reason may be that the ZS can greatly reduce the problem complexity, and the BSO algorithm has good global search capability. Namely, the proposed algorithm can integrate the advantages of “soft isolation” and “hard isolation” to maintain the population diversity. Therefore, compared with other competitors, the ZS-MMBSO can preserve more equivalent Pareto optimal solutions. Compared to the MMODE_ICD, the ZS-MMBSO wins 20 test functions. Clearly, the overall performance of the proposed algorithm is significantly better than that of the MMODE_ICD. For the other two remaining MMOPs (i.e., the SYM_PART simple and the Omni_test), the MMODE_ICD performs better. For the SYM_PART simple, most PSs are distributed in the boundary regions of subspaces, thus it is difficult for the ZS-MMBSO to search equivalent Pareto optimal solutions. For the Omni_test, the distribution of PSs in different subspaces is imbalanced, thus the proposed algorithm may waste computing resources. To visualize the performance comparison of all algorithms, the Friedman test rankings are illustrated in Figure 1 and the ZS-MMBSO owns the best ranking among all compared algorithms. The above statistical results indicate the superiority of the ZS-MMBSO in decision space.
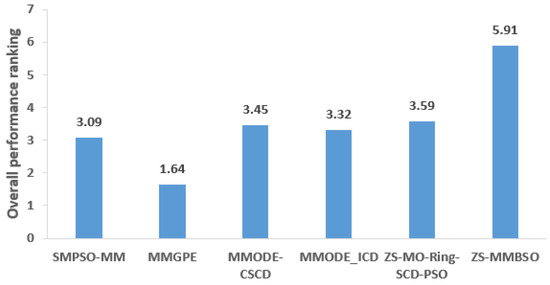
Figure 1.
Performance rankings of all compared algorithms in terms of PSP values.
Table 2 lists the HV results for these comparison algorithms. It is observed that the ZS-MMBSO outperforms the MMGPE on all test functions in terms of HV. Compared with the ZS-MO_Ring_PSO_SCD and SMPSO_MM, the proposed algorithm achieves better results on 21 test functions and similar result on one test function. The ZS-MMBSO is superior to the MMODE_CSCD on 20 test functions. For the MMF10, the proposed algorithm is surpassed by the MMODE_CSCD. The reason is that the global PS of MMF10 is simple, and it is easier for MMODE_CSCD to find the PF approximation. The MMODE_ICD performs better than the ZS-MMBSO on the MMF1_e, but their difference is small. In general, the proposed algorithm is competitive in the objective space. One of the reasons is that the ZS-MMBSO integrates the “soft isolation” and the “hard isolation” to find more PSs, which the population diversity in both decision space and objective space will be improved. The novel individual generation strategy can achieve a trade-off between global exploration and local exploitation, which can balance diversity and convergence. However, the performance improvement of the proposed algorithm in the objective space is not more significant than that in the decision space. In the MMOPs, there are multiple equivalent solutions in the decision space that are corresponding to the same objective value. It is easier for MMOEAs to find a good PF approximation than to locate equivalent solutions in the decision space. As a result, the performance difference of the comparison algorithms in the objective space is relatively small. Figure 2 shows Friedman’s test results of the overall performance ranking. The ZS-MMBSO gets the first ranking, followed by MMODE_ICD, MMODE_CSCD, ZS-MO_Ring_PSO_SCD, SMPSO_MM, and MMMGPE. The above observations fully indicate the ZS-MMBSO performs better in the objective space.
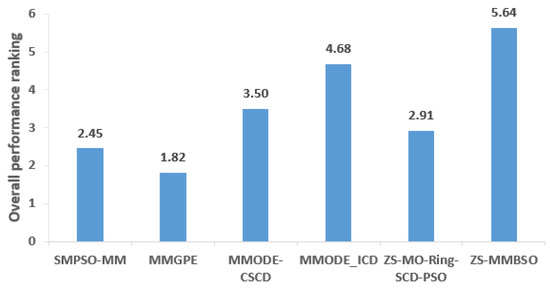
Figure 2.
Performance rankings of all compared algorithms in terms of HV values.
Based on the above analyses, the ZS-MMBSO performs the best among all competitors in both decision space and objective space. The proposed algorithm is an effective tool to solve different types of MMOPs.
5.3. Experimental Analysis
5.3.1. The Effectiveness of the ZS
To validate the effectiveness of the ZS, the ZS-MMBSO and ZS-MMBSO without the ZS strategy (denoted as ZS-MMBSO_1) are used to compare 22 functions in terms of PSP. The parameter settings are consistent with Section 5.1. For each function, the optimal value is displayed in bold, and the results are analyzed by Wilcoxon’s rank sum test.
In Table 3, the mean PSP values of the ZS-MMBSO and its variant are presented. It can be found that ZS-MMBSO performs better than ZS-MMBSO_1 on all test functions. So, the search space segmentation has a significant impact on the proposed algorithm in the decision space. It is because the search complexity is reduced by the ZS, this is important for solving complex problems. In summary, the ZS is effective to assist the proposed algorithm in locating more equivalent PSs.

Table 3.
Mean and standard deviation values of PSP obtained by ZS-MMBSO and ZS-MMBSO_1.
5.3.2. The Effectiveness of the Novel Individual Generation Strategy
To demonstrate the effectiveness of the novel individual generation strategy, the PSP is used to testify the performance of the proposed algorithm and its variant. The ZS-MMBSO and ZS-MMBSO which adopts the Gaussian mutation to generate the offspring individuals (named as ZS-MMBSO_2) are compared on 22 test functions. The parameter settings are shown in Section 5.1. The Wilcoxon’s rank sum test is used to analyze the results and the best results are showed in bold.
From Table 4, it can be observed that ZS-MMBSO achieves the best results in 19 out of 22 cases. On the MMF14_a and the SYM_PART simple, the ZS-MMBSO_2 obtains the best results. The statistical results indicate the effectiveness of the novel individual generation strategy. It is because the novel individual generation strategy can balance the global exploration and local exploitation. The Gaussian mutation used in the early stage can explore the entire search space and find the potential regions where the optimal solution may be located. By using the information of the non-dominated solutions, the DE/current-to-best/1 can guide individuals to search the potential regions and locate more equivalent solutions. The mutation strategy used in the latter stage has a good exploitation ability and can speed up the population convergence. For MMF14_a and SYM_PART simple, the ZS-MMBSO_2 performs better than ZS-MMBSO, but the difference is small. Overall, the novel individual generation strategy can help the proposed algorithm locate the equivalent PSs in the decision space.

Table 4.
Mean and standard deviation values of PSP obtained by ZS-MMBSO and ZS-MMBSO_2.
5.3.3. Impact of the Number of Clusters
The number of clusters may impact the performance of the BSO. If there are too many clusters, the population diversity will be improved. Conversely, if the number of clusters is too small, the population may converge quickly, and the equivalent solutions will be difficult to preserve. To validate the influence of different K values on the performance of the ZS-MMBSO, K is set to be 10, 15, 20, 25, and 30, respectively. In addition, ZS-MMBSO with different K values is independently run 20 times on 22 functions. The best results are marked in bold. And Friedman’s test [40] is employed to analyze the experimental results.
In Table 5, it is observed that for different K values, the ZS-MMBSO can only achieve the best results on a few problems. Namely, the differences for different K values are small. This means that users can easily set the K value. The Friedman rankings with different K values are represented in Figure 3. From Figure 3, if the number of clusters is too large or small, the performance of the proposed algorithm will be degraded. When K = 20, the ZS-MMBSO can balance diversity and convergence and its overall performance is the best. Hence, the K value of ZS-MMBSO is set to 20.

Table 5.
Mean and standard deviation values of PSP obtained by different K values.
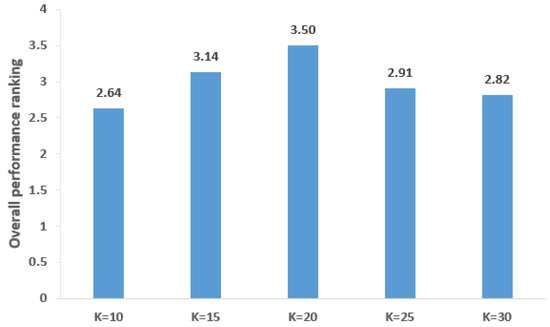
Figure 3.
Performance rankings of PSP values with different K values.
6. Discussion
In this study, a zoning search-based multimodal multi-objective brain storm optimization (ZS-MMBSO) is proposed. In the ZS-MMBSO, the ZS is employed to reduce the complexity of MMOPs. A novel individual generation strategy is proposed to strengthen the global exploration ability in the early stage and improve local exploitation in the late stage. To demonstrate the effectiveness of the ZS-MMBSO, it is compared with five famous MMOEAs on 22 test functions. The results demonstrate ZS_MMBSO is competitive in both decision space and objective space. The effectiveness of the proposed strategy is analyzed in Section 5.3.1 and Section 5.3.2. The experimental analysis results indicate that these strategies can help the ZS-MMBSO solve MMOPs. Section 5.3.3 analyzed the sensitivity of the cluster number K.
Author Contributions
Conceptualization, J.F. and Q.F.; methodology, J.F., W.H., Q.J. and Q.F; investigation, J.F., W.H., Q.J. and Q.F.; writing—original draft preparation, J.F.; writing—review and editing, J.F., W.H., Q.J. and Q.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China-Shandong joint fund (U2006228), the National Natural Science Foundation of China (No. 61603244, No. 71904116), and the Shanghai Pujiang Program (No. 22PJD030).
Data Availability Statement
Data supporting reported results are available from the authors upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Hartikainen, M.; Miettinen, K.; Wiecek, M.M. PAINT: Pareto front interpolation for nonlinear multiobjective optimization. Comput. Optim. Appl. 2012, 52, 845–867. [Google Scholar] [CrossRef]
- Nedjah, N.; Mourelle, L.D. Evolutionary multi-objective optimisation: A survey. Int. J. Bio-Inspired Comput. 2015, 7, 1–25. [Google Scholar] [CrossRef]
- Liang, J.J.; Yue, C.T.; Qu, B.Y. Multimodal multi-objective optimization: A preliminary study. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 2454–2461. [Google Scholar]
- Li, G.; Wang, W.; Chen, H.; You, W.; Wang, Y.; Jin, Y.; Zhang, W. A SHADE-based multimodal multi-objective evolutionary algorithm with fitness sharing. Appl. Intell. 2021, 51, 8720–8752. [Google Scholar] [CrossRef]
- Liang, J.; Qiao, K.; Yue, C.; Yu, K.; Qu, B.; Xu, R.; Li, Z.; Hu, Y. A clustering-based differential evolution algorithm for solving multimodal multi-objective optimization problems. Swarm Evol. Comput. 2021, 60, 100788. [Google Scholar] [CrossRef]
- Qu, B.; Li, C.; Liang, J.; Yan, L.; Yu, K.; Zhu, Y. A self-organized speciation based multi-objective particle swarm optimizer for multimodal multi-objective problems. Appl. Soft Comput. J. 2020, 86, 105886. [Google Scholar] [CrossRef]
- Wang, W.; Li, G.; Wang, Y.; Wu, F.; Zhang, W.; Li, L. Clearing-based multimodal multi-objective evolutionary optimization with layer-to-layer strategy. Swarm Evol. Comput. 2022, 68, 100976. [Google Scholar] [CrossRef]
- Li, W.; Zhang, T.; Wang, R.; Ishibuchi, H. Weighted Indicator-Based Evolutionary Algorithm for Multimodal Multiobjective Optimization. IEEE Trans. Evol. Comput. 2021, 25, 1064–1078. [Google Scholar] [CrossRef]
- Li, G.; Wang, W.; Zhang, W.; Wang, Z.; Tu, H.; You, W. Grid search based multi-population particle swarm optimization algorithm for multimodal multi-objective optimization. Swarm Evol. Comput. 2021, 62, 100843. [Google Scholar] [CrossRef]
- Qu, B.; Li, G.; Yan, L.; Liang, J.; Yue, C.; Yu, K.; Crisalle, O.D. A grid-guided particle swarm optimizer for multimodal multi-objective problems. Appl. Soft Comput. 2022, 117, 108381. [Google Scholar] [CrossRef]
- Liang, J.; Guo, Q.; Yue, C.; Qu, B.; Yu, K. A self-organizing multi-objective particle swarm optimization algorithm for multimodal multi-objective problems. In Proceedings of the 9th International Conference on Swarm Intelligence, ICSI 2018, Shanghai, China, 17–22 June 2018; Springer: Shanghai, China, 2018; pp. 550–560. [Google Scholar]
- Fan, Q.; Yan, X. Solving Multimodal Multiobjective Problems Through Zoning Search. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 4836–4847. [Google Scholar] [CrossRef]
- Fan, Q.; Ersoy, O.K. Zoning Search With Adaptive Resource Allocating Method for Balanced and Imbalanced Multimodal Multi-Objective Optimization. IEEE/CAA J. Autom. Sin. 2021, 8, 1163–1176. [Google Scholar] [CrossRef]
- Guo, Y.-N.; Jiang, D.-Z.; Wang, R.-R.; Gong, D.-W. Structural design of heat exchanger plate with wide-channel based on multi-objective brain storm optimization. Kongzhi Yu Juece/Control Decis. 2022, 37, 2314–2322. [Google Scholar] [CrossRef]
- Hou, Y.; Wang, H.; Fu, Y.; Gao, K.; Zhang, H. Multi-Objective brain storm optimization for integrated scheduling of distributed flow shop and distribution with maximal processing quality and minimal total weighted earliness and tardiness. Comput. Ind. Eng. 2023, 179, 109217. [Google Scholar] [CrossRef]
- Cheng, S.; Chen, J.; Lei, X.; Shi, Y. Locating Multiple Optima via Brain Storm Optimization Algorithms. IEEE Access 2018, 6, 17039–17049. [Google Scholar] [CrossRef]
- Dai, Z.; Fang, W.; Li, Q.; Chen, W.-N. Modified Self-adaptive Brain Storm Optimization Algorithm for Multimodal Optimization. In Proceedings of the 14th International Conference on Bio-inspired Computing: Theories and Applications, BIC-TA 2019, Zhengzhou, China, 22–25 November 2019; Springer Science and Business Media Deutschland GmbH: Zhengzhou, China, 2020; pp. 384–397. [Google Scholar]
- Dai, Z.; Fang, W.; Tang, K.; Li, Q. An optima-identified framework with brain storm optimization for multimodal optimization problems. Swarm Evol. Comput. 2021, 62, 100827. [Google Scholar] [CrossRef]
- Guo, X.; Wu, Y.; Xie, L. Modified brain storm optimization algorithm for multimodal optimization. In Proceedings of the 5th International Conference on Advances in Swarm Intelligence, ICSI 2014, Hefei, China, 17–20 October 2014; pp. 340–351. [Google Scholar]
- Pourpanah, F.; Wang, R.; Wang, X.; Shi, Y.; Yazdani, D. mBSO: A Multi-Population Brain Storm Optimization for Multimodal Dynamic Optimization Problems. In Proceedings of the 2019 IEEE Symposium Series on Computational Intelligence (SSCI), Xiamen, China, 6–9 December 2019; pp. 673–679. [Google Scholar]
- Yue, C.; Qu, B.; Yu, K.; Liang, J.; Li, X. A novel scalable test problem suite for multimodal multiobjective optimization. Swarm Evol. Comput. 2019, 48, 62–71. [Google Scholar] [CrossRef]
- Yue, C.; Qu, B.; Liang, J. A Multiobjective Particle Swarm Optimizer Using Ring Topology for Solving Multimodal Multiobjective Problems. IEEE Trans. Evol. Comput. 2018, 22, 805–817. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Shi, Y. Brain storm optimization algorithm. In Proceedings of the Advances in Swarm Intelligence—Second International Conference, ICSI 2011, Chongqing, China, 12–15 June 2011; pp. 303–309. [Google Scholar]
- Deb, K.; Tiwari, S. Omni-optimizer: A procedure for single and multi-objective optimization. In Evolutionary Multi-Criterion Optimization; Coello, C.A.C., Aguirre, A.H., Zitzler, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3410, pp. 47–61. [Google Scholar]
- Zhang, J.-X.; Chu, X.-K.; Yang, F.; Qu, J.-F.; Wang, S.-W. Multimodal and multi-objective optimization algorithm based on two-stage search framework. Appl. Intell. 2022, 52, 12470–12496. [Google Scholar] [CrossRef]
- Li, G.; Zhou, T. A multi-objective particle swarm optimizer based on reference point for multimodal multi-objective optimization. Eng. Appl. Artif. Intell. 2022, 107, 104523. [Google Scholar] [CrossRef]
- Li, W.; Yao, X.; Zhang, T.; Wang, R.; Wang, L. Hierarchy Ranking Method for Multimodal Multiobjective Optimization With Local Pareto Fronts. IEEE Trans. Evol. Comput. 2023, 27, 98–110. [Google Scholar] [CrossRef]
- Hu, Z.B.; Zhou, T.; Su, Q.H.; Liu, M.F. A niching backtracking search algorithm with adaptive local search for multimodal multiobjective optimization. Swarm Evol. Comput. 2022, 69, 101031. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, J.; Liang, J.; Wang, Y.L.; Ashraf, U.; Yue, C.T.; Yu, K.J. A two-archive model based evolutionary algorithm for multimodal multi-objective optimization problems. Appl. Soft Comput. 2022, 119, 108606. [Google Scholar] [CrossRef]
- Gao, W.; Xu, W.; Gong, M.; Yen, G.G. A decomposition-based evolutionary algorithm using an estimation strategy for multimodal multi-objective optimization. Inf. Sci. 2022, 606, 531–548. [Google Scholar] [CrossRef]
- Han, H.; Liu, Y.; Hou, Y.; Qiao, J. Multi-modal multi-objective particle swarm optimization with self-adjusting strategy. Inf. Sci. 2023, 629, 580–598. [Google Scholar] [CrossRef]
- Ming, F.; Gong, W.Y.; Wang, L.; Gao, L. Balancing Convergence and Diversity in Objective and Decision Spaces for Multimodal Multi-Objective Optimization. IEEE Trans. Emerg. Top. Comput. Intell. 2022, 7, 474–486. [Google Scholar] [CrossRef]
- Dang, Q.-L.; Xu, W.; Yuan, Y.-F. A Dynamic Resource Allocation Strategy with Reinforcement Learning for Multimodal Multi-objective Optimization. Mach. Intell. Res. 2022, 19, 138–152. [Google Scholar] [CrossRef]
- Ji, H.; Chen, S.; Fan, Q. Zoning Search and Transfer Learning-based Multimodal Multi-objective Evolutionary Algorithm. In Proceedings of the 2022 IEEE Congress on Evolutionary Computation, CEC 2022, Padua, Italy, 18–23 July 2022; Institute of Electrical and Electronics Engineers Inc.: Padua, Italy, 2022. [Google Scholar]
- Zhou, T.; Hu, Z.B.; Zhou, Q.; Yuan, S.X. A novel grey prediction evolution algorithm for multimodal multiobjective optimization. Eng. Appl. Artif. Intell. 2021, 100, 104173. [Google Scholar] [CrossRef]
- Yue, C.T.; Suganthan, P.N.; Liang, J.; Qu, B.Y.; Yu, K.J.; Zhu, Y.S.; Yan, L. Differential evolution using improved crowding distance for multimodal multiobjective optimization. Swarm Evol. Comput. 2021, 62, 100849. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual Comparisons by Ranking Methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
- Friedman, M. The Use of Ranks to Avoid the Assumption of Normality Implicit in the Analysis of Variance. J. Am. Stat. Assoc. 1937, 32, 675–701. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).