Abstract
Practical entanglement distillation is a critical component in quantum information theory. Entanglement distillation is often utilized for designing quantum computer networks and quantum repeaters. The practical entanglement distillation problem is formulated as a bilevel optimization problem. A fuzzy formulation is introduced to estimate the quantum state (density matrix) from pseudo-likelihood functions (i.e., quantum state tomography). A scale-independent relationship between fuzzy relations in terms of the pseudo-likelihood functions is obtained. The entanglement distillation optimization problem is solved using the combined coupled map lattice and dual annealing approach. Comparative analysis of the results is then conducted against a standard dual annealing algorithmic implementation.
1. Introduction
Entanglement distillation is a critical aspect of quantum information systems. The key idea of entanglement distillation is to preserve or restore the quality of diluted entanglement states of quantum information transmitted over large distances. Decoherence effects during transmission cause the dilution of entanglement states. Past theoretical and experimental research works have focused on the study of quantum distillation frameworks [1,2,3]. Recently, pairs of single photons (entangled in multiple degrees of freedom) were used to experimentally determine the domain of distillable states and their relative fidelity [4]. In Ecker et al., 2021 [4], comparative studies were also carried out on various distillation schemes to gain a deeper understanding in terms of resilient quantum network design. A proof-of-concept experiment was recently conducted to study the application of filtering protocols (in atomic ensembles) for constructing quantum repeater nodes [5]. The experiment was conducted in a crystal (rare-earth-ion-doped). In that setting, the entanglement states were prepared. The relationship between bit thread, entanglement distillation, and entanglement purification (in the holographic framework) was recently studied [6]. In Lin et al., 2021 [6], a bit thread interpretation of the one-shot entanglement distillation tensor network was provided. It was shown that the holographic entanglement purification process could be viewed as a special case of a type of surface growth scheme. The objective of the study in Lin et al., 2021 [6] was to develop an accurate framework for describing physical entanglement structures. Another interesting work is seen in the theoretical investigation of entanglement distillability presented in [7]. In that work, the authors studied the mentioned subject with regards to the undistillability conjecture of specific Werner states and gained deeper understanding of the distillability problem. Recent developments of entanglement distillation are seen in [8], He et al., 2021 [9], Gour and Scandolo, 2021 [10], Yan et al., 2022 [11], Shchukin and van Loock, 2022 [12], and Riera-Sàbat et al., 2021 [13].
In the past few years, much research in quantum information systems has been directed towards optimization. This can be seen in the work of Gyongyosi and Imre [14]. In that work, the optimization of the read-out procedure of local unitaries of a high-retrieval efficiency quantum memory was performed. The authors also studied the retrieval efficiency of quantum memory and the signal-to-noise ratio. A similar work is seen in Gyongyosi et al., 2020 [15], where an approach for obtaining the optimal quantum state and computational path evaluation for gate-model quantum computing devices was proposed. Efficient algorithms for attaining generation time and transmission fidelity of entangled pairs between the end nodes of quantum chains is seen in Brand et al., [16].
Quantum state tomography (QST) is an effective method to reconstruct or estimate quantum states from measurements of identical quantum states. This directly impacts the development of reliable quantum resources, as well as quantum devices for quantum information processing. A recent interesting study on information gain in QST is seen in the work of Sahu et al., [17]. In that work, the authors discuss the effects of chaotic dynamics on the information transfer during QST. Their investigations also uncovered operational insights into the mechanisms of fidelity gain during actual quantum information tomography protocols. In Schmale et al., [18], the authors improve the accuracy of observable measurements from tomographic data. This was done by using a QST scheme that approximates a probability distribution over a measurement (informationally complete) within a variational manifold characterized by a convolutional neural network. In that work, the authors regenerated high classical-fidelity states, which performed more efficiently as compared to standard techniques (e.g., maximum likelihood estimation). Another recent approach in QST is observed in the work of Farooq et al., [19]. In that work, the authors developed a formulation for pure quantum state reconstruction via eigenvalue decomposition. In Farooq et al., [19], the authors demonstrated that the proposed approach is robust against depolarizing noise (high-strength white noise) where the quantum states were reconstructed accurately similar to the noiseless case. A computational-focused strategy for QST is seen in the work of Ahmad et al., 2022 [20]. In that research, the authors proposed a simultaneous perturbation stochastic approximation algorithm with high-speed convergence. The central idea in that work was to develop a computational technique for estimating quantum states under limited computational conditions using a Barzilai–Borwein two-point step size gradient method. In Choi, 2022 [21], a low-complexity effective QST scheme was proposed. The proposed scheme requires the measurement of only three observables for systems of any scale. The key concept was the coupling of the system and the ‘pointer’ of a single qubit.
Complex nonlinear dynamical systems have been successfully modeled using chaotic maps such as coupled map lattices (CML). For instance, in Lu et al., [22] an urban rail transit system under cascading failure was modeled with respect to network vulnerability using CMLs. In that work, the authors quantified the relationship between passenger flow and the perturbation index. In addition to investigations of the anti-risk resistance capability of stations, the dependency of cascading failures on location and type of stations were identified. In Stenzinger and Tragtenberg, 2022 [23], CMLs were for a biomedical-focused application. In that work, the authors utilized spatiotemporal chaos in the CML to simulate cardiac reentry. Among their key research findings were clinical manifestations of certain types of tachycardia in the electrocardiogram, as well as a novel type of dynamical pattern (with wavefronts comprised of harmonized bursts and cardiac plateaus). In Wang and Liu, 2021 [24], a one-dimensional, two-parameter with a wide-range system mixed coupled map lattice model was proposed for image encryption. The authors of that work performed simulations to establish the effectiveness of the proposed encryption algorithm for grayscale and color images. In addition, they also carried out security tests to ensure that the proposed method could hold against conventional security attacks. CMLs have also been recently employed in the field of wireless communication. For instance, in Xie et al., [25], a CML model was developed to assess the vulnerability of an unmanned aerial vehicle (UAV) network. The authors in that work showed that precision interference on critical UAV nodes could inflict significant damage to the entire UAV network. In addition, the authors of Xie et al., 2022 [25] also discovered that network vulnerability increases with the intensity of external interference.
This work reformulates the practical entanglement distillation problem as a bilevel optimization model. This work extends the practical entanglement distillation problem to account for approximating the quantum state (density matrix) using QST using fuzzy relations. The bilevel practical entanglement distillation optimization problem is then solved using the combined CML and the dual annealing approach. The central idea is to leverage on the complex behavior of the CML to enhance the optimization capabilities of the dual annealing algorithm. This paper is organized as follows: the Section 2 describes the model formulation for the bilevel practical entanglement distillation problem. In this section, the novel QST formulation using fuzzy relations is presented. The Section 3 discusses the CML and its hybridization with the dual annealing algorithm. The Section 4 presents analysis on the results generated by the numerical experiments. The paper concludes with some final remarks and recommendations for future research works.
2. Entanglement Distillation with Fuzzy Relations for QST
In this work, a bipartite practical entanglement distillation model is considered, where the central idea is to convert a state, (density matrix form), into a state which is close to a maximally entangled state, utilizing only local operations and classical communication. In contrast to theoretical entanglement distillation, practical entanglement distillation frameworks allow for the possibility of failure [26]. The mentioned communication takes place between two nodes of a communication network A and B. This can be represented mathematically as follows:
where is the fidelity—i.e., closeness of the converted state to the maximally entangled state. A and B are the input registers while and are the output registers. is the dimension of the quantum state and is the converted state (). is the maximally entangled state across output registers and . If the dimension, , then one possible example of would be as follows:
In this view, a technically simplified subcategory of local operations and classical communication (between network nodes, and ) called measure and exchange operations scheme is employed as presented in Rozpędek et al., [27]. In this scheme, the positive operator-valued measurement performed on the input register, is defined as with and where . The parameter, defines the trade-off between fidelity and the probability of success. This measurement follows the map: , where the symbol, represents the Kronecker product. A similar formulation would apply for a positive operator-valued measurement performed on the input register, . Both measurements are declared a success if fA = fB = 1 for option . Since practical entanglement distillation frameworks allow for the possibility of failure, the fidelity parameter would only be relevant to the analysis if the entanglement distillation is a success [26]. This then creates a multilevel scenario with the probability of distillation success, cascaded by the fidelity parameter, F. Since the local quantum memory utilized to store the quantum entanglement is imperfect/non-ideal, this entanglement cannot be preserved for an arbitrary amount of time. Hence, the probability of distillation success, would control the rate at which high-fidelity entanglement between the different nodes in the network is aimed.
Practical entanglement distillation uses schemes involving the application of local operation and measurement on A and B registers. This is then followed by a measurement outcome (single exchange) using classical communication to determine distillation success/failure. In this work, the practical quantum distillation scheme presented in Rozpędek et al., [27] is considered. The central idea is to search for the following optimal parameters: (i) output dimension, d; (ii) input state, ; and (iii) quantum channels (i.e., quantum operations). To optimize quantum operations, Choi isomorphism can be utilized, where a one-to-one correspondence between quantum channels and quantum states is established (with certain properties) (Jiang et al., 2013). A unique Choi state, , exists for any quantum channel, from a system, to a system, with as the density matrix of the normalized maximally entangled state, as presented in Equation (1) with dimensions, . This unique Choi state satisfies and . In the measurement and exchange operations, the Choi states take a product representation achieved using the Kronecker product operations. After a series of simplifications presented in Rozpędek et al., the Choi states for the case of register, are obtained: . A similar formulation could be achieved for register, B. This way, the isomorphism carries over all the information from the original channel to the Choi state. Following the problem formulation in Rozpędek et al., [27], the bilevel optimization formulation of entangle distillation is as follows:
subject to,
where and are Choi state equivalent for output registers A and B. Similarly, and are matrices depicting Choi states which correspond to quantum channels. The symbol represents the Kronecker product and the dimensions of the identity matrices, and depend on the dimensions of the registers and .
In designing practical quantum information processing systems, quantum state tomography (QST) is employed to approximate a certain state of the density matrix. This is done by using measurement results of repeated state preparations. Unfortunately, QST becomes very challenging as the system scales up in terms of size—i.e., dimensions, . Current methods for QST formulation include linear inversion, maximum likelihood, Bayesian, hybrid Bayesian-Monte Carlo, and neural network approaches [28,29]. In this work, a fuzzy approach is developed and employed for QST. In Recasens, [30], it was demonstrated that symmetric positive semi-definite matrices could be constructed from the application of fuzzy relations on certain sets (fuzzy subsets). For example, if sets and , with both having cardinality of and , are fuzzy subsets of and with the additive generator of the -norm being: , then the following matrix is constructed:
In the case of estimating the density matrix, in Equations (2) and (3), is considered as symmetric and positive semi-definite with the additional normalization condition: . In this view, the and are fuzzy sets that act as pseudo-likelihood functions obtained from measurement data (empirical). Since and are quantum states for , it can be stated that . The measurements of these quantum states in the form of fuzzy memberships may not be equal: and the normalization condition: holds. Using the simplified notations for the pseudolikelihood measurements and , Equation (4) then becomes: . An interesting result is obtained from the symmetric semi-definite density matrix construction when the differential form of Equation (4) is obtained:
Equation (5) is then obtained by taking the partial differential for the density matrix in Equation (4) and assuming and to be continuous parameters. Similarly, the analysis is extended to seek for an analogue to approximate the factor in Equation (5) using the binomial formula and Maclaurin series:
Therefore, a generalized partial differential equation (PDE) independent of scale (i.e., cardinality or dimension) is obtained:
The measurements and are treated as continuous parameters and the solution to the scale-free exact solution to the PDE in Equation (7) is obtained:
where is a constant. Considering and to be subsequent measurements, pseudo-likelihood measurements are conjectured to have the Markov property such that:
where is an transition or stochastic matrix. With this conjecture, the density matrix, is approximated using data from the current pseudo-likelihood measurement, and the previous pseudo-likelihood function, . The current pseudo-likelihood measurement, could be generated using the stochastic matrix, as in Equation (9). QST is highly efficient when estimating density matrices, for small quantum systems. However, as the system scales-up and increases in dimensions, effective QST becomes a challenging feat [28]. The fuzzy formulation for pseudo-likelihood relations presented in Equations (4)–(9) aim to enable effective estimation of density matrices, at larger scales. Treating density matrices, as symmetric and positive semi-definite are critical requirements for this analysis.
3. Chaotic Dual Annealing Optimization
In recent times, optimization problems have grown in terms of complexity—i.e., nonlinearity, nonconvexity, multilevel, and uncertainty in parameters. This directly results in stagnation in the solution method upon implementation, where the algorithmic technique gets trapped in a local optimum. This causes the task of optimizing such problems to become exceedingly difficult. An effective approach to tackle such issues is the utilization of stochastic optimization approaches. One such approach is simulated annealing (SA) [31]. SA is based on the idea of the physical concept of annealing, where a solid is repeatedly heated and cooled until it reaches a configurational state of minimal energy. In this work, we use the dual annealing optimization approach, which is a coupled technique inspired by the classical simulated annealing as well as the fast simulated annealing approaches [32]. The dual annealing optimization approach used in this work implements a distorted Cauchy-Lorentz visiting distribution, with (the distribution’s shape controlling parameter):
where and are constants, is artificial time, is the trial jump distance and is the artificial temperature. The candidate solution’s acceptance probability is set by defining an acceptance parameter, is determined as follows:
The decrease of the artificial temperature, is given by the following relation:
In this work, the dual annealing technique is coupled with coupled map lattices (CML) to enhance its optimization capability by simulating chaotic non-linear dynamics. CMLs have applications in diverse fields of research and implementation: system identification, process modeling, design optimization, internet of things (IoT), and cryptography [24,33,34,35]. For a specific discreet-time dynamical map, CMLs consist of discreet interacting elements. These elements make up a multidimensional dynamical system. Hence, the CML model could be designed to simulate a dynamical system, where its macroscopic field variables are defined on a lattice. Independent processes then decompose the dynamical system. In this sense, each process represents a procedure in the CML. Nonlinear transformations are generated using each state variable (i.e., lattice points) and coupling terms, which are executed iteratively. Since CMLs commonly generate chaotic behavior, a logistic map is introduced in this work to induce such dynamics by setting the constant, . The logistic map is given as follows:
where is the iteration count. The recursive map for CML is as follows:
where s is the index for the vertices on the lattice and the coupling parameter, . The second term in the CML recursive map is for the neighboring lattice points. In this work a unidirectional coupling approach is taken with the convex map. The proposed techniques that combine the CML and the dual annealing optimization approaches is given in Algorithm 1:
| Algorithm 1: Combined Coupled Map Lattice and Dual Annealing Optimization Approach |
| START 1. Initialize dual annealing parameters: maximum iterations, . 2. Initialize CML parameters: Logistic map parameter, number of lattice vertices (N), coupling parameter (). 3. Solve using dual annealing algorithm to find optimal quantum state, and Choi states: and . 4. Initiate and run CML simulation. 5. IF Iteration = 1: Randomly initialize lattice values, . 6. IF Iteration > 1 and fitness function = 1: Back-substitute the improved computed lattice values. 7. IF Iteration > 1 and fitness function = 0: Back-substitute the lattice values from the previous iteration () (so it does not lead the CML algorithm towards non-optimal regions). 8. Compute new lattice values () using CML (with logistic map). 9. Check fitness of solution candidates (binary decision function). 10. IF Candidate solution is improved: 10.1. Fitness function is Satisfied: Fitness = 1, HALT PROGRAM. 10.2. Fitness function is NOT Satisfied: Fitness = 1, Repeat Step 4. 11. IF Candidate solution is NOT improved: 11.1. Fitness is Satisfied: Fitness function = 0, HALT PROGRAM. 11.2. Fitness is NOT Satisfied: Fitness function = 0, Repeat Step 5. 12. Determine statistical moments on CML simulation data—mean and variance. 13. Using statistical moments on a Gaussian distribution, simulate random values for quantum state . 14. Using standard PRNG, simulate random values for Choi states: and . 15. Solve for F in the upper-level problem. 16. Re-initialize Stackelberg game framework until fitness function cannot be further improved. END |
The bilevel optimization problem presented in Equation (3) is solved within a Stackelberg game-theoretic framework [34]. The fidelity objective function, F is the upper level/leader, while the probability of success, is the lower level/follower. The leader’s strategy is to optimize the objective of the sub-problem (. This influences the follower’s strategy, optimizing the objective (F). The numerical framework iteratively solves every level of the optimization problem as a Stackelberg game reaches the optimal solution. In this work, the entanglement distillation problem was solved using: Combined Coupled Map Lattice and Dual Annealing (CML-DA) technique and dual annealing method using pseudo-random number generators (PRNG-DA). The sub-problem problem is solved using the DA-PRNG approach by searching for the optimal dimension, d that maximizes . The quantum state, and the Choi states, and are generated using the PRNG. Consequently, using the obtained dimension d, and the density states, and the probability of success, , the upper-level problem is solved by searching for the best Choi states, and using the PRNG. As for the proposed CML-DA technique, the Stackelberg framework is employed, and each level of the problem is solved iteratively. In the CML-DA approach, the quantum state of the qubit before conversion () is estimated using the CML and PRNG techniques. The parameter settings employed for the numerical experiments in this work, for both the CML and DA techniques, are given in Table 1 and Table 2:

Table 1.
Parameter settings for the DA technique.

Table 2.
Parameter settings for the CML.
4. Computational Analysis
Similar to many research efforts in QST, the ideas presented in this work have been built on previous instrumental efforts in quantum parameter estimation—e.g., estimating one-parameter unitary gates for qubit systems and the use of entanglement for quantum parameter estimation to improve overall measurement stability [36,37,38,39,40]. The Stackelberg game-theoretic framework was utilized for the entanglement distillation problem, with a QST using fuzzy relations to estimate the quantum state. The pseudolikelihood measurements were simulated and the optimization problem was then solved using: the combined CML and dual annealing technique (CML-DA); and the conventional dual annealing approach with pseudo-random number generators (PRNG-DA). The numerical experiments were performed using the Python programming language on Google Collaboratory platform on a cloud with Python 3 Google Compute Engine (RAM 12.68 GB and Disk space:107.72 GB). Each technique was executed a total of 40 times, where each time the technique was run 3 times and the best solution taken for each execution. Therefore, both techniques were individually executed a total of 120 times. The computational results obtained using both techniques were measured using the weighted hypervolume indicator for the bilevel problem:
where the optimal solution candidate is and the nadir point is ). The weights and enable the relative importance of the contribution of the upper-level problem (1) and lower-level problem (2). In these experiments, the weights and . The nadir point is for the upper-level problem (or fidelity objective) (1), and the lower-level subproblem (or probability of success) (2) is ). The larger the value of the wHVI metric, the better the optimization performance. Due to the complexity of the optimization problem given in Equation (3), the existence of a global optima cannot be confirmed. Thus, the computational techniques present a framework to find a local optimal for the given entanglement distillation protocol. The rated individual solutions obtained using the PRNG-DA approach are given in Table 3, and the optimal quantum state of the best solution (pure state density matrix) is shown in Figure 1:

Table 3.
Rated individual solutions obtained using the PRNG-DA approach.
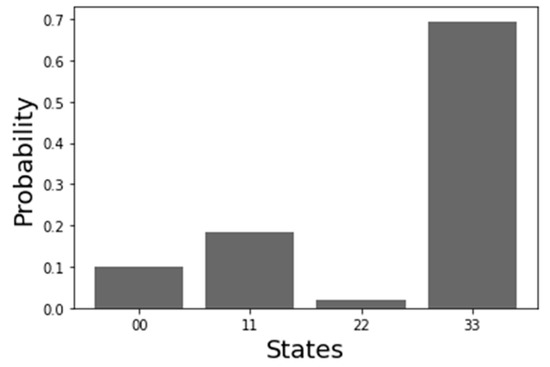
Figure 1.
The quantum state, for the best individual solution generated using the PRNG-DA approach.
The individual solutions obtained using the CML-DA technique are ranked and shown in Table 4. The generated optimal quantum state (pure density matrix) for the individual best solution is given in Figure 2:

Table 4.
Rated individual solutions obtained using the CML-DA approach.
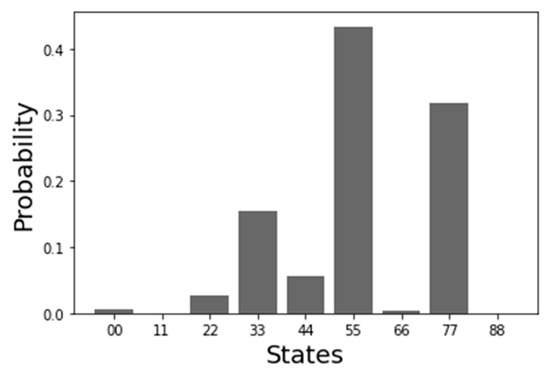
Figure 2.
The quantum state, for the best individual solution generated using the CML-DA approach.
The best individual solutions reached by the PRNG-DA and CML-DA techniques have a quantum state, with the dimensions: and , respectively. The difference in terms of the level of optimality reached by the individual best solutions, measured using the wHVI, was about . The scatter plot in Figure 3 shows the spread of the individual solutions generated using the PRNG-DA and CML-DA:
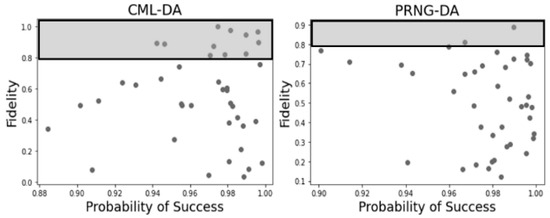
Figure 3.
Spread objective values for individual solutions generated using the PRNG-DA and CML-DA.
In Figure 3, it can be seen that the shaded area highlights the optimal region in the objective space, where the optimality of the fidelity objective is given more importance as compared to the cascaded objective function: probability of success. Thus, more solutions generated by the CML-DA technique fall into the optimal region as compared to the PRNG-DA approach. This is reflected in the value of the overall optimality of the solutions measured using the weighted HVI. The overall optimality of the CML-DA and PRNG-DA approaches are 27,109 and 25,718, respectively. The CML-DA outperforms the PRNG-DA in terms of overall optimization performance by approximately 5.267%. The key factor influencing the techniques in this study is the CML component. The chaotic dynamics exhibited by the CML enables wide-range dynamical behavior as compared the standard PRNG. This boosts the performance of the CML-DA approach, enabling it to perform a more thorough search of the objective landscape as compared to standard techniques (PRNG-based approaches). The CML is thus able to adapt better to the multilevel structure of the optimization problem and avoid scenarios that may cause stagnation. In other words, the CML manages to escape local optima traps in the objective space. The programs developed using the mentioned computational techniques did not encounter convergent issues and performed smoothly during execution. The execution time taken for the overall solution generation using the CML-DA technique was 156,804 s while the PRNG-DA approach took about 27 s. Thus, the trade-off experienced by the CML-DA in terms of optimization efficiency is the execution time as compared to the PRNG-DA approach. The additional algorithmic complexity embedded in the CML chaotic simulator comes with an additional computational cost. Nevertheless, both techniques showed stable performance when solving the entanglement distillation problem with the fuzzy relations for QST. In that work, the authors also developed a similarly scalable efficient maximum likelihood computational framework for approximating states from incomplete statistical data.
5. Conclusions and Recommendations
In this work, the entanglement distillation optimization was formulated using a bilevel structure. Using fuzzy relations, the quantum state of the system (density matrix, ), represented as a symmetric positive semidefinite matrix, was estimated using pseudo-likelihood measurements. A scale-independent partial differential equation (PDE) was derived (see Equation (7)). The solution to the PDE was employed for the QST of the quantum state. This multilevel optimization formulation was then solved using the CML-DA and PRNG-DA approaches within a Stackelberg game theoretic-framework. Comparative analysis showed that the CML-DA technique proved more efficient as compared to the PRNG-DA approach. The CML-DAs capacity for wide-range chaotic behavior enables it to navigate the objective space efficiently as compared to conventional techniques such as the PRNG-DA.
Due to the complexity of the problem, as well as the difficulty in analytically identifying the global optima, future works could be directed towards rigorous testing and analysis using other metaheuristics/optimization algorithms to obtain solutions closer to the global optima. Future works could also be directed on testing the performance of other novel meta-heuristics or evolutionary algorithms for other practical entanglement distillation protocols. In addition, research efforts could be focused on reformulating the practical entanglement distillation problem using pseudo-likelihood measurements, including environmental factors influencing the density matrix estimation in QST. This could be carried out by considering the quantum Liouville equation or the Gorini–Kossakowski–Sudarshan–Lindblad equation [41,42].
Author Contributions
Conceptualization, T.G. and I.E.; methodology, T.G. and I.E.; software, T.G. and I.E.; validation, T.G. and I.E.; formal analysis, T.G. and I.E.; investigation, T.G. and I.E.; resources, T.G. and I.E.; data curation, T.G. and I.E.; writing—original draft preparation, T.G. and I.E.; writing—review and editing, T.G. and I.E.; visualization, T.G. and I.E.; supervision, T.G. and I.E.; project administration, T.G. and I.E.; funding acquisition, T.G. and I.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kalb, N.; Reiserer, A.A.; Humphreys, P.C.; Bakermans, J.J.; Kamerling, S.J.; Nickerson, N.H.; Benjamin, S.C.; Twitchen, D.J.; Markham, M.; Hanson, R. Entanglement distillation between solid-state quantum network nodes. Science 2017, 356, 928–932. [Google Scholar] [CrossRef]
- Li, M.; Fei, S.; Li-Jost, X. Bell inequality, separability and entanglement distillation. Chin. Sci. Bull. 2011, 56, 945–954. [Google Scholar] [CrossRef]
- Ruan, L.; Dai, W.; Win, M.Z. Adaptive recurrence quantum entanglement distillation for two-Kraus-operator channels. Phys. Rev. A 2018, 97, 052332. [Google Scholar] [CrossRef]
- Ecker, S.; Sohr, P.; Bulla, L.; Huber, M.; Bohmann, M.; Ursin, R. Experimental single-copy entanglement distillation. Phys. Rev. Lett. 2021, 127, 040506. [Google Scholar] [CrossRef]
- Liu, C.; Tu, T.; Li, P.Y.; Liu, X.; Zhu, X.Y.; Zhou, Z.Q.; Li, C.F.; Guo, G.C. Towards entanglement distillation between atomic ensembles using high-fidelity spin operations. Commun. Phys. 2022, 5, 67. [Google Scholar] [CrossRef]
- Lin, Y.Y.; Sun, J.R.; Sun, Y. Bit thread, entanglement distillation, and entanglement of purification. Phys. Rev. D 2021, 103, 126002. [Google Scholar] [CrossRef]
- Qian, L.; Chen, L.; Chu, D.; Shen, Y. A matrix inequality for entanglement distillation problem. Linear Algebra Its Appl. 2021, 616, 139–177. [Google Scholar] [CrossRef]
- Kondra, T.V.; Datta, C.; Streltsov, A. Catalytic transformations of pure entangled states. Phys. Rev. Lett. 2021, 127, 150503. [Google Scholar] [CrossRef] [PubMed]
- He, M.; Malaney, R.; Burnett, B.A. Noiseless linear amplifiers for multimode states. Phys. Rev. A 2021, 103, 012414. [Google Scholar] [CrossRef]
- Gour, G.; Scandolo, C.M. Entanglement of a bipartite channel. Phys. Rev. A 2021, 103, 062422. [Google Scholar] [CrossRef]
- Yan, P.S.; Zhou, L.; Zhong, W.; Sheng, Y.B. Measurement-based logical qubit entanglement purification. Phys. Rev. A 2022, 105, 062418. [Google Scholar] [CrossRef]
- Shchukin, E.; van Loock, P. Optimal entanglement swapping in quantum repeaters. Phys. Rev. Lett. 2022, 128, 150502. [Google Scholar] [CrossRef]
- Riera-Sàbat, F.; Sekatski, P.; Pirker, A.; Dür, W. Entanglement-assisted entanglement purification. Phys. Rev. Lett. 2021, 127, 040502. [Google Scholar] [CrossRef] [PubMed]
- Gyongyosi, L.; Imre, S. Optimizing high-efficiency quantum memory with quantum machine learning for near-term quantum devices. Sci. Rep. 2020, 10, 135. [Google Scholar] [CrossRef] [PubMed]
- Gyongyosi, L. Quantum state optimization and computational pathway evaluation for gate-model quantum computers. Sci. Rep. 2020, 10, 1–12. [Google Scholar] [CrossRef]
- Brand, S.; Coopmans, T.; Elkouss, D. Efficient computation of the waiting time and fidelity in quantum repeater chains. IEEE J. Sel. Areas Commun. 2020, 38, 619–639. [Google Scholar] [CrossRef]
- Sahu, A.; Sreeram, P.G.; Madhok, V. Effect of chaos on information gain in quantum tomography. Phys. Rev. E 2022, 106, 024209. [Google Scholar] [CrossRef]
- Schmale, T.; Reh, M.; Gärttner, M. Efficient quantum state tomography with convolutional neural networks. NPJ Quantum Inf. 2022, 8, 115. [Google Scholar] [CrossRef]
- Farooq, A.; Khalid, U.; ur Rehman, J.; Shin, H. Robust Quantum State Tomography Method for Quantum Sensing. Sensors 2022, 22, 2669. [Google Scholar] [CrossRef]
- Ahmad, S.T.; Farooq, A.; Shin, H. Self-guided quantum state tomography for limited resources. Sci. Rep. 2022, 12, 5092. [Google Scholar] [CrossRef]
- Choi, M.S. Single-qubit reaped quantum state tomography. Sci. Rep. 2022, 12, 10983. [Google Scholar] [CrossRef] [PubMed]
- Lu, Q.C.; Zhang, L.; Xu, P.C.; Cui, X.; Li, J. Modeling network vulnerability of urban rail transit under cascading failures: A Coupled Map Lattices approach. Reliab. Eng. Syst. Saf. 2022, 221, 108320. [Google Scholar] [CrossRef]
- Stenzinger, R.V.; Tragtenberg, M.H.R. Cardiac reentry modeled by spatiotemporal chaos in a coupled map lattice. Eur. Phys. J. Spec. Top. 2022, 231, 847–858. [Google Scholar] [CrossRef]
- Wang, X.; Liu, P. A new full chaos coupled mapping lattice and its application in privacy image encryption. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 69, 1291–1301. [Google Scholar] [CrossRef]
- Xie, X.; Li, J.; Huang, Z.; Yang, Q.; Kwak, K.S. Coupled-Map-Lattices-Based Vulnerability Assessment of UAV Network in Interference Scenarios. Wirel. Commun. Mob. Comput. 2022, 2022, 1–14. [Google Scholar] [CrossRef]
- Xu, F.; Ma, X.; Zhang, Q.; Lo, H.K.; Pan, J.W. Secure quantum key distribution with realistic devices. Rev. Mod. Phys. 2020, 92, 025002. [Google Scholar] [CrossRef]
- Rozpędek, F.; Schiet, T.; Elkouss, D.; Doherty, A.C.; Wehner, S. Optimizing practical entanglement distillation. Phys. Rev. A 2018, 97, 062333. [Google Scholar] [CrossRef]
- Lukens, J.M.; Law, K.J.; Jasra, A.; Lougovski, P. A practical and efficient approach for Bayesian quantum state estimation. New J. Phys. 2020, 22, 063038. [Google Scholar] [CrossRef]
- Quek, Y.; Fort, S.; Ng, H.K. Adaptive quantum state tomography with neural networks. NPJ Quantum Inf. 2021, 7, 105. [Google Scholar] [CrossRef]
- Recasens, J. On the relationship between positive semi-definite matrices and t-norms. Fuzzy Sets Syst. 2022, 446, 26–37. [Google Scholar] [CrossRef]
- Guilmeau, T.; Chouzenoux, E.; Elvira, V. Simulated annealing: A review and a new scheme. In Proceedings of the 2021 IEEE Statistical Signal Processing Workshop (SSP), Rio de Janeiro, Brazil, 11–14 July 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 101–105. [Google Scholar]
- Xiang, Y.; Gubian, S.; Martin, F. Generalized simulated annealing. In Computational Optimization in Engineering—Paradigms and Applications; InTechOpen: London, UK, 2017; pp. 25–46. [Google Scholar]
- Zia, U.; McCartney, M.; Scotney, B.; Martinez, J.; Sajjad, A. A novel pseudo-random number generator for IoT based on a coupled map lattice system using the generalised symmetric map. SN Appl. Sci. 2022, 4, 1–17. [Google Scholar] [CrossRef]
- Ganesan, T.; Vasant, P.; Litvinchev, I. Chaotic simulator for bilevel optimization of virtual machine placements in cloud computing. J. Oper. Res. Soc. China 2022, 10, 703–723. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Teng, L.; Jiang, D. A novel meaningful image encryption algorithm based on newly-designed coupled map lattice and adaptive embedding. Optik 2022, 270, 170073. [Google Scholar] [CrossRef]
- Genoni, M.G.; Olivares, S.; Paris, M.G. Optical phase estimation in the presence of phase diffusion. Phys. Rev. Lett. 2011, 106, 153603. [Google Scholar] [CrossRef]
- Teklu, B.; Olivares, S.; Paris, M.G. Bayesian estimation of one-parameter qubit gates. J. Phys. B At. Mol. Opt. Phys. 2009, 42, 035502. [Google Scholar] [CrossRef]
- Rossi, M.A.; Paris, M.G. Entangled quantum probes for dynamical environmental noise. Phys. Rev. A 2015, 92, 010302. [Google Scholar] [CrossRef]
- Brivio, D.; Cialdi, S.; Vezzoli, S.; Gebrehiwot, B.T.; Genoni, M.G.; Olivares, S.; Paris, M.G. Experimental estimation of one-parameter qubit gates in the presence of phase diffusion. Phys. Rev. A 2010, 81, 012305. [Google Scholar] [CrossRef]
- Marchetti, B. Particle Beam Diagnostics. arXiv 2020, arXiv:2008.05896, preprint. [Google Scholar]
- Kim, H.W.; Rhee, Y.M. Two-oscillator mapping modification of the Poisson bracket mapping equation formulation of the quantum–classical Liouville equation. J. Chem. Phys. 2020, 153, 214103. [Google Scholar] [CrossRef]
- Manzano, D. A short introduction to the Lindblad master equation. Aip Adv. 2020, 10, 025106. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).