Optimizing Multidimensional Pooling for Variational Quantum Algorithms
Abstract
1. Introduction
2. Background
2.1. Quantum Bits and States
2.2. Quantum Gates
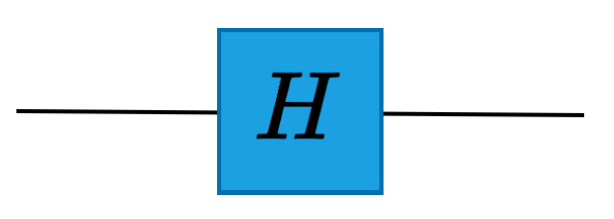
2.2.1. Hadamard Gate
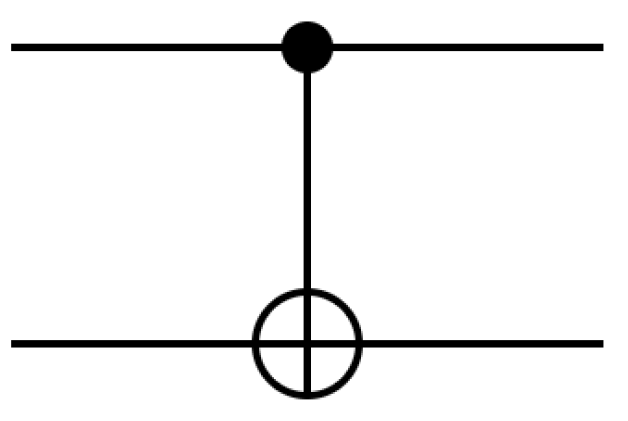
2.2.2. Controlled-NOT (CNOT) Gate
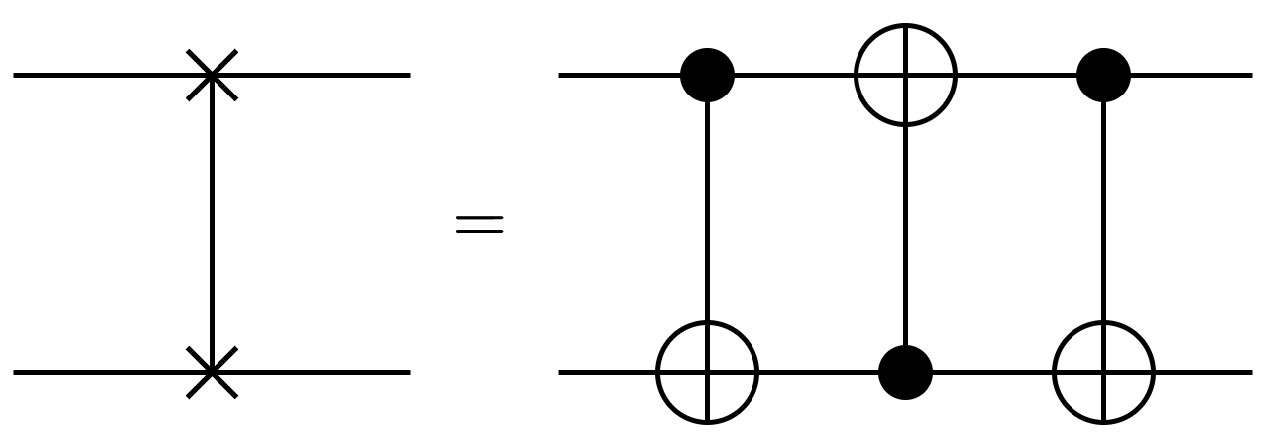
2.2.3. SWAP Gate
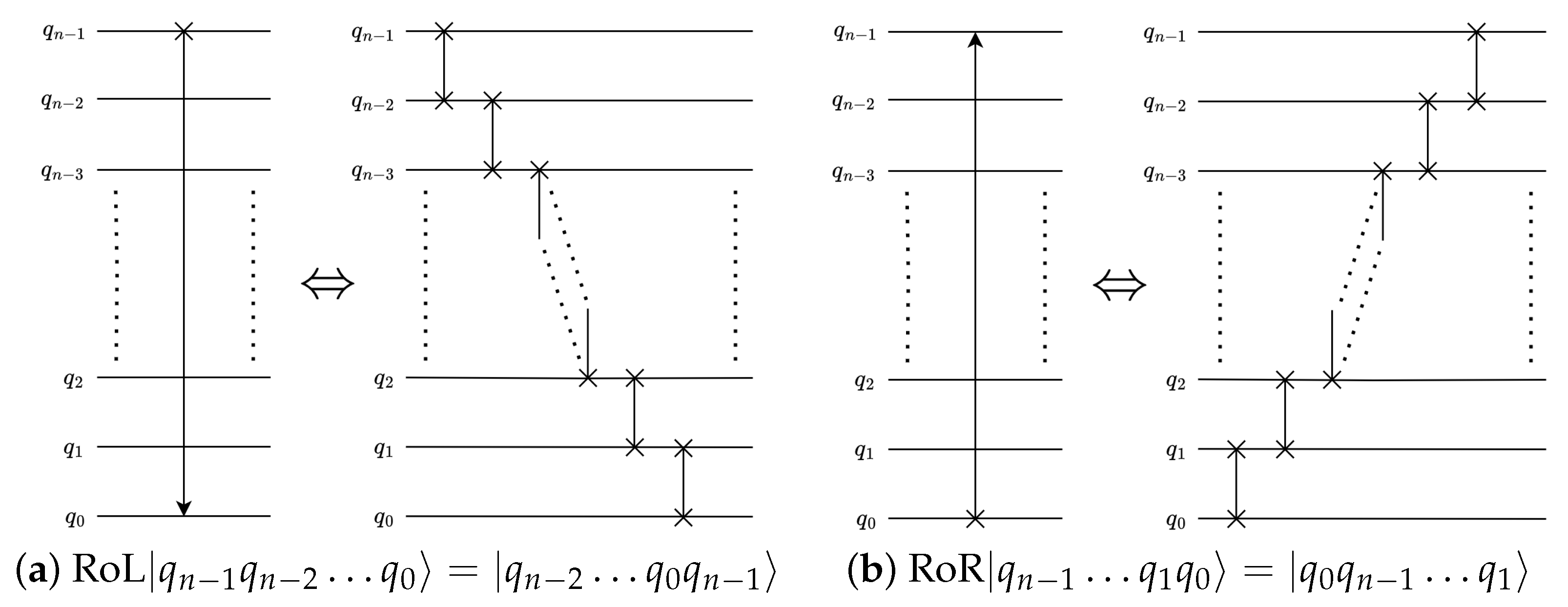
2.2.4. Quantum Perfect Shuffle Permutation (PSP)
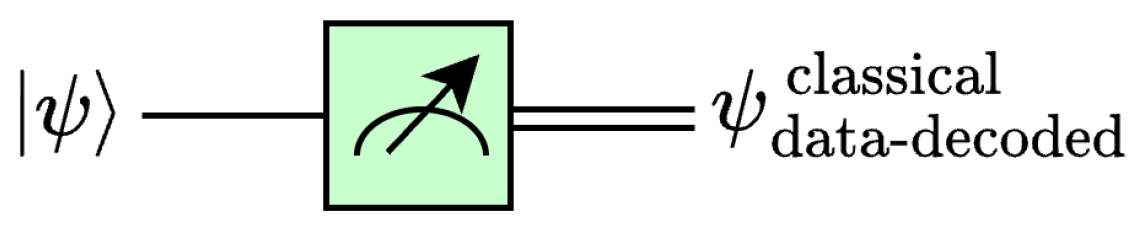
2.2.5. Quantum Measurement
3. Related Work
4. Materials and Methods
4.1. Quantum Average Pooling via Quantum Haar Transform
- Haar Wavelet Operation: By applying Hadamard (H) gates (see Section 2.2.1) in parallel, the high- and low-frequency components are decomposed from the input data.
- Data Rearrangement: By applying quantum rotate-right (RoR) operations (see Section 2.2.4), the high- and low-frequency components are grouped into contiguous regions.
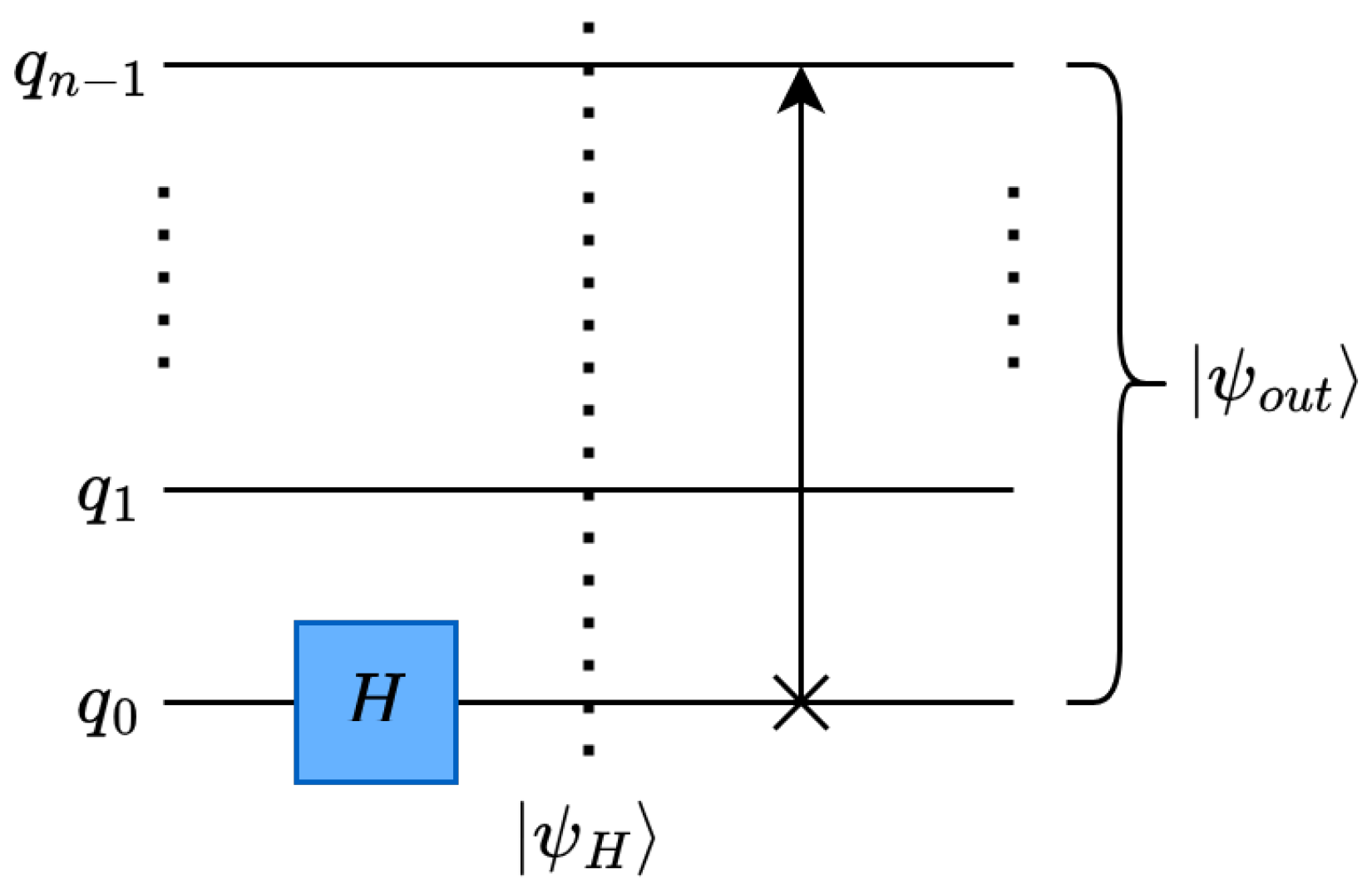
4.1.1. Single-Level One-Dimensional Quantum Haar Transform
Haar Wavelet Operation on Single-Level One-Dimensional Data
Data Rearrangement Operation
Circuit Depth
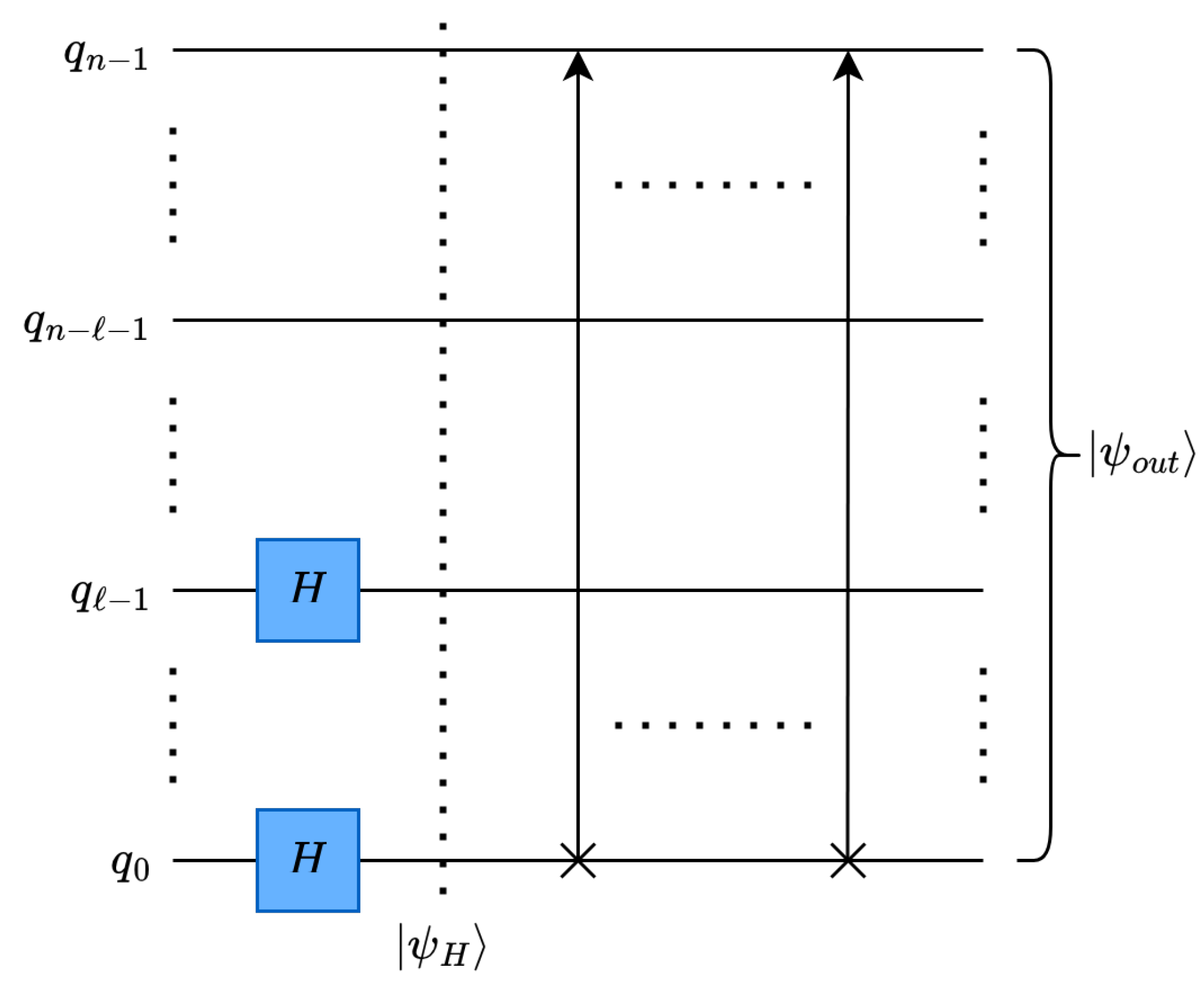
4.1.2. Multilevel One-Dimensional Quantum Haar Transform
Haar Wavelet Operation on Multilevel One-Dimensional Data
Data Rearrangement Operation
Circuit Depth
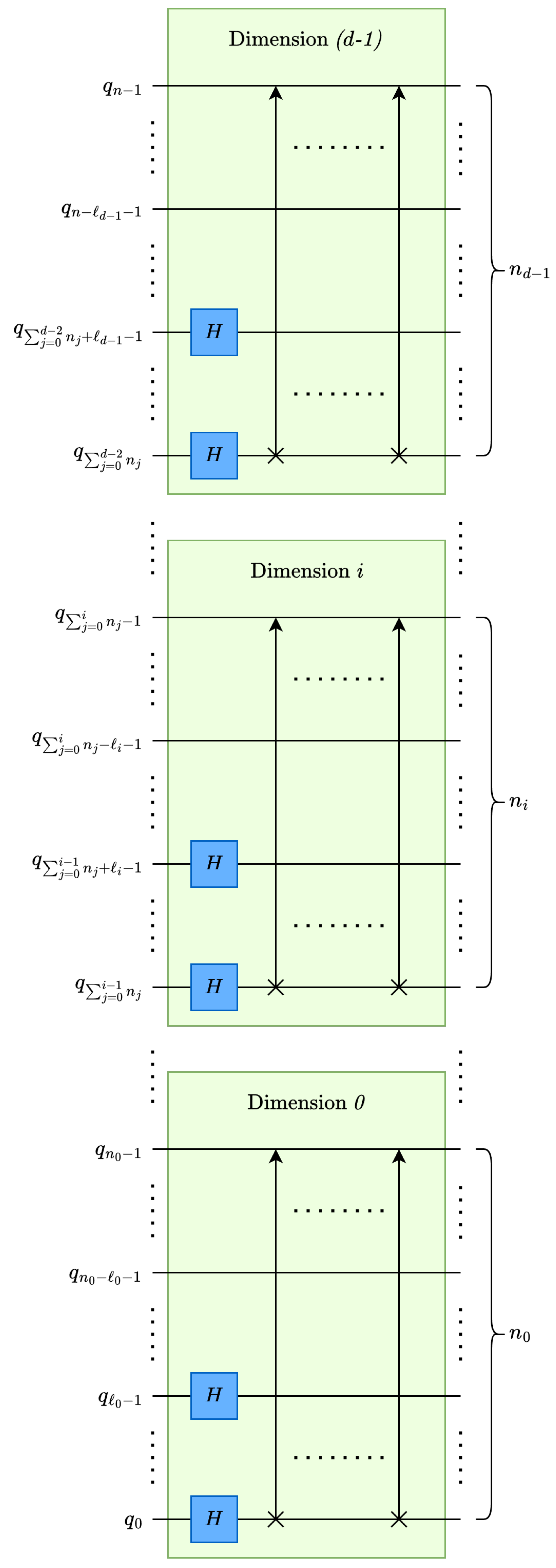
4.1.3. Multilevel Multidimensional Quantum Haar Transform
Haar Wavelet Operation on Multidimensional Data
Data Rearrangement Operation
Circuit Depth
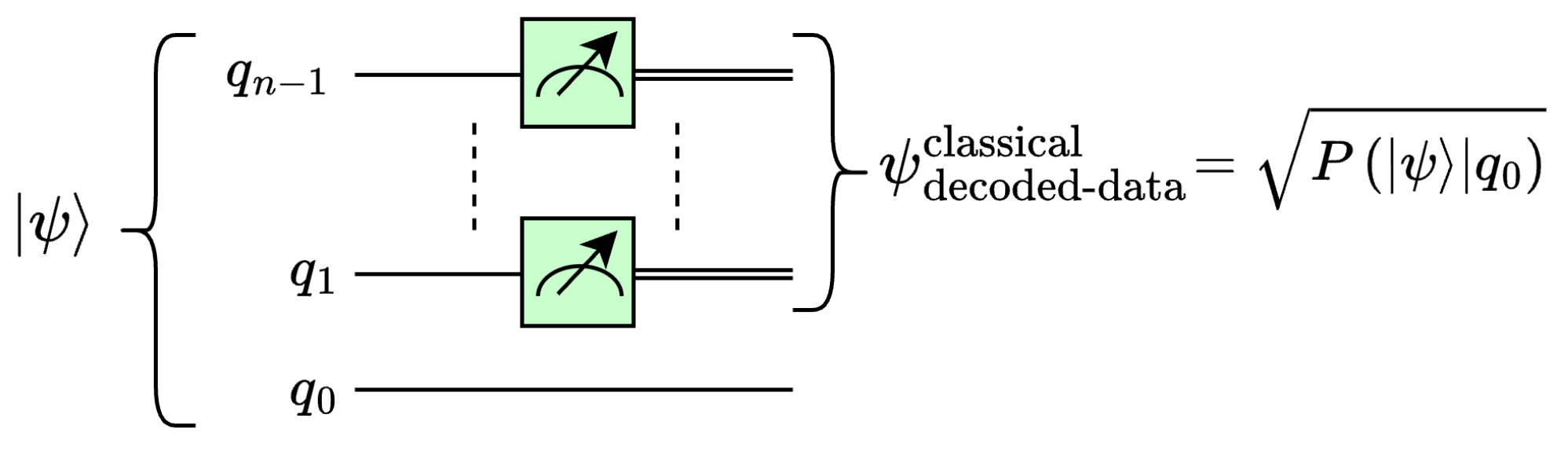
4.2. Quantum Euclidean Pooling Using Partial Measurement
4.2.1. Single-Level One-Dimensional Quantum Euclidean Pooling
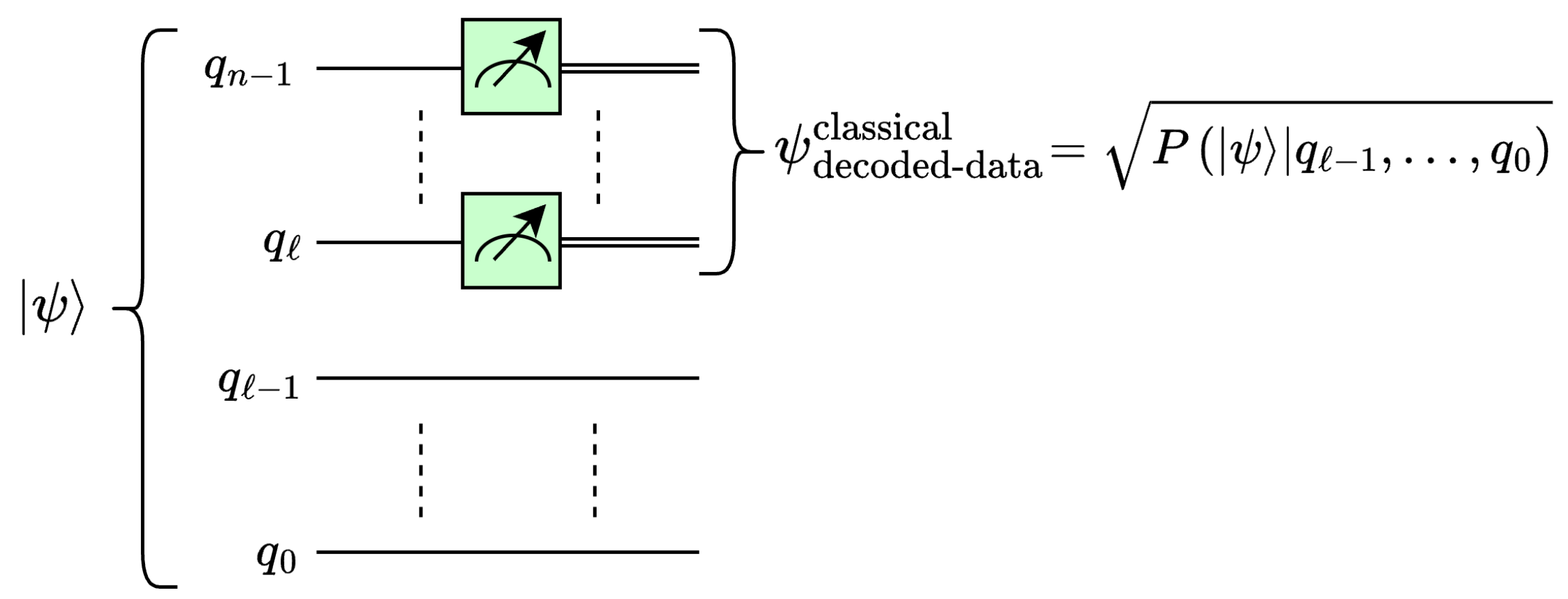
4.2.2. Multilevel One-Dimensional Quantum Euclidean Pooling
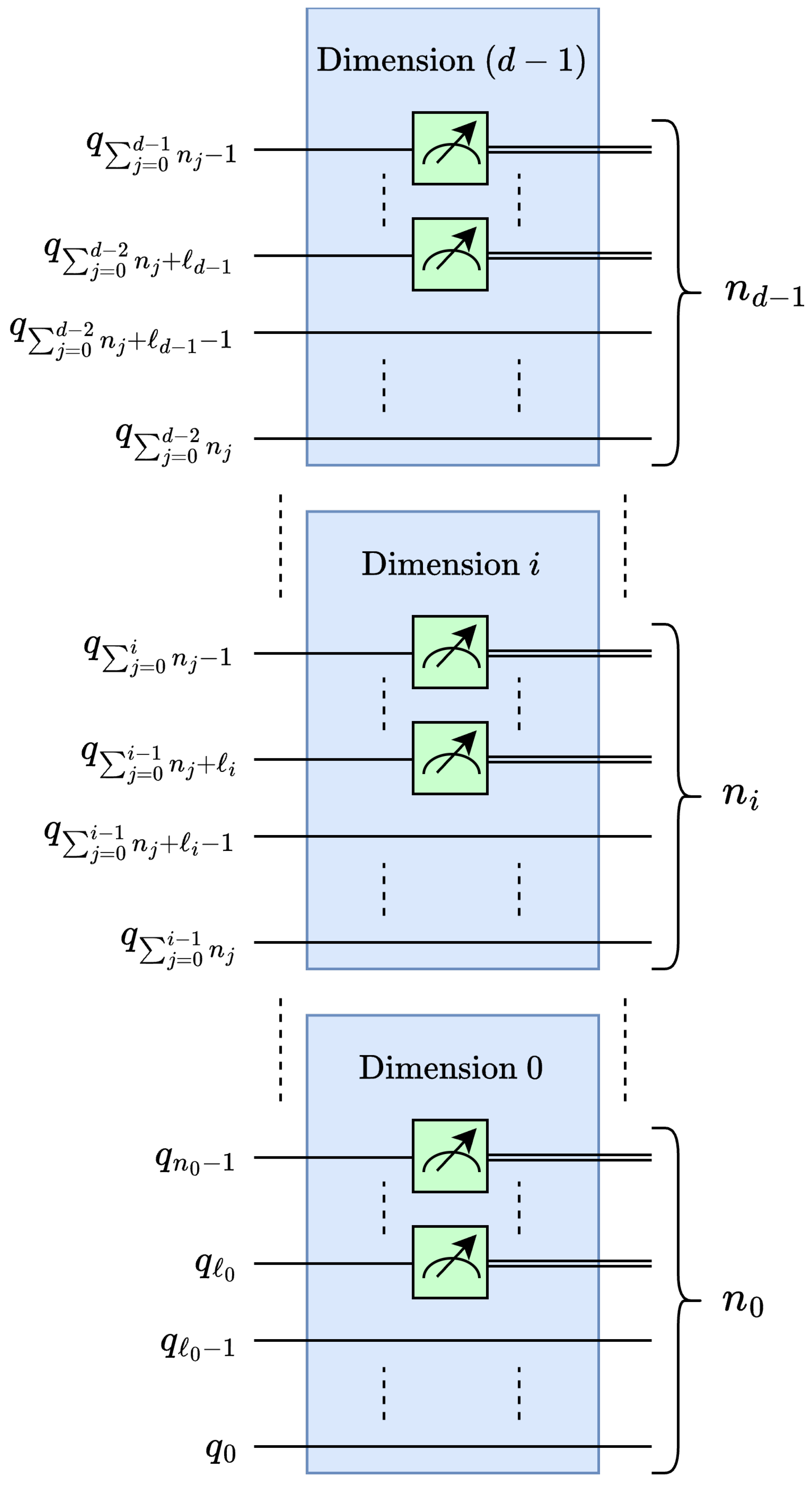
4.2.3. Multilevel Multidimensional Quantum Euclidean Pooling
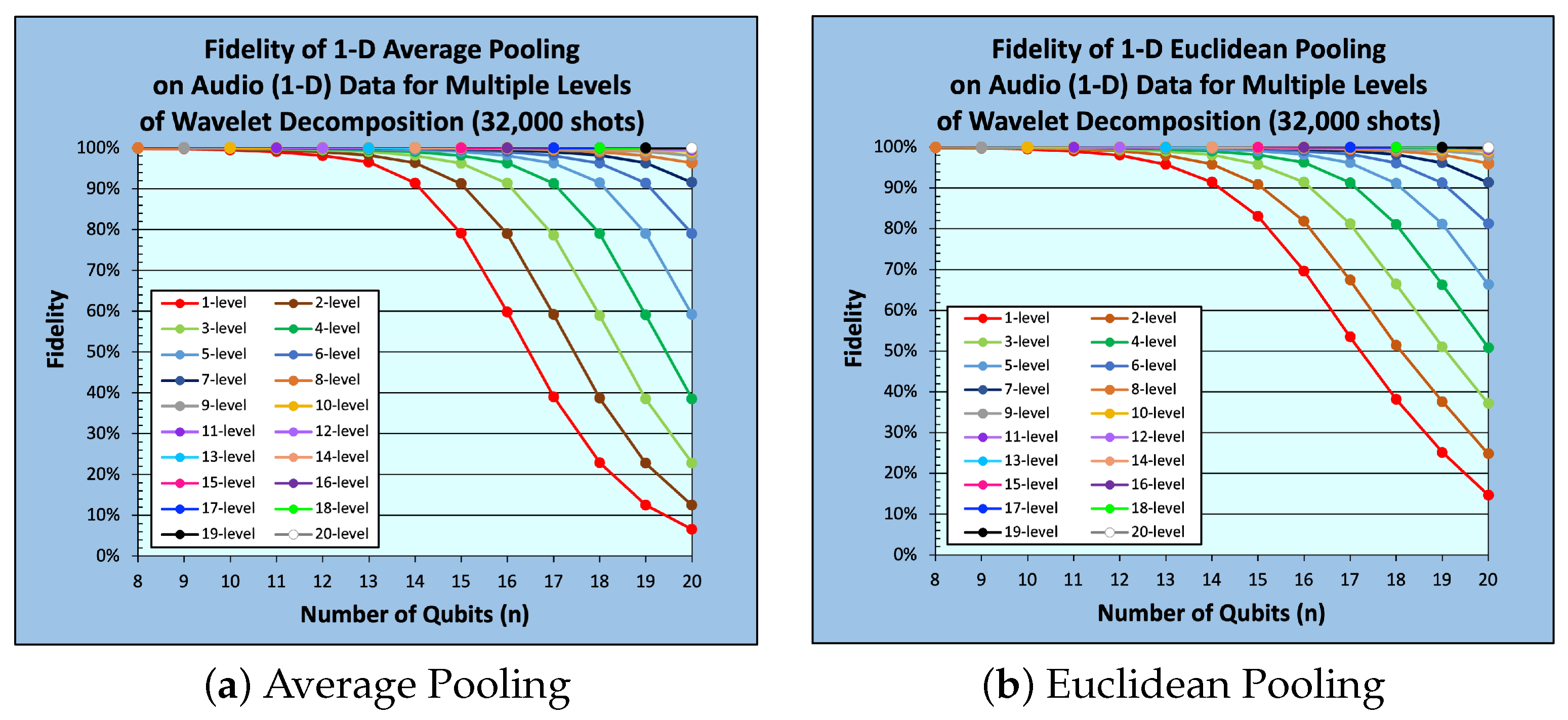
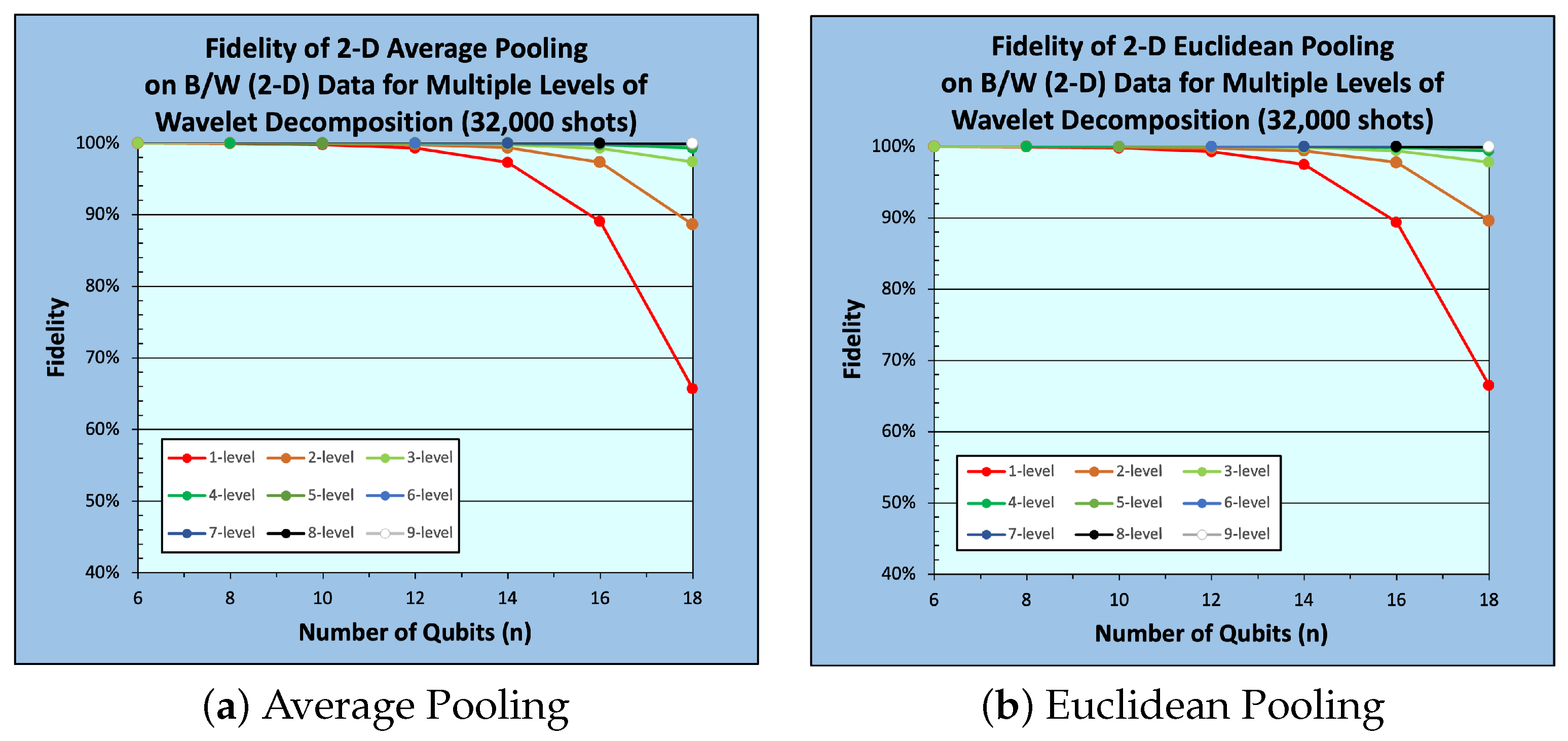
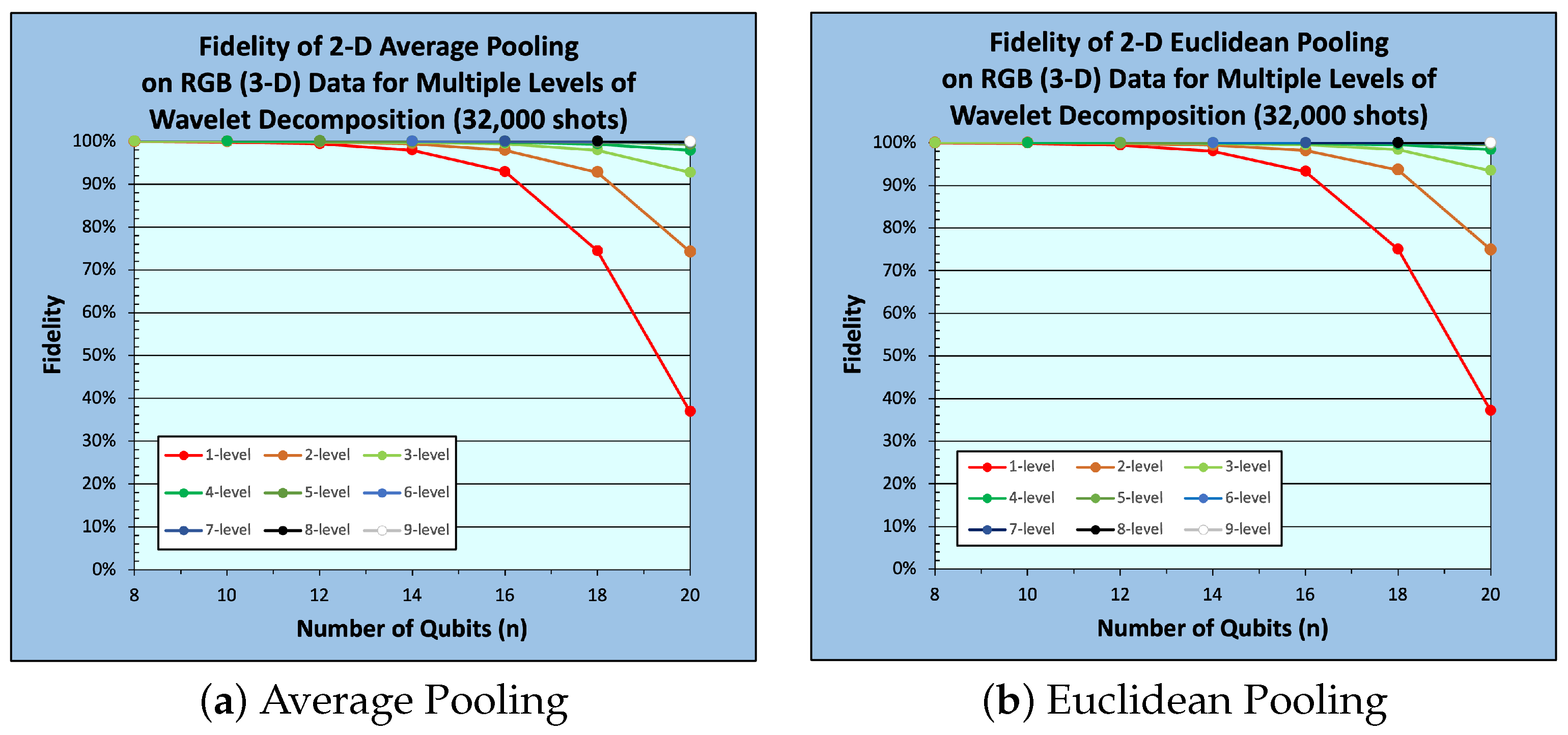
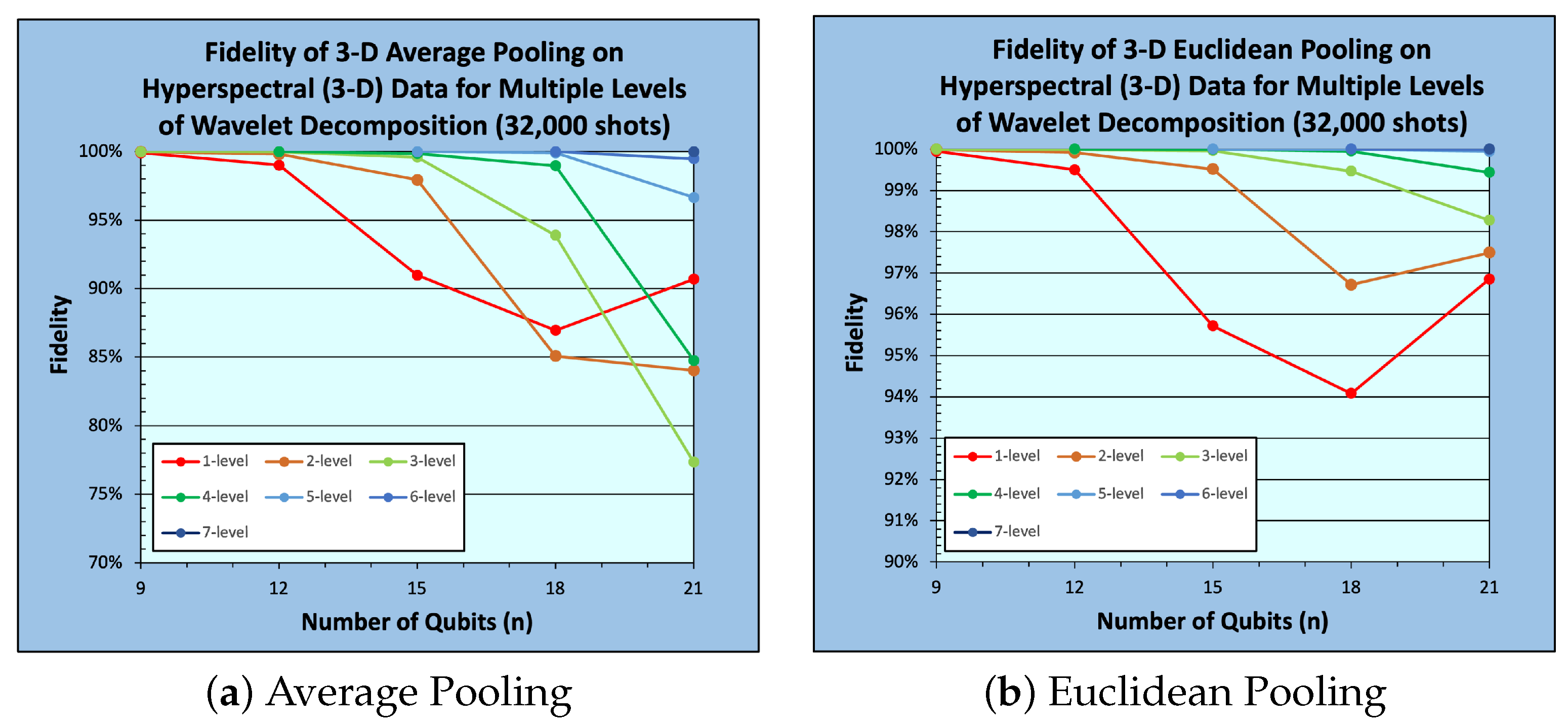
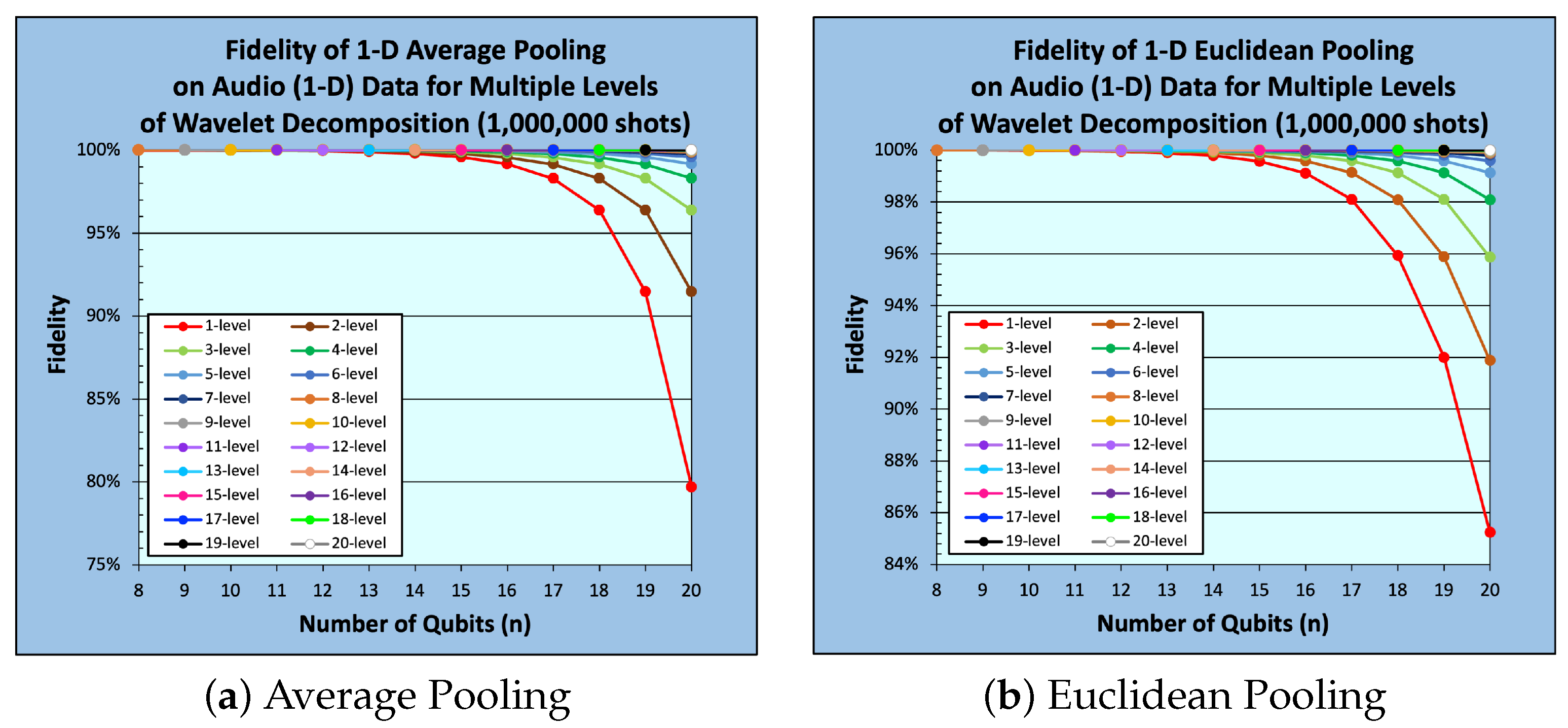
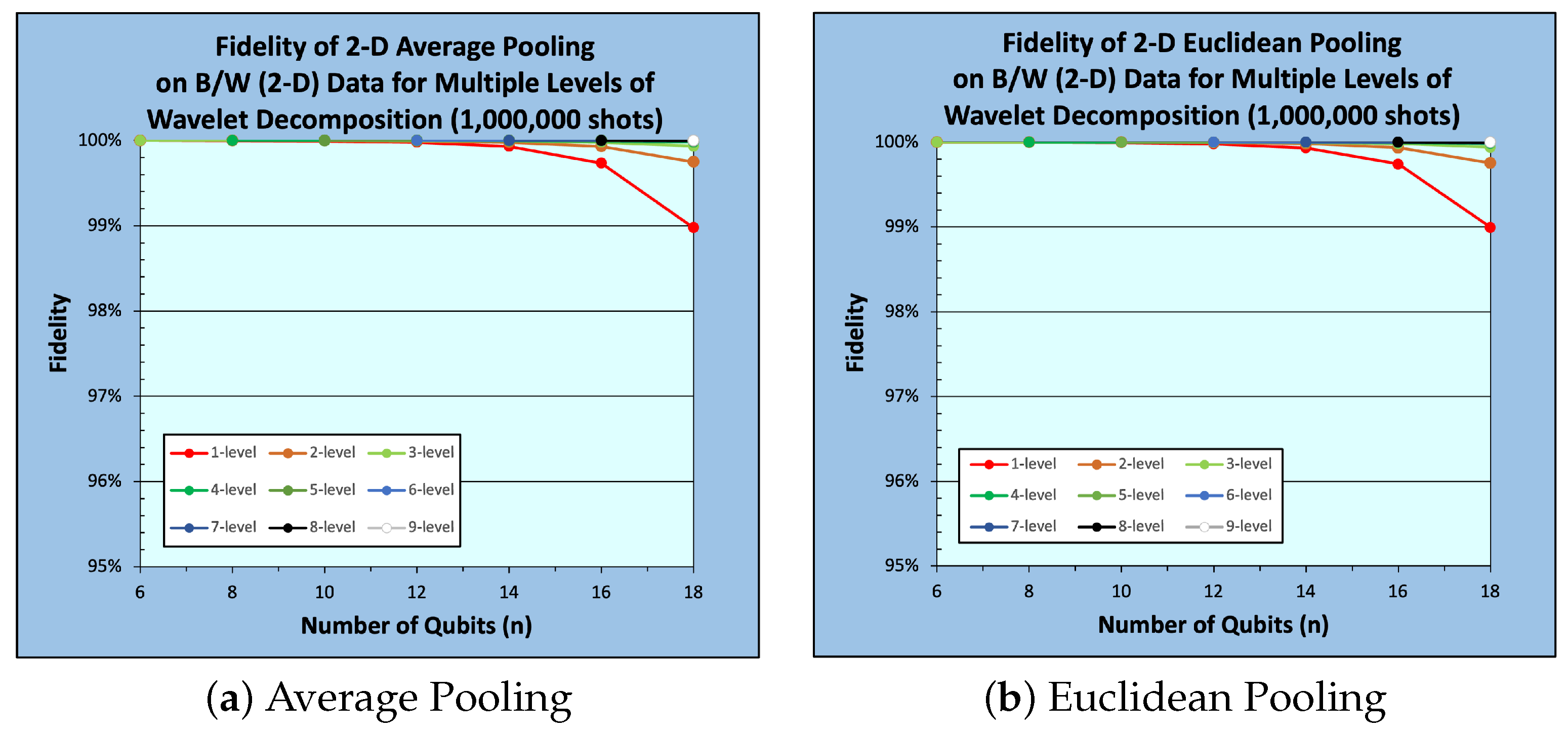
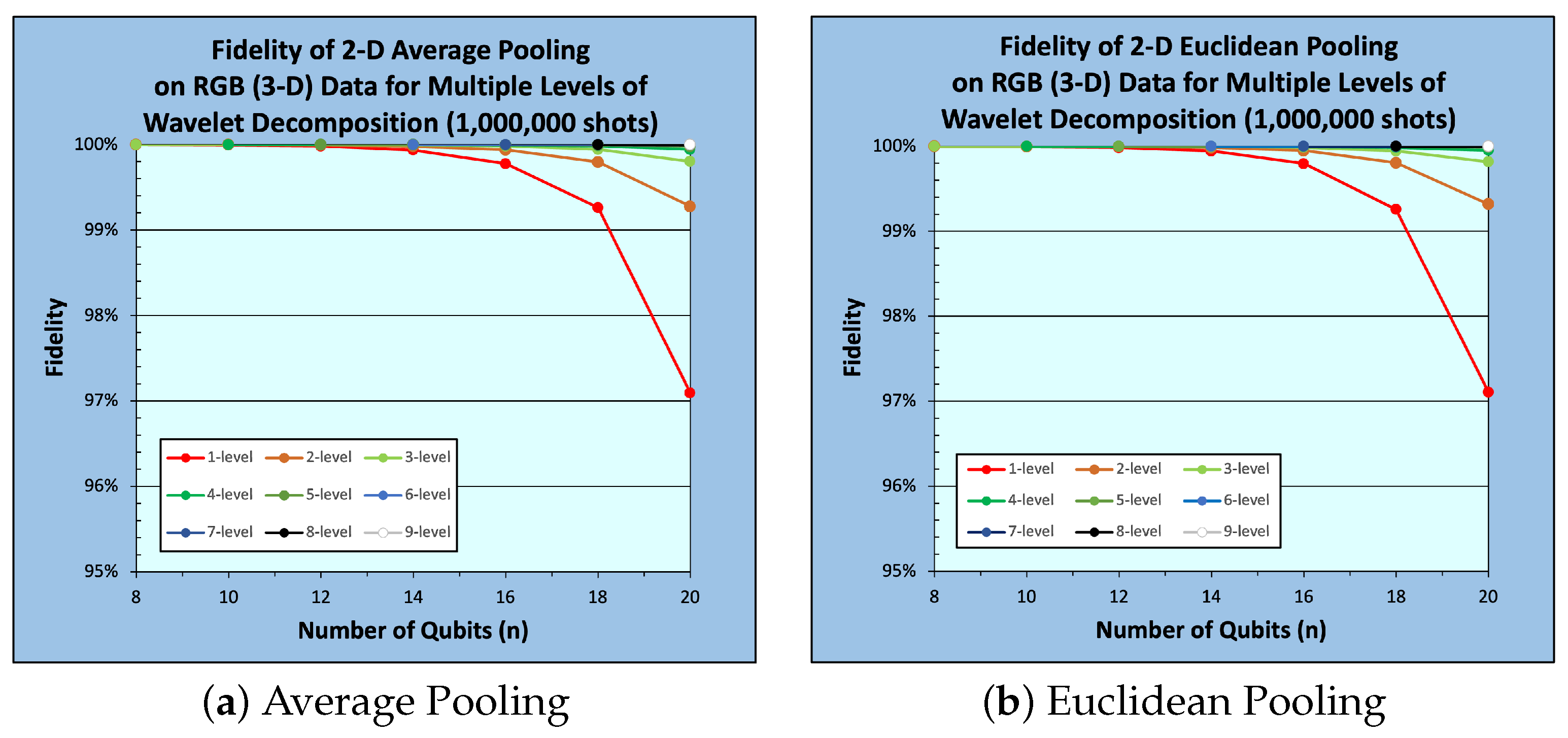
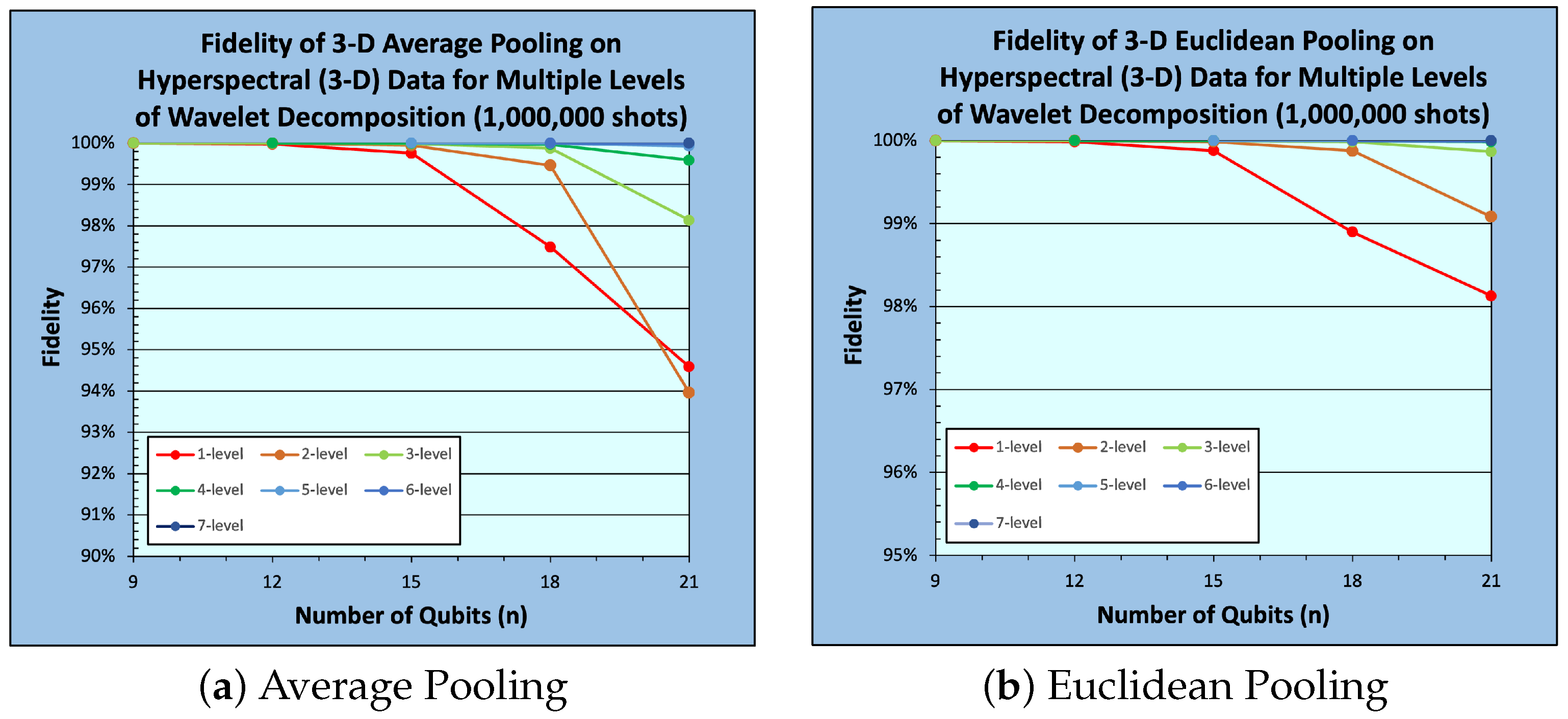
5. Experimental Work
5.1. Experimental Setup
5.2. Results and Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- LeCun, Y.; Kavukcuoglu, K.; Farabet, C. Convolutional networks and applications in vision. In Proceedings of the 2010 IEEE International Symposium on Circuits and Systems, Paris, France, 30 May–2 June 2010; IEEE: New York, NY, USA, 2010; pp. 253–256. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Gholamalinezhad, H.; Khosravi, H. Pooling methods in deep neural networks, a review. arXiv 2020, arXiv:2009.07485. [Google Scholar]
- Chen, F.; Datta, G.; Kundu, S.; Beerel, P.A. Self-Attentive Pooling for Efficient Deep Learning. In Proceedings of the the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–7 January 2023; pp. 3974–3983. [Google Scholar]
- Tabani, H.; Balasubramaniam, A.; Marzban, S.; Arani, E.; Zonooz, B. Improving the efficiency of transformers for resource-constrained devices. In Proceedings of the 2021 24th Euromicro Conference on Digital System Design (DSD), Sicily, Italy, 1–3 September 2021; IEEE: New York, NY, USA, 2021; pp. 449–456. [Google Scholar]
- Jeng, M.; Islam, S.I.U.; Levy, D.; Riachi, A.; Chaudhary, M.; Nobel, M.A.I.; Kneidel, D.; Jha, V.; Bauer, J.; Maurya, A.; et al. Improving quantum-to-classical data decoding using optimized quantum wavelet transform. J. Supercomput. 2023, 79, 20532–20561. [Google Scholar] [CrossRef]
- Rohlfing, C.; Cohen, J.E.; Liutkus, A. Very low bitrate spatial audio coding with dimensionality reduction. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 741–745. [Google Scholar] [CrossRef][Green Version]
- Ye, J.; Janardan, R.; Li, Q. GPCA: An efficient dimension reduction scheme for image compression and retrieval. In Proceedings of the Tenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Seattle, WA, USA, 22–25 August 2004; ACM: New York, NY, USA, 2004; pp. 354–363. [Google Scholar] [CrossRef]
- Hur, T.; Kim, L.; Park, D.K. Quantum convolutional neural network for classical data classification. Quantum Mach. Intell. 2022, 4, 3. [Google Scholar] [CrossRef]
- Cong, I.; Choi, S.; Lukin, M.D. Quantum convolutional neural networks. Nature Phys. 2019, 15, 1273–1278. [Google Scholar] [CrossRef]
- Biamonte, J.; Wittek, P.; Pancotti, N.; Rebentrost, P.; Wiebe, N.; Lloyd, S. Quantum machine learning. Nature 2017, 549, 195–202. [Google Scholar] [CrossRef] [PubMed]
- Monnet, M.; Gebran, H.; Matic-Flierl, A.; Kiwit, F.; Schachtner, B.; Bentellis, A.; Lorenz, J.M. Pooling techniques in hybrid quantum-classical convolutional neural networks. arXiv 2023, arXiv:2305.05603. [Google Scholar]
- Peruzzo, A.; McClean, J.; Shadbolt, P.; Yung, M.H.; Zhou, X.Q.; Love, P.J.; Aspuru-Guzik, A.; O’Brien, J.L. A variational eigenvalue solver on a photonic quantum processor. Nature Commun. 2014, 5, 4213. [Google Scholar] [CrossRef] [PubMed]
- Williams, C.P. Explorations in Quantum Computing, 2nd ed.; Springer: London, UK, 2011. [Google Scholar]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information: 10th Anniversary Edition; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar] [CrossRef]
- Walsh, J.L. A Closed Set of Normal Orthogonal Functions. Am. J. Math. 1923, 45, 5–24. [Google Scholar] [CrossRef]
- Shende, V.; Bullock, S.; Markov, I. Synthesis of quantum-logic circuits. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2006, 25, 1000–1010. [Google Scholar] [CrossRef]
- El-Araby, E.; Mahmud, N.; Jeng, M.J.; MacGillivray, A.; Chaudhary, M.; Nobel, M.A.I.; Islam, S.I.U.; Levy, D.; Kneidel, D.; Watson, M.R.; et al. Towards Complete and Scalable Emulation of Quantum Algorithms on High-Performance Reconfigurable Computers. IEEE Trans. Comput. 2023, 72, 2350–2364. [Google Scholar] [CrossRef]
- IBM Quantum. Qiskit: An Open-Source Framework for Quantum Computing. Zenodo. 2023. Available online: https://zenodo.org/records/8190968 (accessed on 30 December 2023).
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- NVIDIA. cuDNN—cudnnPoolingForward() [Computer Software]. 2023. Available online: https://docs.nvidia.com/deeplearning/cudnn/api/index.html#cudnnPoolingForward (accessed on 30 December 2023).
- NVIDIA. TensorRT—Pooling [Computer Software]. 2023. Available online: https://docs.nvidia.com/deeplearning/tensorrt/operators/docs/Pooling.html (accessed on 30 December 2023).
- NVIDIA. Pooling. 2023. Available online: https://docs.nvidia.com/deeplearning/performance/dl-performance-memory-limited/index.html#pooling (accessed on 30 December 2023).
- Schlosshauer, M. Quantum decoherence. Phys. Rep. 2019, 831, 1–57. [Google Scholar] [CrossRef]
- Mahmud, N.; MacGillivray, A.; Chaudhary, M.; El-Araby, E. Decoherence-optimized circuits for multidimensional and multilevel-decomposable quantum wavelet transform. IEEE Internet Comput. 2021, 26, 15–25. [Google Scholar] [CrossRef]
- MacCormack, I.; Delaney, C.; Galda, A.; Aggarwal, N.; Narang, P. Branching quantum convolutional neural networks. Phys. Rev. Res. 2022, 4, 013117. [Google Scholar] [CrossRef]
- Chen, G.; Chen, Q.; Long, S.; Zhu, W.; Yuan, Z.; Wu, Y. Quantum convolutional neural network for image classification. Pattern Anal. Appl. 2023, 26, 655–667. [Google Scholar] [CrossRef]
- Zheng, J.; Gao, Q.; Lü, Y. Quantum graph convolutional neural networks. In Proceedings of the 2021 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; IEEE: Piscataway, NY, USA, 2021; pp. 6335–6340. [Google Scholar]
- Wei, S.; Chen, Y.; Zhou, Z.; Long, G. A quantum convolutional neural network on NISQ devices. AAPPS Bull. 2022, 32, 1–11. [Google Scholar] [CrossRef]
- Bieder, F.; Sandkühler, R.; Cattin, P.C. Comparison of Methods Generalizing Max- and Average-Pooling. arXiv 2021, arXiv:2104.06918. [Google Scholar]
- PyTorch. torch.nn.LPPool1d [Computer Software]. 2023. Available online: https://pytorch.org/docs/stable/generated/torch.nn.LPPool1d.html (accessed on 30 December 2023).
- Geneva, S. Sound Quality Assessment Material: Recordings for Subjective Tests. 1988. Available online: https://tech.ebu.ch/publications/sqamcd (accessed on 30 December 2023).
- Brand Center; University of Kansas. Jayhawk Images. Available online: https://brand.ku.edu/ (accessed on 30 December 2023).
- Graña, M.; Veganzons, M.A.; Ayerdi, B. Hyperspectral Remote Sensing Scenes. Available online: https://www.ehu.eus/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes#Kennedy_Space_Center_(KSC) (accessed on 30 December 2023).
- IBM Quantum. qiskit.circuit.QuantumCircuit.measure [Computer Software]. 2023. Available online: https://docs.quantum.ibm.com/api/qiskit/qiskit.circuit.QuantumCircuit#measure (accessed on 30 December 2023).
- Jeng, M.; Nobel, M.A.I.; Jha, V.; Levy, D.; Kneidel, D.; Chaudhary, M.; Islam, S.I.U.; El-Araby, E. Multidimensional Quantum Convolution with Arbitrary Filtering and Unity Stride. In Proceedings of the IEEE International Conference on Quantum Computing and Engineering (QCE23), Bellevue, WA, USA, 17–22 September 2023. [Google Scholar]
- Lee, G.R.; Gommers, R.; Waselewski, F.; Wohlfahrt, K.; O’Leary, A. PyWavelets: A Python package for wavelet analysis. J. Open Source Softw. 2019, 4, 1237. [Google Scholar] [CrossRef]
- KU Community Cluster, Center for Research Computing, University of Kansas. Available online: https://crc.ku.edu/systems-services/ku-community-cluster (accessed on 30 December 2023).
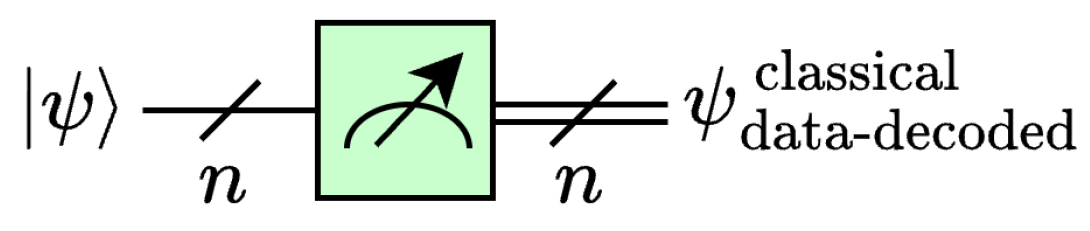

| Levels of Decomposition | Average Pooling (32,000 Shots) | Average Pooling (1,000,000 Shots) | Euclidean Pooling (32,000 Shots) | Euclidean Pooling (1,000,000 Shots) |
|---|---|---|---|---|
| 1 Level |  | 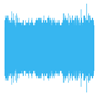 | 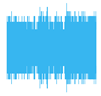 | 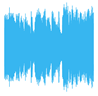 |
| 2 Levels |  |  |  |  |
| 4 Levels |  | 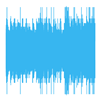 | 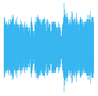 | 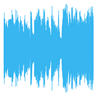 |
| 8 Levels | 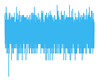 | 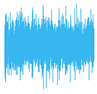 | 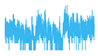 | 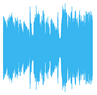 |
| Levels of Decomposition | Average Pooling (32,000 Shots) | Average Pooling (1,000,000 Shots) | Euclidean Pooling (32,000 Shots) | Euclidean Pooling (1,000,000 Shots) |
|---|---|---|---|---|
| 1 Level |  |  |  |  |
| 2 Levels | 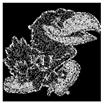 |  | 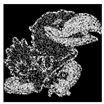 |  |
| 4 Levels |  |  |  |  |
| 8 Levels |  |  |  |  |
| Levels of Decomposition | Average Pooling (32,000 Shots) | Average Pooling (1,000,000 Shots) | Euclidean Pooling (32,000 Shots) | Euclidean Pooling (1,000,000 Shots) |
|---|---|---|---|---|
| 1 Level |  |  |  |  |
| 2 Levels | 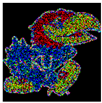 |  | 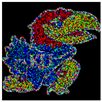 |  |
| 4 Levels |  |  |  |  |
| 8 Levels |  |  |  |  |
| Levels of Decomposition | Average Pooling (32,000 Shots) | Average Pooling (1,000,000 Shots) | Euclidean Pooling (32,000 Shots) | Euclidean Pooling (1,000,000 Shots) |
|---|---|---|---|---|
| 1 Level |  | 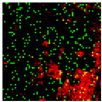 |  | 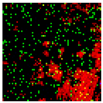 |
| 2 Levels |  | 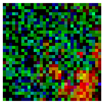 |  | 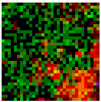 |
| 4 Levels |  |  |  |  |
| 7 Levels |  |  |  |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeng, M.; Nobel, A.; Jha, V.; Levy, D.; Kneidel, D.; Chaudhary, M.; Islam, I.; Baumgartner, E.; Vanderhoof, E.; Facer, A.; et al. Optimizing Multidimensional Pooling for Variational Quantum Algorithms. Algorithms 2024, 17, 82. https://doi.org/10.3390/a17020082
Jeng M, Nobel A, Jha V, Levy D, Kneidel D, Chaudhary M, Islam I, Baumgartner E, Vanderhoof E, Facer A, et al. Optimizing Multidimensional Pooling for Variational Quantum Algorithms. Algorithms. 2024; 17(2):82. https://doi.org/10.3390/a17020082
Chicago/Turabian StyleJeng, Mingyoung, Alvir Nobel, Vinayak Jha, David Levy, Dylan Kneidel, Manu Chaudhary, Ishraq Islam, Evan Baumgartner, Eade Vanderhoof, Audrey Facer, and et al. 2024. "Optimizing Multidimensional Pooling for Variational Quantum Algorithms" Algorithms 17, no. 2: 82. https://doi.org/10.3390/a17020082
APA StyleJeng, M., Nobel, A., Jha, V., Levy, D., Kneidel, D., Chaudhary, M., Islam, I., Baumgartner, E., Vanderhoof, E., Facer, A., Singh, M., Arshad, A., & El-Araby, E. (2024). Optimizing Multidimensional Pooling for Variational Quantum Algorithms. Algorithms, 17(2), 82. https://doi.org/10.3390/a17020082








