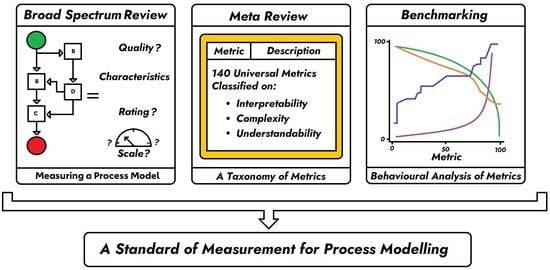
An Experimental Outlook on Quality Metrics for Process Modelling: A Systematic Review and Meta Analysis

Abstract

The ideology behind process modelling is to visualise lengthy event logs into simple representations interpretable to the end user. Classifying process models as simple or complex is based on criteria that evaluate attributes of models and quantify them on a scale. These metrics measure various characteristics of process models and describe their qualities. Over the years, vast amounts of metrics have been proposed in the community, making it difficult to find and select the appropriate ones for implementation. This paper presents a state-of-the-art meta-review that lists and summarises all the evaluation metrics proposed to date. We have studied the behaviour of the four most widely used metrics in process mining with an experiment. Further, we have used seven healthcare domain datasets of varying natures to analyse the behaviour of these metrics under different threshold conditions. Our work aims to propose and demonstrate the capabilities to use our selected metrics as a standard of measurement for the process mining domain.

1. Introduction

Process mining has advanced rapidly within the past two decades and is presently shaping itself into a foundational domain. Since the coining of the term “Process Mining”, the amount of research and evolution that has taken place within is vast. These spheres of expansion are majorly classifiable into topics such as algorithmic approaches, visualisations, modularity, optimisation, data interpretation and analysis. Together, the progress from these spheres gave rise to the commercialisation and expansion of the domain from a theoretical concept into a practical reality. Experimental articles on data discovery algorithms and mining concepts have transformed into software toolkits and marketable products used in the field by organizations to track and improve their processes. The years leading up to 2010 depict that most research efforts were focused on the conceptual part of analysis aimed at creating new mining algorithms, improving visualisations and other core elements utilised in process modelling [1,2,3,4,5,6]. Further on, the focus shifted towards enhancement and evaluation of generated models [7,8,9,10]. This transition was in sync with the presence of better technology. Upon achieving progress, process modelling was employed in many fields at various levels of application (i.e. from basic procedural descriptions to supply chain routines). This brought along the issue of complexity. Excess or lack of information in the model proved to be a failure of process mining as a technique. The only remaining solutions is to analyse the model and determine if it is fit for the end user. Hence, by evaluating and measuring a process model, insight into the level of interpretability and the technical viability of the data is revealed. The cornerstone is being able “To make sure we achieve the objective” (i.e. in principle, a better understanding of our data).

In the pipeline of process modelling, the stages are generally in the order of data collection, application of algorithms, visualisation and evaluation. Our work aims to propose a solution on the part of process model evaluation. The main motivation for our study was derived from a situation where we wanted to measure a model. To do so we had to learn the fundamentals of process model assessment and comb through multiple articles to find a matching metric for our data. Further, we had to interpret the meaning of the metric in relation to a scale and continue searching until the right fit was found. This was a tedious and time-consuming task.

When trying to find suitable measures, we encountered a never-ending supply of metrics described within individual works and a few summarised in review works. We did not find a clear solution such as an ISO standard that recommends the use of certain techniques or measures for the whole sector. Further, we observed that many metrics proposed by researchers in the community have both unique and universal applicability. This implies that every metric has its specific use and cannot be overlooked. However, from the perspective of universal modelling, we did not find a concise set of metrics that can be applied to all process models with universal attributes. Our work aims to address these issues by presenting a definitive solution to approach process model evaluation and metric-based assessment. Thus, our research objectives were crafted as follows:

• OBJ 1: To propose a concise solution to the vast amount of metrics in the scientific community;
• OBJ 2: To demonstrate the use of metrics aimed to showcase the evaluation of process models.

We have performed two individual literature reviews that provide insight into process model evaluation and its history. A taxonomy presents a comprehensive solution to the vast amount of metrics proposed in the community. In our work, we have focused on the technical aspect of model evaluation and have created a classification of metrics based on human-centric qualities of understandability, complexity and interpretability. Lastly, we have summarised the four most widely used metrics in the sector and have benchmarked their performance using real-world healthcare event logs. We have analysed their behaviours under various control conditions and have proposed to use them as a standard of measurement within process modelling.

Further, the paper is divided into the following sections: Section 2 consists of the background and the literature survey. Section 3 elaborates on the methodology, implementation and results of our benchmarking experiment. Section 4 consists of an open discussion of various thoughts, ideas and questions faced over the course of this work. Section 5 is the conclusion. Appendix A, Appendix B and Appendix C consists of material that can be used by the community for future research.

2. Literature

2.1. Background

As mentioned earlier in Section 1, process modelling has been flourishing since the early 2000s. Today, it has become a commercialised sector and is further developing into its own field. During this phase of transitioning into a sector, there came a stage when we needed to assess the fruition of results. This is where the evaluation of process models is primarily required. Much research has been carried out and numerous metrics have been proposed, yet there still exists an uncertainty on how to perfectly evaluate process models. The measurement of models is commonly performed using their characteristic attributes, but as the volume and variety of data grew, many secondary features were being introduced for modelling. By utilising non-universal features for assessment, newly developed metrics were restricted to the type of data that can be used for measurement. Therefore, there is a need to distinguish and classify metrics that can be used on models generated from universal event logs. In our work, we have prioritised selecting metrics and models that use universal elements for assessment and generation.

Today, we have reached a point where metric evaluation can produce a numeric value of sorts that describes the model. However, the details of this rating are left to the user to decode (i.e., the meaning of the metric itself and its relational rating of the process model on that respective metric scale). This creates a complex environment for approaching metrics. Further, the volume of metrics already proposed in the community makes it difficult to specifically choose a metric without overlooking another. Process model qualities were created to address this issue. They were used to distinguish certain properties of the model that can be interpreted by the user via metrics. In our work, we have chosen three major qualities crucially relevant to describe the technical properties and the human perception of the model.

We collectively address these issues using three crafted research questions. By answering these questions, we were able to achieve our research objectives:

• RQ1: What are the methods to evaluate a process model?;
• RQ2: How has process model evaluation progressed over the years?;
• RQ3: How do we measure the understandability, complexity and interpretability of process models using metrics?

Research questions RQ1, RQ2 and RQ3 are addressed as follows. RQ1 and RQ2 are answered using a broad spectrum study along with a meta-review. The broad review gives a ground-up perspective of model measurement and provides a simplified outlook on its evaluation and assessment. The meta-review is a state-of-the-art review of reviews. It presents a taxonomy of established metrics proposed by the community and aims to list all the viable metrics within a tabulation. RQ3 is answered in Section 2 using a diagram and via an experiment in Section 3. This answers the question of evaluating process models based on their understandability, complexity and interpretability. The experiment demonstrating the usage of evaluatory metrics on healthcare event logs is also described in Section 3. We have filtered down to four prime metrics that operate based on the fundamental principles of process modelling (i.e., using universal features). The latter objective of having uniform metrics for the process mining domain as a whole is answered using the results generated from our experiment. Our work further aims to provide “A once and for all solution” to the vast amount of metrics in the community and propose a standard of measurement for process modelling.

2.2. What Are the Methods to Evaluate a Process Model?

This research question is answered using a broad-spectrum study. It aims to give a general idea of metric definitions, conditions and criteria required to qualify as a measure.

Search and Approach: The broad spectrum study utilises a rebounding fashion of analysis. We have navigated through the area of model measurement, contrasting various information sources and aiming to obtain an overview of how to evaluate process models. The literature search for this study was relatively mainstream. Figure 1 provides an overview of the search methodology. For this review, the idea was to present wide-ranging information and not dive into specific topics. Hence, generalised search terms were selected to include wide-ranging topics of modelling and evaluation. We considered the risk of bias factor when creating the keyword search strategy and addressed this aspect by using wider terms therefore almost nullifying the tendency to tilt towards a single area.

We used Google Scholar’s advanced search options to find research works as it allows for a bounded exploration of the literature. It was set up as follows: the articles with "the exact phrase" occurring "anywhere in the article" between the dates 2010 and 2022, with the remaining fields left blank. The generation and usage of keywords were carried out in two different ways. The first approach involved using individual keywords such as “Process models”, “Business process models”, “Process mining” and “Process modelling” as singular terms in the field. The second approach employed the use of multiple terms, where the first word “Process Model” remained constant and singular words such as “Metrics”, “Evaluation”, “Quality”, “Measurement”, “Complexity”, “Interpretability”, “Quality dimensions”, “Quality metrics” were substituted in place of each other (i.e., "Process Model" "Metrics"). Similarly, a second search was conducted using the second approach with the following terms: “Process Modelling” and “Framework”, “Guidelines”, “Rules”. From the above search queries, 624 articles were identified to be within the scope of the broad spectrum review. This number of articles is massive. To solve this, we crafted generalised queries and utilised them as pillars of reference when reading the full text. Query 1: Understanding metrics for process models—the query directs focus towards studying the literature that defines metrics for process models. Query 2: Perceiving methods and approaches to evaluate process models—this query focuses on analysing works that propose and demonstrate the usage of metrics. Query 3: Scrutinising criterion to qualify as a metric—this query concentrates on works that highlight rules, conditions and criteria for metrics. The selected works were classified into five groups. We cross-referenced between these sources to obtain definitive solutions to our questions.

• Process Modelling Books: Works listed in this group consist of books written to cover prime directions and overview of the field [11,12,13,14,15,16,17];
• Existing Metric Articles: This group consists of works that present metrics and quality dimensions to the community [18,19,20,21,22,23,24,25,26];
• Frameworks: This group consists of articles that showcase the quality metric framework specifically used to address the classification of metrics and their characteristics [9,27,28];
• Guidelines: These articles consist of publications that emphasise and describe conditions required for quality dimensions to qualify as a metric [29,30,31,32,33,34];
• Evaluatory Applications: These works present exemplar applications that demonstrate the usage of metrics and quality dimensions on actual data [21,35,36,37,38,39,40,41,42].

Results of the Broad Spectrum Review:

Query 1: Understanding metrics for process models. Within process modelling, the terminology of evaluation is broad. Evaluation, metrics and quality dimension are a few terms used to showcase the variation in features of a process model. To obtain a clear understanding of the definition of a metric we looked towards the ISO org [43], which says that a metric is a quantifiable measure used to assess the performance of an object relative to a scale. In process modelling, process graphs are the main objects of measurement generated from the data. Likewise, we should aim to evaluate the model and not the event log. It was determined that any generated model has to satisfy a specific set of requirements and criteria to classify as fit-for-purpose. A model can be considered of high quality only when it is fit-for-purpose. Utilising global characteristics from the event log and the process graphs yields insight into the model’s viability for purpose [44,45,46,47]. Additionally, quality dimensions can be used to measure traits of the model. These dimensions are differentiated based on their constituting attributes from the process model and the resulting quality shown as in the CPMQF framework [48]. Query 2: Perceiving methods and approaches to evaluate a process model. The query is answered by splitting the analysis into two major categories. Syntax-based evaluation: This category involves using attributes of the process model that are directly extractable and do not require additional features for calculation (e.g., lines of code, number of nodes, number of elements, number of connections, etc.) Characteristics-based evaluation: These are defined terminologies that exhibit behaviour extracted from the process model (e.g., understandability, simplicity, modifiability, comparability, complexity etc.) Query 3: Scrutinising criterion to qualify as a metric. This query elaborates the conditions for a dimension to be termed a metric. To understand how metrics were established and accepted, we have turned towards works that certified and created criteria for researchers to propose their evaluatory metrics. It involved articles including [29,30,31,32], where there are specific conditions that a metric has to satisfy to qualify as a quality measure. The ideal information for query 3 is present in frameworks, guidelines and standards. The following are five of the most widely used guidelines for process modelling metrics:

• Guidelines for business process modelling (2000) (GoM) [49]: This is one of the first foundational guidelines and frameworks developed to create an approach to measure the qualities of process models;
• The 7PMG (2010) [30]: A revised and pinpointed version of conditions that a quality dimension or a measure should aim to fulfill in order to generate a process model of good quality;
• Pragmatic guidelines for business process modelling (2014) [29]: A detailed approach to understand the logical and model generation part of quality defintion;
• Quality assessment strategy (2017) [50]: A quality assessment strategy proposed to create evaluation criteria to assess new models;
• Process modelling guidelines (2018) [31]: This is a systematic literature review and experiment showcasing the various metrics, summarised using an internal relevance.

Other frameworks and regulations mentioned along with these works are CPMQF [48], SEQUAL [51,52], CMQF [53], GoM [49], SIQ [54], BPMQ [55] Frameworks and the ISO standard (ISO 25010:2011) [43].

Overall, from the broad spectrum study, it was found that process models are evaluated based on particular attributes. These attributes vary between the syntax features of process models and properties of the event log itself. According to the search, the ideal way to evaluate a process model is to perform calculations between the model and its respective event log. These calculations are founded upon the Basic Three features (i.e., Unique ID, Activity and Time Stamp) [56]. Further, secondary attributes can be used for extended analysis of the process model and the event log, but with customised methods of calculation.

2.3. Meta Review and Evolution

The research questions RQ2 and RQ3 are addressed within this section. The meta-review provides a collective overview of process model measurement over the years and summarises the vast amount of metrics using a taxonomy. The practical part of RQ3 is extended into an experiment in Section 3.

Early approaches for process model evaluation were solely based on software engineering techniques. However, standalone tools and software (e.g., ProFIT [57], PM4PY [58] etc), are replacing these techniques. The current generation of metrics is established on the three basic attributes. In our work, we have focused on the quality dimensions of understandability, complexity and interpretability [59,60,61,62]. We believe these qualities provide a balanced outlook on human assessment of the models. The level of easiness in perceiving a model is called understandability. The amount of detail shown via the process model from the event log is called complexity. A combination of both complexity and understandability is termed as interpretability [63,64]. When trying to evaluate models, it seemed as though there was a non-stop supply of research works aimed at process model evaluation and quality analysis. Hence, a clear representation of viable metrics for process modelling is required. Even after obtaining an understanding and overview of the various metrics present in the community, there remains a small gap. Implementation and demonstration, it follows through by providing results to the community, which will further aid researchers in shaping the evaluatory phase of process modelling. We have covered the demo of our selected metrics in Section 3. The meta-review aims to answer the follow-up questions from RQ1 and create a taxonomy of metrics. Our search approach for the meta-review was rather unique. The results from our broad spectrum review were taken forward and used to create a search procedure that is more efficient than manual searches.

The meta-review is a review of reviews. The goal is to create a taxonomy of all the metrics proposed within the field of process modelling. The taxonomy can be considered a crucial element for researchers who aim to work in conformance checking and evaluation of models, as it provides an explicit representation of the various metrics present. To create this taxonomy, literature reviews published through the years that summarise the most sought-after metrics were used as critical sources. The taxonomy is included in Appendix C. It lists all the metrics proposed between 1997 and 2023. An individual study of metrics was not performed, since it is tedious and might leave us with a bulk of information with broad relevance. Other issues such as metrics with different names but the same working principle, metrics with very distinct methods of evaluation (i.e., using non-universal features that might not be available in all datasets) and metrics with lengthy calculations or unverifiable performance were considered as possible instances that would exponentially increase the time and energy required to perform a study. Hence, review articles were selected as the source of metrics. As most review works explicitly mention the source of metrics, it makes them efficient sources to analyse. A motto was kept in mind when creating the meta-review, “i.e., to make sure that the proposed information will be useful to the community and not be an additional study weight”.

Search Procedure: The literature search for the meta-review was far-reaching and compact. As our strategy was to use review articles, we were able to minimise the depth of each search term in exchange for a wider array of topics. This, in turn, allowed us to precisely find review articles that are in the sphere of process model assessment and not singular works. Similar to the broad spectrum review, we considered the risk of bias factor when creating the keyword search strategy; this resulted in an increased number of search terms. The search terms were generated based on the spheres that deal with process model evaluation, metrics, quality, modularity and assessment. Since process mining has many neighbouring fields that share the same form of evaluation (e.g., business process modelling, workflow), we specifically selected terms to avoid any bias or overlooking any research works. The primary search was performed using Google Scholar search and the secondary search was conducted through Scopus. The search using Scopus was mainly to recover any missing articles that were not found during the primary search via Google Scholar. Similar to that of the broad spectrum review, the Google Scholar advanced search option was set up in two ways.

The first approach was set up as follows. The articles with "the exact phrase" occurring "anywhere in the article" between the dates 1997 and 2023 with the Review articles only field enabled and the remaining fields were left blank. The keywords used for this search were “Workflow learning”, “Workflow Quality”, “Workflow discovery”, “Workflow Discovery Quality”, “Workflow Discovery Evaluation”, “Business Process Modelling”, “Business Process Modelling Metrics”, “Business Process Modelling Quality”, “Business Process Model Quality”, “Business Process model quality indicators”, “Process Learning”, “Process Mining”, “Process Mining Metrics”, “Process Modelling”, “Process Model Notation”, “Process Model Quality”, “Process Model Evaluation Quality”, “Process Model Understandability”, “Process Model Complexity”, “Process Model Understandability”, “Process Modelling Metrics”, “Knowledge discovery workflow”.

The second search approach was set up as follows. The articles with "with all of the words" and "with the exact phrase" occurring "anywhere in the article" between the dates 1997 and 2023 with the review articles only field enabled and the remaining fields were left blank. The keywords were used as follows. The first part of the phrase was entered in the first field of "with all of the words" (i.e., the phrase before AND) and the second part of the phrase was entered in the field "with the exact phrase" (i.e., the phrase after AND). The search terms were (“Quality assessment” AND “Business process models”), “(Quality indicators” AND “Business process models)”, “(Process model complexity” AND “Metrics)”, “(Process learning” AND “Process mining)”, “(Process discovery” AND “Process mining)”, “(Modularity representation” AND “Business process models)”, “(Presentation medium” AND “Business process models)”, “(Experimental evaluation” AND “Business process modelling)”, “(Business process model” AND “Quality)”, “(Business process model” AND “Complexity)”.

The articles obtained from the search terms were examined by their abstract and full text to make sure they did not fall into neighbouring fields such as networking and business informatics. Figure 2 exhibits the search procedure for the meta-review. The following inclusion and exclusion criteria were used to filter works:

Inclusion criteria:

• Should be a review paper;
• Should have been published between 1997 and 2023 (when performing this study, articles published until January 2023 were considered for analysis);
• Should be relevant to process mining and business process modelling;
• Should be aimed at quality, measurement, modularity, evaluation, metrics and complexity for process models or modelling.

Exclusion criteria:

• Works that focus on topics other than evaluation (e.g., process algorithms, languages, tools or mining approaches, visualisations, oncology);
• Works that focus only on one metric or one characteristic;
• Works not in English.

Results of the Meta Review: We found 379 review articles published in the time frame between 1997 to 2023. Each work summarises various evaluation methods and metrics for process modelling. Upon filtering works based on inclusion and exclusion criteria, a total of 63 articles were obtained. After reading the full text, 36 articles were eligible for analysis and inclusion in the meta-review [65,66,67,68,69,70]. We listed 140 metrics proposed by fellow authors within our meta-review. They are categorised based on their impact on the model qualities of understandability, complexity or interpretability. Additionally, we have included new fields that would aid researchers in selecting and implementing proposed metrics. The taxonomy of metrics consists of the following fields of data (the respective acronyms are included in parentheses):

• The Name of the metric (Metric);
• The Year of proposal (Year);
• Authors of the metric (Auth);
• Working Definition (Def.);
• Status of Demonstration by the authors (Yes/No) (Demo):
  • Yes (Y)—A demonstration of the metric has been provided by the authors in their works;
  • No (N)—A demonstration of the metric has not been provided by the authors;
• Type of Metric (Type):
  • Scratch (S)—Metrics that are completely designed by the author(s);
  • Partially Derived (PD)—Metrics that borrow ideologies but have their own mechanism;
  • Derived (D)—Metrics implemented based on existing concepts and measures;
• Source to Original paper (Src).

Evaluation History: Early literature collectively describes metrics as one of the “goals of models” [71]. We have come up with a simple representation of metrics in retrospect to process mining as a whole. Figure 3 represents the viewpoint of evaluation and its branching. Level 1 consists of the main branches of the field and splits into process discovery, knowledge mining and conformance checking. Level 2 consists of topics which come under each level 1 division. These topics are subdivisions that focus on specific aspects of evaluating models. Knowledge mining consists of methods used to extract information from logs and datasets. Conformance checking encompasses approaches to analyse the mining performance while discovering the event logs and extracting information. The process discovery division deals with performing visualisations and implementation of algorithms to generate models. We believe that these subdivisions work hand-in-hand when dealing with evaluation. Level 3 is a combination of L1 and L2. It ideally performs the model quality analysis. Level 3 is classified as quality dimensions, evaluation and metrics.

The goal of evaluation is to have metrics that can measure specific qualities of a process model. Hence, we have focused on model qualities that aid in improving the human perception of the model. We believe that understandability, complexity and interpretability can be coined as crucial qualities for human perception of process models [72]. To ensure that our taxonomy remains simple and allows for easy traceability to the original works, we adapted strategies to enhance the results:

• Ensure the metrics listed were within the scope of modelling qualities: understandability, complexity and interpretability;
• Link metrics that were conceptually the same but with different authors and explicitly mention them;
• Perform a viability check of the measures (metrics listed should be ideal for universal application, i.e., should utilize the basic three);
• Scrutinise and check if the proposed metric is demonstrated by the author and can be replicated by prospective researchers;
• Mention redundant metrics where necessary;
• Include a mini description to improve readability;
• List the original source of the metric.

The work by [4] in 1997 exhibits the necessity of evaluation in business process modelling. The authors emphasise representing factual data in a simplified manner (i.e., to improve the human perception of the data). With this in mind, if a generated process model does not provide a certain level of data interpretability, then the modelling procedure may be termed a failure. Authors of [73], in 1998, coined the term direct flows graph. It is a more flexible and less accessory-oriented representation for process modelling. The use of DFG has simplified the learning curve to approach process modelling. It has also aided in minimising the gap between data modellers and the end user. Unlike Petri nets and process graphs, the DFG shows only required information such as flow, activities and other peripheral details. The logical section is hidden under a layer and need not be shown along with the final resultant. Using DFGs as a tool was scarce during the early 2000s, as it was a fresh concept still in adaptation.

The boom in technology played its part in the rapid digitisation of the world. It gave rise to enormous amounts of process data usable for analysis and experimentation. As data increases, so does the complexity of the process model. Thus, the trend started from here; to resolve the complexity of modern processes, we need a way to distinguish simple and complex models, i.e., easy vs. hard to interpret. During this time, process mining was also gaining a foothold in the markets as it helped analysts visualise and understand their processes much better than traditional methods [74,75].

Initially, measuring the complexity of a process model was performed by borrowing methods from neighbouring fields of software engineering and networking [76,77,78]. Lines of code and correctness are a few examples of metrics migrated for usage in process modelling. An increase in data generated resulted in these metrics reaching a saturation point, after which using these metrics became very tedious and cumbersome. Hence, frameworks and dimensions of measurements were proposed and developed, e.g., CPMQF [48]. Frameworks such as SEQUEL [51,52] and QME [9] (Quality Assessment framework) suggested using notations, statistics of activities, algorithm variations and many more as features to analyse the metrics of a model. From the year 2006, many works summarised the progress in the field and crafted a path to create a bridge between process mining technologies and operational business processes. The works highlighted many issues faced in the sector based on the approaches, quantifiers, analysis of results, representation and differences within. Nevertheless, the principle remained the same: ensuring process information was conveyed easily using process models [79,80,81,82].

Parallelly, the implementation of new algorithms took place with enhanced feedback. The results focused on improving the algorithms and not just the visualisations. Ref. [83] lists the most-ideal ways to judge the complexity of the model at the time. With insight into algorithms and better feedback, modelling transformed from a static to a dynamic phase. Mining and modelling were no longer only used on past data but also for simulation and designing future usage. The usage of non-universal data attributes was high during this time. These are fields of information that might not be available in datasets of various domains. This led to a shift in using the basic three as the minimal standard for any event log analysis. The 7PMG [30] proposed seven basic guidelines for process modelling. It gave a baseline platform for evaluators and fellow modellers to generate a unified procedure for model development. The years beyond 2013 saw many researchers propose metrics linked to specific process modelling qualities (e.g., activity period, exclusiveness, generalisation, flexibility, etc.).

At the same time, Wil van der Aalst and Jan Mendling published the process mining discovery and metrics books [11,84]. Wil van der Aalst explicitly explained and started the trend of using the four prominent metrics. Other authors proposed their metrics and drove efforts to review and revise older frameworks to develop concise and present-gen versions. The progressing years saw many authors start to use a handful of metrics as a scale to compare and quantify their proposed metrics. Quality metrics including recall fitness, precision, size and generalisation were widely utilised as an informal standard.

Figure 4 shows all the metrics discovered in our meta-review; they are classified based on the three quality dimensions: understandability, complexity and interpretability. This representation of metrics by the three qualities allows researchers to select metrics that majorly read and impact a certain quality of the model. These types of diagrams can be created in the community for various process modelling qualities that list the metrics impacting them.

Appendix C lists all the metrics from our meta-review in detail.

We found that the metrics can be subdivided based on their technique of calculation, as follows. Primitive: These are metrics that utilise older methods to be evaluated. They use brute force approaches and are evaluated directly without mathematical formulation or complex calculations. Calculative: Metrics under this category require performing mathematical or algorithmic calculations to be evaluated. Behavioural: These metrics are specific to the understandability quality, as they depend heavily on features of the log and require analysis of log history to be evaluated. It should be noted that some metrics are repeated within the modelling diagram and have been marked with a star (*).

One of the main motives to perform the meta-review of metrics was derived from the initial objectives: “to rate the extent to which a process model is understandable and can be interpreted without the need for simplification” or, in simple words, “to be able to judge a process model based on its understandability and complexity”. Hence, in the quest to find a suitable approach, we began searching and experimenting with various metrics already published in the community. However, the thought of selecting research articles only after a certain year and ignoring the history (i.e., evolution to that point) puts us at a loss. Hence, the meta-review was conducted to give a background analysis and summary of the various approaches and techniques of evaluation to date.

3. Methodology

This section addresses RQ3 with an experiment involving real-world datasets. Using the insight from the broad spectrum study and meta-review, we found four metrics that have an ideal balance in representing the complexity and understandability of process models. We have termed them the QUAD metrics. The mathematical adaptations of these metrics were created and implemented via a process mining environment. Using real-world datasets, we have analysed the behaviour of these metrics under various control conditions. The results provide insight into how these metrics describe the technical aspect of process models.

3.1. The QUAD Metrics

We have termed Fitness, Precision, Simplicity and Generalisation as the QUAD metrics [85]. From the results of our meta-review, we have seen vast usage of the four metrics. They have been used as primary dimensions for evaluating process models. Initial testing revealed them to have a direct impact on the modelling qualities of understandability and complexity. We performed technical analysis and derived mathematical equations for each metric specific to our modelling environment and dataset attributes.

We have considered the following notations and terms to explain and describe the formulations of the metrics. Let E be an event log with n events and M be a process model of the same event log. T is a trace of events. C is the unique cases of events. Then, the metrics are derived as follows:

• Replay Fitness: Fitness is a measure that denotes how much of the behaviour present in the event log can be reproduced by the process model. It can be elaborated as the extent to which the model can reproduce the traces recorded in the event log. We have based replay fitness of the work [86]. They have used an alignment-based approach to identify the fitness of process models. This technique aligns as many events as possible from the trace with activities in a single execution of the model. The formulation is as follows:

  $$ReplayFitness=1-\frac{|T_E\cap T_M|}{|C_E|}$$

  (1)

  where, $T_E$ is the traces from the event log, $T_M$ is the traces from the process model, $|T_E\cap T_M|$ is the number of traces, that occur in event log and process model and $C_E$ is the unique cases of events in the event log.
  In our implementation, the numerator is calculated by aligning every case ID in the event log from start to end and observing if the model can align all of them. In simpler terms, we determine if the process model can replay every single trace as in the event log. The denominator here is the total number of unique case IDs present in the event log. On calculating, we obtain a rating between 0–1, where 1 indicates the process model can fully replay every single trace present in the event log via the generated process model and vice versa. This metric is measured on a scale of 0 to 100%, where 100% indicates the complete alignment of the traces in the event log to that of the model;
• Precision: Precision is a measure used to show how clearly the process behaviour depicted in the event logs can be captured by the model without oversimplifying the model [86]. The metric aims to find out if there exist decisions that are possible in the model but never made in the log. At first glance, it may seem rather odd, as any mining tool by definition would not intentionally add additional behaviour or, rather, what is not given as input cannot be obtained as output. However, we found that it is possible to have behaviour that is not seen in the event log since there is always a possibility of not including every combination of edges and activities within the log. The measure here is inspired by the so-called escaping edges concept [87,88], where escaping edges are representations of decisions that are not made in the log but exist only in the model. In situations when there are no escaping edges, the model is precise (state = 1). It is formulated as follows:

  $$Precision=1-\frac{|T_E^{\prime }\cap T_M|}{|C_E|}$$

  (2)

  where $T_E$ represents the traces from the event log, $T_M$ represents the traces from the process model, $|T_E^{\prime }\cap T_M|$ is the number of traces that occur in exclusively in the process model and not the event log and $C_E$ is the unique cases of events in the event log.
  In our adaption, the numerator is calculated by checking if the process model has additional behaviour which does not exist in the log. Additional behaviour is analysed using individual traces from the event log. The denominator is calculated as the total number of traces in the event log. When new data observed in the process model is not seen in the event log, the model is considered not precise for that respective trace. It is rated between 0 and 1, where 1 signifies the model has high precision. This metric is measured on a scale of 0 to 100%, where 100% indicates no existence of unseen behaviour in the model, as per the log. There is also a contradiction with calculating precision that we have addressed in the discussions in Section 4. Another approach for precision is seen in [89];
• Generalisation: Generalisation is a measure of the level of abstraction in a process model. It deals with overly precise models and tries to make sure over-abstraction is not performed. It estimates how well the process model describes an unknown system and not only the existing activities. If all parts of the process model are frequently used, then the process model is likely to be generic, i.e., generalisation is high. If parts of the model are infrequently visited then the generalisation is low. The authors [86] have based generalisation off replay fitness. They use the data obtained from fitness as a leading edge towards generalisation. The authors explain that, if a node is visited more often, then it is certain that the behaviour is more frequent and, hence, more generalised. However, if some parts of the process model are less frequently visited, then the generalisation is bad. Our adaption is based on the same concept. The formulation is as follows:

  $$Generalisation=1-\frac{{\Sigma }_{a\in M_A}\sqrt{Ex{\left(a\right)}^{-1}}}{|M_A|}$$

  (3)

  where a denotes activities, $M_A$ is the activities present in the model and $Ex\left(a\right)$ is the number of executions of each activity referred.
  In our version of generalisation, the numerator is calculated by determining the number of times an activity in the model has been executed. The root inverse of the value is generated and a cumulative sum of all individual unique events is calculated. This metric is measured on a scale of 0 to 100%, where 100% indicates a generalised model in which all parts are used equally;
• Simplicity: Simplicity is a measure that describes how easily a model can be perceived by a human subject. It can parallelly be termed model complexity. Simplicity is measured by comparing the size of the model with the number of activities in the log. Using the information from the model itself, simplicity is defined on the following principle: if each activity is represented exactly once in the process graph, then that graph is considered to be as simple as possible [86]. Therefore, simplicity is calculated as follows:

  $$Simplicity=\frac{|M_D|+|E_A-MA|}{|M_A|+|E_A|}$$

  (4)

  where $M_D$ is the duplicate activities present in the model, $E_A$ is the unique activities present in the event log, $M_A$ is the unique activities present in the process model and $E_A-M_A$ is the number of missing events in the model w.r.t to the log.
  The numerator is calculated as the sum of the count of duplicate activities present in the model and the count of missing activities in the model when compared to the event log. The denominator is calculated as the sum of unique activities present in the model and the unique activities present in the event log. This metric is also measured on a scale of 0 to 100%, where 100% indicates a complex model with many events and a lower value represents a simpler model.

3.2. Experimentation

To demonstrate the use of the QUAD metrics, we used a combination of python3 and ProFIT. ProFIT is a process mining tool that works based on the fuzzy heuristic miner algorithm and generates process models specifically in the direct flows graph format. The tool works similarly to other famous process mining software (PM4PY and ProM). Initially, we started the implementation of these metrics on both ProFIT and PM4PY; however, the PM4PY package did not provide the appropriate raw information to perform a ground-level implementation of metrics. Hence, ProFIT was chosen as the main tool for implementation. Currently, our implementation of metrics is specifically designed to work with input data from ProFIT; our long game is to create an open-source library (e.g., GitHub) that can be used by fellow researchers and the community to measure process models using any modelling tool. Python3 was used to mathematically design and implement the metrics for calculation.

3.2.1. Datasets Background and Information

The datasets chosen for this analysis and experimental study of metrics were specific to the medical sphere. The selection criteria to choose the datasets are listed here:

• Should be a medical/healthcare domain dataset;
• Datasets should be open source;
• Should have sufficient events, activities and samples to generate sizeable process maps.

We searched for these datasets using Google Search and Kaggle datasets. Seven datasets fit our criteria and application. Their statistics are summarised in

Table 1. Statistics of selected healthcare datasets.

#	Dataset Name	Number of Entries	Number of Unique Traces	Average Trace length	Max Trace Size	Min Trace Size	Number of Unique Events
1	Remote Patient Monitoring Data	35,358	272	130	673	3	17
2	Real-Life Event logs	150,291	1143	131	1814	1	615
3	Hospital Billing Event Log	89,088	18,278	5	217	1	18
4	Nurse Work Flow Event log	13,644	187	73	440	1	228
5	Data Driven Process Discovery—Artificial Event log	99,589	11,112	9	11	2	8
6	Central Venous Catheter Process	697	20	35	59	26	29
7	Sepsis Treatment Careflow Dataset	15,214	26	586	8111	1	16

.

• Remote Patient Monitoring Data—Almazov Institute: This dataset was provided by PMT online (an online patient healthcare monitoring system). It contains events triggered by in-home blood pressure measurements made by patients suffering from arterial hypertension [90];
• Hospital Records of Dutch Hospital—Eindhoven University: This dataset was published by Eindhoven University of Technology. The dataset consists of real-life event logs of a Dutch academic hospital [91];
• Hospital Billing Log—Eindhoven University: This event log was sourced from Eindhoven University of Technology. The event log was obtained from the financial modules of the ERP system of a regional hospital [92];
• Nurse Work Flow—Almazov Institute: This event log was provided by Almazov National Research centre. It consists of data from the hospital access control system concerning staff activities, laboratory procedures, branch communications. etc. [93];
• Data Driven Process Discovery (An Artificial Event log)—Eindhoven University: This dataset was generated by Eindhoven University. It is a synthetic event log that simulates an artificial process log of a hospital (we have used the dataset with 0% noise) [94];
• Central Venous Catheter Process—Conformance checking challenge 2019: This is a dataset produced by Eindhoven University. It is also the dataset used for a Conformance checking challenge in 2019. The dataset describes the procedure to perform central venous catheter with ultrasound [95];
• Sepsis Treatment Pathway Dataset—Eindhoven University: This dataset was sourced from Eindhoven University. It is a real-life event log consisting of events of sepsis cases from a hospital and its treatment [96].

Upon acquiring these datasets, we explored the data using Python3 and the PM4PY and ProFIT toolkits. The discovery of data was performed in two stages:

• Stage 1: This stage involved sparsely overseeing the various attributes of the process model and filtering fields that may not be useful to our application (e.g., Dataset 2 had 128 fields of information, such as “special code”, “diagnosis index”, etc.). These additional fields were excluded and the basic three were retained in all datasets;
• Stage 2: In this stage, process models were visualised using Python3 and ProFIT. The Activity field in all the datasets was cleaned and made uniform with respect to all event logs. The filtering and cleaning were performed using a self-built Python script which removed all unnecessary elements in the event data (e.g., ‘.’, ‘-’, ‘_’, etc.).

The two-stage filtered data were then used for all further experiments.

3.2.2. Setup

ProFIT produces a direct flows graph to visualise the process model. Direct flows graphs are a robust method that facilitate the requirements of experts and novice users. The miner in ProFIT has two control parameters to change the amount of information depicted in the process model: Activity rate and Path rate. The activity rate controls the number of events (activities) shown, based on their total frequency of occurrence in the event log. The path rate controls the number of pathways (edges) connecting relative activities in the event log. Similar to the activity rate, it is controlled based on the total frequency of usage. Both rates can be varied on a scale of (0–100). In our experiment, the control parameters were varied over two regimes. These specific variations generated process models that produced a uniform pattern for analysis and generation of model ratings. The parameters were varied in the following format:

Regime 1 (R1): 

The Activity rate (AR) is varied in steps of 1 between [0 and 100] (S1) and the Path rate (PR) is varied in stages of [5], [20], [40], [60], [80], [100] (S2). (R1) can be observed in Figure 5;

Regime 2 (R2): 

The Path Rate (PR) is varied in steps of 1 between [0 and 100] (S1) and the Activity rate (AR) is varied in stages of [5], [20], [40], [60], [80], [100] (S2). (R2) can be observed in Figure 5.

3.2.3. Metric Calculation

Each metric was individually programmed in Python3. The metric algorithms utilise information extracted from the generated process model and respective event log. In ProFIT, the process models are rendered using graphviz. A netgraph with text-based information is parsed from ProFIT to the graphviz renderer in order to visualise the process model. We used the net graph data as model interpretation for our algorithms. The source event log remained the same for both the miner and the metric algorithms. Each metric algorithm is split into phases which perform specific calculations and produce a numeric measure at the end.

• Calculation of Fitness: Fitness is calculated according to Formula (1). The full flow of fitness calculation can be seen in Figure A1:
  • Phase 1: Input of event log, activity rate and path rate;
  • Phase 2: The event log is mined and the process model is generated. (The miner function performs filtering and cleaning of the netgraph for metric calculation);
  • Phase 3: Generation of a one-dimensional dictionary containing the source and destination of all activities in the model;
  • Phase 4: Generation of individual traces for each caseID and verification of replay via the process model. E.g., a trace is chosen from the event log and is traversed per caseID throughout the generated process model. If the trace is completely retractable from start to end, then the respective caseID is deemed fit (1), else it is deemed not fit (0);
  • Phase 5: Once all the caseIDs have been checked for replayability, the final formula of fitness is applied where the total number of traces that can be aligned with the model and log is contrasted against the total number of unique caseIDs in the log;
  • Phase 6: Generation of the percentage of fitness and output of final fitness.

For every iteration in path rate and activity rate, the algorithm is executed from phases 1 to 6. In each cycle, all caseIDs are verified for their respective fitness.

2.

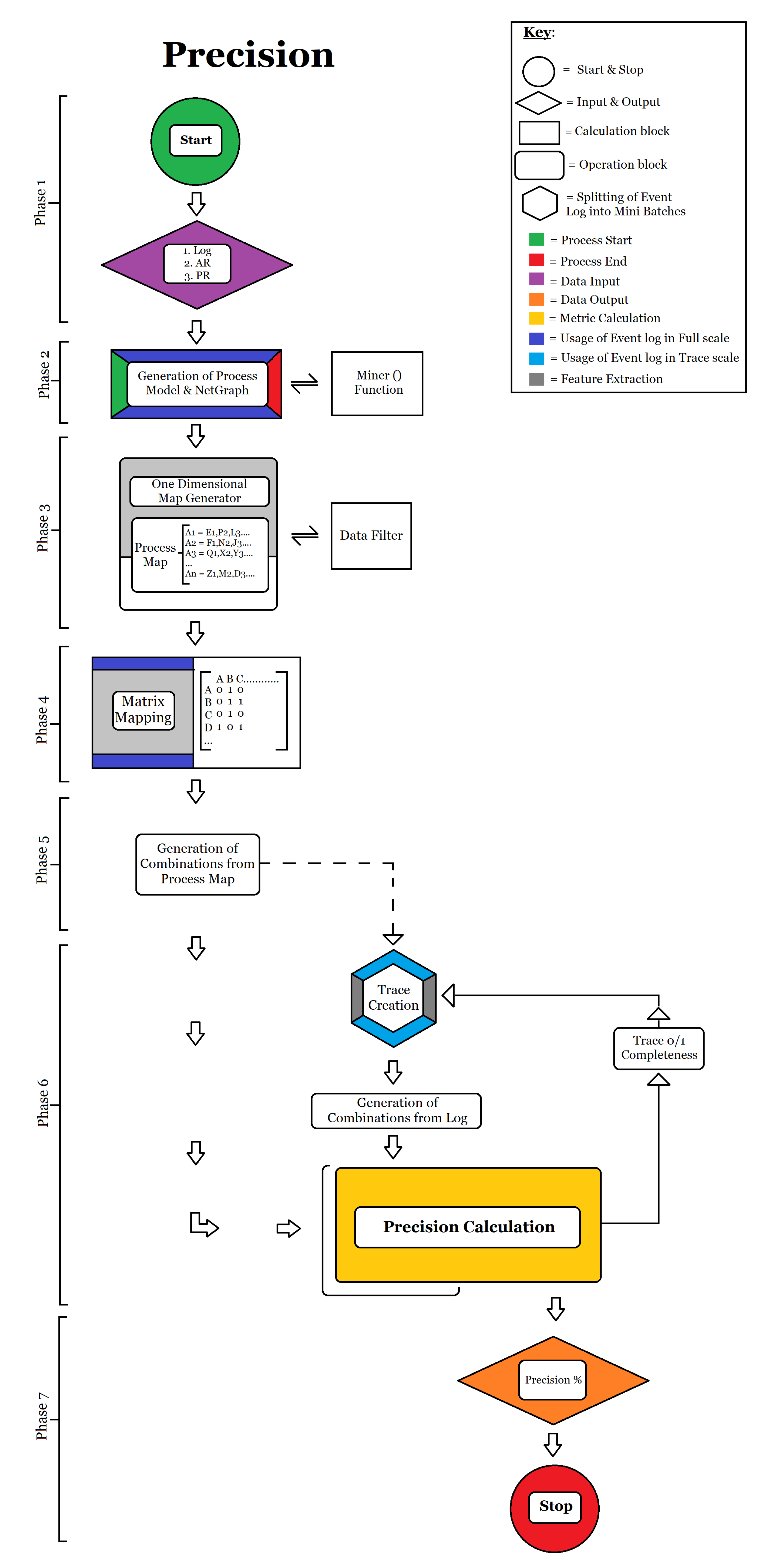
Calculation of Precision: The precision of a model is by far the most complicated metric to be calculated, as there is a lot of ambiguity to deal with. The full flow of precision calculation can be seen in Figure A2. It is generated as follows:

• Phase 1: Input of event log, activity rate and path rate;
• Phase 2: The event log is mined and the process model is generated. (The miner function performs filtering and cleaning of the netgraph for metric calculation);
• Phase 3: Generation of a one-dimensional dictionary containing the source and destination of all activities in the model;
• Phase 4: Conversion of the one-dimensional matrix into a path matrix which uses 0s and 1s to indicate the existence of “Path" and “No Path" between all activities in the model. The matrix is used to generate all possible combinations from the model to verify existing and imaginary paths in the process model;
• Phase 5: Generation of all possible combinations of traces in the process model. A permutation algorithm generates them in sets of two activities (AB, BC, AC, AA, BB, CC, etc.). Duplicates and redundancies are filtered before proceeding to phase 6;
• Phase 6: The trace creator, generates all possible combinations of traces from the event log in pairs of two (AB, BC, AC, AA, BB, CC, etc.). Duplicates and redundancies are filtered. The generated results are used to check combinations that occur only in the process model and not in the log. This value is evaluated against the total number of traces in the event log. The raw precision value of the model is generated using Formula (2). As in Fitness, for every iteration of path rate and activity rate, the algorithm is executed from phase 1 to 6. The precision is likewise calculated at every iteration;
• Phase 7: Generation of the percentage of precision and output of final model precision.

In phase 5, we faced an issue with the concept of precision itself, i.e., “how many repetitions of an event can be considered for evaluation from the process model e.g., AA, AA, AA?”. We have discussed this in Section 4. In our calculation of precision, we have limited the repetitions to one (i.e., a combination can only occur once in the model).

• Calculation of Generalisation: Generalisation is calculated according to Formula (3). The full flow of generalisation calculation can be seen in Figure A3. It is calculated as follows:
  • Phase 1: Input of event log, activity rate and path rate;
  • Phase 2: Data extraction of all activities in the event log and all activities in the process model.;
  • Phase 3: Information from phase 2 is used to calculate the number of executions of each event in the process model and the total number of events present in the process map. These values are then used in Formula (3) to calculate the raw generalisation;
  • Phase 4: Generation of the percentage of generalisation and output of final model generalisation.

The generalisation is calculated for every iteration of path and activity rate and the algorithm is executed from phase 1 to 4. Individual trace extraction is not required in generalisation.

• Calculation of Simplicity: The simplicity of a model is calculated as per Fromula (4). The full flow of simplicity calculation can be seen in Figure A4. It is calculated as follows:
  • Phase 1: Input of event log, activity rate and path rate;
  • Phase 2: Data extraction of all activities in the event log and all activities in the process model;
  • Phase 3: Information generated from phase 2 is used to calculate The sum of all duplicate and missing activities. It is evaluated against the sum of all events in the process model and the event log;
  • Phase 4: The percentage of simplicity is generated for the model.

The simplicity is calculated for every iteration in activity and path rate by repeating phases 1 to 4. Similar to generalisation, individual trace extraction is not required.

3.3. Results

To understand the behaviour of metrics on the datasets, we plotted the performance of each metric in both regimes. The performance graph depicts the changes in quality ratings against one control element (either activity or path rate). We have analysed each metric individually and contrasted them against each other as groups. Every metric has two performance graphs showcasing either regime individually for all seven datasets. Within the performance graphs, each sample (S) is represented using abbreviations S1–S7.

“Fitness is the amount of behaviour present in the event log that can be reproduced by the model”. Figure 6 and Figure 7 show the fitness in R1 and R2, respectively. At a glance, there seems to be more than one behaviour of fitness in R1. However, by observing individually, the fitness for all datasets increases gradually or stays steady. Fitness in S1, S2 and S3 differ in steps of varying sizes. These steps indicate the addition of an event into the process model. Adding new events increases the number of paths within the model. This allows for an increased number of replayable traces. Therefore, the overall fitness of the model increases with the addition of new events. Figure A5 and Figure A6 show an example of S1 in R1 @ PR 80. The number of paths is seen to be increasing as the number of activities increases from 9 to 12. At path rates less than 100, we can observe that the fitness does not reach 100% in any dataset. This is because there is always a certain number of paths hidden due to their low frequency of occurrence; they are only viewable at 100% control rates. Hence, the fitness does not reach 100%, as all traces cannot be replayed by the process model. In S4, S5, S6 and S7, the fitness remains constant for certain periods of activity rates as no new paths are being added to the model; therefore, there is no increase in the number of repayable traces.

In R2, we see similar behaviour as in R1, except the increasing nature of fitness is faster and more gradual. The number of paths seems to have more influence in replaying the traces when activities remain constant.

A measure of the amount of behaviour only possible in the model and not in the event log is called Precision. Figure 8 and Figure 9 show the behaviour of precision in R1 and R2, respectively.

In general, the precision for all the datasets is decreasing in R1. In Figure 8, activity rate gradually impacts the precision of the model. As the path rate increases, the precision reduces. All the samples follow consistent behaviour of gradual decrease in precision with varying step sizes. The precision reaches the lowest value when both path rate and activity rate are at 100%. This is because, despite showing all available traces and events, there are still many possible combinations that were not shown in the log but are theoretically possible in the model. The slow change in precision is seen in path rates of smaller magnitude; for path rates with higher magnitude, the precision reduces faster since the number of possible combinations increases exponentially. Similar to R1, the precision in R2, shown in Figure 9, reduces as it approaches 100% of activity rate and path rate. The rate of precision reduction in R2 is lesser than in R1, as the number of activities does not have a major impact on creating paths for new combinations.

Generalisation is a measure of the level of abstraction that takes place in a process model. A model with uniform usage across all parts has good generalisation, while a model with infrequent usage across some parts has bad generalisation. Figure 10 and Figure 11 show the behaviour of generalisation in R1 and R2.

The behaviour of generalisation across all datasets is similar in R1. The generalisation rating is constant for majority of the time, which indicates all parts of the model are being used consistently. When reaching 100% activity rate, there is a sudden drop observed in S2 and S3, while S1 and S4 have a gradual decrease in their generalisation. S5, S6 and S7 are mostly constant throughout, with minor fluctuations nearing 100% activity rate. The variation in generalisation indicates the addition of an event into the model. In S1 and S4, the events being added after 50% activity rate are less frequently used; hence, all parts of the model are not equally used, thereby reducing the overall generalisation of the model. In S2 and S3, the huge dip in generalisation is due to the appearance of sparsely occurring events added at 100% activity rate. These events cause the process model to be less generic, resulting in low overall generalisation rating. In S5 and S6, the frequency of events have very similar thresholds. This causes most of the events to be shown within very small intervals of the activity rate. Hence, the number of activities remains constant throughout. This also means that all the activities are equally utilised in the event log itself, thus making the process model generic.

The activity rate controls the number of activities shown in the process model; therefore, an increase in activities impacts the generalisation based on the frequency of occurrence of the events. When frequent events are shown, the generalisation is high, since the events are used consistently throughout. When infrequent events are added, the generalisation is low, since certain parts of the model are not always used. This can be observed in Figure A7 and Figure A8, where the number of infrequent activities correlates to the reduction in generalisation. The red circles indicate the new events that were added at each iteration of activity rate in R1. In our adaptation of this metric, the path rate does not have an impact on the generalisation in R1, since we account only for the activities and not the edges. By adding edges for the calculation, the results might not be conclusive, as the concept of generalisation is designed to measure the events in the model that is most often used. The addition and removal of paths will not have a direct effect directly the threshold of activities is maximum.

The behaviour of generalisation in R2 is straightforward, as observable in Figure 11.

The generalisation stays constant throughout the increase in path rate because the number of activities is fixed in R2. E.g., at activity rate = 5, only 5% of the most frequent activities are shown. Thereby, the model will have a fixed number of events throughout the variation in path rate in R2. In S1, at activity rates 5 to 80, the generalisation is almost maximum. This is due to the total number of activities being constant throughout the analysis. All the events are used in the model equally throughout R2. At AR = 100, the generalisation decreases, due to the addition of all paths present in the event log. These paths are not utilised as much as the major ones; hence, the model is less generic than before. Figure A9 and Figure A10 showcases this behaviour. Similarly, in datasets 2–7, each stage of activity holds the total amount of events constant. Therefore, the generalisation in R2 has no impact on the change in path rate and only changes when the activity rate is varied by its stages.

Simplicity is a measure to understand how easily the model can be perceived by a human subject.Figure 12 and Figure 13 show the behaviour of simplicity in R1 and R2. The behaviour of simplicity is equated to the complexity or difficulty in understanding the model. The greater amount of events present in the model, the more difficult it is to understand for a human subject. In this adaptation of Simplicity, the number of interconnections was not involved in calculating the metric. Hence, in R2, despite the change in path rate producing a change in the model, the simplicity remains at the same level, (i.e., due to the mathematical formulation not accounting for the paths).

In R1, the behaviours of the datasets have an increasing trend with gradual steps and constant behaviour. Samples S1, S2, S3, S4, S6 and S7 have a step-wise increasing behaviour for simplicity. These steps are instances when new events are added to the process model. Thus, increasing the number of activities and edges impacts the complexity of the process model. The Figure A11 and Figure A12 show an example of S7 in R1. The increase in activity rates at path rate 100 correlates to the increase in complexity, as in Figure 12 (i.e., the rapid change in complexity is seen only at the end process models, visible in Figure A12). S2 and S3 have a smoother curve, which is due to the presence of many activities with varied thresholds.

S5, as seen in generalisation, has many activities with similar frequency counts, thereby passing the threshold at the same time. This results in many of the activities being shown most of the time and no addition of new events except in the extremes. Figure A13 shows an example of when the model stays constant throughout, from activity rate 5 to 95% at path rate 100%, after which there is a change in the model and it continues to remain constant.

Simplicity in R2 is similar to the behaviour of generalisation in R2. Its behaviour is shown in Figure 13. In all the datasets, the number of activities remains constant throughout the cycle of path rates from 0 to 100. With the number of activities remaining constant throughout, the number of paths is the only feature that can be increased. However, since the paths can only be drawn for existing activities on the process model and it not being included in the calculation, all the models have constant activities but with varying levels of interconnections. Hence, this version of the simplicity formulation produces a constant behaviour in R2, yet, if a formulation is created to measure the paths, it would take into account the detail being produced from the interconnections. The behaviour can be seen in Figure A13; dataset 5 is in R2 and the simplicity remains the same throughout.

Further, we have included full-scale process graphs for select datasets in R1 and R2. Due to the limitation of size and detail, only four datasets were compact enough to be reproduced on sheets. Figure A14, Figure A15, Figure A16, Figure A17, Figure A18, Figure A19, Figure A20 and Figure A21 show full-scale process models for datasets 1, 3, 5 and 7, respectively. The process maps can be correlated with the behaviour of the QUAD metrics in Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 in both R1 and R2. When observed horizontally (from left to right) the process maps are in R1 order and when observed vertically (from top to bottom) the process maps are in R2 order.

4. Discussion

Our work provided a ton of insight into metrics and the evaluation of process models. In this section, we have listed important issues that were encountered during this work. Addressing these issues will further improve the understanding of process models.

Metrics, preferences and their application. Every person is accustomed to their preferences. Complex process models are suitable for industry professionals, as they portray information in greater detail. However, beginners would find complex models very hard to understand. Using a constant model for both audiences results in differences in detail being experienced by either party. This causes a loss of information. To answer this issue, there are several ways we have considered. The first method would be the generation of personalised models depending on the intended user’s preferences, background and subject knowledge. The possible backdrop of this method would be the aggressive collection of personal data. A more realistic approach involves creating a universal model that describes a process within a balance of complexity (i.e., a model that can be useful for both beginners and experts). Metrics and evaluation techniques can be used to determine the optimal range of information to be described via the model. The accuracy of this range can be further improved by incorporating secondary data from the process model (e.g., size of traces, avg. size, number of unique events, etc.).

Figure 14 describes the behaviour of QUAD metrics when an event log is tested in R1. This graph explains the performance of the model and, by analysis, we find the optimal range where models have a balance between all the metrics.

At activity rate 50%, it can be observed that the fitness is greater than 75%, indicating that 3/4 of the traces from the event log can be replayed by the model. The generalisation is good, signalling that most parts of the model are used equally. The precision at the same point has started to reduce but is greater than 75%, signalling that the model might have a small amount of behaviour unseen in the event log. The simplicity is low, indicating that the model is easy to interpret. From these observations, it can be concluded that the region near the 50% mark can be termed as the optimal range, since the models generated within this area during simulation have a good balance between all metrics. This result proves that the model is not aligned with any party (expert or novice). Hence, by using metrics, balanced models can be estimated and used for universal purposes. When required, individual models with weightings on specific features such as complexity, fitness, etc. can be explicitly created for usage (e.g., if all traces should be shown in the model, then the point at which fitness is 100% should be chosen).

Looping in precision. During our experiment, we encountered an issue while calculating precision. It is best explained with an example. Consider a process model with the following flow {AB, BC, CA, BA}. To calculate precision, we calculate the various possible paths between two points. To evaluate, we utilise the full trace of individual caseIDs to check for behaviour not seen in the event log. In the exemplar process model depicted in Figure 15, the model starts at A and ends at C. It has one intermediate event B.

We can notice there exists a looping construct BA and CA. The presence of loops gives rise to uncertainty, i.e., How many times should an occurrence of a loop be included for evaluating precision? For example, a trace in this event log could consist of the sequence ABABABABABC as one of its entries. If we set our looping threshold to three (i.e., any activity can repeat only three times), the precision of this example would be negative. This is because of the existence of duplicate events that are not recorded, giving an impression of too much existing behaviour. This can also be seen in our experimentation of precision in R1. Some samples cross the 0% mark and start generating negative precision values. This is due to the same issue [97,98,99].

Specific changes occurring due to variations in the event log during process map creation. This is an example of the inclusion and exclusion of events causing changes in the metrics recorded. In our experiment, we faced issues with our datasets when using “START” and “STOP” events within our models (i.e., the trace begins with an event “START” and ends with “STOP”). Some of our datasets did not explicitly have this event within them, while a few did. We decided to remove the START and STOP events and then evaluate our metrics. Before taking this decision, we analysed the possible issues that may arise by including and excluding these events.

By excluding START and STOP

• The traces are uniform for universal analysis;
• Traces begin and end with activities from the log, resulting in directly analyzable pure information;
• By excluding START and STOP, instances of measurement are scaled exactly to their logs and not the collective size.

By including START and STOP

• In datasets without the keywords, traces have to be explicitly extracted and modified, thereby increasing pre-processing time;
• When there is more than one event that leads to a STOP, there is an imbalance in precision and generalisation, since they would be additional events that individually (tracewise) lead to the end but collectively result in a mismatch [100,101,102,103].

Why choose understandability and complexity? From our study, we find that the main motive and objective of process modelling is to present event log data to humans in a simple form. The quality of complexity covers many terminologies that give the idea of "not difficult". Understandability gives the idea of “easy to understand”. These two qualities appreciate each other and provide a certain platform to clearly state whether a model is simple or complex without forgetting about metric constructs [104].

Emphasis on using pre-processed data for analysis of events: This is a crucial issue. As mentioned earlier in Section 2, the basic three are vital for process mining and modelling. However, the task data should undergo careful pre-processing, as this can cause issues when evaluating metrics. In our experiment, we faced an issue when there was the usage of English and Cyrillic alphabets together. Our pre-processing was designed for filtering and cleaning English alphabets. However, we overlooked the Cyrillic alphabet which led to more events being present than in the event log, resulting in process models with an increased number of activities to be generated. The evaluation of models with proper per-processing was found to have an equal number of activities as in the event log, thus avoiding irregular metric ratings.

Limitations of the work: By performing this study and experiment, we found certain limitations in the technical aspect. In our work, we have focused on three human-centric qualities (understandability, interpretability and complexity). However, many more qualities can be explored and used to classify metrics (e.g., modifiability, expressiveness, compatibility, etc.). Classifying metrics based on such qualities requires an increased depth of research and narrow exploration strategies.

ProFIT process mining toolkit currently works only using the fuzzy heuristic mining algorithm and visualises data using the direct flows graph (DFG). In comparison to other mining algorithms and visualisations, there are limitations with using this technique (e.g., the Petri-nets can show more event data that is hidden in DFGs and other mining algorithms may project the data in a different perspective). Hence, there is an opportunity to explore the various mining and visualisation techniques; however, our experiment focuses only on the behaviour of the fuzzy heuristic miner and the DFG visualisation.

In our adaptation of the QUAD metrics, we noticed that Simplicity and Generalisation produce constant graphs in R2. At first, we assumed this was an error. However, the reason for this behaviour is due to the non-inclusion of interconnections (edges) from the model into the calculation of the metric (i.e., the paths connecting the model are not used in the calculation of the event log). From our experimental results, we plan to improve these metrics and produce a version that utilises all elements of the process model for evaluation.

The source code created in Python3 for cleaning the data was specifically crafted only for the selected event logs. To use new event logs with variable characters present, a universal filtering system should be created for each event log.

In our work, we have focused on using medical datasets as the prime domain to showcase the usage of QUAD metrics and their behaviour. Nevertheless, the metrics are expandable to all domains with adaptations. By using the QUAD metrics, major characteristics of medical procedures can be identified and optimised. For instance, the generalisation metric can verify the frequency of elements in the medical procedure and eradicate operations that may increase the duration of the process. Fitness can be used as a scale to visualise the whole process and analyse the complete medical procedure without the need to extract metadata of the operation. Similarly, other metrics can be used to identify individual characteristics of medical procedures that allow for the optimisation and restructuring of processes. By applying these aspects, medical procedures can be improved, therefore, benefiting the medical community and, ultimately, the end user (i.e., the patient).

In our experiment, we observed instances where the process models had bottlenecks and peculiar operations that impacted the overall interpretability of the model. For example, in dataset 5, the process models present in Figure A18 and Figure A19 show that the events “Triage" and “Register" occur in almost all the process models but, with increased activity rates, a third event “Check" tends to bottleneck all events taking place after it. This causes the medical process to be dependent on the “Check" event at every iteration and may also increase the duration of the medical procedure. An ideal solution would be to split this event into smaller sub-events that are relevant to the medical operations being performed, thereby improving the efficiency of all processes after. This change can also be viewed via the metrics where the complexity of the model will slightly increase at the expense of better interpretability, generalisation and fitness.

5. Conclusions and Future Work

Achieving a balance between complexity and interpretability is vital to fulfilling the goal of process mining. Process models can be understood by the end user only if they are fit for purpose. Hence, metrics and evaluation techniques mentioned in this work provide researchers with a guide to enter and dive into assessment techniques for process modelling. The taxonomy of metrics collectively cumulates all the viable measures proposed by fellow authors during the time frame of 1997 to 2023 and classifies them based on three human-centric process modelling qualities. We present a once-and-for-all solution to the vast amount of metrics in the community using the taxonomy. Researchers can use our work to find metrics and evaluation techniques instead of studying many articles to find the right fit. Together with the broad spectrum review, the taxonomy follows through by summarising the history of how to evaluate a process model and provides a steady learning curve for beginners in the domain. We have chosen the four most widely used metrics from the tracked literature and termed them the QUAD metrics. These metrics utilise universal attributes of a process model for evaluation and can be used to assess the vital properties of the model. The performance and behaviour of these metrics under various control conditions have been showcased using real-world healthcare event logs. The conclusions drawn from the experiment will aid researchers in the analysis and selection of metrics for future applications. Our implementations of the QUAD metrics are adaptable to datasets from all domains with reconfiguration (i.e., they are universal). Modellers can obtain significant insight into the interpretability of their models by evaluating their process graphs with these metrics. Therefore, we propose to use the QUAD metrics as a universal standard of evaluation for process models. The insight from these metrics can be used to fine-tune and craft visualisations specific to certain qualities or audiences. We believe that our experiment provides crucial information that will aid future researchers to progress in the evaluation phase of modelling.

In future studies, we aim to create open-source access to our implementation of the QUAD metrics and introduce add-ons for universally used process mining software such as PM4PY. We consider the insights from our study to be generalised input for the community and scalable to all domains. We aim to resolve the limitations of this study by including more process modelling qualities for metric analysis and implementing re-conceptualised versions of simplicity and generalisation metrics to account for both activity and path rates. We plan to create a universal filtering script that is applicable to all domain data types within process modelling.