Adding a Tail in Classes of Perfect Graphs

Abstract

Consider a graph G which belongs to a graph class $\mathcal{C}$. We are interested in connecting a node $w\notin V\left(G\right)$ to G by a single edge $uw$ where $u\in V\left(G\right)$; we call such an edge a tail. As the graph resulting from G after the addition of the tail, denoted $G+uw$, need not belong to the class $\mathcal{C}$, we want to compute the number of non-edges of G in a minimum $\mathcal{C}$-completion of $G+uw$, i.e., the minimum number of non-edges (excluding the tail $uw$) to be added to $G+uw$ so that the resulting graph belongs to $\mathcal{C}$. In this paper, we study this problem for the classes of split, quasi-threshold, threshold and $P_4$-sparse graphs and we present linear-time algorithms by exploiting the structure of split graphs and the tree representation of quasi-threshold, threshold and $P_4$-sparse graphs.

1. Introduction

Given a graph G, an edge connecting a vertex $w\notin V\left(G\right)$ to a vertex u of G is a tail added to G; let us denote the resulting graph as $G+uw$. If G belongs to a class $\mathcal{C}$ of graphs, this need not hold for the graph $G+uw$. Hence, we are interested in computing the number of non-edges of G in a minimum $\mathcal{C}$-completion of $G+uw$, i.e., the minimum number of non-edges (excluding the tail $uw$) to be added to $G+uw$ so that the resulting graph belongs to $\mathcal{C}$; such non-edges are called fill edges. The problem is trivial for several graph classes (e.g., planar, bipartite, chordal, weakly chordal, {gem}-free, {house,hole,domino}-free, perfect graphs) but is not so for many other classes. Furthermore, we note that this problem is an instance of the more general ($\mathcal{C},+k$)-MinEdgeAddition problem [1] in which we add k given non-edges in a graph belonging to a class $\mathcal{C}$ and we want to compute a minimum $\mathcal{C}$-completion of the resulting graph.

Computing a minimum completion of an arbitrary graph into a specific graph class is an important and well-studied problem with applications in areas involving graph modeling with missing edges due to lacking data, e.g., molecular biology and numerical algebra [2,3]. Unfortunately, minimum completions into many interesting graph classes, such as split graphs, chordal graphs and cographs, are NP-hard to compute [4,5,6,7,8]. This led researchers towards the computation of minimal completions [9,10,11,12,13,14,15,16], the solution of problems with restricted input [17,18,19,20,21], parameterized algorithms [22,23,24,25] and approximation algorithms [26].

A related field is that of the dynamic recognition (or on-line maintenance) problem on graphs: a series of requests for the addition or the deletion of an edge or a vertex (potentially incident on a number of edges) are submitted and each is executed only if the resulting graph remains in the same class of graphs. Several authors have studied this problem for different classes of graphs and have given algorithms supporting some or all the above operations [27,28,29,30,31].

The motivation of our work is that many classes of perfect graphs arise quite naturally in real-world applications. More specifically, split, cographs, threshold, quasi-threshold, $P_4$-sparse graphs are used in computer storage optimization, analysis of genetic structure, information hiding, synchronization of parallel processes, etc [32]. The classes of threshold and quasi-threshold graphs find applications in set-packing problems, parallel processing and resource allocation problems [33,34,35]. The importance of the study of $P_4$-sparse graphs in practical applications is due to the fact that graphs that are unlikely to have more than a few chordless paths of length 3 appear in a number of contexts [36]; applications in scheduling, clustering and computational semantics have been the driving forces behind the study of $P_4$-sparse graphs, as well as their natural generalization of cographs, which have a nice tree structure and bounded clique width, implying efficient algorithms for several problems [37,38,39,40].

In this paper, we consider the tail addition problem, a special case of the general completion problem and we show that it admits minimum completions for the classes of split, threshold, quasi-threshold and $P_4$-sparse graphs. Given the ($K,S$)-partition of a given split graph or the tree representation of a given quasi-threshold, threshold or $P_4$-sparse graph, our algorithms run in optimal $O\left(n\right)$ time where n is the number of vertices of G. These algorithms are a first step towards the solution of the ($\mathcal{C},+1$)-MinEdgeAddition problem [1] for each of these four classes $\mathcal{C}$ of graphs.

2. Theoretical Framework

We consider finite undirected graphs with no loops or multiple edges. For a graph G, we denote by $V\left(G\right)$ and $E\left(G\right)$ the vertex set and edge set of G, respectively. The subgraph of G induced by a subset S of vertices of G is denoted $G\left[S\right]$. The neighborhood $N_G\left(x\right)$ of a vertex x of the graph G is the set of all the vertices of G which are adjacent to x. The closed neighborhood of x is defined as $N_G\left[x\right]:=N_G\left(x\right)\cup \left\{x\right\}$. The degree of a vertex x in G, denoted $de{g}_G\left(x\right)$, is the number of vertices adjacent to x in G; thus, $de{g}_G\left(x\right)=\left|N_G\left(x\right)\right|$. A vertex of a graph is universal if it is adjacent to all other vertices of the graph. We extend this notion to a subset of the vertices of a graph G and we say that a vertex is universal in a set $S\subseteq V\left(G\right)$, if it is universal in the induced subgraph $G\left[S\right]$.

Finally, $2K_2$ is the disconnected graph on 4 vertices in which each vertex is incident on exactly 1 edge and $P_k$ ($C_k$ resp.) denotes the chordless path (chordless cycle resp.) on k vertices; in each $P_4$, the unique edge incident on its first or last vertex is called a wing.

3. Split Graphs

Split graphs were first studied by Földes and Hammer [41] and independently introduced by Tyshkevich and Chernyak [42]; since then, they have been the focus of many research papers. An undirected graph G is split if its vertex set $V\left(G\right)$ admits a partition $K\cup S$ such that K induces a clique and S induces an independent set [32,43]; the partition into $K,S$ can be computed in time proportional to the size of the graph [44]. It also holds that a graph is split if and only if it contains no induced $C_4$, $C_5$ or $2K_2$. As a result of the definition, the complement and every induced subgraph of a split graph is split.

Lemma 1.

Let G be a split graph with vertex partition into a clique K and an independent set S, u a vertex of G, $uw$ a tail and $Q_{K,S}$ the set of vertices in K that have no neighbors in S. Then, in a minimum split-completion of the graph $G+uw$, the number of fill edges (excluding the tail $uw$) is 0 if $u\in K$, $\left|K\right|-de{g}_G\left(u\right)$ if $u\in S$ and $Q_{K,S}=\varnothing$ and $\left|K\right|-1-de{g}_G\left(u\right)$ if $u\in S$ and $Q_{K,S}\ne \varnothing$.

Proof. 

If $u\in K$, no fill edge (in addition to $uw$) is needed, which is optimal, since $G+uw$ is a split graph with clique K and independent set $S\cup \left\{w\right\}$. Below, we consider that $u\in S$.

First, assume that $Q_{K,S}=\varnothing$. A split completion of $G+uw$ can be obtained by connecting u to all its non-neighbors in K; the resulting graph is split with clique $K\cup \left\{u\right\}$ and independent set $S\cup \left\{w\right\}$. To prove its optimality, suppose for contradiction that there existed a split completion of $G+uw$ that uses fewer than $\left|K\right|-de{g}_G\left(u\right)$ fill edges. Then, there would exist a vertex $a\in K\setminus N_G\left(u\right)$ which is not incident on any fill edge. If there existed one more vertex $b\in K\setminus (N_G\left(u\right)\cup \left\{a\right\})$ not incident on any fill edge as well, then the edges $ab$ and $uw$ would form a $2K_2$, a contradiction. Thus, all the fill edges would be incident on the vertices in $K\setminus (N_G\left(u\right)\cup \left\{a\right\})$; note that these vertices induce a clique in G. However, then, because $Q_{K,S}=\varnothing$, there exists $z\in S\cap N_G\left(a\right)$ and the edges $az$ and $uw$ would form a $2K_2$, a contradiction again.

Next assume that $u\in S$ and $Q_{K,S}\ne \varnothing$; let p be any vertex in $Q_{K,S}$. Then, the graph G is split with clique $K^{\prime }=K\setminus \left\{p\right\}$ and independent set $S^{\prime }=S\cup \left\{p\right\}$ and for each $x\in K^{\prime }$, it holds that $N_G\left(x\right)\cap S^{\prime }\ne \varnothing$, which implies that $Q_{K^{\prime },S^{\prime }}=\varnothing$. Then, from the case for $u\in S$ and $Q_{K,S}=\varnothing$, we conclude that the number of fill edges (excluding $uw$) in a minimum split-completion of $G+uw$ is $|K^{\prime }|-de{g}_G\left(u\right)=\left|K\right|-1-de{g}_G\left(u\right)$.    □

We note that the above case is a special case of the minimum completion for the vertex addition case in [28].

Lemma 1 directly implies that given a split partition of the given graph G with a maximal independent set, the minimum number of fill edges can be computed in $O\left(\right|V\left(G\right)\left|\right)$ time; otherwise, the time complexity is $O\left(\right|V\left(G\right)|+|E\left(G\right)\left|\right)$.

4. Threshold and Quasi-Threshold Graphs

Threshold Graphs. A well-known subclass of perfect graphs called threshold graphs are those whose independent vertex set subsets can be distinguished by using a single linear inequality: a graph G is threshold if there exists a threshold assignment $[\alpha ,t]$ consisting of a labeling $\alpha$ of the vertices by non-negative integers and an integer threshold t such that a set $S\subseteq V\left(G\right)$ is independent if and only if $\alpha \left(v_1\right)+\alpha \left(v_2\right)+\cdots +\alpha \left(v_p\right)\le t$ where $v_i\in S,1\le i\le p$. Chvátal and Hammer [33] first proposed threshold graphs in 1973 and proved that the threshold graphs are precisely the graphs that contain no induced $C_4$, $P_4$ or $2K_2$.

Nikolopoulos [45] proved that every threshold graph admits a unique rooted tree representation as shown in Figure 1(left): each tree node stores a vertex set $V_{i,j}$ (these sets partition the vertex set of the graph) with each $V_{i,1}$ inducing a clique and each of the remaining sets containing a single vertex (note that the tree nodes that store these singleton sets have no descendants) and the vertices in the union of the sets stored in the nodes on a path from a tree node to any one of its descendants induce a clique. Thus, the vertices in $V_{k,1}$ are adjacent to all the vertices in ${\bigcup }_{i>k}{V}_{i,j}$, the vertices in ${\bigcup }_i{V}_{i,1}$ induce a clique and the vertices in ${\bigcup }_i{\bigcup }_{j\ge 2}{V}_{i,j}$ form an independent set.

Regarding the addition of a tail to a threshold graph, we show the following lemma.

Lemma 2.

Let G be a threshold graph and let the nodes of its tree representation $T_G$ store the sets $V_{i,j}$ for all $0\le i\le h$ and $1\le j\le k_i$ where $k_0=1$ and $k_i\ge 2$ for $i\ge 1$ (Figure 1(left)). Consider the addition of a tail $uw$ where $u\in V\left(G\right)$. Then, there exists a minimum threshold completion of the graph $G+uw$ which uses f fill edges (excluding the tail $uw$) where:

(i) 

If $u\in V_{p,1}$, then $f={min}_{0\le \ell \le p}\left\{\left({\sum }_{s=\ell +1}^p(k_s-1)\right)+{\sum }_{s=0}^{\ell -1}\left|V_{s,1}\right|\right\}$;

(ii) 

If $u\in V_{p,j}$ where $2\le j\le k_p$, then $f=min\{f_1,f_2\}$ where

$f_1={\sum }_{r=p}^h\left|V_{r,1}\right|+{min}_{p\le \ell \le h}\left\{\left({\sum }_{s=\ell +1}^h(k_s-1)\right)+{\sum }_{s=0}^{\ell -1}\left|V_{s,1}\right|\right\}$ and

$f_2={\sum }_{r=p}^h\left|V_{r,1}\right|+{min}_{0\le \ell \le p-1}\left\{\left({\sum }_{s=\ell +1}^h(k_s-1)\right)+{\sum }_{s=0}^{\ell -1}\left|V_{s,1}\right|\right\}-1$.

Proof. 

Let $G_{OPT}$ be a minimum threshold completion of the graph $G+uw$ whose tree representation $T_{OPT}$ has nodes storing sets $V_{i,j}^{\prime }$ where $0\le i\le h^{\prime }$, $1\le j\le k_i^{\prime }$ where $k_0^{\prime }=1$ and $k_i^{\prime }\ge 2$ for $i\ge 1$; moreover, let $K^{\prime }={\bigcup }_{s=0}^{h^{\prime }}{V}_{s,1}^{\prime }$ and $S^{\prime }={\bigcup }_{s=1}^{h^{\prime }}{\bigcup }_{t=2}^{k_s^{\prime }}{V}_{s,t}^{\prime }=(V\left(G\right)\cup \left\{w\right\})\setminus K^{\prime }$. Below, we give the properties of the structure of $T_{OPT}$.

Since $u,w$ are adjacent in $G_{OPT}$, $u,w$ cannot both belong to $S^{\prime }$. Additionally, we can assume that $u\in K^{\prime }$; if $u\in S^{\prime }$ then $w\in K^{\prime }$ which implies that $N_{G_{OPT}}\left[u\right]\subseteq K^{\prime }\subseteq N_{G_{OPT}}\left[w\right]$ and thus we can exchange u and w, obtaining a threshold completion of $G+uw$ using the same number of fill edges in which $u\in K^{\prime }$. The $u,w$ exchange can also be applied if $u\in V_{i,1}^{\prime }$ and $w\in V_{j,1}^{\prime }$ with $i>j$; thus, if $u,w\in K^{\prime }$ with $u\in V_{i,1}^{\prime }$ and $w\in V_{j,1}^{\prime }$, we can assume that $i\le j$.

In fact, it is not possible that both $u,w$ belong to $K^{\prime }$ unless $V_{h^{\prime },1}^{\prime }=\{u,w\}$: if $u,w\in V_{h^{\prime },1}^{\prime }$ and $|V_{h^{\prime },1}^{\prime }|>2$, then if we replace the treenode containing the set $V_{h^{\prime },1}^{\prime }$ by the 3-treenode subtree with $V_{h^{\prime },1}^{\prime }=\left\{u\right\}$, $V_{h^{\prime }+1,1}^{\prime }=V_{h^{\prime },1}^{\prime }\setminus \{u,w\}$ and $V_{h^{\prime }+1,2}^{\prime }=\left\{w\right\}$, we obtain a threshold completion of $G+uw$ using fewer fill edges than in $G_{OPT}$, a contradiction; if $u\in V_{i,1}^{\prime }$ where $i<h^{\prime }$, then, if $w\in V_{p,1}^{\prime }$ with $p>i$ or if $w\in V_{p,q}^{\prime }$ where $p>i+1$ and $q\ge 2$, we move w in a new set $V_{i+1,k_{i+1}^{\prime }+1}^{\prime }$ and thus obtain fewer fill edges again. Hence, $u\in V_{i,1}^{\prime }$ and either $i=h^{\prime }$ and $V_{h^{\prime },1}^{\prime }=\{u,w\}$ or $i<h^{\prime }$ and $w\in V_{i+1,j}^{\prime }$ with $j\ge 2$. We consider separately these two cases:

A.

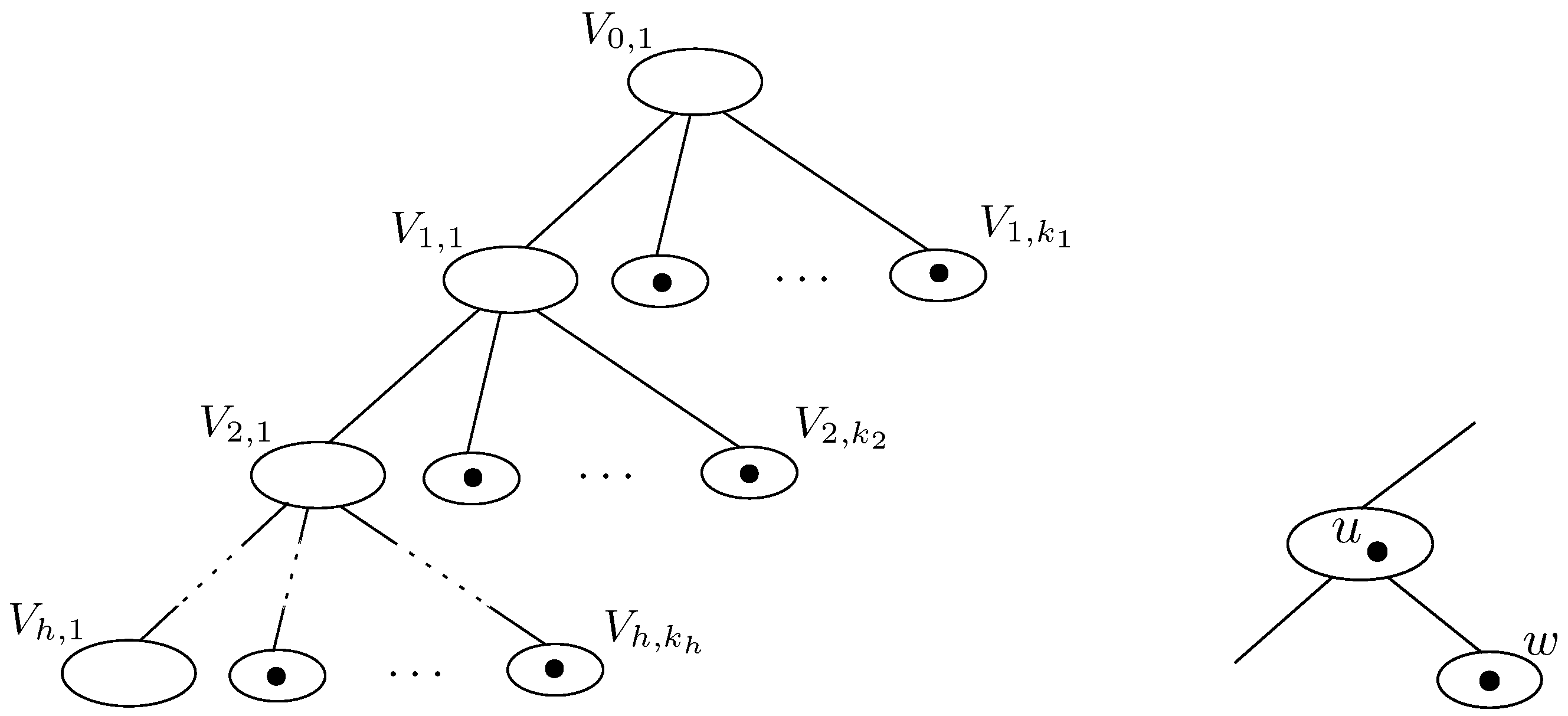
Consider that $u\in V_{i,1}^{\prime }$ with $i<h^{\prime }$ and $w\in V_{i+1,j}^{\prime }$ with $j\ge 2$. Then, $V_{i,1}^{\prime }=\left\{u\right\}$ since otherwise removing $u,w$ from $T_{OPT}$ (note that if $k_{i+1}^{\prime }=2$ then the set $V_{i,1}^{\prime }\setminus \left\{u\right\}$ is merged with the set $V_{i+1,1}^{\prime }$) and then reinserting them as in the formation of Figure 1(right) just above the node storing $V_{i,1}^{\prime }\setminus \left\{u\right\}$ would lead to the omission of the fill edges connecting w to the vertices in $V_{i,1}^{\prime }\setminus \left\{u\right\}$, in contradiction with the optimality of $G_{OPT}$.

Let $B^{\prime }={\bigcup }_{s=i+1}^{h^{\prime }}{\bigcup }_{t=1}^{k_s^{\prime }}{V}_{s,t}^{\prime }$; the set $B^{\prime }$ contains the vertices (including w) stored in all the descendants in $T_{OPT}$ of the node storing $\left\{u\right\}$. Let r be the smallest index such that there exists a vertex $z\in V_{r,1}\cap B^{\prime }$ and let $X={\bigcup }_{s=r+1}^h{\bigcup }_{t=1}^{k_s}{V}_{s,t}$; note that $V_{r,1}\cup X\subseteq N_G\left[z\right]$. Then, $V_{r,1}\cup X\subseteq B^{\prime }$, since otherwise any vertex in $D=B^{\prime }\setminus (V_{r,1}\cup X)$ would belong to ${\bigcup }_{s=0}^{i-1}{V}_{s,1}^{\prime }$ (because $D\subseteq N_G\left[z\right]$) and thus would be incident on a fill edge connecting it to w in $G_{OPT}$; this would imply that $G_{OPT}$ is not optimal compared to replacing $G_{OPT}[B^{\prime }\cup V_{r,1}\cup D\cup \left\{u\right\}]$ by $G[(B^{\prime }\setminus \left\{w\right\})\cup V_{r,1}\cup D]$ along with u being universal in $B^{\prime }\cup V_{r,1}\cup D$ and w being adjacent to all vertices in $\left\{u\right\}\cup (\left({\bigcup }_{s=0}^{i-1}{V}_{s,1}^{\prime }\right)\setminus D)$ which does not use the fill edges connecting w to the vertices in D. In the same way, we can show that if $u\in V_{p,1}$, the vertices in ${\bigcup }_{s=p+1}^h{\bigcup }_{t=1}^{k_s}{V}_{s,t}$ also belong to $B^{\prime }$.

The optimality of $G_{OPT}$ also implies that the subtree resulting from $T_{OPT}$ after having removed the descendants of the node storing $\left\{u\right\}$ is identical to the tree for $G[V\left(G\right)\setminus (B^{\prime }\cup V_{r,1}\cup D)]=G\left[\left\{u\right\}\cup \left({\bigcup }_{s=0}^{r-1}{\bigcup }_{t=1}^{k_s}{V}_{s,t}\right)\cup {\bigcup }_{t=2}^{k_r}{V}_{r,t}\right]$ with the node for $\left\{u\right\}$ placed at the leftmost node in the lowermost level. Therefore,

−

if $u\in V_{p,1}$, the tree $T_{OPT}$ results from the tree $T_G$ of G after we have removed u from $V_{p,1}$ and have inserted the Formation of Figure 1(right) just above any of the nodes storing the set $V_{s,1}$ for $s=0,\dots ,p$ (note that if $V_{p,1}=\left\{u\right\}$, then the removal of u implies that the nodes storing $V_{p+1,t}$ for $2\le t\le k_{p+1}$ are linked to the node of the formation of Figure 1(right) storing $\left\{u\right\}$ if the formation is placed just above the node storing $V_{p,1}$; otherwise, they are linked to the node storing $V_{p-1,1}$);

−

if $u\in V_{p,j}$ with $j\ge 2$, the tree $T_{OPT}$ results from $T_G$ after we have removed the node for $V_{p,j}$ and have inserted the formation of Figure 1(right) just above any of the nodes storing the set $V_{s,1}$ for $s=0,\dots ,h$ (as mentioned, if $p<h$ and $k_p=2$, the removal of u implies that the nodes storing $V_{p,1}$ and $V_{p+1,1}$ will be merged and if $p=h$ and $k_p=2$, the removal of u implies that the node storing $V_{p,1}$ will be merged with the node storing $\left\{u\right\}$ in the formation of Figure 1(right) if the formation is placed just above the node storing $V_{p,1}$ or with the node storing $V_{p-1,1}$ in any other placement of the formation).

B.

Consider that $V_{h^{\prime },1}^{\prime }=\{u,w\}$. Then, it has to be the case that in G either $u\in V_{h,1}$ or $u\in V_{p,j}$ where $j\ge 2$. First, suppose, for contradiction, that $u\in V_{p,1}$ with $p<h$; then, if we link a node storing $\left\{w\right\}$ as a child of the node storing $V_{p,1}$ in $T_G$, we obtain a threshold completion of the graph $G+uw$ with fewer fill edges, a contradiction. Next, if $u\in V_{h,1}$ then $V_{h,1}=\left\{u\right\}$; otherwise, in order to obtain $V_{h^{\prime },1}^{\prime }=\{u,w\}$ in $T_{OPT}$, we need to move all vertices in $V_{h,1}\setminus \left\{u\right\}$ into the set $V_{h-1,1}$, thus adding the fill edges connecting these vertices to $\left\{w\right\}\cup {\bigcup }_{t=2}^{k_h}{V}_{h,t}$, but if we replace the node storing $V_{h,1}$ by the 3-treenode subtree with $V_{h,1}=\left\{u\right\}$, $V_{h+1,1}=V_{h,1}\setminus \left\{u\right\}$ and $V_{h+1,2}=\left\{w\right\}$, we obtain a threshold completion of $G+uw$ without these fill edges, a contradiction.

Next, we rely on the structure of the tree $T_{OPT}$ shown above; we consider the two cases in the statement of the lemma; we have:

(i)

Consider that $u\in V_{p,1}$ in $T_G$. We consider two cases:

(a)

Assume that $p<h$ or if $p=h$ and $|V_{h,1}|\ge 2$. Then, we remove u from $V_{p,1}$ and add the formation of Figure 1(right) just above each node storing $V_{\ell ,1}$ for $0\le \ell \le p$ which results in fill edges connecting u to all vertices in ${\bigcup }_{s=\ell +1}^p{\bigcup }_{t=2}^{k_s}{V}_{s,t}$ and w to all vertices in ${\bigcup }_{s=0}^{\ell -1}{V}_{s,1}$ which yields the number of fill edges stated in the lemma taking into account that ${\sum }_{t=2}^{k_s}\left|V_{s,t}\right|=k_s-1$.

(b)

Assume that $p=h$ and $V_{h,1}=\left\{u\right\}$. Then, we try

*

adding w in $V_{h,1}$ which results in fill edges connecting w to all vertices in ${\bigcup }_{s=0}^{h-1}{V}_{s,1}$ and

*

removing u from $V_{h,1}$ (and linking the nodes for the sets $V_{h,t}$ for all $t=2,\dots ,k_h$ to the node storing $V_{h-1,1}$) and adding the formation of Figure 1(right) just above each node storing $V_{\ell ,1}$ for $0\le \ell \le h-1$ which results in the fill edges stated in Case (a) for $p=h$ and $0\le \ell \le h-1$.

Combining the two cases, we obtain the number of fill edges stated in the lemma in this case too.

(ii)

Consider that $u\in V_{p,j}$ where $2\le j\le k_p$. Then, we remove u (that is, we assume that $V_{p,j}$ becomes empty) and add the formation of Figure 1(right) just above each node storing $V_{\ell ,1}$ for $0\le \ell \le h$ which results in fill edges connecting u to all vertices in $\left({\bigcup }_{r=p}^h{V}_{r,1}\right)\cup {\bigcup }_{s=\ell +1}^h{\bigcup }_{t=2}^{k_s}{V}_{s,t}$ and w to all vertices in ${\bigcup }_{s=0}^{\ell -1}{V}_{s,1}$ which yields the number of fill edges stated in the lemma taking into account that ${\sum }_{t=2}^{k_s}\left|V_{s,t}\right|=k_s-1$ and that if $\ell <p$ we must subtract 1 for the removed u.

   □

The number of fill edges in Lemma 2 results from using the formation in Figure 1(right) above each node in the path from the node storing $V_{p,1}$ to the root of $T_G$ in Case (i) and above each node in the path from the node storing $V_{h,1}$ to the root of $T_G$ in Case (ii) taking into account the removal of the node storing the set $V_{p,j}=\left\{u\right\}$.

Lemma 2 implies that given the tree representation $T_G$ of the given threshold graph G, the minimum number of fill edges can be computed in $O\left(\right|V\left(G\right)\left|\right)$ time; otherwise, the time complexity is $O\left(\right|V\left(G\right)|+|E\left(G\right)\left|\right)$.

Quasi-threshold Graphs. A graph G is called quasi-threshold or QT-graph for short, if G contains no induced $C_4$ or $P_4$ [34,46,47,48]. The class of quasi-threshold graphs is a subclass of the class of cographs and properly contains the class of threshold graphs [32,49,50,51]. Brades et al. [52] proposed the heuristic Quasi-Threshold Mover algorithm to solve the problem of transforming a given graph into a quasi-threshold graph using a small number of edge additions and deletions, which they later used to solve the inclusion-minimal version of the problem [53].

Nikolopoulos and Papadopoulos [54] have shown, among other properties, a unique rooted tree representation of QT-graphs which is a generalization of the tree representation of threshold graphs (Figure 2): the tree nodes store disjoint vertex subsets, each inducing a clique and the vertex sets stored in the tree nodes on a path from a tree node to any of its descendants, induce a clique. It has been proven that a graph is QT-graph if and only if it admits such a tree representation [55,56]. Then, by generalizing the approach in Case (i) of Lemma 2, we can show the following lemma.

Lemma 3.

Let G be a QT-graph and $T_G$ its tree representation. Moreover, let u be a vertex of G for which we assume without loss of generality that $u\in V_{p,1}$ and that the vertex sets stored in the tree nodes on the path from the root of $T_G$ to the node storing $V_{p,1}$ are in order $V_{0,1},V_{1,1},\dots ,V_{p,1}$. Consider the addition of a tail $uw$ to G. Then, any minimum QT completion of the graph $G+uw$ uses ${min}_{0\le \ell \le p}\left\{\left({\sum }_{s=\ell +1}^p{\sum }_{t=2}^{k_s}\left|V_{s,t}\right|\right)+{\sum }_{s=0}^{\ell -1}\left|V_{s,1}\right|\right\}$ fill edges (excluding the tail $uw$).

As previously, Lemma 3 implies that given the tree representation of the given quasi-threshold graph G, the minimum number of fill edges can be computed in $O\left(\right|V\left(G\right)\left|\right)$ time; otherwise, the time complexity is $O\left(\right|V\left(G\right)|+|E\left(G\right)\left|\right)$.

5. ${\mathit{P}}_{\mathbf{4}}$-Sparse Graphs

A graph in which every set of five vertices induces at most one $P_4$ is $P_4$-sparse [57] (Figure 3 depicts the seven forbidden subgraphs for the class of $P_4$-sparse graphs). The $P_4$-sparse graphs are perfect and also perfectly orderable [57] and properly contain many graph classes, such as the cographs, the $P_4$-reducible graphs, etc (see [37,38,58]). They have received considerable attention in recent years and find applications in applied mathematics and computer science (e.g., communications, transportation, clustering, scheduling, computational semantics) in problems that deal with graphs featuring “local density” properties.

For a $P_4$-sparse graph, either the graph or its complement is disconnected with the connected components inducing $P_4$-sparse graphs or it induces a spider. A graph H is called a spider if its vertex set $V\left(H\right)$ admits a partition into sets $S,K,R$ such that:

• The set S is an independent set, the set K is a clique and $\left|S\right|=\left|K\right|\ge 2$;
• Every vertex in R is adjacent to every vertex in K and to no vertex in S;
• There exists a bijection $f:S\to K$ such that for each vertex $s\in S$ either $N_G\left(s\right)\cap K=\left\{f\left(s\right)\right\}$ or $N_G\left(s\right)\cap K=K-\left\{f\left(s\right)\right\}$; in the former case, the spider is thin, in the latter it is thick (see Figure 4).

Note that for $\left|S\right|=\left|K\right|=2$, the spider is simultaneously thin and thick. To avoid ambiguity, in the following, for thick spiders we assume that $\left|K\right|\ge 3$.

In [38], Jamison and Olariu showed that each $P_4$-sparse graph G admits a unique tree representation, up to isomorphism, called the $P_4$-sparse tree $T\left(G\right)$ of G, which is a rooted tree such that:

(i)

Each internal node of $T\left(G\right)$ has at least two children provided that $\left|V\right(G\left)\right|\ge 2$;

(ii)

The internal nodes are labeled by one of 0, 1 or 2 (0-, 1-, 2-nodes, respectively) and the parent node of each 0- or 1-node t has a different label than t;

(iii)

The leaves of the $P_4$-sparse tree are in a one-to-one correspondence with the vertices of G; if the least common ancestor of the leaves corresponding to two vertices $v_i,v_j$ of G is a 0-node (1-node, resp.) then the vertices $v_i,v_j$ are non-adjacent (adjacent, resp.) in G, whereas the vertices corresponding to the leaves of a subtree rooted at a 2-node induce a spider.

The structure of the $P_4$-sparse tree implies the following lemma.

Lemma 4.

Let G be a $P_4$-sparse graph and let $H=(S,K,R)$ be a thin spider of G. Moreover, let $s\in S$ and $k\in K$ be vertices that are adjacent in the spider.

P1. 

Every vertex of the spider is adjacent to all vertices in $N_G\left(s\right)\setminus \left\{k\right\}$.

P2. 

Every vertex $z\in K\setminus \left\{k\right\}$ is adjacent to all vertices in $N_G\left(k\right)\setminus \{s,z\}$.

Let G be a given graph to which we want to add the tail $uw$ with $u\in V\left(G\right)$. Let $t_0{t}_1\cdots t_{h}u$ be the path from the root $t_0$ of the $P_4$-sparse tree $T_G$ of G to the leaf associated with u. Moreover, let $V_i$ ($0\le i<h$) be the set of vertices associated with the leaves of the subtrees rooted at the children of $t_i$ except for $t_{i+1}$, and $V_h$ be the set of vertices associated with the leaves of the subtrees rooted at the children of $t_h$ except for the leaf associated with u (see Figure 5). The sets $V_0,V_1,\dots ,V_h$ form a partition of $V\left(G\right)\setminus \left\{u\right\}$.

We show that there always exists a minimum $P_4$-sparse completion of the graph $G+uw$ in which u and w appear together in a small number of different formations.

Lemma 5.

Let G be a $P_4$-sparse graph and $T_G$ be its $P_4$-sparse tree. Consider the addition of a tail $uw$ incident on a node u of G. Then, there exists a minimum $P_4$-sparse completion $G^{\prime }$ of the graph $G+uw$ such that for the $P_4$-sparse tree $T_{G^{\prime }}$ of $G^{\prime }$, one of the following three cases holds:

1.

The nodes $u,w$ in $T_{G^{\prime }}$ have the same parent node which is a 2-node corresponding to a thin spider $(S,K,R)$ with $u\in K$ and $w\in S$.

2.

The $P_4$-sparse tree $T_{G^{\prime }}$ results from $T_G$ by replacing the leaf for u by the 3-treenode Formation 1 shown in Figure 6(left).

3.

The $P_4$-sparse tree $T_{G^{\prime }}$ results from $T_G$ by removing the leaf for u and replacing a 1- or a 2-node t in the path from the root of $T_G$ to the leaf for u by the 5-treenode Formation 2 in Figure 6(right).

Proof. 

Let $G_{OPT}$ be a minimum $P_4$-sparse completion of the graph $G+uw$ and let $T_{OPT}$ be its $P_4$-sparse tree. We consider the following cases:

A.

The leaves associated with $u,w$ in $T_{OPT}$ do not have the same parent node: Let $T_R$ be the $P_4$-sparse tree obtained from $T_{OPT}$ by using Formation 2 just above the least common ancestor t of w and u in $T_{OPT}$ (Figure 7); let $G_R$ be the $P_4$-sparse graph corresponding to the tree $T_R$. Then, $G_R$ uses no more fill edges than $T_{OPT}$. To see this, let $t^{\prime }$ be the child of t that is an ancestor of the leaf for u (note that $t^{\prime }$ may coincide with the leaf for u). Since $u,w$ are adjacent in $G_{OPT}$, t is a 1- or a 2-node. In either case, w is adjacent to all vertices in $(Z\cup \{u\left\}\right)\setminus X$ corresponding to the leaves of the subtree of $T_{OPT}$ rooted at $t^{\prime }$ and all these edges, except for the tail $uw$, are fill edges. If t is a 1-node, then u is adjacent to all vertices in X (Figure 7) and thus $G_R$ uses no more fill edges than $G_{OPT}$. If t is a 2-node, then u is adjacent to all the vertices in the clique $K_X$ of the corresponding spider (which includes w). Moreover, because $w\in K_X$, w is adjacent to all the vertices in $K_X\setminus \left\{w\right\}$ and to at least one vertex in the independent set for a total of $|K_X|$ fill edges; these fill edges can be used to connect u to the vertices in the independent set of the spider and thus $G_R$ uses no more fill edges in this case too. Therefore, the graph $G_R$ is a minimum $P_4$-sparse completion of $G+uw$.

Recall that in the $P_4$-sparse tree $T_G$ of G, the path from the root $t_0$ to u is $t_0{t}_1\cdots t_{h}u$ and $V_i$ ($0\le i\le h$) is the set of vertices associated with the leaves of the subtrees rooted at the children of $t_i$ except for $t_{i+1}$ (where $t_{h+1}$ is the leaf associated with u); see Figure 5.

We first observe that the induced subgraph $G_R\left[Z\right]$ induced by the set of vertices Z corresponding to the leaves of the subtree of $T_R$ rooted at node t coincides with the induced subgraph $G\left[Z\right]$ (otherwise, $G_{OPT}$ would include fill edges that could be removed in contradiction to its optimality); then, let $t=t_k$. It also holds that node t in $T_R$ is a 1- or a 2-node, since node t was a 1- or a 2-node in $T_{OPT}$, as well. Let $A=V\left(G\right)\setminus (Z\cup \{u\left\}\right)$. Note that there is no set $V_j$ such that $x\in V_j\cap A$, $y\in V_j\cap Z$ and x is a neighbor of u in G; otherwise, we can move x to Z together with y; because y is in Z, all adjacencies from y to all the vertices in $V\left(G\right)\setminus (V_j\cup \left\{u\right\})$ in G are maintained and this will also hold for x and the fill edge $xw$ will be removed, a contradiction to the optimality of $G_R$. Similarly, there is no set $V_j$ such that $x\in V_j\cap A$, $y\in V_j\cap Z$ and y is a non-neighbor of u in G; otherwise, we can move y to A together with x, thus omitting the fill edge $uy$. This implies that for each $i=0,1,\dots ,h$, either $V_i\subseteq A$ or $V_i\subseteq Z$ and since $t=t_k$, $V_k\subseteq Z$.

Finally, there exists no $j>k$ such that $V_j\subseteq A$. Suppose that there existed such a $V_j$ and let j be the largest such index. Then, because $t=t_k$ is a 1- or a 2-node and $k<j$, there would exist a vertex $z\in V_k$ which would be adjacent to all vertices in $V_j$. This implies that in $T_R$, the least common ancestor of z and the vertices in $V_k$ would be a 1-node; thus, u and w would be adjacent to all vertices in $V_j$ and if we moved $V_j$ to Z then we would have fewer fill edges, a contradiction to the optimality of $G_R$. Therefore, the tree $T_R$ is as described in Case 3 of the statement of the lemma.

B.

The leaves associated with $u,w$ in $T_{OPT}$ have the same parent node p: Then, since $u,w$ are adjacent, the parent node p is either a 1-node or a 2-node.

(i)

The parent node p of $u,w$ in $T_{OPT}$ is a 1-node: Then, the leaves associated with u and w are the only children of p (Formation 1): otherwise, we can use Formation 2 as shown in Figure 8 which requires fewer fill edges. Then, w will be adjacent to all neighbors of u in $T_{OPT}$; this and the optimality of $G_{OPT}$ imply that $T_{OPT}$ results from $T_G$ by replacing the leaf for u by Formation 1.

(ii)

The parent node p of $u,w$ in $T_{OPT}$ is a 2-node: Let $H=(S,K,R)$ be the corresponding spider. If H is thick (thus $\left|K\right|\ge 3$), then no matter whether the tail $uw$ is an S-K, K-K or R-K edge, the sum of degrees of $u,w$ in H (excluding $uw$) is at least $\left|V\right(H\left)\right|-3+\left|K\right|-2$ (consider an S-K edge). However, we would have added no more fill edges if we had made u universal in $G\left[V\right(H)\setminus \{w\left\}\right]$ and then applied Formation 2 at the parent of the leaf for u (then $Z=V\left(H\right)\setminus \{u,w\}$) using $\left|V\right(H\left)\right|-2\le \left|V\right(H\left)\right|+\left|K\right|-5$ fill edges.

In the same way, we show that we would have added no more fill edges if H were a thin spider and the tail $uw$ were a K-K or K-R edge. Then, either $u\in K$ and $w\in S$ or $u\in S$ and $w\in K$; in the latter case, we exchange u and w for the same total number of fill edges and obtain $u\in K$ and $w\in S$ again.

   □

5.1. Adding a Tail to a Spider

In this section, we consider adding a tail $uw$ to a spider $H=(S_H,K_H,R_H)$ where $u\in V\left(H\right)$. In the following two lemmas, we address the cases of a thin or a thick spider H, respectively.

Lemma 6.

Consider the addition of a tail $uw$ to a thin spider $H=(S_H,K_H$, $R_H)$ where u is a vertex of H. Then, for the number f of fill edges (excluding the tail $uw$) in a minimum $P_4$-sparse completion of the graph $H+uw$, the following holds:

1.

if $u\in S_H$, $f=|K_H|-1$ if $R_H=\varnothing$ and $f=|K_H|$ otherwise;

2.

If $u\in K_H$, $f=|K_H|-1$;

3.

If $u\in R_H$, Then $f=min\left\{\right|R_H\setminus N_H\left[u\right]|,|K_H|+f^{\prime }\}$ where $f^{\prime }$ is the number of fill edges (excluding $uw$) in a minimum $P_4$-sparse completion of the graph $H\left[R_H\right]+uw$.

Proof. 

1. Let $v\in K_H$ be the neighbor of u in H. Then, we can obtain a $P_4$-sparse graph as follows: if $R_H=\varnothing$, we connect u to all vertices in $K_H\setminus \left\{v\right\}$ (we obtain a thin spider with $S=(S_H\setminus \left\{u\right\})\cup \left\{w\right\}$, $K=(K_H\setminus \left\{v\right\})\cup \left\{u\right\}$ and $R=\left\{v\right\}$; that is, the tail $uw$ is a wing of a $P_4$ of a thin spider); otherwise, we connect v to all vertices in $\left\{w\right\}\cup (S_H\setminus \left\{u\right\})$, which makes v universal in $V\left(H\right)\cup \left\{w\right\}$ and $u,w$ form a separate connected component in $G\left[V\right(G)\setminus \{v\left\}\right]$; the total number of fill edges (excluding the tail $uw$) is precisely $|K_H|-1$ if $R_H=\varnothing$ and $K_H$ otherwise.

Moreover, this is the minimum number of fill edges (excluding $uw$) needed. First, we note that for each pair $k_i,s_i$ where $k_i\in K_H\setminus \left\{v\right\}$ and $s_i\in S_H\setminus \left\{u\right\}$, the vertices $v,u,w,k_i,s_i$ define an $F_5$ or an $F_3$ depending on whether the vertices $v,w$ are adjacent or not, which implies that at least $|K_H|-1$ fill edges (excluding $uw$) are needed. Then, if there is a way of obtaining a $P_4$-sparse graph by adding fewer than the number of fill edges mentioned in Case 1 of the statement of the lemma, it has to be the case that (i) $R_H\ne \varnothing$, (ii) each pair $k_i,s_i$ where $k_i\in K_H\setminus \left\{v\right\}$ and $s_i\in S_H\setminus \left\{u\right\}$ is incident on exactly 1 fill edge and (iii) no more fill edges exist. Let $r\in R_H$ and $k\in K_H\setminus \left\{v\right\}$. Then, the vertices $v,u,w,k,r$ induce a forbidden subgraph (an $F_5$ if k is non-adjacent to both $u,w$ or an $F_6$ ($F_1$, resp.) if k becomes adjacent to u (w, resp.) by means of a fill edge); thus, at least $K_H$ fill edges are needed in this case.

2. Let $v\in S_H$ be the neighbor in H of $u\in K_H$. Then, connecting u to all vertices in $S_H\setminus \left\{v\right\}$ (which makes u universal in H) or connecting w to all vertices in $K_H\setminus \left\{u\right\}$ yields a $P_4$-sparse graph. Moreover, this is the minimum number of fill edges (excluding the tail $uw$) that need to be added. Suppose, for contrast, that we obtain a $P_4$-sparse graph after having added fewer than $|K_H|-1$ fill edges (excluding $uw$) to the thin spider H. Then, there exists a pair of adjacent vertices $s,k$ with $s\in S_H\setminus \left\{v\right\}$ and $k\in K_H\setminus \left\{u\right\}$ such that neither s nor k is incident on a fill edge. Then, the vertices $u,v,w,s,k$ induce a forbidden subgraph $F_5$ or $F_3$ if w and v are adjacent or not, respectively, a contradiction.

3. The term $R_H\setminus N_H\left[u\right]$ corresponds to making u universal in $H\left[R_H\right]$, in which case the resulting graph is $P_4$-sparse (it is a thin spider with $S=S_H\cup \left\{w\right\}$, $K=K_H\cup \left\{u\right\}$ and $R=R_H\setminus \left\{u\right\}$). The term $|K_H|+f^{\prime }$ corresponds to adding $|K_H|$ fill edges connecting w to the vertices in $K_H$ and then computing a minimum $P_4$-sparse completion of the graph $H\left[R_H\right]+uw$. Note that no minimum $P_4$-sparse completion of $H+uw$ exists with u not being universal in $R_H$ and with using fewer than $|K_H|$ fill edges incident on the vertices in $S_H\cup K_H$: if there were such a minimum $P_4$-sparse completion $H^{\prime }$ of $H+uw$, then in $H^{\prime }$, there would exist a non-neighbor $r\in R_H$ and a pair of adjacent vertices $s,k$ where $s\in S_H$ and $k\in K_H$ such that neither s nor k would be incident on a fill edge; but then, in $H^{\prime }$, the vertices $u,w,r,s,k$ induce an $F_4$ or an $F_3$ if $w,r$ have been connected by a fill edge or not, respectively, which leads to a contradiction. In turn, if $H^{\prime }$ has at least $|K_H$ fill edges incident on vertices in $S_H\cup K_H$ then $H^{\prime }[R_H\cup \left\{w\right\}]$ would be $P_4$-sparse using fewer than $f^{\prime }$ fill edges in contradiction to the minimality of $f^{\prime }$.    □

(If $u\in R_H$, the former case corresponds to making u universal in $G\left[R_H\right]$ and the latter to inserting w in $R_H$ by making it adjacent to all the vertices in $K_H$. Furthermore, note that if $u\in R_H$ and u’s parent node is the 2-node corresponding to the thin spider H, then $R_H=\left\{u\right\}$ and no fill edges are needed.)

Lemma 7.

Consider the addition of a tail $uw$ to a thick spider $H=(S_H$, $K_H$, $R_H$) where u is a vertex of H. Then, for the number f of fill edges (excluding the tail $uw$) in a minimum $P_4$-sparse completion of the graph $H+uw$, the following holds:

1.

If $u\in S_H$,

$$f=\left\{\begin{array}{cc}|K_H|-1=2\hfill & if |K_H|=3 and R_H=\varnothing \hfill \\ |K_H|=3\hfill & if |K_H|=3 and |R_H|=1\hfill \\ |K_H|+1=4\hfill & if |K_H|=3 and |R_H|\ge 2\hfill \\ |K_H|\hfill & if |K_H|\ge 4 and R_H=\varnothing \hfill \\ |K_H|+1\hfill & if |K_H|\ge 4 and |R_H|\ge 1;\hfill \end{array}\right.$$

2.

If $u\in K_H$, $f=1$;

3.

If $u\in R_H$, then $f=|K_H|+f^{\prime }$ where $f^{\prime }$ is the number of fill edges (excluding $uw$) in a minimum $P_4$-sparse completion of the graph $H\left[R_H\right]+uw$.

Proof. 

1. Let $v\in K_H$ be the non-neighbor of u in H. Let us first consider the case $|K_H|=3$. If $|R_H|\le 2$, we can obtain a $P_4$-sparse graph after having added the fill edges $vu$ and $vw$ (this implies that v becomes universal in $\left(V\right(H)\setminus \{v\left\}\right)\cup \left\{w\right\}$) and those connecting u to the vertices in $R_H$ if $R_H$ is non-empty; then the vertices in $\left(V\right(H)\setminus \{v\left\}\right)\cup \left\{w\right\}$ induce a thin spider with $K=(K_H\setminus \left\{v\right\})\cup \left\{u\right\}$, $S=(S_H\setminus \left\{u\right\})\cup \left\{w\right\}$ and $R=R_H$, for a total of $|K_H|-1+|R_H|$ fill edges (excluding the tail $uw$). If $|R_H|\ge 2$, a $P_4$-sparse graph is obtained after in addition to the tail $uw$ we add the fill edges $vu$, $vw$ (again v is universal in $\left(V\right(H)\setminus \{v\left\}\right)\cup \left\{w\right\}$) and the fill edges connecting w to the vertices in $K_H\setminus \left\{v\right\}$ (then the vertices in $\left(V\right(H)\setminus \{v\left\}\right)\cup \left\{w\right\}$ induce a thin spider with $K=K_H\setminus \left\{v\right\}$, $S=S_H\setminus \left\{u\right\}$ and $R=R_H\cup \{u,w\}$), for a total of $|K_H|+1$ fill edges (excluding $uw$).

Now, consider the case that $|K_H|\ge 4$. If $|R_H|\le 1$, we obtain a $P_4$-sparse graph after having made u universal by connecting it to the remaining vertices in $S_H$ by using $|K_H|-1$ fill edges and adding the fill edge $uv$ and those connecting u to the vertices in $R_H$ if $R_H$ is non-empty, for a total of $|K_H|+|R_H|$ fill edges (excluding $uw$). If $|R_H|\ge 1$, a $P_4$-sparse graph is obtained after having made v universal (by adding the fill edges $vu$ and $vw$) and after having connected w to all vertices in $K_H\setminus \left\{v\right\}$ (then the vertices in $\left(V\right(H)\setminus \{v\left\}\right)\cup \left\{w\right\}$ induce a thick spider with $K=K_H\setminus \left\{v\right\}$, $S=S_H\setminus \left\{u\right\}$ and $R=R_H\cup \{u,w\}$) for a total of $|K_H|+1$ fill edges (excluding $uw$).

Below we show the minimality of this solution. Recall that $v\in K_H$ is the non-neighbor of u in H. We consider each of the five cases.

(i)

$|K_H|=3$ and $R_H=\varnothing$: Suppose, for contrast, that there is a $P_4$-sparse completion of $H+uw$ with at most $|K_H|-2=1$ fill edge (excluding $uw$). If v is incident on the unique fill edge (which connects v to u or w), then the vertices in $S\cup \{v,w\}$ induce an $F_3$. Now suppose that the fill edge is not incident on v. Moreover, there exists at least one vertex $s\in S_H\setminus \left\{u\right\}$ that is not incident on the fill edge either. Then, the vertices $u,v,w,s,k$ (where $k\in K_H$ is the non-neighbor of s in H) induce an $F_5$ if $k,w$ are connected by the fill edge or an $F_2$ otherwise.

(ii)

$|K_H|=3$ and $|R_H|=1$: Let $R_H=\left\{r\right\}$. Suppose, for contrast, that there is a $P_4$-sparse completion of $H+uw$ with at most $|K_H|-1=2$ fill edges (excluding $uw$). We distinguish three cases depending on whether v is incident on 0, 1 or 2 fill edges:

•

v is not incident on a fill edge: If there exists a pair $s,k$ of non-neighbors with $s\in S_H\setminus \left\{u\right\}$ and $k\in K_H\setminus \left\{v\right\}$ such that none of $s,k$ is incident on a fill edge to u or w, the vertices $u,v,w,s,k$ induce an $F_2$. Otherwise, since the number of such pairs is 2, for each such pair $s,k$, exactly one of $s,k$ is incident on a fill edge to u or w and no other fill edges exist. If there exists a vertex $k\in K_H\setminus \left\{v\right\}$ not incident on a fill edge to w, the vertices $u,v,w,k,r$ induce an $F_5$; otherwise, each of the fill edges connects each of the vertices in $K_H\setminus \left\{v\right\}$ to w and then $u,v,w,s,k$ (for any pair $s,k$ of non-neighbors with $s\in S_H\setminus \left\{u\right\}$ and $k\in K_H\setminus \left\{v\right\}$) induce an $F_5$.

•

v is incident on 1 fill edge (to u or w): Then, there is 1 more fill edge; hence, there exist 2 vertices in the set $(S_H\setminus \left\{u\right\})\cup \left\{r\right\}$ that are not incident on a fill edge connecting them to u or w and let these vertices be $p_1,p_2$. Then, the vertices $u,v,w,p_1,p_2$ induce an $F_5$ if $p_1,p_2$ are connected by a fill edge or an $F_3$ otherwise.

•

v is incident on 2 fill edges connecting it to u and w: Then, there is no other fill edge. Then, the vertices $u,w,k,k^{\prime },r$ (where $\{k,k^{\prime }\}=K_H\setminus \left\{v\right\}$) induce an $F_6$.

(iii)

$|K_H|=3$ and $|R_H|\ge 2$: Let $r_1,r_2$ be two vertices in $R_H$. Suppose, for contrast, that there is a $P_4$-sparse completion of $H+uw$ with at most $|K_H|=3$ fill edges (excluding $uw$). Again, we distinguish three cases depending on whether v is incident on 0, 1 or 2 fill edges:

•

v is not incident on a fill edge: Consider the case that there exists a vertex $k\in K_H\setminus \left\{v\right\}$ that is not incident on a fill edge to w. Let $s\in S_H$ be the non-neighbor of k in H and $A=(S_H\setminus \{u,s\})\cup \{r_1,r_2\}$; the set A contains 3 vertices which are common neighbors of $v,k$. If at least one of these 3 vertices (say, p) is not incident on a fill edge to $u,w$, then the vertices $u,v,w,k,p$ induce an $F_5$; otherwise, all 3 of these vertices are incident on a fill edge to $u,w$ (then these are all the fill edges) and the vertices $u,v,w,s,k$ induce an $F_2$. On the other hand, if no such vertex k exists, then both vertices in $K_H\setminus \left\{v\right\}$ are incident on a fill edge to w, accounting for 2 of the 3 fill edges; then there exists a vertex $s^{\prime }\in S_H\setminus \left\{u\right\}$ which is not incident on a fill edge to w and the vertices $u,v,w,s^{\prime },k^{\prime }$ (where $k^{\prime }\in K_H$ is the non-neighbor of $s^{\prime }$) induce an $F_5$.

•

v is incident on 1 fill edge (to u or w): There are 2 more fill edges; hence, there exist 2 vertices in the set $(S_H\setminus \left\{u\right\})\cup \{r_1,r_2\}$ that are not incident on a fill edge connecting them to u or w and let these vertices be $p_1,p_2$. Then, the vertices $u,v,w,p_1,p_2$ induce an $F_5$ if $p_1,p_2$ are connected by a fill edge or an $F_3$ otherwise.

•

v is incident on 2 fill edges connecting it to u and w: Then, there is 1 more fill edge; hence, there exists a vertex $k\in K_H\setminus \left\{v\right\}$ that is not incident on the fill edge. Moreover, there exist 2 vertices in the set $(S_H\setminus \{u,s\})\cup \{r_1,r_2\}$ that are not incident on a fill edge connecting them to u or w (where $s\in S_H$ is the non-neighbor of k); let these vertices be $p_1,p_2$. Then, the vertices $u,w,k,p_1,p_2$ induce an $F_5$ if $p_1,p_2$ are adjacent or an $F_3$ otherwise.

(iv)

$|K_H|\ge 4$ and $R_H=\varnothing$: Suppose, for contrast, that there is a $P_4$-sparse completion of $H+uw$ with at most $|K_H|-1$ fill edges (excluding the tail $uw$). Again, we distinguish three cases depending on whether v is incident on 0, 1 or 2 fill edges:

•

v is not incident on a fill edge: If there exists a vertex $s\in S_H\setminus \left\{u\right\}$ not incident on a fill edge to u, w or to its non-neighbor $k\in K_H$ in H, the vertices $u,v,w,s,k$ induce an $F_5$ if $k,w$ are connected by a fill edge or an $F_2$ otherwise; if all vertices in $S_H\setminus \left\{u\right\}$ are incident on a fill edge to u, w or their non-neighbor in $K_H$, then there are no more fill edges and the vertices $u,v,w,k,k^{\prime }$ (for any $k,k^{\prime }\in K_H\setminus \left\{v\right\}$) induce an $F_6$.

•

v is incident on 1 fill edge (to u or w): Then, the remaining fill edges are at most $|K_H|-2$ in total. If there exist two vertices $s_1,s_2\in S_H\setminus \left\{u\right\}$ not incident on a fill edge to u or w, the vertices $u,v,w,s_1,s_2$ induce an $F_5$ or an $F_3$ depending on whether $s_1,s_2$ are connected by a fill edge or not. Thus, there cannot be two such vertices $s_1,s_2$; this implies that the remaining fill edges are precisely $|K_H|-2$ and they connect all but one vertex in $S_H\setminus \left\{u\right\}$ to u or w; let that vertex be s. Then, the vertices $u,v,w,s,k^{\prime }$ (where $k^{\prime }\in K_H\setminus \left\{v\right\}$ is a neighbor of s in H) induce an $F_6$ or an $F_1$ if the fill edge incident on v connects it to u or w, respectively.

•

v is incident on 2 fill edges connecting it to u and w: Then, the remaining fill edges are at most $|K_H|-3$ in total; hence, there exist two pairs of non-adjacent vertices $s_1,k_1$ and $s_2,k_2$ with $s_1,s_2\in S_H\setminus \left\{u\right\}$ and $k_1,k_2\in K_H\setminus \left\{v\right\}$ such that none of $s_1,s_2,k_1,k_2$ are incident on a fill edge to u or w. Let $A=S_H\setminus \{u,s_1,s_2\}$; the set A is the set of $|K_H|-3$ common neighbors of $k_1,k_2$ in $S_H$ other than u. If there exists a vertex $s\in A$ not incident on a fill edge to u or w, then the vertices $u,w,k_1,k_2,s$ induce an $F_6$; otherwise, the remaining fill edges are precisely $|K_H|-3$ and they connect each of the vertices in A to u or w; that is, none of the vertices in $K_H\setminus \left\{v\right\}$ are incident on a fill edge. Then, the vertices $u,w,s_1,s_2,k$ (where k is any vertex in $K_H\setminus \{v,k_1,k_2\}$) induce an $F_3$.

(v)

$|K_H|\ge 4$ and $|R_H|\ge 1$: Let $r\in R_H$. Suppose, for contrast, that there is a $P_4$-sparse completion of $H+uw$ with at most $|K_H|$ fill edge (excluding the tail $uw$). Again, w distinguishes three cases depending on whether v is incident on 0, 1 or 2 fill edges:

•

v is not incident on a fill edge: If there exists a vertex $s\in S_H\setminus \left\{u\right\}$ not incident on a fill edge to u, w or to its non-neighbor $k\in K_H$ in H, the vertices $u,v,w,s,k$ induce an $F_5$ if $k,w$ are connected by a fill edge or an $F_2$ otherwise; if all vertices in $S_H\setminus \left\{u\right\}$ are incident on a fill edge to u, w or their non-neighbor in $K_H$, which account for the $|K_H|-1$ of the $|K_H|$ fill edges, there exist vertices $k,k^{\prime }\in K_H\setminus \left\{v\right\}$ which are not incident on a fill edge and then the vertices $u,v,w,k,k^{\prime }$ induce an $F_6$.

•

v is incident on 1 fill edge (to u or w): Then, the remaining fill edges are at most $|K_H|-1$ in total. If all vertices in $K_H\setminus \left\{v\right\}$ are incident on a fill edge to w, then no more fill edges exist and the vertices $u,v,w,s_1,s_2$ (for any $s_1,s_2\in S_H\setminus \left\{u\right\}$) induce an $F_3$. Thus, there exists $k\in K_H\setminus \left\{v\right\}$ which is not incident on a fill edge to w. The number of common neighbors of $v,k$ in $S_H\cup r$ is $|K_H|-1$. If each of these vertices is incident on a fill edge to u or w, then no more fill edges exist and the vertices $u,v,w,s,k^{\prime }$ induce an $F_6$ or an $F_1$ depending on whether the fill edge incident on v connects it to u or w, respectively, where $s\in S_H$ is the non-neighbor of k and $k^{\prime }$ is any vertex in $K_H\setminus \{v,k\}$; hence, there exists a common neighbor p not incident on a fill edge to u or w and the vertices $u,v,w,k,p$ induce an $F_6$ or an $F_1$ depending on whether the fill edge incident on v connects it to u or w, respectively.

•

v is incident on 2 fill edges connecting it to u and w: Then, the remaining fill edges are at most $|K_H|-2$ in total; hence, there exists a pair of non-adjacent vertices $s,k$ (where $s\in S_H\setminus \left\{u\right\}$ and $k\in K_H\setminus \left\{v\right\}$) which are not incident on a fill edge to u or w. Let $A=(S_H\setminus \{u,s\})\cup \left\{r\right\}$; the set A is a set of $|K_H|-1$ neighbors of k other than u. Then, there exists a vertex $p_1$ in A which is not incident on a fill edge to u or w. If there exists a second vertex $p_2$ in A not incident on a fill edge to u or w, then the vertices $u,w,k,p_1,p_2$ induce an $F_5$ if $p_1,p_2$ are connected by a fill edge or an $F_3$ otherwise. If each vertex in $A\setminus \left\{p_1\right\}$ is incident on a fill edge to u or w, then the fill edges incident on these vertices account for the remaining $|K_H|-2$ fill edges and the vertices $u,w,s,k_1,k_2$ (for any vertices $k_1,k_2\in K_H\setminus \{v,k\}$) induce an $F_6$.

Therefore, if we use fewer than the stated number of fill edges, in each case, the resulting graph contains an induced forbidden subgraph, a contradiction.

2. Let $v\in S_H$ be the non-neighbor of u in H. Then, we obtain a $P_4$-sparse graph by connecting u to v; thus, u becomes universal in $V\left(H\right)\cup \left\{w\right\}$. This is the minimum number of fill edges (excluding the tail $uw$) that need to be added since for any pair of non-neighbors $s,k$ with $s\in S_H\setminus \left\{v\right\}$ and $k\in K_H\setminus \left\{u\right\}$, the vertices $u,v,w,s,k$ induce a forbidden subgraph $F_3$, a contradiction.

3. By connecting w to all vertices in $K_H$ and then computing a minimum $P_4$-sparse completion of $H[R_H\cup \left\{w\right\}]$, we obtain a $P_4$-sparse graph and the number of fill edges needed is $|K_H|+f^{\prime }$.

To prove the minimality of this number of fill edges, suppose, for contrast, that we can obtain a $P_4$-sparse graph from $H+uw$ after having added at most $|K_H|-1$ fill edges incident on vertices in $S_H\cup K_H$ (excluding the tail $uw$). Then, there exists a pair $s_1,k_1$ of non-neighbors in H with $s_1\in S_H$ and $k_1\in K_H$, none of which is incident on a fill edge to u or w. We distinguish the following two cases that cover all possibilities.

• Each of the vertices in $K_H\setminus \left\{k_1\right\}$ is incident on a fill edge to w. These are precisely all the $|K_H|-1$ fill edges; hence none of the vertices in $S_H\setminus \left\{s_1\right\}$ is incident on a fill edge. Then, the vertices $u,w,k_1,s_2,s_3$ (for any $s_2,s_3\in S_H\setminus \left\{s_1\right\}$) induce an $F_3$.
• There exists at least one vertex in $K_H\setminus \left\{k_1\right\}$ that is not incident on a fill edge to w. Let that vertex be $k_2$. Then, if there exists another vertex $k_3\in K_H\setminus \{k_1,k_2\}$ that is not incident on a fill edge to w as well, the vertices $u,w,k_2,k_3,s_1$ induce an $F_6$. On the other hand, if each of the vertices in $K_H\setminus \{k_1,k_2\}$ is incident on a fill edge to w (which implies that $k_3$ is adjacent to w), then these fill edges are $|K_H|-2$ in total, with only 1 remaining. If the non-neighbor $s_3$ of $k_3$ in $S_H$ is not incident on a fill edge to u or w, then the vertices $u,w,k_1,k_2,s_3$ induce an $F_6$, whereas if it is adjacent to u or w, then there are no more fill edges. In particular, if $s_3$ is adjacent to u, the vertices $u,k_1,k_3,s_1,s_3$ induce an $F_6$ and if it is adjacent to w, the vertices $u,w,k_2,s_1,s_3$ induce an $F_4$.

In each case, we get a contradiction. Thus every minimum $P_4$-sparse completion of $H+uw$ requires at least $|K_H|$ fill edges incident on vertices of $S_H\cup K_H$. Now, if there exists a minimum $P_4$-sparse completion $H^{\prime }$ of $H+uw$ having fewer than $|K_H|+f^{\prime }$ fill edges, then the fact that at least $|K_H|$ of them are incident on vertices in $S_H\cup K_H$ implies that $H^{\prime }[R_H\cup \left\{w\right\}]$ is $P_4$-sparse using fewer than $f^{\prime }$ fill edges in contradiction to the minimality of $f^{\prime }$.    □

If the (thin or thick) spider H belongs to a more general $P_4$-sparse graph, then Lemmas 6 and 7 imply the following result.

Corollary 1.

Let u be a vertex of a $P_4$-sparse graph to which we add the tail $uw$. Let $t_0\cdots t_{h}u$ be the path in the $P_4$-sparse tree of G from the the root $t_0$ to the leaf for u and let $V_0,\dots ,V_h$ be the corresponding vertex sets as mentioned before. Then, if node $t_i$ ($0\le i\le h$) is a 2-node corresponding to a spider H, the number of fill edges needed for a minimum $P_4$-sparse completion of the graph $G+uw$ (excluding the tail $uw$) does not exceed the minimum number given by Lemmas 6 and 7 (if H is thin or thick, respectively) augmented by $|(V_0\cup \cdots \cup V_{i-1})\cap N_G\left(u\right)|$.

The number of fill edges given in Corollary 1 corresponds to doing a minimum $P_4$-completion of the graph $H+uw$ and not changing the rest of the $P_4$-sparse tree $T_G$ of G.

5.2. The Algorithm

Recall that $t_0{t}_1\cdots t_{h}u$ is the path in the $P_4$-sparse tree $T_G$ of G from the root $t_0$ to the leaf for u and $V_i$ ($0\le i<h$) is the set of vertices associated with the leaves of the subtrees rooted at the children of $t_i$ except for $t_{i+1}$ and $V_h$ is the set of vertices associated with the leaves of the subtrees rooted at the children of $t_h$ except for the leaf corresponding to u (see Figure 5).

Next we prove the conditions under which a minimum $P_4$-sparse completion of the graph $G+uw$ uses fewer fill edges than when using Formation 1 or 2.

Lemma 8.

There exists a minimum $P_4$-sparse completion $G_{OPT}$ of the graph $G+uw$ which uses fewer fill edges than when using Formation 1 or 2 if and only if $uw$ is a wing of a $P_4$ in $G_{OPT}$ which implies that

(i) 

either u is a vertex of a spider in G (Lemmas 6 and 7 apply)

(ii) 

or there exists j ($0\le j<h$) such that $t_j$ is a 1-node, $t_{j+1}$ is a 0-node and there exist vertices $a,b$ such that $a\in V_j$ is universal in $G\left[V_j\right]$ and $b\in V_{j+1}$ is isolated in $G\left[V_{j+1}\right]$.

Then, in $G_{OPT}$, the vertices $u,w,a,b$ induce a $P_4$ in a spider $(S,K,R)$ with $S=\{w,b\}$, $K=\{u,a\}$ and $R=(V_{j+1}\setminus \left\{b\right\})\cup V_{j+2}\cup \cdots \cup V_h$.

Proof. 

If Formation 1 or Formation 2 cannot be used then Lemma 5 implies that $uw$ is the wing of a $P_4$ in $G_{OPT}$. If u is a vertex of a spider in G, then Lemmas 6 and 7 apply. So, below, assume that u is not a vertex of a spider in G.

For the tail $uw$ to be the wing of a $P_4$ in $G_{OPT}$, we can show that there exist vertices $x,y$ such that $uxy$ is a $P_3$ in the graph G: if $u,x,y$ do not all belong to the same connected component of G, then we could add the tail $uw$ to the connected component of G to which u belongs; thus, all the fill edges in $G_{OPT}$ incident on vertices in different connected components (among which is at least one of $ux$ and $uy$) will not be needed, a contradiction; if $u,x,y$ belong to the same connected component of G but do not form a $P_3$, then because $u,y$ are not adjacent in $G_{OPT}$ and thus neither are in G, $u,y$ are at distance 2 in G and there exists a $P_3$ $uay$ in G (note that $u,y$ cannot be at distance $\ge 4$ in G since then G would contain an induced $P_5=F_2$ and they cannot be at distance 3 either since then there exists a $P_4$ $uaby$ in G and u would be a vertex of a spider in G).

Therefore, in the following, consider that the minimum $P_4$-sparse completion $G_{OPT}$ of $G+uw$ contains an induced $P_4$ $wuab$ such that the graph G contains the induced $P_3$ $uab$; suppose that $a\in V_j$ and $b\in V_k$. Then, since $u,b$ are not adjacent in $G_{OPT}$, they are not adjacent in G either and thus their least common ancestor $t_k$ in the $P_4$-sparse tree $T_G$ of G is a 0-node; it cannot be a 2-node since then u would be a vertex of a spider. Moreover, a is a common neighbor of both $u,b$ and thus the least common ancestor $t_j$ of $a,u$ in $T_G$ is a 1- or a 2-node (in the latter case, a is a vertex of the clique of the spider) and $j<k$.

Let us now try forming the $P_4$ $wuab$, which clearly will belong to a spider, say $W=(S_W,K_W,R_W)$. We show that $|S_W|=|K_W|=2$. First, note that the edge $ab$ cannot belong to a spider in G, since then u would belong to that spider as well (note that the vertices of G not belonging to a spider are either adjacent to all vertices of the spider or to none of them). So, suppose for contrast that the spider W has $|S_W|=|K_W|\ge 3$ and let $w,b,d\in S_W$ and $u,a,c\in K_W$ with the corresponding S-K pairs being w and u, b and a and d and c. The spider W can be thin or thick.

• The spider W is thin. Then, $ab\in E\left(G\right)$; otherwise, the removal of $ab$ would produce a $P_4$-sparse graph with fewer fill edges (b is isolated in $G\left[V\right(W\left)\right]$), a contradiction; similarly, $cd\in E\left(G\right)$. Moreover, $ac\in E\left(G\right)$: as above, if $a,c$ do not belong to the same connected component of the induced subgraph $G\left[V\right(W\left)\right]$, then adding the tail $uw$ to the connected component of $G\left[V\right(W\left)\right]$ to which u belongs would result in fewer fill edges (e.g., the fill edge $ac$ will not be needed); if $a,c$ belong to the same connected component of $G\left[V\right(W\left)\right]$ but $ac\notin E\left(G\right)$, then there exists a chordless path $\rho$ connecting them in the subgraph $G[K_W\cup R_W]$ and the vertices in $V\left(\rho \right)\cup \{b,d\}$ induce a $P_{\ell }$ with $\ell \ge 5$, in contradiction to the $P_4$-sparseness of G. However, then, G contains the $P_4$ $baks$ and $ab$ belongs to a spider.
• The spider W is thick. Then, $w\in S_W$ is incident on the tail $uw$ and $|K_W|-2\ge 1$ fill edges. Since we can make u universal in $G\left[V\right(W)\setminus \{w\left\}\right]$ by using a single fill edge and then use Formation 2, it is clear that building spider W does not result in fewer fill edges.

Thus, $G_{OPT}$ with a spider W with $|K_W|\ge 3$ has no fewer fill edges than if we use Formation 2. Therefore, the $P_4$ $wuab$ belongs to a spider with clique size equal to 2, which thus is thin. Then, Property P1 in Lemma 4 implies that w, u and a are adjacent to all the neighbors of b except for a in $G_{OPT}$ and thus at least to the neighbors of b except for a in G; thus, in $G_{OPT}$,

• Fill edges connect vertex w to the vertices in $((V_0\cup \cdots \cup V_{k-1})\setminus \left\{a\right\})\cap N_G\left(b\right)=[(V_0\cup \cdots \cup V_{k-1})\setminus \left\{a\right\}]\cap N_G\left(u\right)$;
• Vertex u and w are adjacent to all neighbors of b in $V_k$; that is, fill edges connect u to the vertices in $(V_k\cap N_G\left(b\right))\setminus N_G\left(u\right)$ and w to the vertices in $V_k\cap N_G\left(b\right)$;
• Vertex a is adjacent to all the vertices in $(V_j\cap N_G\left(b\right))$ and thus fill edges connect a to all vertices in $(V_j\cap N_G\left(b\right))\setminus N_G\left[a\right]$$=(V_j\cap N_G\left(u\right))\setminus N_G\left[a\right]$.

Additionally, Property P2 in Lemma 4 implies that because a is adjacent to all the vertices in $V_{j+1}\cup \cdots \cup V_h$ and to the vertices in $V_j\cap N_G\left(a\right)$ in $G_{OPT}$ (because it is adjacent to them in G), then so must be vertex u in $G_{OPT}$; thus, in $G_{OPT}$, fill edges connect u to the vertices in $(V_{j+1}\cup \cdots \cup V_h)\setminus N_G\left(u\right)$ and to the vertices in $(V_j\cap N_G\left(a\right))\setminus N_G\left(u\right)$ (the set $(V_j\cap N_G\left(a\right))\setminus N_G\left(u\right)$ is non-empty if and only if $t_j$ is a 2-node).

Now, let us consider using Formation 2 right below node $t_j$ in the $P_4$-sparse tree $T_G$ of G; then, the number of fill edges is $|(V_{j+1}\cup \cdots \cup V_h)\setminus N_G\left(u\right)|+|(V_0\cup \cdots \cup V_j)\cap N_G\left(u\right)|$; the former term corresponds to fill edges incident on u, the latter to fill edges incident on w. Then, because $j<k$ and $|((V_0\cup \cdots \cup V_{k-1})\setminus \left\{a\right\})\cap N_G\left(u\right)|=|(V_0\cup \cdots \cup V_{k-1})\cap N_G\left(u\right)|-1$, the only possibility for $G_{OPT}$ to use fewer fill edges than using Formation 2 after node $t_j$ requires that

• $k-1=j⟹k=j+1$;
• $(V_j\cap N_G\left(u\right))\setminus N_G\left[a\right]=\varnothing$;
• $V_k\cap N_G\left(b\right)=\varnothing$ which implies that b is isolated in $G\left[V_k\right]$ and also implies that $(V_k\cap N_G\left(b\right))\setminus N_G\left(u\right)=\varnothing$;
• $(V_j\cap N_G\left(a\right))\setminus N_G\left(u\right)=\varnothing$ which implies that $t_j$ is a 1-node.

Requirement 4 implies that $V_j\cap N_G\left(u\right)=V_j$ which together with Requirement 2 imply that $N_G\left[a\right]=V_j$; that is, a is universal in $G\left[V_j\right]$ and we have the second case in the statement of the lemma.    □

Now we are ready to describe our algorithm for counting the number of fill edges in a minimum $P_4$-sparse completion of the graph $G+uw$. Note that every graph on 4 vertices is $P_4$-sparse since every forbidden graph for the class of $P_4$-sparse graphs has 5 vertices (Figure 3).

Algorithm 1 can be easily augmented to return a minimum cardinality set of fill edges. The correctness of the algorithm follows from Lemmas 5, 6, 7 and 8 and Corollary 1. Let G be the given graph and let n be the number of its vertices. If the $P_4$-sparse tree $T_G$ of G is given, an $O\left(n\right)$-time traversal of the tree enables us to compute the path $t_0{t}_1\cdots t_{h}u$, the sets $V_0,\dots ,V_h$ and the number of neighbors and non-neighbors of u in each of these sets; additionally, the height of $T_G$ is $O\left(n\right)$ and thus $h=O\left(n\right)$. To avoid duplicate work in the recursive calls, we store the numbers of neighbors and non-neighbors of u in each of the sets $V_0,\dots ,V_h$ for easy access and work from the highest 2-node and up, leaving the rest for the recursive call at that node. Since all conditions can be checked in $O\left(1\right)$-time, the entire algorithm runs in $O\left(n\right)$ time.

Theorem 1.

Let G be a $P_4$-sparse graph on n vertices and let $uw$ be a tail attached at node u of G. If the $P_4$-sparse tree of G is given, Algorithm $P_4$-sparse-Tail-Addition computes the minimum number of fill edges to be added to $G+uw$ so that the resulting graph is $P_4$-sparse in $O\left(\right|V\left(G\right)\left|\right)$ time.

If the $P_4$-sparse tree $T_G$ of G is not given, then it can be computed in $O(n+m)$ time where m is the number of edges of G [37] and the entire algorithm takes $O(n+m)$ time.

Algorithm 1 $P_4$-sparse-Tail-Addition(G,u,$uw$)

Input: a $P_4$-sparse graph G, a vertex $u\in V\left(G\right)$ and a tail $uw$ to be added to G. Output: the number of fill edges (excluding the tail $uw$) needed in a minimum      $P_4$-sparse completion of the graph $G+uw$. if $\left|V\right(G\left)\right|\le 3$ then    {the graph $G+uw$ is $P_4$-sparse}   return(0); compute the $P_4$-sparse tree $T_G$ of G and the path $t_0{t}_1\dots t_h$ ($h\ge 1$) from the root $t_0$ of $T_G$ to the parent node $t_h$ of the leaf corresponding to u; compute the sets of vertices $V_i$, $0\le i\le h$ (see Figure 5); $min\leftarrow |N_G\left(u\right)|$;    {corresponds to Formation 1} {apply (Lemma 5(iii) and Corollary 1} for each $t_i$ ($i=0,1,\dots ,h$) that is a 1- or a 2-node do    {use Formation 2 above each 1- or 2-node $t_i$ (Lemma 5(iii))}    $\ell \leftarrow |(V_0\cup \cdots \cup V_{i-1})\cap N_G\left(u\right)|+|(V_i\cup \cdots \cup V_h)\setminus N_G\left(u\right)|$;    update $min$ if $\ell <min$;    {if $t_i$ is a 2-node, apply Lemmas 6 or 7 and Corollary 1}    if $t_i$ is a 2-node then    {spider $H=(S_H,K_H,R_H)$}      if $u\in S_H\cup K_H$ then       $\ell \leftarrow$ number of fill edges according to Lemmas 6 or 7;      else    {$u\in R_H$}        if H is thin then         $\ell \leftarrow min\left\{\right|R_H\setminus N_H\left[u\right]|,|K_H|+P_4$-sparse-Tail-Addition(H,u,$uw$) };        else    {H is thick}         $\ell \leftarrow |K_H|+P_4$-sparse-Tail-Addition(H,u,$uw$);      $\ell \leftarrow \ell +|(V_0\cup \cdots \cup V_{i-1})\cap N_G\left(u\right)|$;       {Corollary 1}      update $min$ if $\ell <min$; {check for new $P_4$ formation (Lemma 8)} for each $i=0,1,\dots ,h-1$ such that $t_i$ is a 1-node and $t_{i+1}$ is a 0-node do    if there exist vertex $a\in V_i$ such that a is universal in $V_i$ and          vertex $b\in V_{i+1}$ such that b has no neighbors in $V_{i+1}$ then      $\ell \leftarrow |(V_0\cup \cdots \cup V_{i-1})\cap N_G\left(u\right)|+|V_i\setminus \left\{a\right\}|+|V_{i+1}\setminus \left\{b\right\}|$                 $+|(V_{i+2}\cup \cdots \cup V_h)\setminus N_G\left(u\right)|$;      update $min$ if $\ell <min$; return($min$);

6. Open Problems

An immediate open problem is to try to devise fast algorithms for the tail addition problem on other subclasses of perfect graphs such as interval, comparability and permutation graphs. Moreover, in light of the results in this paper, it would be interesting to try to extend our approach to the ($\mathcal{C},+1$)-MinEdgeAddition problem [1] in which we want to compute a minimum $\mathcal{C}$-completion of the graph that results after the addition of 1 given non-edge for the classes $\mathcal{C}$ of split, threshold, quasi-threshold and $P_4$-sparse graphs, as well as for other graph classes.

Finally, it is worth investigating the complexity of the ($\mathcal{C},+k$)-MinEdgeAddition problem for fixed $k\ge 1$ for different classes $\mathcal{C}$ of graphs.