Abstract
In the context of big-data analysis, the clustering technique holds significant importance for the effective categorization and organization of extensive datasets. However, pinpointing the ideal number of clusters and handling high-dimensional data can be challenging. To tackle these issues, several strategies have been suggested, such as a consensus clustering ensemble that yields more significant outcomes compared to individual models. Another valuable technique for cluster analysis is Bayesian mixture modelling, which is known for its adaptability in determining cluster numbers. Traditional inference methods such as Markov chain Monte Carlo may be computationally demanding and limit the exploration of the posterior distribution. In this work, we introduce an innovative approach that combines consensus clustering and Bayesian mixture models to improve big-data management and simplify the process of identifying the optimal number of clusters in diverse real-world scenarios. By addressing the aforementioned hurdles and boosting accuracy and efficiency, our method considerably enhances cluster analysis. This fusion of techniques offers a powerful tool for managing and examining large and intricate datasets, with possible applications across various industries.
1. Introduction
Clustering is a key technique in unsupervised learning and is employed across various domains such as computer vision, natural language processing, and bioinformatics. Its primary objective is to assemble related items and disclose hidden patterns within data. Confronting complex datasets, however, can prove challenging, as conventional clustering approaches may not be effective. In response to this issue, Bayesian nonparametric methods have gained popularity in recent years as a potent means of organising large datasets. These approaches offer a versatile and potent solution for managing the data’s unpredictability and complexity, making them a crucial tool in the field of clustering. Clustering is crucial in the fields of information science and big-data management for organizing and handling huge volumes of data. In recent years, exponential data proliferation has increased the demand for efficient and effective solutions to handle, manage, and analyse enormous data volumes. Clustering can accomplish this by grouping comparable data points together, hence lowering the dataset’s size and making it simpler to examine. Apart from traditional techniques, there are much more promising ones. The product partition model (PPM) is one of the most widely used Bayesian nonparametric clustering algorithms. PPMs are a class of models that classify data into clusters and assign a set of parameters to each cluster. They use a prior over the parameters to draw conclusions about the clusters. Despite the efficacy of PPMs, a single clustering solution may not be enough for complicated datasets, resulting in the development of consensus clustering. Consensus clustering is a kind of ensemble clustering that produces a final grouping by combining the results of numerous clustering methods [1,2].
The motivation behind this work lies in addressing the challenges associated with clustering complex datasets, which is crucial for efficient big-data management and analysis. The determination of the number of clusters and handling of high-dimensional data are significant challenges that arise while dealing with these complex datasets. To tackle these challenges, we propose an innovative method that combines Bayesian mixture models with consensus clustering.
Our method is designed to address the challenges of clustering extensive datasets and identifying the ideal number of clusters. By merging the strengths of PPMs, Markov chain Monte Carlo (MCMC), and consensus clustering, we aim to produce reliable and precise clustering outcomes. MCMC methods enable the estimation of PPM parameters, making them a powerful tool for sampling from intricate distributions. Moreover, split-and-merge techniques allow the MCMC algorithm to navigate the parameter space and generate samples from the posterior distribution of the parameters [3,4,5].
The incorporation of consensus clustering with Bayesian mixture models facilitates the examination of complex and high-dimensional datasets, thereby improving the effectiveness and efficiency of big-data management. Our suggested approach also holds the potential to uncover hidden data patterns, which can lead to improved decision-making processes and offer a competitive edge across various industries.
The proposed utilization of Bayesian nonparametric ensemble methods for clustering intricate datasets demonstrates considerable promise in the realms of information science and big-data management. Combining PPMs, MCMC, and consensus clustering results in a robust and accurate clustering solution. Further research could refine this method and explore its application in real-world situations.
The remainder of this article is structured as follows: Section 2 presents a concise overview of Bayesian nonparametric methods, particularly PPMs, and their applicability in clustering. Section 3 describes consensus clustering and its application to ensemble methods. In Section 3.3, we present our proposed method, which incorporates PPMs and consensus clustering. Section 4 conducts experiments to illustrate the efficacy of the proposed method for clustering complex datasets. Finally, Section 6 concludes the paper, discussing potential future research and the significance of our proposed method in the field of big-data analysis and management.
2. Related Work
Cluster analysis has been utilised extensively in numerous disciplines to identify patterns and structures within data. Caruso et al. [6] applied cluster analysis to an actual mixed-type dataset and reported their findings. Meanwhile, Absalom et al. [7] provided a comprehensive survey of clustering algorithms, discussing the state-of-the-art machine learning applications, taxonomy, challenges, and future research prospects. Jiang et al. [8] conducted a survey of cluster analysis for gene expression data. Furthermore, Huang et al. [9] proposed a locally weighted ensemble clustering method that assigns weights to individual partitions based on local information. These studies demonstrate the diversity of clustering methods and their applications, emphasizing the importance of choosing the appropriate method for specific datasets.
Consensus clustering utilises W runs of a base model or learner (such as K-means clustering) and combines the W suggested partitions into a consensus matrix, where the -th entries reflect the percentage of model runs in which the ith and jth individuals co-cluster. This ratio indicates the degree of confidence in the co-clustering of any two elements. Moreover, ensembles may reduce computational execution time. This occurs because individual learners may be weaker (and hence consume less of the available data or stop before complete convergence), and the learners in the vast majority of ensemble techniques are independent of one another, enabling the use of a parallel environment for each of the faster model runs [10].
Bayesian clustering is a popular machine-learning technique for grouping data points into clusters based on their probability distributions. Hidden Markov models (HMM) [11] have been used to model the underlying probabilistic structure of data in Bayesian clustering. Accelerating hyperparameters via Bayesian optimizations can also help in building automated machine learning (AutoML) schemes [12], while such optimizations can also be applied in Tiny Machine Learning (TinyML) environments wherein devices can be trained to fulfil ML tasks [13]. Ensemble Bayesian Clustering [14] is a variation of Bayesian clustering that combines multiple models to produce more robust results, while cluster analysis [15] extends traditional clustering methods by considering the uncertainty in the data, which leads to more accurate results.
Traditional clustering algorithms require a preset selection of the number of clusters K, which can be challenging as it plagues many investigations, with researchers often depending on certain rules to choose a final model. Various selections of K are compared, for instance, using an evaluation metric for K. Techniques for selecting K using the consensus matrix are offered in [16]; however, this implies that any uncertainty over K is not reflected in the final clustering, and each model run utilises the same, fixed number of clusters. An alternative clustering technique incorporates cluster analysis within a statistical framework [17], which implies that models may be formally compared and issues such as choosing K can be represented as a model-selection problem using relevant tools.
In recent years, various clustering techniques have been developed to address the challenges associated with traditional clustering methods. Locally weighted ensemble clustering [9] leverages the advantages of ensemble clustering while accounting for the local structure of the data, leading to more accurate and robust results. Consensus clustering, a type of ensemble clustering, combines multiple runs of a base model into a consensus matrix to increase confidence in co-clustering [16]. Enhanced ensemble clustering via fast propagation of cluster-wise similarities [18,19] improves the efficiency and effectiveness of clustering by propagating cluster-wise similarities more rapidly. Real-world applications of these clustering techniques can be found in various domains, such as gene expression analysis, cell classification in flow cytometry experiments, and protein localization estimation [20,21,22].
Recent advancements in ensemble clustering have addressed various challenges posed by high-dimensional data and complex structures. Yan and Liu [23] proposed a consensus clustering approach specifically designed for high-dimensional data, while Niu et al. [24] developed a multi-view ensemble clustering approach using a joint affinity matrix to improve the quality of clustering. Huang et al. [25] introduced an ensemble hierarchical clustering algorithm that considers merits at both cluster and partition levels. In addition, Zhou et al. [26] presented a clustering ensemble method based on structured hypergraph learning, and Zamora and Sublime [27] proposed an ensemble and multi-view clustering method based on Kolmogorov complexity. Huang et al. [28] tackled the challenge of high-dimensional data by developing a multidiversified ensemble clustering approach, focusing on various aspects such as subspaces, metrics, and more. Huang et al. [29] also proposed an ultra-scalable spectral clustering and ensemble clustering technique. Wang et al. [30] developed a Markov clustering ensemble method, and Huang et al. [31] presented a fast multi-view clustering approach via ensembles for scalability, superiority, and simplicity. These studies showcase the diverse range of ensemble clustering techniques developed to address complex data challenges and improve the performance of clustering algorithms.
Clustering ensemble techniques have been developed and applied across various domains, addressing the challenges and limitations of traditional clustering methods. Nie et al. [32] concentrated on the analysis of scRNA-seq data, discussing the methods, applications, and difficulties associated with ensemble clustering in this field. Boongoen and Iam-On [33] presented an exhaustive review of cluster ensembles, highlighting recent extensions and applications. Troyanovsky [34] examined the ensemble of specialised cadherin clusters in adherens junctions, demonstrating the versatility of ensemble clustering methods. Zhang and Zhu [35] introduced Ensemble Clustering based on Bayesian Network (ECBN) inference for single-cell RNA-seq data analysis, offering a novel method for addressing the difficulties inherent to this data format. Hu et al. [36] proposed an ultra-scalable ensemble clustering method for cell-type recognition using scRNA-seq data of Alzheimer’s disease. Bian et al. [37] developed an ensemble consensus clustering method, scEFSC, for accurate single-cell RNA-seq data analysis based on multiple feature selections. Wang and Pan [38] introduced a semi-supervised consensus clustering method for gene expression data analysis, while Yu et al. [39] explored knowledge-based cluster ensemble approaches for cancer discovery from biomolecular data. Finally, Yang et al. [40] proposed a consensus clustering approach using a constrained self-organizing map and an improved Cop-Kmeans ensemble for intelligent decision support systems, showcasing the broad applicability of ensemble clustering techniques in various fields.
Bayesian mixture models, with their adaptable densities, are highly attractive for data analysis across various types. The number of clusters K can be inferred directly from the data as a random variable, resulting in joint modelling of K and the clustering process [41,42,43,44,45,46]. Inference of the number of clusters can be achieved through methods such as the Dirichlet process [41], finite mixture models [42,43], or over-fitting mixture models [44]. These models have found success in a wide range of biological applications, including gene expression profiles [20], cell classification in flow cytometry experiments [21,47] and scRNAseq experiments [48], as well as protein localization estimation [22]. Bayesian mixture models can also be extended to jointly cluster multiple datasets [49,50].
MCMC techniques are the most-used method for executing Bayesian inference, and they are used to build a chain of clusterings. The convergence of the chain is evaluated to see if its behaviour conforms to the asymptotic theory predicted. However, despite the ergodicity of MCMC approaches, individual chains often fail to investigate the complete support of the posterior distribution and have lengthy runtimes. Some MCMC algorithms attempt to overcome these issues, often at the expense of higher computing cost every iteration (see [51,52]).
Preliminaries
Dirichlet processes (DPs) are a family of stochastic processes. A Dirichlet process defines a distribution over probability measures , where for any finite partition of , say , the random vector
is jointly generalized under a Dirichlet Distribution ( is a random variable since G itself is a random measure and is sampled from the Dirichlet process), written as
where is called the concentration parameter and is the base distribution; collectively is called the base measure.
Dirichlet processes are really useful in the task of nonparametric clustering via using a mixture of Dirichlet processes (commonly DP mixture models or Infinite mixture models). In fact, a DP mixture model can be seen as an extension of Gaussian mixture models over a nonparametric setting. The basic DP mixture model follows the following generative story:
where DP denotes sampling from a Dirichlet process given a base measure.
When we are dealing with DP mixture models for clustering, it helps to integrate out G with respect to the prior on G [53]. Therefore, we can write the clustering problem in an alternate representation, although the underlying model remains the same.
where is the cluster assignment for the point and are the likelihood parameters for each cluster. K denotes the number of clusters, and being a nonparametric model, we assume .
If the likelihood and the base distribution are conjugate, we can easily derive a posterior representation for the cluster assignments or the latent classes and use inference techniques such as mean-field VB and Markov chain Monte Carlo. The work [53] also describes various inference methods in the case of a non-conjugate base distribution.
Dirichlet processes are extremely useful for clustering purposes as they do not assume an inherent base distribution, and therefore it is possible to apply Dirichlet process priors over complex models.
3. Methodology
3.1. Finite Mixture of Normals
Suppose we have a set of samples that can be modelled as
where N(.) denotes the Normal distribution and represents the weight of the j-th component, with and . In addition, let us introduce the latent variable to induce the mixture. Thus, we have that . Given the introduction of the latent variable, we can rewrite the likelihood function as
where if , and otherwise. In addition, the latent variables . That is,
where represents the number of observations falling into component j. With that, we can define the joint distribution of and as
For notational convenience, let us denote , and . Given the expressions above, we have that conditioned on are independent with a probability of classification given by
In the end, we have that
To estimate the components of the finite mixture of Normals under the Bayesian paradigm, we consider the following priors:
To construct the MCMC structure, we need the full conditionals for , , and , which are given below.
where
and
where
From the above, we have:
where .
3.2. Product Partition Models
Let be an n-dimensional vector of a variable we have interest in clustering. We define a partition as a collection of clusters , which are assumed to be non-empty and mutually exclusive. Following [54], the parametric PPM is presented as
where
for some is the cohesion function. From the above, T can be approximated as
and such that .
3.3. Integration of PPM and Consensus Clustering
Following Section 5 in [54], let us consider that
Further, let us denote and k as the number of distinct clusters. Below, we present the full conditionals of the quantities/parameters of interest.
which is
which is
which is
For more details about the marginalization of and for the full conditional of , see Appendix A. To simulate the posterior distribution of the PPM, we use Algorithm 8 introduced by [53]. This algorithm was proposed in the context of Dirichlet process mixture models, but it can be used for PPMs as well.
Definition 1
(Singleton). The definition of a singleton is a cluster consisting of only one observation. In contrast, any cluster comprising more than one observation is not considered a singleton.
Let the cluster labels be denoted as with values ranging from . For each i, where , let , where k represents the number of distinct cluster labels excluding observation i.
- If observation i belongs to a singleton cluster such that for all , the cluster label is assigned the value of . Independent values are then drawn from the prior distribution of and for all .
- If observation i does not belong to a singleton cluster such that for some , independent values are drawn from the prior distribution of and for all .
For both cases, draw a new value for from using the following probabilities:
where is the number of observations (excluding i) that have , and is the Dirichlet process concentration parameter. Change the state to contain only those and that are now associated with one or more observations. Here, is an appropriate normalising constant given by (28).
For all : draw new values from , , , and .
The singleton (Definition 1) is an essential concept in the proposed Bayesian nonparametric clustering approach for several reasons:
- Algorithm efficiency: By identifying singleton clusters, the algorithm can handle them differently in the MCMC sampling process. This distinction allows the algorithm to efficiently explore the space of possible cluster assignments, improving the overall performance of the algorithm and potentially leading to more accurate cluster assignments.
- Flexibility in clustering: The Bayesian nonparametric clustering approach is designed to accommodate an unknown and potentially infinite number of clusters. The notion of singleton clusters enables the method to contemplate the possibility of new cluster construction, resulting in a more flexible, data-adaptive clustering solution.
- Addressing overfitting: In the MCMC sampling process, the presence of singleton clusters helps prevent overfitting. By allowing new clusters to be created, the algorithm can effectively control the complexity of the clustering model, avoiding the risk of assigning too many data points to the same cluster when they may, in fact, belong to separate clusters.
- Model interpretability: Singleton clusters can provide insights into the underlying structure of the data. Identifying singleton clusters can help reveal potential outliers or unique observations, allowing for a more granular understanding of the data’s patterns and relationships.
Generally, the concept of singletons plays a crucial role in the proposed Bayesian nonparametric clustering approach, improving the algorithm’s efficiency, flexibility, and interpretability, as well as addressing potential overfitting issues.
Based on all the preceding information, we propose a Bayesian nonparametric clustering method within an MCMC framework. This is illustrated as a flowchart in Figure 1, while the full inner structure is given in Algorithm 1. The algorithm initiates by inputting the y observations and , m hyperparameters as well as the MCMC iterations of the program. The outputs of the algorithm are the K clusters as well as their means and variances.
| Algorithm 1 Bayesian nonparametric clustering in MCMC framework |
|
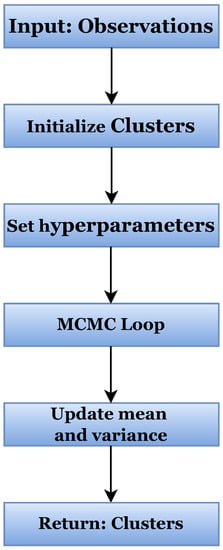
Figure 1.
Flowchart of Bayesian nonparametric clustering in MCMC framework.
4. Experimental Results
In this section, we present the experimental results based on the methods from the preceding sections. Figure 2a shows the frequency histogram of y observations of the data, while Figure 2b shows the histogram of x and the density of the data.
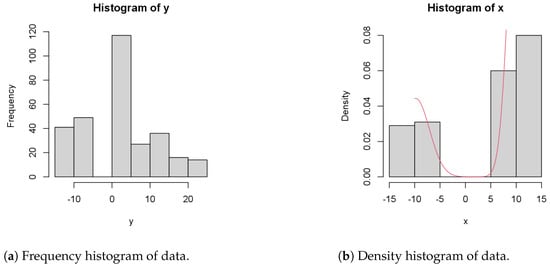
Figure 2.
Statistical sampling analysis of the PPM model.
Figure 3a shows the MCMC sampling structure and the repetitive areas on y points over 300 iterations, while Figure 3b shows the posterior similarity matrix.
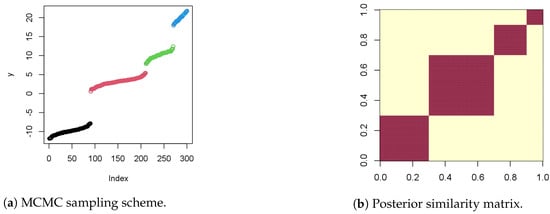
Figure 3.
Statistical sampling analysis of the PPM and consensus clustering.
For the experimental results, the following posterior parameters were utilized , which represent the means of the posterior distributions for each of the four clusters; represent the variances of the posterior distributions for each of the four clusters; represent the proportions (or mixing weights) of the posterior distributions for each of the four clusters. The simulation parameters are the means and variances of the clusters, as well as the mixing proportions of the Poisson process mixture. The values represent the estimated proportion of each of the four clusters in the PPM. The standard deviations give the uncertainty around these estimated proportions, with the lower and upper bounds indicating the credible interval. It is worth noting that the results presented in the table are just one possible output of the simulation study, and other simulations with different parameter settings may produce different results. Table 1 shows the results of a simulation study of PPM and consensus clustering.

Table 1.
Results of PPM and consensus clustering.
The clustering results of the proposed method in the MCMC framework are shown in Table 2. We conduct tests by adjusting the hyperparameters for different scenarios for which various numbers of clusters are produced, and their means and variances are calculated.

Table 2.
Experimental results using the proposed Bayesian nonparametric clustering in MCMC framework.
5. Further Extensions for Big Data Systems
In this section, we propose further extensions for big-data systems and how these methods can be applied to the information science sector. Algorithm 2 is a method for clustering big datasets into groups based on the similarities between observations, with a variety of applications in fields such as information science, big-data systems, and businesses. The algorithm uses Hamiltonian Monte Carlo (HMC) sampling to estimate the posterior distribution of the clusters and their means and variances. One of the main challenges in dealing with big data is the processing time required to analyse and cluster large datasets. By partitioning the MCMC iterations into equal portions and allocating each part to a worker, parallelization of the algorithm helps to surmount this difficulty. This parallelizes the clustering procedure, thereby substantially reducing the processing time.
| Algorithm 2 Parallel Bayesian nonparametric clustering using HMC |
|
Algorithm 2 boasts a wide range of applications spanning numerous fields such as computer science, big-data systems, and business. In the realm of information science, this algorithm can be employed to consolidate extensive datasets based on similarities, thereby uncovering the data’s underlying structure. In the context of business, the algorithm can be applied to cluster customers according to their purchasing behaviours and preferences, yielding valuable insights that enable targeted marketing and sales strategies.
In the domain of big-data systems, the algorithm is capable of clustering massive datasets into groups sharing similar traits, which reduces data storage and processing demands. Moreover, clustering analogous data facilitates parallel processing, consequently boosting efficiency and accelerating processing times. Beyond business and information science, the algorithm can also be utilized in human resource management, where it can group employees based on their skill sets and experiences. This clustering empowers organizations to streamline talent acquisition, leading to increased productivity and employee satisfaction.
Ultimately, the algorithm serves as a potent instrument for analysing vast datasets, generating insightful information, and improving decision-making processes across various sectors. Future research could explore the algorithm’s additional applications and assess its performance in diverse contexts.
Algorithm 1 can be adapted in Apache Spark by dividing the data into smaller chunks and distributing them among different nodes in a cluster. The algorithm can be executed in parallel on each node and the results can be combined to get the final clustering results. Each iteration of the MCMC loop can be implemented as a map-reduce operation, wherein the map operation performs the MCMC updates on a portion of the data and the reduce operation aggregates the results from all the map operations to get the updated clustering results. The map operation includes the operations mentioned in the initial algorithm: updating the and and adjusting the cluster labels if needed. The reduce operation combines the results from all the map operations and produces the updated clustering results, allowing for efficient parallel processing of large datasets and meeting big-data processing requirements in a scalable manner using Apache Spark.
The results of Algorithm 2 are shown in Table 3. This method is similar to Algorithm 1; however, here we utilize Hamiltonian Monte Carlo instead of MCMC.

Table 3.
Experimental results using parallel Bayesian nonparametric clustering with HMC.
Integrating Algorithm 2 with Apache Spark, as demonstrated in Algorithm 3, allows for efficient and scalable processing of massive datasets in a distributed computing environment. Leveraging Spark’s capabilities, the algorithm can handle the increasing demands of big-data systems by dividing the data into P partitions and executing parallel MCMC iterations across multiple nodes within a cluster. This approach enables faster processing times and accommodates growing data sizes while maintaining the accuracy and effectiveness of the clustering method. Additionally, the implementation in Spark paves the way for further development and optimization of Bayesian nonparametric clustering techniques in distributed computing environments, enabling better insights and more effective decision-making processes in various application domains. Finally, the results of Algorithm 3 are shown in Table 4.

Table 4.
Experimental results using the Bayesian nonparametric clustering in MCMC on Apache Spark.
Ultimately, we present the performance of all of the proposed algorithms in Table 5. We utilize famous real-world datasets such as CIFAR-10, MNIST, and Iris. The hyperparameters for each experiment are and m, and we evaluate the clustering accuracy and the time required for the method to complete. The time column is measured in seconds. As we can observe from the table, the fastest clustering was on the Iris dataset, but note that this dataset is smaller in terms of size compared with the other two. As for the method with the highest accuracy, it appears that BNP-MCMC (Algorithm 1) has the highest accuracy on the Iris dataset while having satisfactory accuracy on the other methods. Moreover, the parallel method appears to further improve the accuracy by some decimal points. Lastly, the Spark version of the proposed method produces similar results but outperforms the other methods with regards to time.
| Algorithm 3 Bayesian nonparametric clustering in MCMC on Apache Spark |
|

Table 5.
Experimental results for real-world datasets using different algorithms and hyperparameters.
6. Conclusions and Future Work
In the context of this work, we have proposed a novel approach for clustering complex datasets using Bayesian nonparametric ensemble methods that have the potential to revolutionize the field of information science and big-data management. Our approach generates a robust and accurate final clustering solution, addressing the challenges related to determining the number of clusters and managing high-dimensional datasets. By combining the strengths of PPMs, MCMC, and consensus clustering, our proposed method provides a more comprehensive and informative clustering solution, enabling efficient and effective management of massive datasets.
Further study could concentrate on improving the proposed method in a variety of ways. One area of research could be the creation of more efficient algorithms for computing the consensus matrix, thereby reducing the execution time of the approach. In addition, the incorporation of additional data sources into the model could result in more exhaustive clustering solutions. In addition, the use of more adaptive methods for determining optimal hyperparameters and the development of sophisticated techniques for dealing with data noise and outliers could improve the efficacy of the approach. Improving the comprehensibility and clarity of the proposed method for non-expert users could foster its widespread adoption across a more extensive array of applications and industries.
Exploration of the proposed implementation in various real-world contexts presents a promising avenue for future research. For example, the technique could be deployed to discern and classify diverse tumour types by examining their presentation in medical imaging data. Within the realm of natural language processing, the method could be harnessed to categorize text into specific topics. Additionally, in the financial industry, the suggested approach could be employed to cluster financial data, facilitating the recognition of patterns for stock price forecasting and fraud detection.
In summary, the proposed strategy of employing Bayesian nonparametric ensemble methods for clustering intricate datasets holds substantial promise for the proficient and effective handling of enormous datasets and has the potential to transform the landscape of information science and big-data management. Future research in this area could lead to significant advancements in the field, enabling the solution of increasingly complex problems in various disciplines.
Author Contributions
C.K., A.K., K.C.G., M.A. and S.S. conceived of the idea, designed and performed the experiments, analysed the results, drafted the initial manuscript and revised the final manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
In this section, we try to marginalise and for the full conditional of .
The expression for is a product of integrals, where each integral is over the variables and . The integral of a Gaussian distribution is a Gaussian distribution with a modified mean and variance. Hence, we can simplify the expression as follows:
References
- Coleman, S.; Kirk, P.D.; Wallace, C. Consensus clustering for Bayesian mixture models. BMC Bioinform. 2022, 23, 1–21. [Google Scholar] [CrossRef]
- Lock, E.F.; Dunson, D.B. Bayesian consensus clustering. Bioinformatics 2013, 29, 2610–2616. [Google Scholar] [CrossRef] [PubMed]
- Jain, S.; Neal, R.M. A split-merge Markov chain Monte Carlo procedure for the Dirichlet process mixture model. J. Comput. Graph. Stat. 2004, 13, 158–182. [Google Scholar] [CrossRef]
- Jain, S.; Neal, R.M. Splitting and merging components of a nonconjugate Dirichlet process mixture model. Bayesian Anal. 2007, 2, 445–472. [Google Scholar] [CrossRef]
- Bouchard-Côté, A.; Doucet, A.; Roth, A. Particle Gibbs split-merge sampling for Bayesian inference in mixture models. J. Mach. Learn. Res. 2017, 18, 868–906. [Google Scholar]
- Caruso, G.; Gattone, S.A.; Balzanella, A.; Di Battista, T. Cluster Analysis: An Application to a Real Mixed-Type Data Set. In Models and Theories in Social Systems; Springer International Publishing: Cham, Switzerland, 2019; pp. 525–533. [Google Scholar] [CrossRef]
- Ezugwu, A.E.; Ikotun, A.M.; Oyelade, O.O.; Abualigah, L.; Agushaka, J.O.; Eke, C.I.; Akinyelu, A.A. A comprehensive survey of clustering algorithms: State-of-the-art machine learning applications, taxonomy, challenges, and future research prospects. Eng. Appl. Artif. Intell. 2022, 110, 104743. [Google Scholar] [CrossRef]
- Jiang, D.; Tang, C.; Zhang, A. Cluster analysis for gene expression data: A survey. IEEE Trans. Knowl. Data Eng. 2004, 16, 1370–1386. [Google Scholar] [CrossRef]
- Huang, D.; Wang, C.D.; Lai, J.H. Locally weighted ensemble clustering. IEEE Trans. Cybern. 2017, 48, 1460–1473. [Google Scholar] [CrossRef]
- Ghaemi, R.; Sulaiman, M.N.; Ibrahim, H.; Mustapha, N. A survey: Clustering ensembles techniques. Int. J. Comput. Inf. Eng. 2009, 3, 365–374. [Google Scholar]
- Can, C.E.; Ergun, G.; Soyer, R. Bayesian analysis of proportions via a hidden Markov model. Methodol. Comput. Appl. Probab. 2022, 24, 3121–3139. [Google Scholar] [CrossRef]
- Karras, A.; Karras, C.; Schizas, N.; Avlonitis, M.; Sioutas, S. AutoML with Bayesian Optimizations for Big Data Management. Information 2023, 14, 223. [Google Scholar] [CrossRef]
- Schizas, N.; Karras, A.; Karras, C.; Sioutas, S. TinyML for Ultra-Low Power AI and Large Scale IoT Deployments: A Systematic Review. Future Internet 2022, 14, 363. [Google Scholar] [CrossRef]
- Zhu, Z.; Xu, M.; Ke, J.; Yang, H.; Chen, X.M. A Bayesian clustering ensemble Gaussian process model for network-wide traffic flow clustering and prediction. Transp. Res. Part Emerg. Technol. 2023, 148, 104032. [Google Scholar] [CrossRef]
- Greve, J.; Grün, B.; Malsiner-Walli, G.; Frühwirth-Schnatter, S. Spying on the prior of the number of data clusters and the partition distribution in Bayesian cluster analysis. Aust. N. Z. J. Stat. 2022, 64, 205–229. [Google Scholar] [CrossRef]
- Monti, S.; Tamayo, P.; Mesirov, J.; Golub, T. Consensus clustering: A resampling-based method for class discovery and visualization of gene expression microarray data. Mach. Learn. 2003, 52, 91–118. [Google Scholar] [CrossRef]
- Fraley, C.; Raftery, A.E. Model-based clustering, discriminant analysis, and density estimation. J. Am. Stat. Assoc. 2002, 97, 611–631. [Google Scholar] [CrossRef]
- Huang, D.; Wang, C.D.; Peng, H.; Lai, J.; Kwoh, C.K. Enhanced ensemble clustering via fast propagation of cluster-wise similarities. IEEE Trans. Syst. Man Cybern. Syst. 2018, 51, 508–520. [Google Scholar] [CrossRef]
- Cai, X.; Huang, D. Link-Based Consensus Clustering with Random Walk Propagation. In Proceedings of the Neural Information Processing: 28th International Conference, ICONIP 2021, Sanur, Bali, Indonesia, 8–12 December 2021; Proceedings, Part V 28. Springer: Berlin/Heidelberg, Germany, 2021; pp. 693–700. [Google Scholar]
- Medvedovic, M.; Sivaganesan, S. Bayesian infinite mixture model based clustering of gene expression profiles. Bioinformatics 2002, 18, 1194–1206. [Google Scholar] [CrossRef]
- Chan, C.; Feng, F.; Ottinger, J.; Foster, D.; West, M.; Kepler, T.B. Statistical mixture modeling for cell subtype identification in flow cytometry. Cytom. Part A J. Int. Soc. Anal. Cytol. 2008, 73, 693–701. [Google Scholar] [CrossRef]
- Crook, O.M.; Mulvey, C.M.; Kirk, P.D.; Lilley, K.S.; Gatto, L. A Bayesian mixture modelling approach for spatial proteomics. PLoS Comput. Biol. 2018, 14, e1006516. [Google Scholar] [CrossRef]
- Yan, J.; Liu, W. An ensemble clustering approach (consensus clustering) for high-dimensional data. Secur. Commun. Netw. 2022, 2022, 5629710. [Google Scholar] [CrossRef]
- Niu, X.; Zhang, C.; Zhao, X.; Hu, L.; Zhang, J. A multi-view ensemble clustering approach using joint affinity matrix. Expert Syst. Appl. 2023, 216, 119484. [Google Scholar] [CrossRef]
- Huang, Q.; Gao, R.; Akhavan, H. An ensemble hierarchical clustering algorithm based on merits at cluster and partition levels. Pattern Recognit. 2023, 136, 109255. [Google Scholar] [CrossRef]
- Zhou, P.; Wang, X.; Du, L.; Li, X. Clustering ensemble via structured hypergraph learning. Inf. Fusion 2022, 78, 171–179. [Google Scholar] [CrossRef]
- Zamora, J.; Sublime, J. An Ensemble and Multi-View Clustering Method Based on Kolmogorov Complexity. Entropy 2023, 25, 371. [Google Scholar] [CrossRef] [PubMed]
- Huang, D.; Wang, C.D.; Lai, J.H.; Kwoh, C.K. Toward Multidiversified Ensemble Clustering of High-Dimensional Data: From Subspaces to Metrics and Beyond. IEEE Trans. Cybern. 2022, 52, 12231–12244. [Google Scholar] [CrossRef]
- Huang, D.; Wang, C.D.; Wu, J.S.; Lai, J.H.; Kwoh, C.K. Ultra-Scalable Spectral Clustering and Ensemble Clustering. IEEE Trans. Knowl. Data Eng. 2020, 32, 1212–1226. [Google Scholar] [CrossRef]
- Wang, L.; Luo, J.; Wang, H.; Li, T. Markov clustering ensemble. Knowl.-Based Syst. 2022, 251, 109196. [Google Scholar] [CrossRef]
- Huang, D.; Wang, C.D.; Lai, J.H. Fast multi-view clustering via ensembles: Towards scalability, superiority, and simplicity. IEEE Trans. Knowl. Data Eng. 2023. [Google Scholar] [CrossRef]
- Nie, X.; Qin, D.; Zhou, X.; Duo, H.; Hao, Y.; Li, B.; Liang, G. Clustering ensemble in scRNA-seq data analysis: Methods, applications and challenges. Comput. Biol. Med. 2023, 106939. [Google Scholar] [CrossRef]
- Boongoen, T.; Iam-On, N. Cluster ensembles: A survey of approaches with recent extensions and applications. Comput. Sci. Rev. 2018, 28, 1–25. [Google Scholar] [CrossRef]
- Troyanovsky, S.M. Adherens junction: The ensemble of specialized cadherin clusters. Trends Cell Biol. 2022, 33, 374–387. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Zhu, Y. ECBN: Ensemble Clustering based on Bayesian Network inference for Single-cell RNA-seq Data. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 5884–5888. [Google Scholar]
- Hu, L.; Zhou, J.; Qiu, Y.; Li, X. An Ultra-Scalable Ensemble Clustering Method for Cell Type Recognition Based on scRNA-seq Data of Alzheimer’s Disease. In Proceedings of the 3rd Asia-Pacific Conference on Image Processing, Electronics and Computers, Dalian, China, 14–16 April 2022; pp. 275–280. [Google Scholar]
- Bian, C.; Wang, X.; Su, Y.; Wang, Y.; Wong, K.C.; Li, X. scEFSC: Accurate single-cell RNA-seq data analysis via ensemble consensus clustering based on multiple feature selections. Comput. Struct. Biotechnol. J. 2022, 20, 2181–2197. [Google Scholar] [CrossRef]
- Wang, Y.; Pan, Y. Semi-supervised consensus clustering for gene expression data analysis. BioData Min. 2014, 7, 1–13. [Google Scholar] [CrossRef]
- Yu, Z.; Wongb, H.S.; You, J.; Yang, Q.; Liao, H. Knowledge based cluster ensemble for cancer discovery from biomolecular data. IEEE Trans. Nanobiosci. 2011, 10, 76–85. [Google Scholar]
- Yang, Y.; Tan, W.; Li, T.; Ruan, D. Consensus clustering based on constrained self-organizing map and improved Cop-Kmeans ensemble in intelligent decision support systems. Knowl.-Based Syst. 2012, 32, 101–115. [Google Scholar] [CrossRef]
- Ferguson, T.S. A Bayesian analysis of some nonparametric problems. Ann. Stat. 1973, 1, 209–230. [Google Scholar] [CrossRef]
- Miller, J.W.; Harrison, M.T. Mixture models with a prior on the number of components. J. Am. Stat. Assoc. 2018, 113, 340–356. [Google Scholar] [CrossRef]
- Richardson, S.; Green, P.J. On Bayesian analysis of mixtures with an unknown number of components (with discussion). J. R. Stat. Soc. Ser. B Stat. Methodol. 1997, 59, 731–792. [Google Scholar] [CrossRef]
- Rousseau, J.; Mengersen, K. Asymptotic behaviour of the posterior distribution in overfitted mixture models. J. R. Stat. Soc. Ser. B Stat. Methodol. 2011, 73, 689–710. [Google Scholar] [CrossRef]
- Law, M.; Jain, A.; Figueiredo, M. Feature selection in mixture-based clustering. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2002; Volume 15. [Google Scholar]
- Scrucca, L.; Fop, M.; Murphy, T.B.; Raftery, A.E. mclust 5: Clustering, classification and density estimation using Gaussian finite mixture models. R J. 2016, 8, 289. [Google Scholar] [CrossRef]
- Hejblum, B.P.; Alkhassim, C.; Gottardo, R.; Caron, F.; Thiébaut, R. Sequential Dirichlet process mixtures of multivariate skew t-distributions for model-based clustering of flow cytometry data. Ann. Appl. Stat. 2019, 13, 638–660. [Google Scholar] [CrossRef]
- Prabhakaran, S.; Azizi, E.; Carr, A.; Pe’er, D. Dirichlet process mixture model for correcting technical variation in single-cell gene expression data. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016; PMLR: Baltimore, MD, USA, 2016; pp. 1070–1079. [Google Scholar]
- Gabasova, E.; Reid, J.; Wernisch, L. Clusternomics: Integrative context-dependent clustering for heterogeneous datasets. PLoS Comput. Biol. 2017, 13, e1005781. [Google Scholar] [CrossRef] [PubMed]
- Kirk, P.; Griffin, J.E.; Savage, R.S.; Ghahramani, Z.; Wild, D.L. Bayesian correlated clustering to integrate multiple datasets. Bioinformatics 2012, 28, 3290–3297. [Google Scholar] [CrossRef] [PubMed]
- Karras, C.; Karras, A.; Avlonitis, M.; Giannoukou, I.; Sioutas, S. Maximum Likelihood Estimators on MCMC Sampling Algorithms for Decision Making. In Proceedings of the AIAI 2022 IFIP WG 12.5 International Workshops, Artificial Intelligence Applications and Innovations, Crete, Greece, 17–20 June 2022; Maglogiannis, I., Iliadis, L., Macintyre, J., Cortez, P., Eds.; Springer: Cham, Switzerland, 2022; pp. 345–356. [Google Scholar]
- Karras, C.; Karras, A.; Avlonitis, M.; Sioutas, S. An Overview of MCMC Methods: From Theory to Applications. In Proceedings of the AIAI 2022 IFIP WG 12.5 International Workshops, Artificial Intelligence Applications and Innovations, Crete, Greece, 17–20 June 2022; Maglogiannis, I., Iliadis, L., Macintyre, J., Cortez, P., Eds.; Springer: Cham, Switzerland, 2022; pp. 319–332. [Google Scholar]
- Neal, R.M. Markov chain sampling methods for Dirichlet process mixture models. J. Comput. Graph. Stat. 2000, 9, 249–265. [Google Scholar]
- Quintana, F.A.; Loschi, R.H.; Page, G.L. Bayesian Product Partition Models. Wiley StatsRef Stat. Ref. Online 2018, 1, 1–15. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).