Abstract
This work presents an efficient and effective system allowing hospitals to share patients’ private information while ensuring that each hospital database’s medical records will not be leaked; moreover, the privacy of patients who access the data will also be protected. We assume that the thread model of the hospital’s security is semi-honest (i.e., curious but honest), and each hospital hired a trusted medical records department administrator to manage patients’ private information from other hospitals. With the help of Homomorphic Encryption- and Private Set Intersection -related algorithms, our proposed system protects patient privacy, allows physicians to obtain patient information across hospitals, and prevents threats such as troublesome insider attacks and man-in-the-middle attacks.
1. Introduction
The ever-increasing medical treatment and service progress has reduced patients’ burden of seeking appropriate medical care. For example, the migration from paper-based medical records to electronic medical records has significantly enhanced the quality of medical treatments. However, with the coming of an aging society, the medical services required by elderly patients, especially those with chronic diseases, are usually dominated by medicine-taking only. For convenience, medical institutions close to home are often the principal places to seek medical services. However, it can be challenging for regional medical institutions to provide comprehensive medical services. So, patients will seek medical services in different institutions due to etiology and location considerations. This phenomenon usually occurs in densely populated areas, such as Tokyo in Japan and Soul in South Korea, if we take Asia as an example. However, seeking medical assistance from different institutions, diagnosis-related information that should be paid attention to is often overlooked due to the lack of or distributed storage of the patient’s past medical treatment records. This fact damages the rights and interests of both physicians and patients. Before successfully constructing a national unified medical information database, an alternative way to solve the abovementioned problems is to enable various medical institutions to exchange patient medical information under safe and secure conditions and regulations.
From the viewpoint of the physician side, according to the law, physicians do not have the right to review a patient’s past medical records without obtaining the patient’s authorization because this might infringe on the patient’s privacy. Worryingly, suppose doctors cannot know the patient’s past medical history; in that case, they may be unable to make a precise diagnosis and may have more concerns when making decisions, such as whether it will cause drug allergies and adverse side effects. From the viewpoint of the patient side: When a patient wants to retrieve his past medical records from a hospital, the patient needs to justify his identification (e.g., providing his ID number) to the hospital to verify the patient’s legitimate identity. Although examining the ID allows the hospital to complete her system-level identification, the patient may not want to be identified by the hospital if data retrieving is his only objective. For example, discovering from the hospital’s past records and knowing there is a medical dispute with the hospital may infringe on the patient’s privacy and, more seriously, the patient’s rights and interests in treatment.
In addition to regulatory limitations, it may also be against the institution’s interests to disclose the relevant medical records of patients receiving medical services there. Nevertheless, adequate and complete records of patient visits are necessary for medical institutions to provide optimal patient care. To meet the conflicting needs of both sides, we propose a system that allows patients to retrieve or even consult their past medical records stored in other hospitals to help doctors make a precise diagnosis. The system is operated under the guidance of the Hospital’s electronic medical records system (EMRS) administrator and the corresponding patient’s consent. To safeguard privacy, other institutions should not know which patients’ past medical records have been retrieved except the current medical institution the patient is visiting. This system relieves the patient’s burden of remembering or possessing all medical histories while maintaining patient privacy. It also allows doctors to provide the best medical services with adequate patient medical records.
Notice that, with the aid of Homomorphic Encryption algorithms, our proposed system provides an end-to-end secure secret exchanging capability and can operate directly between hospitals. In other words, except for those who must be legally involved, there is no need to acquire assistance from another third party. In addition, to overcome the substantial computational load and memory space usage brought by the Homomorphic Encryption schemes, we enhanced a series of existing acceleration mechanisms to improve the system’s usability vastly. So, it can be treated as an effective and efficient system for accessing or sharing private information among medical institutions. We justify our claim through experiments with system parameters at a practice scale.
This article is organized as follows: in Section 2, we conduct a system security analysis, identify the problems to be solved, discuss several feasible solutions to these problems, and justify why we narrow the problem down to homomorphic encryption and private set intersection schemes; Section 3 elaborates on how to retrieve private data with optimization processes on homomorphic encryption and private set intersection schemes; Section 4 introduces the enhancement of labeled private set intersections and illustrates the entire system protocol with the sequence diagram; Section 5 demonstrates the system’s feasibility by providing the results of the execution time with different parameters; and Section 6 presents conclusions and future work.
For clarity, the glossary and acronyms are listed in Table 1.

Table 1.
Glossary and Acronyms.
2. Problem Formulation and Related Work on Possible Solutions
2.1. The Strawman Protocol and Its Security Threat
The strawman protocol for providing symptom retrieval is used and monitored by the administrator, A, of a hospital HA’s EMRS. For convenience, hereafter, we will not indicate the name of the responsive hospital but directly refer the corresponding EMRS to the administrator’s name, A. Therefore, the task of transmitting patients’ ID numbers from hospital HA to other Hospitals, say Hospitals HB, HC, and HD, can be represented by the information flow diagram shown in Figure 1. If Hospitals HB and HC did have the relevant medical records of the searched patients, administrators B and C would send the related symptoms back to administrator A, respectively.
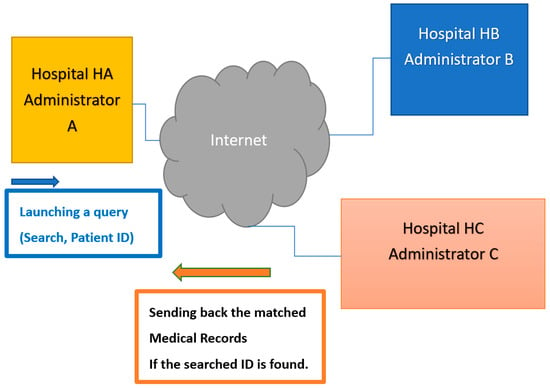
Figure 1.
The Information Flow of the Considered Symptom Retrieving Protocol with the aid of a Cooperative Electronic Medical Recording System.
The security threats of the Strawman protocol presented in Figure 1 can be understood as follows. Suppose a doctor or other interested person in the hospital pretends to be the administrator of the EMRS and initiates a request for symptom retrieval to other hospitals without authorization. In that case, it will infringe on the patient’s privacy. This kind of threat is tough to deal with and is well-known as an insider attack. An essential idea to face insider attacks is that we can introduce a digital signature mechanism, allowing the administrator of the EMRS to sign the message, and other hospitals will verify the message’s origin after receiving it. On the one hand, if Hospitals receive the querying messages in plaintext form, the hospitals can know which patient from which hospital is currently doing the search and whose patient’s records are now being searched; both situations infringe on the patient’s privacy. On the other hand, suppose Hospitals transmit medical records in ciphertext form but the patient’s ID information in plaintext form through insecure channels (such as the Internet). Then, they will still be subjected to another severe security threat, the so-called man-in-the-middle attacks, leading to contaminated sensitive information.
To conquer the threat caused by the middleman, encrypting all communication-related messages, i.e., converting both patient ID and treatment records into the ciphertext domain, is a feasible solution. However, using conventional encryption schemes such as DES and AES, other hospitals have to decrypt the encrypted searching-related message, say the patients’ ID, before conducting the record-seeking task. Consequently, this intermediate decryption process will reveal the footprints of the search pattern. Moreover, after the Hospitals find the records, they must encrypt them again before sending the documents back to the Hospital that initiates the search.
Searchable Encryption and Homomorphic Encryption are two well-known applicable cryptographic approaches to provide ways to relieve the burdens mentioned above. Many searchable encryption schemes and Algorithms [1,2,3,4,5,6] have been proposed to provide various exciting features, such as fine-grained access control, dynamic updates, and attribute revocations. However, searching capabilities must be more potent in most schemes fulfilling actual needs. Usually, they can embed only a single or limited number of keywords into ciphertexts, which is inconvenient and makes searching time-consuming. Although some schemes allow combining multiple keywords and providing ranked search results, users can only fetch files containing all the keywords. Exploring efficient searchable encryption systems to secure medical information circulation and exchange is another exciting and valuable work. We list it as one of our main future research topics. In contrast, in this write-up, we will focus on the second method mentioned above: the Homomorphic Encryption schemes.
2.2. The Homomorphic Encryption Schemes
Homomorphic encryption schemes provide efficient ways for computing and verifying all the processed sensitive data while keeping data confidentiality simultaneously because we can directly conduct all the computations in the encrypted domain. An encryption scheme is called homomorphic over an operation “×” if it satisfies the following equality of equation:
where denotes the encryption algorithm, is an encryption domain operation, and M is the set of all plaintext messages.
Rivest, Dertouzos, and Adleman, [7] first mentioned the concept of “privacy homomorphism” in 1978. RSA [8] is a well-known multiplicatively homomorphic encryption scheme; however, it is not semantically secure. Goldwasser and Micali [9] proposed the first semantically secure homomorphic encryption scheme, which is additively homomorphic over 2. More precisely, homomorphic encryption schemes can be classified into the following three categories: Partially homomorphic encryption (PHE), Somewhat homomorphic encryption (SHE), and Fully homomorphic encryption (FHE).
The category of PHE includes additively homomorphic encryption (AHE) and multiplicatively homomorphic encryption (MHE) schemes. AHE and MHE schemes can only do add/sub and multiplication in the encrypted domain but not simultaneously. AHE schemes with proofs of semantic security include Benaloh, Naccache-Stern, Okamoto and Uchiyama, Paillier, Damgard, Jurik, Kawachi, Tanaka, and Xgawa. On the other hand, RSA and ElGamal are the most well-known MHE schemes. Interested readers can find the definitions and properties of all the PHE schemes mentioned above from the HE-related Wikipedia website [10]. By definition, SHE schemes support both additive and multiplicative operations. However, they can only do a limited number of operations because the accumulated “rounding error” will contaminate the original data or the computational results during the encryption process. When the SHE scheme has been applied several times, the rounding errors mentioned above will grow proportionally and finally cause a decryption failure. Some valuable SHEs have been proposed recently, such as Sander, Young, Boneh, Goh, Nissim, Ishai, and Paskin. Likewise, interested readers can find the definitions and properties of all the schemes mentioned above from the SHE-related survey work [11]. The theoretical proof of the existence of FHE schemes was first provided by Craig Gentry [12] in 2009. With the help of bootstrapping mechanism proposed by Gentry, an unlimited number of arithmetic operations over the encrypted data is doable. Gentry’s work inspired many researchers to pay attention to developing various FHE schemes. According to the FHE-related survey given by Martins, Paulo, Leonel Sousa, and Artur Mariano [13], FHE schemes can be categorized into the following four types: Ideal Lattice-based, Integer-based, (R) LWE-based, and NTRU-like. The following two video records give thorough and comprehensible reviews of the historical development, recent progress, and the challenges that remained on FHE:
- (i)
- “A Decade (or so) of fully homomorphic encryption, by Craig Gentry.” (https://www.youtube.com/watch?v=487AjvFW1lk (accessed on 4 May 2023)), and
- (ii)
- “Fully Homomorphic Encryption: Definitional issues and open problems, by Daniele Micciancio” (https://youtu.be/b24WJyS0dmg (accessed on 4 May 2023)).
By its nature to represent and process messages in ciphertext form, by applying FHE, our system not only can prevent the misconduct caused by the mediator but also ensures that the fraud of leaking and infringing on patients’ privacy can be avoided.
In addition to conducting search operations in the encryption domain, we have to grasp how to retrieve the patient’s symptoms in the plaintext domain to achieve our goal and then analyze the challenges of escalating the problem to the ciphertext domain. Let us probe into the problem in more detail. Assume the patient list sent by the administrator of the EMRS of Hospital HA is plaintext; after another hospital, say Hospital HB, receives the patient list, the easiest way to achieve our goal is to traverse HB’s database to find out whether there is a matching patient. If the answer is yes, the related symptoms of the patient in the database will be fed back to the administrator of the HB’s EMRS. Unfortunately, HE only supports additions and multiplications on ciphertext, but not conditional branching in a programming loop. In other words, no complex program logic, such as “if-else,” exists in the HE-encrypted domain, which brings a significant obstacle to developing HE-based applications in practice.
Therefore, we need to accomplish two tasks with the help of homomorphic encryption algorithms. Task 1: Confirm whether the patient list sent by the administrator of Hospital HA and the medical record databases of other hospitals have found matched patients. Task 2: If there is, return the symptoms corresponding to the matched patients. We can formulate task 1 as “finding the intersection of two sets without leaking the elements of both sets,” a.k.a. the Private Set Intersection (PSI) problem. Let us denote the set of patients in other hospitals be X and the set of patients that the administrator of the EMRS of Hospital HA wants to retrieve every day be Y. In our situation, it usually satisfies |X| >> |Y| (that is, the number of elements of the set X is much larger than that of the set Y). To accomplish Tasks 1 and 2, we will apply the PSI-related techniques, as detailed in Section 2.3.
2.3. The Private Set Intersection Problem and Its Possible Solutions
Reference [14] is one of the first papers to address the concept of PSI. That paper aims to solve the authentication problem of two distrusting parties through an impartial third party. [15] proposed a PSI protocol that does not require an impartial third party. It mainly uses asymmetric cryptography mechanisms, supplemented by hash functions, so that group members can know the intersection with other members. The protocol’s key idea is to protect members’ privacy through signature and verification mechanisms. However, this method faces a trade-off between information leakage and ease of use, and insiders can also spoof this protocol. Then, [16] proposed a protocol based on Oblivious Polynomial Evaluation; the primary polynomial can be expressed in the following formula:
where ∈ Y, ∈ X, and i = 1, …, n. From Equation (2), if is included in the set X, the result after evaluating the polynomial will be 0, and otherwise, if it is not. Notice that we can apply the above polynomial to transform the PSI problem into an HE realizable form.
Different from the conventional polynomial-based solution, [17] proposed the secure Pseudorandom Function (PRF)-based solution for PSI, in which the security of PRF is ensured by introducing an oblivious transfer (OT) protocol. Inspired by [17], many follow-ups OT-based methods have been proposed to solve the PSI problem. For example, [18] uses OT-extension optimization, which significantly improves the speed of Circuit-based and Bloom-filter-based PSI. [19,20,21] also applied the OT method to find the optimal solution for PSI. However, all the above OT-based methods have a common disadvantage: the communication cost will be proportional to the sets of two parties. This condition does not fit the requirement for our application landscapes (one set is large, and the other is relatively small in size).
Reference [22] provided a HE-based PSI protocol. However, due to the time-consuming calculation of HE, it is prone to calculation errors once the number of operations is extensive. Hence, it took work to develop a practical PSI system with HE in the past. However, [22] did improve the computational and communication complexity of the HE-based PSI problem by combining many optimization methods so that it might be feasible to cope with an immense amount of computation and speed up the execution time. Reference [23] extends the work on [22] to deal with the Labeled PSI problem. Suppose a client wants to initiate a Labeled PSI request to a server. The Labeled PSI can be interpreted as each element in the set of servers having a corresponding label in the database, allowing the client to obtain the labels of the intersection elements. A simple illustrative example is as follows: Suppose there are three pieces of data on the Server, namely D1, D2, and D3, the labels corresponding to these three pieces of data are L6, L11, and L18, respectively, denoted as X = {(Di, Li)} = {(D1, L6), (D2, L11), (D3, L18)}. Suppose a client has two pieces of data, D2 and D5, denoted as Y = {Di} = {D2, D5}. Then, when the client initiates a PSI request to the Server, the answer will be {D2} (because the intersection element of the two sets is D2). When the client initiates a Labeled PSI request to the Server, the answer will be {(D2, L11)} (because the intersection element of the two sets is D2, the corresponding label is L11).
Both [22] and [23] provide HE-based PSI solutions, and they meet the needs of our system to suppress the adverse effects brought by the man-in-the-middle attack. Moreover, both works have conducted optimization processes to deal with the case that |X| >> |Y|, which aligns with our application landscape’s assumptions. Since [22,23] build up the backbone of our system architecture, we will explain how [22,23] solves the PSI and the labeled PSI with HE-related approaches in the next Section.
3. Retrieving Private Data with Optimization Processes on Homomorphic Encryption Schemes
For convenience, in the following, we treat EMRSs of other hospitals as the Server side and the administrator of the EMRS of Hospital HA who initiates the request as the Client side. Moreover, we denote the Servers as X and the Clients as Y.
3.1. Transform the PSI Problem into a HE-Operatable Form
Reference [22] converts the PSI problem into the following polynomial form to meet the types of operable operations (addition and multiplication) supported by HE and asks the Server to calculate it on the encryption domain:
where ∈ Y is an element on the Client side, and ∈ X is an element on the Server side. If the result of is 0, it indicates that is also one of the elements on the server side (i.e., there is an intersection between X and Y). If the result is not 0, does not belong to the Intersection Set. It is worth noting that for the Server when calculating , is the plaintext form, while is in the ciphertext form transmitted by the Client after conducting the HE operations.
However, when the result of is not 0, the Client could infer the elements on the Server by initiating multiple PSI requests to the Server, resulting in indirect leakage of the elements on the Server. To eliminate the concerns about leaking elements on the Server, multiplying the above polynomial by a random number is an ingenious way, that is:
This simple operation can ensure that the Client cannot speculate the data on the Server. We can now learn whether the two sets have an intersection through the evaluation of Fx (y; r) on Y by the similar expounds associated with . That is, we regard the the Client requests the Server to evaluate the encryption domain as a PSI-checking request. Next, if there is an intersection between X and Y, we hope to obtain the corresponding labels of the intersected elements. As suggested in [23], a new polynomial could be created based on to fulfill this requirement. That is
In Equation (5), is used to determine whether there is an intersection, and is a curve-fitting polynomial passing through a sequence of given data points which is used to retrieve the corresponding labels of the intersected elements. Taking the two-dimensional space as an example, given the coordinates of k points, we can use the well-known Lagrange Interpolation Formula to find the polynomial that passes through all the given k points on the plane. Therefore, we can transform the server’s database into the coordinate and retrieve the corresponding data label by polynomial interpolation. Suppose there are three data on the server, say 1, 2, and 3, and the corresponding labels are 6, 11, and 18. Then, we can regard the data and the corresponding labels as three points (1, 6), (2, 11), (3, 18) in the two-dimensional space. Then, through the polynomial-based curve-fitting, we can find the desired polynomial. Taking the Lagrange interpolation as an example, can be written as:
It can be easily checked that generated above does satisfy , , .
So far, we can use to complete Task 1 (by ) and Task 2 (by ) mentioned at the end of Section 2.2. Moreover, we can regard the Server’s evaluation of based on the request sent from the Client in the homomorphic encryption domain as a labeled PSI, which retrieves the corresponding labels of the intersected data on both sides of the databases without leaking any sensitive information.
Let us focus on the situation of the pre-described symptom retrieval system. Suppose that the administrator of the EMRS has a set of patient ID numbers Y = {A123456789, X298659978, Z297466383, and so on}, and another hospital, say Hospital HA, has the patient ID numbers and the associated symptoms set X = {(A123456789, hypertension), (T203584780, heart disease, diabetes), (B119641539, asthma), and so on}. The administrator of the EMRS initiates a labeled PSI request to the hospital HA to retrieve the patient’s symptoms, ensuring that the remaining patient information stored in the hospital HA’s database will not be known to the requester. Moreover, the administrator of hospital HA’s EMRS cannot know which patients’ symptoms are being retrieved. Nonetheless, there are still some issues to be resolved.
In HE schemes, there is noise associated with each ciphertext, and sequence operations on the ciphertext will increase the noise progressively. The nature of HE has the operation (whether it is addition or multiplication) on a ciphertext always be a ciphertext. Therefore, we can regard as multiplication operations among the server’s ciphertexts. Further note, that when the noise is too loud, the ciphertext cannot be decrypted correctly. Adding ciphertext and ciphertext, multiplying ciphertext and plaintext, and adding ciphertext and plaintext will not enlarge the noise too much. However, if two ciphertexts are multiplied, the noise will be amplified quickly. Notice that the larger the noise is, the slower the calculation of the ciphertext will be. Therefore, we must resolve these issues; otherwise, when the number of reaches an application-dependent threshold, say more than 10 million items, it will be difficult for the Server to calculate the polynomial correctly within a short period. Therefore, we must optimize the server’s polynomial calculation in the HE domain. The following Section briefly introduces the optimization methods proposed in [22].
Before applying any optimization process, we summarize the above-mentioned labeled PSI protocol between the Client and the Server as follows:
- Step 1: The Client encrypts each element in Y with the homomorphic public key and transmits each encrypted element to the Server one by one.
- Step 2: The server samples two random numbers, and , for each received ciphertext y and calculates Fx (y; r) and = + in the HE domain.
- Step 3: The Server returns the calculated result of and corresponding to each received ciphertext to the Client.
- Step 4: The Client decrypts the received results of and with the HE decryption key. If the decrypted result of is 0, is at the intersection of X and Y, and then refer to the decrypted result of as the label associated with . On the contrary, if the decrypted result of is not 0, it means that is not at the intersection of X and Y, so the result of cannot be referred to as the corresponding label.
The complexity of the above-mentioned labeled PSI protocol before applying any optimization process is shown in Table 2.

Table 2.
The Complexity of the non-optimized labeled PSI protocol.
For the convenience of explanation, the following complexity analysis of optimized Labeled PSI will take the complexity of its non-optimized version as a benchmark. Starting from Section 3.2, we will briefly explain each optimization method proposed in [22,23]. The prerequisite is that the Server and the Client share the following public information:
- |X|: The number of elements in the Server set
- |Y|: The number of elements in the Client set
- H: a secure Hash function
- h: The number of involved hash functions
- The bit length of an element in the data set (e.g., 8 bits, 16 bits, or 32 bits).
3.2. The Batching Process
Reference [24] proposed a technique for data batching in the HE domain. Batching is a skill to encrypt multiple pieces of data into one ciphertext at a time so that multiple pieces of data can be simultaneously processed on the encryption domain. In terms of architectural language, those pieces can be operated in the Single Instruction Multiple Data (SIMD) modes. If n pieces of data are encrypted into one ciphertext at a time, the complexity after optimization through batch processing is listed in Table 3.

Table 3.
The Complexity of the Labeled PSI Protocol after Applying the Batch-based Optimization.
3.3. The Combined Process of Cuckoo Hashing, Multi-Hashing, and Permutation-Based Hashing
Theoretically, with hashing, the time complexity of data access can be reduced to O (1); however, the hash collision problem should first be tackled using hashing. When a hash collision occurs frequently, the time complexity of accessing the hash table will increase, and in the worst case, it may degrade the measure to O (n). This problem has been solved using Cuckoo hashing [25], a hashing algorithm that significantly reduces the probability of hash collision. The trick is to use h (h > 1) hash functions to improve the usage rate of the Hash-Table (where h hash functions will make each data corresponding to h different hashing addresses), and the data access time of O (1) can be guaranteed. Therefore, with both the Client and Server doing cuckoo hashing, the bucket-wise comparison between the Client and the Server can produce the correct intersection. Among them, the Client’s Hash Table has m (>|Y|) buckets, and each bucket has one slot, while the Server’s Hash Table has m (>|Y|) buckets, and each bucket has s slots.
First, let the Client and the Server agree on the value of h and which hash functions H1, H2, …, Hh to use, then both the Client and the Server insert their data into the Hash Tables by using the Cuckoo hashing. Then, when the Client sends y to the Server to confirm an intersection, we expect the Server also to check whether there is a y in the corresponding bucket through Cuckoo hashing within O (1) time complexity. However, the Server cannot know which Hash function was used to insert the elements in each bucket of the Client’s Hash Table, so we need the Server to do multi-hashing.
Multi-hashing means the Server must insert data into the buckets at the hashing addresses according to the outputs of all hash functions. In this way, no matter which hash function the Client uses to insert the data during Cuckoo hashing; the Server can always find the data in the bucket at the hashing address corresponding to one of the hash functions. After the Server completes multi-hashing, the data may be gathered in the earlier slots of each bucket if no processing is performed. In order to avoid data being located in specific slots and indirectly leaking the Hash Table information on the Server, all the slots in each bucket should be shuffled after all data was inserted into the Hash Table.
The permutation-based hashing proposed by [26] is a hashing technique that reduces the data bit length that needs to be stored on the Hash Table by encoding a part of the data in the bucket’s index. It can be used to cope with the problem that the bit number of the data is too high and reduce the memory required to store the data. Suppose the bucket size of the Hash Table is m (here we assume that m is a power of 2, interested readers can learn how to generalize to other sizes from [26]), and split the bit representation of the data x into xL and xR, where |xR| = log (m). Moreover, we denote the hashing address as Location (x) = f (xL) ⊕ xR, where the actual Hash Table data is represented by |xL| bits and f is a random function whose range is in [0, m). Compared with the original approach, only |xL| bits are needed to store the entire x; that is, permutation-based hashing saves log (m) bits.
Combined with the permutation-based hashing and the Cuckoo hashing, we can denote the data hashed with the i-th hash function and its new hashing address as <xL, i> and Locationi (x) = Hi (xL) ⊕ xR, respectively. This approach reduces the size of each data by (log (m) − ⌈log (h)⌉) bits, where ⌈.⌉ denotes the ceiling function. Assuming that the bucket size of the Hash Table is m, and there are s slots in each bucket, the complexity of the Labeled PSI Protocol after applying all the hashing processes mentioned above is listed in Table 4.

Table 4.
The Complexity of the Labeled PSI Protocol after Applying All Hashing-based Optimization (with s slots in each bucket).
3.4. The Windowing Process
In HE operations, the addition and multiplication results between a ciphertext and a plaintext will be in the ciphertext domain. If the depth of multiplication between two ciphertexts is too high, it is easy to cause errors in the obtained results. Therefore, if the Server directly performs the item-by-item operation on , it is equivalent to doing |X| times of inter-ciphertext multiplications. When |X| is a large number (e.g., |X| > 220), the Server is prone to miscalculate the result.
Assuming that the Client wants to retrieve the labels corresponding to y on the Server, an optimization method to reduce the multiplication depth is to let the Client send the ciphertexts (y1) encrypted, (y2) encrypted, (y3) encrypted, …, (y|x|) encrypted to a Server. Next, the Server can expand into = Σai yi, where 0 ≤ i ≤ |X| and ai is the coefficient of the corresponding term of y raised to the power of i. From the Server’s perspective, ai is a plaintext, and yi is a ciphertext sent by the Client, so the Server only needs to multiply the plaintext and the ciphertext for each item and adds these items up to obtain the answer. The communication cost after this optimization is O (|Y||X|), and the multiplication depth of HE reduces to O (1). Although the multiplication depth of the Server becomes O (1), the Client must send the ciphertext’s power of one to power of |X| to the Server for each y, which will increase the communication cost of the Client by |X| times. In our case, |Y| is much smaller than |X|, so this approach causes too much burden for the Client.
Instead of having the Client send the ciphertext y (from the power of one to the power of |X|) to the Server, the above-mentioned communication cost can be mitigated by having the Client only send the y i∙2^(j𝓁) to the Server, where 𝓁 is the window size, for all 1 ≤ i ≤ 2𝓁 − 1 and 0 ≤ j ≤ ⌊log2(|X|/𝓁)⌋. After the Server receives these terms, we can calculate the ciphertexts corresponding to y’s power one to power |X| efficiently and correctly. For example, if 𝓁 is 1, the Client needs to send the encrypted y, y2, y4, y8, …, y2^⌊log2(|X|)⌋ to the Server. This pre-computing process can significantly reduce the multiplication depth of HE operations on the Server, and the extra communication cost paid by the Client will not be too high. The complexity of the labeled PSI protocol after applying the windowing optimization is shown in Table 5.

Table 5.
The Complexity of the Labeled PSI Protocol after Applying the Windowing Optimization Process.
3.5. The Partitioning Process
Since the data stored on the Server have no dependencies with each other, the Server can split the dataset X into α independent parts. We can then conduct the labeled PSI once for each part and send the result of each PSI operation back to the Client so that the Client will receive α split-PSI operation results. There is an intersection if any split-PSI operation result is 0 and vice versa. After applying the Partitioning-based optimization, the complexity of the labeled-PSI protocol is given in Table 6.

Table 6.
The Complexity of the Labeled PSI Protocol after Applying the Partitioning-based optimization Process.
Although the HE-related multiplication depth is indeed improved after applying the partitioning process, the communication cost of the Server to the Client has also increased by α times. In our case, |Y| is a small value; we can still alleviate the increased communication cost due to partitioning. For this, we can use the following modulus switching technique.
3.6. The Modulus Switching Process
When performing homomorphic encryption operations, we will use a set of encryption parameters to encrypt the data, one of which is the modulus q which defines the algebraic structure of the ciphertext. In general, q is a product of multiple prime numbers, which determines the ciphertext noise tolerance for correct decryption. The larger the q value, the greater the noise tolerance, which means that more operations can be performed on the ciphertext, and the size of the ciphertext would be more extensive. When the noise tolerance of the ciphertext is less than or equal to 0, subsequent operations are prone to produce erroneous results. Therefore, at the beginning of encryption, we should choose a larger q to make the ciphertext capable of performing more operations and producing the correct result. When it is determined that the ciphertext will not be subjected to subsequent operations, the q value of the ciphertext can be switched to a smaller q′, thereby reducing the size of the ciphertext and the transmission cost. In addition, replacing q with q′ will not affect the correctness of the decrypted ciphertext. The above statement’s correctness is because the ciphertext size is proportional to log (q). Optimizing this step will reduce the ciphertext size by log (q)/log (q′) times. Similarly, Table 7 depicts the complexity of the Labeled-PSI after applying the Modulus Switching Process.

Table 7.
The Complexity of the Labeled PSI Protocol after Applying the Modulus Switching Process.
4. The Enhanced Labeled-PSI System and the Full Protocol
This Section presents an improved version of the pre-described Labeled-PSI System in which the system’s security level has been enhanced by combining Digital Signature and Homomorphic Encryption Schemes. Figure 2 illustrates the full protocol of Enhanced Labeled-PSI from a high-level perspective. A more in-depth sequence diagram is attached as supplementary material to ease the procedure-checking addressed later and for readers interested in an in-depth sequence diagram. The chart is big in size because it presents the global view and the detailed interactions among all modules of our system. The specific precautions and procedures can be understood as follows:
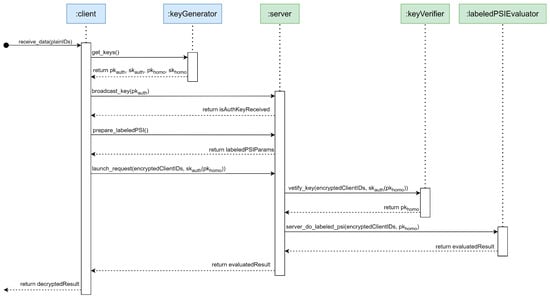
Figure 2.
Sequence Diagram of the Enhanced Labeled Private Set Intersection protocol from a high-level perspective.
- Step 1: The administrator of the EMRS randomly generates a pair of new public-key and private-key, respectively denoted as pkauth and skauth, every day to allow other hospitals to do authentication tasks. In addition, the administrator of the EMRS also needs to generate a pair of new public-key and private-key, respectively denoted as pkhomo and skhomo, for encrypting and decrypting the data into/from the homomorphic domain.
- Step 2: The administrator of the EMRS broadcasts the randomly generated authentication public key, pkauth, to other hospitals through a secure channel so that other hospitals can record that key in their databases.
- Step 3: The administrator of the EMRS needs to obtain the required parameters from other hospitals that need to participate in labeled PSI, such as the partitioning size of server data.
- Step 4: When initiating a request for symptom retrieval from other hospitals, the administrator of the EMRS needs to encrypt the patient’s ID number with a homomorphic public key (cf. pkhomo) into ciphertexts (denoted as IDencrypted). In order to prevent insider attacks, the administrator uses skauth to sign pkhomo, (denoted as skauth (pkhomo)). The administrator of the EMRS can then initiate a labeled PSI request to other hospitals. The administrator needs to transmit IDencrypted and skauth (pkhomo) to other hospitals.
- Step 5: When other hospitals receive skauth (pkhomo), they can try to decrypt it with the stored authentication public key (i.e., pkauth) in their databases. If the decryption is successful, that is pkauth (skauth (pkhomo)) = pkhomo; it means the authentication is successful. Under this condition, other hospitals can accept the labeled PSI request initiated by the Hospital HA’s EMRS administrator and safely use this authenticated pkhomo to retrieve symptoms from their EMRS in the HE domain. Otherwise, the authentication process will fail if an insider wants to use the pk’homo created by himself to initiate a request to retrieve symptoms from other hospitals. In this case, other hospitals can ignore such labeled PSI requests, indirectly preventing insiders from launching denial-of-service attacks.
- Step 6: The administrator of the EMRS can then perform decryption with skhomo after obtaining the evaluated result from the server. All hospitals should clear their stored public key for authentication in the database at the end of each day to prevent replay attacks. In other words, pkauth should be highly timing-sensitive.
5. Feasibility Analyses and Simulation Results
To justify the feasibility and applicability of our optimized labeled-PSI protocol, we have conducted a series of experiments associated with different polynomial degrees, the Client’s dataset size, and the Server’s dataset size. Our experimental settings are as follows:
- Hardware Setup: Asus X550JX 8-core CPU (i7-4720HQ) (CPU clock frequency is fixed at 3.6 GHz)
- Memory: 8 GB
- Operating System: Ubuntu 18.04.5 LTS
- Homomorphic Encryption Framework: SEAL (BFV Scheme)
- Multi-threading Framework: OpenMP
Table 8 and Table 9, respectively, report our protocol’s Single-thread and Multi-thread runtime timing performances associated with testing parameters that are practical for regular-sized hospitals in Taiwan.

Table 8.
The execution time associated with various testing parameters under the Single-thread computation mode.

Table 9.
The execution time associated with various testing parameters under the multi-thread computation mode.
In Table 8, it is observed that when the size of the Server’s dataset is fixed, the size of the Client’s dataset has little effect on the protocol’s execution time. This preferable property came from our insertion of a hash table into the Client’s dataset during optimization and did operations in batching mode. Although the Client’s dataset size is only 100, 1000, or 10,000, those remaining empty slots in the Hash Table will still be used by the Server as the Server is unaware of which slot is empty. In addition, since the HE scheme cannot support branching, there is no similar program logic in our protocol, such as if (empty slot), then skip.
Table 9 shows a similar experimental result to Table 8 under the multi-thread execution mode. There are 8 CPU cores in our testing machine, which means up to 8 times acceleration can be expected in an ideal case. However, only some of the entire program can be parallelly executed as there are dependencies and costs for thread creation, lock acquisition, and aggregation. Nevertheless, we can still see that the overall performance improved after involving multi-threading.
To further prove the feasibility of our protocol, we enlarge the Server’s dataset size to 224, which is the limitation of our testing hardware settings. We demonstrate the runtime timing performance in Table 10.

Table 10.
The execution time associated with various testing parameters under the Multi-thread computation mode and large Server dataset.
In the above tables, Client data size = 100 means sending 100 data to the server. The polynomial degree decides the maximum number of client data sent to the server. For example, polynomial degree = 16,384 means the number of client data that can be sent to the server < 16,384. 8192 and 16,384 are the mostly used degree for homomorphic encryption. The larger the degree, the longer the calculation time. Kindly remember that this article intends to handle the case where the client set size is much smaller than the server. So, in the Tables, we have reported the results associated with client data is 10,000, which should be sufficient for a hospital. Hospital administrators are encouraged to request multiple protocol runs if there is a case where more than 10,000 data is required.
6. Conclusions
Our proposed system can retrieve private data between hospitals through digital signature and HE schemes and prevent insider and man-in-the-middle attacks. In addition, the adopted optimization processes in our system proved the feasibility of private data retrieval using HE schemes while achieving a considerable speedup in execution time. Furthermore, we use the BFV HE scheme [27] in our implementation to encode the data as integers to ensure the correctness of operations. As one of the anonymized reviewers pointed out, our proposed system can apply not only to the case of Hospitals but also to Banks, Department Stores, Research Institutes, and so force. Our proposed protocol aims to preserve users’ privacy meanwhile allows for secure data transmission. Based on this, we analyze many situations in practical usage, such as that the client set size is usually much smaller than the server data size and the flexibility of use of BFV homomorphic implementation to ensure 100% data security.
In other words, if the data can be encoded or indexed as integers, detailed information about the symptoms can be accessed, such as diabetes and hypertension indexes. This consideration can be extended to other scenarios, such as the interactions between insurance companies and hospitals. According to our experiments, even if the Server’s dataset size becomes huge, our protocol can complete one PSI task within 2.33 min with multi-threading execution (eight threads in our setup). In practice, the frequency of secure patient data exchanges among hospitals’ EMRSs is limited daily due to various administration considerations. In other words, with the proposed protocol, each hospital can do secure patient data exchanges with other hospitals approximately 600 times a day. In more precious, let us take the longest execution time in our experiments into account (where polynomial degree = 16,384, client data size = 100, server data size = 224, and the time spent is 139.77 s). Then, considering we have 86,400 s per day, it takes 139.77 s for our proposed protocol. So, 86,400/139.77 621.58. That is the reason why we state that the hospital can perform 600 such operations per day.
In the future, we will look for more possibilities to accelerate our protocol from the hardware perspective and analyze more on memory usage optimization. Most recently, Aner Ben Efraim, Olga Nissenbaum, Eran Omri, and Anat Paskin-Cherniavsky presented a non-homomorphic encryption-based protocol, PSImple [28], to solve the Multiparty Maliciously-Secure Private Set Intersection Problem. Instead of using homomorphic encryption schemes, the construction of PSImple is based on oblivious transfer and garbled Bloom filters. To demonstrate the practicality of PSImple, the authors implemented their protocol and ran experiments with up to 32 parties and 220 inputs. Experimental results showed that PSImple is competitive even with the state-of-the-art concretely efficient semi-honest multiparty PSI protocols. Inspired by [28], how to extend our protocol to a malicious threat model and integrate our protocol with non-homomorphic-based approaches, such as PSImple, to further enhance the values of PSI in practical applications are listed at the top of our future research list.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/a16050244/s1.
Author Contributions
Formal analysis, Y.-W.W.; Funding acquisition, J.-L.W.; Investigation, Y.-W.W. and J.-L.W.; Methodology, Y.-W.W.; Project administration, J.-L.W.; Resources, J.-L.W.; Software, Y.-W.W.; Supervision, J.-L.W.; Writing—original draft, Y.-W.W.; Writing—review & editing, Y.-W.W. and J.-L.W. All authors have read and agreed to the published version of the manuscript.
Funding
The Minister of Science and Technology, Taiwan: MOST 111-2221-E-002-134-MY3 and Taiwan Semiconductor Manufacturing Company: TSMC: 112H1002-D.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, H.; Liu, D.; Jia, K.; Lin, X. Achieving authorized and ranked multi-keyword search over encrypted cloud data. In Proceedings of the 2015 IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 7450–7455. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, D.; Zhang, Y.; Liu, L. Efficiently revocable and searchable attribute-based encryption scheme for mobile cloud storage. IEEE Access 2018, 6, 30444–30457. [Google Scholar] [CrossRef]
- Liu, L.; Wang, S.; He, B.; Zhang, D. A Keyword-searchable ABE scheme from lattice in cloud storage environment. IEEE Access 2019, 7, 109038–109053. [Google Scholar] [CrossRef]
- Miao, Y.; Deng, R.H.; Liu, X.; Choo, K.-K.R.; Wu, H.; Li, H. Multi-authority attribute-based keyword search over encrypted cloud data. IEEE Trans. Dependable Secur. Comput. 2021, 18, 1667–1680. [Google Scholar] [CrossRef]
- Khan, S.; Khan, S.; Zareei, M.; Alanazi, F.; Kama, N.; Alam, M.; Anjum, A. Abkspbm: Attribute-based keyword search with partial bilinear map. IEEE Access 2021, 9, 46313–46324. [Google Scholar] [CrossRef]
- Wang, H.; Ning, J.; Huang, X.; Wei, G.; Poh, G.S.; Liu, X. Secure fine-grained encrypted keyword search for e-Healthcare cloud. IEEE Trans. Dependable Secur. Comput. 2021, 18, 1307–1319. [Google Scholar] [CrossRef]
- Rivest, R.L.; Dertouzos, M.L.; Adleman, L. On data banks and privacy homomorphisms. In Foundations of Secure Computation; Academic Press: New York, NY, USA, 1978; pp. 169–179. [Google Scholar]
- Rivest, R.L.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Goldwasser, S.; Micali, S. Probabilistic encryption & how to play mental poker keeping secret all partial information. In Proceedings of the Fourteenth Annual ACM Symposium on Theory of Computing, San Francisco, CA, USA, 5–7 May 1982; pp. 365–377. [Google Scholar] [CrossRef]
- Wikipedia: Homomorphic Encryption. Available online: https://en.wikipedia.org/wiki/Homomorphic_encryption (accessed on 4 May 2023).
- Fan, J.; Vercauteren, F. Somewhat Practical Fully Homomorphic Encryption. Cryptology ePrint Archive, Paper 2012/144. Available online: https://ia.cr/2012/144 (accessed on 4 May 2023).
- Gentry, C. Fully homomorphic encryption using ideal lattices. In Proceedings of the STOC ‘09: Proceedings of the Forty-First Annual ACM Symposium on Theory of Computing, Bethesda, MD, USA, 31 May–2 June 2009; pp. 169–178. [Google Scholar] [CrossRef]
- Martins, P.; Sousa, L.; Mariano, A. A Survey on fully homomorphic encryption: An engineering perspective. ACM Comput. Surv. (CSUR) 2017, 50, 1–33. [Google Scholar] [CrossRef]
- Meadows, C. A More efficient cryptographic matchmaking protocol for use in the absence of a continuously available third party. In Proceedings of the IEEE Symposium on Security and Privacy, Oakland, CA, USA, 7–9 April 1986; p. 134. [Google Scholar] [CrossRef]
- Huberman, B.A.; Franklin, M.; Hogg, T. Enhancing privacy and trust in electronic communities. In Proceedings of the EC ‘99: Proceedings of the 1st ACM Conference on Electronic Commerce, Denver, CO, USA, 3–5 November 1999; pp. 78–86. [Google Scholar] [CrossRef]
- Freedman, M.J.; Nissim, K.; Pinkas, B. Efficient private matching and set intersection. In Proceedings of the Advances in Cryptology-EUROCRYPT, International Conference on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, 2–6 May 2004; pp. 1–19. [Google Scholar] [CrossRef]
- Hazay, C.; Lindell, Y. Efficient protocols for set intersection and pattern matching with security against malicious and covert adversaries. In Proceedings of the Theory of Cryptography Conference, New York, NY, USA, 19–21 March 2008; pp. 155–175. [Google Scholar] [CrossRef]
- Pinkas, B.; Schneider, T.; Zohner, M. Faster private set intersection based on OT extension. Usenix Secur. 2014, 14, 797–812. Available online: https://www.usenix.org/conference/usenixsecurity14/technical-sessions/presentation/pinkas (accessed on 4 May 2023).
- Pinkas, B.; Schneider, T.; Zohner, M. Scalable Private Set Intersection Based on OT Extension. Cryptology ePrint Archive, Report 2016/930. 2016. Available online: http://eprint.iacr.org/2016/930 (accessed on 4 May 2023).
- Orrù, M.; Orsini, E.; Scholl, P. Actively secure 1-out-of-n ot extension with application to private set intersection. In Proceedings of the Cryptographers’ Track at the RSA Conference, San Francisco, CA, USA, 14–17 February 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 381–396. [Google Scholar]
- Kolesnikov, V.; Kumaresan, R.; Rosulek, M.; Trieu, N. Efficient Batched Oblivious PRF with Applications to Private Set Intersec-tion. Cryptology ePrint Archive, Report 2016/799. 2016. Available online: http://eprint.iacr.org/2016/799 (accessed on 4 May 2023).
- Chen, H.; Laine, K.; Rindal, P. Fast private set intersection from homomorphic encryption. In Proceedings of the CCS ‘17: Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, Dallas, TX, USA, 30 October–3 November 2017; pp. 1243–1255. [Google Scholar] [CrossRef]
- Chen, H.; Huang, Z.; Laine, K.; Rindal, P. Labeled PSI from fully homomorphic encryption with malicious security. In Proceedings of the CCS ‘18: Proceedings of ACM SIGSAC Conference on Computer and Communications Security, Toronto, ON, Canada, 15–19 October 2018; pp. 1223–1237. [Google Scholar] [CrossRef]
- Gentry, C.; Halevi, S.; Smart, N.P. Homomorphic evaluation of the AES circuit. In Proceedings of the 32nd Annual Cryptology Conference (CRYPTO’12), Santa Barbara, CA, USA, 19–23 August 2012; pp. 850–867. [Google Scholar] [CrossRef]
- Pagh, R.; Rodler, F.F. Cuckoo Hashing. J. Algorithms 2004, 51, 122–144. [Google Scholar] [CrossRef]
- Arbitman, Y.; Naor, M.; Segev, G. Backyard cuckoo hashing: Constant worst-case operations with a succinct representation. In Proceedings of the 2010 51st Annual IEEE Symposium on Foundations of Computer Science (FOCS), Las Vegas, NV, USA, 23–26 October 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 787–796. Available online: https://www.cs.huji.ac.il/w~segev/papers/BackyardCuckooHashing.pdf (accessed on 4 May 2023).
- Kuo, T.-H.; Wu, J.-L. A High Throughput BFV-Encryption-Based Secure Comparison Protocol. Mathematics 2023, 11, 1227. [Google Scholar] [CrossRef]
- Ben-Efraim, A.; Nissenbaum, O.; Omri, E.; Paskin-Cherniavsky, A. PSImple: Practical Multiparty Maliciously-Secure Private Set Intersection. In Proceedings of the ASIA CCS ‘22: Proceedings of the 2022 ACM on Asia Conference on Computer and Communications Security, Nagasaki, Japan, 30 May–3 June 2022; pp. 1098–1112. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).