Abstract
Page stream segmentation (PSS) is the task of retrieving the boundaries that separate source documents given a consecutive stream of documents (for example, sequentially scanned PDF files). The task has recently gained more interest as a result of the digitization efforts of various companies and organizations, as they move towards having all their documents available online for improved searchability and accessibility for users. The current state-of-the-art approach is neural start of document page classification on representations of the text and/or images of pages using models such as Visual Geometry Group-16 (VGG-16) and BERT to classify individual pages. We view the task of PSS as a clustering task instead, hypothesizing that pages from one document are similar to each other and different to pages in other documents, something that is difficult to incorporate in the current approaches. We compare the segmentation performance of an agglomerative clustering method with a binary classification model based on images on a new publicly available dataset and experiment with using either pretrained or finetuned image vectors as inputs to the model. To adapt the clustering method to PSS, we propose the switch method to alleviate the effects of pages of the same class having a high similarity, and report an improvement in the scores using this method. Unfortunately, neither clustering with pretrained embeddings nor clustering with finetuned embeddings outperformed start of document page classification for PSS. However, clustering with either pretrained or finetuned representations is substantially more effective than the baseline, with finetuned embeddings outperforming pretrained embeddings. Finally, having the number of documents K as part of the input, in our use case a realistic assumption, has a surprisingly significant positive effect. In contrast to earlier papers, we evaluate PSS with the overlap weighted partial match F1 score, developed as a Panoptic Quality in the computer vision domain, a metric that is particularly well-suited to PSS as it can be used to measure document segmentation.
1. Introduction
The task of page stream segmentation (PSS) is concerned with the segmentation of consecutive streams of pages into their original source documents. This task is of great importance to digitalization efforts in many different domains, such as archiving and the digitization of records from financial institutions [1,2].
The current state-of-the-art approaches to PSS view segmentation as a classification problem; binary classifiers are trained to detect whether or not a page is the first of a document [1,2,3,4]. However, using this approach, efficiently incorporating information from the surrounding pages is complicated. This information might be highly relevant to the task, for example, for streams of documents where starting pages have very different layouts. Instead, we approach PSS as an agglomerative clustering problem in which each page is compared to its neighbouring pages and pages are represented as either finetuned or pretrained vectors. This way, we leverage the relationships between pages, instead of viewing them as stand-alone objects. We do this under the hypothesis that pages in a document are more similar to each other than pages from other documents. This method has been used before, by Thompson and Nikolov in 2002 [5], but they used a combination of rule-based representations and a classification model to determine similarity. We follow a similar strategy, but instead use representations obtained from deep learning models. Although both text and images are used by the current state-of-the-art approaches [2,3], early experiments in our research showed almost no improvement when including text and therefore we focus only on images.
Research Aim Our aim is to improve PSS performance by using restricted connectivity agglomerative clustering and vector representations of pages taken from finetuned and pretrained deep learning models. We will answer the following research questions:
- RQ1
- Does the clustering performance improve when we use supervision? That is, with vector representations from a finetuned neural model [2] instead of from a pretrained classification model (VGG16) [6].
- RQ2
- How can we adapt agglomerative clustering to PSS, and does this lead to an improved performance?
- RQ3
- Does treating the number of documents, K, in a stream as given lead to a substantially higher classification performance?
In our experiments, we found that neither clustering with pretrained models nor finetuned neural page representations outperformed current start of document page classification methods. Clustering with both representations is substantially more effective than the baseline, with finetuned vectors outperforming pretrained vectors. Having the number of documents K as part of the input, in our use case a realistic assumption, has a surprisingly significant positive effect.
Although our results were negative, we still feel it has merit for the community to communicate them. We tried the most natural—in our experience, this is how humans do it—approach to PSS: agglomerative clustering. One simply keeps on adding pages to a document as long as they are similar to the pages already collected. However, through an extensive analysis we found that the underlying hypothesis—pages from the same document have higher similarity than pages from different documents—does not hold with state-of-the-art vector representations of pages. Maybe humans use a more versatile representation of pages, choosing and combining on the fly content, structure, layout, style and other clues in their similarity judgements.
2. Background and Related Work
2.1. Agglomerative Clustering
Agglomerative clustering was developed by Joe Ward in 1963 [7] as a way to cluster large groups of items based on many variables. In the field of text analysis, agglomerative clustering has mainly been used for two different purposes: clustering documents and topical clustering of text. In 2013, Su et al. [8] combined agglomerative clustering with keyword frequency comparisons for document clustering. In the same year, Alfred et al. [9] used TF–IDF (Term Frequency–Inverse Document Frequency) document vectors for clustering and in 2019, Franciscus et al. [10] used word embeddings instead of TF–IDF to cluster tweets.
Regarding topic clustering in documents, Wu et al. [11] created a linear segmentation algorithm based on hierarchical clustering and in 2020 Bodrunova et al. [12] used agglomerative clustering based on sentence embeddings to find topics in news articles.
2.2. Page Stream Segmentation
Regarding page stream segmentation, the field has developed from using statistical approaches based on page similarity to using machine learning approaches. In 2002, Thompson and Nikolov [5] used bottom-up hierarchical clustering in combination with a classifier working on rule-based page representations which yields page similarities to segment streams into documents. The main difference between their approach and the approach used in this paper is that we do not rely on handcrafted feature vectors containing layout information, but that we instead use vectors obtained from a neural vision model, which is expected to encode many of these features implicitly. Additionally, we limit our studies to clustering pages on their visual features, instead of incorporating textual information.
In 2009, Meilender and Belaïd [13] extracted specific fields from the images of pages as features for a left-to-right (Bakis) hidden Markov model. The first study that viewed PSS only as a classification problem was that of Agin et al. [14], who used a Bag of Visual Words (BoVW) representation and three different classifiers: Support Vector Machines (SVM), Random Forest and Multilayer Perceptron (MLP). In 2014, Rusinol et al. [15] used both image and text as input for their SVM and were the first to use multimodal machine learning for PSS. In 2021, with the use of transfer learning, Wiedemann and Heyer [2] achieved state-of-the-art PSS performance by creating a multimodal classification model using the VGG16 architecture [6] for images and a pretrained FastText [16] model for word embeddings. Guha et al. [3] experimented with using domain specific BERT [17] models and found that this only yielded a minor improvement. Although these neural binary classification methods have proven successful, there is still room for improvement, as these models learn to rely solely on the features of individual pages for classification, instead of leveraging interpage relationships. By using agglomerative clustering, we explicitly model these interpage dependencies, allowing the model to utilize the information from surrounding pages. Our work is related to that of Demirtas et al. [1], where they included the interpage context by adding page dependencies using 33 semantic classes, which increased the performance substantially. The main difference in our method is that we do not add explicit relationship information to the data, but rather model these relationships by using agglomerative clustering, which makes these possible relationships explicit.
3. Materials and Methods
3.1. Materials
In this study, we use a newly released open dataset for page stream segmentation that contains streams of Dutch governmental documents collected during the period from January to August 2022. In our experiments, we only consider streams that contain at least two documents. The dataset contains 108 streams with an average stream length of 827 pages and an average of 226 documents per stream. It contains 89,491 pages and 24,181 documents, with roughly of these documents consisting of only one page. Figure 1 contains an illustration of the task, with a stream of documents which contains seven pages and three separate documents. The task of a PSS model is to retrieve the boundaries given these seven consecutive pages. As mentioned in the Introduction, we only consider the images of the scanned pages as input to the models in this research, working only on the visual representations and not making direct use of the textual information present in the pages. For both the binary classification method and the agglomerative clustering method, we extract pages from streams as png files with a dpi of 300, and then convert them to the input format required by the CNN model (maximum size of 224 by 224 pixels).
Figure 1.
Illustration of the PSS task, where the numbered rectangles indicate the pages. In this illustration, we have a stream of seven pages that are contained within three documents. The task is to identify pages one, four and six as pages that start a new document.
The dataset and code used to run the experiments in this paper are available on Zenodo and GitHub via https://github.com/irlabamsterdam/PSS_clustering (accessed on 16 May 2023).
3.2. Method
In this research, we compare our approach based on agglomerative clustering to a binary classification algorithm that uses the VGG16 architecture for image classification [6], both using pretrained vectors from this model, as well as vectors that were extracted after the model had been finetuned on the PSS task. In addition, we also compare our method to a non-learned baseline that uses only information on the mean number of documents in a stream.
The VGG16 model is an image classification model that has been trained on data from the ImageNet classification task [18]. The model is often used to extract feature vectors from images by feeding images through the network trained on ImageNet and extracting the output from the last layer, where these embeddings can then be used in downstream tasks. As the VGG16 model was not trained on the specific dataset, these will be referred to as pretrained embeddings, and the intuition is that these vectors contain general information on the features of an image. However, the model can also be finetuned for a specific classification task, further training the model to extract features specific to the dataset. We will refer to embeddings extracted after this dataset-specific training step as finetuned embeddings.
For both the clustering and the classification methods, streams are represented as binary vectors, where one indicates that the page is the first page of a document and a zero indicates that it is the continuation of a document.
For the VGG16 model from Wiedemann and Heyer, we used png images converted to the appropriate format for required the model. Then, we used those images to finetune the model—based on the study of Wiedemann and Heyer [2]—for 20 epochs with a batch size of 32 and a learning rate of .
Finetuned vector representations are taken from the last dense layer of our VGG16 model and pretrained vectors are taken from the last dense layer of the pretrained VGG16 model [6]. Finetuned and pretrained vectors have 256 and 4096 dimensions, respectively. These pretrained and finetuned embeddings will then be used as input to the agglomerative clustering method.
For the implementation of the agglomerative clustering algorithm, we use the sklearn AgglomerativeClustering [19] implementation. We calculate the cosine distance for each page representation and its neighbouring pages, restrict connectivity to only neighbouring pages, normalize the distances and use the average linkage function to perform clustering. Restricting the connectivity to neighbouring pages is necessary, as pages cannot belong to the same document if pages between them are not part of the same documents, given the fact that the pages are represented in a specific order.
Both the use of cosine similarity and the average linkage function were found to yield the best results in a hyperparameter search. When we performed agglomerative clustering, we assumed that the number of clusters is known and use it in the model.
Since we assume the number of documents K in a stream to be known, we differentiate between normal classification predictions, in which we use a threshold of 0.5 to assign a page a positive label, and Top-K classification predictions, in which we set the K highest predicted scores in a stream to 1.
For the experiments in this paper, we split the data into a training and test set, with 70% and 30% of the total streams, respectively.
3.3. Metrics
Since we view the task of PSS as a clustering task, we also report the performance of models using a clustering/segmentation metric from the computer vision domain, called Panoptic Quality (PQ) [20], as well as also reporting the scores of models using the P1 metric on the page labels alone, as this has several drawbacks, which have been discussed at length in the literature [21,22].
In the computer vision domain, the Panoptic Quality metric is used to measure how well a model is able to recognize and segment parts of images. As an example, consider a task in which we have to detect animals in an image, and our model returns bounding boxes of pixels where it predicts an animal. The metric is most easily understood when broken down into two components, namely the Recognition Quality and the Segmentation Quality. The former measures how many of the objects have been recognized, and the latter measures how well these detected objects are recognized. (In the case of the animal pictures, how close are the predicted bounding boxes to the actual boundaries?) For computation of the Recognition Quality, the Jaccard similarity between a document in the gold standard and all documents in the predicted stream is used to calculate true positives. If there exists a predicted cluster p for which the Jaccard similarity with a gold standard cluster t is higher than , this is counted as a true positive, which also forces each gold standard document to be matched to at most one predicted document. In the case of documents, this would give the ratio of how many pages were in the same document for predicted and gold standard.
The recognition quality is then calculated as , where FP are the false positives and FN are the false negatives.
For the segmentation metric, we want to know how well the true positives were matched, which we will calculate using the Jaccard similarity, and this yields the formula below:
Combining both the Recognition Quality and the Segmentation Quality, the complete Panoptic Quality metric is defined as the multiplication of the two, where the Segmentation Quality in essence weights the Recognition Quality.
For both clustering and classification we measure results using the F1 score for the positive class, i.e., pages that mark the start of a new document.
We report the average scores over all streams in the test set and compare obtained scores against a non-learned baseline, in which every predicted document has the mean document length of that stream, which we will refer to as the Mean Document Length Baseline.
4. Results and Discussion
Table 1 contains the results of our experiments. All methods outperform the baseline, most of them substantially. The switch method is explained in Section 4.2.

Table 1.
Average F1 scores over 33 streams (6.476 docs with 25.124 pages) for the classification and clustering methods as well as the mean document length baseline. For the clustering methods, we assume K to be known.
We now briefly answer our research questions. After that we will dive deeper and give an explanation for the somewhat disappointing result. Our main conclusion is that boundary page classification is far superior to clustering for PSS, even if the number of documents is not known. Regarding the subquestions, we find that supervision does help with clustering, and even more so when we apply the switch method, with the Doc F1 increasing from 0.25 to 0.52.
Concerning classification, the Page F1 score of 0.86 obtained on our corpus is in line with that reported in [2] on their corpus. Our main positive result is that when the number of documents K is known, we obtain a 28% performance gain in Doc F1. In our use case, this K can often be obtained through knowledge extraction. This result shows that it pays to invest in estimating the number of documents in a stream.
4.1. RQ1: How Much Does Supervision Help Clustering?
By using finetuned embeddings from the VGG16 binary classification model trained on the dataset, some of the label information is retained in the embeddings. We expect this to be reflected in the vectors, and as a result we expect the vectors are tuned towards more specific regions of the pages.
With the use of GradCam [23], we found that the finetuned vectors from the classification model focus primarily on email headers or contact information in letters, as visible in Figure 2a,b. For the pretrained vectors, this is not the case, and the pretrained representations are based on more general features such as the page structure or whether or not a page contains an image or a table, as seen in Figure 2c,d. We believe that these pretrained embeddings yield a more intuitive separation of pages. For example, with pretrained representations, the distance is high between a page with only an image and a page with only text. The finetuned embeddings from the classification model on the other hand see both these pages as “uninteresting” (classified as 0), which causes the distance to be low. However, as can be seen in Table 1, this intuitive way of separating pages is too simplistic for a complex task such as PSS. We calculated the average distance between pages from the same documents and with pages from different documents and found that there was almost no difference, with an average cosine distance of 0.232 and 0.236, respectively. Therefore, we have to conclude that our hypothesis was wrong and that pages from the same document are not more similar to each other than pages from different documents. In fact, documents in our dataset do not have a big variety and start pages can be identified by considering only a few features. We suspect that with more variety in documents, clustering might perform better. Simultaneously, if there are more types of start pages, classification would likely perform worse.

Figure 2.
GradCam visualization of pretrained and finetuned vectors of a starting (left) and a non-starting (right) page. (a) Finetuned vector of starting page. (b) Finetuned vector of non-starting page. (c) Pretrained vector of the same (starting) page. (d) Pretrained vector of the same (non-starting) page.
4.2. RQ2: What Goes Wrong with Clustering and Can We Repair It?
Since the finetuned representations are taken from a classifier, these representations reflect its prediction; that is, whether or not a page starts a new document (class 1 or 0).
This is supported by Table 2, where we see that the cosine distance between pages of the same class is lower than the cosine distance between pages of the other class. Two of these four scenarios cause a problem: we want (1, 1) to be clustered into different groups, which will not occur given that they have a low distance. Conversely, (1, 0) should be clustered together, as the 0 here represents the second page of a new document. We call this the similarity problem and attempt to solve it by using the “switch” cluster method.

Table 2.
Mean normalized cosine distances of finetuned representations grouped by classifier predictions.
Here, if a distance between two consecutive pages is higher than a threshold—set to the highest distance in the stream with K is the number of documents—we set (“switch”) as the distance between the next pair of pages, and to , where is the average distance, clipping the distance to zero if the resulting distance is negative. In essence, this formula causes page pairs with a high distance to have a lower distance, and page pairs with a low distance to have a higher distance. The intuition behind this is that if the distance between two pages is high, it is either a transition from a boundary page to a non-boundary page or vice versa. After the first page of the stream, we will always encounter the (0, 1) transition first; thus, this transition is indicated by encountering a high similarity. The next transition is then either (1, 0) or (1, 1), the two problematic cases we described above. By switching this distance, we obtain the desired low/high distance in both cases. Figure 3 shows an example of the switch method for an example stream. We can see the effectiveness of this method back in the results in Table 1; the highest score using clustering was obtained with the switch.
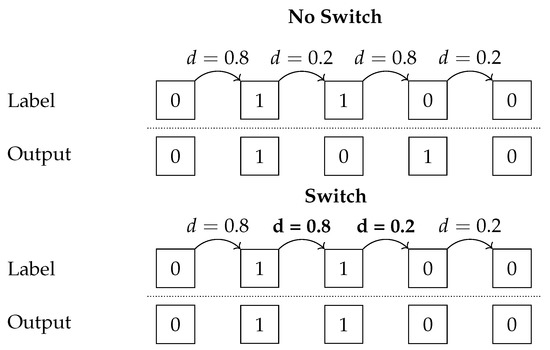
Figure 3.
Example of the similarity problem for part of a five-page example stream and the fix proposed by the switch method, with boldfaced numbers indicating changed distances. , K = 2 and threshold = .
Clustering still suffers from another problem introduced by using the switch method, in which one mistake is multiplied into many. We call this the entry problem. In explanation, Figure 4 contains the binary predictions versus the gold standard of an example from our test set. We only consider the part of the stream indicated by the 0s and 1s. The first two pages are in reality both start pages , but the switched distance is not enough to classify them apart and thus they are grouped together in the prediction . What follows after this first mistake is that the cluster model is able to properly identify document boundaries, but because the entry value of this chain was wrong all predictions are exactly the opposite of what they should be (the 40 page long red part in the figure).

Figure 4.
The entry problem in a stream from the test set.
We were not able to solve both this problem and the similarity problem, as we cannot predict where the cluster model is wrong. The impact of this problem on the scores is large. We consider the entry problem to be the case when at least 11 pages with a minimum of four different document boundaries are predicted to be the opposite of the ground truth. With this definition, the entry problem is the cause of 1107 wrongly predicted pages (4.4% of all pages in the test set). If we could repair the entry problem and only count the initial mistake, Page F1 would increase from 0.61 to 0.72 and Doc F1 from 0.53 to 0.63.
4.3. RQ3: How Much Does Knowing K Help?
If we focus on the effect of K on the performance of the binary classification methods, we see in Table 3 that the normal classification models and top-K classification models make almost the same total number of mistakes, but with the top-K method, false positives and false negatives are completely balanced while they are not when K is not given.

Table 3.
FPs and FNs for start page classification.
The equal precision and recall caused an increase in their harmonic mean. When K is given, the classifier is forced to assign more pages to the True class, increasing the recall. This naturally comes with more false positives, but the increase in correctly identified starting pages is so large that the precision goes up as well. The effect on Doc F1 is even larger: a 29% increase to 0.87. Indeed, knowing K causes 230 extra correctly identified start pages, but almost 1300 correctly identified documents. Of these 1300, 830 are one- or two-page documents, for which the Panoptic Quality requires a complete match between the predicted and true pages. Our task PSS is after all about segmenting a stream into documents, so a high score on the document metric is the ultimate goal.
5. Conclusions and Future Work
We found that classification substantially outperforms clustering for PSS, even more so when the number of documents in a stream is given. Clustering with representations of the classification model gives better results than with pretrained representations. However, clustering with finetuned representations still faces two problems: the similarity problem, which we solved using “switch clustering”, and the entry problem, which we were not able to solve. We conclude that pretrained representations are too simplistic for such a complicated task as PSS.
In future work, we will consider changing certain parameters of the agglomerative clustering method to more suit the task of PSS. One such change could be the definition of the linkage function to only consider specific pages when merging clusters, such as the first N pages and the last N pages of documents, as this seems to be more in line with human intuition on how to perform the task. Another interesting direction for future work is to investigate the robustness of these models across different datasets, as their focus on interpage relationships might prove beneficial in scenarios with limited training data.
We suggest not ruling out clustering entirely, as more variety in documents could both favor clustering and hinder classification.
Author Contributions
Conceptualization, L.B., M.M. and R.v.H.; resources, M.M. and R.v.H.; data curation, M.M. and R.v.H.; software L.B.; formal analysis, L.B., M.M. and R.v.H.; supervision, M.M. and R.v.H.; funding acquisition, M.M.; validation, R.v.H. and M.M.; investigation, L.B., R.v.H. and M.M.; visualization, L.B., R.v.H. and M.M.; methodology, L.B., R.v.H. and M.M.; writing—original draft, L.B.; project administration, R.v.H. and M.M.; writing—review and editing, all authors. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported in part by the Netherlands Organization for Scientific Research (NWO) through the ACCESS project grant CISC.CC.016.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Both the data and the code used in this research are publicly available via a GitHub Link (https://github.com/irlabamsterdam/PSS_clustering) (accessed on 16 May 2023).
Conflicts of Interest
The authors have no conflict of interest to declare that are relevant to the content of this article.
References
- Demirtaş, M.A.; Oral, B.; Akpınar, M.Y.; Deniz, O. Semantic Parsing of Interpage Relations. arXiv 2022, arXiv:2205.13530. [Google Scholar]
- Wiedemann, G.; Heyer, G. Multi-modal page stream segmentation with convolutional neural networks. Lang. Resour. Eval. 2021, 55, 127–150. [Google Scholar] [CrossRef]
- Guha, A.; Alahmadi, A.; Samanta, D.; Khan, M.Z.; Alahmadi, A.H. A Multi-Modal Approach to Digital Document Stream Segmentation for Title Insurance Domain. IEEE Access 2022, 10, 11341–11353. [Google Scholar] [CrossRef]
- Braz, F.A.; da Silva, N.C.; Lima, J.A.S. Leveraging effectiveness and efficiency in Page Stream Deep Segmentation. Eng. Appl. Artif. Intell. 2021, 105, 104394. [Google Scholar] [CrossRef]
- Collins-Thompson, K.; Nickolov, R. A clustering-based algorithm for automatic document separation. In Proceedings of the SIGIR 2002 Workshop on Information Retrieval and OCR: From Converting Content to Grasping, Meaning, Tampere, Finland, 11–15 August 2002. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Ward, J.H., Jr. Hierarchical Grouping to Optimize an Objective Function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Su, C.; Zhou, J.; Bao, F.; Takagi, T.; Sakurai, K. Collaborative agglomerative document clustering with limited information disclosure. Secur. Commun. Netw. 2013, 7, 964–978. [Google Scholar] [CrossRef]
- Alfred, R.; Fun, T.S.; Tahir, A.; On, C.K.; Anthony, P. Concepts Labeling of Document Clusters Using a Hierarchical Agglomerative Clustering (HAC) Technique. In Proceedings of the The 8th International Conference on Knowledge Management in Organizations; Uden, L., Wang, L.S., Corchado Rodríguez, J.M., Yang, H.C., Ting, I.H., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 263–272. [Google Scholar]
- Franciscus, N.; Ren, X.; Wang, J.; Stantic, B. Word Mover’s Distance for Agglomerative Short Text Clustering. In Proceedings of the Intelligent Information and Database Systems; Nguyen, N.T., Gaol, F.L., Hong, T.P., Trawiński, B., Eds.; Springer: Cham, Switzerland, 2019; pp. 128–139. [Google Scholar]
- Wu, J.W.; Tseng, J.C.; Tsai, W.N. An Efficient Linear Text Segmentation Algorithm Using Hierarchical Agglomerative Clustering. In Proceedings of the 2011 Seventh International Conference on Computational Intelligence and Security, Sanya, China, 3–4 December 2011; pp. 1081–1085. [Google Scholar] [CrossRef]
- Bodrunova, S.S.; Orekhov, A.V.; Blekanov, I.S.; Lyudkevich, N.S.; Tarasov, N.A. Topic Detection Based on Sentence Embeddings and Agglomerative Clustering with Markov Moment. Future Internet 2020, 12, 144. [Google Scholar] [CrossRef]
- Meilender, T.; Belaïd, A. Segmentation of continuous document flow by a modified backward-forward algorithm. In Proceedings of the Document Recognition and Retrieval XVI, International Society for Optics and Photonics, San Jose, CA, USA, 18–22 January 2009; Volume 7247, p. 724705. [Google Scholar]
- Agin, O.; Ulas, C.; Ahat, M.; Bekar, C. An approach to the segmentation of multi-page document flow using binary classification. In Proceedings of the Sixth International Conference on Graphic and Image Processing (ICGIP 2014), Beijing, China, 24–26 October 2014; Wang, Y., Jiang, X., Zhang, D., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2015; Volume 9443, pp. 216–222. [Google Scholar]
- Rusinol, M.; Frinken, V.; Karatzas, D.; Bagdanov, A.D.; Lladós, J. Multimodal page classification in administrative document image streams. Int. J. Doc. Anal. Recognit. (IJDAR) 2014, 17, 331–341. [Google Scholar] [CrossRef]
- Bojanowski, P.; Grave, E.; Joulin, A.; Mikolov, T. Enriching Word Vectors with Subword Information. Trans. Assoc. Comput. Linguist. 2017, 5, 135–146. [Google Scholar] [CrossRef]
- Devlin, J.; Chang, M.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Kirillov, A.; He, K.; Girshick, R.; Rother, C.; Dollár, P. Panoptic segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 9404–9413. [Google Scholar]
- Beeferman, D.; Berger, A.; Lafferty, J. Statistical models for text segmentation. Mach. Learn. 1999, 34, 177–210. [Google Scholar] [CrossRef]
- Pevzner, L.; Hearst, M.A. A critique and improvement of an evaluation metric for text segmentation. Comput. Linguist. 2002, 28, 19–36. [Google Scholar] [CrossRef]
- Selvaraju, R.R.; Das, A.; Vedantam, R.; Cogswell, M.; Parikh, D.; Batra, D. Grad-CAM: Why did you say that? Visual Explanations from Deep Networks via Gradient-based Localization. arXiv 2016, arXiv:1611.07450. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).