Unsupervised Cyclic Siamese Networks Automating Cell Imagery Analysis
Abstract
1. Introduction
- Smudges, in some cases larger than cells. Simple background filtering does not work, as these can move during the experiment.
- Ongoing cell divisions (Figure 1 right), making it unclear in some cases what the actual correct target variable would be, but giving a meaning to comma values as they can represent an ongoing division.
- Varying contrast and light conditions.
- Dying, appearance, and vanishing of cells.
- Overpopulation of the cell chamber or the end of an experiment due to escape of the cells.
- Overlapping and close adherence of cells.
- Continuous changes in the cell membrane and inner organelles, changing the orientation of cells, with variations in shape and perceived size.
- We achieve high prediction preciseness on the target variable where the state of the art fails to do so.
- We build an effective translation learning pipeline and show, on multiple microscopy data sets, that this pipeline is stable and reliable throughout this domain.
- We gain additional insight into the inner state of the neural network by performing translations twice (cycling), leading to critical parts of the architecture to optimize the network for the domain without overfitting to the specific data, thus contributing to the understanding of deep neural network representations, especially for Siamese networks [6].
2. Related Work
3. Methodology
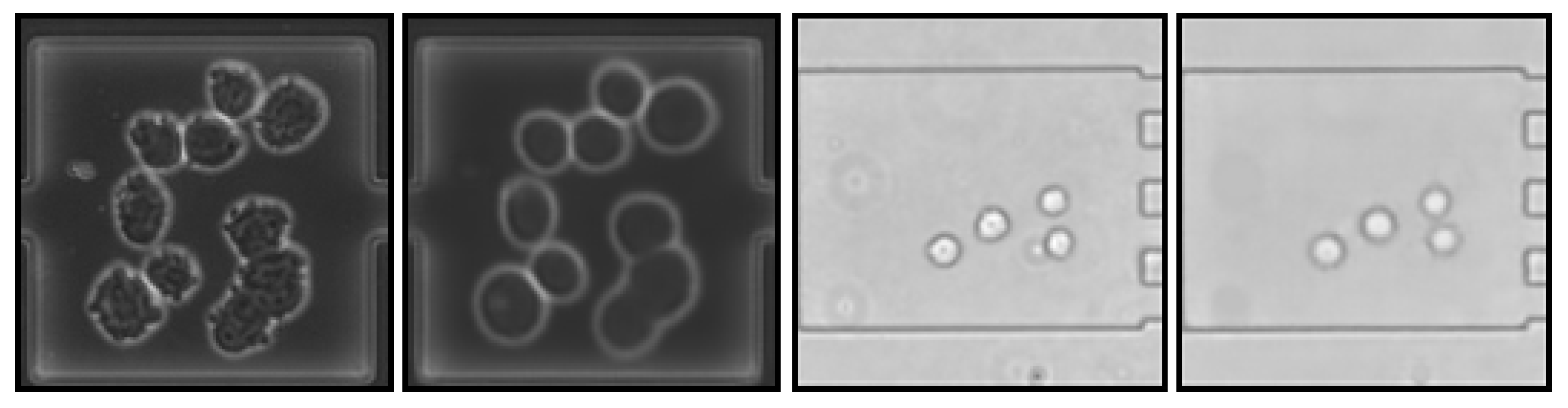
3.1. Natural Data
3.2. Synthetic Data
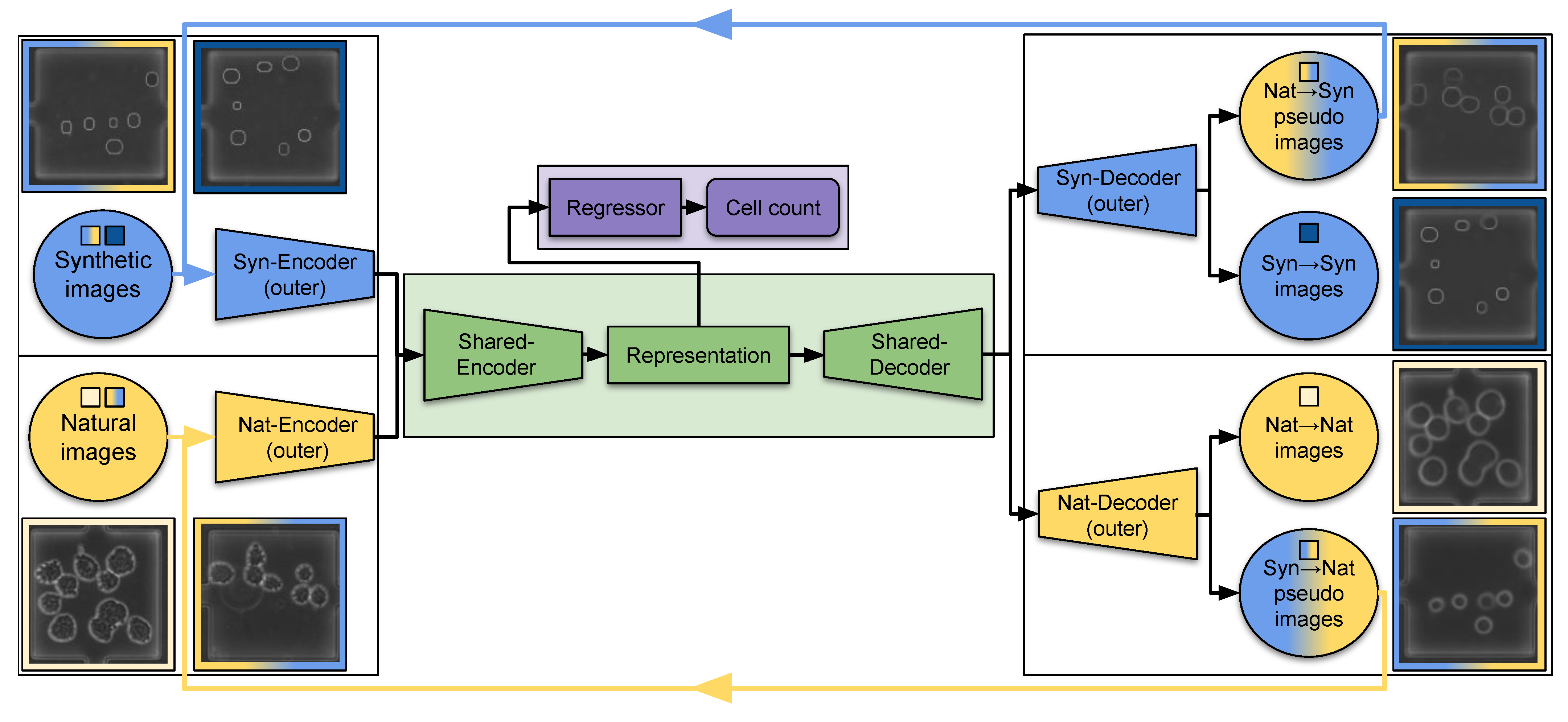
3.3. Architecture and Learning Scheme
3.3.1. Architecture
3.3.2. Learning Scheme
3.3.3. Baselines
4. Results
4.1. Comparison
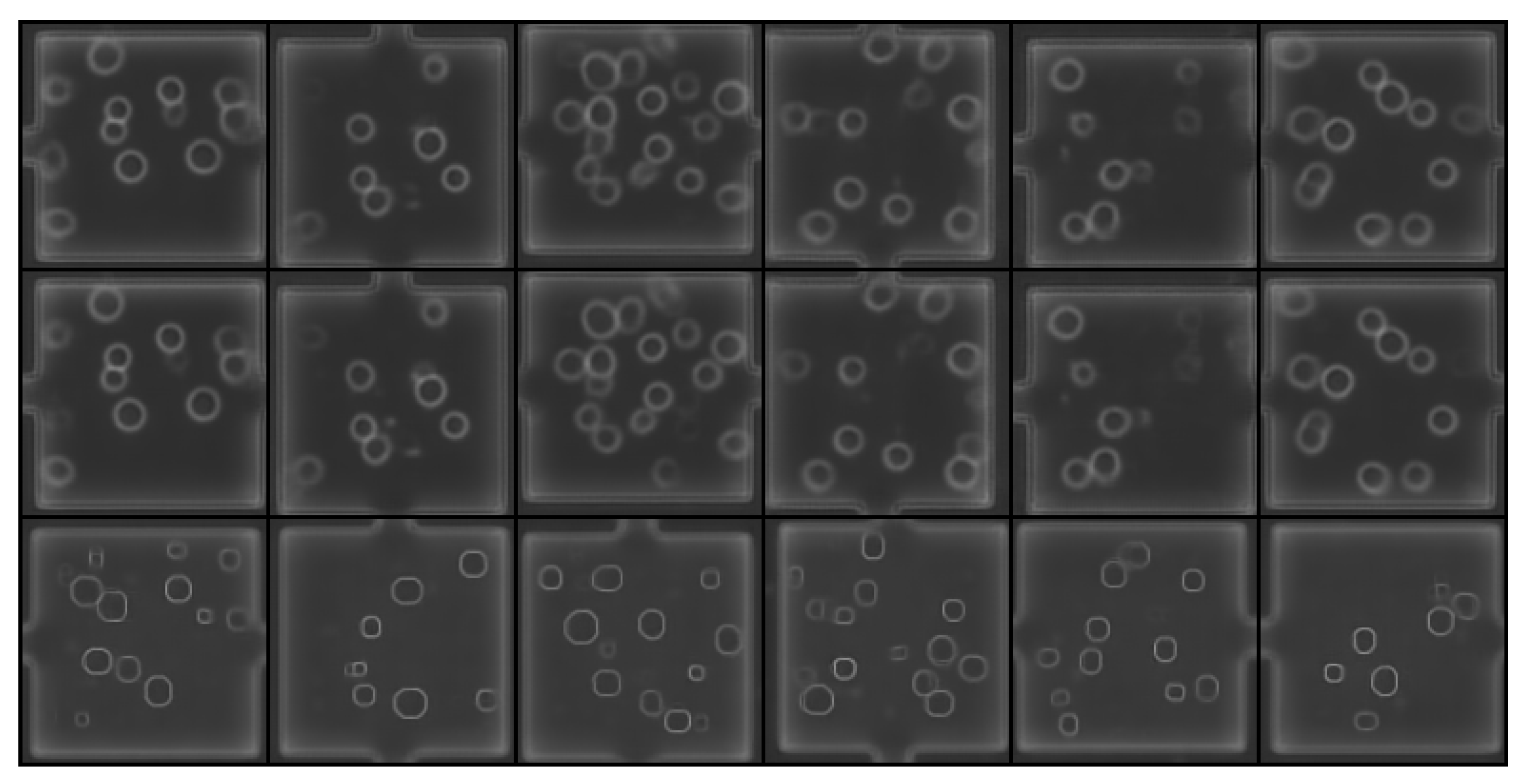
4.2. Image Reconstruction and Representation
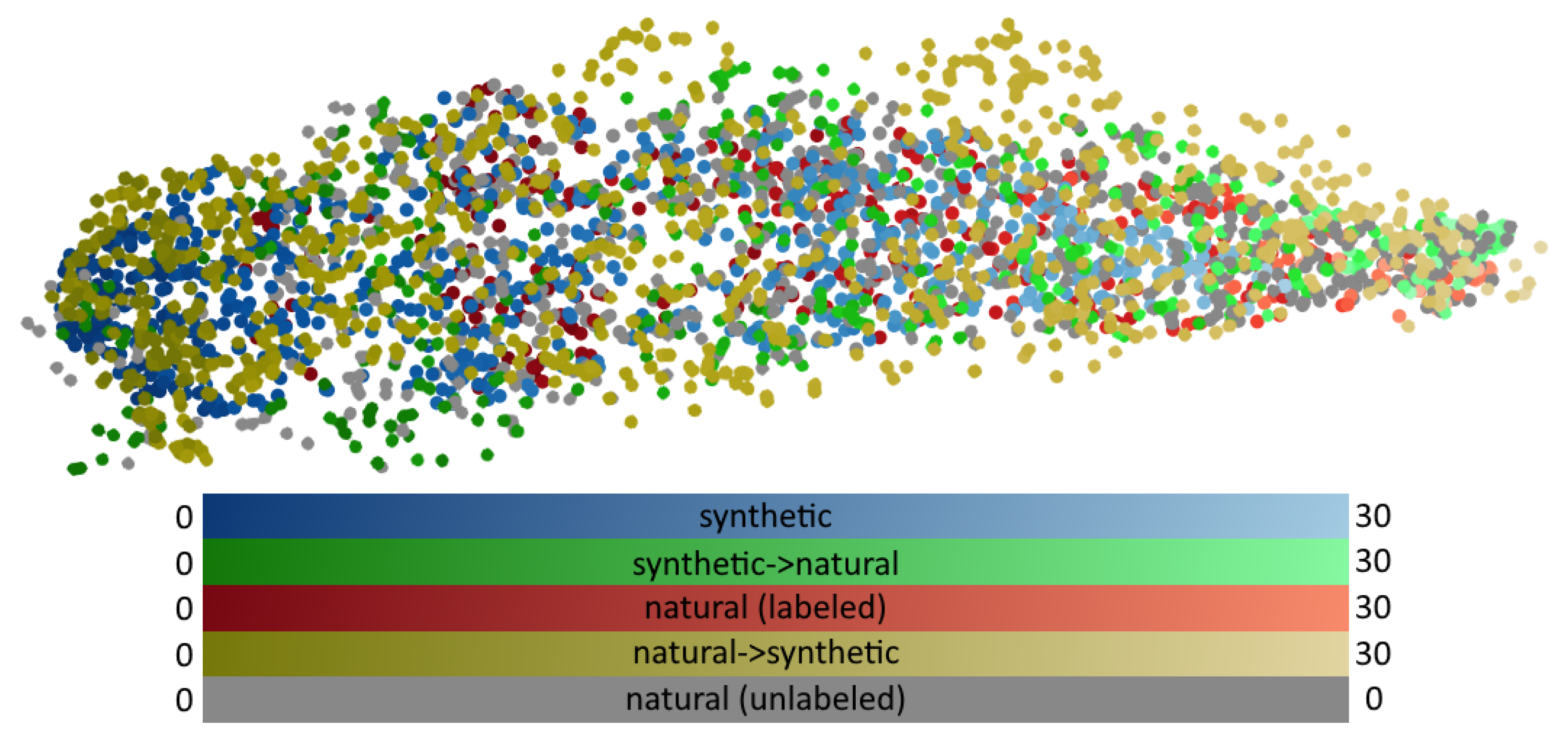
4.3. Shared Representation
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Anggraini, D.; Ota, N.; Shen, Y.; Tang, T.; Tanaka, Y.; Hosokawa, Y.; Li, M.; Yalikun, Y. Recent advances in microfluidic devices for single-cell cultivation: methods and applications. Lab Chip 2022, 22, 1438–1468. [Google Scholar] [CrossRef] [PubMed]
- Sachs, C.C. Online high throughput microfluidic single cell analysis for feed-back experimentation. Ph.D. Thesis, Technische Hochschule Aachen, Aachen, Germany, 2018. RWTH-2018-231907. [Google Scholar] [CrossRef]
- Stallmann, D.; Göpfert, J.P.; Schmitz, J.; Grünberger, A.; Hammer, B. Towards an Automatic Analysis of CHO-K1 Suspension Growth in Microfluidic Single-cell Cultivation. Bioinformatics 2020, 37, 3632–3639. [Google Scholar] [CrossRef]
- Kenneweg, P.; Stallmann, D.; Hammer, B. Novel transfer learning schemes based on Siamese networks and synthetic data. Neural Comput. Appl. 2022, 35, 8423–8436. [Google Scholar] [CrossRef] [PubMed]
- Theorell, A.; Seiffarth, J.; Grünberger, A.; Nöh, K. When a single lineage is not enough: Uncertainty-Aware Tracking for spatio-temporal live-cell image analysis. Bioinformatics 2019, 35, 1221–1228. [Google Scholar] [CrossRef] [PubMed]
- Jacob, G.; Rt, P.; Katti, H.; Arun, S. Qualitative similarities and differences in visual object representations between brains and deep networks. Nat. Commun. 2021, 12, 1872. [Google Scholar] [CrossRef] [PubMed]
- Ioannidou, A.; Chatzilari, E.; Nikolopoulos, S.; Kompatsiaris, I. Deep Learning Advances in Computer Vision with 3D Data: A Survey. ACM Comput. Surv. 2017, 50, 3042064. [Google Scholar] [CrossRef]
- Lempitsky, V.; Zisserman, A. Learning To Count Objects in Images. In Proceedings of the Advances in Neural Information Processing Systems 23; Lafferty, J.D., Williams, C.K.I., Shawe-Taylor, J., Zemel, R.S., Culotta, A., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2010; pp. 1324–1332. [Google Scholar]
- Razzak, M.I.; Naz, S.; Zaib, A. Challenges and the Future. In Classification in BioApps: Automation of Decision Making; Springer: Cham, Switzerland, 2018; pp. 323–350. [Google Scholar] [CrossRef]
- Moen, E.; Bannon, D.; Kudo, T.; Graf, W.; Covert, M.; Van Valen, D. Deep learning for cellular image analysis. Nat. Methods 2019, 16, 1233–1246. [Google Scholar] [CrossRef]
- Ulman, V.; Maška, M.; Magnusson, K.E.G.; Ronneberger, O.; Haubold, C.; Harder, N.; Matula, P.; Matula, P.; Svoboda, D.; Radojevic, M.; et al. An objective comparison of cell-tracking algorithms. Nat. Methods 2017, 14, 1141–1152. [Google Scholar] [CrossRef]
- Berg, S.; Kutra, D.; Kroeger, T.; Straehle, C.N.; Kausler, B.; Haubold, C.; Schiegg, M.; Ales, J.; Beier, T.; Rudy, M.; et al. ilastik: interactive machine learning for (bio)image analysis. Nat. Methods 2019, 16, 1226–1232. [Google Scholar] [CrossRef]
- Hughes, A.J.; Mornin, J.D.; Biswas, S.K.; Beck, L.E.; Bauer, D.P.; Raj, A.; Bianco, S.; Gartner, Z.J. Quanti.us: a tool for rapid, flexible, crowd-based annotation of images. Nat. Methods 2018, 15, 587–590. [Google Scholar] [CrossRef]
- Schmitz, J.; Noll, T.; Grünberger, A. Heterogeneity Studies of Mammalian Cells for Bioproduction: From Tools to Application. Trends Biotechnol. 2019, 37, 645–660. [Google Scholar] [CrossRef] [PubMed]
- Brent, R.; Boucheron, L. Deep learning to predict microscope images. Nat. Methods 2018, 15, 868–870. [Google Scholar] [CrossRef] [PubMed]
- Falk, T.; Mai, D.; Bensch, R.; Çiçek, Ö.; Abdulkadir, A.; Marrakchi, Y.; Böhm, A.; Deubner, J.; Jäckel, Z.; Seiwald, K.; et al. U-Net: deep learning for cell counting, detection, and morphometry. Nat. Methods 2019, 16, 67–70. [Google Scholar] [CrossRef] [PubMed]
- Di Carlo, D.; Wu, L.Y.; Lee, L.P. Dynamic single cell culture array. Lab Chip 2006, 6, 1445–1449. [Google Scholar] [CrossRef]
- Kolnik, M.; Tsimring, L.S.; Hasty, J. Vacuum-assisted cell loading enables shear-free mammalian microfluidic culture. Lab Chip 2012, 12, 4732–4737. [Google Scholar] [CrossRef]
- Arteta, C.; Lempitsky, V.; Noble, J.A.; Zisserman, A. Interactive Object Counting. In Computer Vision—ECCV 2014; Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2014; Volume 8691, pp. 504–518. [Google Scholar] [CrossRef]
- Arteta, C.; Lempitsky, V.; Noble, J.A.; Zisserman, A. Detecting overlapping instances in microscopy images using extremal region trees. Med Image Anal. 2016, 27, 3–16. [Google Scholar] [CrossRef]
- Chen, S.W.; Shivakumar, S.S.; Dcunha, S.; Das, J.; Okon, E.; Qu, C.; Taylor, C.J.; Kumar, V. Counting Apples and Oranges With Deep Learning: A Data-Driven Approach. IEEE Robot. Autom. Lett. 2017, 2, 781–788. [Google Scholar] [CrossRef]
- Xie, W.; Noble, J.A.; Zisserman, A. Microscopy cell counting and detection with fully convolutional regression networks. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2018, 6, 283–292. [Google Scholar] [CrossRef]
- Koh, W.; Hoon, S. MapCell: Learning a Comparative Cell Type Distance Metric with Siamese Neural Nets With Applications Toward Cell-Type Identification Across Experimental Datasets. Front. Cell Dev. Biol. 2021, 9, 767897. [Google Scholar] [CrossRef]
- Müller, T.; Pérez-Torró, G.; Franco-Salvador, M. Few-Shot Learning with Siamese Networks and Label Tuning. In Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), Dublin, Ireland, 22–27 May 2022; pp. 8532–8545. [Google Scholar] [CrossRef]
- Yang, L.; Chen, Y.; Song, S.; Li, F.; Huang, G. Deep Siamese Networks Based Change Detection with Remote Sensing Images. Remote. Sens. 2021, 13, 13173394. [Google Scholar] [CrossRef]
- Mehmood, A.; Maqsood, M.; Bashir, M.; Shuyuan, Y. A Deep Siamese Convolution Neural Network for Multi-Class Classification of Alzheimer Disease. Brain Sci. 2020, 10, 84. [Google Scholar] [CrossRef] [PubMed]
- Figueroa-Mata, G.; Mata-Montero, E. Using a Convolutional Siamese Network for Image-Based Plant Species Identification with Small Datasets. Biomimetics 2020, 5, 10008. [Google Scholar] [CrossRef] [PubMed]
- Tan, M.; Le, Q.V. EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks. arXiv 2019, arXiv:1905.11946. [Google Scholar]
- Rahman, M.S.; Islam, M.R. Counting objects in an image by marker controlled watershed segmentation and thresholding. In Proceedings of the 3rd IEEE International Advance Computing Conference (IACC), Ghaziabad, India, 22–23 February 2013; pp. 1251–1256. [Google Scholar] [CrossRef]
- Kolesnikov, A.; Beyer, L.; Zhai, X.; Puigcerver, J.; Yung, J.; Gelly, S.; Houlsby, N. Large Scale Learning of General Visual Representations for Transfer. arXiv 2019, arXiv:1912.11370. [Google Scholar]
- Sam, D.B.; Sajjan, N.N.; Maurya, H.; Babu, R.V. Almost Unsupervised Learning for Dense Crowd Counting. Proc. AAAI Conf. Artif. Intell. 2019, 33, 8868–8875. [Google Scholar] [CrossRef]
- Schönfeld, E.; Ebrahimi, S.; Sinha, S.; Darrell, T.; Akata, Z. Generalized Zero- and Few-Shot Learning via Aligned Variational Autoencoders. arXiv 2019, arXiv:1812.01784. [Google Scholar]
- Jaderberg, M.; Simonyan, K.; Vedaldi, A.; Zisserman, A. Synthetic data and artificial neural networks for natural scene text recognition. In Proceedings of the Workshop on Deep Learning, Advances in Neural Information Processing Systems (NIPS); Palais des Congrès de Montréal, Montréal, QC, Canada, 7 December 2018. [Google Scholar]
- Nikolenko, S.I. Synthetic Data for Deep Learning. arXiv 2019, arXiv:1909.11512. [Google Scholar]
- van Engelen, J.E.; Hoos, H.H. A survey on semi-supervised learning. Mach. Learn. 2020, 109, 373–440. [Google Scholar] [CrossRef]
- Göpfert, C.; Ben-David, S.; Bousquet, O.; Gelly, S.; Tolstikhin, I.O.; Urner, R. When can unlabeled data improve the learning rate? In Proceedings of the Conference on Learning Theory, COLT 2019, PMLR, Phoenix, AZ, USA, 25–28 June 2019; Beygelzimer, A., Hsu, D., Eds.; Proceedings of Machine Learning Research. Volume 99, pp. 1500–1518. [Google Scholar]
- Göpfert, J.P.; Göpfert, C.; Botsch, M.; Hammer, B. Effects of variability in synthetic training data on convolutional neural networks for 3D head reconstruction. In Proceedings of the 2017 IEEE Symposium Series on Computational Intelligence (SSCI), Honolulu, HI, USA, 27 November–1 December 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Ullrich, K.; Meeds, E.; Welling, M. Soft Weight-Sharing for Neural Network Compression. arXiv 2017, arXiv:1702.04008. [Google Scholar]
- McInnes, L.; Healy, J.; Saul, N.; Grossberger, L. UMAP: Uniform Manifold Approximation and Projection. J. Open Source Softw. 2018, 3, 861. [Google Scholar] [CrossRef]
- Schmitz, J.; Täuber, S.; Westerwalbesloh, C.; von Lieres, E.; Noll, T.; Grünberger, A. Development and application of a cultivation platform for mammalian suspension cell lines with single-cell resolution. Biotechnol. Bioeng. 2021, 118, 992–1005. [Google Scholar] [CrossRef] [PubMed]
- Sandfort, V.; Yan, K.; Pickhardt, P.J.; Summers, R.M. Data augmentation using generative adversarial networks (CycleGAN) to improve generalizability in CT segmentation tasks. Sci. Rep. 2019, 9, 16884. [Google Scholar] [CrossRef] [PubMed]
- Saxe, A.M.; McClelland, J.L.; Ganguli, S. Exact solutions to the nonlinear dynamics of learning in deep linear neural networks. In Proceedings of the International Conference on Learning Representations, ICLR 2013, Scottsdale, AZ, USA, 2–4 May 2013. [Google Scholar]
- Liu, L.; Jiang, H.; He, P.; Chen, W.; Liu, X.; Gao, J.; Han, J. On the Variance of the Adaptive Learning Rate and Beyond. arXiv 2020, arXiv:1908.03265. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for Hyper-Parameter Optimization. In Proceedings of the Advances in Neural Information Processing Systems; Shawe-Taylor, J., Zemel, R., Bartlett, P., Pereira, F., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2011; Volume 24. [Google Scholar]
- Williams, C.K.I.; Rasmussen, C.E. Gaussian Processes for Regression. In Advances in Neural Information Processing Systems 8; Touretzky, D.S., Mozer, M.C., Hasselmo, M.E., Eds.; MIT Press: Cambridge, MA, JUSA, 1996; pp. 514–520. [Google Scholar]
- Tan, M.; Le, Q.V. EfficientNetV2: Smaller Models and Faster Training. arXiv 2021, arXiv:2104.00298. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]





| Data Set Name | No. of Phase-Contrast Images | No. of Bright-Field Images |
|---|---|---|
| Nat | Nat-PC | Nat-BF |
| Nat-U-Tr | 3.152 | 2.469 |
| Nat-L-Te | 792 | 514 |
| Syn | Syn-PC | Syn-BF |
| Syn-L-Tr | 3.152 | 2.469 |
| Syn-L-Te | 792 | 514 |
| Method | MAE (Syn) ↓ | MRE (Syn) ↓ | Acc. (Syn) ↑ | MAE (Nat) ↓ | MRE (Nat) ↓ | Acc. (Nat) ↑ |
|---|---|---|---|---|---|---|
| PC (phase-contrast microscopy) | ||||||
| EfficientNet (ss) | 4.987 | 79.4% | 5.0% | 1.67 | 25.12% | 23.4% |
| BiT (ss) | N/A | N/A | N/A | 2.32 | 29.7% | 25.4% |
| Twin-VAE (ss) | 0.09 | 0.68% | 68.2% | 0.60 | 5.92% | 57.8% |
| Transfer Twin-VAE (ss) | 0.15 | 0.43% | 85.0% | 0.66 | 6.46% | 53.7% |
| Dual Transfer Twin-VAE (ss) | 0.12 | 0.43% | 85.0% | 0.58 | 5.56% | 58.7% |
| Watershed (u) | 0.94 | 18.0% | 24.0% | 1.66 | 29.0% | 23.1% |
| C-VAE (u) | 0.24 | 2.65% | 54.2% | 1.03 | 19.1% | 28.9% |
| S-VAE (u) | 0.09 | 0.53% | 76.3% | 2.64 | 41.2% | 11.6% |
| SC-VAE (u) | 0.11 | 0.83% | 66.1% | 0.49 | 5.16% | 61.7% |
| SC-VAE-B (u) | 0.10 | 0.81% | 67.9% | 0.48 | 5.12% | 61.8% |
| BF (bright-field microscopy) | ||||||
| EfficientNet (ss) | 6.502 | 67.1% | 4.5% | 1.13 | 17.2% | 33.9% |
| BiT (ss) | N/A | N/A | N/A | 1.79 | 22.45% | 38.7% |
| Twin-VAE (ss) | 0.48 | 4.27% | 60.1% | 0.68 | 7.6% | 53.2% |
| Transfer Twin-VAE (ss) | 0.40 | 3.87% | 66.6% | 0.52 | 5.47% | 60.7% |
| Dual Transfer Twin-VAE (ss) | 0.35 | 3.73% | 66.8% | 0.51 | 5.43% | 60.8% |
| Watershed (u) | 1.92 | 39.0% | 2.0% | 2.39 | 32.0% | 32.0% |
| C-VAE (u) | 0.67 | 5.72% | 50.8% | 1.96 | 21.8% | 26.3% |
| S-VAE (u) | 0.33 | 3.66 % | 67.3% | 2.09 | 34.2% | 18.6% |
| SC-VAE (u) | 0.41 | 3.88% | 62.5% | 0.60 | 7.1% | 56.6% |
| SC-VAE-B (u) | 0.39 | 3.77% | 62.6% | 0.56 | 6.51% | 58.7% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stallmann, D.; Hammer, B. Unsupervised Cyclic Siamese Networks Automating Cell Imagery Analysis. Algorithms 2023, 16, 205. https://doi.org/10.3390/a16040205
Stallmann D, Hammer B. Unsupervised Cyclic Siamese Networks Automating Cell Imagery Analysis. Algorithms. 2023; 16(4):205. https://doi.org/10.3390/a16040205
Chicago/Turabian StyleStallmann, Dominik, and Barbara Hammer. 2023. "Unsupervised Cyclic Siamese Networks Automating Cell Imagery Analysis" Algorithms 16, no. 4: 205. https://doi.org/10.3390/a16040205
APA StyleStallmann, D., & Hammer, B. (2023). Unsupervised Cyclic Siamese Networks Automating Cell Imagery Analysis. Algorithms, 16(4), 205. https://doi.org/10.3390/a16040205





