How to Open a Black Box Classifier for Tabular Data
Abstract
1. Introduction
1.1. Related Work on Self-Explaining Neural Networks
1.2. Contributions to the Literature
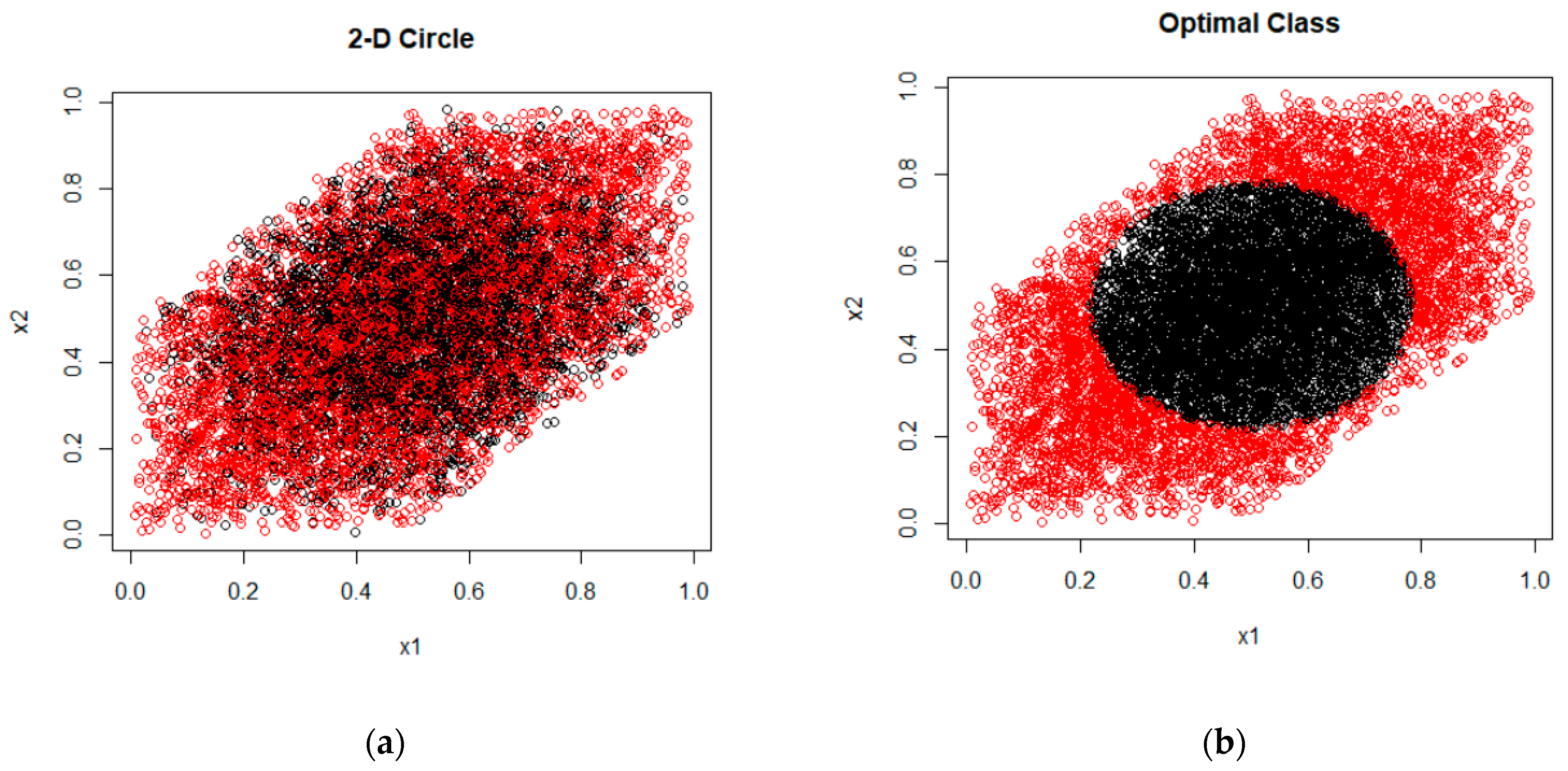
- Comprehensive presentation of the generic framework for deriving PRiSM models from arbitrary black box binary classifiers, reviewing the orthogonality properties of ANOVA for two alternative measures: the Dirac measure, which is similar to partial dependence functions in visualisation algorithms [11] and produces component functions that are tied to the data median; the Lebesgue measure, which involves estimates of marginal effects and is related to the quantification of effect sizes [7]. The method is tested on nine-dimensional synthetic data to verify that it retrieves the correct generating variables and achieves close to optimal classification performance;
- Derivation of a commonly used indicator of feature attribution, Shapley values [22]. When applied to the logit of model predictions from GAMs and SENNs, it is shown to be identical to the value of the contributions of the partial responses derived from ANOVA;
- Mapping of the properties of the PRiSM models to a formal framework for interpretability, demonstrating compliance with its main requirements [23], known as the three Cs of interpretability. This is complemented by an in-depth analysis of the component functions estimated from three real-world data sets.
2. Materials and Methods
2.1. Methods
2.1.1. ANOVA Decomposition
- Dirac measure
- Lesbesgue measure
2.1.2. Model Selection with the LASSO
2.1.3. Second Training Iteration
- (1)
- Univariate partial response corresponding to the input
- (2)
- Bivariate partial response for the input pair {,}
- (3)
- Finally, an amount is added to the total sum of the values calculated for the bias term in the structured neural network. This amount is equal to the intercept of the logistic Lasso, .
2.1.4. Summary of the Method
2.1.5. Exact Calculation of Shapley Values
2.1.6. Experimental Settings
2.2. Data sets used
2.2.1. Synthetic Data
2.2.2. Real-World data
- (a)
- Diabetes data set:
- (b)
- Statlog German Credit Card data set:
- (c)
- Statlog Shuttle data set:
3. Results
3.1. Synthetic Data
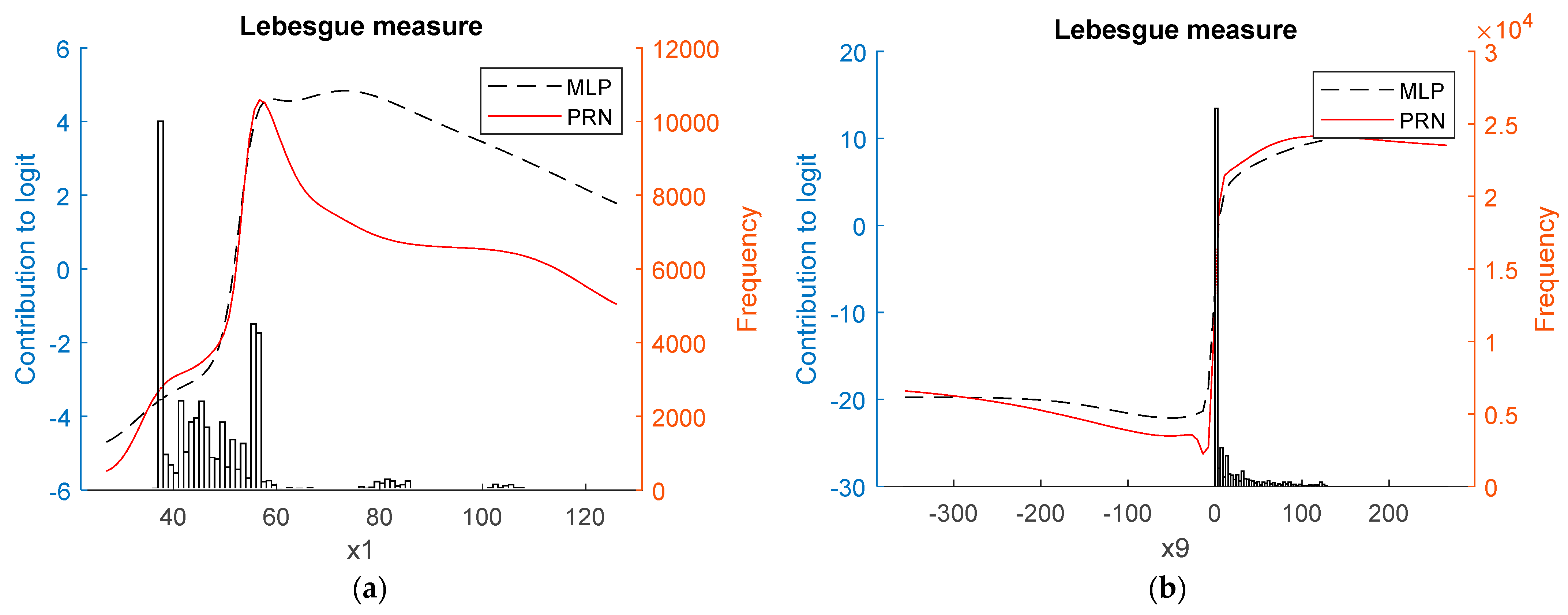
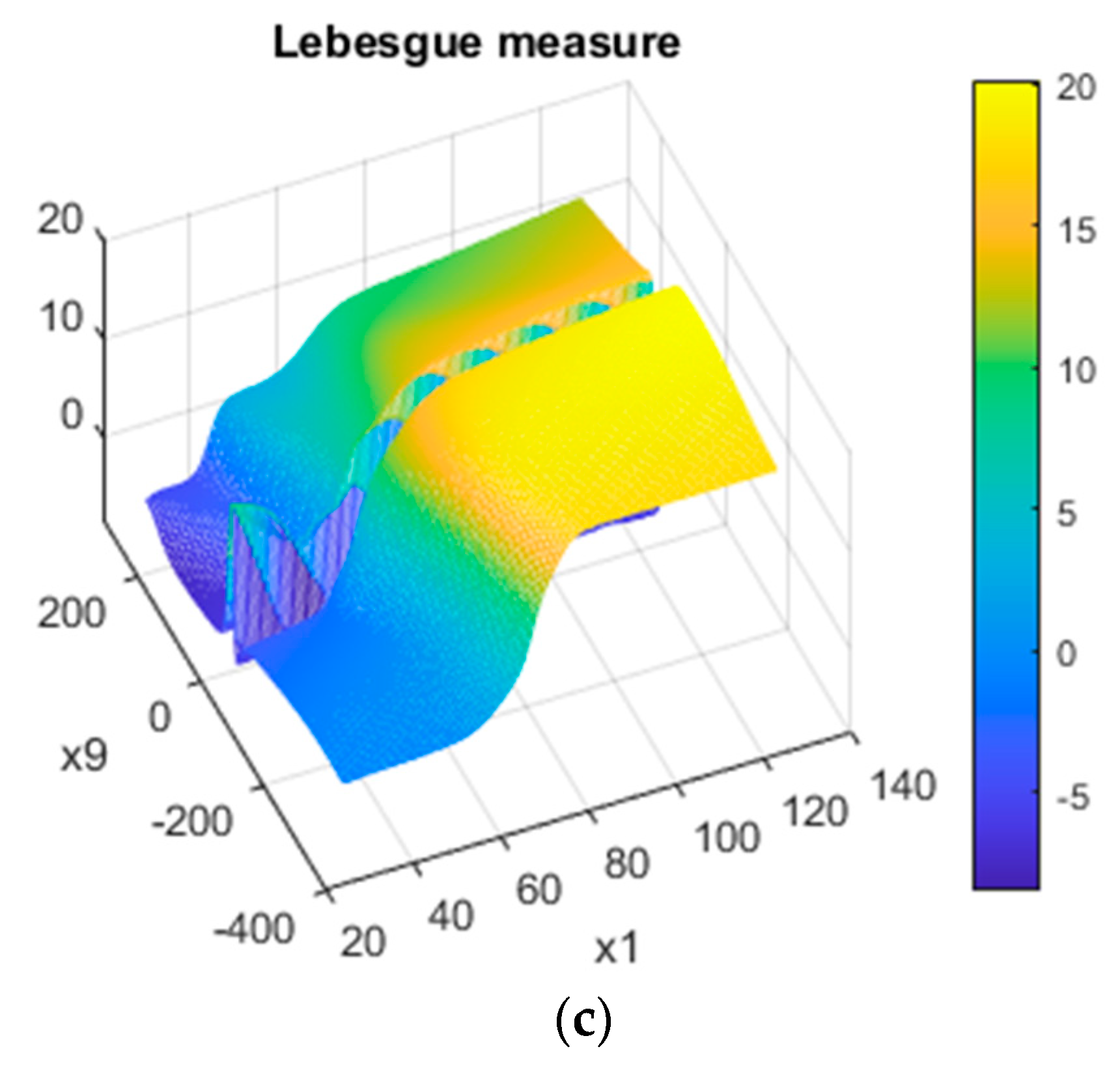
3.2. Real-World Data
4. Discussion
4.1. Predictive Accuracy
4.2. Stability
4.3. Interpretability
- Completeness—the proposed models have global coverage in the sense that they provide a direct and causal explanation of the model output from the input data, over the complete range of input data. The validity of the model output is evidenced by the AUC and calibration measures;
- Compactness—the explanations are as succinct, ensured by the application of logistic regression modelling with the Lasso. The component functions, both univariate and bivariate, are shown in the results to be stable, as are the derived GAMs;
- Correctness—the explanation generates trust in the sense that:
- -
- They are sufficiently correct to ensure good calibration for all data sets. This means that deviations from the theoretical curves for the synthetic data occur in regions where the model is close to saturated, i.e., making predictions close to 0 or 1;
- -
- The label coherence of the instances covered by the explanation is assured by the shape of the component functions so that the neighbouring instances have similar explanations.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Angelino, E.; Larus-Stone, N.; Alabi, D.; Seltzer, M.; Rudin, C. Learning Certifiably Optimal Rule Lists for Categorical Data. J. Mach. Learn. Res. 2018, 18, 1–78. [Google Scholar]
- Rögnvaldsson, T.; Etchells, T.A.; You, L.; Garwicz, D.; Jarman, I.; Lisboa, P.J.G. How to Find Simple and Accurate Rules for Viral Protease Cleavage Specificities. BMC Bioinform. 2009, 10, 149. [Google Scholar] [CrossRef]
- Poon, A.I.F.; Sung, J.J.Y. Opening the Black Box of AI-Medicine. J. Gastroenterol. Hepatol. 2021, 36, 581–584. [Google Scholar] [CrossRef]
- Christodoulou, E.; Ma, J.; Collins, G.S.; Steyerberg, E.W.; Verbakel, J.Y.; van Calster, B. A Systematic Review Shows No Performance Benefit of Machine Learning over Logistic Regression for Clinical Prediction Models. J. Clin. Epidemiol. 2019, 110, 12–22. [Google Scholar] [CrossRef] [PubMed]
- Guidotti, R.; Monreale, A.; Ruggieri, S.; Turini, F.; Giannotti, F.; Pedreschi, D. A Survey of Methods for Explaining Black Box Models. ACM Comput. Surv. 2018, 51, 93. [Google Scholar] [CrossRef]
- Sarle, W.S. Neural Networks and Statistical Models. In Proceedings of the Nineteenth Annual SAS Users Group International Conference, Dallas, TX, USA, 10–13 April 1994; pp. 1538–1550. [Google Scholar]
- Brás-Geraldes, C.; Papoila, A.; Xufre, P. Odds Ratio Function Estimation Using a Generalized Additive Neural Network. Neural Comput. Appl. 2019, 32, 3459–3474. [Google Scholar] [CrossRef]
- Lee, C.K.; Samad, M.; Hofer, I.; Cannesson, M.; Baldi, P. Development and Validation of an Interpretable Neural Network for Prediction of Postoperative In-Hospital Mortality. NPJ Digit. Med. 2021, 4, 8. [Google Scholar] [CrossRef]
- Alvarez-Melis, D.; Jaakkola, T.S. Towards Robust Interpretability with Self-Explaining Neural Networks. In Proceedings of the 32nd Conference on Neural Information Processing Systems (NeurIPS 2018), Montréal, QC, Canada, 2–8 December 2018. [Google Scholar]
- Hooker, G. Generalized Functional ANOVA Diagnostics for High-Dimensional Functions of Dependent Variables. J. Comput. Graph. Stat. 2007, 16, 709–732. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Agarwal, R.; Melnick, L.; Frosst, N.; Zhang, X.; Lengerich, B.; Caruana, R.; Hinton, G.E. Neural Additive Models: Interpretable Machine Learning with Neural Nets. Adv. Neural Inf. Process. Syst. 2020, 6, 4699–4711. [Google Scholar] [CrossRef]
- Nori, H.; Jenkins, S.; Koch, P.; Caruana, R. InterpretML: A Unified Framework for Machine Learning Interpretability. arXiv 2019, arXiv:1909.09223 2019. [Google Scholar]
- Yang, Z.; Zhang, A.; Sudjianto, A. GAMI-Net: An Explainable Neural Network Based on Generalized Additive Models with Structured Interactions. Pattern Recognit. 2021, 120, 108192. [Google Scholar] [CrossRef]
- Ravikumar, P.; Lafferty, J.; Liu, H.; Wasserman, L. Sparse Additive Models. J. R. Stat. Soc. Ser. B 2009, 71, 1009–1030. [Google Scholar] [CrossRef]
- Chen, H.; Wang, X.; Deng, C.; Huang, H. Group Sparse Additive Machine. Adv. Neural Inf. Process. Syst. 2017, 30, 97–207. [Google Scholar]
- van Belle, V.; Lisboa, P. White Box Radial Basis Function Classifiers with Component Selection for Clinical Prediction Models. Artif. Intell. Med. 2014, 60, 53–64. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance Based Sensitivity Analysis of Model Output. Design and Estimator for the Total Sensitivity Index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Rudin, C. Stop Explaining Black Box Machine Learning Models for High Stakes Decisions and Use Interpretable Models Instead. Nat. Mach. Intell. 2019, 1, 206–215. [Google Scholar] [CrossRef]
- Walters, B.; Ortega-Martorell, S.; Olier, I.; Lisboa, P.J.G. Towards Interpretable Machine Learning for Clinical Decision Support. In Proceedings of the International Joint Conference on Neural Networks, Padua, Italy, 18–23 July 2022. [Google Scholar] [CrossRef]
- Lisboa, P.J.G.; Jayabalan, M.; Ortega-Martorell, S.; Olier, I.; Medved, D.; Nilsson, J. Enhanced Survival Prediction Using Explainable Artificial Intelligence in Heart Transplantation. Sci. Rep. 2022, 12, 19525. [Google Scholar] [CrossRef]
- Lundberg, S.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 4765–4774. [Google Scholar]
- Carvalho, D.V.; Pereira, E.M.; Cardoso, J.S. Machine Learning Interpretability: A Survey on Methods and Metrics. Electronics 2019, 8, 832. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection Via the Lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- The MathWorks Inc. MATLAB; The MathWorks Inc.: Natick, MA, USA, 1994. [Google Scholar]
- MacKay, D.J.C. The Evidence Framework Applied to Classification Networks. Neural Comput. 1992, 4, 720–736. [Google Scholar] [CrossRef]
- Nabney, I. NETLAB: Algorithms for Pattern Recognitions; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Tsukimoto, H. Extracting Rules from Trained Neural Networks. IEEE Trans. Neural Netw. 2000, 11, 377–389. [Google Scholar] [CrossRef] [PubMed]
- Ripley, B.D. Pattern Recognition and Neural Networks; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Smith, J.W.; Everhart, J.E.; Dickson, W.C.; Knowler, W.C.; Johannes, R.S. Using the ADAP Learning Algorithm to Forecast the Onset of Diabetes Mellitus. In Proceedings of the Annual Symposium on Computer Application in Medical Care, Washington, DC, USA, 6–9 November 1988; p. 261. [Google Scholar]
- Newman, D.J.; Hettich, S.; Blake, C.L.; Merz, C.J. UCI Repository of Machine Learning Databases. Available online: http://www.ics.uci.edu/~mlearn/MLRepository.html (accessed on 1 January 2022).
- Abe, N.; Zadrozny, B.; Langford, J. Outlier Detection by Active Learning. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Philadelphia, PA, USA, 20–23 August 2006; pp. 504–509. [Google Scholar] [CrossRef]
- Balachandran, V.P.; Gonen, M.; Smith, J.J.; DeMatteo, R.P. Nomograms in Oncology: More than Meets the Eye. Lancet Oncol. 2015, 16, e173–e180. [Google Scholar] [CrossRef] [PubMed]
- Roder, J.; Maguire, L.; Georgantas, R.; Roder, H. Explaining Multivariate Molecular Diagnostic Tests via Shapley Values. BMC Med. Inform. Decis. Mak. 2021, 21, 1–18. [Google Scholar] [CrossRef]
- Biganzoli, E.; Boracchi, P.; Mariani, L.; Marubini, E. Feed Forward Neural Networks for the Analysis of Censored Survival Data: A Partial Logistic Regression Approach. Stat. Med. 1998, 17, 1169–1186. [Google Scholar] [CrossRef]









| AUC [CI] | No. Input Variables | Training (n = 6000) | Optimisation (n = 2000) | Performance Estimation (n = 2000) |
|---|---|---|---|---|
| Optimal classifier | 2 | 0.676 [0.662,0.689] | 0.657 [0.634,0.681] | 0.666 [0.643,0.690] |
| MLP | 9 | 0.676 [0.663,0.690] | 0.659 [0.635,0.682] | 0.660 [0.636,0.684] |
| SVM | 9 | 0.695 [0.682,0.708] | 0.646 [0.622,0.670] | 0.648 [0.624,0.672] |
| GBM | 9 | 0.697 [0.684,0.710] | 0.649 [0.625,0.673] | 0.641 [0.617,0.665] |
| PRiSM models | Components | Dirac measure | ||
| Lasso | 2 | 0.675 [0.661,0.688] | 0.658 [0.634,0.682] | 0.661 [0.637,0.685] |
| PRN | 2 | 0.676 [0.662,0.689] | 0.659 [0.636,0.683] | 0.664 [0.640,0.687] |
| PRN–Lasso | 2 | 0.676 [0.662,0.689] | 0.659 [0.636,0.683] | 0.664 [0.640,0.688] |
| prSVM | 2 | 0.676 [0.662,0.689] | 0.658 [0.634,0.681] | 0.664 [0.640,0.688] |
| prGBM | 5 | 0.681 [0.667,0.694] | 0.655 [0.631,0.679] | 0.655 [0.632,0.679] |
| PRiSM models | Components | Lebesgue measure | ||
| Lasso | 2 | 0.675 [0.662,0.689] | 0.659 [0.636,0.683] | 0.661 [0.637,0.685] |
| PRN | 2 | 0.676 [0.662,0.689] | 0.659 [0.636,0.683] | 0.664 [0.640,0.687] |
| PRN–Lasso | 2 | 0.676 [0.662,0.689] | 0.660 [0.636,0.683] | 0.664 [0.640,0.687] |
| prSVM | 3 | 0.675 [0.662,0.689] | 0.657 [0.634,0.681] | 0.665 [0.641,0.689] |
| prGBM | 2 | 0.673 [0.659,0.686] | 0.656 [0.632,0.679] | 0.654 [0.630,0.678] |
| AUC [CI] | No. Input Variables | Training (n = 6000) | Optimisation (n = 2000) | Performance Estimation (n = 2000) |
|---|---|---|---|---|
| Optimal classifier | 1 | 0.689 [0.675,0.702] | 0.663 [0.639,0.687] | 0.671 [0.648,0.695] |
| MLP | 9 | 0.692 [0.678,0.705] | 0.665 [0.641,0.688] | 0.669 [0.646,0.693] |
| SVM | 9 | 0.708 [0.695,0.721] | 0.652 [0.628,0.676] | 0.660 [0.637,0.684] |
| GBM | 9 | 0.713 [0.700,0.726] | 0.586 [0.561,0.610] | 0.609 [0.584,0.633] |
| PRiSM models | Components | Dirac measure | ||
| Lasso | 1 | 0.688 [0.675,0.701] | 0.663 [0.639,0.686] | 0.672 [0.648,0.695] |
| PRN | 1 | 0.690 [0.677,0.703] | 0.664 [0.640,0.687] | 0.670 [0.646,0.694] |
| PRN–Lasso | 1 | 0.688 [0.675,0.702] | 0.663 [0.639,0.686] | 0.672 [0.648,0.695] |
| prSVM | 14 | 0.691 [0.678,0.705] | 0.663 [0.640,0.687] | 0.671 [0.648,0.695] |
| prGBM | 1 | 0.687 [0.674,0.700] | 0.656 [0.633,0.680] | 0.661 [0.638,0.685] |
| PRiSM models | Components | Lebesgue measure | ||
| Lasso | 1 | 0.689 [0.676,0.702] | 0.664 [0.640,0.688] | 0.670 [0.647,0.694] |
| PRN | 1 | 0.690 [0.677,0.703] | 0.664 [0.640,0.687] | 0.670 [0.646,0.693] |
| PRN–Lasso | 1 | 0.690 [0.676,0.703] | 0.664 [0.641,0.688] | 0.670 [0.647,0.694] |
| prSVM | 7 | 0.690 [0.677,0.703] | 0.633 [0.640,0.687] | 0.672 [0.648,0.695] |
| prGBM | 1 | 0.688 [0.675,0.702] | 0.656 [0.632,0.680] | 0.659 [0.635,0.682] |
| AUC [CI] | No. Input Variables | Training (n = 6000) | Optimisation (n = 2000) | Performance Estimation (n = 2000) |
|---|---|---|---|---|
| Optimal classifier | 3 | 0.816 [0.802,0.830] | 0.836 [0.813,0.860] | 0.817 [0.793,0.841] |
| MLP | 9 | 0.816 [0.803,0.830] | 0.833 [0.809,0.857] | 0.815 [0.791,0.839] |
| SVM | 9 | 0.803 [0.790,0.817] | 0.797 [0.772,0.821] | 0.786 [0.762, 0.809] |
| GBM | 9 | 0.822 [0.810,0.834] | 0.826 [0.805,0.847] | 0.808 [0.787,0.830] |
| PRiSM models | Components | Dirac measure | ||
| Lasso | 3 | 0.815 [0.801,0.828] | 0.833 [0.809,0.857] | 0.813 [0.789,0.837] |
| PRN | 3 | 0.816 [0.802,0.829] | 0.835 [0.811,0.858] | 0.814 [0.790,0.838] |
| PRN–Lasso | 3 | 0.816 [0.802,0.830] | 0.835 [0.811,0.859] | 0.814 [0.791,0.838] |
| prSVM | 6 | 0.800 [0.787,0.813] | 0.813 [0.790,0.835] | 0.797 [0.774, 0.820] |
| prGBM | 6 | 0.820 [0.807,0.832] | 0.828 [0.807,0.848] | 0.807 [0.786,0.829] |
| PRiSM models | Components | Lebesgue measure | ||
| Lasso | 3 | 0.815 [0.801,0.828] | 0.832 [0.808,0.856] | 0.813 [0.789,0.837] |
| PRN | 3 | 0.816 [0.802,0.829] | 0.835 [0.811,0.858] | 0.814 [0.790,0.838] |
| PRN–Lasso | 3 | 0.816 [0.802,0.830] | 0.835 [0.811,0.858] | 0.815 [0.791,0.839] |
| prSVM | 4 | 0.799 [0.786,0.812] | 0.812 [0.790,0.834] | 0.796 [0.773,0.819] |
| prGBM | 8 | 0.817 [0.805,0.829] | 0.828 [0.808,0.849] | 0.810 [0.789,0.831] |
| AUC [CI] | No. Input Variables | Training (n = 6000) | Optimisation (n = 2000) | Performance Estimation (n = 2000) |
|---|---|---|---|---|
| Optimal classifier | 3 | 0.840 [0.822,0.859] | 0.817 [0.783,0.851] | 0.836 [0.805,0.868] |
| MLP | 9 | 0.840 [0.822,0.859] | 0.809 [0.775,0.843] | 0.832 [0.801,0.864] |
| SVM | 9 | 0.797 [0.779,0.815] | 0.764 [0.729,0.798] | 0.786 [0.755,0.817] |
| GBM | 9 | 0.831 [0.816,0.847] | 0.796 [0.767,0.826] | 0.813 [0.786,0.840] |
| PRiSM models | Components | Dirac measure | ||
| Lasso | 3 | 0.837 [0.818,0.855] | 0.811 [0.777,0.845] | 0.821 [0.797,0.861] |
| PRN | 3 | 0.837 [0.819,0.856] | 0.812 [0.778,0.846] | 0.830 [0.799,0.862] |
| PRN–Lasso | 3 | 0.837 [0.819,0.856] | 0.812 [0.778,0.846] | 0.830 [0.799,0.862] |
| prSVM | 6 | 0.813 [0.796,0.829] | 0.777 [0.744,0.810] | 0.807 [0.778,0.836] |
| prGBM | 3 | 0.832 [0.817,0.847] | 0.797 [0.768,0.826] | 0.813 [0.786,0.841] |
| PRiSM models | Components | Lebesgue measure | ||
| Lasso | 3 | 0.834 [0.816,0.853] | 0.808 [0.774,0.842] | 0.828 [0.796,0.860] |
| PRN | 3 | 0.837 [0.819,0.856] | 0.812 [0.778,0.846] | 0.831 [0.799,0.862] |
| PRN–Lasso | 3 | 0.837 [0.819,0.856] | 0.812 [0.778,0.846] | 0.831 [0.799,0.862] |
| prSVM | 6 | 0.808 [0.792,0.824] | 0.776 [0.745,0.808] | 0.805 [0.777,0.833] |
| prGBM | 4 | 0.825 [0.809,0.841] | 0.798 [0.768,0.828] | 0.810 [0.781,0.839] |
| AUC [CI] | D | Diabetes | D | Credit Card | D | Shuttle |
|---|---|---|---|---|---|---|
| MLP | 7 | 0.902 [0.850,0.954] | 24 | 0.815 [0.758,0.872] | 6 | 0.999 [0.998,1.000] |
| SVM | 7 | 0.817 [0.749,0.884] | 24 | 0.793 [0.733,0.852] | 6 | 0.999 [0.999,1.000] |
| GBM | 7 | 0.816 [0.748,0.884] | 24 | 0.784 [0.724,0.845] | 6 | 1.000 [0.999,1.000] |
| PRiSM models | Dirac measure | |||||
| MLP–Lasso | 5 | 0.902 [0.851,0.954] | 12 | 0.818 [0.762,0.875] | 3 | 0.999 [0.999,1.000] * |
| PRN | 5 | 0.903 [0.851,0.954] | 12 | 0.809 [0.752,0.867] | 3 | 0.999 [0.998,1.000] * |
| PRN–Lasso | 5 | 0.903 [0.851,0.955] | 12 | 0.815 [0.758,0.872] | 2 | 0.998 [0.997,0.999] * |
| prSVM | 5 | 0.884 [0.829,0.940] | 13 | 0.798 [0.739,0.857] | 3 | 0.998 [0.997,0.999] * |
| prGBM | 8 | 0.847 [0.784,0.910] | 10 | 0.763 [0.700,0.825] | 2 | 0.998 [0.997,0.999] |
| PRiSM models | Lebesgue measure | |||||
| MLP–Lasso | 4 | 0.889 [0.835,0.944] | 12 | 0.819 [0.763,0.876] | 3 | 0.999 [0.998,1.000] * |
| PRN | 4 | 0.903 [0.852,0.955] | 12 | 0.817 [0.760,0.874] | 3 | 0.999 [0.998,1.000] * |
| PRN–Lasso | 4 | 0.905 [0.853,0.956] | 11 | 0.819 [0.762,0.875] | 2 | 0.999 [0.998,1.000] * |
| prSVM | 6 | 0.896 [0.842,0.949] | 12 | 0.803 [0.745,0.861] | 3 | 0.998 [0.997,0.999] * |
| prGBM | 7 | 0.881 [0.824,0.937] | 9 | 0.791 [0.732,0.851] | 2 | 0.997 [0.995,0.998] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Walters, B.; Ortega-Martorell, S.; Olier, I.; Lisboa, P.J.G. How to Open a Black Box Classifier for Tabular Data. Algorithms 2023, 16, 181. https://doi.org/10.3390/a16040181
Walters B, Ortega-Martorell S, Olier I, Lisboa PJG. How to Open a Black Box Classifier for Tabular Data. Algorithms. 2023; 16(4):181. https://doi.org/10.3390/a16040181
Chicago/Turabian StyleWalters, Bradley, Sandra Ortega-Martorell, Ivan Olier, and Paulo J. G. Lisboa. 2023. "How to Open a Black Box Classifier for Tabular Data" Algorithms 16, no. 4: 181. https://doi.org/10.3390/a16040181
APA StyleWalters, B., Ortega-Martorell, S., Olier, I., & Lisboa, P. J. G. (2023). How to Open a Black Box Classifier for Tabular Data. Algorithms, 16(4), 181. https://doi.org/10.3390/a16040181






