Abstract
The identification of fault locations (FL) on overhead power lines (OHPLs) in the shortest possible time allows for a reduction in the time to shut down OHPLs in case of damage. This helps to improve the reliability of power systems. FL devices on OHPLs according to the emergency mode parameters (EMPs) are widely used, as they have a lower cost. However, they have a larger error than FL devices that record traveling wave processes. Most well-known algorithms for FL on OHPL by EMP assume a uniform distribution of resistivity along the OHPL. In real conditions, this is not the case. The application of these algorithms in FL devices on OHPLs with inhomogeneities leads to significant errors in calculating the distance to the fault location. The use of search algorithms for unconditional one-dimensional optimization is proposed to increase the speed of the implementation of iterative procedures in FL devices on OHPLs by EMPs. Recommendations have been developed for choosing optimization criteria, as well as options for implementing computational procedures. Using the example of a two-sided FL on OHPL, it is shown that the use of search algorithms can significantly (from tens to hundreds of times) reduce the number of steps of the computational iterative procedure. The implementation of search algorithms is possible in the software of typical relay protection and automation terminals, without upgrading their hardware.
1. Introduction
Optimization methods are included in the areas of applied mathematics that combine algorithmic implementations of effective control of various systems. In the general case, the optimization task is reduced to finding the extremum of some objective function. Based on the objective function, technical applications of optimization methods in the problems of the electric power industry can be different [1,2,3,4,5].
One of the important operational tasks of electric grid companies, solved on the basis of optimization methods, is the determination of fault locations (FL) on overhead power lines (OHPLs) [6,7,8]. The transmission of electricity from power plants to remote consumers is carried out through the main and distribution overhead transmission lines. In a number of countries, high- and ultra-high-voltage power transmission lines have a length of tens and even hundreds of kilometers, pass through rough terrain, and are also operated in difficult climatic conditions [9,10,11,12,13,14,15]. Therefore, finding the faults on the overhead transmission line, through detours and inspections for emergency recovery work, takes a lot of time. Starting in the 1950s, power grid companies have been massively introducing FL devices installed at substations [16,17,18,19,20]. This makes it possible to reduce the time of switching off the OHPL in case of an accident due to the rapid detection and elimination of faults. Ultimately, this affects the reliability of power systems [21,22,23].
Most FL algorithms for OHPLs, implemented in relay protection and automation (RPA) terminals, neglect the unevenness and inhomogeneity of the distribution of resistivity along the OHPL. Such inhomogeneity of OHPLs occurs for the following reasons:
- Availability of cable inserts with transition points;
- The use of different types of OHPL towers in certain areas [24];
- Change in the grounding resistance of towers caused by the passage of OHPL through areas with different soils, crossings of rivers, swamps, and reservoirs [25,26];
- Convergence with other high-voltage power lines in joint corridors;
- The presence or absence of a ground wire in certain sections of OHPL;
- Different span lengths of overhead transmission lines [27];
- Use of different wires types and cross-sections in high-voltage power lines;
- Other factors.
There are two main classes of FL on OHPL methods implemented in relay protection and automation terminals: methods based on assessing the parameters of emergency mode currents and voltages (EMP) [28,29,30] and traveling wave methods [31,32,33]. Moreover, traveling wave methods include the use of active sounding of high-voltage power lines, as well as passive registration of wave processes propagating to the ends of the power line and arising when it is faulted.
In practice, FL devices on OHPLs by EMP have a higher error than devices that record traveling wave processes. However, FL devices on OHPLs by EMP have become the most widely used, since they have a lower cost. This is due to a simpler technical implementation, since the components of currents and voltages of industrial frequency are used in FL devices on OHPLs and it does not require the use of analog-to-digital converters with a high sampling rate, as well as high-performance processors [34]. In such devices, algorithms for the FL devices on OHPL by EMP can be implemented, involving single-ended and double-ended (multi-ended) measurements in currents and voltages [35]. Single-ended algorithms do not require the use of communication channels to exchange information about the measured currents and voltages but have a higher error compared to double-ended ones [36].
The inhomogeneity of the OHPL leads to the need to use complex and, as a rule, iterative algorithms with sequential step-by-step organization of calculations. To ensure a smaller error of the FL on OHPL, the step size of the iterative procedure must be small so as not to exceed the maximum allowable error in calculating the distance to the fault. For extended OHPLs, the number of steps in the iterative procedure of FL can range from hundreds to thousands of units [37,38,39].
In the conditions of the decentralization of generating capacities, with mass integration into the main and distribution networks of distributed generation facilities, including those based on renewable energy sources, the solution to the problem of FL on OHPLs becomes even more complicated [40,41]. As a rule, these generation facilities are connected to OHPLs by taps, which significantly complicates their configuration. In addition, multidirectional power flows in the OHPLs and their taps are fixed due to the rapidly changing modes of generation and power consumption at the network nodes [42,43].
An urgent task is to develop the simplest iterative algorithms for the software of specialized FL devices of OHPLs, which increase speed, operate in an automated mode, and, at the same time, do not require significant modernization of the device hardware, as well as an increase in the cost of devices [44,45,46].
The authors propose the use of search algorithms for unconditional one-dimensional optimization to increase the speed of the implementation of iterative procedures in FL devices on OHPLs. As examples of the implementation of search algorithms, the results of the work of the following methods are demonstrated: sequential enumeration, dichotomy, and bitwise search. The authors have developed recommendations for choosing optimization criteria, as well as options for implementing computational procedures. Using the example of double-ended FL on OHPLs, it is shown that the use of search algorithms can significantly (from tens to hundreds of times) reduce the number of steps of the computational iterative procedure. This leads to a significant reduction in the time to eliminate fault on OHPLs.
2. Materials and Methods
Let us perform an analysis of the implementation FL procedure on the example of the OHPL with a double-sided power supply L km long. Figure 1 shows a simplified scheme of a single OHPL with a double-sided power supply in the case of fault.
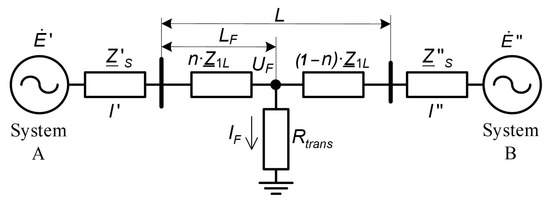
Figure 1.
Simplified scheme of single OHPL with a double-sided power supply in case of short circuit.
In Figure 1 OHPL has the parameters Z1L, Z2L, and Z0, which are full impedances of the positive, negative, and zero sequence, respectively, while Z1L = Z2L; Z′1S and Z″1S, Z′2S и Z″2S, Z′0S и Z″0S are equivalent impedances of the positive, negative, and zero sequences from system A and from system B, respectively; и is equivalent EMF from system A and from system B, respectively; Rtrans is transition resistance at the place of fault; LF is distance to the place of fault from the beginning of the OHPL (system A); and n = LF /L.
The RZA terminals installed at the ends of the OHPL record three currents and three voltages in the case of short circuit (SC). SC in the place of fault can be calculated using Equation (1):
If the distance to the fault location LF is known, then six equations can be drawn up (for three phases and three sequences):
where ν is the phase index (A, B or C) or the sequence index (1, 2 or 0) and ∆v and ∆v are voltage drops in the section to the left and to the right, respectively of the SC point. For individual sequences, they are determined by Equations (3):
Various variants of solving Equation (2) are known. The most general solution is associated with obtaining the objective function and applying a special computational procedure [47]. At the same time, the general criterion for the FL on OHPL with a minimum error is the condition for achieving the global minimum using the objective function on a set of variable parameters. The simplest objective function can be the discrepancy of Equation (2), that is, the difference in their right side from zero. The formation of residual values ǀσǀ is implemented by changing the distance to the fault n (for example, for LF ∈ [0; L]). Next, the modulus of the right side is determined depending on the expected fault location. An example of four such dependences for Rtrans = 0 is shown in Figure 2 for the OHPL of 220 kV and 100 km long [18].
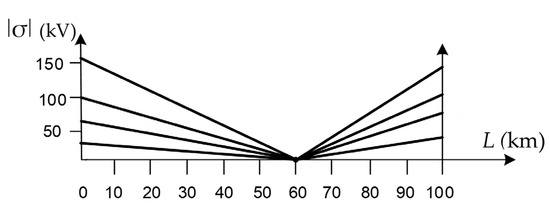
Figure 2.
The graph of the dependence of the discrepancies of Equation (2) on the distance to the place of fault.
Along with the general approach, there are many private criteria for single-, double- and multi-ended methods of FL on OHPL, which can be applied in the implementation of the optimization task:
- Minimum (equality of zero) reactive power at the place of fault [47];
- Minimum (equality of zero) reactive resistance in the place of fault [48];
- Compliance of the current distribution coefficient with registered currents at the ends of the power transmission line [49];
- Compliance of the voltage at the place of fault with the values calculated from different sides of the OHPL for registered currents and voltages [50];
- Criteria based on the theory of remote measurement (resistance measurement) [18];
- Criteria based on the use of instant values of currents and voltages [50];
- Other criteria used for various OHPL configurations [19].
Options for the practical application of optimization iteration procedures for FL on OHPLs by EMPs can be different [51,52,53]. However, the widespread use of the Newton–Rafson algorithm should be distinguished [54,55,56,57,58]. Such a choice is justified by the fact that even in simple tasks of single- and double-ended methods of FL, it is advisable to minimize the error of calculating the distance to the place of fault in the conditions of unknown resistance of the fault. Therefore, it is necessary to implement optimization algorithms that simultaneously reach the extremum of the target function in a minimum of two parameters.
Another approach for FL on OHPL based on optimization procedures used in OHPLs with taps [59,60,61] is known. At the same time, the following iteration algorithm is applied:
- Implementation of simulation of the analyzed OHPL;
- Moving the fault point when simulating along the OHPL and fixing on each iteration currents and voltages at the ends of the OHPL;
- Comparison of the parameters of currents and voltages obtained by simulation with oscillograms of the emergency mode, recorded on the ends of the OHPL at the fault time;
- Calculation of deviations of simulated currents and voltages from the result of processing oscillograms of the emergency mode;
- Finding the fault location on the OHPL by minimizing deviations of current parameters and voltages using optimization algorithms.
The parameters of currents and voltages may include amplitudes and phases [61], coefficients of current distribution, power distribution, etc. [51,52,53]. For the implementation of optimization procedures, both traditional parametric algorithms and non-parametric can be used: the genetic algorithm [61], an algorithm based on the methods of optimization of whales [60], etc.
The analysis showed that publications have not paid sufficient attention to the methods of one-dimensional optimization and, in particular, the search algorithms. For example, the use of the “golden section” [62] and tangent [63] can reduce the number of steps of the computational iteration procedure. When EMPs implement FL on OHPLs by using simple methods, one-dimensional optimization can contribute to the creation of effective FL devices for the following reasons:
- There are stable algorithms of the FL on OHPL by EMP, in which the error of calculating the distance to the place of fault does not depend on the transition resistance at the place of fault [64,65];
- Methods of one-dimensional optimization are significantly easier from the point of technical implementation and require a smaller number of computing operations and a smaller amount of time to calculate the extremum of the target function, etc. Therefore, their use in FL devices will not lead to complications and a rise in the cost of hardware and software [66,67].
- The vast majority of the FL algorithms on OHPLs suggest uniform distribution of resistance along the OHPL. However, in practice, OHPLs always have heterogeneous areas. Therefore, algorithms of multi-parametric optimization are significantly complicated, and their use in the FL devices for heterogeneous OHPL becomes difficult, and sometimes impossible [68,69,70].
3. Results
3.1. Influence of the Heterogeneity at Overhead Transmission Line on the Accuracy of the Fault Location
According to the requirements of the standard [71], the inhomogeneity of the resistivity distribution along the OHPL can be neglected if the error of the FL increases by no more than 2%.
Sections of extended OHPLs operated by electric grid companies may include wires of different brands suspended on towers of various types. Additionally, the line route often passes through terrain with different soil characteristics [72,73].
The equivalent circuit of a single-circuit OHPL, consisting of two heterogeneous sections of different lengths n1∙L and n2∙L with resistances Z1L∙n1∙L and (Z1L + ∆ZL2)∙n2∙L, is shown in Figure 3.
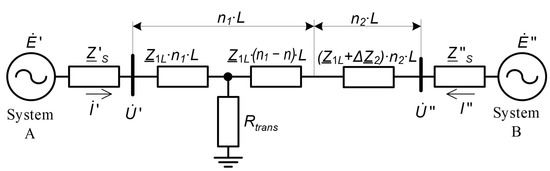
Figure 3.
Equivalent circuit of a heterogeneous single-circuit OHPL with two sections.
Taking into account the metallic SC (Rtrans = 0), as well as the uniform resistivity of the OHPL sections, the error in calculating the distance to the fault place in the section n1∙L will be determined by Equation (4):
where
At the same time, the maximum value of the FL error of OHPL is achieved when the SC occurs at the end of the section n1∙L and corresponds to Equation (5):
In the event of a SC in the second OHPL section, the error in calculating the distance to the fault place should be determined by Equation (6):
which takes the maximum value at n = n2.
An analysis of Equations (4) and (6) shows that the error value changes according to a linear law, and ∆ZL2 can have both a positive and a negative sign. Figure 4 shows the dependence of the calculation error in the FL on OHPL for cases where ∆ZL2 < 0 and ∆ZL2 > 0, and the maximum error value is reached at the end of the first section of the OHPL.
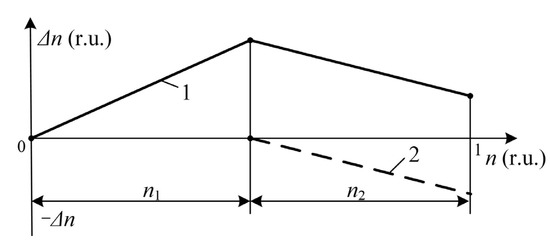
Figure 4.
Dependence of the calculation error in the case of FL on OHPL: 1 corresponds to ∆ZL2 < 0; 2 corresponds to ∆ZL2 > 0.
Generalizing the approaches to calculating the error of the FL on OHPL, including N inhomogeneous sections, let us move on to Equation (8) for calculating the error during an SC in the Nth section of the OHPL:
Based on the requirements of [71], when estimating the magnitude of the maximum error, it is necessary to consider SC at the end of each section of the OHPL and choose the largest of them, which determines the admissibility of neglecting the inhomogeneity of the OHPL. The value of the maximum error in the Nth section should be determined using Equation (9):
For FL on OHPLs with a smaller error, inhomogeneous sections should be taken into account. In the event of fault in each of the sections, there is an individual error of the FL (Equation (8)), which depends on the ratios of the resistance values of individual OHPL sections. This significantly complicates the procedure for calculating the distance to the fault place.
3.2. Analysis of the Application of Iterative Procedures in Case of Fault Location on OHPLs
Let us consider the application of numerical methods of one-dimensional optimization for FL on OHPLs. The problem of the FL on OHPLs can be reduced to finding the smallest value of some function, which is chosen as the target one. This approach is universal and can be applied to both homogeneous and heterogeneous OHPLs. It can be assumed that the objective functions characterizing the distribution of the OHPL parameters of the recorded currents and voltages are continuous and differentiable.
Let f(x) be a continuous function on the interval [a, b]. The task of finding the minimum of a function can be written as
The solution of task (10) will be denoted by хopt:
Note that maximizing the objective function (f(x) → max) is equivalent to minimizing the opposite value (−f(x) → min); therefore, without loss of generality, we will consider only minimization tasks.
Due to the specific features of the FL on OHPLs, when solving the optimization task, as a rule, unimodal functions take place, in which the local minimum is simultaneously global. Therefore, f(x) is a convex function (the second derivative f″(x) ≥ 0 on the section [a, b]).
The use of some one-dimensional optimization methods is possible only when the rate of change of the objective function f(x) in any parts of the segment [a, b] is limited by a certain number, the same for all sections. Then, we say that f(x) satisfies the Lipschitz condition. It is observed if there exists a number Θ > 0 (Lipschitz constant) such that
for all x′ and x″ belonging to [a, b].
Methods that use only the values of the function and do not require the calculation of derivatives are called direct optimization methods. In this case, the function f(x) may not be specified in an analytical form, but it is important that it is possible to determine the function f(x) at given points. The classification of search algorithms for unconditional one-dimensional optimization based on various mathematical methods is shown in Figure 5.
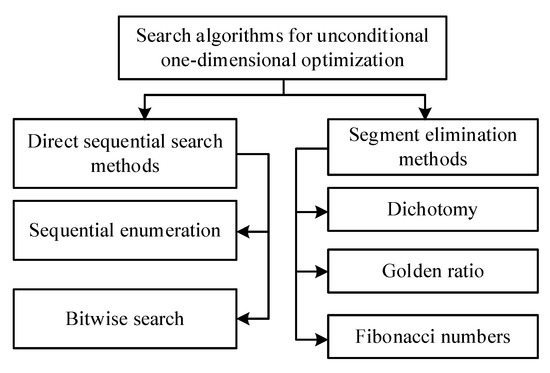
Figure 5.
Classification of search algorithms for unconditional one-dimensional optimization.
The simplest way to solve the problem is the method of sequential enumeration (Figure 5). A typical example of the use of sequential enumeration is the iterative method of FL by EMP for single-ended measurements on OHPLs [49]. This method is applicable not only to homogeneous OHPLs but also, with some modernization, to OHPLs that include heterogeneous sections. Let us explain the implementation of the iterative FL using the example of a single homogeneous OHPL (Figure 1).
In the event of a SC on the OHPL, the currents (from the side of System A) and (from the side of System B) and voltages (on the buses of System A) and (on the buses of System B). The total SC current through the transition resistance F is the sum of the components of the SC current from System A Fab and from System B Fab in emergency mode.
The voltage in the FL devices at the beginning of the OHPL is equal to the sum of the voltage drops on the OHPL to the point of fault ∆F and at the transient resistance ∆R trans, which is calculated by Equation (13):
where n = LF/L is the distance from System A to the fault place, p.u.
In Equation (13), the , and F values are determined depending on the type of fault in accordance with the recommendations [16,18].
There are two unknowns in Equation (13); these are the distance to the fault location n and the current at the fault location F. To determine them, the current is needed not only from the side of System A, but also from the side of System B. Therefore, the exact distance to the fault place on the OHPL according to Equation (13) can only be determined using an iterative process. During this process, the value of the current at the fault place is specified by approaching the true value of the current distribution coefficient.
The problem of FL on OHPLs can be solved using the algorithm shown in Figure 6. It is called the impedance method [49].
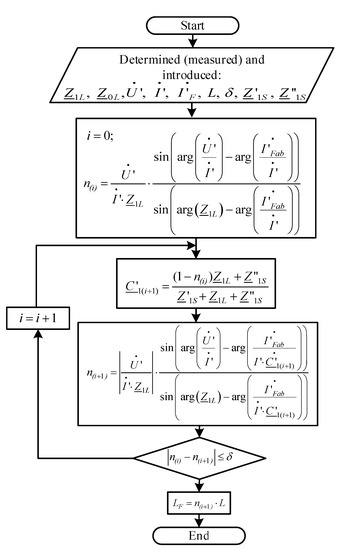
Figure 6.
Block diagram of the FL algorithm based on the impedance method for a single-circuit OHPL with two-way power supply.
Let us explain the sequence of implementation of the steps in FL on OHPLs using the impedance method (Figure 6).
- To perform the FL procedure, the following characteristics must be entered into the FL device: the total length of the power line—L; the value of δ, which determines the calculation error (reducing the error leads to an increase in the number of iterations); full longitudinal resistances of the positive and zero sequences of OHPLs (Z1L и Z0L); and the resistance from the side of System A (place of installation of the FL device). These resistances are calculated from the emergency-mode parameters according to Equation (14):
- 2.
- The resistance from System B (the opposite end of the OHPL in relation to the place of installation of the FL device)—Z″1S, in contrast to the resistance from System A–Z′1S (the beginning of the OHPL)—cannot be calculated from the parameters of the emergency mode. This is true since the single-ended FL method by EMP does not use communication channels to transmit information from the opposite end of the OHPL. Therefore, this resistance must be set in advance or changed depending on the currents and voltages at the beginning of the OHPL, based on the accumulated empirical data. In this case, an error arises, since at the moment of a SC, the resistance from System B differs from the resistance in the pre-emergency mode due to the operation of automatic excitation regulators of synchronous generators at power plants, as well as changes in the network configuration.
- 3.
- At the time of fault on the OHPL, based on the entered settings, the distance to the fault place n(i) is determined as a first approximation using the assumption that the current distribution coefficient C′1(i) is a real number (for i = 0).
- 4.
- An iterative process is launched, and in its course, the current distribution coefficient C′1(i + 1) is specified, as well as the distance to the fault place n(i + 1), where i is the iteration number.
- 5.
- At the end of each iteration, the following condition is checked:
If the inequality condition (15) is not met, then the process goes to the next iteration and repeats step 3. If the inequality condition (15) is met, then the iterative process ends and the distance to the fault place in relative units (r.u.) is determined by Equation (16):
The high accuracy of the iterative method of FL on OHPLs is confirmed by the results of simulation [49].
An improved method of sequential enumeration is called the bitwise search method and is characterized by a reduced number of f(x) values that must be found in the process of searching for the extremum of the function. If f(xi) ≤ f(xi + 1), then there is no need to calculate f(x) at the points xi + 2, xi + 3, etc. since the unimodality of the function implies that xopt ≤ xi + 1.
It is advisable to first determine the section of the OHPLs containing the point xopt with a small accuracy and then search for it in this section with a smaller step. It is this logic that is implemented in the bitwise search method. The enumeration of the section points occurs first with a step ∆х = xi + 1 − xi > δ until the condition f(xi) ≤ f(xi + 1) is satisfied or until the next of these points coincides with the end of the OHPL section. After that, the step decreases (usually four times) and the enumeration of points with a new step is carried out in the opposite direction until the values of f(x) stop decreasing or the next point coincides with the end of the OHPL section. The algorithm for the FL on OHPLs based on the bitwise search method is shown in Figure 7a.
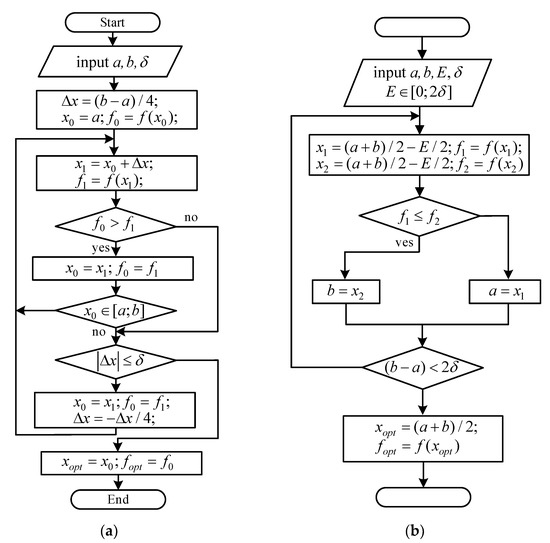
Figure 7.
Block diagrams of the FL algorithm for OHPLs based on the following methods: (a) bitwise search; (b) dichotomies.
The process of calculating the distance to the fault place is completed when the enumeration in the given direction is completed. In this case, the discretization step does not exceed the error δ.
Let us consider the issue of applying the methods of excluding sections for FL on OHPLs. One of the most efficient ways to search for xopt follows from the definition of unimodal functions when organizing the FL procedure.
Let а < x1 < x2 < b; then, by comparing the values of f(x1) and f(x2), we can shorten the search area xopt by going to the area [а, x1], if f(x1) < f(x2) or to the area [x1, b], if f(x1) > f(x2).
The above procedure can be repeated several times, successively reducing the section of the OHPL containing the minimum point. There are various methods (Figure 5) for excluding segments depending on the method of choosing the analyzed points (dichotomy, golden section, Fibonacci numbers, etc.).
Let us consider the application of methods for eliminating segments using the example of a dichotomy. In this case, a small value E is chosen, which belongs to the interval Е ϵ [0; 2δ], where δ is the FL error (Figure 7b).
Relative to the middle of the segment [a, b], the points are determined according to Equation (17):
as well as the values of the function f(x) at these points f1 = f(x1), f2 = f(x2).
Let us verify the condition f1 ≤ f2 (Figure 7b) and select points for forming a segment for subsequent analysis depending on the ratio of f1 and f2. The ratio of the new segment length to the length of the previous one will be as follows:
The iterative process ends when the length of the next segment is (b − a) < 2δ. At the last step of the iterative process, the optimal value of the function f(x) argument is determined, which is хopt = (a + b)/2.
When using the dichotomy method to ensure a given error δ of the FL on OHPL, the required number of iterations is determined from the condition:
The required number of calculations of the objective function f(x) should be M = 2m, and the guaranteed calculation error after m iterations will be
4. Discussion
Let us consider examples of the application of bitwise search and dichotomy methods in the case of FL on an inhomogeneous OHPL.
It was noted above that for an accurate FL on OHPL, it is necessary to take into account its inhomogeneous sections. In the case of fault on each of the OHPL sections, an individual error of the FL takes place. It depends on the ratio of the specific resistance values of individual OHPL sections and significantly complicates the procedure for calculating the distance to the fault place.
In [74], the following requirements are established for determining the inspection area of the OHPL. After an emergency shutdown of the OHPL, according to the data of the FL devices, the length of the inspection zone should be no more than
- ±15% of the OHPL length with its length up to 50 km inclusive;
- ±10% for OHPLs with a length of more than 50 km up to 100 km inclusive;
- ±7% for OHPLs with a length from 100 to 300 km inclusive; and
- ±5% for OHPLs with a length from 300 km or more.
Taking the size of the inspection zone based on operating experience and statistical data from the indications of FL devices is allowed in a given electric grid company.
Therefore, on an OHPL with a non-uniform distribution of resistivity along the overhead line, the inspection area should be increased by the value of the maximum error (Equation (9)). This is necessary to exclude cases when the fault place on the OHPL is outside the inspection area. For the implementation of high-speed and accurate FL on OHPLs, the most promising approach is to first calculate the distance to the fault place using the equation for homogeneous OHPLs. Next, an extended inspection area is determined, taking into account the error of the FL due to the inhomogeneous distribution of resistivity along the OHPL. Further, within the extended inspection area, the algorithm of FL is implemented for a non-uniform OHPL in order to clarify the size of the inspection area.
To illustrate the application of numerical methods of one-dimensional optimization, we will use the data obtained from the operated OHPL, 220 kV and 120 km long, with a short circuit on its section. The OHPL is heterogeneous, consisting of three sections:
where n1 = n2 = n3 = 1/3; ∆ZL2 = −0.15∙Z1L; and ∆ZL3 = −0.3∙Z1L.
For simplicity of calculations, let us move from complex values to amplitude values of currents and voltages. The recorded actual values of the amplitudes of currents and voltages at the ends of a real OHPL were I′ = 2.0 kA, I″ = 0.56 kA, U′ = 40 kV, U″ = 28 kV. Let us implement a distance-to-fault calculation using double-ended current and voltage measurements.
At the first stage, we will not take into account the inhomogeneity of the resistances in the sections of the OHPL (Figure 1). We will form the main calculation relations of the FL method based on measurements of the modules of currents and voltages at the ends of the OHPL I′, I″, U′, U″, as well as Equation (21):
where UF is the voltage at the place of the SC (fault).
The calculation according to Equation (21) is performed by the components of the zero sequence. In this case, the resistivity Z0 = 30,426 = 1278 Ohm/km, and ZL = L∙Z0. Let us calculate the distance to the fault place on the OHPL by jointly solving Equation (21), with the substitution Z0, which corresponds to the calculation equation:
Let us set the permissible error in calculating the distance to the FL on OHPLs with a nonuniform distribution of resistivity based on the operating experience of an OHPL. The operational and technological personnel of electric grid companies consider the error in calculating the distance to the FL on OHPL to be low if it does not exceed the length of one OHPL span. The length of one span of 220 kV OHPL is 250–350 m, so we will set the allowable error in calculating the distance to the fault place in the form δ = 0.3 km.
Let us assume that according to the results of preliminary calculations of the FL on OHPL, taking into account the heterogeneity of the sections of the OHPL, the average distance to the fault place was L′F = 19.2 km. The simulation may include multiple random factors to obtain the average distance to a fault, and the results may differ from the actual values due to the current combination of random factors. Therefore, the error in the implementation of the FL on OHPL due to the non-uniform distribution of resistivity along the overhead line will be equal to
Let us form an extended inspection area of OHPLs by a line crew for the example under consideration (±7%) for OHPLs with a length from 100 to 300 km inclusive (±120∙0.07 = 8.4 km), taking into account the FL error with the value ±∆LF = 3.382 km. The extended inspection area of the OHPL will be ±12.382 km, and relative to the fault place LК = 22.582 km, it will correspond to the section of the OHPL from 10.2 km to 34.964 km.
When implementing the developed method of FL on OHPLs, we will use an iterative algorithm based on the bitwise search method, which provides a calculation of the distance to the fault place on the OHPL with a non-uniform distribution of resistivity along the OHPL with a given allowable error δ = 0.3 km. The computational algorithm of the iterative bitwise search procedure (Figure 7a) is implemented within the extended inspection area of the OHPL within a = 10.2 km and b = 34.964 km.
The application of the criterion of equality of voltages calculated from two ends of the OHPL makes it possible to form the required objective function of the iterative algorithm f(х) = ∆U, which provides a minimum of the module of the voltage difference ∆U at the fault point (UF) (Equation (21)), calculated from different ends of power lines:
Equation (23) is valid for a homogeneous OHPL; therefore, in the presence of sections with non-uniform resistance, it is necessary to specifically take into account the voltage drop in these sections.
FL devices that involve the use of search algorithms are made by both European and North American manufacturers, which use different processors and controllers. Therefore, the operating time is estimated by the number of steps of the iterative procedure in order not to be tied to a particular manufacturer and to ensure the comparability of the effect for different devices.
Let us apply a step-by-step calculation of the distance to the fault place for an inhomogeneous OHPL using the bitwise search method with the chosen objective function (23).
In the first step:
х0 = а = 10.2 km; ∆х = (b − a)/4 = (34.964 − 10.2)/4 = 6.191 km;
f0 = f(х0) = ∆U = ǀ[2.0∙10.2∙1.278 + 40] − [0.56∙1.278·(40 − 10.2 + 40·0.85 + 40·0.7) + 28]ǀ = 27.63 kV;
х1 = х0 + (b − a)/4 = 10.2 + (34.964 − 10.2)/4 = 16.391 km;
f1 = f(х1) = ∆U = ǀ[2.0∙16.391∙1.278 + 40] − [0.56∙1.278·(40 − 16.391 + 40·0.85 + 40·0.7) + 28]ǀ = 7.37 kV.
f0 = f(х0) = ∆U = ǀ[2.0∙10.2∙1.278 + 40] − [0.56∙1.278·(40 − 10.2 + 40·0.85 + 40·0.7) + 28]ǀ = 27.63 kV;
х1 = х0 + (b − a)/4 = 10.2 + (34.964 − 10.2)/4 = 16.391 km;
f1 = f(х1) = ∆U = ǀ[2.0∙16.391∙1.278 + 40] − [0.56∙1.278·(40 − 16.391 + 40·0.85 + 40·0.7) + 28]ǀ = 7.37 kV.
In the second step:
х0 = 16.391 (km); f0 = f(х0) = ∆U = 7.37 kV; х1 = х0 + ∆х = 16.391 + 6.191 = 22.582 km;
f1 = f(х1) = ∆U = ǀ[2.0∙22.582∙1.278 + 40] − [0.56∙1.278·(40 − 22.582 + 40·0.85 + 40·0.7) + 28]ǀ = 12.88 kV;
∆х = −∆х/4 = −1.55.
f1 = f(х1) = ∆U = ǀ[2.0∙22.582∙1.278 + 40] − [0.56∙1.278·(40 − 22.582 + 40·0.85 + 40·0.7) + 28]ǀ = 12.88 kV;
∆х = −∆х/4 = −1.55.
In the third step:
х0 = 16.391 (km); f0 = f(х0) = ∆U = 7.37 kV; х1 = х0 + ∆х = 16.391 − 1.55 = 14.841 km;
f1 = f(х1) = ∆U= ǀ[2.0∙14.841∙1.278 + 40] − [0.56∙1.278·(40 − 14.841 +
+ 40·0.85 + 40·0.7) + 28]ǀ = 12.44 (kV);
∆х = −∆х/4 = 1.55/4 = 0.39.
f1 = f(х1) = ∆U= ǀ[2.0∙14.841∙1.278 + 40] − [0.56∙1.278·(40 − 14.841 +
+ 40·0.85 + 40·0.7) + 28]ǀ = 12.44 (kV);
∆х = −∆х/4 = 1.55/4 = 0.39.
The variables obtained in a similar way according to the algorithm in Figure 7a are listed in Table 1.

Table 1.
An example of the FL implementation on OHPLs based on the bitwise search method.
Thus, the distance to the fault place is LF = 18.641 km, and its calculation requires m1 = 20 steps of the iterative procedure organized by the bitwise search method (Figure 8).
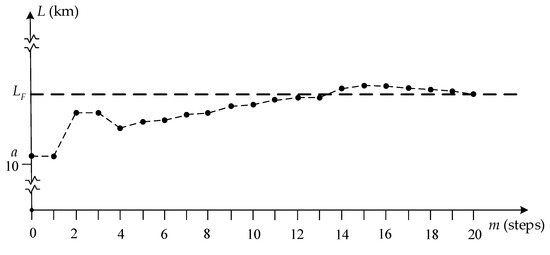
Figure 8.
Graph for the FL implementation on OHPLs by an EMP based on the bitwise search method.
We will refine the inspection zone of the OHPL by the line crew in accordance with the requirements of [74], i.e., (±7%) for the OHPL with a length from 100 to 300 km inclusive (±120∙0.07 = 8.4 km). Thus, the revised survey zone will correspond to the section of the OHPL from 10,241 km to 27,041 km.
Since, in the implementation of the FL on OHPL, the alleged fault place can be at any point of an inhomogeneous OHPL, under the conditions of the example for a simple method of sequential enumeration, the required number of iteration steps in the case of fault at the end of the overhead transmission line will be m2 = L/δ = 120/0.3 = 400. The gain in speed when implementing the bitwise search method, compared with the sequential search method, will be w = m2/m1 = 20 times.
The gain in the speed of iterative procedures w largely depends on the pre-specified error δ of the FL line (Figure 8). The smaller the error, the more significant the gain.
According to the calculation results (Table 1), the error in the implementation of the FL on OHPL due to the non-uniform distribution of resistivity along the overhead line will be
or 3.28% of the length of the high-voltage transmission line.
∆LF = LF − L’F = 22.582 − 18.641 = 3.941 km,
The proposed variant of the FL implementation on OHPL has an error that does not exceed δ = 0.3 km or 0.25% of the OHPL length.
If we do not use a two-stage procedure and implement an iterative FL throughout the entire length of the overhead line, then the number of steps m can be significantly increased.
х0 = 0 (n = 0); f0 = f(х0) = ∆U = ǀU1 − [I2 0.85∙120∙ZL + U2]ǀ
= ǀ40 − 0.85∙0.56∙120∙1.278 + 28ǀ = 61.0 kV;
х1 = х0 + (b − a)/4 = 30 km (n = 0.25); f1 = f(х1) = ∆U = ǀ[2.0∙0.25∙120∙1.278 +40]
− [0.56∙0.6∙120∙1.278 + 28]ǀ = 37.15 kV;
∆х = 120/4 = 30 km.
= ǀ40 − 0.85∙0.56∙120∙1.278 + 28ǀ = 61.0 kV;
х1 = х0 + (b − a)/4 = 30 km (n = 0.25); f1 = f(х1) = ∆U = ǀ[2.0∙0.25∙120∙1.278 +40]
− [0.56∙0.6∙120∙1.278 + 28]ǀ = 37.15 kV;
∆х = 120/4 = 30 km.
The variables obtained in a similar way are shown in Table 2.

Table 2.
An example of the implementation of the FL on OHPLs in the case of refusal from the two-stage procedure.
Analysis of the data from Table 2 shows that the distance to the fault place was LF = хopt = 18.621 km, which corresponds to the value from Table 1, but it took m1 = 30 steps of the iterative procedure organized by the bitwise search method to calculate it.
In this case, the speed gain associated with the use of the bitwise search method compared to sequential enumeration is equal to w = m2/m1 = 13.33 times.
Ensuring a large gain in speed can be achieved by using methods for eliminating segments (Figure 5). For example, the dichotomy method (Equation (19)) for the considered example with Е = δ requires the implementation of the minimum number m3 = log2 [(L − δ)/δ] = log2 [(120 − 0.3)/ 0.3] = log2 [399] 9 steps, with a corresponding gain w = m2/m3 = 44.44 times.
5. Conclusions
Most of the well-known FL algorithms for OHPLs by EMP are based on the assumption of a uniform distribution of resistivity along the OHPL. The use of these FL algorithms for OHPLs with inhomogeneities will lead to significant errors in calculating the distance to the fault place.
The expediency of using simple search and optimization methods (sequential enumeration, dichotomy, and bitwise search) that do not require changes in the hardware of the device and increase its cost, but give an effect in terms of speed, is substantiated.
The results of the calculations prove that the use of the search algorithms proposed by the authors makes it possible to reduce the time required to calculate the distance to the fault place from tens to hundreds of times.
An additional advantage of using the search algorithms proposed by the authors for FL on OHPLs is that their implementation is possible in the software of typical relay protection and automation terminals, without the need to upgrade their hardware.
Along with undeniable advantages, the use of search methods leads to an insignificant complication of the software in the implementation of FL on OHPLs.
Author Contributions
Conceptualization, A.K. and P.I.; methodology, A.K. and S.F.; software, A.K. and A.L.; validation, P.I. and S.F.; formal analysis, A.K. and S.F.; investigation, A.L.; resources, P.I.; data curation, P.I.; writing—original draft preparation, A.K. and P.I.; writing—review and editing, S.F. and A.L; visualization, A.L.; supervision, A.K.; project administration, P.I.; funding acquisition, S.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing is not applicable. No new data were created or analyzed in this study.
Conflicts of Interest
The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Montoya, F.G.; Baños, R.; Alcayde, A.; Manzano-Agugliaro, F. Optimization Methods Applied to Power Systems. Energies 2019, 12, 2302. [Google Scholar] [CrossRef]
- Lu, Z.; Xu, X.; Yan, Z.; Wu, J.; Sang, D.; Wang, S. Overview on Data-Driven Optimal Scheduling Methods of Power System in Uncertain Environment. Autom. Electr. Power Syst. 2020, 44, 172–183. [Google Scholar]
- Al-Shahri, O.A.; Ismail, F.B.; Hannan, M.A.; Lipu, M.S.H.; Al-Shetwi, A.Q.; Begum, R.A.; Al-Muhsen, N.F.O.; Soujeri, E. Solar Photovoltaic Energy Optimization Methods, Challenges and Issues: A Comprehensive Review. J. Clean. Prod. 2021, 284, 125465. [Google Scholar] [CrossRef]
- Huang, Х.; Dong, Z.; Zhang, F.; Zhang, L. Model-free adaptive integral sliding mode constrained control withmodified prescribed performance. IET Control Theory Appl. 2023, 1–17. [Google Scholar] [CrossRef]
- Zabudsky, G.G.; Veremchuk, N.S. About One-Dimensional Space Allocation Problem with forbidden zones. Mech. Sci. Technol. Update 2019, 1260, 082006. [Google Scholar] [CrossRef]
- Stringfield, T.W.; Marihart, D.J.; Stevens, R.F. Fault location methods for overhead lines. IEEE Trans. Power Appar. Syst. 1957, 76, 518–530. [Google Scholar] [CrossRef]
- Born, E.; Jaeger, J. Device locates point of fault on transmission lines. Electr. World 1967, 168, 133–134. [Google Scholar]
- Senderovich, G.A.; Gryb, O.G.; Karpaliuk, I.T.; Shvets, S.V.; Zaporozhets, A.O.; Samoilenko, I.A. Automation of determining the location of damage of overhead power lines. Stud. Syst. Decis. Control. 2021, 359, 35–53. [Google Scholar]
- Farkhadzeh, E.M.; Muradaliev, A.Z.; Abdullaeva, S.A.; Nazarov, A.A. Quantitative Assessment of The Operational Reliability of Overhead Power Transmission Lines. Power Technol. Eng. 2022, 55, 790–796. [Google Scholar] [CrossRef]
- Zainuddin, N.M.; Rahman, M.S.A.; Kadir, M.Z.A.A.; Ali, N.H.N.; Ali, Z.; Osman, M.; Mansor, M.; Ariffin, A.M.; Nor, S.F.M.; Nasir, N.A.F.M. Review of Thermal Stress and Condition Monitoring Technologies for Overhead Transmission Lines: Issues and Challenges. IEEE Access 2020, 8, 120053–120081. [Google Scholar] [CrossRef]
- Beryozkina, S. Evaluation Study of Potential Use of Advanced Conductors in Transmission Line Projects. Energies 2019, 12, 822. [Google Scholar] [CrossRef]
- Khalyasmaa, A.I.; Dmitriev, S.A.; Romanov, A.M. Robotic Intelligence Laboratory for Overhead Transmission Lines Assessment. In Proceedings of the 2016 57th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON 2016), Riga, Latvia, 13–14 October 2016; p. 7763123. [Google Scholar]
- Palangar, M.F.; Mohseni, S.; Siada, A.; Mirzaie, М. Online Condition Monitoring of Overhead Insulators Using Pattern Recognition Algorithm. IEEE Trans. Instrum. Meas. 2022, 71, 6007111. [Google Scholar] [CrossRef]
- Palangar, M.F.; Amin, U.; Bakhshayesh, H.; Ahmad, G.; Siada, A.; Mirzaie, М. Identification of Composite Insulator Criticality Based on a New Leakage Current Diagnostic Index. IEEE Trans. Instrum. Meas. 2021, 70, 9004110. [Google Scholar] [CrossRef]
- Roman, R.-C.; Precup, R.-E.; Petriu, E.M.; Muntyan, M. Fictitious Reference Iterative Tuning of Discrete-Time Model-Free Control for Tower Crane Systems. Stud. Inform. Control. 2023, 32, 1. [Google Scholar] [CrossRef]
- Maly, A.S.; Shalyt, G.M.; Eisenfeld, A.I. Determination of the Places of Damage to Power Transmission Lines According to the Parameters of the Emergency Mode; Energiya: Moscow, Russia, 1972; 215p. (In Russian) [Google Scholar]
- Schweitzer, E.O. A review of impedance-based fault locating experience. In Proceedings of the 14th Annual Iowa–Nebraska System Protection Seminar, Omaha, NE, USA, 16 October 1990; pp. 1–31. [Google Scholar]
- Arzhannikov, E.A.; Lukoyanov, V.Y.; Misrikhanov, M.S. Determining the Location of a Short Circuit on High−Voltage Power Transmission Lines; Shuin, V.A., Ed.; Energoatomizdat: Moscow, Russia, 2003; 272p. (In Russian) [Google Scholar]
- Saha, M.M.; Izykowski, J.; Rosolowski, E. Fault Location on Power Networks; Springer: London, UK, 2010; 437p. [Google Scholar]
- Senderovich, G.A.; Gryb, O.G.; Karpaliuk, I.T.; Shvets, S.V.; Zaporozhets, A.O.; Samoilenko, I.A. Experimental studies of the method for determining location of damage of overhead power lines in the operation mode. Stud. Syst. Decis. Control. 2021, 359, 55–77. [Google Scholar]
- Voropai, N. Electric Power System Transformations: A Review of Main Prospects and Challenges. Energies 2020, 13, 21. [Google Scholar] [CrossRef]
- Ilyushin, P.V.; Pazderin, A.V. Approaches to organization of emergency control at isolated operation of energy areas with distributed generation. In Proceedings of the International Ural Conference on Green Energy (URALCON 2018), Chelyabinsk, Russia, 4–6 October 2018. [Google Scholar] [CrossRef]
- Voropai, N.I.; Golub, I.I.; Efimov, D.N.; Iskakov, A.B.; Yadykin, I.B. Spectral and Modal Methods for Studying Stability and Control of Electric Power Systems. Autom. Remote Control. 2020, 81, 1751–1774. [Google Scholar] [CrossRef]
- Voitovich, P.A.; Lavrov, Y.A.; Petrova, N.F. Innovative technical solutions for the construction of ultra-compact high-voltage overhead power transmission lines. New Russ. Electr. Power Ind. 2018, 8, 44–57. (In Russian) [Google Scholar]
- Kosyakov, A.A.; Kuleshov, P.V.; Pogudin, A.L. The influence of the grounding device structure of a substation on the voltage of conducted interference of lightning currents. Russ. Electr. Eng. 2019, 90, 752–755. [Google Scholar] [CrossRef]
- Sharipov, U.B.; Égamnazarov, G.A. Calculating currents in lightning protection cables and in optical cables built into them during asymmetric short circuits in overhead transmission lines. Power Technol. Eng. 2017, 50, 673–678. [Google Scholar] [CrossRef]
- Shevchenko, N.Y.; Ugarov, G.G.; Kirillova, S.N.; Lebedeva, Y.V. Review and analysis of the design features of overhead power line wires with increased resistance to icy-wind loads. Quest. Electr. Technol. 2018, 4, 53–63. (In Russian) [Google Scholar]
- Lebedev, V.; Filatova, G.; Timofeev, A. Increase of accuracy of the fault location methods for overhead electrical power lines. Adv. Mater. Sci. Eng. 2018, 2018, 3098107. [Google Scholar] [CrossRef]
- Shalyt, G.M.; Eisenfeld, A.I.; Maly, A.S. Determination of Places of Damage to Power Transmission Lines According to the Parameters of the Emergency Mode; Energoatomizdat: Moscow, Russia, 1983; 208p. (In Russian) [Google Scholar]
- Kulikov, A.L. Digital Remote Detection of Power Line Damage; Misrikhanov, M.S., Ed.; Publishing House of the Volga-Vyatka Academy of State Services: Nizhniy Novgorod, Russia, 2006; 315p. (In Russian) [Google Scholar]
- Krzysztof, G.; Kowalik, R.; Rasolomampionona, D.D.; Anwar, S. Traveling wave fault location in power transmission systems: An overview. J. Electr. Syst. 2011, 7, 287–296. [Google Scholar]
- Minullin, R.G. Detecting the faults of overhead electric-power lines by the location-probing method. Russ. Electr. Eng. 2017, 88, 61–70. [Google Scholar] [CrossRef]
- Kulikov, A.L. Remote Determination of Power Line Damage Sites by Active Sensing Methods; Energoatomizdat: Moscow, Russia, 2006; 148p. (In Russian) [Google Scholar]
- Ilyushin, P.V.; Shepovalova, O.V.; Filippov, S.P.; Nekrasov, A.A. Calculating the sequence of stationary modes in power distribution networks of Russia for wide-scale integration of renewable energy-based installations. Energy Rep. 2021, 7, 308–327. [Google Scholar] [CrossRef]
- Lebedev, V.D.; Yablokov, A.A.; Filatova, G.A.; Lebedeva, N.V.; Petrov, A.E. Development and research of fault location algorithm for double-end feed lines in the multifunctional system. In Proceedings of the 2019 2nd International Youth Scientific and Technical Conference on Relay Protection and Automation (RPA 2019), Moscow, Russia, 24–25 October 2019; p. 8958174. [Google Scholar]
- Kulikov, A.; Ilyushin, P.; Suslov, K.; Filippov, S. Estimating the Error of Fault Location on Overhead Power Lines by Emergency State Parameters Using an Analytical Technique. Energies 2023, 16, 1552. [Google Scholar] [CrossRef]
- Izykowski, J. Fault Location on Power Transmission Line; Springer: London, UK, 2008; 221p. [Google Scholar]
- Obalin, M.D.; Kulikov, A.L. Application of adaptive procedures in algorithms for determining the location of damage to power lines. Ind. Power Eng. 2013, 12, 35–39. (In Russian) [Google Scholar]
- Kulikov, A.L.; Obalin, M.D. The development of software to support decision-making in the elimination of damage on power transmission lines. News High. Educ. Inst. Electromech. 2015, 2, 70–75. (In Russian) [Google Scholar]
- Filippov, S.P.; Dilman, M.D.; Ilyushin, P.V. Distributed Generation of Electricity and Sustainable Regional Growth. Therm. Eng. 2019, 66, 869–880. [Google Scholar] [CrossRef]
- Ilyushin, P.V.; Pazderin, A.V.; Seit, R.I. Photovoltaic power plants participation in frequency and voltage regulation. In Proceedings of the 17th International Ural Conf. on AC Electric Drives (ACED 2018), Ekaterinburg, Russia, 26–30 March 2018. [Google Scholar] [CrossRef]
- Suslov, K.; Shushpanov, I.; Buryanina, N.; Ilyushin, P. Flexible power distribution networks: New opportunities and applications. In Proceedings of the 9th International Conference on Smart Cities and Green ICT Systems (SMARTGREENS), Prague, Czech Republic, 2–4 May 2020; pp. 57–64. [Google Scholar] [CrossRef]
- Rylov, A.; Ilyushin, P.; Kulikov, A.; Suslov, K. Testing Photovoltaic Power Plants for Participation in General Primary Frequency Control under Various Topology and Operating Conditions. Energies 2021, 14, 5179. [Google Scholar] [CrossRef]
- Brimberg, J.; Hansen, P.; Mladenovic, N.; Salhi, S. A Survey of Solution Methods for the Continuous Location-Allocation Problem. Int. J. Oper. Res. 2008, 5, 1–12. [Google Scholar]
- Pardalos, P.M.; Khachay, M.; Kochetov, Y. Special Issue: 18th International conference on mathematical optimization theory and operations research (MOTOR 2019). J. Glob. Optim. 2022, 83, 403–404. [Google Scholar] [CrossRef]
- Hansen, P.; Mladenovic, N. Variable Neighborhood Search Methods. Les. Cah. GERAD 2007, 24, 1097–1100. [Google Scholar] [CrossRef]
- Lyamets, Y.Y.; Antonov, V.I.; Efremov, V.A. Diagnostics of power transmission lines. In Electrotechnical Microprocessor Devices and Systems: Interuniversity Collection of Scientific Papers; Publishing House of the Chuvash State University: Cheboksary, Russia, 1992. (In Russian) [Google Scholar]
- Takagi, T.; Yamakoshi, Y.; Yamaura, Y.; Kondow, R.; Matsushima, T. Development of a new type fault locator using the one-terminal voltage and current data. IEEE Trans. Power App. Syst. 1982, 8, 2892–2898. [Google Scholar] [CrossRef]
- Ustinov, A.A.; Visyashchev, A.N. Iterative methods for determining the location of damage by the parameters of the emergency mode during one-way measurements on overhead power lines. Bull. IrSTU 2010, 5, 260–266. (In Russian) [Google Scholar]
- Kulikov, A.L.; Lukicheva, I.A. Determination of the place of damage to the power transmission line by the instantaneous values of the oscillograms of emergency events. Bull. Ivanovo State Power Eng. Univ. 2016, 5, 16–21. (In Russian) [Google Scholar]
- Bahmanyar, A.; Jamali, S.; Estebsari, A.; Bompard, E. A comparison framework for distribution system outage and fault location methods. Electr. Power Syst. Res. 2017, 145, 19–34. [Google Scholar] [CrossRef]
- Yu, C.S.; Liu, C.W.; Jiang, J.A. A new fault location algorithm for series compensated lines using synchronized phasor measurements. In Proceedings of the 2000 Power Engineering Society Summer Meeting, Seattle, WA, USA, 16–20 July 2000. [Google Scholar] [CrossRef]
- Aboshady, F.M.; Thomas, D.W.P. A Wideband Single End Fault Location Scheme for Active Untransposed Distribution Systems. IEEE Trans. Smart Grid 2020, 11, 2115–2124. [Google Scholar] [CrossRef]
- Simeon, O.; Faithpraise, F.O.; Ibanga, J. Iterative Newton-Raphson-Based Impedance Method for Fault Distance Detection on Transmission Line. Int. Multiling. J. Sci. Technol. 2020, 5, 2805–2810. [Google Scholar] [CrossRef]
- Thongkrajay, U.; Poolsawat, N.; Ratniyomchai, T.; Kulworawanichpong, T. Alternative Newton-Raphson power flow calculation in unbalanced three-phase power distribution systems. In Proceedings of the 5th WSEAS International Conference on Applications of Electrical Engineering, Prague, Czech Republic, 12–14 March 2006; pp. 24–29. [Google Scholar]
- Nagendra Reddy, P.L.V.; Mukunda, V.K.S.; Sushyanth, C.; Vanitha, V. Implementation of Novosel Simple Impedance Algorithm for fault location. IJCTA 2016, 9, 7589–7596. [Google Scholar]
- Liao, Y. Transmission Line Fault Location Algorithms without Requiring Line Parameters. Electr. Power Compon. Syst. 2008, 36, 1218–1225. [Google Scholar] [CrossRef]
- Panahi, H.; Zamani, R.; Sanaye-Pasand, M.; Mehrjerdi, H. Advances in Transmission Network Fault Location in Modern Power Systems: Review, Outlook and Future Works. IEEE Access 2021, 9, 158599–158615. [Google Scholar] [CrossRef]
- Azizi, S.; Sanaye-Pasand, M. A Straightforward Method for Wide-Area Fault Location on Transmission Networks. IEEE Trans. Power Deliv. 2015, 30, 264–272. [Google Scholar] [CrossRef]
- Bahmanyar, A.; Borhani-Bahabadi, H.; Jamali, S. Fault Location in Active Distribution Networks Using Improved Whale Optimization Algorithm. Iran. J. Electr. Electron. Eng. 2020, 16, 302–312. [Google Scholar]
- Kezunovic, M.; Knezev, M. Selection of optimal fault location algorithm. In Proceedings of the Conference: Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008. [Google Scholar] [CrossRef]
- Yang, H.; Liu, X.; Guo, Y.; Zhang, P. Fault Location of Active Distribution Networks Based on the Golden Section Method. Math. Probl. Eng. 2020, 2020, 6937319. [Google Scholar] [CrossRef]
- Dalcastagne, A.L.; Filho, S.N.; Zurn, H.H.; Seara, R. An Iterative Two-Terminal Fault-Location Method Based on Unsynchronized Phasors. IEEE Trans. Power Deliv. 2008, 23, 2318–2329. [Google Scholar] [CrossRef]
- Izykowski, J. Location of complex faults on overhead power line. Prz. Elektrotechniczny 2016, 1, 81–84. [Google Scholar] [CrossRef]
- Dong, A.H.; Geng, X.L.; Yang, Y.; Su, Y.; Li, M.Y. Overhead Power Line Fault Positioning System. Appl. Mech. Mater. 2013, 329, 299–303. [Google Scholar] [CrossRef]
- Visyashchev, A.N. Devices and Methods for Determining the Location of Damage on Power Transmission Lines: A Textbook; At 2 h. h. 1; Publishing House of IrSTU: Irkutsk, Russia, 2001; 188p. (In Russian) [Google Scholar]
- Belyakov, Y.S. Actual issues of determining the places of damage to overhead power lines. Electr. Eng. Libr. 2010, 11, 80. (In Russian) [Google Scholar]
- Suslov, K.; Solonina, N.; Solonina, Z.; Akhmetshin, A. Development of the method of determining the location of a short circuit in transmission lines. J. Phys. Conf. Ser. 2021, 2061, 012033. [Google Scholar] [CrossRef]
- Eroshenko, S.A.; Ilyushin, P.V. Features of implementing multi-parameter islanding protection in power districts with distributed generation units. In Proceedings of the 2018 IEEE 59th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON 2018), Riga, Latvia, 12–14 November 2018. [Google Scholar] [CrossRef]
- Minullin, R.G.; Akhmetova, I.G.; Kasimov, V.A.; Piunov, A.A. Location monitoring with determination of damage location and current operability of overhead power transmission lines. Electr. Station. 2022, 11, 30–38. (In Russian) [Google Scholar]
- STO 56947007-29.240.55.224-2016; Standard of the Organization of PJSC FGC UES. Guidelines for Determining the Places of Damage to Overhead Lines with a Voltage of 110 kV and Higher. Publishing House PJSC FGC UES: Moscow, Russia, 2016.
- Ahmedova, O.; Soshinov, A.; Shevchenko, N. Analysis of influence of external atmospheric factors on the accuracy of fault location on overhead power lines. In Proceedings of the High-Speed Turbomachines and Electrical Drives Conference 2020 (HSTED-2020), Prague, Czech Republic, 14–15 May 2020. [Google Scholar]
- Margitova, A.; Kolcun, M.; Kanalik, M. Impact of the Ground on the Series Impedance of Overhead Power Lines. Trans. Electr. Eng. 2018, 7, 47–54. [Google Scholar] [CrossRef]
- STO 56947007–29.240.55.159–2013; Standard of the Organization of PJSC FGC UES. Standard Instructions for the Organization of Work to Determine the Places of Damage to Overhead Power Lines with a Voltage of 110 kV and Above. Publishing House PJSC FGC UES: Moscow, Russia, 2013.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).