Blow-Up Dynamics and Synchronization in Tri-Trophic Food Chain Models
Abstract
1. Introduction
- The UR and HP models individually can exhibit chaotic dynamics for the same parameter regimes. However, they will synchronize when coupled accordingly.
- This synchronization will occur only for small-to-moderate initial conditions.
- For larger initial conditions, the UR and HP models will not synchronize. This is shown numerically and analytically.
- For small initial conditions, the modified UR and HP models will synchronize, but for larger initial conditions, it is numerically seen that they will not synchronize.
- Thus, we reaffirm that the synchronization of three species’ food chains with different top-down control (differently behaving top predators) is caused solely by the top predator.
2. Generalized Synchronization Using the OPCL Coupling Method
3. Model Systems
3.1. Upadhyay–Rai (UR) Model
3.2. Hastings–Powell (HP) Model
4. Generalized Synchronization of the UR Model and HP Model Using the OPCL Coupling Method
5. Numerical Results
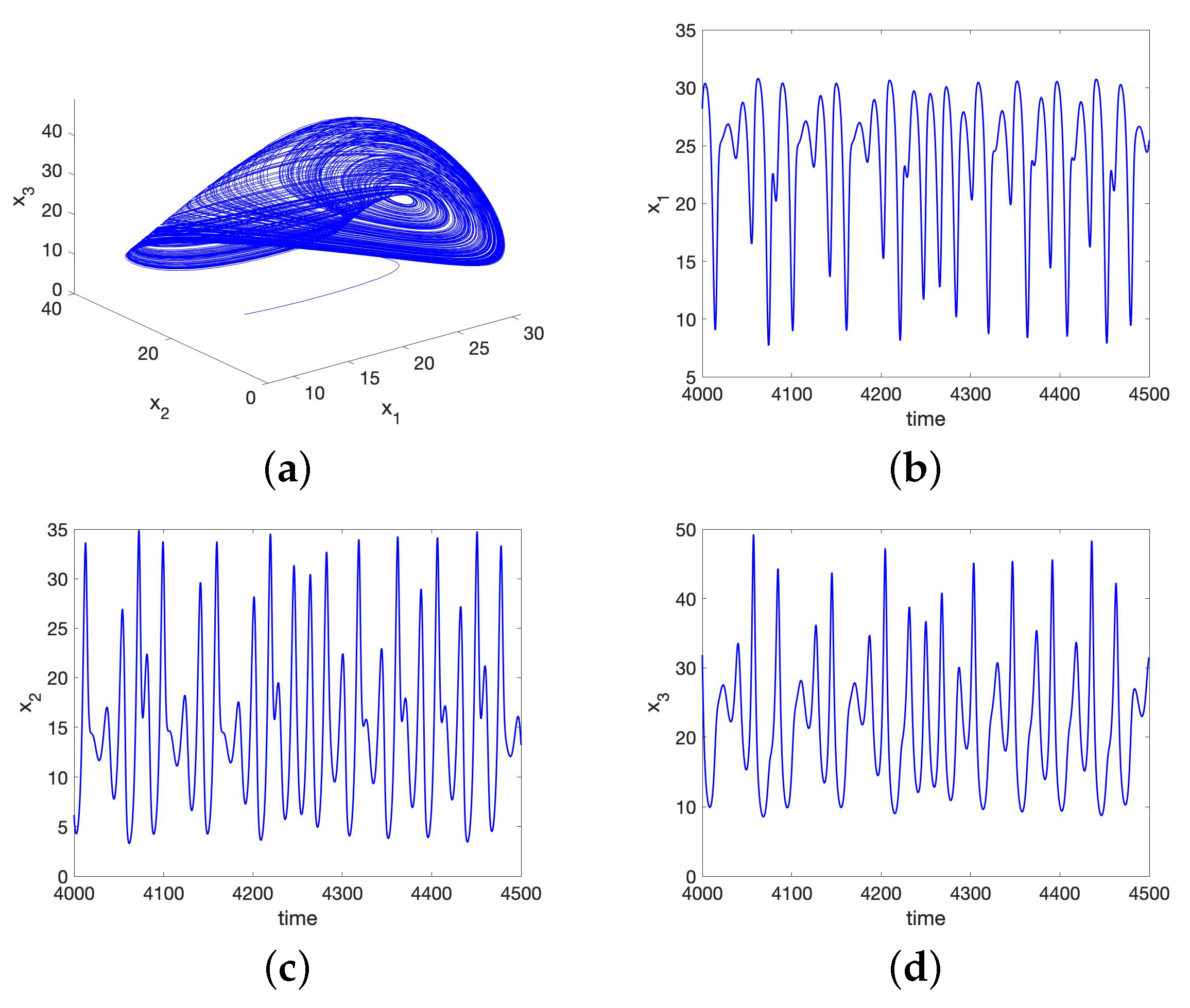
5.1. Chaos in the UR Model and HP Model for Small Initial Data
5.2. GS for the UR Model and HP Model for Small Initial Data
6. Possible Causes of a Lack of Synchronization
No Synchronization for the UR Model or HP Model for Large Initial Data
7. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
- Step 1.
- Identify the driver and response systems.
- Step 2.
- Compute the Jacobian of the response system.
- Step 3.
- Construct an H-matrix from the Jacobian and choose values for the H-matrix such that the Routh–Hurwitz criterion is satisfied.
- Step 4.
- Construct the transformation matrix which ensures the desired goal dynamics.
- Step 5.
- Propose a coupling to achieve the GS state.
References
- Blasius, B.; Stone, L. Chaos and phase synchronization in ecological systems. Int. J. Bifurc. Chaos 2000, 10, 2361–2380. [Google Scholar] [CrossRef]
- Arenas, A.; Díaz-Guilera, A.; Kurths, J.; Moreno, Y.; Zhou, C. Synchronization in complex networks. Phys. Rep. 2008, 469, 93–153. [Google Scholar] [CrossRef]
- Néda, Z.; Ravasz, E.; Brechet, Y.; Vicsek, T. The sound of many hands clapping. Nature 2000, 403, 849–850. [Google Scholar] [CrossRef] [PubMed]
- Mirollo, R.E.; Strogatz, S.H. Synchronization of pulse-coupled biological oscillators. SIAM J. Appl. Math. 1990, 50, 1645–1662. [Google Scholar] [CrossRef]
- Medvedev, G.S.; Kopell, N. Synchronization and transient dynamics in the chains of electrically coupled Fitzhugh-Nagumo oscillators. SIAM J. Appl. Math. 2001, 61, 1762–1801. [Google Scholar] [CrossRef]
- Prindle, A.; Samayoa, P.; Razinkov, I.; Danino, T.; Tsimring, L.S.; Hasty, J. A sensing array of radically coupled genetic ‘biopixels’. Nature 2012, 481, 39. [Google Scholar] [CrossRef]
- Dominguez, L.G.; Wennberg, R.A.; Gaetz, W.; Cheyne, D.; Snead, O.C.; Velazquez, J.L.P. Enhanced synchrony in epileptiform activity? Local versus distant phase synchronization in generalized seizures. J. Neurosci. 2005, 25, 8077–8084. [Google Scholar] [CrossRef]
- Schnitzler, A.; Gross, J. Normal and pathological oscillatory communication in the brain. Nat. Rev. Neurosci. 2005, 6, 285. [Google Scholar] [CrossRef]
- Strogatz, S.H.; Abrams, D.M.; McRobie, A.; Eckhardt, B.; Ott, E. Theoretical mechanics: Crowd synchrony on the millennium bridge. Nature 2005, 438, 43. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821–824. [Google Scholar] [CrossRef]
- Upadhyay, R.K.; Rai, V. Complex dynamics and synchronization in two non-identical chaotic ecological systems. Chaos Solitons Fractals 2009, 40, 2233–2241. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, W.; Gao, J. Synchronization of interconnected heterogeneous networks: The role of network sizes. Sci. Rep. 2019, 9, 6154. [Google Scholar] [CrossRef] [PubMed]
- Pinto, R.D.; Varona, P.; Volkovskii, A.R.; Szücs, A.; Abarbanel, D.I.; Rabinovich, M.I. Synchronous behavior of two coupled electronic neurons. Phys. Rev. E 2000, 62, 2644. [Google Scholar] [CrossRef] [PubMed]
- Pikovsky, A.; Rosenblum, M.; Kurths, J. Synchronization: A universal concept in nonlinear science. Am. J. Phys. 2002, 70, 655. [Google Scholar] [CrossRef]
- Roy, P.K.; Hens, C.; Grosu, I.; Dana, S.K. Engineering generalized synchronization in chaotic oscillators. Chaos Interdiscip. J. Nonlinear Sci. 2011, 21, 013106. [Google Scholar] [CrossRef] [PubMed]
- Grosu, I. Robust synchronization. Phys. Rev. E 1997, 56, 3709. [Google Scholar]
- Jackson, E.A.; Grosu, I. An open-plus-closed-loop (OPCL) control of complex dynamic systems. Phys. D Nonlinear Phenom. 1995, 85, 1–9. [Google Scholar] [CrossRef]
- Rulkov, N.F.; Sushchik, M.M.; Tsimring, L.S.; Abarbanel, H.D. Generalized synchronization of chaos in directionally coupled chaotic systems. Phys. Rev. E 1995, 51, 980. [Google Scholar] [CrossRef]
- Abarbanel, H.D.; Rulkov, N.F.; Sushchik, M.M. Generalized synchronization of chaos: The auxiliary system approach. Phys. Rev. E 1996, 53, 4528. [Google Scholar] [CrossRef]
- Hastings, A.; Powell, T. Chaos in a three-species food chain. Ecology 1991, 72, 896–903. [Google Scholar] [CrossRef]
- Aziz-Alaoui, M.A. Study of a Leslie-Gower type tri-trophic population model. Chaos Solitons Fractals 2002, 14, 1275–1293. [Google Scholar] [CrossRef]
- Letellier, C.; Aziz-Alaoui, M.A. Analysis of the dynamics of a realistic ecological model. Chaos Solitons Fractals 2002, 13, 95–107. [Google Scholar] [CrossRef]
- Kumari, N. Pattern Formation in Spatially Extended Tritrophic Food Chain Model Systems: Generalist versus Specialist Top Predator. ISRN Biomath. 2013, 2013, 198185. [Google Scholar] [CrossRef]
- Parshad, R.D.; Kumari, N.; Kouachi, S. A remark on “Study of a Leslie-Gower-type tritrophic population model” [Chaos, Solitons & Fractals 2002, 14, 1275–1293]. Chaos Solitons Fractals 2015, 71, 22–28. [Google Scholar]
- Mishra, P.; Raw, S.N.; Tiwari, B. Study of a Leslie-Gower predator-prey model with prey defense and mutual interference of predators. Chaos Solitons Fractals 2019, 120, 1–16. [Google Scholar] [CrossRef]
- Gakkhar, S.; Singh, B. Complex dynamic behavior in a food web consisting of two preys and a predator. Chaos Solitons Fractals 2005, 24, 789–801. [Google Scholar] [CrossRef]
- Li, G.-H. Generalized synchronization of chaos based on suitable separation. Chaos Solitons Fractals 2009, 39, 2056–2062. [Google Scholar] [CrossRef]
- Grosu, I.; Banerjee, R.; Roy, P.K.; Dana, S.K. Design of coupling for synchronization of chaotic oscillators. Phys. Rev. E 2009, 80, 016212. [Google Scholar] [CrossRef] [PubMed]
- Upadhyay, R.K.; Rai, V. Why chaos is rarely observed in natural populations? Chaos Solitons Fractals 1997, 8, 1933–1939. [Google Scholar] [CrossRef]
- Aziz-Alaoui, M.A.; Okiye, M.D. Boundedness and global stability for a predator-prey model with modified Leslie-Gower and Holling-type II schemes. Appl. Math. Lett. 2003, 16, 1069–1075. [Google Scholar] [CrossRef]
- Allen, J.C.; Schaffer, W.M.; Rosko, D. Chaos reduces species extinction by amplifying local population noise. Nature 1993, 364, 229–232. [Google Scholar] [CrossRef]
- Said, K.; Zaidi, A. Blow up in finite time of solutions to a Leslie-Gower predator-prey model in absence of the middle predator. Authorea Prepr. 2022. [Google Scholar] [CrossRef]
- Parshad, R.D.; Qansah, E.; Black, K.; Beauregard, M. Biological control via “ecological” damping: An approach that attenuates non-target effects. Math. Biosci. 2016, 273, 23–44. [Google Scholar] [CrossRef] [PubMed]
- Kumari, N.; Kumar, V. Controlling chaos and pattern formation study in a tritrophic food chain model with cannibalistic intermediate predator. Eur. Phys. J. Plus 2022, 137, 1–23. [Google Scholar] [CrossRef]









| Symbols | Description |
|---|---|
| prey | |
| middle predator | |
| top predator | |
| intrinsic growth rate of prey | |
| measure of competition among prey | |
| intrinsic death rate of in the absence of food only | |
| D, | measure of the level of protection offered to the prey by the environment |
| value of at which its per capita removal rate becomes | |
| Loss of due to lack of favorite food | |
| c | growth rate of via sexual reproduction |
| maximum value that per capital rate can attain |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takyi, E.M.; Parshad, R.D.; Upadhyay, R.K.; Rai, V. Blow-Up Dynamics and Synchronization in Tri-Trophic Food Chain Models. Algorithms 2023, 16, 180. https://doi.org/10.3390/a16040180
Takyi EM, Parshad RD, Upadhyay RK, Rai V. Blow-Up Dynamics and Synchronization in Tri-Trophic Food Chain Models. Algorithms. 2023; 16(4):180. https://doi.org/10.3390/a16040180
Chicago/Turabian StyleTakyi, Eric M., Rana D. Parshad, Ranjit Kumar Upadhyay, and Vikas Rai. 2023. "Blow-Up Dynamics and Synchronization in Tri-Trophic Food Chain Models" Algorithms 16, no. 4: 180. https://doi.org/10.3390/a16040180
APA StyleTakyi, E. M., Parshad, R. D., Upadhyay, R. K., & Rai, V. (2023). Blow-Up Dynamics and Synchronization in Tri-Trophic Food Chain Models. Algorithms, 16(4), 180. https://doi.org/10.3390/a16040180




