Abstract
Decentralized identity (DID) systems aim to give users full control over their identities by using completely decentralized technologies, such as blockchain or distributed ledgers, as identity providers. However, when user credentials are compromised, it is impossible in existing DID systems for the users to detect credential misuse. In this paper, we propose new DID authentication protocols with two properties: auditability and privacy. The former enables the detection of malicious authentication events, while the latter prevents an adversary from linking an authentication event to the corresponding user and service provider. We present two protocols that achieve auditability with varying privacy and performance guarantees. The first protocol has high performance, but it reveals information about the user. The second protocol achieves full privacy, but it incurs a higher performance overhead. We present a formal security analysis of our privacy-preserving protocols by using the Tamarin prover. We implemented them and evaluated their performance with a permissioned blockchain deployed over the Amazon AWS and a local cloud infrastructure. The results demonstrate that the first protocol is able to support realistic authentication workloads, while the second is nearly practical.
1. Introduction
Decentralized identity (DID) [1] is an identity system in which users have full control over their identities, and it helps to achieve identity sovereignty. Today, DID systems (or DIDs) leverage decentralized storage systems, such as a distributed ledger (DLT) or a blockchain, to manage the mapping between identifiers and other data, such as cryptographic credentials (usually stored as URIs or dereferenceable documents on the web). DID is standardized by W3C [2] and has been adopted in different frameworks, such as Hyperledger Indy [3], Hyperledger Aries [4], Evernym [5], Nuggets [6], Blockstack [7], CanDID [8], and so on. Though DID technologies are revolutionizing the web, the security of these systems depends on a strong assumption of the underlying storage system (DLT). In particular, identities are tamper-evident and highly available without relying on centralized trusted parties. However, achieving identity sovereignty comes at a price, since existing DIDs cannot detect the misuse of compromised credentials. More specifically, it is impossible to detect that a user’s credentials have been stolen and used by an adversary to authenticate them with a service provider in a fully decentralized way. This is a limitation compared to centralized identity systems that log all authentication events. For example, Google’s last-login feature [9] provides users with the details of all login events by their accounts.
Our goal is to design DID authentication protocols that enable users to detect credential misuse. We define two security properties for such protocols: auditability, which allows users to detect unauthorized authentication events that use their credentials, and privacy, which prevents adversaries from linking an authentication to the corresponding user and service provider. The challenge here is to design protocols that have both properties and reasonable performance. One naive solution is to store the full content of all authentication events in distributed append-only storage (in our implementation, a blockchain). This achieves auditability because the user can see the complete history of their credential usage, but both the user and the service provider of every event are revealed, thus achieving no privacy.
We propose two protocols that achieve auditability with varying privacy and performance guarantees. The first protocol has high performance, but limited privacy. It works as follows. For each authentication, the user increments a counter and signs it with a key associated with their DID. This signed counter is sent to the service provider, who tries to log it in the DLT or blockchain. If successful, the user is authenticated. The blockchain ensures that it only accepts consecutive counter values from the correct user. The user can detect malicious authentication by checking if a future counter value has been logged on the blockchain by keeping track of the latest counter value. However, because counter values are signed, each authentication event reveals who the user is by associating it with the DID.
The second protocol achieves full privacy, but incurs a high performance overhead. The key challenge in designing this protocol is how to hide user information (such as the DID or keys associated with it) from the authentication event. To illustrate this, we describe a protocol using verifiable random functions (VRFs) and show that it only works under strong security assumptions. We address this challenge by using the Zero-Knowledge Succinct Non-Interactive Argument of Knowledge (zk-SNARK) primitive [10]. More specifically, the client generates a token based on a counter value and a zero-knowledge proof with which the blockchain can verify that some token derived from the value is already in the blockchain, but without revealing this token or the counter value. Our evaluation shows a performance that is three orders of magnitude lower than that of the first protocol. This overhead is due to the cost of the verification performed by the blockchain.
In summary, we make the following contributions: (1) We define two security properties for detecting credential misuse in DID authentication (DIDAuth), namely, auditability and privacy. (2) We propose two protocols that achieve auditability with varying privacy and performance guarantees. The first has high performance but limited privacy, and the second has full privacy but low performance. (3) We provide a formal security analysis of our privacy-preserving protocol by using the Tamarin Prover. (4) We implement and evaluate the two protocols by using Hyperledger Fabric v0.6 (Hyperledger Fabric v0.6 has higher performance and security guarantees than those of v1.4 [11]). The results confirm that the overhead for privacy is substantial—the protocol can only handle one authentication event for every 3s. However, by lowering the privacy guarantee, our protocol can perform over 380 events per second, which means that it can handle the average workload of today’s centralized authentication systems.
The rest of this paper is organized as follows. Section 2 provides the relevant background and related work on blockchain, DIDs, and cryptographic primitives. Section 3 describes the system model, threat model, and security properties. Section 4 and Section 5 present the two protocols in detail. Section 6 gives a formal security analysis by using the Tamarin Prover. Section 7 discusses the implementation and performance of the two protocols before Section 8 provides the conclusions.
2. Background and Related Works
2.1. Blockchain
A blockchain system consists of distrusting nodes that implement a replicated, tamper-evident, append-only log data structure called a ledger. The ledger comprises blocks, each block contains transactions that modify some global states, and the blocks are linked through cryptographic hash pointers. The nodes keep the global chain of blocks consistent through a consensus protocol. In addition, most blockchains support smart contracts, which are user-defined functions executed by all nodes in the network.
Existing blockchains can be broadly classified into permissionless and permissioned based on their consensus protocol [11]. Examples of the former include Bitcoin [12] and Ethereum [13], in which any nodes can join and leave. Examples of the latter include Hyperledger Fabric [14] and Quorum [15], in which membership is strictly enforced. Permissionless blockchains use variants of the proof-of-work (PoW) consensus protocol, whereas permissioned ones use variants of Byzantine fault-tolerant (BFT) protocols [16].
A blockchain executes and stores user transactions in the ledger. The user can ask for proof that their transaction is included in the ledger without downloading and re-executing the entire ledger. In a permissioned blockchain, this proof consists of a statement (that the transaction is included) signed by nodes (f is the maximum number of Byzantine nodes that can be tolerated). In a permissionless blockchain, all transactions are represented by a Merkle root hash included in the block; thus, the proof consists of the valid Merkle path to the root hash of the latest block.
2.2. Decentralized Identity Authentication
Decentralized identity (DID) [1] is an identity system in which identity information is owned by the entity that creates it, as opposed to a centralized identity management system, such as Microsoft’s Active Directory, in which third party stores and modifies identities. Most DIDs today use blockchains to store a mapping between a unique identifier (representing an entity), which is called did, and other metadata, such as cryptographic keys.
An entity registers a new did with the corresponding metadata, meta, by executing a smart contract on a blockchain, which stores (did, meta) on the blockchain. To retrieve the corresponding metadata of a given did, i.e., to resolve the did, the user provides the string (<did>:<method-specific identifier>:<method>) as input to the DID (which points to a resolver). The system then triggers the specified method on the specified blockchain, which returns the (did, meta) tuple.
The benefits of DIDs are derived directly from those of blockchains—the (did, meta) tuples are tamper-evident and highly available. In addition, DIDs can guarantee that only the original owner of a registered did can update the corresponding metadata, thereby giving the user full control of their identity.
DID-based authentication. A DID can replace centralized PKI systems in public-key-based authentication [17]. Figure 1a shows how OAuth works with centralized identity management systems. In particular, to authenticate with a service provider, the user first presents their credentials to their identity provider, which issues a signed token after verification. The user submits this token to the service provider, which verifies it by using PKI before establishing a session with the user. Then, by using the DID, as shown in Figure 1b, the user sends a signed, fresh authentication request by using their private key (the public key for which is stored in the metadata). The service provider resolves the user’s did to verify the request, and then establishes a session with the user.
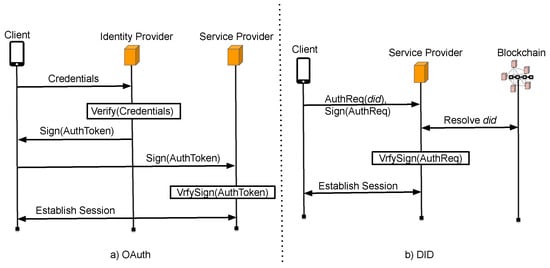
Figure 1.
Comparison between OAuth and DID authentication.
2.3. Cryptographic Primitives
Hash function. A cryptographic hash function is defined as , where is called the domain, and is called the range. The function is collision-resistant, meaning that it is hard to find two different inputs producing the same output. Additionally, it is pre-image-resistant, i.e., given an element in the range, it should be computationally infeasible to find an input that maps to that element.
Unforgeable signatures. A signature scheme is defined with the three following algorithms.
- (a)
- is a key generation algorithm that takes a security parameter as input and outputs the (signing) secret key and the verification key .
- (b)
- is a signing algorithm that takes the secret key and a message as inputs, and it outputs a signature .
- (c)
- is a signature verification algorithm that takes a verification key , a message , and a signature as input, and it outputs “True” if the signature matches the key and the message, or “False” otherwise.
We assume that the digital scheme used is existentially unforgeable under chosen message attacks, i.e., it is EUF-CMA (existential unforgeability under chosen message attack) secure.
Verifiable random function (VRF). A VRF [18] is the following tuple of algorithms.
- (a)
- is a key generation algorithm that takes a security parameter as input and outputs a keypair, i.e., the secret key and the verification key ( and , respectively).
- (b)
- is an algorithm that takes the secret key and X as inputs and outputs a pseudorandom hash h and a proof (the value h is unique for the inputs and X).
- (c)
- is a verification algorithm that takes the verification key with the values X, h, and ; it returns “True” if proves that h was created for X with the corresponding key , and “False” otherwise.
In practice, VRFs can be implemented with unique signatures.
zk-SNARK. zk-SNARK (Zero-Knowledge Succinct Non-Interactive Argument of Knowledge) [19] is a non-interactive zero-knowledge proving system that allows one to prove and verify the integrity of an arbitrary computation (represented as an arithmetic circuit). zk-SNARK consists of the following algorithms.
- (a)
- is a key generation algorithm that takes an arbitrary circuit C and secret parameter as inputs, and it generates a proving key and a verification key . The generation of these keys constitutes a setup phase and is trusted.
- (b)
- is a function that takes public inputs and the private witness w as inputs, and it outputs a succinct-integrity proof of computation .
- (c)
- is a function that takes as input a verification key , a proof , and public inputs , and it returns “True” if the proof is valid, and “False” otherwise.
Although we describe one of our protocols by using zk-SNARKs, it can be combined with any proving system with the same capabilities—in particular, with systems that offer better performance or do not require a trusted setup [20].
2.4. Related Work
Our work is the first to propose DID authentication protocols that achieve auditability and privacy. In the following, we discuss related works with similar properties.
Blockstack [21] introduces a distributed namespace in which a binding of a name to a key can be published on a public blockchain. Similarly, CONIKS [22] supports name-to-key binding, and it provides publicly verifiable proof that the binding has been added to a public (centralized) log. The integrity of this log depends on a number of auditors that frequently check the log. This design is implemented in Google’s Key Transparency (KT) [23]. These systems provide similar guarantees to those of a DID system, that is, full user control of the name-to-key binding and data transparency. However, like existing DIDs, they do not have the auditability property, as defined in this paper. Chu et al. [24] introduced Ticket Transparency, an accountable single-sign-on system with a privacy-preserving public log. The system allows users to detect if an identity provider has signed a fraudulent ticket and if a ticket has been used to sign on to a service provider. The problem addressed by Ticket Transparency is similar to that of ours, but it is specific to existing single-sign-on systems with centralized identity providers. Our work focuses on DIDs in which users manage their own identities.
Privacy Pass [25] is an anonymous user authentication scheme that provides users with the ability to create and sign cryptographically “blinded” tokens for services that require PoW authentication. Extending this, Facebook built a privacy-preserving logging scheme known as DIT [26], which addressed the constraints of implementing an anonymized logging infrastructure that involved mobile clients and additional requirements of lower latency. Though both addressed token anonymity achieving it while checking for token consistency could lead to a similar overhead to that of our privacy-preserving approach.
Coconut [27] is a privacy-preserving verifiable credential scheme with a selective disclosure property supporting threshold credential issuances. The users can obtain a credential from the blockchain and authenticate with multiple services while being unlinkable across different usages. EL Passo [28] provides a privacy-preserving single-sign-on (SSO) system based on verifiable credentials that provide the same security guarantee as that of the traditional OAuth protocol without compromising on usability. The credential usage is similar to that of Coconut, and both use a PS signature [29] to implement a verifiable credential scheme. Unlike in our scheme, neither EL Passo nor Coconut aims to detect credential misuse. They can be seen as orthogonal to our work, and combining them with our solution could be a possibility for future work.
WAVE [30] and Droplet [31] are decentralized authorization systems that aim to replace centralized solutions, such as OAuth. WAVE proposes novel cryptographic protocols for delegating access permissions without relying on trusted parties. It uses a secure log based on Google’s Trillian [32] data store. The log can be efficiently audited to detect any forks in its history, similarly to CONIKS. In addition, WAVE supports user privacy by using a reverse-discoverable encryption scheme to encrypt authorization policies so that only users with appropriate permissions can see them. Droplet is very specific to the management of access to time-series data in an IoT environment. WAVE and Droplet are complementary to our work, since we focus on authentication instead of authorization.
Going beyond authentication, SAMPL [33] proposes a blockchain-based system for auditing the user surveillance process. The auditability property targeted by this system is different from that in our definition, as it refers to the detection of non-compliance with the surveillance process—for example, when a user is being over-surveilled. SAMPL requires the authority and relevant entities to log surveillance requests and responses to the blockchain and ensure the privacy of such data when auditing.
Another orthogonal work with which our technology can be integrated to provide privacy-preserving auditing is that of Kim et al. [34] on a blockchain-based energy trading scheme for a V2V environment by using decentralized identity technology. Li et al. [35] proposed a double-layer blockchain and decentralized identifier-assisted secure registration and authentication (BDRA) mechanism for decentralized VANETs. In their implementation, they used Hyperledger Fabric as a blockchain framework; hence, our solution can easily be integrated into decentralized VANETs, since our implementation uses the same blockchain framework. The concept of DID was applied in electric vehicles (EVs) [36] to provide privacy to users by anonymizing user identities, but this work did not consider credential misuse or propose a privacy-preserving mechanism for detecting credential misuse, which is the focus of our paper.
3. Overview
In this section, we first give an overview of our protocols. We then present the system model, the desired security and system properties, and the threat model.
3.1. Overview
With centralized identity providers such as Google or Facebook, users rely on the provider to manage their identity and log all associated authentication events. The provider can ensure that one user cannot see another user’s authentication log. There are two problems associated with this setting. First, the provider has to be trusted to log all authentication events, including malicious ones. Second, the provider can see all of the logs; thus, there is no user privacy against the provider.
Current DID-based authentication systems [17] do not solve these two problems. Although they do not rely on trusted, centralized parties, they do not enforce the logging of all authentication events. As a result, users cannot detect misuse of their credentials. Furthermore, simply moving the logs from a centralized system to the blockchain violates user privacy, as data in the blockchain are publicly visible.
We address these two problems in this paper. We define two properties: auditability, which allows the user to see the complete log of all authentication events associated with their credentials, and privacy, which prevents linking an authentication event to the corresponding user and service provider. We propose two DID authentication protocols that achieve auditability and varying privacy guarantees. The first protocol, i.e., the baseline, stores authentication tokens to the blockchain for each authentication event. It is simple and efficient, but reveals links between authentication events and identities. The second protocol addresses the challenge in hiding user information in authentication events, by using a combination of VRF and zk-SNARK primitives. We highlight why both are needed by showing an intermediate protocol that only uses VRF and demonstrating that it fails to achieve auditability within our model. The final protocol ensures privacy, but at the cost of a high performance overhead.
3.2. System and Threat Model
Our system consists of three types of entities: the blockchain, service providers, and clients.
- The blockchain is a blockchain system, such as Hyperledger Fabric or Ethereum, in which users can register their dids and retrieve valid proof that a transaction has been added to the blockchain.
- The client represents the user. It stores secret data, such as private keys associated with the user’s did, and it runs the DID protocol on behalf of the user.
- The service provider (or service) provides resources that the user wants to access. It runs a DID authentication protocol to authenticate the user before giving them access to a resource.
We define our threat model with respect to each entity in the system as follows. The blockchain is trusted to protect the integrity of the stored data. It is also highly available, i.e., not subject to denial-of-service attacks. The client is trusted to follow the protocol, but the adversary can steal its credentials (corresponding to the client’s identity). The service provider can be compromised. In this case, it can collude with an adversary that has stolen a user’s credentials to prevent the user from detecting the credential misuse. When not compromised, the service provider is semi-honest; that is, it follows the authentication protocol correctly, but it wants to learn information other than what the authentication protocol reveals. In particular, it may want to learn which client authenticated with which (other) service providers, since knowledge of clients’ behavior may give a service provider an important competitive advantage.
3.3. Properties
Our goal is to design and implement DID authentication protocols that achieve a good trade-off among three desirable properties.
- Auditability: The user can detect unauthorized authentication events that use their credentials. More specifically, whenever an adversary uses stolen credentials with an honest server, this fact can be detected later on by the compromised client. Our protocols support “passive” detection, which is when the client detects the misuse while authenticating with an honest server, or “active”, when the client queries the blockchain to find the misuse.
- Privacy: Given an authentication event that is logged in the blockchain, the adversary cannot link it (a) to the identity that is the subject of the authentication event, (b) to the service provider involved, or (c) to any previous authentication events triggered by the identity. We assume that in privacy attacks, the adversary can constantly observe the blockchain’s content, but we leave network-level de-anonymization attacks out of the scope of this submission (i.e., the adversary cannot eavesdrop on the network connections of clients and services).
- Performance: The protocol achieves sufficient throughput to handle realistic authentication workloads.
Table 1 compares our protocols with existing DID authentication protocols according to the three properties. We note that the first two security properties are in addition to what is provided by existing DID protocols.

Table 1.
Comparison of our protocols with existing DID authentication protocols.
4. Baseline Protocol
The baseline protocol is simple and achieves most, but not all, of the desired system properties with minimal overhead. It is based on a naive idea in which, for each authentication event, the corresponding counter is logged on the blockchain, and it is verified that the owner of a generated it and that the counter is consistent with the previous one. We discuss the protocol in two phases: (1) registration, in which a user publishes their identity in the blockchain, and (2) authentication, where we show a protocol for logging authentication counters.
4.1. Registration
In the registration phase, the client first generates its keypair , then derives its identity , and initializes its authentication counter . With these values, the client creates a registration request
which includes , other human-readable information (e.g., a name or a comment), and the signature computed over the content of the request. The request is sent to the blockchain, where the smart contract method handles it. The method implements basic sanity checks, including signature validation and the insertion of the verification key and other information into the identity map (), which is a mapping between the (key) and a tuple (value), whereupon the registration is set to 0.
Upon successful execution of the code, blockchain nodes create an inclusion proof , which states that the identity was successfully registered and is part of the blockchain. The registration process is complete, and the client is ready to use its for authentication.
4.2. Extended Authentication
Our protocol extends the standard authentication process. In the authentication phase, the client first derives a new counter by incrementing it by 1, generates an ephemeral keypair (a new ephemeral keypair is created in each session, and we describe its purpose later in this section), and creates the requests
with its , proof of inclusion of the , a new (consecutive) counter, and the signatures over and . The request is sent to the service, which, upon receiving the request, verifies the proof of inclusion and the signatures.
At this point, the client and service run any authentication protocol that they wish to use. We do not mandate a specific scheme, since we foresee that our protocol will be integrated within existing protocols, such as DIDAuth or a TLS, which may require additional message flows or may provide additional security properties (such as service authentication). However, we require that during the authentication process, the service ensures that the client possesses the secret keys corresponding to its “long-term” key () and its ephemeral key . (We also envision that the ephemeral key pair can be used to provide other session security features, such as perfect forward secrecy.) A way of realizing such authentication, similarly to some popular TLS authentication modes, would be to require the client (a) to sign with and send the corresponding signature to the service and (b) to use to sign the authentication context, which would contain all exchanged messages and a nonce provided by the service. This “standard” authentication phase, which ensures the possession of and , is also part of other protocols that we propose later in this paper (i.e., the protocols from Section 5.1 and Section 5.2).
After a successful authentication, the service extracts and forwards cntReq to the blockchain platform, where the incrementCounter smart contract method handles the request, as shown in Algorithm 1. The method verifies (1) the signature and ensures that it belongs to the right , and (2) the current counter mapped to has the value , which confirms that there is no occurrence of credential misuse. Once validated, the counter value in the identity map is incremented. Upon successful execution of the code, blockchain nodes create an inclusion proof (i.e., a statement signed by at least nodes) that states that the request was successfully processed by the platform. The service validates the inclusion proof, as shown in Algorithm 2, and forwards it to the client, who verifies that the inclusion proof is correct and matches the intended cntReq message. After the process is finished, the service proceeds to establish a session with the client.
| Algorithm 1: Logging authentication events (the baseline protocol). |
incrementCounter (, , σ) 1 assert 2 assert 3 4 assert 5 |
| Algorithm 2: Verification of the inclusion proof of object . |
vrfyInclusion (, ) 1 assert fordo 2 assert 3 assert k is unique 4 assert end |
Signing cntReq with an ephemeral key prevents replay attacks, thus guaranteeing the client that the blockchain processed their request. Since an adversary can control the service and the client’s long-term credentials (i.e., ) without signing the request with an ephemeral key, the adversary could create the same cntReq (even if a random nonce accompanied it), use it to authenticate with an honest service, and replay the blockchain inclusion proof to the client. With an honest service verifying the possession of ephemeral , such a replay attack is impossible.
The baseline protocol satisfies the auditability property, since for each authentication event using , the identity map’s entry corresponding to is updated with the consecutive counter value. The client can easily audit the consistency between its local counter value with the counter value stored in the identity map to check for any credential misuse. Moreover, detection can also be passive, since for any authentication after a misuse happens, the blockchain would not process cntReq successfully, which would be noticed by the client. We focus on the basic functionality of our protocol; however, the protocol can be extended. For instance, to identify the service against which a malicious authentication was performed, additional metadata encrypted with the client’s public key could also be logged along with the counter.
4.3. Limitations
Counter requests do not reveal the services to which a given identity is authenticated. However, since the authentication counters are publicly logged and service providers submit identity information, such as a and signature, along with the counter, to the blockchain, anyone who can see the transactions on the blockchain can notice how often a user authenticates using their identity. A privacy-cautious user may not want to share this information with the public, which may be challenging, as, by design, the information on the blockchain is public. Although privacy-preserving blockchain platforms, such as Solidus [37] and zkLedger [38], which allow storage of encrypted content on-chain, have been proposed, they require trusted third-party auditors. However, such an assumption in the DID ecosystem would be against its principles of self-sovereign identity (i.e., an owner has full control of their identity). Therefore, in the next protocol, we explain how to provide auditability with a privacy guarantee over an open blockchain.
5. Privacy-Preserving Protocol
In this section, we address the limitations described in Section 4.3. First, in Section 5.1, we sketch an intermediate protocol in which deploying VRFs can provide the desired properties, but this requires additional security assumptions. Then, we extend this idea to the final protocol, which, in addition to VRFs, deploys a computational zero-knowledge proving system.
5.1. Intermediate Protocol
While investigating the drawbacks of the baseline scheme, it becomes clear that the privacy issues are caused by the linkage between the sent counters and the identity that issued them. One idea for breaking such a linkage is to allow a client to prove that the counters are consecutive and authentic (i.e., created by the client), but without leaving public evidence of that fact. We present a protocol that requires services to verify the linkage (thus, they become trusted in that scope). In our construction, we use a VRF that outputs a unique and deterministic hash for a given counter with a proof guaranteeing its authenticity. Hash–proof pairs can ensure services that the hashes are authentic, while hashes recorded in the blockchain ensure privacy (since without their proofs, they cannot be attributed to identities) and give clients the ability to audit which of their counter values have been used. Based on those insights, in the following sections, we give more details of this protocol. (Designs alternative to those presented in this section could include a system in which authentication counters are encrypted under the identity’s public key and the corresponding ciphertexts are submitted to the blockchain. Unfortunately, such a solution (a) would require clients to constantly keep validating all new ciphertexts (in order to audit them) and (b) would allow anyone to use the public key to generate and submit a valid ciphertext, which would be interpreted by the client as a credential misuse).
5.1.1. Registration
The registration process is similar to that in the baseline protocol. First, a client generates its key pair , derives its identity , sets its local counter , computes , where the VRF’s hash is called an authentication token, and sends the following registration request (for a simple description, we assume that the clients use the same keypair in the VRFs and digital signatures; in practice, different cryptographic primitives may require different keypairs) to the blockchain platform:
The blockchain smart contract (a) verifies the signature, (b) adds a to the identity map (in contrast to the previous protocol, counter values are not associated with identities), (c) checks that is not in the token set, and, if so, (d) adds the token to this set. The token set is the set of all tokens that the blockchain platform has accepted. If all of these checks pass, the blockchain nodes return the and token inclusion proofs ( and , respectively), proving that the identity and the token are part of the blockchain. After receiving and validating the proofs, the client can use their identity for authentication.
5.1.2. Extended Authentication
Prior to any authentication, the client increments its counter and generates an ephemeral key pair (which, as in the previous protocol, is used for replay protection). Then, the clients initiate the process, whose goal is to convince the service that (a) the client’s identity is registered with the blockchain, and (b) the authentication process is consistent with the previous authentication of this client. The client prepares the following messages:
and it sends to the service, which runs the standard authentication of and (as in the baseline protocol—Section 4.2) and validates the messages, thus verifying (1) that the tokens and are authentically generated by the client for the inputs and , respectively, i.e., (, , ) and (, , ) both output “True”, (2) that the identity inclusion proof is correct and corresponds to , (3) that the token inclusion proof corresponds to the authentication token , (4) is signed correctly, and (5) that the authentication token is not registered in the blockchain.
For the last check, the service needs to contact the blockchain platform and obtain proof that was not appended to the blockchain’s token set (this can be efficiently realized with authenticated dictionaries [39]). Therefore, the token request is submitted to the blockchain, where nodes only check if the token is not in the token set. (The nodes cannot check ’s authenticity, since it is not accompanied by its corresponding proof .) If so, is inserted into the token set, and the blockchain platform returns an inclusion proof (claiming that the was processed correctly and that became part of the blockchain) to the service, which forwards it to the client (the client will use the proof for the next authentication). With these checks, the service and the client are confident that the previous and current tokens are consistent with each other and that no credential misuse has occurred. Since we assumed the network level in Section 3.3, the request’s origin (i.e., the service) cannot be de-anonymized. (This also applies to the requests sent in the final protocol from Section 5.2.) To relax this assumption, the service could use an anonymity network [40] while interacting with the blockchain platform.) At any time, the client can audit its authentications by simply checking whether the next token value that is computed from is in the blockchain (if it is, then this implies that its credentials were misused).
5.1.3. Discussion
The use of a VRF guarantees that the service can verify that the tokens were computed by the given identity holder and that they are consecutive, while submitted tokens do not reveal corresponding identities or previous tokens to the public, since VRF hashes (i.e., tokens) cannot be verified without their corresponding proofs (we also note that the token set acts as the anonymity set in this case). Moreover, tokens are deterministic; thus, clients can easily check for potential credential misuses by using blockchain lookups that query their next token values.
Unfortunately, the protocol assumes that the participating services are honest as they verify the continuity between tokens (the blockchain platform checks only for the token uniqueness in the token set). To illustrate this, let us assume that an adversary compromises the client’s secret key and a service controlled by the adversary (in fact, nothing prevents the adversary from acting as a service, too). In such a case, the adversary would produce and insert into the blockchain’s token set a token computed from , where k is significantly larger than the client’s counter . With this malicious token inserted, the adversary can keep authenticating with honest services by using consecutive tokens (starting from ). However, since the client would be auditing the blockchain for ’s consecutive tokens, they would not be able to detect the malicious token (at least for a long time period).
Below, we show how this intermediate protocol can be turned into the final protocol, where the linkage between tokens and identities is verified by the blockchain (i.e., services do not have to be trusted in that scope) while not revealing the linkage to the public, thus preventing the described attack.
5.2. Final Protocol
The insecurity of the previous approach is caused by the fact that the verification is implemented only at the service, since verifying the token authenticity with the blockchain nodes would violate privacy. In our final protocol, we employ a computational integrity proofing system, such as zk-SNARK, to “move” the verification from the service to the blockchain nodes, but while preserving privacy. Therefore, in addition to ensuring consecutive counters, a client needs to—non-interactively (as the proof is to be verified by the blockchain nodes) and with zero knowledge—prove that tokens were created under the same private key, and the previous token is in the blockchain. This requires a composition of non-interactive zero-knowledge VRF and signature verifications. Although a system such as zk-SNARK can be seen as a “heavyweight” tool, it seems unavoidable to realize this. We see the optimization of this construction as interesting future work.
The registration process in the final protocol is the same as that in the intermediate protocol (see Section 5.1.1). In addition, the blockchain platform in this protocol maintains the same data structures (i.e., the identity map and the token set). Prior to the protocol’s deployment, the proofing system requires a setup phase in which the proving and verification keys are generated for a circuit, i.e., in our case, and the blockchain platform is pre-loaded with the verification key. In some systems, the setup phase is assumed to be run by a trusted party. zk-SNARK shares this limitation, and, in practice, this assumption can be relaxed by a multi-party computation ceremony [41].
5.2.1. New Token and Its Consistency
To generate a new token , the client increments the counter and computes the token and its proof as in the previous protocol, i.e., . We emphasize that, due to the properties of VRFs, the value of each token is unique and deterministic. After a new token is computed, the client has to create proof that this token is consecutive to its previous token , which is already logged in the blockchain’s token set, but without revealing any information about this token (in particular, this can be proof of the initial token). To accomplish this, we use a non-interactive zero-knowledge computation integrity proofing system (Section 2.3) together with the circuit used to conduct the relevant computations (see Section 3). The circuit takes as an input the client’s verification key, the current counter, the VRF outputs corresponding to the new and previous tokens, and the inclusion proof of the previous token. Note that only the new token is passed as a public argument; thus, the computation integrity proof will not reveal any other information, such as the client’s counter or identity. In the first two lines, the circuit ensures that the tokens are created by an entity that possesses the same secret key and that they are for consecutive values of the counter . The third line validates the inclusion proof , thus ensuring that the previous token is indeed in the blockchain.
For a new token and a list of secret arguments (as shown in Algorithm 3), the client generates a computation integrity proof , where w is a witness. The proof will ensure a verifier (i.e., the blockchain platform) that the two tokens are created by using the same secret key and the consecutive counter values, and that the previous token is part of the blockchain. Once the proof is generated, the client is ready to contact the service and conduct the authentication process. Although generating the proof is relatively time-consuming (i.e., seconds), it does not have to be conducted just before the authentication. It can be computed at any point between two consecutive authentications.
| Algorithm 3: Circuit for proving that the previous token of the client is in the blockchain. The boxed arguments are secret and are known only to the client (i.e., the prover). |
Token() 1 assert2 assert 3 vrfyInclusion (see Algorithm 2) |
5.2.2. Extended Authentication
After deriving a new token and proving its computations as described above, the client generates an ephemeral keypair (as previously, this is used against replay attacks)
and it initiates the authentication with the service by sending .
The service authenticates the client’s and keys with a standard authentication protocol (as in the previous protocols in Section 4.2). In addition, the service (a) validates the inclusion proof and checks whether it corresponds to the claimed and (b) ensures that the VRF output is correct and authentic, i.e., outputs “True” (the associated with the for the VRF verification is obtained from ). With these checks, the service ensures that the new token corresponds to the . The service does not have to validate the computation integrity proof, since it will be validated by the blockchain platform in the next step. The service passes to the blockchain, where the request is handled by the TokenVrfy smart contract method (see Algorithm 4). This verifies that (a) the integrity computation proof is correct, calling , and that (b) is not in the token set. These checks ensure the blockchain platform that the new token is not yet added and that it was created with the same secret key and as a consecutive counter of some other (unrevealed) token that has already been logged. After successful validation, the new token is added to the token set, and the blockchain nodes create an inclusion proof , which states that the request was processed correctly and the new token is added to the blockchain. The service receives and validates the proof, it sends it to the client (who validates it, too), and proceeds with session establishment.
| Algorithm 4: Smart contract method for logging authentication events (the final protocol). |
TokenVrfy(π, )
1
assert2 assert 3 |
The protocol provides auditability, since the client can query the token set from the blockchain for its consecutive tokens or just notice the blockchain’s error response (while processing ) during an authentication. In contrast to the previous protocol, a token added to the token set (except for the registration) has to be accompanied by proof that its preceding token is already in the set (which proves the tokens’ continuity with zero knowledge).
5.2.3. Discussion
This protocol hides token–identity mappings and login frequency from an adversary observing the blockchain (i.e., the adversary sees new tokens, but is unable to link them to their originators or other tokens). However, if a client uses its identity with a service multiple times, the service learns the corresponding counters. Any pair of counters allows the service to deduce how many authentications with other services for which the identity has been used between these two counters. Although we do not believe that this is a major privacy issue, our protocol can be extended with the following modifications to mitigate it:
- (a)
- Prior to the registration, the client generates its counter as a large secret number.
- (b)
- For every authentication, a new token and its proof are computed as (the only difference is that the counter is internally hashed).
- (c)
- The service receives —not , as previously—and verifies the token’s authenticity by calling .
- (d)
- The circuit verifies two tokens analogically, thus guaranteeing that the hashes are for the two consecutive values.
These changes would hide counter values from services, as they would learn only counters’ hashes. This would eliminate the mentioned privacy leak; however, it would require a more complicated circuit.
6. Security Proofs with Tamarin
We used the Tamarin Prover [42] to prove the security properties that provide both auditability and privacy for the DID authentication protocol. To the best of our knowledge, this is the first formal security modeling of a DID authentication protocol. All of the Tamarin code can be found in [43].
6.1. The Tamarin Prover
The Tamarin Prover [42] is a powerful automated tool for the modeling and analysis of security protocols. In Tamarin, protocols and adversaries are described by using multiset rewriting rules, and trace properties such as authentication and secrecy are specified in first-order logical statements. These rules are represented by states or facts in which the symbolic representation of the adversary’s knowledge, network messages, and freshly generated information are stored. The protocols and adversaries interact by updating and generating network messages based on the rules. The security properties are modeled as trace properties, which specify a sequence of the rules’ actions.
Tamarin works on the Dolev–Yao (DY) model, which is a symbolic model in which messages are represented as terms. In the DY model, the attacker controls the network, can see all of the messages, and can manipulate, block, or re-order them. However, the attacker is not capable of breaking cryptographic primitives, such as forging the signature.
In the Tamarin protocol, execution is represented by a labeled state transition system. A state is a finite multiset of facts that include arguments of the state and their current snapshots of protocol execution. The facts include the local states of all participants, messages sent over the network, and messages that an attacker can construct from these messages. The action performed by the protocol participants and the attacker is specified by rules, which rewrite one state to another. The rules are of the form , where a is a set of premises, b is a set of actions (optional), and c is a set of conclusions. Executing the rules requires all premises to be currently present in the state, satisfy requirements of all actions, and result in adding conclusions to the state while the premises are deleted. The following are some of the important prefixes used in Tamarin:
- denotes the fresh variable x;
- denotes the public variable x;
- denotes the timestamp i;
- denotes a persistent .
Here, the only difference between persistent facts (with the ! prefix) and linear facts is that persistent facts are never removed from the state, while linear facts can be removed after executing some rules. Specifically, if there is a linear fact as a premise, but it does not appear as a conclusion, then it will be removed (consumed by the corresponding rule). To handle this, persistent facts are sometimes utilized.
Builtins, Functions, and Equations
In Tamarin, a function is an expression involving variables that maps some arguments to other arguments. We can define our functions or use builtin functions. However, an equation is a statement used to model the properties of a function. Equations can also be user-defined or extracted from builtin message theories.
In our Tamarin model for DID authentication, we use various builtins, such as:
- Signing: This theory models the signature scheme. The function’s symbols are , , , and , which satisfy the equation .
- Hashing: This theory models a hash function. The function’s symbol is , and there are no equations.
- Multiset: This theory introduces the associative–commutative operator "+", which is usually used to model multisets.
The custom functions with their respective equations are as follows:
- and with helps to obtain the zero-knowledge proof and verify the proof.
- , , and with, ,help to obtain and verify the VRF output with the token and token proof (gamma).
- and with, .
- with with,.Both t1 and g1 are getter functions. For example, given a pair of tokens, t1 takes the first element of the token.
6.2. Privacy-Preserving DID Authentication Model in Tamarin
We modeled DID authentication in a standard way and explain the set of rules that we defined to verify the security properties.
We start with rules that help the clients to initialize their new identifiers and the authentication tokens corresponding to them:
rule Register_pk:
[ Fr(~ltkA) ] --> [!Ltk($A, ~ltkA), !Pk($A, pk(~ltkA))]
rule Register_did:
[!Pk($A, pkA)] --> [!Did($A, h(pkA))]
rule Register_tkn:
[!Ltk($A, ltkA)]
-->
[!Token($A, token(’0’, ltkA)), !Gamma($A, gamma(’0’, ltkA))]
The Register_tkn rule consists of the fact, which ensures that token and the token VRF proof belong to a specific client.
Next, we have a registration request rule that is created by the client that uses it; it can register the initialized values to the blockchain:
rule Registration_request:
let p = <pkA, ~info, token(’0’, ltkA)>
in
[ Fr(~info), !Token($A, token(’0’, ltkA)),
!Ltk($A, ltkA), !Pk($A, pkA) ]
--[ Send_RR($A) ]->
[ Out(<p, sign(p, ltkA)>)]
Here, we take freshly generated information, a token fact, and both the secret key and public key as premises and output a public statement with its respective signature. This action will be called Send_RR, as stated in the rule.
In the next rule, as stated, we demonstrate how the blockchain verifies the signature on the public inputs (included in p) from the client and checks whether the token that it received from the client is not registered with the blockchain using the received action facts:
rule Blockchain_receive:
[!Pk($A, pkA), In(<p, sig>), !Token($A, tkn),
!Did($A, did)]
--[Recv_RR($A)],
Eq(verify(sig, p, pkA), true), Unique(token) ]->
[!Did($A, did), !Betadid(did), !Betatkn(tkn)]
Here, and are called restrictions such that, to execute the premises, all of the respective variables should satisfy the specified restrictions. is an equality restriction denoted by , which means that , while is a unique restriction denoted by , which means that x can only be executed once. If the signature verification is successful and the token is unique, then it outputs the that belongs to the client and the corresponding inclusion proofs as facts.
After the registration step, we define rules for the client to authenticate with a specific service, which involves generating a new token and its corresponding computational integrity proof (which is the zkSNARK proof). As premises, we take the previous token, gamma (token proof), betatoken (token inclusion proof), fresh variable w as the witness, and the setup phase proving key. Then, we check whether both the token and gamma share the same counter and secret key, as well as whether the betatoken corresponds to the token. Finally, we return a new token and gamma with its counter increased by 1 and the computational integrity proof denoted as .
rule Generate_tkn:
[ !Token($A, tkn), !Gamma($A, gam),
!Betatkn(betatoken), Fr(~w), !Ltk($Z, ltkz) ]
--[ Eq(g1(gam), t1(tkn)),
Eq(g2(gam), t2(tkn)),
Eq(betatoken, tkn) ]->
[ !Token($A, token(t1(tkn)+’1’, t2(tkn))),
!Gamma($A, gamma(g1(gam)+’1’, g2(gam))),
Phi($A, prove(token(t1(tkn)+’1’, t2(tkn)),
~w, ltkz)) ]
Now, we move towards defining rules for privacy-preserving verification of the authentication token at the blockchain. As the first step, we generate an ephemeral keypair, which is done in a slightly different way from the standard, since it needs to be signed with the client’s secret key,
rule Generate_pke:
[ Fr(~ltkB), !Ltk($A, ltkA) ]
-->
[ Ltk2($A, ~ltkB), Pk2($A, sign(pk(~ltkB), ltkA)) ]
The ephemeral key helps to protect the client against a reply attack; hence, it plays an important role. Once we have the ephemeral key, we define the next rule, , to model the authentication request that is initiated by the client and then sent to the service.
rule Auth_req:
let tknreq = <<proof, tkn>, sign(<proof, tkn>, ltkB), pkB>
in [Phi($A, proof), !Token($A, tkn), Ltk2($A, ltkB),
Pk2($A, pkB), !Did($A, did), !Betadid(betadid),
!gamma($A, gam) ] --[ Send_to_service($A), Eq(t1(tkn),
g1(gam))] -> [ Authreq(<did, betadid, t1(tkn), gam,
tknreq>) ]
Here, the new token and token integrity proof are signed with the freshly generated ephemeral secret key to generate the , which is embedded into the and sent to the service. Next, we model the rule , which defines how the service handles the authentication request from a client.
rule Service_receive:
let tknreq = <<proof, tkn>, sig, pkB>
in [ Authreq(<did, betadid, cnt, gamma, tknreq>,
!Pk($A, pkA))]--[ Recv_AR($A)],
Eq(vrfyVRF(cnt, tkn, gamma, pkA), true),
Eq(did, betadid) ]->
[ Tokenreq(tknreq) ]
This is sent to the blockchain, after which we model the rule to receive the token from the service and output with an inclusion proof .
rule Blockchain_receive:
let tkereq = <<proof, tkn>, sig, pkB>
in [ Tokenreq(tknreq), !Pk($Z, pkz)
--[ Recv_TR(),
Eq(vrfy(proof, tkn, pkz), true), Unique(tkn) ]-->
[ !Betatkn(tkn) ]
The is defined with a persistent fact . In the final step, we model the rule, which models how the service verifies the inclusion proof received from the blockchain and establishes a session with the client.
rule return_to_service:
[ !Token($A, tkn), !Betatkn(betatoken) ]
--[ Eq(betatoken, tkn), Finish() ]->
[ St_Session($A) ]
The rule takes a token and betatoken as premises, checks whether the betatoken corresponds to the token, and then initiates the session.
6.3. Security Property
An attacker cannot login to an honest service by using an identity on the blockchain without being detected. The client will be able to detect its credentials being misused at an honest service through active surveillance of the blockchain or its subsequent authentication events. An honest service or blockchain is an entity that is not controlled by the attacker. We formalize it as follows.
Definition 1.
A DID authentication protocol can achieve auditability and privacy with honest client C, honest service S, and blockchain B if C can register an identity on B, use it to authenticate with S, and successfully and anonymously log the event onto B; then, C holds a valid identity on B, and an adversary has not used it to authenticate to an honest S.
For the DID authentication protocol, we use the following formalization.
lemma executable:
exists-trace
"Ex #i. Finish() @i
& (All x y #i #j. (Send_RR(x)@i & Send_RR(y)@j)
==> x = y & #i = #j)
& (All x y #i #j. (Recv_RR(x)@i & Recv_RR(y)@j)
==> x = y & #i = #j)
& (All x y #i #j. (Send_to_service(x)@i &
Send_to_service(y)@j) ==> x = y)
& (All x y #i #j. (Recv_AR(x)@i & Recv_AR(y)@j)
==> x = y & #i = #j)
& (All #i #j. (Recv_TR()@i & Recv_TR()@j)
==> #i = #j)"
The above lemma checks whether there is a trace from the client registration to the start session passing all rules associated with the following:
- The client sends a registration request to the blockchain.
- The blockchain receives the registration request, verifies the signature, ensures that the token received is unique, and returns the did and token inclusion proof.
- The client generates an authentication request to be sent to the service after deriving a new token and proving its computation.
- The service receives the authentication request, verifies that the token is created with the respective counter and secret key, verifies whether the corresponds to its did inclusion proof, and sends a token request to the blockchain.
- The blockchain receives the token request and verifies it, after which the service establishes a session with the client.
We provide a Tamarin model that has 128 lines of code. The model was computed automatically on a desktop machine with 8 CPUs of the type Intel(R) Core (TM) i7-8550U at1.80 GHz, with 16 GB for RAM, running Ubuntu 20.04.2 LTS. The runtime for our model was 3.716 s, and the code is available at [43]. In Appendix A, we also provide a UC modeling of our DID authentication protocol.
6.4. Privacy with Token Unlinkability
Our protocol achieves auditability while providing the privacy property defined as token unlinkability between (, token) and (service provider, token). To formulate token unlinkability, we should depend on a typical indistinguishability game that an adversary plays with a challenger. However, to facilitate our token unlinkability analysis, we analyze it through the following three informal anonymity sets.
- Anonymity client set . A client with a registered is anonymous with respect to logging a token onto the blockchain if and only if is anonymous within a set of clients defined as the anonymity set.
- Anonymity service set . A service provider is anonymous with respect to logging tokens to the blockchain on behalf of the clients in the set if and only if is anonymous within a set of service providers defined as the service anonymity set.
- Anonymity token set . A token on the blockchain is anonymous if and only if is indistinguishable from other tokens within a set defined as the token anonymity set.
The privacy guarantee of our protocol depends on the size of the anonymity set. If there is only a single client and one token , then a union set with a set size of, at most, compromises privacy with the probability . This is similar in the case of service providers.
7. Evaluation
7.1. Performance Evaluation
We implemented our baseline and privacy-preserving protocols on Hyperledger Fabric. (We used an old version of Hyperledger Fabric, i.e., v0.6, instead of the newer versions because it had better security and performance.) This is a permissioned blockchain that uses PBFT consensus and supports Turing-complete smart contracts called chaincodes. It executes smart contracts inside Docker containers.
Our implementation consisted of smart contract functions written in Golang, which provides rich support for complex data structures and cryptographic libraries. Signatures were implemented by using the crypto/ecdsa library with the ed25519 curve. The TokenVrf function in Algorithm 3, which contained the most complex logic for verification, was implemented by using go-snark [44].
The client and service provider were written in Golang. They interacted with the blockchain via REST APIs. The client used the circom compiler [45] to compile the circuit from Algorithm 3. To make the circuit more efficient, we used EdDSA with the Babyjub [46] elliptic curve to implement VRFs and MiMC7 [47] as the hash function. Computation integrity proofs were generated by using websnark (https://github.com/iden3/websnark (accessed on 18 October 2020).
7.1.1. Methodology
We evaluated the performance of our protocols by using the following metrics: (1) throughput: the number of authentication events completed per second; (2) latency: the end-to-end latency at the client; (3) cost breakdown: the computation cost at the client, service provider, and the blockchain node. We pre-generated the proofs and used up to 5 clients to generate increasing loads on the blockchain. Throughput was computed as the number of transactions included in the blockchain over the measurement period, which was set to 10 min. End-to-end latency was computed as the time from when the client submitted the transaction to when the transaction was included in the blockchain.
We varied the size of the blockchain by varying its fault tolerance threshold f. The number of nodes was . We varied f from 0 to 6. This was to measure the impact of the consensus protocol on the overall performance. At , there was no consensus. At , the cost of the consensus increased with f.
Our experiments were run on both a local cluster and on AWS. Each cluster node had 8 GB of RAM, a 2.10 GHz CPU, and 1 Gbps Ethernet, and each was run on Ubuntu 18.04 OS. For AWS, we used t1.xlarge instances (4 vCPUs, 16 GB of RAM) across two regions (Singapore and Hong Kong). Unless stated otherwise, the results presented below are for a local cluster averaged over 5 runs.
7.1.2. Results
We first measured the throughput by varying client request rates. The results for (or 13 nodes) are shown in Figure 2 (the results for other values of f are similar).
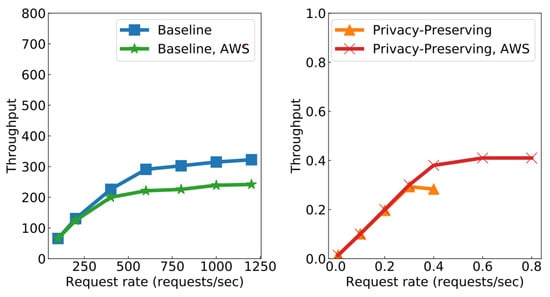
Figure 2.
Throughput with varying client request rates ().
The throughput of the baseline protocol increased to 380 authentication events per second, whereas that of the privacy-preserving protocol peaked at authentication events per second (or roughly one authentication for every 3 s). The low throughput of the latter was due to the overhead of the zkSNARK primitives. Each proof was only 784 bytes, but verifying it took 3.18 s on average. The baseline performance was lower than but consistent with the results in [11] because of the overhead in signature verification.
Figure 3 shows the peak throughputs for varying f and the latencies at these throughputs. It can be seen that increasing the number of blockchain nodes did not effect the privacy-preserving protocol. In particular, the throughput remained at authentication events per second. In contrast, the baseline protocol suffered a drop of from 380 to 280 events per second. Furthermore, the latency remained constant with increasing f, with 3 s on average for the baseline and 30 s on average for the privacy-preserving protocol. We observed that the throughputs running on AWS were slightly lower for the baseline and higher for the other protocol. This was because the network bandwidth across the AWS regions was lower than that of the local cluster, and the AWS instances had more powerful CPUs than the local cluster’s VMs.
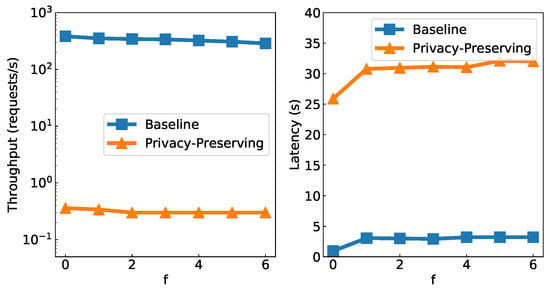
Figure 3.
Peak throughput and latency.
We examined the cost breakdown at the blockchain node to better understand the performance difference. In particular, we measured the cost of consensus and transaction execution at the blockchain. Figure 4 compares these costs for the two protocols, with different values of f. Consensus was the major cost in the baseline protocol, whereas transaction execution contributed the most to the cost in the privacy-preserving protocol. In particular, for , the consensus and execution latency in the baseline protocol were and s, respectively ( and s for AWS). In the privacy-preserving protocol, they were and s, respectively ( and s for AWS). As a result, the baseline protocol was sensitive to the consensus cost, which increased with f, whereas the other protocol was only affected by the execution cost.
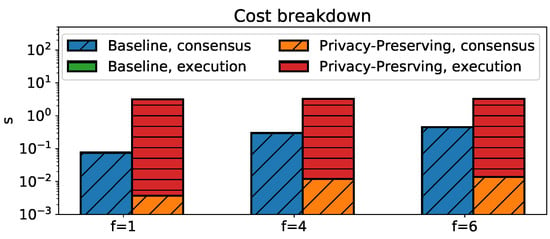
Figure 4.
Cost breakdown at blockchain nodes.
So far, we have ignored the cost of generating proofs at the client. Before generating proofs, the system first has to perform a one-time setup phase (i.e., executing ), after which clients can generate proofs (i.e., calling ). The costs of the setup phase and proof generation are shown in Table 2. It can be seen that the setup phase was expensive, and its cost increased when more signatures were included in the proof (since the circuit size increased). For example, with (or 16 nodes), the setup took almost 2 h to complete. We note, however, that this cost was incurred only once and can be amortized over time.

Table 2.
The costs of setup and generating proofs at the client.
7.2. Discussion
We remark that even though the throughput of the privacy-preserving protocol was low, the baseline protocol achieved a high enough throughput for it to be practical. In particular, we note that the authentication workload at Google is reported to be 20 requests per second over a dataset of users [48]. Extrapolating from this, the baseline protocol can support workloads of up to 13 M users. Importantly, this protocol can scale horizontally with a sharded blockchain because different identities can be partitioned and processed independently in multiple shards. This means that the protocol can scale out to support billions of users.
7.3. Integration
Our privacy-preserving protocol can be integrated with the latest verifiable credential schemes, such as Coconut [27] and EL Passo [28], to provide logging of authentication events, which can help users detect credential misuse. We briefly explain how our protocol can be integrated.
Coconut is a selective disclosure credential scheme in which a user first sends a coconut issue request to a set of authorities (identity providers) with public and private attributes, using which each authority issues a partial credential. Next, the user aggregates a threshold number of shares to obtain a consolidated credential and then invokes a show protocol to selectively disclose attributes or make statements about them to a service (doing authentication). This credential can be used across multiple services without connecting with the authorities during every show protocol execution. Our approach is to associate a token with each credential issue request (during which a token is initialized and registered with the blockchain managed by the authorities), and before each show protocol, the user needs to generate a new token consistent with the previous token and the token integrity proof, which is then sent to a service that redirects it to the blockchain. The service will be able to alert users (or users can audit) of misuse if the verification of the integrity proof fails at the blockchain.
EL Passo uses a verifiable credential to overcome the privacy issues of traditional single-sign-on (SSO) systems. The user can obtain a verifiable credential from an identity provider and use it across multiple relying parties (service) without going through the identity provider, thus preventing the identity provider from tracking user activities. However, the drawback is that this also prevents the users’ ability to detect any possible credential misuse. Since the user cannot rely on the identity provider to log the authentication events, we propose the deployment of an additional blockchain infrastructure in which the user can log an authentication event (or choose their own blockchain and then deploy a smart contract to log the event; during the authentication, the user needs to specify to the relying party the blockchain on which the token needs to be logged). So, during the setup phase, along with generating a user secret, the user initializes a token and obtains a credential from the identity provider associated with both of these values. They then must register this token on the blockchain before using the credential to authenticate with any relying party. The credential usage and subsequent misuse detection during the sign-on phase are similar to those of Coconut.
8. Conclusions and Future Work
In this paper, we proposed two DID authentication protocols that allow users to detect credential misuse. The first protocol achieves high performance, but with limited privacy. The second protocol achieves full privacy, but with a high performance overhead. We gave a formal security analysis of the final protocol by using the Tamarin Prover. We implemented these protocols by using Hyperledger Fabric and evaluated their performance on a local cluster. The results showed that the first protocol achieved throughput sufficient to support realistic workloads. However, the second protocol incurred significant overhead and suffered from a throughput that was three orders of magnitude lower. In future work, we plan to improve the two protocols by using more efficient blockchains with sharding and parallel execution. In addition, we also plan to tackle other security issues, such as token integrity (ensuring that the attacker does not tamper with the token, for example, by storing the counter value externally), and to compare this with other implementations of DIDAuth and privacy-preserving logging protocols.
Author Contributions
Conceptualization, B.A., P.S. and T.T.A.D.; Methodology, B.A., P.S. and T.T.A.D.; Software, B.A., S.M. and J.I.G.; Validation, Z.L.; Formal analysis, S.M. and J.I.G.; Investigation, S.M.; Resources, K.M.M.A.; Writing—original draft, B.A.; Writing—review & editing, S.M.; Supervision, K.M.M.A. and Z.L.; Project administration, K.M.M.A. and Z.L.; Funding acquisition, K.M.M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by A*STAR under its RIE2020 Advanced Manufacturing and Engineering (AME) Programmatic Programme (Award A19E3b0099).
Data Availability Statement
The data presented in this study are available in the present article.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A
Here, we formally model the final protocol (Section 5.2) under the UC framework [49] by using the ideal-world/real-world paradigm, in which parties are modeled as probabilistic polynomial-time interactive Turing machines.
A protocol is secure if there exists no environment that can distinguish whether it is interacting with adversary and parties running protocol or with the ideal process for carrying out the desired task, where the ideal adversary and dummy parties interact with the ideal functionality . Every functionality and every protocol invocation should be instantiated with a unique session ID that distinguishes them from other instantiations. More formally, we say that the protocol emulates the ideal process if, for any adversary , there exists a simulator such that for all environments , the ensembles and are computationally indistinguishable, i.e., We outline a security proof in the UC framework to show the registration and authentication subprotocols that match and under a concurrent composition.
Appendix A.1. UC Modeling of the Final Protocol
Functionality: We briefly re-formalize our privacy-perserving protocol with a UC model, which consists of three phases: (1) initialization, (2) registration, and (3) authentication. The functionality is parameterized with the security parameter and the algorithms of cryptographic primitives. In the initialization phase, receives a command from the client and forwards a notification to the simulator (and stores this session). During registration, it receives a command (Register, , , ) from the client . checks for a possible entry; if not, it makes a new entry and sets ; otherwise, the command is ignored, and it returns (Unregistered, , , Error) to and halts. After that, it forwards the command (Register, , , 1) to the adversary . Next, it receives from , to which it responds with and records . In addition, passes the message to along with the and token inclusion proofs ( and , respectively), and it records (the client is registered). Finally, in the authentication phase, it receives a command from , where . The ideal functionality checks for a possible entry and then sends a notification to and . Otherwise, it outputs ⊥ and aborts. Now, the input (Token-match, , , ) is received from , after which checks for an entry (, , , 1). Once confirmed, it sends a notification (Token-match, , , ) to ; otherwise, the command is ignored. Lastly, it receives (Token-match, , , ) from , and it validates that no entry (, , , 0) has been recorded before. In the case of validation failure, returns to and halts; otherwise, it returns (Token-match, , , ) to and records the entry (, , , 1).
Functionality: is parameterized with a relation R and communicates with a prover P, a verifier V, and an adversary . It receives a command (ZKProver, , ) from P for a statement x associated with a witness w; if , then, it sends to V and and exits. Otherwise, it exits.
Functionality: The ideal blockchain functionality runs with a set of clients , a service provider , and an ideal adversary . holds a database indexed on integers and initializes a counter . First, it receives a command (Write, , , ) from in the registration phase, after which checks whether is stored in the database under the index that corresponds to from the client. It sends a notification (Write,, ) to and updates the counter: . Next, it receives (Token-match, , , ) from (i.e., the service provider ) in the authentication phase; if there is an entry (, , , 1), then, it checks for a tuple stored under the index . If there is, then it passes (Token-match, , ) to .
Functionality: This functionality is parameterized with the participants and for authentication. It receives (Login, , , ) from . If there is a record , then it forwards it to , and then returns (Token-match, , , ) to . After this, it interacts with by sending a command (Token-match, , , ), to which it responds with (Token-match,, , ). records and forwards (Token-match, , ,) to .
Appendix A.2. Formalized Final Protocol
Protocol: Our construction operates in the (, , )-hybrid model and in the phases explained in the previous section. In the initialization phase, it receives a command from the environment ; then, the client initializes the required keys. After this step, it sends the command (Write, , , , , ) to and . The smart contract is initialized and created; it keeps privately and sends to the client by invoking (, , C) for a circuit C. In the registration phase, generates the keys, derives the from the public key, and then interacts with to obtain the inclusion proofs , which it stores locally. In the authentication phase, the protocol receives the command from the environment , which helps a client to authenticate with a service provider. First, derives a new token and associates zero-knowledge proof of computation, as explained in Section 5.2.1. Once the proof is derived, it sends a command to and obtains as a response. The legitimacy of the new token and its consistency are verified as shown in Algorithm 3.
Once validation is complete, is sent to . After receiving, it sends (Token-match, , , ) to . At the ledger, the smart contract verifies the new token request from a service provider, as shown in Algorithm 4, and returns the notification (Token-match, , , ) from . then fetches from and validates the legitimacy, i.e., returns (Token-match, , , ) to the client .
Theorem A1.
Let and be an ideal functionality and a probabilistic polynomial-time (PPT) adversary for our proposed scheme, respectively, and let be an ideal-world PPT simulator for . Then, the proposed scheme UC-realizes the ideal functionality for any PPT-distinguishing environment in the (, , )-hybrid model.
Construction of . In a nutshell, if a message is sent by an honest party to , emulates appropriate real-world communications among participants for with information obtained from . If a message is sent to by a corrupted party, extracts the input and interacts with the corrupted party with the help of .
Hybrid H.1 proceeds as in the real-world protocol, except that emulates . In particular, invokes the signature scheme and generates a keypair , and then keeps and publishes . Whenever wants to communicate with , records ’s messages and faithfully emulates ’s behavior. Similarly, emulates by storing items internally. As ’s view in H.1 is perfectly simulated as in the real world, cannot distinguish between H.1 and H.0.
Hybrid H.2 proceeds as in H.1, except for a modification in how the signature is generated. The indistinguishability between H.1 and H.2 can be shown by the following reduction to the EU-CMA property of the signature scheme. In more detail, if sends forged attestations to ,the signature verification conducted by will fail with all but a negligible probability. If can distinguish H.2 from H.1, and can be used to win the game of signature forgery. As assumed, unforgeability is guaranteed by the signature scheme used.
Hybrid H.3 proceeds as in H.2, but it has emulate the authentication, which means that honest clients will send the command to . emulates messages from , as described above, and to . It is clear that ’s view is distributed exactly as in H.2, as can perfectly emulate and .
Hybrid H.4 proceeds as in H.3 except that, under the random oracle model, the adversary does not know the secret VRF key , but must distinguish between pairs , where is the VRF hash output on the counter input , and pairs , where r is a random value. This adversary knows the public values , and it can easily compute if they know . However, is kept private. In addition, even looks random in the random oracles that know ; thus, pseudo-randomness is guaranteed because the adversary cannot distinguish from a random distribution, and is pseudo-random in the range of H. Further, suppose an adversary, given the secret key . The verification can satisfy both and for and , and the uniqueness adversary cannot distinguish them unless because of the uniqueness property of the VRF. Hence, the indistinguishability between H.4 and H.3 can be directly reduced to the uniqueness and the pseudo-randomness properties of the VRF.
Hybrid H.5 proceeds as in H.4, except for a modification in how the hash value is generated. The indistinguishability between H.5 and H.4 can be shown by a reduction to the second pre-image resistance property of the hash function. In H.4, the output of the VRF will be hashed via ; in H.5, a value is sampled from a uniform distribution at random and input into . If can distinguish H.5 from H.4, this implies that can break the second pre-image resistance, which contradicts our assumptions.
It remains to observe that H.5 is identical to the ideal protocol. Then, combining all of them together with this invariant ensures that H.5 precisely reflects the ideal execution of in the -hybrid model.
References
- Decentralized Identity Foundation. 2018. Available online: https://identity.foundation/ (accessed on 19 October 2020).
- DID Specification. 2020. Available online: https://www.w3.org/TR/did-core/ (accessed on 21 June 2021).
- Hyperledger Indy. 2018. Available online: https://tinyurl.com/yycca4ek (accessed on 19 October 2020).
- Hyperledger Aries. 2019. Available online: https://www.hyperledger.org/projects/aries (accessed on 19 October 2020).
- Evernym. 2018. Available online: https://www.evernym.com (accessed on 19 October 2020).
- Nuggets. 2018. Available online: https://nuggets.life/ (accessed on 19 October 2020).
- Blockstack. 2018. Available online: https://blockstack.org/ (accessed on 19 October 2020).
- Maram, D.; Malvai, H.; Zhang, F.; Jean-Louis, N.; Frolov, A.; Kell, T.; Lobban, T.; Moy, C.; Juels, A.; Miller, A. CanDID: Can-Do Decentralized Identity with Legacy Compatibility, Sybil-Resistance, and Accountability. IACR Cryptol. ePrint Arch. 2020, 2020, 934. [Google Scholar]
- Google Last Login. 2019. Available online: https://tinyurl.com/lqlg2xz (accessed on 21 June 2021).
- Bowe, S.; Gabizon, A.; Miers, I. Scalable Multi-party Computation for zk-SNARK Parameters in the Random Beacon Model. IACR Cryptol. ePrint Arch. 2017, 1050, 1–24. [Google Scholar]
- Dinh, T.T.A.; Liu, R.; Zhang, M.; Chen, G.; Ooi, B.C.; Wang, J. Untangling blockchain: A data processing view of blockchain systems. TKDE 2018, 30, 1366–1385. [Google Scholar] [CrossRef]
- Nakamoto, S. Bitcoin: A peer-to-peer electronic cash system. Decentralized Bus. Rev. 2019, 21260. [Google Scholar]
- Wood, G. Ethereum: A secure decentralised generalised transaction ledger. Ethereum Proj. Yellow Pap. 2014, 151, 1–32. [Google Scholar]
- Hyperledger Fabric. 2020. Available online: https://tinyurl.com/ydaswf3j (accessed on 21 June 2021).
- Quorum. 2020. Available online: https://www.goquorum.com (accessed on 21 June 2021).
- Castro, M.; Liskov, B. Practical Byzantine fault tolerance. In OSDI; USENIX: Berkeley, CA, USA, 1999; pp. 173–186. [Google Scholar]
- DIDAuth. 2018. Available online: https://tinyurl.com/y89tahad (accessed on 19 October 2020).
- Micali, S.; Rabin, M.; Vadhan, S. Verifiable random functions. In Proceedings of the 40th Annual Symposium on Foundations of Computer Science, Washington, DC, USA, 17–18 October 1999. [Google Scholar]
- Bitansky, N.; Canetti, R.; Chiesa, A.; Tromer, E. From extractable collision resistance to succinct non-interactive arguments of knowledge, and back again. In Proceedings of the 3rd Innovations in Theoretical Computer Science Conference, Berkeley, CA, USA, 31 January–3 February 2022. [Google Scholar]
- Ben-Sasson, E.; Bentov, I.; Horesh, Y.; Riabzev, M. Scalable, transparent, and post-quantum secure computational integrity. IACR Cryptol. ePrint Arch. 2018, 2018, 46. [Google Scholar]
- Ali, M.; Nelson, J.; Shea, R.; Freedman, M.J. Blockstack: A Global Naming and Storage System Secured by Blockchains. In Proceedings of the 2016 USENIX Annual Technical Conference, Denver, Colorado, USA, 22–24 June 2016. [Google Scholar]
- Melara, M.S.; Blankstein, A.; Bonneau, J.; Felten, E.W.; Freedman, M.J. CONIKS: Bringing Key Transparency to End Users. In Proceedings of the 24th USENIX Security Symposium, Washington, DC, USA, 12–14 August 2015. [Google Scholar]
- Key Transparency. 2020. Available online: https://tinyurl.com/ybhedmfs (accessed on 21 June 2021).
- Chu, D.; Lin, J.; Li, F.; Zhang, X.; Wang, Q.; Liu, G. Ticket Transparency: Accountable Single Sign-On with Privacy-Preserving Public Logs. In Proceedings of the International Conference on Security and Privacy in Communication Systems, Orlando, FL, USA, 23–25 October 2019. [Google Scholar]
- Davidson, A.; Goldberg, I.; Sullivan, N.; Tankersley, G.; Valsorda, F. Privacy Pass: Bypassing Internet Challenges Anonymously. Proc. Priv. Enhancing Technol 2018, 3, 164–180. [Google Scholar] [CrossRef]
- Huang, S.; Jeyaraman, S.I.S.; Kushwah, S.; Lee, C.K.; Luo, Z.; Raghunathan, P.M.A.; Shaikh, S.; Sung, Y.C.; Zhang, A. DIT: De-Identified Authenticated Telemetry at Scale. Available online: https://scontent.fsin10-1.fna.fbcdn.net/v/t39.8562-6/246534149_588854725718321_8923613326138589821_n.pdf?_nc_cat=103&ccb=1-7&_nc_sid=ad8a9d&_nc_ohc=sgqd5Qn5r-YAX_F9X4W&_nc_ht=scontent.fsin10-1.fna&oh=00_AfDK48w6piGcXrn2W3zsEvHTqbVqp_6-ugYzHVoZwjNJmQ&oe=63A75882 (accessed on 21 June 2021).
- Sonnino, A.; Al-Bassam, M.; Bano, S.; Meiklejohn, S.; Danezis, G. Coconut: Threshold issuance selective disclosure credentials with applications to distributed ledgers. arXiv 2018, arXiv:1802.07344. [Google Scholar]
- Zhang, Z.; Król, M.; Sonnino, A.; Zhang, L.; Rivière, E. EL PASSO: Privacy-preserving, Asynchronous Single Sign-On. arXiv 2020, arXiv:2002.10289. [Google Scholar]
- Pointcheval, D.; Sanders, O. Short randomizable signatures. In Proceedings of the Cryptographers’ Track at the RSA Conference, San Francisco, CA, USA, 29 February–4 March 2016; pp. 111–126. [Google Scholar]
- Andersen, M.P.; Kumar, S.; AbdelBaky, M.; Fierro, G.; Kolb, J.; Kim, H.S.; Culler, D.E.; Popa, R.A. WAVE: A Decentralized Authorization Framework with Transitive Delegation. In Proceedings of the 28th USENIX Security Symposium, Santa Clara, CA, USA, 14–16 August 2019. [Google Scholar]
- Shafagh, H.; Burkhalter, L.; Ratnasamy, S.; Hithnawi, A. Droplet: Decentralized Authorization and Access Control for Encrypted Data Streams. In Proceedings of the 29th USENIX Security Symposium, Boston, MA, USA, 12–14 August 2020. [Google Scholar]
- Google Trillian. 2020. Available online: https://github.com/google/trillian (accessed on 21 June 2021).
- Panwar, G.; Vishwanathan, R.; Misra, S.; Bos, A. SAMPL: Scalable Auditability of Monitoring Processes using Public Ledgers. In Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security, London, UK, 11–15 November 2019. [Google Scholar]
- Kim, M.; Lee, J.; Oh, J.; Park, K.; Park, Y.; Park, K. Blockchain based energy trading scheme for vehicle-to-vehicle using decentralized identifiers. Appl. Energy 2022, 322, 119445. [Google Scholar] [CrossRef]
- Li, X.; Jing, T.; Li, R.; Li, H.; Wang, X.; Shen, D. BDRA: Blockchain and Decentralized Identifiers Assisted Secure Registration and Authentication for VANETs. IEEE Internet Things J. 2022; Early Access. [Google Scholar] [CrossRef]
- Poolat Parameswarath, R.; Gope, P.; Sikdar, B. Decentralized Identifier-based Privacy-preserving Authenticated Key Exchange Protocol for Electric Vehicle Charging in Smart Grid. arXiv 2022, arXiv:2206.13055. [Google Scholar]
- Cecchetti, E.; Zhang, F.; Ji, Y.; Kosba, A.; Juels, A.; Shi, E. Solidus: Confidential distributed ledger transactions via PVORM. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, Dallas, TX, USA, 30 October–3 November 2017. [Google Scholar]
- Narula, N.; Vasquez, W.; Virza, M. zkLedger: Privacy-Preserving Auditing for Distributed Ledgers. In Proceedings of the 5th USENIX Symposium on Networked Systems Design and Implementation (NSDI 18), Boston, MA, USA, 12–14 April 2021. [Google Scholar]
- Crosby, S.A.; Wallach, D.S. Authenticated dictionaries: Real-world costs and trade-offs. ACM Trans. Inf. Syst. Secur. (TISSEC) 2011, 14, 1–30. [Google Scholar] [CrossRef]
- Dingledine, R.; Mathewson, N.; Syverson, P. Tor: The Second-Generation Onion Router; Naval Research Lab: Washington, DC, USA, 2004. [Google Scholar]
- Zcash: Parameter Generation. 2020. Available online: https://z.cash/technology/paramgen/ (accessed on 21 June 2021).
- Meier, S.; Schmidt, B.; Cremers, C.; Basin, D. The TAMARIN prover for the symbolic analysis of security protocols. In Proceedings of the International Conference on Computer Aided Verification, Saint Petersburg, Russia, 13–19 July 2013; pp. 696–701. [Google Scholar]
- DID Authentication Tamarin Model. 2021. Available online: https://github.com/bithinalangot/DIDAuthTamarin (accessed on 18 March 2022).
- Go-Snark. 2020. Available online: https://github.com/arnaucube/go-snark (accessed on 18 March 2022).
- Circom Compiler. 2019. Available online: https://github.com/iden3/circom (accessed on 18 March 2022).
- Babyjub. 2020. Available online: https://tinyurl.com/yc7kmcsj (accessed on 18 March 2022).
- MiMC7. 2020. Available online: https://tinyurl.com/y99c2khj (accessed on 18 March 2022).
- Thomas, K.; Pullman, J.; Yeo, K.; Raghunathan, A.; Kelley, P.G.; Invernizzi, L.; Benko, B.; Pietraszek, T.; Patel, S.; Boneh, D.; et al. Protecting accounts from credential stuffing with password breach alerting. In Proceedings of the 28th USENIX Security Symposium, Santa Clara, CA, USA, 14–16 August 2019. [Google Scholar]
- Canetti, R. Universally composable security: A new paradigm for cryptographic protocols. In Proceedings of the 42nd IEEE Symposium on Foundations of Computer Science, Las Vegas, NV, USA, 14–17 October 2001. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).