Abstract
Regularized sparse learning with the -norm is important in many areas, including statistical learning and signal processing. Iterative hard thresholding (IHT) methods are the state-of-the-art for nonconvex-constrained sparse learning due to their capability of recovering true support and scalability with large datasets. The current theoretical analysis of IHT assumes the use of centralized IID data. In realistic large-scale scenarios, however, data are distributed, seldom IID, and private to edge computing devices at the local level. Consequently, it is required to study the property of IHT in a federated environment, where local devices update the sparse model individually and communicate with a central server for aggregation infrequently without sharing local data. In this paper, we propose the first group of federated IHT methods: Federated Hard Thresholding (Fed-HT) and Federated Iterative Hard Thresholding (FedIter-HT) with theoretical guarantees. We prove that both algorithms have a linear convergence rate and guarantee for recovering the optimal sparse estimator, which is comparable to classic IHT methods, but with decentralized, non-IID, and unbalanced data. Empirical results demonstrate that the Fed-HT and FedIter-HT outperform their competitor—a distributed IHT, in terms of reducing objective values with fewer communication rounds and bandwidth requirements.
1. Introduction
Sparse learning has emerged as a central topic of study in a variety of fields that require high-dimensional data analysis. Sparsity-constrained statistical models exploit the fact that high dimensional data arising from real-world applications frequently have low intrinsic complexity and have been shown to perform accurate estimation and inference in a variety of data mining fields, such as bioinformatics [1], image analysis [2,3], graph sparsification [4] and engineering [5]. These models often require solving the following optimization problem with a nonconvex, nonsmooth sparsity constraint:
where is a smooth and convex cost function in terms of a vector of parameters to be optimized x, denotes the -norm (cardinality) of x, which computes the number of nonzero entries in x, and is the sparsity level pre-specified for x. Examples of this model include sparsity-constrained linear/logistic regression problems [6,7] and sparsity-constrained graphical models [8].
Extensive research has been conducted for Problem (1). The methods largely fall into the regimes of either matching pursuit methods [9,10,11,12] or iterative hard thresholding (IHT) methods [13,14,15]. Even though matching pursuit methods achieve remarkable success in minimizing quadratic loss functions (such as the -constrained linear regression problems), they require finding an optimal solution to min over the identified support after hard thresholding at each iteration, which lacks analytical solutions for arbitrary losses and can be time-consuming [16]. Hence, gradient-based IHT methods have gained significant interest and become popular for nonconvex sparse learning. IHT methods currently include the gradient descent HT (GD-HT) [14], stochastic gradient descent HT (SGD-HT) [15], hybrid stochastic gradient HT (HSG-HT) [17], and stochastic variance reduced gradient HT (SVRG-HT) [18,19] methods. These methods update the iterate as follows: , where is the learning rate, can be the full gradient, stochastic gradient or variance reduced gradient at the t-th iteration, and denotes the HT operator that preserves the top elements in x and sets other elements to 0. However, finding a solution to Problem (1) is generally NP-hard because of the non-convexity and non-smoothness of the cardinality constraint [20].
Local datasets can be sensitive to sharing during the construction of a sparse inference model when sparse learning becomes distributed and uses data collected by distributed devices. For instance, meta-analyses may integrate genomic data from a large number of labs to identify (a sparse set of) genes contributing to the risk of a disease without sharing data across the labs [21,22]. Smartphone-based healthcare systems may need to learn the most important mobile health indicators from a large number of users; however, the personal health information gathered on the phone is private [23]. Furthermore, communication efficiency can be the main challenge to distributively training a sparse learning model. Due to the power and bandwidth limitations of various sensors, the signal processing community, for instance, has been seeking more communication-efficient methods [24].
Federated learning (FL) is a recently proposed communication-efficient distributed computing paradigm that enables collaborations among a collection of clients while preserving data privacy on each device by avoiding the transmission of local data to the central server [25,26,27]. Hence, sparse learning can benefit from the setting of federated learning. In this paper, we solve the federated nonconvex sparsity-constrained empirical risk minimization problem with decentralized data as follows:
where is a smooth and convex function, is the loss function of the i-th client (or device) with weight , , is the distribution of data located locally on the i-th client, and N is the total number of clients. It is thus desirable to solve Problem (2) in a communication-efficient way and investigate theory and algorithms applicable to a broader class of sparse constrained learning problems in high-dimensional data analyses [6,7,8,28].
We thus propose federated HT algorithms with lower communication costs and provide the corresponding theoretical analysis under practical federated settings. The analysis of proposed methods is difficult due to the fact that distributions of training data on each client may be non-identical and the data weights can be unbalanced across devices.
Our main contributions are summarized as follows.
(a) We develop two schemes for the federated HT method: the Federated Hard Thresholding (Fed-HT) algorithm and Federated Iterative Hard Thresholding (FedIter-HT) algorithm. In Fed-HT, we apply the HT operator at the central server right before distributing the aggregated model to clients. To further improve the communication efficiency and the ability of sparsity recovery, in FedIter-HT, we consider applying to both local updates and the central server aggregate. Note that this is the first trial to explore IHT algorithms under federated learning settings.
(b) We provide a set of theoretical results for the federated HT method, particularly of Fed-HT and FedIter-HT, under the realistic condition that the distributions of training data over devices can be unbalanced and non-independent and non-identical (non-IID), i.e., for , and are different. We prove that both algorithms enjoy a linear convergence rate and have a strong guarantee for sparsity recovery. In particular, Theorems 1 (for the Fed-HT) and 2 (for the FedIter-HT) show that the estimation error between the algorithm iterate and the optimal solution is upper bounded as: where is the initial guess of the solution, the convergence rate factor is related to the algorithm parameter K (the number of SGD steps on each device before communication), and the closeness between the pre-specified sparsity level and the true sparsity , and determines a statistical bias term related not only to K but also to the gradient of f at the sparse solution and the measurement of the non-IIDness of the data across the devices.
The theoretical results allow us to evaluate and compare the proposed methods. For example, greater non-IIDness among clients increases the bias of both algorithms. More local iterations may reduce but increase the statistical bias. Due to the utilization of the HT operator on local updates, the statistical bias induced by the FedIter-HT in Theorem 2 matches the best known upper bound for traditional IHT methods [17], which exhibits the powerful capability of sparsity recovery.
(c) When instantiating the general loss function by concrete squared or logistic loss, we arrive at specific sparse learning problems, such as sparse linear regression and sparse logistic regression. We provide statistical analysis of the maximum likelihood estimators (M-estimators) of these problems when using the FedIter-HT to solve them. This result can be regarded as federated HT analysis for generalized linear models.
(d) Extensive experiments in simulations and on real-life datasets demonstrate the effectiveness of the proposed algorithms over standard distributed IHT learning.
Related Work
Distributed sparse learning. Existing IHT algorithms can be extended to their distributed version—Distributed IHT (see Appendix A.1. for details), in which the central server aggregates (averages) the local parameter updates from each client and broadcasts the latest model parameters to individual clients, whereas each client updates the parameters based on the distributed local data with one step of stochastic gradient descend and sends them back to the central server. However, Distributed IHT is communication expensive since it needs to send dense local models to the central server after each step of stochastic gradient updates. Even though variants of the Distributed IHT, such as [29,30], have been developed, information must be exchanged at each iteration, making communication costly and limiting bandwidth. Other distributed methods have also been proposed. For instance, Ref. [31] tries to solve a relaxed -norm regularized problem and thus introduces extra bias to Problem (2); Ref. [32] experimentally studies gradient compression with practical gradient clipping techniques (i.e., the local nodes have to select threshold) in distributed training; Ref. [33] proposed a modified distributed top-k sparsification by choosing the largest absolute gradients before updating the model to reduce communication. The distributed algorithms proposed in [32,33] use some techniques to reduce communication and bandwidth but are not designed for constrained optimization such as sparse model optimization.
Federated learning. FL is a privacy-preserving learning framework for large-scale machine learning on edge computing devices and solves the data-decentralized optimization problem: (without the sparsity constraint in Problem (2).) The FedAvg algorithm proposed in [25] can significantly reduce the communication cost by running multiple local SGD steps before each communication round and has become the de facto federated learning technique. Later, the client drift problem was observed for FedAvg [34,35,36], and the FedProx algorithm came to exist [37] in which the individual clients attempt to add a proximal operator to the local subproblem to address the issue of FedAvg. Researchers also study FL in the quantization strategy and the IoT (Internet of Things) systems, and the local updates are sparsified and compressed using signSGD [38,39,40]. Ref. [41] presents an online gradient sparsification method, which ensures that different clients provide a similar amount of updates and automatically determines the near-optimal communication and computation trade-off that is controlled by the degree of gradient sparsity. Yuan et al. recently studied a federated -regularized logistic regression problem and proposed federated mirror descent algorithm [42] to solve (convex) nonsmooth composite optimization. However, federated optimization of -norm regularized sparse learning (as described in Problem (2)) is still under explored.
Organization of the paper is as follows: Section 2 provides the preliminaries formally, which include the notations used in this study as well as several generally held assumptions and lemmas. In Section 3 and Section 4, the Fed-HT and FedIter-HT algorithms are proposed and studied, respectively. In Section 4, we normally perform a statistical analysis for M-estimators in order to emphasize the advantageous property of the FedIter-HT. Experiments simulating numerical performance are presented in Section 5.1, and benchmark datasets are analyzed in Section 5.2. Section 6 summarizes our outcomes. Appendix A contains the proof of our theoretical results and additional experiment details.
2. Preliminaries
We formalize our problem as Problem (2) and provide the notations (Table 1), assumptions and prepared lemmas used in this paper. We denote vectors by lowercase letters, e.g., x. The model parameters form a vector . The -norm, -norm and the -norm of a vector are denoted by , and , respectively. Let represent the asymptotic upper bound, be the integer set . The support is associated with the -th iteration in the t-th round on device i. For simplicity, we use , throughout the paper without ambiguity, and .

Table 1.
Brief summary of notations in this paper.
We use the same conditions employed in the theoretical analysis of other IHT methods by assuming that the objective function satisfies the following conditions:
Assumption 1.
We assume that the loss function on each device i
- 1.
- is restricted -strongly convex (RSC [43]) at the sparsity level s for a given , i.e., there exists a constant such that with , , we have
- 2.
- is restricted -strongly smooth (RSS [43]) at the sparsity level s for a given , i.e., there exists a constant such that with , , we have
- 3.
- has -bounded stochastic gradient variance, i.e.,
Remark 1.
When , the above assumption is no longer restricted to the support at a sparsity level, and is actually -strongly convex and -strongly smooth.
Following the same convention in FL [35,37], we also assume the dissimilarity between the gradients of the local functions and the global function f is bounded as follows.
Assumption 2.
The functions () are -locally dissimilar, i.e., there exists a constant , such that
for any .
From the assumptions mentioned in the main text, we have the following lemmas to prepare for our theorems.
Lemma 1
([44]). For and for any parameter , we have
where and .
Lemma 2.
A differentiable convex function is restricted -strongly smooth with parameter s, i.e., there exists a generic constant such that for any , with and
then we have:
The above two inequalities also hold for the global smoothness parameter .
The proof of Lemma 2 can be found in Appendix A.3.
3. The Fed-HT Algorithm
In this section, we first describe our new federated -norm regularized sparse learning framework via hard thresholding—Fed-HT, and then discuss the convergence rate of our proposed algorithm.
A high level summary of Fed-HT is described in Algorithm 1. The Fed-HT algorithm generates a sequence of —sparse vectors , , ⋯, from an initial sparse approximation . At the -th round, clients receive the global parameter update from the central server, then run K steps of minibatch SGD based on local private data. In each step, the i-th client updates for , i.e., . Clients send for back to the central server; then, the server averages them to obtain a dense global parameter vector and applies the HT operator to obtain a sparse iterate . Unlike the commonly used FedAvg, the Fed-HT is designed to solve the family of federated -norm regularized sparse learning problems. It has a strong ability to recover the optimal sparse estimator in decentralized non-IID and unbalanced data settings while at the same time reducing the communication cost by a large margin because the central server broadcasts a sparse iterate for each of the T rounds.
| Algorithm 1. Federated Hard Thresholding (Fed-HT) |
|
The following theorem characterizes our theoretical analysis of Fed-HT in terms of its parameter estimation accuracy for sparsity-constrained problems. Although this paper is focused on the cardinality constraint, the theoretical result is applicable to other sparsity constraints, such as a constraint based on matrix rank. Then, we have the main theorem and the detailed proof.
Theorem 1.
Let be the optimal solution to Problem (2), , and suppose satisfies Assumptions 1 and 2. The condition number . Let stepsize and the batch size , , , , the sparsity level . Then the following inequality holds for the Fed-HT:
where , , , .
The proof can be found in Appendix A.4.
Note that if the sparse solution is sufficiently close to an unconstrained minimizer of , then is small, so the first exponential term on the right-hand side can be a dominating term, which approaches 0 when T goes to infinity. We further obtain the following corollary that bounds the number of rounds T to obtain a sub-optimal solution, i.e., the difference between the solution and is bounded only by the second term.
Corollary 1.
If all the conditions in Theorem 1 hold, for a given precision , we need at most rounds to obtain
where , , and .
Remark 2.
Corollary 1 indicates that under proper conditions and with sufficient rounds, the estimation error of the Fed-HT is determined by the second term—the statistical bias term—which we denote as . The term can become small if is sufficiently close to an unconstrained minimizer of , so it represents the sparsity-induced bias to the solution of the unconstrained optimization problem. The upper bound result guarantees that the Fed-HT can closely approach arbitrarily under a sparsity-induced bias, and the speed of approaching the biased solution is linear (or geometric) and determined by . In Theorem 1 and Corollary 1, is closely related to the number of local updates K. The condition number , so . When K is larger, is smaller, so is the number of rounds T required for reaching a target ϵ. In other words, the Fed-HT converges faster with fewer communication rounds. However, the bias term will increase when K increases. Therefore, K should be chosen to balance the convergence rate and statistical bias.
We further investigate how the objective function approaches the optimal .
Corollary 2.
If all the conditions in Theorem 1 hold, let , and , we have
The proof details can be found in Appendix A.5.
Because the local updates on each device are based on SGD with dense parameters, without the HT operator, -smoothness and -strongly convexity are required, which depend on dimension d and are stronger requirements for f. Furthermore, , i.e., and are , which are suboptimal compared with the results for traditional IHT methods in terms of dimension d. In order to solve such drawbacks, we develop a new algorithm in the next section.
4. The FedIter-HT Algorithm
If we apply the HT operator to each local update as well, we obtain the FedIter-HT algorithm, as described in Algorithm 2. Hence, the local update on each device performs multiple SGD-HT steps, which further reduces the communication cost because model parameters sent back from clients to the central server are also sparse. If a client has a communication bandwidth so small that it can not effectively pass the full set of parameters, the FedIter-HT provides a good solution and also can relax the strict requirements for the objective function f and reduce the statistical bias. In this section, we first present a more communication-efficient federated -norm regularized sparse learning framework—FedIter-HT; then, we theoretically show it enjoys a better convergence rate compared with Fed-HT, and we further provide statistical analysis for M-estimators under the framework of FedIter-HT.
We again examine the convergence of the FedIter-HT by developing an upper bound on the distance between the estimator and the optimal , i.e., in the following theorem.
| Algorithm 2. Federated Iterative Hard Thresholding (FedIter-HT) |
|
Theorem 2.
Let be the optimal solution to (2), , and suppose satisfies Assumptions 1 and 2. The condition number . Let stepsize and the batch size , , , , the sparsity level . Then, the following inequality holds for the FedIter-HT:
where , , , , , and .
The proof details can be found in Appendix A.6.
Remark 3.
The factor , compared with in Theorem 1, is smaller if , which means that the FedIter-HT converges faster than the Fed-HT when the beforehand-guessed sparsity τ is much larger than the true sparsity. Both and will decrease when the number of internal iterations K increases, but decreases faster than because is smaller than . Thus, the FedIter-HT is more likely to benefit by increasing K than the Fed-HT. The statistical bias term can be much smaller than in Theorem 1 because only depends on the norm of restricted to the support of size . Because the norm of the gradient is a dominating term in and , slightly increasing K does not significantly vary the statistical bias terms (when ).
Using the results in Theorem 2, we can further derive Corollary 3 to specify the number of rounds required to achieve a given estimation precision.
Corollary 3.
If all the conditions in Theorem 2 hold, for a given , the FedIter-HT requires the most rounds to obtain
where .
Because , and we also know and in high dimensional statistical problems, the result in Corollary 3 gives a tighter bound than the one obtained in Corollary 1. Similarly, we also obtain a tighter upper bound for the convergence performance of the objective function .
Corollary 4.
If all the conditions in Theorem 2 hold, let , and , we have
The proof details can be found in Appendix A.7.
The theorem and corollaries developed in this section only depend on the -restricted smoothness and -restricted strong convexity, where , which are the same conditions used in the analysis of existing IHT methods. Moreover, , which means and are , where is the size of support . Therefore, our results match the current best-known upper bound for the statistic bias term compared with the results for traditional IHT methods.
Statistical Analysis for M-Estimators
Due to the good property of the FedIter-HT, we also study its constrained M-estimators derived from more concrete learning formulations. Although we focus on the sparse linear regression and sparse logistic regression in this paper, our method can be used to analyze other statistical learning problems as well.
Sparse Linear Regression can be formulated as follows:
where is a design matrix associated with client i. For each row of matrix , we further assume that they are independently drawn from a sub-Gaussian distribution with parameter , denotes the response vector, and is a noise vector following Normal distribution , with is the underlying sparse regression coefficient vector.
Corollary 5.
If all the conditions in Theorem 2 hold, with and a sufficiently large number of communication rounds T, we have
with a probability of at least , where is a universal constant.
Proof.
Let be the overall design matrix of the linear regression problem, and each row of Z can be treated as drawn IID from a sub-Gaussian distribution with parameter . is the random Gaussian noise. Then Lemma C.1 in [45] immediately implies that is restricted -strongly convex and restricted -strongly smooth with and , respectively, with a probability of at least if the total sample size , where and are universal constants. Furthermore, we know that , with a probability of at least , where are universal constants. Gathering everything together yields the following bound with a high probability. □
Sparse Logistic Regression can be formulated as follows:
where for is a predictive vector and drawn from a sub-Gaussian distribution associated with client i, each observation on client i is drawn from the Bernoulli distribution , and with is the underlying true parameter that we want to recover.
Corollary 6.
If all the conditions in Theorem 2 hold, , for and and and with a sufficiently large number of communication rounds T, we have
with a probability of at least , where , and are constants.
Proof.
If we further assume and for and , the sparse logistic regression objective function is restricted -strongly convex and restricted -strongly smooth with and , respectively, with a probability of at least if , where , , and are constants. Furthermore, according to Corollary 2 in [46], we have with a probability of at least , where , and are universal constants. Therefore, we can obtain the following corollary. Based on the above result, the estimation error specified in terms of the distances and decreases when the total sample size is large or the dissimilarity level and the dimension d are small. □
5. Experiments
We empirically evaluate our methods in both simulations and on three real-world datasets: E2006-tfidf, RCV1 and MNIST (Table 2, which are downloaded from the LibSVM website (https://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/, accessed on 1 July 2022)), and compare them against a baseline method. The baseline method is a standard Distributed IHT and communicates every local update to the central server, which then aggregates and broadcasts back to clients (see Appendix A.1 for more details). Specifically, experiments for simulation I and on the E2006-tfidf dataset are conducted for sparse linear regression. We solve the sparse logistic regression problem in simulation II and for the RCV1 data set. The last experiment uses MNIST data in a multi-class softmax regression problem. The exact loss functions for the various problems are available in the Appendix A.2.

Table 2.
Statistics of three real-world datasets in the federated setting.
Following the convention in the federated learning literature, we use the number of communication rounds to measure the communication cost. For a comprehensive comparison, we also include the number of iterations. For both synthetic and real-world datasets, algorithm parameters are determined by the following criteria. The number of local iterations K is searched from . We have tested the performance of our proposed algorithms under different K conditions (see Figure 1). The stepsize for each algorithm is set by a grid search from . All the algorithms are initialized with . The sparsity is 500 for the MNIST dataset and 200 for the other two datasets.
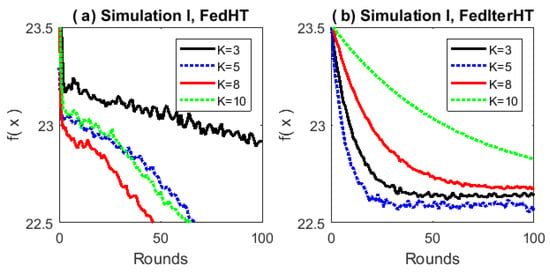
Figure 1.
The comparison of proposed algorithms for different K values in terms of the objective function value vs. communication rounds (a,b).
5.1. Simulations
To generate synthetic data, we follow a similar setup to that in [37]. In simulation I, for each device , we generate samples for according to , where , . The first 100 elements of are drawn from and the remaining elements in are zeros, , , , where is a diagonal matrix with the i-th diagonal element equal to . Each element in the mean vector is drawn from , . Therefore, controls how much the local models differ from each other, and controls how much the local on-device data differ between one another; hence, we have simulated Non-IID federated data. In simulation I, . The data generation procedure for simulation II is the same as the procedure of simulation I, except that ; then, for the i-th client, we set corresponding to the top 100 of for ; otherwise, . In simulation II, we also set .
The results in Figure 2 show that, with a higher degree of Non-IID, both Fed-HT and FedIter-HT tend to converge slower. We also compare the proposed methods with the baseline method—Distributed IHT. In Figure 3, we observe that in simulation I, FedIter-HT only needs 20 (∼ less) communication rounds to reach the same objective value that the Distributed-IHT obtains with more than 100 communication rounds; in simulation II, the FedIter-HT needs 50 communication rounds (∼ less) to achieve the same objective value that the Distributed-IHT obtains with 200 communication rounds.
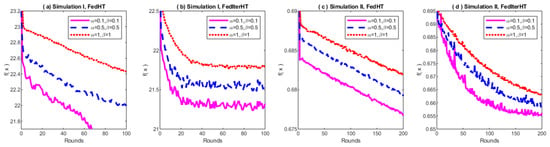
Figure 2.
The objective function value vs. communication rounds for regression (a,b) and classification (c,d), and for Fed-HT (a,c) and FedIter-HT (b,d) with varying degrees of non-IID data.
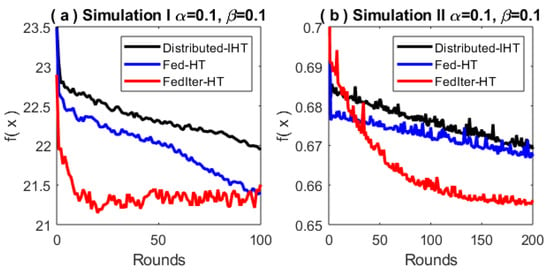
Figure 3.
The comparison of different algorithms in terms of the objective function value vs. communication rounds (a,b) and for regression (a) and classification (b). Note that the Distributed-IHT is the baseline method that communicates every local update (so the number of rounds equals the number of iterations) and may be the best scenario for reducing the objective value.
5.2. Benchmark Datasets
We use the E2006-tfidf dataset [47] to predict the volatility of stock returns based on the SEC-mandated financial text report, represented by tf-idf. It was collected from thousands of publicly traded U.S. companies, for which data from different companies are inherently non-identical and the privacy consideration for financial data demands federated learning. The RCV1 dataset [48] is used to predict categories of newswire stories recently collected by Reuters, Ltd. The RCV1 can be naturally partitioned based on the news category and used for federated learning experiments since readers may only be interested in one or two categories of news. Our model training process mimics the personalized privacy-preserving news recommender system where we use the K-means method to partition the datasets, respectively, into 10 clusters. Each device randomly selects two of the clusters for use in the learning. We run t-SNE to visualize the hidden structures found by K-means as shown in Figure 4 and Figure 5, respectively, for the E2006-tfidf dataset (sparse linear regression) and the RCV1 dataset (sparse logistic regression). For the MNIST images, there are 10 digits that automatically serve as the clusters.
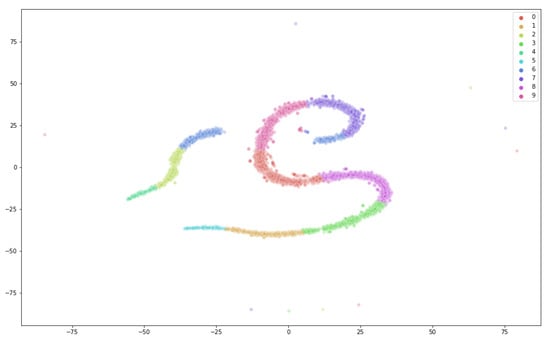
Figure 4.
Visualization of 10 K-means clusters for E2006-dfidf using t-SNE.
Figure 5.
Visualization of 10 K-means clusters for RCV1 using t-SNE.
For all datasets, the data in each cluster are evenly partitioned into 20 parts, and each client randomly picks two clusters and selects one part of data from each of the clusters. Because the MNIST images are evenly collected for each digit, the partitioned decentralized MNIST data are balanced in terms of categories, whereas the other two datasets are unbalanced.
Figure 6 shows that our proposed Fed-HT and FedIter-HT can significantly reduce the communication rounds required to achieve a given accuracy. In Figure 6a,c, we further notice that federated learning displays more randomness when approaching the optimal solution. This may be caused by dissimilarity across clients. For instance, the three different algorithms in Figure 6c reach the neighborhood of different solutions at the end, where the proposed FedIter-HT obtains the lowest objective value. These behaviors may be worth exploring further in the future.
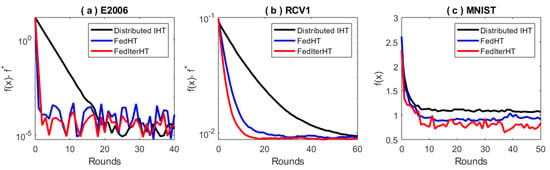
Figure 6.
Comparison of the algorithms on different datasets in terms of the objective function value vs. communication rounds. is a lower bound of . FedIter-HT performs consistently better across all datasets, which confirms our theoretical result.
6. Conclusions
In this paper, we propose two communication-efficient federated IHT methods—Fed-HT and FedIter-HT—to deal with -norm regularized sparse learning with decentralized non-IID data. The Fed-HT algorithm is designed to impose a hard thresholding operator at a central server, whereas the FedIter-HT applies this operator at each update regardless of local clients or a central server. Both methods reduce communication costs—in both the communication rounds and the communication load at each round. Theoretical analyses show a linear convergence rate for both algorithms where the Fed-HT has a better convergence rate , but the FedIter-HT has a better statistical estimation bias. Similar to the conventional IHT methods with IID data, there is still a guarantee to recover the best sparse estimator even with decentralized non-IID data. They outperform the traditional Distributed-IHT in simulations and on benchmark datasets, according to empirical findings.
Author Contributions
Conceptualization, Q.T. and G.L.; methodology, Q.T. and J.B.; software, G.L.; validation, G.L., J.D. and T.Z.; formal analysis, Q.T. and G.L.; investigation, Q.T.; resources, Q.T., G.L. and J.B.; writing—original draft preparation, Q.T., G.L. and J.B.; writing—review and editing, J.B. and M.P.; visualization, Q.T., G.L., J.D. and T.Z.; supervision, J.B.; project administration, J.B. All authors have read and agreed to the published version of the manuscript.
Funding
The work of Q.T. and G.L. was partially funded by the U.S. National Science Foundation (NSF) under grants IIS-1718738 to J.B. T.Z. was partially funded by a grant of National Institutes of Health (NIH) 5K02DA043063-03 to J.B. J.B. was also funded by an NIH R01-DA051922-01 grant. The work of J.D. and M.P. was funded in part by the NSF under grants US CNS-1801925 and CNS-2029569 to M.P.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| IHT | iterative hard thresholding |
| SGD | stochastic gradient descent |
| HT | hard thresholding |
| FL | federated learning |
| IID | independent and identically distributed |
Appendix A
Appendix A.1. Distributed IHT Algorithm
Here we describe the distributed implementation of the IHT method in Algorithm A1, and we use it as a baseline to compare with the two federated IHT methods proposed in the present paper.
| Algorithm A1. Distributed-IHT |
|
Appendix A.2. More Experimental Details
In more detail, experiments in simulation I and on the real-life dataset E2006-tfidf were conducted with sparse linear regression,
Experiments in simulation II and on the RCV1 dataset were conducted with sparse logistic regression
The last experiment solves a multi-class softmax regression problem on the MNIST dataset as follows:
Appendix A.3. Proof of Lemma 2
Results of Lemma 2 are used particularly in the proof of the Corollary 2, we provide a brief proof of this lemma.
Proof.
Let , then is restricted -strongly smooth with parameter s too. Because is convex, is also convex, and x is a minimizer of due to . We define
where the equality (A1) is due to ; inequality (A2) is due to restricted -strongly smoothness.
Let and and reorganize, we have
Furthermore, for the global smoothness parameter , we have
□
Appendix A.4. Proof of Theorem 1
Proof.
For the Fed-HT algorithm:
Equation (A3) holds due to Lemma 1, Equation (A4) holds because , Equation (A5) holds due to Jensen’s Inequality, and the sampling procedures across different clients are independent of each other.
We calculate the stochastic gradient, which is essential in a local update, and we split the stochastic gradient into three terms. Note that the last inequality holds due to bounded variance on support assumption and the inequality .
Next, we want to build the connection of and . Let . Consider the inner loop iteration:
Plug in (A6), and we further derive
where the last inequality holds due to strongly restricted convexity and . Then, iteratively, we have
Let and . Then, we have
Since , we derive the relation between and ,
We further set and assume is large enough such that
where is a positive constant and will be set later.
We now use mathematical induction to prove that there exists a such that the following inequality holds.
When , the above inequality is true. Now we assume that for , it holds. Then, for , we have
We now find an appropriate value for . Let , we have , and then further obtain
Furthermore, there exists a large , such that . Then we have . If we require , (and we also set ), we can derive the restriction on sparse parameter . □
Appendix A.5. Proof of Corollary 2
Proof of Corollary 2
In the next stage, we use a previous upper bound for and -restricted strongly smooth conditions to establish epoch-based convergence of .
We first use -restricted strongly smooth conditions and and obtain:
Take the expectation on both sides,
From the upper bound of ,
We can obtain the final convergence result:
where , . □
Appendix A.6. Proof of Theorem 2
Proof.
For the FedIter-HT Algorithm, we also begin with
This time we calculate the stochastic gradient on support, which is different from the analysis of the Fed-HT Algorithm. We also split the stochastic gradient on support into three terms,
where the last inequality holds due to bounded variance on the support assumption and the inequality .
Next, we want to build the connection of and . Let . Consider the inner loop iteration,
Further deriving from the above result yields
and then we can have
Similarly, we have the following result:
where , , and . Furthermore, there exists a large , such that . Therefore, we have . Then, we can derive the restriction on sparse parameter . □
Appendix A.7. Proof of Corollary 4
Proof.
In the next stage, we use the previous upper bound for and -restricted strongly smooth conditions to establish epoch-based convergence of .
We first use -restricted strongly smooth conditions and and obtain:
Take the expectation on both sides,
From the upper bound of ,
Then, we can obtain the final convergence result:
where , . □
References
- Mohamed, S.; Heller, K.; Ghahramani, Z. Bayesian and l1 approaches to sparse unsupervised learning. arXiv 2011, arXiv:1106.1157. [Google Scholar]
- Quattoni, A.; Collins, M.; Darrell, T. Transfer learning for image classification with sparse prototype representations. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Lu, X.; Huang, Z.; Yuan, Y. MR image super-resolution via manifold regularized sparse learning. Neurocomputing 2015, 162, 96–104. [Google Scholar] [CrossRef]
- Chen, K.; Che, H.; Li, X.; Leung, M.F. Graph non-negative matrix factorization with alternative smoothed L0 regularizations. Neural Comput. Appl. 2022, 1–15. [Google Scholar] [CrossRef]
- Ravishankar, S.; Bresler, Y. Learning sparsifying transforms. IEEE Trans. Signal Process. 2012, 61, 1072–1086. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Boufounos, S.; Raj, P.; Bahmani, S.; Boufounos, P.; Raj, B. Greedy Sparsity-Constrained Optimization. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.365.3874&rep=rep1&type=pdf (accessed on 1 July 2022).
- Jalali, A.; Johnson, C.; Ravikumar, P. On learning discrete graphical models using greedy methods. Adv. Neural Inf. Process. Syst. 2011, 24, 1935–1943. [Google Scholar]
- Mallat, S.G.; Zhang, Z. Matching pursuits with time-frequency dictionaries. IEEE Trans. Signal Process. 1993, 41, 3397–3415. [Google Scholar] [CrossRef]
- Pati, Y.C.; Rezaiifar, R.; Krishnaprasad, P.S. Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition. In Proceedings of the 27th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 1–3 November 1993; pp. 40–44. [Google Scholar]
- Needell, D.; Tropp, J.A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples. Appl. Comput. Harmon. Anal. 2009, 26, 301–321. [Google Scholar] [CrossRef]
- Foucart, S. Hard thresholding pursuit: An algorithm for compressive sensing. SIAM J. Numer. Anal. 2011, 49, 2543–2563. [Google Scholar] [CrossRef]
- Blumensath, T.; Davies, M.E. Iterative hard thresholding for compressed sensing. Appl. Comput. Harmon. Anal. 2009, 27, 265–274. [Google Scholar] [CrossRef]
- Jain, P.; Tewari, A.; Kar, P. On iterative hard thresholding methods for high-dimensional m-estimation. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 685–693. [Google Scholar]
- Nguyen, N.; Needell, D.; Woolf, T. Linear convergence of stochastic iterative greedy algorithms with sparse constraints. IEEE Trans. Inf. Theory 2017, 63, 6869–6895. [Google Scholar] [CrossRef]
- Bahmani, S.; Raj, B.; Boufounos, P.T. Greedy sparsity-constrained optimization. J. Mach. Learn. Res. 2013, 14, 807–841. [Google Scholar]
- Zhou, P.; Yuan, X.; Feng, J. Efficient stochastic gradient hard thresholding. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 1988–1997. [Google Scholar]
- Li, X.; Zhao, T.; Arora, R.; Liu, H.; Haupt, J. Stochastic variance reduced optimization for nonconvex sparse learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 917–925. [Google Scholar]
- Shen, J.; Li, P. A tight bound of hard thresholding. J. Mach. Learn. Res. 2017, 18, 7650–7691. [Google Scholar]
- Natarajan, B.K. Sparse approximate solutions to linear systems. SIAM J. Comput. 1995, 24, 227–234. [Google Scholar] [CrossRef] [Green Version]
- Wahlsten, D.; Metten, P.; Phillips, T.J.; Boehm, S.L.; Burkhart-Kasch, S.; Dorow, J.; Doerksen, S.; Downing, C.; Fogarty, J.; Rodd-Henricks, K.; et al. Different data from different labs: Lessons from studies of gene–environment interaction. J. Neurobiol. 2003, 54, 283–311. [Google Scholar]
- Kavvoura, F.K.; Ioannidis, J.P. Methods for meta-analysis in genetic association studies: A review of their potential and pitfalls. Hum. Genet. 2008, 123, 1–14. [Google Scholar]
- Lee, Y.G.; Jeong, W.S.; Yoon, G. Smartphone-based mobile health monitoring. Telemed. E-Health 2012, 18, 585–590. [Google Scholar] [CrossRef]
- Qin, Z.; Fan, J.; Liu, Y.; Gao, Y.; Li, G.Y. Sparse representation for wireless communications: A compressive sensing approach. IEEE Signal Process. Mag. 2018, 35, 40–58. [Google Scholar] [CrossRef]
- McMahan, H.B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B.A. Communication-efficient learning of deep networks from decentralized data. arXiv 2016, arXiv:1602.05629. [Google Scholar]
- Yang, Q.; Liu, Y.; Chen, T.; Tong, Y. Federated machine learning: Concept and applications. ACM Trans. Intell. Syst. Technol. (TIST) 2019, 10, 1–19. [Google Scholar] [CrossRef]
- Kairouz, P.; McMahan, H.B.; Avent, B.; Bellet, A.; Bennis, M.; Bhagoji, A.N.; Bonawitz, K.; Charles, Z.; Cormode, G.; Cummings, R.; et al. Advances and open problems in federated learning. Found. Trends® Mach. Learn. 2021, 14, 1–210. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Patterson, S.; Eldar, Y.C.; Keidar, I. Distributed compressed sensing for static and time-varying networks. IEEE Trans. Signal Process. 2014, 62, 4931–4946. [Google Scholar] [CrossRef]
- Lafond, J.; Wai, H.T.; Moulines, E. D-FW: Communication efficient distributed algorithms for high-dimensional sparse optimization. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 4144–4148. [Google Scholar]
- Wang, J.; Kolar, M.; Srebro, N.; Zhang, T. Efficient distributed learning with sparsity. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 3636–3645. [Google Scholar]
- Lin, Y.; Han, S.; Mao, H.; Wang, Y.; Dally, W.J. Deep gradient compression: Reducing the communication bandwidth for distributed training. arXiv 2017, arXiv:1712.01887. [Google Scholar]
- Shi, S.; Wang, Q.; Zhao, K.; Tang, Z.; Wang, Y.; Huang, X.; Chu, X. A distributed synchronous SGD algorithm with global top-k sparsification for low bandwidth networks. In Proceedings of the 2019 IEEE 39th International Conference on Distributed Computing Systems (ICDCS), Dallas, TX, USA, 7–10 July 2019; pp. 2238–2247. [Google Scholar]
- Hsu, T.M.H.; Qi, H.; Brown, M. Measuring the effects of non-identical data distribution for federated visual classification. arXiv 2019, arXiv:1909.06335. [Google Scholar]
- Karimireddy, S.P.; Kale, S.; Mohri, M.; Reddi, S.J.; Stich, S.U.; Suresh, A.T. SCAFFOLD: Stochastic controlled averaging for on-device federated learning. arXiv 2019, arXiv:1910.06378. [Google Scholar]
- Reddi, S.; Charles, Z.; Zaheer, M.; Garrett, Z.; Rush, K.; Konečnỳ, J.; Kumar, S.; McMahan, H.B. Adaptive Federated Optimization. arXiv 2020, arXiv:2003.00295. [Google Scholar]
- Li, T.; Sahu, A.K.; Zaheer, M.; Sanjabi, M.; Talwalkar, A.; Smith, V. Federated optimization in heterogeneous networks. arXiv 2018, arXiv:1812.06127. [Google Scholar]
- Bernstein, J.; Zhao, J.; Azizzadenesheli, K.; Anandkumar, A. signSGD with majority vote is communication efficient and fault tolerant. arXiv 2018, arXiv:1810.05291. [Google Scholar]
- Sattler, F.; Wiedemann, S.; Müller, K.R.; Samek, W. Robust and communication-efficient federated learning from non-iid data. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 3400–3413. [Google Scholar] [CrossRef]
- Li, C.; Li, G.; Varshney, P.K. Communication-efficient federated learning based on compressed sensing. IEEE Internet Things J. 2021, 8, 15531–15541. [Google Scholar] [CrossRef]
- Han, P.; Wang, S.; Leung, K.K. Adaptive gradient sparsification for efficient federated learning: An online learning approach. In Proceedings of the 2020 IEEE 40th International Conference on Distributed Computing Systems (ICDCS), Singapore, 29 November–1 December 2020; pp. 300–310. [Google Scholar]
- Yuan, H.; Zaheer, M.; Reddi, S. Federated composite optimization. In Proceedings of the International Conference on Machine Learning, Baltimore, MD, USA, 18–24 July2021; pp. 12253–12266. [Google Scholar]
- Agarwal, A.; Negahban, S.; Wainwright, M.J. Fast Global Convergence Rates of Gradient Methods for High-Dimensional Statistical Recovery. Available online: https://proceedings.neurips.cc/paper/2010/file/7cce53cf90577442771720a370c3c723-Paper.pdf (accessed on 1 July 2022).
- Li, X.; Arora, R.; Liu, H.; Haupt, J.; Zhao, T. Nonconvex sparse learning via stochastic optimization with progressive variance reduction. arXiv 2016, arXiv:1605.02711. [Google Scholar]
- Wang, L.; Gu, Q. Differentially Private Iterative Gradient Hard Thresholding for Sparse Learning. In Proceedings of the 28th International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019. [Google Scholar]
- Loh, P.L.; Wainwright, M.J. Regularized M-estimators with nonconvexity: Statistical and algorithmic theory for local optima. J. Mach. Learn. Res. 2015, 16, 559–616. [Google Scholar]
- Kogan, S.; Levin, D.; Routledge, B.R.; Sagi, J.S.; Smith, N.A. Predicting risk from financial reports with regression. In Proceedings of the Human Language Technologies: The 2009 Annual Conference of the North American Chapter of the Association for Computational Linguistics, Boulder, CO, USA, 31 May–5 June 2009; Association for Computational Linguistics: Boulder, CO, USA, 2009; pp. 272–280. [Google Scholar]
- Lewis, D.D.; Yang, Y.; Rose, T.G.; Li, F. Rcv1: A new benchmark collection for text categorization research. J. Mach. Learn. Res. 2004, 5, 361–397. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).