Personalized Federated Multi-Task Learning over Wireless Fading Channels
Abstract
1. Introduction
- We propose the FedGradNorm algorithm. The proposed algorithm takes advantage of the GradNorm [19] dynamic weighting strategy in a PFL setup for achieving a more effective and fair learning performance when the clients have a diverse set of tasks to perform.
- We propose HOTA-FedGradNorm. The proposed algorithm takes into account the characteristics of the communication channel by defining a hierarchical structure for the PFL setting.
- We provide the convergence analysis for adaptive weighting strategy for MTL in PFL setting. Existing works either do not provide convergence analysis or do it in special cases. We demonstrate that FedGradNorm has an exponential convergence rate.
- We conduct several experiments on our framework using Multi-Task Facial Landmark (MTFL) dataset [28], and RadComDynamic dataset on the wireless communication domain [29]. We investigate the changes in task loss during training to compare the learning speed and fairness of FedGradNorm with a similar PFL setting which uses equal weighting technique, namely FedRep. Experimental results exhibit a better and faster learning performance for FedGradNorm than FedRep. In addition, we demonstrate that HOTA-FedGradNorm results in faster training over the wireless fading channel compared to algorithms with naive static equal weighting strategies since dynamic weight selection process takes the channel conditions into account.
2. System Model and Problem Formulation
2.1. Federated Learning (FL)
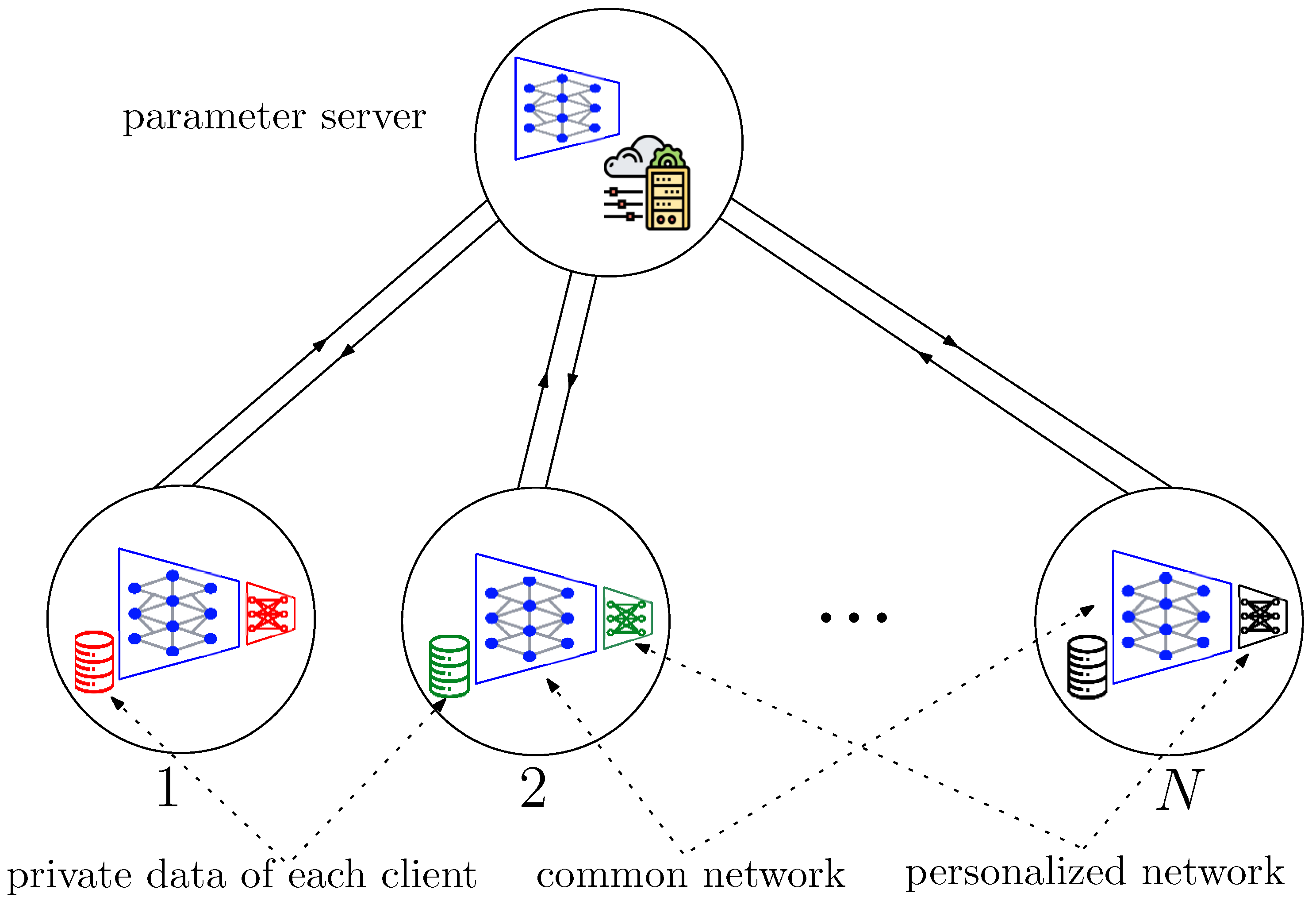
2.2. Personalized Federated Multi-Task Learning (PF-MTL)
2.3. PF-MTL as Bilevel Optimization Problem
| Algorithm 1 Iterative differentiation (ITD) algorithm. |
Input: K, D, step sizes , , initialization , . fork = 0, 1, 2, …, K do Set = if otherwise . for t = 1, …, D do Update Compute Update |
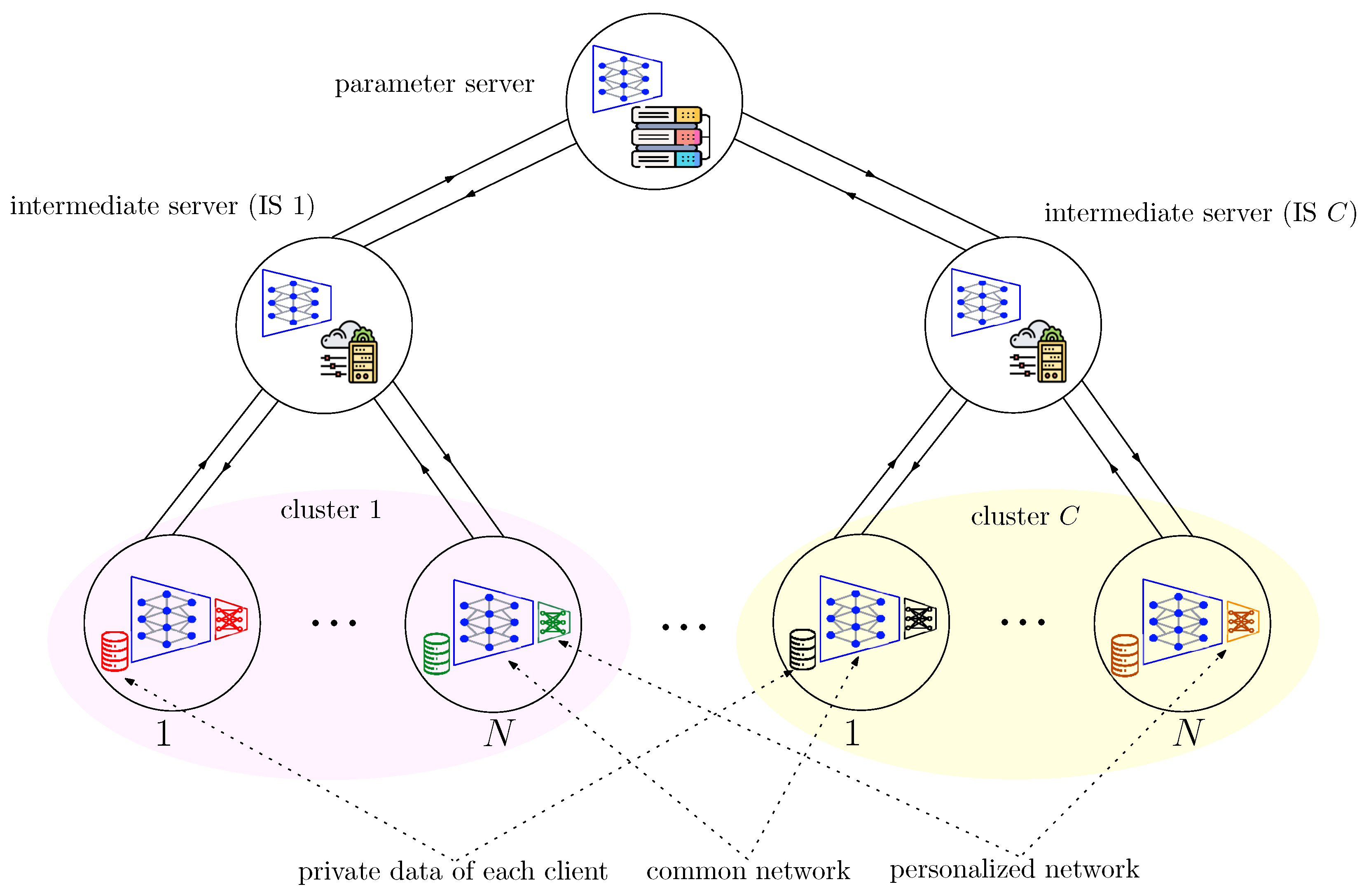
2.4. Hierarchical Federated Learning (HFL) for Wireless Fading Channels
3. Algorithm Description
3.1. Definitions and Preliminaries
- : A subset of the global shared network parameters . FedGradNorm is applied on ⊂, which is a subset of the global shared network parameters at client i at iteration k. is generally chosen as the last layer of the global shared network at client i at iteration k.
- : The norm of the gradient of the weighted task loss at client i at iteration k with respect to the chosen weights .
- = : The average gradient norm across all clients (tasks) at iteration k.
- = : Inverse training rate of task i (at client i) at iteration k, where is the loss for client i at iteration k, and is the initial loss for client i.
- =: Relative inverse training rate of task i at iteration k.
- is the average of gradient updates at client i at iteration k, where is the jth local update of the global shared representation at client i at iteration k. Note that is a subset of since .
- is the client-specific head parameters after the jth local update on the client-specific network of client i at iteration k, .
- is the global shared network parameters of client i after the jth local update at iteration k, . Additionally, denotes for brevity.
3.2. FedGradNorm Description
| Algorithm 2 Training with FedGradNorm |
Initialize , , fork=1 toKdo The parameter server sends the current global shared network parameters to the clients. for Each client do Initialize global shared network parameters for local updates by for do = for do += Client i sends , and to the parameter server After collecting , and for active clients , the parameter server performs the following operations in the order: • Constructs using and as given in Equation (12). • Updates , . • Aggregates the gradient for the global shared network by . • Updates the global shared network parameters with the aggregated gradient by . • Broadcasts to clients for the next global iteration. |
3.3. Hierarchical Over-the-Air (HOTA) FedGradNorm
| Algorithm 3 HOTA-FedGradNorm |
|
| Algorithm 4 FGN_Server |
|
4. Convergence Analysis
- is μ-strongly convex with respect to
- is μ-strongly convex with respect to , where , and .
5. Experiments
5.1. Dataset Specifications
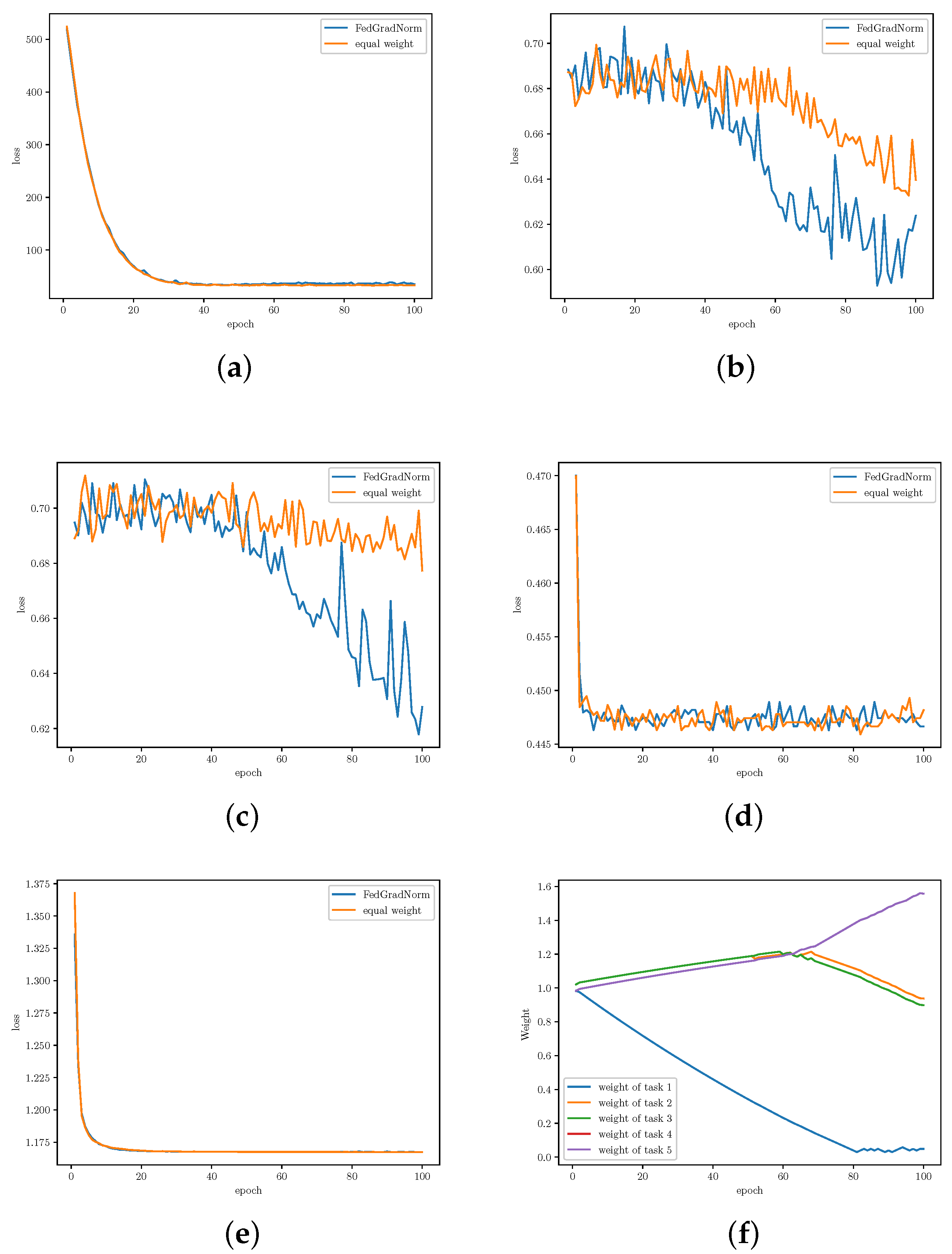
- Multi-Task Facial Landmark (MTFL) [28]: This dataset contains 10,000 training and 3000 test images, which are human face images annotated by (1) five facial landmarks, (2) gender, (3) smiling, (4) wearing glasses, and (5) head pose. The first task (five facial landmarks) is a regression task, and other tasks are classification tasks.
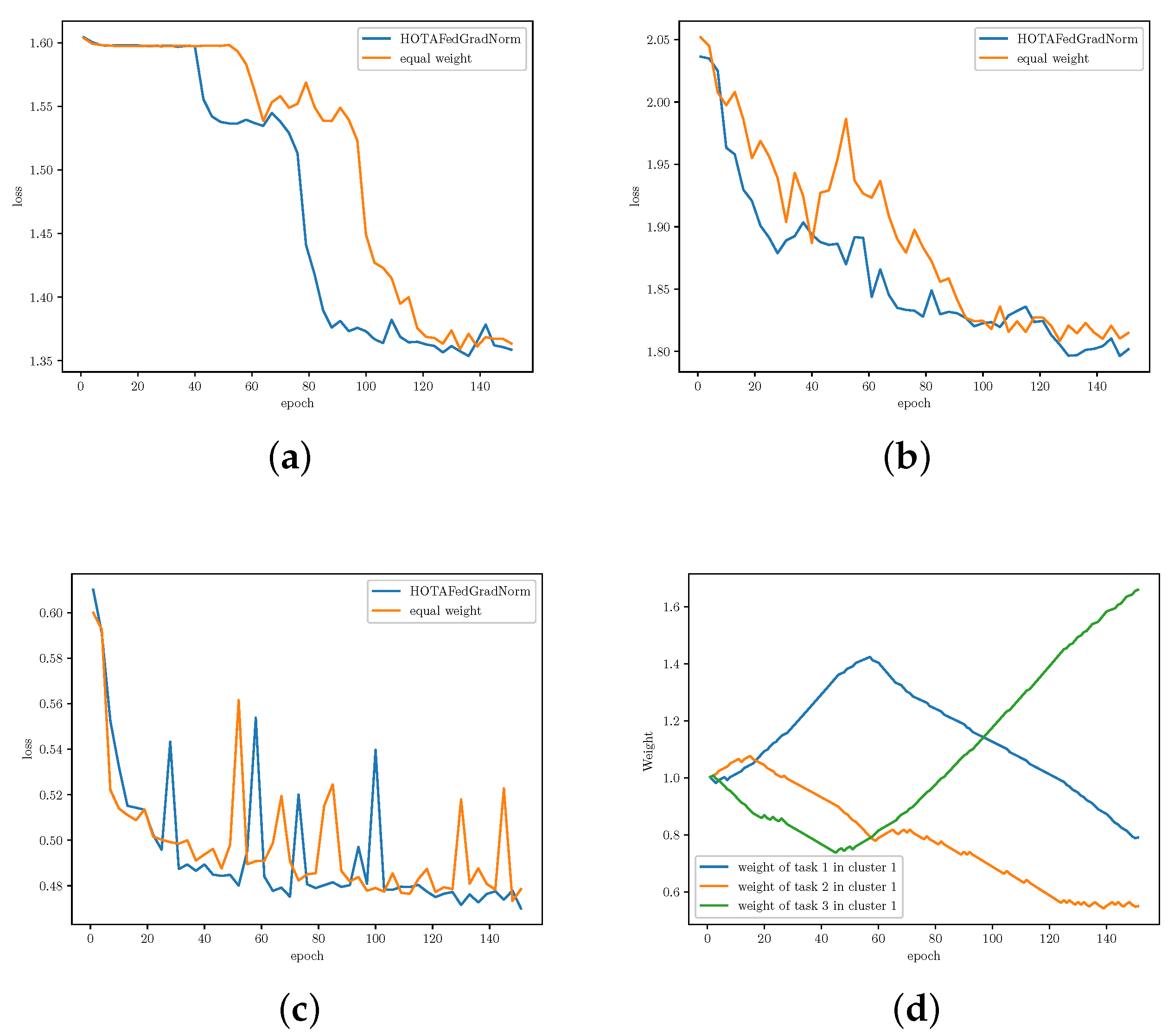
- RadComDynamic [29]: This dataset is a multi-class wireless signal dataset which contains 125,000 samples. Samples are radar and communication signals from GNU Radio Companion derived for different SNR values. The dataset contains six modulation types and eight signal types. Dynamic parameters for samples are listed in Table 1. We perform 3 different tasks over RadComDynamic dataset, (1) modulation classification, (2) signal type classification, and (3) anomaly detection.
- –
- Task 1. Modulation classification: The modulation classes are amdsb, amssb, ask, bpsk, fmcw, and pulsed continous wave (PCW).
- –
- Task 2. Signal type classification: The signal classes are AM radio, short-range, Radar-Altimeter, Air-Ground-MTI, Airborne-detection, Airborne-range, Ground-mapping.
- –
- Task 3. Anomaly behavior: Signal to noise ratio (SNR) can be considered as a proxy for geo-location information. We define anomaly behavior as having SNR lower than −4 dB.
5.2. Hyperparameters and Model Specifications
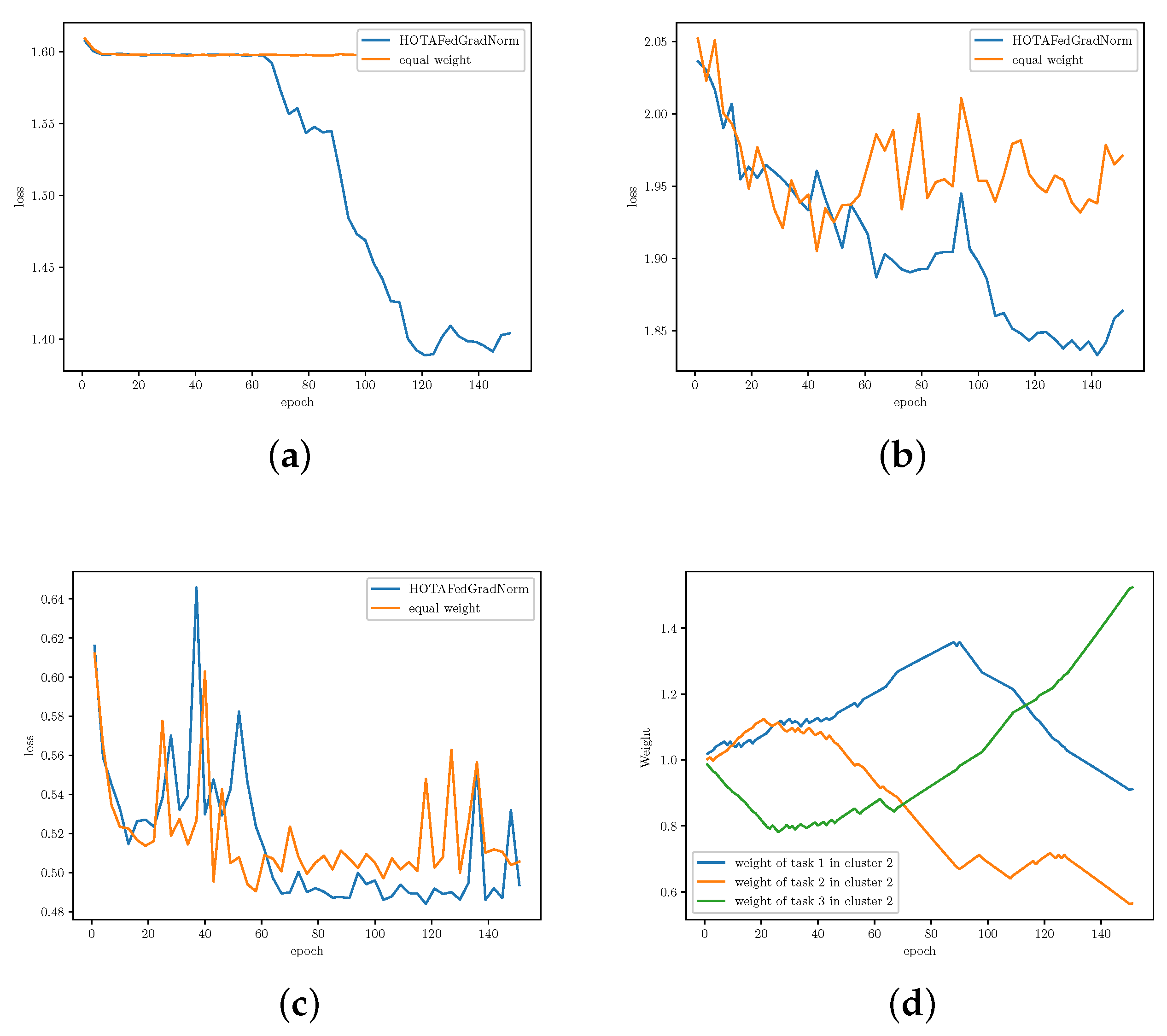
5.3. Results and Analysis
6. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Caruana, R. Multitask learning. Mach. Learn. 1997, 28, 41–75. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Q. A survey on multi-task learning. arXiv 2017, arXiv:1707.08114. [Google Scholar] [CrossRef]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; Aguera y Arcas, B. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the AISTATS, Fort Lauderdale, FL, USA, 20–22 April 2017. [Google Scholar]
- Li, T.; Sahu, A.K.; Zaheer, M.; Sanjabi, M.; Talwalkar, A.; Smith, V. Federated optimization in heterogeneous networks. In Proceedings of the MLSys, Austin, TX, USA, 2–4 March 2020. [Google Scholar]
- Karimireddy, S.P.; Kale, S.; Mohri, M.; Reddi, S.; Stich, S.; Suresh, A.T. SCAFFOLD: Stochastic controlled averaging for federated learning. In Proceedings of the ICML, Virtual, 13–18 July 2020. [Google Scholar]
- Fifty, C.; Amid, E.; Zhao, Z.; Yu, T.; Anil, R.; Finn, C. Measuring and harnessing transference in multi-task learning. arXiv 2020, arXiv:2010.15413. [Google Scholar]
- Collins, L.; Hassani, H.; Mokhtari, A.; Shakkottai, S. Exploiting shared representations for personalized federated learning. In Proceedings of the ICML, Virtual, 18–24 July 2021. [Google Scholar]
- Arivazhagan, M.G.; Aggarwal, V.; Singh, A.K.; Choudhary, S. Federated learning with personalization layers. arXiv 2019, arXiv:1912.00818. [Google Scholar]
- Deng, Y.; Kamani, M.; Mahdavi, M. Adaptive personalized federated learning. arXiv 2020, arXiv:2003.13461. [Google Scholar]
- Fallah, A.; Mokhtari, A.; Ozdaglar, A. Personalized federated learning with theoretical guarantees: A model-agnostic meta-learning approach. In Proceedings of the NeurIPS, Virtual, 6–12 December 2020. [Google Scholar]
- Lan, G.; Zhou, Y. An optimal randomized incremental gradient method. Math. Program. 2018, 171, 167–215. [Google Scholar] [CrossRef]
- Smith, V.; Chiang, C.K.; Sanjabi, M.; Talwalkar, A.S. Federated multi-task learning. In Proceedings of the NeurIPS, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Hanzely, F.; Richtárik, P. Federated learning of a mixture of global and local models. arXiv 2020, arXiv:2002.05516. [Google Scholar]
- Liang, P.P.; Liu, T.; Ziyin, L.; Allen, N.B.; Auerbach, R.P.; Brent, D.; Salakhutdinov, R.; Morency, L.P. Think locally, act globally: Federated learning with local and global representations. arXiv 2020, arXiv:2001.01523. [Google Scholar]
- Agarwal, A.; Langford, J.; Wei, C.Y. Federated residual learning. arXiv 2020, arXiv:2003.12880. [Google Scholar]
- Hanzely, F.; Zhao, B.; Kolar, M. Personalized federated learning: A unified framework and universal optimization techniques. arXiv 2021, arXiv:2102.09743. [Google Scholar]
- Kendall, A.; Gal, Y.; Cipolla, R. Multi-task learning using uncertainty to weigh losses for scene geometry and semantics. In Proceedings of the CVPR, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Qian, W.; Chen, B.; Zhang, Y.; Wen, G.; Gechter, F. Multi-task variational information bottleneck. arXiv 2020, arXiv:2007.00339. [Google Scholar]
- Chen, Z.; Badrinarayanan, V.; Lee, C.; Rabinovich, A. GradNorm: Gradient normalization for adaptive loss balancing in deep multitask networks. In Proceedings of the ICML, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Mortaheb, M.; Vahapoglu, C.; Ulukus, S. FedGradNorm: Personalized federated gradient-normalized multi-task learning. In Proceedings of the IEEE SPAWC, Oulu, Finland, 4–6 July 2022. [Google Scholar]
- Amiri, M.M.; Gündüz, D. Machine learning at the wireless edge: Distributed stochastic gradient descent over-the-air. In Proceedings of the IEEE ISIT, Paris, France, 7–12 July 2019. [Google Scholar]
- Amiri, M.M.; Gündüz, D. Over-the-air machine learning at the wireless edge. In Proceedings of the IEEE SPAWC, Cannes, France, 2–5 July 2019. [Google Scholar]
- Vahapoglu, C.; Mortaheb, M.; Ulukus, S. Hierarchical over-the-air FedGradNorm. In Proceedings of the IEEE Asilomar, Pacific Grove, CA, USA, 1–4 November 2022. [Google Scholar]
- Abad, M.S.H.; Ozfatura, E.; Gündüz, D.; Erçetin, Ö. Hierarchical federated learning across heterogeneous cellular networks. In Proceedings of the IEEE ICASSP, Virtual, 4–8 May 2020. [Google Scholar]
- Liu, L.; Zhang, J.; Song, S.H.; Letaief, K.B. Client-edge-cloud hierarchical federated learning. In Proceedings of the IEEE ICC, Virtual, 7–11 June 2020. [Google Scholar]
- Luo, S.; Chen, X.; Wu, Q.; Zhou, Z.; Yu, S. HFEL: Joint edge association and resource allocation for cost-efficient hierarchical federated edge learning. IEEE Trans. Wirel. Commun. 2020, 19, 6535–6548. [Google Scholar] [CrossRef]
- Wang, J.; Wang, S.; Chen, R.R.; Ji, M. Demystifying why local aggregation helps: Convergence analysis of hierarchical SGD. arXiv 2020, arXiv:2010.12998. [Google Scholar] [CrossRef]
- Zhang, Z.; Luo, P.; Loy, C.; Tang, X. Facial landmark detection by deep multi-task learning. In Proceedings of the ECCV, Zurich, Switzerland, 6–12 September 2014. [Google Scholar]
- Jagannath, A.; Jagannath, J. Multi-task learning approach for automatic modulation and wireless signal classification. In Proceedings of the IEEE ICC, Virtual, 7–11 December 2021. [Google Scholar]
- Bonawitz, K.; Eichner, H.; Grieskamp, W.; Huba, D.; Ingerman, A.; Ivanov, V.; Kiddon, C.; Konecný, J.; Mazzocchi, S.; McMahan, H.; et al. Towards federated learning at scale: System design. In Proceedings of the MLSys, Stanford, CA, USA, 31 March–2 April 2019. [Google Scholar]
- Sinha, A.; Malo, P.; Deb, K. A review on bilevel optimization: From classical to evolutionary approaches and applications. IEEE Trans. Evol. Comput. 2017, 22, 276–295. [Google Scholar] [CrossRef]
- Hansen, P.; Jaumard, B.; Savard, G. New branch-and-bound rules for linear bilevel programming. SIAM J. Sci. Comput. 1992, 13, 1194–1217. [Google Scholar] [CrossRef]
- Shi, C.; Lu, J.; Zhang, G. An extended kuhn-tucker approach for linear bilevel programming. Appl. Math. Comput. 2005, 162, 51–63. [Google Scholar] [CrossRef]
- Bennett, K.P.; Moore, G.M. Bilevel programming algorithms for machine learning model selection. In Proceedings of the Rensselaer Polytechnic Institute, 9 March 2010. [Google Scholar]
- Domke, J. Generic methods for optimization-based modeling. In Proceedings of the AISTATS, La Palma, Canary Islands, 21–23 April 2012. [Google Scholar]
- Ghadimi, S.; Wang, M. Approximation methods for bilevel programming. arXiv 2018, arXiv:1802.02246. [Google Scholar]
- Grazzi, R.; Franceschi, L.; Pontil, M.; Salzo, S. On the iteration complexity of hypergradient computation. In Proceedings of the ICML, Virtual, 13–18 July 2020. [Google Scholar]
- Shaban, A.; Cheng, C.A.; Hatch, N.; Boots, B. Truncated back-propagation for bilevel optimization. In Proceedings of the AISTATS, Naha, Okinawa, Japan, 16–18 April 2019. [Google Scholar]
- Maclaurin, D.; Duvenaud, D.; Adams, R. Gradient-based hyperparameter optimization through reversible learning. In Proceedings of the ICML, Lille, France, 6–11 July 2015. [Google Scholar]
- Ji, K.; Yang, J.; Liang, Y. Bilevel optimization: Convergence analysis and enhanced design. In Proceedings of the ICML, Virtual, 18–24 July 2021. [Google Scholar]
- Hsieh, K.; Harlap, A.; Vijaykumar, N.; Konomis, D.; Ganger, G.R.; Gibbons, P.B.; Mutlu, O. Gaia: Geo-distributed machine learning approaching LAN speeds. In Proceedings of the NSDI, Boston, MA, USA, 27–29 March 2017; pp. 629–647. [Google Scholar]
- Yang, Z.; Chen, M.; Wong, K.; Poor, H.V.; Cui, S. Federated learning for 6G: Applications, challenges, and opportunities. Engineering 2022, 8, 33–41. [Google Scholar] [CrossRef]


| Dynamic Parameters | Value |
|---|---|
| Carrier frequency offset std. dev/sample | 0.05 Hz |
| Maximum carrier frequency offset | 250 Hz |
| Sample rate offset std. dev/sample | 0.05 Hz |
| Maximum sample rate offset | 60 Hz |
| Num. of sinusoids in freq. selective fading | 5 |
| Maximum doppler frequency | 2 Hz |
| Rician K-factor | 3 |
| Fractional sample delays comprising PDP | [0.2, 0.3, 0.1] |
| Number of multipath taps | 5 |
| List of magnitudes corresponding to each delay in PDP | [1, 0.5, 0.5] |
| Hyperparameter | Value |
|---|---|
| Optimizer | Adam |
| FedGradNorm | |
| 0.9 | |
| Learning rate () | 0.0002 |
| Learning rate () | 0.004 |
| HOTA-FedGradNorm | |
| Number of clusters C | 10 |
| Number of clients in each cluster N | 3 |
| for | 1 |
| 0.6 | |
| Learning rate () | 0.0003 |
| Learning rate () | 0.008 |
| Network 1 | Network 2 |
|---|---|
| Conv2d(1, 16, 5) | FC(256, 512) |
| MaxPool2d(2, 2) | FC(512, 1024) |
| Conv2d(16, 48, 3) | FC(1024, 2048) |
| MaxPool2d(2, 2) | FC(2048, 512) |
| Conv2d(48, 64, 3) | FC(512, 256) |
| MaxPool2d(2, 2) | |
| Conv2d(64, 64, 2) |
| Tasks | Face Landmark | Gender | Smile | Glass | Pose |
|---|---|---|---|---|---|
| FedRep loss | 33.28 | 0.66 | 0.60 | 0.44 | 1.1 |
| FedGradNorm loss | 33.25 | 0.56 | 0.57 | 0.43 | 1.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mortaheb, M.; Vahapoglu, C.; Ulukus, S. Personalized Federated Multi-Task Learning over Wireless Fading Channels. Algorithms 2022, 15, 421. https://doi.org/10.3390/a15110421
Mortaheb M, Vahapoglu C, Ulukus S. Personalized Federated Multi-Task Learning over Wireless Fading Channels. Algorithms. 2022; 15(11):421. https://doi.org/10.3390/a15110421
Chicago/Turabian StyleMortaheb, Matin, Cemil Vahapoglu, and Sennur Ulukus. 2022. "Personalized Federated Multi-Task Learning over Wireless Fading Channels" Algorithms 15, no. 11: 421. https://doi.org/10.3390/a15110421
APA StyleMortaheb, M., Vahapoglu, C., & Ulukus, S. (2022). Personalized Federated Multi-Task Learning over Wireless Fading Channels. Algorithms, 15(11), 421. https://doi.org/10.3390/a15110421





