k-Pareto Optimality-Based Sorting with Maximization of Choice and Its Application to Genetic Optimization
Abstract
1. Introduction
- Based on the proposed ranking metric Pareto-optimality, we study three genetic algorithms in detail: PO-count, PO-prob, and PO-prob*; see Section 4 for the detailed description. All three algorithms are based on NSGA-II and differ from the latter in the selection procedure by:
- PO-count: counting PO, which consists of counting the number of dominating solutions (counting PO);
- PO-prob: approximating PO via a probabilistic procedure (probabilistic PO);
- PO-prob*: sequentially combining probabilistic calculation of PO and Pareto dominance sorting from NSGA-II.
- We compare the proposed methods with NSGA-II and NSGA-III using the knapsack problem with the number of objectives varying from 2 to 25. Our experimental results with random and tournament selection show the following:
- Ranking by counting PO provides almost identical results as ranking by Pareto dominance;
- Using probabilistic PO ranking allows us to increase the hypervolume of the resulting solutions for many-objective and most multi-objective optimization problems;
- With the increase in the number of the objectives, probabilistic PO yields a set of solutions that are almost never dominated by the solutions of other algorithms;
- In general, PO-prob and NSGA-III algorithms yield fewer extreme solutions when the number of objectives increases;
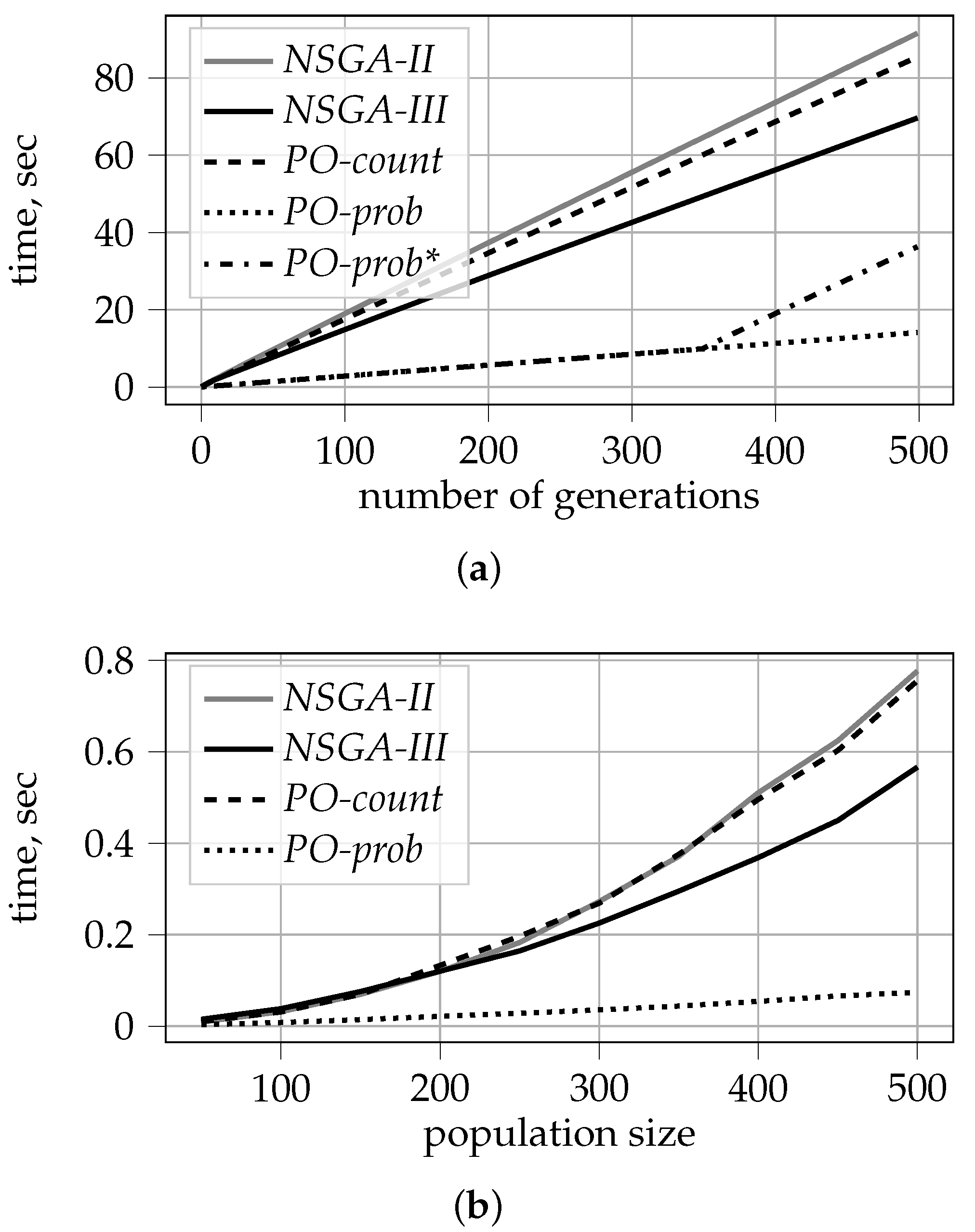
- We demonstrate that probabilistic PO ranking is computationally much more efficient. It allows for reducing the time complexity of the sorting procedure from to , where N is the population size and M is the number of objectives.
- Our algorithms are implemented as an extension of the Python library for evolutionary computation DEAP (https://deap.readthedocs.io/en/master/, accessed on 28 January 2022). They are available as open source (https://github.com/marharyta-aleksandrova/kPO, accessed on 28 January 2022).
- We also discuss how Pareto optimality can contribute to the problem of interpretability, see Section 6.
2. Related Work
2.1. Searchability Deterioration of Pareto Dominance-Based Sorting
2.2. Computational Complexity
3. -Pareto Optimality-Based Sorting for Genetic Optimization
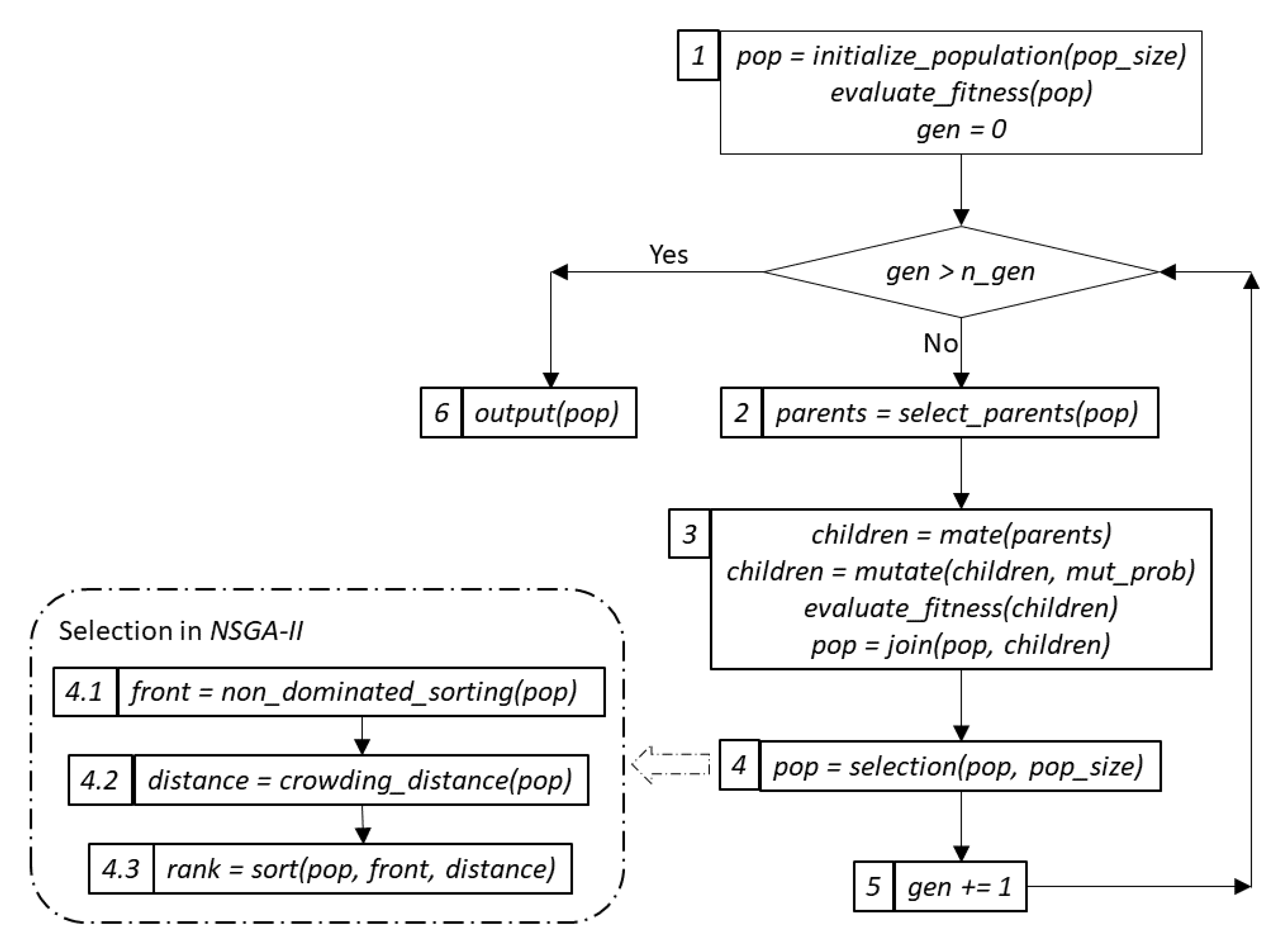
3.1. Genetic Optimization Overview
- First, we create an initial population of solutions (or individuals) of a predefined size, , and evaluate the fitness of every individual with respect to a predefined fitness function, step 1. In the case of multi- or many-objective optimization, this is a function with multi-dimensional output.
- Second, we select a subset of individuals for “procreation” based on a chosen parent selection criterion, step 2. Two popular criteria are random and tournament selection. In random selection, the parents are chosen randomly; in tournament selection, the choice is made based on fitness among a set of randomly selected individuals of a predefined size.
- Next, on the step 3, the chosen parents are “mated” to create a required number of children or offspring. This operation is also known as crossover. Often, the number of children is equal to the size of the original population. The generated offspring can also be mutated. The latter process is controlled by the value of the mutation probability, . After evaluating the fitness values for the newly created offspring, the two sets of solutions are joined.
- Finally, on the selection step, step 4, the combined population is sorted according to a specific criterion, and the best individuals are advanced to the next generation. The evolution continues until a certain criterion is fulfilled. Often, the process is controlled by the maximum number of generations, .
3.2. Formal Definition of k-Pareto Optimality
3.3. Illustrative Example
4. Experimental Setup
5. Experimental Results
5.1. Characteristics of the Proposed Approach
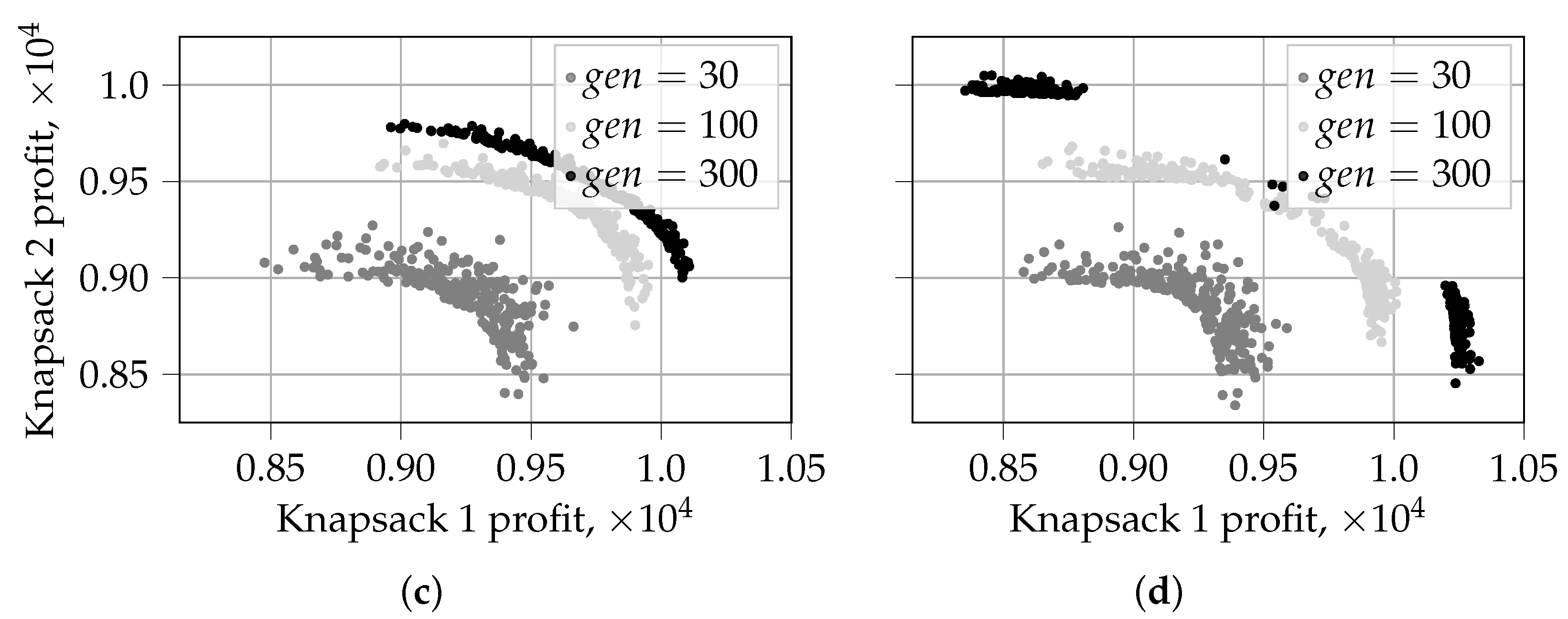
5.1.1. Evolution of Solutions for
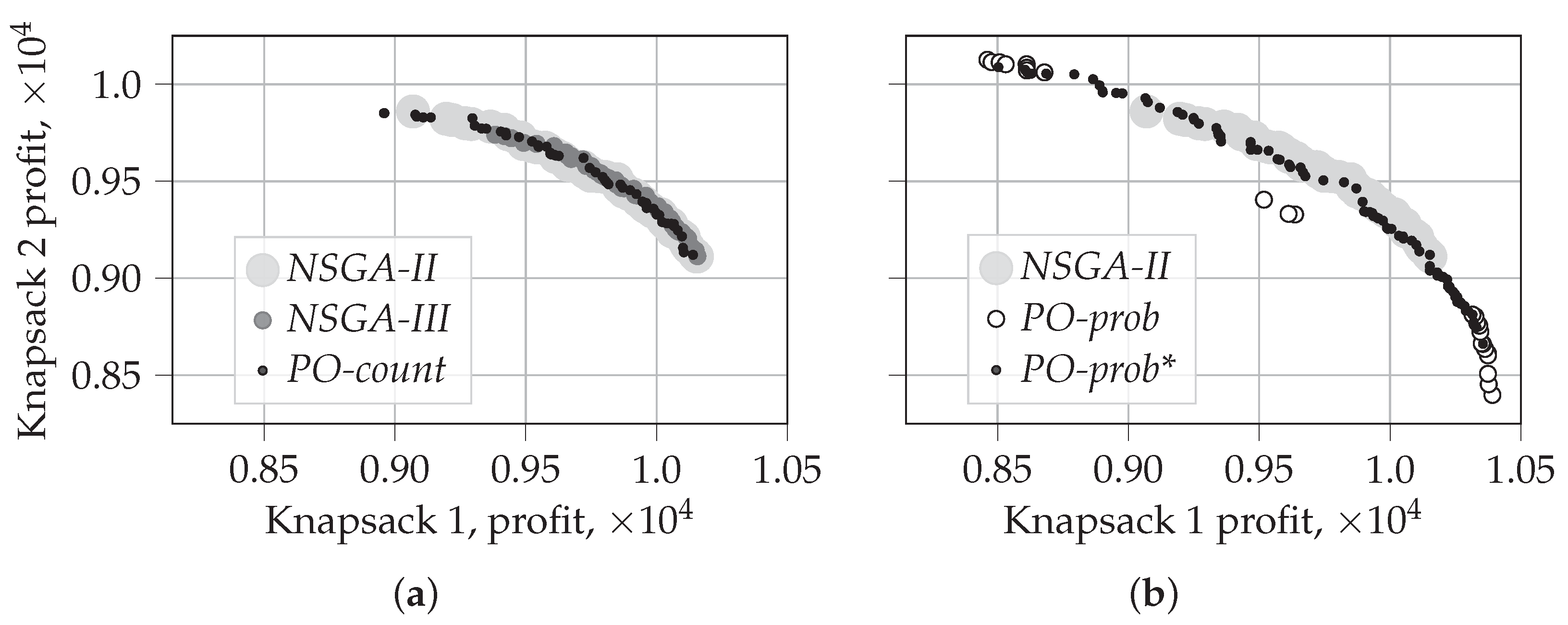
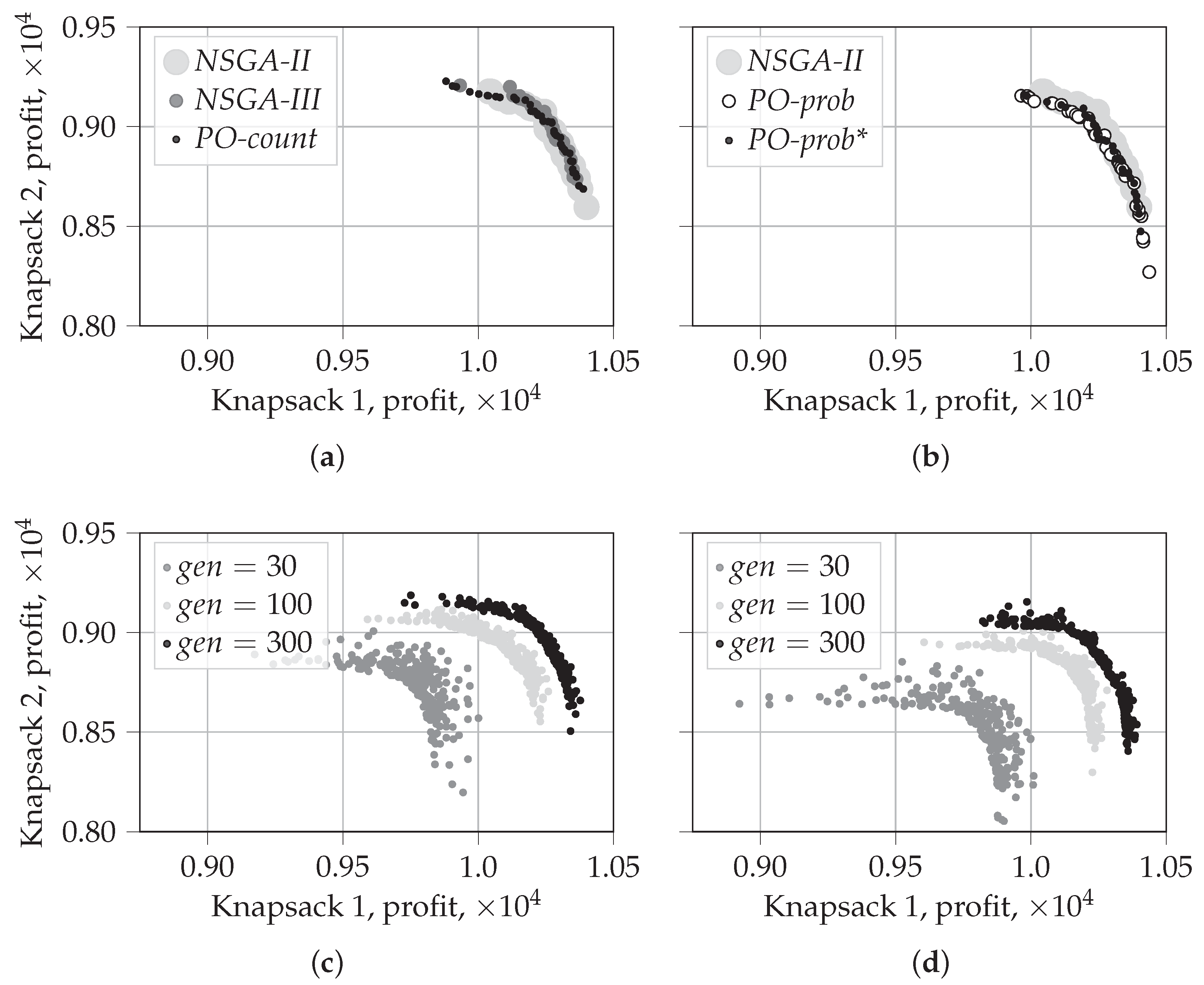
5.1.2. Visualization of the First Front for
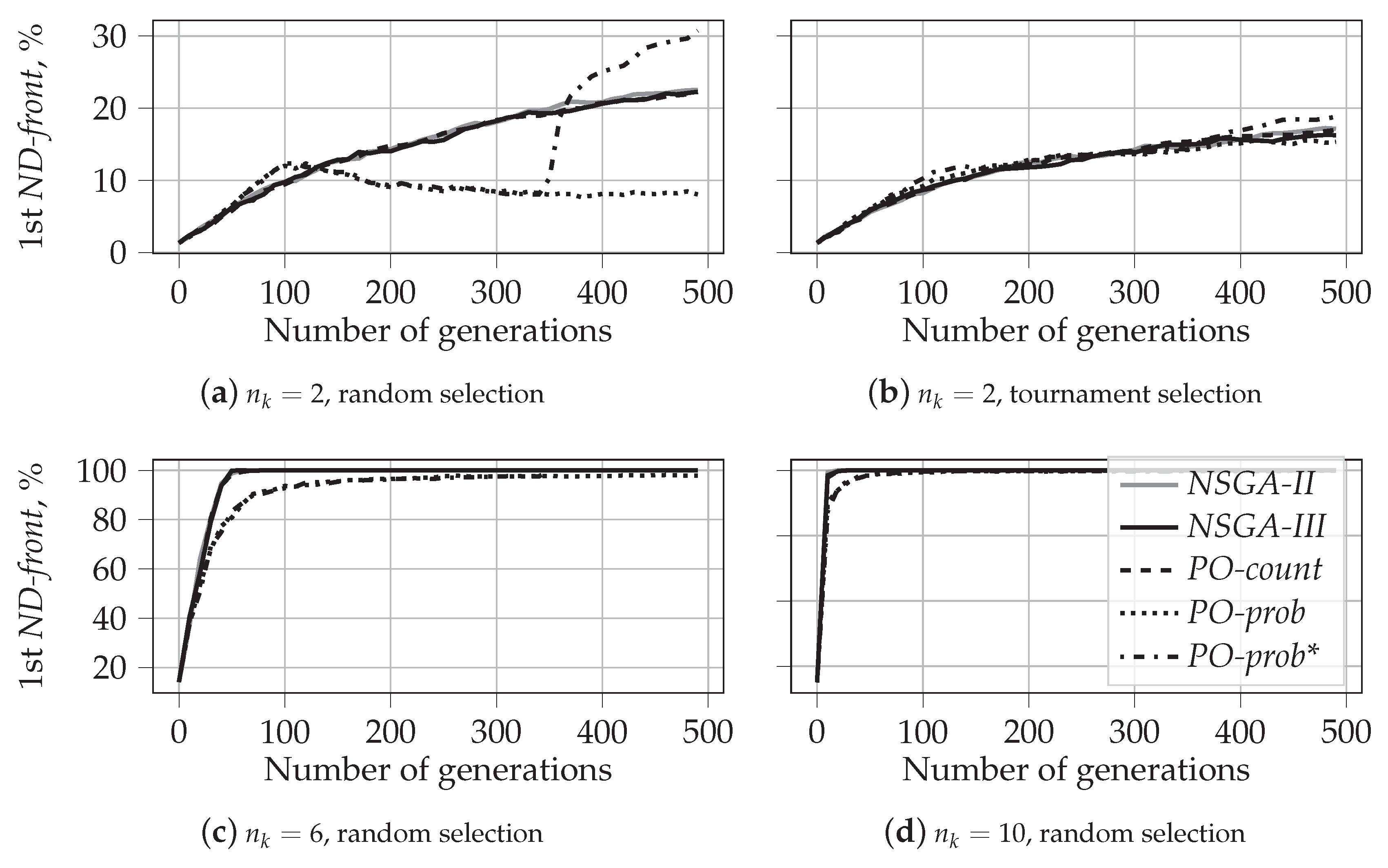
5.1.3. Fraction of Non-Dominated Solutions
5.1.4. Characteristics: Main Findings
- For two knapsakcs, :
- –
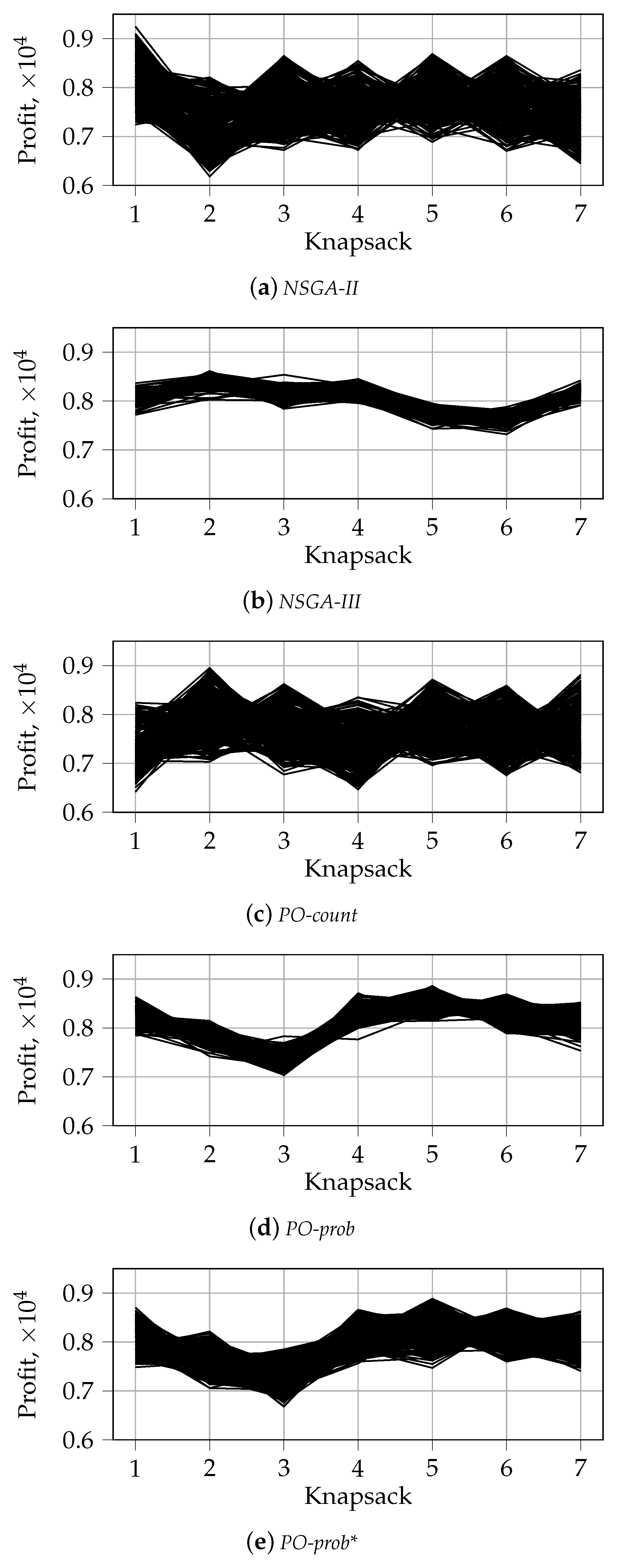
- PO-prob performs better in identifying extreme solutions. In the case of random selection, it also results in fragmented coverage of the Pareto-frontier. This tendency can, however, be repaired by using traditional non-dominated sorting during later generations, as in PO-prob*.
- –
- NSGA-II performs the best in covering the middle part of the Pareto-frontier. The behavior and performance of NSGA-III and PO-count are similar to that of NSGA-II.
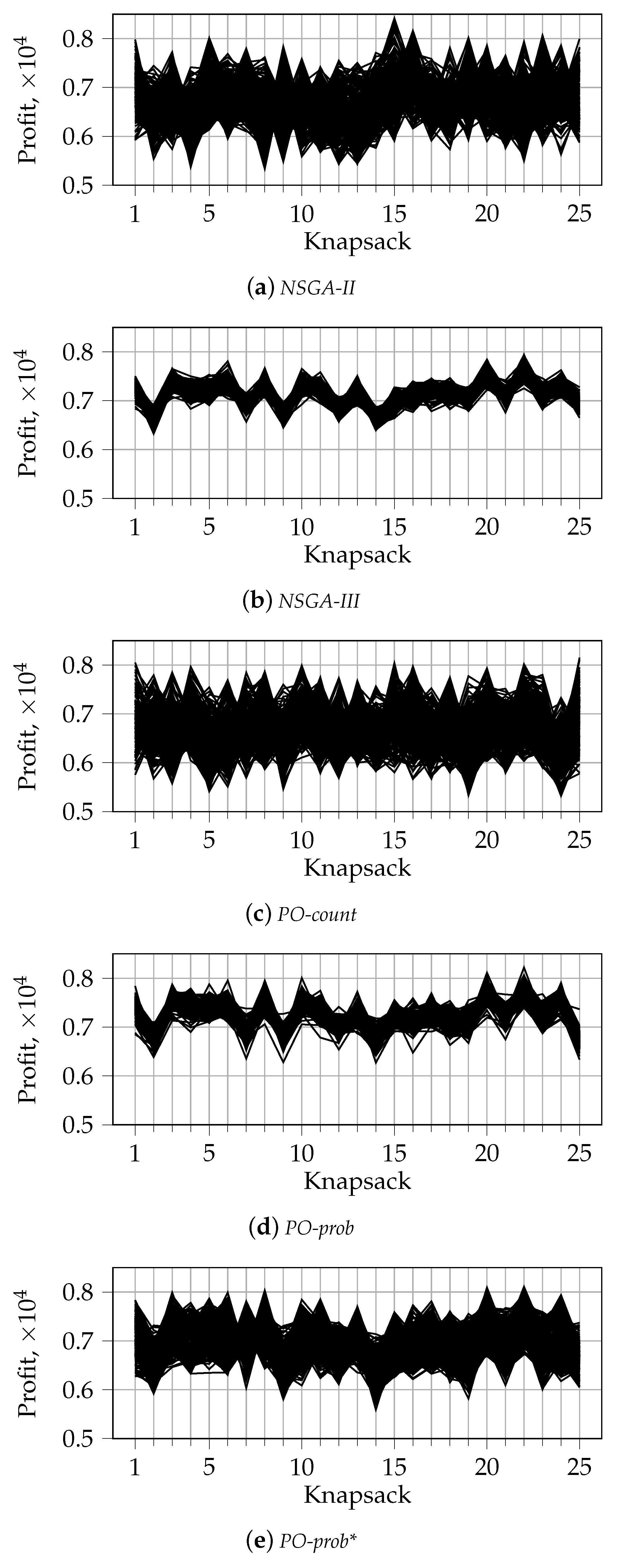
- When , the tendency changes:
- –
- PO-prob does not result in fragmented sets of solutions; this is observed for in our experiments.
- –
- PO-prob and NSGA-III result in fewer extreme solutions than other algorithms; this is observed for in our experiments.
- Ranking based on probabilistic PO results in a very low number of incomparable solutions, which is not the case for PO-count and PD sorting. This demonstrates the ability of the probabilistic PO sorting to distinguish between the solutions and find the direction for further evolution.
5.2. Performance
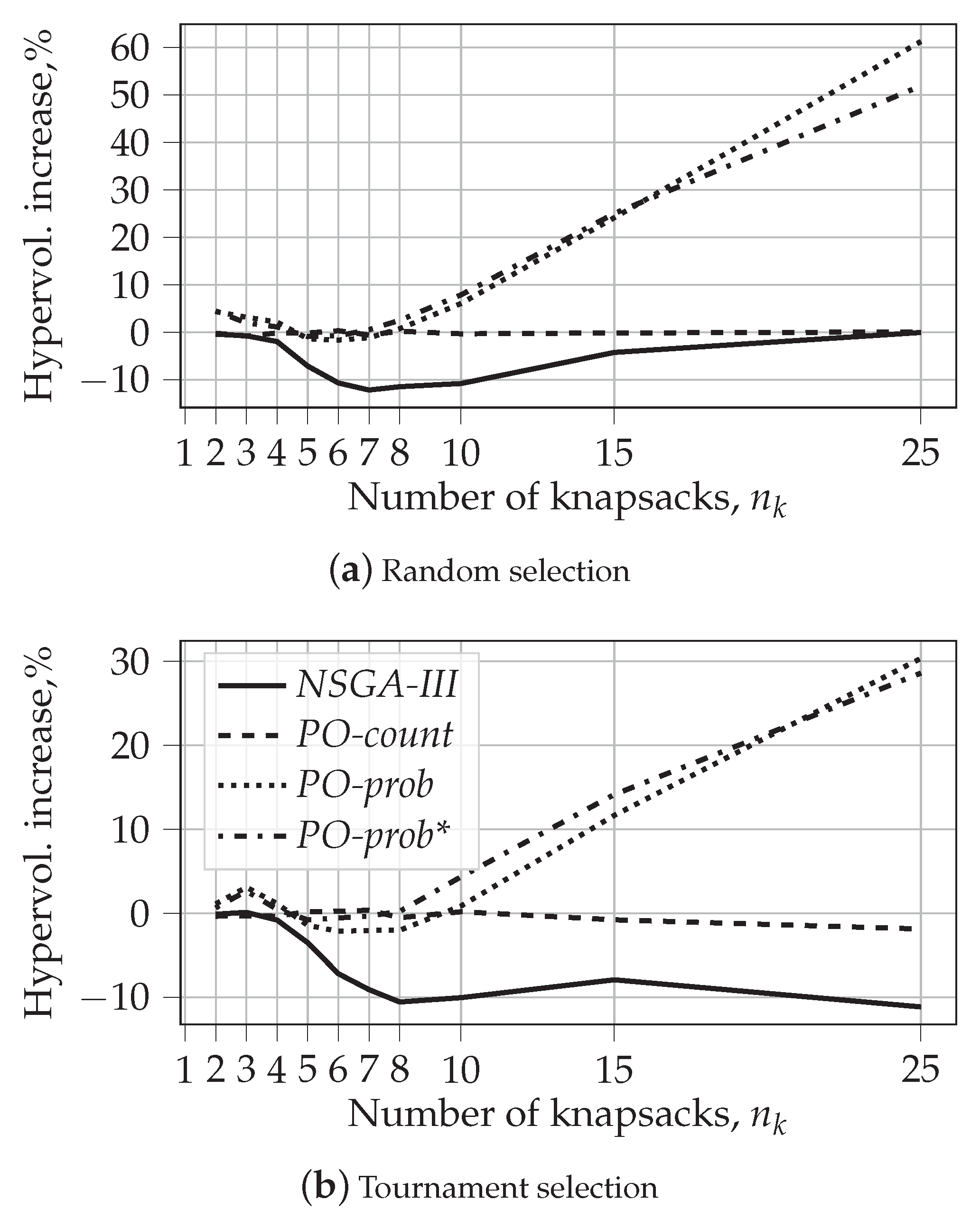
5.2.1. Hypervolume
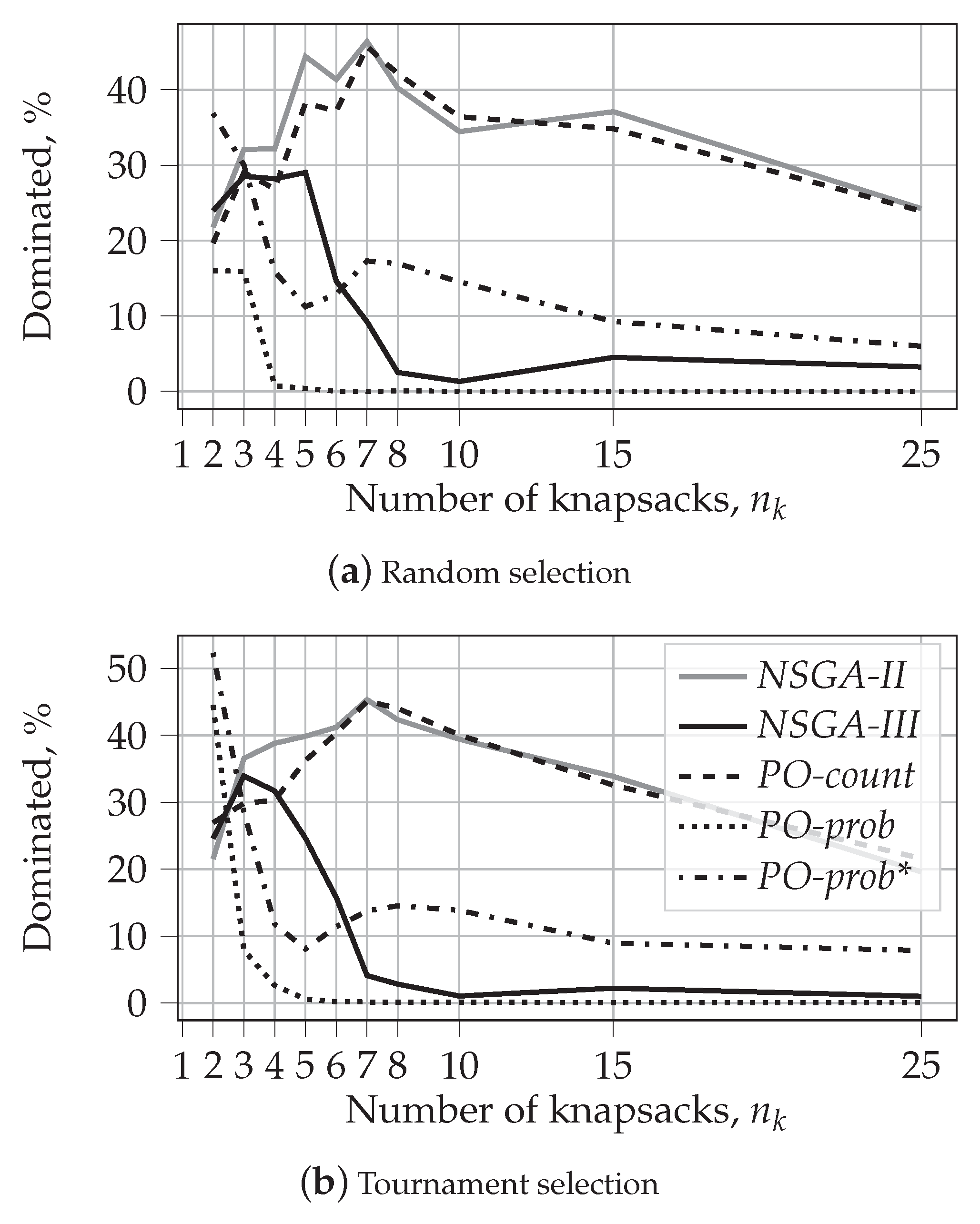
5.2.2. Fraction of Dominated Solutions
5.2.3. Performance: Main Findings
- The performance of PO-count is very close to that of NSGA-II, both in terms of hypervolume and the fraction of dominated solutions.
- Our results support the finding from [39]. We show that, contrary to expectations, NSGA-III results in lower values of hypervolume than NSGA-II for large numbers of objectives. However, we also show that for large values of , the solutions produced by NSGA-III are rarely dominated by those produced by NSGA-II. At the same time, NSGA-III does dominate some fraction of solutions produced by NSGA-II. This shows that NSGA-III can be beneficial for many-objective optimization problems. This observation was not reported in [39].
- Finally, our experiments clearly demonstrate the advantages of probability-based algorithms for many-objective optimization problems. Both PO-prob and PO-prob* result in solutions that cover larger hypervolumes and are less often dominated by the solutions of other algorithms.
5.3. Time Complexity
6. Conclusions
7. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| NSGA-II | Non-dominated Sorting Genetic Algorithm II [6] |
| NSGA-III | Non-dominated Sorting Genetic Algorithm III [16] |
| PD | Pareto dominance-based sorting, as used in NSGA-II |
| PESA-II | Pareto Envelope-based Selection Algorithm II [5] |
| (k-)PO | (k-)Pareto Optimality [14] |
| PO-count | Pareto Optimality computed via counting |
| PO-prob | Pareto Optimality computed using probabilistic approximation |
| PO-prob* | PO-prob sequentially combined with Pareto dominance sorting |
| SPEA2 | Strength Pareto Evolutionary Algorithm 2 [7] |
Appendix A. 0/1 Multi-objective Knapsack Problem Formulation
Appendix B. Visualization of the First front with Parallel Coordinates for n_k = 2
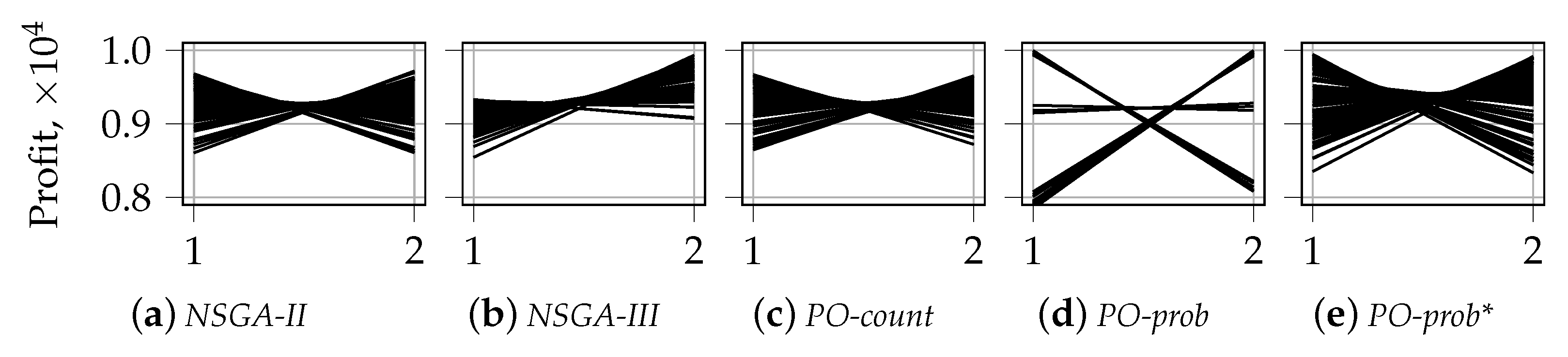

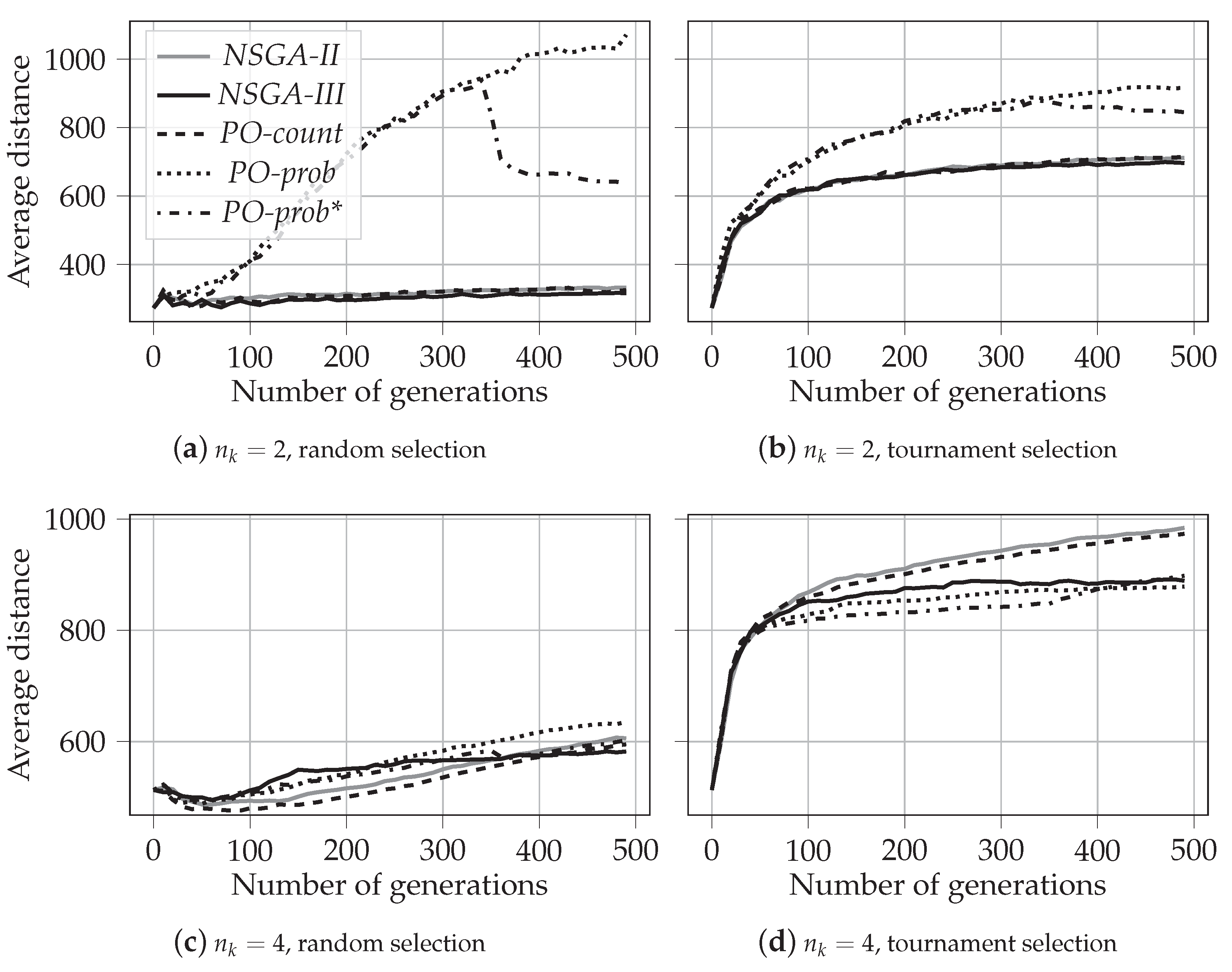
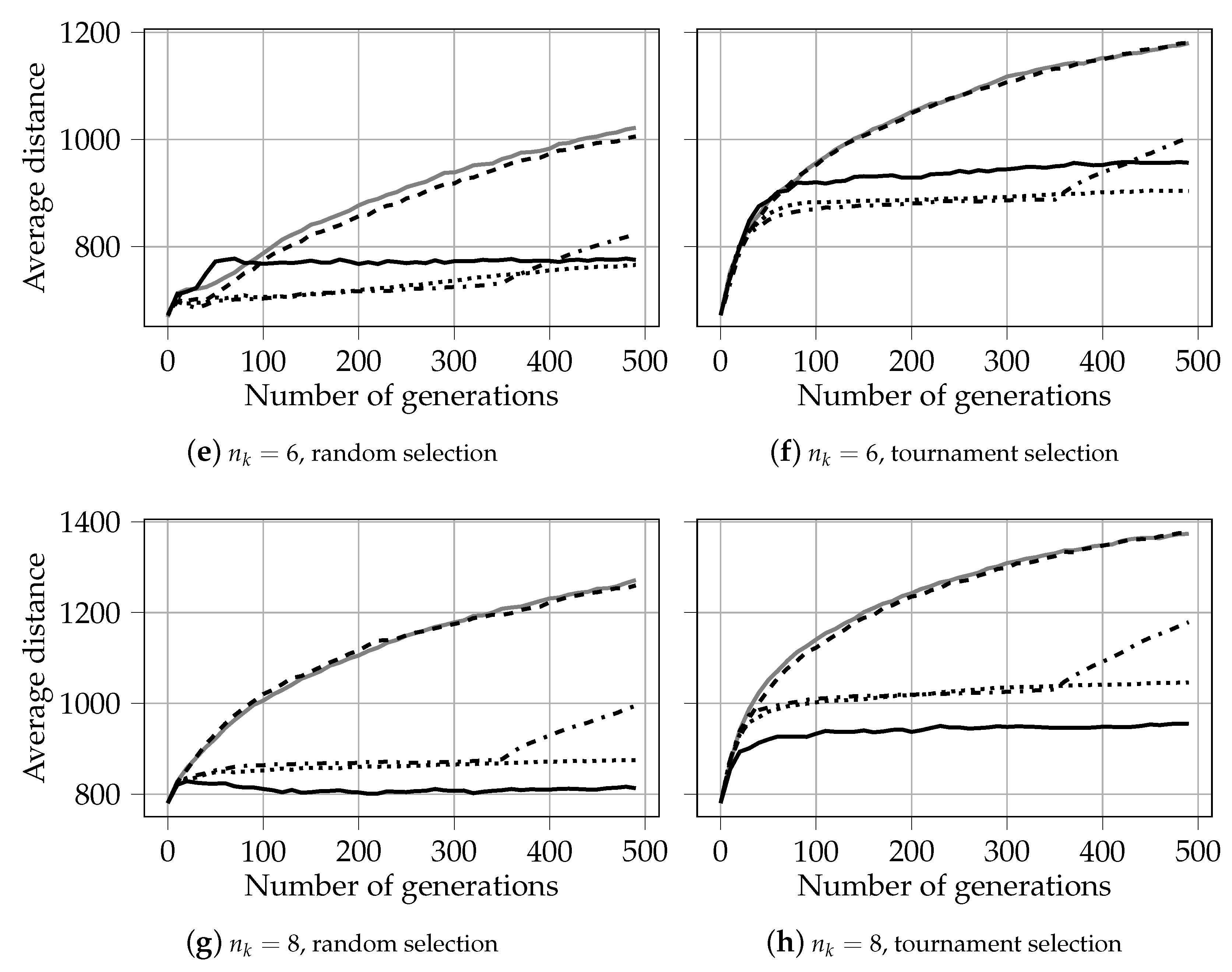
Appendix C. Average Distance to Diagonal
References
- Imene, L.; Sihem, S.; Okba, K.; Mohamed, B. A third generation genetic algorithm NSGAIII for task scheduling in cloud computing. J. King Saud Univ. Comput. Inf. Sci. 2022, 34, 7515–7529. [Google Scholar] [CrossRef]
- Bobadilla, J.; Ortega, F.; Hernando, A.; Alcalá, J. Improving collaborative filtering recommender system results and performance using genetic algorithms. Knowl. Based Syst. 2011, 24, 1310–1316. [Google Scholar] [CrossRef]
- Amorim, F.M.D.S.; Arantes, M.D.S.; Toledo, C.F.M.; Frisch, P.E.; Almada-Lobo, B. Hybrid genetic algorithms applied to the glass container industry problem. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Ishibuchi, H.; Tsukamoto, N.; Nojima, Y. Evolutionary many-objective optimization: A short review. In Proceedings of the 2008 IEEE Congress on Evolutionary Computation, Hong Kong, China, 1–6 June 2008; pp. 2419–2426. [Google Scholar]
- Corne, D.W.; Jerram, N.R.; Knowles, J.D.; Oates, M.J. PESA-II: Region-based selection in evolutionary multiobjective optimization. In Proceedings of the 3rd Annual Conference on Genetic and Evolutionary Computation, San Francisco, CA, USA, 7–11 July 2001; pp. 283–290. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the strength Pareto evolutionary algorithm. TIK Rep. 2001, 103, 1–21. [Google Scholar]
- Zhang, X.; Tian, Y.; Cheng, R.; Jin, Y. An efficient approach to non-dominated sorting for evolutionary multi-objective optimization. IEEE Trans. Evol. Comput. 2014, 19, 201–213. [Google Scholar] [CrossRef]
- Zhang, X.; Tian, Y.; Jin, Y. A knee point-driven evolutionary algorithm for many-objective optimization. IEEE Trans. Evol. Comput. 2014, 19, 761–776. [Google Scholar] [CrossRef]
- Palakonda, V.; Ghorbanpour, S.; Mallipeddi, R. Pareto dominance-based MOEA with multiple ranking methods for many-objective optimization. In Proceedings of the 2018 IEEE Symposium Series on Computational Intelligence (SSCI), Bangalore, India, 18–21 November 2018; pp. 958–964. [Google Scholar]
- Li, B.; Li, J.; Tang, K.; Yao, X. Many-objective evolutionary algorithms: A survey. ACM Comput. Surv. (CSUR) 2015, 48, 1–35. [Google Scholar] [CrossRef]
- Hughes, E.J. Evolutionary many-objective optimisation: Many once or one many? In Proceedings of the 2005 IEEE Congress on Evolutionary Computation, Edinburgh, UK, 2–5 September 2005; Volume 1, pp. 222–227. [Google Scholar]
- Wagner, T.; Beume, N.; Naujoks, B. Pareto-, aggregation-, and indicator-based methods in many-objective optimization. In Proceedings of the International Conference on Evolutionary Multi-Criterion Optimization, Shenzhen, China, 28–31 March 2007; pp. 742–756. [Google Scholar]
- Ruppert, J.; Aleksandrova, M.; Engel, T. k-pareto optimality-based sorting with maximization of choice. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Virtual, 28–30 March 2022; pp. 1138–1160. [Google Scholar]
- Palakonda, V.; Mallipeddi, R. KnEA with ensemble approach for parameter selection for many-objective optimization. In Proceedings of the International Conference on Bio-Inspired Computing: Theories and Applications, Harbin, China, 1–3 December 2019; pp. 703–713. [Google Scholar]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, Part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2013, 18, 577–601. [Google Scholar] [CrossRef]
- Palakonda, V.; Mallipeddi, R. Pareto dominance-based algorithms with ranking methods for many-objective optimization. IEEE Access 2017, 5, 11043–11053. [Google Scholar] [CrossRef]
- Wang, P.; Tong, X. A dimension convergence-based evolutionary algorithm for many-objective optimization Problems. IEEE Access 2020, 8, 224631–224642. [Google Scholar] [CrossRef]
- Gupta, A.S. Objective Reduction in Many-Objective Optimization Problems. Master’s Thesis, Brock University, St. Catharines, ON, Canada, 2019. Available online: https://dr.library.brocku.ca/bitstream/handle/10464/14540/Brock_Sengupta_Arpi_2019.pdf?sequence=1&sequence=1 (accessed on 19 September 2022).
- Ghorbanpour, S.; Palakonda, V.; Mallipeddi, R. Ensemble of Pareto-based selections for many-objective optimization. In Proceedings of the 2018 IEEE Symposium Series on Computational Intelligence (SSCI), Bengaluru, India, 18–21 November 2018; pp. 981–988. [Google Scholar]
- Gu, Q.; Wang, R.; Xie, H.; Li, X.; Jiang, S.; Xiong, N. Modified non-dominated sorting genetic algorithm III with fine final level selection. Appl. Intell. 2021, 51, 1–34. [Google Scholar] [CrossRef]
- Laumanns, M.; Thiele, L.; Deb, K.; Zitzler, E. Combining convergence and diversity in evolutionary multiobjective optimization. Evol. Comput. 2002, 10, 263–282. [Google Scholar] [CrossRef]
- Farina, M.; Amato, P. On the optimal solution definition for many-criteria optimization problems. In Proceedings of the 2002 Annual Meeting of the North American Fuzzy Information Processing Society Proceedings, NAFIPS-FLINT 2002 (Cat. No. 02TH8622), New Orleans, LA, USA, 27–29 June 2002; pp. 233–238. [Google Scholar]
- Zou, X.; Chen, Y.; Liu, M.; Kang, L. A new evolutionary algorithm for solving many-objective optimization problems. IEEE Trans. Syst. Man Cybern. Part B 2008, 38, 1402–1412. [Google Scholar]
- Köppen, M.; Vicente-Garcia, R.; Nickolay, B. Fuzzy-pareto-dominance and its application in evolutionary multi-objective optimization. In Proceedings of the International Conference on Evolutionary Multi-Criterion Optimization, Shenzhen, China, 28–31 March 2005; pp. 399–412. [Google Scholar]
- Wang, G.; Jiang, H. Fuzzy-dominance and its application in evolutionary many objective optimization. In Proceedings of the 2007 International Conference on Computational Intelligence and Security Workshops (CISW 2007), Harbin, China, 15–19 December 2007; pp. 195–198. [Google Scholar]
- Yuan, Y.; Xu, H.; Wang, B.; Yao, X. A new dominance relation-based evolutionary algorithm for many-objective optimization. IEEE Trans. Evol. Comput. 2015, 20, 16–37. [Google Scholar] [CrossRef]
- Palakonda, V.; Pamulapati, T.; Mallipeddi, R.; Biswas, P.P.; Veluvolu, K.C. Nondominated sorting based on sum of objectives. In Proceedings of the 2017 IEEE Symposium Series on Computational Intelligence (SSCI), Honolulu, HI, USA, 27 November–1 December 2017; pp. 1–8. [Google Scholar]
- Zhang, X.; Tian, Y.; Cheng, R.; Jin, Y. Empirical analysis of a tree-based efficient non-dominated sorting approach for many-objective optimization. In Proceedings of the 2016 IEEE Symposium Series on Computational Intelligence (SSCI), Athens, Greece, 6–9 December 2016; pp. 1–8. [Google Scholar]
- Zhang, X.; Tian, Y.; Jin, Y. Approximate non-dominated sorting for evolutionary many-objective optimization. Inf. Sci. 2016, 369, 14–33. [Google Scholar] [CrossRef]
- Tian, Y.; Wang, H.; Zhang, X.; Jin, Y. Effectiveness and efficiency of non-dominated sorting for evolutionary multi-and many-objective optimization. Complex Intell. Syst. 2017, 3, 247–263. [Google Scholar] [CrossRef]
- Palakonda, V.; Mallipeddi, R. MOEA with approximate nondominated sorting based on sum of normalized objectives. In Swarm, Evolutionary, and Memetic Computing and Fuzzy and Neural Computing; Springer: Berlin/Heidelberg, Germany, 2019; pp. 70–78. [Google Scholar]
- Coello, C.A.C.; Lamont, G.B.; Van Veldhuizen, D.A. Evolutionary Algorithms for Solving Multi-Objective Problems; Springer: Berlin/Heidelberg, Germany, 2007; Volume 5. [Google Scholar]
- Calder, J.; Esedoglu, S.; Hero, A.O. A Hamilton–Jacobi equation for the continuum limit of nondominated sorting. SIAM J. Math. Anal. 2014, 46, 603–638. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Setoguchi, Y.; Masuda, H.; Nojima, Y. Performance of decomposition-based many-objective algorithms strongly depends on Pareto front shapes. IEEE Trans. Evol. Comput. 2016, 21, 169–190. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Sato, H. Evolutionary many-objective optimization. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Prague, Czech Republic, 13–17 July 2019; pp. 614–661. [Google Scholar]
- Shang, K.; Ishibuchi, H.; He, L.; Pang, L.M. A survey on the hypervolume indicator in evolutionary multiobjective optimization. IEEE Trans. Evol. Comput. 2020, 25, 1–20. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Imada, R.; Setoguchi, Y.; Nojima, Y. Performance comparison of NSGA-II and NSGA-III on various many-objective test problems. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 3045–3052. [Google Scholar]
- Ishibuchi, H.; Akedo, N.; Nojima, Y. Behavior of multiobjective evolutionary algorithms on many-objective knapsack problems. IEEE Trans. Evol. Comput. 2014, 19, 264–283. [Google Scholar] [CrossRef]
- He, C.; Tian, Y.; Wang, H.; Jin, Y. A repository of real-world datasets for data-driven evolutionary multiobjective optimization. Complex Intell. Syst. 2019, 6, 189–197. [Google Scholar] [CrossRef]
- Wangsom, P.; Lavangnananda, K. Extreme solutions NSGA-III (E-NSGA-III) for multi-objective constrained problems. In Proceedings of the OLA’2019 International Conference on Optimization and Learning, Bangkok, Thailand, 29–30 January 2019. [Google Scholar]
- Wangsom, P.; Bouvry, P.; Lavangnananda, K. Extreme solutions NSGA-III (E-NSGA-III) for scientific workflow scheduling on cloud. In Proceeding of the 2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA), Jinan, China, 26–28 May 2018; pp. 1139–1146. [Google Scholar]
- Ishibuchi, H.; Matsumoto, T.; Masuyama, N.; Nojima, Y. Effects of dominance resistant solutions on the performance of evolutionary multi-objective and many-objective algorithms. In Proceedings of the 2020 Genetic and Evolutionary Computation Conference, Cancun, Mexico, 8–12 July 2020; pp. 507–515. [Google Scholar]
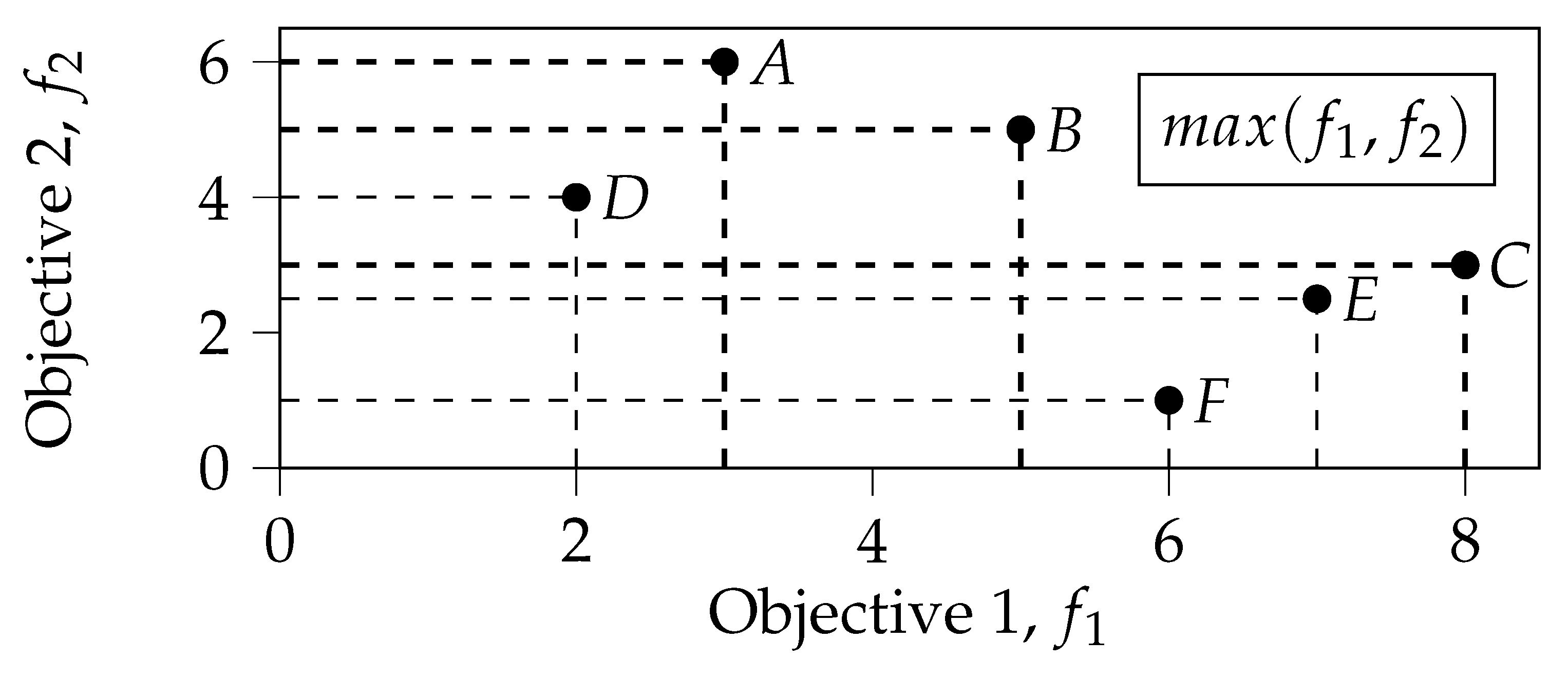
| Front | PD | PO-count | PO-prob | PO-prob, | |||
|---|---|---|---|---|---|---|---|
| Points | Val. | Points | Val. | Points | Val. | ||
| 1 | A, B, C | A, B, C | 0 | A, C | 0.00 | C | 0.05 |
| 2 | D, E | E | 1 | B | 0.08 | A | 0.07 |
| 3 | F | D, F | 2 | E | 0.11 | B | 0.08 |
| 4 | D, F | 0.28 | E | 0.11 | |||
| 5 | D, F | 0.28 | |||||
| Problem | knapsack, , 250 items |
| Baseline | NSGA-II, NSGA-III |
| Algorithms | PO-count, PO-prob, PO-prob* |
| Implementation | python package DEAP |
| Parent selection | random, binary tournament |
| Crossover | uniform |
| Parameters | , , |
| Runs | 30 |
| NSGA-II, h-Vol. | NSGA-III | PO-Count | PO-Prob | PO-Prob* | |
|---|---|---|---|---|---|
| Random selection | |||||
| 2 | –0.40 | –0.19 | 4.36 | 4.48 | |
| 3 | –0.73 | –0.80 | 3.18 | 1.97 | |
| 4 | –1.95 | –0.13 | 2.15 | 1.14 | |
| 5 | –7.11 | –0.15 | –1.36 | –0.90 | |
| 6 | –10.67 | 0.33 | –1.63 | –0.74 | |
| 7 | –12.15 | –0.56 | –1.14 | 0.55 | |
| 8 | –11.45 | 0.23 | 0.76 | 2.53 | |
| 10 | –10.78 | –0.31 | 6.07 | 7.88 | |
| 15 | –4.23 | –0.14 | 24.13 | 25.02 | |
| 25 | –0.04 | 0.07 | 61.23 | 51.88 | |
| Tournament selection | |||||
| 2 | –0.09 | –0.33 | 1.14 | 0.67 | |
| 3 | 0.12 | –0.29 | 3.11 | 2.66 | |
| 4 | –0.79 | –0.33 | 1.16 | 0.48 | |
| 5 | –3.49 | 0.22 | –1.42 | –0.77 | |
| 6 | –7.18 | 0.24 | –2.13 | –0.54 | |
| 7 | –9.07 | 0.39 | –2.02 | –0.31 | |
| 8 | –10.54 | –0.51 | –2.01 | 0.25 | |
| 10 | –10.02 | 0.20 | 0.90 | 4.35 | |
| 15 | –7.90 | –0.76 | 11.67 | 14.14 | |
| 25 | -11.12 | –1.86 | 30.35 | 28.59 | |
| Dominated algorithm, | |||||
| NSGA-II | NSGA-III | PO-count | PO-prob | PO-prob* | |
| NSGA-II | 44.24 | 39.21 | 13.52 | 47.38 | |
| NSGA-III | 37.50 | 34.51 | 13.52 | 44.76 | |
| PO-count | 43.34 | 45.01 | 13.52 | 46.94 | |
| PO-prob | 0.00 | 0.00 | 0.00 | 8.37 | |
| PO-prob* | 6.24 | 6.64 | 5.02 | 23.46 | |
| mean, | 21.77 | 23.97 | 19.60 | 16.01 | 36.86 |
| Dominated algorithm, | |||||
| NSGA-II | NSGA-III | PO-count | PO-prob | PO-prob* | |
| NSGA-II | 0.00 | 8.57 | 0.00 | 0.04 | |
| NSGA-III | 39.72 | 40.51 | 0.08 | 19.00 | |
| PO-count | 9.99 | 0.00 | 0.00 | 0.05 | |
| PO-prob | 66.73 | 27.51 | 66.72 | 48.65 | |
| PO-prob* | 61.52 | 1.41 | 63.31 | 0.07 | |
| mean, | 44.49 | 7.23 | 44.78 | 0.04 | 16.94 |
| Dominated algorithm, | |||||
| NSGA-II | NSGA-III | PO-count | PO-prob | PO-prob* | |
| NSGA-II | 0.00 | 8.28 | 0.00 | 0.15 | |
| NSGA-III | 18.97 | 18.83 | 0.00 | 8.48 | |
| PO-count | 6.40 | 0.00 | 0.00 | 0.20 | |
| PO-prob | 36.55 | 9.59 | 36.52 | 18.76 | |
| PO-prob* | 30.13 | 0.80 | 31.89 | 0.00 | |
| mean, | 23.01 | 2.60 | 23.88 | 0.00 | 6.90 |
| Dominated algorithm, | |||||
| NSGA-II | NSGA-III | PO-count | PO-prob | PO-prob* | |
| NSGA-II | 43.93 | 46.67 | 47.81 | 61.20 | |
| NSGA-III | 35.99 | 43.17 | 45.71 | 59.33 | |
| PO-count | 35.83 | 36.70 | 42.32 | 57.43 | |
| PO-prob | 6.61 | 7.75 | 7.53 | 31.29 | |
| PO-prob* | 7.78 | 9.95 | 10.41 | 42.26 | |
| mean, | 21.55 | 24.58 | 26.95 | 44.52 | 52.31 |
| Dominated algorithm, | |||||
| NSGA-II | NSGA-III | PO-count | PO-prob | PO-prob* | |
| NSGA-II | 0.00 | 11.21 | 0.00 | 0.09 | |
| NSGA-III | 42.92 | 44.00 | 0.53 | 15.69 | |
| PO-count | 12.16 | 0.00 | 0.01 | 0.03 | |
| PO-prob | 63.32 | 14.72 | 63.73 | 39.24 | |
| PO-prob* | 62.91 | 1.71 | 61.52 | 0.11 | |
| mean, | 45.33 | 4.11 | 45.12 | 0.16 | 13.76 |
| Dominated algorithm, | |||||
| NSGA-II | NSGA-III | PO-count | PO-prob | PO-prob* | |
| NSGA-II | 0.00 | 6.69 | 0.03 | 0.32 | |
| NSGA-III | 17.35 | 20.83 | 0.03 | 10.60 | |
| PO-count | 5.57 | 0.00 | 0.01 | 0.12 | |
| PO-prob | 29.77 | 3.60 | 30.92 | 20.40 | |
| PO-prob* | 25.71 | 0.44 | 27.97 | 0.23 | |
| mean, | 19.60 | 1.01 | 21.60 | 0.07 | 7.86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruppert, J.; Aleksandrova, M.; Engel, T. k-Pareto Optimality-Based Sorting with Maximization of Choice and Its Application to Genetic Optimization. Algorithms 2022, 15, 420. https://doi.org/10.3390/a15110420
Ruppert J, Aleksandrova M, Engel T. k-Pareto Optimality-Based Sorting with Maximization of Choice and Its Application to Genetic Optimization. Algorithms. 2022; 15(11):420. https://doi.org/10.3390/a15110420
Chicago/Turabian StyleRuppert, Jean, Marharyta Aleksandrova, and Thomas Engel. 2022. "k-Pareto Optimality-Based Sorting with Maximization of Choice and Its Application to Genetic Optimization" Algorithms 15, no. 11: 420. https://doi.org/10.3390/a15110420
APA StyleRuppert, J., Aleksandrova, M., & Engel, T. (2022). k-Pareto Optimality-Based Sorting with Maximization of Choice and Its Application to Genetic Optimization. Algorithms, 15(11), 420. https://doi.org/10.3390/a15110420





