Abstract
Decomposition-based evolutionary algorithms are popular with solving multi-objective optimization problems. It uses weight vectors and aggregate functions to keep the convergence and diversity. However, it is hard to balance diversity and convergence in high-dimensional objective space. In order to discriminate solutions and equilibrate the convergence and diversity in high-dimensional objective space, a two-archive many-objective optimization algorithm based on D-dominance and decomposition (Two Arch-D) is proposed. In Two Arch-D, the method of D-dominance and adaptive strategy adjusting parameter are used to apply selection pressure on the population to identify better solutions. Then, it uses the two archives’ strategy to equilibrate convergence and diversity, and after classifying solutions in convergence archive, the improved Tchebycheff function is used to evaluate the solution set and retain the better solutions. For the diversity archive, the diversity is maintained by making any two solutions as far apart and different as possible. Finally, the Two Arch-D is compared with other four multi-objective evolutionary algorithms on 45 many-objective test problems (including 5, 10 and 15 objectives). Good performance of the algorithm is verified by the description and analysis of the experimental results.
1. Introduction
The introduction many-objective optimization problems (MaOPs) have been widely used in real life. Generally speaking, a MaOP can be described mathematically as follows [1]
where is an n-dimensional decision vector; is an n-dimensional decision space; contains m conflicting objective functions. Here are some important concepts: suppose there are two solutions , if and only if , then is said to be pareto dominant compared with , denoted as . is called the Pareto optimal solution if and only if .
At present, many MaOPs have been widely used in network optimization [2,3], power system [4], chemical process and structure optimization [5]. So, to solve MaOPs, many many-objective evolutionary algorithms have been coming out in recent years. In 2017, Delice et al. proposed a particle swarm optimization algorithm [6] based on negative knowledge, which can effectively search in the solution space. Khajehzadeh et al. combined the adaptive gravitational search algorithm with pattern search [7] to improve the local search ability of the algorithm. Reference [8] proposed a firefly algorithm based on opposite learning, which uses opposite learning concepts to generate the initial population and update location.
With the development of optimization technology, the many-objective optimization algorithm is used to solve many-objective optimization problems [9,10,11]. The larger the number of objectives, the greater the proportion of nondominated solutions in the candidate solutions, which worsens the selection pressure of PF. Maintaining population diversity in high-dimensional objective space is also a challenging task [12]. For these problems, scholars have proposed that many algorithms can be divided into the following three types according to the different methods.
The first is indicator-based algorithms, e.g., an optimization algorithm [13] based on a new enhanced inverted generation distance indicator is proposed, which automatically adjusts the reference points according to the new indicator contribution. A many-objective optimization algorithm [14] based on IGD indicator and nadir estimation is proposed. IGD is used to select solutions with convergence and diversity. They use indicators to evaluate the convergence and diversity of solutions and guide the search process, the final solution set depends mainly on the indicator characteristics included, such as hypervolume (HV) indicator [15], R2 indicator [16], indicator [17] and the inverted generational distance (IGD). HV is one of the commonly used indicators [18,19], but it requires a large amount of calculation, which is generally exponential. Evaluating IGD requires the real Pareto front, which is unknown in real-life problems.
The second category is based on the Pareto dominance relationship, e.g., NSGA-II/SDR [20], GrEA [21], VaEA [22] and B-NAGA-III [23], which uses improved Pareto domination to select solutions. The larger the number of objectives, the larger the number of dominant solutions [24]. The method based on Pareto dominance mainly relies on diversity measurement to distinguish solutions, so the population will lose the selection pressure and cannot ensure diversity. To address these issues, more efforts should be made to design diversity maintenance mechanisms to ensure diversity.
The third is based on decomposition. The main idea is to transform a MaOP into a set of subproblems by decomposition method and optimize the subproblems in a collaborative way using evolutionary search. The most representative algorithm is the MOEA/D proposed in 2007 [25]. Many similar algorithms have since emerged, such as MOEA/DD [26], MOEA/AD [10], MOEA/D-SOM [27], MOEA/D-AM2M [28], hpaEA [29] and ar-MOEA [30], etc. These algorithms have gained wide popularity due to their good performance. The decomposition-based method uses the objective value of subproblems to update the whole, which reduces the calculation cost. However, it uses a set of weight vectors to decompose MaOPs. The weight vector guides the evolution of the subproblem, which makes the performance of the algorithm strongly depend on the weight vectors.
To better equilibrate the convergence and diversity of population and reduce the influence of the weight vector on algorithm performance, this paper combines the “two-archive” algorithm with the decomposition methods, and its main contribution can be summarized as follows.
- The method of D-dominance and adaptive strategy adjusting parameter are used to apply selection pressure on the population to identify better solutions. Meanwhile, the dominant and dominated regions can be adjusted by parameter , which means that D-dominance is more flexible when dealing with MaOPs;
- In this paper, two-archive strategy is used to balance the convergence and diversity of solutions, and a set of solutions with good convergence can be obtained.
The rest of the article is structured as follows: The second part describes the algorithm and its method detailly. The third part presents the experimental results and related analysis and discussion. Finally, the conclusion is drawn in the fourth part.
2. Materials and Methods
2.1. D-Dominance Methods
Penalty-based Boundary Intersection (PBI) is one of the most common decomposition methods, and its definition formula is as follows:
where , is a preset parameter, which usually takes 0.5. is the projection distance of in direction λ, and is the distance from the vertical projection of in direction λ. The farther away from λ, the greater the penalty value , which constrains the direction of the algorithm weight vector to generate solutions. Suppose is the projection of on line , as shown in Figure 1, the distance from to is represented by , and the distance from to is represented by .
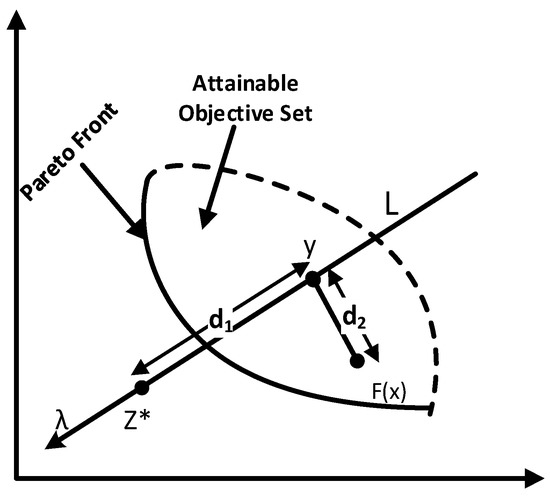
Figure 1.
Penalty-based Boundary Intersection (PBI).
Chen and Liu established a new relationship between decomposition and dominance through PBI decomposition, namely D-dominance [31]. According to the definition of and in the PBI decomposition, the parameter and the unit decomposition vector , D-dominance is defined as follows.
If , then let us say is D-dominated by , expressed by .
Otherwise, if , let us say is D-dominated by , expressed by .
Otherwise, and are called mutually non-D-dominated. and are calculated by Equation (4). We used to evaluate the convergence of and to measure population diversity, and we wanted to be as small as possible and increased for diversity. If , deviated from the unit vector by an angle greater than in the direction, and was greater than in the distance. Conversely, if , deviated from the unit vector by an angle greater than in the direction, and was greater than in the distance.
Figure 2 shows D-dominance example diagram. In the figure, there are three groups of solutions , , , and , and three decomposition vectors and , where is the moving vectors of . To judge whether is D-dominated by , move the vector to to intersect with to get the β projection; that is, the PBI-β decomposition value of with respect to is . From the figure, we can see intuitively that is greater than the projection value ; that is, is D-dominated by . To determine whether is D-dominated by , one only needs the moving decomposition vector intersected with , and then one can find the β projection value, i.e., , but is less than . At the same time, the projection from to is intuitively greater than . Therefore, and are not D-dominated.
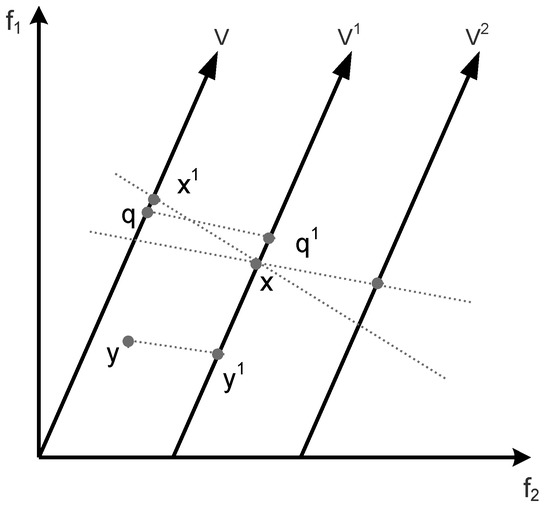
Figure 2.
D-dominance example diagram.
The D-dominated method reduces the dependence on the decomposition vector and enables each individual to update around itself. At the same time, D-dominated region can pass parameter flexible adjustment. In order to set reasonably, we used Formula (5) to adjust automatically.
where stands for current generation, and denotes the maximal generation. The initial value of is the largest and monotonically decreases with the increase of the current generation. As the increases, the selection pressure also increases, which results in fewer non-D-domination solutions. This is designed to exert more selective pressure on the population at an early stage of evolution, bringing it rapidly closer to PF, and then gradually reduce selection pressure so that the population has better expansion along PF. Compared with Pareto domination, D-domination has an adjustable domination area and dominated area, which means that D-domination will be more flexible in dealing with MaOPs.
2.2. Two Archives Strategy
The two-archive algorithm is a multi-objective evolutionary algorithm for balancing the convergence and diversity using the diversity archive (DA) and convergence archive (CA). The non-dominated solution and its descendants are added to CA, while the dominated solution and its descendants are added to DA. Solutions that exceed the CA and DA thresholds will be deleted. However, as the objective dimension increases, the size of CA increases enormously, leaving little space for DA. When the total size of both archives’ overflows, the removal strategy should be applied.
First, the solutions in CA are classified by a set of weight vectors generated by the initial population. The purpose of this is to obtain a uniformly distributed solution set to maintain its diversity. The following formula is used to classify the solutions in CA.
where is a reference point, and is cosine of the angle between and .
In the DA archive, to maintain the diversity, select the solution with the largest difference between any two distances in the population. The distance value of any solution is calculated by Formula (8).
where represent the distance and difference of the two solutions individually.
2.3. Updating Strategy
In order to update population, the algorithm adopts non-D-dominated sorting and Tchebycheff aggregate functions to preserve better convergent and distributed solutions. It is important to maintain the distribution of the population, given a set of weight vectors . According to the cosine value of the angle between the solution and the weight vector, each solution in CA is divided into the group of the nearest weight vector, and only one solution is retained in each group. First, calculate the cosine value of the angle between the solution in CA and the given weight vector according to Formula (6). The larger the cosine of the angle, the smaller the angle. After all partitions are completed, all solutions in CA are divided into groups. For each weight vector, if there is only one corresponding solution, the solution is kept directly. If the corresponding solution is more than one, the solution of each group needs to be evaluated according to the improved Tchebycheff function, then the D-dominance method is used to increase the selection pressure and, finally, the best solution in each group is retained. Therefore, the solution with the smallest Tchebycheff function value is selected according to Formula (9). If there is no corresponding solution, the selection range is extended to the whole CA, and the solution with the smallest Tchebycheff function value in CA is retained.
2.4. The Proposed Algorithm
In order to discriminate better solutions and better equilibrate convergence and diversity in high-dimensional objective space, we proposed Two Arch-D. Benefiting from the D-dominance, the decomposition vectors are free vectors in Two Arch-D, and the subpopulation search and update no longer rely on the decomposition vector but take themselves as the center, which greatly reduces the individual’s high dependence on the relevant decomposition vector in the process of evolution.
This section describes in detail how the proposed D-domination method and update strategy based on the Two Arch framework works. The main ideas are as follows.
First, use unit vectors to divide the objective space into sub-regions, and each sub-region satisfies Formula (10). That is, is in if and only if the angle between and is the smallest among all direction vectors. (1) is decomposed into multiple objective optimization subproblems and solved them in a cooperative manner. subpopulations are maintained in each generation, and each subpopulation always contains multiple feasible solutions. Finally, these feasible solutions are output to the population EPOP.
In order to get a good set of convergent solutions, Formulas (6) and (7) are used to classify the CA. The improved Tchebycheff function is used to assess solutions, and the solution with the smallest value of Tchebycheff function is selected to be retained. To keep the diversity of solutions, use Formula (8) to select any two solutions with a large distance difference in the population into the diversity archives. In Algorithm 1, the framework of the algorithm is given. At the same time, the pseudo-code to determine CA in this paper is also given in Algorithm 2.
| Algorithm 1: Proposed algorithm framework |
| Input: |
| MaOP(1). |
| A set of weight vectors . |
| K: number of subproblems. |
| MaxGen: the maximal generation. |
| Genetic operators and their associated parameters. |
| Output: EPOP |
| Initialization: unit direction vectors and population. |
| while the stop requirements are not met do |
| The new solution was obtained by genetic manipulation. for 1 to do |
| for do |
| Pick a solution at random from |
| A new solution was obtained by genetic operation; |
| ; |
| end |
| end |
| Find all solutions in . |
| Determine the convergence archive . |
| Defining the diversity archive : use Formula (8) to select solutions. |
| . |
| end while |
| Algorithm 2: Determine the convergence archive CA |
| Input: |
| : a set of solutions. |
| weight vectors . |
| Output:: . |
| Classifying solutions in CA according to Formulas (6) and (7). |
| Using non-D-dominated sorting and Tchebycheff aggregate functions to preserve better convergent and distributed solutions. |
| for, do |
| if |
| Evaluate the solution in by formula (9), keep only the best solution in each group. |
| end if |
| end |
3. Results and Discussion
3.1. Test Problem
In this part, Two Arch-D is compared with the running results of other seven MOEAs (NSGAIII, MOEA/DD, KnEA, RVEA, hpaEA, VaEA and NSGAIISDR) on 15 test functions of CEC2018 MaOP optimization to verify the effectiveness of Two Arch-D. NSGAIII [32] uses the method based on reference points when selecting the Pareto solution set, while NSGAII uses the way of crowding distance to screen. MOEA/DD [26] combines dominance and decomposition methods, using their advantages to equilibrate the convergence and diversity. The KnEA [33] algorithm does not need to introduce an additional diversity maintenance mechanism, thus reducing the computational complexity. RVEA [34] is a multi-objective optimization algorithm guided by reference vector. In the high-dimensional objective space, RVEA employs an angle-penalized distance to select solutions. HpaEA [29] is an evolutionary algorithm based on adjacent hyperplanes to select non-dominated solutions using the newly proposed selection strategy. In VaEA [22], in order to maintain the diversity and convergence of solutions, the maximum vector angle-first strategy is used to select solutions, and worse solutions are replaced by other solutions. NSGA-II/SDR [20] is an improved many-objective optimization algorithm based on NSGA-II, which uses a new domination relation based on the angle of candidate solutions to select convergent solutions.
In order to test the ability of Two Arch-D algorithm to solve various MOPs, 15 benchmark functions with different characteristics of the CEC2018 MaOP competition [35] were selected for testing. The 15 benchmark functions with different properties used in the experiments can well represent various real-world scenarios, such as multimodal, disconnected and degenerate. The main features, expressions and PF features of these 15 test functions are referred to the literature [36]. For testing the performance of the Two Arch-D algorithm, the objective number of each test function is set to 5, 10 and 15, respectively, with a total of 45 sets of problems.
3.2. Parameter Setting
The experiment is tested by PlatEMO (http://bimk.ahu.edu.cn/12957/list.htm, accessed on 10 September 2022) [37], an evolutionary multi-objective optimization platform based on MATLAB. Each algorithm runs independently 20 times when solving each test function. The parameter of the Two Arch-D algorithm is set as follows: the outside population is twice as large as N, and the maximum function evaluation time is 100,000. Other parameter settings are the same as those of the CEC2018 MaOP competition [35]. The population size N and maximum function evaluation times of NSGAIII, MOEA/DD, KnEA, RVEA, hpaEA, VaEA and NSGAIISDR comparison algorithms are the same as those of Two Arch-D, and the default parameters of PlatEMO platform are used for other parameter settings.
3.3. Performance Indicator
In the experimental part, the IGD [38] index is used to evaluate algorithm. It mainly evaluates the convergence and diversity of the algorithm by calculating the sum of the minimum distance between each individual on the real Pareto front and the individual set obtained by algorithm. If IGD is smaller and the population is closer to the Pareto front, the better performance of the algorithm. Computing IGD requires a real Pareto front. However, in reality, the real Pareto front of optimization problems is often unknown. In the experiment, we uniformly selected 10,000 points on the Pareto fronts of each test question to calculate the IGD. In addition, the average IGD values of each algorithm were compared using Wilcoxon rank-sum test [38] with a significance level of 0.05. The IGD is calculated by Formula (11).
where is the solution set obtained by algorithm, is a set of points sampled from PF and is the Euclidean distance between point in the reference set and point in the solution set . The smaller the average IGD is, the closer P is to the true PF, and it is evenly distributed on the whole PF. Therefore, the IGD index can measure the convergence and diversity of the algorithm solutions to a certain extent.
3.4. Comparison and Analysis of Results
Table 1 and Table 2 show the average and standard deviation of IGD obtained by Two Arch-D and other seven comparison algorithms running independently 20 times on 45 test problems (including 5, 10 and 15 objectives). In the table, the best performance for each test question is highlighted in bold. “+” indicates that the comparison algorithm performs better than Two Arch-D, “−” indicates that the comparison algorithm performs worse than Two Arch-D and “=“ indicates that the two algorithms are similar.

Table 1.
IGD mean and standard deviation values of each algorithm.

Table 2.
IGD mean and standard deviation values of each algorithm.
From the experimental results, it can be seen that on the first 15 test questions (5 objectives), the average IGD values obtained by Two Arch-D on the problems of MaF1, MaF3, MaF4, MaF6, MaF7, MaF9 and MaF12 are significantly better than other compared algorithms. On the test problems of 10 objectives, the average IGD values obtained by Two Arch-D on the six problems of MaF3, MaF5, MaF6 and MaF10–12 are outperformed the compared algorithms. On the last 15 test problems (15 objectives), the average IGD values obtained by Two Arch-D on the problems of MaF2 and MaF5 are outperformed the other comparison algorithms.
Among the 45 problems, the performance of Two Arch-D on 15 problems is statistically better than other compared algorithms, which indicates that the Two Arch-D algorithm has a good performance on IGD. On 23, 23, 23, 26, 17, 14 and 18 problems, Two Arch-D performed better than NSGAIII, MOEA/DD, KnEA, RVEA, hpaEA, VaEA and NSGAIISDR. However, NSGAIII, MOEA/DD, KnEA, RVEA, hpaEA, VaEA and NSGAIISDR performed similarly to Two Arch-D on two, two, three, two, two, four and zero problems. On 20, 17, 19, 17, 26, 27 and 27 problems, the average IGD of Two Arch-D was smaller than other compared algorithms, respectively. In summary, it can be seen from the experimental data that the performance of Two Arch-D algorithm is superior to NSGAIII, MOEA/DD, KnEA and RVEA algorithms for most test problems. This also shows the excellent performance of Two Arch-D algorithm in estimating convergence and diversity.
The test problem MaF3 can clearly show the convergence of the algorithm, so the IGD value obtained by algorithm Two Arch-D on the MaF3 problem (5 objective, 10 objective and 15 objective) varies with the evaluation numbers as shown Figure 3, Figure 4 and Figure 5. It can be seen that the proposed algorithm performs well in terms of convergence.
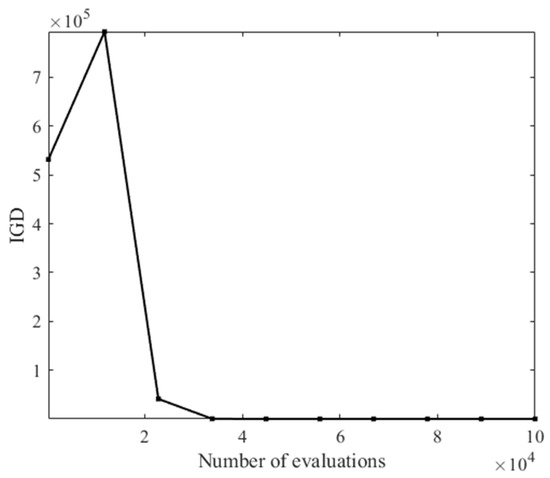
Figure 3.
Change of IGD value with the number of assessments (5 objective).
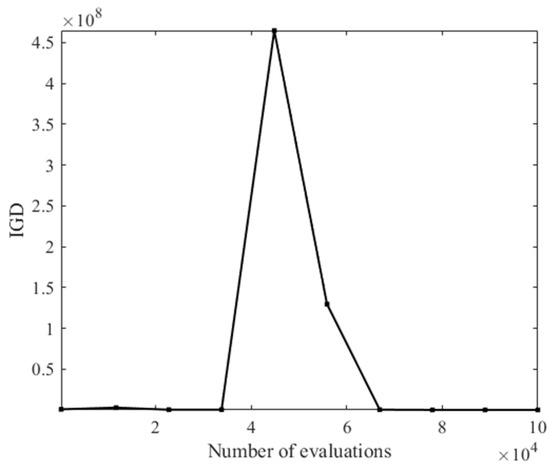
Figure 4.
Change of IGD value with the number of assessments (10 objective).
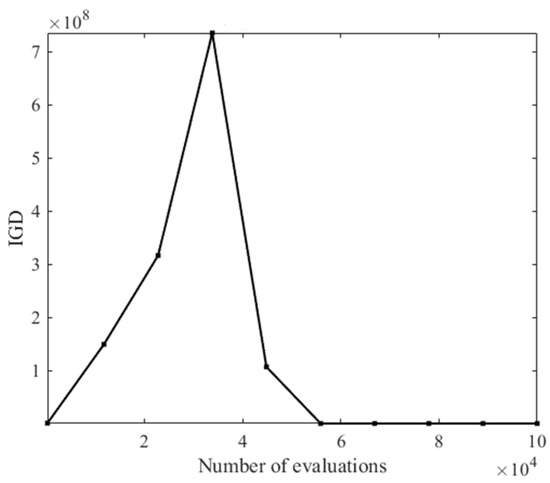
Figure 5.
Change of IGD value with the number of assessments (15 objective).
3.5. Value of Parameter β
In order to make the comparison results more accurate, the population size, target dimension and function evaluation times to be input for each test problem are the same, and only the value of parameter is changed. The value range of parameter is . In order to determine the optimal value of β, the performance of the algorithm with different values of β is tested in 15 test problems. Each test question was run independently 20 times, and the average IGD measurements obtained are shown in Table 3, Table 4 and Table 5. In conclusion, different values of parameter β have different effects on the algorithm performance in most problems. For the problem MaF1–MaF5, the algorithm performs well when β is 0.2, 0.6, 0.8, 0.9 and 1.2. For MaF6–MaF10, the average value of IGD is small when β is 0.2 and 1.0; for MaF11–MaF15, different values of β had little effect on the algorithm, and the average value of IGD changed little. Especially for MaF11, MaF12 and MaF13, the algorithm was more stable. Overall, among the 15 test questions, with the parameter β of 0.2, 0.3 and 1.0, better times are obtained.

Table 3.
IGD mean obtained by Two Arch-D with different β.

Table 4.
IGD mean obtained by Two Arch-D with different β.

Table 5.
IGD mean obtained by Two Arch-D with different β.
3.6. Discusion
The high-dimensional many-objective optimization problem is closely related to our life and production and has been widely used in various fields, such as power scheduling, network optimization, chemical production, structure design and path planning, so the research on the high-dimensional many-objective optimization algorithm has important practical significance. For example, the algorithm proposed can be applied to the operation and scheduling of high-speed railway trains. Due to the continuous growth of passenger traffic volume and the increasing demand for high-speed railway service quality, it is necessary to optimize the operation adjustment method of high-speed railway trains. Taking the punctuality rate of train operation, passenger comfort and delay time as optimization objectives, a multi-objective optimization model is established to minimize the total number of train delays, and the proposed algorithm is applied to provide a fast and reasonable train operation adjustment scheme for dispatchers.
4. Conclusions
This paper uses CA archives and DA archives to equilibrate diversity and convergence. On this basis, the adaptive strategy D-domination method and the improved Tchebycheff are used to preserve the convergent solutions, and a set of uniformly distributed solutions are obtained. The adaptive strategy D-domination method is adopted. On the one hand, the β value is automatically adjusted during the algorithm execution, which makes the β value more reasonable. On the other hand, the implementation of the D-domination method is based on PBI decomposition, making the update of each individual in the population centered on itself, reducing the dependence on the decomposition vector. At the same time, the improved Tchebycheff function is used to exert selection pressure on the population to select solutions with better convergence. The goal of better identifying solutions and balancing convergence and diversity in high-dimensional objective space is realized. The effectiveness of the proposed method is verified by a series of comparative experiments. The main work in the future is to apply the proposed algorithm to the operation and scheduling of high-speed railway trains mentioned in Section 3.6.
Author Contributions
Conceptualization, N.Y., X.X. and C.D.; methodology, N.Y., X.X. and C.D.; software, N.Y. and X.X.; validation, N.Y.; formal analysis, N.Y. and C.D.; data curation, N.Y., X.X. and C.D.; writing—original draft preparation, N.Y.; writing—review and editing, N.Y. and C.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by National Natural Science Foundations of China (no.12271326, no. 61806120, no. 61502290, no. 61401263, no. 61672334, no. 61673251), China Postdoctoral Science Foundation (no. 2015M582606), Industrial Research Project of Science and Technology in Shaanxi Province (no. 2015GY016, no. 2017JQ6063), Fundamental Research Fund for the Central Universities (no. GK202003071), Natural Science Basic Research Plan in Shaanxi Province of China (no. 2022JM-354).
Data Availability Statement
The data used to support the findings of this study are available from the corresponding author upon request.
Acknowledgments
In this work, Xinyu Liang, Zhu Liu, Cheng Peng and Zhibin Zhou provided some helps. Thanks for their help.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Coello Coello, C.A.; Lamont, G.B.; Van Veldhuizen, D.A. (Eds.) Basic Concepts; Springer: Boston, MA, USA, 2007; pp. 1–60. [Google Scholar]
- Koessler, E.; Almomani, A. Hybrid particle swarm optimization and pattern search algorithm. Optim. Eng. 2021, 22, 1539–1555. [Google Scholar] [CrossRef]
- Cherki, I.; Chaker, A.; Djidar, Z.; Khalfallah, N.; Benzergua, F. A Sequential Hybridization of Genetic Algorithm and Particle Swarm Opti mization for the Optimal Reactive Power Flow. Sustainability 2019, 11, 3862. [Google Scholar] [CrossRef]
- Eslami, M.; Shareef, H.; Mohamed, A.; Khajehzadeh, M. Damping controller design for power system oscillations using hybrid ga-sqp. Int. Rev. Electr. Eng. 2011, 6, 888–896. [Google Scholar]
- Kaveh, A.; Ghazaan, M.; Abadi, A.A. An improved water strider algorithm for optimal design of skeletal structures. Period. Polytech. Civ. Eng. 2020, 64, 1284–1305. [Google Scholar] [CrossRef]
- Delice, A.Y.; Aydoan, E.K.; Özcan, U.; lkay, M.S. A modified particle swarm optimization algorithm to mixed-model two-sided assembly line balancing. J. Intell. Manuf. 2017, 28, 23–36. [Google Scholar] [CrossRef]
- Mohammad, A.K.; Raihan, T.M.; Mahdiyeh, E. Multi-objective optimisation of retaining walls using hybrid adaptive gravitational search algorithm. Civ. Eng. Environ. Syst. 2014, 31, 229–242. [Google Scholar]
- Khajehzadeh, M.; Taha, M.R.; Eslami, M. Opposition-based firefly algorithm for earth slope stability evaluation. China Ocean Eng. 2014, 28, 713–724. [Google Scholar] [CrossRef]
- Dong, N.; Dai, C. An improvement decomposition-based multi-objective evolutionary algorithm using multi-search strategy. Knowl.-Based Syst. 2019, 163, 572–580. [Google Scholar] [CrossRef]
- Wu, M.; Li, K.; Kwong, S.; Zhang, Q. Evolutionary many-objective optimization based on adversarial decomposition. IEEE Trans. Cybern. 2020, 50, 753–764. [Google Scholar] [CrossRef]
- Liu, S.; Lin, Q.; Tan, K.C.; Gong, M.; Coello, C.A.C. A fuzzy decomposition-based multi/many-objective evolutionary algorithm. IEEE Trans. Cybern. 2022, 52, 3495–3509. [Google Scholar] [CrossRef]
- Ji, H.; Dai, C. A simplified hypervolume-based evolutionary algorithm for many-objective optimization. Complexity 2020, 2020, 8353154. [Google Scholar] [CrossRef]
- Tian, Y.; Cheng, R.; Zhang, X.; Cheng, F.; Jin, Y. An indicator-based multiobjective evolutionary algorithm with reference point adaptation for better versatility. IEEE Trans. Evol. Comput. 2018, 22, 609–622. [Google Scholar] [CrossRef]
- Sun, Y.; Yen, G.G.; Yi, Z. Igd indicator-based evolutionary algorithm for many-objective optimization problems. IEEE Trans. Evol. Comput. 2019, 23, 173–187. [Google Scholar] [CrossRef]
- Bader, J.; Zitzler, E. Hype: An algorithm for fast hypervolume-based many-objective optimization. Evol. Comput. 2011, 19, 45–76. [Google Scholar] [CrossRef]
- Shang, K.; Ishibuchi, H. A new hypervolume-based evolutionary algorithm for many-objective optimization. IEEE Trans. Evol. Comput. 2020, 24, 839–852. [Google Scholar] [CrossRef]
- Liang, Z.; Luo, T.; Hu, K.; Ma, X.; Zhu, Z. An indicator-based many-objective evolutionary algorithm with boundary protection. IEEE Trans. Cybern. 2021, 51, 4553–4566. [Google Scholar] [CrossRef]
- While, L.; Hingston, P.; Barone, L.; Huband, S. A faster algorithm for calculating hypervolume. IEEE Trans. Evol. Comput. 2006, 10, 29–38. [Google Scholar] [CrossRef]
- Menchaca-Mendez, A.; Coello, C.A.C. A new selection mechanism based on hypervolume and its locality property. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 924–931. [Google Scholar]
- Tian, Y.; Cheng, R.; Zhang, X.; Su, Y.; Jin, Y. A strengthened dominance relation considering convergence and diversity for evolutionary many-objective optimization. IEEE Trans. Evol. Comput. 2019, 23, 331–345. [Google Scholar] [CrossRef]
- Yang, S.; Li, M.; Liu, X.; Zheng, J. A grid-based evolutionary algorithm for many-objective optimization. IEEE Trans. Evol. Comput. 2013, 17, 721–736. [Google Scholar] [CrossRef]
- Xiang, Y.; Zhou, Y.; Li, M.; Chen, Z. A vector angle-based evolutionary algorithm for unconstrained many-objective optimization. IEEE Trans. Evol. Comput. 2017, 21, 131–152. [Google Scholar] [CrossRef]
- Seada, H.; Abouhawwash, M.; Deb, K. Multiphase balance of diversity and convergence in multiobjective optimization. IEEE Trans. Evol. Comput. 2019, 23, 503–513. [Google Scholar] [CrossRef]
- Xiang, Y.; Zhou, Y.; Yang, X.; Huang, H. A many-objective evolutionary algorithm with pareto-adaptive reference points. IEEE Trans. Evol. Comput. 2020, 24, 99–113. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. Moea/d: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Li, K.; Deb, K.; Zhang, Q.; Kwong, S. An evolutionary many-objective optimization algorithm based on dominance and decomposition. IEEE Trans. Evol. Comput. 2015, 19, 694–716. [Google Scholar] [CrossRef]
- Gu, F.; Cheung, Y.-M. Self-organizing map-based weight design for decomposition-based many-objective evolutionary algorithm. IEEE Trans. Evol. Comput. 2018, 22, 211–225. [Google Scholar] [CrossRef]
- Liu, H.-L.; Chen, L.; Zhang, Q.; Deb, K. Adaptively allocating search effort in challenging many-objective optimization problems. IEEE Trans. Evol. Comput. 2018, 22, 433–448. [Google Scholar] [CrossRef]
- Chen, H.; Tian, Y.; Pedrycz, W.; Wu, G.; Wang, R.; Wang, L. Hyperplane assisted evolutionary algorithm for many-objective optimization problems. IEEE Trans. Cybern. 2020, 50, 3367–3380. [Google Scholar] [CrossRef]
- Yi, J.; Bai, J.; He, H.; Peng, J.; Tang, D. ar-moea: A novel preference-based dominance relation for evolutionary multiobjective optimization. IEEE Trans. Evol. Comput. 2019, 23, 788–802. [Google Scholar] [CrossRef]
- Chen, L.; Liu, H.; Tan, K.C.; Cheung, Y.; Wang, Y. Evolutionary many-objective algorithm using decomposition-based dominance relationship. IEEE Trans. Cybern. 2019, 49, 4129–4139. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part i: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Zhang, X.; Tian, Y.; Jin, Y. A knee point-driven evolutionary algorithm for many-objective optimization. IEEE Trans. Evol. Comput. 2015, 19, 761–776. [Google Scholar] [CrossRef]
- Cheng, R.; Jin, Y.; Olhofer, M.; Sendhoff, B. A reference vector guided evolutionary algorithm for many-objective opti-mization. IEEE Trans. Evol. Comput. 2016, 20, 773–791. [Google Scholar] [CrossRef]
- Cheng, R.; Li, M.; Tian, Y.; Xiang, X.; Zhang, X.; Yang, S.; Jin, Y.; Yao, X. Benchmark functions for cec’2018 competition on many-objective optimization. Complex Intell. Syst. 2017, 3, 1–22. [Google Scholar] [CrossRef]
- Steel, R.G.D.; Torrie, J.H. Principles and Procedures of Statistics. (With Special Reference to the Biological Sciences.); McGraw-Hill Book Company: New York, NY, USA; Toronto, ON, Canada; London, UK, 1960; pp. 207–208. [Google Scholar]
- Tian, Y.; Cheng, R.; Zhang, X.; Jin, Y. Platemo: A matlab platform for evolutionary multi-objective optimization [educational forum]. IEEE Comput. Intell. Mag. 2017, 12, 73–87. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L.; Laumanns, M.; Fonseca, C.M.; da Fonseca, V.G. Performance assessment of multiobjective optimizers: An analysis and review. IEEE Trans. Evol. Comput. 2003, 7, 117–132. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).