Abstract
Currently, the User-PC computingsystem (UPC) has been studied as a low-cost and high-performance distributed computing platform. It uses idling resources of personal computers (PCs) in a group. The job-worker assignment for minimizing makespan is critical to determine the performance of the UPC system. Some applications need to execute a lot of uniform jobs that use the identical program but with slightly different data, where they take the similar CPU time on a PC. Then, the total CPU time of a worker is almost linear to the number of assigned jobs. In this paper, we propose a static assignment algorithm of uniform jobs to workers in the UPC system, using simultaneous linear equations to find the lower bound on makespan, where every worker requires the same CPU time to complete the assigned jobs. For the evaluations of the proposal, we consider the uniform jobs in three applications. In OpenPose, the CNN-based keypoint estimation program runs with various images of human bodies. In OpenFOAM, the physics simulation program runs with various parameter sets. In code testing, two open-source programs run with various source codes from students for the Android programming learning assistance system (APLAS). Using the proposal, we assigned the jobs to six workers in the testbed UPC system and measured the CPU time. The results show that makespan was reduced by on average, which confirms the effectiveness of the proposal.
1. Introduction
Currently, the User-PC computing (UPC) system has been studied as a low-cost and high-performance distributed computing platform [1]. The UPC system uses idling resources of personal computers (PCs) in a group to handle a number of various computing jobs from users. Then, the proper assignment of incoming jobs to workers is very important to effectively deal with them by using computational resources properly. As a result, the job assignment algorithm is critical to achieve the minimization for makespan to complete all the demanded jobs in the UPC system.
Previously, we proposed the algorithm of assigning non-uniform jobs to workers in the UPC system [2]. In non-uniform jobs, the programs are much different from each other, including the developed programming languages, the number of threads, and the requiring data. The execution time for each non-uniform job is highly different from the others. The previous algorithm can find the job-worker assignment through two stages sequentially, of which are heuristic due to the nature of the NP-hardness and cannot guarantee the optimality of the solution.
Some applications need to execute a lot of uniform jobs that use the identical program but with slightly different data/files, where they take a similar CPU time on a PC. The applications include deep learning (machine learning), physics simulations, software testing, computer network simulations, mathematical modeling, and mechanics modeling. These jobs have the common feature of a similar CPU time when they run on a specific PC. The uniform jobs often need a long CPU time. For example, in physics or network simulations, it can take several days to run one job. Nevertheless, it will be necessary to find the best result of all the input data by repeating them to slightly change some parameter values for the program and running them. This work can be common in research activities using computer simulations.
In this paper, we propose a static assignment algorithm of uniform jobs to workers in the UPC system, using simultaneous linear equations to find the lower bound on makespan, where every worker requires the same CPU time to complete the assigned jobs. The simultaneous linear equations describe the equality of the estimated CPU time among the workers, and the equality of the total number of assigned jobs to workers with the number of given jobs. The estimated CPU time considers simultaneous executions of multiple jobs on one worker by using its multiple cores. Since solutions of simultaneous linear equations become real numbers in general, the integer number of jobs assigned to each worker is introduced to them in a greedy way.
For evaluations of the proposal, we consider uniform jobs in the three applications for the UPC system, namely, OpenPose [3], OpenFOAM [4], and code testing [5,6]. For OpenPose, the CNN-based program runs with 41 images of human bodies. For OpenFOAM, the physics simulation program runs with 32 parameter sets. For unit testing, the open-source programs run with 578 source codes that were submitted from students to the server in the Android programming learning assistance system (APLAS). These jobs were applied to the proposed algorithm and were assigned to six workers in the testbed UPC system by following the results. Then, the CPU time was measured by running them. For comparisons, two simple algorithms were also implemented where the jobs were applied, and the CPU time was measured. The evaluation results show that the difference between the longest CPU time and the shortest one among the six workers became 92 s, and makespan of the UPC system was reduced by on average from the results by comparative algorithms. Thus, the effectiveness of the proposal was confirmed.
The proposed algorithm limits the application to the jobs where the CPU time is nearly equal to a worker. This limitation can simplify the job scheduling algorithm to only considering the number of jobs assigned to each worker, while neglecting the differences between individual jobs. Fortunately, it is possible to alleviate this limitation to a certain degree by considering the granularity of the CPU time on a worker. The CPU time of a job that is applicable to the proposal is often proportional to the number of iteration steps before the termination, or to the number of elements in the computational model. For example, in computer network simulations, the number of iteration steps need to be selected with the unit time before simulations, where the CPU time is usually proportional to it. By considering a multiple of a constant number of iteration steps, such as 100, the CPU time can be estimated even if the number of iteration steps is widely changed with this granularity. In future works, we will study this extension of the proposed algorithm to increase its applicable applications.
The rest of this paper is organized as follows: Section 2 discusses related works. Section 3 reviews the UPC system, OpenPose, OpenFOAM, and code testing in APLAS. Section 4 presents the static assignment algorithm of uniform jobs to workers in the UPC system. Section 5 evaluates the proposal through experiments. Section 6 extends the proposal to multiple job-type assignments. Finally, Section 7 concludes this paper with future works.
2. Related Works in the Literature
In this section, we discuss some related works in the literature.
In [7], Lin proposed several linear programming models and algorithms for identical jobs (uniform jobs) on parallel uniform machines for individual minimizations of several different performance measures. The proposed linear programming models provide structured insights of the studied problems and provide an easy way to tackle the scheduling problems.
In [8], Mallek et al. addressed the problem of scheduling identical jobs (uniform jobs) on a set of parallel uniform machines. The jobs are subjected to conflicting constraints modeled by an undirected graph G, in which adjacent jobs are not allowed to be processed on the same machine. The minimization of the maximum makespan in the schedule is known to be NP-hard. To solve the general case of this problem, they proposed mixed-integer linear programming formulations alongside lower bounds and heuristic approaches.
In [9], Bansal et al. proposed the two-stage Efficient Refinery Scheduling Algorithm (ERSA) for distributed computing systems. In the first stage, it assigns a task according to the min–max heuristic. In the second stage, it improves the scheduling by using the refinery scheduling heuristic that balances the loads across the machines and reduces makespan.
In [10], Murugesan et al. proposed a multi-source task scheduler to map the tasks to the distributed resources in a cloud. The scheduler has three phases: the task aggregation, the task selection, and the task sequencing. By using the ILP formulation, this scheduler minimizes makespan while satisfying the budget allotted by the cloud user based on the divisible load theory.
In [11], Garg et al. proposed the adaptive workflow scheduling (AWS) for grid computing using the dynamic resources based on the rescheduling method. The AWS has three stages of the initial static scheduling, the resource monitoring, and the rescheduling, to minimize makespan using the directed acyclic graph workflow model for grid computing. It deals with the heterogeneous dynamic grid environment, where the availability of computing nodes and link bandwidths are inevitable due to existences of loads.
In [12], Gawali et al. proposed the two-stage Standard Deviation-Based Modified Cuckoo Optimization Algorithm (SDMCOA) for the scheduling of distributed computing systems. In the first stage, it calculates the sample initial population among all the available number of task populations. In the second stage, the modified COA immigrates and lays the tasks.
In [13], Bittencourt et al. reviewed existing scheduling problems in cloud computing and distributed systems. The emergence of distributed systems brought new challenges on scheduling in computer systems, including clusters, grids, and clouds. They defined a taxonomy for task scheduling in cloud computing, namely, pre-cloud schedulers and cloud schedulers, and classified existing scheduling algorithms in the taxonomy. They introduced future directions for scheduling research in cloud computing.
In [14], Attiya et al. presented a modified Harris hawks optimization (HHO) algorithm based on the simulated annealing (SA) for scheduling the jobs in a cloud environment. In this approach, SA is employed as a local search algorithm to improve the convergence rate and the solution quality generated by the standard HHO algorithm. HHO is a novel population-based, nature-inspired optimization paradigm proposed by Heidari et al. [15]. The main inspiration of HHO is the cooperative behavior and the chasing style of Harris’ hawks in nature. In the HHO model, several hawks explore prey, respectively, and simultaneously after attacking the target from different directions to surprise it.
In [16], Al-Maytami et al. presented a novel scheduling algorithm using Directed Acyclic Graph (DAG) based on the Prediction of Tasks Computation Time algorithm (PTCT) to estimate the preeminent scheduling algorithm for prominent cloud data. The proposed algorithm provides a significant improvement with respect to makespan and reduces the computational complexity via employing Principal Components Analysis (PCA) and reducing the Expected-Time-to-Compute (ETC) matrix.
In [17], Panda et al. proposed an energy-efficient task scheduling algorithm (ETSA) to address the demerits associated with the task consolidation and scheduling. The proposed algorithm ETSA takes into account the completion time and the total utilization of a task on the resources, and follows a normalization procedure to make a scheduling decision. The ETSA provides an elegant trade-off between energy efficiency and makespan, more so than the existing algorithms.
3. Reviews of UPC System and Three Applications
In this section, we review the User-PC computing system (UPC) system and the three applications in this paper.
3.1. UPC System
First, we review the UPC system. The UPC system can provide computational powers efficiently for members in a group, such as engineers in a company or students in a laboratory, by using idling computing resources of their PCs. To allow various application programs to run on different PC environments, the UPC system adopts Docker. Docker is a popular software tool that has been designed to create, deploy, and execute various application programs on various platforms by packaging the necessary dependencies of the application [18].
Figure 1 shows the overview of the UPC system. The UPC system adopts the master-worker model. Users submit computing jobs to the UPC master through the UPC web server. After synchronizations of the jobs, the UPC master assigns the submitted jobs to the appropriate UPC workers. Each worker computes its assigned jobs and returns the results to the master upon completion. Users can access the results at the web browser.
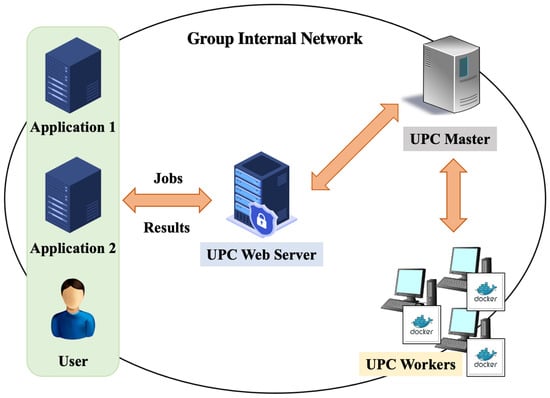
Figure 1.
Overview of UPC system.
For further details, the usage flow of the UPC system will be described:
- 1.
- Job reception: A user submits jobs from the web browser and requests to compute them in the UPC system.
- 2.
- Worker assignment: The UPC master selects an appropriate active worker to compute each job using a job-worker assignment algorithm.
- 3.
- Docker image generation: The UPC master generates the Docker image to execute the job on the assigned worker.
- 4.
- Docker image transmission: The master sends the Docker image to the assigned worker.
- 5.
- Job execution: The worker generates the Docker container from the image and executes the job there.
- 6.
- Result transmission: The worker returns the result to the master upon completion.
- 7.
- Result response: The master shows the computing results of the jobs to the user through the web server.
3.2. OpenPose
Next, we review OpenPose. It has been developed by researchers at Carnegie Mellon University and is an popular open-source software for real-time human pose estimation [3]. It extracts the feature points, called keypoints, of the human body in the given image using Convolutional Neural Network (CNN). The keypoints represent the important joints in a human body, the contours of eyes, lips in the face, fingertips, and joints in the hands and feet. Using the keypoints, the shapes of a body, face, hands, and feet can be described. Since it has been developed based on CNN, the CPU time is very long when computed on a conventional PC.
OpenPose is used in our group for developing the exercise and performance learning assistant system (EPLAS) to assist practicing exercises or learning performances by themselves at home [19]. EPLAS offers video content of Yoga poses by instructors whose performances should be followed by users. During the practice, it automatically takes photos of important scenes of the user. Then, it extracts the keypoints of the human body using OpenPose to rate the poses in the photos by comparing the coordinates of them between the user and the instructor.
3.3. OpenFOAM
Then, we review OpenFOAM. It is an open-source software for the computational fluid dynamics (CFD) simulations and has been developed primarily by OpenCFD Ltd. (Bracknell, UK) It has an extensive range of features to solve anything from complex fluid flows involving chemical reactions, turbulence, and heat transfer, to acoustics, solid mechanics, and electromagnetics [4]. Furthermore, the optimal parameter selection is critical for the high accuracy of the results, and it needs a lot of iterations of selecting parameters in OpenFOAM and running it with the parameter values. We applied the parameter optimization method for OpenFOAM [20]; it needs to run OpenFOAM with a lot of different parameters.
Meanwhile, it is also applied for developing the air conditioning guidance system [21] in our research. The estimation or prediction of the distributions of the temperature or humidity inside a room using this simulation model is necessary to properly control the air conditioner. By estimating the room environment changes under various actions, it will be possible to decide when the air conditioner is turned on or off. Even the timing to open or close windows in the room can be selected. To estimate or predict the distributions in a room together with sensors, the CFD simulation using OpenFOAM has been investigated. Then, the optimization of the parameters in OpenFOAM is critical in order to fit the simulation results well with the corresponding measured ones.
3.4. Code Testing
Finally, we review the code testing in the Android programming learning assistance system (APLAS). APLAS has been developed in our group as the automatic and self-learning system for Android programming using Java and XML [5,6]. The code testing is the process to validate a source code by running the corresponding test code on a testing framework. To confirm the validity of the answer source code from a student in satisfying the required specifications in the assignment, APLAS implements the code testing function using JUnit for unit testing of Java codes [22] and Robolectric for integration testing with XML codes [23,24]. APLAS needs to run the code testing function with a lot of different source codes from many students, which usually takes a long time.
In ALPAS, Java codes can be directly tested on JUnit. However, the Android-specific components, such as the Layout, the Activity, the Event Listener, and the Project Resources that will be described in XML, cannot be directly tested on JUnit. The building tool Gradle is used to build and integrate them as Java classes. Then, Robolectric is used to generate Java objects—called shadow objects—for them, so that they can be tested on JUnit.
4. Proposal of Static Uniform Job Assignment Algorithm
In this section, we present the static uniform job assignment algorithm to workers in the UPC system.
4.1. Objective
To design the algorithm, it is observed that when the makespan of every worker becomes equal, the objective of the problem on the makespan minimization can be achieved. Otherwise, the maximum makespan can be reduced by moving some jobs at the bottleneck worker which determines this maximum makespan to other workers, if the number of assigned jobs to any worker can take a real number. Only when every worker has the same makespan, the maximum makespan cannot be reduced.
The minimization of the maximum makespan among all the workers is given as the objective of the problem, where makespan at worker w for type t is given by the summation of the CPU time for preparation and execution.
4.2. Simultaneous Linear Equations
In this paper, the following simultaneous linear equations have been derived to find the optimal job-worker assignment, such that the estimated CPU time required to complete the assigned jobs becomes equal among all the workers. The solutions of the simultaneous linear equations will be the lower bound on makespan. Since the solutions become real numbers in general, the integer number of assigned jobs to each worker should be introduced to them.
To satisfy the objective of the equal CPU time among the workers, gives the best CPU time to solve one job at worker w by running jobs.
4.3. Problem Formulation
To present the static uniform jobs assignment algorithm to workers in the UPC system, the problem to be solved is formulated here.
4.3.1. Variables
The following variables are defined for the problem to be solved:
- t: Particular job type;
- w: Particular worker;
- : # of the assigned jobs to worker w for type t;
- : Makespan at worker w to complete all the assigned jobs for type t;
- : # of running jobs in parallel using multi-threads at worker w.
4.3.2. Constants
The following constants are given as the inputs to this problem:
- T: Set of job types;
- W: Set of workers;
- : Total # of jobs for type t;
- : # of jobs for the best throughput at worker w for any type;
- : CPU time at worker w to prepare job executions for type t;
- : CPU time at worker w to execute d jobs for type t in parallel.
Here, represents the number of simultaneously running jobs for job type t at worker w, which maximizes the number of completed jobs per unit time. This is constant for any job type in each application, because it depends on the common program in the application for every job type.
represents the CPU time required to initiate the execution of the program at worker w. For example, in the code testing application, it represents the CPU time to initiate the Gradle Wrapper daemon and generate shadow objects that are necessary to run the code testing function.
can be measured using any worker by running jobs for job type t while increasing the number of running jobs in parallel from 1 until .
4.3.3. Constraints
The following two constraints must be satisfied in the problem:
- The total number of the assigned jobs to workers must be equal to for any type t.
- Any worker cannot run d jobs in parallel when d is larger than the (let for worker w) due to the PC specifications.
4.4. Conditions for Uniform Job Assignment
For the uniform job assignment to workers in the UPC system, the following conditions are assumed:
- Several job types may exist for uniform jobs in each application, where different job types may need the different CPU time, memory size, and number of CPU cores due to the differences in data;
- Each job is fully executed on one worker until it is completed;
- Each worker may have different performance specifications from the others;
- Each worker may have a different number of running jobs in parallel, using multi-threads for the best throughput;
- The CPU time to run the certain number of jobs in parallel is given for each worker and job type.
4.5. Static Uniform Job Assignment Algorithm
Here, we note that the CPU time may be different depending on the number of running jobs in parallel in each worker that has multiple cores. To reduce the CPU time by increasing the job completion throughput, jobs of type t should run at worker w as much as possible, since it will give the best throughput. Based on this observation, we present the three-step static uniform job assignment algorithm. Figure 2 shows the flowchart of the proposal.
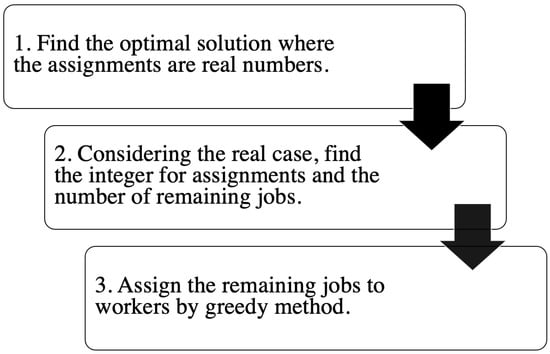
Figure 2.
Flowchart of the proposal.
4.5.1. First Step
4.5.2. Second Step
The solution in the first step becomes feasible only when is a multiple of for type t. Unfortunately, does not satisfy the condition, in general. Therefore, in the second step, as the closest integer number to satisfy the condition, the following jobs will be assigned to the worker (worker w), where gives the largest integer equal to or smaller than y:
Then, the number of the remaining jobs (let for type t) is calculated by:
Besides, the estimated makespan for each worker (let for worker w and job type t) after the job assignment is calculated by:
Therefore, after completing the procedures for all the job types, the estimated makespan for each worker is calculated by:
As the objective of the algorithm, the maximum estimated makespan among the workers is calculated by:
4.5.3. Third Step
In the third step, the remaining jobs () in the second step will be assigned to workers in a greedy way, such that the increase in the maximum estimated makespan is minimized. It is noted that the remaining jobs may exist for any job type. Here, to utilize the parallel job computation using multiple threads on multiple cores for each worker as much as possible, the simultaneous assignment of multiple jobs to one worker is always considered.
- 1.
- Find the worker whose is smallest among the workers (let worker w).
- 2.
- Assign jobs to worker w.
- 3.
- Update the number of the remaining jobs (), and the number of assigned jobs and makespan of the worker w by:
- 4.
- If the number of the remaining jobs becomes zero (), terminate the procedure.
- 5.
- Go to 1.
5. Evaluation
In this section, we evaluate the proposal through extensive experiments which are running jobs in three applications on the testbed UPC system.
5.1. Testbed UPC System
Table 1 shows the PC specifications in the testbed UPC system. One master and six workers are used here.

Table 1.
PC specifications.
5.2. Jobs
Table 2 shows the specifications of the jobs for the eight job types in our experiments. For the code testing application in APLAS, six job types are prepared, where each job type represents one assignment to students in APLAS. These job types run the same programs of JUnit and Robolectric, but accept many different data of answer source codes and test codes. For the other applications, only one job type is considered.

Table 2.
Job specifications.
5.3. CPU Time
Table 3 shows the constant CPU time required to start running the jobs on each worker for each of the six job types. Table 4, Table 5 and Table 6 show the increasing CPU time when the number of jobs is increased by one until the number for the best throughput for each type.

Table 3.
Constant CPU time to start jobs (s).

Table 4.
Increasing CPU time at PC1∼PC4 (s).

Table 5.
Increasing CPU time at PC5 (s).

Table 6.
Increasing CPU time at PC6 (s).
Through preliminary experiments, we found the number of simultaneously running jobs for the highest throughput for each worker. For code testing in APLAS, PC1, PC2, and PC3 can run only one job in parallel due to the low specifications. This number is two for PC4, five for PC5, and six for PC6. For OpenPose, any worker can only execute one job because it uses a lot of threads to compute CNN. For OpenFOAM, for each worker, the CPU time is constant at any number of simultaneously running jobs until it reaches the number of cores in the worker.
5.4. Comparative Algorithms
For performance comparisons, we implemented two simple algorithms to assign non-uniform jobs to workers.
The first one is the First-Come-First-Serve (FCFS) algorithm. It assigns each job to the first available worker, starting from the worker with the highest specification until the one with the lowest. It limits the worker to executing only one job at a time.
The second is the best throughput-based FCFS (T-FCFS) algorithm. The difference between T-FCFS and FCFS is that each worker may execute multiple jobs simultaneously until the best throughput.
5.5. Total Makespan Results
Table 7 compares the maximum makespan results for each job type when the testbed UPC system runs the jobs by following the assignments found by the algorithms. Furthermore, it shows the lower bound (LB) on the maximum makespan found at First Step of the proposed algorithm for the reference of them.

Table 7.
Maximum makespan results (s).
The results indicate that for any job type, the maximum makespan result by the proposal is better than the results by the two compared algorithms and is close to the lower bound. Thus, the effectiveness of the proposal is confirmed. It is noted that the results by FCFS are far larger than the ones by the others because FCFS does not consider simultaneous multiple job executions for a worker.
5.6. Individual Makespan Results
For reference, Table 8, Table 9 and Table 10 show makespan or the total CPU time of each worker and the largest CPU time difference between the workers and the three algorithms. For OpenFOAM, no job was assigned to PC1–PC4, because all of the 32 jobs can be executed simultaneously at PC5 and PC6. The largest CPU time difference by the proposal is smaller than the ones by the others, except for ColorGame, SoccerMatch, AnimalTour, and MyLibrary, where in Table 4, the increasing CPU time of PC1 is much larger than other workers, and the far smaller number of jobs was assigned. Therefore, the proposal can balance well the job assignments among the workers.

Table 8.
FCFS makespan detail (s).

Table 9.
T-FCFS makespan detail (s).

Table 10.
Proposal makespan detail (s).
5.7. Discussions
The results in Table 7 show improvements of maximum makespan results by the proposed algorithm if compared with T-FCFS. However, some differences can be observed against the lower bound.
The current algorithm can find the assignment of some remaining jobs to workers, and assign an integer number of jobs to any worker in a greedy way, after the real number solutions are obtained by solving the simultaneous linear equations. A greedy method is usually difficult to give a near-optimum solution, since it only considers the local optimality under the current assignment.
To improve the solution quality, a local search method using iterations has often been adopted for solving combinatorial optimization problems, including this study. Therefore, we will study the use of a local search method for the remaining job assignment in the proposed algorithm.
6. Extension to Multiple Job Types Assignment
In this section, we extend the proposed algorithm to the case when jobs for multiple job types are assigned together.
6.1. Algorithm Extension
In First Step of the proposed algorithm, the linear equations are modified in this extension to consider the CPU time to complete all the jobs for the plural job types assigned to each worker:
The number of variables to be solved is , where represents the number of workers and represents the number of job types, respectively. Thus, linear equations are necessary to solve them. In the original algorithm, for each job type, linear equations are derived for the CPU time equality and one equation is for the job number. Thus, equations can be introduced.
However, in this extension, the total number of linear equations for the CPU time equality is reduced to because all the job types need to be considered together here. Therefore, to solve the linear equations uniquely, the following linear equations will be introduced by considering the total CPU time for job types together for combinations of job types, in addition to the total CPU time for job types together in (13):
where represents the set of the job types in T except for job type u.
The combinations of job types are selected by excluding the combination where the following estimated total CPU time to execute all the jobs in the remaining job types on PC6 is smallest:
Then, in Second Step and Third Step, the estimated makespan for each worker and the maximum estimated makespan among the workers are modified to consider all the given job types together.
6.2. Total Makespan Results
Table 11 shows the maximum makespan results when the testbed UPC system runs the jobs by following the assignments by the extended algorithm. When compared with the result by the original algorithm, it is reduced by , and becomes closer to the lower bound. The difference between our result and the lower bound is very small. Thus, this extension is effective when plural job types are requested at the UPC system together.

Table 11.
Maximum makespan results (s) by proposal.
6.3. Discussions
The result in Table 11 confirms some reduction in the total makespan result by the extended algorithm. However, there is still a difference when compared to the lower bound. Thus, it is necessary to further improve the algorithm.
One idea for this improvement in the extended algorithm will not be to limit the exclusion of one job type combination—where the estimated total CPU time to execute all jobs in the remaining job types on PC6 is the smallest—and to generate the linear equations for the CPU time equality. Instead, every combination will be excluded one by one to obtain the result for each combination exclusion. Then, the best one will be selected among them.
7. Conclusions
This paper proposed the static uniform job assignment algorithm to workers in the UPC system. The simultaneous linear equations have been derived to find the optimal assignment of minimizing the maximum makespan among the workers, where the CPU time to complete the assigned jobs becomes equal among all the workers.
For an evaluation, the 651 uniform jobs in three applications, OpenPose, OpenFOAM, and code testing in APLAS, were considered to run on six workers in the testbed UPC system, and the makespan was compared with the results by two simple algorithms and the lower bounds. The comparisons confirmed the effectiveness of the proposal.
The novelty of the proposal is that with a very simple formula, it is able to provide the near-optimal solutions to NP-complete problems in the User-PC computing (UPC) system, a typical distributed system. The current algorithm limits the jobs whereby the computing time for a worker is nearly equal. This limitation can simplify our approach of considering the simple assignment of the number of jobs for each worker without considering the differences among individual jobs.
Fortunately, it is possible to alleviate this limitation by considering the granularity of the CPU time for a worker. The CPU time of a job in suitable applications to the proposal is often proportional to the number of iteration steps before the termination or the number of elements in the model. By considering a multiple of a constant number of iteration steps, the CPU time can be estimated even if the number of iteration steps is widely changed with this granularity; this finding will be in future studies.
In future studies, we will also improve the algorithm for remaining job assignments and simultaneous job assignments of multiple job types, and we will study the combination of uniform jobs and non-uniform jobs in the job-worker assignment algorithm for the UPC system.
Author Contributions
Conceptualization, N.F.; Data curation, X.Z. and H.H.; Resources, H.H., A.K., I.T.A., Y.H. and Y.W.S.; Software, X.Z.; Supervision, N.F.; Writing–original draft, X.Z.; Writing–review & editing, N.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this paper:
| UPC | User-PC Computing System |
| PC | Personal Computer |
| APLAS | Android Programming Learning Assistance System |
| CNN | Convolutional Neural Network |
| CFD | Computational Fluid Dynamics |
| XML | Extensible Markup Language |
| CPU | Central Processing Unit |
| ERSA | Efficient Refinery Scheduling Algorithm |
| ILP | Integer Linear Programming |
| AWS | Adaptive Workflow Scheduling |
| COA | Cuckoo Optimization Algorithm |
| SDMCOA | Standard Deviation-Based Modified Cuckoo Optimization Algorithm |
| HHO | Harris Hawks optimization |
| PTCT | Prediction of Tasks Computation Time algorithm |
| PCA | Principal Components Analysis |
| ETC | Expected Time to Compute |
| ETSA | Energy-Efficient Task Scheduling Algorithm |
| SA | Simulated Annealing |
| AC | Air Conditioners |
| LOC | Lines Of Codes |
| FCFS | First Come First Serve |
| T-FCFS | Best Throughput-Based FCFS |
| LB | Lower Bound |
References
- Htet, H.; Funabiki, N.; Kamoyedji, A.; Kuribayashi, M.; Akhter, F.; Kao, W.-C. An implementation of user-PC computing system using Docker container. Int. J. Future Comput. Commun. 2020, 9, 66–73. [Google Scholar]
- Kamoyedji, A.; Funabiki, N.; Htet, H.; Kuribayashi, M. A proposal of job-worker assignment algorithm considering CPU core utilization for user-PC computing system. Int. J. Future Comput. Commun. 2022, 11, 40–46. [Google Scholar] [CrossRef]
- OpenPose 1.7.0. Available online: Cmu-perceptual-computing-lab.github.io/openpose/web/html/doc/index.html (accessed on 15 August 2022).
- OpenFOAM. Available online: ww.openfoam.com (accessed on 15 August 2022).
- Syaifudin, Y.W.; Funabiki, N.; Kuribayashi, M.; Kao, W.-C. A proposal of Android programming learning assistant system with implementation of basic application learning. Int. J. Web Inf. Syst. 2019, 16, 115–135. [Google Scholar] [CrossRef]
- Syaifudin, Y.W.; Funabiki, N.; Mentari, M.; Dien, H.E.; Mu’aasyiqiin, I.; Kuribayashi, M.; Kao, W.-C. A web-based online platform of distribution, collection, and validation for assignments in Android programming learning assistance system. Eng. Lett. 2021, 29, 1178–1193. [Google Scholar]
- Lin, Y. Fast LP models and algorithms for identical jobs on uniform parallel machines. Appl. Math. Model. 2013, 37, 3436–3448. [Google Scholar] [CrossRef]
- Mallek, A.; Bendraouche, M.; Boudhar, M. Scheduling identical jobs on uniform machines with a conflict graph. Comput. Oper. Res. 2019, 111, 357–366. [Google Scholar] [CrossRef]
- Bansal, S.; Hota, C. Efficient refinery scheduling heuristic in heterogeneous computing systems. J. Adv. Inform. Technol. 2011, 2, 159–164. [Google Scholar] [CrossRef]
- Murugesan, G.; Chellappan, C. Multi-source task scheduling in grid computing environment using linear programming. Int. J. Comput. Sci. Eng. 2014, 9, 80–85. [Google Scholar] [CrossRef]
- Garg, R.; Singh, A. Adaptive workflow scheduling in grid computing based on dynamic resource availability. Eng. Sci. Technol. 2015, 18, 256–269. [Google Scholar] [CrossRef][Green Version]
- Gawali, M.B.; Shinde, S.K. Standard deviation based modified Cuckoo optimization algorithm for task scheduling to efficient resource allocation in cloud computing. J. Adv. Inform. Technol. 2017, 8, 210–218. [Google Scholar] [CrossRef]
- Bittencourt, L.F.; Goldman, A.; Madeira, E.R.M.; da Fonseca, N.L.S.; Sakellariou, R. Scheduling in distributed systems: A cloud computing perspective. Comput. Sci. Rev. 2018, 30, 31–54. [Google Scholar] [CrossRef]
- Attiya, I.; Elaziz, M.A.; Xiong, S. Job scheduling in cloud computing using a modified Harris Hawks optimization and simulated annealing algorithm. Comput. Intelli. Neuro. 2020, 2020, 3504642. [Google Scholar] [CrossRef] [PubMed]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris Hawks optimization: Algorithm and applications. Future Gen. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Al-Maytami, B.A.; Hussain, P.F.A.; Baker, T.; Liatsis, P. A Task Scheduling Algorithm With Improved Makespan Based on Prediction of Tasks Computation Time algorithm for Cloud Computing. IEEE Access 2019, 7, 160916–160926. [Google Scholar] [CrossRef]
- Panda, S.K.; Jana, P.K. An energy-efficient task scheduling algorithm for heterogeneous cloud computing systems. Clust. Comput. 2019, 22, 509–527. [Google Scholar] [CrossRef]
- Mouat, A. Using Docker: Developing and Deploying Software with Containers, 1st ed.; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2015. [Google Scholar]
- Anggraini, I.T.; Basuki, A.; Funabiki, N.; Lu, X.; Fan, C.-P.; Hsu, Y.-C.; Lin, C.-H. A proposal of exercise and performance learning assistant system for self-practice at home. Adv. Sci. Technol. Eng. Syst. J. 2020, 5, 1196–1203. [Google Scholar] [CrossRef]
- Zhao, Y.; Kojima, K.; Huo, Y.-Z.; Funabiki, N. CFD parameter optimization for air-conditioning guidance system using small room experimental model. In Proceedings of the 4th Global Conference on Life Sciences and Technologies, Osaka, Japan, 7–9 March 2022; pp. 252–253. [Google Scholar]
- Huda, S.; Funabiki, N.; Kuribayashi, M.; Sudibyo, R.W.; Ishihara, N.; Kao, W.-C. A proposal of air-conditioning guidance system using discomfort index. In InInternational Conference on Broadband and Wireless Computing, Communication and Applications; Springer: Cham, Switzerland, 2020; pp. 154–165. [Google Scholar]
- Wahid, M.; Almalaise, A. JUnit framework: An interactive approach for basic unit testing learning in software engineering. In Proceedings of the 3rd International Conference on Engineering Education and Information Technology, Kuala Lumpur, Malaysia, 17–19 May 2011. [Google Scholar]
- Robolectric. Available online: www.robolectric.org (accessed on 15 August 2022).
- Linares-Vásquez, M.; Bernal-Cardenas, C.; Moran, K.; Poshyvanyk, D. How do developers test android applications. In Proceedings of the 2017 IEEE International Conference on Software Maintenance and Evolution, Shanghai, China, 17–22 September 2017. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).