A Survey on Fault Diagnosis of Rolling Bearings
Abstract
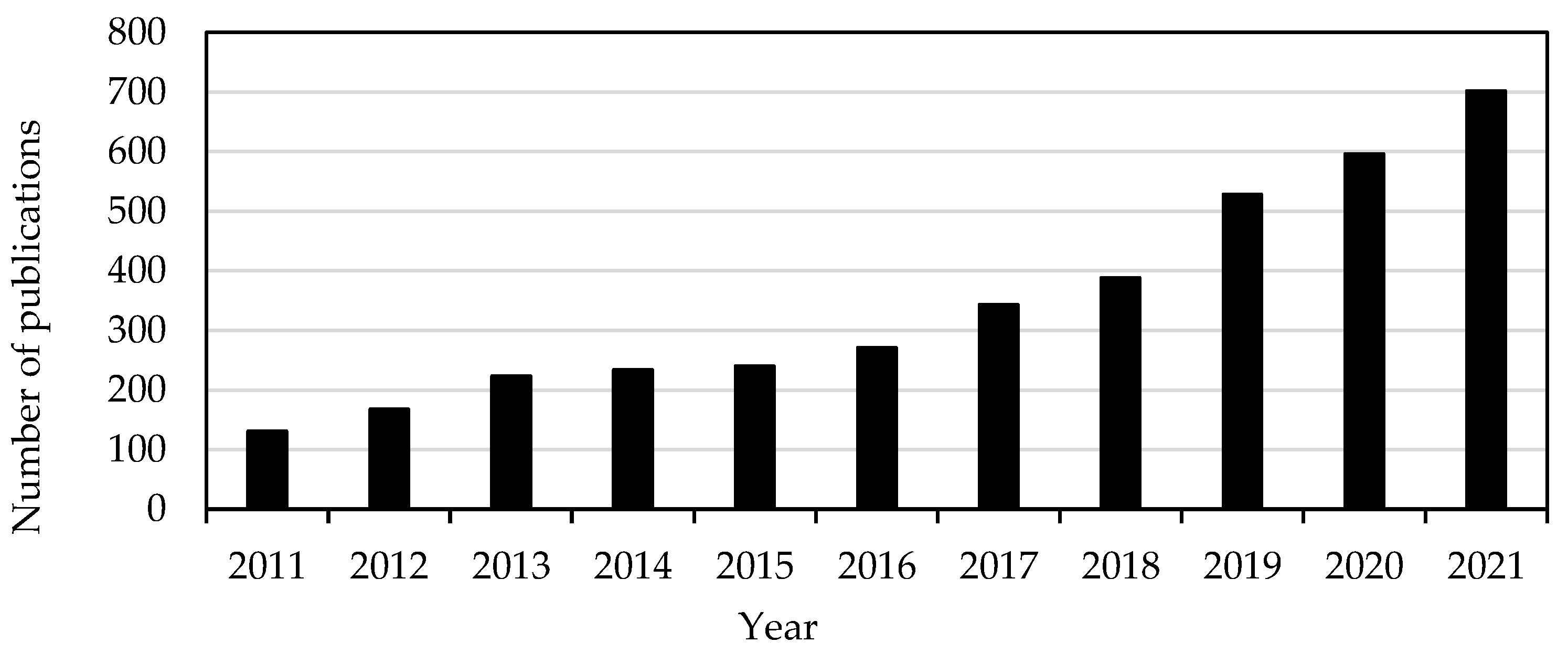
1. Introduction
2. Background, Taxonomy, and Scope
2.1. Fault Forms/Types of Rolling Bearing
- (1)
- Fatigue
- (2)
- Wear
- (3)
- Deformation
- (4)
- Corrosion
- (5)
- Fracture
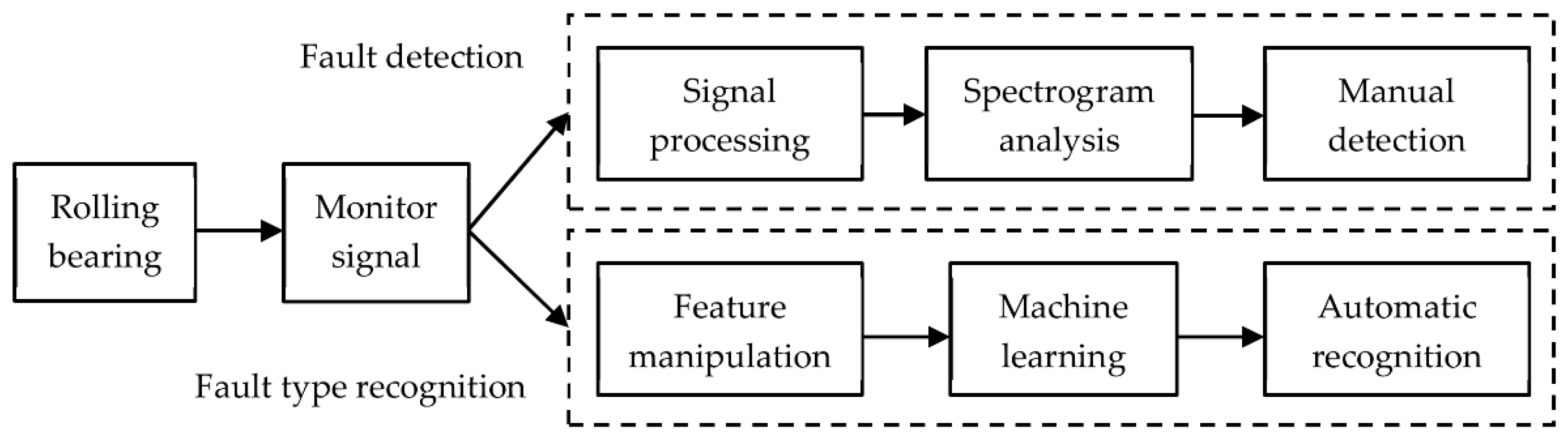
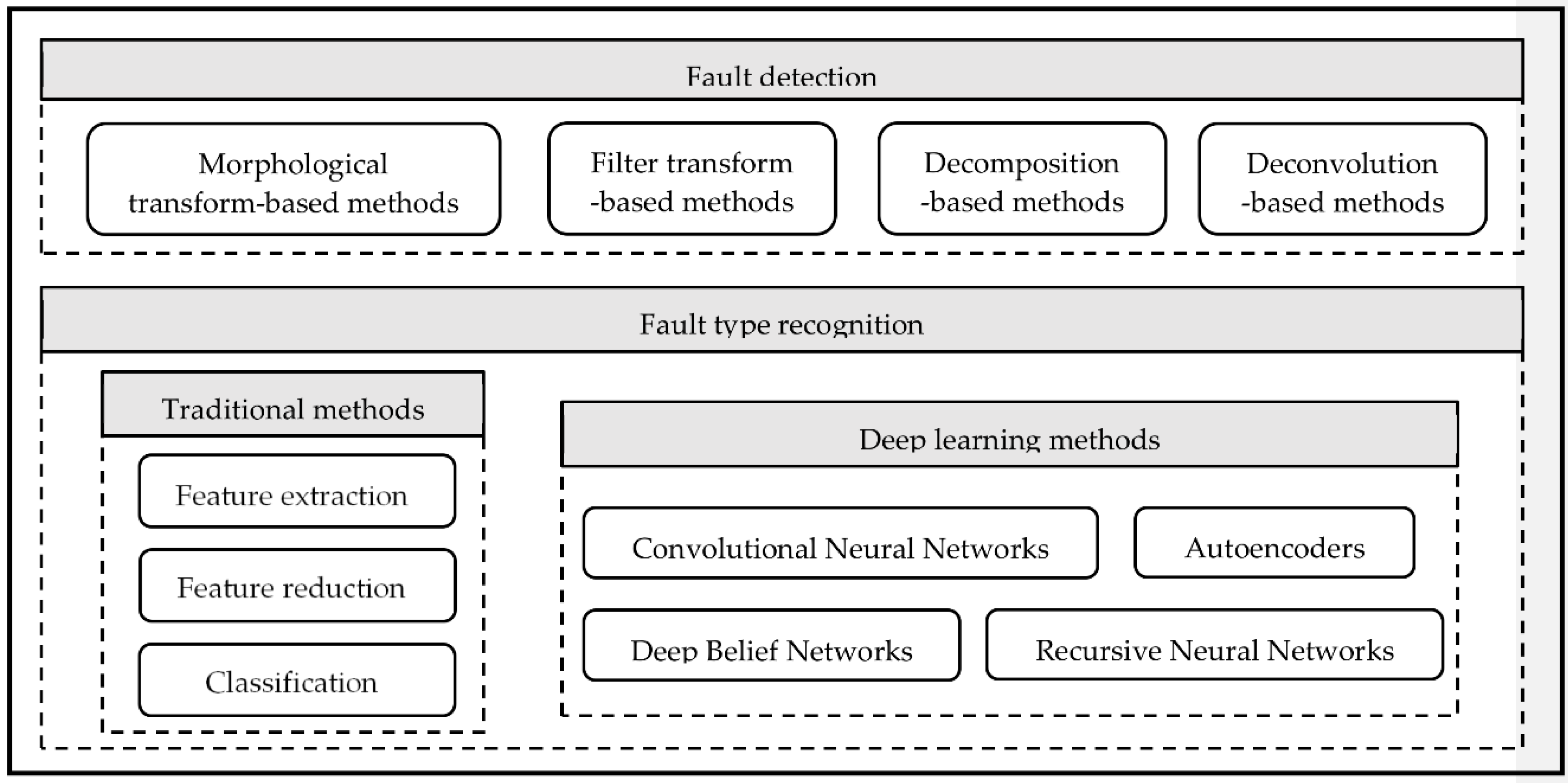
2.2. Taxonomy and Scope
3. Rolling Bearing Fault Detection
3.1. Morphological Transform-Based Fault Detection Methods
3.2. Filter-Based Fault Detection Methods
3.3. Decomposition-Based Fault Detection Methods
3.4. Deconvolution-Based Fault Detection Methods
4. Rolling Bearing Fault Type Recognition
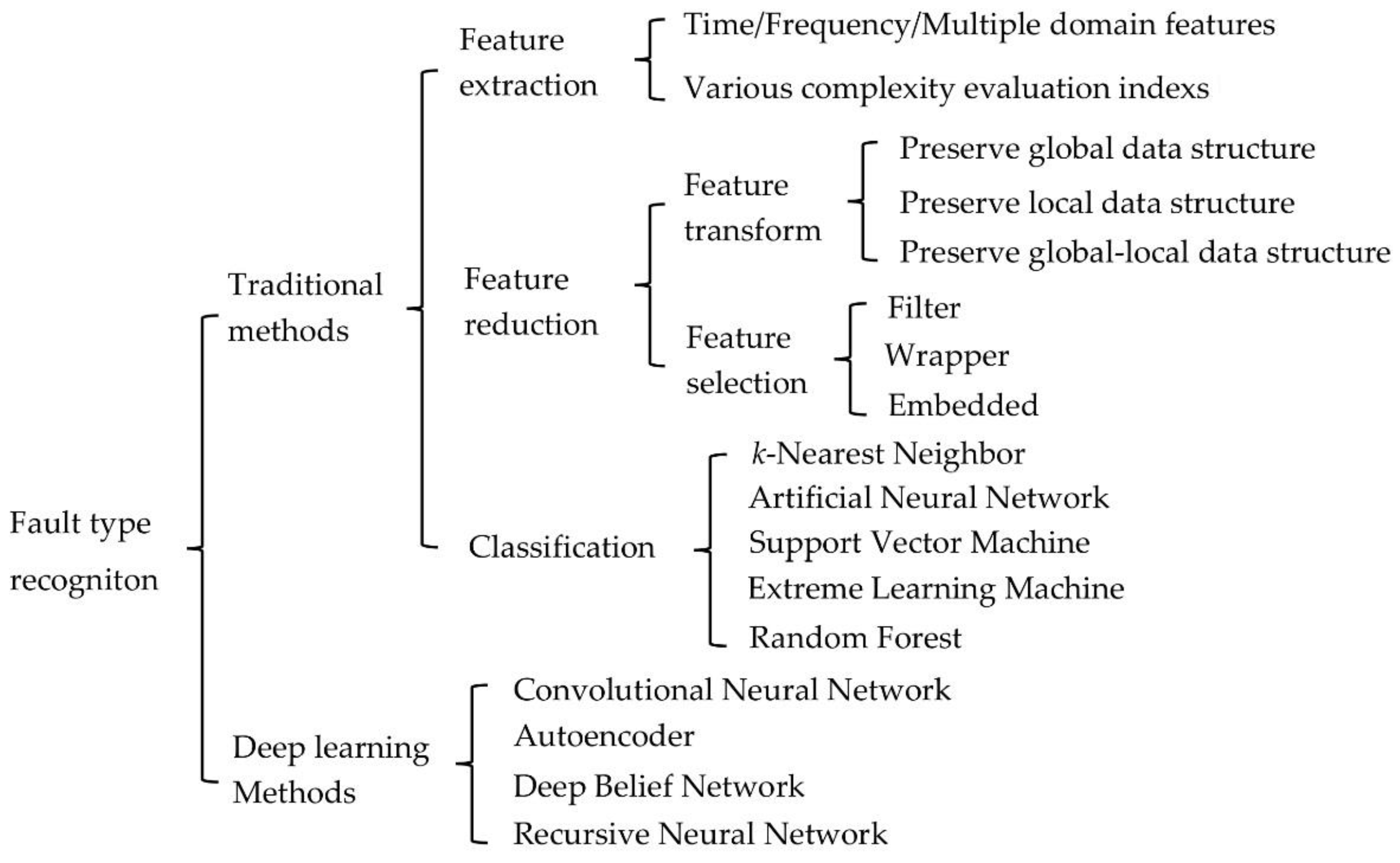
4.1. Traditional Fault Type Recognition Methods
- (1)
- Feature extraction
- (2)
- Feature reduction
- (3)
- Classification
4.2. Deep Learning Based Fault Type Recognition Methods
5. Datasets, Practices, Limitations/Challenges, and Future Research Trends
5.1. Commonly Used Datasets and Practices
5.2. Limitations and Challenges
- (1)
- Limitations of fault detection methods: Some rolling bearing fault detection methods, such as morphological transform-based methods, filter-based methods, decomposition-based methods, and deconvolution-based methods, often need rich domain/prior knowledge to design and use. For example, it should be known in advance how these methods operate, what their advantages and disadvantages are, and whether they are suitable or effective for the task at hand. However, experts with such knowledge are often costly to employ. In addition, the running condition of rolling bearings in actual services is complex and dynamic, making it very hard to develop a method to meet the actual environment. Capturing the periodic impact component caused by the fault in the signal is a good way to achieve fault detection but very challenging. To address this limitation, it is promising to develop an intelligent method that can automatically generate a detection model to adaptively remove the background interference and effectively retain the fault-related impulses.
- (2)
- Limitations of traditional fault type recognition methods: Traditional rolling bearing fault type recognition methods often include three key steps, i.e., feature extraction, feature reduction, and classification. The results of a previous step may influence the outcomes of the following step. To ensure the whole diagnostic process is feasible and effective, each step must be designed elaborately by experienced researchers, such as determining which type of features to choose/extract, which features to use, which classifier to use, and whether the classifier needs to be optimized. However, it should be noted that such a well-designed diagnostic method may only be effective for a specific fault diagnosis task. Therefore, it is promising to design methods that can automatically deal with these subtasks of fault type recognition. In addition, obtaining representative features of sample signals is the key to achieving good results. Therefore, it is a good research direction that develops a diagnostic method to automatically and simultaneously extract and construct representative features from the original bearing signals, to reduce the difficulty of distinguishing samples and improve the accuracy of fault type recognition.
- (3)
- Limitations of deep learning-based fault type recognition methods: Although the deep-learning-based rolling bearing fault type recognition methods can automatically achieve feature extraction, feature reduction, and classification, most of the methods are based on neural networks, which need researchers to design their architectures and adjust the corresponding parameters. The process of model design and parameter adjustment process will consume a significant amount of time and resources. Moreover, the interpretability of the neural network-based methods is not good, i.e., cannot directly express the fault identification process. In addition, these methods usually require a large number of samples to train. However, in practical engineering applications, it is typically difficult to obtain a large number of fault samples, which will limit the use of deep learning-based diagnosis methods.
5.3. Future Research Directions
- (1)
- Transfer learning-based methods: The effective performance of the fault type recognition methods usually needs to meet a basic assumption, namely, that the training samples and test samples are independent and identically distributed. However, the monitor information of rolling bearing is generally subject to working conditions, such as the characteristic frequency and amplitude changing with rotational speed, resulting in a large distribution difference between training data and test data, thereby presenting a domain migration issue. Transfer learning (TL) can extract knowledge from one or more related scenes to help improve the learning performance of scenarios in the target domain [165]. TL can relax the assumption of independent and identical distributions and provide a new solution to address the above deficiencies. The TL-based rolling bearing fault type recognition methods were proposed and achieved desirable results [166,167,168]. The TL-based recognition model, learning the common feature space from the source domain data and the target domain data to reduce the distribution difference between different domains, cannot adaptively adjust its parameters for target domain tasks, thereby affecting its domain adaptability and recognition accuracy. Thus, the further development of TL-based fault type recognition methods is a good direction for future research to improve the classification performance, recognition accuracy, and generalization under variable operating conditions.
- (2)
- Few-shot learning methods: A large amount of labelled data is also the key to ensuring the performance of existing fault type recognition methods, especially for deep learning-based methods. In real-world scenarios, it is easy to obtain enough normal samples due to the rolling bearing mostly running under normal conditions, but the fault samples are typically difficult to obtain and require extensive manual effort to label. The absence of labelled fault samples will either lead to overfitting in the training process or the class imbalance problem. Few-shot learning (FSL) is effective for distinguishing failure attribution accurately under very limited data conditions [169,170]. Data augmentation, data/model transfer, and meta-learning constitute the three main threads of FSL methods. Thus, the comprehensive exploration of FSL-based fault type recognition methods is a good direction for future research for reducing the dependence on large amounts of data, avoiding the risk of overfitting, and improving the applicability and recognition performance.
- (3)
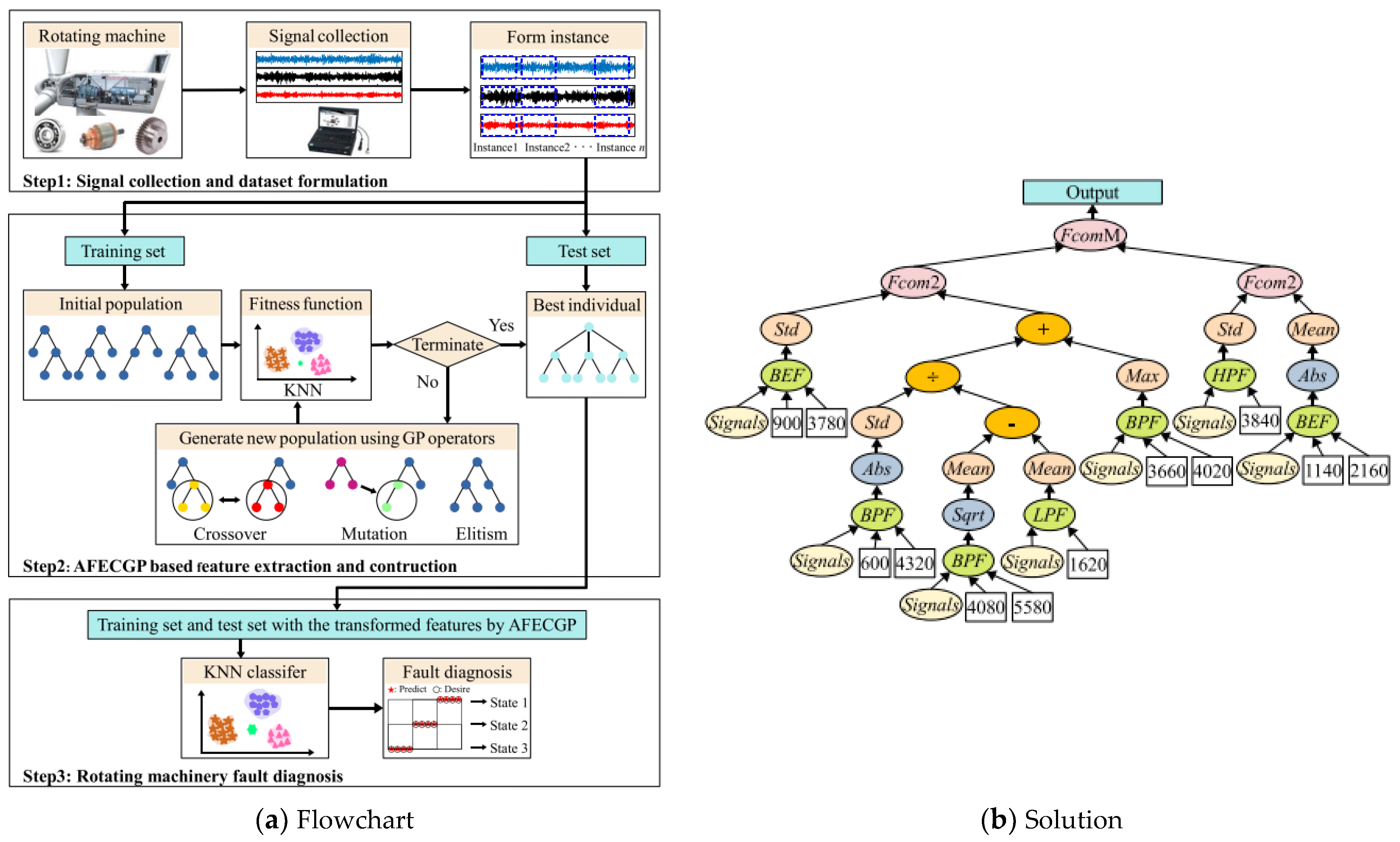
- Evolutionary deep learning methods: Evolutionary deep learning methods aim to deal with the limitations of deep learning methods, particularly neural networks, by using evolutionary computation (EC) techniques. This direction includes two main topics, i.e., using EC methods to automatically design neural networks and using EC methods to evolve deep models by themselves. On the first topic, some work was performed to evolve neural networks for fault diagnosis by finding the optimal numbers of layers, network connections, numbers of filters, etc. [171,172,173,174,175]. These methods can reduce the requirement of expertise from both the neural network domain and the problem domain, improve recognition performance, and decrease the number of parameters in the evolved models. On the second topic, pure EC methods, particularly genetic programming methods, are used to evolve deep models. GP is a computational intelligence algorithm to achieve automatic programming without human intervention and domain knowledge [176,177]. With a flexible program expression, GP can automatically evolve variable-length models to solve a task. GP has shown promise in the computer vision domain by evolving deep models [178,179,180,181]. The models evolved by GP typically have better interpretability than neural networks. However, there is little work on GP for fault diagnosis [182,183,184]. Figure 6 shows an example of using GP to solve fault type recognition, where the GP method is used to automatically generate informative and discriminative features from original vibration signals for recognizing different fault types. The left example tree of Figure 6 is the solution evolved by GP, showing high interpretability. In addition, the solutions are often creative and even not considered by human experts [183,184]. However, both topics have not been fully investigated in the fault diagnosis community. Therefore, it is promising to develop effective evolutionary deep learning approaches to fault diagnosis.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, S.; Peng, Z.; Zhou, P. Review of signal decomposition theory and its applications in machine fault diagnosis. J. Mech. Eng. 2020, 56, 91–107. [Google Scholar]
- Yan, G.; Chen, J.; Bai, Y.; Yu, C.; Yu, C. A Survey on Fault Diagnosis Approaches for Rolling Bearings of Railway Vehicles. Processes 2022, 10, 724. [Google Scholar] [CrossRef]
- Kuang, P.; Xu, F.; Liu, Y. Modern Machinery Fault Diagnosis: Principles and Techniques; China Agriculture Press: Beijing, China, 1991. [Google Scholar]
- Wang, X. Research on Fault Diagnosis Method of Rolling Bearing Based on Vibration Signal Processing. Ph.D. Thesis, North China Electric Power University, Beijing, China, 2017. [Google Scholar]
- Zhang, X.; Zhao, B.; Lin, Y. Machine Learning Based Bearing Fault Diagnosis Using the Case Western Reserve University Data: A Review. IEEE Access 2021, 9, 155598–155608. [Google Scholar] [CrossRef]
- Singh, J.; Azamfar, M.; Li, F.; Lee, J. A systematic review of machine learning algorithms for prognostics and health management of rolling element bearings: Fundamentals, concepts and applications. Meas. Sci. Technol. 2020, 32, 012001. [Google Scholar] [CrossRef]
- Lin, H.; Ye, Y. Reviews of bearing vibration measurement using fast Fourier transform and enhanced fast Fourier transform algorithms. Adv. Mech. Eng. 2019, 11, 1687814018816751. [Google Scholar] [CrossRef]
- Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial intelligence for fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- Wang, Y.; Xiang, J.; Markert, R.; Liang, M. Spectral kurtosis for fault detection, diagnosis and prognostics of rotating machines: A review with applications. Mech. Syst. Signal Process. 2016, 66, 679–698. [Google Scholar] [CrossRef]
- Rai, A.; Upadhyay, S. A review on signal processing techniques utilized in the fault diagnosis of rolling element bearings. Tribol. Int. 2016, 96, 289–306. [Google Scholar] [CrossRef]
- Neupane, D.; Seok, J. Bearing fault detection and diagnosis using case western reserve university dataset with deep learning approaches: A review. IEEE Access 2020, 8, 93155–93178. [Google Scholar] [CrossRef]
- Yang, Z. Oil Liquid State Monitoring technolgoy and application in equipment maintenance management. Mech. Manag. Dev. 2006, 89, 51–52. [Google Scholar]
- Sun, B.; Wang, Y.; Yang, L. Study of fault diagnosis of induction motor bearing based on infrared inspection. Elect. Mach. Control 2012, 16, 50–55. [Google Scholar]
- Wang, Y. Acoustic-Based Condition Monitoring of Machinery Using Blind Signal Processing. Ph.D. Thesis, Kunming University of Science and Technology, Kunming, China, 2010. [Google Scholar]
- Singh, S.; Vishwakarma, M. A review of vibration analysis techniques for rotating machines. Int. J. Eng. Res. T. 2015, 4, 757–761. [Google Scholar]
- Randall, R.; Jérme, A. Rolling element bearing diagnostics—A tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Ripley, B.; Matheron, G. Random sets and integral geometry. J. R. Stat. Soc. 1975, 139, 277–278. [Google Scholar] [CrossRef]
- Maragos, P.; Schafer, R. Morphological filters. Part 1. Their set-theoretic analysis and relations to linear shift-invariant filters. IEEE Trans. Acous. Speech Signal Process. 1987, 35, 1153–1169. [Google Scholar] [CrossRef]
- Maragos, P.; Schafer, R. Morphological filters. Part 2. Their set-theoretic analysis and relations to linear shift-invariant filters. IEEE Trans. Acous. Speech Signal Process. 1987, 35, 1170–1184. [Google Scholar] [CrossRef]
- Wang, J.; Xu, G.; Zhang, Q.; Liang, L. Application of improved morphological filter to the extraction of impulsive attenuation signals. Mech. Syst. Signal Process. 2009, 23, 236–245. [Google Scholar] [CrossRef]
- Shen, C.; Zhu, Z.; Kong, F.; Huang, W. An improved morphological filtering method and its application in bearing fault feature extraction. J. Vib. Eng. 2012, 25, 468–473. [Google Scholar]
- He, W.; Jiang, Z.; Qin, Q. A joint adaptive wavelet filter and morphological signal processing method for weak mechanical impulse extraction. J. Mech. Sci. Technol. 2010, 24, 1709–1716. [Google Scholar] [CrossRef]
- Raj, A.; Murali, N. Early classification of bearing faults using morphological operators and fuzzy inference. IEEE Trans. Ind. Electron. 2013, 60, 567–574. [Google Scholar] [CrossRef]
- Osman, S.; Wang, W. An Hilbert-huang spectrum technique for fault detection in rolling element bearings. IEEE Trans. Instrum. Meas. 2016, 65, 2646–2656. [Google Scholar] [CrossRef]
- Li, Y.; Liang, X.; Zuo, M. A new strategy of using a time-varying structure element for mathematical morphological filtering. Measurement 2017, 106, 53–65. [Google Scholar] [CrossRef]
- Li, Y.; Zuo, M.; Lin, J.; Liu, J. Fault detection method for railway wheel flat using an adaptive multiscale morphological filter. Mech. Syst. Signal Process. 2017, 84, 642–658. [Google Scholar] [CrossRef]
- Li, Y.; Liang, X.; Zuo, M. Diagonal slice spectrum assisted optimal scale morphological filter for rolling element bearing fault diagnosis. Mech. Syst. Signal Process. 2017, 85, 146–161. [Google Scholar] [CrossRef]
- Wang, D.; Tse, P.; Tse, Y. A morphogram with the optimal selection of parameters used in morphological analysis for enhancing the ability in bearing fault diagnosis. Meas. Sci. Technol. 2012, 23, 65001–65015. [Google Scholar] [CrossRef]
- Meng, L.; Xiang, J.; Wang, Y.; Jiang, Y.; Gao, H. A hybrid fault diagnosis method using morphological filter-translation invariant wavelet and improved ensemble empirical mode decomposition. Mech. Syst. Signal Process. 2015, 50–51, 101–115. [Google Scholar] [CrossRef]
- Deng, F.; Tang, G.; He, Y. Fault feature extraction for rolling element bearings based on cepstrum pre-whitening and morphology self-complementary top-hat transformation. J. Vib. Shock 2015, 34, 77–81. [Google Scholar]
- Yan, X.; Jia, M. Parameter optimized combination morphological filter-hat transform and its application in fault diagnosis of wind turbine. J. Mech. Eng. 2016, 52, 103–110. [Google Scholar] [CrossRef]
- Li, Y.; Zuo, M.; Chen, Y.; Feng, K. An enhanced morphology gradient product filter for bearing fault detection. Mech. Syst. Signal Process. 2018, 109, 166–184. [Google Scholar] [CrossRef]
- Deng, F.; Yang, S.; Guo, W.; Liu, Y. Fault feature extraction method for rolling bearing based on adaptive multi-scale morphological AVG-Hat filtering. J. Vib. Eng. 2017, 30, 178–187. [Google Scholar]
- Zou, F.; Zhang, H.; Sang, S.; Li, X.; He, W.; Liu, X. Bearing fault diagnosis based on combined multi-scale weighted entropy morphological filtering and bi-LSTM. Appl. Intell. 2021, 51, 6647–6664. [Google Scholar] [CrossRef]
- Li, Y.; Liang, X.; Lin, J.; Chen, Y.; Liu, J. Train axle bearing fault detection using a feature selection scheme based multi-scale morphological filter. Mech. Syst. Signal Process. 2018, 101, 435–448. [Google Scholar] [CrossRef]
- Zhu, D.; Zhang, Y.; Zhu, Q. Fault feature extraction for rolling element bearings based on multi-scale morphological filter and frequency-weighted energy operator. J. Vibroeng. 2018, 20, 2892–2907. [Google Scholar] [CrossRef]
- Wu, Z.; Yang, S.; Ren, B.; Ma, X.; Zhang, J. Rolling element bearing fault diagnosis method based on NAMEMD and multi-scale morphology. J. Vib. Shock 2016, 35, 127–133. [Google Scholar]
- Chen, Q.; Chen, Z.; Sun, W.; Yang, G. A new structuring element for multi-scale morphology analysis and its application in rolling element bearing fault diagnosis. J. Vib. Control 2015, 21, 765–789. [Google Scholar] [CrossRef]
- Antoni, J. The spectral kurtosis: A useful tool for characterising non-stationary signals. Mech. Syst. Signal Process. 2006, 20, 282–307. [Google Scholar] [CrossRef]
- Antoni, J.; Randall, R. The spectral kurtosis: Application to the vibratory surveillance and diagnostics of rotating machines. Mech. Syst. Signal Process. 2006, 20, 308–331. [Google Scholar] [CrossRef]
- Lei, Y.; Lin, J.; He, Z.; Zi, Y. Application of an improved kurtogram method for fault diagnosis of rolling element bearings. Mech. Syst. Signal Process. 2011, 25, 1738–1749. [Google Scholar] [CrossRef]
- Wang, D.; Tse, P.; Tsui, K. An enhanced kurtogram method for fault diagnosis of rolling element bearings. Mech. Syst. Signal Process. 2013, 35, 176–199. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, Z.; Zi, Y.; He, Z.; Sun, C. Detecting of transient vibration signatures using an improved fast spatial-spectral ensemble kurtosis kurtogram and its applications to mechanical signature analysis of short duration data from rotating machinery. Mech. Syst. Signal Process. 2013, 40, 1–37. [Google Scholar] [CrossRef]
- Moshrefzadeh, A.; Fasana, A. The autogram: An effective approach for selecting the optimal demodulation band in rolling element bearings diagnosis. Mech. Syst. Signal Process. 2018, 105, 294–318. [Google Scholar] [CrossRef]
- Gu, X.; Yang, S.; Liu, Y.; Liao, Y. An improved kurtogram method and its application in fault diagnosis of rolling element bearings under complex interferences. J. Vib. Shock 2017, 36, 187–193. [Google Scholar]
- Tse, P.; Wang, D. The design of a new sparsogram for fast bearing fault diagnosis: Part 1 of the two related manuscripts that have a joint title as “Two automatic vibration-based fault diagnostic methods using the novel sparsity measurement-Parts 1 and 2”. Mech. Syst. Signal Process. 2013, 40, 499–519. [Google Scholar] [CrossRef]
- Antoni, J. The infogram: Entropic evidence of the signature of repetitive transients. Mech. Syst. Signal Process. 2016, 74, 73–94. [Google Scholar] [CrossRef]
- Wan, S.; Zhang, X.; Dou, L. Shannon entropy of binary wavelet packet subbands and its application in bearing fault extraction. Entropy 2018, 20, 260. [Google Scholar] [CrossRef]
- Miao, Y.; Zhao, M.; Lin, J. Improvement of kurtosis-guided-grams via Gini index for bearing fault feature identification. Meas. Sci. Technol. 2017, 28, 125001. [Google Scholar] [CrossRef]
- Mo, Z.; Wang, J.; Zhang, H.; Miao, Q. Weighted cyclic harmonic-to-noise ratio for rolling element bearing fault diagnosis. IEEE Trans. Instrum. Meas. 2020, 69, 432–442. [Google Scholar] [CrossRef]
- Tse, P.; Wang, D. The automatic selection of an optimal wavelet filter and its enhancement by the new sparsogram for bearing fault detection. Mech. Syst. Signal Process. 2013, 40, 520–544. [Google Scholar] [CrossRef]
- Gu, X.; Yang, S.; Liu, Y.; Ren, B.; Zhang, J. Fault Feature Extraction of Wheel-bearing Based on Multi-objective Cross Entropy Optimization. J. Mech. Eng. 2018, 54, 304–311. [Google Scholar] [CrossRef]
- Wan, S.; Peng, B. Adaptive asymmetric real Laplace wavelet filtering and its application on rolling bearing early fault diagnosis. Shock Vib. 2019, 2019, 7475868. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, K.; Ma, C.; Sheng, Z.; Shen, H. An adaptive spectrum segmentation method to optimize empirical wavelet transform for rolling bearings fault diagnosis. IEEE Access 2019, 7, 30437–30456. [Google Scholar] [CrossRef]
- Guo, J.; Shi, Z.; Zhen, D.; Meng, Z.; Gu, F.; Ball, A.D. Modulation signal bispectrum with optimized wavelet packet denoising for rolling bearing fault diagnosis. Struct. Health Monit. 2022, 21, 984–1011. [Google Scholar] [CrossRef]
- Huang, N.; Shen, Z.; Long, S.; Wu, M.; Shih, H.; Zheng, Q.; Yen, N.; Tung, C.; Liu, H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Huang, N.; Zheng, S.; Long, S. A new view of nonlinear water waves: The Hilbert spectrum. Annu. Rev. Fluid Mech. 1999, 31, 417–457. [Google Scholar] [CrossRef]
- Gao, Q.; Du, X.; Fan, H.; Meng, Q. An empirical mode decomposition based method for rolling bearing fault diagnosis. J. Vib. Eng. 2007, 20, 19–22. [Google Scholar]
- Wu, Z.; Huang, N. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Li, H.; Liu, T.; Wu, X.; Chen, Q. Application of EEMD and improved frequency band entropy in bearing fault feature extraction. ISA Trans. 2019, 88, 170–185. [Google Scholar] [CrossRef]
- Tomes, M.; Colominas, M.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Prague, Czech Republic, 22–27 May 2011. [Google Scholar]
- Rabah, A.; Abdelhafid, K.; Azeddine, B.; Derouiche, Z. Rolling bearing fault diagnosis based on an improved denoising method using the complete ensemble empirical mode decomposition and the optimized thresholding operation. IEEE Sens. J. 2018, 18, 7166–7172. [Google Scholar]
- Huang, H.; Sun, S.; Ren, X.; Liu, H. Early fault diagnosis of rolling bearing based on CEEMDAN and 1.5 dimension spectrum. China Meas. Test 2019, 4, 155–160. [Google Scholar]
- Gao, S.; Wang, Q.; Zhang, Y. Rolling bearing fault diagnosis based on CEEMDAN and refined composite multiscale fuzzy entropy. IEEE Trans. Instrum. Meas. 2021, 70, 1–8. [Google Scholar] [CrossRef]
- Smith, S. The local mean decomposition and its application to EEG perception data. J. R. Soc. Interface 2005, 2, 443–454. [Google Scholar] [CrossRef]
- Cheng, J.; Yang, Y.; Yang, Y. A rotating machinery fault diagnosis method based on local mean decomposition. Digital Signal Process. 2012, 22, 356–366. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Z.; Miao, Q.; Zhang, X. Complete ensemble local mean decomposition with adaptive noise and its application to fault diagnosis for rolling bearings. Mech. Syst. Signal Process. 2018, 106, 24–39. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, K.; Ma, C.; Li, S.; Zhang, H. Optimized LMD method and its applications in rolling bearing fault diagnosis. Meas. Sci. Technol. 2019, 30, 125017. [Google Scholar] [CrossRef]
- Li, X.; Ma, J.; Wang, X.; Wu, J.; Li, Z. An improved local mean decomposition method based on improved composite interpolation envelope and its application in bearing fault feature extraction. ISA Trans. 2020, 97, 365–383. [Google Scholar] [CrossRef]
- Frei, M.; Osorio, I. Intrinsic time-scale decomposition: Time-frequency-energy analysis and real-time filtering of non-stationary signals. Proc. Math. Phys. Eng. Sci. 2007, 463, 321–342. [Google Scholar] [CrossRef]
- Yu, J.; Liu, H. Sparse coding shrinkage in intrinsic time-scale decomposition for weak fault feature extraction of bearings. IEEE Trans. Instrum. Meas. 2018, 67, 1579–1592. [Google Scholar] [CrossRef]
- Ma, J.; Zhan, L.; Li, C.; Li, Z. An improved intrinsic time-scale decomposition method based on adaptive noise and its application in bearing fault feature extraction. Meas. Sci. Technol. 2020, 32, 025103. [Google Scholar] [CrossRef]
- Yang, Y.; Zeng, M.; Cheng, J. A New Time-frequency analysis method-the local characteristic-scale decomposition. J. Hunan Univ. (Nat. Sci.) 2012, 39, 35–39. [Google Scholar]
- Cheng, J.; Yang, Y.; Yang, Y. Local characteristic-scale decomposition method and its application to gear fault diagnosis. J. Mech. Eng. 2012, 48, 64–71. [Google Scholar] [CrossRef]
- Cheng, J.; Yang, Y.; Li, X.; Pan, H.; Cheng, J. An early fault diagnosis method of gear based on improved symplectic geometry mode decomposition. Measurement 2019, 151, 107140. [Google Scholar] [CrossRef]
- Luo, S.; Yang, W.; Luo, Y. A novel fault detection scheme using improved inherent multiscale fuzzy entropy with partly ensemble local characteristic-scale decomposition. IEEE Access 2020, 8, 6650–6661. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Bian, J. Fault Diagnosis of bearing combining parameter optimized variational mode decomposition based on genetic algorithm with 1.5-dimensional spectrum. J. Propul. Technol. 2017, 38, 1618–1624. [Google Scholar]
- Yan, X.; Jia, M. Application of CSA-VMD and optimal scale morphological slice bispectrum in enhancing outer race fault detection of rolling element bearings. Mech. Syst. Signal Process. 2019, 122, 56–86. [Google Scholar] [CrossRef]
- Li, H.; Liu, T.; Wu, X.; Chen, Q. An optimized VMD method and its applications in bearing fault diagnosis. Measurement 2020, 166, 108185. [Google Scholar] [CrossRef]
- Bonizzi, P.; Karel, J.; Meste, O.; Peeters, R. Singular spectrum decomposition: A new method for time series decomposition. Adv. Adapt. Data Anal. 2014, 6, 107–109. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, Z.; Ma, C.; Zhang, J. Improved singular spectrum decomposition and its applications in rolling bearing fault diagnosis. J. Vib. Eng. 2019, 32, 168–175. [Google Scholar]
- Wang, X.; Tang, G.; He, Y. Weak fault diagnosis for rolling bearing based on COT-SSD under variable rotating speed. Elec. Power Autom. Equip. 2019, 39, 187–193. [Google Scholar]
- Mao, Y.; Jia, M.; Yan, X. A new bearing weak fault diagnosis method based on improved singular spectrum decomposition and frequency-weighted energy slice bispectrum. Measurement 2020, 166, 108235. [Google Scholar] [CrossRef]
- Wiggins, R. Minimum entropy deconvolution. Geophys. Prospect. Petrole 1980, 16, 21–35. [Google Scholar] [CrossRef]
- Endo, H.; Randall, R. Enhancement of autoregressive model based gear tooth fault detection technique by the use of minimum entropy deconvolution filter. Mech. Syst. Signal Process. 2007, 21, 906–919. [Google Scholar] [CrossRef]
- McDonald, G.; Zhao, Q.; Zuo, M. Maximum correlated kurtosis deconvolution and application on gear tooth chip fault detection. Mech. Syst. Signal Process. 2012, 33, 237–255. [Google Scholar] [CrossRef]
- Miao, Y.; Zhao, M.; Lin, J.; Xu, X. Sparse maximum harmonics-to-noise-ratio deconvolution for weak fault signature detection in bearings. Meas. Sci. Technol. 2016, 27, 105004. [Google Scholar] [CrossRef]
- McDonald, G.; Zhao, Q. Multipoint optimal minimum entropy deconvolution and convolution fix: Application to vibration fault detection. Mech. Syst. Signal Process. 2017, 82, 461–477. [Google Scholar] [CrossRef]
- Buzzonia, M.; Antoni, J.; D’Elia, G. Blind deconvolution based on cyclostationarity maximization and its application to fault identification. J. Sound Vib. 2018, 432, 569–601. [Google Scholar] [CrossRef]
- Zhang, Z.; Entezami, M.; Stewart, E.; Roberts, C. Enhanced fault diagnosis of roller bearing elements using a combination of empirical mode decomposition and minimum entropy deconvolution. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 655–671. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, Z.; Zhang, W.; Huang, G. Particle swarm optimization algorithm to solve the deconvolution problem for rolling element bearing fault diagnosis. ISA Trans. 2019, 90, 244–267. [Google Scholar] [CrossRef]
- Wang, X.; Yan, X.; He, Y. Weak fault detection for wind turbine bearing based on ACYCBD and IESB. J. Mech. Sci. Technol. 2020, 34, 1399–1413. [Google Scholar] [CrossRef]
- Hu, Q.; He, Z.; Zhang, S.; Zi, Y.; Lei, Y. Intelligent diagnosis for incipient fault based on lifting wavelet package transform and support vector machines ensemble. J. Mech. Eng. 2006, 42, 20–26. [Google Scholar] [CrossRef]
- Lei, Y.; He, Z.; Zi, Y. Fault diagnosis based on novel hybrid intelligent model. J. Mech. Eng. 2008, 44, 112–117. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Y.; Zhu, Y. Intelligent fault diagnosis of rolling element bearing based on SVMs and fractal dimension. Mech. Syst. Signal Process. 2007, 21, 2012–2024. [Google Scholar] [CrossRef]
- Caesarendra, W.; Kosasih, B.; Tieu, A.; Moodie, C. Application of the largest Lyapunov exponent algorithm for feature extraction in low speed slew bearing condition monitoring. Mech. Syst. Signal Process. 2015, 50–51, 116–138. [Google Scholar] [CrossRef]
- Yan, R.; Gao, R. Approximate entropy as a diagnostic tool for machine health monitoring. Mech. Syst. Signal Process. 2007, 21, 824–839. [Google Scholar] [CrossRef]
- Su, W.; Wang, F.; Zhu, H.; Guo, Z.; Zhang, Z.; Zhang, H. Feature extraction of rolling element bearing fault using wavelet packet sample entropy. J. Vib. Meas. Diag. 2011, 31, 33–37+134. [Google Scholar]
- Zheng, J.; Cheng, J.; Yang, Y. A rolling bearing fault diagnosis approach based on LCD and fuzzy entropy. Mech. Mach. Theory 2013, 70, 441–453. [Google Scholar] [CrossRef]
- Yan, R.; Liu, Y.; Gao, R. Permutation entropy: A nonlinear statistical measure for status characterization of rotary machines. Mech. Syst. Signal Process. 2012, 29, 474–484. [Google Scholar] [CrossRef]
- Fu, W.; Tang, J.; Wang, K. Semi-supervised fault diagnosis of bearings based on the VMD dispersion entropy and improved SVDD with modified grey wolf optimizer. J. Vib. Shock 2019, 38, 190–197. [Google Scholar]
- Pincus, S. Approximate entropy (ApEn) as a complexity measure. Chaos 1998, 5, 110–117. [Google Scholar] [CrossRef]
- Richman, J.; Randall, M. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart C. 2000, 278, 2039–2049. [Google Scholar] [CrossRef]
- Chen, W. A Study of Feature Extraction from sEMG Singal Based on Entropy. Ph.D. Thesis, Shanghai University, Shanghai, China, 2008. [Google Scholar]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Rostaghi, M.; Azami, H. Dispersion entropy: A measure for time-series analysis. IEEE Signal Process. Lett. 2016, 23, 610–614. [Google Scholar] [CrossRef]
- Yan, X.; Jia, M.; Zhao, Z. A novel intelligent detection method for rolling bearing based on IVMD and instantaneous energy distribution-permutation entropy. Measurement 2018, 130, 435–447. [Google Scholar] [CrossRef]
- Tang, G.; Pang, B.; He, Y.; Tian, T. Gearbox fault diagnosis based on hierarchical instantaneous energy density dispersion entropy and dynamic time warping. Entropy 2019, 21, 593. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.; Peng, C. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2007, 89, 705–708. [Google Scholar] [CrossRef]
- Liu, H.; Han, M. A fault diagnosis method based on local mean decomposition and multi-scale entropy for roller bearings. Mech. Mach. Theory 2014, 75, 67–78. [Google Scholar] [CrossRef]
- Zhang, L.; Huang, W.; Xiong, G. Assessment of rolling element bearing fault severity using multi-scale entropy. J. Vib. Shock 2014, 33, 185–189. [Google Scholar]
- Aziz, W.; Arif, M. Multiscale permutation entropy of physiological time series. In Proceedings of the INMIC 2005 9th International Multitopic Conference, Karachi, Pakistan, 1–5 December 2005. [Google Scholar]
- Tiwari, R.; Gupta, V.; Kankar, P. Bearing fault diagnosis based on multi-scale permutation entropy and adaptive neuro fuzzy classifier. J. Vib. Control 2015, 21, 461–467. [Google Scholar] [CrossRef]
- Zheng, J.; Cheng, J.; Yang, Y. Multi-scale Permutation entropy and its applications to rolling bearing fault diagnosis. China Mech. Eng. 2013, 24, 2641–2646. [Google Scholar]
- Azami, H.; Kinney-Lang, E.; Ebied, A.; Fernández, A.; Escudero, J. Multiscale dispersion entropy for the regional analysis of resting-state magnetoencephalogram complexity in Alzheimer’s disease. In Proceedings of the 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Jeju Island, South Korea, 11–15 July 2017. [Google Scholar]
- Azami, H.; Rostaghi, M.; Abasolo, D.; Escudero, J. Refined composite multiscale dispersion entropy and its application to biomedical signals. IEEE Trans. Biomed. Eng. 2017, 64, 2872–2879. [Google Scholar]
- Xu, Z.; Liu, K.; Zhang, H.; Wnag, D.; Zhang, M. A fault diagnosis method for rolling bearings based on empirical mode decomposition and principal component analysis. J. Vib. Shock 2014, 33, 133–139. [Google Scholar]
- Ahmed, H.; Nandi, A. Three-stage hybrid fault diagnosis for rolling bearings with compressively-sampled data and subspace learning techniques. IEEE Trans. Ind. Electron. 2018, 66, 5516–5524. [Google Scholar] [CrossRef]
- Ding, X.; He, Q.; Luo, N. A fusion feature and its improvement based on locality preserving projections for rolling element bearing fault classification. J. Sound Vib. 2015, 335, 367–383. [Google Scholar] [CrossRef]
- Jiang, L.; Shi, T.; Xuan, J. Fault diagnosis of rolling bearings based on marginal fisher analysis. J. Vib. Control 2014, 20, 470–480. [Google Scholar] [CrossRef]
- Yu, J. Local and global principal component analysis for process monitoring. J. Process Control 2012, 22, 1358–1373. [Google Scholar] [CrossRef]
- Chen, J.; Ma, Z.; Liu, Y. Local coordinates alignment with global preservation for dimensionality reduction. IEEE Trans. Neural Netw. Learn. 2013, 24, 106–117. [Google Scholar] [CrossRef]
- Zhang, M.; Ge, Z.; Song, Z.; Fu, R. Global-local structure analysis model and its application for fault detection and identification. Ind. Eng. Chem. Res. 2011, 50, 6837–6848. [Google Scholar] [CrossRef]
- Gao, Y.; Yu, D.; Wang, H.; Chen, T. Fault feature extraction method of rolling bearing based on spectral graph indices. J. Aeronaut. Power 2018, 33, 2033–2040. [Google Scholar]
- Cheng, J.; Zheng, J.; Yang, Y.; Luo, S. Fault diagnosis model for rolling bearing based on partly ensemble local characteristic-scale decomposition and Laplacian score. J. Vib. Eng. 2014, 27, 942–950. [Google Scholar]
- Vakharia, V.; Gupta, V.; Kankar, P. Efficient fault diagnosis of ball bearing using ReliefF and Random Forest classifier. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 2969–2982. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Y.; Li, G.; Xu, M.; Huang, W. A fault diagnosis scheme for planetary gearboxes using modified multi-scale symbolic dynamic entropy and mRMR feature selection. Mech. Syst. Signal Process. 2017, 91, 295–312. [Google Scholar] [CrossRef]
- Wang, X.; Qiu, J.; Liu, G. New feature selection method in machine fault diagnosis. Chin. J. Mech. Eng. 2005, 18, 251–254. [Google Scholar] [CrossRef]
- Pan, X.; Huang, J.; Mao, H.; Liu, Z. Fault-characteristic extracting technology based on particle swarm optimization. J. Vib. Shock 2008, 27, 144–147. [Google Scholar]
- Kadri, O.; Mouss, L.; Mouss, M. Fault diagnosis of rotary kiln using SVM and binary ACO. J. Mech. Sci. Technol. 2012, 26, 601–608. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Q.; Chen, M.; Sun, Y.; Qin, X.; Li, H. A two-stage feature selection and intelligent fault diagnosis method for rotating machinery using hybrid filter and wrapper method. Neurocomputing 2017, 275, 2426–2439. [Google Scholar] [CrossRef]
- Xue, R.; Zhao, R. The fault feature selection algorithm of combination of ReliefF and QPSO. J. Vib. Shock 2020, 39, 176–181+213. [Google Scholar]
- Zhu, X.; Zhang, Y.; Zhu, Y. Intelligent fault diagnosis of rolling bearing based on kernel neighborhood rough sets and statistical features. J. Mech Sci. Technol. 2012, 26, 2649–2657. [Google Scholar] [CrossRef]
- Zhao, X.; Tang, X.; Zhao, J.; Zhang, Y. Fault diagnosis of asynchronous induction motor based on BP neural network. In Proceedings of the International Conference on Measuring Technology and Mechatronics Automation, Changsha, China, 13–14 March 2010. [Google Scholar]
- Gunerkar, R.S.; Jalan, A.K.; Belgamwar, S.U. Fault diagnosis of rolling element bearing based on artificial neural network. J. Mech. Sci. Technol. 2019, 33, 505–511. [Google Scholar] [CrossRef]
- Zhu, K.; Chen, L.; HU, X. Rolling element bearing fault diagnosis based on multi-scale global fuzzy entropy, multiple class feature selection and support vector machine. Trans. Inst. Meas. Control 2019, 41, 4013–4022. [Google Scholar] [CrossRef]
- Chen, X.; He, W.; Ma, D.; Zhao, D. Symbol entropy and svm based rolling bearing fault diagnosis. China Mech. Eng. 2010, 21, 67–70. [Google Scholar]
- Tian, Y.; Ma, J.; Lu, C.; Wang, Z. Rolling bearing fault diagnosis under variable conditions using LMD-SVD and extreme learning machine. Mech. Mach. Theory 2015, 90, 175–186. [Google Scholar] [CrossRef]
- Han, T.; Jiang, D. Rolling bearing fault diagnostic method based on VMD-AR model and random forest classifier. Shock Vib. 2016, 6, 1–11. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Q.; Qin, X.; Sun, Y. Rolling bearing fault diagnosis based on ITD Lempel-Ziv complexity and PSO-SVM. J. Vib. Shock 2016, 35, 102–107+138. [Google Scholar]
- Tang, G.; Pang, B.; Tian, T.; Zhou, C. Fault diagnosis of rolling bearings based on improved fast spectral correlation and optimized random forest. Appl. Sci. 2018, 8, 1859. [Google Scholar] [CrossRef]
- Wu, J.; Qin, W.; Liang, H.; Jin, S.; Luo, W. Transformer fault identification method based on self-adaptive extreme learning machine. Elec. Power Autom. Equip. 2019, 39, 181–186. [Google Scholar]
- Zhao, R.; Yan, R.; Chen, Z.; Mao, K.; Wang, P.; Gao, R. Deep learning and its applications to machine health monitoring. Mech. Syst. Signal Process. 2019, 115, 213–237. [Google Scholar] [CrossRef]
- Singh, S.; Howard, C.; Hansen, C. Convolutional neural network based fault detection for rotating machinery. J. Sound Vib. 2016, 377, 331–345. [Google Scholar]
- Wen, L.; Li, X.; Gao, L.; Zhang, Y. A new convolutional neural network-based data-driven fault diagnosis method. IEEE Trans. Ind. Electron. 2017, 65, 5990–5998. [Google Scholar] [CrossRef]
- Wang, J.; Zhuang, J.; Duan, L.; Cheng, W. A multi-scale convolution neural network for featureless fault diagnosis. In Proceedings of the International Symposium on Flexible Automation, Cleveland, OH, USA, 1–3 August 2016. [Google Scholar]
- Zhang, W.; Peng, G.; Li, C.; Chen, Y.; Zhang, Z. A new deep learning model for fault diagnosis with good anti-noise and domain adaptation ability on raw vibration signals. Sensors 2017, 17, 425. [Google Scholar] [CrossRef]
- Sun, W.; Deng, A.; Deng, M.; Zhu, J.; Zhai, Y. Multi-view feature fusion for rolling bearing fault diagnosis using random forest and autoencoder. J. Southeast Univ. 2019, 35, 33–40. [Google Scholar]
- Shi, P.; Guo, X.; Han, D.; Fu, R. A sparse auto-encoder method based on compressed sensing and wavelet packet energy entropy for rolling bearing intelligent fault diagnosis. J. Mech. Sci. Technol. 2020, 34, 1445–1458. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, X.; Zhang, W.; Xia, X. Fault diagnosis of rolling bearing under fluctuating speed and variable load based on TCO spectrum and stacking auto-encoder. Measurement 2019, 138, 162–174. [Google Scholar]
- Gu, Y.; Cao, J.; Song, X.; Yao, J. A Denoising autoencoder-based bearing fault diagnosis system for time-domain vibration signal. Wirel. Commun. Mob. Com. 2021, 2021, 9790053. [Google Scholar] [CrossRef]
- Oh, H.; Jung, J.H.; Jeon, B.C.; Youn, B.D. Scalable and unsupervised feature engineering using vibration-imaging and deep learning for rotor system diagnosis. IEEE Trans. Ind. Electron. 2018, 65, 3539–3549. [Google Scholar] [CrossRef]
- Chen, Z.; Li, W. Multisensor feature fusion for bearing fault diagnosis using sparse autoencoder and deep belief network. IEEE Trans. Instrum. Meas. 2017, 66, 1693–1702. [Google Scholar] [CrossRef]
- Shao, H.; Jiang, H.; Li, X.; Liang, T. Rolling bearing fault detection using continuous deep belief network with locally linear embedding. Comput. Ind. 2018, 96, 27–39. [Google Scholar] [CrossRef]
- Yuan, M.; Wu, Y.; Lin, L. Fault diagnosis and remaining useful life estimation of aero engine using LSTM neural network. In Proceedings of the IEEE International Conference on Aircraft Utility Systems, Austin, TX, USA, 30 October 2016. [Google Scholar]
- Zhao, R.; Wang, J.; Yan, R.; Mao, K. Machine health monitoring with LSTM networks. In Proceedings of the International Conference on Sensing Technology, Nanjing, China, 11–13 November 2016. [Google Scholar]
- Zhao, K.; Shao, H. Intelligent fault diagnosis of rolling bearing using adaptive deep gated recurrent unit. Neural Process. Lett. 2020, 51, 1165–1184. [Google Scholar] [CrossRef]
- Case Western Reserve University Bearing Data Center. Available online: http://csegroups.case.edu/bearingdatacenter/home/ (accessed on 1 April 2018).
- Nectoux, P.; Gouriveau, R.; Medjaher, K.; Ramasso, E.; Chebel-Morello, B.; Zerhouni, N.; Varnier, C. PRONOSTIA: An experimental platform for bearings accelerated degradation tests. In Proceedings of the IEEE International Conference on Prognostics and Health Management, PHM’12, Mineapollis, MN, USA, 23–27 September 2012. [Google Scholar]
- Gousseau, W.; Antoni, J.; Girardin, F.; Griffaton, J. Analysis of the Rolling Element Bearing data set of the Center for Intelligent Maintenance Systems of the University of Cincinnati. In Proceedings of the CM2016, Paris, France, 10–12 October 2016. [Google Scholar]
- Huang, H.; Baddour, N. Bearing vibration data collected under time-varying rotational speed conditions. Data Brief 2018, 21, 1745–1749. [Google Scholar] [CrossRef]
- Wang, B.; Lei, Y.; Li, N.; Li, N. A hybrid prognostics approach for estimating remaining useful life of rolling element bearings. IEEE Trans. Reliab. 2020, 69, 401–412. [Google Scholar] [CrossRef]
- Deng, J.; Dong, W.; Socher, R.; Li, L.; Li, K.; Li, F. ImageNet: A large-scale hierarchical image databas. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009. [Google Scholar]
- Weiss, K.; Khoshgoftaar, T.M.; Wang, D. A survey of transfer learning. J. Big Data 2016, 3, 1–40. [Google Scholar] [CrossRef]
- Guo, L.; Lei, Y.; Xing, S.; Yan, T.; Li, N. Deep convolutional transfer learning network: A new method for intelligent fault diagnosis of machines with unlabeled data. IEEE Trans. Ind. Electron. 2018, 66, 7316–7325. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, D.; Lu, W.; Yang, J.; Li, Z.; Liang, B. A deep transfer model with wasserstein distance guided multi-adversarial networks for bearing fault diagnosis under different working conditions. IEEE Access 2019, 7, 65303–65318. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Ma, H.; Luo, Z.; Li, X. Deep learning-based adversarial multi-classifier optimization for cross-domain machinery fault diagnostics. J. Manuf. Syst. 2020, 55, 334–347. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, M.; Xu, Y.; Lu, W.; Yang, J.; Zhang, T. Metric-based meta-learning model for few-shot fault diagnosis under multiple limited data conditions. Mech. Syst. Signal Process. 2021, 155, 107510. [Google Scholar] [CrossRef]
- Wu, J.; Zhao, Z.; Sun, C.; Yan, R.; Chen, X. Few-shot transfer learning for intelligent fault diagnosis of machine. Measurement 2020, 166, 108202. [Google Scholar] [CrossRef]
- Fuan, W.; Hongkai, J.; Haidong, S.; Wenjing, D.; Shuaipeng, W. An adaptive deep convolutional neural network for rolling bearing fault diagnosis. Meas. Sci. Technol. 2017, 28, 095005. [Google Scholar] [CrossRef]
- Gao, S.; Xu, L.; Zhang, Y.; Pei, Z. Rolling bearing fault diagnosis based on intelligent optimized self-adaptive deep belief network. Meas. Sci. Technol. 2020, 31, 055009. [Google Scholar] [CrossRef]
- Tong, J.; Luo, J.; Pan, H.; Zheng, J.; Zhang, Q. A Novel Cuckoo Search Optimized Deep Auto-Encoder Network-Based Fault Diagnosis Method for Rolling Bearing. Shock Vib. 2020, 2020, 8891905. [Google Scholar] [CrossRef]
- Xiao, M.; Zhang, W.; Wen, K.; Zhu, Y.; Yiliyasi, Y. Fault Diagnosis Based on BP Neural Network Optimized by Beetle Algorithm. Chin. J. Mech. Eng. 2021, 34, 119. [Google Scholar] [CrossRef]
- Chen, J.; Jiang, J.; Guo, X.; Tan, L. A self-Adaptive CNN with PSO for bearing fault diagnosis. Syst. Sci. Control Eng. 2021, 9, 11–22. [Google Scholar] [CrossRef]
- Koza, J. Genetic Programming: On The Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Bi, Y.; Xue, B.; Zhang, M. Genetic Programming for Image Classification: An Automated Approach to Feature Learning; Springer International Publishing: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Shao, L.; Liu, L.; Li, X. Feature learning for image classification via multiobjective genetic programming. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 1359–1371. [Google Scholar] [CrossRef]
- Fu, W.; Johnston, M.; Zhang, M. Genetic programming for edge detection: A Gaussian-based approach. Soft. Comput. 2016, 20, 1231–1248. [Google Scholar] [CrossRef]
- Bi, Y.; Xue, B.; Zhang, M. Genetic programming with image-related operators and a flexible program structure for feature learning in image classification. IEEE Trans. Evolut. Comput. 2020, 25, 87–101. [Google Scholar] [CrossRef]
- Bi, Y.; Xue, B.; Zhang, M. An effective feature learning approach using genetic programming with image descriptors for image classification. IEEE Comput. Intell. Mag. 2020, 15, 65–77. [Google Scholar] [CrossRef]
- Guo, H.; Jack, L.; Nandi, A. Feature generation using genetic programming with application to fault classification. IEEE Trans. Syst. Man Cyber. Part B 2005, 35, 89–99. [Google Scholar] [CrossRef]
- Peng, B.; Wan, S.; Bi, Y.; Xue, B.; Zhang, M. Automatic feature extraction and construction using genetic programming for rotating machinery fault diagnosis. IEEE Trans. Cyber. 2020, 51, 4909–4923. [Google Scholar] [CrossRef]
- Peng, B.; Bi, Y.; Xue, B.; Zhang, M.; Wan, S. Multi-view feature construction using genetic programming for rolling bearing fault diagnosis. IEEE Comput. Intell. Mag. 2021, 16, 79–94. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, B.; Bi, Y.; Xue, B.; Zhang, M.; Wan, S. A Survey on Fault Diagnosis of Rolling Bearings. Algorithms 2022, 15, 347. https://doi.org/10.3390/a15100347
Peng B, Bi Y, Xue B, Zhang M, Wan S. A Survey on Fault Diagnosis of Rolling Bearings. Algorithms. 2022; 15(10):347. https://doi.org/10.3390/a15100347
Chicago/Turabian StylePeng, Bo, Ying Bi, Bing Xue, Mengjie Zhang, and Shuting Wan. 2022. "A Survey on Fault Diagnosis of Rolling Bearings" Algorithms 15, no. 10: 347. https://doi.org/10.3390/a15100347
APA StylePeng, B., Bi, Y., Xue, B., Zhang, M., & Wan, S. (2022). A Survey on Fault Diagnosis of Rolling Bearings. Algorithms, 15(10), 347. https://doi.org/10.3390/a15100347






