Power Flow Solution in Bipolar DC Networks Considering a Neutral Wire and Unbalanced Loads: A Hyperbolic Approximation
Abstract
1. Introduction
1.1. Motivation
1.2. Brief State of the Art
1.3. Contributions and the Article’s Outline
- A generalized power flow approximation based on the Taylor expansion of the nonlinear relation between currents and voltages, which includes a neutral pole that is either solidly grounded or non-grounded. This approximation could be used for different studies, such as planning and operation, among others.
- A set of numerical experiments in different benchmark test systems confirms that the hyperbolic approximation is applicable for meshed and radial grids, demonstrating the scalability of the model and the low number of iterations, even for large networks.
2. Formulation of the Power Flow Problem
2.1. General Representation
2.2. Solidly Grounded Case
2.3. Non-Grounded Neutral Wire
3. Test Feeders
3.1. The Four-Bus System
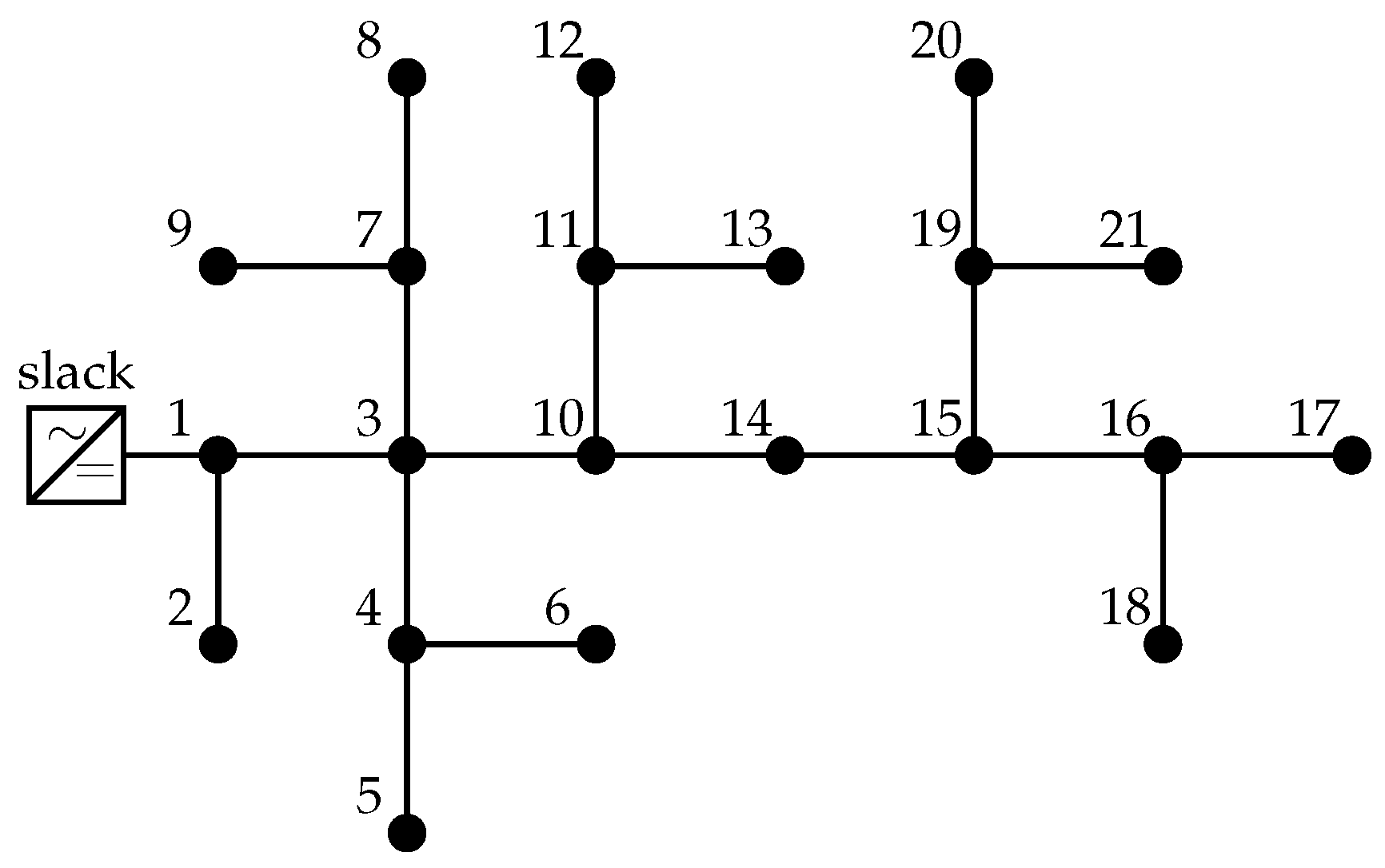
3.2. The 21-Bus System
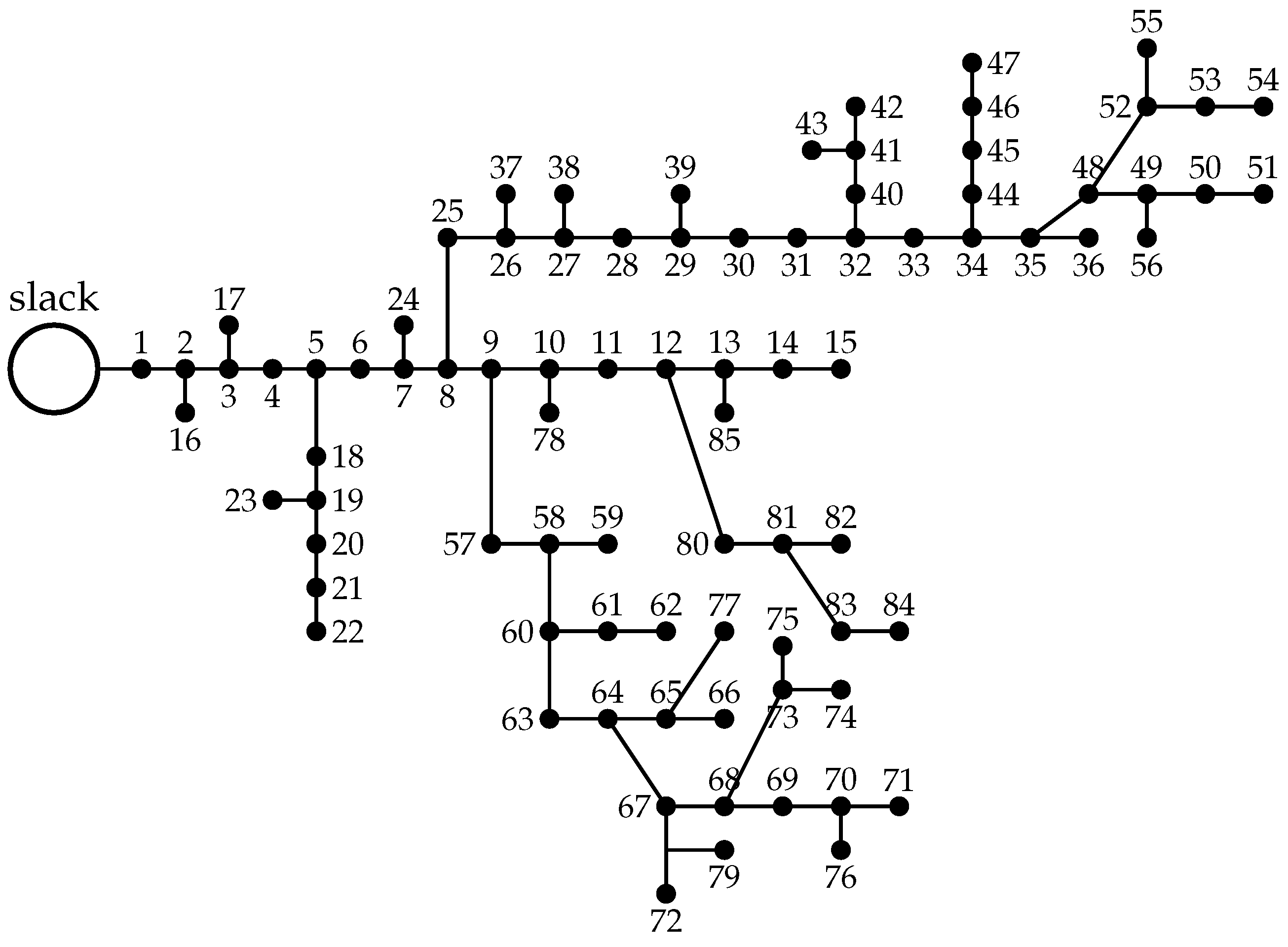
3.3. The 85-Bus System
4. Computational Validation
4.1. Results in the Four-Bus Grid
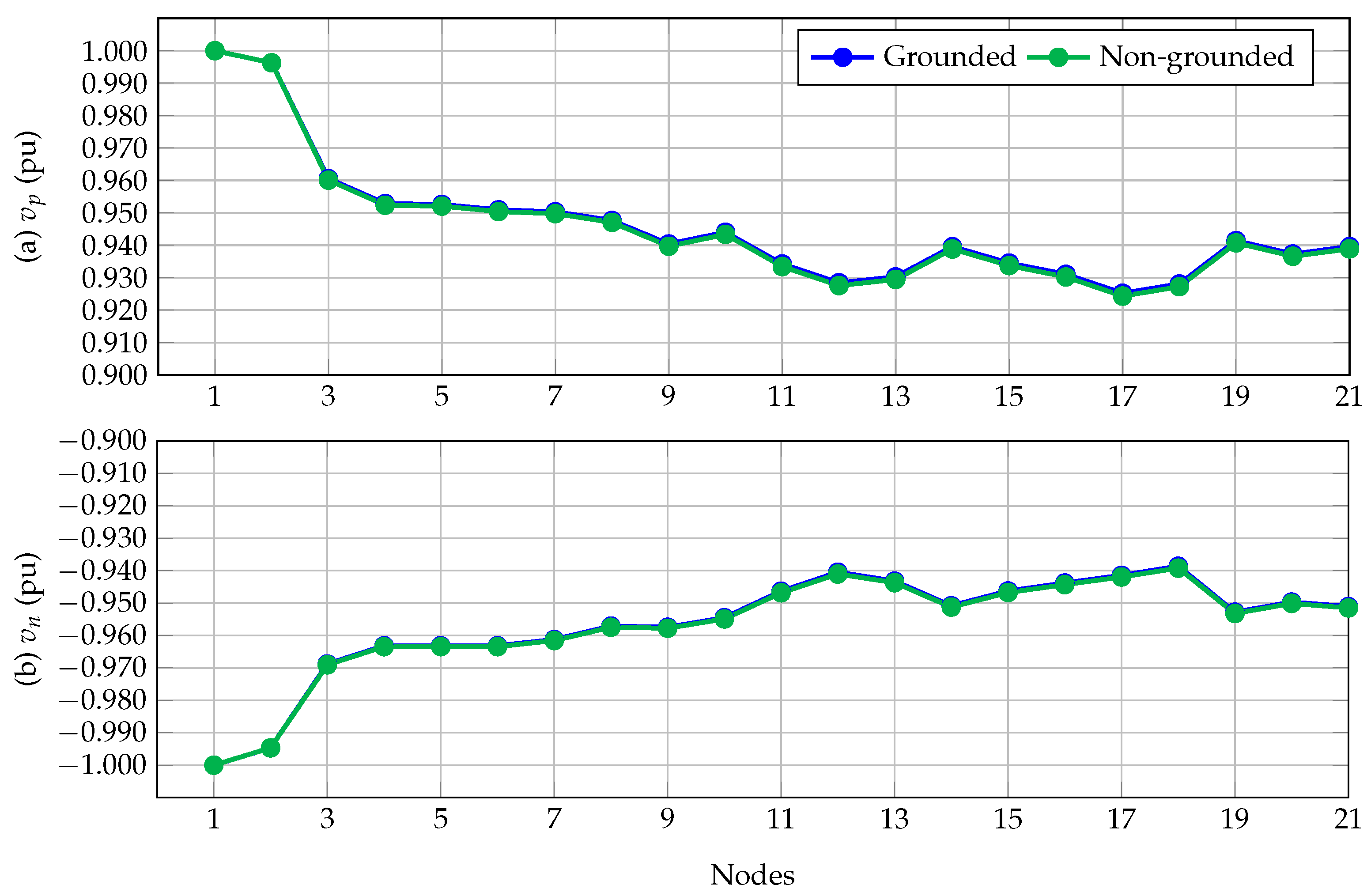
4.2. Results in the 21-Bus Grid
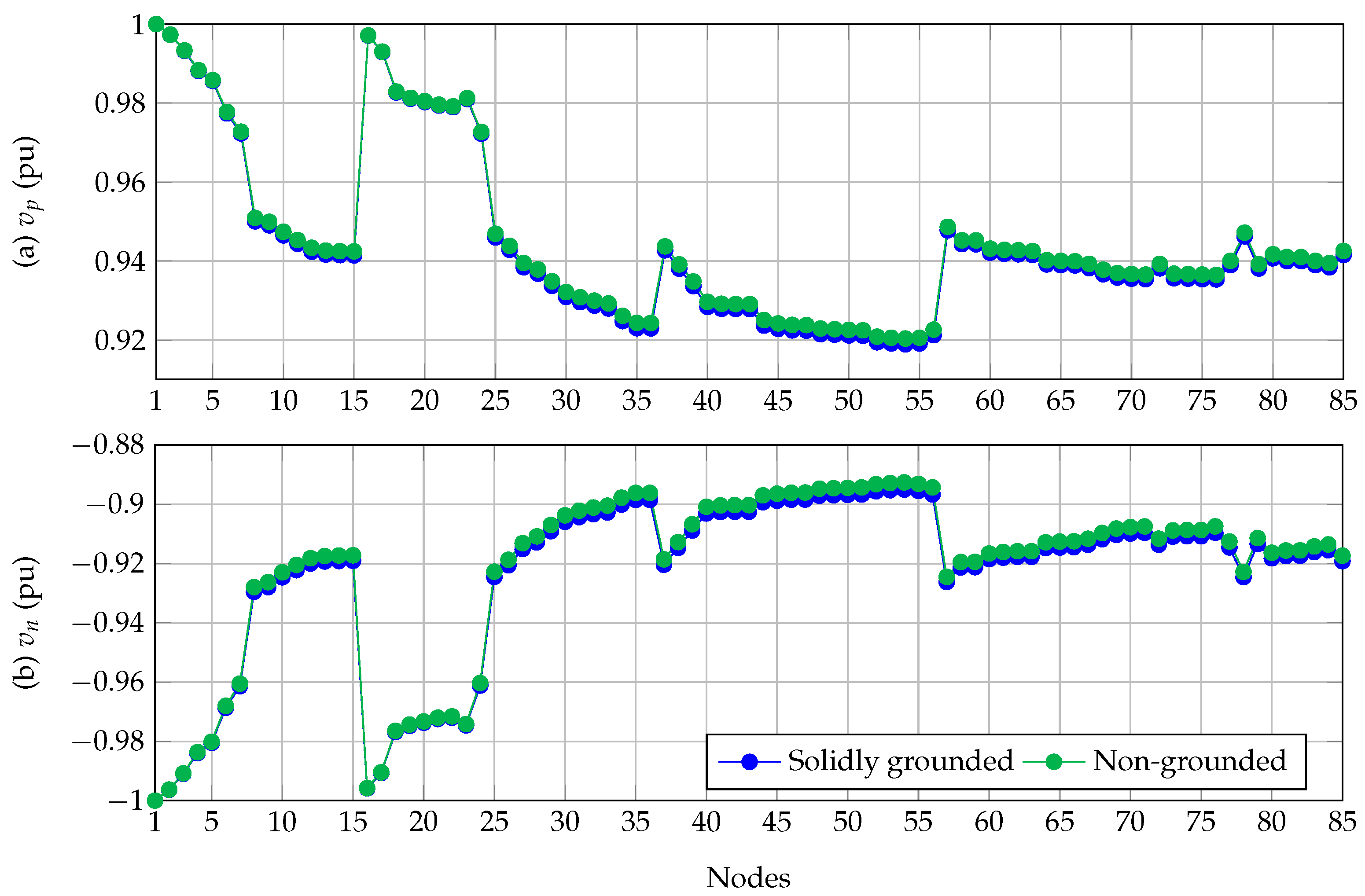
4.3. Results in the 85-Bus Grid
4.4. Simulations Using the Quasi-Newton Formulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lotfi, H.; Khodaei, A. AC Versus DC Microgrid Planning. IEEE Trans. Smart Grid 2017, 8, 296–304. [Google Scholar] [CrossRef]
- Barros, J.; de Apráiz, M.; Diego, R. Power Quality in DC Distribution Networks. Energies 2019, 12, 848. [Google Scholar] [CrossRef]
- Elsayed, A.T.; Mohamed, A.A.; Mohammed, O.A. DC microgrids and distribution systems: An overview. Electr. Power Syst. Res. 2015, 119, 407–417. [Google Scholar] [CrossRef]
- Mackay, L.; van der Blij, N.H.; Ramirez-Elizondo, L.; Bauer, P. Toward the Universal DC Distribution System. Electr. Power Components Syst. 2017, 45, 1032–1042. [Google Scholar] [CrossRef]
- Kumar, J.; Agarwal, A.; Agarwal, V. A review on overall control of DC microgrids. J. Energy Storage 2019, 21, 113–138. [Google Scholar] [CrossRef]
- Parhizi, S.; Lotfi, H.; Khodaei, A.; Bahramirad, S. State of the Art in Research on Microgrids: A Review. IEEE Access 2015, 3, 890–925. [Google Scholar] [CrossRef]
- Chauhan, R.K.; Rajpurohit, B.S.; Pindoriya, N.M. DC Power Distribution System for Rural Applications. In Proceedings of the 8th National Conference on Indian Energy Sector Synergy with Energy, Ahmadabad, India, 11–12 October 2012. [Google Scholar] [CrossRef]
- Justo, J.J.; Mwasilu, F.; Lee, J.; Jung, J.W. AC-microgrids versus DC-microgrids with distributed energy resources: A review. Renew. Sustain. Energy Rev. 2013, 24, 387–405. [Google Scholar] [CrossRef]
- Kalair, A.; Abas, N.; Khan, N. Comparative study of HVAC and HVDC transmission systems. Renew. Sustain. Energy Rev. 2016, 59, 1653–1675. [Google Scholar] [CrossRef]
- Dastgeer, F.; Gelani, H.E. A Comparative analysis of system efficiency for AC and DC residential power distribution paradigms. Energy Build. 2017, 138, 648–654. [Google Scholar] [CrossRef]
- Vossos, V.; Garbesi, K.; Shen, H. Energy savings from direct-DC in U.S. residential buildings. Energy Build. 2014, 68, 223–231. [Google Scholar] [CrossRef]
- Kakigano, H.; Miura, Y.; Ise, T. Low-Voltage Bipolar-Type DC Microgrid for Super High Quality Distribution. IEEE Trans. Power Electron. 2010, 25, 3066–3075. [Google Scholar] [CrossRef]
- Rivera, S.; Lizana, R.; Kouro, S.; Dragičević, T.; Wu, B. Bipolar DC Power Conversion: State-of-the-Art and Emerging Technologies. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 1192–1204. [Google Scholar] [CrossRef]
- Tavakoli, S.D.; Mahdavyfakhr, M.; Hamzeh, M.; Sheshyekani, K.; Afjei, E. A unified control strategy for power sharing and voltage balancing in bipolar DC microgrids. Sustain. Energy Grids Netw. 2017, 11, 58–68. [Google Scholar] [CrossRef]
- Gwon, G.H.; Kim, C.H.; Oh, Y.S.; Noh, C.H.; Jung, T.H.; Han, J. Mitigation of voltage unbalance by using static load transfer switch in bipolar low voltage DC distribution system. Int. J. Electr. Power Energy Syst. 2017, 90, 158–167. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Garces, A. Numerical methods for power flow analysis in DC networks: State of the art, methods and challenges. Int. J. Electr. Power Energy Syst. 2020, 123, 106299. [Google Scholar] [CrossRef]
- Mishra, M.; Patnaik, B.; Biswal, M.; Hasan, S.; Bansal, R.C. A systematic review on DC-microgrid protection and grounding techniques: Issues, challenges and future perspective. Appl. Energy 2022, 313, 118810. [Google Scholar] [CrossRef]
- Mandal, S.; Pahwa, A. Optimal Selection of Conductors for Distribution Feeders. IEEE Power Eng. Rev. 2002, 22, 71. [Google Scholar] [CrossRef]
- Wang, P.; Wang, W.; Xu, D. Optimal Sizing of Distributed Generations in DC Microgrids With Comprehensive Consideration of System Operation Modes and Operation Targets. IEEE Access 2018, 6, 31129–31140. [Google Scholar] [CrossRef]
- Altun, T.; Madani, R.; Yadav, A.P.; Nasir, A.; Davoudi, A. Optimal Reconfiguration of DC Networks. IEEE Trans. Power Syst. 2020, 35, 4272–4284. [Google Scholar] [CrossRef]
- Meng, L.; Luna, A.; Diaz, E.; Sun, B.; Dragicevic, T.; Savaghebi, M.; Vasquez, J.; Guerrero, J.; Graells, M. Flexible System Integration and Advanced Hierarchical Control Architectures in the Microgrid Research Laboratory of Aalborg University. IEEE Trans. Ind. Appl. 2015, 52, 1736–1749. [Google Scholar] [CrossRef]
- Roncero-Clemente, C.; Gonzalez-Romera, E.; Barrero-Gonzalez, F.; Milanes-Montero, M.I.; Romero-Cadaval, E. Power-Flow-Based Secondary Control for Autonomous Droop-Controlled AC Nanogrids With Peer-to-Peer Energy Trading. IEEE Access 2021, 9, 22339–22350. [Google Scholar] [CrossRef]
- Abdi, H.; Beigvand, S.D.; Scala, M.L. A review of optimal power flow studies applied to smart grids and microgrids. Renew. Sustain. Energy Rev. 2017, 71, 742–766. [Google Scholar] [CrossRef]
- Li, J.; Liu, F.; Wang, Z.; Low, S.H.; Mei, S. Optimal Power Flow in Stand-Alone DC Microgrids. IEEE Trans. Power Syst. 2018, 33, 5496–5506. [Google Scholar] [CrossRef]
- Grisales-Noreña, L.F.; Montoya, O.D.; Gil-González, W.J.; Perea-Moreno, A.J.; Perea-Moreno, M.A. A Comparative Study on Power Flow Methods for Direct-Current Networks Considering Processing Time and Numerical Convergence Errors. Electronics 2020, 9, 2062. [Google Scholar] [CrossRef]
- Medina-Quesada, A.; Montoya, O.D.; Hernández, J.C. Derivative-Free Power Flow Solution for Bipolar DC Networks with Multiple Constant Power Terminals. Sensors 2022, 22, 2914. [Google Scholar] [CrossRef]
- Lee, J.O.; Kim, Y.S.; Jeon, J.H. Generic power flow algorithm for bipolar DC microgrids based on Newton–Raphson method. Int. J. Electr. Power Energy Syst. 2022, 142, 108357. [Google Scholar] [CrossRef]
- Lee, J.O.; Kim, Y.S.; Moon, S.I. Current Injection Power Flow Analysis and Optimal Generation Dispatch for Bipolar DC Microgrids. IEEE Trans. Smart Grid 2021, 12, 1918–1928. [Google Scholar] [CrossRef]
- Mackay, L.; Guarnotta, R.; Dimou, A.; Morales-Espana, G.; Ramirez-Elizondo, L.; Bauer, P. Optimal Power Flow for Unbalanced Bipolar DC Distribution Grids. IEEE Access 2018, 6, 5199–5207. [Google Scholar] [CrossRef]
- Chew, B.S.H.; Xu, Y.; Wu, Q. Voltage Balancing for Bipolar DC Distribution Grids: A Power Flow Based Binary Integer Multi-Objective Optimization Approach. IEEE Trans. Power Syst. 2019, 34, 28–39. [Google Scholar] [CrossRef]
- Tamilselvan, V.; Jayabarathi, T.; Raghunathan, T.; Yang, X.S. Optimal capacitor placement in radial distribution systems using flower pollination algorithm. Alex. Eng. J. 2018, 57, 2775–2786. [Google Scholar] [CrossRef]
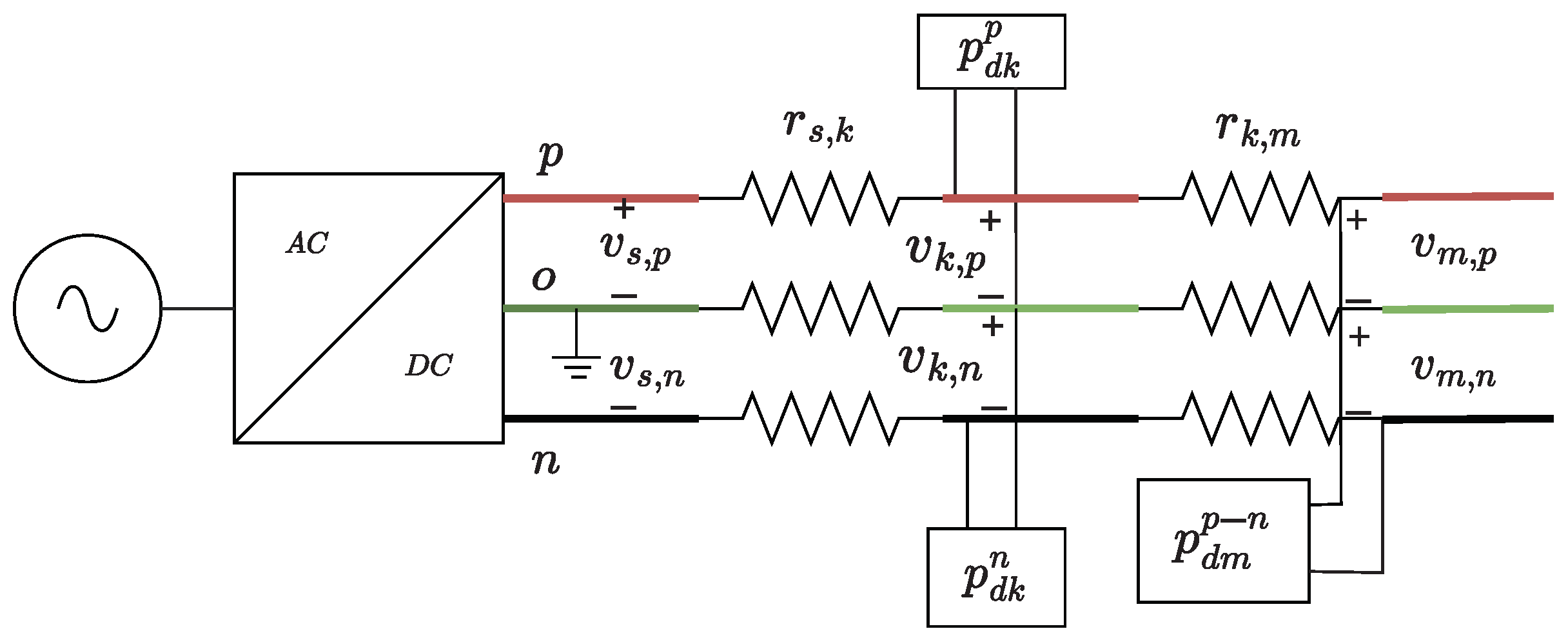

| Node j | Node k | () | (W) | (W) | (W) |
|---|---|---|---|---|---|
| 1 | 2 | 0.25 | 500 | 700 | 950 |
| 2 | 3 | 0.50 | 750 | 350 | 0 |
| 3 | 4 | 0.45 | 250 | 600 | 700 |
| Node j | Node k | () | |||
|---|---|---|---|---|---|
| 1 | 2 | 0.053 | 70 | 100 | 0 |
| 1 | 3 | 0.054 | 0 | 0 | 0 |
| 3 | 4 | 0.054 | 36 | 40 | 120 |
| 4 | 5 | 0.063 | 4 | 0 | 0 |
| 4 | 6 | 0.051 | 36 | 0 | 0 |
| 3 | 7 | 0.037 | 0 | 0 | 0 |
| 7 | 8 | 0.079 | 32 | 50 | 0 |
| 7 | 9 | 0.072 | 80 | 0 | 100 |
| 3 | 10 | 0.053 | 0 | 10 | 0 |
| 10 | 11 | 0.038 | 45 | 30 | 0 |
| 11 | 12 | 0.079 | 68 | 70 | 0 |
| 11 | 13 | 0.078 | 10 | 0 | 75 |
| 10 | 14 | 0.083 | 0 | 0 | 0 |
| 14 | 15 | 0.065 | 22 | 30 | 0 |
| 15 | 16 | 0.064 | 23 | 10 | 0 |
| 16 | 17 | 0.074 | 43 | 0 | 60 |
| 16 | 18 | 0.081 | 34 | 60 | 0 |
| 14 | 19 | 0.078 | 9 | 15 | 0 |
| 19 | 20 | 0.084 | 21 | 10 | 50 |
| 19 | 21 | 0.082 | 21 | 20 | 0 |
| Node j | Node k | () | |||
|---|---|---|---|---|---|
| 1 | 2 | 0.108 | 0 | 0 | 10.075 |
| 2 | 3 | 0.163 | 50 | 0 | 40.35 |
| 3 | 4 | 0.217 | 28 | 28.565 | 0 |
| 4 | 5 | 0.108 | 100 | 50 | 0 |
| 5 | 6 | 0.435 | 17.64 | 17.995 | 25.18 |
| 6 | 7 | 0.272 | 0 | 8.625 | 0 |
| 7 | 8 | 1.197 | 17.64 | 17.995 | 30.29 |
| 8 | 9 | 0.108 | 17.8 | 350 | 40.46 |
| 9 | 10 | 0.598 | 0 | 100 | 0 |
| 10 | 11 | 0.544 | 28 | 28.565 | 0 |
| 11 | 12 | 0.544 | 0 | 40 | 45 |
| 12 | 13 | 0.598 | 45 | 40 | 22.5 |
| 13 | 14 | 0.272 | 17.64 | 17.995 | 35.13 |
| 14 | 15 | 0.326 | 17.64 | 17.995 | 20.175 |
| 2 | 16 | 0.728 | 17.64 | 67.5 | 33.49 |
| 3 | 17 | 0.455 | 56.1 | 57.15 | 50.25 |
| 5 | 18 | 0.820 | 28 | 28.565 | 200 |
| 18 | 19 | 0.637 | 28 | 28.565 | 10 |
| 19 | 20 | 0.455 | 17.64 | 17.995 | 150 |
| 20 | 21 | 0.819 | 17.64 | 70 | 152.5 |
| 21 | 22 | 1.548 | 17.64 | 17.995 | 30 |
| 19 | 23 | 0.182 | 28 | 75 | 28.565 |
| 7 | 24 | 0.910 | 0 | 17.64 | 17.995 |
| 8 | 25 | 0.455 | 17.64 | 17.995 | 50 |
| 25 | 26 | 0.364 | 0 | 28 | 28.565 |
| 26 | 27 | 0.546 | 110 | 75 | 175 |
| 27 | 28 | 0.273 | 28 | 125 | 28.565 |
| 28 | 29 | 0.546 | 0 | 50 | 75 |
| 29 | 30 | 0.546 | 17.64 | 0 | 17.995 |
| 30 | 31 | 0.273 | 17.64 | 17.995 | 0 |
| 31 | 32 | 0.182 | 0 | 175 | 0 |
| 32 | 33 | 0.182 | 7 | 7.14 | 12.5 |
| 33 | 34 | 0.819 | 0 | 0 | 0 |
| 34 | 35 | 0.637 | 0 | 0 | 50 |
| 35 | 36 | 0.182 | 17.64 | 0 | 17.995 |
| 26 | 37 | 0.364 | 28 | 30 | 28.565 |
| 27 | 38 | 1.002 | 28 | 28.565 | 25 |
| 29 | 39 | 0.546 | 0 | 28 | 28.565 |
| 32 | 40 | 0.455 | 17.64 | 0 | 17.995 |
| 40 | 41 | 1.002 | 10 | 0 | 0 |
| 41 | 42 | 0.273 | 17.64 | 25 | 17.995 |
| 41 | 43 | 0.455 | 17.64 | 17.995 | 0 |
| 34 | 44 | 1.002 | 17.64 | 17.995 | 0 |
| 44 | 45 | 0.911 | 50 | 17.64 | 17.995 |
| 45 | 46 | 0.911 | 25 | 17.64 | 17.995 |
| 46 | 47 | 0.546 | 7 | 7.14 | 10 |
| 35 | 48 | 0.637 | 0 | 10 | 0 |
| 48 | 49 | 0.182 | 0 | 0 | 25 |
| 49 | 50 | 0.364 | 18.14 | 0 | 18.505 |
| 50 | 51 | 0.455 | 28 | 28.565 | 0 |
| 48 | 52 | 1.366 | 30 | 0 | 15 |
| 52 | 53 | 0.455 | 17.64 | 35 | 17.995 |
| 53 | 54 | 0.546 | 28 | 30 | 28.565 |
| 52 | 55 | 0.546 | 38 | 0 | 48.565 |
| 49 | 56 | 0.546 | 7 | 40 | 32.14 |
| 9 | 57 | 0.273 | 48 | 35.065 | 10 |
| 57 | 58 | 0.819 | 0 | 50 | 0 |
| 58 | 59 | 0.182 | 18 | 28.565 | 25 |
| 58 | 60 | 0.546 | 28 | 43.565 | 0 |
| 60 | 61 | 0.728 | 18 | 28.565 | 30 |
| 61 | 62 | 1.002 | 12.5 | 29.065 | 0 |
| 60 | 63 | 0.182 | 7 | 7.14 | 5 |
| 63 | 64 | 0.728 | 0 | 0 | 50 |
| 64 | 65 | 0.182 | 12.5 | 25 | 37.5 |
| 65 | 66 | 0.182 | 40 | 48.565 | 33 |
| 64 | 67 | 0.455 | 0 | 0 | 0 |
| 67 | 68 | 0.910 | 0 | 0 | 0 |
| 68 | 69 | 1.092 | 13 | 18.565 | 25 |
| 69 | 70 | 0.455 | 0 | 20 | 0 |
| 70 | 71 | 0.546 | 17.64 | 38.275 | 17.995 |
| 67 | 72 | 0.182 | 28 | 13.565 | 0 |
| 68 | 73 | 1.184 | 30 | 0 | 0 |
| 73 | 74 | 0.273 | 28 | 50 | 28.565 |
| 73 | 75 | 1.002 | 17.64 | 6.23 | 17.995 |
| 70 | 76 | 0.546 | 38 | 48.565 | 0 |
| 65 | 77 | 0.091 | 7 | 17.14 | 25 |
| 10 | 78 | 0.637 | 28 | 6 | 28.565 |
| 67 | 79 | 0.546 | 17.64 | 42.995 | 0 |
| 12 | 80 | 0.728 | 28 | 28.565 | 30 |
| 80 | 81 | 0.364 | 45 | 0 | 75 |
| 81 | 82 | 0.091 | 28 | 53.75 | 0 |
| 81 | 83 | 1.092 | 12.64 | 32.995 | 62.5 |
| 83 | 84 | 1.002 | 62 | 72.2 | 0 |
| 13 | 85 | 0.819 | 10 | 10 | 10 |
| Node | +Pole (V) | 0 Pole (V) | −Pole (V) |
|---|---|---|---|
| Grounded neutral | |||
| 1 | 220 | 0 | −220 |
| 2 | 217.2970 | 0 | −217.1193 |
| 3 | 214.1348 | 0 | −214.0633 |
| 4 | 212.8650 | 0 | −212.0487 |
| Power losses | 113.6987 W | ||
| Number of iterations | 3 | ||
| Non-grounded neutral | |||
| 1 | 220 | 0 | −220 |
| 2 | 217.2990 | −0.1834 | −217.1155 |
| 3 | 214.1399 | −0.0864 | −214.0535 |
| 4 | 212.8721 | −0.8384 | −212.0337 |
| Power losses | 115.2222 W | ||
| Number of iterations | 3 | ||
| Node | +Pole (V) | 0 Pole (V) | −Pole (V) |
|---|---|---|---|
| Grounded neutral | |||
| 1 | 220 | 0 | −220 |
| 2 | 217.2970 | 0 | −217.1193 |
| 3 | 214.1348 | 0 | −214.0633 |
| 4 | 212.8650 | 0 | −212.0487 |
| Power losses | 113.6987 W | ||
| Number of iterations | 7 | ||
| Non-grounded neutral | |||
| 1 | 220 | 0 | −220 |
| 2 | 217.2990 | −0.1834 | −217.1155 |
| 3 | 214.1399 | −0.0864 | −214.0535 |
| 4 | 212.8721 | −0.8384 | −212.0337 |
| Power losses | 115.2222 W | ||
| Number of iterations | 8 | ||
| Node | +Pole (V) | 0 Pole (V) | −Pole (V) |
|---|---|---|---|
| Grounded neutral | |||
| 1 | 1000 | 0 | −1000 |
| 2 | 996.2761 | 0 | −994.6716 |
| 3 | 960.0683 | 0 | −968.4100 |
| 4 | 952.3714 | 0 | −962.7830 |
| 5 | 952.1067 | 0 | −962.7830 |
| 6 | 950.4396 | 0 | −962.7830 |
| 7 | 953.7448 | 0 | −964.5412 |
| 8 | 951.0867 | 0 | −960.4284 |
| 9 | 943.8619 | 0 | −960.7609 |
| 10 | 937.4888 | 0 | −948.4698 |
| 11 | 930.9220 | 0 | −942.8952 |
| 12 | 925.1152 | 0 | −936.9933 |
| 13 | 926.9467 | 0 | −939.7613 |
| 14 | 916.4715 | 0 | −930.2940 |
| 15 | 905.4444 | 0 | −921.0085 |
| 16 | 896.1420 | 0 | −913.9505 |
| 17 | 890.1027 | 0 | −911.4861 |
| 18 | 893.0582 | 0 | −908.6017 |
| 19 | 909.9528 | 0 | −924.3558 |
| 20 | 905.7061 | 0 | −921.1448 |
| 21 | 908.0565 | 0 | −922.5781 |
| Power losses | 91.2701 kW | ||
| Number of iterations | 4 | ||
| Non-grounded neutral | |||
| 1 | 1000 | 0 | −1000 |
| 2 | 996.2821 | −1.6193 | −994.6628 |
| 3 | 959.5205 | 9.2157 | −968.7363 |
| 4 | 951.7636 | 11.3722 | −963.1358 |
| 5 | 951.4955 | 11.6403 | −963.1358 |
| 6 | 949.8030 | 13.3327 | −963.1358 |
| 7 | 953.1183 | 11.7700 | −964.8884 |
| 8 | 950.4291 | 10.3922 | −960.8213 |
| 9 | 943.1110 | 17.9963 | −961.1073 |
| 10 | 936.5746 | 12.4855 | −949.0602 |
| 11 | 929.9259 | 13.6204 | −943.5464 |
| 12 | 924.0247 | 13.7095 | −937.7342 |
| 13 | 925.9357 | 14.4762 | −940.4119 |
| 14 | 915.1628 | 15.9904 | −931.1532 |
| 15 | 903.9040 | 18.1140 | −922.0181 |
| 16 | 894.4081 | 20.6576 | −915.0657 |
| 17 | 888.2594 | 24.3408 | −912.6002 |
| 18 | 891.2522 | 18.5786 | −909.8309 |
| 19 | 908.5513 | 16.7359 | −925.2872 |
| 20 | 904.2616 | 17.8323 | −922.0939 |
| 21 | 906.6158 | 16.9276 | −923.5434 |
| Power losses | 95.4237 kW | ||
| Number of iterations | 4 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sepúlveda-García, S.; Montoya, O.D.; Garcés, A. Power Flow Solution in Bipolar DC Networks Considering a Neutral Wire and Unbalanced Loads: A Hyperbolic Approximation. Algorithms 2022, 15, 341. https://doi.org/10.3390/a15100341
Sepúlveda-García S, Montoya OD, Garcés A. Power Flow Solution in Bipolar DC Networks Considering a Neutral Wire and Unbalanced Loads: A Hyperbolic Approximation. Algorithms. 2022; 15(10):341. https://doi.org/10.3390/a15100341
Chicago/Turabian StyleSepúlveda-García, Simón, Oscar Danilo Montoya, and Alejandro Garcés. 2022. "Power Flow Solution in Bipolar DC Networks Considering a Neutral Wire and Unbalanced Loads: A Hyperbolic Approximation" Algorithms 15, no. 10: 341. https://doi.org/10.3390/a15100341
APA StyleSepúlveda-García, S., Montoya, O. D., & Garcés, A. (2022). Power Flow Solution in Bipolar DC Networks Considering a Neutral Wire and Unbalanced Loads: A Hyperbolic Approximation. Algorithms, 15(10), 341. https://doi.org/10.3390/a15100341







