RSB: Robust Successive Binarization for Change Detection in Bitemporal Hyperspectral Images
Abstract
:1. Introduction
- Successive binarization techniques are proposed by varying the thresholding value, which can be considered fixed every time, i.e., not adaptively varying and not a free parameter, if the proposed types of error functions are the ones adopted here.
- Among the used error functions, a new one based on the Pearson correlation coefficient is introduced.
- Robustness with respect to the error function is achieved by computing a suitable mean image: the produced output is a suitable weighted sum of every contribution.
2. Methodology
2.1. Error Functions
- Euclidean distance (): The difference between every spectral row vector in and is computed. Then, the second norm of the resulting difference vectors is calculated. The computational cost for this metric is proportional to .
- Manhattan distance (): The norm 1 is computed on the spectral difference vectors. The computational cost is proportional to .
- SAM-ZID ()—see [16]: Firstly, the sinus of the angle between every spectral row vector in and is computed and then scaled in ; secondly, the obtained result is multiplied by the standardized difference vector, again scaled in . The computational cost is proportional to .
- Spatial Mean SAM—in short, SAM-MEAN (): The arithmetic mean of the angles between two pairs of spectral vectors (i.e., one row vector in and another row vector in ) inside a local window is computed. The computational cost is , where, by , we denote the chosen window size; see [28] for the details about this parameter.
- Spatial Mean Spectral Angles Deviation Mapper—in short, SMSADM (): The arithmetic mean of the deviation angles from their spectral mean is computed inside a local window, which slides through the considered image. The computational cost is , where, again, by , we denote the chosen window size.
- A complementary measure of the Pearson correlation coefficient, denoted in short as Pearson cc, (): The Pearson correlation coefficient [29] is computed between every pair of spectral row vectors. This is not a common error function to measure changes, but it is experimentally proven to be insightful; see [30]. Here, we propose the following novel formulation. The Pearson coefficient, computed for every spectral row vector, is a value between and 1. In particular, means a negative linear correlation, while means a positive linear correlation. Values of near the 0 mean either very low or no correlation at all. In order to use as a suitable indicator for the change detection task, firstly, it is computed as , to eliminate any negative numbers (which would be meaningless in terms of pixel intensity values) and then it is mirrored with respect to one, so . In fact, a high correlation is expected among the unchanged pixels, in the background, since the same area is analyzed at two different time steps, and hence, for those pixels, the corresponding should be close to 1. Meanwhile, regarding the changed pixels, it is unlikely to obtain any possible linear correlation, i.e., the values should be small or even 0. Therefore, to obtain a suitable output that highlights changes, the produced for every spectral row vector is mirrored with respect to one, so that 0 or close to 0 values will become closer to 1 and the corresponding pixels will have higher intensity values. The computational cost is .
| Algorithm 1: RSB pseudo-code |
Data: Given HS vectorized images Result: Binary change map  output: ; |
2.2. The Algorithm
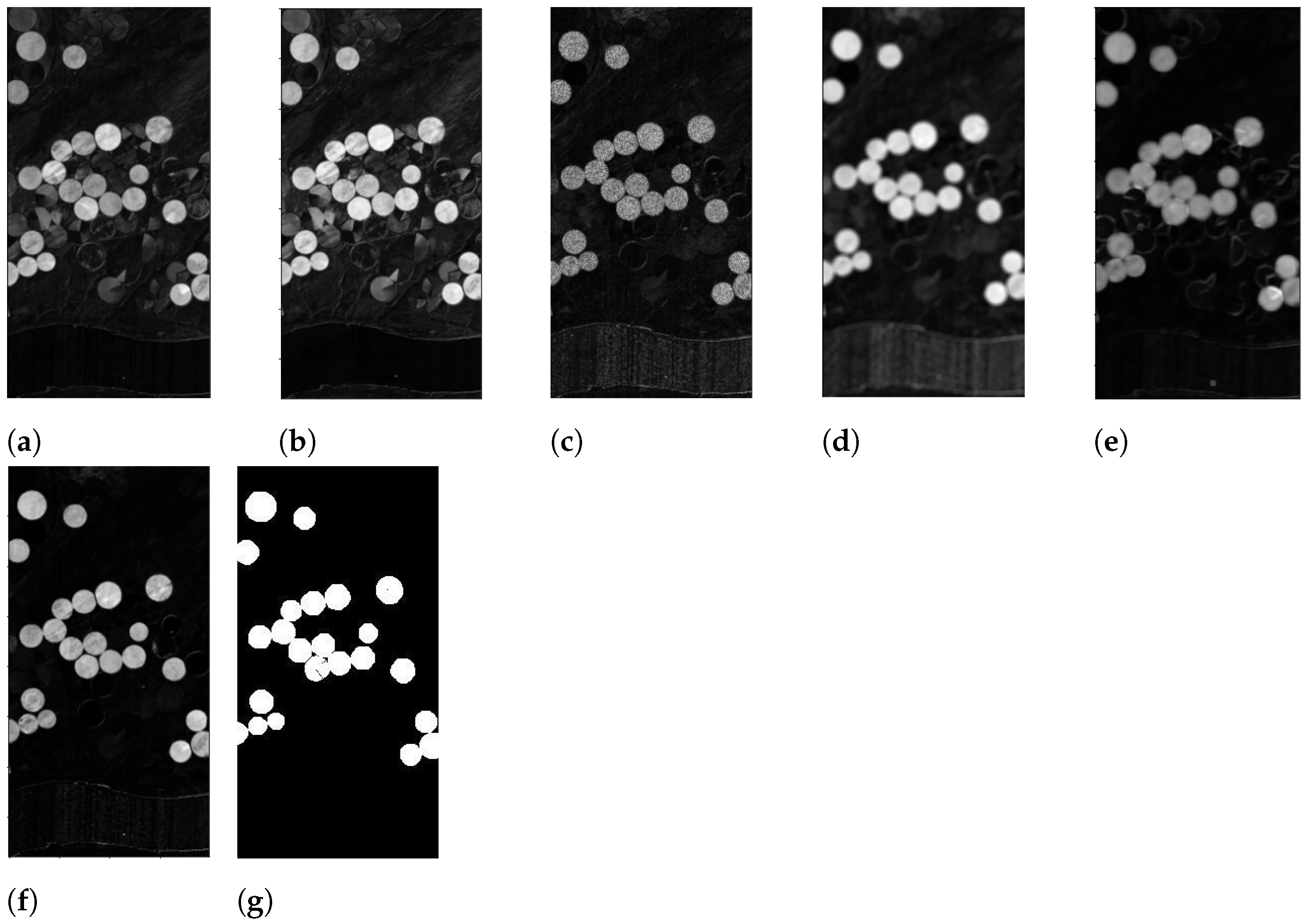
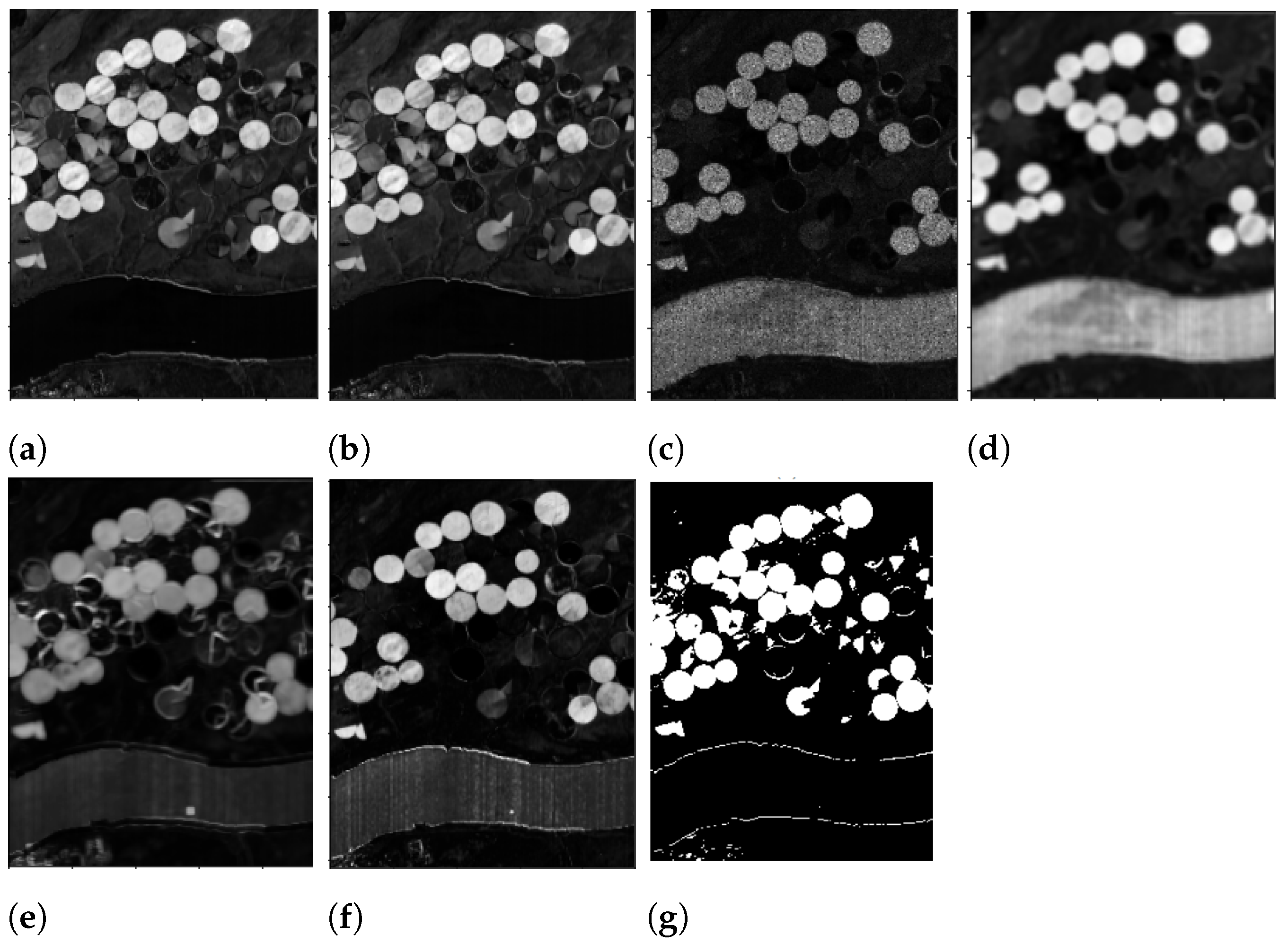
- Application of an error function , which gives as output an image denoted by , for every , line 2 in Algorithm 1.
- Scaling in the range the intensity values of , to obtain , line 3 in Algorithm 1.
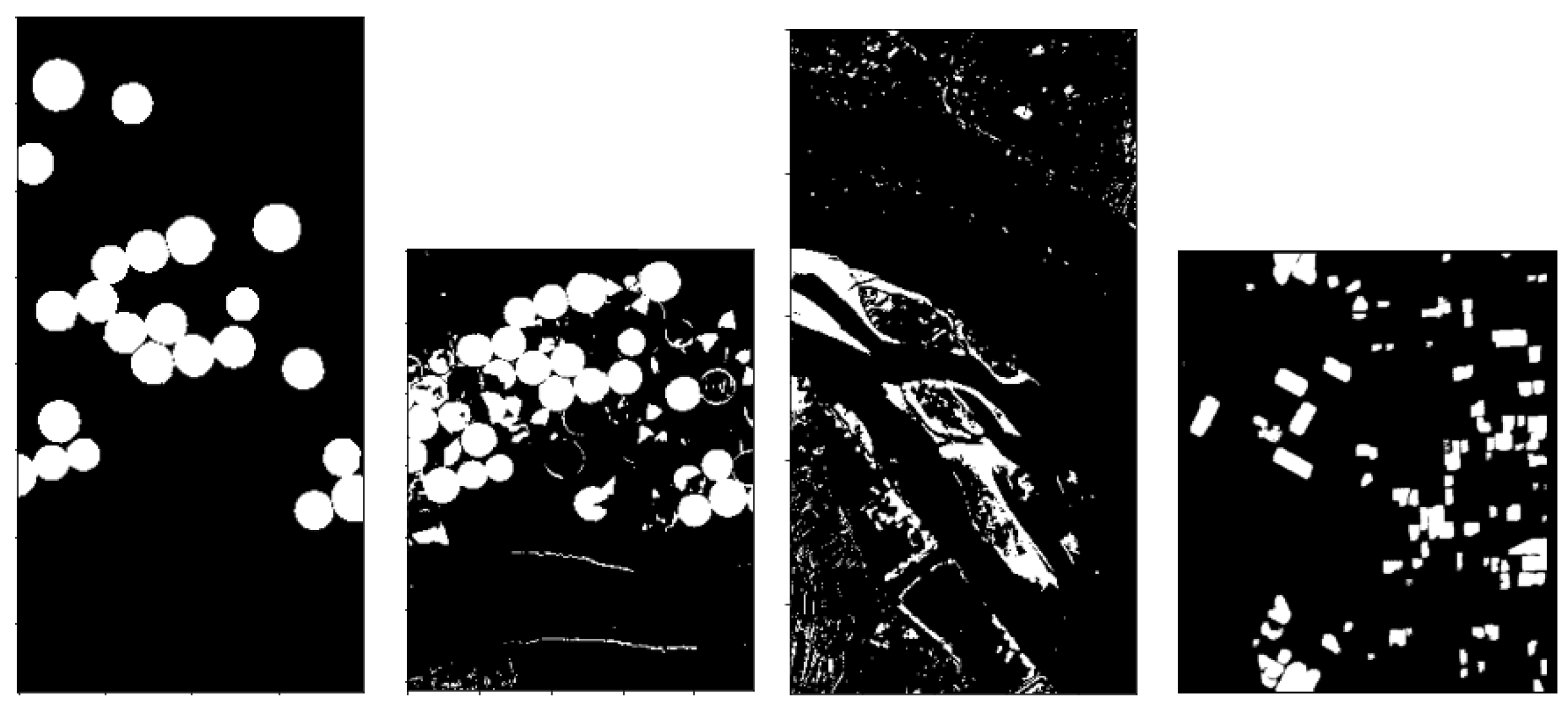
- Binarize by applying different threshold values, line 3 in Algorithms 1 and 2. In particular, let us denote with the chosen thresholds. The pixels in are screened against the values of , producing 5 differently binarized images, for every analyzed . Hence, selecting any , the pixels greater than or equal to the value of the current are set to 1 (i.e., they will be white), and the others, less than , will be set to 0, i.e., black pixels. We denote the resulting image with , for the chosen value of . The computational cost for this procedure is . It should be noted that this process is commonly performed by an automatic thresholding technique, such as Otsu’s thresholding method; see [34]. The choice to produce 5 different outputs though is preferable here, as we are not seeking to produce the best binarized possible image, for which an adapting thresholding technique should be employed. The goal here is to produce a set of different possible binary images, which is achieved more easily in the following.
- A suitable mean image is then computed asThe choice to divide by 2 rather than by 5, as it would be in the common mean definition, is motivated by the fact that we are looking to sum together the contributions of the two sought classes of changed and unchanged pixels. Since it is not a priori known which of the 5 produced binary images are the best ones to make the two classes fairly separable, all are considered, but it is assumed that the contribution provided by these 5 images, under a theoretical point of view, should sum up to 2.
- Every image , for , is then itself binarized (line 5 in Algorithms 1 and 3) by setting to 1, i.e., white, the pixels whose intensity is greater than or equal to 1, and setting to 0, i.e., black, the pixels with intensity values less than 1. The computational cost for this procedure is . This step, for every fixed i, will produce an image denoted with whose entries are only integer values of 0 s and 1 s.
- The next step consists in computing the following image:
- Since T is obtained by summing integer quantities, when the white pixels are present on the same areas, the resulting entries in T will be equal to 6; on the contrary, if only black pixels are present in a certain spot, the corresponding entries in T will be 0. An interesting case arises when, on the same regions, in some cases, there are white pixels, and in other cases, there are black ones. In particular, T is binarized according to the following rule:
- Pixels with an intensity value greater than or equal to 3 are set to 1 and hence will be white, i.e., changed ones;
- Pixels with values less than 3 are set to 0, and hence they will denote unchanged areas.
This procedure is summarized in Algorithm 4 and it costs .The adopted error functions are dissimilarity measures; hence, the higher values are provided when different areas, either in the spatial domain or in the spectral domain, are analyzed. However, it can happen that, due to different light conditions, similar areas could be perceived as different ones, and hence, as a result, the corresponding pixels could receive a high intensity value in the computed image. This possible scenario does not necessarily appear in every for every used error function ; thus, the best value to threshold the computed output is set to 3 for the following reason. There are two error functions to detect changes in the spatial domain (i.e., ) and in the spectral domain (i.e., ); then, there is a hybrid error function for the spectral–spatial domain () and another function for detecting any linear correlation in the background (). The functions and on the one side, and the functions and on the other, behave pair-wise similarly. Therefore, any analyzed pixel cannot be wrongly classified more than twice, since is a hybrid function that should smooth out any contradictory behaviors of the previous functions and measures a different indicator.
| Algorithm 2: Binarize1 pseudo-code |
Data: Given a matrix A Result: Binary mask 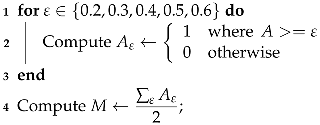 output: M; |
| Algorithm 3: Binarize2 pseudo-code |
Data: Given a matrix M Result: Binary mask 1 Compute ; output: ; |
| Algorithm 4: Binarize3 pseudo-code |
Data: Given a matrix T Result: Binary mask 1 Compute ; output: |
3. Numerical Experiments
- Hermiston dataset (The dataset can be downloaded at: https://gitlab.citius.usc.es/hiperespectral/ChangeDetectionDataset/-/tree/master/Hermiston access date 15 August 2022) consists of two coregistered HS images over the city of Hermiston, Oregon, in 2004 and in 2007. The images are acquired by the Hyperion sensor and consist of pixels with 242 spectral bands; see Figure 1 for the RGB rendering of this dataset.
- USA dataset (The dataset can be downloaded at: https://rslab.ut.ac.ir/documents/81960329/82034892/Hyperspectral_Change_Datasets.zip access date 15 August 2022) consists again of two HS images acquired by the Hyperion sensor over Hermiston in Umatilla County, on 1 May 2004, and 8 May 2007, respectively. The land cover types are soil, irrigated fields, river, building, types of cultivated land, and grassland. These two HS images consist of pixels and 154 spectral bands; see Figure 2 for the RGB rendering of this dataset.
- River (The dataset can be downloaded at: http://crabwq.github.io access date 15 August 2022) dataset [35] contains two HS images taken in Jiangsu Province, China, acquired on 3 May 2013 and on 31 December 2013, respectively, by the (EO-1) Hyperion sensor; see Figure 3 for the RGB rendering of this dataset. These two images consist of pixels with only 198 spectral bands after noise removal.
- Bay Area (The dataset can be downloaded at https://gitlab.citius.usc.es/hiperespectral/ChangeDetectionDataset/-/tree/master/bayArea access date 15 August 2022) dataset consists of two HS images taken in the years 2013 and 2015 with the AVIRIS sensor surrounding the city of Patterson (California). The spatial dimension is pixels and there are 224 spectral bands. In the available ground truth, of the total number of pixels are not classified, i.e., do not have any label. These images were coregistered by using the HypeRvieW desktop tool; see [36,37] and Figure 4 for the RGB rendering.
3.1. Preliminary Discussion
3.2. Thresholding Robustness
3.3. Results Evaluation
- -
- TP: true positive,
- -
- TN: true negative,
- -
- FP: false positive,
- -
- FN: false negative.
4. Post-Processing
4.1. Morphological Transformations
4.2. Supervised Classifier
5. Discussion
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Radke, R.J.; Andra, S.; Al-Kofahi, O.; Roysam, B. Image change detection algorithms: A systematic survey. IEEE Trans. Image Process. 2005, 14, 294–307. [Google Scholar] [CrossRef] [PubMed]
- Hame, T.; Heiler, I.; San Miguel-Ayanz, J. An unsupervised change detection and recognition system for forestry. Int. J. Remote Sens. 1998, 19, 1079–1099. [Google Scholar] [CrossRef]
- Koltunov, A.; Ustin, S. Early fire detection using non-linear multitemporal prediction of thermal imagery. Remote Sens. Environment 2007, 110, 18–28. [Google Scholar] [CrossRef]
- Kwan, C. Methods and challenges using multispectral and hyperspectral images for practical change detection applications. Information 2019, 10, 353. [Google Scholar] [CrossRef]
- Rivera, V.O. Hyperspectral Change Detection Using Temporal Principal Component Anaylsis; University of Puerto Rico: Mayaguez, Puerto Rico, 2005. [Google Scholar]
- Schaum, A.; Stocker, A. Advanced algorithms for autonomous hyperspectral change detection. In Proceedings of the 33rd Applied Imagery Pattern Recognition Workshop (AIPR’04), Washington, DC, USA, 13–15 October 2004; pp. 33–38. [Google Scholar]
- Zhan, T.; Sun, Y.; Tang, Y.; Xu, Y.; Wu, Z. Tensor Regression and Image Fusion-Based Change Detection Using Hyperspectral and Multispectral Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 9794–9802. [Google Scholar] [CrossRef]
- Zhang, L.; Du, B. Recent advances in hyperspectral image processing. Geo-Spat. Inf. Sci. 2012, 15, 143–156. [Google Scholar] [CrossRef]
- Hu, M.; Wu, C.; Zhang, L.; Du, B. Hyperspectral anomaly change detection based on autoencoder. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 3750–3762. [Google Scholar] [CrossRef]
- López-Fandiño, J.; Garea, A.S.; Heras, D.B.; Argüello, F. Stacked autoencoders for multiclass change detection in hyperspectral images. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 1906–1909. [Google Scholar]
- Zeng, H.; Xie, X.; Cui, H.; Yin, H.; Ning, J. Hyperspectral Image Restoration via Global L 1-2 Spatial–Spectral Total Variation Regularized Local Low-Rank Tensor Recovery. IEEE Trans. Geosci. Remote Sens. 2020, 59, 3309–3325. [Google Scholar] [CrossRef]
- Xue, J.; Zhao, Y.; Liao, W.; Chan, J.C.W. Nonlocal low-rank regularized tensor decomposition for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5174–5189. [Google Scholar] [CrossRef]
- Xue, J.; Zhao, Y.; Huang, S.; Liao, W.; Chan, J.C.W.; Kong, S.G. Multilayer sparsity-based tensor decomposition for low-rank tensor completion. IEEE Trans. Neural Netw. Learn. Syst. 2021, 1–15. [Google Scholar] [CrossRef]
- Xue, J.; Zhao, Y.; Bu, Y.; Chan, J.C.W.; Kong, S.G. When Laplacian Scale Mixture Meets Three-Layer Transform: A Parametric Tensor Sparsity for Tensor Completion. IEEE Trans. Cybern. 2022, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Huang, F.; Yu, Y.; Feng, T. Hyperspectral remote sensing image change detection based on tensor and deep learning. J. Vis. Commun. Image Represent. 2019, 58, 233–244. [Google Scholar] [CrossRef]
- Seydi, S.T.; Hasanlou, M. A new land-cover match-based change detection for hyperspectral imagery. Eur. J. Remote Sens. 2017, 50, 517–533. [Google Scholar] [CrossRef]
- Appice, A.; Guccione, P.; Acciaro, E.; Malerba, D. Detecting salient regions in a bi-temporal hyperspectral scene by iterating clustering and classification. Appl. Intell. 2020, 50, 3179–3200. [Google Scholar] [CrossRef]
- Ou, X.; Liu, L.; Tu, B.; Zhang, G.; Xu, Z. A CNN Framework with Slow-Fast Band Selection and Feature Fusion Grouping for Hyperspectral Image Change Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Bovolo, F.; Bruzzone, L. A theoretical framework for unsupervised change detection based on change vector analysis in the polar domain. IEEE Trans. Geosci. Remote Sens. 2006, 45, 218–236. [Google Scholar] [CrossRef]
- López-Fandiño, J.; Heras, D.B.; Argüello, F.; Duro, R.J. CUDA multiclass change detection for remote sensing hyperspectral images using extended morphological profiles. In Proceedings of the 2017 9th IEEE International Conference on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications (IDAACS), Bucharest, Romania, 21–23 September 2017; Volume 1, pp. 404–409. [Google Scholar]
- Andresini, G.; Appice, A.; Dell’Olio, D.; Malerba, D. Siamese Networks with Transfer Learning for Change Detection in Sentinel-2 Images. In Proceedings of the International Conference of the Italian Association for Artificial Intelligence, Virtual Event, 1–3 December 2021; Springer: Berlin/Heidelberg, Germany, 2022; pp. 478–489. [Google Scholar]
- Moustafa, M.S.; Mohamed, S.A.; Ahmed, S.; Nasr, A.H. Hyperspectral change detection based on modification of UNet neural networks. J. Appl. Remote Sens. 2021, 15, 028505. [Google Scholar] [CrossRef]
- Song, A.; Choi, J.; Han, Y.; Kim, Y. Change detection in hyperspectral images using recurrent 3D fully convolutional networks. Remote Sens. 2018, 10, 1827. [Google Scholar] [CrossRef]
- Zhan, T.; Song, B.; Xu, Y.; Wan, M.; Wang, X.; Yang, G.; Wu, Z. SSCNN-S: A spectral-spatial convolution neural network with Siamese architecture for change detection. Remote Sens. 2021, 13, 895. [Google Scholar] [CrossRef]
- Yuan, Z.; Wang, Q.; Li, X. ROBUST PCANet for hyperspectral image change detection. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 4931–4934. [Google Scholar]
- Appice, A.; Lomuscio, F.; Falini, A.; Tamborrino, C.; Mazzia, F.; Malerba, D. Saliency detection in hyperspectral images using autoencoder-based data reconstruction. In Proceedings of the International Symposium on Methodologies for Intelligent Systems, Graz, Austria, 23–25 September 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 161–170. [Google Scholar]
- Falini, A.; Tamborrino, C.; Castellano, G.; Mazzia, F.; Mininni, R.M.; Appice, A.; Malerba, D. Novel reconstruction errors for saliency detection in hyperspectral images. In Proceedings of the International Conference on Machine Learning, Optimization, and Data Science, Siena, Italy, 19–23 July 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 113–124. [Google Scholar]
- Falini, A.; Castellano, G.; Tamborrino, C.; Mazzia, F.; Mininni, R.M.; Appice, A.; Malerba, D. Saliency detection for hyperspectral images via sparse-non negative-matrix-factorization and novel distance measures. In Proceedings of the 2020 IEEE Conference on Evolving and Adaptive Intelligent Systems (EAIS), Bari, Italy, 27–29 May 2020; pp. 1–8. [Google Scholar]
- Pearson, K., VII. Note on regression and inheritance in the case of two parents. Proc. R. Soc. Lond. 1895, 58, 240–242. [Google Scholar]
- De Carvalho, O.A.; Meneses, P.R. Spectral Correlation Mapper (SCM): An Improvement on the Spectral Angle Mapper (SAM). Available online: https://popo.jpl.nasa.gov/pub/docs/workshops/00_docs/Osmar_1_carvalho__web.pdf (accessed on 30 August 2022).
- Kruse, F.A.; Lefkoff, A.; Boardman, J.; Heidebrecht, K.; Shapiro, A.; Barloon, P.; Goetz, A. The spectral image processing system (SIPS)—Interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- Yang, Z.; Mueller, R. Spatial-spectral cross-correlation for change detection: A case study for citrus coverage change detection. In Proceedings of the ASPRS 2007 Annual Conference, Tampa, FL, USA, 7–11 May 2007; Volume 2, pp. 767–777. [Google Scholar]
- Choi, S.S.; Cha, S.H.; Tappert, C.C. A survey of binary similarity and distance measures. J. Syst. Cybern. Informat. 2010, 8, 43–48. [Google Scholar]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Wang, Q.; Yuan, Z.; Du, Q.; Li, X. GETNET: A general end-to-end 2-D CNN framework for hyperspectral image change detection. IEEE Trans. Geosci. Remote Sens. 2018, 57, 3–13. [Google Scholar] [CrossRef]
- Garea, A.S.; Ordóñez, Á.; Heras, D.B.; Argüello, F. HypeRvieW: An open source desktop application for hyperspectral remote-sensing data processing. Int. J. Remote Sens. 2016, 37, 5533–5550. [Google Scholar] [CrossRef]
- López-Fandiño, J.; B Heras, D.; Argüello, F.; Dalla Mura, M. GPU framework for change detection in multitemporal hyperspectral images. Int. J. Parallel Program. 2019, 47, 272–292. [Google Scholar] [CrossRef]
- Magnusson, M.; Sigurdsson, J.; Armansson, S.E.; Ulfarsson, M.O.; Deborah, H.; Sveinsson, J.R. Creating RGB images from hyperspectral images using a color matching function. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 2045–2048. [Google Scholar]
- Glasbey, C.A. An analysis of histogram-based thresholding algorithms. CVGIP Graph. Model. Image Process. 1993, 55, 532–537. [Google Scholar] [CrossRef]
- Li, C.; Tam, P.K.S. An iterative algorithm for minimum cross entropy thresholding. Pattern Recognit. Lett. 1998, 19, 771–776. [Google Scholar] [CrossRef]
- Sauvola, J.; Pietikäinen, M. Adaptive document image binarization. Pattern Recognit. 2000, 33, 225–236. [Google Scholar] [CrossRef]
- Zack, G.W.; Rogers, W.E.; Latt, S.A. Automatic measurement of sister chromatid exchange frequency. J. Histochem. Cytochem. 1977, 25, 741–753. [Google Scholar] [CrossRef]
- Yen, J.C.; Chang, F.J.; Chang, S. A new criterion for automatic multilevel thresholding. IEEE Trans. Image Process. 1995, 4, 370–378. [Google Scholar] [PubMed]
- Prewitt, J.M.; Mendelsohn, M.L. The analysis of cell images. Ann. N. Y. Acad. Sci. 1966, 128, 1035–1053. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, R.; Wood, R. Digital Image Processing; Pretice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Haralick, R.M.; Shapiro, L.G. Computer and Robot Vision; Addison-Wesley Reading: Boston, MA, USA, 1992; Volume 1. [Google Scholar]
- Zhang, H. The Optimality of Naive Bayes. Available online: https://www.aaai.org/Papers/FLAIRS/2004/Flairs04-097.pdf (accessed on 30 August 2022).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Appice, A.; Di Mauro, N.; Lomuscio, F.; Malerba, D. Empowering change vector analysis with autoencoding in bi-temporal hyperspectral images. In Proceedings of the MACLEAN@ PKDD/ECML, Würzburg, Germany, 16–20 September 2019. [Google Scholar]
- Falini, A.; Mazzia, F. Approximated Iterative QLP for Change Detection in Hyperspectral Images. In Proceedings of the AIP Conference—20th International Conference of Numerical Analysis and Applied Mathematics, Heraklion, Greece, 19–25 September 2022. [Google Scholar]
- Andresini, G.; Appice, A.; Iaia, D.; Malerba, D.; Taggio, N.; Aiello, A. Leveraging autoencoders in change vector analysis of optical satellite images. J. Intell. Inf. Syst. 2022, 58, 433–452. [Google Scholar] [CrossRef]
- Baisantry, M.; Negi, D.; Manocha, O. Change vector analysis using enhanced PCA and inverse triangular function-based thresholding. Def. Sci. J. 2012, 62, 236–242. [Google Scholar] [CrossRef]
- Nielsen, A.A.; Conradsen, K.; Simpson, J.J. Multivariate alteration detection (MAD) and MAF postprocessing in multispectral, bitemporal image data: New approaches to change detection studies. Remote Sens. Environ. 1998, 64, 1–19. [Google Scholar] [CrossRef]
- Marpu, P.; Gamba, P.; Benediktsson, J.A. Hyperspectral change detection with ir-mad and initial change mask. In Proceedings of the 2011 3rd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Lisbon, Portugal, 6–9 June 2011; pp. 1–4. [Google Scholar]
- Nielsen, A.A.; Canty, M.J. Multi-and hyperspectral remote sensing change detection with generalized difference images by the IR-MAD method. In Proceedings of the International Workshop on the Analysis of Multi-Temporal Remote Sensing Images, Groton, MA, USA, 28–30 July 2005; pp. 169–173. [Google Scholar]
- Seydi, S.; Hasanlou, M. Binary hyperspectral change detection based on 3D convolution deep learning. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 43, 1629–1633. [Google Scholar] [CrossRef]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3-D–2-D CNN feature hierarchy for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2019, 17, 277–281. [Google Scholar] [CrossRef]
- Hu, M.; Wu, C.; Du, B.; Zhang, L. Binary Change Guided Hyperspectral Multiclass Change Detection. arXiv 2021, arXiv:2112.04493. [Google Scholar]
- Nemmour, H.; Chibani, Y. Multiple support vector machines for land cover change detection: An application for mapping urban extensions. ISPRS J. Photogramm. Remote Sens. 2006, 61, 125–133. [Google Scholar] [CrossRef]





| Thresholding | Hermiston | USA | River | Bay Area | ||||
|---|---|---|---|---|---|---|---|---|
| OA | K | OA | K | OA | K | OA | K | |
| RSB | 0.9867 | 0.9410 | 0.9076 | 0.7060 | 0.9624 | 0.7250 | 0.8935 | 0.5873 |
| Otsu | 0.9633 | 0.8522 | 0.7323 | 0.3939 | 0.9061 | 0.5970 | 0.8335 | 0.5134 |
| Mean | 0.7691 | 0.4155 | 0.6939 | 0.3960 | 0.5637 | 0.1595 | 0.6585 | 0.2882 |
| Li | 0.9028 | 0.6710 | 0.7276 | 0.4225 | 0.8091 | 0.3946 | 0.7190 | 0.3525 |
| Sauvola | 0.2029 | 0.0223 | 0.2822 | 0.0302 | 0.1403 | 0.0104 | 0.2833 | 0.0483 |
| Triangle | 0.2543 | 0.0415 | 0.2330 | 0.0043 | 0.8474 | 0.4628 | 0.7427 | 0.3820 |
| Yen | 0.8579 | 0.5663 | 0.7117 | 0.4079 | 0.9409 | 0.6977 | 0.8865 | 0.5962 |
| Datasets | 1 Iteration | 2 Iterations | ||
|---|---|---|---|---|
| OA | K | OA | K | |
| USA | 0.9535 | 0.8609 | 0.9579 | 0.8781 |
| River | 0.9609 | 0.7711 | 0.9681 | 0.8014 |
| Method | Hermiston | |
|---|---|---|
| OA | K | |
| RSB+PP | 0.9876 | 0.9447 |
| AI-QLP [50] | 0.9856 | 0.9400 |
| Method [10] | 0.9874 | − |
| BIC2 [17] | 0.9881 | − |
| ORCHESTRA [51] | 0.9871 | − |
| GETNET [18] | 0.9540 | 0.7810 |
| CVA [18] | 0.9390 | 0.6610 |
| PCA-CVA [18] | 0.9790 | 0.9060 |
| CNN [18] | 0.9470 | 0.7600 |
| CUDA [20] | 0.9848 | − |
| AICA [49] | 0.9887 | − |
| SFBS-FFGNET [18] | 0.9850 | 0.9310 |
| Method | USA | |
|---|---|---|
| OA | K | |
| RSB+PP | 0.9579 | 0.8781 |
| GETNET-1 [35] | 0.9289 | 0.7764 |
| GETNET-2 [35] | 0.9332 | 0.7897 |
| CVA [19] | 0.9272 | 0.7670 |
| MAD-SVM [56] | 0.8612 | 0.4760 |
| IR-MAD-SVM [56] | 0.9285 | 0.7700 |
| Method [56] | 0.9490 | 0.8310 |
| BIC2 [17] | 0.9728 | − |
| AICA [49] | 0.9417 | − |
| HybridSN [24] | 0.9553 | 0.8701 |
| SCNN-S [24] | 0.9631 | 0.8848 |
| SSCNN-S [24] | 0.9651 | 0.8918 |
| TRIFCD-MS [7] | 0.8848 | 0.7024 |
| TRIFCD-Fusion [7] | 0.9263 | 0.7813 |
| BCG-Net [58] | 0.9546 | 0.8662 |
| Method | River | |
|---|---|---|
| OA | K | |
| RSB+PP | 0.9681 | 0.8014 |
| GETNET-1 [35] | 0.9497 | 0.7662 |
| GETNET-2 [35] | 0.9514 | 0.7539 |
| CVA [19] | 0.9529 | 0.7967 |
| PCA-CVA [52] | 0.9434 | 0.7326 |
| IR-MAD [54,55] | 0.8963 | 0.6632 |
| SVM [59] | 0.9046 | 0.6360 |
| CNN [35] | 0.9440 | 0.6867 |
| HybridSN [57] | 0.9614 | 0.7371 |
| SCNN-S [24] | 0.9610 | 0.7300 |
| SSCNN-S [24] | 0.9640 | 0.7431 |
| TRIFCD-MS [7] | 0.9442 | 0.7063 |
| TRIFCD-Fusion [7] | 0.9529 | 0.7573 |
| SFBS-FFGNET [18] | 0.9670 | 0.7710 |
| Method | Bay Area | |
|---|---|---|
| OA | K | |
| RSB+PP | 0.9274 | 0.6540 |
| ORCHESTRA [51] | 0.9561 | − |
| EUC+EM [37] | 0.8884 | − |
| EUC + Otsu [37] | 0.8501 | − |
| SAM + Otsu [37] | 0.9493 | − |
| EUC + WAT + Otsu [37] | 0.8666 | − |
| SAM + WAT + EM [37] | 0.9437 | − |
| SAM + WAT + Otsu [37] | 0.9694 | − |
| AICA [51] | 0.8529 | − |
| BIC2 [17] | 0.9551 | − |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Falini, A. RSB: Robust Successive Binarization for Change Detection in Bitemporal Hyperspectral Images. Algorithms 2022, 15, 340. https://doi.org/10.3390/a15100340
Falini A. RSB: Robust Successive Binarization for Change Detection in Bitemporal Hyperspectral Images. Algorithms. 2022; 15(10):340. https://doi.org/10.3390/a15100340
Chicago/Turabian StyleFalini, Antonella. 2022. "RSB: Robust Successive Binarization for Change Detection in Bitemporal Hyperspectral Images" Algorithms 15, no. 10: 340. https://doi.org/10.3390/a15100340
APA StyleFalini, A. (2022). RSB: Robust Successive Binarization for Change Detection in Bitemporal Hyperspectral Images. Algorithms, 15(10), 340. https://doi.org/10.3390/a15100340






