Hyper-Heuristic Based on ACO and Local Search for Dynamic Optimization Problems †
Abstract
:1. Introduction
- We integrate one of the best ACO variations with advanced and effective local search operators, i.e., the Lin–Kernighan and the Unstringing and Stringing heuristics, resulting in a powerful hyper-heuristic (HULK).
- The proposed HULK combines the adaptation capabilities of ACO for DOPs and the superior performance of the local search operators. This is done with a smart and self-adaptive way to choose the LSO that is applied using a weighted roulette wheel, based on the objective function value of the previous solutions.
- We include arc blocking and dropped the frequency of dynamic changes without losing quality.
- The proposed method can provide better solutions, especially in asymmetric dynamic test cases.
2. Proposed Dynamic Changes
2.1. Base Problem Formulation
2.2. Generating Dynamic Test Cases
3. HULK: Hyper-Heuristic Based on ACO and Local Search Operators
3.1. Building Solutions Inside ACO
3.2. Choosing and Applying Local Search Operator
| Algorithm 1 Procedure for Applying LSO | |
|
1: 2: 3: 4: 5: 6: 7: 8: 9: 10: 11: 12: 13: | ApplyLSO() if () then ApplyLocalSearchUS() if (Solution was improved?) then Update and as show in Equation (11) end if else ApplyLocalSearchLK() if (Solution was improved?) then Update and as show in Equation (12) end if end if OUTPUT: %best TSP solution after local search |
3.2.1. Lin–Kernighan Local Search Operator
- Each arc removed must share a node with its added counterpart. After the first arc exchange in each cycle, each arc being removed must also share a node with the previously added arc. Figure 1 illustrates an example of a 2-opt move, where in the first step arc (,) is removed and arc (,), which shares the node with its removed counterpart, is added. In the second step arc (,), which shares node with the previously added arc, is removed and arc (,) is added, closing the tour.
- No exchanges that result in the tour being broken into multiple closed circuits are allowed. An example of this type of exchange is shown in Figure 2, where arcs (,) and (,) are removed and arcs (,) and (,) are added. In this case, the addition of any arcs would not be accepted because it would result in a segment of tour forming a cycle.
- Each pair of arcs exchanged must be gainful, meaning that each arc being added must be shorter than its removed counterpart. If the problem is asymmetric, both orientations of the resulting tour must be analysed.
- Once an arc is removed, it cannot be reinserted until the tour is closed.
3.2.2. Unstringing and Stringing Local Search Operator
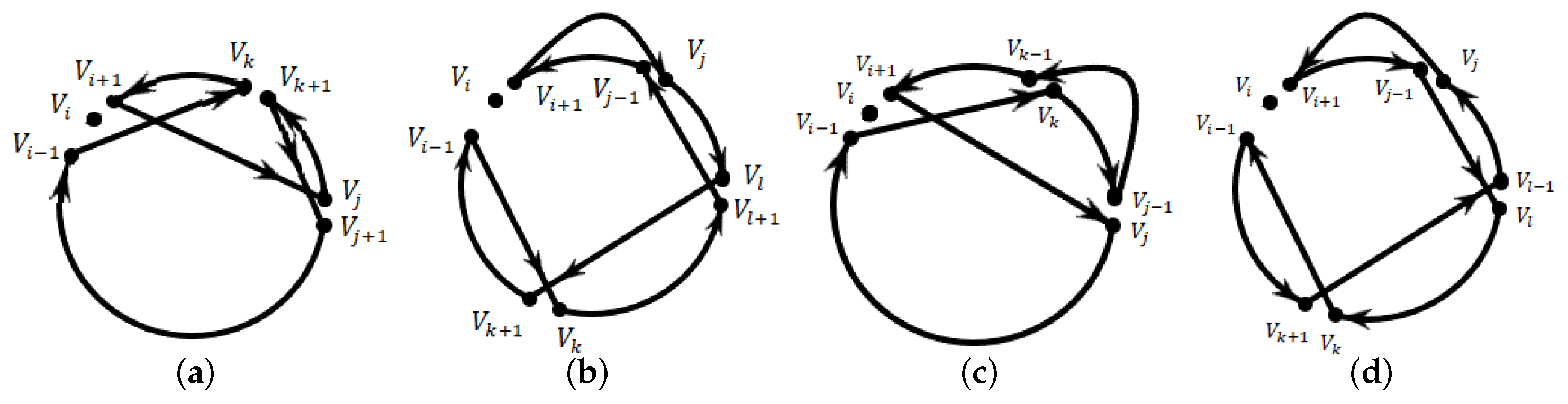
- Unstringing Type I: consider belonging to the neighbourhood of and belonging to the neighbourhood of , with being part of the sub tour . The removal of node results in the deletion of arcs , , and and the insertion of arcs and . Additionally, the sub tours and are reversed.
- Unstringing Type II: consider belonging to the neighbourhood of , belonging to the neighbourhood of , with being part of the subtour , and belonging to the neighbourhood of , with being part of the sub tour . The removal of node results in the deletion of arcs , , , and and the insertion of arcs , , and . As before, the sub tours and are reversed.
- Unstringing Type III: consider belonging to the neighborhood of and belonging to the neighborhood of with being part of the sub tour . The removal of node results in the deletion of arcs , , , and and the insertion of arcs , , and . As before, the sub tours and are reversed.
- Unstringing Type IV: consider belonging to the neighborhood of , belonging to the neighborhood of with being part of the sub tour , and belonging to the neighborhood of with being part of the sub tour . The removal of node results in the deletion of arcs , , , , and and the insertion of arcs , , , and . As before, the sub tours and are reversed.
- Stringing Type I: Assuming and . The insertion of results in the deletion of arcs , and and the insertion of arcs , , and . Additionally, the sub tours and are reversed.
- Stringing Type II: assuming , , , and . The insertion of results in the deletion of arcs , , and and the insertion of arcs , , , and . As before, the sub tours and are reversed.
- Stringing Type III: this stringing type can be seen as the inverse of Stringing Type I. Notice that when node is inserted between and , the sub tour of nodes is rearranged in such a way that almost the entire sequence is reversed. The objective is to explore other promising regions of the search space. As in Stringing Type I, assume that and . The insertion of results in the deletion of arcs , and and the insertion of arcs , , and . As before, the sub tours and are reversed.
- Stringing Type IV: similarly, this type of insertion can be seen as the reverse of Stringing Type II. As in Stringing Type II, assume that , , and . The insertion of results in the deletion of arcs , , and and the insertion of arcs , , , and . As above, the sub tours and are reversed.
3.3. Pheromone Trail Update
3.4. Keeping Solution Diversity
3.5. Responding to Dynamic Changes
3.6. Integration between Algorithms in the Dynamic Test Environment
| Algorithm 2 Hyper-heuristic HULK Dynamic Test Running Environment. | |
| 1: | Initialize parameters:T(the period of dynamic change), M(the maximum number of iterations for the test),(the magnitude of change for the iterationi) and(where is the percentage of choice of US, andis the percentage of choice of LK) |
| 2: 3: 4: 5: 6: 7: | (the current number of iterations for the test) (the current number of iterations without improvement for the test) (the current period of dynamic change) ReadProblem() InitializeEnvironment InitializePheromoneTrails() |
| 8: | SelectAusing a weighted roulette wheel (biased byfor US andfor LK) to be the first algorithm to interact with ACO, A’ will be the LSO who was not chosen |
| 9: 10: 11: 12: 13: 14: 15: 16: 17: 18: 19: 20: 21: 22: 23: 24: 25: 26: 27: 28: 29: 30: 31: 32: | while () do if () then ApplyDynamicChanges() end if ConstructSolutions FindIterationBest if ( and ) then end if if () then ApplyLSO() ApplyLSO() else if or then ApplyLSO() end if end if PheromoneUpdate if then end if |
| 33: | Select A using a weighted roulette wheel to be the algorithm to interact with ACO in the next iteration, A’ will be the LSO that was not chosen |
|
34: 35: 36: 37: |
end while OUTPUT: %best TSP solution |
4. Computational Tests
4.1. Experimental Setup
- AS + US: for each best-so-far ant found by AS, we apply the US local search operator pursuing improvements (detailed in [8]).
- AS + LK: for each best-so-far ant found by AS, we apply the LK local search operator pursuing improvements (detailed in [8]).
- HULK: proposed hyper-heuristic that combines ACO with the LSOs LK and US, biased by a self-adjusting weighted roulette wheel (detailed in Algorithm 2).
4.2. Experimental Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Burke, E.K.; Hyde, M.; Kendall, G.; Ochoa, G.; Özcan, E.; Woodward, J.R. A classification of hyper-heuristic approaches. In Handbookof Metaheuristics; Gendreau, M., Potvin, J.-Y., Eds.; Springer: New York, NY, USA, 2010; pp. 449–468. [Google Scholar]
- Macias-Escobar, T.; Dorronsoro, B.; Cruz-Reyes, L.; Rangel-Valdez, N.; Gómez-Santillán, C. A Survey of hyper-heuristics for dynamic optimization problems. In Intuitionistic and Type-2 Fuzzy Logic Enhancements in Neural and Optimization Algorithms: Theory and Applications; Castillo, O., Melin, P., Kacprzyk, J., Eds.; Studies in Computational Intelligence; Springer: Cham, Switzerland, 2020; Volume 862, pp. 463–477. [Google Scholar] [CrossRef]
- Dorigo, M.; Stützle, T. Ant Colony Optimization; MIT Press: Cambridge, MA, USA, 2004; 304p. [Google Scholar]
- Applegate, D.L.; Bixby, R.E.; Chvatal, V.; Cook, W.J. The Traveling Salesman Problem: A Computational Study; Princeton University Press: Princeton, NJ, USA, 2007; 608p. [Google Scholar]
- Jin, Y.; Branke, J. Evolutionary optimization in uncertain environments—A survey. IEEE Trans. Evol. Comput. 2005, 9, 303–317. [Google Scholar] [CrossRef] [Green Version]
- Emelogu, A.; Chowdhury, S.; Marufuzzaman, M.; Bian, L.; Eksioglu, B. An enhanced sample average approximation method for stochastic optimization. Int. J. Prod. Econ. 2016, 182, 230–252. [Google Scholar] [CrossRef]
- Hart, E.; Ross, P. An immune system approach to scheduling in changing environments. In Proceedings of the 1st Annual Conference on Genetic and Evolutionary Computation, Orlando, FL, USA, 13–17 July 1999. [Google Scholar]
- Mavrovouniotis, M.; Bonilha, I.S.; Müller, F.M.; Ellinas, G.; Polycarpou, M. Effective ACO-Based Memetic Algorithms for Symmetric and Asymmetric Dynamic Changes. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 2567–2574. [Google Scholar] [CrossRef] [Green Version]
- Mavrovouniotis, M.; Müller, F.M.; Yang, S. An ant colony optimization based memetic algorithm for the dynamic travelling salesman problem. In Proceedings of the Conference on Genetic and Evolutionary Computation Conference (GECCO2015), Madrid, Spain, 11–15 July 2015; pp. 49–56. [Google Scholar]
- Mavrovouniotis, M.; Müller, F.M.; Yang, S. Ant colony optimization with local search for the dynamic travelling salesman problems. IEEE Trans. Cybern. 2017, 47, 1743–1756. [Google Scholar] [CrossRef] [Green Version]
- Mavrovouniotis, M.; Yang, S. Ant colony optimization with immigrants schemes for the dynamic travelling salesman problem with traffic factors. Appl. Soft Comput. 2013, 13, 4023–4037. [Google Scholar] [CrossRef]
- Mavrovouniotis, M.; Yang, S. A memetic ant colony optimization algorithm for the dynamic travelling salesman problem. Soft Comput. 2011, 15, 1405–1425. [Google Scholar] [CrossRef]
- Sama, M.; Pellegrini, P.; D’Ariano, A.; Rodriguez, J.; Pacciarelli, D. Ant colony optimization for the real-time train routing selection problem. Trans. Res. Part B Methodol. 2016, 85, 89–108. [Google Scholar] [CrossRef]
- Cheng, H.; Yang, S. Genetic algorithms with elitism-based immigrants for dynamic load balanced clustering problem in mobile ad hoc networks. In Proceedings of the 2011 IEEE Symposium on Computational Intelligence in Dynamic and Uncertain Environments (CIDUE), Paris, France, 11–15 April 2011. [Google Scholar]
- Cheng, H.; Yang, S. Genetic algorithms with immigrants schemes for dynamic multicast problems in mobile ad hoc networks. Eng. Appl. Artif. Intell. 2010, 23, 806–819. [Google Scholar] [CrossRef] [Green Version]
- Cheng, H.; Yang, S. Multi-population genetic algorithms with immigrants scheme for dynamic shortest path routing problems in mobile ad hoc networks. In Proceedings of the European Conference on the Applications of Evolutionary Computation, Istanbul, Turkey, 7–9 April 2010. [Google Scholar]
- Du, W.; Li, B. Multi-strategy ensemble particle swarm optimization for dynamic optimization. Inf. Sci. 2010, 178, 3096–3109. [Google Scholar] [CrossRef]
- Eddaly, M.; Jarboui, B.; Siarry, P. Combinatorial particle swarm optimization for solving blocking flowshop scheduling problem. J. Comput. Des. Eng. 2016, 3, 295–311. [Google Scholar] [CrossRef]
- Liu, J. Rank-based ant colony optimization applied to dynamic traveling salesman problems. Eng. Optim. 2005, 37, 831–847. [Google Scholar] [CrossRef]
- Guntsch, M.; Middendorf, M. Pheromone modification strategies for ant algorithms applied to dynamic TSP. In Proceedings of the Workshops on Applications of Evolutionary Computation, Como, Italy, 18–20 April 2001. [Google Scholar]
- Eyckelhof, C.J.; Snoek, M. Ant systems for a dynamic TSP. In Proceedings of the International Workshop on Ant Algorithms, Brussels, Belgium, 12–14 September 2002. [Google Scholar]
- Mavrovouniotis, M.; Yang, S.; Yao, X. Multi-colony ant algorithms for the dynamic travelling salesman problem. In Proceedings of the IEEE Symposium on Computational Intelligence in Dynamic and Uncertain Environments, Orlando, FL, USA, 9–12 December 2014. [Google Scholar]
- Guntsch, M.; Middendorf, M. A population based approach for ACO. In Proceedings of the Workshops on Applications of Evolutionary Computation, Kinsale, Ireland, 3–4 April 2002. [Google Scholar]
- Angus, D. Niching for ant colony optimisation. Biol.-Inspired Optim. Methods 2009, 210, 165–188. [Google Scholar]
- Angus, D. Niching for population-based ant colony optimization. In Proceedings of the Second IEEE international Conference on e-Science and Grid Computing, Amsterdam, The Netherlands, 4–6 December 2006. [Google Scholar]
- Mavrovouniotis, M.; Yang, S. Memory-based immigrants for ant colony optimization in changing environments. In Proceedings of the European Conference on the Applications of Evolutionary Computation, Torino, Italy, 27–29 April 2011. [Google Scholar]
- Chowdhury, S.; Marufuzzaman, M.; Tunc, H.; Bian, L.; Bullington, W. A modified ant colony optimization algorithm to solve a dynamic traveling salesman problem: A case study with drones for wildlife surveillance. J. Comput. Des. Eng. 2019, 6, 368–386. [Google Scholar] [CrossRef]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B Cybern. 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stützle, T.; Hoos, H. – ant system. Future Gener. Comput. Syst. 2000, 16, 889–914. [Google Scholar] [CrossRef]
- Ulder, N.; Aarts, E.; Bandelt, H.-J.; van Laarhoven, P.; Pesch, E. Genetic local search algorithms for the traveling salesman problem. In Parallel Problem Solving from Nature; Schwefel, H.-P., Männer, R., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1991; Volume 496, pp. 109–116. [Google Scholar]
- Stodola, P.; Michenka, K.; Nohel, J.; Rybanský, M. Hybrid Algorithm Based on Ant Colony Optimization and Simulated Annealing Applied to the Dynamic Traveling Salesman Problem. Entropy 2020, 22, 884. [Google Scholar] [CrossRef] [PubMed]
- Gendreau, M.; Hertz, A.; Laporte, G. New insertion and postoptimization procedures for the traveling salesman problem. Oper. Res. 1992, 40, 1086–1094. [Google Scholar] [CrossRef]
- Lin, S.; Kernighan, B. An effective heuristic algorithm for the traveling salesman problem. Oper. Res. 1973, 21, 498–516. [Google Scholar] [CrossRef] [Green Version]
- Helsgaun, K. An effective implementation of the Lin–Kernighan traveling salesman heuristic. Eur. J. Oper. Res. 2000, 126, 106–130. [Google Scholar] [CrossRef] [Green Version]
- Mavrovouniotis, M.; Yang, S. Ant colony optimization with immigrants schemes in dynamic environments. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Krakov, Poland, 11–15 September 2010. [Google Scholar]
- Mavrovouniotis, M.; Yang, S. Adapting the pheromone evaporation rate in dynamic routing problems. In Applications of Evolutionary Computation; Esparcia-Alcázar, A., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2013; Volume 7835, pp. 606–615. [Google Scholar]
- Tinós, R.; Whitley, D.; Howe, A. Use of explicit memory in the dynamic traveling salesman problem. In Proceedings of the Conference on Genetic and Evolutionary Computation, Vancouver, BC, Canada, 12–16 July 2014; pp. 999–1006. [Google Scholar]
- Dantzig, G.; Fulkerson, R.; Johnson, S. Solution of a large-scale traveling-salesman problem. J. Oper. Res. Soc. Am. 1954, 2, 393–410. [Google Scholar] [CrossRef] [Green Version]
- Roberti, R.; Toth, P. Models and algorithms for the Asymmetric Traveling Salesman Problem: An experimental comparison. EURO J. Transp. Logist. 2012, 1, 113–133. [Google Scholar] [CrossRef] [Green Version]
- Mele, U.J.; Gambardella, L.M.; Montemanni, R. A New Constructive Heuristic Driven by Machine Learning for the Traveling Salesman Problem. Algorithms 2021, 14, 267. [Google Scholar] [CrossRef]
- Stützle, T.; Hoos, H. – ant system and local search for the traveling salesman problem. In Proceedings of the IEEE International Conference on Evolutionary Computation, Indianapolis, IN, USA, 13–16 April 1997; pp. 309–314. [Google Scholar]
- Jonker, R.; Volgenant, T. Transforming asymmetric into symmetric traveling salesman problems. Oper. Res. Lett. 1983, 2, 161–163. [Google Scholar] [CrossRef]
- França, P.M.; Gendreau, M.; Laporte, G.; Müller, F.M. A tabu search heuristic for the multiprocessor scheduling problem with sequence dependent setup times. Int. J. Prod. Econ. 1996, 43, 79–89. [Google Scholar] [CrossRef]
- Mavrovouniotis, M.; Li, C.; Yang, S. A survey of swarm intelligence for dynamic optimization: Algorithms and applications. Swarm Evol. Comput. 2017, 33, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Gambardella, L.M.; Dorigo, M. Ant-Q: A reinforcement learning approach to the traveling salesman problem. In Proceedings of the International Conference on Machine Learning, Tahoe City, CA, USA, 9–12 July 1995; pp. 252–260. [Google Scholar]
- Angus, D.; Hendtlass, T. Ant colony optimisation applied to a dynamically changing problem. In Developments in Applied Artificial Intelligence; Hendtlass, T., Ali, M., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2358, pp. 618–627. [Google Scholar]
- Guntsch, M.; Middendorf, M. Applying population based ACO to dynamic optimization problems. In Ant Algorithms; Dorigo, M., Di Caro, G., Sampels, M., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2463, pp. 111–122. [Google Scholar]
- Bonilha, I.S.; Mavrovouniotis, M.; Müller, F.M.; Ellinas, G.; Polycarpou, M. Ant colony optimization with heuristic repair for the dynamic vehicle routing problem. In Proceedings of the IEEE Symposium Series on Computational Intelligence (SSCI), Canberra, ACT, Australia, 1–4 December 2020; pp. 313–320. [Google Scholar]
- Krolak, P.; Felts, W.; Nelson, J. A Man-Machine Approach Toward Solving the Generalized Truck-Dispatching Problem. Transp. Sci. 1972, 6, 149–170. [Google Scholar] [CrossRef]
- Grötschel, M.; Jünger, M.; Reinelt, G. Optimal control of plotting and drilling machines: A case study. ZOR-Methods Models Oper. Res. 1991, 35, 61–84. [Google Scholar] [CrossRef]
- Grötschel, M.; Pulleyblank, W.R. Clique Tree Inequalities and the Symmetric Travelling Salesman Problem. Math. Oper. Res. 1986, 11, 537–569. [Google Scholar] [CrossRef]
- Branke, J.; Schmeck, H. Designing evolutionary algorithms for dynamic optimization problems. In Advances in Evolutionary Computing; Ghosh, A., Tsutsui, S., Eds.; Natural Computing Series; Springer: Berlin/Heidelberg, Germany, 2003; pp. 239–262. [Google Scholar]





| Problem Instance | m | + LK | + US | HULK |
|---|---|---|---|---|
| KROA100.tsp | 0.05 | 20,500.7 (1.2) | 20,275.6 (0.1) | 20,262.9 |
| 0.1 | 20,101.1 (0.3) | 20,079.3 (0.2) | 20,045.5 | |
| 0.2 | 20,439.7 (2.7) | 19,985.4 (0.4) | 19,899.1 | |
| 0.4 | 20,323.7 (2.4) | 20,013.0 (0.8) | 19,852.8 | |
| KROA150.tsp | 0.05 | 27,929.4 (2.4) | 25,350.3 (0.1) | 25,318.9 |
| 0.1 | 25,564.0 (2.1) | 25,079.8 (0.2) | 25,028.1 | |
| 0.2 | 25,605.1 (1.8) | 25,212.7 (0.2) | 25,158.6 | |
| 0.4 | 25,538.7 (3.0) | 24,868.3 (0.3) | 24,803.8 | |
| KROA200.tsp | 0.05 | 27,942.6 (2.4) | 27,334.7 (0.1) | 27,299.6 |
| 0.1 | 27,945.7 (1.7) | 27,521.8 (0.2) | 27,465.4 | |
| 0.2 | 28,343.7 (2.9) | 27,586.8 (0.2) | 27,531.9 | |
| 0.4 | 28,407.6 (3.4) | 27,545.5 (0.2) | 27,482.5 | |
| KROA100.atsp | 0.05 | 20,340.2 (2.3) | 19,937.4 (0.3) | 19,876.4 |
| 0.1 | 20,124.9 (1.9) | 19,864.8 (0.6) | 19,755.3 | |
| 0.2 | 20,109.1 (0.9) | 20,014.6 (0.6) | 20,028.3 | |
| 0.4 | 20,175.0 (3.0) | 19,768.2 (0.9) | 19,593.8 | |
| KROA150.atsp | 0.05 | 25,471.1 (1.3) | 25,241.8 (0.3) | 25,133.7 |
| 0.1 | 25,382.5 (1.1) | 25,219.6 (0.5) | 25,098.6 | |
| 0.2 | 25,277.0 (1.4) | 25,078.4 (0.6) | 24,933.4 | |
| 0.4 | 25,320.4 (2.0) | 25,036.3 (0.9) | 24,824.0 | |
| KROA200.atsp | 0.05 | 28,210.2 (1.7) | 27,821.4 (0.3) | 27,725.9 |
| 0.1 | 28,273.7 (2.1) | 27,825.8 (0.4) | 27,703.2 | |
| 0.2 | 28,169.9 (1.8) | 27,868.3 (0.7) | 27,676.0 | |
| 0.4 | 28,498.2 (3.6) | 27,742.0 (0.9) | 27,498.0 |
| Instance | HULK | RIACO | EIACO | MIACO | ALNS |
|---|---|---|---|---|---|
| KROA100.tsp | 20,045.5 | 23,635.8 (17.9) | 23,417.2 (16.8) | 23,398.7 (16.7) | 21,407.5 (6.8) |
| KROA150.tsp | 25,028.1 | 30,343.8 (21.2) | 29,892.6 (19.4) | 29,893.0 (19.4) | 28,203.7 (12.7) |
| KROA200.tsp | 27,465.4 | 34,203.1 (24.5) | 33,496.6 (22.0) | 33,576.9 (22.3) | 31,468.3 (14.6) |
| Problem Instance | m | + LK | + US | HULK |
|---|---|---|---|---|
| KROA100.tsp | 0.05 | 20,383.9 (0.7) | 20,254.8 (0.1) | 20,235.5 |
| 0.1 | 20,457.7 (0.9) | 20,334.4 (0.3) | 20,280.3 | |
| 0.2 | 20,482.0 (2.0) | 20,178.2 (0.5) | 20,073.3 | |
| 0.4 | 20,373.5 (1.8) | 20,188.4 (0.8) | 20,022.9 | |
| KROA150.tsp | 0.05 | 25,477.0 (0.8) | 25,347.2 (0.3) | 25,274.2 |
| 0.1 | 25,635.1 (2.4) | 25,189.4 (0.6) | 25,043.1 | |
| 0.2 | 25,758.1 (2.5) | 25,419.6 (1.2) | 25,128.6 | |
| 0.4 | 25,800.4 (3.3) | 25,275.1 (1.2) | 24,969.3 | |
| KROA200.tsp | 0.05 | 28,118.8 (2.2) | 27,524.4 (0.0) | 27,521.0 |
| 0.1 | 28,250.7 (2.2) | 27,645.6 | 27,649.7 (0.0) | |
| 0.2 | 28,814.1 (4.4) | 27,595.1 | 27,842.3 (0.9) | |
| 0.4 | 29,038.8 (4.8) | 28,067.7 (1.3) | 27,705.5 | |
| d198.tsp | 0.05 | 13,280.9 | 14,157.0 (6.6) | 13,403.0 (0.9) |
| 0.1 | 13,078.4 | 13,837.3 (5.8) | 13,393.0 (2.4) | |
| 0.2 | 13,147.6 | 14,014.3 (6.6) | 13,513.9 (2.8) | |
| 0.4 | 12,943.2 | 13,887.8 (7.3) | 38,842.3 (3.1) | |
| lin318.tsp | 0.05 | 39,520.4 (0.4) | 40,624.7 (3.2) | 39,355.2 |
| 0.1 | 39,371.9 (0.3) | 40,615.7 (3.5) | 39,252.9 | |
| 0.2 | 39,057.7 (0.1) | 40,312.8 (3.3) | 39,032.5 | |
| 0.4 | 38,795.8 (0.0) | 40,091.8 (3.3) | 38,793.8 | |
| pcb442.tsp | 0.05 | 48,811.3 | 49,709.1 (1.8) | 48,944.7 (0.3) |
| 0.1 | 48,776.4 | 49,683.1 (1.9) | 49,044.5 (0.5) | |
| 0.2 | 48,692.5 | 49,770.8 (2.2) | 49,359.8 (1.4) | |
| 0.4 | 48,501.4 | 49,615.1 (2.3) | 49,416.6 (1.9) | |
| u574.tsp | 0.05 | 37,456.7 (8.5) | 35,920.9 (4.1) | 34,521.9 |
| 0.1 | 37,260.4 (8.1) | 35,698.2 (3.6) | 34,473.1 | |
| 0.2 | 36,997.4 (5.5) | 35,564.3 (1.5) | 35,055.9 | |
| 0.4 | 36,964.7 (5.9) | 35,451.3 (1.6) | 34,907.4 | |
| rat783.tsp | 0.05 | 8173.1 (0.5) | 8364.1 (2.9) | 8129.6 |
| 0.1 | 8064.4 (0.6) | 8267.5 (3.1) | 8019.9 | |
| 0.2 | 8034.6 (0.1) | 8239.4 (2.7) | 8024.4 | |
| 0.4 | 7995.4 (0.2) | 8202.9 (2.8) | 7980.0 | |
| pcb1173.tsp | 0.05 | 54,478.8 | 55,930.7 (2.7) | 54,639.2 (0.3) |
| 0.1 | 54,321.4 | 55,904.8 (2.9) | 54,476.0 (0.3) | |
| 0.2 | 54,419.8 (0.2) | 55,991.1 (3.1) | 54,287.6 | |
| 0.4 | 59,943.1 (10.8) | 55,814.4 (3.2) | 54,105.2 |
| Problem Instance | m | + LK | + US | HULK |
|---|---|---|---|---|
| KROA100.atsp | 0.05 | 20,279.1 (1.5) | 20,058.4 (0.4) | 19,981.4 |
| 0.1 | 20,051.2 (0.4) | 20,120.6 (0.3) | 19,975.4 | |
| 0.2 | 20,050.9 (0.9) | 20,038.6 (0.8) | 19,875.4 | |
| 0.4 | 20,090.3 (1.5) | 19,978.9 (0.9) | 19,802.0 | |
| KROA150.atsp | 0.05 | 25,447.8 (1.3) | 25,236.0 (0.5) | 25,109.0 |
| 0.1 | 25,277.0 (0.8) | 25,291.1 (0.8) | 25,083.7 | |
| 0.2 | 25,451.3 (2.6) | 25,062.8 (1.0) | 24,808.1 | |
| 0.4 | 25,268.0 (2.5) | 24,907.7 (1.0) | 24,651.8 | |
| KROA200.atsp | 0.05 | 28,110.2 | 28,183.5 (0.3) | 28,131.3 (0.1) |
| 0.1 | 28,170.0 (0.9) | 27,988.0 (0.3) | 27,910.7 | |
| 0.2 | 28,326.1 (2.6) | 27,595.1 | 27,626.3 (0.0) | |
| 0.4 | 28,433.7 (3.6) | 27,796.9 (1.3) | 27,453.0 | |
| d198.atsp | 0.05 | 14,582.0 (5.5) | 14,999.4 (8.6) | 13,815.4 |
| 0.1 | 14,489.4 (5.3) | 14,831.4 (7.8) | 13,761.6 | |
| 0.2 | 14,236.4 (2.9) | 14,842.6 (7.3) | 13,834.8 | |
| 0.4 | 13,789.3 (6.3) | 14,578.9 (12.4) | 12,967.4 | |
| lin318.atsp | 0.05 | 41,768.9 (2.6) | 41,924.9 (3.0) | 40,700.7 |
| 0.1 | 41,615.0 (3.0) | 42,168.5 (4.4) | 40,394.4 | |
| 0.2 | 41,587.3 (3.7) | 42,457.0 (5.8) | 40,111.2 | |
| 0.4 | 41,314.8 (3.5) | 42,675.8 (6.9) | 39,928.6 | |
| pcb442.atsp | 0.05 | 51,549.2 (3.2) | 50,997.1 (2.1) | 49,970.9 |
| 0.1 | 51,763.4 (2.9) | 51,543.3 (2.5) | 50,305.6 | |
| 0.2 | 51,694.0 (3.0) | 51,844.5 (3.3) | 50,175.4 | |
| 0.4 | 51,471.9 (3.3) | 52,153.3 (4.6) | 49,846.4 | |
| u574.atsp | 0.05 | 37,363.4 (2.0) | 38,305.9 (4.6) | 36,620.7 |
| 0.1 | 36,893.0 (0.8) | 38,369.8 (4.0) | 36,587.3 | |
| 0.2 | 36,775.8 (2.9) | 38,385.6 (4.4) | 35,727.4 | |
| 0.4 | 36,437.0 (2.8) | 38,383.5 (5.3) | 35,442.5 | |
| rat783.atsp | 0.05 | 8678.9 (1.1) | 8722.9 (1.6) | 8586.5 |
| 0.1 | 8649.5 (2.6) | 8800.3 (4.4) | 8431.1 | |
| 0.2 | 8567.1 (2.0) | 8790.2 (4.7) | 8395.5 | |
| 0.4 | 8491.7 (2.5) | 9103.6 (9.8) | 8288.3 | |
| pcb1173.atsp | 0.05 | 60,343.1 (2.4) | 61,194.5 (3.9) | 58,920.1 |
| 0.1 | 60,197.8 (2.7) | 61,655.1 (5.1) | 58,636.8 | |
| 0.2 | 60,027.8 (2.6) | 62,008.5 (6.0) | 58,515.8 | |
| 0.4 | 59,639.9 (2.3) | 62,706.6 (7.6) | 58,270.7 |
| Problem Instance | m | Symmetric | Asymmetric | ||||
|---|---|---|---|---|---|---|---|
| HULK vs. ALK | HULK vs. AUS | ALK vs. AUS | HULK vs. ALK | HULK vs. AUS | ALK vs. AUS | ||
| KROA100 | 0.05 | + | ∼ | − | + | + | − |
| 0.1 | + | + | − | + | + | ∼ | |
| 0.2 | + | + | − | + | + | ∼ | |
| 0.4 | + | + | − | + | + | − | |
| KROA150 | 0.05 | + | + | − | + | + | − |
| 0.1 | + | − | + | + | ∼ | ||
| 0.2 | + | − | + | − | |||
| 0.4 | + | − | + | − | |||
| KROA200 | 0.05 | ∼ | ∼ | + | + | ||
| 0.1 | ∼ | + | + | − | |||
| 0.2 | ∼ | ∼ | |||||
| 0.4 | + | + | |||||
| d198 | 0.05 | − | |||||
| 0.1 | |||||||
| 0.2 | |||||||
| 0.4 | |||||||
| lin318 | 0.05 | + | + | ||||
| 0.1 | + | + | |||||
| 0.2 | ∼ | ||||||
| 0.4 | ∼ | ||||||
| pcb442 | 0.05 | − | + | + | − | ||
| 0.1 | − | + | + | − | |||
| 0.2 | − | + | + | ||||
| 0.4 | − | + | + | ||||
| u574 | 0.05 | + | |||||
| 0.1 | + | ||||||
| 0.2 | + | ||||||
| 0.4 | + | ||||||
| rat783 | 0.05 | + | + | + | + | ||
| 0.1 | + | + | |||||
| 0.2 | ∼ | + | |||||
| 0.4 | + | ||||||
| pcb1173 | 0.05 | − | + | ||||
| 0.1 | − | ||||||
| 0.2 | + | ||||||
| 0.4 | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Müller, F.M.; Bonilha, I.S. Hyper-Heuristic Based on ACO and Local Search for Dynamic Optimization Problems . Algorithms 2022, 15, 9. https://doi.org/10.3390/a15010009
Müller FM, Bonilha IS. Hyper-Heuristic Based on ACO and Local Search for Dynamic Optimization Problems . Algorithms. 2022; 15(1):9. https://doi.org/10.3390/a15010009
Chicago/Turabian StyleMüller, Felipe Martins, and Iaê Santos Bonilha. 2022. "Hyper-Heuristic Based on ACO and Local Search for Dynamic Optimization Problems " Algorithms 15, no. 1: 9. https://doi.org/10.3390/a15010009
APA StyleMüller, F. M., & Bonilha, I. S. (2022). Hyper-Heuristic Based on ACO and Local Search for Dynamic Optimization Problems . Algorithms, 15(1), 9. https://doi.org/10.3390/a15010009






