Finite-Time Control of Singular Linear Semi-Markov Jump Systems

Abstract

The problem of finite-time control for singular linear semi-Markov jump systems (SMJSs) with unknown transition rates is considered in this paper. By designing a new semi-positive definite Lyapunov-like function, state feedback controller design methods are given that allow closed-loop singular linear SMJSs to be regular, impulse-free and stochastically finite-time-stable without external disturbance, and stochastically finite-time bounded with external disturbance. The obtained conditions are expressed by a set of strict matrix inequalities, which can be simplified to a set of linear matrix inequalities by a one dimensional search for a scalar. Two numerical examples are given to illustrate the effectiveness of proposed method.

1. Introduction

During the past few years, the research of Markov jump systems (MJSs) has gotten a lot of attention due to the fact that those systems can effectively describe the dynamics of physical systems suffering from some changes in structure and parameters, random sudden variations and unexpected environment disturbances [1]. Various fundamental problems, including stability [2], state feedback stabilization [3], output feedback stabilization [4] and filter design [5], have been fully addressed within this topic. The sojourn times of continuous-time MJSs obey a unique exponential distribution, whereas those of discrete-time MJSs follow the geometric distribution, which results in constant transition rates and certain limitations on the MJSs in practical applications. Compared with the standard Markov process, the semi-Markov jump process [6] is subject to a nonexponential distribution, such as the Weibull distribution [7] or phase type distribution [8], and has time-varying transition rates. For this reason, the semi-Markov system model can describe more general practical systems and has a wider range of applications in many real-life situations [9]—epidemic infectious systems [10], social networks [11] and so on. In addition to the above stochastic processes, there are more general stochastic processes, such as regenerative processes and Markovian regenerative processes. The regenerative switched linear system was studied in [12]. The mean stability of this system was investigated and represented by the spectral radius of a expectation matrix. In [13], a Markovian regenerative process was applied to a RAID storage system to obtain more accurate performance prediction. Sufficient conditions for the stochastic stability of linear SMJSs were given in [6], where the information for the upper and lower bounds of the transition rates was required. Moreover, for positive SMJSs, conditions to verify the exponential and stochastic mean stability were given in [14], where the spectral radius of a matrix and a discretization method were introduced. Numerically testable criteria on the basis of a semi-Markov kernel and the emission probability of hidden SMJSs were obtained in [15], with the aid of certain techniques that can eliminate the terms containing products of matrices.

Singular systems, also known as descriptor systems and differential-algebraic systems, have wide applications in actual systems, including power systems [16], singular perturbation systems [17], chemical processes [18] and nuclear energy reaction processes [19], since such systems can contain both dynamic and algebraic relations between state variables and can better describe the complex dynamic systems than the normal state-space ones. By using the fast–slow subsystems decomposition approach, singular systems can be decomposed to fast subsystems depicted by algebraic equations and slow subsystems depicted by differential equations or difference equations [19]. The structural characteristics of singular systems were analyzed in [19], and some criteria for the regularity, absence of impulse and asymptotic stability were given in [20]. For singular MJSs, sufficient and necessary conditions for stability and stabilization of continuous-time singular MJSs were given in [21], and the dynamic output feedback control for singular MJSs was given in [22] by using linear matrix inequality technology. When the system was subject to amplitude bounded disturbance, the PD state feedback control method was extended to the reachable set synthesis problem [23]. The dissipative control problem for T-S fuzzy singular MJSs was studied in [24], where the state-dependent noise and asynchronous modes were considered. Based on the extended passivity theory, a non-fragile filter was designed for singular MJSs with time-varying delay and missing measurements in [25]. For singular semi-Markov jump systems (SSMJSs), the problem of a sliding mode control for nonlinear uncertain SSMJSs with stochastic disturbance was studied by using the weak infinitesimal operator from the viewpoints of probability distribution in [26].

For dynamic systems, stability is an important concept for the control system. Lyapunov stability focuses on the asymptotic behavior in an infinite time domain, which is a concept relating to qualitative research in fact. Sometimes, a system which is asymptotically stable may have bad steady-state performance. In practical engineering, the attention may be paid to the system’s performance in a prescribed finite time interval [27], which may be considered as a quantitative concept. Motivated by this, the concept of finite-time stability was given to analyze the transient behavior within a finite time interval. Given some initial conditions, the dynamic system is finite-time-stable if the trajectory of the state does not exceed a given threshold in a certain time interval [28]. Annular finite-time stability not only defines that the state trajectory of the system is limited to a certain upper threshold within a finite time interval, but also considers the lower limit of the state trajectory, which is of great significance under specific requirements. The annular finite-time boundedness for networked switched systems was investigated with an adaptive event-triggered scheme [29]. A finite-time guaranteed cost control algorithm for SMJSs was given by a set of linear matrix inequalities [30]. In that paper, the event-triggered scheme and quantization input were applied. For singular MJSs with time-varying delays and quantization, the finite-time non-fragile filtering problem was addressed in [31] by constructing a Lyapunov–Krasovskii functional. In [32], the asynchronous filter for singular SMJS was designed to guarantee that the filtering error system was finite-time bounded under the dynamic event-based scheme, but there was a equality constraint, which led to some difficulty in solving numerical values. Recently, based on stochastic system theory and the singular value decomposition approach, the finite-time stability and stabilization problem for SSMJSs has been studied, but not enough. One reason is that the SSMJS has a complicated structure; the other is that the research is not mature. For SSMJSs, in order to design a controller and deal with nonlinear items, the singular matrix was decomposed into a left matrix and right matrix, and it should be pointed out that new matrices were introduced to represent the inverse of the matrices in Lyapunov function in [26], which might not be good. In [33], only under a specified expression, could the gain of the controller be obtained in terms of the linear matrix inequality, which implies that the parameters of the controller were constrained.

Motivated by this, the problem of finite-time control for SSMJSs is considered. By designing a new semi-positive definite Lyapunov-like function with different perspectives in mind, a sufficient condition for the design of the desired state feedback control law is given to guarantee the closed-loop system is regular, impulse-free and finite-time-stable. By some matrix decomposition and construction, this criterion is further simplified to a set of strict matrix inequalities. When the integrally bounded disturbance is introduced, a sufficient condition is also given for the closed-loop SSMJSs to be finite-time bounded. It is noted that the obtained criteria are strict matrix inequalities and can be simplified to be linear matrix inequalities by using a one-dimensional search for a scalar. This gives some computational simplicity when those criteria are verified numerically. Two numerical examples are given to verify the applicability and effectiveness of the proposed method.

The main contributions can be organized as

(1)

A suitable semi-positive definite Lyapunov-like function is designed, which gives a sufficient condition for making the considered closed-loop SSMJSs regular, impulse-free and stochastically finite-time-stable.

(2)

To get the solvable condition, the coupling term about a singular parameter and jump matrix is dealt with through matrix transformation and the Schur complement lemma.

(3)

Some matrix decomposition and construction ideas are introduced, which simplify a complex matrix inequality with an equality constraint to a set of strict matrix inequalities and further to a set of linear matrix inequalities using one dimensional searching.

2. Problem Formulation

Consider a class of SSMJSs with an external disturbance:

$$E\dot{x}\left(t\right)=A\left(r\left(t\right)\right)x\left(t\right)+B\left(r\left(t\right)\right)u\left(t\right)+C\left(r\left(t\right)\right)\omega \left(t\right),$$

(1)

where $x\left(t\right)\in {\mathbb{R}}^n$ is the state vector, $u\left(t\right)\in {\mathbb{R}}^m$ is the control input vector and $\omega \left(t\right)\in {\mathbb{R}}^p$ is the disturbance input satisfying ${\int }_0^T{\omega }^T\left(t\right)\omega \left(t\right)\mathrm{d}t\le d$ for given $T>0$ and $d>0$. $r\left(t\right)$ is a semi-Markov chain taking values in the finite space $\mathcal{S}=\{1,2,\dots ,N\}$, which governs the jump parameters in the probabilistic space $(\Omega ,\mathcal{F},\mathcal{P})$. $A\left(r\right(t\left)\right)$, $B\left(r\right(t\left)\right)$, $C\left(r\right(t\left)\right)$ and $r\left(t\right)\in \mathcal{S}$ are known matrices with compatible dimensions, which depend on $r\left(t\right)$. The matrix E is singular, and we assume $\mathrm{rank}\left(E\right)=r\le n$.

The evolution of the semi-Markov process $r\left(t\right),t\ge 0$ in system (1) is governed by the following probability transitions.

$$P\{r(t+\Delta )=j\mid r\left(t\right)=i\}=\left\{\begin{array}{cc}{\mu }_{ij}\left(h\right)\Delta +o(\Delta ),\hfill & r\left(t\right)\mathrm{jumps}\mathrm{from}i\mathrm{to}j,\hfill \\ 1+{\mu }_{ii}\left(h\right)\Delta +o(\Delta ),\hfill & r\left(t\right)\mathrm{stays}\mathrm{at}\mathrm{mode}i,\hfill \end{array}\right.$$

(2)

where $h\ge 0$ is the sojourn time; $\Delta >0$ and ${lim}_{\Delta \to 0}\frac{o(\Delta )}{\Delta }=0$; ${\mu }_{ij}\left(h\right)$ is the transition rate when $r\left(t\right)$ jumps from the mode i to mode j where $i\ne j$ and ${\mu }_{ii}\left(h\right)=-{\sum }_{j=1,j\ne i}^N{\mu }_{ij}\left(h\right)$. Here, it is also assumed that the transition rate ${\mu }_{ij}\left(h\right)$ is not exactly known but bounded by ${\underline{\mu }}_{ij}\le {\mu }_{ij}\left(h\right)\le {\overline{\mu }}_{ij}$ for ${\underline{\mu }}_{ij}\ge 0$ and ${\overline{\mu }}_{ij}\ge 0$.

The objective of this paper is to walk through the design pf a state feedback controller for a SSMJS (1), such that the closed-loop system is regular, impulse-free and stochastically finite-time bounded. To this end, some definitions and lemmas are introduced first.

Definition 1

(Sathishkumar et al. [34]).

1. 

The pair $(E,A_i)$ is said to be regular, if for each $i\in \mathcal{S}$, $det(sE-A_i) \not\equiv 0$, that is, $\exists s\in \mathbb{C}$, $det(sE-A_i)\ne 0$.

2. 

The pair $(E,A_i)$ is said to be impulse-free, if for each $i\in \mathcal{S}$, $deg(det(sE-A_i))=rank\left(E\right)$.

3. 

The SSMJS in (1) with $u\left(t\right)=0$ and $\omega \left(t\right)=0$ is said to be regular and impulse-free, if for each $i\in \mathcal{S}$, the pair $(E,A_i)$ is regular and impulse-free.

Lemma 1

(Xu et al. [20]). The solution of the SSMJS in (1) with $u\left(t\right)=0$ and $\omega \left(t\right)=0$ exists and is unique and impulse-free, if this system is regular and impulse-free.

Definition 2

(Zhang et al. [35]). Consider the SSMJS in (1) with $u\left(t\right)=0$ and $\omega \left(t\right)=0$. For given positive scalars $c_1$, $c_2$ and T with $c_1<c_2$, and symmetric positive-definite matrix R, this system is said to be stochastically finite-time-stable with respect to $(c_1,c_2,T,R)$, if for $\forall t\in [0,T]$, this system is regular, impulse-free and

$$\mathbb{E}\left\{x^T\left(0\right)E^{T}REx\left(0\right)\right\}\le c_1⟹\mathbb{E}\left\{x^T\left(t\right)E^{T}REx\left(t\right)\right\}<c_2.$$

(3)

Definition 3.

Consider the SSMJS in (1) with $\omega \left(t\right)=0$. For given positive scalars $c_1$, $c_2$ and T with $c_1<c_2$, and symmetric positive-definite matrix R, this system is said to be stochastically finite-time stabilizable with respect to $(c_1,c_2,T,R)$, if there exists a state feedback control law such that the closed-loop system is stochastically finite-time-stable with respect to $(c_1,c_2,T,R)$.

Definition 4

(Zhang et al. [35]). Consider the SSMJS in (1). For given positive scalars $c_1$, $c_2$ and T with $c_1<c_2$, symmetric positive-definite matrix R, this system is said to be stochastically finite-time bounded with respect to $(c_1,c_2,T,R,d)$, if there exists a state feedback control law such that the closed-loop system is regular, impulse-free and satisfies (3).

The state feedback control law to be designed is assumed to be dependent on the semi-Markov modes,

$$u(t,r(t\left)\right)=K\left(r\right(t\left)\right)x\left(t\right),$$

and then the closed-loop system can be given as

$$\begin{array}{cc}\hfill E\dot{x}\left(t\right)& =\left(A\right(r\left(t\right))+B(r\left(t\right)\left)K\right(r\left(t\right)\left)x\right(t)+C(r\left(t\right)\left)\omega \right(t)\hfill \\ \hfill & :=\mathcal{A}\left(r\right(t\left)\right)x\left(t\right)+C\left(r\right(t\left)\right)\omega \left(t\right).\hfill \end{array}$$

(4)

For each possible $r\left(t\right)=i$, $i\in \mathcal{S}$, the system matrices can be rewritten as $A_i$, ${\mathcal{A}}_i$, $B_i$ and $C_i$ for notational simplicity.

3. Results

In this section, the design of state feedback control law for the SSMJS in (1) is presented. The stochastically finite-time stabilization algorithm is given first for the SSMJS in (1) with $\omega \left(t\right)=0$, which is summarized in the following theorem.

3.1. Stochastically Finite-Time Stabilization

Theorem 1.

For given positive scalars $c_1$, $c_2$ and T with $c_1<c_2$ and symmetric positive-definite matrix R, the SSMJS in (1) with $\omega \left(t\right)=0$ is stochastically finite-time stabilizable with respect to $(c_1,c_2,T,R)$, if there exists a positive scalar α; a symmetric positive-definite matrix $P_i$; and matrices $Q_i$, $S_i$ and $Y_i$ with appropriate dimensions such that

$$\begin{array}{c}\left[\begin{array}{cc}{\underline{\Pi }}_{11}& {\underline{\Pi }}_{12}\\ *& {\Pi }_{22}\end{array}\right]<0,\end{array}$$

(5a)

$$\begin{array}{c}\left[\begin{array}{cc}{\overline{\Pi }}_{11}& {\overline{\Pi }}_{12}\\ *& {\Pi }_{22}\end{array}\right]<0,\end{array}$$

(5b)

$$\begin{array}{c}{E}^T=E^T{R}^{\frac{1}{2}}{Q}_i{R}^{\frac{1}{2}}E{P}_i{E}^T,\end{array}$$

(5c)

$$\begin{array}{c}{\lambda }_{max}\left(Q_i\right)c_1{e}^{\alpha T}<{\lambda }_{min}\left(Q_i\right)c_2,\end{array}$$

(5d)

where $H\in {\mathbb{R}}^{n\times (n-r)}$ is any matrix with full column rank that satisfies $EH=0$:

${\underline{\Pi }}_{11}=A_i(P_i{E}^T+H{S}_i^T)+{(P_i{E}^T+H{S}_i^T)}^T{A}_i^T+B_i{Y}_i+Y_i^T{B}_i^T+({\underline{\mu }}_{ii}-\alpha )E{P}_i{E}^T$,

${\overline{\Pi }}_{11}=A_i(P_i{E}^T+H{S}_i^T)+{(P_i{E}^T+H{S}_i^T)}^T{A}_i^T+B_i{Y}_i+Y_i^T{B}_i^T+({\overline{\mu }}_{ii}-\alpha )E{P}_i{E}^T$,

${\underline{\Pi }}_{12}=\left[\sqrt{{\underline{\mu }}_{i1}}\cdots \sqrt{{\underline{\mu }}_{i,i-1}}\sqrt{{\underline{\mu }}_{i,i+1}}\cdots \sqrt{{\underline{\mu }}_{iN}}\right]E{P}_i{E}^T$,

${\overline{\Pi }}_{12}=\left[\sqrt{{\overline{\mu }}_{i1}}\cdots \sqrt{{\overline{\mu }}_{i,i-1}}\sqrt{{\overline{\mu }}_{i,i+1}}\cdots \sqrt{{\overline{\mu }}_{iN}}\right]E{P}_i{E}^T,$

${\Pi }_{22}=diag\{{\Pi }_{22,1},\dots ,{\Pi }_{22,i-1},{\Pi }_{22,i+1},\dots ,{\Pi }_{22,N}\},$

with ${\Pi }_{22,l}=P_l-(P_l{E}^T+H{S}_l^T)-{(P_l{E}^T+H{S}_l^T)}^T,l\in \mathcal{S}$. Furthermore, a suitable state feedback control law is given as

$$u\left(t\right)=Y_i{(P_i{E}^T+H{S}_i^T)}^{-1}x\left(t\right).$$

(6)

Proof of Theorem 1.

Firstly, consider the regularity and absence of impulse. Since $\mathrm{rank}\left(E\right)=r\le n$, there must exist nonsingular matrices L and T such that

$$\begin{array}{c}\hfill \overline{E}=LET=\left[\begin{array}{cc}{I}_r& 0\\ 0& 0\end{array}\right].\end{array}$$

(7)

Similar to this matrix decomposition, we can also define

$$\begin{array}{cc}\hfill \overline{{\mathcal{A}}_i}& =L{\mathcal{A}}_{i}T=\left[\begin{array}{cc}{\overline{\mathcal{A}}}_{i11}& {\overline{\mathcal{A}}}_{i12}\\ {\overline{\mathcal{A}}}_{i21}& {\overline{\mathcal{A}}}_{i22}\end{array}\right],{\overline{S}}_i=L{S}_i=\left[\begin{array}{c}{\overline{S}}_{i1}\\ {\overline{S}}_{i2}\end{array}\right],\hfill \\ \hfill {\overline{P}}_i=& T^{-1}{P}_i{T}^{-T}=\left[\begin{array}{cc}{\overline{P}}_{i11}& {\overline{P}}_{i12}\\ {\overline{P}}_{i21}& {\overline{P}}_{i22}\end{array}\right],\overline{H}=T^{-1}H=\left[\begin{array}{c}0\\ {\overline{H}}_2\end{array}\right],\hfill \end{array}$$

(8)

where ${\overline{H}}_2\in {\mathbb{R}}^{(n-r)\times (n-r)}$ is nonsingular.

By multiplying (5a) or (5b) by L and $L^T$ on the left and right, respectively, we get

$$\left[\begin{array}{cc}★& ★\\ ★& {\overline{\mathcal{A}}}_{i22}{\overline{H}}_2{\overline{S}}_{i2}^T+{\overline{S}}_{i2}{\overline{H}}_2^T{\overline{\mathcal{A}}}_{i22}^T\end{array}\right]<0,$$

(9)

where ★ represents the matrix block, which is irrelevant to the following discussion. From this inequality, it can be obtained that ${\mathcal{A}}_{i22}$ must be nonsingular. Otherwise, there exists a nonzero vector $\xi \in {\mathbb{R}}^{n-r}$ such that ${\mathcal{A}}_{i22}^T\xi =0$ and then ${\xi }^T({\overline{\mathcal{A}}}_{i22}{\overline{H}}_2{\overline{S}}_{i2}^T+{\overline{S}}_{i2}{\overline{H}}_2^T{\overline{\mathcal{A}}}_{i22}^T)\xi =0$, which contradicts to (9). Then, the closed-loop SSMJS is regular and impulse-free [19,21].

Next, a Lyapunov-like function is defined as

$$V(x\left(t\right),r\left(t\right))=x^T\left(t\right)E^T{(P\left(r\left(t\right)\right)E^T+HS{\left(r\left(t\right)\right)}^T)}^{-1}x\left(t\right).$$

(10)

With the fact of $EH=0$, it is obtained that ${(P_i{E}^T+H{S}_i^T)}^T{E}^T=E(P_i{E}^T+H{S}_i^T)=E{P}_i{E}^T\ge 0$. Multiplying the last equation by ${(P_i{E}^T+H{S}_i^T)}^{-T}$ and ${(P_i{E}^T+H{S}_i^T)}^{-1}$ on the left and right, respectively, gives

$$E^T{(P_i{E}^T+H{S}_i^T)}^{-1}={(P_i{E}^T+H{S}_i^T)}^{-T}E\ge 0,$$

(11)

and then the Lyapunov-like function (10) is symmetric semi-positive definite.

With the consideration of $r\left(t\right)=i$, the weak infinitesimal generator ℓ can be given as

$$\begin{array}{cc}\hfill \ell V\left(x\right(t),r(t\left)\right)=& \sum _{j=1}^N{\mu }_{ij}\left(h\right)x^T\left(t\right)E^T{(P_j{E}^T+H{S}_j^T)}^{-1}x\left(t\right)+x^T\left(t\right){\mathcal{A}}_i^T{(P_i{E}^T+H{S}_i^T)}^{-1}x\left(t\right)\hfill \\ \hfill & +x^T\left(t\right){(P_i{E}^T+H{S}_i^T)}^{-T}{\mathcal{A}}_{i}x\left(t\right).\hfill \end{array}$$

(12)

Then, it can be obtained that

$$\ell V(x\left(t\right),r\left(t\right))-\alpha V(x\left(t\right),r\left(t\right))=x^T\left(t\right){\Gamma }_{i}x\left(t\right),$$

(13)

where

$$\begin{array}{cc}\hfill {\Gamma }_i=& \sum _{j=1}^N{\mu }_{ij}\left(h\right)E^T{(P_j{E}^T+H{S}_j^T)}^{-1}+{\mathcal{A}}_i^T{(P_i{E}^T+H{S}_i^T)}^{-1}\hfill \\ \hfill & +{(P_i{E}^T+H{S}_i^T)}^{-T}{\mathcal{A}}_i-\alpha E^T{(P_i{E}^T+H{S}_i^T)}^{-1}.\hfill \end{array}$$

By considering the relationship (11) and performing a matrix transformation, we have

$$\begin{array}{cc}\hfill & {(P_i{E}^T+H{S}_i^T)}^T{E}^T{(P_j{E}^T+H{S}_j^T)}^{-1}(P_i{E}^T+H{S}_i^T)\hfill \\ \hfill =& {(P_i{E}^T+H{S}_i^T)}^T{(P_j{E}^T+H{S}_j^T)}^{-T}{(P_j{E}^T+H{S}_j^T)}^T{E}^T{(P_j{E}^T+H{S}_j^T)}^{-1}(P_i{E}^T+H{S}_i^T)\hfill \\ \hfill =& {(P_i{E}^T+H{S}_i^T)}^T{(P_j{E}^T+H{S}_j^T)}^{-T}E{P}_j{E}^T{(P_j{E}^T+H{S}_j^T)}^{-1}(P_i{E}^T+H{S}_i^T)\hfill \\ \hfill =& {(P_i{E}^T+H{S}_i^T)}^T{E}^T{(P_j{E}^T+H{S}_j^T)}^{-1}{P}_j{(P_j{E}^T+H{S}_j^T)}^{-T}E(P_i{E}^T+H{S}_i^T)\hfill \\ \hfill =& E{P}_i{E}^T{(P_j{E}^T+H{S}_j^T)}^{-1}{P}_j{(P_j{E}^T+H{S}_j^T)}^{-T}E{P}_i{E}^T.\hfill \end{array}$$

(14)

Since $P_j$ is symmetric positive-definite, it is obtained that

$$\begin{array}{cc}\hfill & {\left((P_j{E}^T+H{S}_j^T)-P_j\right)}^T{P}_j^{-1}\left((P_j{E}^T+H{S}_j^T)-P_j\right)\hfill \\ \hfill =& {(P_j{E}^T+H{S}_j^T)}^T{P}_j^{-1}(P_j{E}^T+H{S}_j^T)-(P_j{E}^T+H{S}_j^T)-{(P_j{E}^T+H{S}_j^T)}^T+P_j\hfill \\ \hfill >& 0,\hfill \end{array}$$

(15)

and therefore we have

$$\begin{array}{c}\hfill -{(P_j{E}^T+H{S}_j^T)}^T{P}_j^{-1}(P_j{E}^T+H{S}_j^T)<-(P_j{E}^T+H{S}_j^T)-{(P_j{E}^T+H{S}_j^T)}^T+P_j.\end{array}$$

(16)

For any given h, ${\mu }_{ij}\left(h\right)$ can be written as ${\mu }_{ij}\left(h\right)=\underline{m}{\underline{\mu }}_{ij}+\overline{m}{\overline{\mu }}_{ij}$, where $\overline{m}+\underline{m}=1$ and $\overline{m}>0,\underline{m}>0$. According to (14) and (16), by multiplying (5a) by $\underline{m}$ and (5b) by $\overline{m}$, and by applying the Schur complement lemma, the summary is that

$$\begin{array}{c}\hfill \sum _{j=1}^N(\underline{m}{\underline{\mu }}_{ij}+\overline{m}{\overline{\mu }}_{ij}){(P_i{E}^T+H{S}_i^T)}^T{E}^T{(P_j{E}^T+H_j{S}_j^T)}^{-1}(P_i{E}^T+H{S}_i^T)\\ \hfill +{(P_i{E}^T+H{S}_i^T)}^T{A}_i^T+Y_i^T{B}_i^T+A_i(P_i{E}^T+H{S}_i^T)+B_i{Y}_i-\alpha E{P}_i{E}^T<0,\end{array}$$

(17)

which further yields that

$$\begin{array}{c}\hfill \sum _{j=1}^N{\mu }_{ij}\left(h\right){(P_i{E}^T+H{S}_i^T)}^T{E}^T{(P_j{E}^T+H{S}_j^T)}^{-1}(P_i{E}^T+H{S}_i^T)-\alpha E{P}_i{E}^T\\ \hfill +{(P_i{E}^T+H{S}_i^T)}^T{A}_i^T+Y_i^T{B}_i^T+A_i(P_i{E}^T+H{S}_i^T)+B_i{Y}_i<0.\end{array}$$

(18)

By multiplying (18) by ${(P_i{E}^T+H{S}_i^T)}^{-T}$ and ${(P_i{E}^T+H{S}_i^T)}^{-1}$ on the left and right, respectively, noting the closed-loop system (4) and defining $Y_i=K_i(P_i{E}^T+H{S}_i^T)$, we get that ${\Gamma }_i<0$, which further yields

$$\ell e^{-\alpha t}V(x\left(t\right),r\left(t\right))<0.$$

(19)

Applying the generalized Dynkin formula [36] to (19) gives

$$e^{-\alpha t}\mathbb{E}\left\{V(x\left(t\right),r\left(t\right))\right\}-V(x\left(0\right),r\left(0\right))<0,$$

and further gives

$$\mathbb{E}\left\{V(x\left(t\right),r\left(t\right))\right\}<V(x\left(0\right),r\left(0\right))e^{\alpha t}.$$

(20)

From (5c), it follows that $E^T=E^T{R}^{\frac{1}{2}}{Q}_i{R}^{\frac{1}{2}}E(P_i{E}^T+H{S}_i^T)$, and then

$$E^T{(P_i{E}^T+H{S}_i^T)}^{-1}=E^T{R}^{\frac{1}{2}}{Q}_i{R}^{\frac{1}{2}}E.$$

(21)

This yields that

$$\begin{array}{cc}\hfill \mathbb{E}\left\{V\right(x\left(t\right),r\left(t\right)\left)\right\}& =\mathbb{E}\left\{x^T\left(t\right)E^T{(P_i{E}^T+H{S}_i^T)}^{-1}x\left(t\right)\right\}\hfill \\ \hfill & =\mathbb{E}\left\{x^T\left(t\right)E^T{R}^{\frac{1}{2}}{Q}_i{R}^{\frac{1}{2}}Ex\left(t\right)\right\}\hfill \\ \hfill & \ge {\lambda }_{min}\left(Q_i\right)\mathbb{E}\left\{x^T\left(t\right)E^{T}REx\left(t\right)\right\}.\hfill \end{array}$$

(22)

Similarly, we have

$$\begin{array}{c}\hfill V(x\left(0\right),r\left(0\right))\le {\lambda }_{max}\left(Q_i\right)\mathbb{E}\left\{x^T\left(0\right)E^{T}REx\left(0\right)\right\}.\end{array}$$

(23)

From (5d), (20), (22) and (23), if $\mathbb{E}\left\{x^T\left(0\right)E^{T}REx\left(0\right)\right\}\le c_1$, it is obtained that

$$\begin{array}{c}\hfill \mathbb{E}\left\{x^T\left(t\right)E^{T}REx\left(t\right)\right\}<\frac{{\lambda }_{max}\left(Q_i\right)c_1{e}^{\alpha t}}{{\lambda }_{min}\left(Q_i\right)}<c_2.\end{array}$$

(24)

Then, the closed-loop SSMJS is regular, impulse-free and stochastically finite-time-stable, which concludes the proof. □

Remark 1.

A sufficient condition is provided in Theorem 1 for the stochastically finite-time stabilization of the SSMJS in (1). ${\sum }_{j=1}^N{\mu }_{ij}\left(h\right){(P_i{E}^T+H{S}_i^T)}^T{E}^T{(P_j{E}^T+H{S}_j^T)}^{-1}(P_i{E}^T+H{S}_i^T)$ are not MATLAB solvable, but through matrix transformation, we can use the Schur complement lemma to get the solvable condition. If ${\mu }_{ij}\left(h\right)={\mu }_{ij}$, the sufficient condition is presented to ensure that the closed-loop singular MJS is stochastically finite-time-stable, as considered in [37].

Remark 2.

For a matrix E, different Hs may be designed. The differences in H do not influence the feasible solution of the theorem. Now, we assume that in inequality (5a–d), a feasible solution with $P_i$, $Q_i$, $S_i$, $Y_i$ and α exists for each certain matrix $H\in {\mathbb{R}}^{n\times (n-r)}$. We consider two different matrices H and $H^{\prime }$, and it can be obtained that the nonsingular matrix $V{\in }^{(n-r)\times (n-r)}$ exists to make $H^{\prime }=HV$ and $S_i{\left(H^{\prime }\right)}^T=S_i{V}^T{H}^T$. Then, inequality (5a–d) is satisfied for $P_i$, $Q_i$, $S_i^{\prime }=S_i{V}^{-T}$, $Y_i$ and α. From the above discussion, the state feedback gains are the same even if H is a different matrix.

Remark 3.

It should be pointed out that it is required to assume that $P_i{E}^T+H{S}_i^T$ is nonsingular in the proof of Theorem 1. It is assumed that there exists a feasible solution α, in which $P_i$, $Q_i$, $S_i$ and $Y_i$ condition (5a–d) for a prescribed matrix H, but $P_i{E}^T+H{S}_i^T$ is singular. In this case, according to [38], the matrix $\Delta S_i{\in }^{n\times (n-r)}$ with $\parallel \Delta S_i\parallel \ll 1$ must exist so that $P_i{E}^T+H{(S_i+\Delta S_i)}^T$ is a nonsingular matrix. Meanwhile, the condition (5a–d) is satisfied for α, $P_i$, $Q_i$, $S_i+\Delta S_i$ and $Y_i$.

However, the condition (5c) in Theorem 1 is difficult to verify. In the sequel, a numerically tractable condition will be provided in Theorem 2 to get the matrix gains $K_i$ by some strict linear matrix inequalities.

Theorem 2.

For given positive scalars $c_1$, $c_2$ and T with $c_1<c_2$ and symmetric positive-definite matrix R, the SSMJS in (1) with $\omega \left(t\right)=0$ is stochastically finite-time stabilizable with respect to $(c_1,c_2,T,R)$, if there exist positive scalars α and $0<\theta <1$; symmetric positive-definite matrices $P_i$ and $Z_i$; and matrices $S_i$ and $Y_i$ with appropriate dimensions such that (5a,b) and the following matrix inequalities are satisfied:

$$\begin{array}{c}\theta I<R^{\frac{1}{2}}{L}^{-1}\left(\left[\begin{array}{cc}{I}_r& 0\\ 0& 0\end{array}\right]T^{-1}{P}_i{T}^{-T}\left[\begin{array}{cc}{I}_r& 0\\ 0& 0\end{array}\right]+\left[\begin{array}{cc}0& 0\\ 0& Z_i\end{array}\right]\right)L^{-T}{R}^{\frac{1}{2}},\end{array}$$

(25a)

$$\begin{array}{c}{R}^{\frac{1}{2}}{L}^{-1}\left(\left[\begin{array}{cc}{I}_r& 0\\ 0& 0\end{array}\right]T^{-1}{P}_i{T}^{-T}\left[\begin{array}{cc}{I}_r& 0\\ 0& 0\end{array}\right]+\left[\begin{array}{cc}0& 0\\ 0& Z_i\end{array}\right]\right)L^{-T}{R}^{\frac{1}{2}}<I,\end{array}$$

(25b)

$$\begin{array}{c}{c}_1{e}^{\alpha T}-\theta c_2<0.\end{array}$$

(25c)

Furthermore, the control law can be obtained by (6).

Proof of Theorem 2.

First, it follows from (7) and (8) that the matrix $Q_i$ can be also decomposed to

$$\begin{array}{c}\hfill {\overline{Q}}_i=L^{-T}{R}^{\frac{1}{2}}{Q}_i{R}^{\frac{1}{2}}{L}^{-1}=\left[\begin{array}{cc}{\overline{Q}}_{i11}& {\overline{Q}}_{i12}\\ {\overline{Q}}_{i21}& {\overline{Q}}_{i22}\end{array}\right].\end{array}$$

(26)

Multiplying (5c) by $T^T$ and $L^T$ on the left and right, respectively, gives

$$\begin{array}{c}\hfill Z_R^T{E}^T{Z}_L^T=Z_R^T{E}^T{R}^{\frac{1}{2}}{Q}_i{R}^{\frac{1}{2}}E{P}_i{E}^T{Z}_L^T,\end{array}$$

and further gives

$$\begin{array}{c}\hfill {\overline{E}}^T={\overline{E}}^T{\overline{Q}}_i\overline{E}{\overline{P}}_i{\overline{E}}^T,\end{array}$$

(27)

which straightforwardly gives ${\overline{Q}}_{i11}{\overline{P}}_{i11}=I$. With this observation, ${\overline{Q}}_i$ can be constructed as

$$\begin{array}{c}\hfill {\overline{Q}}_i={\left(\left[\begin{array}{cc}{I}_r& 0\\ 0& 0\end{array}\right]{\overline{P}}_i\left[\begin{array}{cc}{I}_r& 0\\ 0& 0\end{array}\right]+\left[\begin{array}{cc}0& 0\\ 0& Z_i\end{array}\right]\right)}^{-1},\end{array}$$

(28)

where $Z_i\in {\mathbb{R}}^{(n-r)\times (n-r)}$ is symmetric positive-definite.

Next we rewrite $Q_i$ as

$$\begin{array}{c}\hfill Q_i=R^{-\frac{1}{2}}{L}^T{\left(\left[\begin{array}{cc}{I}_r& 0\\ 0& 0\end{array}\right]{\overline{P}}_i\left[\begin{array}{cc}{I}_r& 0\\ 0& 0\end{array}\right]+\left[\begin{array}{cc}0& 0\\ 0& Z_i\end{array}\right]\right)}^{-1}L{R}^{-\frac{1}{2}},\end{array}$$

(29)

and its inverse matrix as

$$Q_i^{-1}=R^{\frac{1}{2}}{L}^{-1}\left(\left[\begin{array}{cc}{I}_r& 0\\ 0& 0\end{array}\right]{\overline{P}}_i\left[\begin{array}{cc}{I}_r& 0\\ 0& 0\end{array}\right]+\left[\begin{array}{cc}0& 0\\ 0& Z_i\end{array}\right]\right)L^{-T}{R}^{\frac{1}{2}}.$$

From above discussion, to solve the conditions (5c,d), we can set (25a,b), where $0<\theta <1$ and $\theta <{\lambda }_{min}\left(Q_i^{-1}\right)<{\lambda }_{max}\left(Q_i^{-1}\right)<1$.

If (25c) holds, we have

$${\lambda }_{max}\left(Q_i^{-1}\right)c_1{e}^{\alpha T}<c_1{e}^{\alpha T}<\theta c_2<{\lambda }_{min}\left(Q_i^{-1}\right)c_2.$$

(30)

Note that ${\lambda }_{max}\left(Q_i\right)=\frac{1}{{\lambda }_{min}\left(Q_i^{-1}\right)}$, ${\lambda }_{min}\left(Q_i\right)=\frac{1}{{\lambda }_{max}\left(Q_i^{-1}\right)}$ and (5d) can be guaranteed. □

Remark 4.

One of the main merits of this theorem is that it eliminates the equality constraint (5c). By constructing the matrix $Q_i$ and confining it into an interval, the result (5c,d) in Theorem 1 reduces to a strict matrix inequality condition which is comparatively easy to verify numerically.

Then, a state feedback control gain design algorithm for the SSMJS in (1) with disturbance is given, which can be summarized in the following theorem.

3.2. Stochastically Finite-Time Boundedness

Theorem 3.

For given positive scalars $c_1$, $c_2$ and T; d with $c_1<c_2$; and symmetric positive-definite matrix R, the SSMJS in (1) is stochastically finite-time bounded with respect to $(c_1,c_2,T,R,d)$, if there exist positive scalars α, η and $0<\theta <1$; symmetric positive-definite matrices $P_i$ and $Z_i$; and matrices $S_i$ and $Y_i$ with appropriate dimensions such that (25a,b) and the following matrix inequalities hold:

$$\begin{array}{c}\left[\begin{array}{ccc}{\underline{\Pi }}_{11}& {\underline{\Pi }}_{12}& C_i\\ *& {\Pi }_{22}& 0\\ *& *& -\alpha W_i\end{array}\right]<0,\end{array}$$

(31a)

$$\begin{array}{c}\left[\begin{array}{ccc}{\overline{\Pi }}_{11}& {\overline{\Pi }}_{12}& C_i\\ *& {\Pi }_{22}& 0\\ *& *& -\alpha W_i\end{array}\right]<0,\end{array}$$

(31b)

$$\begin{array}{c}{c}_1{e}^{\alpha T}+\alpha d\eta e^{\alpha T}<\theta c_2,\end{array}$$

(31c)

$$\begin{array}{c}{W}_i<\eta I,\end{array}$$

(31d)

where H, ${\underline{\Pi }}_{11}$, ${\overline{\Pi }}_{11}$, ${\underline{\Pi }}_{12}$, ${\overline{\Pi }}_{12}$ and ${\Pi }_{22}$ are defined the same as in Theorem 2. Furthermore, the control gain is given as

$$\begin{array}{c}\hfill K_i=Y_i{(P_i{E}^T+H{S}_i^T)}^{-1}.\end{array}$$

Proof of Theorem 3.

For the closed-loop SSMJS (4), it is easy to verify that it is regular and impulse-free from (31a–d). A semi-positive definite Lyapunov-like function can also be designed as (10). Similarly, with the consideration of $r\left(t\right)=i$, $r(t+\Delta )=j$, the weak infinitesimal operator ℓ can be obtained as

$$\begin{array}{cc}\hfill \ell V\left(x\right(t),r(t\left)\right)=& \sum _{j=1}^N{\mu }_{ij}\left(h\right)x^T\left(t\right)E^T{(P_j{E}^T+H{S}_j^T)}^{-1}x\left(t\right)+x^T\left(t\right){\mathcal{A}}_i^T{(P_i{E}^T+H{S}_i^T)}^{-1}x\left(t\right)\hfill \\ \hfill & +x^T\left(t\right){(P_i{E}^T+H{S}_i^T)}^{-T}{\mathcal{A}}_{i}x\left(t\right)+{\omega }^T\left(t\right)C_i^T{(P_i{E}^T+H{S}_i^T)}^{-1}x\left(t\right)\hfill \\ \hfill & +x^T\left(t\right){(P_i{E}^T+H{S}_i^T)}^{-T}{C}_i\omega \left(t\right).\hfill \end{array}$$

(32)

Following the same philosophy as that in Theorem 1, we have

$$\ell V(x\left(t\right),r\left(t\right))-\alpha \left(V(x\left(t\right),r\left(t\right))+{\omega }^T\left(t\right)W_i\omega \left(t\right)\right)={\left[\begin{array}{c}x\left(t\right)\\ \omega \left(t\right)\end{array}\right]}^T\Psi \left[\begin{array}{c}x\left(t\right)\\ \omega \left(t\right)\end{array}\right],$$

(33)

where

$$\begin{array}{cc}\hfill \Psi =& \left[\begin{array}{cc}{\Psi }_{11}& {(P_i{E}^T+H{S}_i^T)}^{-T}{C}_i\\ C_i^T{(P_i{E}^T+H{S}_i^T)}^{-1}& -\alpha W_i\end{array}\right],\hfill \\ \hfill {\Psi }_{11}=& \sum _{j=1}^N{\mu }_{ij}\left(h\right)E^T{(P_j{E}^T+H{S}_j^T)}^{-1}+{\mathcal{A}}_i^T{(P_i{E}^T+H{S}_i^T)}^{-1}\hfill \\ & +{(P_i{E}^T+H{S}_i^T)}^{-T}{\mathcal{A}}_i-\alpha E^T{(P_i{E}^T+H{S}_i^T)}^{-1}.\hfill \end{array}$$

By multiplying $\Psi$ by diag$\{{(P_i{E}^T+H{S}_i^T)}^T,I\}$ and its transpose on the left and right, respectively, and defining $Y_i=K_i(P_i{E}^T+H{S}_i^T)$, we get

$$\overline{\Psi }=\left[\begin{array}{cc}{\overline{\Psi }}_{11}& C_i\\ C_i^T& -\alpha W_i\end{array}\right],$$

(34)

where

$$\begin{array}{cc}\hfill {\overline{\Psi }}_{11}=& \sum _{j=1}^N{\mu }_{ij}\left(h\right){(P_i{E}^T+H{S}_i^T)}^T{E}^T{(P_j{E}^T+H{S}_j^T)}^{-1}(P_i{E}^T+H{S}_i^T)\hfill \\ \hfill & +{(P_i{E}^T+H{S}_i^T)}^T{A}_i^T+A_i(P_i{E}^T+H{S}_i^T)+B_i{Y}_i+Y_i^T{B}_i^T-\alpha E{P}_i{E}^T.\hfill \end{array}$$

According to (14) and (16), by applying the Schur complement lemma, and then multiplying (31a) by $\underline{m}$ and (31b) by $\overline{m}$, with $\overline{m}+\underline{m}=1$ and $\overline{m}>0,\underline{m}>0$, we can also obtain

$$\ell V(x\left(t\right),r\left(t\right))<\alpha \left(V(x\left(t\right),r\left(t\right))+{\omega }^T\left(t\right)W_i\omega \left(t\right)\right).$$

(35)

Multiplying it by $e^{-\alpha t}$ on the both sides gives

$$\ell e^{-\alpha t}V(x\left(t\right),r\left(t\right))<\alpha e^{-\alpha t}{\omega }^T\left(t\right)W_i\omega \left(t\right).$$

(36)

From the Dynkin formula, it is easy to obtain that

$$e^{-\alpha t}\mathbb{E}\left\{V(x\left(t\right),r\left(t\right))\right\}-\mathbb{E}\left\{V(x\left(0\right),r\left(0\right))\right\}<\alpha \left({\int }_0^t{e}^{-\alpha s}\mathbb{E}\left\{{\omega }^T\left(s\right)W_i\omega \left(s\right)\right\}\mathrm{d}s\right).$$

For $t\in [0,T]$, one can get

$$\begin{array}{cc}\hfill \mathbb{E}\left\{V\right(x\left(t\right),r\left(t\right)\left)\right\}& <e^{\alpha T}\left(\mathbb{E}\left\{V(x\left(0\right),r\left(0\right))\right\}+\alpha \left({\int }_0^T{e}^{-\alpha s}\mathbb{E}\left\{{\omega }^T\left(s\right)W_i\omega \left(s\right)\right\}\mathrm{d}s\right)\right)\hfill \\ \hfill & <e^{\alpha T}\left(\mathbb{E}\left\{V(x\left(0\right),r\left(0\right))\right\}+\alpha d{\lambda }_{max}\left(W_i\right)\right).\hfill \end{array}$$

(37)

From (31d), it follows ${\lambda }_{max}\left(W_i\right)<\eta$ and therefore (31c) implies

$$\begin{array}{c}\hfill c_1{e}^{\alpha T}+\alpha d{\lambda }_{max}\left(W_i\right)\theta e^{\alpha T}<\theta c_2.\end{array}$$

(38)

From (31c,d), it follows that $\theta <{\lambda }_{min}\left(Q_i^{-1}\right)<{\lambda }_{max}\left(Q_i^{-1}\right)<1$ and then ${\lambda }_{max}\left(Q_i^{-1}\right)c_1{e}^{\alpha T}<c_1{e}^{\alpha T}<\theta \left(c_2-\alpha d{\lambda }_{max}\left(W_i\right)e^{\alpha T}\right)<{\lambda }_{min}\left(Q_i^{-1}\right)\left(c_2-\alpha d{\lambda }_{max}\left(W_i\right)e^{\alpha T}\right)$. Bearing in mind that ${\lambda }_{max}\left(Q_i\right)=\frac{1}{{\lambda }_{min}\left(Q_i^{-1}\right)}$, ${\lambda }_{min}\left(Q_i\right)=\frac{1}{{\lambda }_{max}\left(Q_i^{-1}\right)}$, it can be derived that

$$\begin{array}{c}\hfill {\lambda }_{max}\left(Q_i\right)c_1{e}^{\alpha T}<{\lambda }_{min}\left(Q_i\right)\left(c_2-\alpha d{\lambda }_{max}\left(W_i\right)e^{\alpha T}\right).\end{array}$$

(39)

Similarly to Theorem 2, we have

$$\begin{array}{c}\mathbb{E}\left\{V(x\left(t\right),r\left(t\right))\right\}\ge {\lambda }_{min}\left(Q_i\right)\mathbb{E}\left\{x^T\left(t\right)E^{T}REx\left(t\right)\right\},\end{array}$$

(40a)

$$\begin{array}{c}V(x\left(0\right),r\left(0\right))\le {\lambda }_{max}\left(Q_i\right)\mathbb{E}\left\{x^T\left(0\right)E^{T}REx\left(0\right)\right\}.\end{array}$$

(40b)

If $\mathbb{E}\left\{x^T\left(0\right)E^{T}REx\left(0\right)\right\}\le c_1$, from (37), (39) and (40a,b), we get $\mathbb{E}\left\{x^T\left(t\right)E^{T}REx\left(t\right)\right\}<c_2$. Therefore, the closed-loop system is stochastically finite-time bounded with respect to $(c_1,c_2,T,R,d)$, which completes the proof. □

Remark 5.

The sufficient conditions for mode-dependent controller design of SSMJSs are presented in this theorem, which guarantees the closed-loop SSMJS is stochastically finite-time bounded and of a unique solution. For the existence of scalar α, the matrix inequalities (31a–d) are not linear. If we fix α to be constant, they are linear ones. With this consideration, we can use the one-dimensional search method to obtain the scalar $\alpha \in (0,{\alpha }^{*}]$ to resolve (31a–d).

4. Numerical Examples

Example 1.

Consider the SSMJS in (1) with $\omega \left(t\right)=0$, which operates in two modes. Some detailed system parameters are given as follows.

$$\begin{array}{c}\hfill E=\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right],A_1=\left[\begin{array}{cc}0.2& -0.5\\ 0.3& 0.7\end{array}\right],A_2=\left[\begin{array}{cc}-0.5& -1.2\\ 1& 2\end{array}\right],B_1=\left[\begin{array}{c}1\\ 1\end{array}\right],B_2=\left[\begin{array}{c}1\\ -1\end{array}\right].\end{array}$$

To study the finite-time stabilization problem, the following parameters are given:

$$\begin{array}{c}\hfill R=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right],H=\left[\begin{array}{c}0\\ 1\end{array}\right],c_1=1,c_2=2,T=4.\end{array}$$

Meanwhile, the transition rate matrix is bounded with

$$\left[{\underline{\mu }}_{ij}\right]=\left[\begin{array}{cc}-0.1& 0.1\\ 0.3& -0.3\end{array}\right],\left[{\overline{\mu }}_{ij}\right]=\left[\begin{array}{cc}-0.9& 0.9\\ 0.7& -0.7\end{array}\right].$$

It can be shown that the matrix inequalities in Theorem 2 are feasible, and a solution can be given as

$$\begin{array}{c}\alpha =0.1,\theta =0.7818,Z_1=Z_2=0.8909,\\ Y_1=\left[\begin{array}{cc}-1.1335& -1.8287\end{array}\right],Y_2=\left[\begin{array}{cc}-2.6346& 2.9817\end{array}\right],\\ P_1=\left[\begin{array}{cc}0.8994& 0.8625\\ 0.8625& 1.0564\end{array}\right],P_2=\left[\begin{array}{cc}0.8748& -0.8619\\ -0.8619& 0.9297\end{array}\right],S_1=\left[\begin{array}{c}0.3159\\ 0.8888\end{array}\right],S_2=\left[\begin{array}{c}-0.5487\\ 0.8030\end{array}\right].\end{array}$$

Therefore, the desired controller gain can be obtained as

$$\begin{array}{c}{K}_1=\left[\begin{array}{cc}1.4353& -2.0574\end{array}\right],K_2=\left[\begin{array}{cc}2.9757& 3.7133\end{array}\right],\end{array}$$

and the corresponding closed-loop system matrices are

$$\begin{array}{c}{\mathcal{A}}_1=\left[\begin{array}{cc}1.6353& -2.5574\\ 1.7353& -1.3574\end{array}\right],{\mathcal{A}}_2=\left[\begin{array}{cc}2.4757& 2.5133\\ -1.9757& -1.7133\end{array}\right].\end{array}$$

With this control law, when the semi-Markov jump mode is as Figure 1a, the state trajectories of closed-loop SSMJS are as in Figure 1b, and the evolution of $x^T\left(t\right)E^{T}REx\left(t\right)$ is presented in Figure 1c.

Example 2.

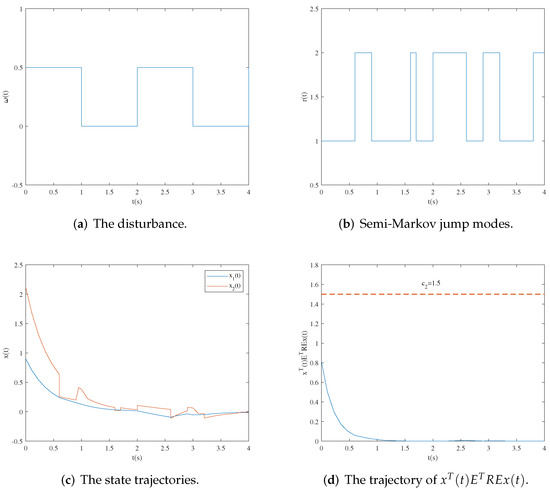
The second example is concerned with the SSMJS in (1) with the following parameters:

$$\begin{array}{c}E=\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right],A_1=\left[\begin{array}{cc}0.9& -0.4\\ 0.5& 0.8\end{array}\right],A_2=\left[\begin{array}{cc}-0.2& -0.4\\ 0.3& -0.5\end{array}\right],\\ B_1=\left[\begin{array}{c}1\\ 1\end{array}\right],B_2=\left[\begin{array}{c}1\\ -1\end{array}\right],C_1=\left[\begin{array}{c}0.1\\ 0\end{array}\right],C_2=\left[\begin{array}{c}0.1\\ 0.1\end{array}\right],\end{array}$$

with $\omega \left(t\right)$ shown in Figure 2a.

Similarly, the following parameters are also given:

$$\begin{array}{c}H=\left[\begin{array}{c}0\\ 1\end{array}\right],R=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right],c_1=1,c_2=1.5,T=4,d=2,\\ \left[{\underline{\mu }}_{ij}\right]=\left[\begin{array}{cc}-0.4& 0.4\\ 0.2& -0.2\end{array}\right],\left[{\overline{\mu }}_{ij}\right]=\left[\begin{array}{cc}-1.2& 1.2\\ 1.3& -1.3\end{array}\right].\end{array}$$

From Theorem 3, it follows that there is a state feedback controller for the closed-loop SSMJS to be stochastically finite-time bounded. A feasible solution to the matrix inequalities is

$$\begin{array}{c}\theta =0.5418,\eta =0.8998,\alpha =0.3,Z_1=Z_2=0.7709,\\ Y_1=\left[\begin{array}{cc}-0.3833& -0.4818\end{array}\right],Y_2=\left[\begin{array}{cc}-0.0196& 0.0027\end{array}\right],W_1=0.6198,W_2=0.6259,\\ P_1=\left[\begin{array}{cc}0.6391& 0.4055\\ 0.4055& 0.3644\end{array}\right],P_2=\left[\begin{array}{cc}0.6571& 0.0038\\ 0.0038& 0.5808\end{array}\right],S_1=\left[\begin{array}{c}0.2095\\ 0.3636\end{array}\right],S_2=\left[\begin{array}{c}0.0077\\ 0.5778\end{array}\right].\end{array}$$

With this solution, we can get the desired controller gain as

$$K_1=\left[\begin{array}{cc}0.6751& -1.3250\end{array}\right],K_2=\left[\begin{array}{cc}-0.0299& 0.0047\end{array}\right],$$

and the corresponding closed-loop system matrices are

$$\begin{array}{c}\hfill {\mathcal{A}}_1=\left[\begin{array}{cc}1.5751& -1.7250\\ 1.1751& -0.5250\end{array}\right],{\mathcal{A}}_2=\left[\begin{array}{cc}-0.2299& -0.3953\\ 0.3299& -0.5047\end{array}\right].\end{array}$$

With this control law, when the semi-Markov jump mode is as in Figure 2b, the state trajectories of closed-loop SSMJS are given in Figure 2c, and the evolution of $x^T\left(t\right)E^{T}REx\left(t\right)$ is presented in Figure 2d.

Remark 6.

In this section, two examples were provided to verify the validity of the results. According to the simulation figures, it can be seen that if the trajectory $x^T\left(0\right)E^{T}REx\left(0\right)$ is less than $c_1$, for $\forall t\in [0,T]$, the trajectories $x^T\left(t\right)E^{T}REx\left(t\right)$ are less than $c_2$—that is, the system is stochastically finite-time-stable. When the singular matrix E of the SSMJS is not a diagonal matrix, the method presented in [39] is not applicable, since it is difficult to simulate due to the existence of equality. The methods in [26,40] can solve the above, but the former has limitations since the controller gain is dependent on many parameters, and the latter, related to the decomposition of singular matrix, is more complicated than the one proposed in this paper.

5. Conclusions

In this paper, the finite-time control problem for SSMJSs was considered. A matrix inequality condition for the design of the desired state feedback controller was given for the closed-loop SSMJS to be regular, impulse-free and finite-time-stable by designing a suitable semi-positive definite Lyapunov-like function, and applying some matrix decomposition and construction. By using a similar method, a matrix inequality condition was also given for the regularity, absence of impulse and finite-time boundedness of the closed-loop SSMJS, when the considered system suffers from an external disturbance integrally bounded within a finite time interval. Using the one-dimensional search method for a scalar variable, those conditions are strict linear matrix inequality conditions that can be easily verified numerically. Numerical examples were used to verify the main results. In order to reduce the conservatism of the conclusion, more consideration should be given to the transition rates in the future, as well as to the coupling term. Moreover, more complex problems for SSMJSs will be studied.