1. Introduction
Pioneering work in the area of the population-based metaheuristics included genetic algorithms (GA) [
1], evolutionary computations—EC [
2], particle swarm optimization (PSO) [
3] and its two offspring—ant colony optimization [
4] and bee colony algorithms (BCA) [
5]. Since the end of the last century, tremendous research effort has brought a variety of approaches and population-based metaheuristics. In 2013 Boussai et al. [
6] proposed the classification of the population-based metaheuristics and grouped them into two broad classes. The first is evolutionary computation with subclasses, including genetic algorithms, evolution strategy, evolutionary programming, genetic programming, estimation of distribution algorithms, differential evolution, coevolutionary algorithms, cultural algorithms and scatter search and path relinking. The second class is swarm intelligence with subclasses, including ant colony optimization, particle swarm optimization, bacterial foraging optimization, bee colony optimization, artificial immune systems and biogeography-based optimization. Over the last 20 years, more than a few thousand new population-based approaches and many new subclasses have been proposed. A recent survey of the population-based techniques can be found in [
7].
Judging from the number of publications appearing during the last two decades, swarm intelligence is one of the fastest-growing areas of research in the population based methods. According to [
8], in the period 2001–2017 more than 3900 swarm intelligence journal publications were indexed by Web of Science. The concept introduced in 1993 by Beni and Wang [
9] is broadly understood as the collective behavior of a decentralized, self-organized population of individuals. The structure and behavior of such a group is usually inspired by a metaphor taken from natural or artificial systems. Swarm intelligence has proven an effective tool for solving variety of difficult optimization and control problems. The importance of the tool in different areas of application has been highlighted in several recent surveys and reviews as, for example [
10,
11,
12,
13,
14].
Researchers tackling difficult optimization problems often focus their efforts on searching for methods able to deal with two famous combinatorial optimization problems—traveling salesman (TSP) and job-shop scheduling (JSSP). Both have attracted numerous teams and labs, resulting in publications and implementations of a huge number of algorithms and approaches. Both problems are important from the point of view of the real life applications, and both belong to the NP hard class. In addition, they are in a certain sense classic, even if they still pose a challenge to researchers in the field of the OR and AI.
Performance of algorithms for solving instances of the TSP and JSSP is, usually, evaluated from the point of view of two criteria—accuracy and computation time. In the quest for approaches providing optimal or near optimal solutions to TSP and JSSP in a reasonable computation time, swarm intelligence and other population-based methods play a leading role. Some well performing recent approaches to solving the TSP include a hybrid method based on particle swarm optimization, ant colony optimization and 3-opt algorithms for traveling salesman problem [
15,
16], discrete bat algorithm for symmetric and asymmetric TSP [
17] and a hybrid ga-PSO algorithm for solving the TSP [
18]. A novel design of differential evolution for solving discrete TSP named NDDA was described in [
19]. The idea is to enhance DE algorithm with several components including the enhanced mapping method transforming the randomly generated initial population with continuous variables into a discrete one. Next, an improved
k-means clustering is adapted as a repairing method for enhancing the discrete solutions in the initial phase. Then, a copy of the modified discrete population is again transformed into a continuous format using the backward mapping method, thus enabling the DE to perform mutation and crossover operations in the continuous landscape. Additionally, an ensemble of DE continuous mutation operators are proposed for increasing the exploration capability of DE.
An effective spider monkey optimization algorithm for TSP named DSMO was proposed in [
20]. In DSMO, every spider monkey represents a TSP solution where swap sequence (SS) and swap operator (SO) based operations are employed, which enables interaction among monkeys in obtaining the optimal or close to the optimal TSP solution. Another swarm intelligence approach called a discrete symbiotic organisms search (DSOS) algorithm for finding a near optimal solution for the TSP was proposed in [
21]. A very good performance in solving TSP instances achieves the approach proposed in [
22]. The authors propose a genetic algorithm with an effective ordered distance vector (ODV) crossover operator, based on the ODV matrix used at the population seeding stage.
With the advance of computational technologies, a number of approaches for solving TSP using parallel computations, have been proposed. One of the first was parallel GA on MapReduce framework using Hadoop cluster [
23]. Another solution using the Hadoop MapReduce for parallel genetic algorithm for TSP can be found in [
24]. Distributed ant colony optimization algorithm for solving the TSP was proposed in [
25]. Parallel version of the population learning metaheuristic applied, among other, to TSP can be found in [
26].
Research efforts on TSP have also produced numerous heuristic and local search algorithms that offer good performance and may serve as the inspiration in constructing hybrid swarm intelligence solutions. One of them is the constructive, insertion and improvement (CII) algorithm proposed in [
27]. CII has three phases. The constructive heuristics of Phase 1 produces a partial tour that includes solely the points of the girding polygon. The insertion heuristic of Phase 2 transforms the partial tour of Phase 1 into a full feasible tour using the cheapest insertion strategy. The tour improvement heuristic of Phase 3 improves iteratively the tour of Phase 2 based on the local optimality conditions using two additional heuristic algorithms.
Population based algorithms including swarm intelligence and evolutionary systems have proven successful in tackling JSSP—another hard optimization problem considered in this study. A state of the art review on application of the AI techniques for solving the JSSP as of 2015 can be found in [
28]. Recently, several interesting swarm intelligence solutions for JSSP were published. In [
29] the local search mechanism of the PSA and large-span search principle of the cuckoo search algorithm are combined into an improved cuckoo search algorithm (ICSA). A hybrid algorithm for solving JSSP integrating PSO and neural network was proposed in [
30]. An improved whale optimization algorithm (IWOA) based on quantum computing for solving JSSP instances was proposed by [
31]. An improved GA for JSSP [
32] offers good performance. Their niche adaptive genetic algorithm (NAGA) involves several rules to increase population diversity and adjust crossover rate and mutation rate according to the performance of the genetic operators. Niche is seen as the environment permitting species with similar features to compete for survival in the elimination process. According to the authors, niche technique prevents premature convergence and improves population diversity. A discrete wolf pack algorithm (DWPA) for job shop scheduling problem was proposed in [
33]. WPA is inspired by the hunting behaviors of wolves. DWPA involves 3 phases: initialization, scouting and summoning. During initialization heuristic rules are used to generate a good quality initial population. The scouting phase is devoted to the exploration while summoning takes care of the intensification. In [
34] a novel biomimicry hybrid bacterial foraging optimization algorithm (HBFOA) was developed. HBFOA is inspired by the behavior of
E. coli bacteria in its search for food. The algorithm is hybridized with simulated annealing. Additionally, the algorithm was enhanced by a local search method. Evaluation of the performance of several PSO based algorithms for solving the JSSP can be found in [
35].
As in the case of other computationally difficult optimization problems, an emerging technology supported development of parallel and distributed algorithms for solving JSSP instances. Scheduling algorithm, called MapReduce coral reef (MRCR) for JSSP instances was proposed in [
36]. The basic idea of the proposed algorithm is to apply the MapReduce platform and the Spark Apache environment to the coral reef optimization algorithm to speed up its response time. More recently, a large scale flexible JSSP optimization by a distributed evolutionary algorithm was proposed in [
37]. The algorithm belongs to the distributed cooperative evolutionary algorithms class and is implemented on Apache Spark.
In this study, we propose to tackle TSP and JSSP instances with a dedicated parallel metaheuristic algorithm implemented in Scala and executed using the Apache Spark environment. The approach was motivated by the following facts:
Performance of the so far developed algorithms and methods for solving TSP and JSSP still leaves a room for improvements in terms of both minimization of computation error and computation time;
Clever use of the available technologies for parallel and distributed combinatorial optimization is an open and not yet fully explored area of research;
The idea of employing a set of simple asynchronous agents exploring the solution space and trying to improve currently encountered solutions has already proven successful in numerous applications of the authors (see for example [
26,
38,
39]).
The proposed algorithm for solving instances of the TSP and JSSP can be classified as belonging to a wide swarm intelligence algorithms class. It is based on the mushroom-picking metaphor where a number of mushroom pickers with different preferences as to the collected mushroom kinds explore the woods in parallel pursuing individual or random, or mixed strategies and trying to improve the current crop. Pickers exchange information indirectly by observing traces left by others and modifying their strategies accordingly. In the proposed mushroom-picking algorithm (MPA) simple agents (alias mushroom pickers) of different skills and abilities are used.
The rest of the article is organized as follows.
Section 2 gives a detailed description of the proposed algorithm and its implementation. It also contains formulation of both considered combinatorial optimization problems.
Section 3 reports on validation experiments carried out. Statistical analysis tools were used to select the best combination of agents solving each problem. The performance of the MPA is next compared with performance of some state-of-the art algorithms for solving TSP and JSSP instances. The final section contains discussion of results and suggestions for future research.
2. Materials and Methods
2.1. MPA Algorithm
The proposed mushroom-picking algorithm is a metaheuristic constructed from the following components:
The initial population of feasible solutions is generated randomly and stored in the common memory. MPA works in cycles. A cycle involves randomly partitioning the solutions from the common memory into several subpopulations of equal size. Each subpopulation is served by a group of the solution-improving agents. Groups are replicated to take care of each subpopulation. Each agent within a group reads the required number of solutions from the subpopulation and tries to improve them. If successful, a worse solution in the population is replaced by the improved one. The required number of solutions depends on the construction of the particular agent. A single argument agent requires a single solution. Double argument agents require two solutions, etc. All groups of agents work in parallel threads. A sequence of improvement attempts within a group is random. After the time span set for the cycle has elapsed the cycle is closed and all current solutions from subpopulations are returned to the common memory. Solutions in the common memory are then shuffled and the next cycle begins. The final stopping criterion is defined as no improvement of the best result (fitness) after the given number of cycles were run. Defining the stopping criterion aims at finding a balance between the quality of the final solution and the overall computation time.
The parallelization of the solutions improvement process is carried out using the Apache Spark, a general-purpose framework for parallel computing [
40].
The general scheme of the MPA is shown in pseudo-code as Algorithm 1.
| Algorithm 1. MPA |
| n = the number of parallel threads |
|
solutions = a set of generated solutions |
| while !stoppingCriterion do { |
| populations = solutions randomly split into n subsets of equal size |
| populationsRDD = populations parallelized in Apache Spark (n threads) |
| populationsRDD = populationsRDD.map( p=>p.applyOptimizations) |
| solutions = populationsRDD.collect |
| bestSolution = solution from solutions with the best fitness |
| } |
| return bestSolution |
ApplyOptimizations attempts to improve current results in each subpopulation of solutions by running the solution-improving agents. The process is carried out for the time span of a given length, called searchTime set by the user. During this period, applyOptimizations draws at random an optimizing agent from the available set of agents and applies it to a random solution from the subpopulation. The number of solutions drawn from the respective subpopulation and temporarily allocated to an agent must be equal to the number of arguments that the agent requires to be able to act. If the agent finds a solution that is different and better than originally obtained as its arguments, applyOptimizations replaces some worse solution with the improved one.
A single solution in the MPA is represented by the ordered list of numbers. The length of the list depends on the problem at hand, but for instances of a particular problem, the length of such a list is constant. For example, for a TSP problem with 6 nodes the solution could be represented by the following: List (2, 1, 4, 3, 5).
The following solution-improving agents were defined and implemented:
randomMove—moves a random element from the list to another, random position,
bestMove—takes a random element from the list and moves it to a position maximizing fitness gain;
randomReverse—takes a random slice of the list and reverses the order of its elements;
bestReverse—takes a random element from the list and reverses the order of elements on all of possible consecutive sublists of different length starting from that element. Solution maximizing fitness gain is finally selected;
crossover—requires two solutions. It takes a slice from one solution and adds to it the missing elements exactly in an order as in the second solution.
Algorithm 2 shows how the crossover operation is implemented as Scala function cross. We also show how the list representing the example solution changes as the result of crossing it with another solution.
| Algorithm 2. Function cross and Example of Its Usage |
| def cross( l1: List[ Int], l2: List[ Int], from: Int, len: Int) = { |
| val slice = l1.slice( from, from+len) |
| val rest = l2 diff slice |
| rest.slice( 0, from) ::: slice ::: rest.slice( from, rest.size) |
| } |
| solution 1: 0,5,9,7,3,1,4,6,8,2 |
| solution 2: 0,1,4,2,8,6,9,5,3,7 |
| slice of solution 1: 1,4,6 |
| result: 0,2,8,9,5,1,4,6,3,7 |
The MPA outlined above may be used for solving various combinatorial optimization problems in which a solution can be represented as the list of numbers. Among such problems there are the traveling salesman problem (TSP) and job shop scheduling problem (JSSP).
2.2. Traveling Salesman Problem
The traveling salesman problem (TSP) is a well-known NP-hard optimization problem. We consider the Euclidean planar traveling salesman problem, a particular case of TSP. For given n cities in the plane and Euclidean distances between these cities, we consider a tour as a closed path visiting each city exactly once. The objective is to find the shortest tour. A solution is represented as the list of indexes of the cities on the path–in the order of visiting them.
2.3. Job Shop Scheduling Problem
Job shop scheduling (JSSP) is another well-known NP-hard optimization problem. There is a set of jobs (J1, …, Jn) and a set of machines (m1, …, mm). Each job j consists of a list of operations that have to be processed in a given order. Each operation within a job must be processed on a specific machine, only after all preceding operations of this job were completed.
The makespan is the total length of a schedule, i.e., the total time needed to process all operations of all jobs. The objective is to find a schedule that minimizes the makespan.
A solution is represented as sequence of jobs of the length n × m. There are m occurrences of each job in such sequence. When examining a sequence from the left to the right, the i–th occurrence of the job j refers to the i–th operation of this job.
2.4. Implementation of the MPA for TSP and JSSP
Although actions of agents are identical for both problems, the implementation is different. The main difference is the manner fitness is calculated. In the TSP, when moving a node to a different position on the list of nodes representing a solution or when reversing the order of nodes on a subpath of the list, the length of the resulting path may be easily adjusted and calculated. Similar, simple, calculations for JSSP do not work. After each change of positions on the list representing a solution, a new value of fitness has to be calculated from the whole list.
Algorithm 3 presents how the function reversing a subpath was implemented within the TSP solution. The algorithm contains part of the definition of the class for TSP solution with the method
reverse. The agent
randomReverse calls it for randomly chosen
from and
len. Algorithm 4 presents similar function for JSSP.
| Algorithm 3. Function reverse (in Scala) in class Solution for TSP |
| class Solution( val task: Task) { |
| var path: List[ Int] = null |
| var fitness: Double = Double.MaxValue |
| def prevI( i: Int) = (i+path.size-1)% path.size //previous index |
| def reverse( from: Int, len: Int) = { |
| //from+len<size |
| val change = task.distance( path( prevI( from)), path( from+len-1)) + |
| task.distance( path( from), path( from+len))– |
| task.distance( path( prevI( from)), path( from))– |
| task.distance( path( prevI( from+len)), path( from+len)) |
| if( change < 0) { //the path is changed only if it improves the fitness |
| var slice = path.slice( from, from + len) |
| slice = slice.reverse |
| path = path.slice( 0, from) ::: slice ::: path.slice( from+len, path.size) |
| fitness = fitness + change |
| } |
| this |
| } |
| } |
| Algorithm 4. Reverse (in Scala) for JSSP
|
| def reverse( from: Int, len: Int) = { |
| val slice = jobs.slice( from, from + len).reverse |
| jobs = jobs.slice( 0, from) ::: slice ::: jobs.slice( from+len, jobs.size) |
| countFitness |
| this |
| } |
The source files of the implementation of MPA for TSP is available at [
41].
3. Results
3.1. Computational Experiments Plan
To validate the proposed approach, we carried out several computational experiments. Experiments were based on publicly available benchmark datasets for TSP [
42] and JSSP [
43], containing instances with known optimal solutions (minimum length of path in the case of TSP or minimum makespan for JSSP). Experiments, besides evaluating the performance of the MPA, aimed at finding the best composition of the self-organized agents, each representing a simple, solution-improving, procedure. Performance of agents was evaluated in terms of the two measures—mean error calculated as the deviation from the optimum or best known solution and computation time. Another analysis covered mean computation time performance versus the number of threads used. This experiment aimed at identifying how increasing the number of threads executed in parallel affects the overall computation time. Finally, we have compared the performance of our approach with the performance of several state-of-the-art algorithms known from the literature.
In the experiments the following settings were used: number of repetitions for calculation of mean values—30 or more, the number of solutions processed in a single thread—2 for TSP and 4 for JSSP. The total number of solutions equals number of threads × number of solutions in a single thread. The number of threads is reported for each experiment.
The initial solutions were generated at random for JSSP, as the number of operations is equal for each job, expression (1) may be used (written in Scala).
In the case of TSP, the next node on the path was chosen as the nearest of the possible nodes with the probability 0.8, second nearest with the probability 0.1, random node of 5 nearest with probability 0.1.
The agent crossover is always called twice less often than any other agent.
All experiments were run on Spark cluster with 8 nodes with 32 VCPU at the Academic Computer Center in Gdansk.
3.2. MPA Performance Analysis
Performance analysis of the proposed mushroom-picking algorithm applied to solving the TSP problem, was based on 23 benchmark instances. For each dataset experiments of four different kinds were run with different sets of agents involved in the process of improving solutions. In each case the crossover was used as two-argument agent and one-argument agents were chosen as follows:
RR—randomMove and randomReverse;
BR—bestMove and randomReverse;
BB—bestMove and bestReverse;
RB—randomMove and bestReverse.
In the experiment 50 threads were used, searchTime (time period used in applyOptimizations) was set to 1 second, stopping criterion was defined as no improvement in the best fitness for 2 rounds.
Mean errors and the respective mean computation times obtained in the experiment are shown in
Table 1. In most cases results produced using pair
BR are better than other results.
Table 2 presents standard deviations of errors and times obtained in the same experiment.
To determine whether there are any significant differences among mean errors produced by different combinations of agents we used the Friedman ANOVA by ranks test. The null hypothesis states that there are no such differences. With Friedman statistics equal to 21.85 and p-value = 0.00007 the null hypothesis should be rejected at the significance level of 0.05. In terms of the computation error BR outperforms the remaining sets of agents. For a similar analysis involving computation times under the null hypothesis that there are no significant differences among mean computation times the Friedman statistics is equal to 46.49 and p-value < 0.00000. Hence, also in the case of mean computation times the null hypothesis should be rejected. In terms of the computation time needed the RR is a looser. However, there are no statistically significant differences between computation times required by the remaining sets of agents.
To identify significant differences among standard deviations produced by different combinations of agents we again used the Friedman ANOVA by ranks test. The null hypothesis state that there are no such differences. With Friedman statistics equal to 17.16 and p-value = 0.00065 the null hypothesis should be rejected at the significance level of 0.05. Similar conclusion can be drawn with respect to standard deviations of computation times.
Performance analysis of the proposed approach applied to solving the JSSP problem was based on 30 benchmark instances. Mean errors and the respective mean computation times obtained in the experiment for pairs
RR and
BR are shown in
Table 3, standard deviations of errors and times are shown in
Table 4. There were 200 threads used in the computations,
searchTime (time span used in
applyOptimizations) was equal to 0.2 s, the stopping criterion was defined as no improvement in the best fitness for 2 rounds. In all considered cases using pair
RR have given the same or better result than
BR. The
BR combination of agents outperforms the remaining ones also in terms of the standard deviation minimization.
In case of the JSSP problem, to determine whether there are any significant differences among mean errors produced by two considered agent groups we used the Wilcoxon Signed Rank Test. The null hypothesis is that the medians of two investigated samples with mean errors are equal. With Z statistics value of 4.20 and p-value equal to 0.00027 the null hypothesis should be rejected at the significance level of 0.05. The agent set RR outperforms statistically BR in terms of the computation errors. Similar analysis was performed to determine whether there are any significant differences among mean computation times needed by two considered kinds of agents. With Z statistics value at 0.42 and p-value equal to 0.673, the null hypothesis that the medians of two investigated samples with mean computation times are statistically equal, holds at the significance level of 0.05. Similar analysis with respect to standard deviations shows that RR outperforms statistically BR, while standard deviations of computation times do not statistically differ between both sets.
Further experiments were carried out to identify some properties of the convergence ability of the MPA.
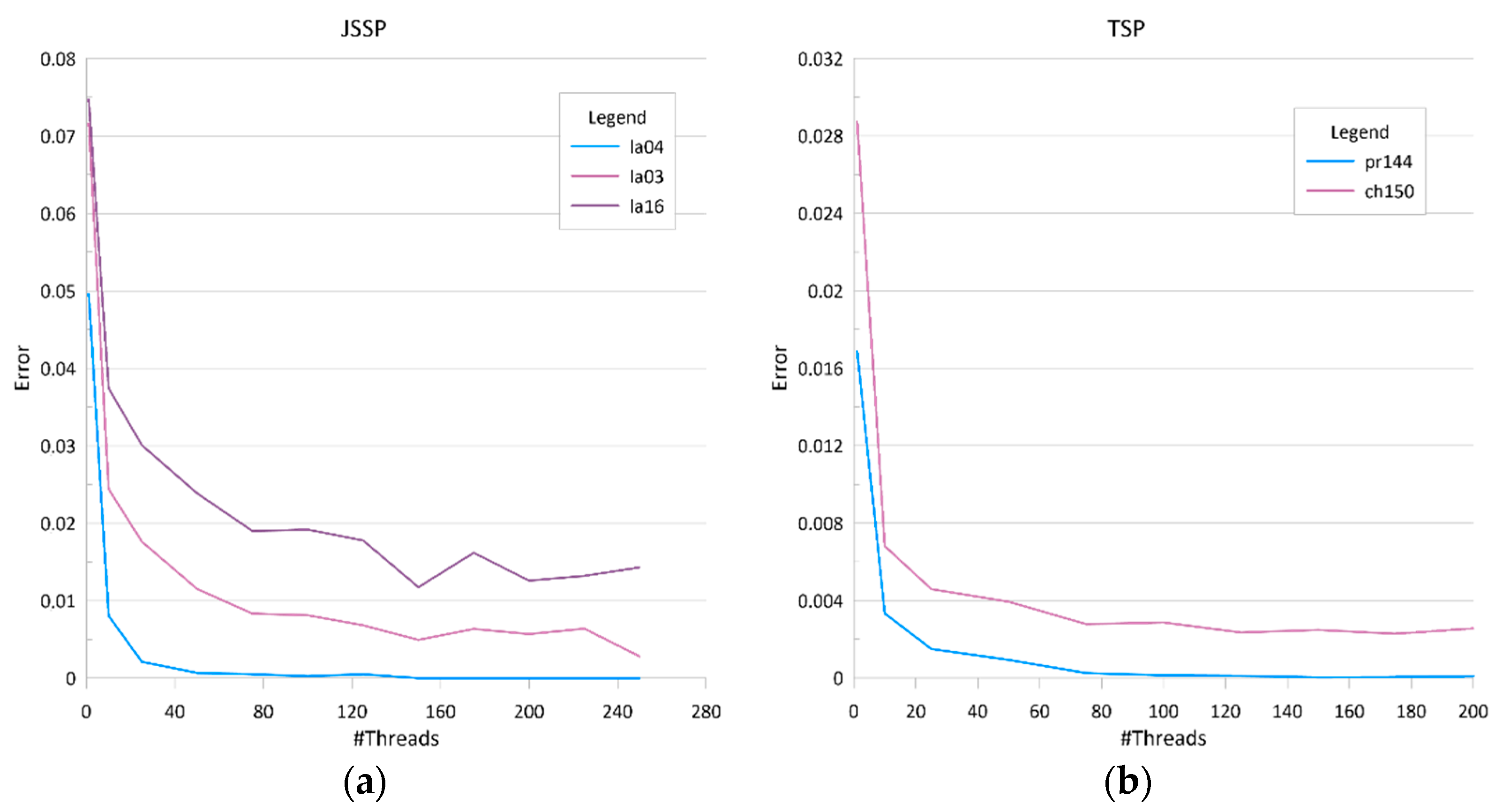
Figure 1 shows the dependency between the number of threads and mean accuracy for example benchmark datasets. Pr144 was solved with 4 solutions processed in each thread, the other datasets used 2 solutions in each thread. Computation results were averaged over 20 runs,
searchTime was equal 0.5 seconds, stopping criterion was defined as no improvement in the best fitness for 2 rounds.
Figure 2 shows dependency between the number of threads and mean computation times in the same experiment. It may be noticed that using more threads results in obtaining better solutions since more solutions from the search space are considered. However, increasing the number of threads also results in increasing the time required for communication. In addition, at some point, depending on the number of nodes in the cluster, some of the threads are executed sequentially.
3.3. MPA Performance versus other Approaches
Further experiments aimed at comparing the performance of the MPA with performance of other, state-of-the-art algorithms.
Table 5 presents results obtained for instances of the TSP for different values of the
searchTime. Calculations were carried out using the set of agents consisting of
bestMove,
randomReverse and
crossover. Computations were carried out using 175 threads. The stopping criterion was defined as no improvement in the best fitness for 5 rounds. In
Table 6 the results are compared with some other results known from the literature,
A comparison with [
27] is especially interesting as in the CII very similar one-argument functions were applied to a single initial solution. CII is much faster (time is expressed in milliseconds in this case) than MPA. In return, our method outperforms CII in terms of the computation errors.
Table 7 presents results obtained for instances of the JSSP. In this case the set of agents consisting of
randomMove, randomReverse and
crossover were used.
searchTime of one round and stopping criterion was defined as 2 deciseconds and 2 rounds with no improvement in the best solution for la01 to la14, and 5 s and 5 rounds with no improvement for la15 to la49. In
Table 8 the MPA results are compared with some other recently published results. Errors for [
33] and [
32] were computed on the base of results given in the respective papers. In [
32] only mean errors were reported with no information on the computation time.
4. Discussion
The proposed mushroom-picking algorithm was validated using benchmark datasets from the TSP and JSSP publicly available repositories. The first of the reported experiments aimed at identifying the best combination of the available agents.
For the TSP, the best combination denoted BR consists of the bestMove and randomReverse agents plus the crossover. The BR, with mean error averaged over all considered dataset at the level of 0.28% was significantly better than RR, BB, RB with the respective mean errors of 0.36%, 0.41% and 0.45%. The above finding was confirmed by the Friedman ANOVA by ranks test at the significance level of 0.05. In the case of the TSP also differences between mean computation times have proven to be statistically significant. The BR not only provides the smallest mean error, but also assures the shortest mean computation time, which was again established by the Friedman ANOVA by ranks test at the significance level of 0.05.
For the JSSP, the best combination denoted RR consists of the randomMove and randomReverse agents plus the crossover. The RR, with the mean computation error averaged over all considered dataset at the level of 3.75% was significantly better than BR with the respective mean error of 11.53%. The above finding was confirmed by the Wilcoxon Signed Rank Test at the significance level of 0.05. However, comparison of the mean computation times by the same method have confirmed that there are no significant differences between mean computation times of RR and BB.
Another feature of the MPA is its stability. In the case of the TSP, the mean value of the standard deviation of the computation error, averaged over all considered datasets, is 0.18% with maximum deviation at 0.95% and minimum at 0.0%. In the case of the JSSP the respective values are 0.92% with maximum at 3.43% and minimum at 0.0%.
Convergence analysis in the case of both TSP and JSSP shows that increasing the number of threads rapidly decreases computation errors. The rule is valid up to certain number of threads. Further increasing of this number decreases computation errors in a much lower pace until a zero or stable error level was reached. Computation time analysis shows that up to a point where the stable computation error was reached, increasing the number of threads increases the computation time at a slow rate. The above dependency is clearly visible in the case of the JSSP as opposed to the case of the TSP where the growth of the computation time with the increase of the number of threads is nearly linear.
The performance of the MPA was compared with performances of the recently published algorithms for solving the TSP and JSSP. Data from
Table 6 show that for the TSP, MPA outperforms other competing approaches including DSOS, NDDE and CII. Unfortunately, due to the high number of missing values for the DSOS and NDDE performance, we were not able to carry out a full statistical analysis of the compared results. The mean computation error in the case of the TSP, calculated over all sample datasets for the MPA is 0.25% while the same value for the CII algorithm is 3.5%. In return, the CII algorithm is much quicker with the mean computation time of 17.05 ms versus 22.17 s in the case of the MPA (both values calculated without pcb442 and pr1002 datasets). Data from
Table 8 show that for JSSP our approach outperforms DWPA and NAGA. Unfortunately, due to the high number of missing values in the case of the NAGA we were not able to carry out the Friedman ANOVA by ranks test. The mean computation error in the case of the JSSP, calculated over all sample datasets for the MPA is 1.44% and 3.53% for the DWPA. DWPA offers, however, a shorter computation time with the average of 6.9 s versus 53.32 s for the MPA.