1. Introduction
In complex production environments in the automotive industry, machine schedules have to be calculated by taking into account frequently changing customer demands and potential failures or unanticipated delays. The calculation of high quality schedules in such an environment is a challenge because the scheduling problem itself usually has significant complexity, tight time restrictions are given, and uncertainty occurs in various production parameters. Even by neglecting uncertainty, the resulting optimization problems are NP-hard and can only be solved exactly with acceptable computation times of some minutes for small and unrealistic configurations. More applicable solution methods for practical problem instances are heuristics and metaheuristics, because they require less computation time and allow one to approximate the optimal schedule with deterministic models, even for larger configurations. However, the parameters of the model have to be set according to the current situation. This means that data from the running production are used to define the actual scheduling problem; a statistical evaluation of past data allows for the determination of safety margins to compensate for scrap or unplanned demands. Before schedules, which were calculated by deterministic optimization methods, should be applied to a production with its statistical effects, they should be tested in stochastic simulation models.
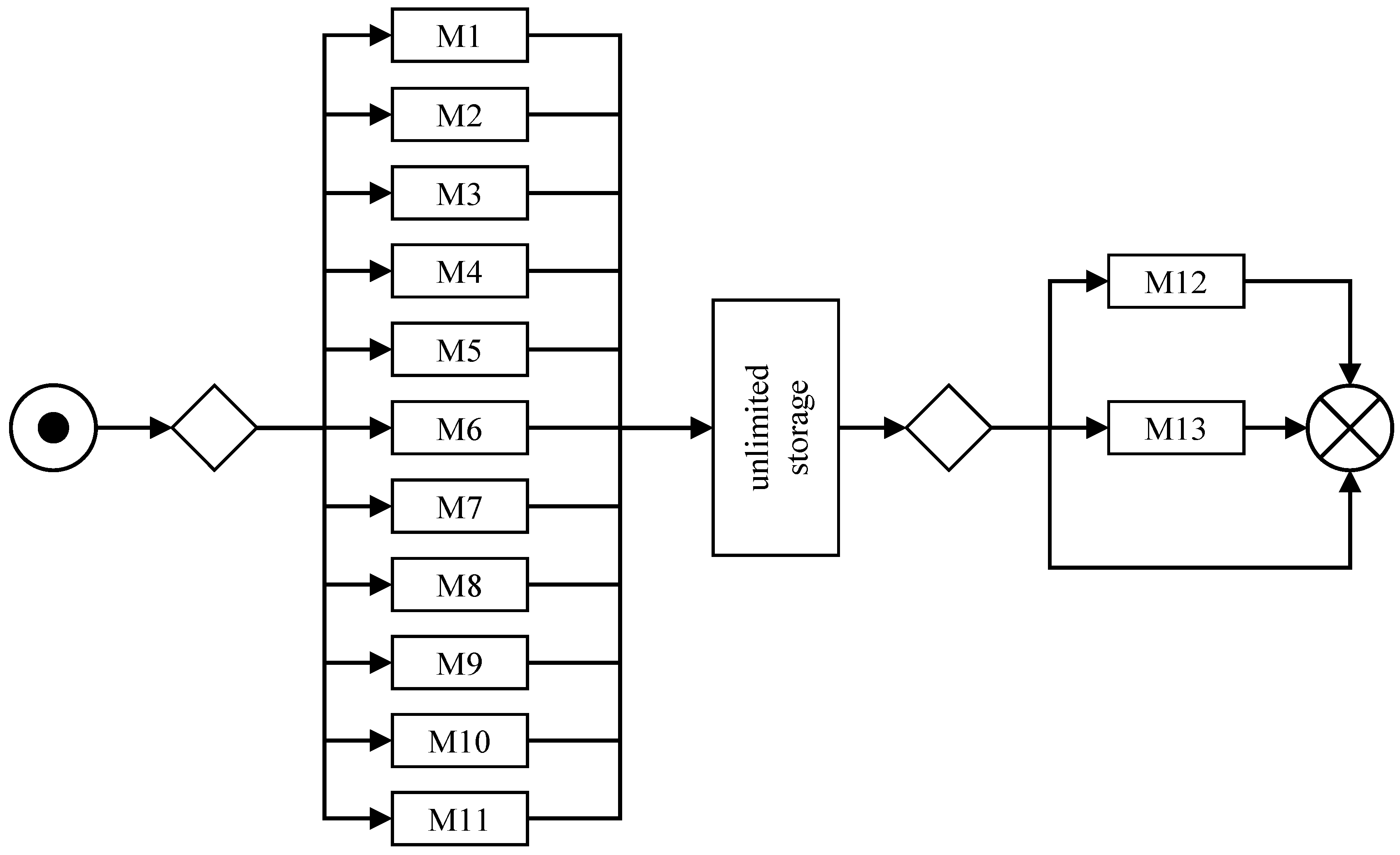
The objective of this paper is to provide combined solutions to various problems at the machine scheduling level for a real application example from a supplier in the automotive industry, which describes a two-stage scheduling problem with parallel machines per stage with uncertainty in several parameters. The system layout of the application case can be found in
Figure 1. The production includes 11 unrelated parallel machines in the first stage. In the second stage, there are two identical parallel machines. The restrictions and characteristics of the basic scheduling problem are machine qualifications, i.e., not every job can be produced on every machine, jobs might skip stages, and the production data show several uncertainties in demands and different production parameters, which need to be handled to provide usefully applicable schedules that perform in production with as few makespans as possible. A composition of forecasting, classification, discrete event simulation, metaheuristic, and heuristic algorithms is developed to identify demand fluctuations, including scrap rates, and to approve schedules for their use in a production environment. So, in contrast to common scheduling approaches, various problems at the machine scheduling level have to be considered in combination. First, based on the available data of past orders, risky jobs that are prone to fluctuations just before or during the production phase are identified by clustering algorithms and corresponding demands are adjusted. Furthermore, the distributions of scrap rates are estimated, and the quantiles of the resulting distribution are used to increase quantities of produced items to avoid costly losses due to unfulfilled demands. Second, we show how deterministic methods solving the described optimization problem are developed from the scheduling problem and how parameters are derived from the available data. Third, a detailed simulation model of the production has been built (see
Figure 2 and Figure 7) using the software AnyLogic 8.5 [
1]. By means of simulation, it is possible to evaluate and improve schedules before they are applied in a real production environment.
The structure of the paper is as follows. In the next section, we present a detailed description of the two-stage hybrid flow shop problem with its restrictions. Related work is summarized afterwards.
Section 4 introduces several metaheuristic and heuristic algorithms to compute schedules for the hybrid flow shop problem. Afterwards, in
Section 5 and
Section 6, the available data from the production are described and methods are presented to estimate all parameters of the optimization problem and to calculate the appropriate production volume from the data. Then in
Section 7, a detailed analysis of the schedules, using simulation and the structure of the simulation model, are introduced. In
Section 8, results of example runs are presented, evaluating makespans and order fulfilment as key indicators. Our findings are summarized in the conclusions, which also outline some steps for future research.
2. Description of the Basic Model
The problem analyzed in this paper is a two-stage hybrid flow shop (), in which a set of jobs has to be completed. To produce the components, there are two production stages i, with with , through which each job follows the same route. At each stage i a job is processed by at most one machine l, with , where .
As far as possible, we set the parameters according to Ruiz et al. [
2] and de Siqueira et al. [
3], to support a more homogeneous notation for machine scheduling studies. The following assumptions hold for our model. In brackets, descriptions of the assumptions from the notation in the paper by Graham et al. [
4] are added.
In the first stage, all jobs are available at time zero.
Jobs that are to be produced in the first and last stage can only start in the second stage, after the job has been finished completely in the first stage.
Each machine can only handle one job at the same time.
Processing of a job on a machine is not interrupted, i.e., preemption is not allowed.
The problem contains machine qualifications (), i.e., each job can only be processed on certain machines at each stage, where the set of eligible machines is , with .
Some jobs visit only one of the stages (). The set of stages to be visited is , where .
Jobs do not need to be dispatched in the same order in all stages. Thus, no fix permutation is considered.
There are infinite buffers in front, between and at the end of the two stages.
Processing times of one product of job j are described by independent stochastic distributions separated by machine, stage and job, i.e., machines are unrelated. Especially in the first stage, processing times differ by machine (), in the second stage, they are machine-independent ().
For setup times , stochastic distributions over all machines and jobs per stage are available.
For scrap rates , job- and stage-related stochastic distributions are available for both stages. Scrap parts are those parts which do not pass the quality check.
Available parts on stock are included to fulfill the demand.
The objective is to minimize the makespan , where is the maximum completion time and defines the completion time of a job j on stage i, where .
Order quantities of the job’s underlie uncertainty and may change even during the week when the job is produced, which results in varying production volumes . The needed processing time for one job is the .
According to Pinedo [
5] and Ruiz and Vázquez-Rodríguez [
6], this problem can be formalized in the Graham et al. [
4] notation as
. In addition, several uncertainties in the model parameters as listed above have to be included, which are not formalized in Graham et al. [
4] notation.
In addition, these other parameters of the Graham et al. [
4] notation are needed in the following sections:
: sequence-dependent setup times
: block times for machines
: block times for machines at the start of the production time
: overlapping or gaps between the processing of jobs in successive stages
: priority relationships between jobs, i.e., one jobs needs to begin production before another job can be started
Following Ruiz et al. [
2] and to support a more homogeneous notation for machine scheduling studies, the variables
and
x are introduced. With these variables, the schedules can be described to their fullest extent with
. The binary variable for the precedence relations
is defined as
Furthermore, is a permutation of jobs. Exemplarily, if jobs should be scheduled to released machines in the order of , , , they are saved as .
3. Related Work
A large number of papers on scheduling in hybrid flow shops are available. Overviews can be found in Ruiz and Vázquez-Rodríguez [
6], Ribas et al. [
7], and Komaki et al. [
8]. In the following, a selected number of studies that deal with problems related to our problem (see
Section 2) are discussed.
Jabbarizadeh et al. [
9] test three constructive heuristics for the problem
. Based on Kurz and Askin [
10], they assign the jobs in the processing stages
in the order of completion times of the previous stage. They evaluate that Shortest Processing Time (SPT) provides better results than Longest Processing Time (LPT). A heuristic based on the algorithm of Johnson [
11] gave the best results in their study. In the field of metaheuristics, a version of simulated annealing, which is a local search algorithm with the acceptance of setbacks, outperforms a genetic algorithm. In each step, the position of a randomly selected job in the first stage is changed. In the following processing steps, the jobs are dispatched according to the Earliest Completion Times (ECT) using the completion times of the previous step.
Ruiz et al. [
2] present a study dealing with an enormous number of realistic components in the problem
. Yet the study only compares constructive heuristics and finds that NEH, a heuristic first published for flow shops by Nawaz et al. [
12], provides the best solutions.
Low et al. [
13] compare for
sixteen combinations of heuristics. They do not consider skipping stages. To form a production sequence for the first stage, Low et al. [
13] use the following methods: random sequence, SPT using processing times of the first stage, LPT using process times of the second processing stage, and Johnson’s algorithm. Once the queue is created, for each method, the jobs are assigned to the machines of the second processing stage with four different rules. They find that the modified Johnson, rule by planning the second stage according to the Earliest Completion Times (ECT) of the first stage,
performs best.
For
Naderi et al. [
14] conduct job sequencing and machine assignment in the same step. All stages
i are scheduled according to the Earliest Completion Times (ECT) of the stage
i itself and they take the arrival times at the stages into account, if
, which result from
. In comparison to other constructive algorithms for their problem and for their test data, this constructive algorithm gives the best results. The paper also uses Iterated Local Search, which outperforms the other tested metaheuristics, like genetic algorithms, up to a number of 80 jobs. Since their problem takes sequence-dependent processing times into account, the problem in combination with applying these algorithms corresponds to unrelated machine problems.
In Burdett and Kozan [
15], several constructive heuristics are compared with simulated annealing (SA) and a genetic algorithm (GA) for the computation of schedules for flow shops with non-unique jobs. Again, SA and GA outperform constructive heuristics but GA does not, in general, do better than SA. Burdett and Kozan [
16] analyze flow shops with resource constraints where limited resources have to be assigned and a schedule has to be computed simultaneously. They show that an evolutionary algorithm gives good results for this class of scheduling problems. The models in the papers differ from our models in several aspects, e.g., they do not consider machine qualification, stochastic demands and scrap.
Dios et al. [
17] compare 24 constructive heuristics for
and the evaluation of their experiments shows that two SPT-based and one LPT-based heuristic generate the best schedules according to
. They do not take unrelated machines into account.
Logendran et al. [
18] use tabu search for
|
,
|
. Since the study works with
, the algorithm contains many details that cannot be used for this work.
Kaczmarczyk et al. [
19] apply tabu search to
|
,
|
. For their sequence of jobs, they swap two jobs in each iteration. The positions of the two exchanged jobs are saved in the tabu list. To schedule the created sequence, the earliest available machine on every stage is chosen for the job and the stages on which the job has to be produced.
De Siqueira et al. [
3] modify a variable neighbourhood search of Geiger [
20] for the problem
|
,
|
. To change the solutions, one of the six neighborhood strategies is applied randomly:
swapping two jobs on one machine;
swapping three jobs on one machine;
shifting the position of a job on one machine;
swapping of two jobs in the schedule (jobs can be scheduled on the same or different machines);
shifting a job within a processing stage;
relocating of a block of three consecutive jobs to a new position in a processing stage.
Thus, no study provides local search and tabu search algorithms for the problem of our paper, which is specified in
Section 2. Furthermore, the above mentioned approaches are all based on a fully parametrized deterministic model. One way to optimize stochastic models is the use of sample average approximations, which are used by Almeder and Hartl [
21] with variable neighborhood search to optimize a two-stage flow shop problem describing a real world production process in the metalworking industry. In contrast to our problem, the number of machines is smaller, machine qualification and setup times are not required, and the behavior of orders seems to be more homogeneous. In this case, production data are not used to determine model parameters. Instead, the sampling averaging of simulation results is used to determine the parameters of the optimization problem, which are analyzed with similar methods to the ones that we apply, but tabu lists do not seem to be used.
Burdett and Kozan [
22] studied buffering in the area of machine scheduling for a parallel machine environment with one stage. They add idle times to the schedule, which depend on the variance of the processing times of the jobs. Uncertainties regarding demand are taken into account by limiting the number of jobs that can be produced in a given production period or by completely blocking resources for unexpected demand. Their study differs from our study since the variance of the processing times in our application case plays a minor role, whereas scrap rates have high influence on the demand. In addition, we can use significant historical data of demand developments to adjust the demand according to the articles through clustering.
Our approach is also related to approaches that combine simulation and optimization [
23]. Regarding the different possibilities in this area to combine optimization and simulation, our study is allocated in the category of first computing a schedule for a deterministic model, which is evaluated afterwards in the detailed simulation model. In a further step, schedules can be enhanced based on the simulation results. Juan et al. [
24] introduced this technique as simheuristics.
In application scenarios, the model has to be built, i.e., parameters have to be estimated and demands have to be forecasted. For parameter estimation and modeling from available data, standard methods of input modeling, as summarized, for example, in Law [
25], may be applied. Classification of products according to their future demands is more demanding. Murray et al. [
26] have examined an application case of order classification in production planning, but they use k-means clustering in order to group customers into segments. The main difference to the problem analyzed in this paper is in the position in the supply chain. Customers are the first layer in a supply chain because they are causing the demand for orders. The demand becomes more distorted and volatile when customers’ order quantities are planned through the different stages of the supply chain [
27]. We consider a problem which is more at the end of a supply chain, so the so-called bullwhip effect can be intense. To forecast demands, regression or time series can be applied. There is no one method with an optimal parameter set that is best to predict demand in different settings; instead, algorithms are developed to select good parameters Kück and Scholz-Reiter [
28] or to even select the optimal prediction method together with the parameters, as carried out by Scholz-Reiter et al. [
29]. According to our results and in order to generate a robust schedule, it is sufficient to oversupply the demand for high-risk jobs, which are identified by clustering algorithms.
Although we do not develop new optimization techniques, the originality of our study is that, to the best of our knowledge, it combines the statistical analysis of production data with heuristic and metaheuristic optimization methods to the specific problem of this paper and the subsequent detailed simulation of a real production problem. The experiments give insights into the behavior of different local search metaheuristics and indicate as expected that local search metaheuristics are able to improve the makespan significantly compared to schedules resulting from simple heuristics like SPT. Moreover, local search and tabu search metaheuristics to the best of our knowledge have not been adapted to the specific problem of this paper in the literature before.
4. Computation of Schedules
Taking the findings of
Section 3 into account, we choose to apply SPT, local searches and tabu searches, and ECT schedules the jobs for the basic model described in
Section 2. We also apply algorithms for the restriction of machine qualifications, skipping stages, and unrelated machines. At first, the first stage is scheduled with one of the algorithms, which then is combined with ECT in each case to schedule the second stage. Thus, we obtain Algorithms 1–4, which were already presented in our conference paper Schumacher et al. [
30].
To create an initial solution, we generate feasible schedules with SPT (Algorithm 1), which uses ECT (Algorithm 2). With Algorithm 1, jobs are ordered according to their increasing average processing times in stage 1 and after that they are scheduled successively to stage 1 on the machines, which becomes available. When the scheduling of all jobs to stage 1 is finished, stage 2 is scheduled with Algorithm 2 according the job completion times of stage 1.
| Algorithm 1:Shortest Processing Time, SPT |
Order jobs j according their increasing average processing times in stage 1 () and save the queue in . Whenever a machine in stage 1 becomes available, select next unscheduled job j of that is qualified for the given machine and schedule j on the available machine. Execute Algorithm 2 (ECT). return schedule x with .
|
| Algorithm 2:Earliest Completion Time, ECT |
Order jobs on stage 2 according to their completion times . If a job is not processed on stage 1, set . Of course, if a job should not be processed on stage 2, the job is not in the sequence for stage 2. If two jobs have the same completion time , order these jobs alphanumerically. Save queue in . Whenever a machine in stage 2 becomes available, select next unscheduled job j of that is qualified for the given machine and schedule j on the available machine.
|
Based on this initial solution, six algorithms of Algorithms 3 and 4 optimize the solution. Both can be computed with one of the variants “shift” or “swap”. With “shift”, one randomly selected job in each iteration is positioned elsewhere in the existing schedule. In contrast, “swap” exchanges the positions of two randomly selected jobs. After one of these moves and the consideration of the eligibility restrictions for machines and stages, the resulting new schedule is compared with the old schedule and checked for improvement by computing and comparing makespans. Random Descent generates a new solution out of the existing one and if this solution performs better, regarding
, the new solution is the starting point for the new testing of solutions. In contrast, Steepest Descent first tests for one job
j the solutions in the neighborhood of the current solution, which are created by shifting or swapping that job to all the other machines that are eligible for that job. Furthermore, Algorithm 4 can be executed with or without tabu list (
). If tabu list is used, the algorithms avoid testing a solution
x again which has already been tested and is currently part of the tabu list. So, the tabu list contains elements
x, which have been tested before. If there is no improvement in the makespan within a predefined amount of iterations, Algorithms 3 and 4 terminate. By choosing all possible combinations of
and
in Algorithm 4, we have four variants of that algorithm. By computing the two possibilities
in Algorithm 3, we have two further algorithms to evaluate. So, in total, with SPT, we get seven different optimization algorithms for the basic model of
Section 2.
| Algorithm 3:Local Search—Random Descent |
Given a feasible initial solution x with makespan . Choose parameter and set . Choose parameter . while - (a)
Duplicate . - (b)
Randomly choose a job j on stage . For this job . According to define l and k. - (c)
Randomly choose a machine . - (d)
if - i.
Shift job j to machine and choose randomly a position to insert job j on this machine .
- (e)
if - i.
Choose randomly a job on selected machine . For this job . According to define . - ii.
Exchange positions of selected jobs j and with setting , , , and .
- (f)
Save solution in , execute Algorithm 2 (ECT) and compute makespan . - (g)
if
returnx with .
|
| Algorithm 4:Tabu and Local Search—Steepest Descent |
Given a feasible initial solution x with makespan . Choose parameter and set . Choose parameter . Choose parameter . if Initialize tabu set . Choose parameter . else Initialize tabu set . repeat - (a)
Duplicate . - (b)
Initialize set .
for all jobs j on stage 1. For the selected job . According to define l and k. for all if Shift job j to machine and choose random a position to insert job j on this machine . Save solution in , execute Algorithm 2 (ECT) and compute makespan . if . if for all on the selected machine According to define . Exchange positions of jobs j and with , . Execute Algorithm 2 (ECT). Save solution in and compute makespan . if . if . if Delete the elements from T, which are added earliest. if Set . for all schedules . if else
returnx with .
|
In the following, the algorithms of [
30] are presented.
5. Parameter Uncertainty
All algorithms presented in the previous section are assumed to have full access to the information about the problem. However, this is rarely found in practical scenarios. Usually, information about a system includes uncertainty and some parameters like processing times underlie statistical fluctuation. Some of the parameters can be described by statistical models like distributions or stochastic processes, whereas for other parameters like machine breakdowns only very little information is available.
If uncertainty is modeled by stochastic distributions, a stochastic optimization problem can be formulated; see Van Hentenryck and Bent [
31]. The complexity of solving stochastic optimization problems is higher than the complexity of solving the related deterministic models. For realistic stochastic hybrid flow shop problems, even the analysis of a single configuration cannot be evaluated analytically with exact methods. Instead, for optimization of such models, stochastic discrete event simulation has to be coupled with metaheuristic optimization methods; see Juan et al. [
32]. Stochastic simulation needs a lot of computation time for function evaluation and metaheuristic optimization methods often need numerous function evaluations. Therefore, the computation of nearly optimal schedules and the evaluation with simulation in every iteration with a random initial schedule can exceed available computation time in production planning of mostly only a few minutes. In order to decrease the computation time, it is more efficient to compare different near-optimal schedules from deterministic optimization models using a detailed simulation model. Furthermore, any model approximates the real system, so that the best solution for the simulation model or deterministic model is not automatically the best schedule for the real-world system. Finding a high-quality schedule which is robust against small changes in the parameters or the description of the random variables is more important.
In production systems, a large amount of data from business information systems are often available. These data can be utilized to model uncertainty. We have to differentiate between internal parameters of the production system on the one hand, like processing times, setup times, scrap rates, and the availability of machines and external parameters, which are mainly described by the varying demand, on the other. We begin with the internal parameters that, to some extent, are under the control of the company and can be measured in the production system. This, of course, does not imply that uncertainty can be deleted from the system but it is often possible to apply standard methods from input modeling to generate a distribution that appropriately models the field data or to use the cleaned data as an empirical distribution.
The availability and quality of production data vary considerably. In
Table 1, we analyzed scenarios where data are available in different levels of detail, and show how these data can be used in deterministic and stochastic models. Another issue to consider are effects of outliers. Due to their high values, it is more realistic for models to use the median instead of the mean for processing times and setup times to compute more realistic schedules by using the deterministic optimization model. In contrast, for scrap rates, it is recommended to use the mean value or some quantile to avoid underproduction. If the needed data are available, the highest category of detail of
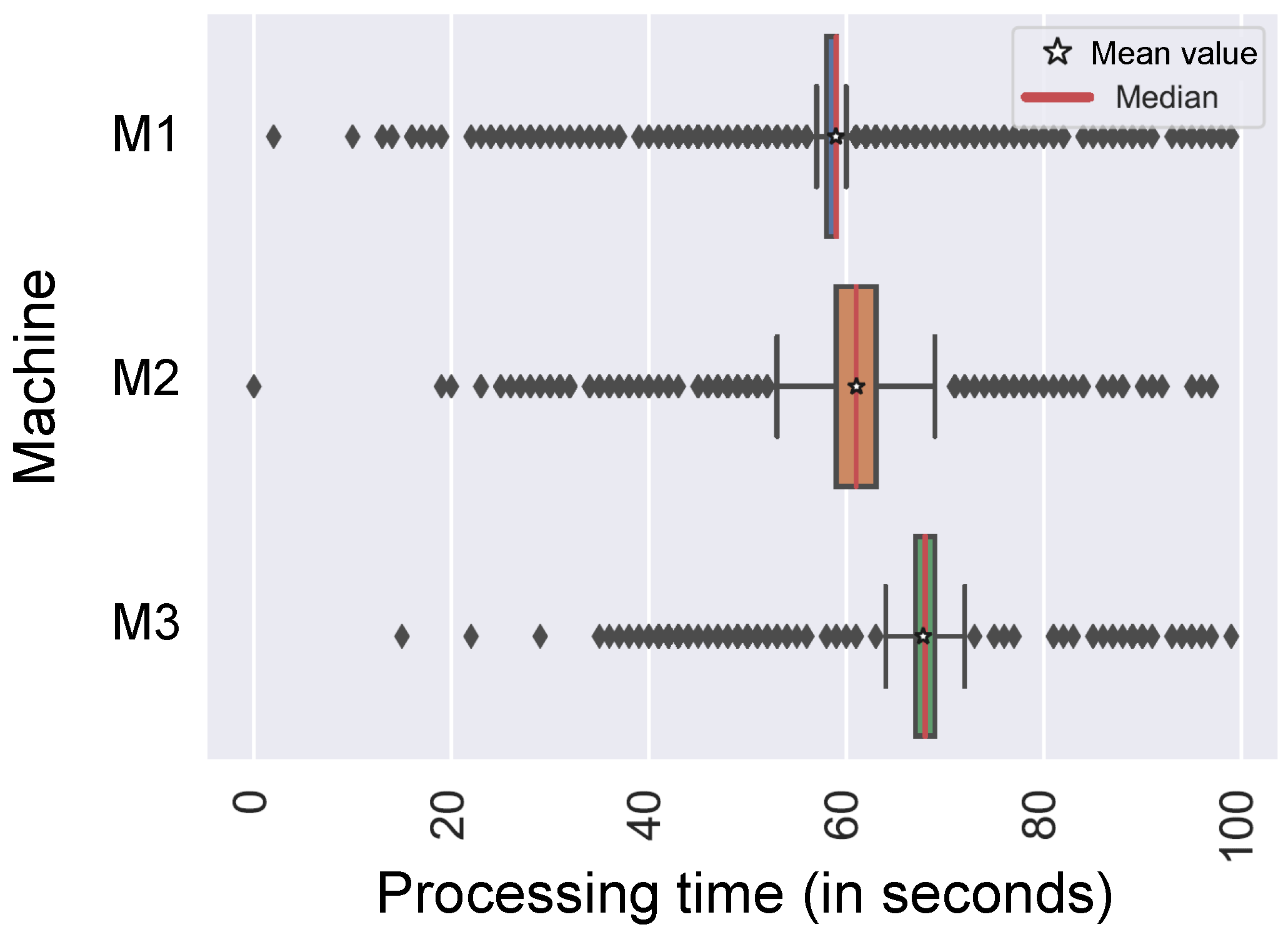
Table 1 should be used for the models. It is possible that job-related and machine-related distributions, even for machines of the same type, like in our application case, differ significantly. Differences result from detailed machine conditions even if machines are nearly identical. For example, in
Figure 3, the processing times of similar jobs on different machines of one type are presented.
External uncertainty, which is part of the problem in this paper, caused by varying demands, is out of the control of the producer. Future demands can be predicted based on historical data. In particular, at the first levels of a longer supply chain, uncertainty in demands grow in volatility and amount throughout the levels [
27].
Figure 4 gives an example of demands over twelve weeks of one specific job and the same production date from a supplier in the automotive industry. The value in the last week in each time series shows the demand that has to be finally supplied to the customer. The other observations illustrate the development of the previously mentioned amount from the customer for the same date.
In the example of
Figure 4, the demand grows in the last week considerably. Thus, if a schedule has been computed with the data of one week in advance, the production will produce less than is needed. Moreover, during the planned week itself, changes occur for high-risk jobs. Fluctuation in demands is, of course, job specific and it is not necessary or possible to model every job in detail. Hence, we first perform a cluster analysis based on historical data to distinguish between low, medium and high-risk jobs. A high-risk job changes its demand often and significantly in the weeks before and in the week of production, whereas for low-risk jobs, ordered quantities and final demand are very similar. For high-risk jobs, we use over-provisioning to avoid situations where the demand cannot be satisfied. The method is specified in the next section.
6. Clustering and Forecasting in the Application Case
In order to allocate the appropriate production volume (
) per job and stage and to meet the final customer demand volume, scrap and customer ordering behavior have to be considered. Therefore, the currently known demand per job and stage (
) as well as historical data of scrap and demand are used. The procedure of including these factors is described in the following and finally results in Equation (
1).
The clustering procedure was first mentioned in Schumacher et al. [
30]. For clustering demand data and identifying high-risk jobs (see
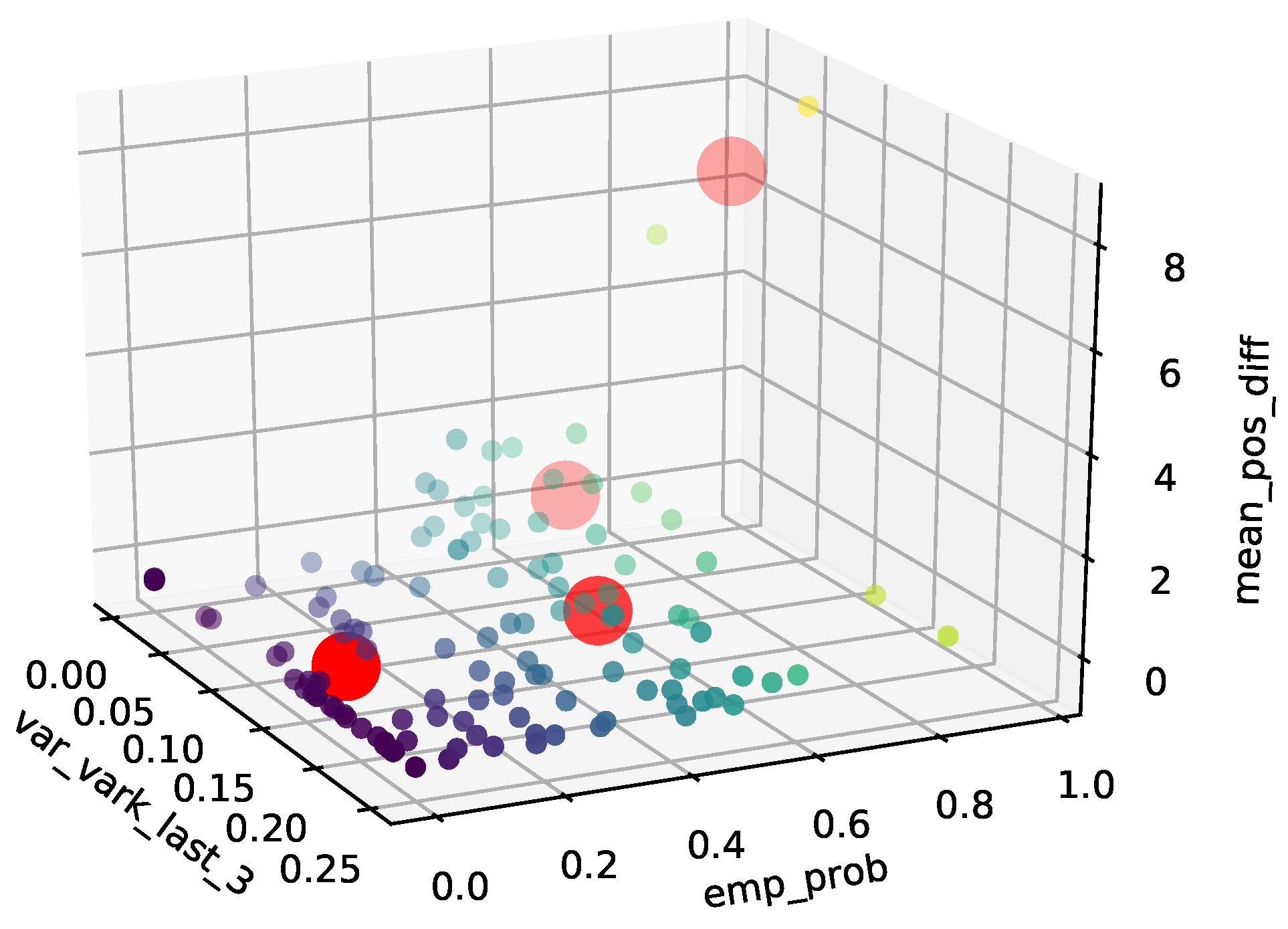
Figure 4), k-means
is applied with three parameters and the result is shown in
Figure 5. For k-means
, Arthur and Vassilvitskii [
33] theoretically prove and show in their results the quality of the algorithm against k-means algorithms for clustering. The three parameters for clustering are namely:
the probability that the demand of a job grows by 500 or more parts in the last week based on historical data ();
the average increase in demand per job (only counted if the demands are increased) ();
and the variance of the variation coefficient for the demands of the last three observations of the previously ordered amount. ().
Following the elbow method, see Leskovec et al. [
34], k-means should be applied for our application case with four clusters. After analyzing the data, we computed the four clusters as shown in
Figure 5 and defined the jobs of cluster 3 and 4 (marked in light red in
Figure 5) as high-risk jobs. The demand for high-risk jobs is multiplied with job-related safety factors, namely
, where
. The safety factor is used to keep the slot for the higher demand in the schedule reserved. Instead of only planning with the
for high-risk-articles, the production volume for risky jobs is extended in this first step to
, where
for high-risk jobs
j. The demands of non high-risk jobs are multiplied with
. These considerations are also finally included in
Figure 6.
The same procedure of reserving slots for required higher amounts in the schedules can also be applied to other non high-risk job demands, e.g., if products are sensitive about producing less than the required demand. So, for these jobs, this method for overproduction compared to
can be applied. The demands can be multiplied with another safety factor, namely
. This bears the possibility to include the knowledge of experienced production planners, e.g., about sensitive demands. A production planner may decide which value to use for the safety factor. At this point, it is important to note that an earlier completion, which can be the cause of slots being reserved for too long in the schedule, is easy to handle with our algorithms presented in
Section 2. Such a schedule causes, at most, only a slightly extended storage cost. In contrast, an unexpected longer slot for jobs would result in drastic delays in the schedule and elaborate rescheduling. With this method, changes in the demand and production quantities can be considered in optimization and simulation models for scheduling.
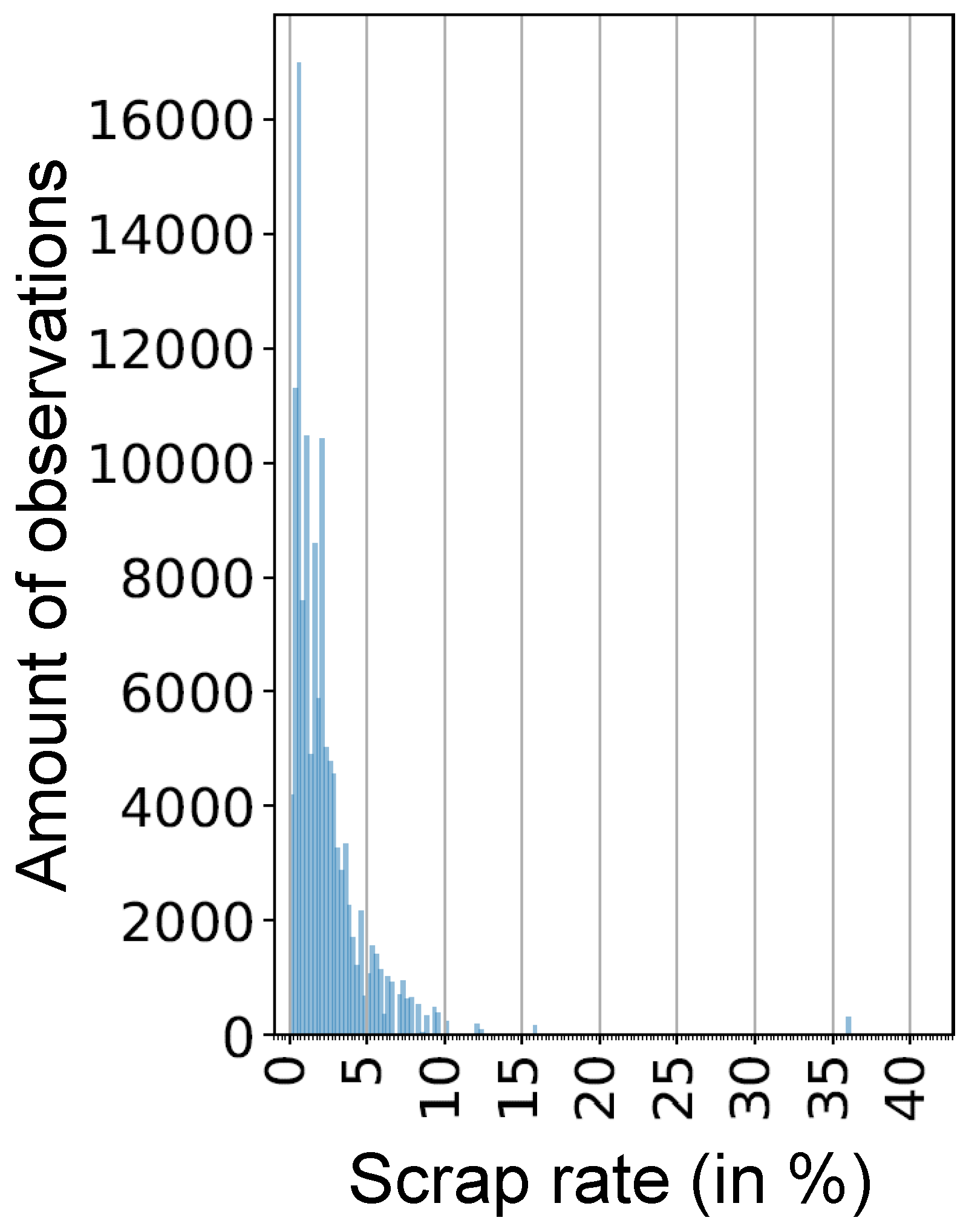
To choose the appropriate scrap rate per job and stage for our application case, different quantile values of the available empirical probability distribution per job and stage are considered.
Figure 6 shows a histogram for the scrap rate of an exemplary job. For every job, we use the same quantile value. Afterwards, per job, the scrap rates
are computed as a function of the quantile value and the probability distribution.
In practice, it is not realistic that the production volume
is completely produced without failure. So, for every job, we have to increase the production volume to finally get the demand that is to be produced. All analyzed factors influencing the demand in the production process in our application case result in the following formula to calculate the appropriate production quantity
:
8. Results
To select one of the schedules created by the seven algorithms, described in
Section 4, that should be applied in the application case and to select the most preferable algorithm for the application case over a defined time horizon, we derive all the algorithms with the historical demands and process data of the production. On the one hand, we evaluate the
values for the algorithms. On the other hand, we test different values for the quantile to reduce and evaluate the risk of producing less demands than the customer order (
Section 5 and
Section 6) and simulate the calculated schedules with our simulation model, described in
Section 7. For the evaluation of different security factor levels, e.g., for
, we refer to Schumacher et al. [
30].
The specific characteristics of the evaluation data for the application case are as follows:
Every week, around 60 jobs are processed in the two-stage system.
In the first stage, there are 11 unrelated parallel machines. In the second stage, there are two identical parallel machines.
In both stages, stochastic distributions for are available. The median at stage 1 is about 80 s per job and at stage 2 it is 4 s per job.
In stage 1, for setup times , the stochastic distribution is available for all machines and products. The median at stage 1 is about 100 min. The median at stage 2 is about 4 min and the given data are deterministic because the second stage is a conveyor belt production stage with a constant flow rate.
For the scrap rate , job-related stochastic distributions are available for both stages.
We have applied the optimization algorithms on a computer with an Intel® Core™ i7-6920 2.9 GHz and 32 GB RAM and we have run the simulation on a Intel® Xeon™ E5-2699 v4 2.2 GHz and 64 GB RAM and an Intel® Core™ i5-4670 3.4 GHz and 16 GB RAM.
The first step for scheduling is to run the seven optimization algorithms that include deterministic processing times and setup times. Therefore, we compare the makespan resulting from the algorithms for six selected calendar weeks in the past. We run the six metaheuristics with the parameter value
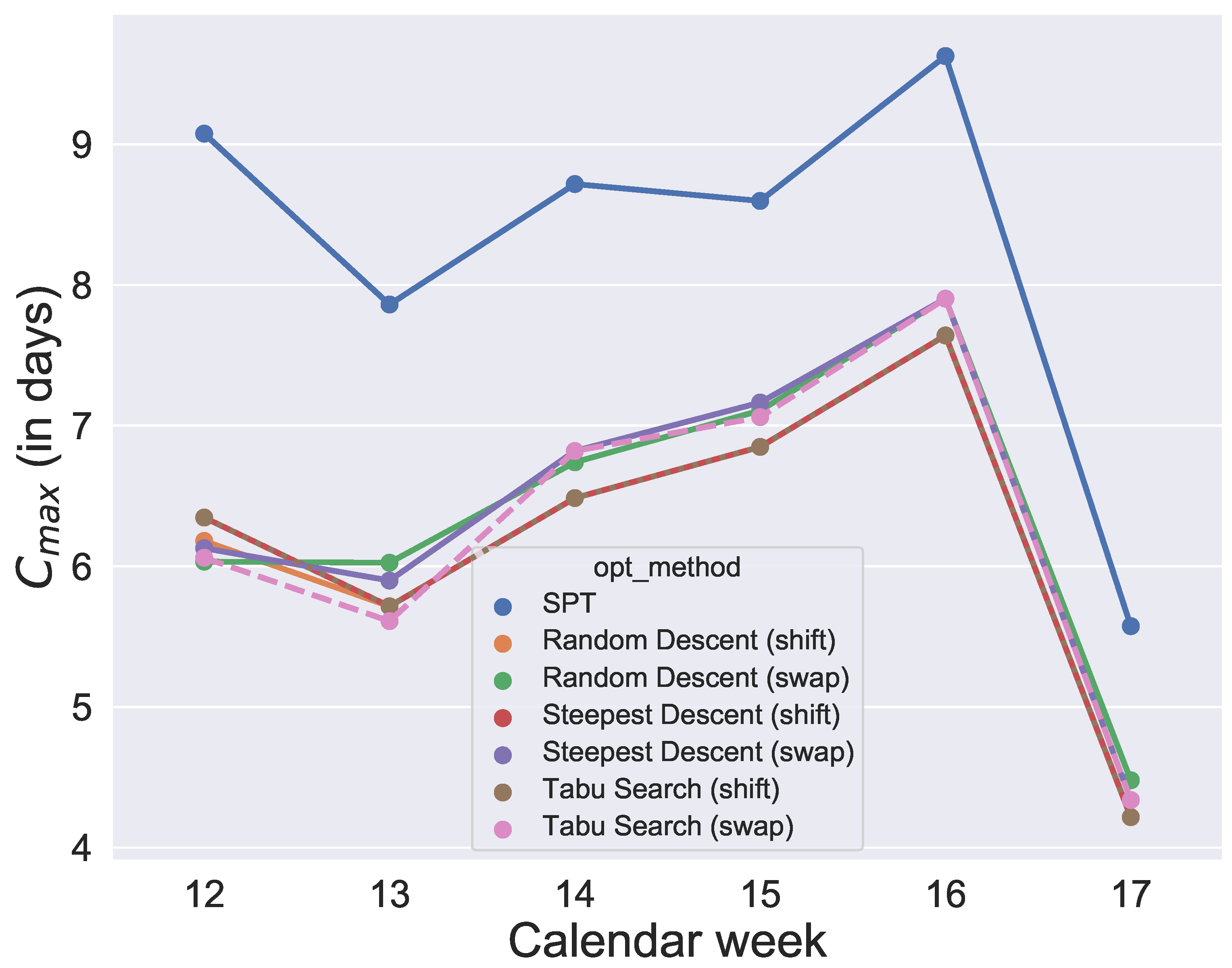
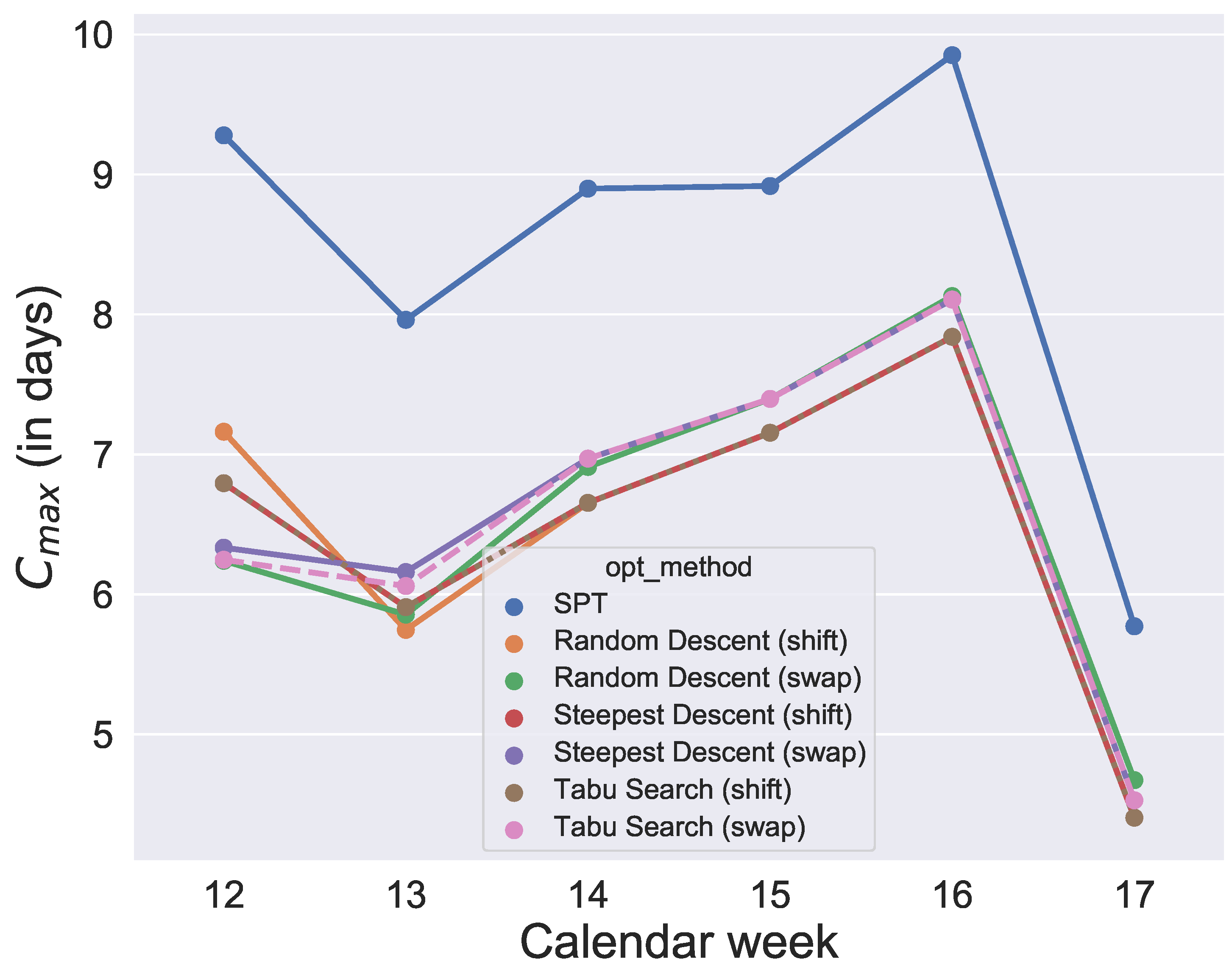
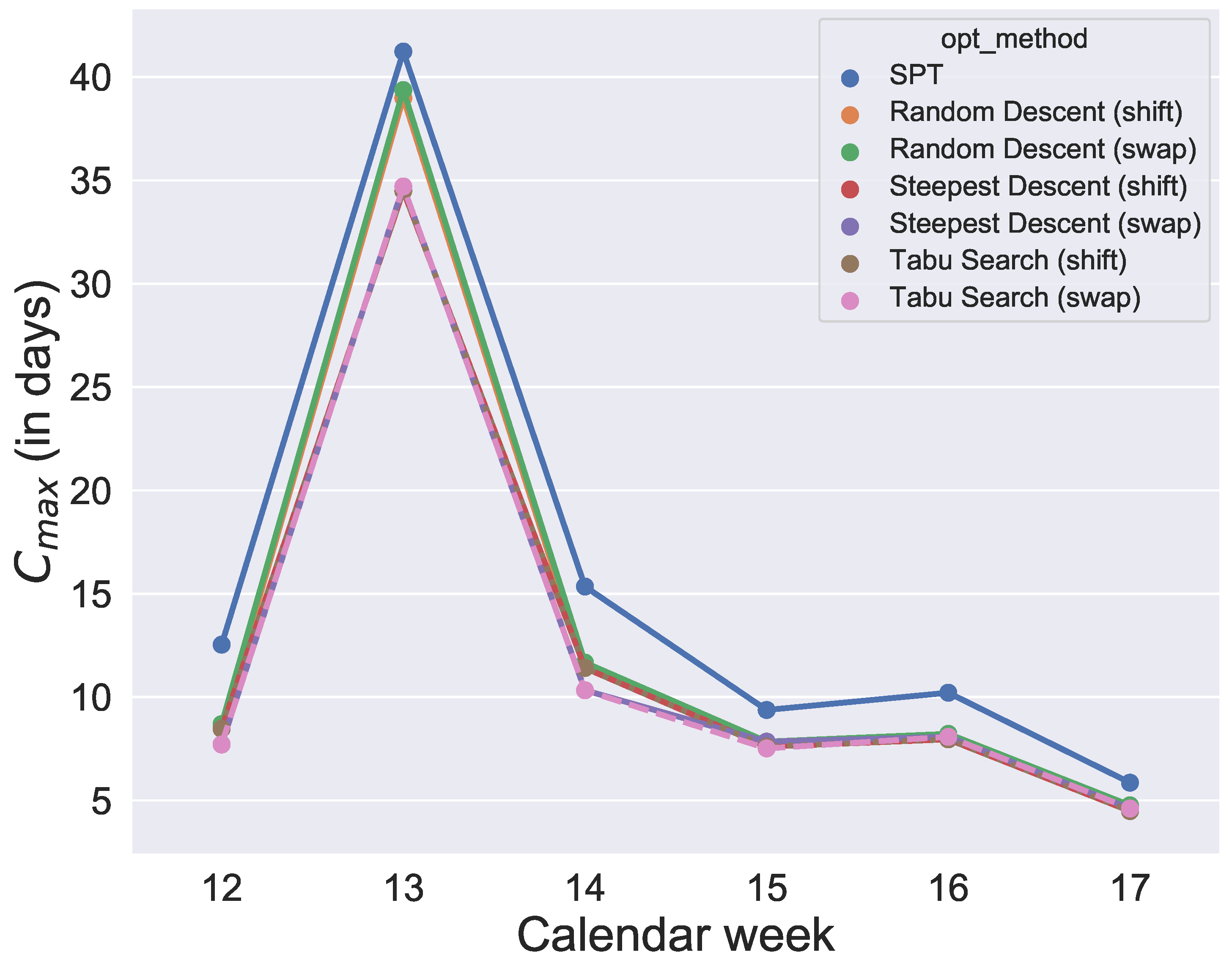
and their initial solution is given by SPT. After running the optimizations, for each week and each quantile value, each algorithm provides an objective value so that, for each algorithm, we get six data points per quantile. The analysis is illustrated in
Figure 8,
Figure 9,
Figure 10,
Figure 11,
Figure 12 and
Figure 13.
In Schumacher et al. [
30], we also analyzed the variation in objective function values caused by stochastic components in the metaheuristics for an exemplary week. Steepest Descent and tabu search algorithms provide the same objective value without variation over different runs. In contrast, the random descent algorithms provide more varying schedules. The majority of their values differ within about a quarter of a day, which means that the influence of the stochastic is relatively small in all of the developed metaheuristics of this paper.
The largest computation time over all algorithms and weeks in optimization was about 4 min 45 s for a tabu search (swap) run and the minimum was less than 1 s for the calculation of SPT.
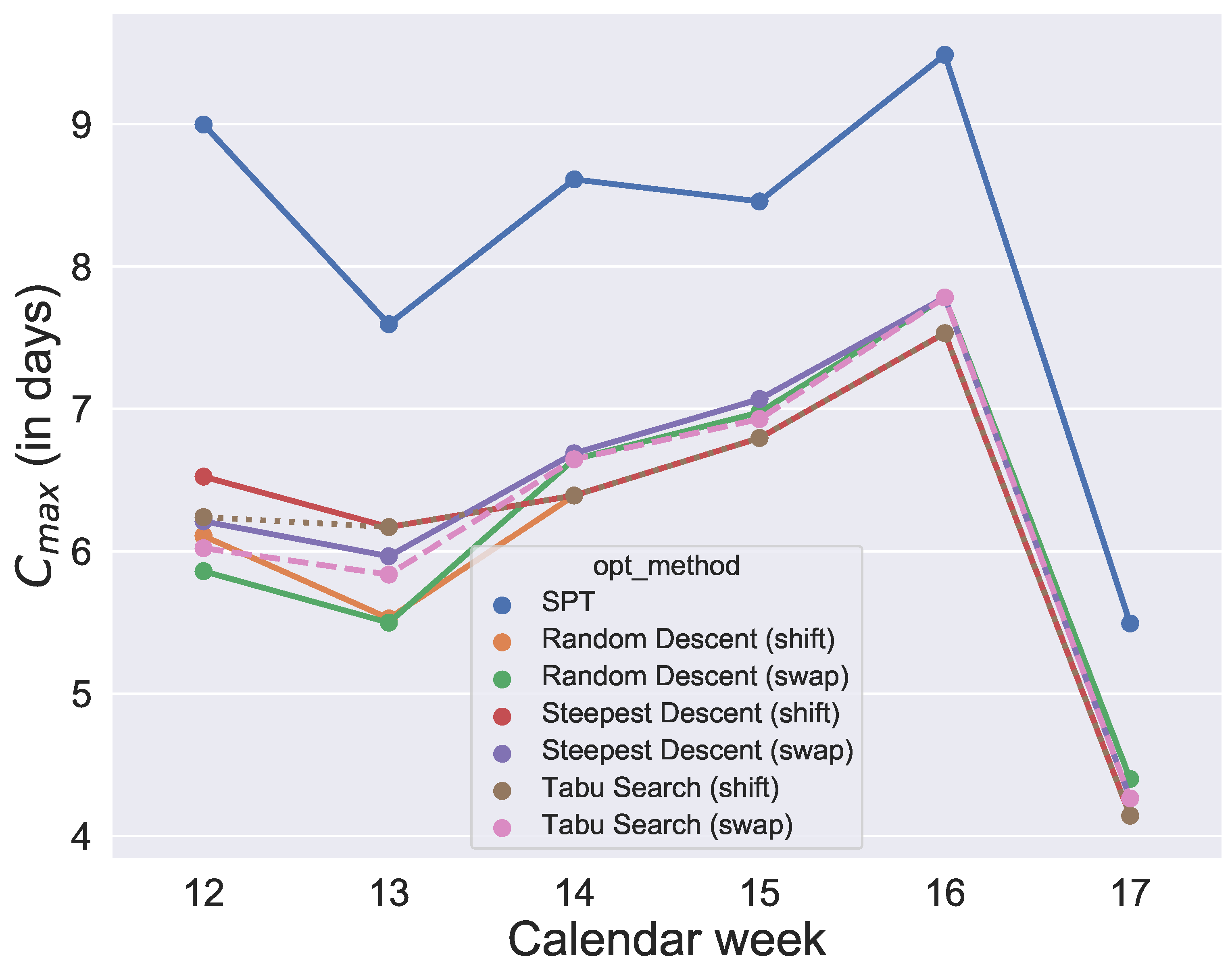
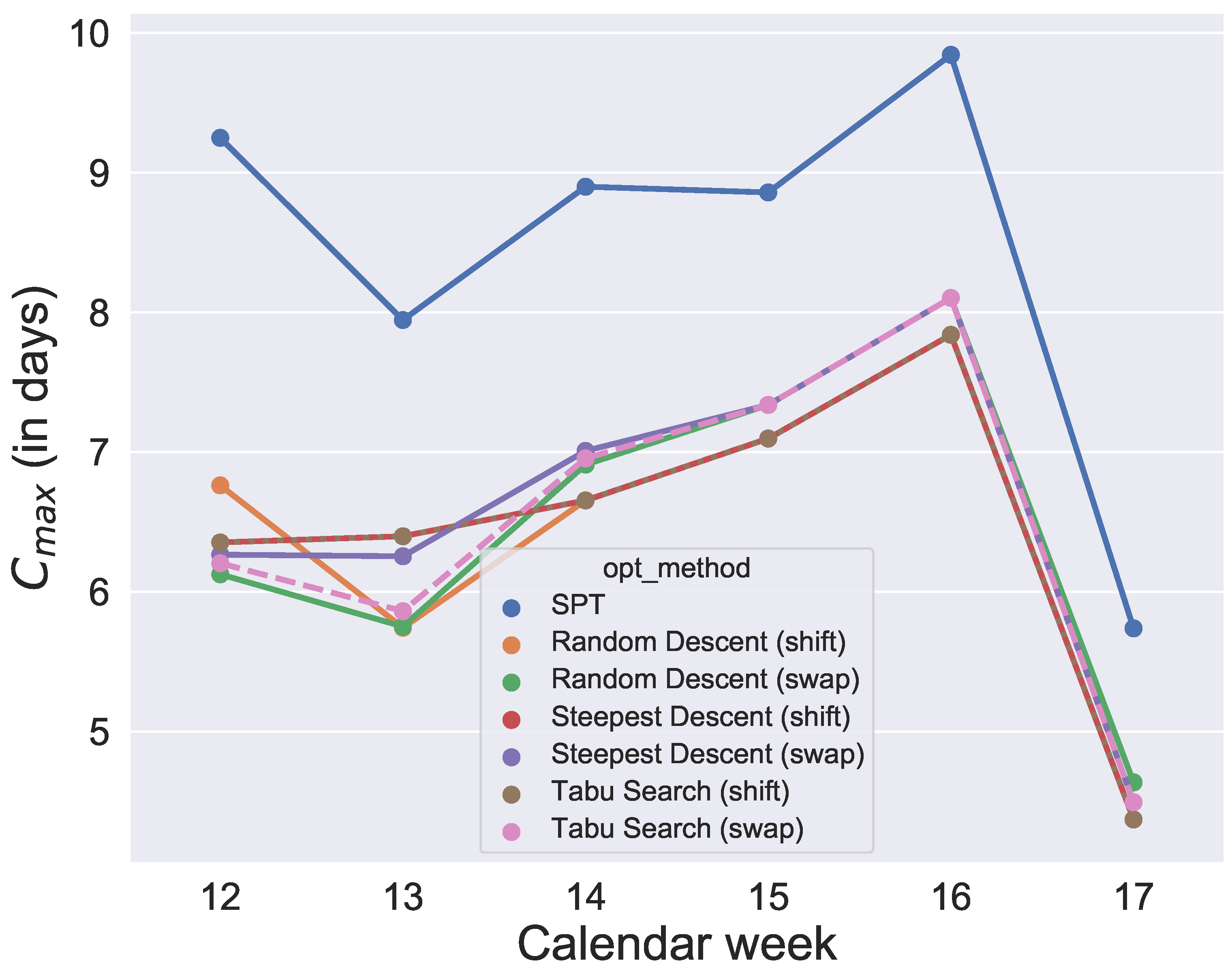
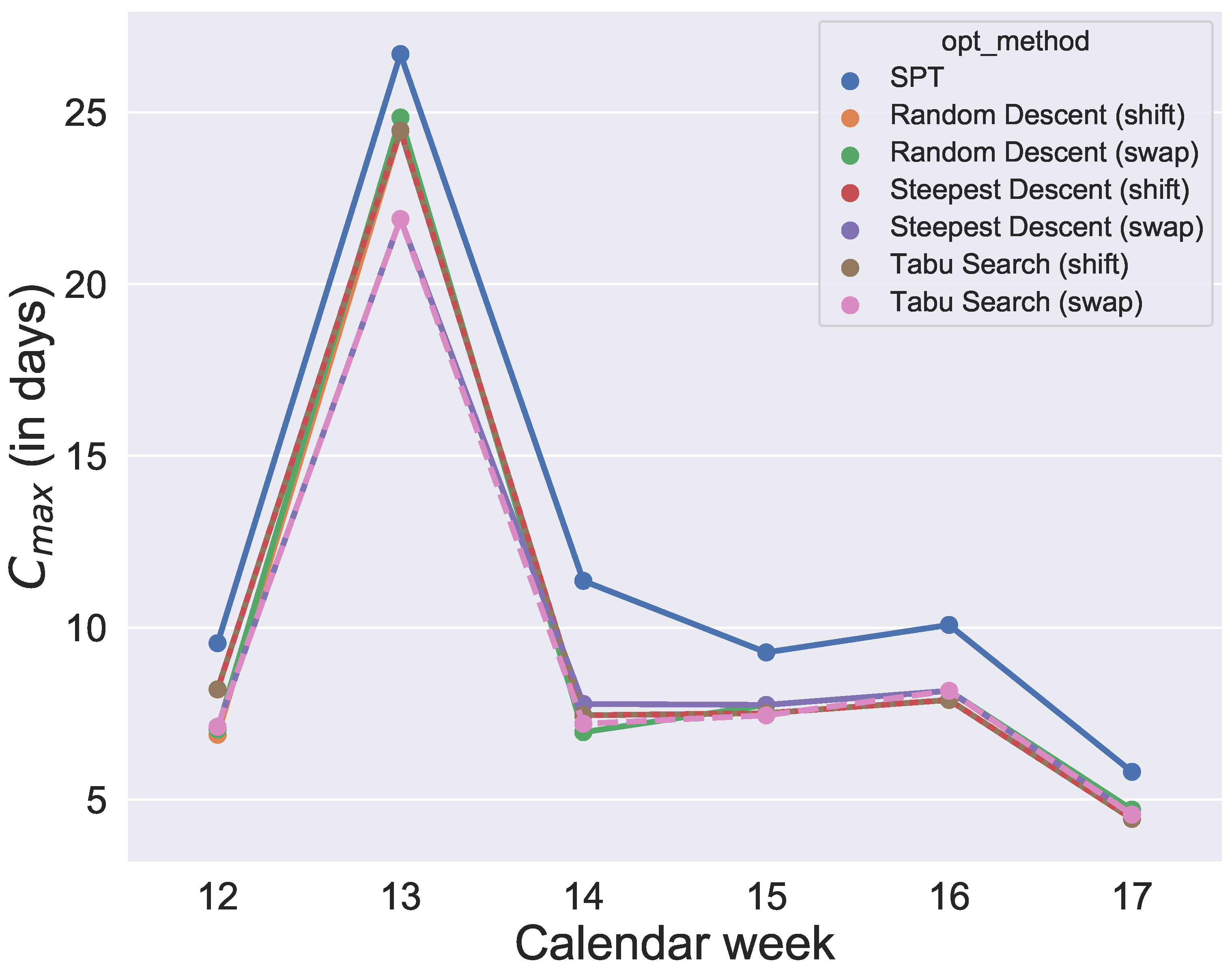
The results of
are visualized in
Figure 8,
Figure 9,
Figure 10,
Figure 11,
Figure 12 and
Figure 13. Since the initial solution for the local search and tabu search algorithms is given by SPT, it is not surprising that, over all selected values for the quantile, the six metaheuristics provide better results than SPT. However, the difference between the
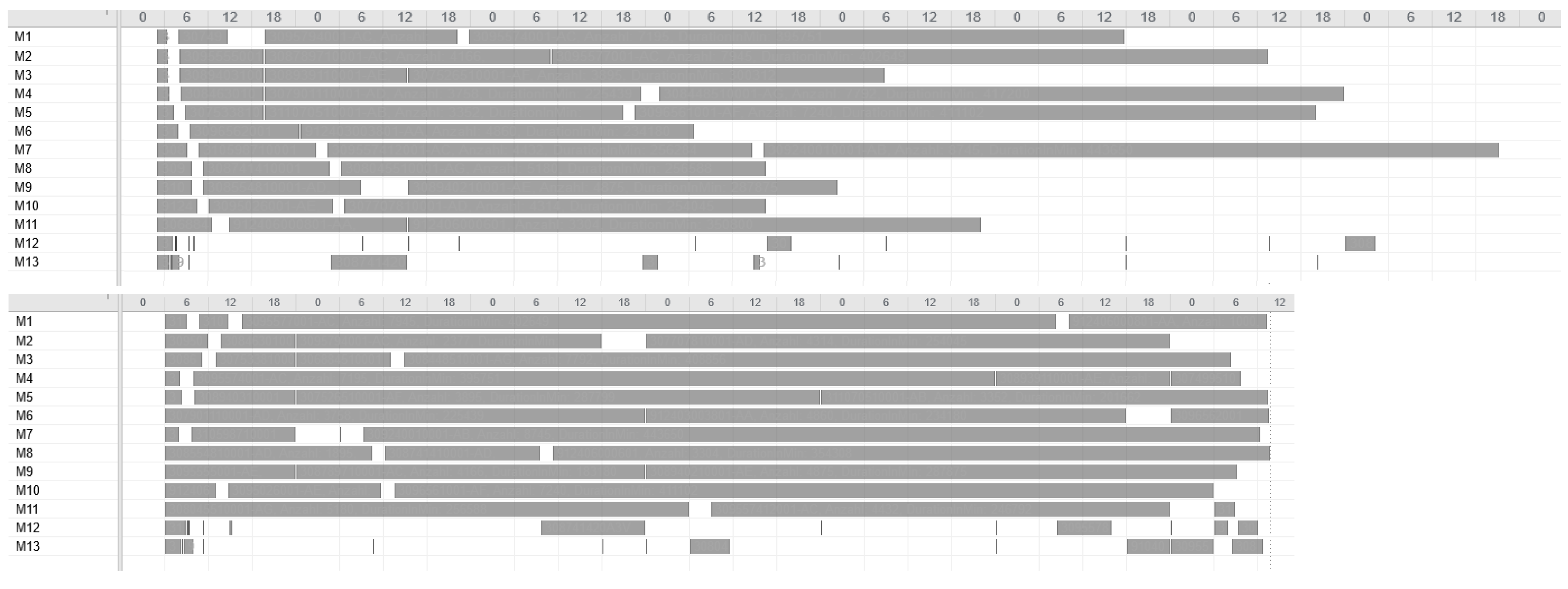
values and SPT is respectable. To show how the degree of usage for the machines increases in the production period by using metaheuristics rather than a static approach like SPT,
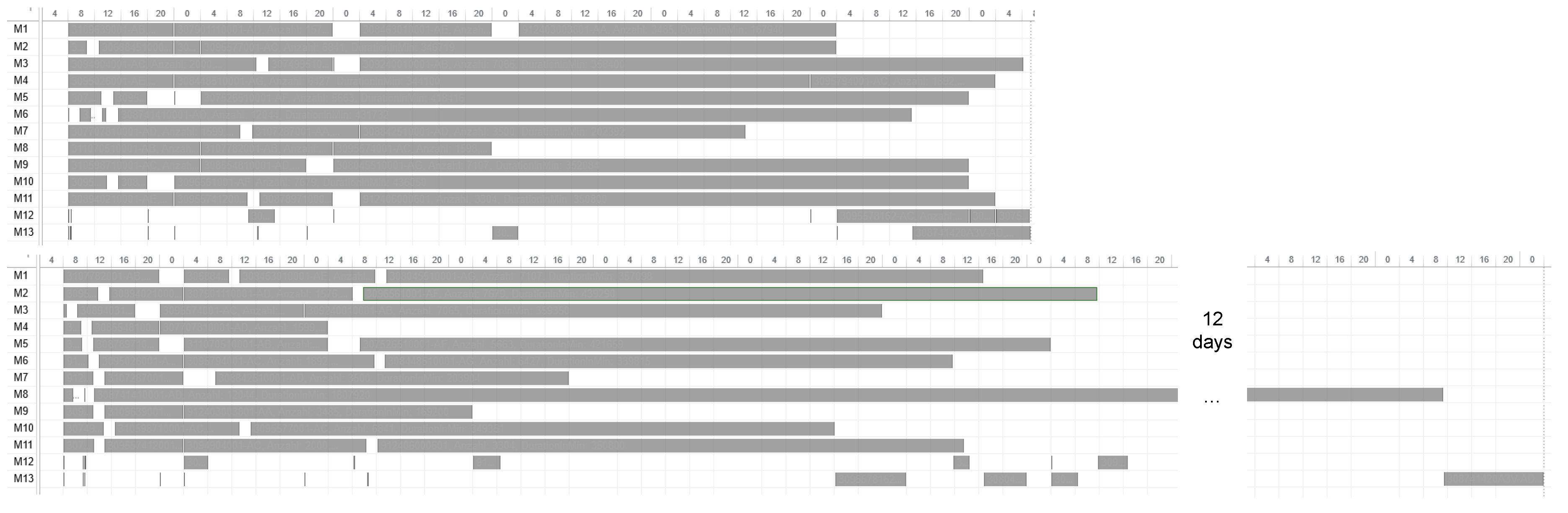
Figure 14 compares one schedule of SPT and one schedule of a metaheuristic, namely the random descent (swap) exemplar for week 12. In contrast, the difference in makespan when comparing only the six metaheuristics for each week is minor. Hence, with this evaluation, we cannot determine which of the metaheuristics will perform best in the application case and which schedule should be applied in practice. Instead, we need simulation to see which solution of the metaheuristics is the most convenient and robust.
Due to the high importance in our application case of fulfilling weekly demands as completely as possible, we also evaluate which quantile value for scrap performs best in optimization with regard to the makespan
. The results are also shown in
Figure 8,
Figure 9,
Figure 10,
Figure 11,
Figure 12 and
Figure 13. It was found that the quantiles 60%, 80%, 90% and 91% provide similar good results for makespan. In contrast, comparing the
values of the 60%, 80%, 90% and 91% group of quantiles, and the 92% and 93% group shows large differences. The differences between 91% and 92% are also illustrated in an exemplary comparison of schedules in
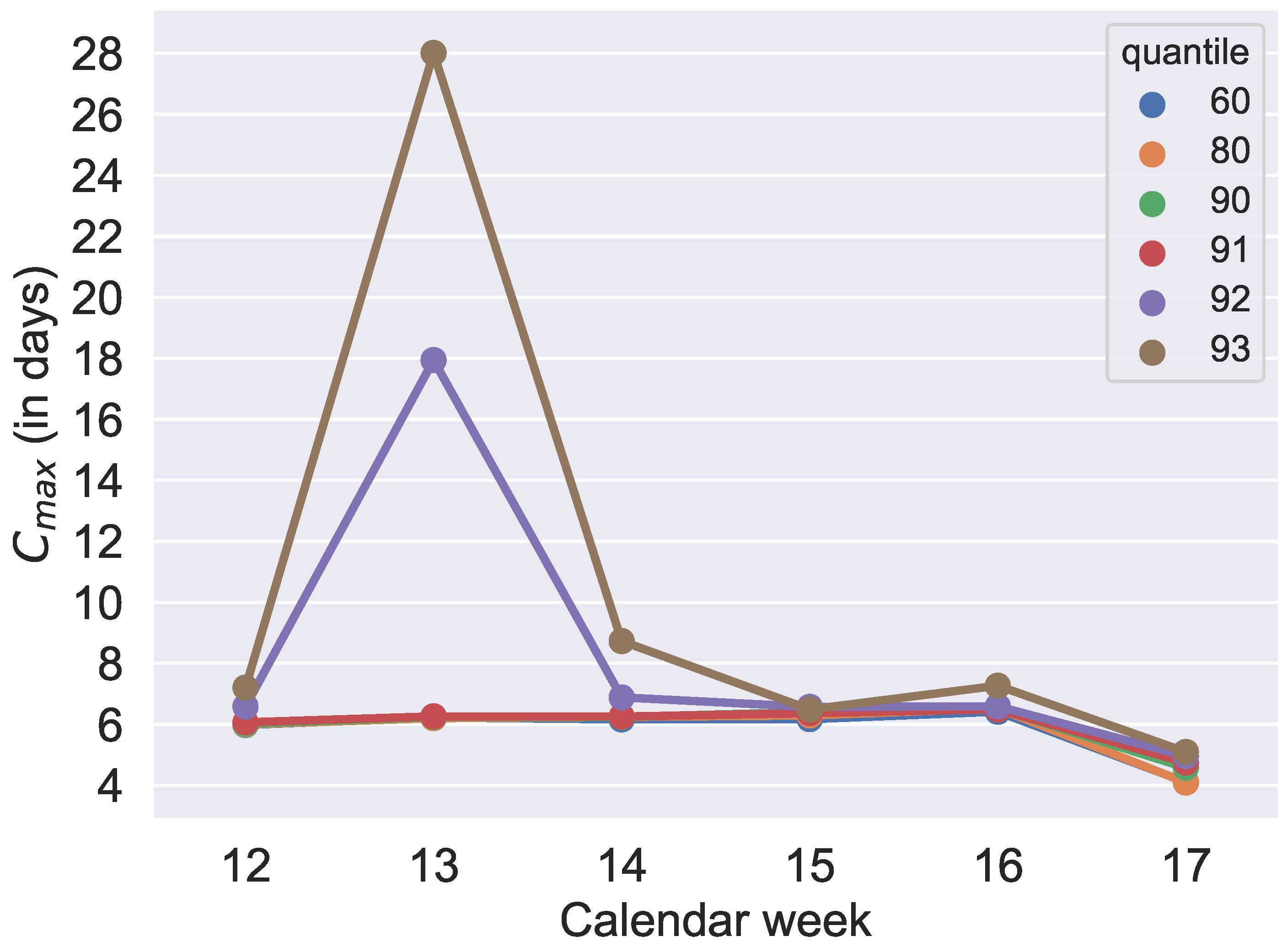
Figure 15. By increasing the value of the quantile by one percent in this exemplary week, the production volume
of one specific product increases from around 13 thousand parts to about 60 thousand parts and causes the extreme extension of the makespan shown in
Figure 15. Considering the results of
Figure 8,
Figure 9,
Figure 10,
Figure 11,
Figure 12 and
Figure 13, a production with a quantile higher than 91% seems uneconomical in this application case. To guarantee a sufficiently high degree of fulfilled orders and avoid extreme overproduction, we recommend the 91% quantile for the selected period of the application case.
For comparing the fulfillment of orders and evaluating the makespan under near-realistic conditions for the different quantile values, we use simulation.
Figure 16,
Figure 17,
Figure 18 and
Figure 19 show the variation in four different key indicators of the simulation results per quantile. For each algorithm and each calendar week, we run the simulation 40 times so that, per data point, we take the average of up to 280 simulation runs. Accordingly, for every figure, 280 key indicators are extracted from the simulation per data point. Only for
Figure 17 are the SPT results excluded, mainly in order to highlight the possible achievable
values.
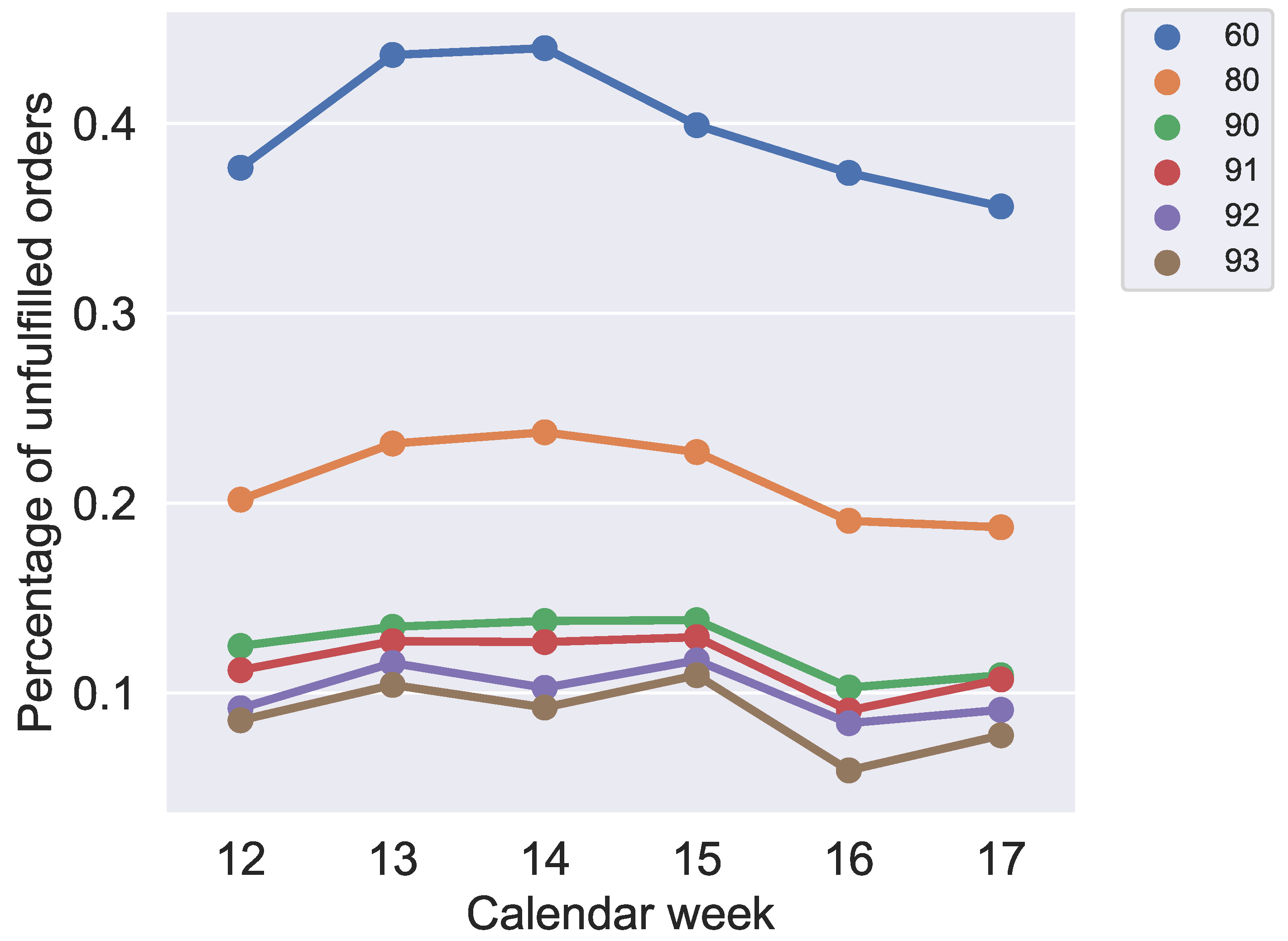
Figure 16 shows the ratio of orders that produce at least one less than the weekly demand. So, jobs are identified for that the weekly demand did not fulfil. This figure also validates our method to use scrap quantiles to avoid as many unfulfilled orders as possible. This demonstrates that the probability of unfulfilled orders decreases with increasing values for the different quantile values in the expected rates. The effects on the makespan show that the quantile value of 91% is preferable and can already be found in the optimization results of
Figure 8,
Figure 9,
Figure 10,
Figure 11,
Figure 12 and
Figure 13 and are also validated by simulation with
Figure 17.
Figure 16 and
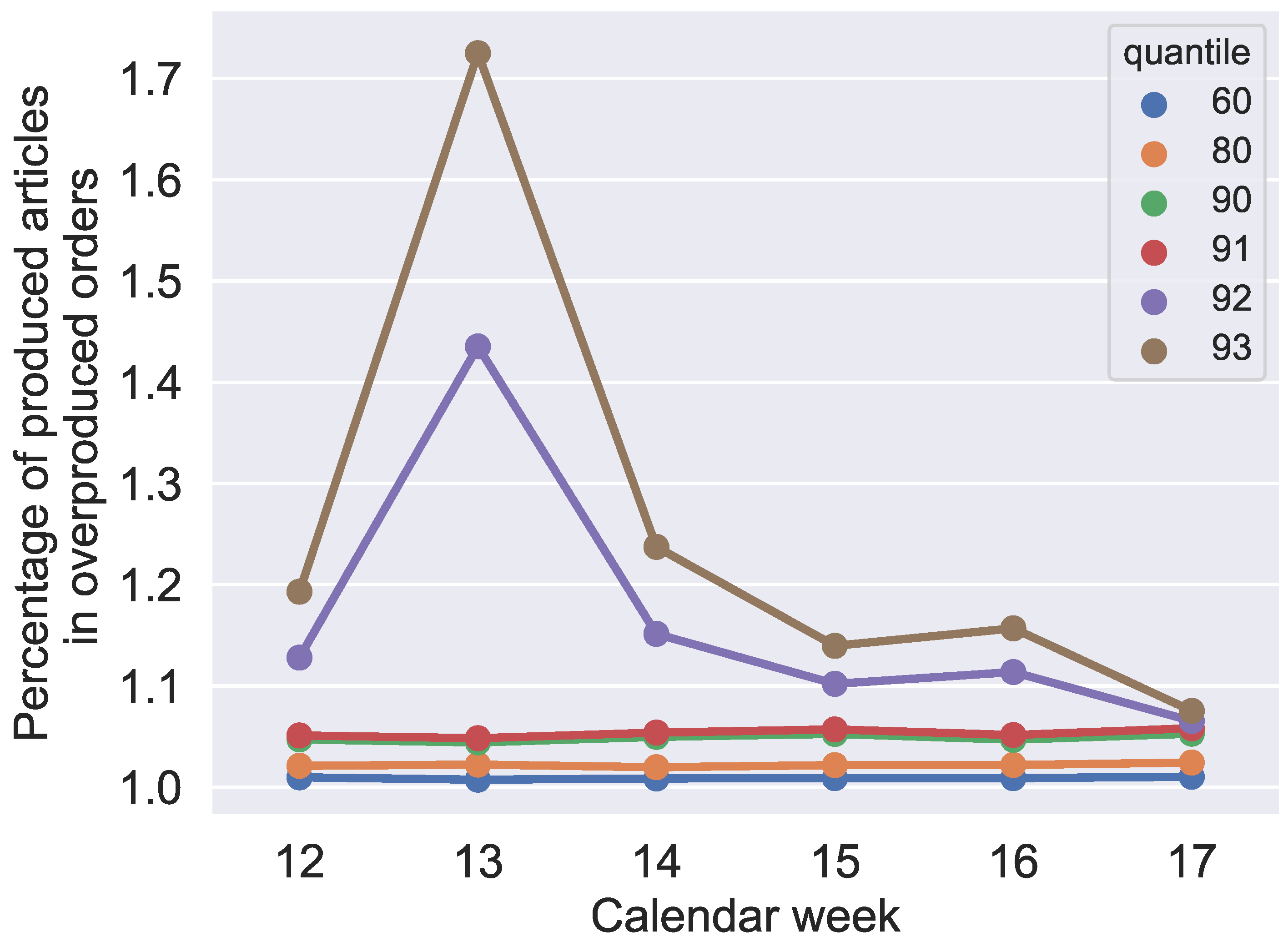
Figure 19, when analyzed together, show that it is not realistic to reduce the probability of unfulfilled orders below 10 % without an extreme overproduction of orders. Furthermore,
Figure 19 also confirms what could be expected from
Figure 8,
Figure 9,
Figure 10,
Figure 11,
Figure 12 and
Figure 13, and
Figure 17: the makespan increases, starting with the 92% quantile, because of significantly more overproduced parts in orders with overproduction.
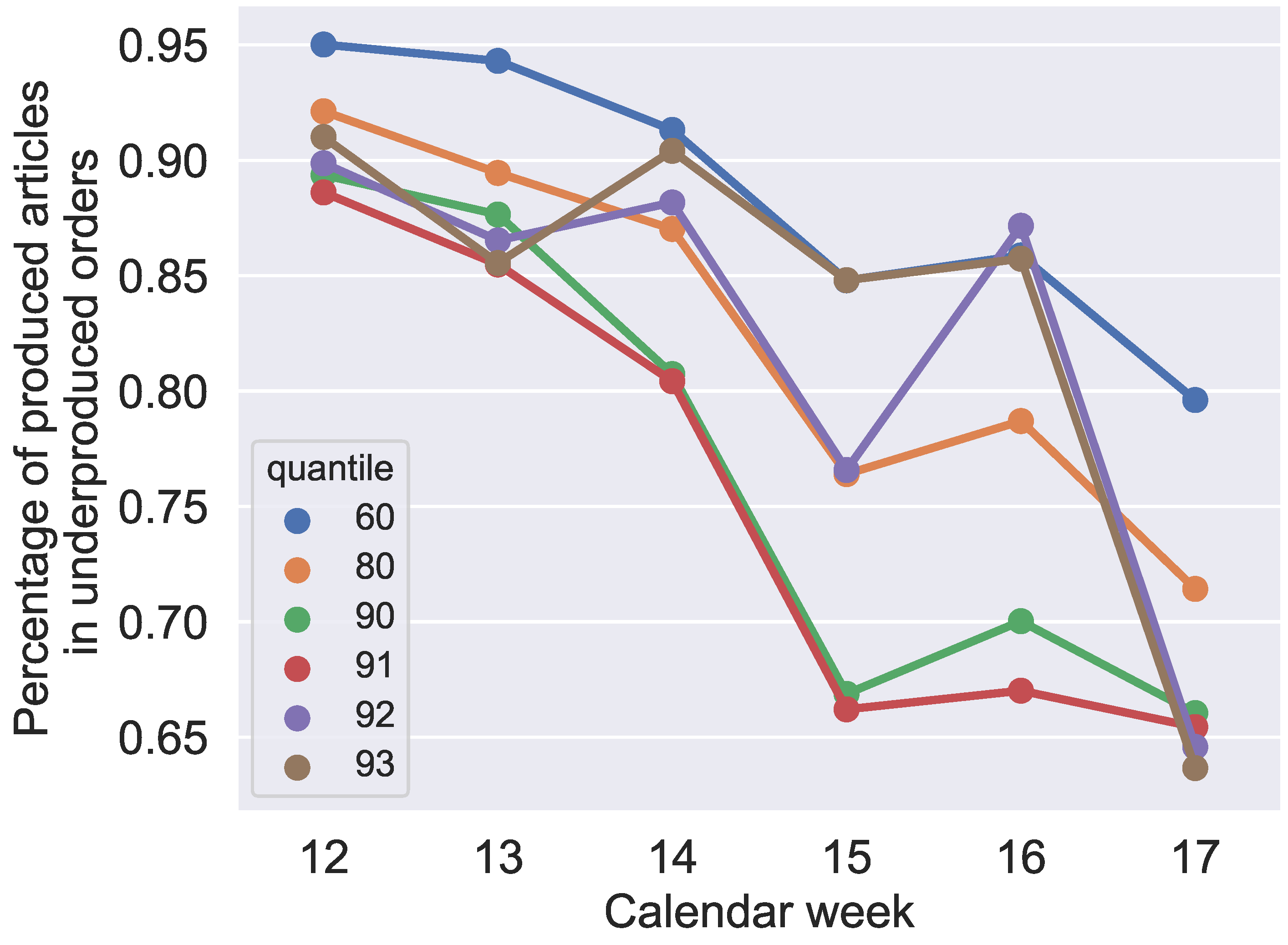
In contrast, the results in
Figure 18 do not indicate a clear correlation. For quantiles 60–91%, the rate of produced jobs decreases by increasing the quantile value, but quantiles 92% and 93% do not validate this assumption. Considering only this figure, quantiles 92% and 93% provide more preferable results. Although
Figure 18 indicates that another quantile value should be chosen instead of the 91% quantile, the analyses of
Figure 16,
Figure 17 and
Figure 19 confirm that the 91% quantile should be preferred for production planning in the application case. Because the most important indicators in our application case are the unfulfilled orders, in the following, we use the 91% quantile for our analysis.
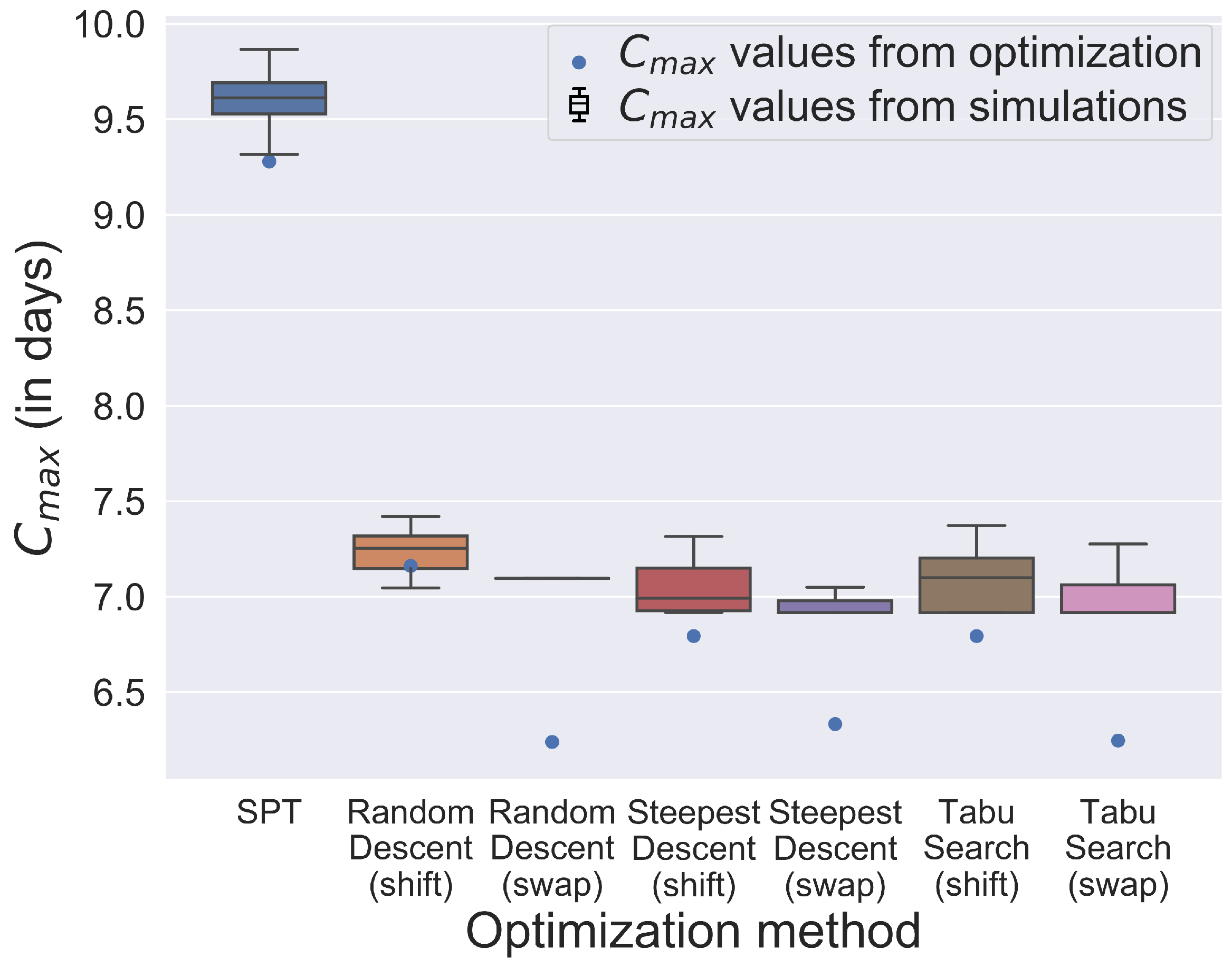
To summarize the results under almost real conditions and to indicate which method returns the schedules with the best makespan and which schedule is most robust against uncertainties, e.g., in processing times or setup times,
Figure 20 shows the makespans for week 12 of different schedules resulting from the seven algorithms analyzed by simulation. The box plots also indicate how the makespan varies in simulation runs of the same schedule. The borders of the boxes describe the first and third quartiles. Upper and lower limits show the minimum and maximum makespan of the simulation runs. Outliers are not included in
Figure 20. For each schedule, 40 parallel replications are performed, requiring about 9 min. A good schedule should result in a small value for makespan and a small box, indicating robustness. The most robust solution in this week is provided by random descent (swap), but the average makespan is higher than the one provided by Steepest Descent (swap). Since the schedule resulting from Steepest Descent (swap) shows only small differences between the results of the different simulation runs and has a small average makespan for the production program of week 12, it should be selected for this week.
9. Conclusions
In this paper, we solve a hybrid flow shop scheduling problem under uncertainties derived from a real industrial use case. It is shown that the combination of data analysis to estimate model parameters, heuristic and metaheuristic optimization and detailed stochastic simulation results in robust schedules that can be used in real systems. In addition, we have shown that, depending on the application, quantile analysis for scrap is an adequate method to reduce unfulfilled orders. Above a certain value of the quantile, their effect on preventing incompletely fulfilled demand positions is adversely affected by extreme overproduction and increased makespans. Thus, it is of high importance to analyze the quantiles and makespans depending on the application case.
Our approach can be developed further by using more efficient forecasting techniques to predict model parameters, by developing an upper bound for scrap rates, by additional heuristics and metaheuristics to generate schedules for the optimization model, and by combining the simulation model with additional techniques to optimize schedules. With the mentioned extensions, more efficient schedules are possible with regard to limiting overproduction, and achieving optimum production is possible. However, it is not expected that we will obtain significantly closer results to the simulation with modifications to the optimization methods because the simulation results are already very near to the results of the deterministic optimization.