Using Zigzag Persistent Homology to Detect Hopf Bifurcations in Dynamical Systems
Abstract
1. Introduction
2. Materials and Methods
2.1. Homology and Persistent Homology
2.2. Time-Delay Embedding
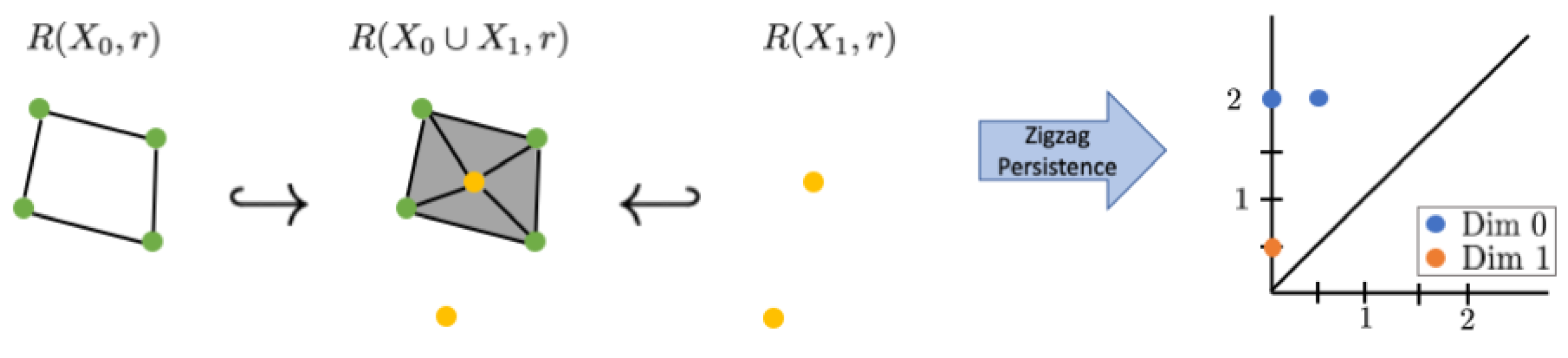
2.3. Zigzag Persistent Homology



2.4. Bifurcations Using Zigzag (Buzz)
2.5. Algorithms
3. Results
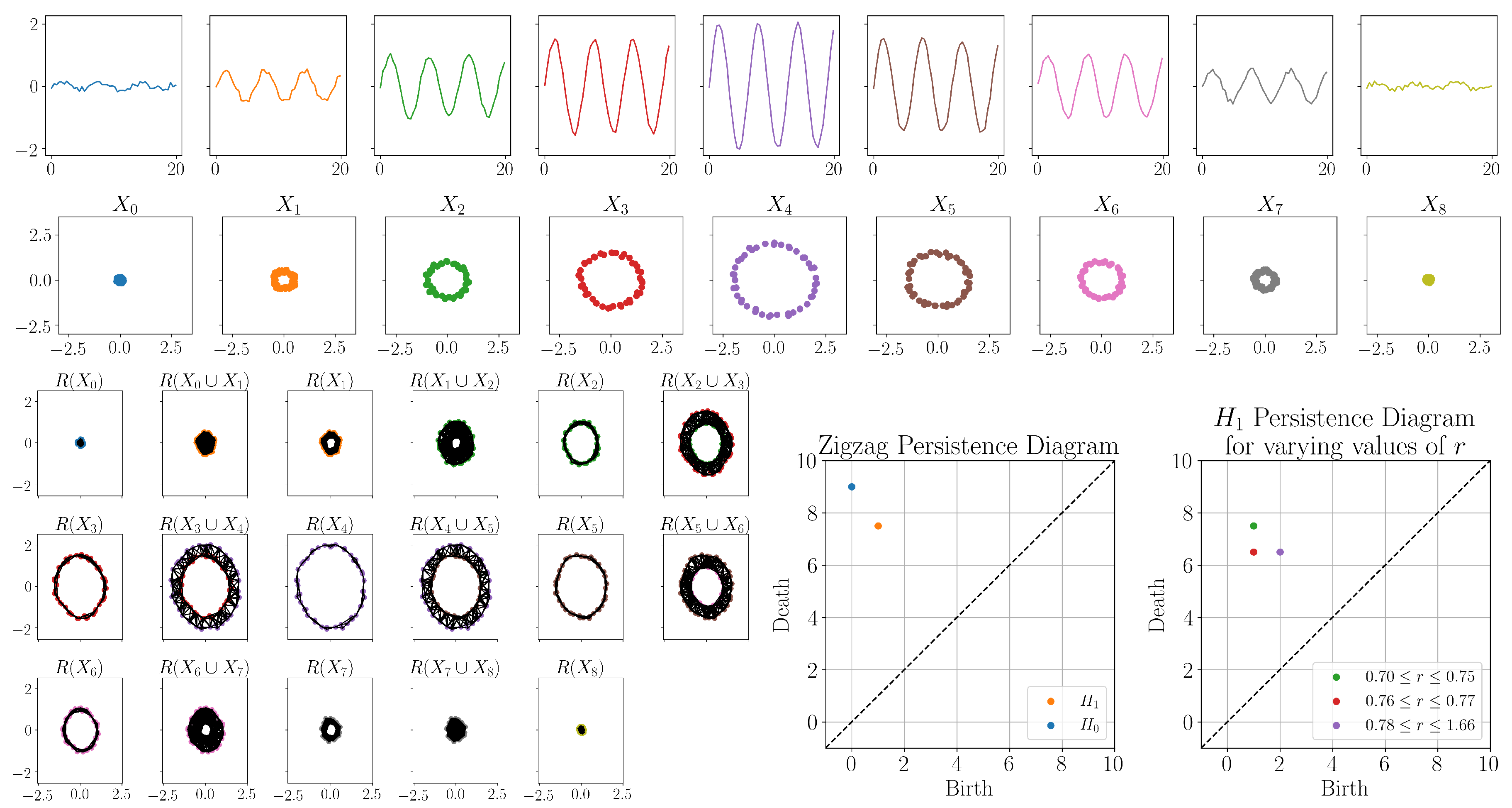
3.1. Synthetic Point Cloud Example
3.2. Synthetic Time-Series Example
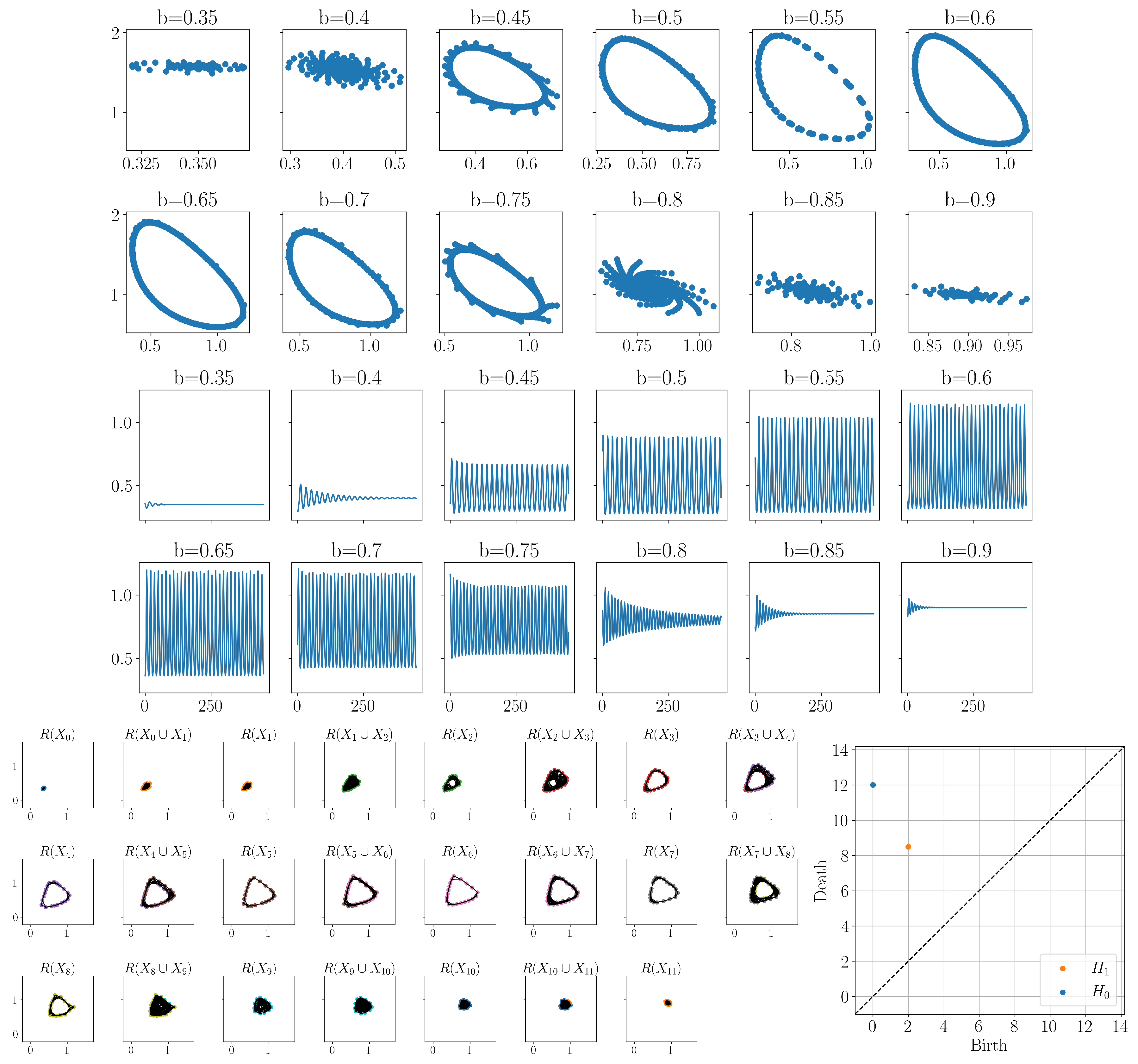
3.3. Sel’kov Model
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Perea, J.A.; Harer, J. Sliding Windows and Persistence: An Application of Topological Methods to Signal Analysis. Found. Comput. Math. 2015, 15, 799–838. [Google Scholar] [CrossRef]
- Sanderson, N.; Shugerman, E.; Molnar, S.; Meiss, J.D.; Bradley, E. Computational Topology Techniques for Characterizing Time-Series Data. arXiv 2017, arXiv:1708.09359. [Google Scholar]
- Tempelman, J.R.; Khasawneh, F.A. A Look into Chaos Detection through Topological Data Analysis. arXiv 2019, arXiv:1902.05918. [Google Scholar] [CrossRef]
- Maletić, S.; Zhao, Y.; Rajković, M. Persistent topological features of dynamical systems. Chaos Interdiscip. J. Nonlinear Sci. 2016, 26, 053105. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Tralie, C.J.; Antia, A.; Lin, M.; Perea, J.A. Twisty Takens: A Geometric Characterization of Good Observations on Dense Trajectories. arXiv 2018, arXiv:1809.07131. [Google Scholar] [CrossRef]
- Myers, A.; Munch, E.; Khasawneh, F.A. Persistent homology of complex networks for dynamic state detection. Phys. Rev. E 2019, 100, 022314. [Google Scholar] [CrossRef]
- Khasawneh, F.A.; Munch, E. Chatter detection in turning using persistent homology. Mech. Syst. Signal Process. 2016, 70-71, 527–541. [Google Scholar] [CrossRef]
- Khasawneh, F.A.; Munch, E. Utilizing Topological Data Analysis for Studying Signals of Time-Delay Systems. In Advances in Delays and Dynamics; Springer International Publishing: Basel, Switzerland, 2017; pp. 93–106. [Google Scholar] [CrossRef]
- Khasawneh, F.A.; Munch, E. Topological data analysis for true step detection in periodic piecewise constant signals. Proc. R. Soc. A Math. Phys. Eng. Sci. 2018, 474, 20180027. [Google Scholar] [CrossRef]
- Yesilli, M.C.; Khasawneh, F.A.; Otto, A. Topological Feature Vectors for Chatter Detection in Turning Processes. arXiv 2019, arXiv:1905.08671v2. [Google Scholar]
- Yesilli, M.C.; Tymochko, S.; Khasawneh, F.A.; Munch, E. Chatter Diagnosis in Milling Using Supervised Learning and Topological Features Vector. In Proceedings of the 2019 18th IEEE International Conference On Machine Learning And Applications (ICMLA), Boca Raton, FL, USA, 16–19 December 2019. [Google Scholar] [CrossRef]
- Khasawneh, F.A.; Munch, E.; Perea, J.A. Chatter Classification in Turning Using Machine Learning and Topological Data Analysis. In Proceedings of the 14th IFAC Workshop on Time Delay Systems TDS 2018, Budapest, Hungary, 28–30 June 2018; Insperger, T., Ed.; Elsevier: Amsterdam, The Netherlands, 2018; Volume 51, pp. 195–200. [Google Scholar] [CrossRef]
- Khasawneh, F.A.; Munch, E. Stability Determination in Turning Using Persistent Homology and Time Series Analysis. In Volume 4B: Dynamics, Vibration, and Control; American Society of Mechanical Engineers: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Berwald, J.; Gidea, M. Critical transitions in a model of a genetic regulatory system. Math. Biosci. Eng. 2014, 11, 723–740. [Google Scholar] [CrossRef]
- Gidea, M. Topological Data Analysis of Critical Transitions in Financial Networks. In Proceedings of the 3rd International Winter School and Conference on Network Science NetSci-X 2017, Tel-Aviv, Israel, 15–18 January 2017; Shmueli, E., Barzel, B., Puzis, R., Eds.; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Tralie, C.J.; Perea, J.A. (Quasi) Periodicity quantification in video data, using topology. SIAM J. Imaging Sci. 2018, 11, 1049–1077. [Google Scholar] [CrossRef]
- Tralie, C. High-dimensional geometry of sliding window embeddings of periodic videos. In Proceedings of the 32nd International Symposium on Computational Geometry (SoCG 2016), Boston, MA, USA, 14–18 June 2016; Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik: Wadern, Germany, 2016. [Google Scholar]
- Chung, Y.M.; Hu, C.S.; Lo, Y.L.; Wu, H.T. A persistent homology approach to heart rate variability analysis with an application to sleep-wake classification. arXiv 2019, arXiv:1908.06856. [Google Scholar]
- Tymochko, S.; Singhal, K.; Heo, G. Classifying sleep states using persistent homology and Markov chain: A Pilot Study. arXiv 2020, arXiv:2002.07810. [Google Scholar]
- Bubenik, P. Statistical Topological Data Analysis using Persistence Landscapes. J. Mach. Learn. Res. 2015, 16, 77–102. [Google Scholar]
- Adams, H.; Emerson, T.; Kirby, M.; Neville, R.; Peterson, C.; Shipman, P.; Chepushtanova, S.; Hanson, E.; Motta, F.; Ziegelmeier, L. Persistence Images: A Stable Vector Representation of Persistent Homology. J. Mach. Learn. Res. 2017, 18, 218–252. [Google Scholar]
- Reininghaus, J.; Huber, S.; Bauer, U.; Kwitt, R. A stable multi-scale kernel for topological machine learning. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015. [Google Scholar] [CrossRef]
- Perea, J.A.; Munch, E.; Khasawneh, F.A. Approximating Continuous Functions on Persistence Diagrams Using Template Functions. arXiv 2019, arXiv:1902.07190. [Google Scholar]
- Adams, H.; Bush, J.; Carr, B.; Kassab, L.; Mirth, J. On the nonlinear statistics of optical flow. In Proceedings of the International Workshop on Computational Topology in Image Context, Málaga, Spain, 24–25 January 2019; Springer: Berlin, Germany, 2019; pp. 151–165. [Google Scholar]
- Adams, H.; Bush, J.; Carr, B.; Kassab, L.; Mirth, J. A torus model for optical flow. Pattern Recognit. Lett. 2020, 129, 304–310. [Google Scholar] [CrossRef]
- Mata, G.; Morales, M.; Romero, A.; Rubio, J. Zigzag persistent homology for processing neuronal images. Pattern Recognit. Lett. 2015, 62, 55–60. [Google Scholar] [CrossRef]
- Tausz, A.; Carlsson, G. Applications of zigzag persistence to topological data analysis. arXiv 2011, arXiv:1108.3545. [Google Scholar]
- Hatcher, A. Algebraic Topology; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Edelsbrunner, H.; Harer, J. Computational Topology: An Introduction; American Mathematical Society: Providence, RI, USA, 2010. [Google Scholar]
- Carlsson, G.; de Silva, V. Zigzag Persistence. Found. Comput. Math. 2010, 10, 367–405. [Google Scholar] [CrossRef]
- Kantz, H.; Schreiber, T. Nonlinear time Series Analysis; Cambridge University Press: Cambridge, UK, 2004; Volume 7. [Google Scholar]
- Takens, F. Detecting strange attractors in turbulence. In Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1981; pp. 366–381. [Google Scholar] [CrossRef]
- Whitney, H. Differentiable manifolds. Ann. Math. 1936, 37, 645–680. [Google Scholar] [CrossRef]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134–1140. [Google Scholar] [CrossRef] [PubMed]
- Kennel, M.B.; Brown, R.; Abarbanel, H.D.I. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 1992, 45, 3403–3411. [Google Scholar] [CrossRef]
- Pecora, L.M.; Moniz, L.; Nichols, J.; Carroll, T.L. A unified approach to attractor reconstruction. Chaos Interdiscip. J. Nonlinear Sci. 2007, 17, 013110. [Google Scholar] [CrossRef]
- Chelidze, D. Reliable Estimation of Minimum Embedding Dimension Through Statistical Analysis of Nearest Neighbors. J. Comput. Nonlinear Dyn. 2017, 12, 051024. [Google Scholar] [CrossRef]
- Pan, S.; Duraisamy, K. On the structure of time-delay embedding in linear models of non-linear dynamical systems. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 073135. [Google Scholar] [CrossRef]
- Kim, H.; Eykholt, R.; Salas, J. Nonlinear dynamics, delay times, and embedding windows. Phys. D Nonlinear Phenom. 1999, 127, 48–60. [Google Scholar] [CrossRef]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Springer: New York, NY, USA, 1983. [Google Scholar] [CrossRef]
- Berwald, J.; Gidea, M.; Vejdemo-Johansson, M. Automatic recognition and tagging of topologically different regimes in dynamical systems. arXiv 2013, arXiv:1312.2482. [Google Scholar] [CrossRef]
- Gidea, M.; Katz, Y. Topological data analysis of financial time series: Landscapes of crashes. Phys. A Stat. Mech. Its Appl. 2018, 491, 820–834. [Google Scholar] [CrossRef]
- Gidea, M.; Goldsmith, D.; Katz, Y.; Roldan, P.; Shmalo, Y. Topological recognition of critical transitions in time series of cryptocurrencies. Phys. A Stat. Mech. Its Appl. 2020, 548, 123843. [Google Scholar] [CrossRef]
- Vejdemo-Johansson, M.; Pokorny, F.T.; Skraba, P.; Kragic, D. Cohomological learning of periodic motion. Appl. Algebra Eng. Commun. Comput. 2015, 26, 5–26. [Google Scholar] [CrossRef]
- Carlsson, G.; De Silva, V.; Morozov, D. Zigzag persistent homology and real-valued functions. In Proceedings of the Twenty-Fifth Annual Symposium on Computational Geometry, Aarhus, Denmark, 8–10 June 2009; pp. 247–256. [Google Scholar]
- Sel’Kov, E. Self-oscillations in glycolysis. Eur. J. Biochem. 1968, 4, 79–86. [Google Scholar] [CrossRef]
- Cavanna, N.J.; Jahanseir, M.; Sheehy, D.R. A geometric perspective on sparse filtrations. arXiv 2015, arXiv:1506.03797. [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Chaos; Taylor & Francis Inc.: Abingdon, UK, 2014. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tymochko, S.; Munch, E.; Khasawneh, F.A. Using Zigzag Persistent Homology to Detect Hopf Bifurcations in Dynamical Systems. Algorithms 2020, 13, 278. https://doi.org/10.3390/a13110278
Tymochko S, Munch E, Khasawneh FA. Using Zigzag Persistent Homology to Detect Hopf Bifurcations in Dynamical Systems. Algorithms. 2020; 13(11):278. https://doi.org/10.3390/a13110278
Chicago/Turabian StyleTymochko, Sarah, Elizabeth Munch, and Firas A. Khasawneh. 2020. "Using Zigzag Persistent Homology to Detect Hopf Bifurcations in Dynamical Systems" Algorithms 13, no. 11: 278. https://doi.org/10.3390/a13110278
APA StyleTymochko, S., Munch, E., & Khasawneh, F. A. (2020). Using Zigzag Persistent Homology to Detect Hopf Bifurcations in Dynamical Systems. Algorithms, 13(11), 278. https://doi.org/10.3390/a13110278




