Efficient Data Structures for Range Shortest Unique Substring Queries †
Abstract
1. Introduction
1.1. Main Problem and Main Results
- Problem
- Preprocess: String .
- Query: Range , where .
- Output: such that is a shortest string with exactly one occurrence in .
1.2. Paper Organization
2. An -Word Data Structure
2.1. Proof of Lemma 1
- Let , where , then
- Let , where , then .
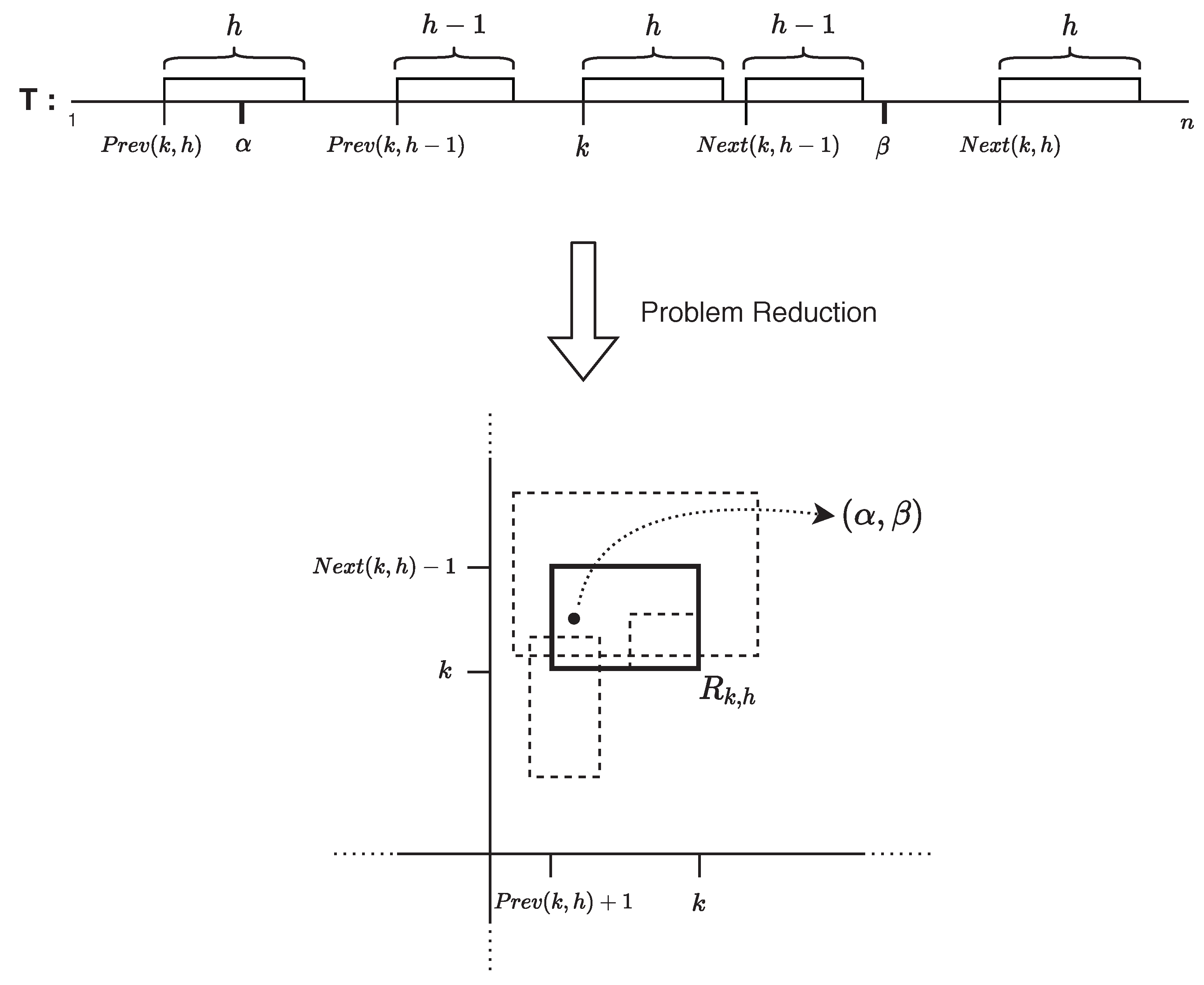
3. An -Word Data Structure
- .
- Computing the Smallest Element in : for each , we compute and report the smallest among them. We handle each query in time , as follows: first find the leaf corresponding to the string position k in the suffix tree of , then the last (resp., first) leaf on its left (resp., right) side, such that the string position x (resp., y) corresponding to it is in , and report . To efficiently enable the computation of x (resp., y), we preprocess the suffix array into an -word data structure that can answer orthogonal range predecessor (resp., successor) queries in time [40].
- Computing the Smallest Element in : for each , we compute the smallest element in and report the smallest among them. The procedure is the following: find the leaf corresponding to the string position r in the suffix tree of and the last (resp., first) leaf on its left (resp., right) side, such that its corresponding string position x (resp., y) is in (via orthogonal range successor/predecessor queries as earlier). Subsequently, is the length of the longest prefix of with an occurrence d in . However, we need to verify whether occurrence d is unique and its . For this, find the two leftmost occurrences of after r, denoted by and (), via two orthogonal range successor queries. If does not exist, set . Then report if . Otherwise, report .
- Computing the Smallest Element in : for each , we compute the smallest element in and report the smallest among them. The procedure is analogous to that of ; i.e., find the length t of the longest prefix of with an occurrence d in . Then, find the two rightmost occurrences of before r, denoted by and (), via two orthogonal range successor queries. If does not exist, set . Subsequently, report if . Otherwise, report .
- Computing the Smallest Element in : the set can be written as , which is now dependent only on and . Therefore, our idea is to pre-compute and explicitly store the minimum element in for all pairs, where both a and b are multiples of , and for that the desired answer can be retrieved in constant time. The additional space needed is .
4. Final Remarks
- Can we design an -word data structure for the problem with polylogarithmic query time?
- Can we design an efficient solution for the k mismatches/edits variation of the problem, perhaps using the framework of [41]?
Author Contributions
Funding
Conflicts of Interest
References
- Lothaire, M. Applied Combinatorics on Words; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Schleiermacher, C.; Ohlebusch, E.; Stoye, J.; Choudhuri, J.V.; Giegerich, R.; Kurtz, S. REPuter: The manifold applications of repeat analysis on a genomic scale. Nucleic Acids Res. 2001, 29, 4633–4642. [Google Scholar] [CrossRef]
- Haubold, B.; Pierstorff, N.; Möller, F.; Wiehe, T. Genome comparison without alignment using shortest unique substrings. BMC Bioinform. 2005, 6, 123. [Google Scholar] [CrossRef]
- Pei, J.; Wu, W.C.; Yeh, M. On shortest unique substring queries. In Proceedings of the 29th IEEE International Conference on Data Engineering (ICDE 2013), Brisbane, Australia, 8–12 April 2013; pp. 937–948. [Google Scholar] [CrossRef]
- Khmelev, D.V.; Teahan, W.J. A Repetition Based Measure for Verification of Text Collections and for Text Categorization. In Proceedings of the 26th Annual International ACM SIGIR Conference on Research and Development in Informaion Retrieval, Toronto, ON, Canada, 28 July–1 August 2003; pp. 104–110. [Google Scholar] [CrossRef]
- Gusfield, D. Algorithms on Strings, Trees, and Sequences: Computer Science and Computational Biology; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar] [CrossRef]
- Weiner, P. Linear Pattern Matching Algorithms. In Proceedings of the 14th Annual Symposium on Switching and Automata Theory (SWAT 1973), Iowa City, IA, USA, 15–17 October 1973; pp. 1–11. [Google Scholar] [CrossRef]
- Ileri, A.M.; Külekci, M.O.; Xu, B. Shortest Unique Substring Query Revisited. In Proceedings of the Combinatorial Pattern Matching—25th Annual Symposium (CPM 2014), Moscow, Russia, 16–18 June 2014; pp. 172–181. [Google Scholar] [CrossRef]
- Tsuruta, K.; Inenaga, S.; Bannai, H.; Takeda, M. Shortest Unique Substrings Queries in Optimal Time. In Proceedings of the 40th International Conference on Current Trends in Theory and Practice of Computer Science, Nový Smokovec, Slovakia, 26–29 January 2014; pp. 503–513. [Google Scholar] [CrossRef]
- Abedin, P.; Külekci, M.O.; V Thankachan, S. A Survey on Shortest Unique Substring Queries. Algorithms 2020, 13, 224. [Google Scholar] [CrossRef]
- Allen, D.R.; Thankachan, S.V.; Xu, B. A Practical and Efficient Algorithm for the k-mismatch Shortest Unique Substring Finding Problem. In Proceedings of the 2018 ACM International Conference on Bioinformatics, Computational Biology, and Health Informatics (BCB 2018), Washington, DC, USA, 29 August–1 September 2018; pp. 428–437. [Google Scholar] [CrossRef]
- Ganguly, A.; Hon, W.; Shah, R.; Thankachan, S.V. Space-Time Trade-Offs for the Shortest Unique Substring Problem. In Proceedings of the 27th International Symposium on Algorithms and Computation (ISAAC), Sydney, Australia, 12–14 December 2016; pp. 34:1–34:13. [Google Scholar] [CrossRef]
- Ganguly, A.; Hon, W.; Shah, R.; Thankachan, S.V. Space-time trade-offs for finding shortest unique substrings and maximal unique matches. Theor. Comput. Sci. 2017, 700, 75–88. [Google Scholar] [CrossRef]
- Inoue, H.; Nakashima, Y.; Mieno, T.; Inenaga, S.; Bannai, H.; Takeda, M. Algorithms and combinatorial properties on shortest unique palindromic substrings. J. Discret. Algorithms 2018, 52, 122–132. [Google Scholar] [CrossRef]
- Hon, W.; Thankachan, S.V.; Xu, B. In-place algorithms for exact and approximate shortest unique substring problems. Theor. Comput. Sci. 2017, 690, 12–25. [Google Scholar] [CrossRef]
- Mieno, T.; Inenaga, S.; Bannai, H.; Takeda, M. Shortest Unique Substring Queries on Run-Length Encoded Strings. In Proceedings of the 41st International Symposium on Mathematical Foundations of Computer Science MFCS, Kraków, Poland, 22–26 August 2016; pp. 69:1–69:11. [Google Scholar] [CrossRef]
- Schultz, D.W.; Xu, B. On k-Mismatch Shortest Unique Substring Queries Using GPU. In Proceedings of the 14th International Symposium, Bioinformatics Research and Applications, Beijing, China, 8–11 June 2018; pp. 193–204. [Google Scholar] [CrossRef]
- Mieno, T.; Köppl, D.; Nakashima, Y.; Inenaga, S.; Bannai, H.; Takeda, M. Compact Data Structures for Shortest Unique Substring Queries. In Proceedings of the 26th International Symposium, String Processing and Information Retrieval, Segovia, Spain, 7–9 October 2019; pp. 107–123. [Google Scholar] [CrossRef]
- Watanabe, K.; Nakashima, Y.; Inenaga, S.; Bannai, H.; Takeda, M. Shortest Unique Palindromic Substring Queries on Run-Length Encoded Strings. In Proceedings of the 30th International Workshop Combinatorial Algorithms, Pisa, Italy, 23–25 July 2019; pp. 430–441. [Google Scholar] [CrossRef]
- Yao, A.C. Space-time Tradeoff for Answering Range Queries (Extended Abstract). In Proceedings of the Fourteenth Annual ACM Symposium on Theory of Computing (STOC ’82), San Francisco, CA, USA, 5–7 May 1982; pp. 128–136. [Google Scholar] [CrossRef]
- Berkman, O.; Vishkin, U. Recursive Star-Tree Parallel Data Structure. SIAM J. Comput. 1993, 22, 221–242. [Google Scholar] [CrossRef]
- Bender, M.A.; Farach-Colton, M. The LCA Problem Revisited. In Proceedings of the 4th Latin American Symposium, LATIN 2000: Theoretical Informatics, Punta del Este, Uruguay, 10–14 April 2000; pp. 88–94. [Google Scholar] [CrossRef]
- Amir, A.; Apostolico, A.; Landau, G.M.; Levy, A.; Lewenstein, M.; Porat, E. Range LCP. J. Comput. Syst. Sci. 2014, 80, 1245–1253. [Google Scholar] [CrossRef]
- Amir, A.; Lewenstein, M.; Thankachan, S.V. Range LCP Queries Revisited. In Proceedings of the 22nd International Symposium, String Processing and Information Retrieval, London, UK, 1–4 September 2015; pp. 350–361. [Google Scholar] [CrossRef]
- Abedin, P.; Ganguly, A.; Hon, W.; Nekrich, Y.; Sadakane, K.; Shah, R.; Thankachan, S.V. A Linear-Space Data Structure for Range-LCP Queries in Poly-Logarithmic Time. In Proceedings of the 24th International Conference, Computing and Combinatorics, Qing Dao, China, 2–4 July 2018; pp. 615–625. [Google Scholar] [CrossRef]
- Ganguly, A.; Patil, M.; Shah, R.; Thankachan, S.V. A Linear Space Data Structure for Range LCP Queries. Fundam. Inform. 2018, 163, 245–251. [Google Scholar] [CrossRef]
- Pissis, S.P. MoTeX-II: Structured MoTif eXtraction from large-scale datasets. BMC Bioinform. 2014, 15, 235. [Google Scholar] [CrossRef] [PubMed]
- Almirantis, Y.; Charalampopoulos, P.; Gao, J.; Iliopoulos, C.S.; Mohamed, M.; Pissis, S.P.; Polychronopoulos, D. On avoided words, absent words, and their application to biological sequence analysis. Algorithms Mol. Biol. 2017, 12, 5:1–5:12. [Google Scholar] [CrossRef][Green Version]
- Ayad, L.A.K.; Pissis, S.P.; Polychronopoulos, D. CNEFinder: Finding conserved non-coding elements in genomes. Bioinformatics 2018, 34, i743–i747. [Google Scholar] [CrossRef]
- Iliopoulos, C.S.; Mohamed, M.; Pissis, S.P.; Vayani, F. Maximal Motif Discovery in a Sliding Window. In Proceedings of the 25th International Symposium, String Processing and Information Retrieval, Lima, Peru, 9–11 October 2018; pp. 191–205. [Google Scholar] [CrossRef]
- Almirantis, Y.; Charalampopoulos, P.; Gao, J.; Iliopoulos, C.S.; Mohamed, M.; Pissis, S.P.; Polychronopoulos, D. On overabundant words and their application to biological sequence analysis. Theor. Comput. Sci. 2019, 792, 85–95. [Google Scholar] [CrossRef]
- Matsuda, K.; Sadakane, K.; Starikovskaya, T.; Tateshita, M. Compressed Orthogonal Search on Suffix Arrays with Applications to Range LCP. In Proceedings of the 31st Annual Symposium on Combinatorial Pattern Matching, Copenhagen, Denmark, 17–19 June 2020; pp. 23:1–23:13. [Google Scholar] [CrossRef]
- Abedin, P.; Ganguly, A.; Pissis, S.P.; Thankachan, S.V. Range Shortest Unique Substring Queries. In Proceedings of the 26th International Symposium, String Processing and Information Retrieval, Segovia, Spain, 7–9 October 2019; pp. 258–266. [Google Scholar] [CrossRef]
- Sleator, D.D.; Tarjan, R.E. A Data Structure for Dynamic Trees. In Proceedings of the 13th Annual ACM Symposium on Theory of Computing, Milwaukee, WI, USA, 11–13 May 1981; pp. 114–122. [Google Scholar] [CrossRef]
- Chan, T.M.; Nekrich, Y.; Rahul, S.; Tsakalidis, K. Orthogonal Point Location and Rectangle Stabbing Queries in 3-d. In Proceedings of the 45th International Colloquium on Automata, Languages, and Programming, Prague, Czech Republic, 9–13 July 2018; pp. 31:1–31:14. [Google Scholar] [CrossRef]
- Harel, D.; Tarjan, R.E. Fast Algorithms for Finding Nearest Common Ancestors. SIAM J. Comput. 1984, 13, 338–355. [Google Scholar] [CrossRef]
- Manber, U.; Myers, E.W. Suffix Arrays: A New Method for On-Line String Searches. SIAM J. Comput. 1993, 22, 935–948. [Google Scholar] [CrossRef]
- Farach, M. Optimal Suffix Tree Construction with Large Alphabets. In Proceedings of the 38th Annual Symposium on Foundations of Computer Science (FOCS ’97), Miami Beach, FL, USA, 19–22 October 1997; pp. 137–143. [Google Scholar] [CrossRef]
- Kärkkäinen, J.; Sanders, P.; Burkhardt, S. Linear work suffix array construction. J. ACM 2006, 53, 918–936. [Google Scholar] [CrossRef]
- Nekrich, Y.; Navarro, G. Sorted Range Reporting. In Proceedings of the 13th Scandinavian Symposium and Workshops (SWAT 2012), Helsinki, Finland, 4–6 July 2012; pp. 271–282. [Google Scholar] [CrossRef]
- Thankachan, S.V.; Aluru, C.; Chockalingam, S.P.; Aluru, S. Algorithmic Framework for Approximate Matching Under Bounded Edits with Applications to Sequence Analysis. In Proceedings of the 22nd Annual International Conference, Research in Computational Molecular Biology (RECOMB 2018), Paris, France, 21–24 April 2018; pp. 211–224. [Google Scholar] [CrossRef]
- Barton, C.; Héliou, A.; Mouchard, L.; Pissis, S.P. Linear-time computation of minimal absent words using suffix array. BMC Bioinform. 2014, 15, 388. [Google Scholar] [CrossRef]
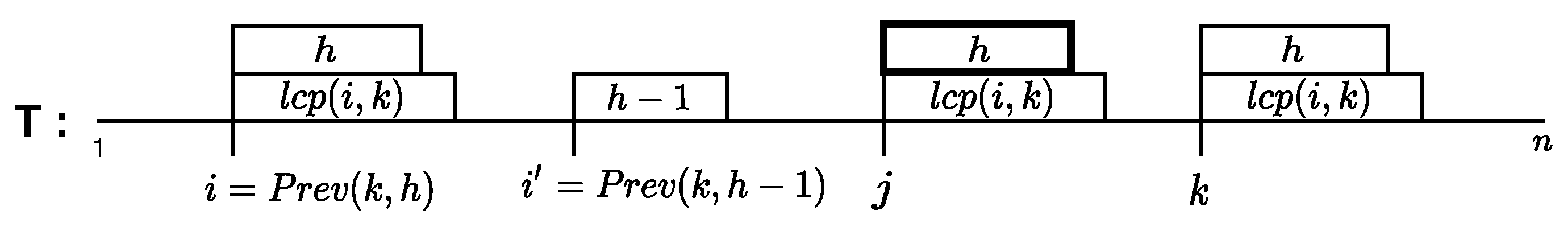
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abedin, P.; Ganguly, A.; Pissis, S.P.; Thankachan, S.V. Efficient Data Structures for Range Shortest Unique Substring Queries. Algorithms 2020, 13, 276. https://doi.org/10.3390/a13110276
Abedin P, Ganguly A, Pissis SP, Thankachan SV. Efficient Data Structures for Range Shortest Unique Substring Queries. Algorithms. 2020; 13(11):276. https://doi.org/10.3390/a13110276
Chicago/Turabian StyleAbedin, Paniz, Arnab Ganguly, Solon P. Pissis, and Sharma V. Thankachan. 2020. "Efficient Data Structures for Range Shortest Unique Substring Queries" Algorithms 13, no. 11: 276. https://doi.org/10.3390/a13110276
APA StyleAbedin, P., Ganguly, A., Pissis, S. P., & Thankachan, S. V. (2020). Efficient Data Structures for Range Shortest Unique Substring Queries. Algorithms, 13(11), 276. https://doi.org/10.3390/a13110276




