An EEG Feature Extraction Method Based on Sparse Dictionary Self-Organizing Map for Event-Related Potential Recognition
Abstract
1. Introduction
1.1. Common EEG Feature Extraction Methods for ERP Classification
1.2. The Proposed Method and Article Structure
2. Methods
2.1. Brief Introduction of EEG Sparse Modeling
2.2. Preprocessing of EEG Signal
- Framing: When the sparse decomposition algorithm processes continuous data, the data should be framed first. For the research needs of the state of cognitive tasks, the cognitive task is generally carried out to the moment when the state transition may occur, which is used as the framing point. The length of time should match the brain-computer interface paradigm.
- Energy normalization: High-energy artifact signals will overwhelm low-energy EEG signals during training, and the energy difference between frames will cause dictionary training distortion. In order to avoid the influence of these factors on the results, before sparse decomposition modeling, we normalize the energy of each frame. For a discrete data frame of length N, the energy is , the normalized frame data are . The energy can be compensated for in the coefficients after the training.
2.3. K-SVD Dictionary Learning Algorithm for EEG Feature Extraction
| Algorithm 1 K-SVD Dictionary-Learning Algorithm. |
| Input: Single-Channel EEG Singal Frames |
| Output: Sparse Dictionary |
|
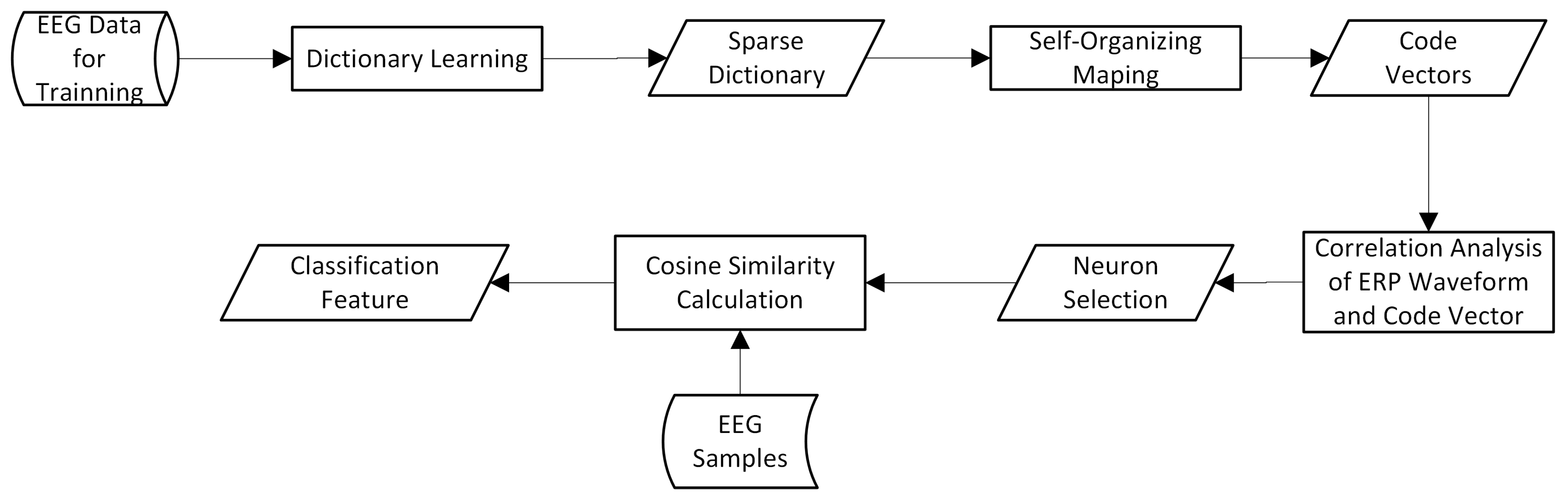
2.4. Feature Extraction Based on Sparse Dictionary Atoms
- Self-organizing mapping of dictionary atoms;
- Calculating the cosine similarity between the weight vector of each neuron and the target ERP waveform, and selecting the most relevant neurons;
- Calculating the cosine similarity between each sample and the selected neuron code vectors as a classification feature.
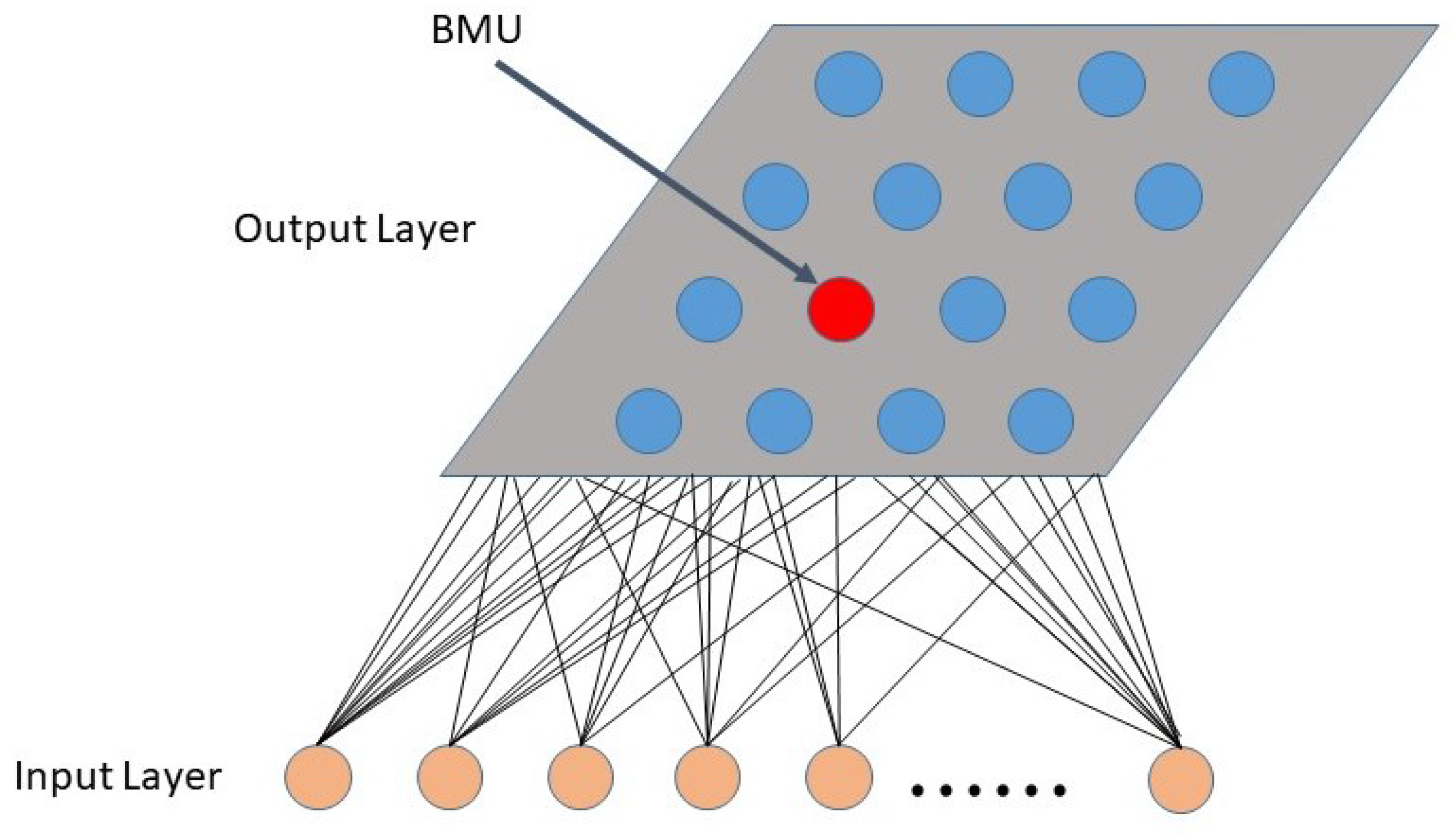
2.4.1. Dictionary Atom Self Organizing Mapping
- Set the weight of each neuron to a random initial value; set a larger initial neighborhood, and set the number of cycles of the network t, set the number of neurons in the network to M;
- Input a dictionary atom Dk into the network : , input into the network; n is the length of the dictionary atom;
- Calculate the weight of and all output neurons, which is the Euclidean distance between the code vector, and select the neuron c with the smallest distance from , that is, , then c is the Winning neuron;
- Update the connection weight of node c and its domain node Among them, is the learning rate, which gradually decreases with time;
- Select another dictionary atom to provide the input layer of the network, and return to step 3 until all the dictionary atoms are provided to the network;
- Let , return to step (2), until . In the learning of self-organizing mapping model, usually 10,000. is the neighbor function, which gradually decreases with the increase in the number of learning. is the learning rate of the network. Since the learning rate gradually tends towards zero with the increase in time, it is guaranteed that the learning process must be convergent.
2.4.2. Neuron Selection and Feature Extraction
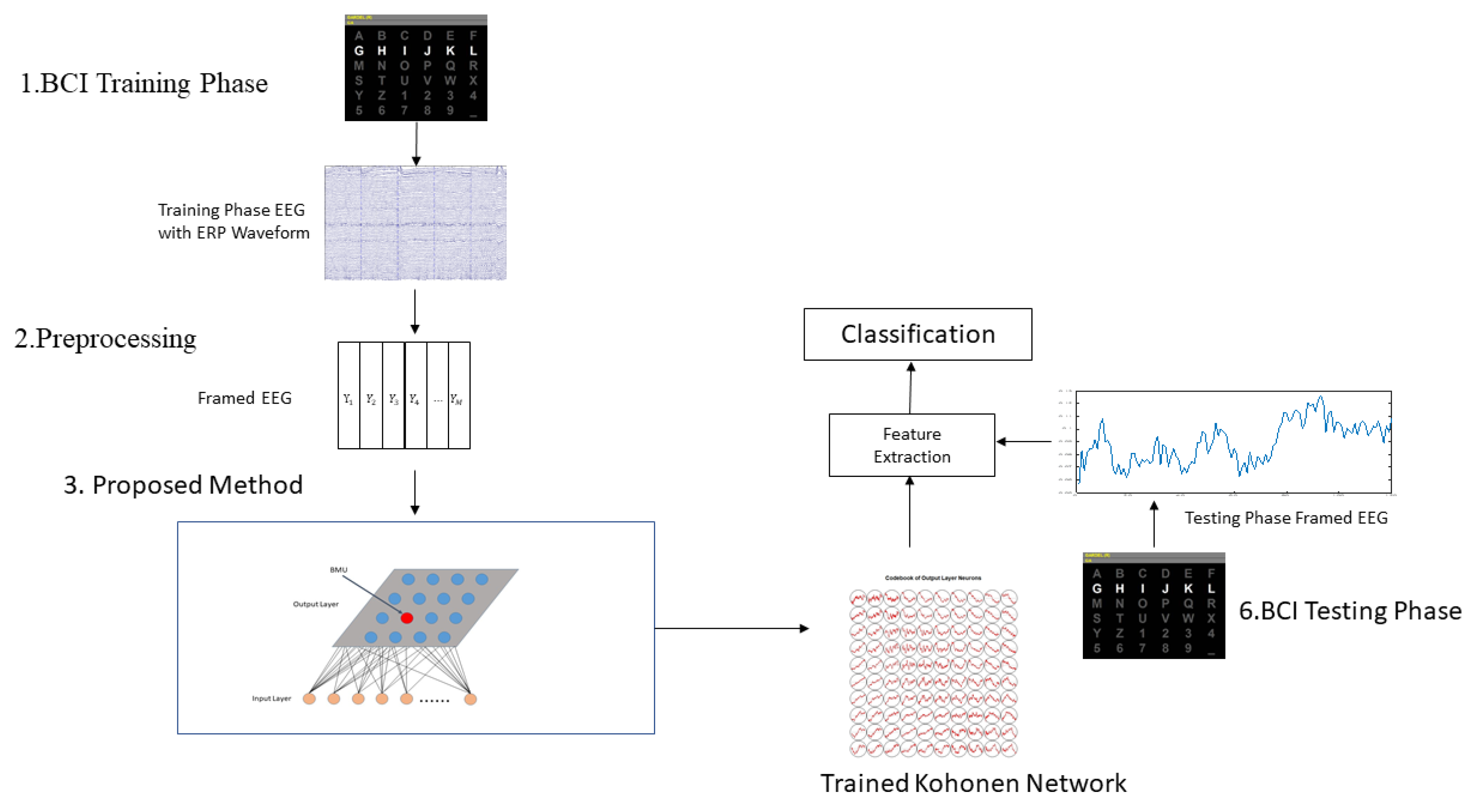
2.5. Application Procedures of Proposed Method in BCI
3. Results
3.1. Dataset Description
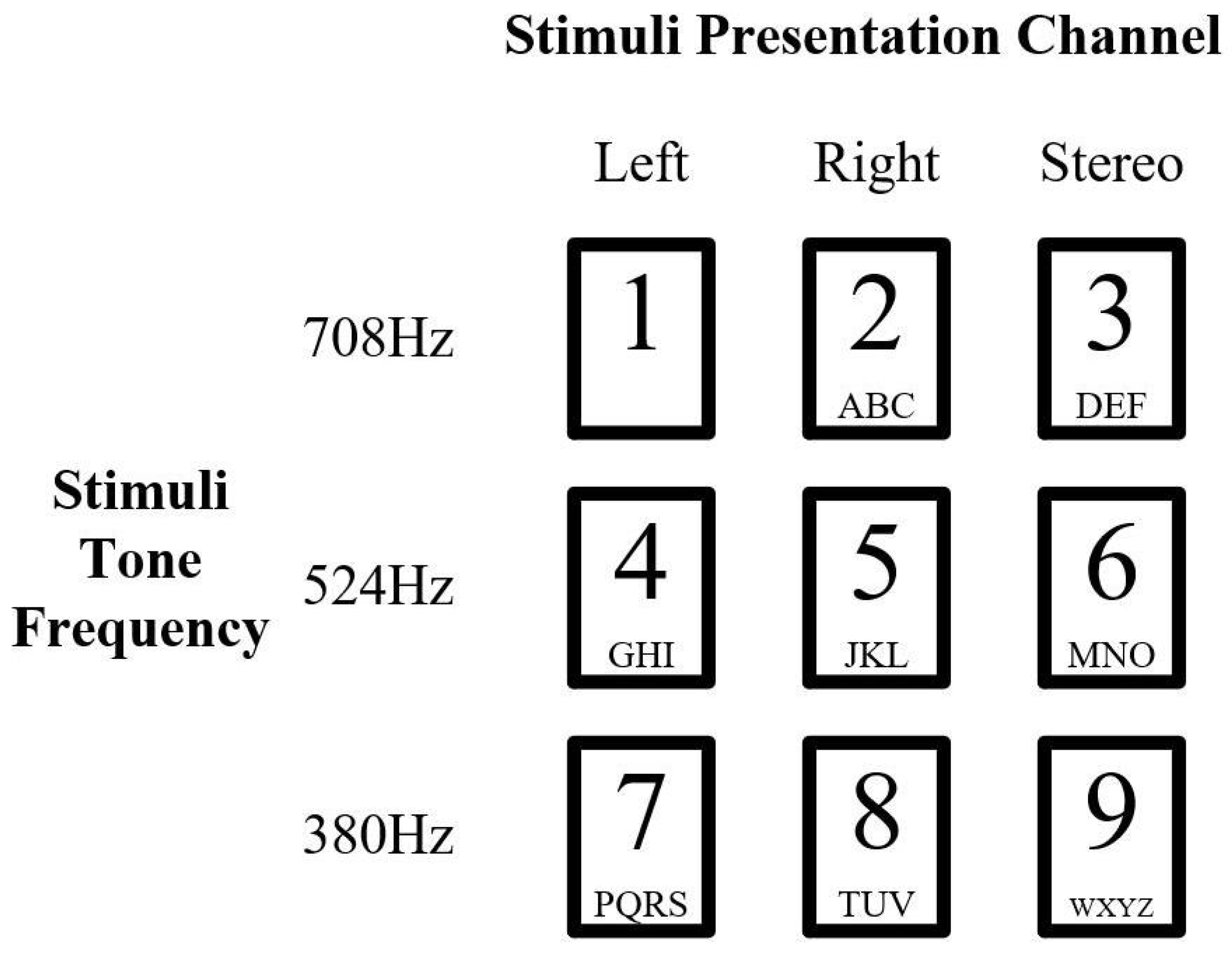
3.1.1. Auditory Stimuli in Experiment Dataset
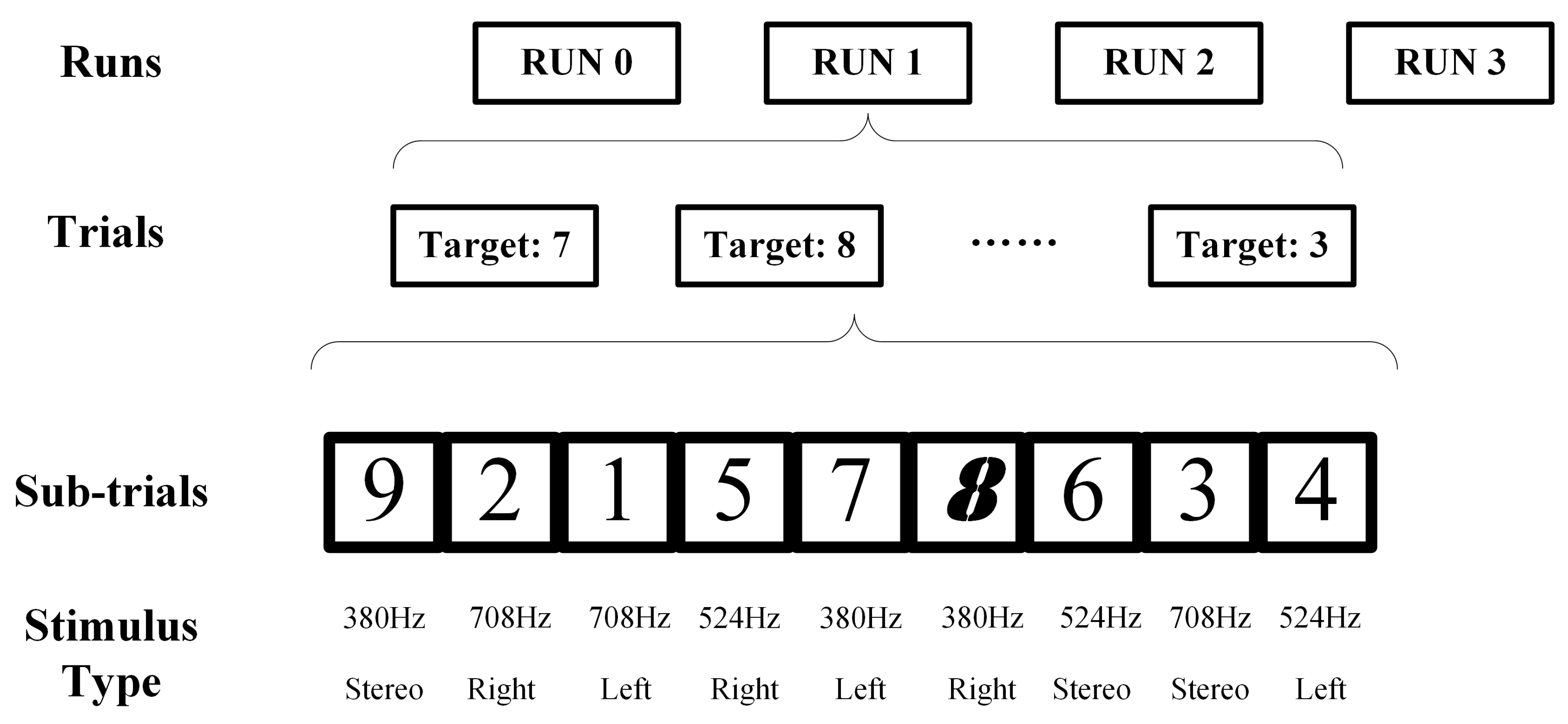
3.1.2. Experiment Paradigm Design in Dataset
3.2. Parameter Selection
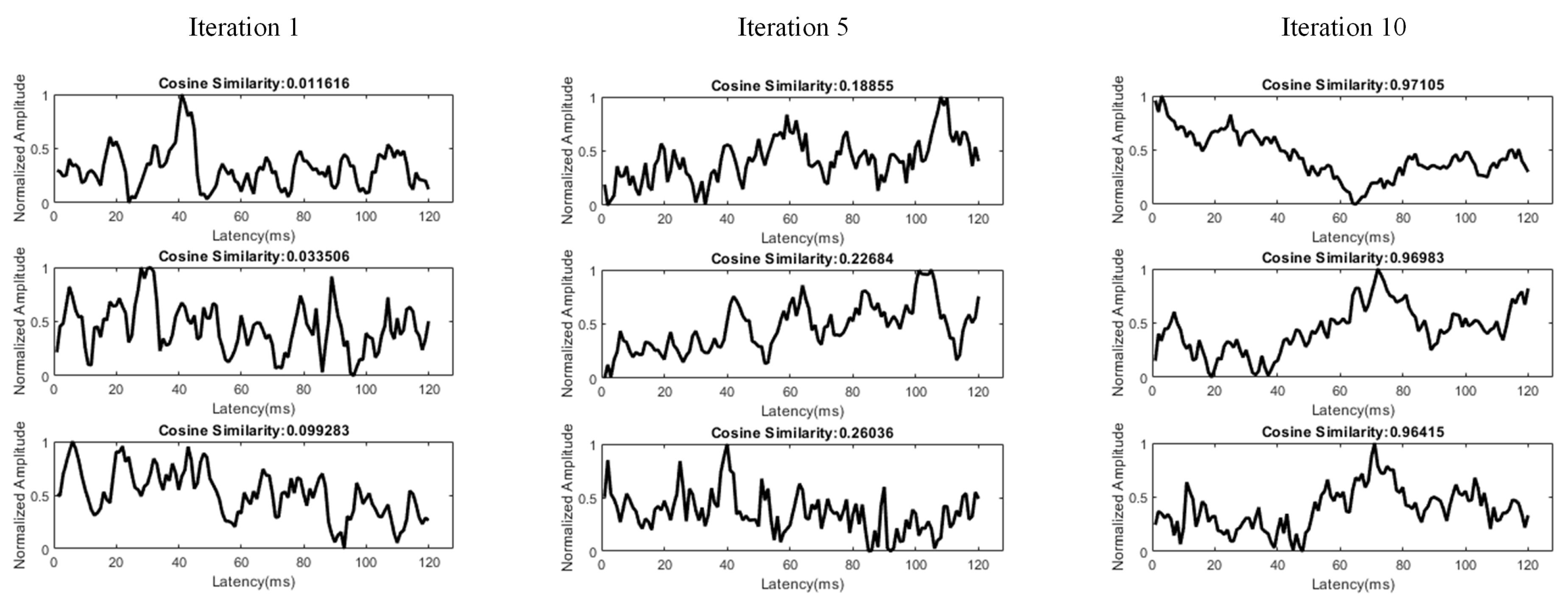
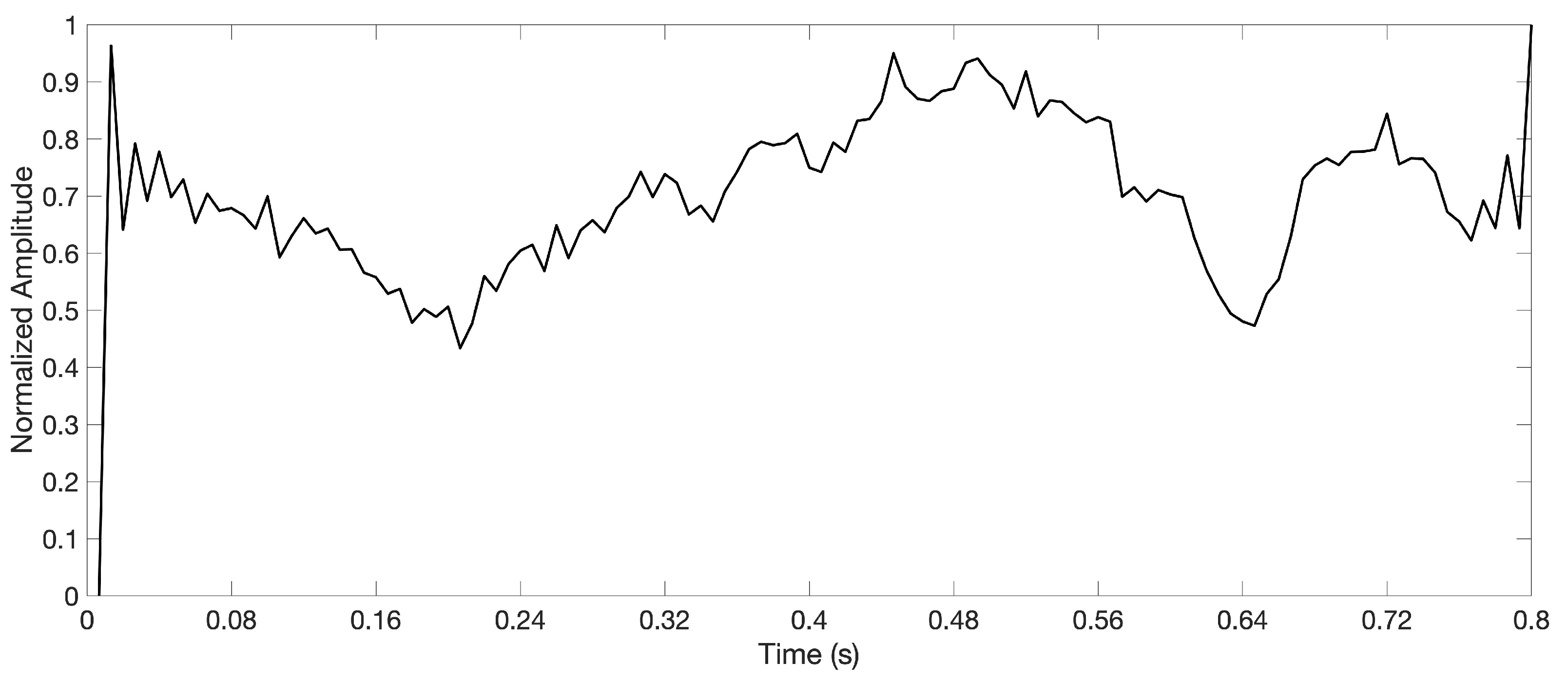
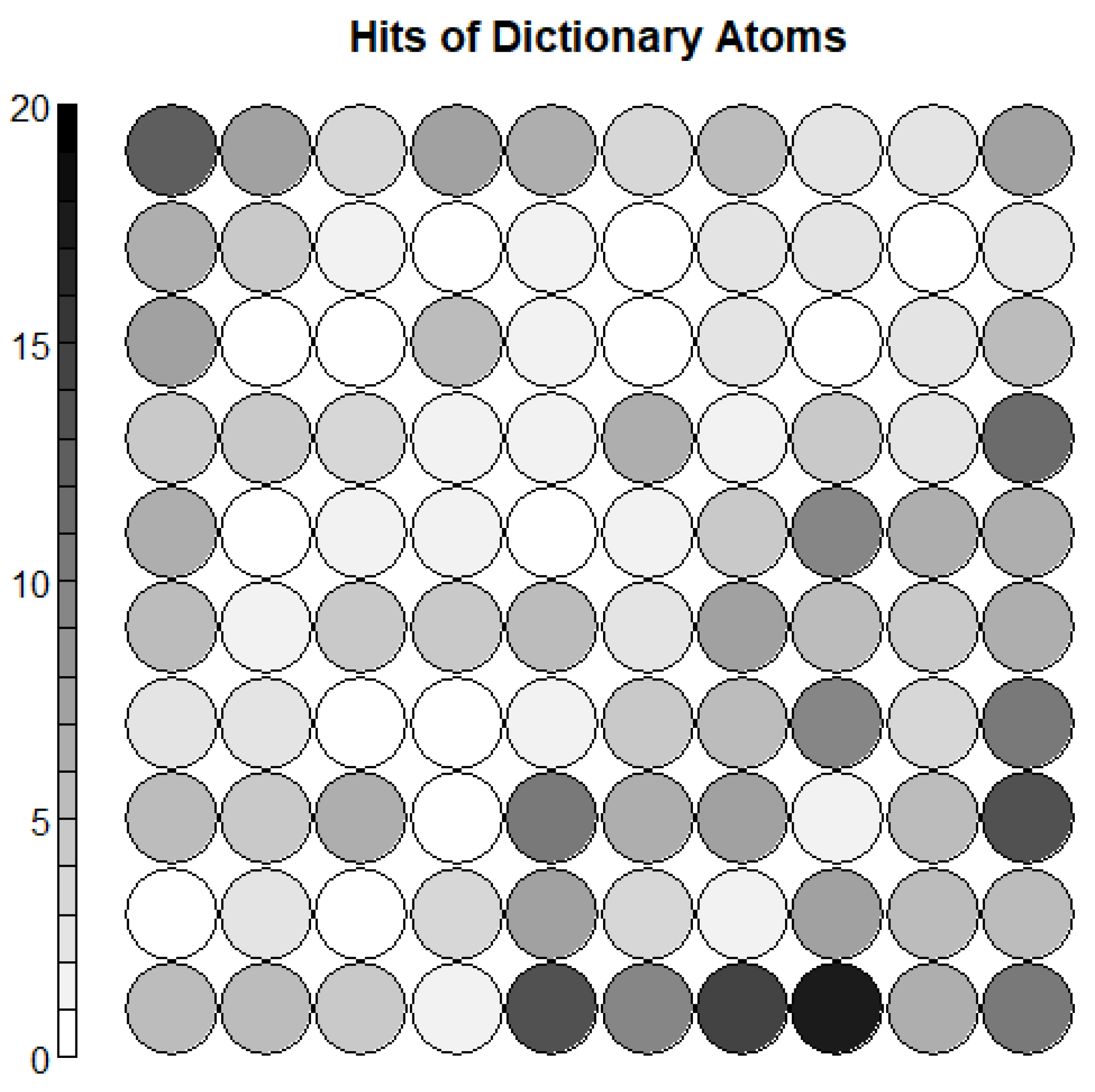
3.3. Dictionary Atom SOM Results
3.4. Neuron Selection and Feature Extraction Results
3.5. Classification Stage and Result Analysis
3.5.1. Classification Stage Design
3.5.2. Classification Result
3.5.3. Review and Comparison of Classification Result
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- James, C.J.; Lowe, D. Extracting multisource brain activity from a single electromagnetic channel. Artif. Intell. Med. 2003, 28, 89–104. [Google Scholar] [CrossRef]
- Hu, L.; Mouraux, A.; Hu, Y.; Iannetti, G.D. A novel approach for enhancing the signal-to-noise ratio and detecting automatically event-related potentials (ERPs) in single trials. Neuroimage 2010, 50, 99–111. [Google Scholar] [CrossRef]
- Azlan, W.A.W.; Low, Y.F. Feature extraction of electroencephalogram (EEG) signal—A review. In Proceedings of the 2014 IEEE Conference on Biomedical Engineering and Sciences (IECBES), Sarawak, Malaysia, 8–10 December 2014; pp. 801–806. [Google Scholar]
- Farwell, L.; Donchin, E. Talking off the top of your head: Toward a mental prosthesis utilizing event-related brain potentials. Electroencephalogr. Clin. Neurophysiol. 1988, 70, 510–523. [Google Scholar] [CrossRef]
- Jung, T.; Makeig, S.; Westerfield, M.; Townsend, J.; Courchesne, E.; Sejnowski, T. Independent component analysis of single-trial event-related potentials. In Proceedings of the International workshop on Independent component analysis and blind signal separation, Aussois, France, 11–15 January 1999; pp. 173–179. [Google Scholar]
- Huang, N.E.; Wu, Z. A review on Hilbert-Huang transform: Method and its applications to geophysical studies. Rev. Geophys. 2008, 46. [Google Scholar] [CrossRef]
- Gao, C.; Ma, L.; Li, H. An ICA/HHT Hybrid Approach for Automatic Ocular Artifact Correction. Int. J. Pattern Recognit. Artif. Intell. 2015, 29, 1558001. [Google Scholar] [CrossRef]
- Lee, W.L.; Tan, T.; Falkmer, T.; Leung, Y.H. Single-trial event-related potential extraction through one-unit ICA-with-reference. J. Neural Eng. 2016, 13, 066010. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Eilbeigi, E.; Setarehdan, S.K. Detecting intention to execute the next movement while performing current movement from EEG using global optimal constrained ICA. Comput. Biol. Med. 2018, 99, 63–75. [Google Scholar] [CrossRef]
- Zhang, J.; Bi, L.; Lian, J.; Guan, C. A Single-Trial Event-Related Potential Estimation Based on Independent Component Analysis and Kalman Smoother. In Proceedings of the 2018 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Auckland, New Zealand, 9–12 July 2018; IEEE: Piscataway, NY, USA, 2018; pp. 7–12. [Google Scholar] [CrossRef]
- Fukami, T.; Watanabe, J.; Ishikawa, F. Robust estimation of event-related potentials via particle filter. Comput. Methods Programs Biomed. 2016, 125, 26–36. [Google Scholar] [CrossRef]
- Ting, C.M.; Salleh, S.H.; Zainuddin, Z.M.; Bahar, A. Modeling and estimation of single-trial event-related potentials using partially observed diffusion processes. Digit. Signal Process. Rev. J. 2015, 36, 128–143. [Google Scholar] [CrossRef]
- Delaney-Busch, N.; Morgan, E.; Lau, E.; Kuperberg, G.R. Neural evidence for Bayesian trial-by-trial adaptation on the N400 during semantic priming. Cognition 2019, 187, 10–20. [Google Scholar] [CrossRef]
- Zeyl, T.; Yin, E.; Keightley, M.; Chau, T. Adding real-time Bayesian ranks to error-related potential scores improves error detection and auto-correction in a P300 speller. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 46–56. [Google Scholar] [CrossRef] [PubMed]
- Wen, D.; Jia, P.; Lian, Q.; Zhou, Y.; Lu, C. Review of sparse representation-based classification methods on EEG signal processing for epilepsy detection, brain-computer interface and cognitive impairment. Front. Aging Neurosci. 2016, 8, 172. [Google Scholar] [CrossRef] [PubMed]
- Dai, Y.; Wang, X.; Li, X.; Tan, Y. Sparse EEG compressive sensing for web-enabled person identification. Meas. J. Int. Meas. Confed. 2015, 74, 11–20. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, Y.; Liu, J.; Sun, J.; Cichocki, A.; Gao, F. Regularized Group Sparse Discriminant Analysis for P300-Based Brain-Computer Interface. Int. J. Neural Syst. 2019, 29. [Google Scholar] [CrossRef] [PubMed]
- Mo, H.; Luo, C.; Jan, G.E. EEG classification based on sparse representation. In Proceedings of the International Joint Conference on Neural Networks, Anchorage, AK, USA, 14–19 May 2017; IEEE: Piscataway, NY, USA, 2017; Volume 2017, pp. 59–62. [Google Scholar] [CrossRef]
- Shin, Y.; Lee, S.; Ahn, M.; Cho, H.; Jun, S.C.; Lee, H.N. Simple adaptive sparse representation based classification schemes for EEG based brain-computer interface applications. Comput. Biol. Med. 2015, 66, 29–38. [Google Scholar] [CrossRef]
- Yuan, S.; Zhou, W.; Yuan, Q.; Li, X.; Wu, Q.; Zhao, X.; Wang, J. Kernel Collaborative Representation- Based Automatic Seizure Detection in Intracranial EEG. Int. J. Neural Syst. 2015, 25, 1550003. [Google Scholar] [CrossRef]
- Yu, H.; Lu, H.; Ouyang, T.; Liu, H.; Lu, B.L. Vigilance detection based on sparse representation of EEG. In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology, Buenos Aires, Argentina, 31 August–4 September 2010; pp. 2439–2442. [Google Scholar] [CrossRef]
- Shin, Y.; Lee, H.N.; Balasingham, I. Fast L1-based sparse representation of EEG for motor imagery signal classification. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; IEEE: Piscataway, NY, USA, 2016; Volume 2016, pp. 223–226. [Google Scholar] [CrossRef]
- Ayesha, S.; Hanif, M.K.; Talib, R. Overview and comparative study of dimensionality reduction techniques for high dimensional data. Inf. Fusion 2020, 59, 44–58. [Google Scholar] [CrossRef]
- Kohonen, T. Self-organized formation of topologically correct feature maps. Biol. Cybern. 1982, 43, 59–69. [Google Scholar] [CrossRef]
- Ngan, S.C.; Yacoub, E.S.; Auffermann, W.F.; Hu, X. Node merging in Kohonen’s self-organizing mapping of fMRI data. Artif. Intell. Med. 2002, 25, 19–33. [Google Scholar] [CrossRef]
- Liao, W.; Chen, H.; Yang, Q.; Lei, X. Analysis of fMRI data using improved self-organizing mapping and spatio-temporal metric hierarchical clustering. IEEE Trans. Med. Imaging 2008, 27, 1472–1483. [Google Scholar] [CrossRef]
- Kurth, C.; Gilliam, F.; Steinhoff, B. EEG spike detection with a Kohonen feature map. Ann. Biomed. Eng. 2000, 28, 1362–1369. [Google Scholar] [CrossRef] [PubMed]
- Hemanth, D.J.; Anitha, J.; Son, L.H. Brain signal based human emotion analysis by circular back propagation and Deep Kohonen Neural Networks. Comput. Electr. Eng. 2018, 68, 170–180. [Google Scholar] [CrossRef]
- Diaz-Sotelo, W.J.; Roman-Gonzalez, A.; Vargas-Cuentas, N.I.; Meneses-Claudio, B.; Zimic, M. EEG Signals Processing Two State Discrimination Using Self-organizing Maps. In Proceedings of the 2018 IEEE International Conference on Automation/XXIII Congress of the Chilean Association of Automatic Control (ICA-ACCA), Concepcion, Chile, 17–19 October 2018; IEEE: Piscataway, NY, USA, 2018; pp. 1–4. [Google Scholar]
- Hämäläinen, T.D. Parallel Implementation of Self-Organizing Maps. In Self-Organizing Neural Networks: Recent Advances and Applications; Springer: Berlin/Heidelberg, Germany, 2001; pp. 245–278. [Google Scholar]
- Aharon, M.; Elad, M.; Bruckstein, A. K-SVD: An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation. IEEE Trans. Signal Process. 2016, 54, 4311–4322. [Google Scholar] [CrossRef]
- Fort, J.C.; Letrémy, P.; Cottrell, M. Advantages and drawbacks of the Batch Kohonen algorithm. In Proceedings of the ESANN 2002, 10th Eurorean Symposium on Artificial Neural Networks, Bruges, Belgium, 24–26 April 2002; pp. 223–230. [Google Scholar]
- Höhne, J.; Schreuder, M.; Blankertz, B.; Tangermann, M. A Novel 9-Class Auditory ERP Paradigm Driving a Predictive Text Entry System. Front. Neurosci. 2011, 5, 99. [Google Scholar] [CrossRef] [PubMed]
- Bostanov, V. BCI competition 2003-data sets Ib and IIb: Feature extraction from event-related brain potentials with the continuous wavelet transform and the t-value scalogram. IEEE Trans. Biomed. Eng. 2004, 51, 1057–1061. [Google Scholar] [CrossRef] [PubMed]
- Saavedra, C.; Salas, R.; Bougrain, L. Wavelet-Based Semblance Methods to Enhance the Single-Trial Detection of Event-Related Potentials for a BCI Spelling System. Comput. Intell. Neurosci. 2019, 2019. [Google Scholar] [CrossRef] [PubMed]
- Kabbara, A.; Khalil, M.; El-Falou, W.; Eid, H.; Hassan, M. Functional Brain Connectivity as a New Feature for P300 Speller. PLoS ONE 2016, 11, e0146282. [Google Scholar] [CrossRef]
- Ogino, M.; Kanoga, S.; Muto, M.; Mitsukura, Y. Analysis of Prefrontal Single-Channel EEG Data for Portable Auditory ERP-Based Brain–Computer Interfaces. Front. Hum. Neurosci. 2019, 13, 250. [Google Scholar] [CrossRef]
- Kundu, S.; Ari, S. Fusion of Convolutional Neural Networks for P300 Based Character Recognition. In Proceedings of the 2019 International Conference on Information Technology (ICIT), Bhubaneswar, India, 19–21 December 2019; IEEE: Piscataway, NY, USA; pp. 155–159. [Google Scholar]
- Lee, J.; Won, K.; Kwon, M.; Jun, S.C.; Ahn, M. CNN with Large Data Achieves True Zero-Training in Online P300 Brain-Computer Interface. IEEE Access 2020, 8, 74385–74400. [Google Scholar] [CrossRef]
- Fazel-Rezai, R.; Allison, B.; Guger, C.; Sellers, E.; Kleih, S.; Kübler, A. P300 brain computer interface: Current challenges and emerging trends. Front. Neuroeng. 2012, 5, 14. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, D. On the Vulnerability of CNN Classifiers in EEG-Based BCIs. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 814–825. [Google Scholar] [CrossRef] [PubMed]
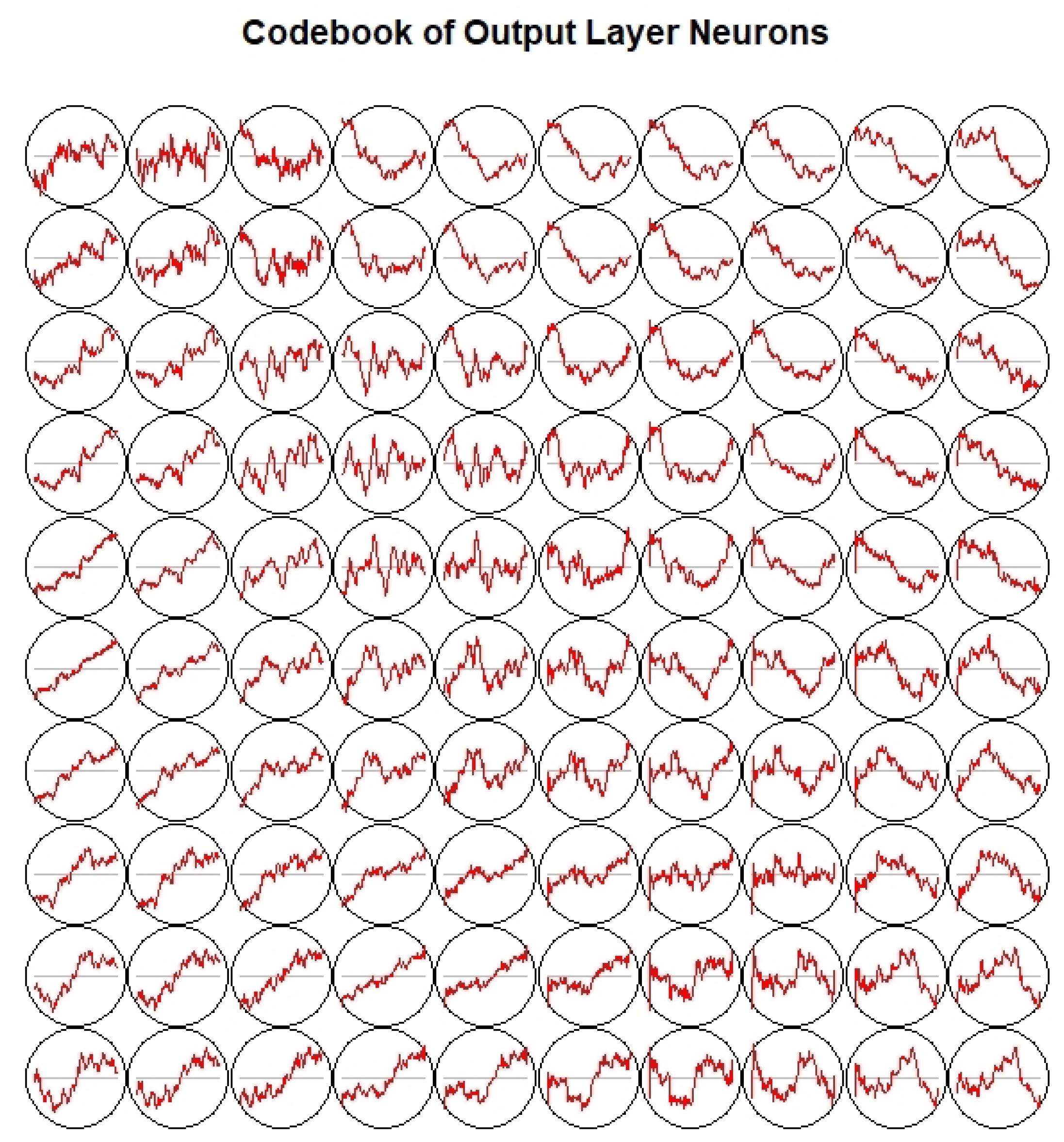
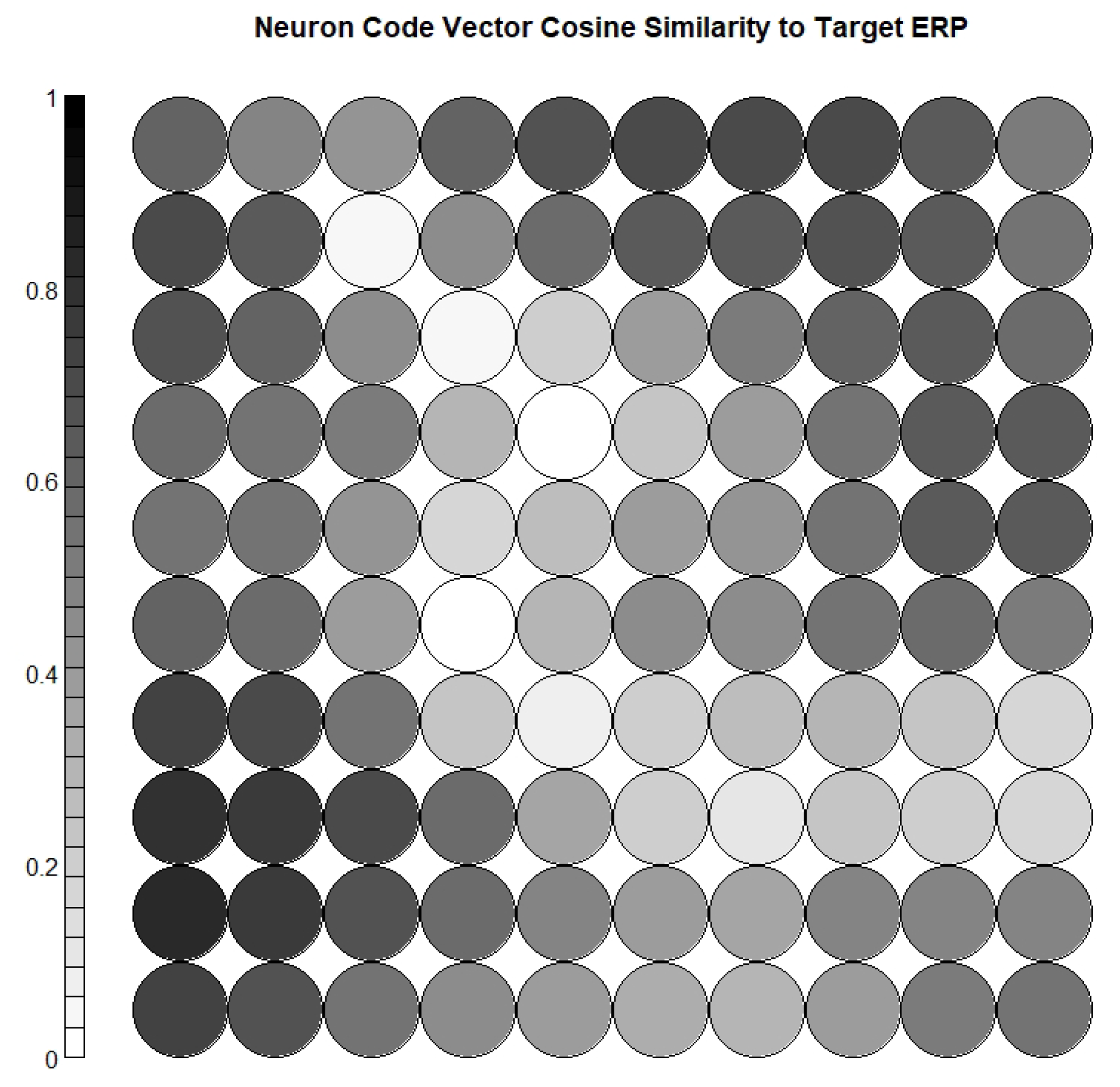

| Parameter | Value |
|---|---|
| K-SVD Sparsity | 10 |
| Number of Atoms in Dictionary | 512 |
| Atom Length | 120 |
| EEGFrame Length | 120 |
| EEG Sample Rate | 150 Hz |
| Number of SOM Neurons | 100 |
| SOM Topology | , Square Topology |
| Method | Subjects | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| VPnv | VPny | VPnz | VPoa | VPob | VPoc | VPod | VPja | VPoe | Avg | |
| Proposed | 78.00% | 75.90% | 75.10% | 73.60% | 79% | 79.50% | 71.20% | 81.00% | 74.50% | 76.42% |
| Original | 77.0% | 75.0% | 74.4% | 72.2% | 78.6% | 79.6% | 70.0% | 82.0% | 73.2% | 75.78% |
| Category | Study | Accuracy | Data Amount Used | Preprocessing Procedures and Computation Required |
|---|---|---|---|---|
| Visual ERP | Saavedra et al. [35] | 75% | Moderate (Multiple Channels) | Moderate for ERP research |
| Bostanov [34] | 77% | Moderate (Multiple Channels) | Moderate for ERP research | |
| Kabbara1 et al. [36] | 80% | Moderate (Multiple Channels) | Moderate for ERP research | |
| Auditory ERP | Ogino et al. [37] | 79% | Moderate (Multiple Channels) | Moderate for ERP research |
| Proposed Method | 76.2% | Minimum (Single Channel) | Only simple procedures minimum computation | |
| Höhne et al. [33] | 75.6% | Moderate (Multiple Channels) | Moderate for ERP research | |
| Deep Learning | Kundu et al. [38] | 90.5% | Large (Multi Channel) (Large Group of Subjects) | Only simple procedures. Huge computation effort. |
| Lee et al. [39] | 93% | Large (Multi Channel) (Large Group of Subjects) | Only simple procedures. Huge computation effort. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, S.; Li, H.; Ma, L.; Xu, Z. An EEG Feature Extraction Method Based on Sparse Dictionary Self-Organizing Map for Event-Related Potential Recognition. Algorithms 2020, 13, 259. https://doi.org/10.3390/a13100259
Feng S, Li H, Ma L, Xu Z. An EEG Feature Extraction Method Based on Sparse Dictionary Self-Organizing Map for Event-Related Potential Recognition. Algorithms. 2020; 13(10):259. https://doi.org/10.3390/a13100259
Chicago/Turabian StyleFeng, Shang, Haifeng Li, Lin Ma, and Zhongliang Xu. 2020. "An EEG Feature Extraction Method Based on Sparse Dictionary Self-Organizing Map for Event-Related Potential Recognition" Algorithms 13, no. 10: 259. https://doi.org/10.3390/a13100259
APA StyleFeng, S., Li, H., Ma, L., & Xu, Z. (2020). An EEG Feature Extraction Method Based on Sparse Dictionary Self-Organizing Map for Event-Related Potential Recognition. Algorithms, 13(10), 259. https://doi.org/10.3390/a13100259




