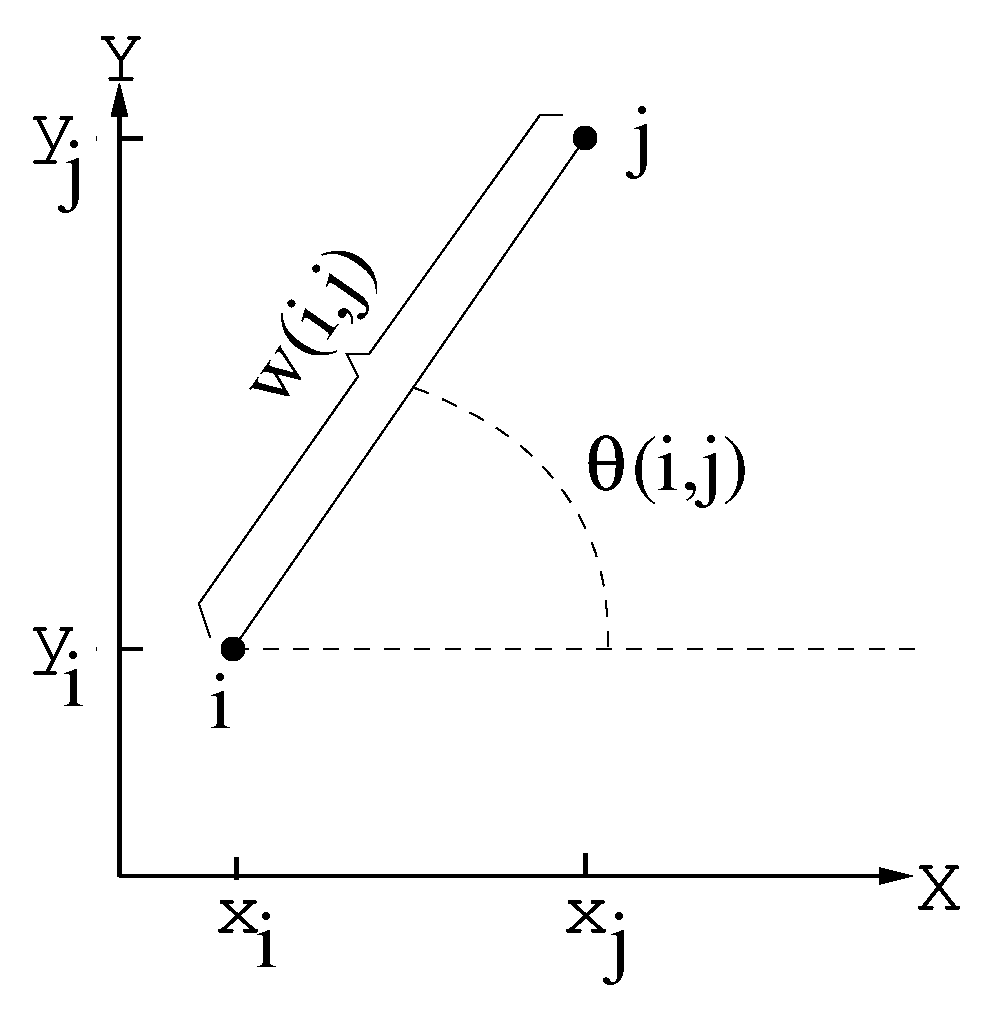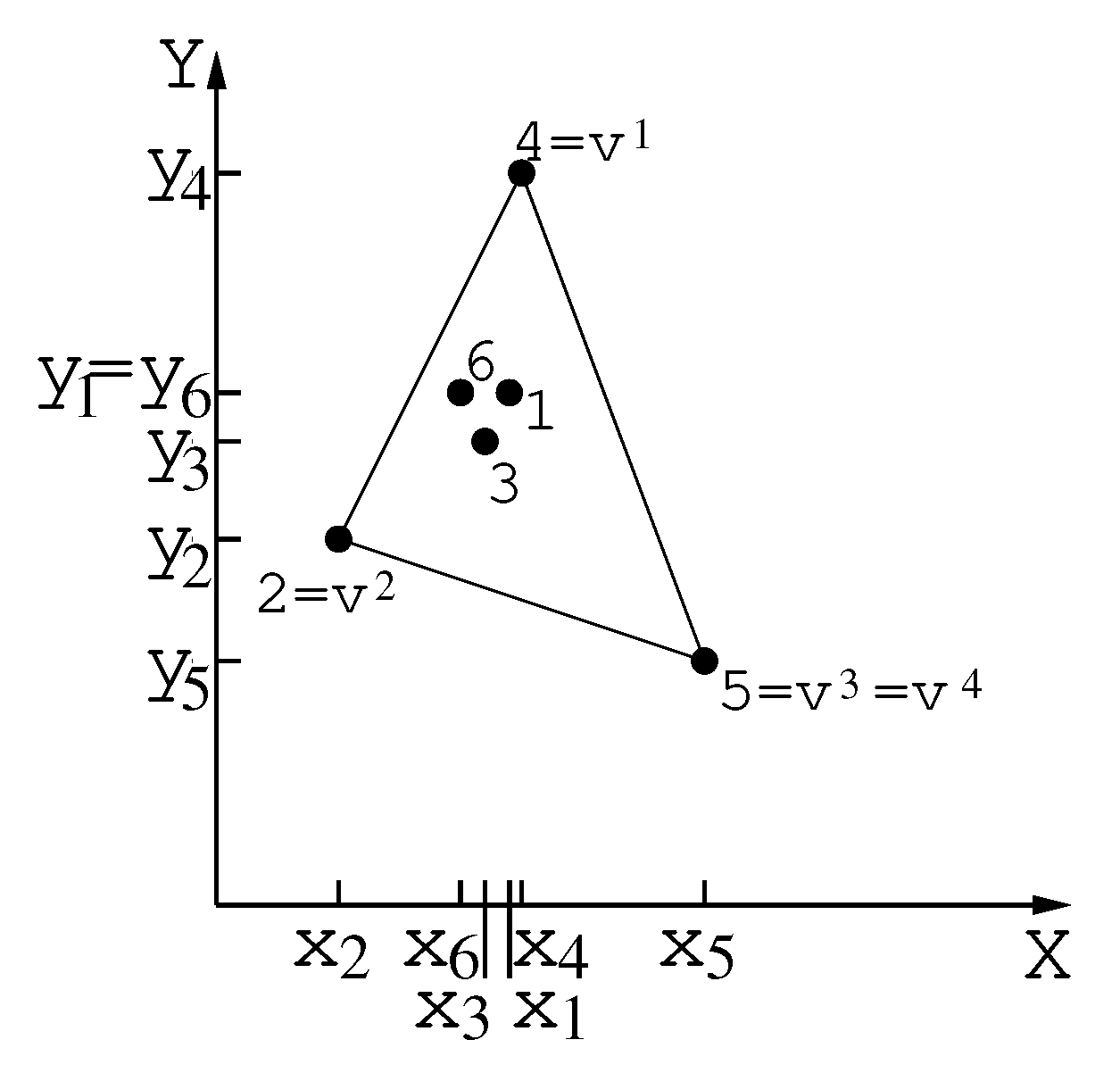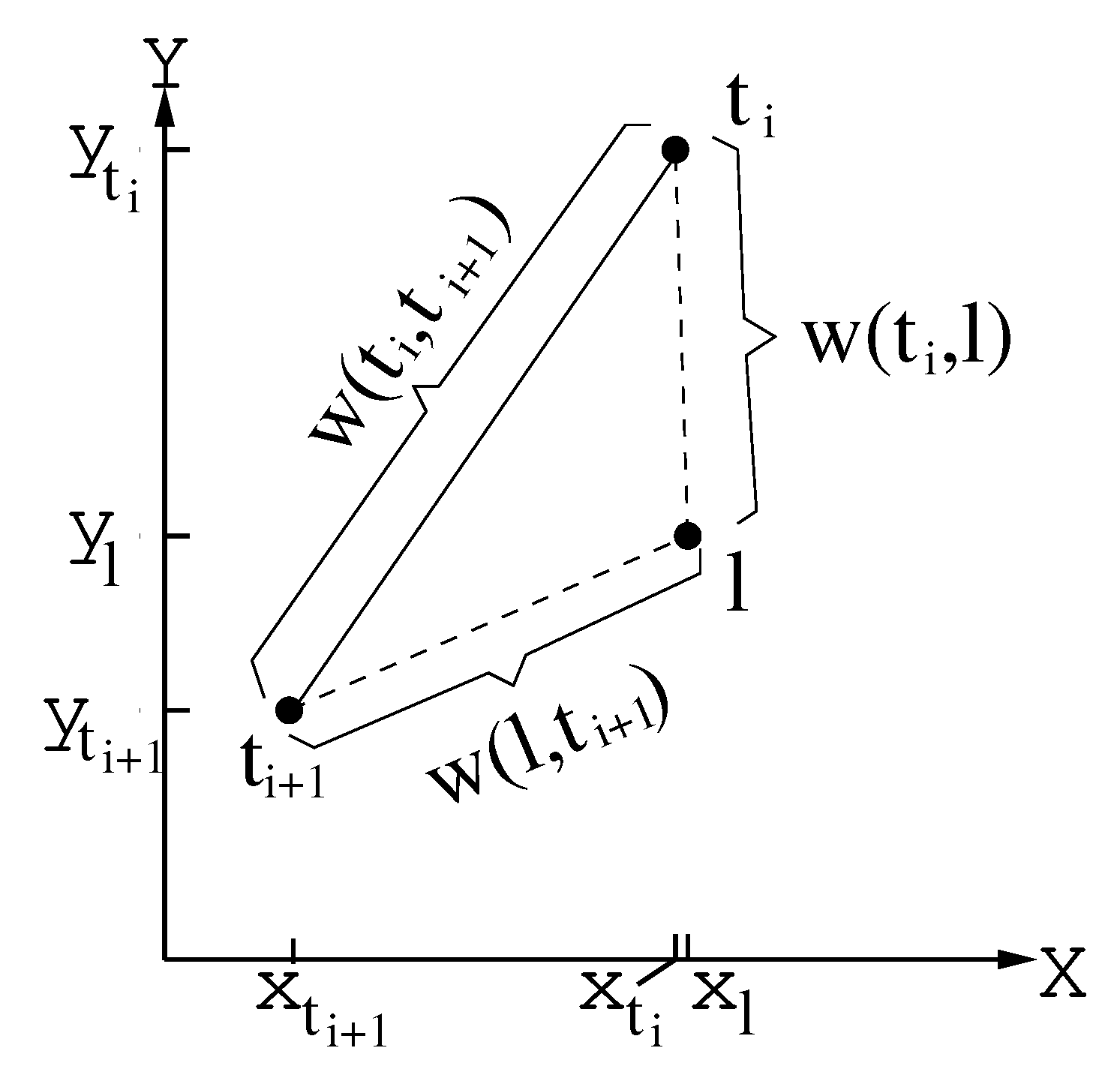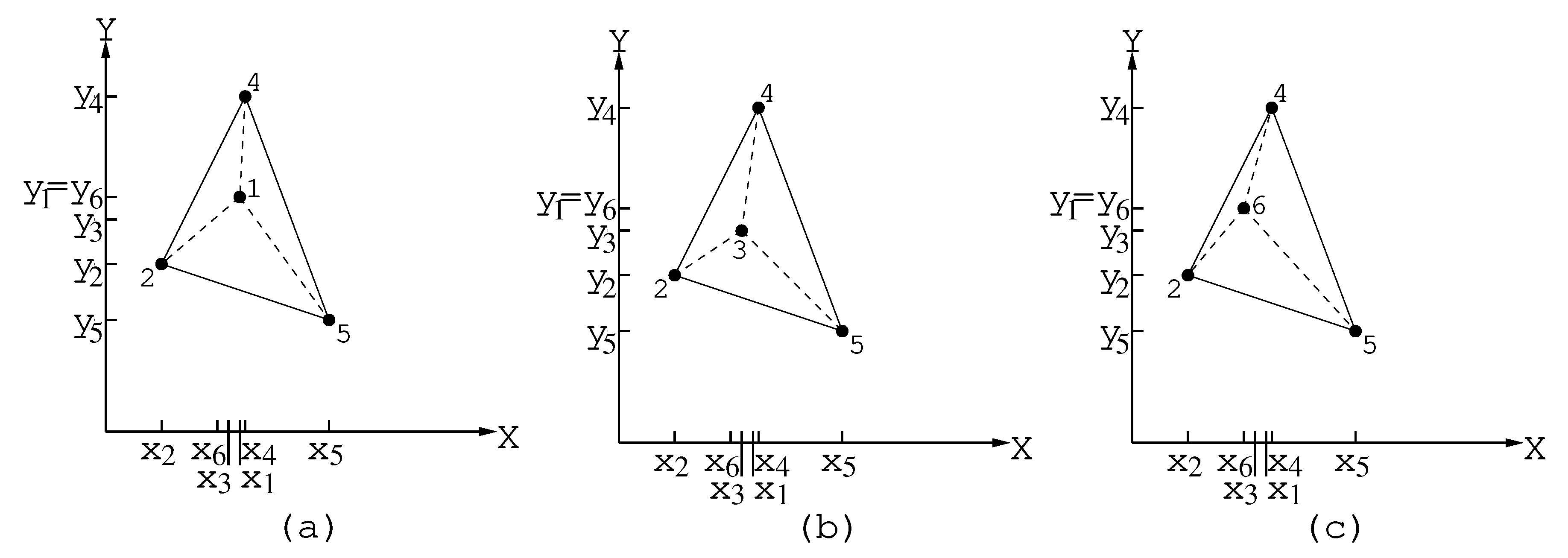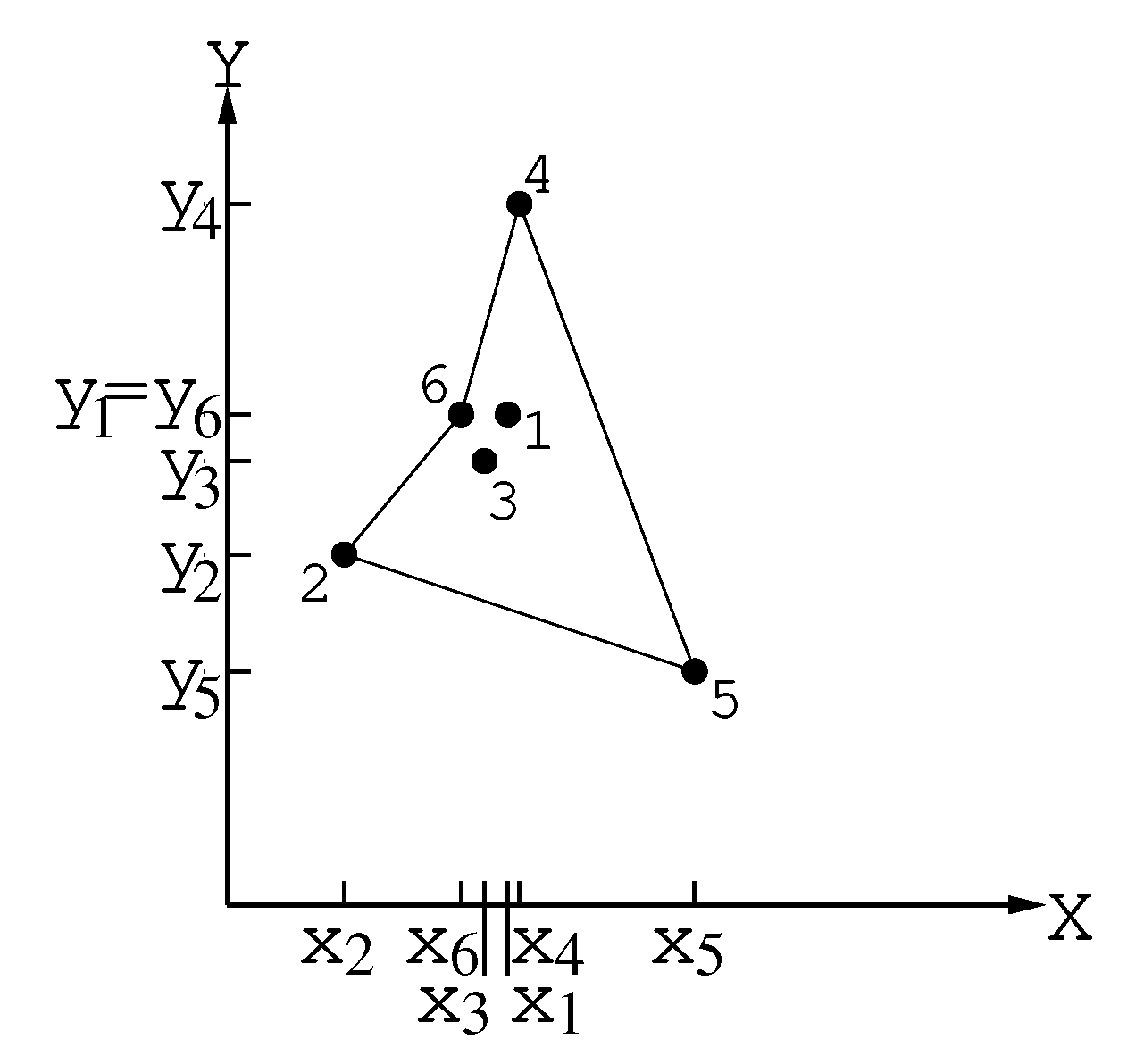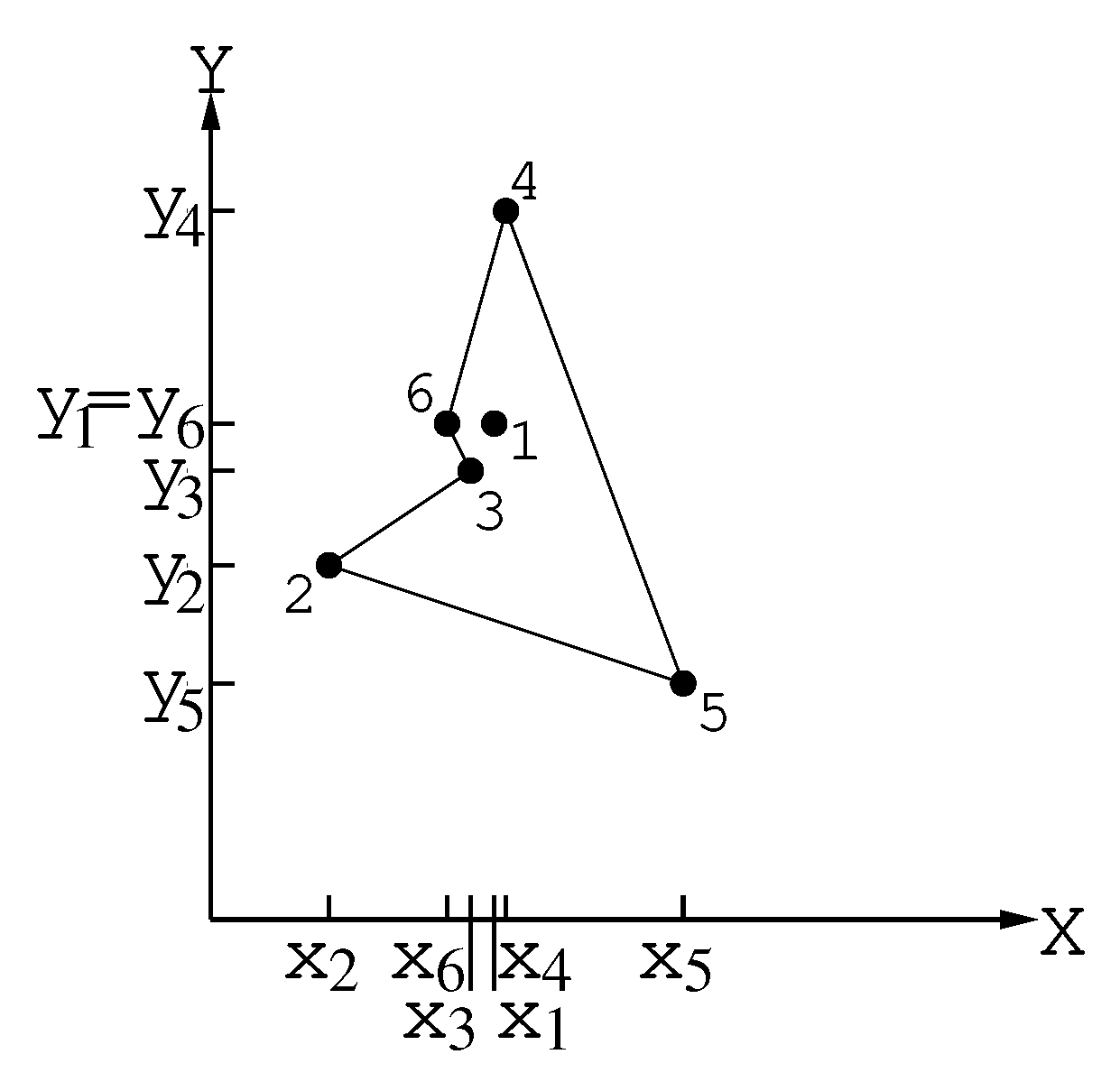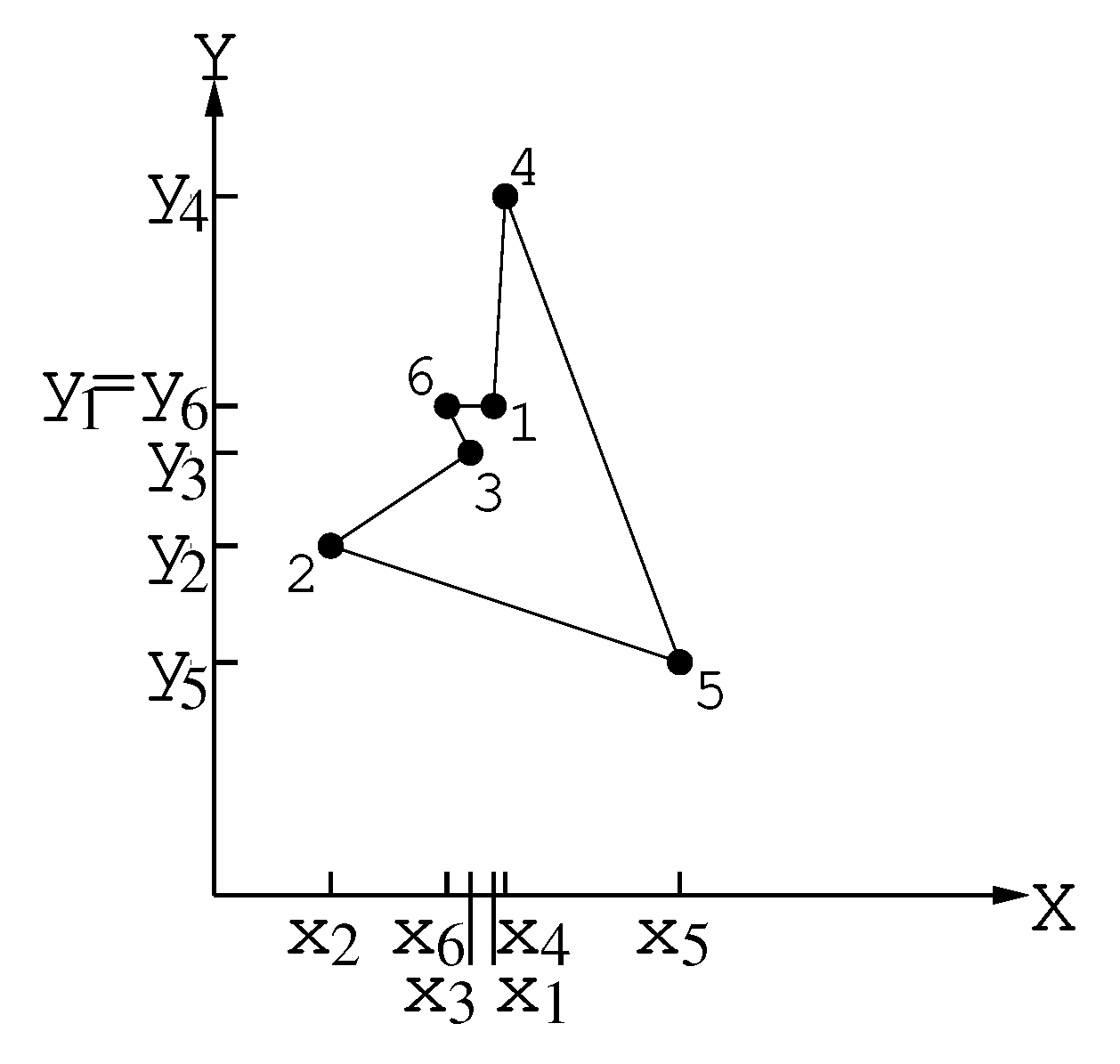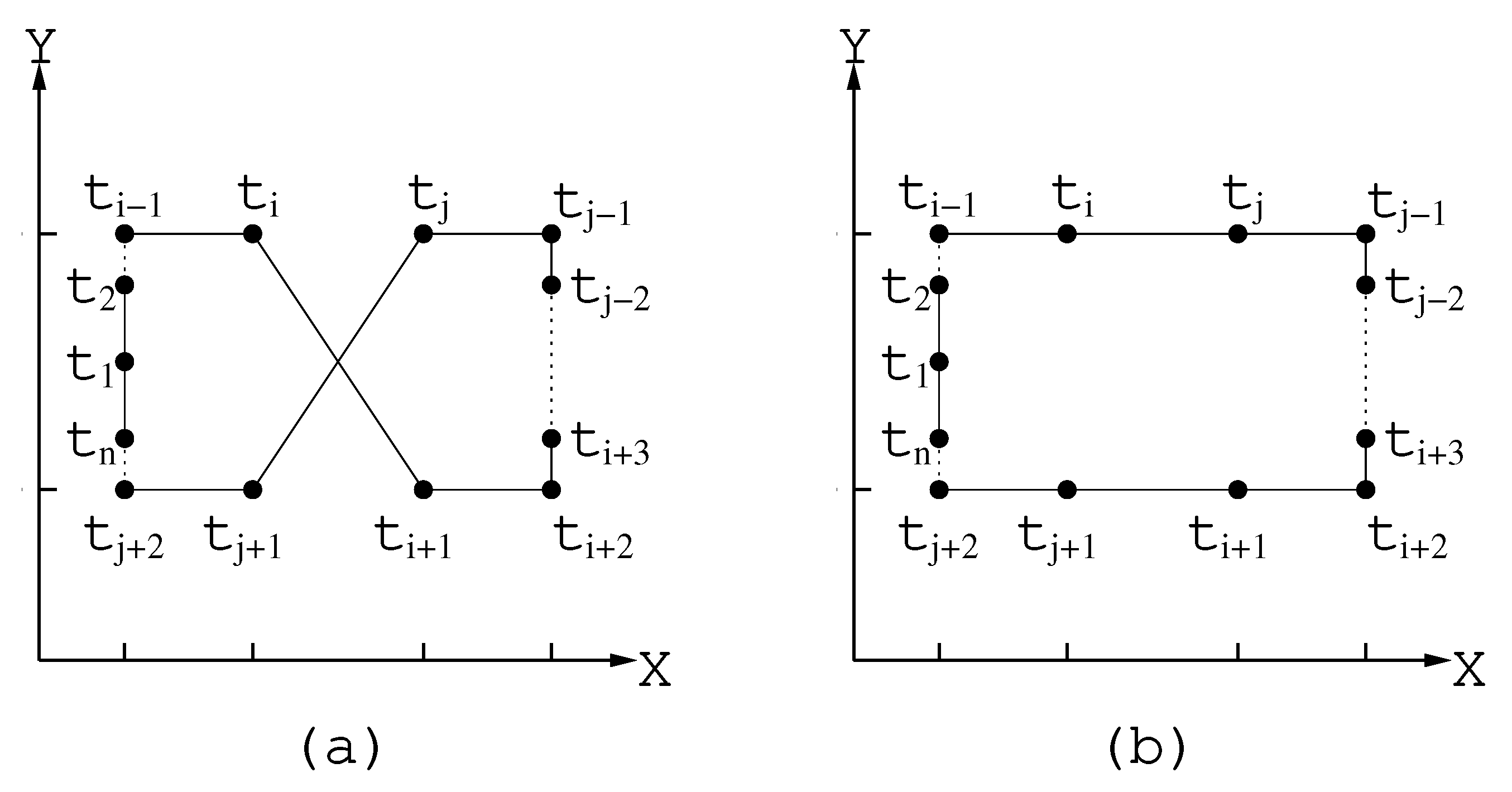Simple Constructive, Insertion, and Improvement Heuristics Based on the Girding Polygon for the Euclidean Traveling Salesman Problem

Abstract

The Traveling Salesman Problem (TSP) aims at finding the shortest trip for a salesman, who has to visit each of the locations from a given set exactly once, starting and ending at the same location. Here, we consider the Euclidean version of the problem, in which the locations are points in the two-dimensional Euclidean space and the distances are correspondingly Euclidean distances. We propose simple, fast, and easily implementable heuristics that work well, in practice, for large real-life problem instances. The algorithm works on three phases, the constructive, the insertion, and the improvement phases. The first two phases run in time $O\left(n^2\right)$ and the number of repetitions in the improvement phase, in practice, is bounded by a small constant. We have tested the practical behavior of our heuristics on the available benchmark problem instances. The approximation provided by our algorithm for the tested benchmark problem instances did not beat best known results. At the same time, comparing the CPU time used by our algorithm with that of the earlier known ones, in about 92% of the cases our algorithm has required less computational time. Our algorithm is also memory efficient: for the largest tested problem instance with 744,710 cities, it has used about 50 MiB, whereas the average memory usage for the remained 217 instances was 1.6 MiB.

1. Introduction

The Traveling Salesman Problem (TSP) is one of the most studied strongly NP-hard combinatorial optimization problems. Given an $n\times n$ matrix of distances between n objects, call them cities, one looks for a shortest possible feasible tour which can be seen as a permutation of the given n objects: a feasible tour visits each of the n cities exactly once except the first visited city with which the tour ends. The cost of a tour is the sum of the distances between each pair of the neighboring cities in that tour. This problem can also be described in graph terms. We have an undirected weighted complete graph $G=(V,E)$, where V is the set of $n=\left|V\right|$ vertices (cities) and E is the set of the $n^2-n$ edges $(i,j)=(j,i)$, $i\ne j$. A non-negative weight of an edge $(i,j)$, $w(i,j)$ is the distance between vertices i and j. There are two basic sets of restrictions that define feasible solution (a tour that has to start and complete at the same vertex and has to contain all the vertices from set V exactly once). A feasible tour T can be represented as:

$$T=(i_1,i_2,\cdots ,i_{n-1},i_n,i_1);i_k\in V,$$

(1)

and its cost is

$$C\left(T\right)=\sum _{k=1}^{n-1}w(i_k,i_{k+1})+w(i_n,i_1).$$

(2)

The objective is to find an optimal tour, a feasible one with the minimum cost ${min}_{T}C\left(T\right)$.

Some special cases of the problem have been commonly considered. For instance, in the symmetric version, the distance matrix is symmetric (i.e., for each edge $(i,j)$, $w(i,j)=w(j,i)$); in another setting, the distances between the cities are Euclidean distances (i.e., set V can be represented as points in the two-dimensional Euclidean space). Clearly, the Euclidean TSP is also a symmetric TSP but not vice versa. The Euclidean TSP has a straightforward immediate application in the real-life scenario when a salesman wishes to visit the cities using the shortest possible tour. Because in the Euclidean version the cities are points in plane, for each pair of points, the triangle inequality holds, which makes the problem a bit more accessible in the sense that simple geometric rules can be used for calculating the cost of a tour or the cost of the inclusion of a new point in a partial tour, unlike the general setting. Nevertheless, the Euclidean TSP remains strongly NP-hard; see Papadimitriou [1] and Garey et al. [2].

The exact solution methods for TSP can only solve problem instances with a moderate number of cities; hence, approximation algorithms are of a primary interest. There exist a vast amount of approximation heuristic algorithms for TSP. The literature on TSP is very wide-ranging, and it is not our goal to overview all the important relevant work here (we refer the reader, e.g., to a book by Lawler et al. [3] and an overview chapter by Jünger [4]).

The literature distinguishes two basic types of approximation algorithms for TSP: tour construction and loop improvement algorithms. The construction heuristics create a feasible tour in one pass so that the taken decisions are not reconsidered later. A feasible solution delivered by a construction heuristic can be used in a loop improvement heuristic as an initial feasible solution (though such initial solution can be constructed randomly). Given the current feasible tour, iteratively, an improvement algorithm, based on some local optimality criteria, makes some changes in that tour resulting in a new feasible solution with less cost. Well-known examples of tour improvement algorithms are 2-Opt Croes 2-Opt, its generalizations 3-Opt and k-Opt, and the algorithm by Lin and Kernighan [5], to mention a few.

The most successful algorithms we have found in the literature for large-scale TSP instances are Ant Colony Optimization (ACO) meta heuristics, with which we compare our results. On one hand, these algorithms give a good approximation. On the other hand, the traditional ACO-based algorithms tend to require a considerable computer memory, which is necessary to keep an $n\times n$ pheromone matrix. Typically, the time complexity of the selection of each next move using ACO is also costly. These drawbacks are addressed in some recent ACO-based algorithms in which, at each iteration of the calculation of the pheromone levels, the intermediate data are reduced storing only a limited number of the most promising tours in computer memory. With Partial ACO (PACO), only some part of a known good tour is altered. A PACO-based heuristic was proposed in Chitty [6] and the experimental results for four problem instances from library Art Gallery were reported. Effective Strategies + ACO (ESACO) uses pheromone values directly in the 2-opt local search for the solution improvement and reduces the pheromone matrix, yielding linear space complexity (see, for example, Ismkman [7]). Parallel Cooperative Hybrid Algorithm ACO (PACO-3Opt) uses a multi-colony of ants to prevent a possible stagnation (see, for example, Gülcü et al. [8]). In a very recent Restricted Pheromone Matrix Method (RPMM) [9], the pheromone matrix is reduced with a linear memory complexity, resulting in an essentially lower memory consumption. Another recent successful ACO-based Dynamic Flying ACO (DFACO) heuristic was proposed by Dahan et al. [10]. Besides these ACO-based heuristics, we have compared our heuristics with other two meta-heuristics. One of them is a parallel algorithm based on the nearest neighborhood search suggested by Al-Adwan et al. [11], and the other one, proposed by Zhong et al. [12], is a Discrete Pigeon-Inspired Optimization (DPIO) metaheuristic. We have also implemented directly the Nearest Neighborhood (NN) algorithm for the comparison purposes (see Section 4 and Appendix A).

In Table A1 in Appendix A, we give a summary of the above heuristics including the information on the type and the number of the instances for which these algorithms were tested and the number of the runs of each of these algorithms. Unlike these heuristics, the heuristic that we propose here is deterministic, in the sense that, for any input, it delivers the same solution each time it is invoked; hence, there is no need in the repeated runs of our algorithm. We have tested the performance of our algorithm on 218 benchmark problem instances (the number of the reported instances for the algorithms from Table A1 vary from 6 to 36). The relative error of our algorithm for the tested instances did not beat the earlier known best results; however, for some instances, our error was better than that of the above-mentioned algorithms (see Table 9 at the end of Section 3). The error percentage provided by our algorithm has varied from 0% to 17%, with an average relative error of 7.16%. The standard error deviation over all the tested instances was 0.03.

In terms of the CPU time, our algorithm was faster than ones from Table A1 except for six instances from Art Gallery RPMM [9] and Partial-ACO [6], and for two instances from TSPLIB DPIO [12] were faster (see Table 10). Among all the comparisons we made, in about 92% of the cases, our algorithm has required less computational time. We have halted the execution of our algorithm for the two of the above-mentioned largest problem instances in 15 days, and for the next largest instance ara238025 with 238,025 cities our algorithm has halted in about 36 h. The average CPU time for the remained instances were 19.2 min. The standard CPU time deviation for these instances was 89.3 min (for all the instances, including the above-mentioned three largest ones, it was 2068.4 min).

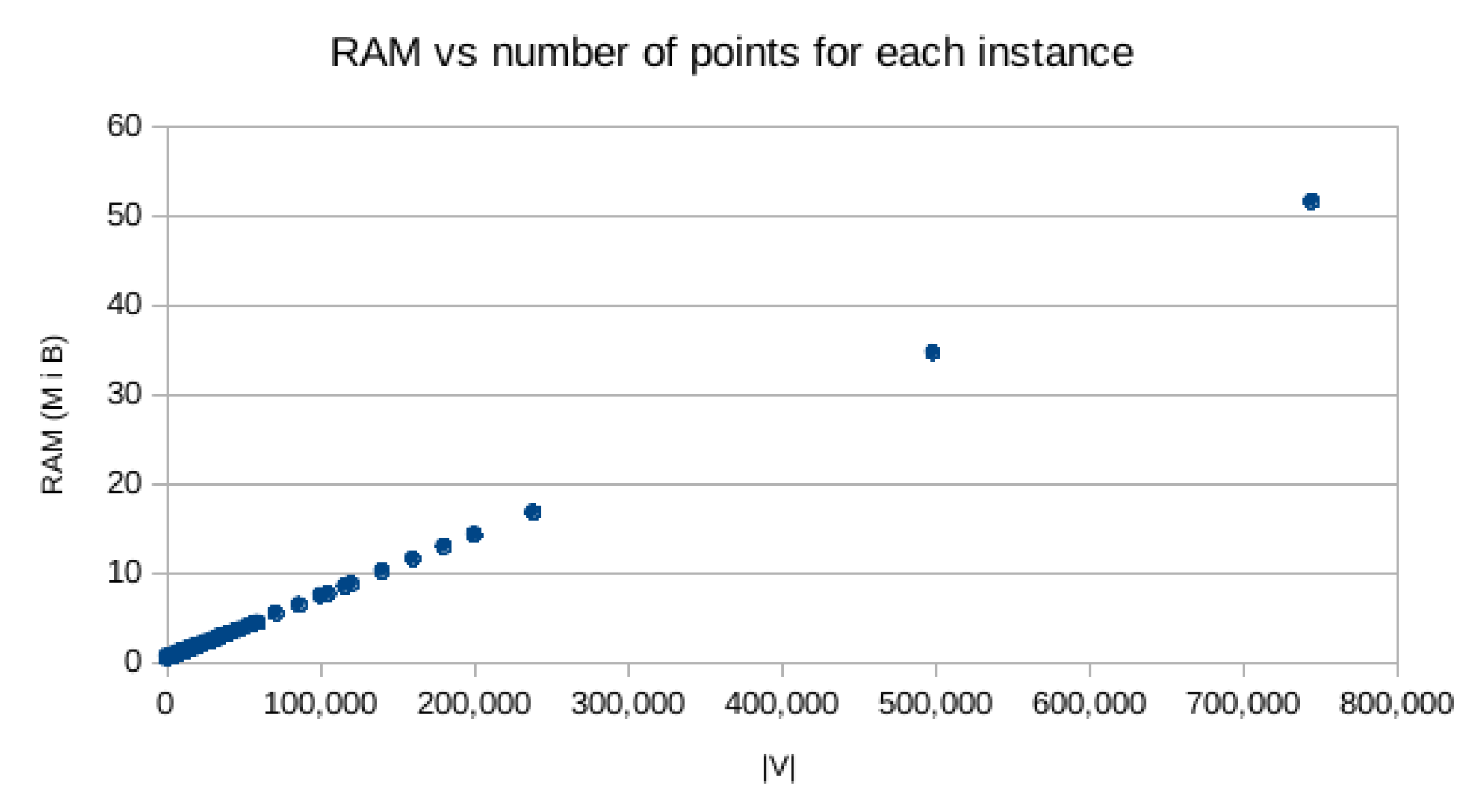
Our algorithm consumes very little computer memory. For the largest problem instance with 744,710 cities, it has used only about 50 MiB (mebibytes). The average memory usage for the remained 217 instances was 1.6 MiB (the average for all the instances including the above largest one was 1.88 MiB). The standard deviation of the usage of the memory is 4.6 MiB. Equation (3) below (see also Figure 15 in Section 3) shows the dependence of the memory required by our algorithm on the total number of cities n. As we can observe, this dependence is linear:

$$RAM=0.0000685n+0.563MiB.$$

(3)

Our algorithm consists of the constructive, the insertion and the improvement phases, we call it the Constructive, Insertion, and Improvement algorithm, the CII-algorithm, for short. The constructive heuristics of Phase 1 deliver a partial tour that includes solely the points of the girding polygon. The insertion heuristic of Phase 2 completes the partial tour of Phase 1 to a complete feasible tour using the cheapest insertion strategy: iteratively, the current partial tour is augmented with a new point, one yielding the minimal increase in the cost in an auxiliary, specially formed tour. We use simple geometry in the decision-making process at Phases 2 and 3. The tour improvement heuristic of Phase 3 improves iteratively the tour of Phase 2 based on the local optimality conditions: it uses two heuristic algorithms which carry out some local rearrangement of the current tour. At Phase 1, the girding polygon for the points of set V and an initial, yet infeasible (partial) tour including the vertices of that polygon is constructed in time $O\left(n^2\right)$. The initial tour of Phase 1 is iteratively extended with the new points from the internal area of the polygon at Phase 2. Phase 2 also runs in time $O\left(n^2\right)$ and basically uses the triangle inequality for the selection of each newly added point. Phase 3 uses two heuristic algorithms. The first one, called 2-Opt, is a local search algorithm proposed by Croes [13]. The second one is based on the procedure of Phase 2. The two heuristics are repeatedly applied in the iterative improvement cycle until a special approximation condition is satisfied. The number of repetitions in the improvement cycle, in practice, is bounded by a small constant. In particular, the average number of the repetitions for all the tested instances was about 9 (the maximum of 49 repetitions was attained for one of the moderate sized instances lra498378, and for the largest instance lrb744710 with 744,710 points, Phase 3 was repeated 18 times).

The rest of the paper is organized as follows. In Section 2, we describe the CII-algorithm and show its time complexity. In Section 3, we give the implementation details and the results of our computational experiments, and, in Section 4, we give some concluding remarks and possible directions for the future work. The tables presented in Appendix A contain the complete data of our computational results.

2. Methods

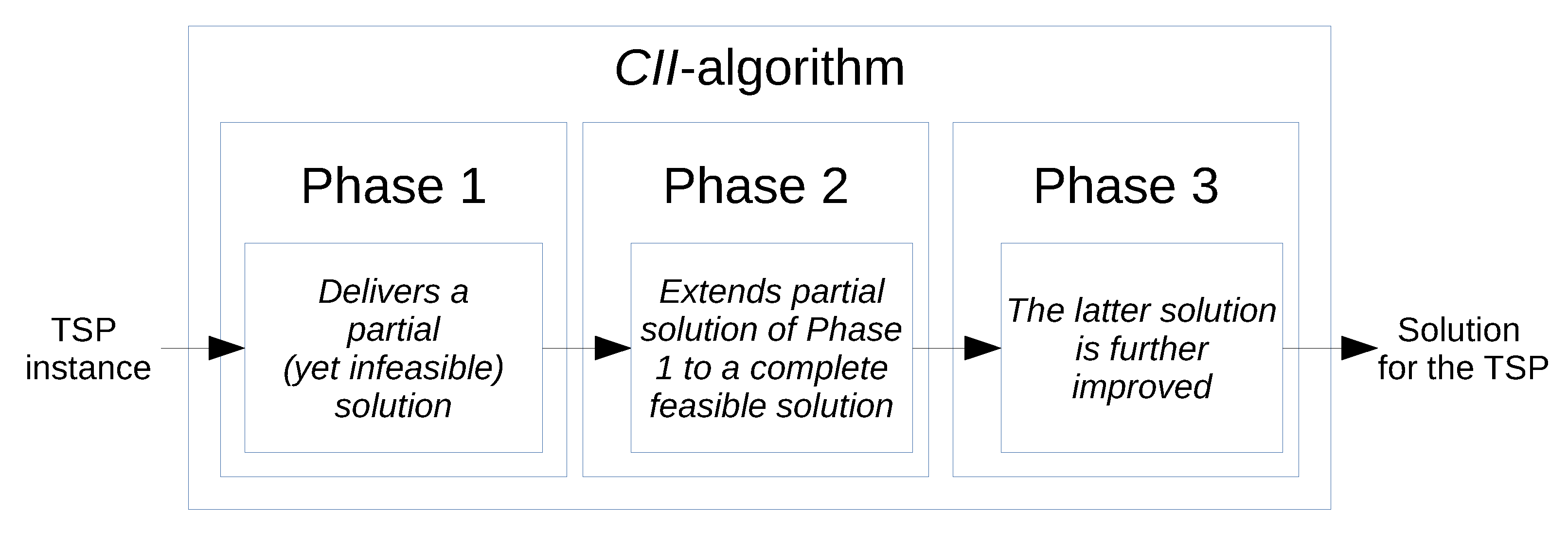
We start this section with a brief aggregated description of our algorithm and in the following subsections we describe its three phases (Figure 1).

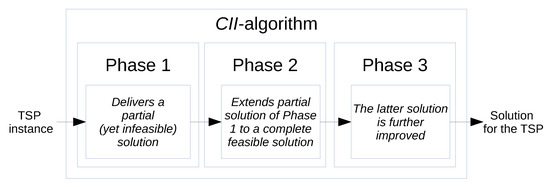
Figure 1. Block diagram of the CII-algorithm: Phase 1 delivers a partial (yet infeasible) solution, Phase 2 extends the partial solution of Phase 1 to a complete feasible solution, and at Phase 3, the latter solution is further improved.

2.1. Phase 1

2.1.1. Procedure to Locate the Extreme Points

At Phase 1, we construct the girding polygon for the points of set V and construct an initial yet infeasible (partial) tour that includes the points of that polygon. The construction of this polygon employs four extreme points $v^1$, $v^2$, $v^3$ and $v^4$; the uppermost, leftmost, lowermost, and rightmost, respectively [14], with ones from set V defined as follows. First, we define the sets of points $T^{\prime },L^{\prime },B^{\prime }$ and $R^{\prime }$ with $T^{\prime }=\{i|y_{i}ismaximum,i\in V\}$, $L^{\prime }=\{i|x_{i}isminimum,i\in V\}$, $B^{\prime }=\{i|y_{i}isminimum,i\in V\}$, and $R^{\prime }=\{i|x_{i}ismaximum,i\in V\}$. Then,

$$v^1=j|x_{j}ismaximum;j\in T^{\prime },$$

(4)

$$v^2=j|y_{j}ismaximum;j\in L^{\prime },$$

(5)

$$v^3=j|x_{j}isminimum;j\in B^{\prime },$$

(6)

and

$$v^4=j|y_{j}isminimum;j\in R^{\prime }.$$

(7)

See the next procedure for the extreme points in Table 1.

Table 1. Procedure extreme_points.

PROCEDURE extreme_points ($\mathit{V}=\{{\mathit{i}}_1,{\mathit{i}}_2,\cdots ,{\mathit{i}}_{\mathit{n}}$})
1	$y_{max}:=y_{i_1}$                                                              //Initializing variables
2	$x_{min}:=x_{i_1}$
3	$y_{min}:=x_{i_1}$
4	$x_{max}:=y_{i_1}$
5	FOR$j:=2$TOnDO
6	IF $y_{i_j}>y_{max}$ THEN $y_{max}:=y_{i_j}$
7	IF $x_{i_j}<x_{min}$ THEN $x_{min}:=x_{i_j}$
8	IF $y_{i_j}<y_{min}$ THEN $y_{min}:=y_{i_j}$
9	IF $x_{i_j}>x_{max}$ THEN $x_{max}:=x_{i_j}$
10	$T^{\prime }=L^{\prime }=B^{\prime }=R^{\prime }:=\varnothing$
11	FOR$j:=1$TOnDO
12	IF $y_{i_j}=y_{max}$ THEN $T^{\prime }:=T^{\prime }\cup \{i_j\}$
13	IF $x_{i_j}=x_{min}$ THEN $L^{\prime }:=L^{\prime }\cup \{i_j\}$
14	IF $y_{i_j}=y_{min}$ THEN $B^{\prime }:=B^{\prime }\cup \{i_j\}$
15	IF $x_{i_j}=x_{max}$ THEN $R^{\prime }:=R^{\prime }\cup \{i_j\}$
16	$v^1:=t_1^{\prime }$        //$T^{\prime }=\{t_1^{\prime },t_2^{\prime },\cdots ,t_{|T^{\prime }|}^{\prime }\}$, $|T^{\prime }|\le n$
17	$v^2:=l_1^{\prime }$        //$L^{\prime }=\{l_1^{\prime },l_2^{\prime },\cdots ,l_{|L^{\prime }|}^{\prime }\}$,   $|L^{\prime }|\le n$
18	$v^3:=b_1^{\prime }$        //$B^{\prime }=\{b_1^{\prime },b_2^{\prime },\cdots ,b_{|B^{\prime }|}^{\prime }\}$, $|B^{\prime }|\le n$
19	$v^4:=r_1^{\prime }$        //$R^{\prime }=\{r_1^{\prime },r_2^{\prime },\cdots ,r_{|R^{\prime }|}^{\prime }\}$, $|R^{\prime }|\le n$
20	FOR$j:=2$TO$|T^{\prime }|$DO
21	IF $x_{t_j^{\prime }}>x_{v^1}$ THEN $v^1:=t_j^{\prime }$
22	FOR$j:=2$TO$|L^{\prime }|$DO
23	IF $x_{l_j^{\prime }}>x_{v^2}$ THEN $v^2:=l_j^{\prime }$
24	FOR$j:=2$TO$|B^{\prime }|$DO
25	IF $x_{b_j^{\prime }}>x_{v^3}$ THEN $v^3:=b_j^{\prime }$
26	FOR$j:=2$TO$|R^{\prime }|$DO
27	IF $x_{r_j^{\prime }}>x_{v^4}$ THEN $v^4:=r_j^{\prime }$
28	RETURN$v^1$, $v^2$, $v^3$, $v^4$

Lemma 1.

The time complexity of Procedure extreme_points is$O\left(n\right)$.

Proof of Lemma 1.

In this and in the following proofs, we only consider those lines in the formal descriptions in which the number of elementary operations, denote it by $f\left(n\right)$, depends on n (ignoring the lines yielding a constant number of operations). In lines 5–9, there is a loop with $n-1$ cycles, hence $\{f(n)=n-1\}$. In lines 11–15, there is a loop with n cycles, hence $\{f(n)=n\}$ In lines 20–21, 22–23, 24–25 and 26–27; there are four loops, each one with at most has n cycles, so $\{f(n)=4n\}$. Hence, the total cost is $O\left(n\right)$. □

2.1.2. Procedure for the Construction of the Girding Polygon

Before we describe the procedure, let us define function $\theta (i,j)$, returning the angle formed between the edge $(i,j)$ and the positive direction of the x-axis (Equation (8) and Figure 2):

$$\theta (i,j)=\left\{\begin{array}{cc}\hfill arccos\frac{x_j-x_i}{w(i,j)}& ifarcsin\frac{y_j-y_i}{w(i,j)}\ge 0,\hfill \\ \hfill -arccos\frac{x_j-x_i}{w(i,j)}& ifarcsin\frac{y_j-y_i}{w(i,j)}<0.\hfill \end{array}\right.$$

(8)

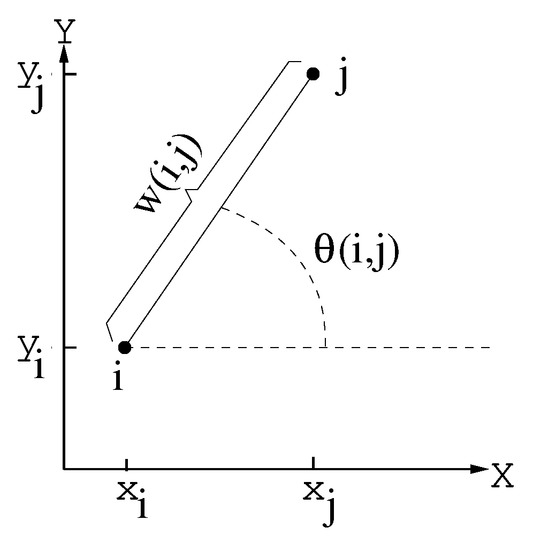
Figure 2. Angle $\theta (i,j)$.

The girding Polygon $P=P\left(V\right)$ is a convex geometric figure in a two-dimensional plane, such that any point in V either belongs to that polygon or to the area of that polygon Vakhania et al. [14].

The input of our procedure for the construction of polygon P (see Table 2), consists of (i) the set of vertices V and (ii) the distinguished extreme points $v^1$, $v^2$, $v^3$ and $v^4$. Abusing slightly the notation, in the description below, we use: (i) P, for the array of the points that form the girding polygon, and (ii) k for the last vertex included so far into the array P. Initially, $P:=\left(v^1\right)$ and $k:=v^1$.

Table 2. Procedure polygon.

PROCEDURE polygon(V, ${\mathit{v}}^1,{\mathit{v}}^2,{\mathit{v}}^3,{\mathit{v}}^4$ )
1	$P:=\left(v^1\right)$                                  //Initializing variables
2	$k:=v^1$
3	WHILE$k\ne v^2$DO                                  //Step 1
4	form a subset of vertices $V^{*}:=\{i|x_i<x_k\wedge y_i\ge y_{v^2};i\in V\}$         //$V^{*}\subset V$
5	form a subset of edges $E^{*}:=\{(k,j);j\in V^{*}\}$                 //$E^{*}\subset E$
6	form a set of angles ${\mathsf{\Theta }}^{*}:=\{\theta (k,j);(k,j)\in E^{*}\}$
7	get the minimum angle $\theta (k,l)$ from ${\mathsf{\Theta }}^{*}$
8	append the vertex l to P and update k equal to l.
9
10	WHILE$k\ne v^3$DO                                  //Step 2
11	form a subset of vertices $V^{*}:=\{i|x_i\le x_{v^3}\wedge y_i<y_k;i\in V\}$
12	form a subset of edges $E^{*}:=\{(k,j);j\in V^{*}\}$
13	form a set of angles ${\mathsf{\Theta }}^{*}:=\{\theta (k,j);(k,j)\in E^{*}\}$
14	get the minimum angle $\theta (k,l)$ from ${\mathsf{\Theta }}^{*}$
15	append the vertex l to P and update k equal to l.
16
17	WHILE$k\ne v^4$DO                                  //Step 3
18	form a subset of vertices $V^{*}:=\{i|x_i>x_k\wedge y_i\le y_{v^4};i\in V\}$
19	form a subset of edges $E^{*}:=\{(k,j);j\in V^{*}\}$
20	form a set of angles ${\mathsf{\Theta }}^{*}:=\{\theta (k,j);(k,j)\in E^{*}\}$
21	get the minimum angle $\theta (k,l)$ from ${\mathsf{\Theta }}^{*}$
22	append the vertex l to P and update k equal to l.
23
24	WHILE$k\ne v^1$DO                                  //Step 4
25	form a subset of vertices $V^{*}:=\{i|x_i\ge x_{v^1}\wedge y_i>y_k;i\in V\}$
26	form a subset of edges $E^{*}:=\{(k,j);j\in V^{*}\}$
27	form a set of angles ${\mathsf{\Theta }}^{*}:=\{\theta (k,j);(k,j)\in E^{*}\}$
28	get the minimum angle $\theta (k,l)$ from ${\mathsf{\Theta }}^{*}$
29	append the vertex l to P and update k equal to l.

Lemma 2.

The time complexity of Procedure polygon is$O\left(n^2\right)$.

Proof of Lemma 2.

There are four independent while statements with similar structure, each of which can be repeated at most n times. In the first line of each of these while statements, in lines 4, 11, 18, and 25, the set of points $V^{*}$ is formed that yields $\{f(n)=2n\}$ operations. In lines 5, 12, 19, and 26, the set of $n-1$ edges $E^{*}$ is formed in time $\{f(n)=n-1\}$. In lines 6, 13, 20, and 27, the set of angles ${\mathsf{\Theta }}^{*}$ consisting of at most $n-1$ elements is formed in time $\{f(n)=n-1\}$. In lines 7, 14, 21, and 28 to find the minimum angle in set ${\mathsf{\Theta }}^{*}$ at most $n-1$ comparisons are needed and the lemma follows. □

In Figure 3, we illustrate an example with $V=\{1,2,\cdots ,6\}$ with coordinates $X=\{x_1,x_2,\cdots ,x_6\}$ and $Y=\{y_1,y_2,\cdots ,y_6\}$. The extreme points are: $v^1=4$, $v^2=2$, $v^3=5$ and $v^4=5$ and $P=(4,2,5,4)$. Initially, $P=\left(4\right)$. Then, vertex 2 is added to polygon in Step 1, vertex 5 is added in Step 2; Step 3 is not carried out because $v^3=v^4$; vertex 4 is added at Step 4.

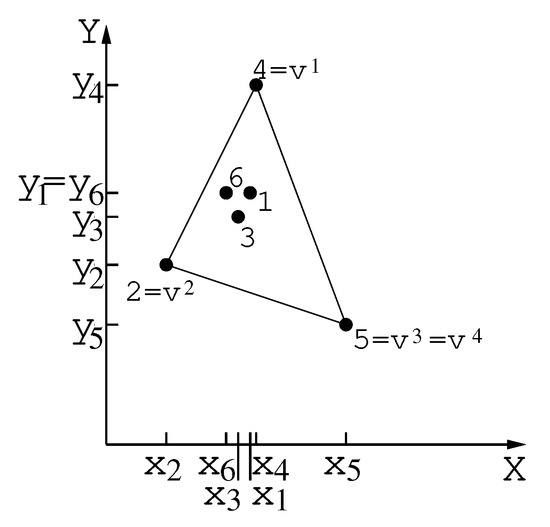
Figure 3. Example that shows the extreme vertices and girding polygon.

Using polygon $P\left(V\right)$ constructed by the Procedure Polygon, we obtain our initial, yet infeasible (partial) tour $T_0=(t_1,t_2,\cdots ,t_m,t_1)$ that is merely formed by all the points $t_1,t_2,\cdots ,t_m$ of that polygon, where $t_1=v^1$ and m is the number of the points.

In the example of Figure 3, P is the initial infeasible tour $T_0=(4,2,5,4)$. $V\backslash T_0=\{1,3,6\}$ is the set of points that will be inserted into the final tour.

2.2. Phase 2

The initial tour of Phase 1 is iteratively extended with new points from the internal area of polygon $P\left(V\right)$ using the cheapest insertion strategy at Phase 2 [15].

Let $l\notin T_{h-1}$ be a candidate point to be included in tour $T_{h-1}$, resulting in an extended tour $T_h$ of iteration $h>0$, and let $t_i\in T_{h-1}$. Due to the triangle inequality, $w(t_i,l)+w(l,t_{i+1})\ge w(t_i,t_{i+1})$; i.e., the insertion of point l between points $t_i$ and $t_{i+1}$, will increase the current total cost $C\left(T_{h-1}\right)$ by $w(t_i,l)+w(l,t_{i+1})-w(t_i,t_{i+1})\ge 0$ (see Figure 4). Once point l is included between points $t_i$ and $t_{i+1}$, for the convenience of the presentation, we let $t_m:=t_{m-1}$, $t_{m-1}:=t_{m-2}$, ⋯, $t_{i+3}:=t_{i+2}$, $t_{i+2}:=t_{i+1}$ and $t_{i+1}:=l$ (due to the way in which we represent our tours, this re-indexing yields no extra cost in our algorithm).

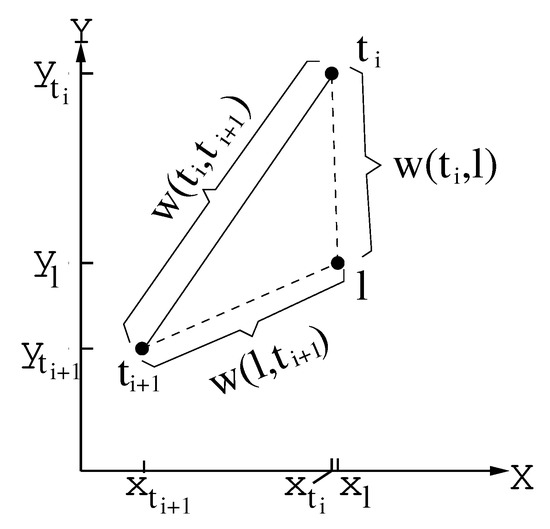
Figure 4. The triangle inequality.

In Table 3, we give a formal description of our procedure that inserts point l between points $t_i$ and $t_{i+1}$ in tour T.

Table 3. Procedure insert_point_in_tour.

PROCEDURE insert_point_in_tour($\mathit{T},\mathit{l},\mathit{i}$)
1	$p:=\left|T\right|$
2	IF$i<p$THEN
3	$j:=p+1$
4	WHILE $j>i+1$ DO
5	$t_j:=t_{j-1}$
6	$j:=j-1$
7	$t_{i+1}:=l$
8	RETURNT

Procedure Construc_tour

At each iteration h, the current tour $T_{h-1}$ is extended by point $l^h\in V\backslash T_{h-1}$ yielding the minimum cost $c_l^h$ (defined below), which represents the increase in the the current total cost $C\left(T_{h-1}\right)$ if that point is included into the current tour $T_{h-1}$. The cost for point $l\in V\backslash T_{h-1}$ is defined as follows:

$$c_l^h=\underset{t_i\in T_{h-1}}{min}\{w(t_i,l)+w(l,t_{i+1})-w(t_i,t_{i+1})\}.$$

(9)

For further references, we denote by $i\left(l\right)$ the index of point $t_i$ for which the above minimum for point l is reached, i.e., $w(t_{i\left(l\right)},l)+w(l,t_{i\left(l\right)+1})-w(t_{i\left(l\right)},t_{i\left(l\right)+1})={min}_{t_i\in T_{h-1}}\{w(t_i,l)+w(l,t_{i+1})-w(t_i,t_{i+1})\}$.

Thus, $l^h$ is a point that attains the minimum

$$min\{c_l^h|l\in V\backslash T_{h-1}\},$$

(10)

whereas the ties can be broken arbitrarily.

To speed up the procedure, we initially calculate the minimum cost for each point $l\in V\backslash T_{h-1}$. After the insertion of point $l^h$, the minimum cost $c_l^h$ is updated as follows:

$$c_l^h:=min\{c_l^{h-1},w(t_i,l)+w(l,t_{i+1})-w(t_i,t_{i+1}),w(t_{i+1},l)+w(l,t_{i+2})-w(t_{i+1},t_{i+2})\}.$$

(11)

We can describe now Procedure construct_tour as shown in Table 4.

Table 4. Procedure construct_tour.

PROCEDURE construct_tour(V, ${\mathit{T}}_0$ )
1	$h:=1$
2	FOR each point $l\in V\backslash T_{h-1}$ DO
3	$c_l^h:={min}_{t_i\in T_{h-1}}\{w(t_i,l)+w(l,t_{i+1})-w(t_i,t_{i+1})\}$
4	WHILE exists a vertex $l\in V\backslash T_{h-1}$ DO
5	get $l^h$
6	insert_point_in_tour ($T_{h-1},l^h,i(l^h)$)
7	FOR each point $l\in V\backslash T_h$ DO
8	$c_l^{h+1}:=min\{c_l^h,w(t_i,l)+w(l,t_{i+1})-w(t_i,t_{i+1}),w(t_{i+1},l)+w(l,t_{i+2})-w(t_{i+1},t_{i+2})\}$
9	$h:=h+1$

Lemma 3.

The time complexity of the Procedure construct_tour is$O(n^2)$.

Proof of Lemma 3.

In lines 2–3, there is a for statement with $n-(m+h-1)$ repetitions. To calculate $c_l^h$ in line 3, the same number of repetitions is needed and the total cost of the for statement is $[n-(m+h-1)][n-(m+h-1)]=[n^2-2(m+h-1)n+{(m+h-1)}^2]$. The while statement in lines 4–9 is repeated at most $n-(m+h-1)$ times. In line 5, to calculate $c_{l^h}^h$ (Equation (10)) $n-(m+h-1)$ comparisons are required. In lines 7–8, there is a for statement nested in the above while statement with $n-(m+h)$ repetitions. Hence, the total cost is $[n^2-2(m+h-1)n+{(m+h-1)}^2]+[n-(m+h-1)]\{[n-(m+h-1)]+[n-(m+h)]\}=[n^2-2(m+h-1)n+(m^2-2m-2h+h^2+1)]+[n-(m+h-1)][2n-(2m+2h-1)]=[n^2-(2m+2h-2)n+(m^2-2m-2h+h^2+1)]+[2n^2-(4m+4h-3)n+(2m^2+4mh-3m-3h+2h^2+1)]=3n^2-(6m+6h-5)n+(3m^2+4mh-5m-5h+3h^2+2)=O\left(n^2\right)$. □

In the example of Figure 5, $T_0=(4,2,5)$. The costs $c_l^1$, $l\in V\backslash T_0$, are calculated as follows: $\begin{array}{ll}{c}_1^1& =min\{w(4,1)+w(1,2)-w(4,2),w(2,1)+w(1,5)-w(2,5),w(5,1)+w(1,4)-w(5,4)\}\\ & =w(5,1)+w(1,4)-w(5,4),\\ c_3^1& =min\{w(4,3)+w(3,2)-w(4,2),w(2,3)+w(3,5)-w(2,5),w(5,3)+w(3,4)-w(5,4)\}\\ & =w(4,3)+w(3,2)-w(4,2),\\ c_6^1& =min\{w(4,6)+w(6,2)-w(4,2),w(2,6)+w(6,5)-w(2,5),w(5,6)+w(6,4)-w(5,4)\}\\ & =w(4,6)+w(6,2)-w(4,2)\end{array}$.

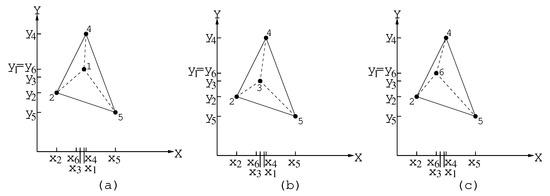
Figure 5. Points 1, 3, and 6 that can be inserted between point 4 and 2, 2 and 5, or 5 and 4 from partial tour $T_0$ are depicted in Figures (a), (b), and (c), respectively.

Hence, $min\{c_1^1,c_3^1,c_6^1\}=c_6^1=w(4,6)+w(6,2)-w(4,2)$; $l^1=6$ and $i\left(6\right)=4$. Therefore, point 6 will be included in tour $T_1$ between points 4 and 2 (Figure 6).

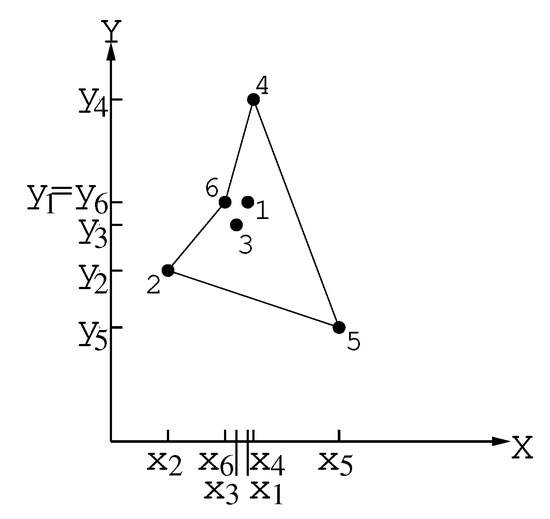
Figure 6. Point 6 was inserted in the tour $T_0$ between points 4 and 2.

Now, $T_1=(4,6,2,5,4)$ and the minimum costs $c_l^2$ for each point $l\in V\backslash T_1$ are: $\begin{array}{ll}{c}_1^2& =\{c_1^1,w(4,1)+w(1,6)-w(4,6),w(6,1)+w(1,2)-w(6,2)\}\\ & =w(4,1)+w(1,6)-w(4,6).\\ c_3^2& =\{c_3^1,w(4,3)+w(3,6)-w(4,6),w(6,3)+w(3,2)-w(6,2)\}\\ & =w(6,3)+w(3,2)-w(6,2)\end{array}$.

Hence, $min\{c_1^2,c_3^2\}=c_3^2=w(6,3)+w(3,2)-w(6,2)$; $l^2=3$ and $i\left(3\right)=6$. Therefore, point 3 will be included in tour $T_2$ between points 6 and 2 (Figure 7).

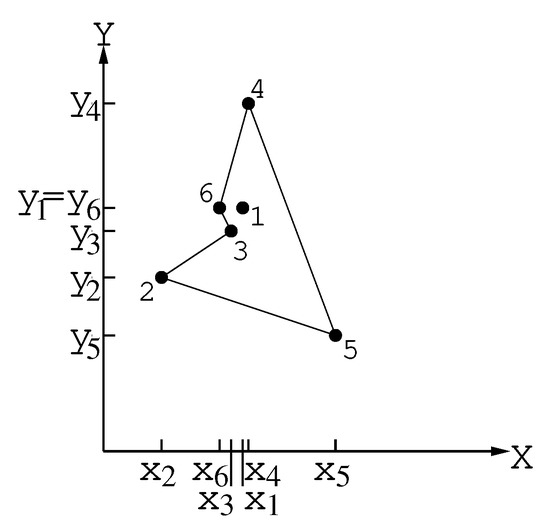
Figure 7. Point 3 was inserted in the tour $T_1$ between points 6 and 2.

Now, $T_2=(4,6,3,2,5,4)$ and the minimum costs $c_l^3$, $l\in V\backslash T_2$ are

$c_1^3=\{c_1^2,w(6,1)+w(1,3)-w(6,3),w(3,1)+w(1,2)-w(3,2)=c_1^2$.

Hence, $min\{c_1^3\}=c_1^2=w(4,1)+w(1,6)-w(4,6)$; $l^3=1$ and $=i\left(1\right)=4$. Therefore, point 1 will be included in tour $T_3$ between points 4 and 6 (Figure 8).

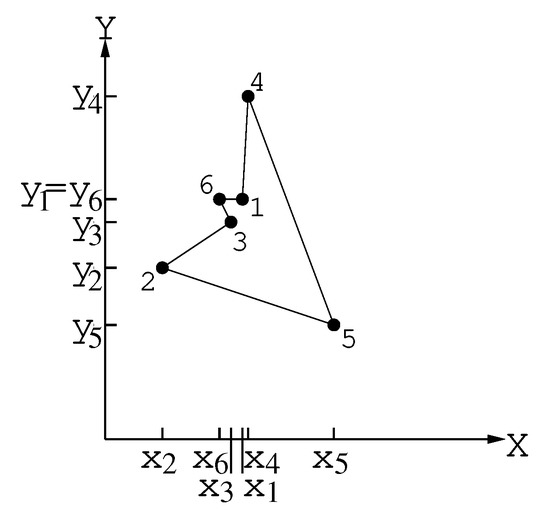
Figure 8. Point 1 be inserted in the tour $T_2$ between points 4 and 6.

The resultant tour $T=T_3=(4,1,6,3,2,5,4)$ includes all points from set V and Procedure construct_tour halts.

2.3. Phase 3

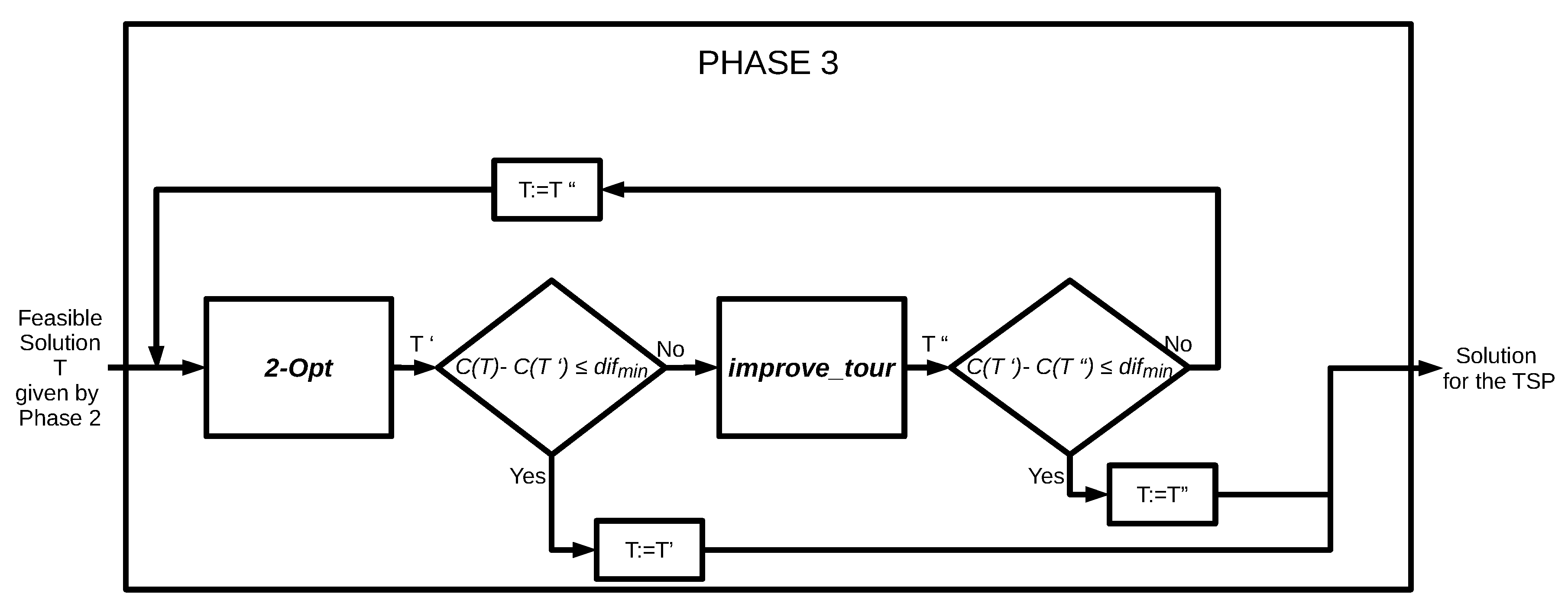
At Phase 3, we iteratively improve the feasible tour T delivered by Phase 2. We use two heuristic algorithms. The first one is called 2-Opt, which is a local search algorithm proposed by Croes [13]. The second one is based on our construct_tour procedure, named improve_tour. The current solution (initially, it is the tour delivered by Phase 2) is repeatedly improved first by 2-Opt-heuristics and then by Procedure improve_tour, until there is an improvement. Phase 3 halts if either the output of one of the heuristics has the same objective value as the input (by the construction, the output cannot be worse than the input) or the following condition is satisfied:

$$C\left(T_{in}\right)-C\left(T_{out}\right)\le di{f}_{min},$$

(12)

where $di{f}_{min}$ is a constant (for instance, we let $di{f}_{min}=0.0001$). Thus, initially, 2-Opt-heuristics runs with input T. Repeatedly, Condition (12) is verified for the the output of every call of each of the heuristics. If it is satisfied, Phase 3 halts; otherwise, for the output of the last called heuristics, the other one is invoked and the whole procedure is repeated; see Figure 9.

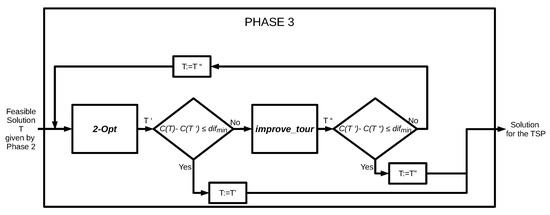
Figure 9. Block diagram of Phase 3.

2.3.1. Procedure 2-Opt

Procedure 2-Opt is a local search algorithm improving feasible solution $T=(t_1,t_2,\cdots ,t_n,t_1)$ ($n=\left|V\right|$). It is well-known that the time complexity of this procedure is $O\left(n^2\right)$. For the completeness of our presentation, we give a formal description of this procedure in Table 5.

Table 5. Procedure 2-Opt.

PROCEDURE 2-Opt(V,T)
1	$i:=1$
2	$n:=\left|V\right|$
3	WHILE$i<n-2$DO
4	$j:=i+1$;
5	WHILE $j<n-1$ DO
6	IF $w(t_i,t_j)+w(t_{i+1},t_{j+1})<w(t_i,t_{i+1})+w(t_j,t_{j+1})$ THEN
7	$x:=i+1$
8	$y:=j$
9	WHILE $x<y$ DO
10	$t_{aux}:=t_x$
11	$t_x:=t_y$
12	$t_y:=t_{aux}$
13	$x:=x+1$
14	$y:=y-1$
15	$j:=j+1$
16	$i:=i+1$
17	RETURNT

The result of a local replacement carried out by the procedure is represented schematically in the Figure 10).

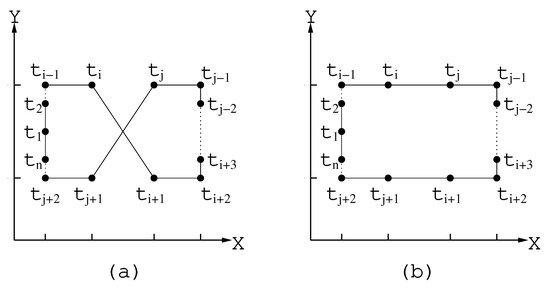
Figure 10. (a) a fragment of a solution before applying the algorithm 2-Opt; (b) the corresponding fragment after applying algorithm 2-Opt.

2.3.2. Procedure improve_tour

We also use our algorithm construct_tour to improve a feasible solution $T=(t_1,t_2,\cdots ,t_n,t_1)$, $n=\left|V\right|$. Iteratively, point $t_{i+1}$, $1\le i<n$, is removed from the tour T and is reinserted by a call of procedure construct_tour $(V,T\backslash \{t_{i+1}\})$. If a removed point gets reinserted in the same position, then $i:=i+1$ and the procedure continues until $i\le n$ (see Table 6).

Table 6. Procedure improve_tour.

PROCEDURE improve_tour(V,T)
1	$i:=1$
2	WHILE$i<n$DO
3	$t_j:=t_{i+1}$
4	remove $t_{i+1}$ from the tour T      //now T is infeasible
5	construct_tour(V, $T\backslash \{t_{i+1}\}$)      //T is feasible again
6	IF $t_{i+1}=t_j$ THEN
7	$i:=i+1$
8	RETURNT

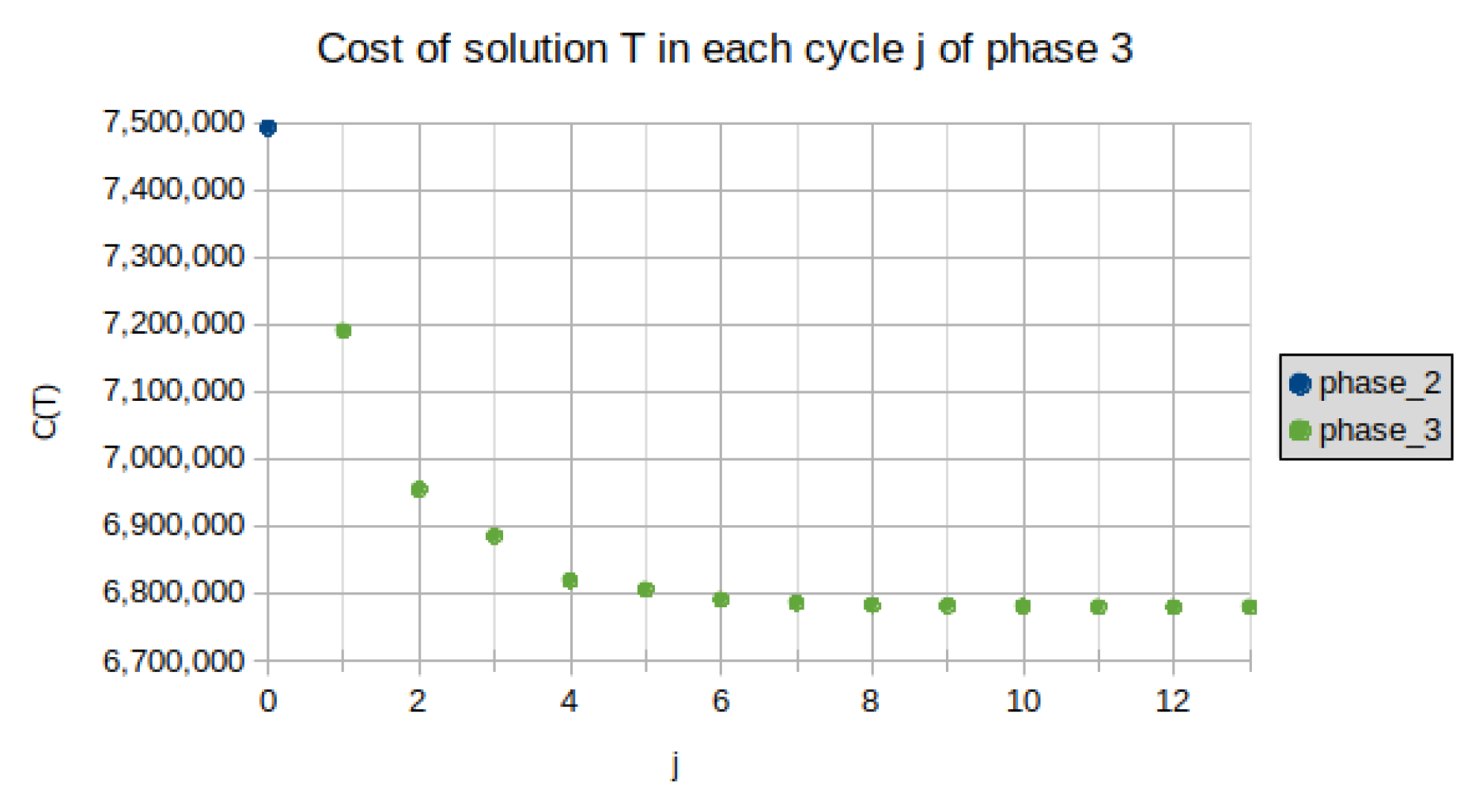
Figure 11 illustrates the iterative improvement in the cost of the solutions obtained at Phase 3 for a sample problem instance usa115475. The initial solution $T_0$ of Phase 2 is iteratively improved as shown in the diagram.

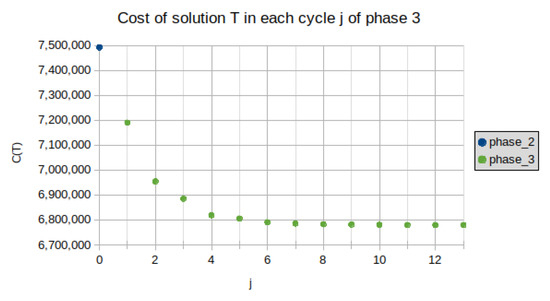
Figure 11. The improvement rate at Phase 3 for instance usa115475.

Lemma 4.

The time complexity of the Procedure improve_tour is$O\left(n^2\right)$.

Proof of Lemma 4.

In lines 2–7, there is a while statement with $n-1$ repetitions. The call of Procedure construct_tour in line 5 yields the cost $O\left(n\right)$ since with $m=n-1$, $h=1$; see the proof of Lemma 3 (m is the number of points in the current partial tour). The lemma follows. □

3. Implementation and Results

CII-algorithm was coded in C++ and compiled in g++ on a server with processor 2x Intel Xeon E5-2650 0 @ 2.8 GHz (Cuernavaca, Mor., Mexico), 32 GB in RAM and Ubuntu 18.04 (bionic) operating system (we have used only one CPU in our experiments). We did not keep the cost matrix in computer memory, but we have rather calculated the costs using the coordinates of the points. This does not increase the computation time too much and saves considerably the required computer memory.

We have tested the performance of CII-algorithm for 85 benchmark instances from TSPLIB [16] library and for 135 benchmark instances from TSP Test Data [17] library. The detailed results are presented in the Appendix. In our tables, parameter “Error” specifies the approximation factor of algorithm H compared to cost of the best known solution (C(BKS)):

$$Erro{r}_H=\left|\frac{C\left(BKS\right)-C\left(T_H\right)}{C\left(BKS\right)}\right|100\%.$$

(13)

In Table 7 below, we give the data on the average performance of our heuristics. The average error percentage of our heuristics is calculated using Formula (13). It shows, for each group of instances, the average error of the solutions delivered by Phase 2 and, at Phase 3, the number of cycles at Phase 3 and the average decrease in the cost of the solution decreased at Phase 3 compared to that Phase 3.

Table 7. Statistics about the solutions delivered by CII.

Description	TSPLIB	NATIONAL	ART GALLERY	VLSI	All
Number of instances	83	27	6	102	218
Average error percentage of the solutions at Phase 2	11.8%	17.7%	6.7%	18.4%	15.4%
Average number of cycles performed at Phase 3	7	11	11	10	9
Average decrease in error at Phase 3	6.5%	9.6%	3.1%	9.8%	8.3%
Final average error percentage	5.3%	8.2%	3.6%	8.6%	7.2%
Average memory usage	0.8 MiB	1.6 MiB	10.9 MiB	2.3 MiB	1.88 MiB

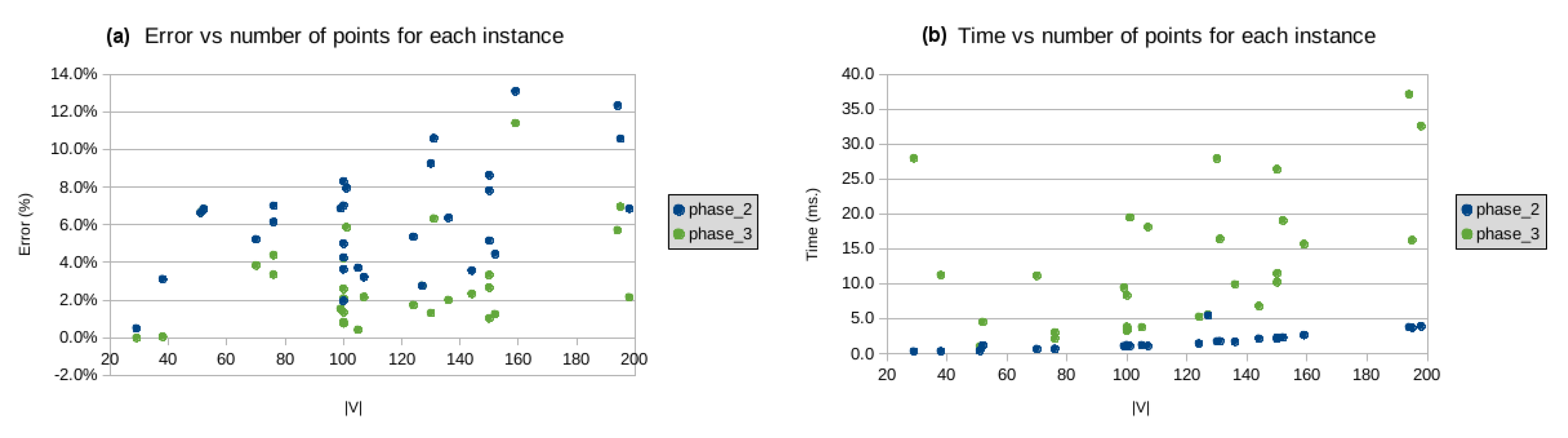
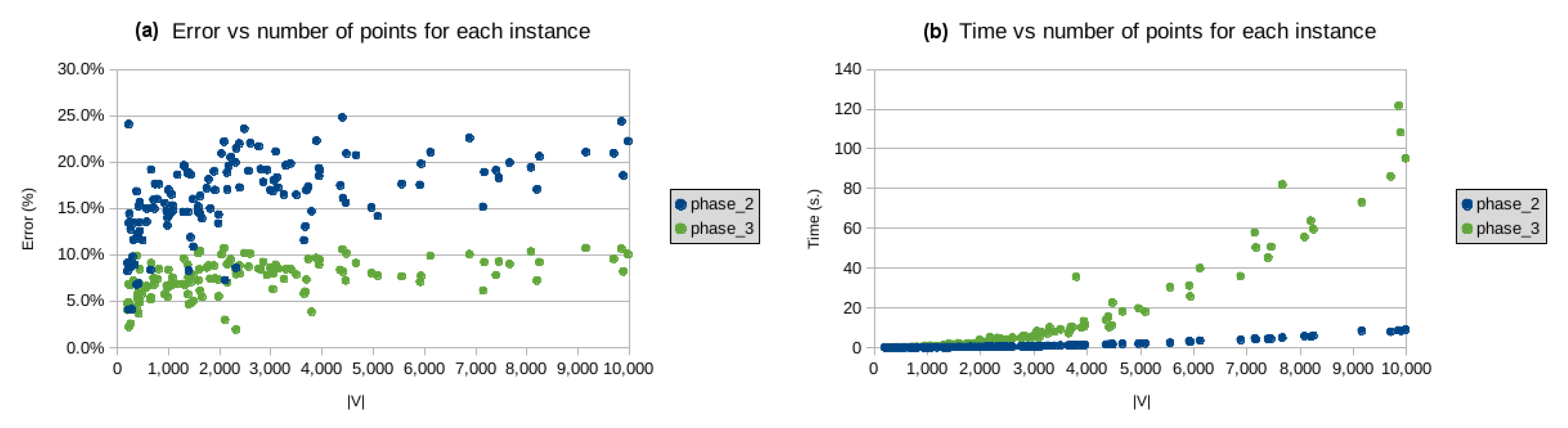
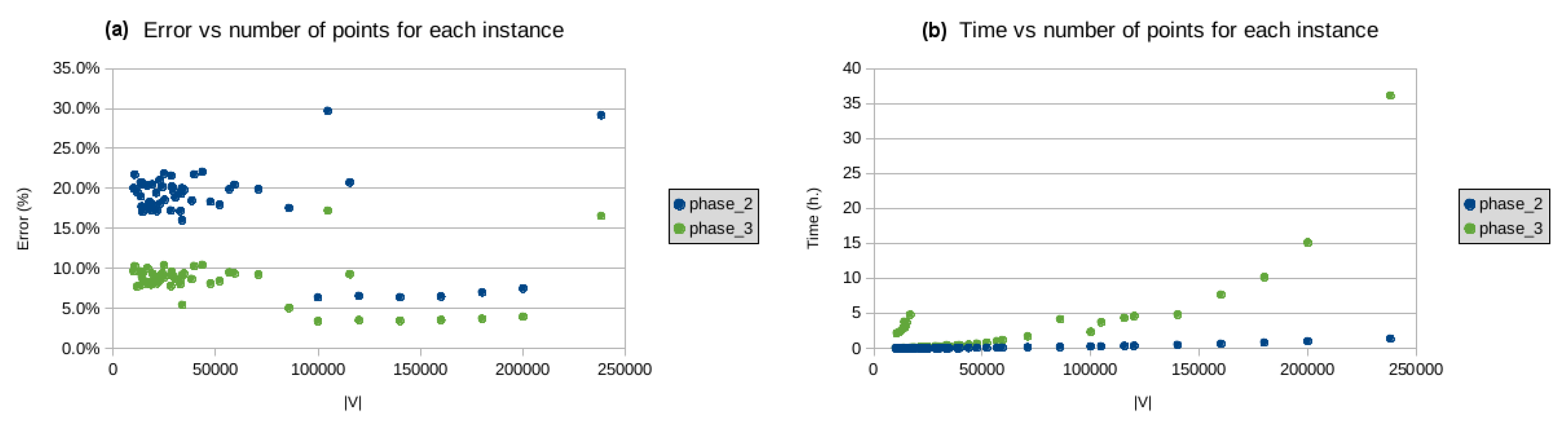
In the diagrams below (on the left hand-side), we illustrate the dependence of the approximation given by our algorithm on the size of the tested instances, and the dependence of the execution time of our algorithm on the size of the instances (right hand-side diagrams). We classify the tested instance into three groups: the small ones (from 1 to 199 points in Figure 12), the middle-sized ones (from 200 to 9999 points in Figure 13), and large instances (from 10,000 to 250,000 in Figure 14). We do not include the data for the largest two problem instances lra498378 and lrb744710 because of the visualization being technically complicated. The error for these instances is 12.5% and 15.9%, respectively, and the CPU time was limited to two weeks for both instances. As we can see, at Phase 3, there is an improvement in the quality of the solutions delivered by Phase 2.

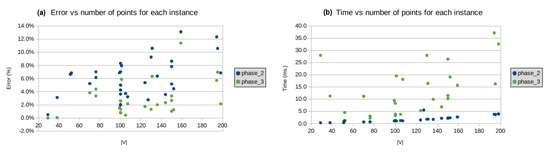
Figure 12. (a) error vs. number of points, and (b) processing time vs. number of points, where $1\le \left|V\right|<200$.

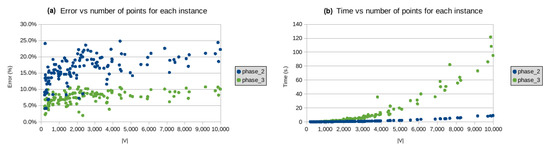
Figure 13. (a) error vs. number of points, and (b) processing time vs. number of points, where $200\le \left|V\right|<10,000$.

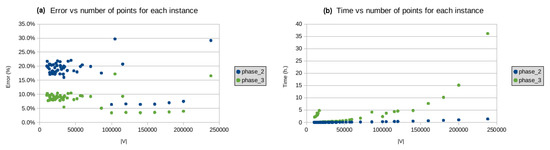
Figure 14. (a) error vs. number of points, and (b) processing time vs. number of points, where $\mathrm{10,000}\le \left|V\right|<\mathrm{250,000}$.

Table 8 shows the summary of the comparison statistics of the solutions delivered by our algorithm CII with the solutions obtained by the heuristics that we have mentioned in the introduction (namely, DFACO [10], ACO-3Opt [10], ESACO [7], PACO-3Opt [8], DPIO [12], ACO-RPMM [9], Partial ACO [6], and PRNN [11]). We may observe in Table 9 that algorithm CII has attained an improved approximation for 17 instances. At the same time, in terms of the execution time, our heuristic dominates the other heuristics.

Table 8. Statistics between CII and other heuristics.

Description	TSPLIB	NATIONAL	ART GALLERY	VLSI	All
Number of instances	83	27	6	102	218
Number of the known results from other heuristics	142	0	10	12	164
Number of time CII gave a better error than other heuristics	2	0	4	12	18
Number of times CII has improved the earlier known best execution time	140	0	0		140

Table 9. Comparative relative errors for some problem instances.

Description	${\mathit{Error}}_{\mathit{CII}}$	${\mathit{Error}}_{\mathit{H}}$
TSPLIB/rat783	7.4%	19.1% and 19.5% (DFACO [10] and ACO-3Opt [10])
ART/Mona-lisa100K	3.4%	5.5% (Partial ACO [6])
ART/Vangogh120K	3.5%	5.8% (Partial ACO [6])
ART/Venus140K	3.4%	5.8% (Partial ACO [6])
ART/Earring200K	3.9%	7.2% (Partial ACO [6])
VLSI/dca1376	7.6%	19.6% (PRNN [11])
VLSI/djb2036	10.0%	23.4% (PRNN [11])
VLSI/xqc2175	9.1%	21.4% (PRNN [11])
VLSI/xqe3891	9.7%	21.7% (PRNN [11])
VLSI/bgb4355	8.4%	22.8% (PRNN [11])
VLSI/xsc6880	10.1%	21.9% (PRNN [11])
VLSI/bnd7168	9.2%	21.7% (PRNN [11])
VLSI/ida8197	7.2%	23.2% (PRNN [11])
VLSI/dga9698	9.6%	21.1% (PRNN [11])
VLSI/xmc10150	9.6%	20.3% (PRNN [11])
VLSI/xvb13584	9.5%	23.6% (PRNN [11])
VLSI/frh19289	9.3%	22.5% (PRNN [11])

In the Table 9, we specify the problem instances for which our algorithm provided a better relative error than some of the earlier cited algorithms.

In terms of the CPU time comparison, see Table 10.

Table 10. Comparative CPU time for the problem instances for which the other heuristics were faster.

Description	${\mathit{Time}}_{\mathit{CII}}$	${\mathit{Time}}_{\mathit{H}}$
TSPLIB/pla33810	25.7 m	21.0 m (DPIO [12])
TSPLIB/pla85900	4.1 h	1.4 h (DPIO [12])
Art Gallery/mona-lisa100K	2.3 h	1.4 h and 1.1 h (ACO-RPMM [9] and Partial ACO [6])
Art Gallery/vangogh120K	4.6 h	1.9 h and 1.5 h (ACO-RPMM [9] and Partial ACO [6])
Art Gallery/venus140K	4.8 h	2.6 h and 2.1 h (ACO-RPMM [9] and Partial ACO [6])
Art Gallery/pareja160K	7.7 h	3.5 h (ACO-RPMM [9])
Art Gallery/coubert180K	10.1 h	4.5 h (ACO-RPMM [9])
Art Gallery/earring200K	15.1 h	6.0 h and 5.1 h (ACO-RPMM [9] and Partial ACO [6])

In the diagram below (Figure 15), we illustrate the dependence of the memory used by our algorithm of all tested instances.

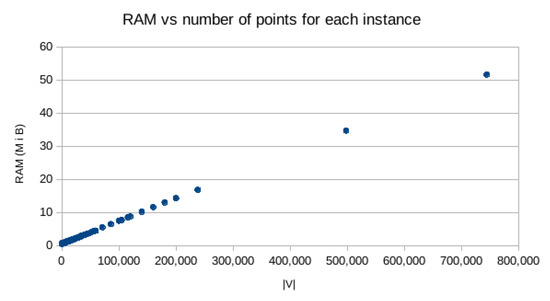
Figure 15. RAM vs. number of points for all the tested instances.

4. Conclusions and Future Work

We have presented a simple, easily implementable and fast heuristic algorithm for the Euclidean traveling salesman problem that solves both small and large scale instances with an acceptable approximation and consumes a little computer memory. Since the algorithm uses simple geometric calculations, it is easily implementable. The algorithm is fast, the first two phases run in time $O\left(n^2\right)$, whereas the number of the improvement repetitions in the third phase, in practice, is not large. The first two phases might be used independently from the third phase, for instance, for the generation of an initial tour in more complex loop improvement heuristics. The quality of the solution delivered already by Phase 2 is acceptable and is expected to greatly outperform that of a random solution used normally to initiate meta-heuristic algorithms. We have implemented NN (Nearest Neighborhood) heuristics and run the code for the benchmark instances (the initial vertex for NN heuristic was selected randomly). Phase 2 gave essentially better results. In average, for the tested 135 instances (6 large, 32 Medium and 97 small ones), the difference between the approximation factor obtained by the procedure of Phase 2 and that of Nearest Neighbor heuristic was $9.65\%$ (the average error of Phase 2 was 16.89% and that of NN was 26.55%, whereas the standard deviations were similar, 0.05% and 0.04%, respectively). As for the overall algorithm, it uses a negligible computer memory. Although for most of the tested benchmark instances it did not improve the best known results, the execution time of our heuristic, on average, was better than the earlier reported best known times. For future work, we intend to create a more powerful, yet more complex, CII-algorithm by augmenting each of the three phases of our algorithm with alternative ways for the creation of the initial tour and alternative insertion and improvement procedures.