Top Position Sensitive Ordinal Relation Preserving Bitwise Weight for Image Retrieval
Abstract
1. Introduction
- (1)
- When learning binary codes and bitwise weights, we propose to penalize data points without preserving an ordinal relation at the top position of a ranking list more than those at the bottom. This measure helps to reduce the probability of chaos ranking occurring at the top position.
- (2)
- Unlike a general two-step mechanism, we simultaneously learn binary codes and bitwise weights by an iterative mechanism, and they can feedback into each other. When the mechanism converges, the binary codes and bitwise weights are effectively adapted to each other.
- (3)
- A tensor ordinal graph (TOG) is precomputed to represent a relative similarity relationship of any two data pairs, which can effectively reduce the training complexity.
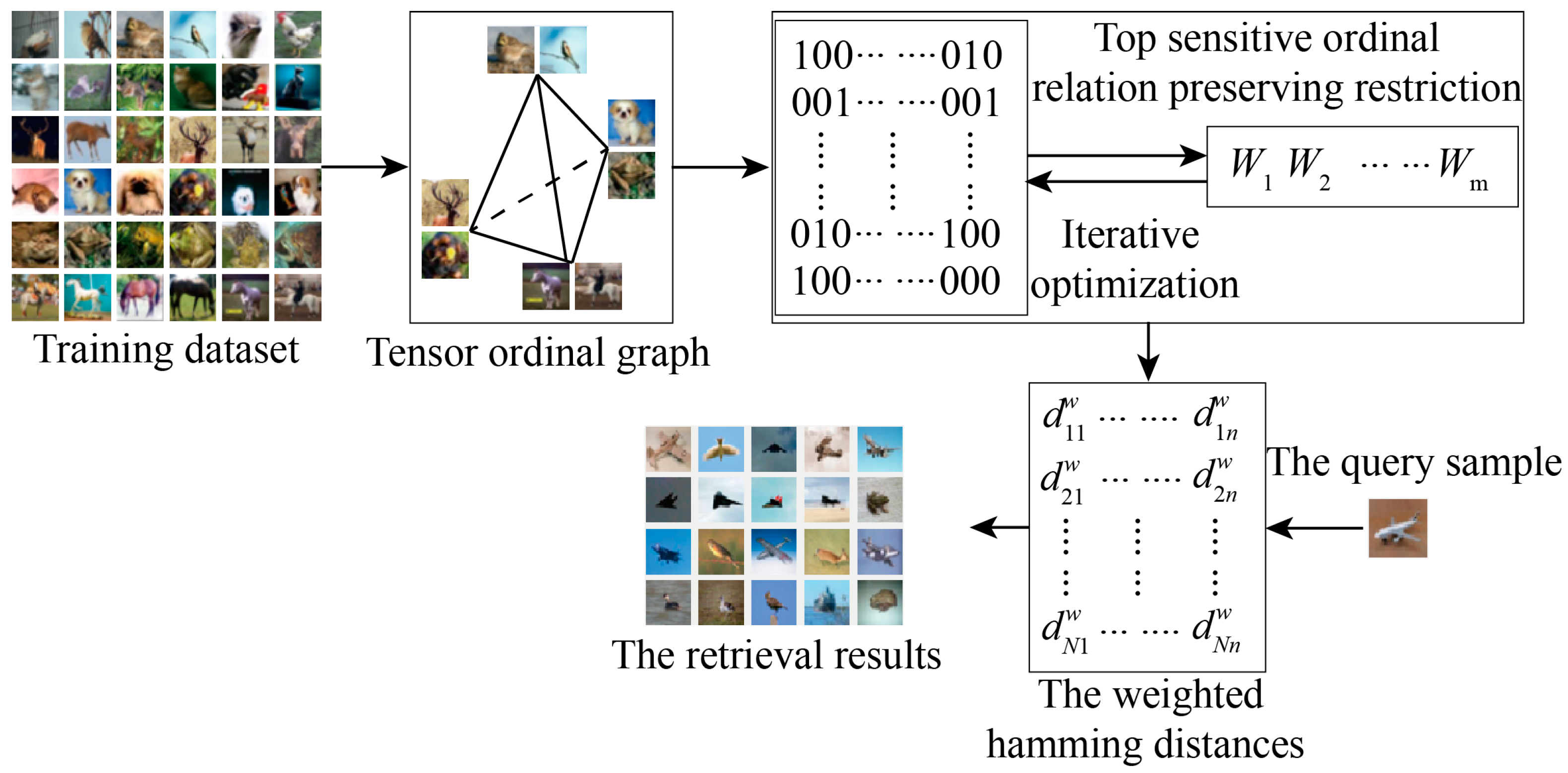
2. Method
2.1. Top-Position-Sensitive Ordinal-Relation-Preserving Restriction
2.2. Relaxation and Iterative Optimization
| Algorithm 1 TORBW |
| Input: Data set X={x1,⋯, xn}, the number of binary bits r, and parameters λ1 and λ2. Output: The coefficients of hash functions (u1, ⋯, ur) and bitwise weight functions (v1, ⋯, vr). 1: Choose training samples from X by the k-means algorithm; 2: Compute an affinity graph S and a dissimilar graph DS by Equation (5); 3: Construct a tensor ordinal graph G by Equation (6); 4: Generate an ordinal relations set of triplet elements (xi, xj, xk) by G 5: for c=1:r 6: repeat 7: Compute the partial derivation by Equation (13); 8: Update the value of uc by Equation (15); 9: Compute the partial derivation by Equation (16); 10: Update the value of vc by Equation (17); 11: until convergence or reaching the maximum iteration number 12: end for. |
3. Experimental Results and Discussion
3.1. Database and Setup
3.2. Compared Methods and Evaluation Metrics
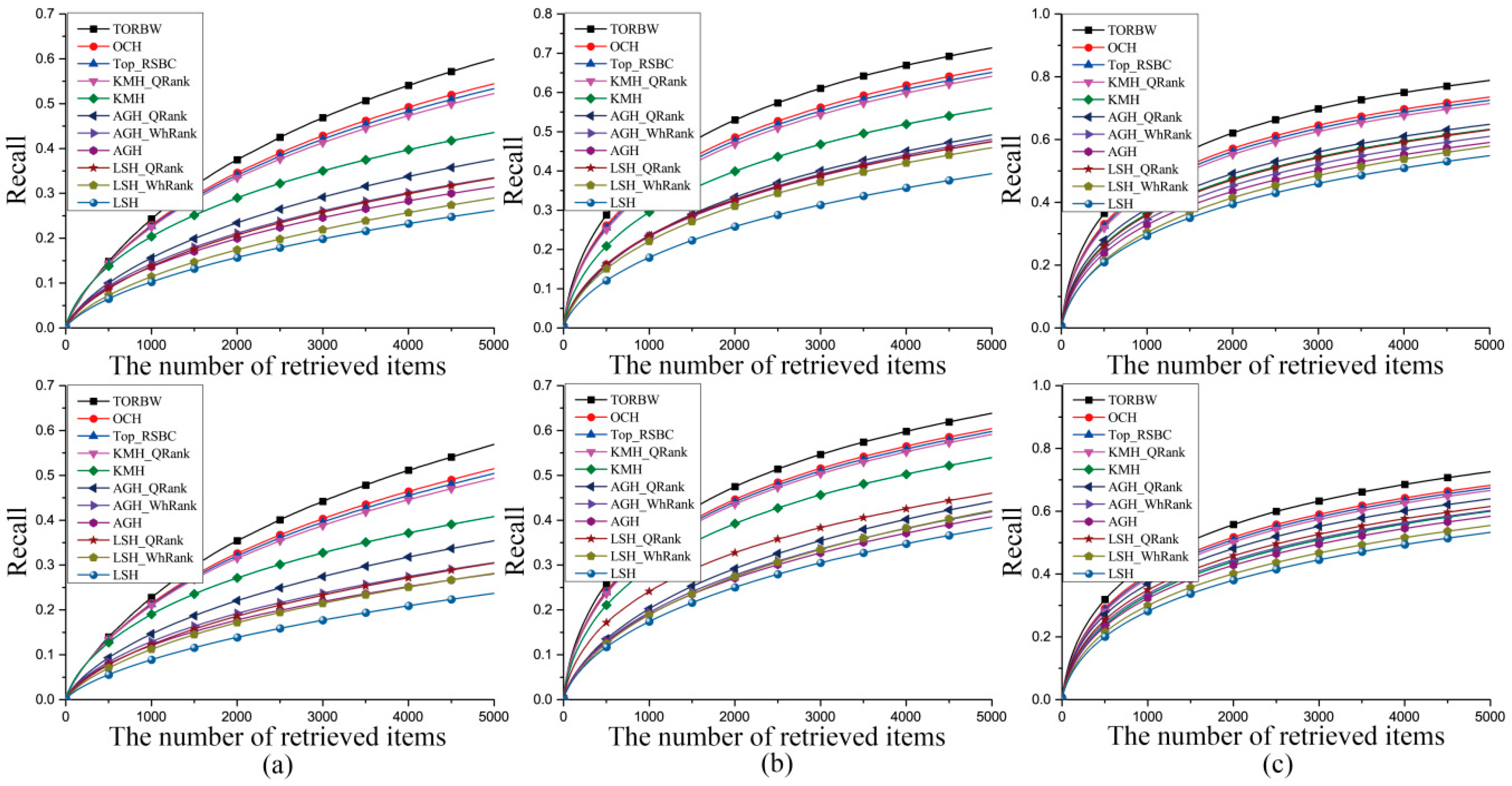
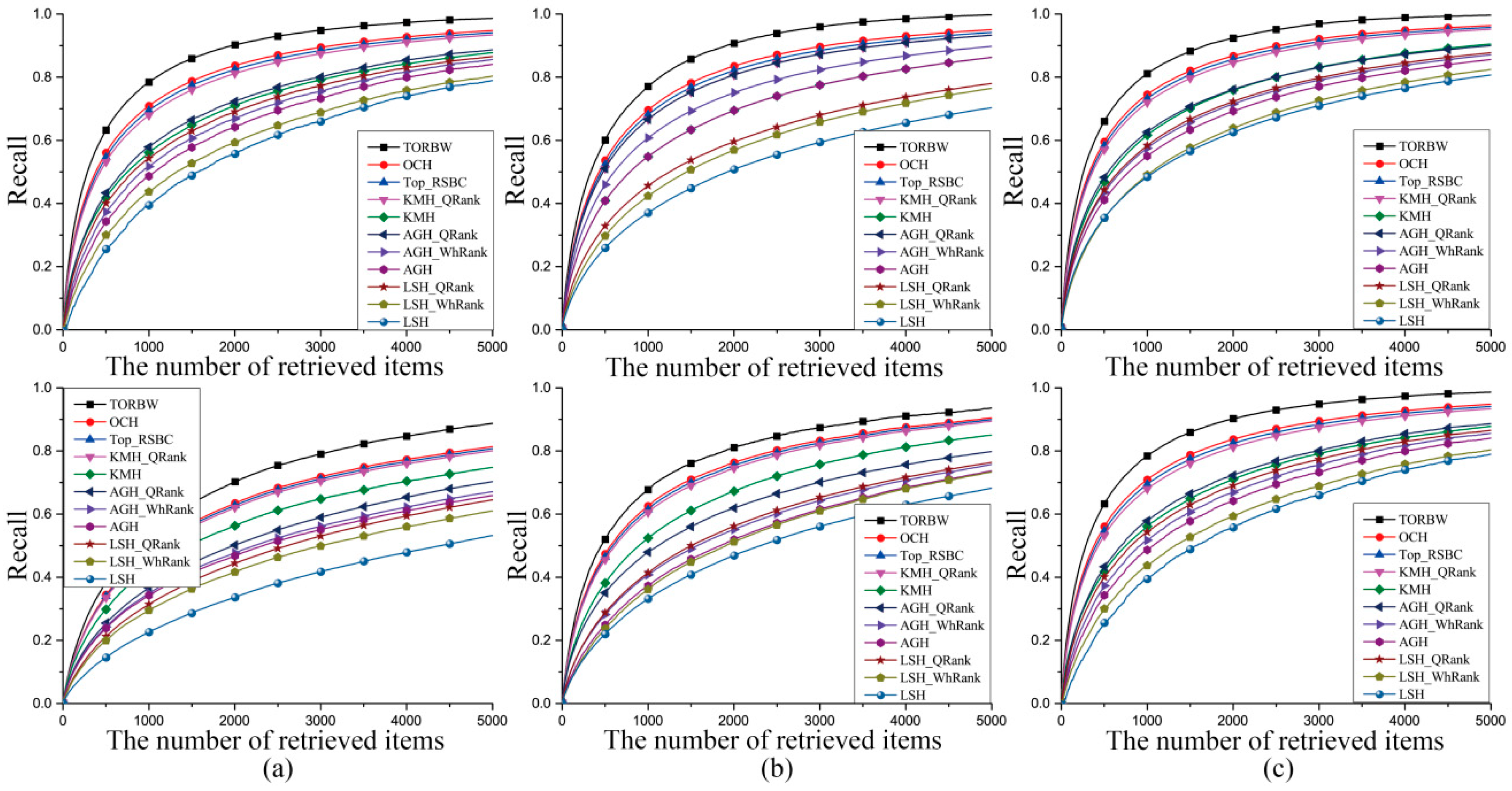
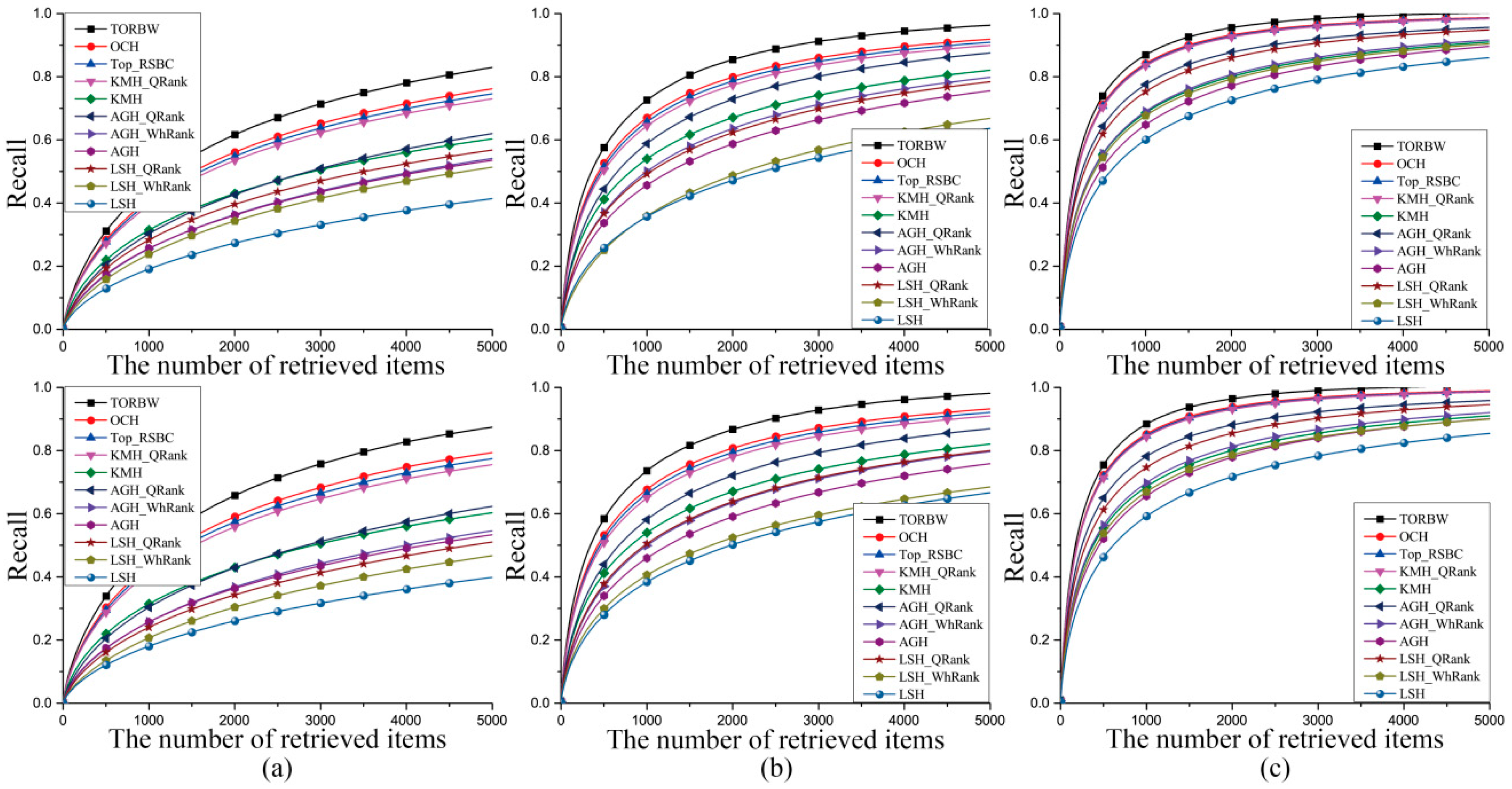
3.3. Experimental Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, H.; Ji, R.; Wu, Y.; Huang, F. Ordinal constrained binary code learning for nearest neighbor search. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2019; Volume 41, pp. 941–955. [Google Scholar]
- Luo, X.; Zhang, P.F.; Huang, Z.; Nie, L.Q.; Xu, X.S. Discrete hashing with multiple supervision. IEEE Trans. Image Process. 2019, 28, 2962–2975. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.S.; Han, J.G.; Guo, Y.C.; Liu, L.; Ding, G.; Ni, Q.; Shao, L. Unsupervised deep video hashing via balanced code for large-scale video retrieval. IEEE Trans. Image Process. 2019, 28, 1993–2007. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.D.; Li, C.X.; Luo, X.; Nie, L.; Zhang, W.; Xu, X.S. Scratch: A scalable discrete matrix factorization hashing framework for cross-modal retrieval. IEEE Trans. Circ. Syst. Video 2019. [Google Scholar] [CrossRef]
- Ding, K.; Yang, Z.; Wang, Y.; Liu, Y. An improved perceptual hash algorithm based on u-net for the authentication of high-resolution remote sensing image. Appl. Sci. 2019, 9, 2972. [Google Scholar] [CrossRef]
- Yang, H.; Yin, J.; Jiang, M. Perceptual image hashing using latent low-rank representation and uniform lbp. Appl. Sci. 2018, 8, 317. [Google Scholar] [CrossRef]
- Datar, M.; Immorlica, N.; Indyk, P.; Mirrokni, V.S. Locality-sensitive hashing scheme based on p-stable distributions. In Proceedings of the Annual Symposium on Computational Geometry, Brooklyn, NY, USA, 8–11 June 2004. [Google Scholar]
- Liu, W.; Wang, J.; Kumar, S.; Chang, S.F. Hashing with graphs. In Proceedings of the International Conference on Machine Learning, Bellevue, WA, USA, 28 June–2 July 2011. [Google Scholar]
- He, K.; Wen, F.; Sun, J. K-means hashing: An affinity-preserving quantization method for learning binary compact codes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013. [Google Scholar]
- Gong, Y.; Lazebnik, S. Iterative quantization: A procrustean approach to learning binary codes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011. [Google Scholar]
- Norouzi, M.; Fleet, D.J. Minimal loss hashing for compact binary codes. In Proceedings of the International Conference on Machine Learning, Bellevue, WA, USA, 28 June–2 July 2011. [Google Scholar]
- Salakhutdinov, R.; Hinton, G. Semantic hashing. Int. J. Approx. Reason. 2009, 50, 969–978. [Google Scholar] [CrossRef]
- Wang, J.; Wang, J.; Yu, N.; Li, S. Order preserving hashing for approximate nearest neighbor search. In Proceedings of the ACM International Conference on Multimedia, Barcelona, Spain, 21–25 October 2013. [Google Scholar]
- Norouzi, M.; Blei, D.M.; Salakhutdinov, R. Hamming distance metric learning. In Proceedings of the Advances in Neural Information Processing Systems, Harrahs and Harveys, Lake Tahoe, Stateline, NV, USA, 3–6 December 2012. [Google Scholar]
- Wang, J.; Liu, W.; Sun, A.X.; Jiang, Y.G. Learning hash codes with listwise supervision. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, NSW, Australia, 1–8 December 2013. [Google Scholar]
- Dizaji, G.K.; Zheng, F.; Nourabadi, S.N.; Yang, Y.; Deng, C.; Huang, H. Unsupervised deep generative adversarial hashing network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Shen, F.; Xu, Y.; Liu, L. Unsupervised deep hashing with similarity-adaptive and discrete optimization. IEEE Trans. Pattern Anal. 2018, 40, 3034–3044. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Liu, L.; Long, Y.; Shao, L. Unsupervised deep hashing with pseudo labels for scalable image retrieval. IEEE Trans. Image Process. 2018, 27, 1626–1638. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Yuan, X.; Lu, J.; Tian, Q.; Zhou, J. Deep hashing via discrepancy minimization. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Jiang, Y.G.; Wang, J.; Chang, S.F. Lost in Binarization: Query-adaptive ranking for similar image search with compact codes. In Proceedings of the ACM International Conference on Multimedia Retrieval, Trento, Italy, 18–20 April 2011. [Google Scholar]
- Jiang, Y.G.; Wang, J.; Xue, X.; Chang, S.F. Query-adaptive image search with hash codes. IEEE Trans. Multimed. 2013, 15, 442–453. [Google Scholar] [CrossRef]
- Shum, H.Y.; Zhang, L.; Zhang, X. QsRank: Query-sensitive hash code ranking for efficient ∊-neighbor search. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012. [Google Scholar]
- Zhang, L.; Zhang, Y.; Tang, J.; Lu, K.; Tian, Q. Binary code ranking with weighted hamming distance. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013. [Google Scholar]
- Ji, T.; Liu, X.; Deng, C.; Huang, L.; Lang, B. Query-adaptive hash code ranking for fast nearest neighbor search. In Proceedings of the ACM International Conference on Multimedia, New York, NY, USA, 10–16 October 2014. [Google Scholar]
- Song, D.; Liu, W.; Ji, R.; Meyer, D.A.; Smith, J.R. Top rank supervised binary coding for visual search. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Jegou, H.; Douze, M.; Schmid, C. Product quantization for nearest neighbor search. IEEE Trans. Pattern Anal. 2011, 33, 117–128. [Google Scholar] [CrossRef] [PubMed]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images; Computer Science Department, University of Toronto: Toronto, ON, Canada, 2009. [Google Scholar]
- Wang, J.; Kumar, S.; Chang, S.F. Semi-supervised hashing for large-scale search. IEEE Trans. Pattern Anal. 2012, 34, 2393–2406. [Google Scholar] [CrossRef] [PubMed]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Oliv, A.; Torralba, A. Modeling the shape of the scene: A holistic representation of the spatial envelope. Int. J. Comput. Vis. 2001, 42, 145–175. [Google Scholar] [CrossRef]
- Le, N.Q.; Ho, Q.T.; Qu, Y.Y. Incorporating deep learning with convolutional neural networks and position specific scoring matrices for identifying electron transport proteins. J. Comput. Chem. 2017, 38, 2000–2006. [Google Scholar] [CrossRef] [PubMed]
- Le, N.Q.K.; Huynh, T.T.; Yapp, E.K.Y.; Yeh, H.Y. Identification of clathrin proteins by incorporating hyperparameter optimization in deep learning and PSSM profiles. Comput. Methods Programs Biomed. 2019, 177, 81–88. [Google Scholar] [CrossRef] [PubMed]
| Ground Truth | 10 | 100 | ||||
|---|---|---|---|---|---|---|
| Binary Bits | 32 | 64 | 128 | 32 | 64 | 128 |
| TORBW | 4.25 | 7.86 | 10.72 | 3.92 | 7.65 | 10.53 |
| OCH | 4.03 | 7.64 | 10.53 | 3.75 | 7.42 | 10.27 |
| Top-RSBC | 3.95 | 7.42 | 10.48 | 3.71 | 7.26 | 10.17 |
| KMH_QRank | 3.87 | 7.18 | 10.22 | 3.61 | 6.85 | 10.03 |
| KMH | 2.35 | 4.42 | 6.79 | 2.17 | 4.27 | 6.54 |
| AGH_QRank | 2.38 | 5.96 | 8.63 | 2.16 | 5.82 | 8.47 |
| AGH_WhRank | 1.93 | 4.89 | 6.31 | 1.62 | 4.63 | 6.08 |
| AGH | 1.62 | 3.21 | 4.19 | 1.35 | 3.01 | 3.96 |
| LSH_QRank | 1.33 | 3.32 | 6.83 | 1.08 | 3.07 | 6.58 |
| LSH_WhRank | 1.09 | 2.13 | 4.86 | 0.85 | 1.88 | 4.62 |
| LSH | 0.89 | 1.99 | 2.75 | 0.67 | 1.67 | 2.56 |
| Ground Truth | 10 | 100 | ||||
|---|---|---|---|---|---|---|
| Binary Bits | 32 | 64 | 128 | 32 | 64 | 128 |
| TORBW | 11.84 | 17.12 | 21.26 | 11.52 | 16.81 | 20.96 |
| OCH | 11.61 | 16.95 | 21.02 | 11.38 | 16.65 | 20.71 |
| Top-RSBC | 11.46 | 16.58 | 20.94 | 11.24 | 16.37 | 20.63 |
| KMH_QRank | 11.25 | 16.37 | 20.73 | 11.02 | 16.08 | 20.45 |
| KMH | 8.56 | 11.59 | 15.12 | 8.31 | 11.35 | 14.86 |
| AGH_QRank | 7.22 | 9.46 | 15.53 | 6.94 | 9.25 | 15.27 |
| AGH_WhRank | 5.06 | 7.94 | 13.92 | 4.85 | 7.76 | 13.53 |
| AGH | 4.02 | 7.68 | 13.21 | 3.72 | 7.45 | 12.98 |
| LSH_QRank | 4.15 | 8.58 | 14.00 | 4.02 | 8.34 | 13.75 |
| LSH_WhRank | 4.03 | 7.30 | 9.99 | 3.76 | 7.18 | 9.67 |
| LSH | 2.68 | 5.83 | 9.36 | 2.47 | 5.57 | 9.03 |
| Ground Truth | 10 | 100 | ||||
|---|---|---|---|---|---|---|
| Binary Bits | 32 | 64 | 128 | 32 | 64 | 128 |
| TORBW | 5.83 | 16.82 | 21.05 | 5.54 | 16.71 | 31.59 |
| OCH | 5.62 | 16.57 | 20.76 | 5.37 | 16.42 | 30.48 |
| Top-RSBC | 5.43 | 16.38 | 20.43 | 5.06 | 16.21 | 25.37 |
| KMH_QRank | 5.05 | 16.21 | 20.06 | 4.82 | 16.07 | 18.35 |
| KMH | 4.38 | 8.89 | 10.17 | 3.98 | 8.76 | 8.92 |
| AGH_QRank | 4.87 | 15.03 | 29.74 | 4.67 | 14.86 | 29.64 |
| AGH_WhRank | 3.12 | 8.73 | 18.02 | 2.92 | 8.53 | 17.75 |
| AGH | 2.93 | 5.64 | 7.85 | 2.81 | 5.46 | 7.62 |
| LSH_QRank | 3.74 | 10.22 | 25.15 | 3.48 | 10.07 | 24.89 |
| LSH_WhRank | 2.81 | 6.14 | 15.92 | 2.67 | 5.94 | 15.71 |
| LSH | 2.24 | 5.44 | 7.47 | 2.03 | 5.17 | 7.18 |
| SIFT1M | GIST1M | Cifar10 | |
|---|---|---|---|
| p value | 6.57 × 10–8 | 1.76 × 10–5 | 1.9 × 10–3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Sun, F.; Zhang, L.; Wang, L.; Liu, P. Top Position Sensitive Ordinal Relation Preserving Bitwise Weight for Image Retrieval. Algorithms 2020, 13, 18. https://doi.org/10.3390/a13010018
Wang Z, Sun F, Zhang L, Wang L, Liu P. Top Position Sensitive Ordinal Relation Preserving Bitwise Weight for Image Retrieval. Algorithms. 2020; 13(1):18. https://doi.org/10.3390/a13010018
Chicago/Turabian StyleWang, Zhen, Fuzhen Sun, Longbo Zhang, Lei Wang, and Pingping Liu. 2020. "Top Position Sensitive Ordinal Relation Preserving Bitwise Weight for Image Retrieval" Algorithms 13, no. 1: 18. https://doi.org/10.3390/a13010018
APA StyleWang, Z., Sun, F., Zhang, L., Wang, L., & Liu, P. (2020). Top Position Sensitive Ordinal Relation Preserving Bitwise Weight for Image Retrieval. Algorithms, 13(1), 18. https://doi.org/10.3390/a13010018





