2.1. Computational Complexity
We assume that the reader is familiar with basic notions from the theory of computational complexity, such as the complexity classes P and NP. For more details, we refer to textbooks on the topic (see, e.g., [
11,
12]).
There are many natural decision problems that are not contained in the classical complexity classes P and NP (under some common complexity-theoretic assumptions). The
Polynomial Hierarchy [
2,
3,
12,
13] contains a hierarchy of increasing complexity classes
, for all
. We give a characterization of these classes based on the satisfiability problem of various classes of quantified Boolean formulas. A
quantified Boolean formula is a formula of the form
, where each
is either ∀ or ∃, the
are disjoint sets of propositional variables, and
is a Boolean formula over the variables in
. The quantifier-free part of such formulas is called the
matrix of the formula. Truth of such formulas is defined in the usual way. Let
be a function that maps some variables of a formula
to other variables or to truth values. We let
denote the application of such a substitution
to the formula
. We also write
to denote
. For each
, the decision problem
QSat is defined as follows.
Input formulas to the problem
QSat are called
-formulas. For each nonnegative integer
, the complexity class
can be characterized as the closure of the problem
QSat under polynomial-time reductions [
2,
3]—that is, all decision problems that are polynomial-time reducible to
QSat. The
-hardness of
QSat holds already when the matrix of the input formula is restricted to
for odd
i, and restricted to
for even
i. Note that the class
coincides with P, and the class
coincides with NP. For each
, the class
is defined as co-
—that is,
.
The classes
and
can also be defined by means of nondeterministic Turing machines with an oracle. Intuitively, oracles are black-box machines that can solve a problem in a single time step—for more details, see, e.g., Chapter 3 of [
11]. For any complexity class
C, we let
be the set of decision problems that are decided in polynomial time by a nondeterministic Turing machine with an oracle for a problem that is in the class
C. Then, the classes
and
, for
, can be equivalently defined by letting
, and for each
letting
and
.
The Polynomial Hierarchy also includes complexity classes between
and
—such as the classes
and
. The class
consists of all decision problems that are decided in polynomial time by a deterministic Turing machine with an oracle for a problem that is in the class
. Similarly, the class
consists of all decision problems that are decided in polynomial time by a deterministic Turing machine with an oracle for a problem that is in the class
, with the restriction that the Turing machine is only allowed to make
oracle queries, where
n denotes the input size [
14,
15]. It holds that
.
There are also natural decision problems that are located between NP and
. The
Boolean Hierarchy (BH) [
16,
17,
18] consists of a hierarchy of complexity classes
, for each
, that can be used to classify the complexity of decision problems between NP and
. Each class
can be characterized as the class of problems that can be reduced to the problem
-
Sat, which is defined inductively as follows. The problem
-
Sat consists of all sequences
of length 1, where
is a satisfiable propositional formula. For even
, the problem
-
Sat consists of all sequences
of propositional formulas such that both
-
Sat and
is unsatisfiable. For odd
, the problem
-
Sat consists of all sequences
of propositional formulas such that
-
Sat or
is satisfiable. The class
is also denoted by DP, and the problem
-
Sat is also denoted by
. The class BH is defined as the union of all
, for
. It holds that
.
2.2. Parameterized Complexity
We introduce some core notions from parameterized complexity theory. For an in-depth treatment, we refer to other sources [
19,
20,
21,
22,
23]. A
parameterized problem L is a subset of
for some finite alphabet
. For an instance
, we call
x the
main part and
k the
parameter. The following generalization of polynomial-time computability is commonly regarded as the main tractability notion of parameterized complexity theory. A parameterized problem
L is
fixed-parameter tractable if there exists a computable function
f and a constant
c such that there exists an algorithm that decides whether
in time
, where
denotes the size of
x. Such an algorithm is called an
fpt-algorithm, and this amount of time is called
fpt-time. FPT is the class of all parameterized problems that are fixed-parameter tractable. If the parameter is constant, then fpt-algorithms run in polynomial time where the order of the polynomial is independent of the parameter. This provides a good scalability in the parameter in contrast to running times of the form
, which are also polynomial for fixed
k, but are already impractical for, say,
.
Parameterized complexity also generalizes the notion of polynomial-time reductions. Let and be two parameterized problems. A (many-one) fpt-reduction from L to is a mapping from instances of L to instances of for which there exist some computable function such that for all : (i) is a yes-instance of L if and only if is a yes-instance of , (ii) , and (iii) R is computable in fpt-time. Let K be a parameterized complexity class. A parameterized problem L is K-hard if for every there is an fpt-reduction from to L. A problem L is K-complete if it is both in K and K-hard. Reductions that satisfy properties (i) and (ii) but that are computable in time , for some fixed computable function f, we call xp-reductions.
The parameterized complexity classes , for , , and can be used to give evidence that a given parameterized problem is not fixed-parameter tractable. These classes are based on the satisfiability problems of Boolean circuits and formulas. We consider Boolean circuits with a single output gate. We call input nodes variables. We distinguish between small gates, with fan-in , and large gates, with fan-in . The depth of a circuit is the length of a longest path from any variable to the output gate. The weft of a circuit is the largest number of large gates on any path from a variable to the output gate. We say that a circuit C is in negation normal form if all negation nodes in C have variables as inputs. A Boolean formula can be considered as a Boolean circuit where all gates have fan-out . We adopt the usual notions of truth assignments and satisfiability of a Boolean circuit. We say that a truth assignment for a Boolean circuit has weight k if it sets exactly k of the variables of the circuit to true. We denote the class of Boolean circuits with depth u and weft t by . We denote the class of all Boolean circuits by CIRC, and the class of all Boolean formulas by FORM. For any class of Boolean circuits, we define the following parameterized problem:
p-WSat Instance: A Boolean circuit , and an integer k. Parameter: k. Question: Does there exist an assignment of weight k that satisfies C?
|
We denote closure under fpt-reductions by —that is, for any set of parameterized problems, is the set of all parameterized problems that are fpt-reducible to some problem . The classes are defined by letting p-WSat for all . The classes and are defined by letting p-WSat and p-WSat .
Let
K be a classical complexity class, e.g., NP. The parameterized complexity class para-K is defined as the class of all parameterized problems
, for some finite alphabet
, for which there exist a computable function
, and a problem
such that
and for all instances
of
L we have that
if and only if
. (Here, we implicitly use a representation of pairs of strings in
as strings in
.) Intuitively, the class para-K consists of all problems that are in
K after a precomputation that only involves the parameter. The class para-NP can also be defined via nondeterministic fpt-algorithms [
24]. The class para-K can be seen as a direct analogue of the class K in parameterized complexity. In particular, for the case of
, we have
.
We consider the following (trivial) parameterization of SAT, the satisfiability problem for propositional logic. We let . In other words, is the parameterized variant of SAT where the parameter is the constant value 1. Similarly, we let . The problem is para-NP-complete, and the problem is para--complete. In other words, the class para-NP consists of all parameterized problems that can be fpt-reduced to , and para- consists of all parameterized problems that can be fpt-reduced to .
Another analogue to the classical complexity class K is the parameterized complexity class
, that is defined as the class of those parameterized problems
Q whose slices
are in K, i.e., for each positive integer
k the classical problem
is in K [
20]. For instance, the class
consists of those parameterized problems whose slices are decidable in polynomial time. Note that this definition is non-uniform, that is, for each positive integer
k, there might be a completely different polynomial-time algorithm that witnesses that
is polynomial-time solvable. There are also uniform variants
of these classes
. We define XP to be the class of parameterized problems
Q for which there exists a computable function
f and an algorithm
A that decides whether
in time
[
20,
22,
24]. Similarly, we define XNP to be the class of parameterized problems that are decidable in nondeterministic time
. Its dual class we denote by Xco−NP. Alternatively, we can view XNP as the class of parameterized problems for which there exists an xp-reduction to
and Xco−NP as the class of parameterized problems for which there exists an xp-reduction to
. (For any
, we know that
L can be xp-reduced to
by following a suitable variant of the proof of the Cook-Levin Theorem [
25,
26]. Conversely, any parameterized problem
L that can be xp-reduced to
we can solve in nondeterministic time
by first carrying out the xp-reduction, and then solving the resulting instance of
. The case for Xco−NP and
is entirely analogous.)
2.3. Fpt-Reductions to SAT and Parameterized Complexity Classes at Higher Levels of the PH
Problems in NP and co-NP can be encoded into SAT in such a way that the time required to produce the encoding and consequently also the size of the resulting SAT instance are polynomial in the input (the encoding is a polynomial-time many-one reduction). Typically, the SAT encodings of problems proposed for practical use are of this kind (see, e.g., [
27]). For problems that are “beyond NP”, say for problems on the second level of the PH, such polynomial SAT encodings do not exist, unless the PH collapses. However, for such problems, there still could exist SAT encodings which can be produced in fpt-time with respect to some parameter associated with the problem. In fact, such fpt-time SAT encodings have been obtained for various problems on the second level of the PH [
28,
29,
30,
31]. The classes para-NP and para-co-NP contain exactly those parameterized problems that admit such a many-one fpt-reduction to
and
, respectively. Thus, with fpt-time encodings, one can go significantly beyond what is possible by conventional polynomial-time SAT encodings.
Fpt-time encodings to SAT also have their limits. Clearly, para-
-hard and para-
-hard parameterized problems do not admit fpt-time encodings to SAT, even when the parameter is a fixed constant, unless the PH collapses. There are problems that apparently do not admit fpt-time encodings to SAT, but seem not to be para-
-hard nor para-
-hard either. Recently, several complexity classes have been introduced to classify such intermediate problems [
7,
8,
30]. These parameterized complexity classes are dubbed the
class and the
hierarchy, inspired by their definition, which is based on the following weighted variants of the quantified Boolean satisfiability problem that is canonical for the second level of the PH. The problem
-
WSat(
) provides the foundation for the
class.
-WSat Instance: A quantified Boolean formula , and an integer k. Parameter: k. Question: Does there exist a truth assignment to X with weight k such that for all truth assignments to Y the assignment satisfies ?
|
Similarly, the problem
-
WSat(
) provides the foundation for the
hierarchy—where
is a class of Boolean circuits. (The parameterized problems
-
WSat(
) seem not to be fpt-reducible to each other for various classes
of Boolean circuits—similarly to the problems
p-
WSat that are used to define the classes
,
, and
. This is in contrast to the case of
-
WSat, where we can use a Tseitin transformation [
32] to reduce arbitrary Boolean circuits to equisatisfiable 3CNF formulas.)
-WSat() Instance: A Boolean circuit over two disjoint sets X and Y of variables, and an integer k. Parameter: k. Question: Does there exist a truth assignment to X such that for all truth assignments to Y with weight k the assignment satisfies C?
|
The parameterized complexity class
(also called the
class) is then defined as follows:
Similarly, the classes of the hierarchy are defined as follows:
= -WSat,
= -WSat(FORM) , and
= -WSat(CIRC) .
Note that these definitions are entirely analogous to those of the parameterized complexity classes of the W-hierarchy [
20]. The following inclusion relations hold between the classes of the
hierarchy:
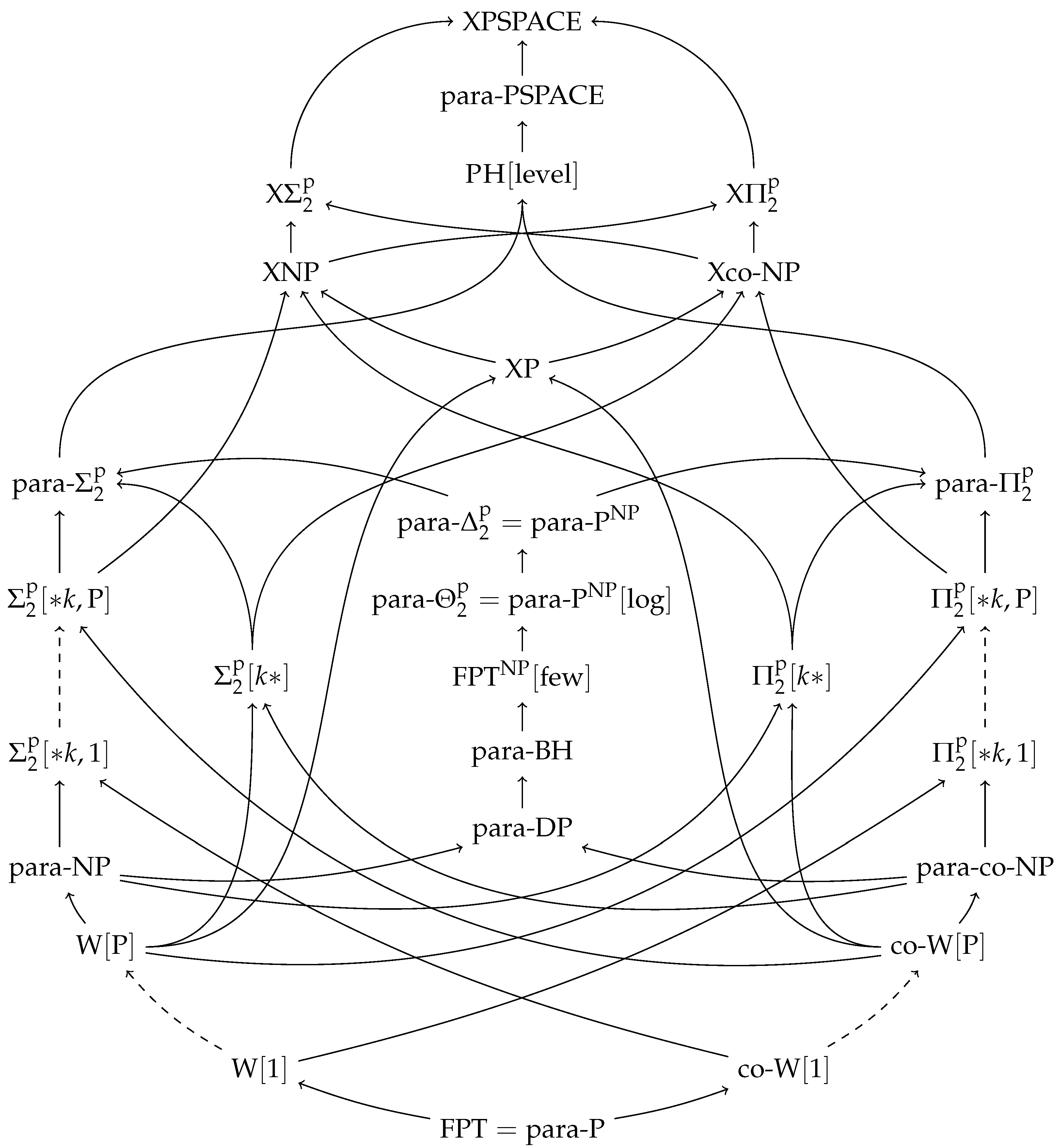
(See also
Figure 1 for a visual overview of these inclusion relations.)
Dual to the classical complexity class is its co-class , whose canonical complete problem is complementary to the problem QSat. Similarly, we can define dual classes for the class and for each of the parameterized complexity classes in the hierarchy. These co-classes are based on problems complementary to the problems -WSat and -WSat—i.e., these problems have as yes-instances exactly the no-instances of -WSat and -WSat, respectively. Equivalently, these complementary problems can be considered as variants of -WSat and -WSat where the existential and universal quantifiers are swapped, and are therefore denoted with -WSat and -WSat. We use a similar notation for the dual complexity classes, e.g., we denote co- by .
The class
includes the class para-
as a subset, and is contained in the class Xco−NP as a subset. Similarly, each of the classes
include the the class para-NP as a subset, and is contained in the class XNP. Under some common complexity-theoretic assumptions, the class
can be separated from para-NP on the one hand, and para-
on the other hand. In particular, assuming that
, it holds that
, that
and that
[
7,
8]. Similarly, the classes
can be separated from para-
and para-
. Assuming that
, it holds that
, that
and thus in particular that
, and that
[
7,
8].
One can also enhance the power of polynomial-time SAT encodings by considering polynomial- time algorithms that can query a SAT solver multiple times—that is, polynomial-time Turing reductions. Such an approach has been shown to be quite effective in practice (see, e.g., [
33,
34,
35]) and extends the scope of SAT solvers to problems in the class
, but not to problems that are
-hard or
-hard. In addition, here, switching from polynomial-time to fpt-time provides a significant increase in power. The class para-
contains all parameterized problems that can be decided by an fpt-algorithm that can query a SAT oracle multiple times—i.e., by an fpt-time Turing reduction to SAT. (One can prove this by following the proof of Theorem 4 in [
24] that
, with the modification that the algorithms are given access to a SAT oracle.) In addition, one could restrict the number of queries that the algorithm is allowed to make. The class para-
consists of all parameterized problems that can be decided by an fpt-algorithm that can query a SAT oracle at most
many times, where
k is the parameter value,
n is the input size, and
f is some computable function. (This statement one can prove by following the proof of Theorem 4 in [
24] that
, with the modification that the algorithms can query a SAT oracle an amount of times that depends logarithmically on the input size.) Restricting the number of queries even further, we define the parameterized complexity class
as the class of all parameterized problems that can be decided by an fpt-algorithm that can query a SAT oracle at most
times, where
k is the parameter value and
f is some computable function [
7,
8].
We get the parameterized analogue para-PSPACE of the class PSPACE by using the definition of para-K for
. Similarly, we can define the parameterized complexity class XPSPACE, consisting of all parameterized problems
Q for which there exists a computable function
f and an algorithm
A that decides whether
in space
. We also consider another parameterized variant of PSPACE, which is based on parameterizing the number of quantifier alternations in
QSat. An unbounded number of quantifier alternations in this problem results in the class PSPACE, and bounding the number of quantifier alternations by a constant leads to some fixed level of the PH. The parameterized complexity class
PH is based on bounding the number of quantifier alternations by the problem parameter [
7,
36]. Formally, we consider the following parameterized problem
QSat(level).
The parameterized complexity class PH is defined to be the class of all parameterized problems that can be fpt-reduced to QSat(level). We have that .
An overview of the parameterized complexity classes relevant for this paper can be found in
Figure 1.
In the early literature on this topic [
6,
28,
30,
37,
38,
39,
40,
41], the class
appeared under the names
and
. Similarly, the classes
appeared under the names
and
. In addition, the class
appeared under the name
.