Using Graph Partitioning for Scalable Distributed Quantum Molecular Dynamics
Abstract
1. Introduction
2. Evaluating Matrix Polynomials on Partitions
- for all ;
- neighbors of vertices in that are themselves not in are contained in .
- Divide into q disjoint sets and define a CH-partition , where has core and halo ;
- Construct submatrices for all ;
- Compute for all i independently using dense matrix algebra;
- Given a vertex i, let k be the index such that the set contains i. Let j be the row in that corresponds to the i-th row in A. Then, define as a matrix whose i-th row equals the j-th row of .
3. Algorithms for Graph Partitioning Considered in Our Study
3.1. Edge Cut Graph Partitioning
3.1.1. METIS
- Starting from the original graph (where ), METIS generates a sequence of graphs for some to coarsen the input graph. The coarsening ends with a suitably small graph (typically with vertices).
- An algorithm of choice is used to partition .
- Using the sequence , the partitions are expanded back from to the full graph .
3.1.2. KaHIP
3.1.3. Hypergraph Partitioning
3.2. Refinement with Simulated Annealing
- Select a random block , select one of its halo nodes v at random and move v into block P.
- Select a random block , select one of its nodes v at random and move v into P.
- Select the block with most halo nodes and (a) move a random node v into P, (b) make a random halo node of P a core node, or (c) move any node of P to another block.
- Like (3.) using the block with the largest sum of core and halo nodes.
| Algorithm 1: Simulated Annealing. |
 |
4. Experiments
4.1. Parameter Choices for METIS and hMETIS
4.2. A Collection of Test Graphs Derived from Molecular Systems
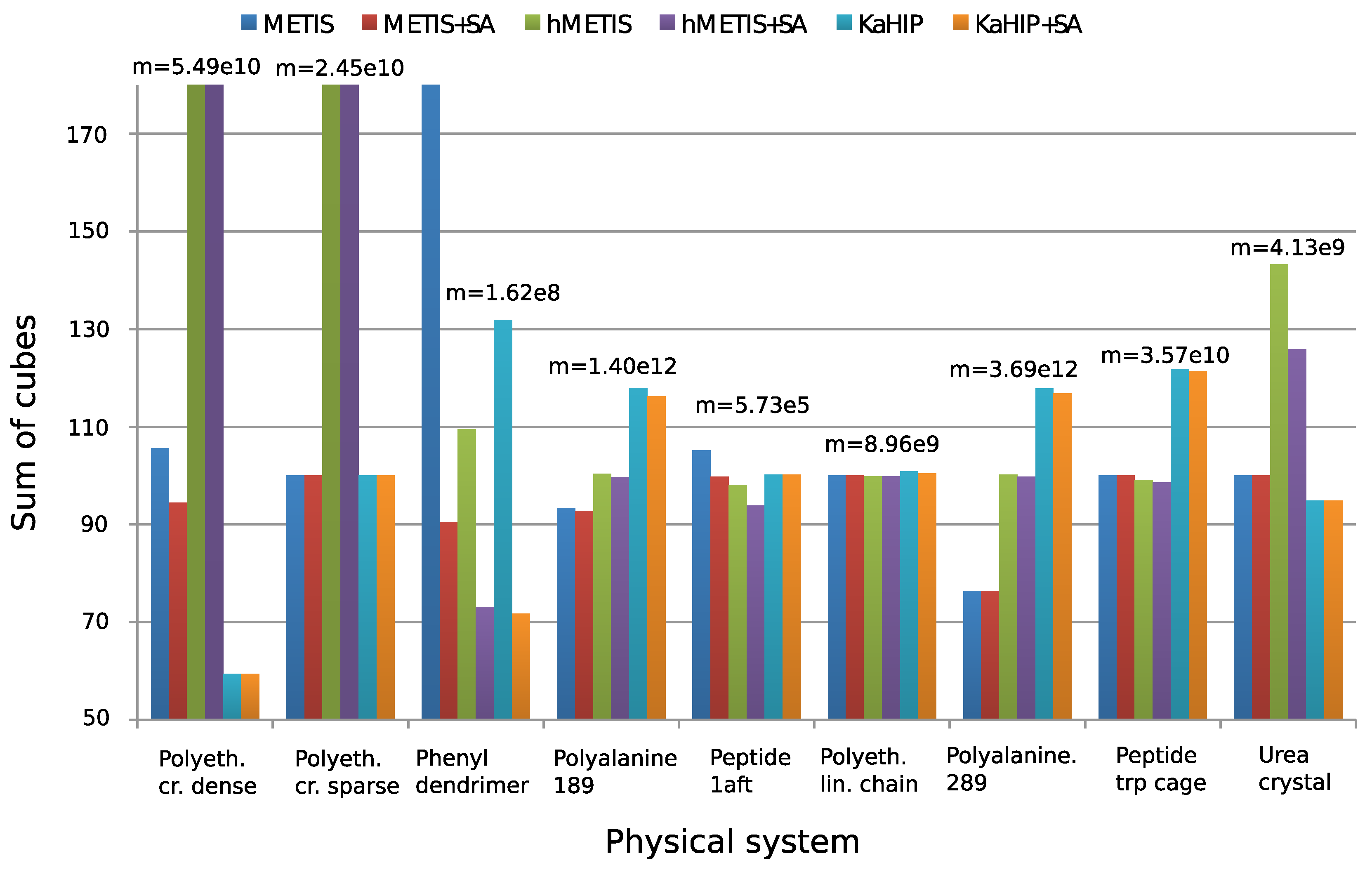
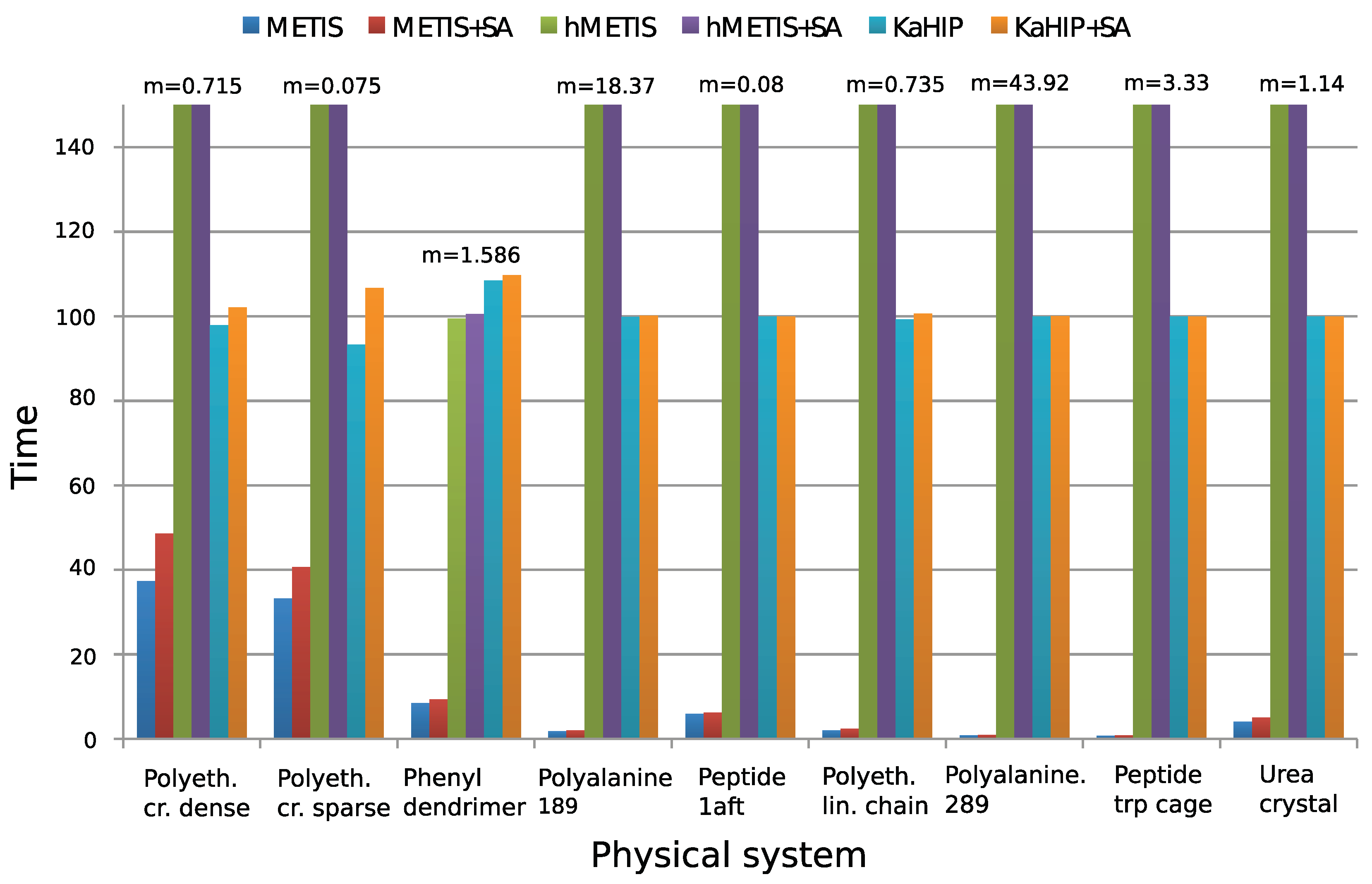
4.3. Comparison of the Partitioning Algorithms
- METIS with parameters of Section 4.1;
- METIS with subsequent simulated annealing (SA);
- hMETIS;
- hMETIS with subsequent SA;
- KaHIP;
- KaHIP with subsequent SA.
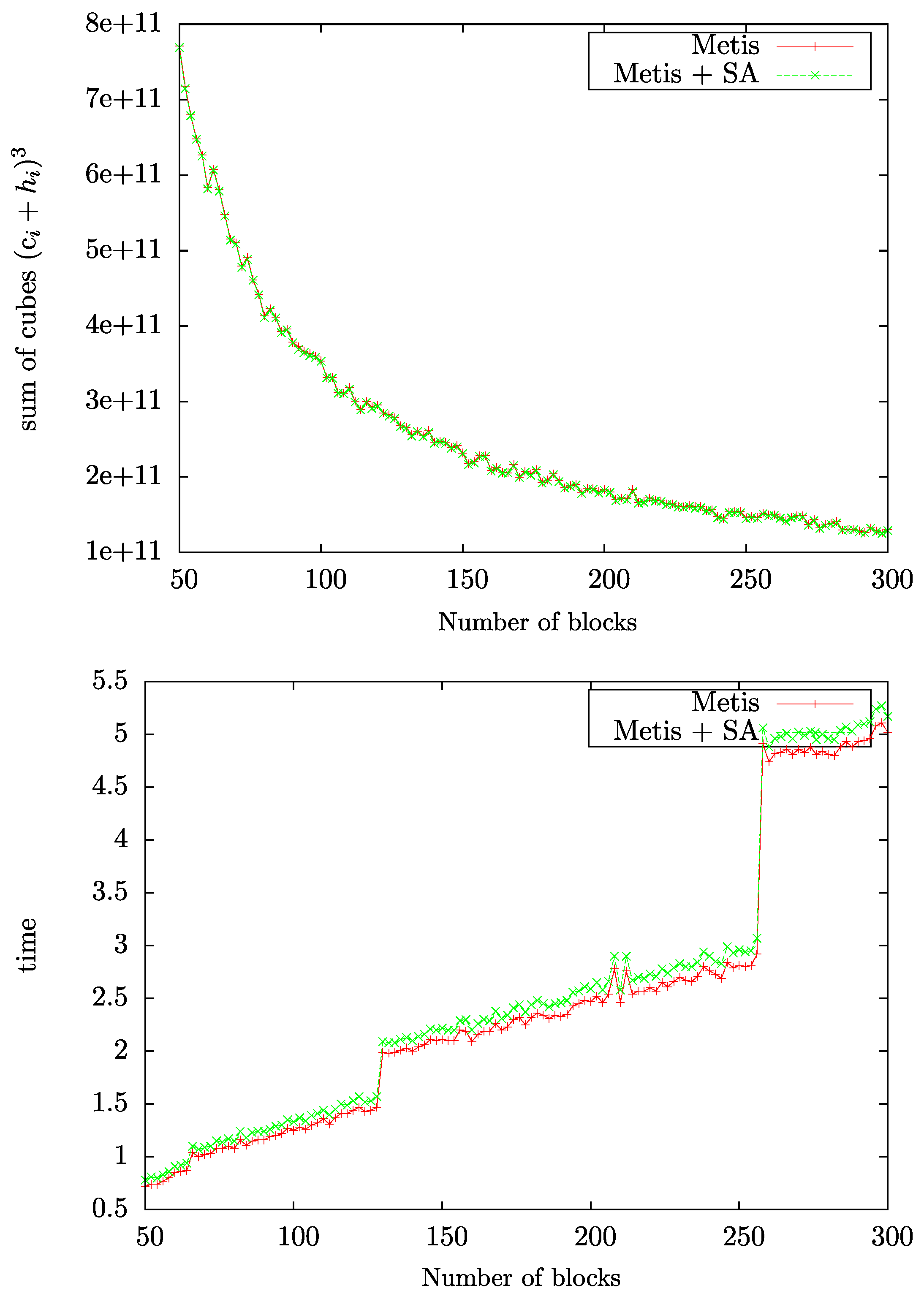
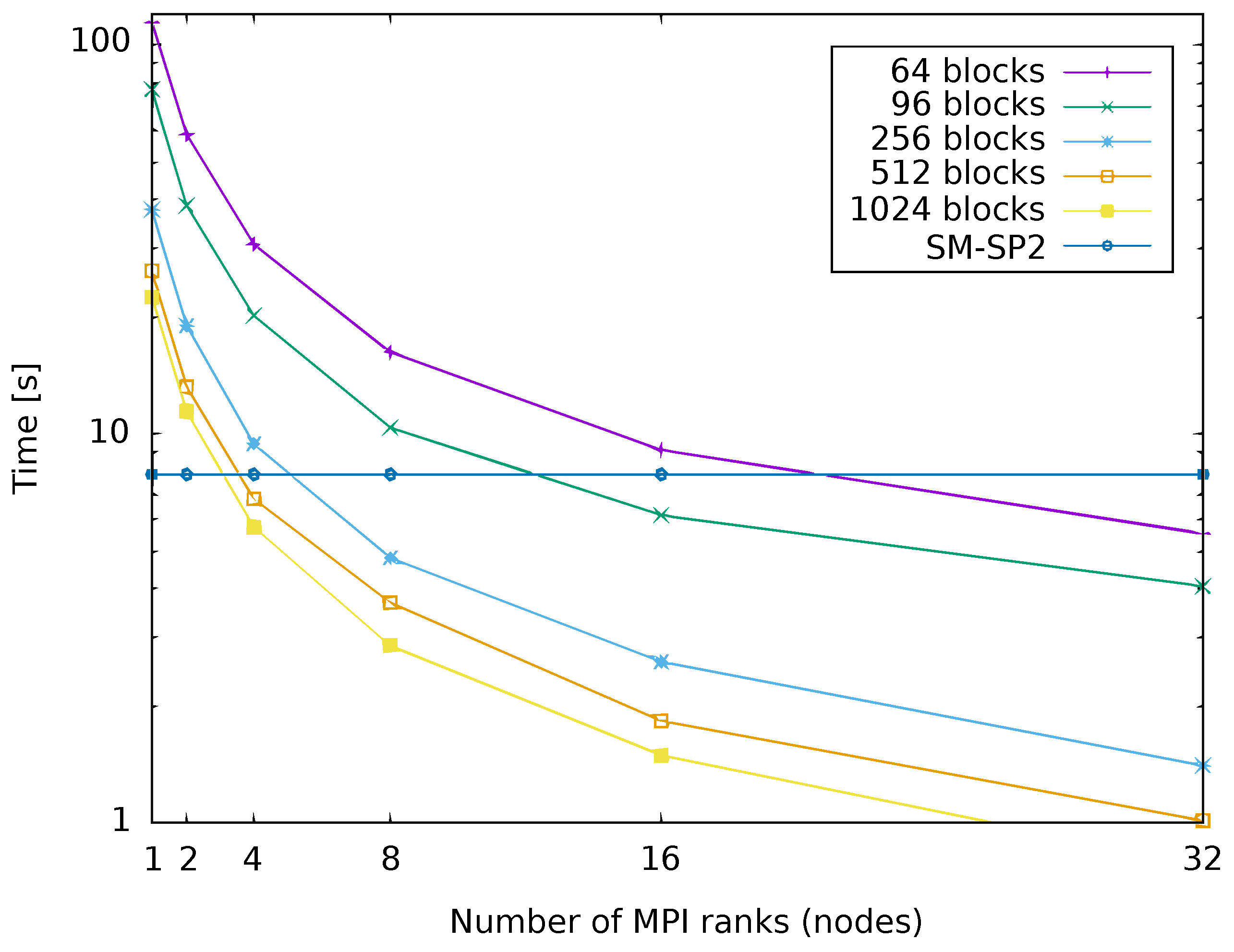
4.4. Parallelized Implementation of G-SP2
4.5. Single-Node SM-SP2 versus Parallelized Implementation of G-SP2
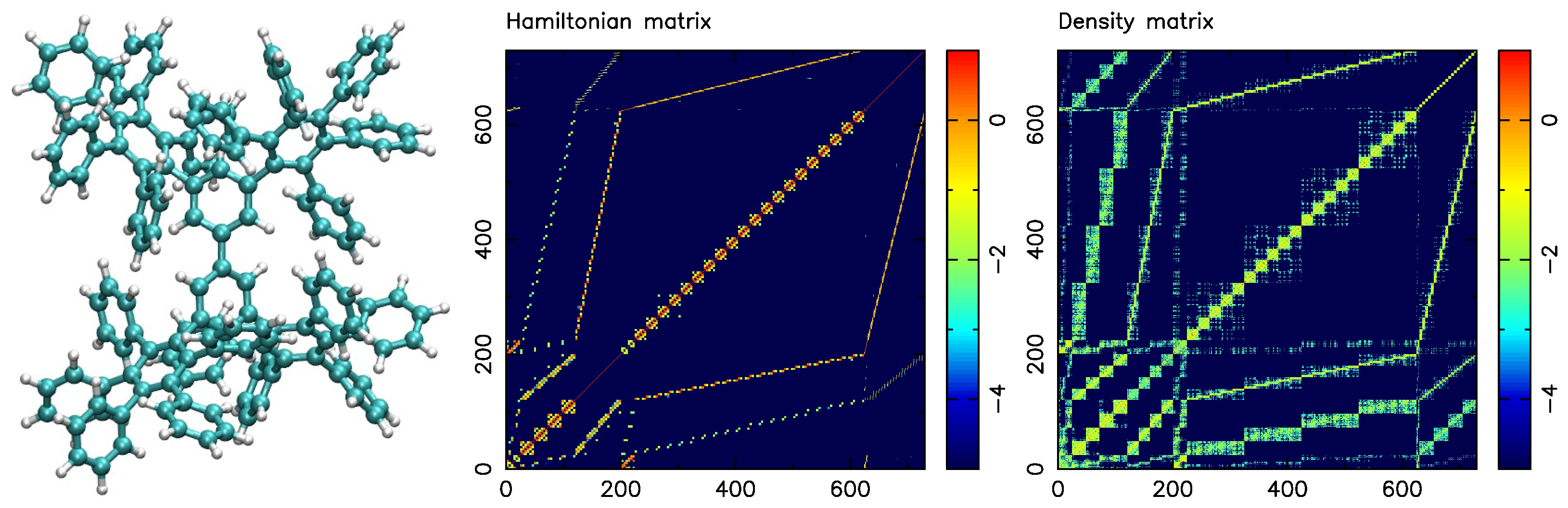
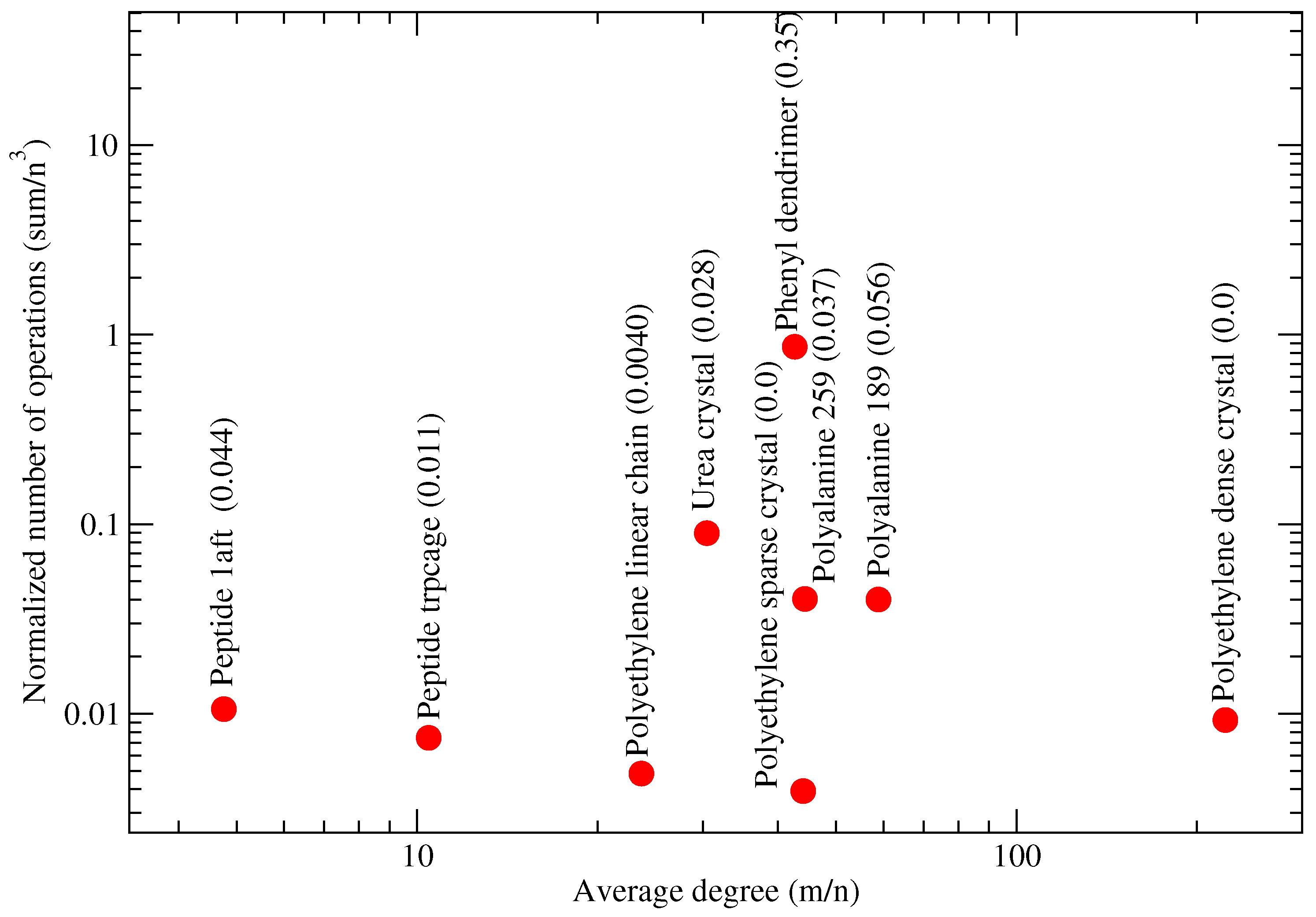
4.6. Relationship between Molecular System and Partitions
5. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Proofs for Section 2
Appendix B. Further Details on Experimental Results
| Test System | Method | Sum | Min | Max | Time [s] |
|---|---|---|---|---|---|
| polyethylene dense crystal | METIS | 57,982,058,496 | 1536 | 1536 | 0.267175 |
| n = 18,432 | METIS + SA | 51,856,752,364 | 976 | 1536 | 0.347209 |
| m = 4,112,189 | HMETIS | 7,126,357,377,024 | 3840 | 9984 | 141.426 |
| p = 16 | HMETIS + SA | 1,362,943,612,944 | 2520 | 5814 | 141.79 |
| KaHIP | 32,614,907,904 | 768 | 1536 | 0.7 | |
| KaHIP + SA | 32,614,907,904 | 768 | 1536 | 0.73 | |
| polyethylene sparse crystal | METIS | 24,461,180,928 | 1152 | 1152 | 0.024942 |
| n = 18,432 | METIS + SA | 24,461,180,928 | 1152 | 1152 | 0.030508 |
| m = 812,343 | HMETIS | 195,689,447,424 | 2304 | 2304 | 55.9726 |
| p = 16 | HMETIS + SA | 170,056,587,295 | 2013 | 2299 | 55.9943 |
| KaHIP | 24,461,180,928 | 1152 | 1152 | 0.07 | |
| KaHIP + SA | 24,461,180,928 | 1152 | 1152 | 0.08 | |
| phenyl dendrimer | METIS | 336,049,081 | 150 | 409 | 0.13482 |
| n = 730 | METIS + SA | 146,550,740 | 0 | 382 | 0.14877 |
| m = 31,147 | HMETIS | 177,436,462 | 135 | 358 | 1.578 |
| p = 16 | HMETIS + SA | 118,409,940 | 0 | 358 | 1.59436 |
| KaHIP | 231,550,645 | 55 | 381 | 1.72 | |
| KaHIP + SA | 116,248,715 | 0 | 324 | 1.74 | |
| polyethylene dense crystal | METIS | 57,982,058,496 | 1536 | 1536 | 0.267175 |
| n = 18,432 | METIS + SA | 51,856,752,364 | 976 | 1536 | 0.347209 |
| m = 4,112,189 | HMETIS | 7,126,357,377,024 | 3840 | 9984 | 141.426 |
| p = 16 | HMETIS + SA | 1,362,943,612,944 | 2520 | 5814 | 141.79 |
| KaHIP | 32,614,907,904 | 768 | 1536 | 0.7 | |
| KaHIP + SA | 32,614,907,904 | 768 | 1536 | 0.73 | |
| peptide 1aft | METIS | 603,251 | 24 | 41 | 0.004755 |
| n = 384 | METIS + SA | 572,281 | 24 | 41 | 0.005007 |
| m = 1833 | HMETIS | 562,601 | 24 | 40 | 0.820561 |
| p = 16 | HMETIS + SA | 538,345 | 24 | 42 | 0.820771 |
| KaHIP | 575,978 | 11 | 44 | 0.08 | |
| KaHIP + SA | 575,978 | 11 | 44 | 0.08 | |
| polyethylene chain 1024 | METIS | 8,961,763,376 | 800 | 848 | 0.01513 |
| n = 12,288 | METIS + SA | 8,961,763,376 | 800 | 848 | 0.017951 |
| m = 290,816 | HMETIS | 8,951,619,584 | 824 | 824 | 27.3297 |
| p = 16 | HMETIS + SA | 8,951,619,584 | 824 | 824 | 27.3332 |
| KaHIP | 9,037,266,968 | 782 | 875 | 0.73 | |
| KaHIP + SA | 9,000,224,048 | 782 | 872 | 0.74 | |
| polyalanine 289 | METIS | 2,816,765,783,803 | 4591 | 6102 | 0.366308 |
| n = 41,185 | METIS + SA | 2,816,141,689,603 | 4591 | 6093 | 0.399265 |
| m = 1,827,256 | HMETIS | 3,694,884,690,563 | 5733 | 6828 | 710.084 |
| p = 16 | HMETIS + SA | 3,681,874,557,307 | 5733 | 6830 | 710.128 |
| KaHIP | 4,347,865,055,912 | 52 | 8955 | 43.9 | |
| KaHIP + SA | 4,309,969,305,955 | 52 | 8907 | 43.94 | |
| peptide trp cage | METIS | 35,742,302,607 | 1228 | 1414 | 0.025795 |
| n = 16,863 | METIS + SA | 35,740,265,780 | 1228 | 1414 | 0.029837 |
| m = 176,300 | HMETIS | 35,428,817,730 | 1214 | 1472 | 31.0506 |
| p = 16 | HMETIS + SA | 35,237,003,004 | 1214 | 1472 | 31.0545 |
| KaHIP | 43,551,196,287 | 515 | 1898 | 2.81 | |
| KaHIP + SA | 43,388,946,192 | 536 | 1896 | 2.81 | |
| urea crystal | METIS | 4,126,744,977 | 608 | 708 | 0.047032 |
| n = 3584 | METIS + SA | 4,126,744,977 | 608 | 708 | 0.057645 |
| m = 109,067 | HMETIS | 5,913,680,136 | 643 | 811 | 15.2321 |
| p = 16 | HMETIS + SA | 5,194,749,106 | 604 | 785 | 15.2443 |
| KaHIP | 3,907,671,473 | 622 | 630 | 1.05 | |
| KaHIP + SA | 3,907,671,473 | 622 | 630 | 1.05 |
References
- Elstner, M.; Porezag, D.; Jungnickel, G.; Elsner, J.; Haugk, M.; Frauenheim, T.; Suhai, S.; Seifert, G. Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys. Rev. B 1998, 58, 7260–7268. [Google Scholar] [CrossRef]
- Finnis, M.W.; Paxton, A.T.; Methfessel, M.; van Schilfgarde, M. Crystal structures of zirconia from first principles and self-consistent tight binding. Phys. Rev. Lett. 1998, 81, 5149. [Google Scholar] [CrossRef]
- Frauenheim, T.; Seifert, G.; Elsterner, M.; Hajnal, Z.; Jungnickel, G.; Poresag, D.; Suhai, S.; Scholz, R. A self-consistent charge density-functional based tight-binding method for predictive materials simulations in physics, chemistry and biology. Phys. Stat. Sol. 2000, 217, 41–62. [Google Scholar] [CrossRef]
- Niklasson, A.M. Expansion algorithm for the density matrix. Phys. Rev. B 2002, 66, 155115–155121. [Google Scholar] [CrossRef]
- Mniszewski, S.M.; Cawkwell, M.J.; Wall, M.; Moyd-Yusof, J.; Bock, N.; Germann, T.; Niklasson, A.M. Efficient parallel linear scaling construction of the density matrix for Born-Oppenheimer molecular dynamics. J. Chem. Theory Comput. 2015, 11, 4644–4654. [Google Scholar] [CrossRef] [PubMed]
- Bock, N.; Challacombe, M. An Optimized Sparse Approximate Matrix Multiply for Matrices with Decay. SIAM J. Sci. Comput. 2013, 35, C72–C98. [Google Scholar] [CrossRef]
- Borstnik, U.; VandeVondele, J.; Weber, V.; Hutter, J. Sparse matrix multiplication: The distributed block-compressed sparse row library. Parallel Comput. 2014, 40, 47–58. [Google Scholar] [CrossRef]
- VandeVondele, J.; Borštnik, U.; Hutter, J. Linear Scaling Self-Consistent Field Calculations with Millions of Atoms in the Condensed Phase. J. Chem. Theory Comput. 2012, 8, 3565–3573. [Google Scholar] [CrossRef] [PubMed]
- Niklasson, A.M.; Mniszewski, S.M.; Negre, C.F.; Cawkwell, M.J.; Swart, P.J.; Mohd-Yusof, J.; Germann, T.C.; Wall, M.E.; Bock, N.; Rubensson, E.H.; et al. Graph-based linear scaling electronic structure theory. J. Chem. Phys. 2016, 144, 234101. [Google Scholar] [CrossRef] [PubMed]
- Pınar, A.; Hendrickson, B. Partitioning for Complex Objectives. In Proceedings of the 15th International Parallel and Distributed Processing Symposium (CDROM), San Francisco, CA, USA, 23–27 April 2001; IEEE Computer Society: Washington, DC, USA, 2001; pp. 1–6. [Google Scholar]
- Von Looz, M.; Wolter, M.; Jacob, C.R.; Meyerhenke, H. Better partitions of protein graphs for subsystem quantum chemistry. arXiv 2016, arXiv:1606.03427, 1–20. [Google Scholar]
- Djidjev, H.N.; Hahn, G.; Mniszewski, S.M.; Negre, C.F.; Niklasson, A.M.; Sardeshmukh, V. Graph Partitioning Methods for Fast Parallel Quantum Molecular Dynamics (full text with appendix). In Proceedings of the SIAM Workshop on Combinatorial Scientific Computing (CSC16), Albuquerque, NM, USA, 10–12 October 2016; pp. 1–17. [Google Scholar]
- Bader, D.A.; Meyerhenke, H.; Sanders, P.; Wagner, D. (Eds.) Graph Partitioning and Graph Clustering—10th DIMACS Implementation Challenge Workshop. Contemp. Math. 2013, 588. [Google Scholar] [CrossRef]
- Karypis, G.; Kumar, V. A Fast and High Quality Multilevel Scheme for Partitioning Irregular Graphs. SIAM J. Sci. Comput. 1999, 20, 359–392. [Google Scholar] [CrossRef]
- Fiduccia, C.; Mattheyses, R. A linear time heuristic for improving network partitions. In Proceedings of the 19th IEEE Design Automation Conference, Las Vegas, NV, USA, 14–16 June 1982; pp. 175–181. [Google Scholar]
- Sanders, P.; Schulz, C. Think Locally, Act Globally: Highly Balanced Graph Partitioning. In Proceedings of the International Symposium on Experimental Algorithms (SEA), Rome, Italy, 5–7 June 2013; Springer: Berlin/Heidelberg, Germany, 2013; Volume 7933, pp. 164–175. [Google Scholar]
- Sanders, P.; Schulz, C. Engineering multilevel graph partitioning algorithms. LNCS 2011, 6942, 469–480. [Google Scholar] [CrossRef]
- Ford, L., Jr.; Fulkerson, D. Maximal flow through a network. Canad. J. Math. 1956, 8, 399–404. [Google Scholar] [CrossRef]
- Karypis, G.; Kumar, V. Multilevel k-way Hypergraph Partitioning. VLSI Des. 2000, 11, 285–300. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C., Jr.; Vecchi, M. Optimization by Simulated Annealing. Science 1983, 200, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Karypis, G.; Kumar, V. A Hypergraph Partitioning Package. Available online: http://glaros.dtc.umn.edu/gkhome/fetch/sw/hmetis/manual.pdf (accessed on 7 September 2019).
- Bunn, C. The crystal structure of long-chain normal paraffin hydrocarbons. The “shape” of the CH2 group. Trans. Faraday Soc. 1939, 35, 482–491. [Google Scholar] [CrossRef]
- Schlag, S.; Henne, V.; Heuer, T.; Meyerhenke, H.; Sanders, P.; Schulz, C. k-way Hypergraph Partitioning via n-Level Recursive Bisection. arXiv 2015, arXiv:1511.03137, 1–21. [Google Scholar]
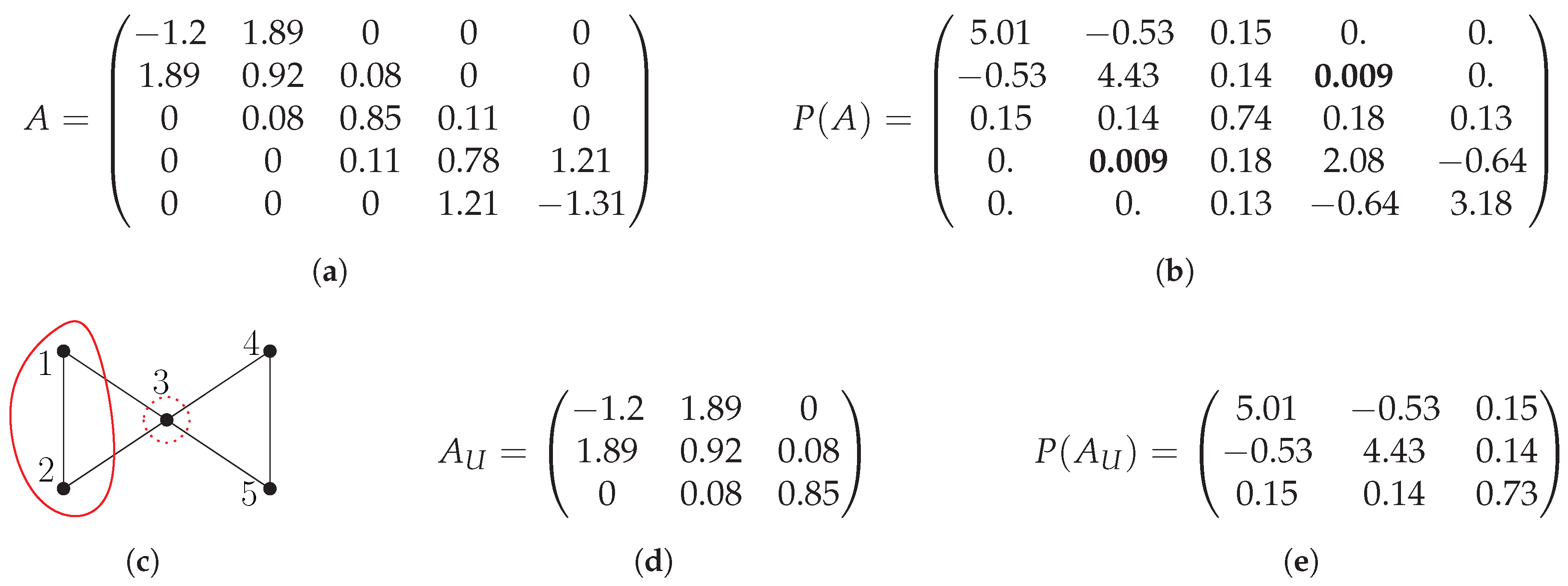
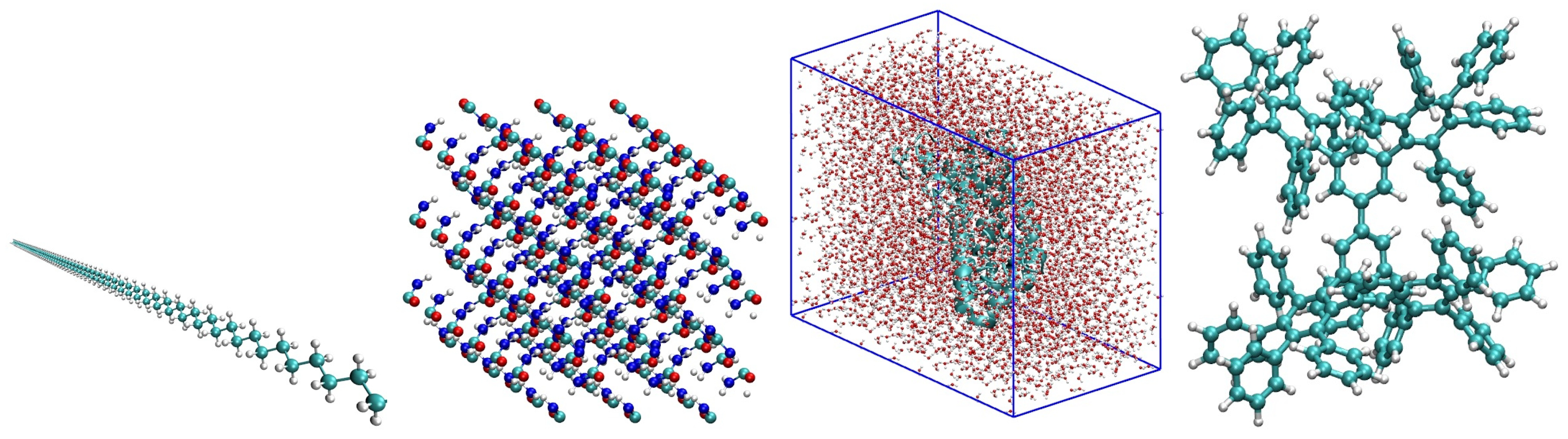

| Name | n | m | Description | |
|---|---|---|---|---|
| polyethylene dense crystal | 18,432 | 4,112,189 | 223.1 | crystal molecule in water solvent (low threshold) |
| polyethylene sparse crystal | 18,432 | 812,343 | 44.1 | crystal molecule in water solvent (high threshold) |
| phenyl dendrimer | 730 | 31,147 | 42.7 | polyphenylene branched molecule |
| polyalanine 189 | 31,941 | 1,879,751 | 58.9 | polyalanine protein solvated in water |
| peptide 1aft | 385 | 1833 | 4.76 | ribonucleoside-diphosphate reductase protein |
| polyethylene chain 1024 | 12,288 | 290,816 | 23.7 | chain of polymer molecule, almost 1-dimensional |
| polyalanine 289 | 41,185 | 1,827,256 | 44.4 | large protein in water solvent |
| peptide trp cage | 16,863 | 176,300 | 10.5 | smallest protein with ability to fold (in water) |
| urea crystal | 3584 | 109,067 | 30.4 | organic compound in living organisms |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Djidjev, H.N.; Hahn, G.; Mniszewski, S.M.; Negre, C.F.A.; Niklasson, A.M.N. Using Graph Partitioning for Scalable Distributed Quantum Molecular Dynamics. Algorithms 2019, 12, 187. https://doi.org/10.3390/a12090187
Djidjev HN, Hahn G, Mniszewski SM, Negre CFA, Niklasson AMN. Using Graph Partitioning for Scalable Distributed Quantum Molecular Dynamics. Algorithms. 2019; 12(9):187. https://doi.org/10.3390/a12090187
Chicago/Turabian StyleDjidjev, Hristo N., Georg Hahn, Susan M. Mniszewski, Christian F. A. Negre, and Anders M. N. Niklasson. 2019. "Using Graph Partitioning for Scalable Distributed Quantum Molecular Dynamics" Algorithms 12, no. 9: 187. https://doi.org/10.3390/a12090187
APA StyleDjidjev, H. N., Hahn, G., Mniszewski, S. M., Negre, C. F. A., & Niklasson, A. M. N. (2019). Using Graph Partitioning for Scalable Distributed Quantum Molecular Dynamics. Algorithms, 12(9), 187. https://doi.org/10.3390/a12090187





