Distributed Balanced Partitioning via Linear Embedding ^†

Abstract

Balanced partitioning is often a crucial first step in solving large-scale graph optimization problems, for example, in some cases, a big graph can be chopped into pieces that fit on one machine to be processed independently before stitching the results together, leading to certain suboptimality from the interaction among different pieces. In other cases, links between different parts may show up in the running time and/or network communications cost, hence the desire to have small cut size. We study a distributed balanced-partitioning problem where the goal is to partition the vertices of a given graph into k pieces so as to minimize the total cut size. Our algorithm is composed of a few steps that are easily implementable in distributed computation frameworks such as MapReduce. The algorithm first embeds nodes of the graph onto a line, and then processes nodes in a distributed manner guided by the linear embedding order. We examine various ways to find the first embedding, for example, via a hierarchical clustering or Hilbert curves. Then we apply four different techniques including local swaps, and minimum cuts on the boundaries of partitions, as well as contraction and dynamic programming. As our empirical study, we compare the above techniques with each other, and also to previous work in distributed graph algorithms, for example, a label-propagation method, FENNEL and Spinner. We report our results both on a private map graph and several public social networks, and show that our results beat previous distributed algorithms: For instance, compared to the label-propagation algorithm, we report an improvement of 15–25% in the cut value. We also observe that our algorithms admit scalable distributed implementation for any number of partitions. Finally, we explain three applications of this work at Google: (1) Balanced partitioning is used to route multi-term queries to different replicas in Google Search backend in a way that reduces the cache miss rates by ≈$0.5\%$, which leads to a double-digit gain in throughput of production clusters. (2) Applied to the Google Maps Driving Directions, balanced partitioning minimizes the number of cross-shard queries with the goal of saving in CPU usage. This system achieves load balancing by dividing the world graph into several “shards”. Live experiments demonstrate an ≈$40\%$ drop in the number of cross-shard queries when compared to a standard geography-based method. (3) In a job scheduling problem for our data centers, we use balanced partitioning to evenly distribute the work while minimizing the amount of communication across geographically distant servers. In fact, the hierarchical nature of our solution goes well with the layering of data center servers, where certain machines are closer to each other and have faster links to one another.

1. Introduction

Graph partitioning is a crucial first step in developing a tool for mining big graphs or solving large-scale optimization problems. In many applications, the partition sizes have to be balanced or almost balanced so that each part can be handled by a single machine to ensure the speedup of parallel computing over different parts. Such a balanced graph partitioning tool is applicable throughout scientific computation for dealing with distributed computations over massive data sets, and serves as a tradeoff between the local computation and total communication amongst machines.

In several applications, a graph serves as a substitute for the computational domain [1]. Each vertex denotes a piece of information and edges denote dependencies between information. Usually, the goal is to partition the vertices such that no part is too large, and the number of edges across parts is small. Such a partition implies that most of the work happens within a part and only minimal work or communication takes place between parts. In these applications, links between different parts may show up in the running time and/or network communications cost. Thus, a good partitioning minimizes the amount of communication during a distributed computation. In other applications, a big graph can be carefully chopped into parts that fit on one machine to be processed independently before finally stitching the individual results together, leading to certain suboptimality arising from the interaction between different parts. To formally capture these situations, we study a balanced partitioning problem where the goal is to partition the vertices of a given graph into k parts so as to minimize the total cut size. We emphasize that our main focus is on the size of the resulting cut and not the resource consumption of our algorithm, although it is fully distributable, uses linear space and runs for all the relevant experiments in reasonable amount of time (more or less comparable to the state of the art). Unfortunately, we cannot reveal the exact running times due to corporate restrictions. Nevertheless, we report in Section 6.4 relative running times of our algorithm on synthetic data of varying sizes to demonstrate its scalability.

This is a challenging problem that is computationally hard even for medium-size graphs [2] as it captures the graph bisection problem [3], hence all attempts at tackling it necessarily relies on heuristics. While the topic of large-scale balanced graph-partitioning has attracted significant attention in the literature [4,5,6,7], the large body of previous work study large-scale but non-distributed solutions to this problem. Several motivations necessitate the quest for a distributed algorithm for these problems: (i) first of all, huge graphs with hundreds of billions of edges that do not fit in memory are becoming increasingly common [4,5]; (ii) in many distributed graph-processing frameworks such as Pregel [8], Apache Giraph [9], and PEGASUS [10], we need to partition the graph into different pieces, since the underlying graph does not fit on a single machine, and therefore for the same reason, we need to partition the graph in a distributed manner; (iii) the ability to run a distributed algorithm using a common distributed computing framework such as MapReduce on a distributed computing platform consisting of commodity hardware makes an algorithm much more widely applicable in practice; and (iv) even if the graph fits in memory of a super-computer, implementing some algorithms requires superlinear memory which is not feasible on a single machine. The need for distributed algorithms has been observed by several practical and theoretical research papers [4,5].

For streaming and some distributed optimization models, Stanton [11] has shown that achieving formal approximation guarantees is information theoretically impossible, say, for a class of random graphs. Given the hardness of this problem, we explore several distributed heuristic algorithms. Our algorithm is composed of a few logical, simple steps, which can be implemented in various distributed computation frameworks such as MapReduce [12].

1.1. Motivation

Following the publication of the extended abstract of this work at WSDM 2016 [13], we have depolyed this algorithm in several applications from various domains (such as Maps, Search and Infrastructure). However, we only mention two motivating applications in this section, in order to keep the reader focused. The interested reader is encouraged to visit Section 7 for more information about applications.

1.1.1. Google Maps Driving Directions

As one of the applications of our balanced-partitioning algorithm, we study a balanced- partitioning problem in the Google Maps Driving Directions. This system computes the optimal driving route for any given source-destination query (pairs of locations on Google Maps). A plausible approach to answer such pairwise queries in this large-scale graph application is to obtain a suitable partitioning of the graph beforehand so that each server handles its own section of the graph, called a shard. In this application, ideally we seek to minimize the number of cross-shard queries, for which the source and destination are not in the same shard, that is, the total cross-shard traffic is as low as possible, since handling cross-shard queries is much more costly and entails extra communication and coordination across multiple servers. In order to reduce the cross-shard query traffic we want to minimize the cut size between the partitions, with the expectation that less directions will be produced where the source and the destination are in different partitions. Reducing the cut size in practice results in denser regions in the same partition, therefore most queries will be contained within one shard. We confirm this observation with extensive studies using historical query data and live experiments (see Section 7.1 for more details).

Conveniently, a linear embedding provides a very simple way of specifying partitions by merely providing two numbers for each shard’s boundaries. Therefore it is straightforward and fast to identify the shard a given query point belongs to. As we will discuss later, our study of linear embedding of graphs while minimizing the cut size is partly motivated by these reasons.

1.1.2. Treatment and Control Groups for Randomized Experiments

Another application where balanced partitioning has historically been found very effective is in the context of causal inference in randomized experiments [14,15]. In most settings there is an underlying interference between experiment units (for example, advertisers). Interference is often modeled by a graph in which nodes are treatment units and there is an edge between two nodes if their potential outcomes depend on each others’ treatment assignment. The graph is then partitioned into clusters of approximately equal size that minimize the total edge weights crossing the clusters. Finding such clusters is equivalent to the balanced-partitioning problem, which is the focus of our study. Once the clusters are generated, a set of clusters can be chosen at random to set up the treatment portion of the experiment.

1.2. Our Contributions

Our contributions in this paper can be divided into five categories.

• We introduce a multi-stage distributed optimization framework for balanced partitioning based on first embedding the graph into a line and then optimizing the clusters guided by the order of nodes on the line. (Embedding into a line is also essential in graph compression; see, e.g., References [16,17]). This framework is not only suitable for distributed partitioning of a large-scale graph, but also it is directly applicable to balanced-partitioning applications like those in Google Maps Driving Directions described above. More specifically, we develop a general technique that first embeds nodes of the graph onto a line, and then post-processes nodes in a distributed manner guided by the order of our linear embedding.
• As for the initialization stage, we examine several ways to find the first embedding: (i) by naïvely using a random ordering, (ii) for map graphs by the Hilbert-curve embedding, and (iii) for general graphs by applying hierarchical clustering on an edge-weighted graph where the edge weights are based either on the number of common neighbors of the nodes in the graph or on the inverse of the distance of the corresponding nodes on the map. Whereas the Hilbert-curve embedding and our hierarchical clustering based on node distances may only be applied to maps graphs, the hierarchical clustering based on the number of common neighbors is applicable to all graphs. While all these methods prove useful, to our surprise, the latter (most general) initial embedding technique is the best initialization technique even for maps. We later explain that all these methods have very efficient and scalable distributed implementations. See the discussion in Section 3.3 regarding the efficiency of the hierarchical clustering, and consult Reference [18] regarding the challenge to construct the similarity metric. (It might be worth studying spectral embedding methods or standard embedding techniques into ${\ell }_1$, but we did not try them due to not having a scalable distributed implementation, and also since the hierarchical clustering-based embedding worked pretty well in practice. We leave this for future research.)
• As a next step, we apply four methods to postprocess the initial ordering and produce an improved cut. The methods include a metric ordering optimization method, a local improvement method based on random swaps, another based on computing minimum cuts in the boundaries of partitions, and finally a technique based on contracting the minimum-cut-based clusters, and applying dynamic programming to compute optimal cluster boundaries. Our final algorithm (called Combination) combines the best of our initialization methods, and iterates on the various postprocessing methods until it converges. The resulting algorithm is quite scalable: it runs smoothly on graphs with hundreds of millions of nodes and billions of edges.
• In our empirical study, we compare the above techniques with each other, and more importantly with previous work. In particular, we compare our results to prior work in (distributed) balanced graph-partitioning, including a label propagation-based algorithm [4], FENNEL [5], Spinner [19] and METIS [20]. Some works such as Reference [21] are indirectly compared to, and others such as Reference [22] did not report cut sizes. We relied for these comparisons on available cut results for a host of large public graphs. We report our results on both a large private map graph, and also on several public social networks studied in previous work [4,5,19,22].
  • First, we show that our distributed algorithm consistently beats the label-propagation algorithm by Ugander and Backstrom [4] (on LiveJournal) by a reasonable margin for all values of k. For example, for $k=20$, we improve the cut by $25\%$ (from $37\%$ to $27.5\%$ of total edge weight), and for $k=100$, we improve the cut by $15\%$ (from $49\%$ to $41.5\%$). The clustering outputs can be found in Reference [23].
  • In addition, for $k>2$ partitions, we show that our algorithm beats METIS and FENNEL (on Twitter) by a reasonable factor. For $k=2$, the results that we obtain beats the output of METIS but it is slightly inferior to the result reported by FENNEL.
  • For both graphs, our results are consistently superior to that of Spinner [19] with a wide margin.
  • We also note that our algorithms admit scalable distributed implementation for small or large number of partitions. More specifically, changing k from 2 to tens of thousands does not change the running time significantly.
  • As for comparing various initialization methods, we observe that while geographic Hilbert-curve techniques outperform the random ordering, the methods based on the hierarchical clustering using the number of common neighbors as the similarity measure between nodes outperform the geography-based initial embeddings, even for map graphs. Note that the computation for the number of common neighbors is needed only once to obtain the initial graph, and the new edge weights in the subsequent rounds are computed via aggregation. Further note that approximate triangle counting can be done efficiently in MapReduce; see, for example, Reference [18].
  • As for comparing other techniques, we observe the random swap techniques are effective on Twitter, and the minimum-cut-based or contract and dynamic program techniques are very effective for the map graphs. Overall, we realize that these techniques complement each other, and combining them in a Combination algorithm is the most effective method.
• As mentioned earlier, we apply our results to the Google Maps Driving Directions application, and deploy two linear-embedding-based algorithms on the world’s map graph. We first examine the best imbalance factor for our cut-optimization technique, and observe that we can reduce $21\%$ of cross-shard queries by increasing the imbalance factor from $0\%$ to $10\%$. The two methods that we examined via live experiments were (i) a baseline approach based on the Hilbert-curve embedding, and (ii) one method based on applying our cut-optimization post-processing techniques. In live experiments on the real traffic, we observe the number of multi-shard queries from our cut-optimization techniques is 40% less compared to the baseline Hilbert embedding technique. This, in turn, results in less CPU usage in response to queries. (The exact decrease in CPU usage depends on the underlying serving infrastructure which is not our focus and is not revealed due to company policies. We note that there are several other algorithmic techniques and system tricks that are involved in setting up the distributed serving infrastructure for Google Maps driving directions. This system is handled by the Maps engineering team, and is not discussed here as it is not the focus of this paper.)

1.3. Other Related Work

Balanced partitioning is a challenging problem to approximate within a constant factor [2,24,25] or to approximate within any factor in several distributed or steaming models [11]. As for heuristic algorithms for this problem in the distributed or streaming models, a number of recent papers have been written about this topic [4,5,21]. Our algorithms are different from the ones studied in these papers. The most similar related work are the label propagation-based methods of Ugander and Backstrom [4] and Martella et al. (Spinner) [19] which develop a scalable distributed algorithm for balanced partitioning. Our random-swap technique is similar in spirit to the label-propagation algorithm studied in Reference [4], however, we also examine three other methods as a postprocessing stage and find out that these methods work well in combination. Moreover, Reference [4] studied two different methods for their initialization, a random initialization, and a geographic initialization. We also examine random ordering, and a Hilbert-curve ordering which is similar to the geographic initialization in Reference [4]. However, we examine two other initialization techniques and observe that even for map-based geographic graphs, the initialization methods based on hierarchical clustering outperform the geography-based initial ordering. Overall, we compare our algorithm directly on a LiveJournal public graph (the only public graph reported in Reference [4]), and improve the cut values achieved in References [4,19] by a large margin for all values of k. In addition, algorithms developed in References [5,21] are suitable for the streaming model but one can implement variants of those algorithms in a distributed manner. We also compare our algorithm directly to the numbers reported on the large-scale Twitter graph by FENNEL [5], and show that our algorithm compares favorably with the FENNEL output, hence indirectly comparing against Reference [21] because of the comparison provided in Reference [5].

Motivated by a variety of big data applications, distributed clustering has attracted significant attention over the literature, both for applications with no strict size constraints on the clusters [26,27,28] or with explicit or implicit size constraints [29]. A main difference between such balanced-clustering problems and the balanced graph-partitioning problems considered here is that in the graph-partitioning problems a main objective function is to minimize the cut size, whereas in those clustering problems, the main goal is minimize the maximum or average distance of nodes to the centers of their clusters.

2. Preliminaries

For an integer n, we define $\left[n\right]=\{1,2,\cdots ,n\}$. We also slightly abuse the notation and, for a function $f:A\mapsto \mathbb{R}$, define $f\left(A^{\prime }\right)={\sum }_{a\in A^{\prime }}f\left(a\right)$ if $A^{\prime }\subseteq A$. For a function $f:S\mapsto T$, we let $f^{-1}\left(t\right)$ for $t\in T$ denote the set of elements in S mapped to t via f; more precisely, $f^{-1}\left(t\right)=\{s\mid f\left(s\right)=t\}$. For a permutation $\pi$, let ${\pi }_i$ denote, for $i\in \left[n\right]$, the element in position i of $\pi$. Moreover, let $\pi (i\to j)=\{{\pi }_i,{\pi }_{i+1},\cdots ,{\pi }_j\}$ for $i\in \left[n\right],j\in \left[n\right]\cup \left\{0\right\}$. Note that, in particular, $\pi (i\to j)=\varnothing$ if $j<i$.

2.1. Problem Definition

Given is a graph $G(V,E)$ of n vertices with nonnegative edge lengths and nonnegative node weights, as well as an integer k, and a real number $\alpha \ge 0$. Let us denote the edge lengths by $d:E\mapsto \mathbb{R}$, and the vertex weights by $w:V\mapsto \mathbb{R}$. A partition of vertices of G into k parts $\{V_i:i\in \left[k\right]\}$ is said to be $\alpha$-balanced if and only if

$$(1-\alpha )\frac{w\left(V\right)}{k}\le w\left(V_i\right)\le (1+\alpha )\frac{w\left(V\right)}{k}.$$

In particular, a zero-balanced (or fully balanced) partition is one where all partitions have the same weight. The cut length of the partition is the total sum of all edges whose endpoints fall in different parts:

$$\begin{array}{c}\hfill \sum _i\sum _{j<i}\sum _{u\in V_i}\sum _{v\in V_j:(u,v)\in E\left(G\right)}w(u,v).\end{array}$$

Our goal is to find an $\alpha$-balanced partition whose cut size is (approximately) minimized.

The problem is NP-hard as the case of $\alpha =0,k=2$ is equivalent to the minimum bisection problem [3]. For arbitrary k, we get the minimum balanced k-cut problem, that is known to be inapproximable within any finite factor [2]; the best known approximation factor for it is $O\left({log}^{1.5}n\right)$ (if $\alpha >0$ is constant).

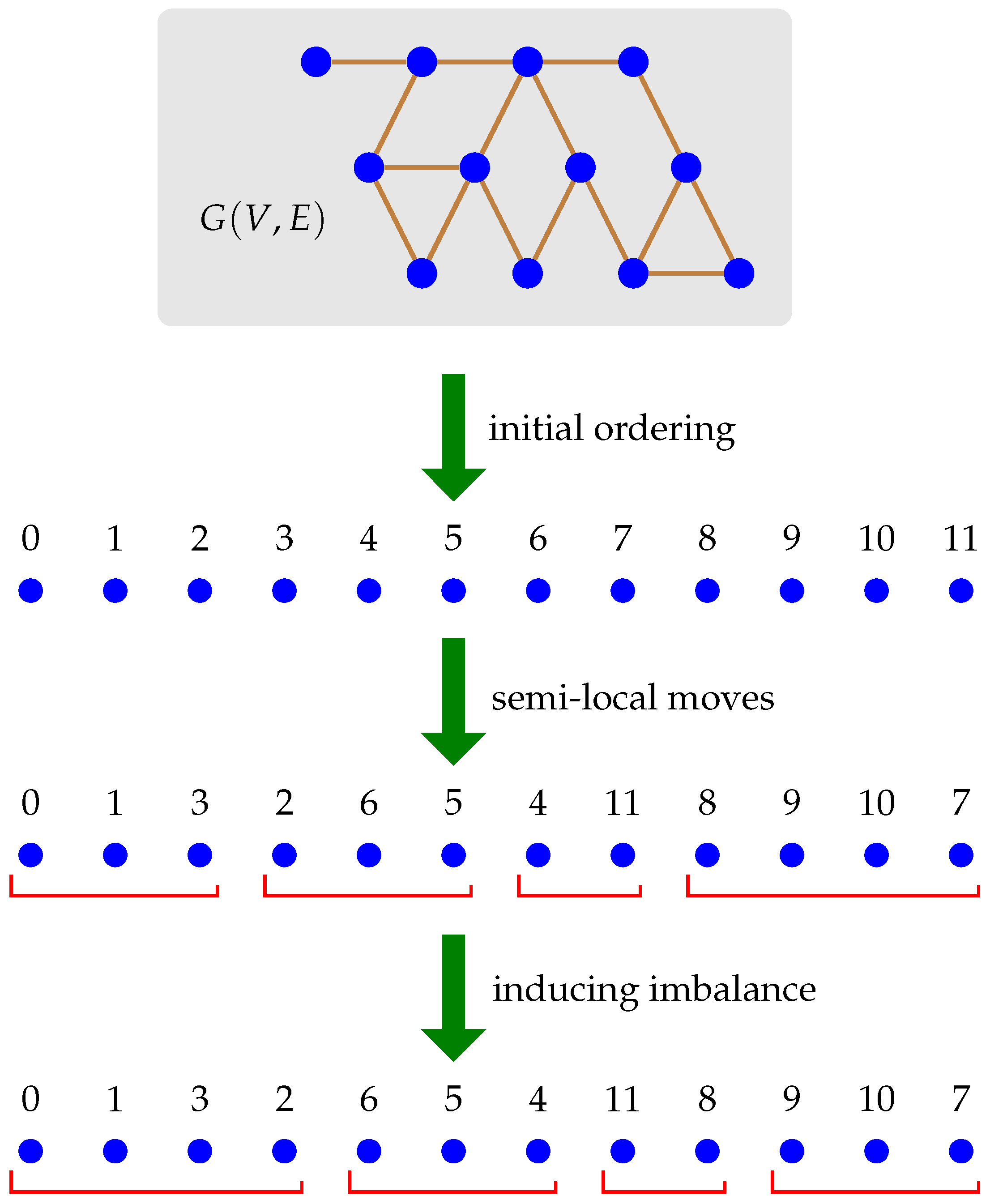
2.2. Our Algorithm

Our algorithm consists of three main parts (depicted in Figure 1):

• We first find a suitable mapping of the vertices to a line. This gives us an ordering of the vertices that presumably places (most) neighbors close to each other, therefore somewhat reduces the minimum-cut partitioning problem to an almost local optimization one.
• We next attempt to improve the ordering mainly by swapping vertices in a semilocal manner. These moves are done so as to improve certain metrics (perhaps, the cut size of a fully balanced partition).
• Finally, we use local postprocessing optimization in the “split windows” (i.e., a small interval around the equal-size partitions cut points taking into account permissible imbalance) to improve the partition’s cut size.

Note that one implementation may use only some of the above, and clearly any implementation will pick one method to perform each task above and mix them to get a final almost balanced partition. Indeed, we report some of our results (specially those in comparison to the previous work) based on Combination, which uses AffCommNeigh to get the initial ordering and then iteratively applies techniques from the second and third stages above (e.g., Metric, Swap, MinCut) until the result converges. (The convergence in our experiments happens in two or three rounds).

Algorithm 1$\mathtt{Combination}(G,k,\alpha )$

Input: Graph G, number of parts k, imbalance parameter $\alpha$ Output: A partition of $V\left(G\right)$ into k parts 1: for all$(u,v)\in E\left(G\right)$do 2:  $w(u,v)\leftarrow$ number of common neighbors of $u,v$ 3: $\pi \leftarrow \mathtt{AffinityOrdering}(G,w)$ 4: for$i=0$tokdo 5:  $q\left(i\right)\leftarrow \lfloor \frac{in}{k}\rfloor$ {fully balanced split points} 6: repeat 7:  $({\pi }^{\prime },q^{\prime })\leftarrow (\pi ,q)$ 8:  Use any (semilocal or imbalance-inducing) postprocessing technique on $(G,{\pi }^{\prime },q^{\prime })$ to obtain $(\pi ,q)$ 9: until$\pi ={\pi }^{\prime }$and$q=q^{\prime }$ 10: for all$i\in \left[k\right]$do 11:  $V_i\leftarrow \pi (q\left(i\right)+1\to q(i+1))$ 12: return$\{V_1,V_2,\cdots ,V_k\}$

3. Initial Mapping to Line

3.1. Random Mapping

The easiest method to produce an ordering for the vertices is to randomly permute them. Though very fast, this method does not seem to lead to much progress towards our goal of finding good cuts. In particular, if we then turn this ordering into a partition by cutting contiguous pieces of equal size, we end up with a random partition of the input (into equal parts) which is almost surely a bad cut: a standard probabilistic argument shows that the cut has expected ratio $1-\frac{1}{k}$. Nevertheless, the next stage of the algorithm (i.e., the semilocal optimization by swapping) can generate a relatively good ordering with this naïve starting point.

3.2. Hilbert Curve Mapping

For certain graphs, geographic/geometric information is available for each vertex. It is fairly easy, then, to construct an ordering using a space-filling curve—prime examples are Peano, Morton and Hilbert curves but we focus on the latter in this work. These methods are known to capture proximity well: nodes that are close in the space are expected to be placed nearby on the line.

There has been extensive study of the applicability of these methods in solving large-scale optimization problems in parallel; see, for example, References [30,31].

Not only can this algorithm be used on its own without any cut guarantees but it can also be employed to break a big instance down into smaller ones that we can afford to run more intensive computations on. Both applications were known previously.

The previous works do not offer any theoretical guarantees on the quality of the cut generated from Hilbert curves. However, certain assumptions on the distributions of edge lengths and node positions let us bound the resulting cut ratio and show that it is significantly less than the result of random ordering [32,33,34]. This is observed in our experiments, too.

3.3. Affinity-Based Mapping

One drawback of the Hilbert-curve cover (even when geographic coordinates are available) is that it ignores the actual edges in the graph. For an illustration, consider using the Hilbert curve to map certain points in an archipalego (or just a small number of islands or peninsulas). The Hilbert curve, unaware of the connectivities, traverses the vertices in a semirandom order, therefore, it may jump from island to island without covering the entire island first.

To address this issue, we use an agglomerative hierarchical clustering method, usually called average-linkage clustering We call the method “affinity clustering” since it takes into account the affinity of vertices. Informally, every node starts in a singleton cluster of its own and then in several stages we group vertices that are closely connected, hence building a tree of these connections. More precisely, at every stage, each node turns on the connection to its closest neighbor, after which the connected components form clusters. The similarities used in the next level between constructed clusters are computed via some function of the similarities between the elements forming the clusters; in particular, we take the average function for this purpose. Typically attributed to Reference [35], this is reminiscent of a parallel version of Borúvka’s algorithm for minimum spanning tree where the min operation is replaced by average [36].

The final ordering is produced by sorting the vertex labels produced as follows. Let the label for each vertex be the concatenation of vertex ID strings from the root to the corresponding leaf. Sorting the constructed labels places the vertices under each branch in a contiguous piece on the line. The same guarantee holds recursively, hence the (edge) proximity is preserved well. A pseudocode for this procedure is given in Algorithm 2: Line 15 uses notation $a\#b$ to denote the concatenation of labels for a and b. Notice that this pseudocode explains a sequential algorithm, however, the procedure can be efficiently implemented in a few rounds of MapReduce. In fact, our algorithm is very similar to that in Reference [37] but uses Distributed Hash Tables as explained in Reference [38]. In fact, as mentioned therein, an implementation of the connected-components algorithm within the same framework and using the same techniques provides a 20–40 times improvement in running time compared to best previously known algorithms.

Algorithm 2$\mathtt{AffinityOrdering}(G,w)$

Input: Graph G, (partial) similarity function w Output: A permutation of vertices 1: ${\mathcal{C}}^0$←$\left\{\right\{v\}\mid v\in V(G\left)\right\}$ 2: for$v\in V\left(G\right)$do 3:  $\ell \left(v\right)\leftarrow v$ 4: $i\leftarrow 0$ 5: repeat 6:  for $s\in {\mathcal{C}}^i$ do 7:   ${\displaystyle p\left(s\right)\leftarrow arg\underset{t\in C^i}{max}w(s,t)}$ 8:  ${\mathcal{C}}^{i+1}\leftarrow \varnothing$ 9:  for $t\in \{p\left(s\right)\mid s\in {\mathcal{C}}^i\}$ do 10:   $S\leftarrow p^{-1}\left(t\right)$ 11:   $S^{\prime }\leftarrow {\bigcup }_{s\in S}s$ 12:   ${\displaystyle {\mathcal{C}}^{i+1}\leftarrow {\mathcal{C}}^{i+1}\cup S^{\prime }}$ 13:   ${\displaystyle r\leftarrow arg\underset{r^{\prime }\in S^{\prime }}{min}s}$ 14:   for $s^{\prime }\in S^{\prime }$ do 15:    $\ell \left(s^{\prime }\right)\leftarrow r\#\ell \left(s^{\prime }\right)$ 16:  $i\leftarrow i+1$ 17: until$|{\mathcal{C}}^i|=|{\mathcal{C}}^{i-1}|$ 18: $\pi \leftarrow$ permutation of vertices sorted according to ℓ 19: return$\pi$

Intuitively, we expect vertices connected in lower levels (farther from the root) to be closer than those connected in later stages. (See Figure 2 for illustration). In particular, we observed that a graph with several connected components gives an advantage to affinity tree ordering over the ordering produced by Hilbert curve.

For this approach to work, we require meaningful distances/similarities between vertices of the graph. Conveniently it does not matter whether we have access to distances or similarity values. However, though theoretically possible to run the affinity clustering algorithm on an unweighted graph with distances 1 and ∞ for edges and non-edges respectively, this leads to a lot of arbitrary tie-breaks that makes the result irrelevant. Practically the worse outcome is a highly unbalanced hierarchical partitioning because arbitrary tie-breaks favor the “first” cluster.

Fortunately, there are standard ways to impose a metric on an unweighted graph: for example, common-neighbors ratio or personalized page rank. We focus on the former metric and compute for every pair of neighbors the ratio of the number of their common neighbors over the total number of their distinct neighbors. Computing the number of common neighbors can be implemented using standard techniques in MapReduce, however, one can use sampling when dealing with high-degree vertices to improve the running time and memory footprint (leading to an approximate result). As alluded earlier in the text, there are very fast distributed algorithms for computing this metric; see, for example, Reference [18].

4. Improve Ordering Using SemiLocal Moves

Given an initial ordering of vertices for example by AffinityOrdering, we can further improve the cut size by applying semilocal moves. The motivation here is that these simple techniques provide us with highly parallelizable algorithms that can be iteratively applied (e.g., by a MapReduce pipeline) so the result converges to high-quality partitions. In the following we discuss two such approaches.

4.1. Minimum Linear Arrangement

Minimum Linear Arrangement (MinLA) is a well-studied NP-hard optimization problem [3], which admits $O(loglogn)$ approximation on planar metrics [39] and $O(\sqrt{logn}loglogn)$ approximation on general graph metrics [40,41]. Given an undirected graph $G=(V,E)$ (with edge weights $w_{uv}$) we seek a one-to-one function $\varphi :V\to \{0,1,\cdots ,n-1\}$ that minimizes

$$\begin{array}{c}\hfill \sum _{(u,v)\in E}|\varphi \left(v\right)-\varphi \left(u\right)|w_{uv}.\end{array}$$

(1)

Optimizing the sum above results in a linear ordering of vertices along a line such that neighbor nodes are near each other. The end result is that dense regions of the graph will be isolated into clusters, which makes it easier to identify cut boundaries on the line.

We have implemented a very simple distributed algorithm (in MapReduce) that directly optimizes MinLA. The algorithm simply iterates on the following MapReduce phases until it converges (or runs up to a specified number of steps):

• MR Phase 1: Each node computes its optimal rank as the weighted median of its neighbors and outputs its new rank. Note that, all else fixed, moving a node to the weighted median of its neighbors—a standard computation in MapReduce—optimizes Equation (1).
• MR Phase 2: Assigns final ranks to each node (i.e., handles duplicate resolution, for example, by simple ID-based ordering).

Note that since Phase 1 is done in parallel for each node and independently of other moves, there will be side effects, hence it is an optimistic algorithm with the hope that it will converge to a stable state after few rounds. Our experimental results show that in practice this algorithm indeed converges for all the graph types that we tried, although the number of rounds depends on the underlying graph.

4.2. Rank Swap

Given an existing linear ordering of vertices in a graph we can further improve the cut size (of the fully balanced partition based on it) via semilocal swaps. Note that unlike MinLA heuristic discussed in Section 4.1, this process depends on the pre-selected cut boundaries, that is, the number of final partitions k. Notice that one expects that the semilocal swap operations will be effective once a good initial ordering provided by either the Affinity-based mapping and/or MinLA. Indeed our experimental results show that this procedure is extremely effective and produces cut sizes better than the competition on some public social graphs we tried.

RankSwap can be implemented in a straightforward way on a distributed (for example, MapReduce) framework as outlined by Algorithm 3.

Algorithm 3$\mathtt{RankSwap}(G,k,r)$

Input: Graph G, number of partitions k, number of intervals per partition r Output: A partition of $V\left(G\right)$ into k parts      – Controller: 1:  Pair nearby partitions 2:  Split each partition into r intervals $I_0,\cdots ,I_{r-1}$ and randomly pair intervals between paired partitions – Map$\langle I_i;I_j\rangle$: 3: repeat 4:  Pick node pair $u\in I_i$, $v\in I_j$ with the best cut improvement 5:  Swap u and v 6: until no pair improves the cut 7: for all$u\in I_i\cup I_j$do 8:  Emit $\langle u;r_u\rangle$. {$r_u$ is the new rank of u} Reduce$\langle u;r_u\rangle$: 9:  Emit $\langle u;r_u\rangle$. {Identity Reducer}

Subdividing each partition into intervals is important, especially for small number of partitions k, to achieve parallelism and allowing possibly more time- and memory-consuming swap operations. Pairing the intervals between two partitions can be done in various ways. One simple example is random pairing. Our experiments showed that this is almost as effective as more complicated ones, hence we do not discuss the other methods in detail here.

The swap operation between two intervals (handled by each Mapper task) can be done in various ways. (The version described in Algorithm 3 is Method 3 below).

Each approach below starts with computing the cut size reduction as a result of moving a node from one interval to the other. Once these values are computed for each node in the two intervals, the following are the alternatives we tried (from the simplest to more complicated):

• Method 1: Sort the nodes in each interval in descending order by their cut size reduction. Then simply do a pairwise swap between entries at i-th place in each interval provided that the swap results in a combined reduction. This method is very simple and fast, however, it may have side effects within the interval (and also outside) since it does not account for those.
• Method 2: This is a modified version of Method 1 with the addition that after each swap is performed, we also update the cut reduction values of other nodes. This method does only one pass from top to bottom and stops when there is no further improvement.
• Method 3: In this method we iterate on Method 2 until we converge to a stable state. In this way we reach a local optimum between two intervals. The other improvement is that instead of pairing entries at i-th position, we find the best pair in the second interval and swap with that. This is because the top entries in each interval can be neighbors of each other and therefore they may not be the best pair to swap.

Our extensive studies with these methods confirmed that Method 3 gives the best results in terms of quality at the expense of an acceptable additional cost. It runs fast in practice due to the relatively small sizes of the intervals because of the parallelism we achieve. We can also afford an additional cost in the swap method because each interval pair is handled by a separate Mapper task.

5. Imbalance-Inducing Postprocessing

We have now an ordering of the vertices that presumably places similar vertices close to each other. Instead of cutting the sequence at equidistant positions to obtain a fully balanced partitioning, we describe in this section several postprocessing techniques that allow us to take advantage of the permissible imbalance and produce better cuts.

First we sketch how the problem can be solved optimally if the number of vertices is not too large. This approach is based on dynamic programming and requires the entire graph to live in memory, which is a barrier for using this technique even if the running time were almost linear. In fact, the procedure proposed here runs in time $O(n^{3}logk)$ but the running time can be improved to almost linear. Despite the memory requirement, this algorithm is usable with the caveat that one first needs to group together blocks of contiguous vertices and contract them into supernodes, such that the graph of supernodes fits in memory and is small enough for the algorithm to handle. The fact that nearby vertices are similar to each other implies that this sort of contraction should not hurt the subsequent optimization significantly. Indeed trying two different block sizes (resulting in 1000 and 5000 blocks) produced similar cuts in our experiments.

The other two approaches work on the concept of “windows” and perform only local optimizations within each. Let $\pi$ denote the permutation of vertices at the start of the local optimization and let ${\pi }_i$ be the i-th vertex in the permutation for $1\le i\le n$. Given that we want to get k parts of (almost) the same size, we consider the ideal split points $q_j=\lfloor \frac{jn}{k}\rfloor$ for $1\le j<k$. Though there are only $k-1$ real split points, we define two dummy split points at either end to make the notation cleaner: $q_0=0$ and $q_k=n$. Then, the ideal partitions, in terms of size, will be formed of $\pi (q_j+1\to q_{j+1})$ for different $0\le j<k$. Given permissible imbalance $\alpha >0$, a window is defined around each (real) split point allowing for $\alpha /2$ imbalance on either side. More precisely, $W_j=\pi ({\pi }_{q_j-{\alpha }^{\prime }}\to {\pi }_{q_j+{\alpha }^{\prime }})$ for ${\alpha }^{\prime }=\lceil \frac{\alpha n}{2k}\rceil$. Essentially we are free to shift the boundaries of partitions within each window without violating the balance requirements. We propose two methods to take advantage of this opportunity. One finds the optimal boundaries within windows, while the other also permutes the vertices in each window arbitrarily to find a better solution.

5.1. Dynamic Program to Optimize Cuts

The partitioning problem becomes more tractable if we fix an ordering $\pi$ of vertices and insist on each partition consisting of consecutive vertices (perhaps, with wrap-around). Let us for now assume that no wrap-around is permissible; that is, each part corresponds to a contiguous subset of vertices on $\pi$.

In the dynamic programming (DP) framework, instead of solving the given instance, we solve several instances (all based on the input and closely related to one another) and do so in a carefully chosen sequence such that the instances already solved make it easier to quickly solve newer instances, culminating in the solution to the real instance.

Let $A_{i,j,q}$ for $1\le i,j\le n,1\le q\le k,j\ge i-1$ denote the smallest cut size achievable for the subgraph induced by vertices $\pi (i\to j)$ if exactly q partitions thereof are desired. Once all these entries are computed, $A_{1,n,k}$ yields the solution to the original problem. As is customary in dynamic programs, we only discuss how to find the “cost”—here, the cut size—of the optimal solution; finding the actual solution—here, the partition—can be achieved in a straight-forward manner by adding certain information to the DP table.

We fill in the table $A_{i,j,q}$ in the order of increasing q. For the case of $q=1$, we clearly have $A_{i,j,q}=0$ if and only if

$$w\left(\pi (i\to j)\right)\le (1+\alpha )\frac{w\left(V\right)}{k},$$

that is, vertices $\pi (i\to j)$ can be placed in one part without violating the balanced property. Otherwise, it is defined as infinity.

We use a recursive formula to compute $A_{i,j,q}$ for $q>1$. The formula depends on $A_{i^{\prime },j^{\prime },q^{\prime }}$ entries where $q^{\prime }<q$, hence these entries have all been already computed. Let us introduce some notation before presenting the recurrence. We define $C(i,j,k)$ as the total length of edges going from $\pi (i\to j)$ to $\pi (j+1\to k)$. We now present the recursive formula for computing $A_{i,j,q}$ as

$$\begin{array}{cc}\hfill A_{i,j,q}& =\underset{i-1\le k\le j}{min}\left[A_{i,k,1}+A_{k+1,j,q-1}+C(i,k,j)\right].\hfill \end{array}$$

(2)

Notice that the first term in the minimization is only used to signify whether $\pi (i\to k)$ is a valid part in the intended $\alpha$-balanced partition: its value is either zero or infinity.

Lemma 1.

Equation (2) is a valid recursion for $A_{i,j,q}$, which coupled with the initialization step given above yields a sound computation for all entries in the DP table.

Proof. 

The argument proceeds by mathematical induction. The initialization step is clearly sound as it is simply verifying feasibility of single parts.

For the inductive part, it suffices to show that the best solution with a part $\pi (i\to k)$ has a cut size $A_{i,k,1}+A_{k+1,j,q-1}+C(i,k,j)$. Then, the first term in (2) accounts for the case when we use one empty part (i.e., we partition $\pi (i\to j)$ using only $q-1$ parts) and the minimization considers the cases when the first part consists of $\pi (i\to k)$. To see the cost of the latter is as in (2), notice that any cut edge in the partition of $\pi (i\to j)$ is either completely inside $\pi (i\to k)$ (i.e., not contributing to the cut size), inside $\pi (k+1\to j)$ (which is accounted for in $A_{k+1,j,q-1}$ or connects $\pi (i\to k)$ to $\pi (k+1\to j)$ (in which case is taken into account by $C(i,k,j)$). □

The above procedure can be implemented to run in time $O\left(n^{3}k\right)$ and consume space $O\left(n^{2}k\right)$. Next we show how to improve this further. See Algorithm 4. The key idea is to avoid computing $A_{i,j,q}$ for all values $1\le q\le k$. Rather we focus on a limited subset of such q’s of size $O(logk)$.

Algorithm 4ImbalanceDP$(G,k,\pi )$

Input: Graph G, number of partitions k, fixed ordering $\pi$ of vertices Output: A partition of $V\left(G\right)$ into k parts 1: Let $n=\left|V\right(G\left)\right|$ be number of vertices in G 2: for all$1\le i\le j\le n$do 3:  Compute $w\left(\pi \right(i\to j\left)\right)$, the total weight of interval $\pi (\to j)$ 4: for all$1\le i\le j\le n$do 5:  if $w\left(\pi (i\to j)\right)\le (1+\alpha )\frac{w\left(V\right)}{k}$ then 6:   $A_{i,j,1}\leftarrow 0$ 7:  else 8:   $A_{i,j,1}\leftarrow \infty$ 9: for all$q=2$tokdo 10:  if $q=\lfloor k/2^l\rfloor$ or $q=\lceil k/2^l\rceil$ for some $l\ge 0$ then 11:   for all $1\le i\le j\le n$ do 12:    for all $i-1\le p<j$ do 13:     Compute $C(i,p,j)$, the total length of edges going from $\pi (i\to j)$ to $\pi (j+1\to k)$ 14:     $v\leftarrow A_{i,p,\lfloor \frac{q}{2}\rfloor }+A_{p+1,j,\lceil \frac{q}{2}\rceil }+C(i,p,j)$ 15:     if $A_{i,j,q}>v$ then 16:      $A(i,j,q)\leftarrow v$ 17: return$A_{1,n,k}$

We start by rewriting the recurrence as

$$\begin{array}{cc}\hfill A_{i,j,q}& =\underset{i-1\le k<j}{min}\left[A_{i,k,\lfloor \frac{q}{2}\rfloor }+A_{k+1,j,\lceil \frac{q}{2}\rceil }+C(i,k,j)\right].\hfill \end{array}$$

(3)

Then, computing the desired value $A_{1,n,k}$ only requires the computation of $A_{i,j,q}$ where q is either $\lfloor \frac{k}{2^l}\rfloor$ or $\lceil \frac{k}{2^l}\rceil$ for some $l\ge 0$. This reduces the running time to $O(n^{3}logk)$ and a bottom-up DP computation needs no more than three different values for q, hence the memory requirement is $O\left(n^2\right)$.

5.2. Scalable Linear Boundary Optimization

Recall the notion of “windows” defined at the beginning of Section 5. We now focus on a window $W=W_j$. This is small enough so that all information on the vertices in the window (including all their edges) fit in the memory (of one Mapper or Reducer). The linear optimization postprocessing finds a new split point in each window, so that the total weight of edges crossing it is minimized.

Let B and A denote the set of vertices appearing before and after W, respectively, in the ordering $\pi$. The edges going from B to A are irrelevant to the local optimization since those edges are necessarily cut no matter what split point we choose. The other edges have at least one endpoint in W. Then, there is a simple algorithm of running time $O\left(\right|V_W|·|E_W\left|\right)$ to find the best split point in W where $V_W$ and $E_W$ denote the set of vertices and edges, respectively, corresponding to W: look at each candidate split point and go over all relevant edges to determine the weight of the associated cut.

This can be done more efficiently to run in time $O\left(\right|V_W|+|E_W\left|\right)$, too. Let $s_v$ for $v\in W$ be the cut value (ignoring the effect of the edges between B and A). Let $s_0=s_{{\pi }_{q_j-{\alpha }^{\prime }}}$ (i.e., the cut value for the first split point in W), which is the total weight of edges between B and W and itself can be computed in time $O\left(\right|V_W|+|E_W\left|\right)$ (without hurting the overall runtime guarantee). We scan the candidate split points from left to right and compute $s_v-s_0$, however, the additive term $-s_0$ does not matter in comparing the different split point candidates.

For each vertex v following u, start with $s_u-s_0$, remove the edges between v and the vertices to its left (these already showed up in the cut value) and add up the edges between u and the vertices to its right; this gives the cut value $s_v-s_0$.

Since the windows are relatively small compared to the entire graph, and their corresponding subproblems can be solved independently, there is a very efficient MapReduce implementation for window-based postprocessing methods.

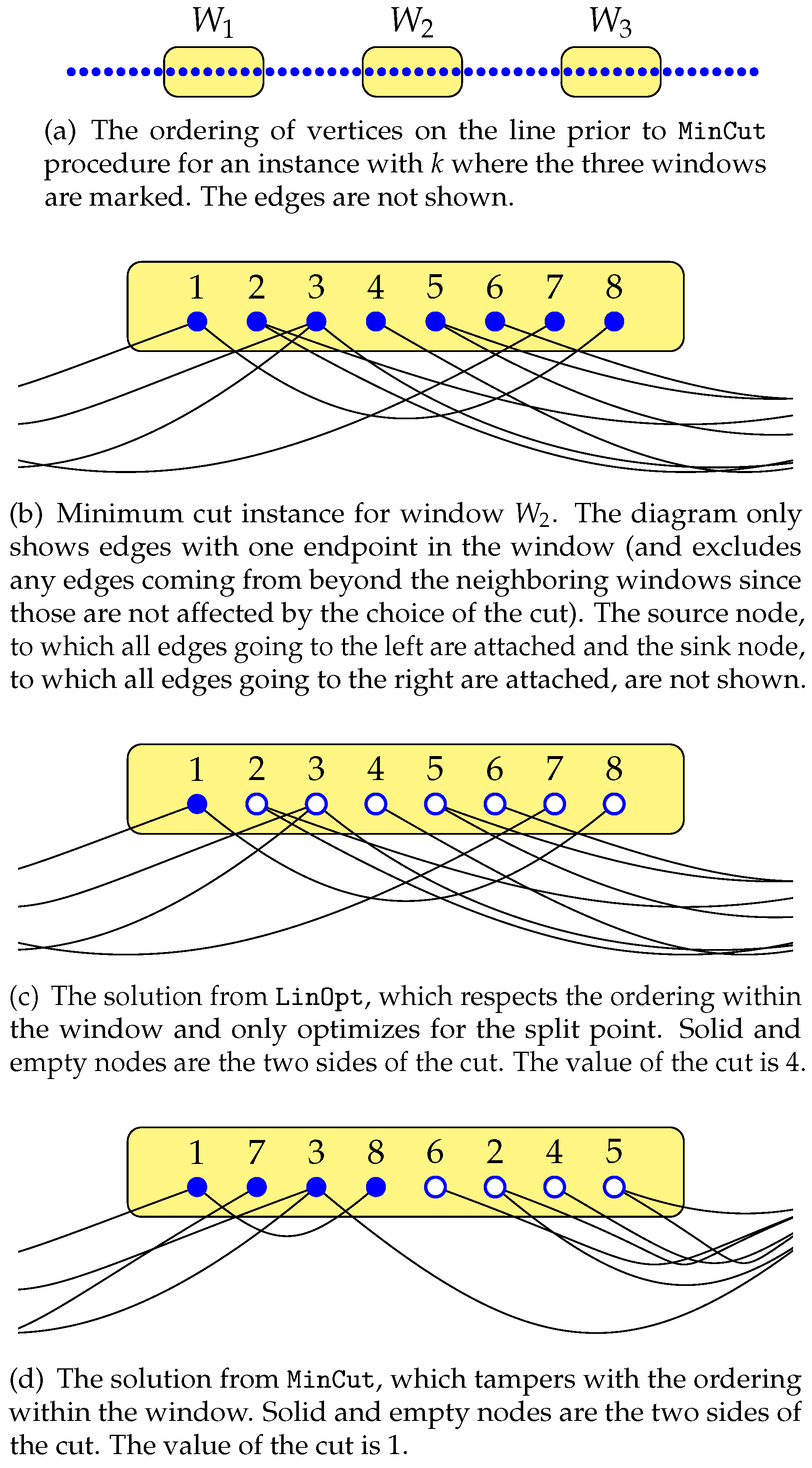
5.3. Scalable Minimum-Cut Optimization

Once again we focus on a window $W=W_j$ and denote by B and A the set of vertices belonging to previous and following vertices. Recall that the linear optimization of the previous section finds the best split point in the window while respecting the ordering of the vertices given in the permutation in $\pi$. The minimum-cut optimization, though, finds the best way to partition W into two pieces $W_L$ and $W_R$ so that the total weight of edges going from $B\cup W_L$ to $A\cup W_R$ is minimized. See Figure 3 for an illustration of this method.

5.4. Parallel Implementation

All the components of our algorithm (described in Section 3, Section 4 and Section 5) may be implemented in a distributed fashion, using a framework such as MapReduce [12]. Indeed the empirical study of Section 6 is based on an internal MapReduce implementation. An immediate advantage of this is that we can run our algorithm on very large graphs (with billions of nodes), as the implementation easily scales horizontally by

• dividing the graph into pieces which can be hosted in a distributed file system and
• launching multiple worker processes that operate on each piece independently.

It is worthwhile to note that in some cases workers might need access to other pieces (for example, the Affinity-based mapping described in Section 3.3). A typical solution that scales well in such cases is to temporarily use Distributed Hash Tables (DHT) [38]. The disadvantage of using a DHT is that it requires additional system resources. Some parts of the algorithm, especially the post-processing operations described in Section 4 and Section 5, may optionally be implemented using a DHT.

In a follow-up work [42], we present more details about the inner workings of the hierarchical clustering algorithm and provide a theoretical backing for its performance. In fact, a recent blog post [43] briefly summarizes the said work and the current paper.

6. Empirical Studies

First we describe the different datasets used in our experiments. Next we compare our results to previous work and we also compare our different methods to each other: that is, we demonstrate through experiments how much value each ingredient of the algorithm adds to the solution. Finally we discuss the scalability of our approach by running the algorithm on instances of varying sizes (but of the same type).

6.1. Datasets

We present our results on three datasets: World-roads, Twitter and LiveJournal (as well as publish our output on Friendster). As the names suggest, the first one is a geographic dataset while the other three are social graphs. All are big graphs, representatives of maps and social networks and we test the quality and scalability of our algorithm on them.

World-roads 

A subset of the entire world road network with hundreds of millions of vertices and over a billion edges. (Due to near-planarity, the average degree is small.) Edges do not have weights but vertices have longitude/latitude information. Our algorithms run smoothly on this graph in reasonable time using a small number of machines, demonstrating their scalability.

Twitter 

The public graph of tweets, with about 41 million vertices (twitter accounts) and 2.4 billion (directed) edges (denoting followership) [44]. This graph is unweighted, too. We run all our algorithms on the undirected underlying graph.

LiveJournal 

The undirected version of this public social graph (snapshot from 2006) has $4.8$ million vertices and $42.9$ million edges [4].

Friendster 

The undirected version of this public social graph (snapshot from 2006) has $65.6$ million vertices and $1.8$ billion [45].

Table 1. Statistics about datasets used. (Numbers for World-roads are approximate).

Dataset	$\left|\mathit{V}\right|$	$\left|\mathit{E}\right|$	Max Degree
LiveJournal	4,847,571	42,851,237	20,333
Twitter	41,652,230	1,202,513,046	2,997,487
Friendster	65,608,366	1,806,067,135	3615
World-roads	>${10}^8$	>${10}^9$	<20

presents a summary for these datasets. Reference [5] contains graphs other than Twitter, which are either small or not public.

6.2. Comparison of Different Techniques

6.2.1. Initial Ordering

We have four methods to obtain an initial ordering for the geographic graphs and two for non-geographic graphs. Here we compare these methods to each other based on the value of the cut obtained by chopping the resulting order into equal contiguous pieces. In order to make this meaningful, we report all the cut sizes as the fraction of cut edges to the total number of edges in the graph.

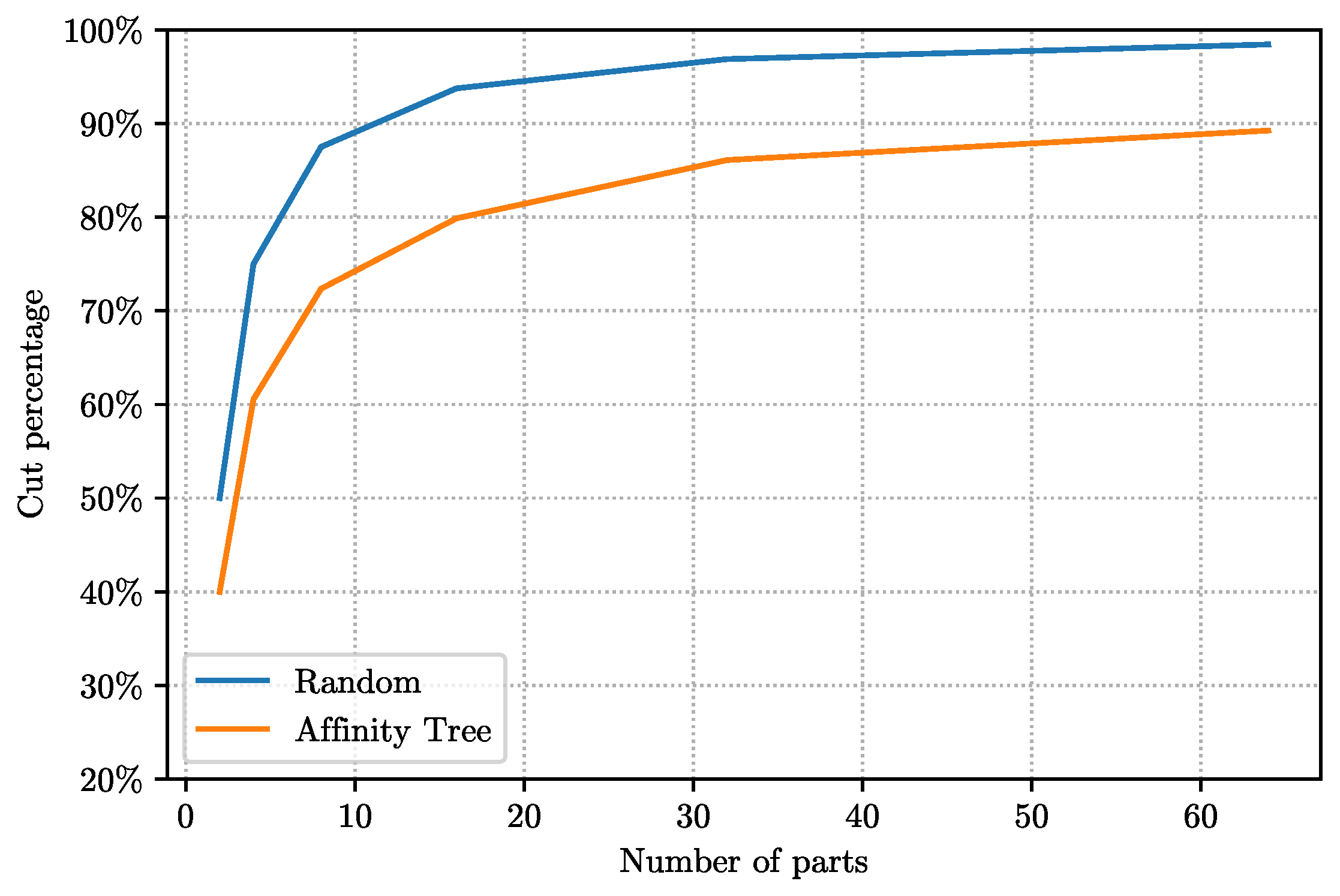
Figure 4 compares the results of two methods: RandInit produces a random permutation of the vertices, hence, as we observed previously, gets a cut size of approximately $1-\frac{1}{k}$; AffCommNeigh  (using the AffinityOrdering with the similarity oracle based on the number of common neighbors) clearly produces better solutions with improvements ranging from 20% to 10% (more improvement for smaller number of parts). The AffCommNeigh tree in this case was pretty shallow (much lower than the theoretical $logn$ upper bound) with only four levels. Whenever we report results for different number of partitions in one plot, $k=2,4,8,16,32,64$ are used for experiments.

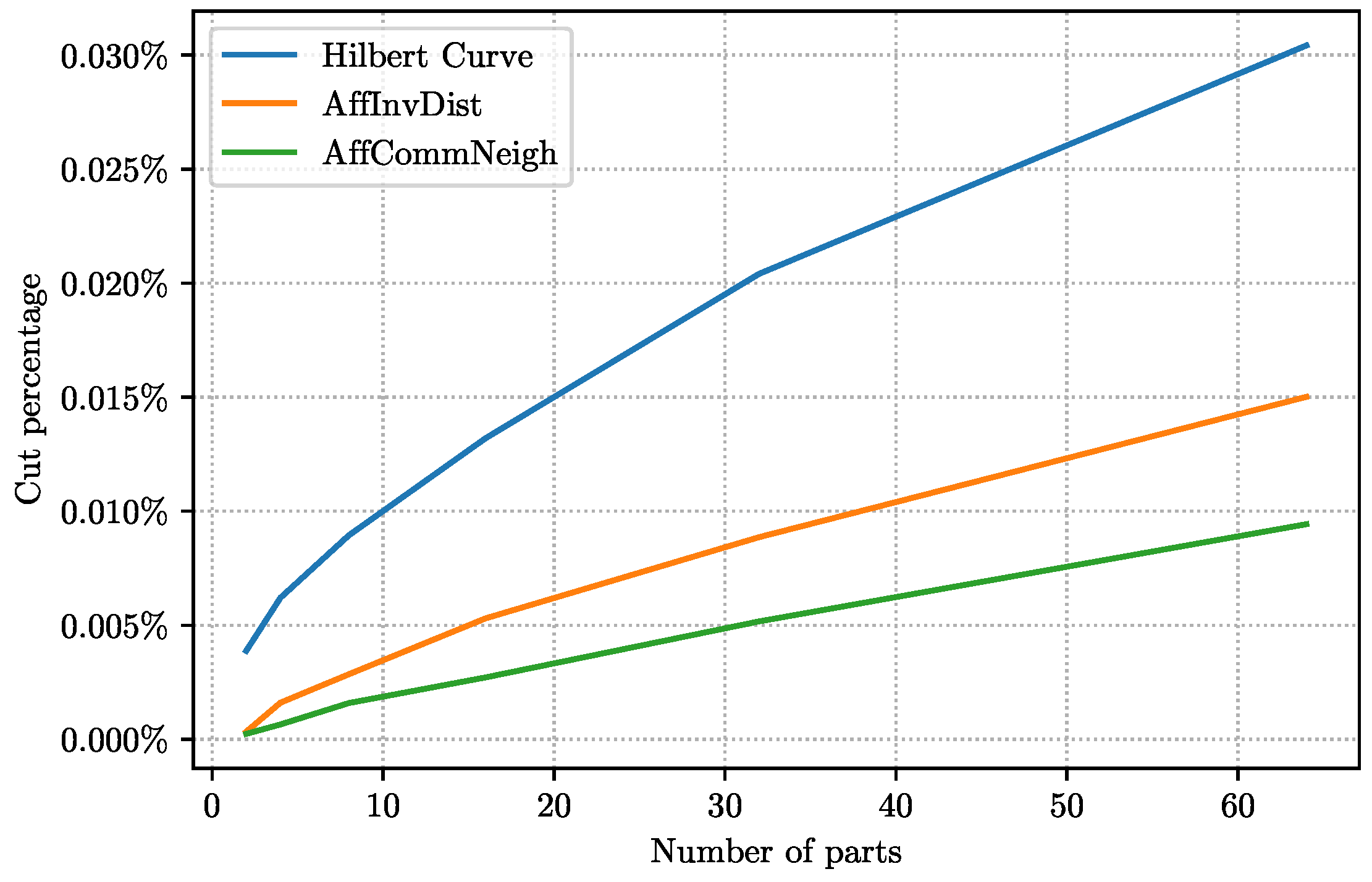
Figure 5 compares the results of three methods, each producing a cut of size at most $3\%$ and significantly improving upon the $1-\frac{1}{k}$ result of RandInit: Compared to Hilbert, the two other methods AffInvDist (using the inverse of geographic distance as the similarity oracle) and AffCommNeigh, respectively, obtain $90\%$ to $50\%$ and $95\%$ to $70\%$ improvement; once again the easier instances are those with smaller k. The corresponding trees, with 13 and 11 levels, respectively, are not as shallow as the one for Twitter. The quality of the cuts correlates with the runtime complexity of the algorithms: RandInit (fastest and worst), Hilbert, AffInvDist and AffCommNeigh (best and slowest). Note that although the implementation of Hilbert seems more complicated, it is significantly faster in practice.

For the following experiments, we focus on AffCommNeigh since it consistently produces better results for different values of k as well as both for Twitter and World-roads. Specially in diagram legends, this initialization step may be abbreviated as Aff.

6.2.2. Improvements and Imbalance

The performance of the semilocal improvement methods, Aff+Metric and Aff+Swap, as well as our main algorithm, Combination, on Twitter is reported in Figure 6. The diagram shows the percentage of improvement of each over the baseline AffCommNeigh for different values of $k=2,4,8,16,32,64$. Except for $k=16,32$, Aff+Swap outperforms Aff+Metric; their performance varies from $7\%$ to $75\%$, with best performance for smaller k. 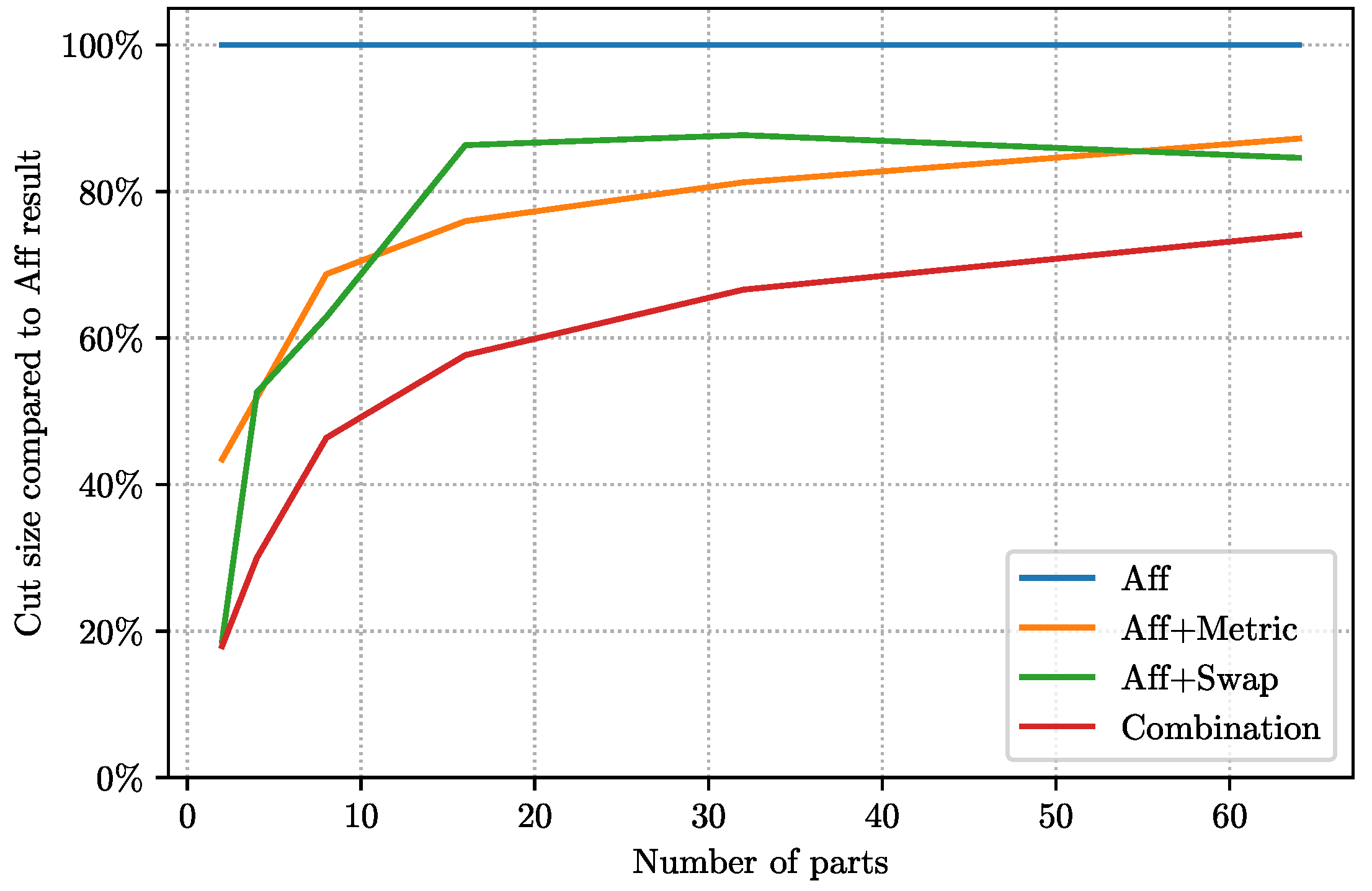Combining the two methods with the imbalance-inducing techniques to get Combination yields results significantly better than every single ingredient, with the relative improvement sometimes as large as 50%. The final results have very little imbalance and indeed cuts of comparable quality can be obtained without any imbalance.

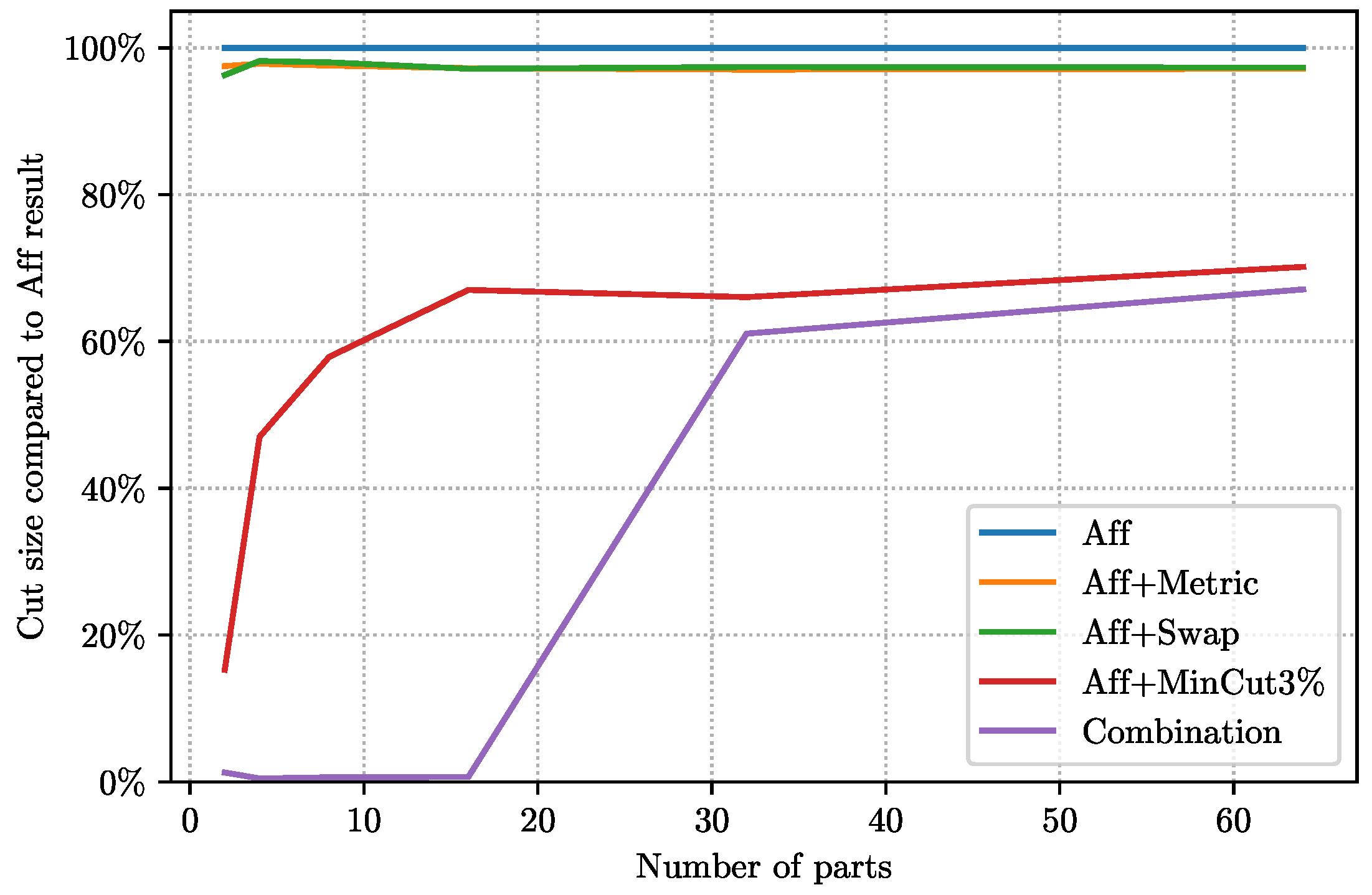
Figure 7 also sets the results of various postprocessing methods against one another and depicts their improvements compared to the baseline of AffCommNeigh when run on World-roads. The first two consists of semilocal optimization methods, Aff+Metric and Aff+Swap, which also appeared in the discussion for Twitter. These do not yield significant improvement over their AffCommNeigh starting point: the results compared to the starting point (baseline) ranges from 95% to 98%. The other two algorithms use imbalance-inducing ideas and yield significantly better results. Our main algorithm, which we call Combination, clearly outperforms all the others specially for small values of k.

All the experiments assume $3\%$ imbalance in partition sizes—each partition may have size within range $(1\pm 0.03)\frac{n}{k}$. However, only Aff+MinCut and Combination use this to improve the quality of the partition.

6.2.3. Convergence Analysis

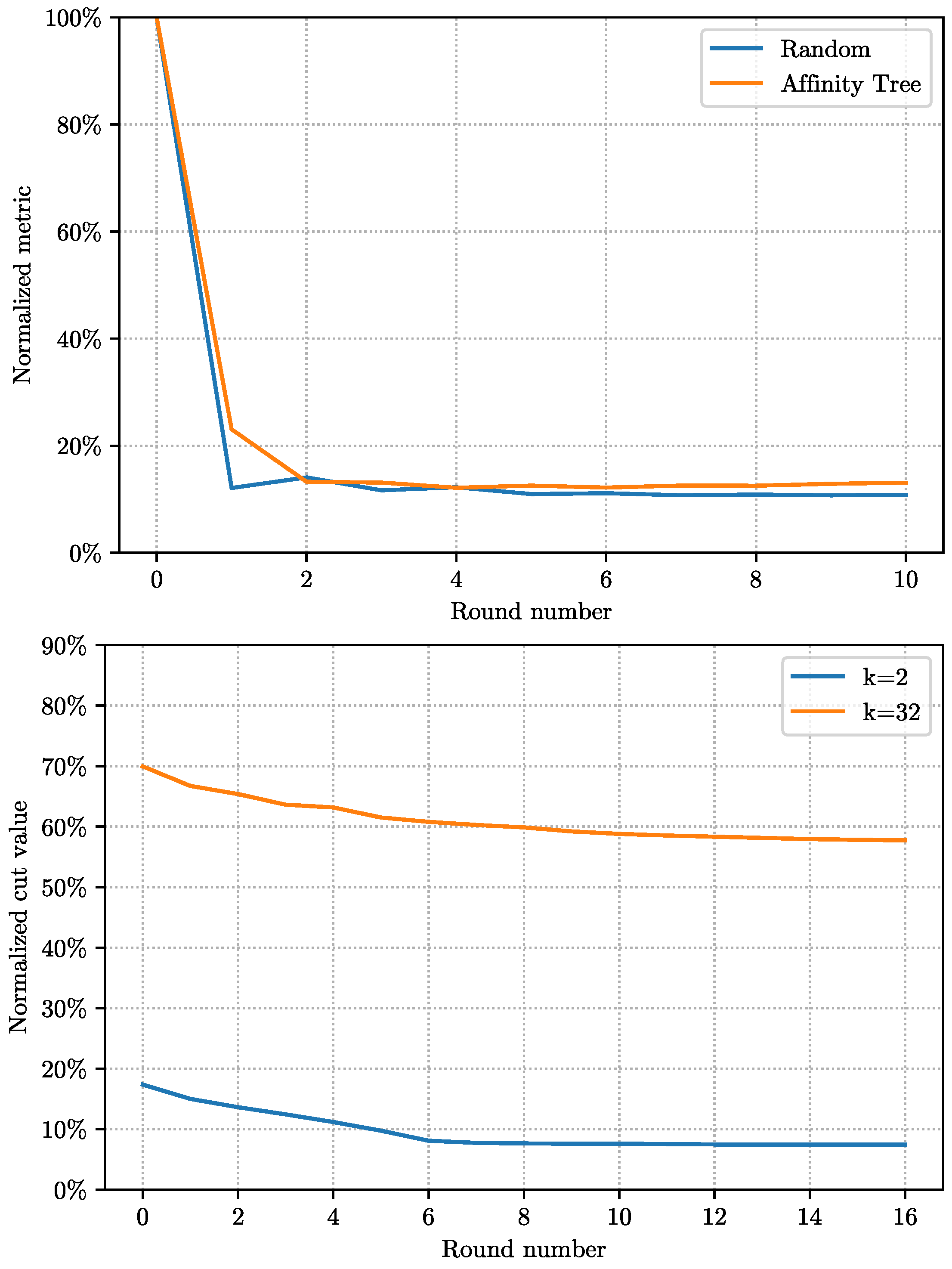
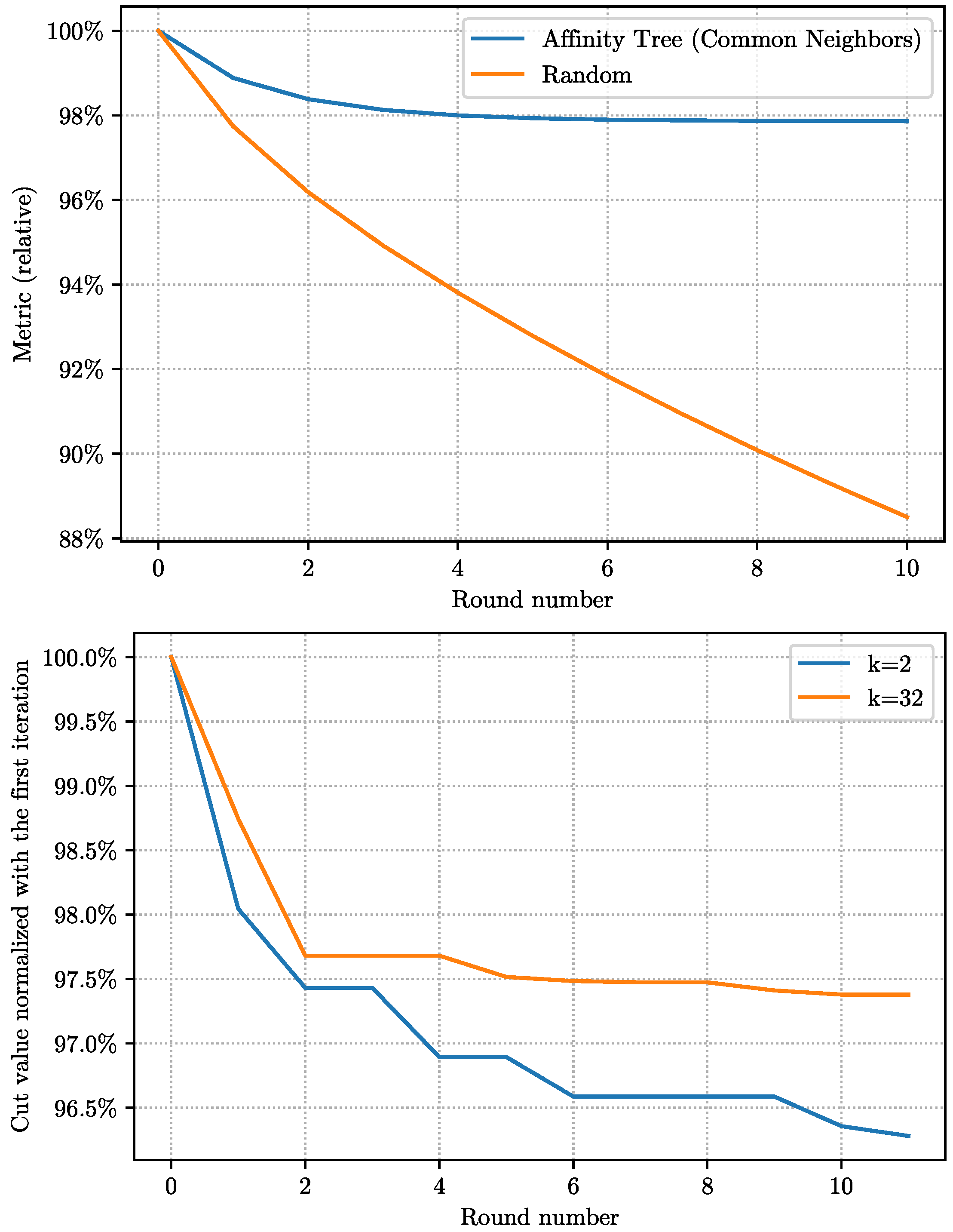
Next we consider the convergence rate of the two semilocal improvement methods on two graphs. For Twitter, the rate of convergence for metric optimization is the same whether we start with AffCommNeigh or RandInit (See Figure 8). The convergence happens essentially in three or four rounds.

The convergence for the rank swap methods happens in 10–15 steps for Twitter and in 5–10 steps for World-roads; more steps required for larger values of k.

The convergence for the metric optimization on World-roads happens in 3–4 steps if the starting point is AffCommNeigh. However, if we start with a random ordering, it may take up to 20 steps for the metric to converge. See Figure 9.

6.3. Comparison to Previous Work

The most relevant among the previous work are the scalable label propagation-based algorithms of Ugander and Backstrom [4] and Martella et al. [19]. The former reports their results on an internal graph (for Facebook) and a public social graph, LiveJournal, while the latter reports results on LiveJournal and Twitter.

Table 2. Comparison to prior work on LiveJournal. The main entries are the ratio of edges cut by the clustering over the total number of edges in the graph. The number of clusters is denoted by k. Numbers in parentheses are permissible imbalance (Best results in each row are typeset in bold for easier spotting).

k	[4] $\begin{array}{c}(-0.5\mathbf{mm})(5\%)\end{array}$	$\begin{array}{c}\mathtt{Spinner}(5\%)\end{array}$	$\begin{array}{c}\mathtt{Aff}(0\%)\end{array}$	$\begin{array}{c}\mathtt{Combination}(0\%)\end{array}$
20	37%	38%	35.71%	27.50%
40	43%	40%	40.83%	33.71%
60	46%	43%	43.03%	36.65%
80	47.5%	44%	43.27%	38.65%
100	49%	46%	45.05%	41.53%

compares our results to prior work on LiveJournal. The cut sizes in the table for $k=40,60,80$ for Reference [4] and all the numbers for Reference [19] are approximates taken from the graph provided in Reference [4] as they do not report the exact values. The numbers in parentheses show the maximum imbalance in partition sizes, and the cut sizes are reported as fractions of total number of edges in the graph.

Even our initial linear embedding (obtained by constructing the hierarchical clustering based on a weighted version of the input, where edge weights denote the number of common neighbors between two vertices) is consistently better than the best previous result. Our algorithm with the postprocessing obtains $15\%$ to $25\%$ improvement over the previous results (better for smaller k) and it only requires a couple of postprocessing rounds to converge. We take note that the results of Reference [4] allow $5\%$ imbalance whereas our results produce almost perfectly balanced partitions.

Twitter is another public graph, for which the results of state-of-the-art minimum-cut partitioning is available. In

Table 3. Comparison to prior work on Twitter. The main entries are the ratio of edges cut by the clustering over the total number of edges in the graph. The number of clusters is denoted by k. Numbers in parentheses denote the permissible imbalance for each algorithm (Best results in each row are typeset in bold for easier spotting).

k	[21] $\begin{array}{c}(4–15\%)\end{array}$	$\begin{array}{c}\mathtt{Spinner}(5\%)\end{array}$	$\begin{array}{c}\mathtt{FENNEL}(10\%)\end{array}$	$\begin{array}{c}\mathtt{METIS}(3\%)\end{array}$	$\begin{array}{c}\mathtt{Combination}(3\%)\end{array}$
2	34%	15%	6.8%	11.98%	7.43%
4	55%	31%	29%	24.39%	18.16%
8	66%	49%	48%	35.96%	33.55%
16	76%	61%	59%	N/A	46.18%
32	80%	69%	67%	N/A	57.67%

we report and compare the results of our main algorithm, Combination, for this graph to the best previous methods. (Numbers for Reference [21] are quoted from Reference [19]).

Algorithms developed in References [5,21] are suitable for the streaming model but one can implement variants of those algorithms in a distributed manner. Our implementation of a natural distributed version of the FENNEL algorithm does not achieve the same results as those reported for the streaming implementation reported in Reference [5]. However, we compare our algorithm directly to the numbers reported on Twitter by FENNEL [5].

Finally we report in

Table 4. Cut sizes produced by our algorithm on Friendster (ratio of cut edges to the total number of edges), where k denotes the number of clusters.

k	2	10	${10}^2$
Cut size	11.9%	41.4%	59.8%

the cut sizes for another public graph, Friendster, so others can compare their results with it. The running time of our algorithms are not affected with large k; the running time difference for $k=2$ and tens of thousands is less than $1\%$, well within the noise associated with the distributed system. In fact, construction of the initial ordering is independent of k, and the post-processing steps may only take advantage of the increased parallelism possible for large k.

We also make our partitions for Twitter, LiveJournal and Friendster publicly available [23].

6.4. Scalability

We noted above that the choice of k does not affect the running time of the algorithm significantly: the running time for two and tens of thousands of partitions differed less than $1\%$ for Friendster.

As another measure of its scalability, we run the algorithm with $k=2$ on a series of random graphs (that are similar in nature) of varying sizes. In particular, we use RMAT graphs [46] with parameter 20, 22, 24, 26 and 28, whose node and edge count is given in

Table 5. General statistics (size) about the RMAT graphs as well as the relative running times of balanced-partitioning algorithm on these graphs.

Graph	$\left|\mathit{V}\right|$	$\left|\mathit{E}\right|$	Max Degree	Running Time
RMAT 20	650 K	31 M	65 K	100%
RMAT 22	2.4 M	130 M	160 K	110%
RMAT 24	8.9 M	525 M	400 K	133%
RMAT 26	32.8 M	2.1 B	1 M	160%
RMAT 28	120 M	8.5 B	2.5 M	402%

. In addition, the last column gives the normalized running time of our algorithm on these graphs. Note that the size of the graph almost quadruples from one graph to the next.

7. Applications

In the past five years, we have applied this algorithm to various applications within Google, including those in Maps, Search and Infrastructure domains. In this section, we briefly explain three examples.

7.1. Google Maps Driving Directions

As discussed in Section 1, we apply our results to the Google Maps Driving Directions application. Note that the evaluation metric for balanced partitioning of the world graph is the expected percentage of cross-shard queries over the total number of queries. More specifically, this objective function can be captured as follows: we first estimate the number of times each edge of graph may be part of the shortest path (or the driving direction) from the source to destination across all the query traffic. This produces an edge-weighted graph in which the weight of each edge is proportional to the number of times we expect this edge appearing in a driving direction and our goal is to partition the graph into a small number of pieces and minimize the total weight of the edges cut. We can estimate edge weights based on historical data and use it as a proxy for the number of times the edge appears on a driving direction on the real data. This objective is aligned with minimizing the weighted cut and we can apply our algorithms to solve this problem.

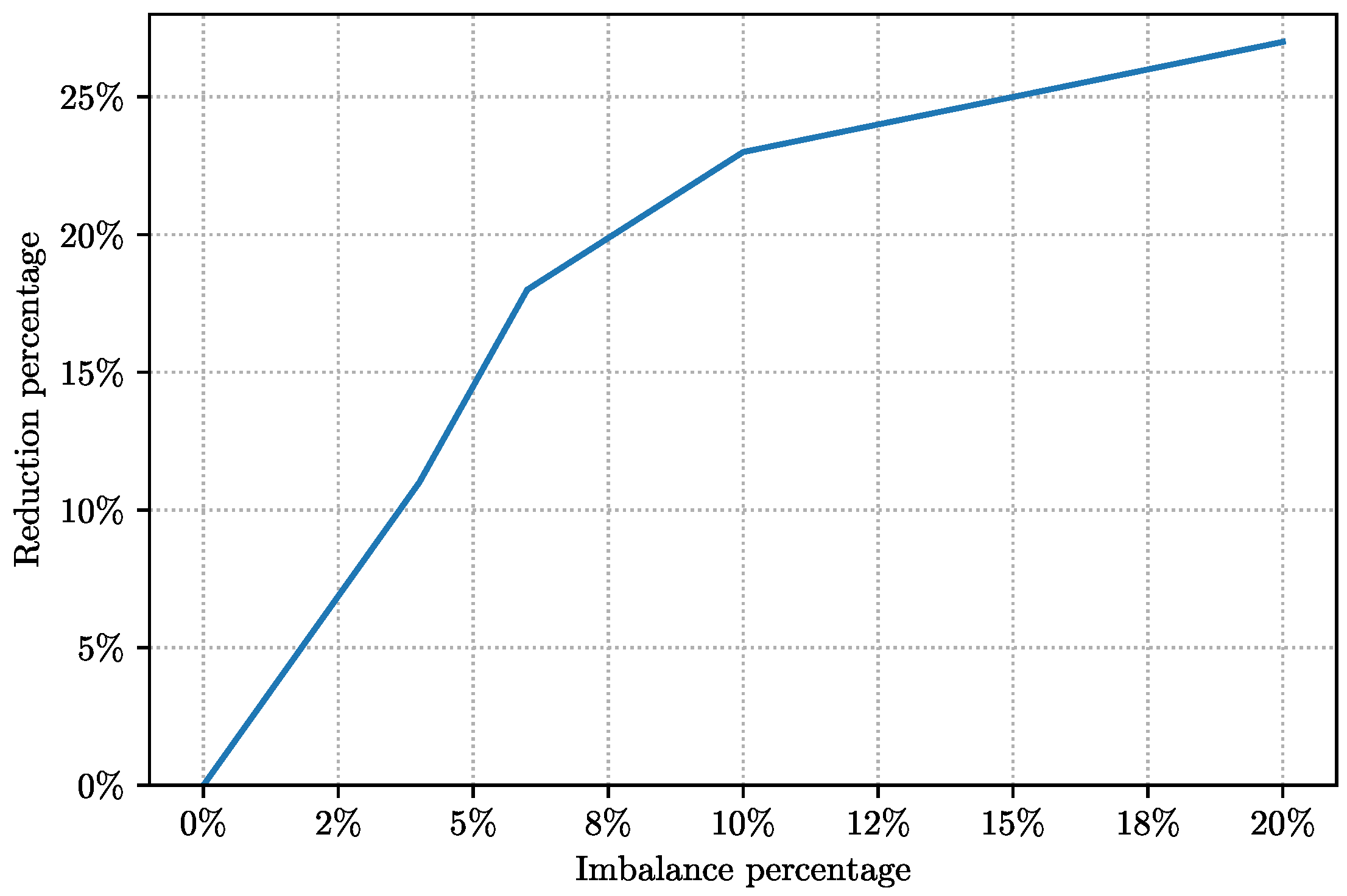
Before deciding about our live experiments, we realized it might be suitable to use an imbalance factor in dividing the graph and as a result, we first examined the best imbalance factor for our cut-optimization technique. The result of this study is summarized in Figure 10. In particular, we observe that we can reduce cross-shard queries by $21\%$ when increasing the imbalance factor from $0\%$ to $10\%$.

The two methods that we examined via live experiments were (i) a baseline approach based on the Hilbert-curve embedding and (ii) one method based on applying our cut-optimization postprocessing techniques. Note that both these algorithms first compute an embedding of nodes into a line, which results in a much simpler system to identify the corresponding shards for the source and destination of each query at serving time. Finally, by running live experiments on the real traffic, we observe that the number of multi-sharded queries from our cut-optimization techniques is almost 40% less than the number of multi-sharded queries compared to the naïve Hilbert embedding technique.

7.2. Load Balancing in Google Search Backend

Another application of this large-scale balanced-partitioning algorithm is in cache-aware load balancing of data centers [47]. While this is not the focus of the present work, we present a brief overview to demonstrate a different application.

The load-balancer of a big search engine distributes search queries among several identical serving replicas. Then the server pulls, for each term in the query, the index of all pages associated with the search term. As significant time and network traffic is consumed in loading these index tables, a cache is employed on the serving replicas. This leads to better utilization if each search term is usually sent to a specific machine. The complication, though, originates from the fact search queries often consist of several search terms, each with its own index table.

The proposed solution is a voting table to select the right replica for each query. The voting table is constructed via a multi-stage algorithm, yet the initial voting table—a decent solution in and of itself—comes from a balanced-partitioning formulation: We aim to partition the search terms in a balanced way, where the sizes denote lengths of index tables, so as to minimize the expected cache miss rate. This is done by carefully building a term-query bipartite graph, whose vertex weights correspond to index table sizes and whose edge weights are related to cache miss rates. See Reference [47] for more information.

Deployed in 2015, the said solution decreases cache miss rate by about $0.5\%$ and increases end-to-end throughput by double-digit percentage.

7.3. Co-Location of Tasks in a Data Center

Yet another application of our balanced-partitioning algorithm is in scheduling of computation tasks within data centers. The cost of intra-network bandwidth in a data center is nonnegligible, and adds up over time. Besides, the underlying network topology may be hierarchical: the machines at a lower-level subtree can have much higher bandwidth and may even be organized as a clique. Consequently the communication cost between machines across different subtrees can be much higher.

One way to reduce network bandwidth usage is to co-locate related tasks within closer physical proximity and therefore optimize the network traffic. As communication patterns of many applications stay stable over time, one can look into historical logs to construct a graph of communication among tasks. In this graph, each node is an application (or task) and the edge weight between two nodes is the communication cost between them. Machines have limited size or memory, thus we naturally cast the problem as balanced partitioning: We cluster the tasks (subject to a physical limit) and minimize the communication cost across clusters.

Our initial implementation of this technique (within a subset of the overall traffic) resulted in a six-fold increase of co-located tasks.

7.4. Randomized Experimental Design via Geographic Clustering

Recently, the authors of Reference [48] used balanced partitioning as a way to cluster geographic regions in order in order to set up randomized experiments over them. This is especially useful in web-based services, since it does not require tracking individual users or browser cookies. Given the fact that users, especially mobile ones, may issue queries from different geographical locations, it cannot be assumed that geographic regions are independent and interference may still be present in the experiments. These characteristics of the problem make it suitable for applying balanced partitioning where the geographic regions are modeled as a graph and the edge weights across output clusters are minimized while producing clusters of almost the same size.

8. Conclusions

We develop a three-stage algorithm for balanced partitioning of a graph, with the main objective of minimizing the overall weight of cut edges.

The first two stages construct an ordering of the vertices based on the neighborhoods in the graph—nearby vertices are expected to be close to each other in the ordering.

The third stage considers the permissible imbalance and moves the boundaries of parts so as to optimize the cut value. It may also permute vertices that are very close to the part boundaries.

Though we give a few variants for each stage, it is not necessary to run all the three stages; some can be replaced by a dummy routine. To get the full potential of the algorithm, one had better use the best variants of every stage, however, even using random ordering in the first stage, for instance, produces a nontrivial result. Similarly, only using a natural balanced partitioning based on the hierarchical agglomerative clustering produces decent results. Interestingly, this outperforms the Hilbert cover-based ordering, even for the geographic graphs where the latter technique is feasible.

For $k>2$, our algorithm beats METIS and FENNEL, and is more scalable than both of them. For $k=2$, that is, the minimum bisection problem, while our algorithm is far superior in terms of running time and scalability, the results that we obtain are on par with (or slightly worse than) those of the other two.

Our algorithm is pretty scalable: for example, it runs smoothly on a portion of the world graph with half a billion vertices and more than a billion edges.

Furthermore, we study or deploy this solution in various applications at Google.

• A simple version of our algorithm (using Hilbert curves for the initial ordering, no optimization in stage two and dynamic programming in the third stage) yields a $40\%$ improvement for the Google Maps Driving Directions application: the improvement is both in terms of overall CPU usage as well as the number of multishard queries.
• In another work [47], we show how to use balanced partitioning to optimize the load balancing component of Google Search backend. Deployed in 2015, the said solution decreases cache miss rate by about $0.5\%$ and increases end-to-end throughput by double-digit percentage.
• This algorithm has been effective in scheduling jobs in data centers with the objective of minimizing communication.
• It is also demonstrated in a separate work [48] that experiment design can benefit from a balanced partitioning of users based on their geography. This helps reduce the dependency between various experiment arms.