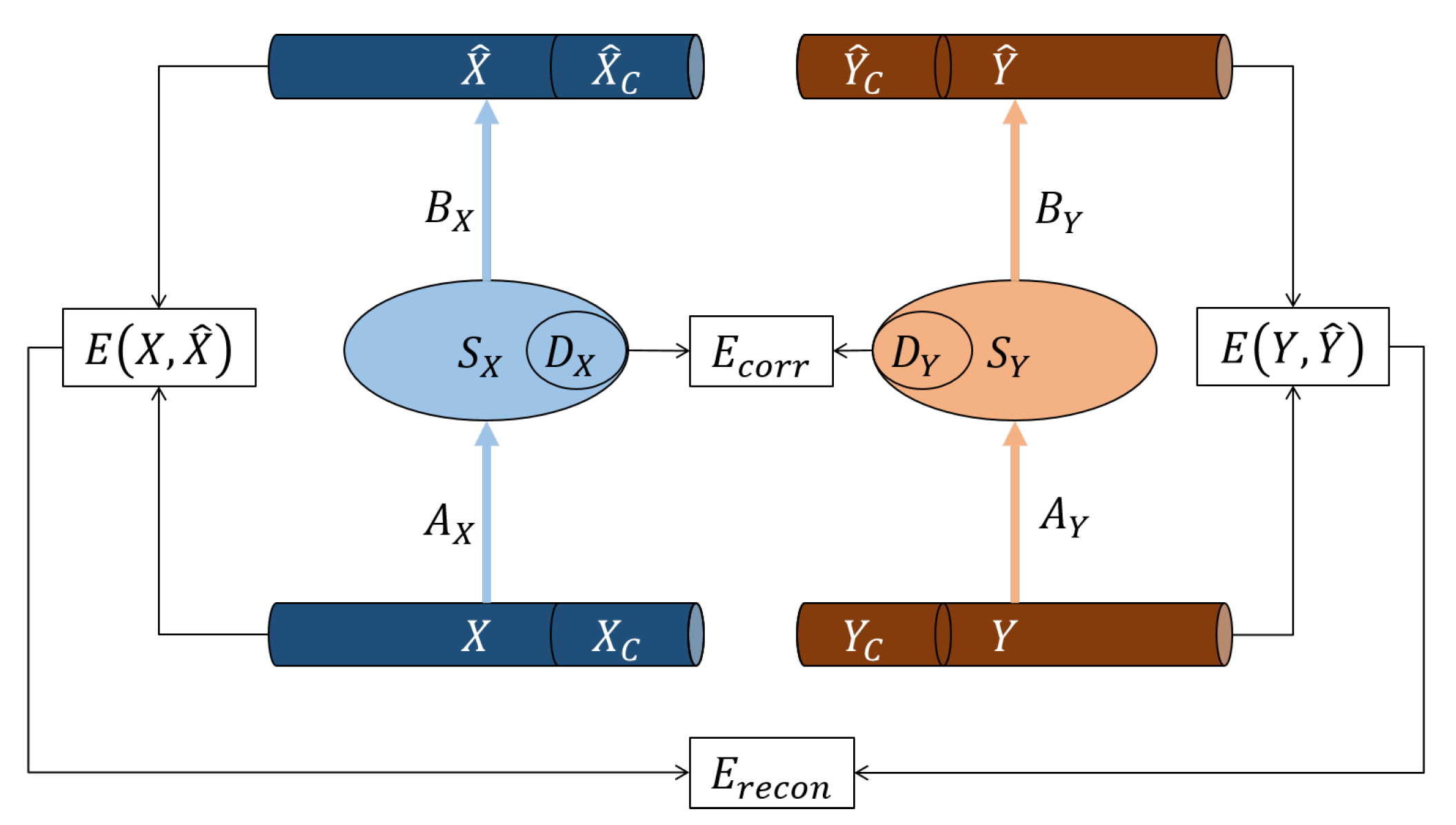
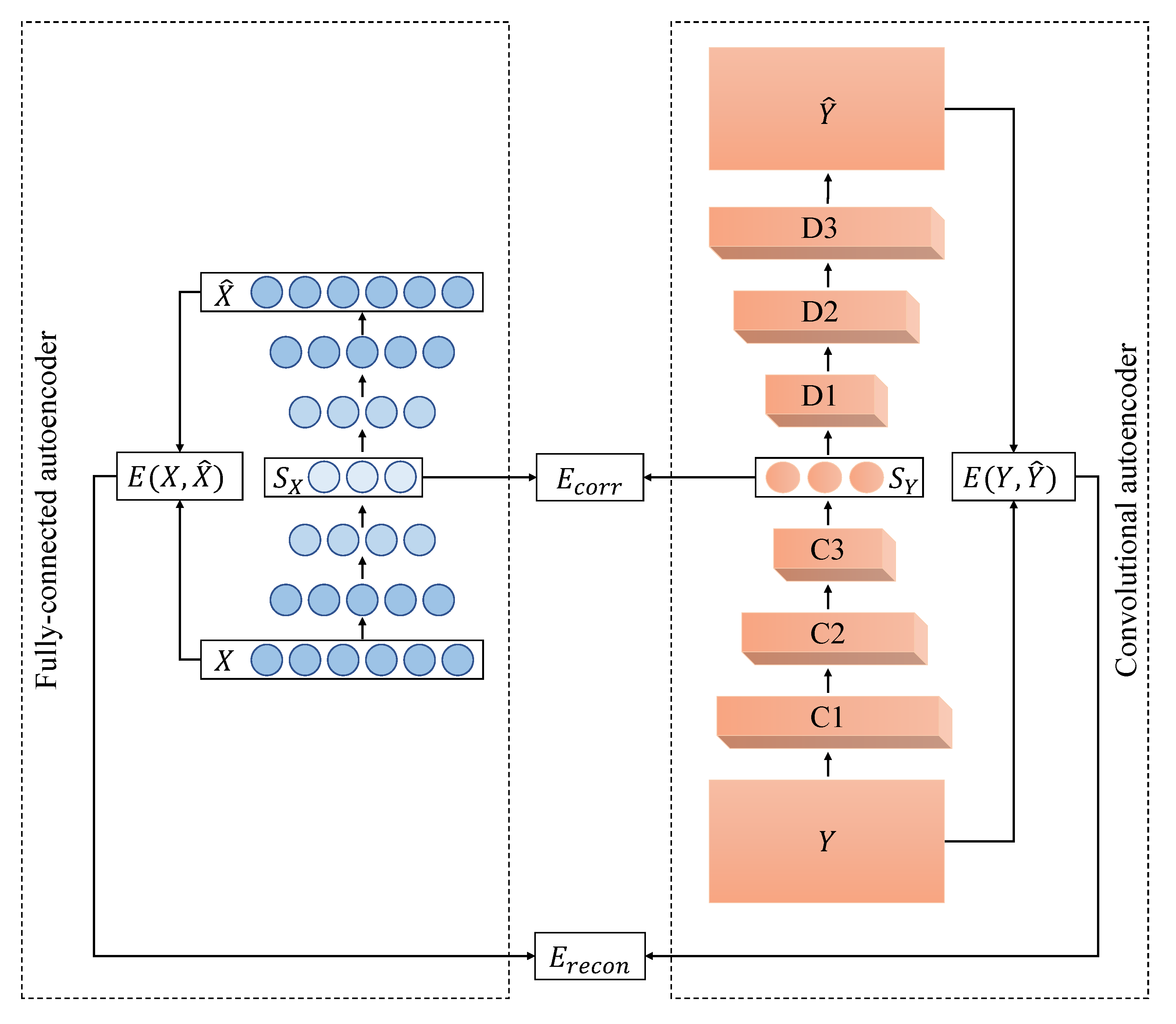
5.2.1. Double Pendulum Datasets
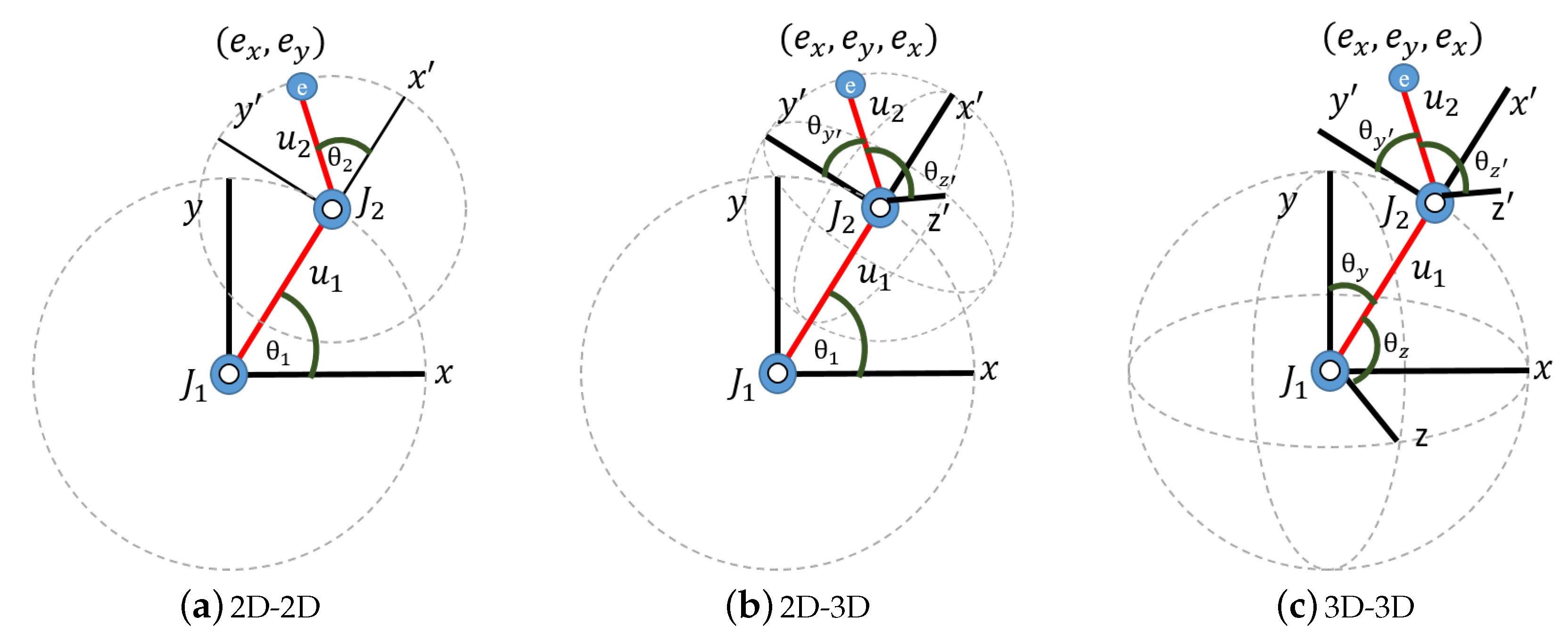
We generated high-dimensional datasets by simulating the motion of double pendulums where three different conditions were considered (
Figure 4): 2D-2D, 2D-3D and 3D-3D. The two limbs of the double pendulum are denoted as
and
, and the joints are denoted as
and
. One end of
is fixed at
, and the limb can rotate around this joint. The other end of
is attached to
at joint
.
can rotate freely around joint
. The free end point
e of the pendulum is referred to as the “end-effector” and has coordinates
in the two-dimensional case and
in the three-dimensional version using a right-handed coordinate system with the origin at joint
.
The data were generated in simulation for the 2D-2D, 2D-3D and 3D-3D cases as follows (
Figure 4):
- (i)
2D-2D motion: The pendulum has two Degrees-Of-Freedom (DOF), that is, both limbs
and
rotate in the two-dimensional (
x-
y)-plane, each of them describing a circle. In
Figure 4a,
and
are the rotation angles of limbs
and
at joints
and
, respectively. Accordingly, the manifold representing the dynamics of the 2D-2D case is the cross-product of two circles,
, which is homeomorphic to the two-dimensional torus, that is a 2-manifold.
- (ii)
2D-3D motion: The pendulum has three DOFs, where limb
can rotate on a two-dimensional sphere
in three-dimensional space, while
is restricted to rotate on a circle
in a two-dimensional plane. That is, the manifold representing the dynamics of the 2D-3D case is homeomorphic to
, which is a 3-manifold. As the pendulum moves in 3D space, the end-effector has the 3D coordinates
. In
Figure 4b,
and
are the angles of
with axes
and
, respectively, and describe the motion on the sphere
.
is the angle between the
x-axis and
and describes the two-dimensional rotation of the sphere’s centre in the (
x-
y)-plane.
- (iii)
3D-3D motion: In this case, the pendulum has four DOFs, where both limbs can rotate on two-dimensional spheres in 3D space. In
Figure 4c,
and
are the angles of
with the
y and
z axes, respectively, and
and
are the angles of
with the
and
axes, respectively. Accordingly, we expected that the manifolds representing the dynamics of the 3D-3D case were homeomorphic to
, which is a 4-manifold.
For each case, two datasets, X and Y, were generated that represented the motion of two similar double pendulums that differed only in different limb lengths and limb length ratios:
that is, we restricted the experiments to the case .
The feature vectors for each sample point (or instance) were calculated from the kinematics at the joints and the coordinates of the end-effector. The end-effector coordinates were calculated using forward kinematics. Then, feature vectors for the 2D-2D, 2D-3D, and 3D-3D cases were defined as:
2D-2D:
2D-3D:
3D-3D:
The data points for the 2D double pendulums were generated using its equations of motion and then sampled at angular increments of in and at both joints. There were instances and six features, resulting in a dataset of size for each of the pendulums X and Y.
In the case of the 2D-3D motion, instances were sampled at angular increments of at three angles , and of the corresponding joints. As a result, the number of instances was , and with the nine features, the size of the two datasets, X and Y, was .
In the 3D-3D case, instances were sampled at angular increments of in the rotational angles , , and at the corresponding joints. As a result, the number of instances was 20,736, and with the 11 features, the size for each of the two datasets X and Y was 20,736 × 11.
In order to challenge the robustness of the different alignment methods and to simulate potential real-world scenarios, two different types of noise were added in separate experiments to the clean datasets X and Y. The first type of noise we refer to as “actuator noise”, and it was added to the joint angles to imitate the noise at actuator joints in a real-world system. The range of actuator noise was incremented from to in steps of . The second type of noise was added to the end-effector coordinates, and we refer to it as “coordinate noise”. This noise could simulate, for example, the jittery motion of robot limbs. In the experiments, the coordinate noise range was increased from to in steps of size .
5.2.2. PDAE Architecture
The deep autoencoders that were used as part of PDAE had six neurons in the input layer for 2D-2D motion alignment where the data matrix had six features. Similarly, for the 2D-3D data, the input layer had nine neurons, and for the 3D-3D motion, the input layer had 11 neurons. Then, the number of neurons was reduced by one in each of the consecutive hidden layers until it reached three at the code layer of the deep autoencoders. The decoder had the same layer architecture as the encoder, but in reverse order. In summary, the architectures of the deep autoencoders were:
The weights of the autoencoders were randomly initialised within using a normal distribution. We plotted the network error for learning rates in the range for 500 epochs to find the best performing learning rate using the Adam optimiser, which was for the 2D-2D case and for the 2D-3D and 3D-3D cases. Then, PDAEs were trained for 10,000 epochs with a stopping criterion of and as the activation function.
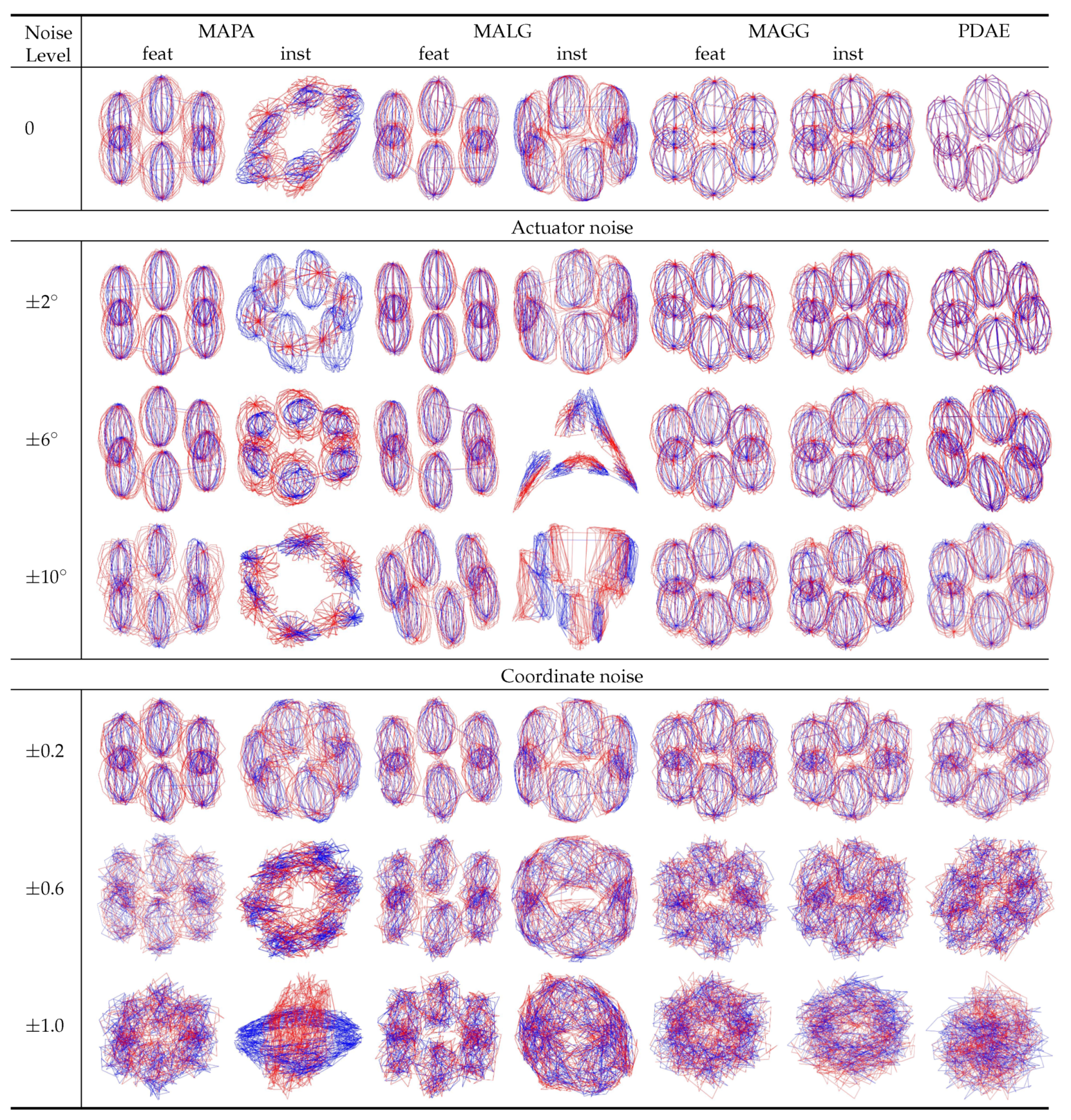
5.2.3. Results of 2-Manifold Alignment
In the case of the 2D-2D motion data, limb
rotated around joint
in a circle and limb
rotated in another circle around joint
. In three-dimensional space, this motion can be represented as a torus
, that is a 2-manifold. In the first row of
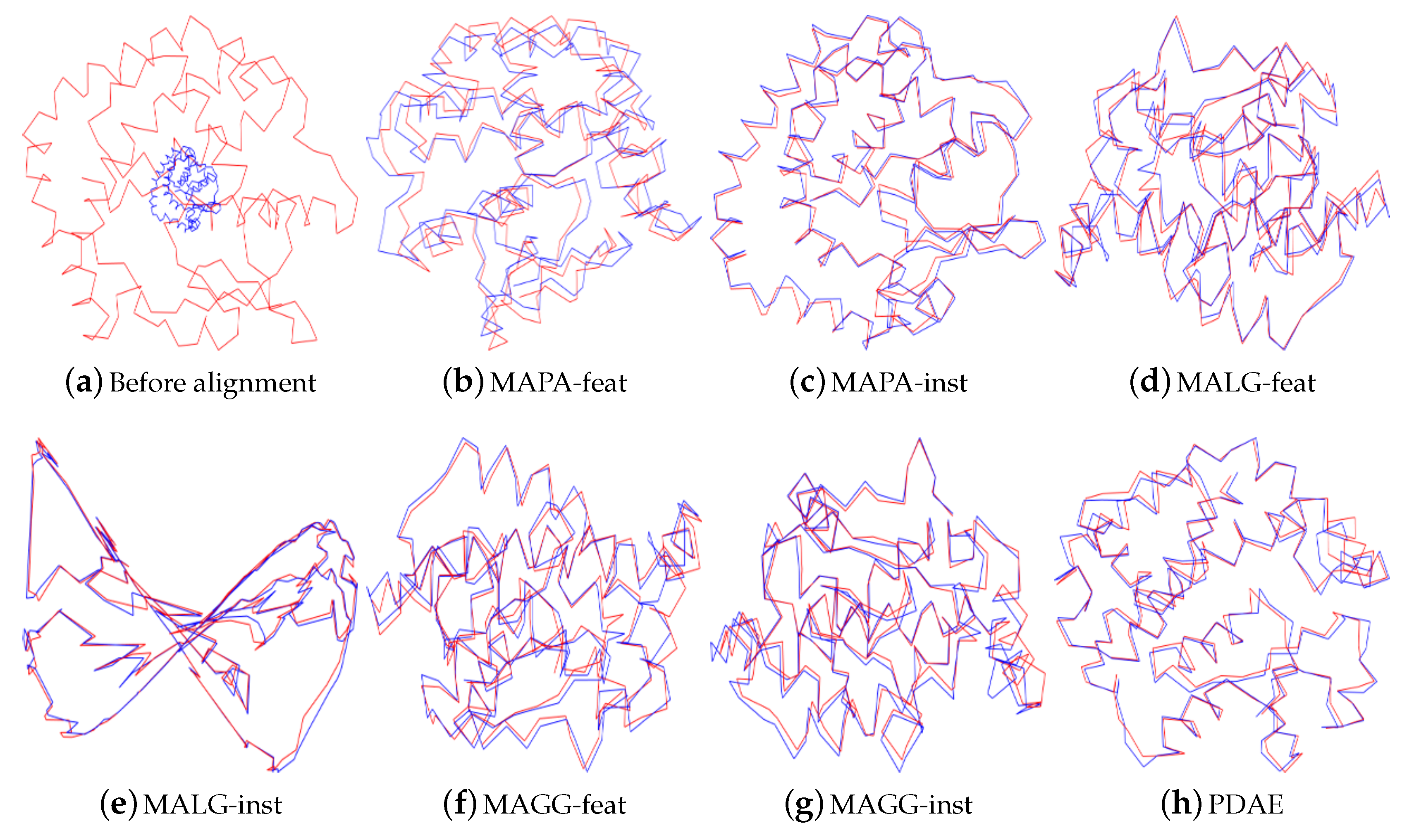
Figure 5, we can see that for zero noise, the visualisations of the results for MAPA-inst, MALG and PDAE resulted in objects that resembled the expected torus-shaped surfaces, while the other methods produced cylinder-like deformations of torus-shaped surfaces. With increasing levels of noise (only three representative levels are displayed), the instance-level alignments were less stable than the feature-level alignments. The addition of noise led all traditional methods to fail by collapsing the resulting manifolds or misaligning the two sets. Visually, the best outcomes were achieved by PDAE where for all levels of noise, an object resembling a torus-like surface with minor deformations was obtained.
The alignment errors
in
Table 2 indicate that MALG-feat resulted in the closest alignment among the conventional methods. The
of the autoencoder was lower than that of MALG-feat for higher levels of noise.
Table 2 also shows that PDAE had the lowest standard deviation (in parentheses) at high levels of noise. This indicates that PDAE more smoothly aligned than the other methods. It should be noted that low values for
or
can also occur when a torus manifold cannot correctly be established and uniformly collapses or projects into a simpler form as, for example, a cylinder in some cases of MALG-feat. We trained and tested PDAE with five different sets of initial random weights, and the standard deviation of the mean of the resulting alignment errors was about
at zero noise. This indicates that the autoencoder results do not depend in a notable way on the selection of the initial random weights.
5.2.5. Results of 4-Manifold Alignment
The 11-dimensional data of the two 3D double pendulums were described in
Section 5.2.1. Each of the two datasets
X and
Y was represented by a 20,736 × 11 data matrix. In the 3D pendulum motion, the rotation of limb
described a sphere
, and the motion of the other limb
described another sphere
, so that the 3D pendulum motion resembled
, which is a 4-manifold. As this was too complex to visualise in full, we took snapshots of the motion around
at
steps and for the motion around
at
steps. This way, the rotation of
resulted in six spherical shapes that were uniformly distributed on a bigger sphere, which represented the motion of
. The visualisations in
Figure 7 show that the instance-level methods were not successful in aligning the high-dimensional nonlinear motion data. The manifolds of the instance-level alignments collapsed even without any noise. Only MAGG-feat and PDAE produced the expected visualisation, comprising six spheres that represented the snapshots we selected in the motion data on
. The outcome of MAGG-feat was also supported by our case study [
47].
For the remaining experiments, random noise was added to the data in several stages as described in
Section 5.2.1. The noisy datasets were aligned using MAPA-feat, MALG-feat and PDAE. All manifolds collapsed after noise addition, and therefore, only visualisations for zero noise are included in
Figure 7.
and
were calculated as described in
Section 4. The numerical results in
Table 4 together with the qualitative visual evaluations of
Figure 7 showed that PDAE performed better than MAGG-feat and the other methods.
The experiments were executed on the university’s high performance computing grid with 60 GB RAM using two parallel k80 GPUs. The huge speed advantage of inference with the autoencoder was representative of all our data and all comparative simulations we conducted (Table 6). However, these speed results can only be indicative for precise benchmarking of a standalone high-performance machine or a specialised setup would be required.