Abstract
This paper deals with the consensus tracking problem of heterogeneous linear multiagent systems under the repeatable operation environment, and adopts a proportional differential (PD)-type iterative learning control (ILC) algorithm based on the fractional-power tracking error. According to graph theory and operator theory, convergence condition is obtained for the systems under the interconnection topology that contains a spanning tree rooted at the reference trajectory named as the leader. Our algorithm based on fractional-power tracking error achieves a faster convergence rate than the usual PD-type ILC algorithm based on the integer-order tracking error. Simulation examples illustrate the correctness of our proposed algorithm.
1. Introduction
In the past decades, the cooperative control problem of multiagent systems [1,2] has been extensively studied due to its wide applications in many engineering fields, e.g., multirobot cooperative control, formation control of unmanned aerial vehicles, traffic control, smart grid, and so on. As a fundamental problem of distributed cooperative control, consensus problem requires all agents to reach an agreement on the states of interest, and various consensus problems have been thoroughly studied, such as leader-following consensus [3], group consensus [4], finite-time consensus [5], and so on.
Iterative learning control (ILC), a classic learning control strategy, is designed to improve tracking performance by applying information obtained from the past control experiment [6,7,8]. The current input signal is usually generated by the previous input signal plus the tracking error (either the derivative of tracking error or the integral of the tracking error). ILC is used to accomplish control tasks that repeat on finite-time intervals, and it does not require an accurate system model. Due to this attractive feature of ILC, it has been widely used in practical systems and engineering practice, for example, industrial robots that perform repetitive tasks such as welding and handling [9], servo systems whose command signals are periodic functions [10], etc.
Many industry issues require repeated execution and coordination among several subsystems, for example, cooperative control of several robotic arms on an industrial production line. Recently, the consensus tracking problem of multiagent systems by ILC strategy has attracted the attention of researchers, since many industry issues can be solved under the ILC algorithm [11,12,13,14]. Unfortunately, existing results on consensus problems by ILC algorithm are mostly given for homogeneous multiagent systems, of which all the agents have the same dynamics. In some real engineering applications subjected to various restrictions or to reach the goals with lowest costs, the dynamics of cooperating agents are required to be distinct, e.g., coordination control of unmanned aerial vehicles and unmanned ground vehicles, so the study on heterogeneous multiagent systems is more practical and meaningful. Yang et al. [15] proposed an ILC algorithm to solve the consensus tracking problems of homogeneous and heterogeneous multiagent systems, respectively, and the output consensus conditions have been obtained based on the concept of graph-dependent matrix norm. Li [16] considered a heterogeneous multiagent system composed of first- and second-order dynamics, and the leader was assumed to have second-order dynamics. Different protocols have been designed for the heterogeneous following agents, so that all the following agents tracked the state of the leader asymptotically [16].
As an important evaluation index of the ILC algorithm, the convergence rate refers to the speed at which the multiagent systems approach the reference trajectory, and has stimulated research interest for a long time. In order to accelerate the convergence rate of the ILC algorithm, taking the proportional differential (PD)-type learning law as an example, an acceleration correction algorithm with variable gain and adjustment of learning interval was designed for the linear time-invariant system [17]. Tao et al. proposed an interpolating algorithm to regulate the reference trajectory in order to achieve faster convergence rate [18]. The convergence rate of closed-loop ILC algorithm is obviously faster than that of open-loop ILC algorithm, due to real-time performance of closed-loop ILC algorithm [19]. The convergence rate was greatly improved by introducing adaptive gains into the ILC algorithm [20]. Sun et al. used the terminal converging strategy for ILC algorithm, and reached the finite-time convergence [21]. For the consensus tracking problem of multiagent systems, Yang et al. proposed an ILC algorithm with input sharing, i.e., each agent exchanged its input information to the neighbors, and obtained a faster convergence rate [22].
This paper focuses on the output consensus tracking problem of heterogeneous linear multiagent systems, in which the following agents are required to track the output trajectory of the leader. It is worth noting that the state dimensions of agents may be different, but the output must have the same dimension. In order to accelerate the consensus convergence rate of multiagent systems, a novel PD-type ILC consensus algorithm is proposed by using the fractional-power tracking error. Sufficient consensus condition, which depends on the control parameters, is obtained based on the operator theory.
2. Preliminaries
2.1. Digraph
In this paper, we study the consensus tracking problem via leader-following coordination control structure. The information flow among following agents forms a digraph G [23], and the leader is denoted by vertex 0.
The digraph composed of the following agents contains the vertex set , the edge set , and the adjacent matrix . A directed edge from i to j in G is denoted by , meaning that the node j can obtain information from the node i. Assume and for all . The set of neighbors of node i is denoted by . The Laplacian matrix of the digraph G is defined as , where is the degree matrix. In the digraph G, a directed path from node to node is a sequence of ordered edges of the form , where . A digraph is said to have a spanning tree if there exists a node that forms a directed path from this node to every other node.
Then, the interconnection among all agents is characterized by a compound digraph , and the coupling weight of the ith following agent to the leader is denoted by . if agent i can obtain information from the leader; otherwise . Besides, let .
Through this paper, we take into account the following topology.
Assumption 1.
The interconnection topology of the following agents and the leader contains a spanning tree with the leader being its root.
Under Assumption 1, the eigenvalues of all have positive real parts [24].
2.2. Critical Definitions
Definition 1.
For a given vector , is any vector norm. For any matrix , is the matrix norm induced by the vector norm. In particular, , , and , where is the spectral radius. For all matrices , , and , the following property is satisfied.
Definition 2.
[21] If a function s.t.
where , then is Hölder continuous in region D.
2.3. Consensus Tracking Problem
The consensus tracking problem analyzed in this paper requires that spatially separative agents track a desired reference trajectory via cooperative control, and we take the ILC strategies for each agent. Additionally, we take into account a class of linear heterogeneous multiagent systems, and the dynamics of agent i are in the following form at the kth iteration.
where , , and are the state and control input and output, respectively, of the agent i, , , and are matrices with proper dimension. The states of agents are different, because this paper studies the consensus problem of heterogeneous multiagent systems, which were mentioned in the article [15]. Since this paper deal with the output tracking problem, the output dimensions of all agents must be consistent with the reference trajectory in order to facilitate comparison with the reference trajectory.
The reference trajectory is defined on a time interval , which is regarded as the leader’s output trajectory. In the distributed coordination control framework, the leader’s output trajectory is only accessed by a subset of the following agents, and the left agents reach the leader’s trajectory indirectly. The control objective is to design a new ILC algorithm so that the output signals of all following agents converge to the reference trajectory asymptotically, i.e.,
Remark 1.
The leader in this paper is a virtual leader, i.e., the reference trajectory is generated by the virtual leader, but the leader does not actually exist, so there will be no collision between the leader and the following agents. Moreover, we assume that there will be no collision between all followers, and we avoid collision by placing all followers in a reasonable position. For example, system (2) formulates the dynamics of a robot in industrial production lines, the output denotes the angle of the robot’s joints, and the robots will not have collision problems due to their judicious distance.
3. Design And Analysis of ILC Consensus Algorithm
Firstly, we define the tracking error of each agent as
and
where and are the tracking errors with the leader and neighboring agents, respectively, of agent i at the kth iteration.
Let denotes the information received or measured of the agent i at the kth iteration, and we get
where is the adjacency elements associated with the edges of the digraph, and is the coupling weight of the ith following agent to the leader.
In terms of ILC algorithm, the tracking error continues to decrease with increasing iteration number, and the convergence rate will be slow when the tracking error is small. Hence, we are encouraged to appropriately amplifying the tracking error when the tracking error is small; the following agents can track the leader’s trajectory more quickly.
In this paper, we adopt the PD type ILC consensus algorithm and introduce a fractional-power proportional part as follows,
where , are the learning gains, , and the sign function is defined as
Moreover, the concrete steps of the algorithm (6) are shown in Algorithm 1.
| Algorithm 1 Iterative learning control (ILC) consensus algorithm based on fractional-power error signals |
| Parameters: agent i, iteration index k, , , ,, Input: the reference trajectory Output: the control input 1: initialize the iteration index k=1 2: while () 3: initialize the initial state 4: calculate the output by the Equation (2), 5: calculate the tracking errors of each agent by the Equation (3), 6: calculate the tracking errors with the neighboring agents by the Equation (4), 7: calculate by the Equation (5) 8: if k=1 9: else 10: end if 11: set k=k+1 12: end while 13: print the control input |
Remark 2.
Mishra et al. [23] used the sliding mode control to solve the finite-time consensus problem, where the sign function is used to force the state trajectories onto the sliding surface from any arbitrary initial location in the phase plane. However, the sign function in this paper is to extract the sign of the tracking errors, and then take fractional-power of the absolute value of the tracking errors. Fractional-power tracking errors can accelerate the convergence rate when the tracking errors are small.
Remark 3.
It should be pointed out that, in order to ensure the convergence of the multiagent systems, α is in the range of 0 to 1 and cannot be too small.
Let , , and the systems (2) are written in the compact-vector form as
where , and . Defining and , and Equation (8) can be written as
where , and L is the Laplacian matrix of G.
Next, we define the following operators and ,
and
Consequently, the compact-vector version of algorithm (6) is
where , and .
To realize the consensus tracking, we need the following assumption on the initial states of agents.
Assumption A2.
The initial tracking error resetting condition is satisfied for all agents, i.e., .
Now, we go to the main result, and some important lemmas are listed first.
Lemma 1.
[25] Let , , and be a real valued continuous function on , and , if
then,
Lemma 2.
[25] Let be a constant sequence that converges to zero. Define an operator: satisfying
where is a constant, and the norm of r dimensional vector takes the maximum value. Suppose that is a continuous function matrix of dimension, and let satisfy
Then, holds uniformly with t, if .
Theorem 1.
Proof.
Available from Assumption 2, we have . Take integral operation of dynamical system (9) with (14), and we get
Then, taking norms on two sides of (16) yields
With Lemma 1 , Equation (17) becomes
where is a continuous vector function.
According to the Hölder continuity of the vector function, there is a constant such that the following formulation holds,
Thus,
Next, we analyze the tracking error, and it follows from (3) that
Recursively, following (16) yields
Evidently, we get
To recall Lemma 2, we define the following operators; and ,
and
It is obvious that P and satisfy the definitions in Lemma 2.
In the following, we consider two simple special cases for the heterogeneous multiagent systems (2) and ILC consensus algorithm (6).
Corollary 1.
Proof.
When , the convergence condition in Theorem 1 becomes
Under Assumption 1, a nonsingular matrix, and its eigenvalues have positive real parts [24]. Therefore, the convergence condition of the spectral radius in Theorem 1 is simplified as the convergence condition of the eigenvalues. □
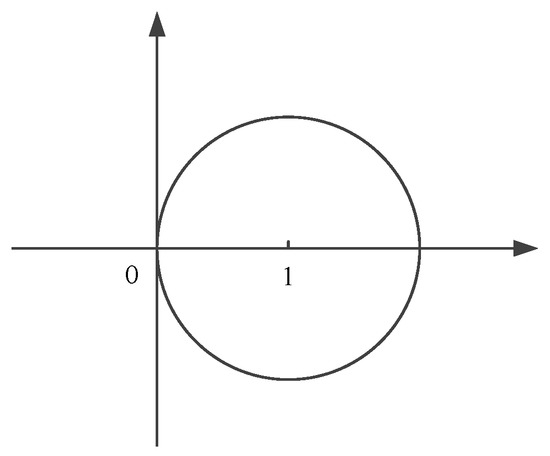
Figure 1.
Location of .
Additionally, we can get a more conservative distributed conditions when the topology is symmetric, i.e., .
Corollary 2.
For heterogeneous multiagent system (2) with algorithm (6), we suppose that , where is a constant. Assume that the topology of agents (2) and leader is symmetric and has a spanning tree rooted at the leader. With Assumption 2, if there exists a positive constant satisfying that
the following agents track the leader’s trajectory with as .
4. Simulation And Discussion
In order to verify the efficiency of our proposed consensus algorithm, we consider a system consisting of the six heterogeneous following agents, given by
The leader’s trajectory is chosen as .
The digraph formed by the six following agents and the leader is shown in Figure 2, where vertex 0 represents the leader and the vertices 1–6 represent the following agents.
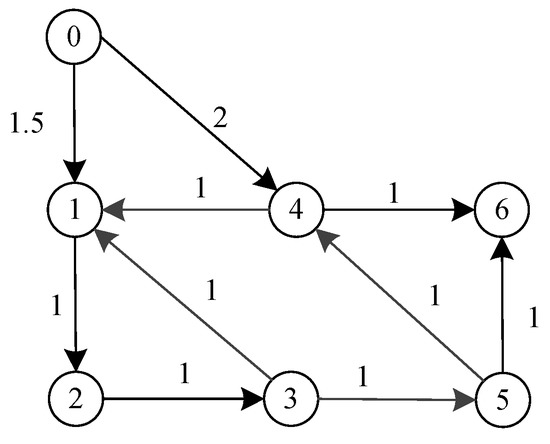
Figure 2.
The communication digraph.
The Laplacian for six following agents is
and , so the eigenvalues of are .
The parameters of fractional-power ILC algorithm (14) are chosen as and , and it is easy to verify that , i.e., these parameters chosen above satisfy the condition (15) of Theorem 1.
It is seen from Assumption 2 that the initial tracking errors are assumed to be zero, so all agents are reset to the same initial position after each iteration. The control input signals for the first iteration of all agents are set to 0.
We choose as , and the tracking processes at the 10th and 70th iteration are represented by Figure 3 and Figure 4, respectively. Figure 5 shows the control input signals when the six following agents fully track the leader’s trajectory. In addition, Figure 6 illustrates the evolution of each agent’s tracking error . Set as the precision requirement, Figure 6 clearly shows that all the following agents track the leader’s trajectory when the iteration reaches 70 times.
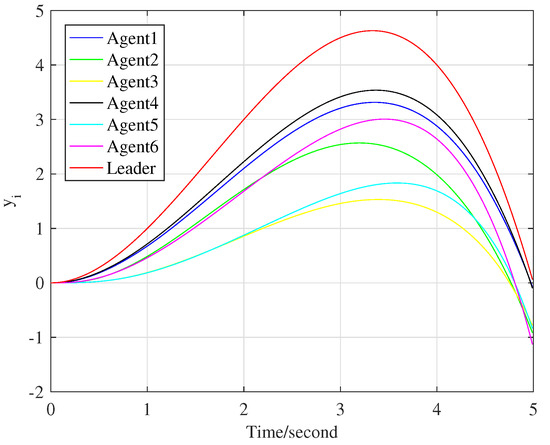
Figure 3.
Tracking process at 10th iteration.
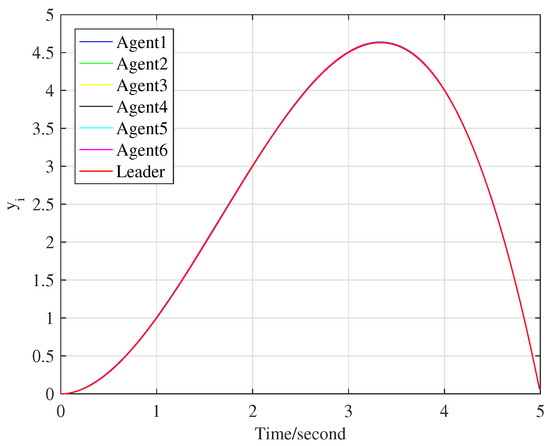
Figure 4.
Tracking process at 70th iteration.
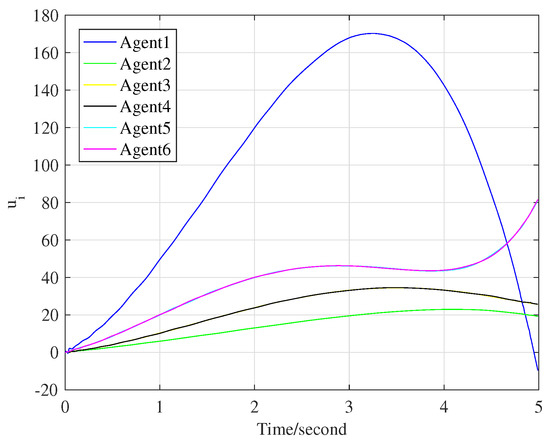
Figure 5.
The control input signals at 70th iteration.
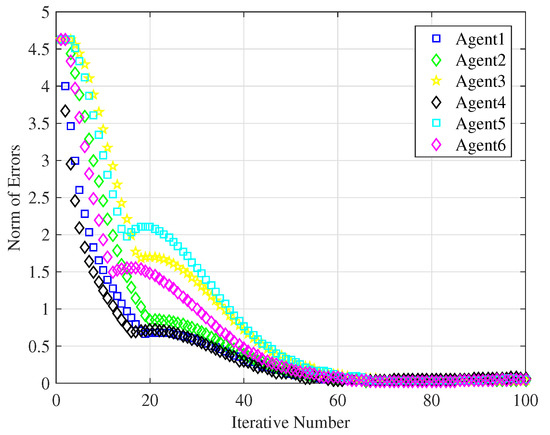
Figure 6.
Tracking error of ILC algorithm based on fractional-power error signals with .
Then, we choose ; other parameters remain unchanged. Figure 7 shows the tracking errors of the six following agents, and the novel ILC consensus algorithm needs to iterate 80 times so that all agents completely track the leader’s trajectory with . Obviously, selecting different control parameters yields distinct consensus convergence rate, and how to get the best control parameters for the algorithm could refer to the main idea of the agent-based simulator for tourist urban routes in the work by the authors of [26].
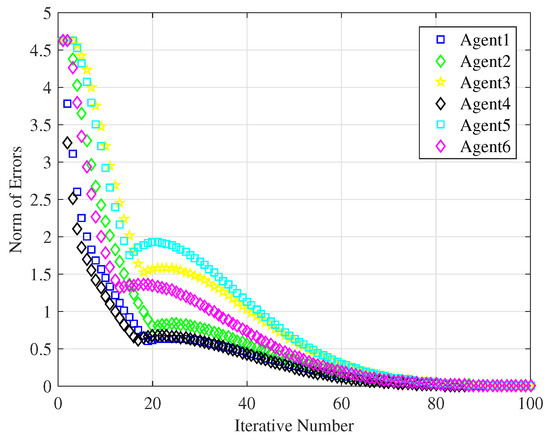
Figure 7.
Tracking error of ILC algorithm based on fractional-power error signals with .
In order to compare the tracking performance of the novel ILC consensus algorithm based on fractional-power error signals with that of the traditional PD-type ILC algorithm, we choose , so the algorithm (14) is converted into the traditional PD-type ILC algorithm. In Figure 8, all agents with the traditional ILC algorithm completely track the leader’s trajectory after the 100th iteration, but the convergence rate is slower than that of the ILC algorithm based on fractional-power error signals with . As discussed above, it is discovered that fractional-power error signals show beneficial influences on the convergence rate.
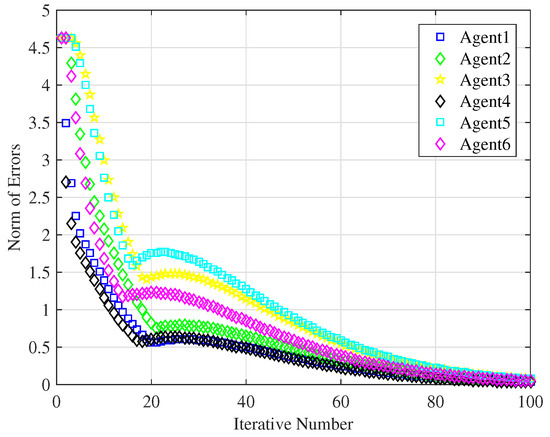
Figure 8.
Tracking error of traditional proportional differential (PD)-type ILC algorithm.
In order to consider the external environmental effects, as well as model uncertainties of the multiagent systems, we use the following model to illustrate the robustness of the proposed ILC algorithm.
where represents unmodeled dynamics and denotes repetitive disturbance. Choose , , , , , , , , ; other parameters remain unchanged. Figure 9 shows that the proposed ILC algorithm is sufficiently robust to model uncertainty and to repetitive disturbances.
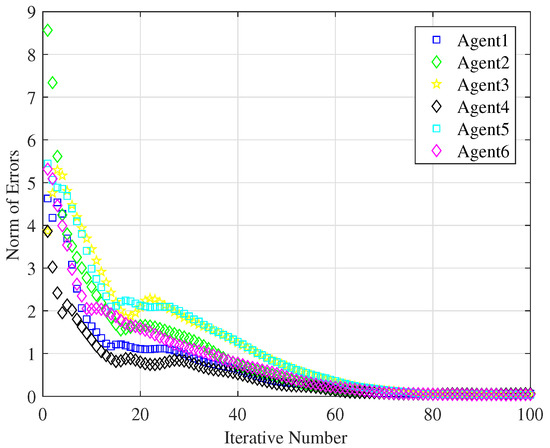
Figure 9.
Tracking error of the model (34) with .
5. Conclusions
In this paper, we adopt a PD-type ILC consensus algorithm to solve the consensus tracking problem of a class of linear heterogeneous multiagent systems. In the algorithm, we replace the normal proportional tracking error part by a fractional-power tracking error. With the interconnection topology, which contains a spanning tree rooted at the leader that denotes the desired trajectory, convergence condition is obtained in the light of graph theory and operator theory. Fractional-power tracking error feedback amplifies the tracking error appropriately when the tracking error is small, so it realizes a faster convergence rate than the integer-power tracking error.
Author Contributions
All authors contributed to the initial motivation of the work, to the research and numerical experiments and to the writing. All authors have read and approved the final manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Grant No. 61973139, 61473138), the Six Talent Peaks Project in Jiangsu Province (Grant No. 2015-DZXX-011), and the Natural Science Foundation of Jiangsu Province (Grant No. BK20151130).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ge, X.; Han, Q.L.; Ding, D. A survey on recent advances in distributed sampled-data cooperative control of multi-agent systems. Neurocomputing 2017, 275, 1684–1701. [Google Scholar] [CrossRef]
- Seyboth, G.S.; Wei, R.; Allgöwer, F. Cooperative control of linear multiagent systems via distributed output regulation and transient synchronization. Automatica 2016, 68, 132–139. [Google Scholar] [CrossRef]
- Liu, K.X.; Duan, P.H.; Duan, Z.S.; Cai, H.; Lu, J. Leader-following consensus of multiagent systems with switching networks and event-triggered control. IEEE Trans. Circuits Syst. I Reg. Pap. 2018, 65, 1696–1706. [Google Scholar] [CrossRef]
- Yu, J.Y.; Wang, L. Group consensus in multiagent systems with switching topologies and communication delays. Syst. Control Lett. 2010, 59, 340–348. [Google Scholar] [CrossRef]
- Wang, H.; Yu, W.W.; Wen, G.H. Finite-time bipartite consensus for multiagent systems on directed signed networks. IEEE Trans. Circuits Syst. I Reg. Pap. 2018, 65, 4336–4348. [Google Scholar] [CrossRef]
- Bristow, D.A.; Tharayil, M.; Alleyne, A.G. A survey of iterative learning control. IEEE Control Syst. Mag. 2006, 26, 96–114. [Google Scholar]
- Chen, Y.Y.; Chu, B.; Freeman, C.T. Point-to-point iterative learning control with optimal tracking time allocation. IEEE Trans. Control Syst. Technol. 2018, 26, 1685–1698. [Google Scholar] [CrossRef]
- Jin, X. Iterative learning control for non-repetitive trajectory tracking of robot manipulators with joint position constraints and actuator faults. Int. J. Adapt. Control Signal Process. 2017, 31, 859–875. [Google Scholar] [CrossRef]
- Lambrecht, J.; Kleinsorge, M.; Rosenstrauch, M. Spatial programming for industrial robots through task demonstration. Int. J. Adv. Robot Syst. 2013, 10, 254. [Google Scholar] [CrossRef]
- Fen, Y.; Xu, J.M. Segment filtering iterative learning control for motor servo systems. In Proceedings of the 27th Chinese Control and Decision Conference, Qingdao, China, 23–25 May 2015; pp. 6103–6106. [Google Scholar]
- Zhang, T.; Li, J.M. Iterative Learning Control for multiagent systems with finite-leveled sigma-delta quantization and random packet losses. IEEE Trans. Circuits Syst. I Reg. Pap. 2017, 64, 2171–2181. [Google Scholar] [CrossRef]
- Li, J.S.; Liu, S.Y.; Li, J.M. Observer-based distributed adaptive iterative learning control for linear multiagent systems. Int. J. Syst. Sci. 2017, 48, 2948–2955. [Google Scholar] [CrossRef]
- Wu, Q.F.; Liu, S. Iterative learning control of multiagent consensus with initial error correction. Comput. Eng. Appl. 2014, 50, 29–35. [Google Scholar]
- Yang, S.P.; Xu, J.X.; Yu, M. An iterative learning control approach for synchronization of multiagent systems under iteration-varying graph. In Proceedings of the 52nd IEEE Conference on Decision and Control, Florence, Italy, 10–13 December 2013; pp. 6682–6687. [Google Scholar]
- Yang, S.P.; Xu, J.X.; Huang, D.Q. Optimal iterative learning control design for multiagent systems consensus tracking. Syst. Control Lett. 2014, 69, 80–89. [Google Scholar] [CrossRef]
- Li, J.S.; Li, J.M. Iterative learning control approach for a kind of heterogeneous multiagent systems with distributed initial state learning. Appl. Math. Comput. 2015, 265, 1044–1057. [Google Scholar]
- Lan, T.Y.; Lin, H. Accelerated iterative learning control algorithm with variable gain and adjustment of interval in sense of Lebesgue-p norm. Control Decis. 2017, 32, 2071–2075. [Google Scholar]
- Tao, H.F.; Dong, X.Q.; Yang, H.Z. Optimal algorithm and application for point to point iterative learning control via updating reference trajectory. Control Theory Appl. 2016, 9, 1207–1213. [Google Scholar]
- Sun, M.X.; Wang, D. Closed-loop iterative learning control for non-linear systems with initial shifts. Int. J. Adapt. Contr. Signal Process. 2002, 16, 515–538. [Google Scholar] [CrossRef]
- Cao, W.; Cong, W.; Li, J. Iterative learning control of variable gain with initial state study. Control Decis. 2012, 27, 473–476. [Google Scholar]
- Sun, M.X.; Bi, H.B.; Zhou, G.L.; Wang, H.F. Feedback assisted PD type iterative learning control: Initial value problem and correction strategy. Acta Autom. Sin. 2015, 41, 157–164. [Google Scholar]
- Yang, S.P.; Xu, J.X.; Li, X.F. Iterative learning control with input sharing for multiagent consensus tracking. Syst. Control Lett. 2016, 94, 97–106. [Google Scholar] [CrossRef]
- Mishra, R.K.; Sinha, A. Event-triggered sliding mode based consensus tracking in second order heterogeneous nonlinear multiagent systems. Eur. J. Control 2019, 45, 30–44. [Google Scholar] [CrossRef]
- Lin, Z.; Francis, B.; Maggiore, M. Necessary and sufficient graphical conditions for formation control of unicycles. IEEE Trans. Autom. Control 2005, 50, 121–127. [Google Scholar]
- Lin, H.; Wang, L. Iterative Learning Control Theory; Northwestern Polytechnical University Press: Xi’an, China, 1998. [Google Scholar]
- García-Magariño, I. ABSTUR: An Agent-based Simulator for Tourist Urban Routes. Expert Syst. Appl. 2015, 42, 5287–5302. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).