1. Introduction
The traditional algorithm development process in theoretical computer science typically involves (i) algorithm design based on abstract and simplified models and (ii) analyzing the algorithm’s behavior within these models using analytical techniques. This usually leads to asymptotic results, mostly regarding the worst-case performance of the algorithm. (While average-case [
1] and smoothed analysis [
2] exist and have gained some popularity, worst-case bounds still make up the vast majority of (e.g., running time) results.) Such worst-case results are, however, not necessarily representative for algorithmic behavior in real-world situations [
3], both for
-complete problems [
4,
5] and poly-time ones [
6,
7]. In case of such a discrepancy, deciding upon the best-fitted algorithm solely based on worst-case bounds is ill-advised.
Algorithm engineering has been established to overcome such pitfalls [
8,
9,
10]. In essence, algorithm engineering is a cyclic process that consists of five iterative phases: (i) modeling the problem (which usually stems from real-world applications), (ii) designing an algorithm, (iii) analyzing it theoretically, (iv) implementing it, and (v) evaluating it via systematic experiments (also known as
experimental algorithmics). Note that not all phases have to be reiterated necessarily in every cycle [
11]. This cyclic approach aims at a symbiosis: the experimental results shall yield insights that lead to further theoretical improvements and vice versa. Ideally, algorithm engineering results in algorithms that are asymptotically optimal
and have excellent behavior in practice at the same time. Numerous examples where surprisingly large improvements could be made through algorithm engineering exist, e.g., routing in road networks [
12] and mathematical programming [
5].
In this paper, we investigate and provide guidance on the experimental algorithmics part of algorithm engineering—from a network analysis viewpoint. It seems instructive to view network analysis, a subfield of
network science [
13], from two perspectives: on the one hand, it is a collection of methods that study the structural and algorithmic aspects of networks (and how these aspects affect the underlying application). The research focus here is on efficient algorithmic methods. On the other hand, network analysis can be the process of interpreting network data using the above methods. We briefly touch upon the latter; yet, this paper’s focus is on experimental evaluation methodology, in particular regarding the underlying (graph) algorithms developed as part of the network analysis toolbox. We use the terms
network and
graph interchangeably.)
In this view, network analysis constitutes a subarea of empirical graph algorithmics and statistical analysis (with the curtailment that networks constitute a particular data type) [
13]. This implies that, like general statistics, network science is not tied to any particular application area. Indeed, since networks are abstract models of various real-world phenomena, network science draws applications from very diverse scientific fields such as social science, physics, biology and computer science [
14]. It is interdisciplinary and all fields at the interface have their own expertise and methodology. The description of algorithms and their theoretical and experimental analysis often differ, sometimes widely—depending on the target community. We believe that uniform guidelines would help with respect to comparability and systematic presentation. That is why we consider our work (although it has limited algorithmic novelty) important for the field of network analysis (as well as network science and empirical algorithmics in general). After all, emerging scientific fields should develop their own best practices.
To stay focused, we concentrate on providing guidelines for the experimental algorithmics part of the algorithm engineering cycle—with emphasis on graph algorithms for network analysis. To this end, we combine existing recommendations from fields such as combinatorial optimization, statistical analysis as well as data mining/machine learning and adjust them to fit the idiosyncrasies of networks. Furthermore, and as main technical contribution, we provide SimexPal, a highly automated tool to perform and analyze experiments following our guidelines. For illustration purposes, we use this tool in a case study—the experimental evaluation of a recent algorithm for approximating betweenness centrality, a well-known network analysis task. The target audience we envision consists of network analysts who develop algorithms and evaluate them empirically. Experienced undergraduates and young PhD students will probably benefit most, but even experienced researchers in the community may benefit substantially from SimexPal.
5. Guidelines for the Experimental Pipeline
Organizing and running all the required experiments can be a time-consuming activity, especially if not planned and carried out carefully. That is why we propose techniques and ideas to orchestrate this procedure efficiently. The experimental pipeline can be divided into four phases. In the first one, we finalize the algorithm’s implementation as well as the scripts/code for the experiments themselves. It is important to use scripts or some external tool in order to automate the experimental pipeline. This also helps to reduce human errors and simplifies repeatability and replicability. Next, we submit the experiments for execution (even if the experiments are to be executed locally, we recommend to use some scheduling/batch system). In the third phase, the experiments run and create the output files. Finally, we parse the output files to gather the information about the relevant performance indicators.
5.1. Implementation Aspects
Techniques for implementing algorithms are beyond the scope for this paper; however, we give an overview of tooling that should be used for developing algorithmic code.
Source code should always be stored in version control systems (VCS); nowadays, the most commonly used VCS is Git [
65]. For scientific experiments, a VCS should also be used to version scripts that drive experiments, valuable raw experimental data and evaluation scripts. Storing instance names and algorithm parameters of experiments in VCS is beneficial, e.g., when multiple iterations of experiments are done due to the AE cycle.
The usual principles for software testing (e.g., unit tests and assertions) should be applied to ensure that code behaves as expected. This is particularly important in growing projects where seemingly local changes can affect other project parts with which the developer is not very familiar. It is often advantageous to open-source code. (We acknowledge that open-sourcing code is not always possible, e.g., due to intellectual property or political reasons). The
Open Source Initiative keeps a list (
https://opensource.org/licenses/alphabetical) of approved open source licenses. An important difference is whether they require users to publish derived products under the same license. If code is open-sourced, we suggest well-known platforms like Github [
66], Gitlab [
67], or Bitbucket [
68] to host it. An alternative is to use a VCS server within one’s own organization, which reduces the dependence on commercial interests. In an academic context, a better accessibility can have the benefit of a higher scientific impact of the algorithms. For long-term archival storage, in turn, institutional repositories may be necessary.
Naturally, code should be well-structured and documented to encourage further scientific participation. Code documentation highly benefits from documentation generator tools such as Doxygen. (
http://www.doxygen.nl.)
Profiling is usually used to find bottlenecks and optimize implementations, e.g., using tools such as the
perf profiler on Linux, Valgrind [
69] or a commercial profiler such as VTune [
70].
5.2. Repeatability, Replicability and Reproducibility
Terminology differs between venues; the Association of Computing Machinery defines repeatability as obtaining the same results when the same team repeats the experiments, replicability for a different team but the same programs and reproducibility for the case of a reimplementation by a different team. Our recommendations are mostly concerned with replicability.
In a perfect world scenario, the behavior of experiments is completely determined by their code version, command line arguments and configuration files. From that point of view, the ideal case for replicability, which is increasingly demanded by conferences and journals (for example, see the
Replicated Computational Results Initiative of the
Journal on Experimental Algorithms,
http://jea.acm.org) in experimental algorithms, looks like this: A single executable program automatically downloads or generates the input files, compiles the programs, runs the experiments and recreates the plots and figures shown in the paper from the results.
Unfortunately, in reality some programs are non-deterministic and give different outputs for the same settings. If randomization is used, this problem is usually avoided by fixing an initial seed of a pseudo-random number generator. This seed is just another argument to the program and can be handled like all others. However, parallel programs might still cause genuine non-determinism in the output, e.g., if the computation depends on the order in which a large search space is explored [
71,
72] or on the order in which messages from other processors arrive. (As an example, some associative calculations are not associative when implemented with floating point numbers [
73]. In such a case, the order of several, say, additions, matters). If these effects are of a magnitude that they affect the final result, these experiments need to be repeated sufficiently often to cover the distribution of outputs. A replication would then aim at showing that its achieved results are, while not identical, equivalent in practice. For a formal way to show such
practical equivalence, see
Section 7.4.1.
Implementations often depend on libraries or certain compiler versions. This might lead to complications in later replications when dependencies are no longer available or incompatible with modern systems. Providing a virtual machine image or container addresses this problem.
5.3. Running Experiments
Running experiments means to take care of many details: Instances need to be generated or downloaded, jobs need to be submitted to batch systems or executed locally, (note that the exact submission mechanism is beyond the scope of this paper, as it heavily depends on the batch system in question. Nevertheless, our guidelines and tooling suggestions can easily be adapted to all common batch system, such as Slurm (
https://slurm.schedmd.com/) or PBS (
https://www.pbspro.org/) running jobs need to be monitored, crashes need to be detected, crashing jobs need to be restarted without restarting all experiments, etc. To avoid human errors, improve reproducibility and accelerate those tasks, scripts and tooling should be employed.
To help with these recurring tasks, we provide as a supplement to this paper
SimexPal, a command-line tool to automate the aforementioned tasks (among others). (
SimexPal can be found at
https://github.com/hu-macsy/simexpal). This tool allows the user to manage instances and experiments, launch jobs and monitor the status of those jobs. While our tool is not the only possible way to automate these tasks, we do hope that it improves over the state of writing custom scripts for each individual experiment.
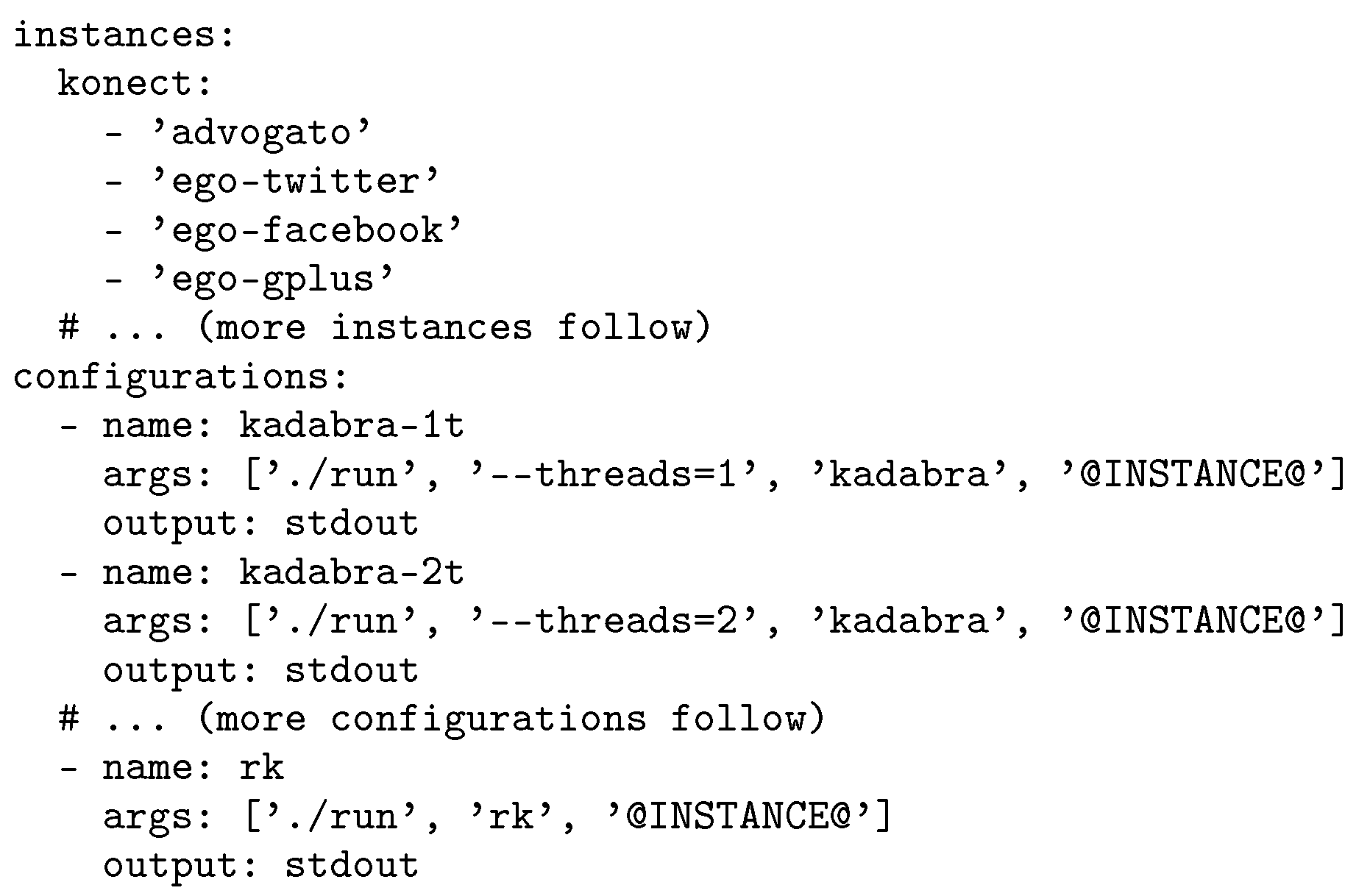
SimexPal is configured using a simple YAML [
74] file and only requires a minimal amount of user-supplied code. To illustrate this concept, we give an example configuration in
Figure 2. Here,
run is the only piece of user-supplied code that needs to be written.
run executes the algorithm and prints the output (e.g., running times) to
stdout. Given such a configuration file, the graph instances can be downloaded using
simex instances download. After that is done, jobs can be started using the command
simex experiments launch.
SimexPal takes care of not launching experiments twice and never overwrites existing output files.
simex experiments list monitors the progress of all jobs. If a job crashes,
simex experiments purge can be used to remove the corresponding output files. The next
launch command will rerun that particular job.
Guideline 5. Use automation tools (e.g., simexpal or others) to manage experiments.
5.4. Structuring Output Files
Output files typically store three kinds of data: (i)
experimental results, e.g., running times and indicators of solution quality, (ii)
metadata that completely specify the parameters and the environment of the run, so that the run can be replicated (see
Section 5.2), and (iii)
supplementary data, e.g., the solution to the input problem that can be used to understand the algorithm’s behavior and to verify its correctness. Care must be taken to ensure that output files are suitable for long-term archival storage (which is mandated by good scientific practices [
75]). Furthermore, carefully designing output files helps to accelerate experiments by avoiding unnecessary runs that did not produce all relevant information (e.g., if the focus of experiments changes after exploration).
Choosing which experimental results to output is problem-specific but usually straightforward. For metadata, we recommend to include enough information to completely specify the executed algorithm version, its parameters and input instance, as well as the computing environment. This usually involves the following data: the VCS commit hash of the implementation and compiler(s) as well as all libraries, the implementation depends on name (or path) of the input instance, values of parameters of the algorithm (including random seeds host name of the machine and current date and time. (Experiments should never run uncommitted code. If there are any uncommitted changes, we suggest to print a comment to the output file to ensure that the experimental data in question does enter a paper). If the implementation’s behavior can be controlled by a large number of parameters, it makes sense to print command line arguments as well as relevant environment variables and (excerpts from) configuration files to the output file. (Date and time help to identify the context of the experiments based on archived output data). Implementations that depend on hardware details (e.g., parallel algorithms or external-memory algorithms) want to log CPU, GPU and/or memory configurations, as well as versions of relevant libraries and drivers.
The relevance of different kinds of supplementary data is highly problem-dependent. Examples include (partial) solutions to the input problem, numbers of iterations that an algorithm performs, snapshots of the algorithm’s state at key points during the execution or measurements of the time spent in different parts of the algorithm. Such supplementary data is useful to better understand an algorithm’s behavior, to verify the correctness of the implementation or to increase confidence in the experimental results (i.e., that the running times or solution qualities reported in a paper are actually correct). If solutions are stored, automated correctness checks can be used to find and debug problems or to demonstrate that no such problems exist.
The
output format itself should be chosen to be both
human readable and
machine parsable. Human readability is particularly important for long-term archival storage, as parsers for proprietary binary formats (and the knowledge of how to use them) can be lost over time. Machine parsability enables automated extraction of experimental results; this is preferable over manual extraction, which is inefficient and error-prone. Thus, we recommend structured data formats like YAML (or JSON [
76]). Those formats can be easily understood by humans; furthermore, there is a large variety of libraries to process them in any commonly used programming language. If plain text files are used, we suggest to ensure that experimental results can be extracted by simple regular expressions or similar tools.
KADABRA Example
Let us apply these guidelines to our example of the
KADABRA algorithm using
SimexPal with the YAML file format. For each instance, we report
KADABRA’s running time, the values of the parameters
and
, the random seed that was used for the run, the number of iterations (i.e., samples) that the run required and the top-25 nodes of the resulting betweenness centrality ranking and their betweenness scores. The number 25 here is chosen arbitrarily, as a good balance between the amount of information that we store to verify the plausibility of the results and the amount of space consumed by the output. To fully identify the benchmark setting, we also report the hostname, our git commit hash, our random generator seed and the current date and time.
Figure 3 gives an example how the resulting output file looks like.
Guideline 6. Use output file formats that are easy to read (by humans) and that can be parsed using existing libraries.
5.5. Gathering Results
When the experiments are done, one has to verify that all runs were successful. Then, the output data has to be parsed to extract the desired experimental data for later evaluation. Again, we recommend the use of tools for parsing. In particular,
SimexPal offers a Python package to collect output data.
Figure 4 depicts a complete script that computes average running times for different algorithms on the same set of instances, using only seven lines of Python code. Note that
SimexPal takes care of reading the output files and checking that all runs indeed succeeded (using the function
collect_successful_results()).
In our example, we assume that the output files are formatted as YAML (thus we use the function yaml.load() to parse them). In case a custom format is used (e.g., when reading output from a competitor where the output format cannot be controlled), the user has to supply a small function to parse the output. Fortunately, this can usually be done using regular expressions (e.g., with Python’s regex module).
It would also be a good time to aggregate data appropriately (unless this has been taken care of before, also see
Section 4.6).
6. Visualizing Results
After the experiments have finished, the recorded data and results need to be explored and analyzed before they can finally be reported. Data visualization in the form of various different plots is a helpful tool both in the exploration phase and also in the final communication of the experimental results and the formal statistical analysis. The amount of data collected during the experiments is typically too large to report in its entirety and hence meaningful and faithful data aggregations are needed. For future reference and repeatability, it may make sense to include relevant raw data in tables in the appendix. However, raw data tables are rarely good for illustrating trends in the data. While descriptive summary statistics such as means, medians, quartiles, variances, standard deviations, or correlation coefficients, as well as results from statistical testing like
p-values or confidence intervals provide a well-founded summary of the data, they do so, by design, only at a very coarse level. The same statistics can even originate from very different underlying data: a famous example is Anscombe’s quartet [
77], a collection of four sets of eleven points in
with very different point distributions, yet (almost) the same summary statistics such as mean, variance, or correlation (for example plots of the four point sets see
https://commons.wikimedia.org/w/index.php?curid=9838454). It is a striking example of how important it can be not to rely on summary statistics alone, but to visualize experimental data graphically. A more recent example is the datasaurus (
https://www.autodeskresearch.com/publications/samestats).
Here we discuss a selection of
plot types for data visualization with focus on algorithm engineering experiments, together with guidelines when to use which type of plot depending on the properties of the data. For a more comprehensive introduction to data visualization, we refer the reader to some of the in-depth literature on the topic [
78,
79,
80]. Furthermore, there are many powerful libraries and tools for generating data plots, e.g., R (
https://www.r-project.org) and the ggplot2 package (
https://ggplot2.tidyverse.org), gnuplot (
http://www.gnuplot.info), matplotlib (
https://matplotlib.org). Additionally, mathematical software such as MATLAB (
https://www.mathworks.com/products/matlab.html) (or even spreadsheet tools) can generate various types of plots from your data. For more details about creating plots in one of these tools, we refer to the respective user manuals and various available tutorials.
When presenting data in two-dimensional plots,
marks are the basic graphical elements or geometric primitives to show data. They can be points (zero-dimensional), lines (1D), or areas (2D). Each mark can be further refined and enriched by visual variables or
channels such as their position, size, shape, color, orientation, texture, etc. to encode different aspects of the data. (The term
attribute is also commonly used to describe the same concept. We use “channel” for compatibility with relevant literature, i.e., [
81,
82]). The most important difference between those channels is that some are more suitable to represent categorical data (e.g., graph properties, algorithms, data sources) by assigning different shapes or colors to them, whereas others are well suited for showing quantitative and ordered data (e.g., input sizes, timings, quantitative quality measures) by mapping them to a spatial position, size, or lightness. For instance, in
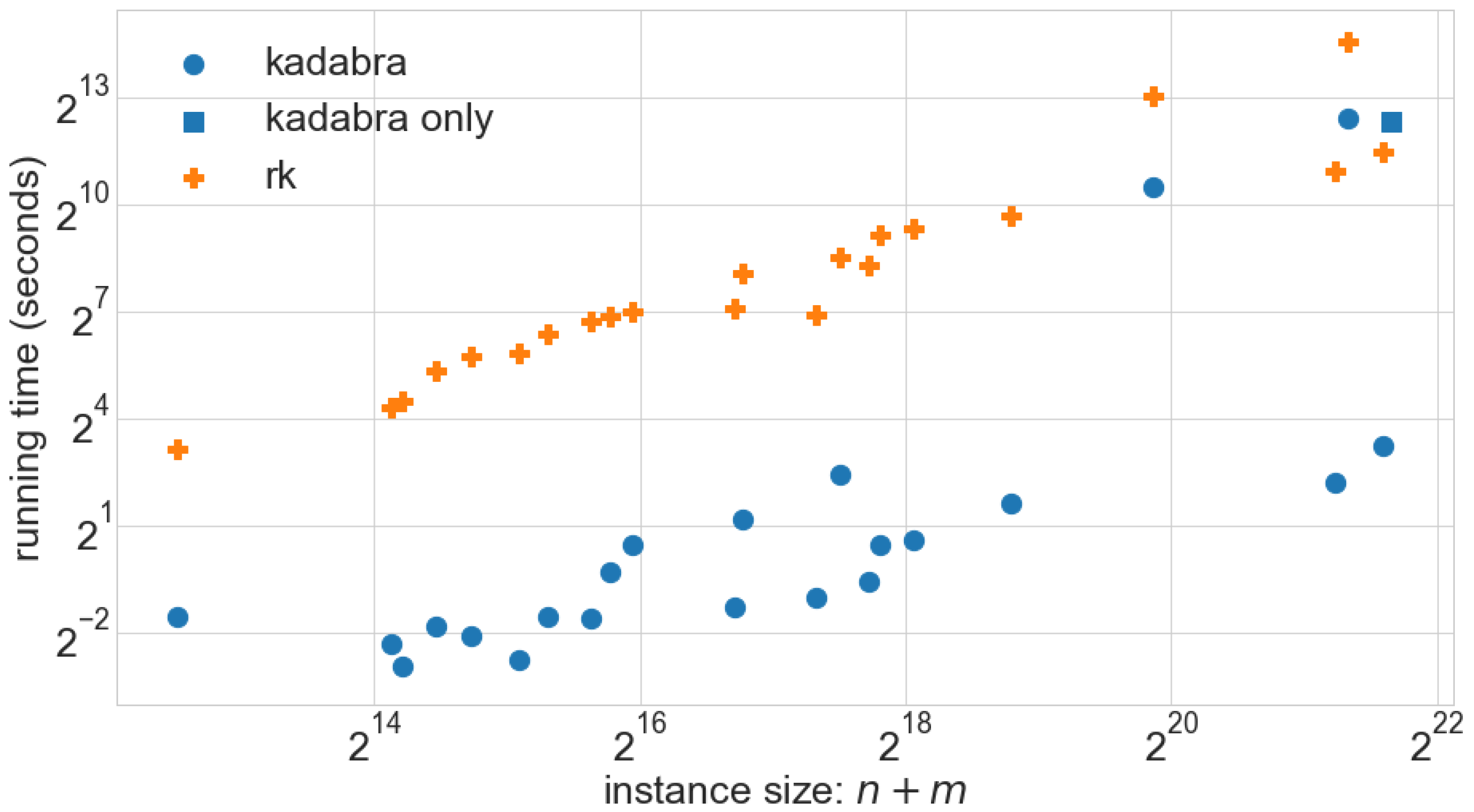
Figure 5 we use blue circles as marks for one of the algorithms, while for the other we use orange crosses. Using different shapes makes sure that the plots are still readable if printed in grey-scale. Not all channels are equally expressive and effective in encoding information for the human visual system, so that one has to carefully select which aspects of the data to map to which channels, possibly also using redundancy. For more details see the textbooks [
81,
82].
As discussed in
Section 4.6, the types of metrics from algorithmic experiments comprise two main aspects: running time data and solution quality data. Both types can consist of absolute or relative values. Typically, further attributes and parameters of the experimental data, of the algorithms, and of the input instances are relevant to include in a visualization to communicate the experimental findings. These can range from hardware-specific parameters, over the set of algorithms and possible algorithm-specific parameters, to instance-dependent parameters such as certain graph properties. Depending on the focus of the experiment, one needs to decide on the parameters to show in a plot and on how to map them to marks and channels. Typically, the most important metric to answer the guiding research question (e.g., running time or solution quality) is plotted along the
y-axis. The
x-axis, in turn, is used for the most relevant parameter describing the instances (e.g., instance size for a scalability evaluation or a graph parameter for evaluating its influence on the solution quality). Additional parameters of interest can then be represented by using distinctly colored or shaped marks for different experimental conditions such as the respective algorithm, an algorithmic parameter or properties of the used hardware; see for example that, in
Figure 5 instances roadNet-PA (rdPA), roadNet-TX (rdTX) are plotted differently for
KADABRA because
RK did not finish within the allocated time frame of 7 h.
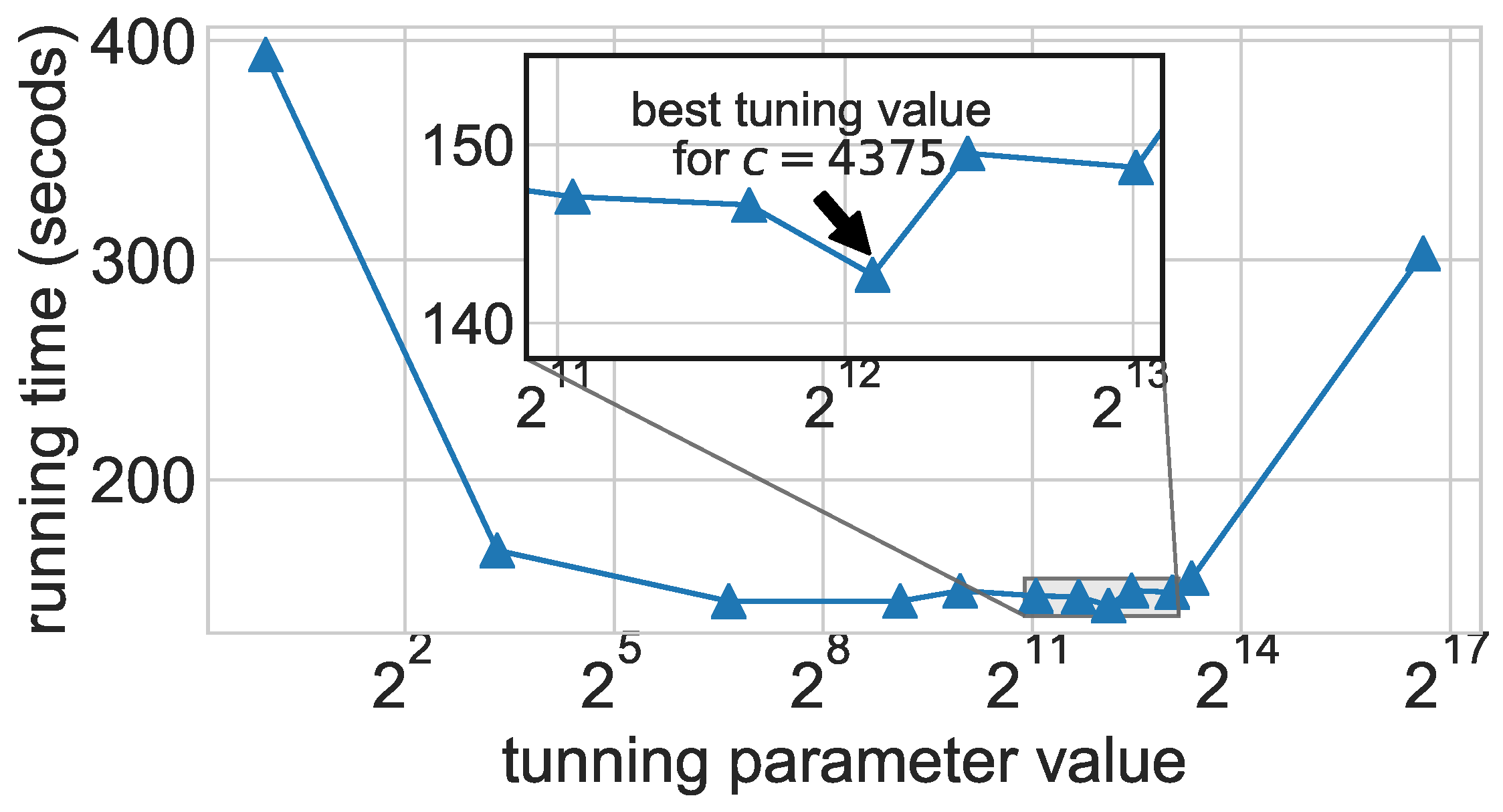
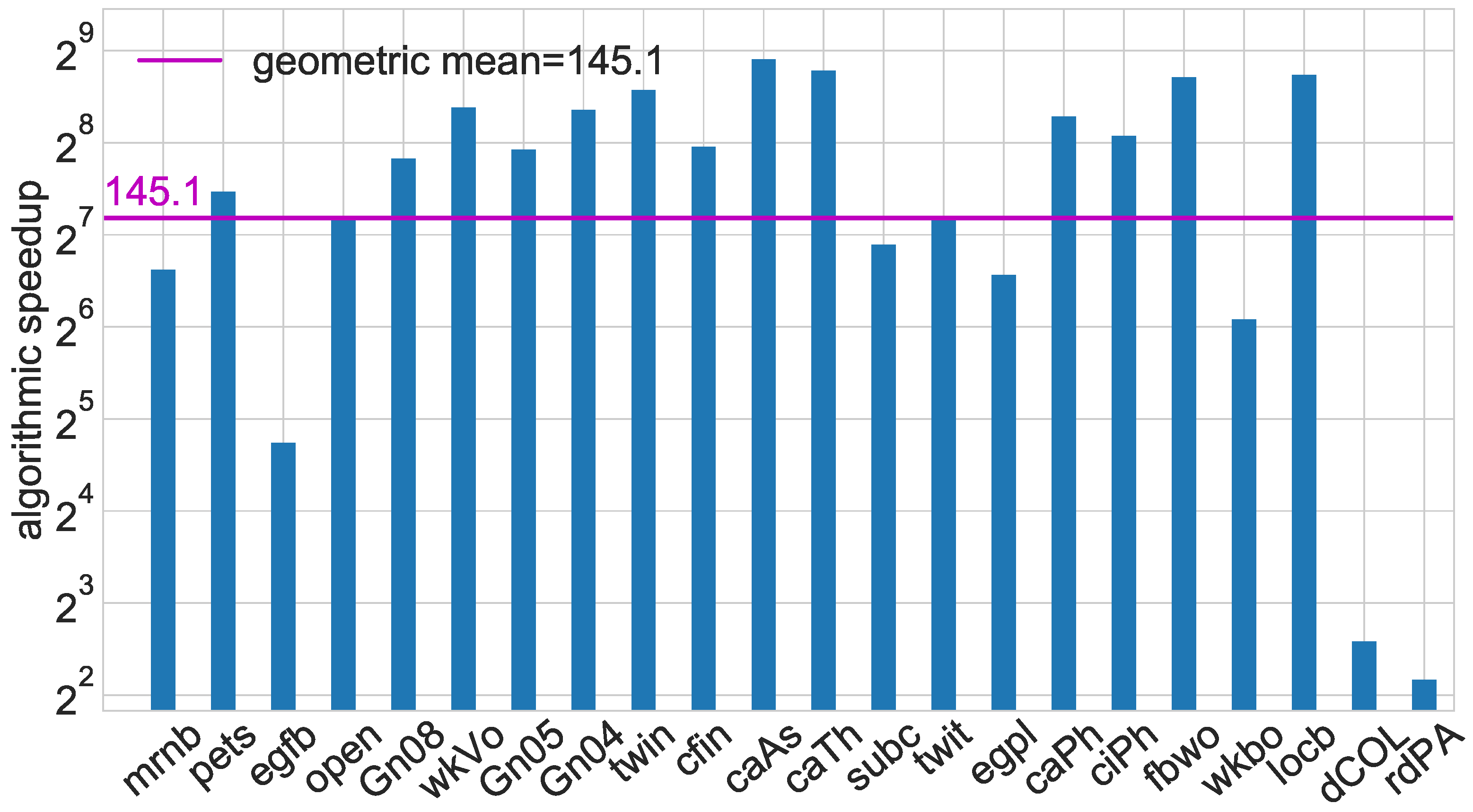
Before starting to plot the data, one needs to decide whether raw absolute data should be visualized (e.g., running times or objective function values) or whether the data should be shown relative to some baseline value, or be normalized prior to plotting. This decision typically depends on the specific algorithmic problem, the experimental setup and the underlying research questions to be answered. For instance, when the experiment is about a new algorithm for a particular problem, the algorithmic speedup or possible improvement in solution quality with respect to an earlier algorithm may be of interest; hence, running time ratios or quality ratios can be computed as a variable to plot—as shown in
Figure 6 with respect to
KADABRA and
RK. Another possibility of data preprocessing is to normalize certain aspects of the experimental data before creating a plot. For example, to understand effects caused by properties of the hardware, such as cache sizes and other memory effects, one may normalize running time measurements by the algorithm’s time complexity in terms of
n and
m, the number of vertices and edges of the input graph, and examine if the resulting computation times are constant or not. A wide range of meaningful data processing and analysis can be done before showing the resulting data in a visualization. While we just gave a few examples, the actual decision of what to show in a plot needs to be made by the designers of the experiment after carefully exploring all relevant aspects of the data from various perspectives. For the remainder of this section, we assume that all data values to be visualized have been selected.
A very fundamental plot is the
scatter plot, which maps two variables of the data (e.g., size and running time) onto the x- and
y-axis, see
Figure 5. Every instance of the experiment produces its own point mark in the plot, by using its values of the two chosen variables as coordinates. Further variables of the data can be mapped to the remaining channels such as color, symbol shape, symbol size, or texture. If the number of instances is not too large, a scatter plot can give an accurate visualization of the characteristics and trends of the data. However, for large numbers of instances, overplotting can quickly lead to scatter plots that become hard to read.
In such cases, the data needs to be aggregated before plotting, by grouping similar instances and showing summaries instead. The simplest way to show aggregated data, such as repeated runs of the same instances, is to plot a single point mark for each group, e.g., using the mean or median, and then optionally putting a vertical error bar on top of it showing one standard deviation or a particular confidence interval of the variable within each group. Such a plot can be well suited for showing how running times scale with the instance size. If the sample sizes in the experiment have been chosen to cover the domain well, one may amplify the salience of the trend in the data by linking the point marks by a line plot. However, this visually implies a linear interpolation between neighboring measurements and therefore should only be done if sufficiently many sample points are included and the plot is not misleading. Obviously, if categorical data are represented on the x-axis, one should never connect the point marks by a line plot.
At the same time, the scale of the two coordinate axes is also of interest. While a linear scale is the most natural and least confusing for human interpretation, some data sets contain values that may grow exponentially. On a linear scale, this results in the large values dominating the entire plot and the small values disappear in a very narrow band. In such cases, axes with a logarithmic scale can be used; however, this should always be made explicit in the axis labeling and the caption of the plot.
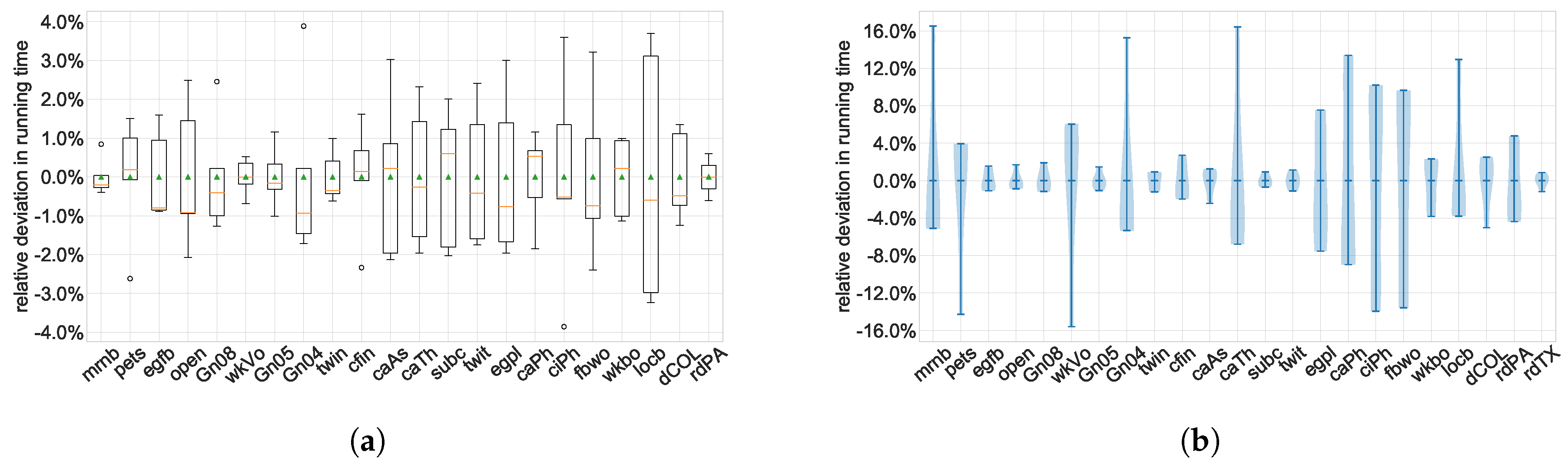
A more advanced summary plot is the
box plot (or
box-and-whiskers plot), where all repeated runs of the same instance or sets of instances with equal or similar size form a group, see
Figure 7a. This group is represented as a single glyph showing simultaneously the median, the quartiles, the minimum and maximum values or another percentile, as well as possibly outliers as individual marks. If the
x-axis shows an ordered variable such as instance size, one can still clearly see the scalability trend in the data as well as the variability within each homogeneous group of instances.
Violin plots take the idea of box plots even further and draw the contour of the density distribution of the variable mapped to the
y-axis within each group, see
Figure 7b. It is thus visually more informative than a simple box plot, but also more complex and thus possibly more difficult to read. When deciding for a particular type of plot, one has to explore the properties of the data and choose a plot type that is neither oversimplifying them nor more complex than needed.
Data from algorithmic experiments may also often be aggregated by some attribute into groups of different sizes. In order to show the distribution of the instances into these groups, bar charts (for categorical data) or histograms (for continuous data) can be used to visualize the cardinality of each group. Such diagrams are often available in public repositories like KONECT (for example, one can find this information for moreno_blogs in
http://konect.uni-koblenz.de/networks/moreno_blogs). For a complex network, for example, one may want to plot the degree distribution of its nodes with the degree (or bins with a specific degree range) on the
x-axis and the number of vertices with a particular degree (or in a particular degree range) on the
y-axis. Such a histogram can then quickly reveal how skewed the degree distribution is. Similarly, histograms can be useful to show solution quality ratios obtained by one or more algorithms by defining bins based on selected ranges of quality ratios. Such a plot quickly indicates to the reader what percentage of instances could be solved within a required quality range, e.g., at least
of the optimum.
A single plot can contain multiple experimental conditions simultaneously. For instance, when showing running time behavior and scalability of a new algorithm compared to previous approaches, a single plot with multiple trend lines in different colors or textures or with visually distinct mark shapes can be very useful to make comparisons among the competing algorithms. Clearly, a legend needs to specify the mapping between the data and the marks and channels in the plot. Here it is strongly advisable to use the same mapping if multiple plots are used that all belong together. But, as a final remark, bear in mind the size and resolution of the created figures. Avoid clutter and ensure that your conclusion remains clearly visible!
Guideline 7. Effectively visualizing the experimental findings is a problem-dependent task, but it is a necessary step towards communicating them to your audience.
7. Evaluating Results with Statistical Analysis
Even if a result looks obvious (it fulfills the “inter-ocular trauma test”, as the saying goes, the evidence hitting you between the eyes), it can benefit from a statistical analysis to quantify it, especially if random components or heuristics are involved. The most common questions for a statistical analysis are:
Do the experimental results support a given hypothesis, or is the measured difference possibly just random noise? This question is addressed by hypothesis testing.
How large is a measured effect, i.e., which underlying real differences are plausible given the experimental measurements? This calls for parameter estimation.
If we want to answer the first two questions satisfactorily, how many data points do we need? This is commonly called
power analysis. As this issue affects the planning of experiments, we discussed it already in
Section 4.3.
The two types of hypotheses we discussed in
Section 4.1 roughly relate to hypothesis tests and parameter estimation. Papers proposing new algorithms mostly have hypotheses of the first type: The newly proposed algorithm is faster, yields solutions with better quality or is otherwise advantageous.
In many empirical sciences, the predominant notion has been
null hypothesis significance testing (NHST), in which a statistic of the measured data is compared with the distribution of this statistic under the
null hypothesis, an assumed scenario where all measured differences are due to chance. Previous works on statistical analysis of experimental algorithms, including the excellent overviews of McGeoch [
38] and Coffin and Saltzmann [
15], use this paradigm.
Due to some limitations of the NHST model, a shift towards
parameter estimation [
83,
84,
85,
86] and also Bayesian methods [
87,
88,
89] is taking place in the statistical community.
We aim at applying the current state of the art in statistical analysis to algorithm engineering, but since no firm consensus has been reached [
85], we discuss both frequentist and Bayesian approaches. As an example for null hypothesis testing, we investigate whether the
KADABRA and the
RK algorithms give equivalent results for the same input graphs. While this
equivalence test could also be performed using Bayesian inference, we use a null hypothesis test for illustration purposes.
It is easy to see from running time plots (e.g.,
Figure 5) that
KADABRA is faster than
RK. To quantify this speedup, we use Bayesian methods to infer plausible values for the algorithmic speedup and different scaling behavior. We further evaluate the influence of the graph diameter on the running time.
7.1. Statistical Model
A statistical model defines a family of probability distributions over experimental measurements. Many experimental running times have some degree of randomness: caching effects, network traffic and influence of other processes contribute to this, sometimes the tested algorithm is randomized itself. Even a deterministic implementation on deterministic hardware can only be tested on a finite set of input data, representing a random draw from the infinite set of possible inputs. A model encodes our assumptions about how these sources of randomness combine to yield the distribution of outputs we see. If, for example, the measurement error consists of many additive and independent parts, the central limit theorem justifies a normal distribution.
To enable useful inferences, the model should have at least one free
parameter corresponding to a quantity of interest. Any model is necessarily an abstraction, as expressed in the aphorism “all models are wrong, but some are useful” [
90].
7.1.1. Example
Suppose we want to investigate whether
KADABRA scales better than RK on inputs of increasing size. (To reproduce this example and the following inferences, one may use the companion Jupyter notebook
Analysis-Example, which is included in the statistics subdirectory of the public repository of this paper:
https://github.com/hu-macsy/ae-tutorial-paper).
Figure 5 shows running times of
KADABRA and
RK with respect to the instance size. These are spread out, implying either that the running time is highly variable, or that it depends on aspects other than the instance size.
In general, running times are modeled as functions of the input size, sometimes with additional properties of the input (or of the output, e.g., in the case of parametrized or output-sensitive algorithms). The running time of KADABRA, for example, possibly depends on the diameter of the input graph. Algorithms in network analysis often have polynomial running times where a reasonable upper bound for the leading exponent can be found. Thus, the running time can be modeled as such a polynomial, written as , with the unknown coefficients of the polynomial being the free parameters of the model.
However, a large number of free model parameters makes inference difficult. This includes the danger of overfitting, i.e., inferring parameter values that precisely fit the measured results but are unlikely to generalize.
To evaluate the scaling behavior, it is thus often more useful to focus on the largest exponent instead. Let
be the running time of the implementation of
RK and
the running time of the implementation of
KADABRA on inputs of size
n, with unknown parameters
and
. (For estimating asymptotic upper bounds, see the work of McGeoch et al. [
33] on curve bounding).
The term
explicitly models the error; it can be due to variability in inputs (some instances might be harder to process than others of the same size) and measurement noise (some runs suffer from interference or caching effects). Since harder inputs are not constrained to additive difficulty and longer runs have more opportunity to experience adverse hardware effects, we choose a multiplicative error term. (Summands with smaller exponents are also subsumed within the error term. If they have a large effect, an additive error might reflect this more accurately). Taking the logarithms of both sides makes the equations linear:
A commonly chosen distribution for additive errors is Gaussian, justified by the central limit theorem [
91]. Since longer runs have more exposure to possibly adverse hardware or network effects we consider multiplicative error terms to be more likely and use a log-normal distribution. (In some cases, it might even make sense to use a hierarchical model with two different error terms: One for the input instances, the other one for the differences on the same input). Since the logarithm of the log-normal distribution is a normal (Gaussian) distribution, Equations (
4) and (
5) can be rewritten as normally distributed random variables:
This form shows more intuitively the idea that a statistical model is a set of probability measures on experimental outcomes. In this example, the set of probability measures modeling the performance of an algorithm are parametrized by the tuple .
A problem remains if the input instances are very inhomogeneous. In that case, both
A and
B have a large estimated variance (
). Even if the variability of performance
on the same instance is small, any genuine performance difference might be wrongly attributed to the large
inter-instance variance. This issue can be addressed with a combined model as recommended by Coffin and Saltzmann [
15], in which the running time
of
A is a function of the running time
of
B on the same instance x:
For a more extensive overview of modeling experimental algorithms, see [
38].
7.1.2. Model Fit
Several methods exist to infer parameters when fitting a statistical model to experimental data. The most well-known is arguably the maximum-likelihood fit, choosing parameters for a distribution that give the highest probability for the observed measurements. In the case of a linear model with a normally distributed error, this is equivalent to a least-squares fit [
92]. Such a fit yields a single estimate for plausible parameter values.
Given random variations in the measurement, we are also interested in the
range of plausible values, quantifying the uncertainty involved in measurement and instance selection. This is covered in
Section 7.3.2 and
Section 7.4.
7.2. Formalizing Hypotheses
Previously (
Section 4.1), we discussed two types of hypotheses. The first type is that a new algorithm is better in some aspect than the state of the art. The second type claims insight into how the behavior of an algorithm depends on settings and properties of the input. We now express these same hypotheses more formally, as statements about the parameters in a statistical model. The two types are then related to the statistical approaches of
hypothesis testing and
parameter estimation.
Considering the scaling model presented in Equation (
8) and the question whether implementation A scales better than implementation B, the parameter in question is the exponent
. The hypothesis that
A scales better than
B is equivalent to
; both scaling the same implies
. Note that the first hypothesis does not imply a fully specified probability distribution on
, merely restricting it to the negative half-plane. The hypothesis of
does completely specify such a distribution (i.e., a point mass of probability 1 at 0), which is useful for later statistical inference.
7.3. Frequentist Methods
Frequentist statistics defines the probability of an experimental outcome as the limit of its relative frequency when the number of experiments trends towards infinity. This is usually denoted as the classical approach.
7.3.1. Null Hypothesis Significance Testing
As discussed above, null hypothesis significance testing evaluates a proposed hypothesis by contrasting it with a null hypothesis, which states that no true difference exists and the observed difference is due to chance. As an example application, we compare the approximation quality of KADABRA and RK. From theory, we would expect higher approximation errors from KADABRA, since it samples fewer paths. We investigate whether the measured empirical difference supports this theory, or could also be explained with random measurement noise, i.e., with the null hypothesis (denoted with ) of both algorithms having the same distribution of errors and just measuring higher errors from KADABRA by coincidence. Here it is an advantage that the proposed alternate hypothesis (i.e., the distributions are meaningfully different) does not need an explicit modeling of the output distribution, as the distribution of differences in our case does not follow an easily parameterizable distribution.
When deciding whether to reject a null hypothesis (and by implication, support the alternate hypothesis), it is possible to make one of two errors: (i) rejecting a null hypothesis, even though it is true (false positive), (ii) failing to reject a false null hypothesis (false negative). In such probabilistic decisions, the error rate deemed acceptable often depends on the associated costs for each type of error. For scientific research, Fisher suggested that a false positive rate of 5% is acceptable [
93], and most fields follow that suggestion. This threshold is commonly denoted as
.
Controlling for the first kind of error, the
p-value is defined as the probability that a
summary statistic as extreme as the observed one would have occurred given the null hypothesis [
94]. Please note that this is
not the probability
, i.e., the probability that the null hypothesis is true given the observations.
For practical purposes, a wide range of
statistical hypothesis tests have been developed, which aggregate measurements to a summary statistic and often require certain conditions. For an overview of which of them are applicable in which situation, see the excellent textbook of Young and Smith [
94].
KADABRA Example
In our example the paired results are of very different instances and clearly not normally distributed. We thus avoid the common t-test and use a Wilcoxon test of pairs [
95] from the SciPy [
96] stats module, yielding a
p-value of
, see cell 14 of the Analysis-Example notebook in the statistics subdirectory. Since this is smaller than our threshold
of 0.05, one would thus say that this result allows us to reject the null hypothesis at the level of
. Such a difference is commonly called
statistically significant. To decide whether it is actually significant in practice, we look at the magnitude of the difference: The error of
KADABRA is about one order of magnitude higher for most instances, which we would indeed call significant.
Multiple Comparisons
The NHST approach guarantees that of all false hypotheses, the expected fraction that seem significant when tested is at most
. Often though, a publication tests more than one hypotheses. For methods to address this problem and adjust the probability that
any null hypothesis in an experiment is falsely rejected (also called the
familywise error rate), see Bonferroni [
97] and Holm [
98].
7.3.2. Confidence Intervals
One of the main criticism of NHST is that it ignores effect sizes; the magnitude of the
p-value says nothing about the magnitude of the effect. More formally,
for every true effect with size and every significance level α, there exists an so that all experiments containing measurements are likely to reject the null hypothesis at level α. Following this, Coffin and Saltzmann [
15] caution against overly large data sets—a recommendation which comes with its own set of problems.
The statistical response to the problem of small but meaningless
p-values with large data sets is a shift away from hypothesis testing to
parameter estimation. Instead of asking whether the difference between populations is over a threshold, the difference is quantified as a parameter in a statistical model, see also
Section 7.2. As Kruschke et al. [
88] put it, the null hypothesis test asks whether the null value of a parameter would be rejected at a given significance level. A
confidence interval merely asks which other parameter values would not be rejected [
88]. We refer to [
99,
100] for a formal definition and usage guidelines.
7.4. Bayesian Inference
Bayesian statistics defines the probability of an experimental outcome as the
uncertainty of knowledge about it. Bayes’s theorem gives a formal way to update probabilities on new observations. In its simplest form for discrete events and hypotheses, it can be given as:
When observing outcome A, the probability of hypothesis is proportional to the probability of A conditioned on multiplied by the prior probability . The conditional probability of an outcome A given an hypothesis is also called the likelihood of . The prior probability reflects the estimation before making observations, based on background knowledge.
Extended to continuous distributions, Bayes’s rule allows to combine a statistical model with a set of measurements and a
prior probability distribution over parameters to yield a
posterior probability distribution over parameters. This posterior distribution reflects both the uncertainty in measurements and possible prior knowledge about parameters. A thorough treatment is given by Gelman et al. [
101].
For our example model introduced in
Section 7.1, we model the running times of implementation B as a function of the time of implementation A, as done in Equation (
8):
This defines the likelihood function as a Gaussian noise with variance
. Since this variance is unknown, we keep it as a model parameter. As we have no specific prior information about plausible values of
and
, we define the following vague prior distributions:
The first two distributions represent our initial—conservative—belief that the two implementations are equivalent in terms of scaling behavior and constants. We model the variance of the observation noise as an inverse gamma distribution instead of a normal distribution, since a variance cannot be negative.
Figure 8 shows how to compute and trace the posterior distribution of these three parameters using SciPy [
96] and PyMC3 [
102]. Results are listed in
Table 4. The interval of
Highest Probability Density (HPD) is constructed to contain 95% of the probability mass of the respective posterior distribution. It is the Bayesian equivalent of the confidence interval (
Section 7.3.2) and also called
credible interval. The most probable values for
and
are
and 1.04, respectively. Taking measurement uncertainty into account, the true values are within the intervals
respective
with 95% probability. This shows that
KADABRA is more than two orders of magnitude faster on average, but results about the relative scaling behavior are inconclusive. While the average for
is 1.04 and suggests similar scaling, the interval
neither excludes the hypothesis that
KADABRA scales better, nor the hypothesis that it scales worse.
7.4.1. Equivalence Testing
Computing the highest density interval can also be used for hypothesis testing. In
Section 7.3.1 we discussed how to show that two distributions are different. Sometimes, though, we are interested in showing that they are sufficiently
similar. An example would be wanting to show that two sampling algorithms give the same distribution of results. This is not easily possible within the NHST paradigm, as the two answers of a classical hypothesis test are “probably different” and “not sure”.
This problem can be solved by calculating the posterior distribution of the parameter of interest and defining a
region of practical equivalence (ROPE), which covers all parameter values that are effectively indistinguishable from 0. If
of the posterior probability mass are in the region of practical equivalence, the inferred parameter is practically indistinguishable with probability
. If
of the probability mass are outside the ROPE, the parameter is meaningfully different with probability
. If the intervals overlap, the observed data is insufficient to come to either conclusion. In our example, the scaling behavior of two algorithms is equivalent if the inferred exponent modeling their relative running times is more or less 1. We could define practical equivalence as
, resulting in a region of practical equivalence of
. The interval
containing
of the probability mass for
is neither completely inside
nor completely outside it, implying that more experiments are needed to come to a conclusion. In
Section 4.3, we discussed that the width of many confidence and credible intervals is inversely proportional to the square root of the number of samples used to compute it. If the scaling is indeed equivalent, we would thus expect to need at least
times as many samples to confirm it.
7.4.2. Bayes Factor
Bayes factors are a way to compare the
relative fit of several models and hypotheses to a given set of observations. To compute this relative fit of two hypotheses
,
to an observation
A, we apply the Bayes theorem (Equation (
9)) to both and consider their ratios:
Crucially, the ratio of prior probabilities, which is subjective, is a separate factor from the ratio of likelihoods, which is objective. This objective part, the ratio , is called the Bayes factor. It models how much the posterior odds ratio differs from the prior odds ratio due to making observation A.
The first obvious difference to NHST is that calculating a Bayes Factor consists of comparing the fit of both hypotheses to the data, not only the null hypothesis. It thus requires that an alternate hypothesis is stated explicitly, including a probability distribution over observable outcomes. If the alternative hypothesis is meant to be vague, for example just that two distributions are different, an uninformative prior with a high variance should be used. However, specific hypotheses like “the new algorithm is at least 20% faster” can also be modeled explicitly.
This explicit modeling allows inference in both directions; using NHST, on the other hand, one can only ever infer that a null hypothesis is unlikely or that the data is insufficient to infer this. Using Bayes factors, it is possible to infer that is more probable than , or that the observations are insufficient to support this statement, or that is more probable than .
In the previous running time analysis, we hypothesized a better scaling behavior, which was not confirmed by the experimental measurements. However, a cursory complexity analysis of the KADABRA algorithm suggests that the diameter has an influence on the running time. Might also the relative scaling of KADABRA and RK depend on the diameter?
To answer this question, we compare the fit of two models: The first model is the same as discussed earlier (Equation (
8)), it models the expected running time of
KADABRA on instance
x as
, where
is the running time of RK on the same instance. The second model has the additional free parameter
, controlling the interaction between the diameter and running times:
Comparing for example the errors of a least-squares fit of the two models would not give much insight, since including an additional free parameter in a model almost always results in a better fit. This does not have to mean that the new parameter captures something interesting.
Instead, we calculate the Bayes factor, for which we integrate over the prior distribution in each model (if favoring frequentist methods, one could compare whether the correlation of running times and diameter is significantly higher than expected by chance). Since this integral over the prior distribution also includes values of the new parameter which are not a good fit, models with too many additional parameters are automatically penalized. Our two models are similar, thus we can phrase them as a hierarchical model with the additional parameter controlled by a boolean random variable, see
Figure 9.
The posterior for the indicator variable
selected_model is
, yielding a Bayes factor of ≈2 in support of including the diameter in the model. This is so inconclusive as to be barely worth mentioning [
103]. A likely reason for this uncertain result is that our high-diameter graphs are also significantly larger and thus have long running times even independent from their high diameter.
Graph Generator Example
Some of the publications that could have been improved by applying these methods are our own. In von Looz et al. [
104], we present an algorithm to efficiently sample random graphs from hyperbolic geometry. To demonstrate its correctness, we compared the distribution of generated graphs with the results of a reference implementation. At the time, we decided to plot the average properties of both generator outputs, which indeed look similar except for random fluctuations.
How can we approach this more rigorously? Showing that the two distributions are
exactly equal is of course impossible, as it requires an infinite number of samples. We set a (somewhat arbitrary) threshold of
instead: When the difference
between the average output of the generators is at least one order of magnitude less than the average difference of two instances sampled from
the same generator, we call them indistinguishable in practice. Due to the central limit theorem, we expect the measurements to be normally distributed. For two normally distributed random variables
and
, their difference is again normally distributed, with
. Estimating this difference
by taking
n samples has a standard error of
, see
Section 4.3. Plausibly judging whether an estimated difference is below
requires that the expected error of the estimate itself is at most
. As
and
are equivalent, this happens if
.
A problem in this scenario is that the real quantities of interest are the probabilities over isomorphic graph classes, which do not lend themselves to understandable modeling. We instead consider the distributions of five network properties: the average degree, the diameter, the clustering coefficient, the degeneracy and the degree assortativity.
Observable differences in these properties will reflect underlying differences in the graphs’ structure. To ensure our results are generally applicable, we explore different parameters for the graph density and degree distributions, 28 combinations in total. We thus generate at least 200 random graphs for each combination of parameters.
A problem remains that when testing 28 combinations of input parameters and 5 properties each, some of the 140 tests are likely to show a difference by chance—the same problem with multiple comparisons in the NHST (
Section 7.3.1) approach (with random draws and such a high number of tests, one could easily show by accident that a distribution is meaningfully different
from itself). We instead define two hypotheses
and
and compute a Bayes factor to decide between them. As the properties have different variances, we estimate the standard deviation
separately for each property. Let
then be the hypothesis that for all properties, the true difference between the average outputs of the generators is at most 10% of the estimated standard deviation
. Let
be the hypothesis that this difference is above 10%.
The notebook Equivalence-BF-Hyperbolic-Generator in the statistics subdirectory contains code to compute the Bayes Factor comparing and . This analysis shows that hypothesis is overwhelmingly more likely, meaning that if there is a difference between the properties of the generated graphs, it is at least one order of magnitude smaller than the average difference between graphs from one generator. It also shows that for some parameters, both our and the reference implementation deviate from the requested degree distribution in the same way, indicating a possible weakness in the shared approximations used to derive internal parameters.
7.5. Recommendations
Different statistical methods fulfill different needs. For almost all objectives, both Bayesian and frequentist methods exist, see
Table 5. In experimental algorithmics, most hypotheses can be expressed as statements constraining parameters in a statistical model, i.e., “the average speedup of A over B is at least 20%”. Thus, in contrast to earlier statistical practice, we recommend to approach evaluation of hypotheses by parameter estimation and to only use the classical hypothesis tests when parameter estimation is not possible. The additional information gained by parameter estimates has a couple of advantages. For example, when using only hypothesis tests, small differences in large data sets can yield impressively small
p-values and thus claims of
statistical significance even when the difference is irrelevant in practice and the significance is statistical only [
15]. Using confidence intervals (
Section 7.3.2) or the posterior distribution in addition with a region of practical equivalence avoids this problem [
88].
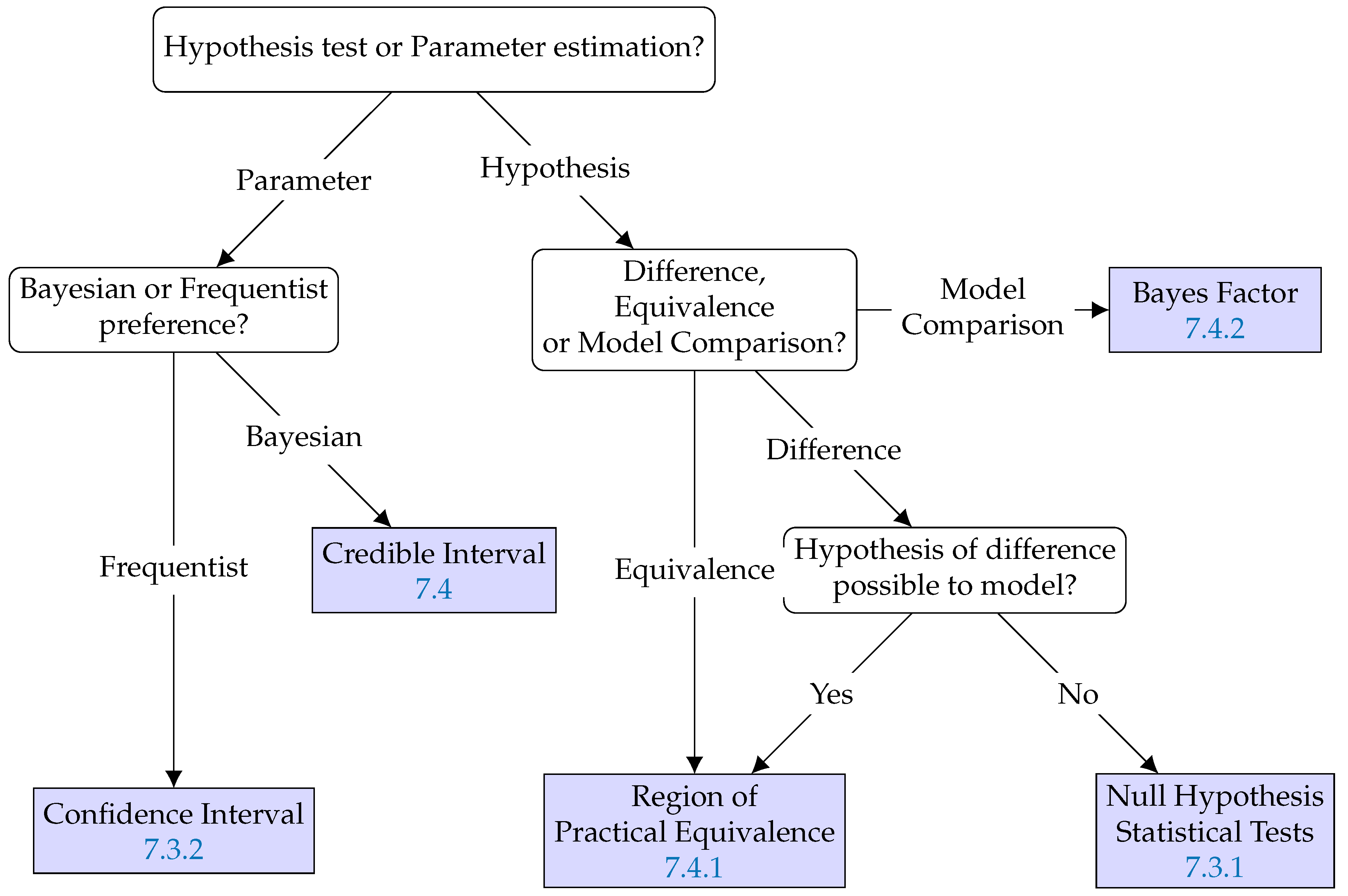
Below is a rough guideline (also shown in
Figure 10) outlining our method selection process. It favors Bayesian methods, since the python library PyMC3 [
102] offering them fits well into our workflow.
Define a model that captures the parts of the measured results that interest you, see
Section 7.1.
Using
confidence intervals (
Section 7.3.2) or
credible intervals (
Section 7.4), estimate plausible values for the model parameters, including their uncertainty. If this proves intractable and you are only interested in whether a measured difference is due to chance, use a significance test instead (
Section 7.3.1).
If you want to show that two distributions (of outcomes of algorithms) are similar, use an equivalence test, in which you define a region of practical equivalence.
If you want to show that two distributions (of outcomes of algorithms) are different, you may also use an equivalence test or alternatively, a significance test.
If you want to compare how well different hypotheses explain the data, for example compare whether the diameter has an influence on relative scaling, compare the
relative fit using a Bayes factor (
Section 7.4.2). Bayes factors are also useful when investigating equivalence or difference of more complex models.
Needless to say, these are only recommendations.
Guideline 8. Statistical methods help a rigorous interpretation of experimental results. The classical approach of using p-values, while common, is often not the most appropriate method.