Abstract
Political parties recently learned that they must use social media campaigns along with advertising on traditional media to defeat their opponents. Before the campaign starts, it is important for a political party to establish and ensure its media presence, for example by enlarging their number of connections in the social network in order to assure a larger portion of users. Indeed, adding new connections between users increases the capabilities of a social network of spreading information, which in turn can increase the retention rate and the number of new voters. In this work, we address the problem of selecting a fixed-size set of new connections to be added to a subset of voters that, with their influence, will change the opinion of the network’s users about a target candidate, maximizing its chances to win the election. We provide a constant factor approximation algorithm for this problem and we experimentally show that, with few new links and small computational time, our algorithm is able to maximize the chances to make the target candidate win the elections.
1. Introduction
Over the past few years, political parties learned that, along with advertising on traditional mediums such as television and newspapers, they must use social media campaigns to defeat their opponents. Many real-life examples exist that show how the political intervention effect in social media [1,2,3,4]. One of the most effective examples of political digital marketing is the recent presidential US election where a study shows that 92% percent of people remembered the pro-Trump fake news, and 23% percent of them remembered the pro-Clinton fake news [5]. Another example, in 2017, where automated accounts in social networks spread a considerable portion of political-related content, mostly fake news, trying to influence the French election [2].
Before the campaign starts, it is important for a political party to establish and ensure its media presence. For example, and this is the case we study in this paper, they can enlarge their number of connections in the social network in order to assure a larger portion of users. Indeed, adding new connections between users increases the capabilities of a social network of spreading information which in turn can increase the retention rate and the number of new voters.
There is an extensive literature on manipulating elections without considering the underlying social network structure; we point the reader to a recent survey [6]. Although there have been few studies that exploits opinion diffusion on social networks in order to manipulate elections, we review them in Section 2.
In this work, we focus on a variant of the election control problem via social influence, introduced in [7]. We consider the scenario in which users of a social network have to vote for elections, i.e., each voter has a preference list over the set of candidates. Based on the model by Wilder et al. [7], there is a subset of users who want to propagate a campaign, i.e., a message, among the users of the network with the aim of changing voters’ opinions about a target candidate. Our goal is to study the case in which an external manipulator can decide to add new links in the network in order to change the outcome and make a specific candidate win.
Original Contribution
We study the problem of selecting a fixed-size set of new connections to a subset of voters who, with their influence, will change the opinion of the network’s users about a target candidate, maximizing its chances to win the election. We provide a -approximation algorithm for the problem of maximizing the score of a target candidate by showing submodularity, where e is the base of the natural logarithm. We exploit such property to provide a -approximation algorithm for the constructive election control problem. Finally, we present an experimental study on heterogeneous real-world networks to validate the model and assess the capability of the algorithm.
2. Related Work
In the literature, there are few studies that exploit social influence in order to solve the problem of constructive/destructive election control considering the social connections between users. This problem consists in changing voters’ opinions with the aim of maximizing/minimizing the margin of victory of target candidate with respect to its most voted opponent.
Wilder et al. [7] considered the Independent Cascade Model [8] as diffusion process in both the constructive and destructive control scenarios providing algorithmic and hardness results, respectively, for maximizing the margin and the probability of victory.
Corò et al. studied the same problem under the Linear Threshold Model [8] and arbitrary scoring rules [9,10]. In both cases, the election control problem can be solved with an approximation factor of in the constructive scenario and in the destructive one. Moreover, Faliszewski et al. [11] studied a variant of the Linear Threshold Model with weighted vertices; in their scenario, each node of the graph is a group of voters with a specific list of candidates and there is an edge between two nodes if they differ by the ordering of a single pair of adjacent candidates. Bredereck et al. [12] instead focused on a simple Linear Threshold Model, where each node holds a binary opinion, each edge has the same fixed weight, and all vertices have a threshold fixed to ; in this scenario, they studied how to manipulate, by means of bribing nodes or adding/deleting edges, the network in order to have control on the majority opinion, i.e., having more than 50% of nodes with the same opinion.
Recently, few studies considered the problem of modifying the network structure in order to minimize/maximize the information diffusion. D’Angelo et al. [13] introduced the Influence Maximization with Augmentation problem (IMA) that consists in adding a limited number of edges incident to a given set of nodes in order to maximize their capability of spreading information under the Independent Cascade Model. They proved that such problem is -hard to approximate within a factor greater than and provide an approximation algorithm that almost matches such upper bound. Furthermore, D’Angelo et al. [14] studied a similar problem for which the budget could be spent to buy either seeds or edges according to a cost function, providing two approximation algorithms that depend on the cost of the edges. Sheldon et al. [15] studied the problem of adding nodes in a network to maximize the diffusion in a network. They showed that their problem is not submodular and proposed exact integer programming formulations. Recently, Amelkin et al. [16] studied the problem of disabling opinion control in a social network by strategically altering the network’s users’ Eigen centralities by recommending new connections between the users. Zhang et al. [17] considered the problem of removing either edges or nodes from the network with the aim of minimizing the information diffusion and developed algorithms with rigorous performance guarantees and good empirical performance. Finally, experimental studies show that increasing the connectivity or the centrality of a node, by adding edges to the graph, lead also to an increase in the expected number of nodes that the diffusion process is able to reach [18,19,20].
3. Preliminaries
The Influence Maximization Problem
The Influence Maximization Problem, introduced by Kempe et al. [21] in 2003, studies a social network, represented by a weighted directed graph , where the set of nodes V represent the users, the set of edges E represent social links between users, and the weight function represents the influence between users. The goal is then to find a set of influential nodes of size B that can maximize the spread of information. The influence is defined based on the information diffusion process among users.
There are many different models to study these processes on graphs, one of the most used being the Independent Cascade Model (ICM) [21]. Given a graph and an initial set of nodes , usually referred as seeds, the diffusion process proceeds iteratively in a synchronous way along a discrete time-axis, starting from . Such set can be seen, for example, as the initial supporters of a product (or an opinion) that start to propagate it in a social network. Let be the set of nodes active at time t, then, for each node , a neighbor node v of u is activated at time with probability , independently, for each edge . Then, if and only if or one of the above independent events is realized. We say that the process has quiesced at the first time such that the set of active nodes would not change in the next round, i.e., time is such that . We define the eventual set of active nodes as . In this case, the goal is to maximize the set A, i.e., the set of active nodes at the end of the process.
Kempe et al. showed that the distribution of the set of active nodes A in the graph starting with under the ICM process is equivalent to the distribution of reachable nodes from the same set in the set of random graphs called live-edge graphs (see Proof of Theorem 4.5 in [8]). A live-edge graph is built as follows: Given a graph , every edge is selected to be inserted to independently at random with a probability proportional to its weight . This equivalent model allow them to provide two important results.
First, they conjectured that evaluating the expected number of active nodes under ICM is -complete, which was later proved by Chen et al. [22]. However, it can be efficiently approximated by using a polynomial number of live-edge graphs ([8], Proposition 4.1). Moreover, under the live-edge model, the problem of selecting the initial seed set of nodes in order to maximize the diffusion is submodular (for a ground set N, a function is submodular if for any two sets such that and for any element it holds that ) [8]. Hence, exploiting a classical result [23], the influence maximization problem admits a approximation using a simple greedy hill-climbing approach that, starting with an empty solution, for B iterations, selects the node that gives the maximal marginal gain on the objective function with respect the solution computed so far.
4. Problem Statement
Consider the scenario in which users of a social network have to vote for elections. In this work, we study the case in which an external manipulator can decide to add new links in the network in order to change the outcome of the elections and make a specific candidate win.
We represent the underlying connections between users as a directed graph . Let be the set of m candidates; we refer to our target candidate, i.e., the one that we want to make win the elections, as . Each voter has a list of preferences for the elections represented as a function that represents the position of a given candidate in the preference list of v, e.g., for a given candidate means that in the preference list of voter v such candidate is ranked as third.
In this work, we use the model presented by Wilder et al. [7]: We use the Independent Cascade Mode as a model for influence diffusion, i.e., each edge has an associated probability , that is the probability to influence the neighbor. Then, the process works as follow: Starting from the seed set, when a voter v is reached by the social influence, i.e., there exists a path from a seed to v, it shifts the ranking of the target candidate by one position up. If is already in first position, i.e., , the message has no effect but the node still shares the message with its neighbors. At the end of the process, each voter casts a vote for their first ranked candidate, i.e., we consider plurality as voting system. Under plurality rule, each voter can only express a single preference among the candidates and that with the plurality of the votes wins, i.e., it is sufficient to have the highest number of votes and there is no need of an absolute majority (50% + 1 of votes).
Recall that in the problem of election control we want to maximize the chances of the target candidate to win the elections. To achieve that, we maximize its expected Margin of Victory (MoV) with respect to the most voted opponent, akin to that defined in [7]. Let us first define the set of voters that rank candidate in the jth position as . Note that initially candidate has votes. After the ICM process has quiesced, the position of in the preference list of each influenced node is changed by one position up, except for the voters that already have in the first position from the beginning.
Given the set of seed nodes and the set S of edges added to G, we define the score of candidate as . Initially, i.e., before the process starts, the score of a candidate is equivalent to the number of voters that have in first position, i.e., . Note that, under this model, we can write the new score of , i.e., the score after the process has quiesced, by the use of live-edge graphs. In fact, the score can be expressed by the number of voters that had in first position before the process plus the expected number of reachable nodes in live-edge graphs that had in second position, starting from the seed set . Recall that a live-edge graph is a subset of graph G where each edge is selected to be part of independently at random with a probability . Hence, X has probability to be sampled equal to . Let us define as the set of reachable nodes in set from the seed set in live-edge graph X and define the set of all possible live-edge graphs. Finally,
Finally, we define as the expected increase of the difference between the score of and that of the most voted opponent. Formally, if c and are the candidates, different from , with the highest score before and after the process has quiesced, respectively, then the is defined as
Let be the initial budget, i.e., the maximum size of the set edges that the manipulator can add to G; the election control problem asks to find a set of edges , of size at most B, that maximizes the MoV, i.e.,
Roughly, we aim to maximize the expected number of votes by which wins the election; however, note that not only candidate gain a vote, but another candidate loses a vote and we need to keep track of the number of votes lost by each other candidate. The definition of MoV given above take into consideration this fact by comparing the votes gained by and the number of votes of the candidate with the largest starting and smallest loss in votes.
As a running example, let us consider five voters and three candidates . Let three voters have , for and two have , for . Since we are considering the plurality rule, we have that the scores of following the elections are .
Now, consider being able to influence voters 3 and 4 using the process presented by Wilder et al., which is the one we consider in this paper. Then, is able to move one position up in and and the new scores are and the value of is . We can make the following observations in this simple example: (1) even if we failed to make the target candidate win the elections, the value of is at its maximum value in this instance, i.e., even the optimal solution, would not have been able to make win; and (2) since, under this model, we can only move the target candidate up to one position, influencing the first three voters would not have changed the outcome of the elections and the scores would have still been .
5. Approximation Result
In this section, we first show that the change in score of the candidate is a monotone and submodular function. This allows us to give a constant factor approximation using the result given in [24]. The authors proved that, if a solution approximates the change in score of the target candidate within a factor , then this solution provides a approximation to the MoV.
Let us first denote the change in score of candidate as
It directly follows that the function is a non-negative linear combination of functions . In the next lemma, we show that in live-edge X is a monotone submodular function of the initial set of nodes . This allows us to prove that also is monotone and submodular with respect to (Theorem 1).
Lemma 1.
Given a set of nodes , two live-edge graphs s.t. and , and an edge . Then,
where and .
Proof.
Note that we can decompose and . Then, since and we have that and . Thus,
We can now prove the following theorem.
Theorem 1.
Given a graph , a seed set , is monotonically increasing submodular function of sets .
Proof.
First, we need to prove that is a monotonically increasing function, formally , for each edge .
The last equation holds since .
To prove submodularity, we show that for each pair of sets such that and, for each edge , the increment in the expected number of influenced nodes that edge causes in is larger than the increment it produces in , that is .
Given two sets of edges , such that , for each live-edge graph X in we denote by the set of live-edge graphs in that have X as a subgraph and possibly contain other edges in . In other words, a live-edge graph in has been generated with the same outcomes as X on the coin flips in the edges of and it has other outcomes for edges in .
Since, for each , and by Lemma 1, then
This result provide us with the fact that a simple greedy hill-climbing approach gives a constant factor approximation to the problem of maximizing , where the constant is . By combining this result and applying Theorem 3 in [24], here reported as Theorem 2, we obtain a -approximation algorithm for the election control problem.
Theorem 2 holds for any scoring rule, i.e., plurality included, and for any model in which the manipulator has the ability to change only the position of a target candidate for a subsets of voters and the increment in score of such candidate is at least equal to the decrement in score of the other candidates. Our model satisfy all of these hypotheses since the manipulator is only able to modify the lists of the voters that are active during the ICM process, i.e., the nodes that are reachable from the seed set. Moreover, using the model from Wilder et al. [7], the manipulator can only change the score of the target candidate by increasing its position in the preference list up by one position. This also implies that the increment in score of is at least equal to the decrement in scoring of the other candidates since the new score of can also be defined as the scores lost by the other candidates, i.e.,
Theorem 2
([24]). An α-approximation algorithm for the problem of maximizing the increment in score of a target candidate gives an -approximation to the election control problem.
Corollary 1.
There is an algorithm that outputs a solution S that satisfies
where denotes an optimal solution of size B to maximizing .
6. Improving the Running Time
In the previous section, we proved that there exists an algorithm that approximate up to a constant factor by showing that the change in score of the target candidate is monotone and submodular with respect to sets (Theorem 1). It follows that Greedy (Algorithm 1) finds a set S of edges whose value is at least times the one of an optimal solution [23].
| Algorithm 1:Greedy |
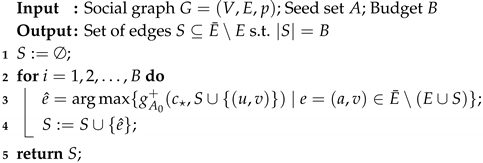 |
As it is stated, Algorithm 1 is clearly infeasible, in terms of running time, for very large real networks, having a computational complexity of , where R is the number of simulations, i.e., live-edge graphs, needed to compute an approximation for . Recall that calculating the expected number of active nodes is -complete but can be approximated by using a polynomial number of live-edge graphs [8,22].
Since our Algorithm 1 is a modified version of the algorithm Greedy2 presented in [25], whose aim was to maximize the influence diffusion in a social network, we can exploit the same reduction to the Limited Seed Selection problem (LSS) that aims at finding a subset of the initial active users in order to maximize the expected number of influenced users. This reduction allows us to adapt the algorithm presented in [26] in such a way that it finds a subset of a given limited set of edges, i.e., .
7. Experimental Study
In this section, we present some experimental results that show how our approximation algorithm performs on real-world networks.
We chose several heterogeneous social and communication networks that are suitable for our problem, taken from KONECT [27], ArnetMiner [28] and SNAP [29] repositories. The size of the graphs are reported in Table 1.

Table 1.
Real-world networks.
We considered three different scenarios, each with a different number of candidates, i.e., . For each scenario, we assigned a random preference list to each node of the networks. Moreover, we chose of the nodes in V as seeds and set the budget to . We generated the probabilities to the edges according to the weighted model presented by Kempe et al. [21], i.e., for each edge , assign , where is the number of incoming neighbour of node v. Note that, for these experiments, the seed nodes were chosen uniformly at random.
All our experiments were performed on a computer equipped with two Intel Xeon E5-2643 CPUs (six cores clocked at 3.4 GHz) and 128 GB RAM; our programs were implemented in C++ (gcc compiler v4.8.2 with optimization level O3).
In Table 2, we report: and that are the differences in MoV of with respect to the most voted opponent before and after the edge addition, i.e., and , where c and are the candidates, different from , with the highest score before and after the process has quiesced; I is the relative increment of MoV after the edge addition computed as ; and T is the time in seconds. Note that negative values in means that the target candidate was not winning before we used our algorithm.

Table 2.
Results for real-world networks. and , where c and are the candidates, different from , with the highest score before and after the process has quiesced.
To prove the capability of our proposed algorithm, we compared the value of MoV in a graph augmented by using Algorithm 1 and in the same graph augmented by using several alternative baselines that connect the given seed set to a set of B nodes chosen accordingly: PrefAtt (PA) selects nodes according to the Preferential Attachment model [30,31]; Jaccard (J) selects the nodes with the highest Jaccard [32] coefficient; Degree (D) selects the nodes with the highest out-degree; Topk (TopK) selects the nodes with the highest harmonic centrality [33]; and Prob (Prob) selects nodes adding the edges with the highest probability. Note that some of these algorithms are well-known algorithms used for link recommendation. For each graph, we report in Table 3 and Table 4 the relative increment of MoV, defined above as I. The experiments clearly show that our proposed algorithm outperforms all the alternative baselines with respect to the final value of MoV.

Table 3.
Baseline results for real-world networks.

Table 4.
Baseline results for real-world networks.
Figure 1 shows the effectiveness of the algorithm in the scenario with candidates running for the elections compared with the other approaches on the Twitter network. Note that this scenario is the “hardest” one among the considered ones, since it has the value of , i.e., the target candidate is not winning before the process starts, and Twitter is the largest network among the ones we considered.
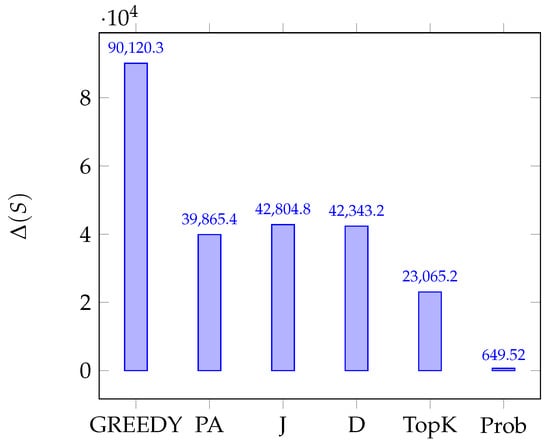
Figure 1.
Value of in Twitter Network.
8. Conclusions
Using social media to influence elections is a major concern in our society and for this reason it is important to study this phenomenon in order to prevent attacks from manipulators. Our result might be a further step to understand and prevent these situations in real-life.
In this work, we address the problem of selecting a fixed-size set of new connections to a subset of voters that, with their influence, will change the opinion of the network’s users about a target candidate, maximizing its chances to win the election. We provide a -approximation algorithm for the problem of maximizing the score of a target candidate by showing submodularity. We then exploit such property to provide a -approximation algorithm for the constructive election control problem. Finally, we present an experimental study on several heterogeneous real-world networks to validate the model and assess the capability of the algorithm comparing our proposed solution with other link recommendation algorithms and showing its effectiveness.
Our results open several research directions. It could be interesting to study the same approach on different models, e.g., changing the model of diffusion, or using different voting rules, e.g., Borda rule that is used, as stated in Wikipedia, in elections by educational institutions or for granting sports awards in the United States. Moreover, future work should concentrate also in uncertainty models for the diffusion process, for example in robust influence maximization where weights on the edges are not known but a probability distribution is given in input.
Author Contributions
Conceptualization, F.C., G.D. and Y.V.; methodology, F.C., G.D. and Y.V.; software, F.C., G.D. and Y.V.; validation, F.C., G.D. and Y.V.; formal analysis, F.C., G.D. and Y.V.; investigation, F.C., G.D. and Y.V.; data curation, Y.V.; writing-original draft preparation, F.C.; writing-review and editing, F.C., G.D. and Y.V.; funding acquisition, G.D.
Funding
This research was partially funded by the Italian MIURPRIN 2017 Project ALGADIMAR “Algorithms, Games, and Digital Markets”.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bond, R.M.; Fariss, C.J.; Jones, J.J.; Kramer, A.D.I.; Marlow, C.; Settle, J.E.; Fowler, J.H. A 61-million-person experiment in social influence and political mobilization. Nature 2012, 489, 295. [Google Scholar] [CrossRef] [PubMed]
- Ferrara, E. Disinformation and social bot operations in the run up to the 2017 French presidential election. First Monday 2017, 22. [Google Scholar] [CrossRef]
- Kreiss, D. Seizing the moment: The presidential campaigns’ use of Twitter during the 2012 electoral cycle. New Media Soc. 2016, 18, 1473–1490. [Google Scholar] [CrossRef]
- Stier, S.; Bleier, A.; Lietz, H.; Strohmaier, M. Election Campaigning on Social Media: Politicians, Audiences, and the Mediation of Political Communication on Facebook and Twitter. Political Commun. 2018, 35, 50–74. [Google Scholar] [CrossRef]
- Allcott, H.; Gentzkow, M. Social Media and Fake News in the 2016 Election; Working Paper 23089; National Bureau of Economic Research: Cambridge, MA, USA, 2017. [Google Scholar] [CrossRef]
- Faliszewski, P.; Rothe, J.; Moulin, H. Control and Bribery in Voting. In Handbook of Computational Social Choice; Cambridge University Press: Cambridge, UK, 2016; pp. 146–168. [Google Scholar] [CrossRef]
- Wilder, B.; Vorobeychik, Y. Controlling Elections through Social Influence. In Proceedings of the AAMAS 2018 17th International Conference on Autonomous Agents and MultiAgent Systems, Stockholm, Sweden, 10–15 July 2018; pp. 265–273. [Google Scholar]
- Kempe, D.; Kleinberg, J.M.; Tardos, É. Maximizing the Spread of Influence through a Social Network. Theory Comput. 2015, 11, 105–147. [Google Scholar] [CrossRef]
- Corò, F.; Cruciani, E.; D’Angelo, G.; Ponziani, S. Vote For Me!: Election Control via Social Influence in Arbitrary Scoring Rule Voting Systems. In Proceedings of the 18th International Conference on Autonomous Agents and MultiAgent Systems AAMAS ’19, Montrea, QC, Canada, 13–17 May 2019; pp. 1895–1897. [Google Scholar]
- Corò, F.; Cruciani, E.; D’Angelo, G.; Ponziani, S. Exploiting Social Influence to Control Elections Based on Scoring Rules. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, IJCAI, Macao, China, 10–16 August 2019; pp. 201–207. [Google Scholar] [CrossRef]
- Faliszewski, P.; Gonen, R.; Koutecký, M.; Talmon, N. Opinion Diffusion and Campaigning on Society Graphs. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, IJCAI-18. International Joint Conferences on Artificial Intelligence Organization, Stockholm, Germany, 13–19 July 2018; pp. 219–225. [Google Scholar] [CrossRef]
- Bredereck, R.; Elkind, E. Manipulating Opinion Diffusion in Social Networks. In Proceedings of the 26th International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017; pp. 894–900. [Google Scholar]
- D’Angelo, G.; Severini, L.; Velaj, Y. Recommending links through influence maximization. Theor. Comput. Sci. 2019, 764, 30–41. [Google Scholar] [CrossRef]
- D’Angelo, G.; Severini, L.; Velaj, Y. Selecting Nodes and Buying Links to Maximize the Information Diffusion in a Network. In Proceedings of the 42nd International Symposium on Mathematical Foundations of Computer Science, Aalborg, Denmark, 21–25 August 2017; pp. 75:1–75:14. [Google Scholar] [CrossRef]
- Sheldon, D.; Dilkina, B.; Elmachtoub, A.N.; Finseth, R.; Sabharwal, A.; Conrad, J.; Gomes, C.; Shmoys, D.; Allen, W.; Amundsen, O.; et al. Maximizing the spread of cascades using network design. In Proceedings of the Twenty-Sixth Conference on Uncertainty in Artificial Intelligence, Catalina Island, CA, USA, 8–11 July 2010. [Google Scholar]
- Amelkin, V.; Singh, A.K. Fighting Opinion Control in Social Networks via Link Recommendation. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019. [Google Scholar]
- Zhang, Y.; Adiga, A.; Vullikanti, A.; Prakash, B.A. Controlling propagation at group scale on networks. In Proceedings of the 2015 IEEE International Conference on Data Mining (ICDM), Atlantic City, NJ, USA, 14–17 November 2015. [Google Scholar]
- Crescenzi, P.; D’angelo, G.; Severini, L.; Velaj, Y. Greedily improving our own closeness centrality in a network. ACM Trans. Knowl. Discov. Data 2016, 11, 9. [Google Scholar] [CrossRef]
- Parotsidis, N.; Pitoura, E.; Tsaparas, P. Centrality-aware link recommendations. In Proceedings of the Ninth ACM International Conference on Web Search and Data Mining, San Francisco, CA, USA, 22–25 February 2016. [Google Scholar]
- Papagelis, M. Refining social graph connectivity via shortcut edge addition. ACM Trans. Knowl. Discov. Data 2015, 10, 12. [Google Scholar] [CrossRef]
- Kempe, D.; Kleinberg, J.M.; Tardos, É. Maximizing the spread of influence through a social network. In Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 24–27 August 2003; pp. 137–146. [Google Scholar] [CrossRef]
- Chen, W.; Wang, C.; Wang, Y. Scalable influence maximization for prevalent viral marketing in large-scale social networks. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 25–28 July 2010; pp. 1029–1038. [Google Scholar] [CrossRef]
- Nemhauser, G.L.; Wolsey, L.A.; Fisher, M.L. An analysis of approximations for maximizing submodular set functions-I. Math. Program. 1978, 14, 265–294. [Google Scholar] [CrossRef]
- Aboueimehrizi, M.; Corò, F.; Cruciani, E.; D’Angelo, G. Election Control with Voters’ Uncertainty: Hardness and Approximation Results. arXiv 2019, arXiv:1905.04694. [Google Scholar]
- Corò, F.; D’Angelo, G.; Velaj, Y. Recommending Links to Maximize the Influence in Social Networks. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, IJCAI, Macao, China, 10–16 August 2019; pp. 2195–2201. [Google Scholar] [CrossRef]
- Cohen, E.; Delling, D.; Pajor, T.; Werneck, R.F. Sketch-based Influence Maximization and Computation: Scaling Up with Guarantees. In Proceedings of the 23rd ACM International Conference on Conference on Information and Knowledge Management, Shanghai, China, 3–7 November 2014. [Google Scholar]
- Kunegis, J. KONECT-The Koblenz Network Collection. In Proceedings of the International World Wide Web Conferen, Rio de Janeiro, Brazi, 13–17 May 2013. [Google Scholar]
- Arnetminer. Available online: http://arnetminer.org (accessed on 15 January 2015).
- Leskovec, J.; Krevl, A. SNAP Datasets: Stanford Large Network Dataset Collection. 2014. Available online: http://snap.stanford.edu/data (accessed on 28 September 2019).
- Bollobás, B.; Borgs, C.; Chayes, J.; Riordan, O. Directed scale-free graphs. In Proceedings of the Fourteenth Annual ACM-SIAM Symposium on Discrete Algorithms, Baltimore, MD, USA, 12–14 January 2003. [Google Scholar]
- Newman, M.E. Clustering and preferential attachment in growing networks. Phys. Rev. E 2001, 64, 025102. [Google Scholar] [CrossRef] [PubMed]
- Jaccard, P. Étude comparative de la distribution florale dans une portion des Alpes et des Jura. Bull. Soc. Vaudoise Sci. Nat. 1901, 37, 547–579. [Google Scholar]
- Boldi, P.; Vigna, S. Axioms for centrality. Internet Math. 2014, 10, 222–262. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).